- 1Department of Mechanical Engineering, Kennesaw State University, Marietta, GA, United States
- 2Department of Physics, University of Toronto, Toronto, ON, Canada
- 3Department of Mechanical Engineering, Johns Hopkins University, Baltimore, MD, United States
- 4Institute for NanoBioTechnology, Johns Hopkins University, Baltimore, MD, United States
- 5Center for Cell Dynamics, Johns Hopkins School of Medicine, Baltimore, MD, United States
Cells lacking a stiff cell wall, e.g., mammalian cells, must actively regulate their volume to maintain proper cell function. On the time scale that protein production is negligible, water flow in and out of the cell determines the cell volume variation. Water flux follows hydraulic and osmotic gradients; the latter is generated by various ion channels, transporters, and pumps in the cell membrane. Compared to the widely studied roles of sodium, potassium, and chloride in cell volume regulation, the effects of proton and bicarbonate are less understood. In this work, we use mathematical models to analyze how proton and bicarbonate, combined with sodium, potassium, chloride, and buffer species, regulate cell volume upon inhibition of ion channels, transporters, and pumps. The model includes several common, widely expressed ion transporters and focuses on obtaining generic outcomes. Results show that the intracellular osmolarity remains almost constant before and after cell volume change. The steady-state cell volume does not depend on water permeability. In addition, to ensure the stability of cell volume and ion concentrations, cells need to develop redundant mechanisms to maintain homeostasis, i.e., multiple ion channels or transporters are involved in the flux of the same ion species. These results provide insights for molecular mechanisms of cell volume regulation with additional implications for water-driven cell migration.
1. Introduction
Mammalian cell volume regulation is an essential process during the cell life cycle (Lang et al., 1998; Kay, 2017; Perez-Gonzalez et al., 2019; Li et al., 2020). Seventy percent of the cell volume fraction consists of incompressible water. Since large molecules are not permeable through the cell membrane, on short time scales where protein production is negligible, water flux in and out of the cell is the primary process that determines the cell volume variation. Water flux across the cell membrane follows hydraulic pressure and osmotic pressure differences (Lang et al., 1998; Tao et al., 2017; Li et al., 2020). The intracellular osmotic pressure arises from the entropy of mixing of water with large molecules that are non-permeable through the membrane and small permeable solutes such as ions and sugar. Major ionic species in cells include Na+, K+, Cl−, , Ca2+, and H+. The cell membrane embeds many different types of channels, transporters, and pumps that allow ions to move in and out of the cell. A net ion flux may lead to a net change in the intracellular osmolarity, which drives water flux, cell volume change, and cell boundary movement (Li et al., 2020).
Unlike Na+, K+, and Cl− which are non-reactive, and H+ are reactive, and their concentrations are correlated. The intracellular concentration of a reactive species is not solely determined by its flux across the cell membrane. Transporters such as the Na+/H+ and Cl−/ exchangers generate ion fluxes for both non-reactive and reactive species. Inhibition of these transporters can potentially lead to chemical reactions in the cell, which modulate the cell volume in a non-trivial manner. With emerging data showing the importance of ion and water fluxes during cell migration, force generation, and morphological change (Klein et al., 2000; Loitto et al., 2002; Stock et al., 2005; Lauritzen et al., 2012; Stroka et al., 2014; Li and Sun, 2018; Li et al., 2019, 2020), it becomes essential to understand the regulation of intracellular and H+. In this work, we investigate how and H+ are involved in cell volume regulation when the activities of relevant ion transporters are perturbed. We will further discuss counter-intuitive ionic concentration changes during ion channel/transporter/pump perturbation.
In general, ions are transported across membranes both passively and actively. Passive ionic transport is carried out by ion-specific channels and pores, some of which are sensitive to cortical tension. Active transport is carried out by energy-consuming ion pumps, which utilize chemical energy (ATP) to transport ions against a chemical potential gradient (Gadsby, 2009). Another type of active transporters is classified as secondary active transporters, which utilize the chemical-electrical potential gradient of one species to facilitate the transport of another species (Shi, 2013). Given the molecular complexity in cell ionic homeostasis, various ion channels/transporters/pumps and the associated fluxes must be considered together. Realistic computational models are necessary to make significant progress. Here we will use mathematical analysis to predict the change of ion concentration.
In this paper, we include the following transporters: Na+/K+ exchanger (NKE), Na+-K+-Cl− cotransporter (NKCC), Na+/H+ exchanger (NHE), Cl−/ exchanger (AE2), and Na+/ cotransporter (NBC) (Figure 1A). The NKE is a ubiquitous and important active ion pump that maintains the membrane potential of cells. It exports three Na+ ions and intakes two K+ ions per ATP molecule. Because the overall flux is positive outwards, the pump's activity depends on the membrane potential (Gadsby et al., 1985). The NKE flux also depends on the concentrations of Na+ and K+ (Gao et al., 1995; Bueno-Orovio et al., 2014) and saturates at high concentration limits (Bueno-Orovio et al., 2014). The Na+-K+-Cl− cotransporter (NKCC), along with its isoforms, is widely expressed in various cell types (Russell, 2000). The NKCC simultaneously transports one Na+, one K+, and two Cl−s into the cell under physiological conditions. The Na+/H+ exchanger (NHE), which has ten identified isoforms, is expressed in almost all tissues (Vallés et al., 2015). It imports one Na+ and extrudes one H+ under physiological conditions. This exchanger has significant effects on water flux, cell volume regulation (Cala, 1980; Ericson and Spring, 1982; Grinstein et al., 1986; Alexander and Grinstein, 2006; Maeno et al., 2006; Hughes et al., 2010), cell migration (Scholz et al., 1995; Lauritzen et al., 2012; Chang et al., 2014; Stroka et al., 2014), and is a major therapeutic target (Mahnensmith and Aronson, 1985; Karmazyn, 2013; Vallés et al., 2015). NHE is quiescent at intracellular pH > 7.2 (Casey et al., 2010). The Cl−/ exchanger (AE2), which imports one Cl− and extrudes one , is also common in cells. This exchanger is almost quiescent at intracellular pH < 6.8 − 7.3. The Na+/ cotransporter (NBC), which transports Na+ and in the same direction, is expressed in both epithelial and non-epithelial cells (Boron and Boulpaep, 1989). The stoichiometry of this cotransporter is cell-type dependent (Gross et al., 2001) and is either or 2:1 (Boron and Boulpaep, 1989; Weinstein, 2013). As a result, NBC is electrogenic and influences the intracellular pH (Boron and Boulpaep, 1989). Depending on the concentrations of the two species and the membrane potential, the flux of NBC can be either in or out of the cell.
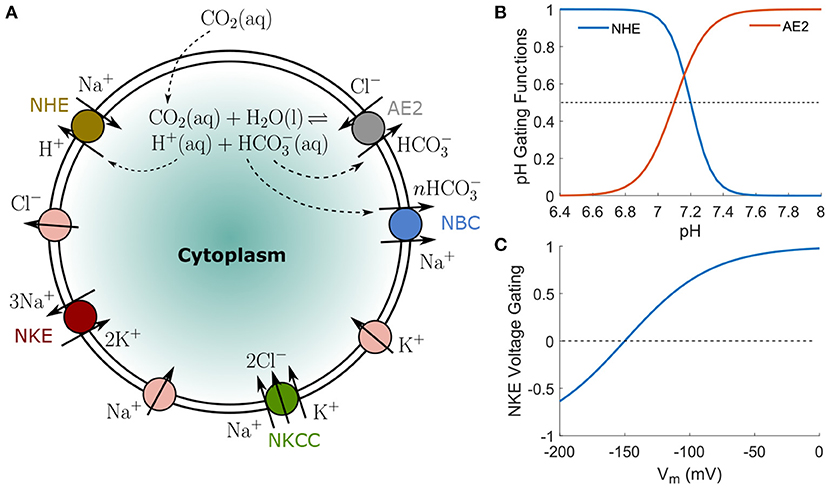
Figure 1. (A) A schematic representation of ion pumps, transporters and passive channels included in the model to compute cell ion homeostasis. The ion fluxes can depend on intracellular and extracellular ion concentrations, transmembrane potential, the tension in the cell cortex, and expression/activation levels of each channel (see Methods). The overall cell ionic composition depends on ion channel/transporter/pump expression and activation. (B) pH-gating profiles of NHE and AE2 transporters, taken from data in Casey et al. (2010). (C) Voltage-gating profile for NKE, taken from data in Gadsby et al. (1985).
Given the large amount of identified ion transporters so far, the ones we include in the model are not meant to be exhaustive, nor do we intend to model the exact expression and activity levels of channels, transporters, and pumps in various cell types (Hoffman, 1969; Landowne and Ritchie, 1970; Baker and Willis, 1972; Burnham and Stirling, 1984a,b; Russell, 2000; Bonar and Casey, 2008; Blaesse et al., 2009; Romero et al., 2013; Vallés et al., 2015), although by varying flux parameters in the model, we can computationally examine cell responses when the activity levels of ion channels, transporters, and pumps are varied. In this work, we will focus on the generic interaction among hydrogen, bicarbonate, and their associated exchangers. A possible explanation of NHE-dependent regulatory cell volume increases will be discussed. Moreover, we demonstrate explicitly how ionic fluxes and cytoskeletal contraction can work together to achieve the final observed cell volume. We also examine how ion transporter expression in several common cell types can lead to variations in cell properties such as cell volume, pH, and transmembrane voltage and compare with experimental results.
2. Materials and Methods
2.1. Model Description
We present a cell volume regulation model through the influence of ion fluxes, intracellular osmolarity, and pH on the time scale of minutes. In the model, we consider the following intracellular species, Na+, K+, Cl−, H+, , A−, Buf−, and HBuf, where A− represents charged organic molecules or proteins that are not permeable across the cell membrane. The total number of intracellular proteins NA is prescribed. The organic molecules or proteins have various charges, and the average charge is negative (Gitlin et al., 2006). We thus lump all the proteins and assume an effective average valence of −1. The impact of the average valence will be discussed. Within the cell, we include an unprotonated buffer (Buf−) and protonated buffer (HBuf) species, both of which are considered as non-permeable across the cell membrane (Weinstein, 1986) and the total, NBuf + NHBuf, is fixed. The extracellular ion concentrations are given based on generic cell culture medium composition or extracellular fluid environment in vivo. is adjusted based on the concentration of other charged ion species so that the electro-neutrality condition of the medium is satisfied. Here c represents concentrations, and the superscript ‘0’ indicates quantities associated with the extracellular environment. We can also include large, non-permeable molecules (G) in the extracellular space to adjust the baseline osmolarity of the medium, in a similar manner as modulating the extracellular hydrostatic pressure, which is determined up to a constant. By default, we let this molecule to be charge-free, but it can assume any valence to ensure the electroneutrality of the extracellular space when other extracellular species are specified. Since the molecule is non-permeable and the electroneutrality condition in the extracellular domain is maintained, it will not affect the membrane potential nor voltage-dependent ion channels, transporters, and pumps.
Considering a generic spherical cell experiencing volume regulation, the rate change of the cell radius, r, is modulated by osmotic and hydrostatic pressure gradients (Li et al., 2020).
where Jwater is water flux across the cell membrane, defined positive inward. αw is the combined permeability coefficient of water from the lipid membrane and aquaporins (AQPs). The water permeability through lipids is several orders of magnitude smaller than that of AQPs. So in most cases αw is dominated by the contribution from AQPs. is the osmotic pressure difference across the cell membrane. The extracellular and intracellular osmolytes in the model are, respectively, and . The hydrostatic pressure difference across the cell membrane, Δp, is related to the combined effective cortical and membrane stress, σ, by the Laplace law Δp = 2hσ/r, where h is the combined effective thickness of the cell cortex and membrane. The stress can be obtained from the constitutive relation of the actomyosin cortex and membrane (Jiang and Sun, 2013) and is composed of two parts, σ = σp+σa, where σp is the passive mechanical stress of the actin network and membrane, which includes contributions from F-actin crosslinkers, filament mechanics, and lipid bilayer. σa is the active myosin contraction from the cortex. The passive stress is typically small compared to the active stress, and in this model, we only consider the active stress such that σ ≃ σa. Hereafter, we will use cortical stress to refer to the combined stress from the cortical layer and the cell membrane. Similarly, we will use cortical tension and cortical thickness to refer to the combined effects from both the cortical layer and the lipid bilayer.
The chemical equilibrium equation for the bicarbonate-carbonic acid pair is , where [CO2]aq is related to the partial pressure of CO2, PCO2, by the Henry constant kH, i.e., [CO2]aq = PCO2/kH. The reaction equilibrium constant for the bicarbonate-carbonic acid pair is . Defining as the extracelluar pH and pKc = −log10kc, we then have , where [CO2]aq = [CO2] since CO2 can move freely across the cell membrane (Vallés et al., 2015). For the intracellular domain, we have
where is the intracelluar pH. The cell contains various buffer solutions. In general, the chemical reaction for the intracellular buffer solution can be written as , where ℓ = 1, 2, 3, … for different buffer species and ZBuf = −ℓ is the valence of the unprotonated buffer. The reaction equilibrium constant is similarly . With pKB,ℓ = −log10kB,ℓ, we have . Without loss of generality, we lump all buffer solutions into one and use ℓ, or equivalently ZBuf, as a model parameter. By default, we let ℓ = 1 and simplify the notation of pKB,ℓ, Bufℓ−, and HℓBuf as pKB, Buf−, and HBuf, respectively. We will discuss the impact of ℓ later.
The conservation equation for the non-reactive ion species is
where Jn is the total ion flux across the membrane for each species and is determined by the boundary conditions of ion fluxes through the membrane channels, transporters, and pumps; V = 4πr3/3 is the cell volume. The conservation equation for the intracellular reactive species is
The total flux for each ionic species is the sum of the fluxes through the relevant channels, transports, and pumps:
The passive ion fluxes, Jn,p, are proportional to the electrochemical potential difference of ions across the membrane (Li et al., 2015) and are typically mechanosensitive (Martinac, 2004),
where Vm is the membrane potential; zn is the valence of each ionic species; is the ratio of extra- to intra-cellular ion concentrations; αn,p is the permeability coefficient of each species, which depends on the channel property and the density of the channels in the membrane; Gm ∈ (0, 1) is a mechanosensitive gating function that generally follows a Boltzmann distribution, i.e., , where β1 and β2 are two constants and τm is the cortical tension given by τm = σh.
Since NKCC is mainly a passive transport, the flux through it can be expressed as (Bennett et al., 2008)
where αNKCC is the permeability coefficient independent of the cortical tension. Given the dependence of NHE on pH, the flux of NHE is expressed as
where αNHE is the permeability coefficient which does not significantly depend on cortical tension (Pang et al., 2012) and we assume it as constant. is a pH-gated function indicating the dependence of the NHE activity on pH (Figure 1B). Similarly, the flux through AE2 takes the form
where αAE2 is the permeability coefficient of AE2 and is assumed to be independent of the cortical tension. is a pH-gated function indicating the dependence of the AE2 activity on pH (Figure 1B). The fluxes through NBC depends on the combined electrochemical potential of the two species, i.e.,
where αNBC is the permeability coefficient of NBC and nNBC = 2 or 3 indicates the stoichiometry of NBC. In the paper, we will take nNBC = 2 in our simulation. Since the NKE is voltage-dependent and its flux saturates at high concentration limits, we model the flux of Na+ and K+ through the Na+/K+ pump as
where αNKE is the permeability coefficient of the pump depending on the density of the pump as well as the concentration of ATP. βNKE,Na and βNKE,K are constants that scale ΓNa and ΓK, respectively. The exponents 3 and 2 are the Hill's coefficients of Na+ and K+, respectively. Equation 15 ensures that the flux is zero when either 1/ΓNa or ΓK approaches zero; the flux saturates if 1/ΓNa and ΓK approaches infinity. GV,NKE captures the voltage-dependence of the pump activity (Gadsby et al., 1985), , where β3 and β4 are constants (Figure 1C).
The electro-neutral condition should be satisfied for both the intracellular and the extracellular spaces. The condition for the intracellular space is maintained by enforcing ∑zncn = 0. The full set of equations for the system is as follows,
In this work, the given quantities (known model inputs) are: , , , , NA, PCO2, and NHBuf + NBuf. The six equations (Equations 16–21) are used to solve for the six unknowns: r, Vm, cNa, cK, cCl, and pH. The rest of the quantities are derived either from the given quantities or from the unknowns.
For steady-state response, Equations (16–21) can be directly implemented to solve for the six unknowns by letting d/dt = 0. The membrane potential, Vm, is solved by Equation (17). To solve for the cell transient response to sudden changes, since Equation (17) does not explicitly contain Vm, it does not give the time-dependent Vm in its original form. We will thus rewrite Equation (17) as follows. At each time step, we have , which explicitly contains Vm and will replace Equation (17) in solving for cell transient responses. In this case, the initial condition for the cell volume should give rise to the concentrations of cA and cBuf such that ∑zncn = 0 is satisfied.
2.2. Brief Model Analysis
Here we will provide some brief analysis that provide useful insights on the responses of the cell. At steady state, all the time-depend terms in Equations (16–21) vanish and the system becomes
We first observe that the permeability coefficient of water, αw, is not present in the steady-state solution, suggesting that the steady-state cell volume variation is independent of the expression level of AQPs, although AQPs are important for water flux. We will discuss the role of AQP in the result sections.
Among the six equations, only Equations (22, 23) explicitly contain r (e.g., cA = NA/V), and Equations (24–27) are ion fluxes as functions of ion concentration, membrane potential, and pH. We can therefore find an equation that solves for the cell volume. Multiplying Equation (23) with RT and adding it to Equation (22) provides a cubic equation in r. To perform a scaling analysis, we let R0 be a generic scale of cell radius. The cell radius can thus be written in a non-dimensional form on the order of one: . The cubic equation becomes
where p3, p2, p0 > 0 and are all in dimension of moles. Denote as the osmolarity difference across the cell membrane. We thus have . Under physiological-relevant conditions, (2cBuf + cHBuf + 2cA − Δc) is on the order of 100 mM, R0 is on the order of 10 μm, h is on the order of 10−7 m, σ is on the order of 1 kPa, NHBuf + NBuf and NA are on the order of 0.1 pmol, and is on the order of 1. Together, , , . If the product of hσ increases by one order of magnitude, p2 will also increase by one order of magnitude. Nevertheless, we have , which indicates that Equation (28) has one unique real solution for . Although the system described by Equations (22–27) is highly nonlinear, when the cell reaches steady state, the cell volume is uniquely determined. We can further find an approximate analytical solution for using the perturbation method. Since p2 ≪ p3 and p2 ≪ p0, let ϵ = p2 be a small parameter for the equation . The solution for is expanded as . The ϵ0-order of equation solves for as and the ϵ1-order of equation solves for as . The solution for is thus approximately
From the order of magnitude analysis, we can see that cn and pH are the primary variables determining the cell volume. σ has an important but secondary effect. αw does not influence the cell volume at a steady state. The factor 2hσ/R0 in p2 can be rewritten as . We then have based on the orders of p2 and p3. Since is on the order of 1, then . Therefore, and 2cBuf + cHBuf + 2cA − Δc ≃ 2cBuf + cHBuf + 2cA. The sum (2cBuf + cHBuf + 2cA) is typically on the order of 100 mM, suggesting that Δc is on the order of 0.01 mM. Given the large overall osmolarity of the intracellular and extracellular environments, which is on the order of 100 mM, the Δc is negligible and is often approximated as zero (Mori, 2012). Equation 29 can further be simplified as
The leading order solution is
On the leading order, the cell volume is
Equation 32 shows that the cell volume is linear in NHBuf + NBuf and NA due to the assumed impermeability of the buffer solution and proteins in the model (Kay, 2017; Yellin et al., 2018). Different cells may have different amounts and types of buffer solutions and proteins. pH plays an important role in cell volume regulation; cells' ability to control pH also affects cells' ability to control volume. The concentration of permeable ion species can be expressed in terms of impermeable species, cBuf, cHBuf, and cA. Of note, Equation (32) is not a result of Equations (24–27) and is thus independent of the choice of ion channels, transporters, and pumps. Equations 32 does depend on the spherical assumption we have made on the cell. In this work, we will limit our study on the volume response of spherical cells under perturbations.
Equations 24 to 27 can be scaled by an arbitrary constant. Without loss of generality, we can choose the passive K+ channel permeability coefficient, αK,p, as the overall permeability scale, α0, of ion dynamics, i.e., α0 = αK,p. We will then rescale all the other permeability coefficients by α0, which is equivalent to rescaling each flux, jn,p = Jn,p/α0, jNKE = JNKE/α0, jNKCC = JNKCC/α0, jNHE = JNHE/α0, jAE2 = JAE2/α0, jNBC = JNBC/α0. Equations 24 to 27 becomes
which provide the same solution as Equations (24–27). Therefore, the overall permeability scale, α0, is a free parameter for the steady-state problem and only affects the time scale of the transient response before the system reaches steady-state. For steady-state solution, the relative values of the permeability coefficients of each species will play the major role in determining the cell response, including the cell volume as seen in Equation (29).
2.3. Parameters
Most of the model parameters can be estimated or obtained from the literature. The overall permeability scale, α0, is chosen such that the predicted transient response upon perturbation lasts about 10 min before the system reaches a steady state. This time scale comes from both our experimental observation when cells typically research steady-state after perturbation (Yellin et al., 2018) and the possible magnitude of fluxes from the average number of ion channels, transporters, or pumps per unit cell surface area (Gadsby, 2009). The relative permeability coefficients of various ion channels, transporters, and pumps, such as αNKE/α0, αNKCC/α0, αNHE/α0, and αAE2/α0, are fitted such that the model output vector, , is consistent with physiological-relevant numbers reported in the literature. For example, the intracellular concentrations of sodium, potassium, and chloride are on the order of 5 mM, 150 mM, and 10–50 mM, respectively. The typical membrane potential is about −65 mV and the intracellular pH is about 7.4. We then solve an inverse problem in which X is given and the relative permeability coefficients of various ion channels, transporters, and pumps are unknowns. The solution for the unknowns determines the order of magnitude for αNKE, αNKCC, αNHE, and αAE2. The value for αNBC is estimated and in this model we allow it to vary across several orders of magnitudes. This variation can come from multiple mechanisms, including regulation via calcium (Yamada et al., 1996; Ruiz et al., 1999; Bachmann et al., 2006) and biochemical signals (Ruiz et al., 1996, 1998).
In the model, we consider two chemical reactions: the bicarbonate-carbonic acid pair and the buffer solution. The buffer solution is generic and contains all possible buffer mechanisms, including the phosphate buffer (Thomas and O'Shea, 2005). The pKB for the intracellular buffer is based on values in literature (Weinstein, 1986). Since different cell types have a different amount of buffer solution, the value of pKB is likely to be cell-type dependent. Since cells can modulate their intracellular biochemical environment such that NHE inhibition does not change the membrane potential (Mahnensmith and Aronson, 1985), we therefore adjust pKB in a way that its value ensures that NHE has a negligible effect on the membrane potential.
The full parameters used in the model are provided in Table 1. These parameters will not change throughout the simulation unless otherwise specified or varied. Most of the parameter choice is generic and does not qualitatively affect the results and conclusions. We instead focus more on the scaling laws of the system and draw a general conclusion on cell volume regulation. MATLABⓇ was used to program and solve the equations. The roots of the non-linear equations at each time step were found by the Newton-Raphson Iteration method (Ben-Israel, 1966).
3. Results and Discussion
3.1. Transient Water Flux and Intracellular Osmolarity
Given the importance of NHE in cellular function, volume regulation, and its coupling to AE2 through the bicarbonate-carbonic acid pair, we will start with NHE as an example to illustrate the transient response of the cell upon channel inhibition. In a theoretical experiment, the inhibition of NHE is achieved by reducing the permeability coefficient of NHE, i.e., αNHE. In a laboratory experiment, NHE inhibition can be achieved by adding inhibitors such as EIPA or by interfering with the expression of NHE using techniques such as siRNA, shRNA, or CRISPR/cas9. Here we use a 103-fold decrease in αNHE to represent a generic inhibition of the transporter; in later sections, we will discuss the effect of different levels of inhibition on the cell response.
We apply NHE inhibition at t0 = 20 min where the cell has reached a steady state (regime i) from an initial condition (Figure 2A). The cell volume is predicted to decrease upon inhibition (Figure 2A); this prediction will be different if the permeability coefficient of NBC increases, which will be discussed later. The time scale of the transient response, τ (Figure 2A), is mainly affected by the overall permeability scale, α0: τ decreases as α0 increases. After the transient regime, the cell reaches a steady state again (regime ii).
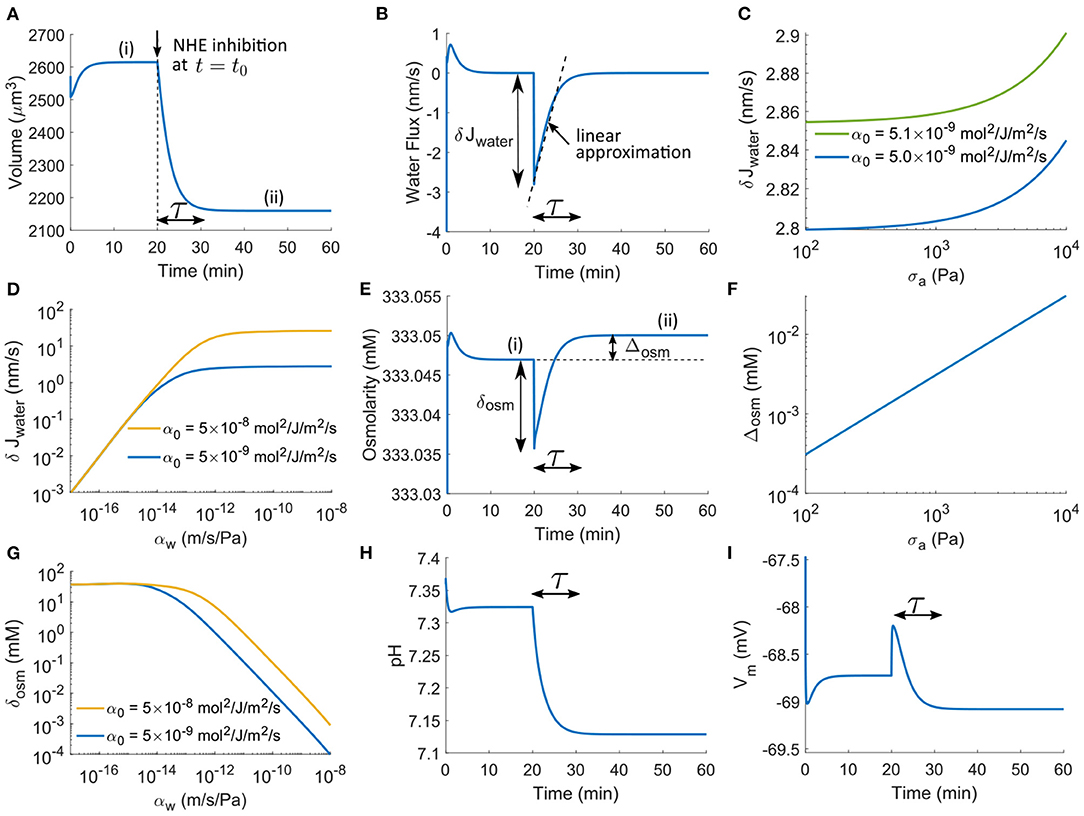
Figure 2. Model prediction on the cell transient response upon NHE inhibition applied at t0 = 20 min by reducing αNHE by three orders of magnitude. (A) Transient response of cell volume as a function of time. τ is the time scale of the transient regime. (B) Transient response of cell water flux. (C) The maximum magnitude of the transient water flux upon NHE inhibition as a function of cortical stress, σ, for different α0. (D) The maximum magnitude of the transient water flux upon NHE inhibition as a function of the water permeability coefficient, αw, for different α0. (E) Transient response of intracellular osmolarity. The extracellular osmolarity is 333 mM. (F) The magnitude of the steady-state osmolarity difference before and after NHE inhibition as a function of cortical stress σa. (G) The magnitude of the osmolarity difference before and after NHE inhibition as a function of αw for different α0. (H) Transient response of the intracellular pH. (I) Transient response of the cell membrane potential.
The cell volume decrease results from the water efflux during the transient regime (Figure 2B). Upon inhibition, an initial efflux with a maximum magnitude of δJwater is seen, followed by a gradually decreasing efflux. The cell volume reduction corresponds to a change in cell radius, Δr. Equation 1 suggests that . If we approximate the water flux as a linear function in time during the time period τ (Figure 2B), we thus have Δr ≈ (δJwater)τ/2. The maximum magnitude can then be expressed in terms of Δr as δJwater = 2Δr/τ. Since Δr is slightly affected by σ (see section Brief Model Analysis), so is δJwater (Figure 2C). The model predicts that the increase of δJwater is only < 2% even if σ has increased two orders of magnitude. Compared to σ, the overall permeability scale, α0, has a more significant effect: 2% increase of α0 leads to about 2% change of δJwater (Figure 2C).
When αw is in the physiological regime ( m/Pa/s), one order of magnitude increase of α0 leads to approximately one order of magnitude increase of δJwater (Figure 2D, see the two lines). Although Δr is independent of αw, δJwater decreases with decreasing αw when αw is several orders of magnitude lower than the physiological-relevant regime, where δJwater becomes independent of α0. However, within the physiological-relevant regime of αw, δJwater remains as a constant (Figure 2D). The lipid membrane of mammalian cells is permeable to water with a permeability around m/s/Pa in the absence of the AQPs (Li et al., 2020). Thus, even if AQP is inhibited, this value of αw will still lead to a permeability-independent δJwater unless the overall permeability scale, α0, is two orders of magnitude higher than expected (Figure 2D). This result indicates that the limiting factor for the maximum water flux δJwater depends on the relative coefficients of water and ion fluxes. Under normal conditions, water permeability is not the limiting factor. Together, the maximum magnitude of water flux across a cell membrane, in addition to the changes in solution concentration, is mainly affected by the overall permeability scale of ion channels, transporters, and pumps.
Water flux results from a hydrostatic pressure and osmotic pressure imbalance. The initial instantaneous water flux δJwater comes from the initial osmolarity change δosm (Figure 2E). At steady states (i) and (ii) the two pressures are in balance. Define as the difference between the osmolarity at the two steady states after and before NHE inhibition (Figure 2E). By Equation (22), we have
Given that the original cell radius r is on the order of 8 μm and the change of radius is on the order of 0.5 μm, the term in the parenthesis is on the order of 10−2 μm−1. Besides,h is on the order of 0.5 μm, and σ is on the order of 103 Pa. We thus find mM, which is <0.02‰ of the absolute value of the intracellular osmolarity, 333.05 mM (the extracellular constant osmolarity is 333 mM in this model). Therefore, the osmolarity difference across the cell membrane is tiny compared to the absolute osmolarity under consideration.
Although Δosm is proportional to σ by Equation (37), two orders of magnitude change of σ will still keep Δosm at a low level much <1 mM (Figure 2F). We thus conclude that before and after ion transporter perturbation, the intracellular osmolarity remains almost the same; the small change in osmolarity comes from the cortical tension. Of note, here we have assumed positive cortical tension; Δosm can be negative if the cortical tension becomes negative upon cell volume decrease. Since the effect from the cortical tension is much smaller than that from solute concentration, δosm can be approximated from Equation (16) as δosm ≈ δJwater/(αwRT) ≈ 2Δr/(ταwRT), which indicates that the immediate change of osmolarity upon transporter perturbation is mainly determined by αw and τ (i.e., α0). Interestingly, small water permeability or large overall permeability scale can increase δosm to the order of 1 mM (Figure 2G). Although αw and α0 do not influence the cell when it reaches a steady state, it has a significant impact on the transient osmolarity. It has also been found that the water permeability can depend on membrane tension (Ozu et al., 2013; Bahari et al., 2020). With this consideration, the transient time scale will be different, i.e., the cell will reach a steady state either faster or slower depends on whether the cell expands or shrinks. This result also has implications on cell migration. When ion transporters are perturbed during cell migration, the expression level of AQPs and ion transporters will collectively determine the transient intracellular concentrations of ions, leading to a modulation of downstream signals that depend on the ionic content.
The pH and membrane potential changes (Figures 2H,I) show the same transient time scale before a steady state is reached. Inhibition of NHE acidifies the cell (Figure 2H) but does not affect the membrane potential (Figure 2I), both being consistent with our understanding of NHE (Boron and Boulpaep, 1989). The acidification comes from the reduced H+ extrusion upon NHE inhibition. We will have further discussion in the following sections on how this acidification leads to cell volume reduction.
3.2. Mechanisms of NHE in Cell Volume Regulation
It is attempting to think that the reduced intracellular sodium concentration is responsible for cell volume reduction upon NHE inhibition. This speculation comes from the following reasoning. NHE intakes one Na+ and removes one H+ at one time. The removed H+ goes with via AE2, a chloride and bicarbonate exchanger (Figure 1A). Since CO2 is permeable to the cell membrane, the cytoplasm can continuously produce H+ and , which will be transported out of the cells. With the NHE in place, the cell would have a net gain of two ions at one time, namely Na+ and Cl− (Lang et al., 1998; Vallés et al., 2015). Inhibition of NHE would reduce this net gain and thus decrease cell volume. Below we will explain why the reduced Na+ influx itself upon NHE inhibition is unlikely to be responsible for cell volume reduction. We will also provide a possible mechanism of NHE-induced cell volume decrease.
Figure 2B shows that the net cell volume change is a result of the integration of Jwater over the time τ. A small instantaneous water flux δJwater with negligible time span (t ≪ τ) is not able to generate significant volume change. We, therefore, infer that the instantaneous osmolarity fluctuation δosm does not lead to volume change, either. The transient osmolarity change over time τ (Figure 2E) is a combination of the concentration change of each ion species inside the cell (Figure 3A). The model predicts that among all the species under consideration, only Na+ experiences an instantaneous (t ≪ τ) concentration change while other species have a time scale of about τ (Figure 3A). This result suggests that the effect of NHE on Na+ is immediate and is thus not expected to contribute to the large volume change seen in Figure 2A. The model also predicts a significant concentration decrease for bicarbonate, . This decrease is expected from the bicarbonate-carbonic acid pair reaction and is one of the main reasons behind the NHE inhibition-induced cell volume reduction.
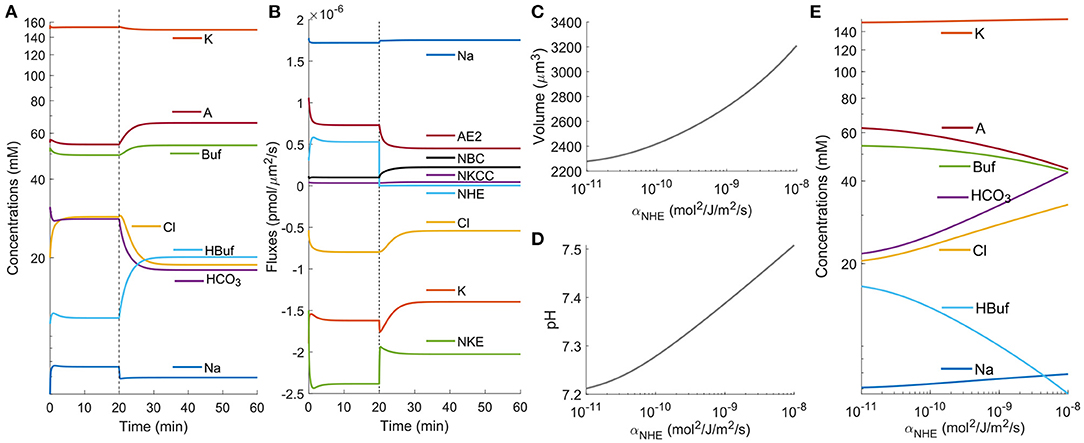
Figure 3. Model predictions of the cellular response upon NHE inhibition. (A) Intracellular ion concentrations upon NHE inhibition at t0 = 20 min. (B) Ion fluxes across each channel and co-transporter upon NHE inhibition at t0 = 20 min. (C) Model prediction of the cell volume when NHE is inhibited. (D) Model prediction of the intracellular pH when NHE is inhibited. (E) Model prediction of the intracellular ion concentrations when NHE is inhibited.
Since NHE inhibition acidifies the cell, let's consider the following scaling analysis. If at the beginning the intracellular pH is 7.4, from Equation (2) we find the intracellular concentration of to be 33.5 mM. If after acidification the intracellular pH is reduced to 7.2, the concentration then becomes 21.1 mM. This ~10 mM change in concentration is significant enough to build up pressure difference to drive water flux, although we recognize that the final cell volume change is a combination of all the ion species, not alone. As a side note, 0.5 mM change in concentration corresponds to 1 kPa change in pressure (Li et al., 2020). A second significance with concentration reduction is that it reduces AE2 flux, bringing in fewer Cl− as a result. The model also predicts a remarkable concentration decrease of Cl− on the order of 10 mM (Figure 3A).
We also observed a concentration increase of A−, Buf−, and HBuf (Figure 3A). This trend is expected because these species are not permeable to the cell membrane, so when the cell volume decreases their concentrations increase. For permeable species, the concentration change is mainly a result of the flux change through the corresponding transporters (Figure 3B), except for the changes that come from the chemical reaction. The model predicts that for channels or transports that directly involve Na+, their transient flux changes are almost immediate (much less than the time scale τ). For example, we see a quick reduction in the magnitude of ion flux through NKE as a result of the reduced intracellular Na+ concentration. This change also leads to a slight reduction for the intracellular K+ (Figure 3A). To summarize, the total intracellular osmolarity change over time τ is a combined effect of the transient responses of ion fluxes and concentration modulation, especially the NHE and AE2 pair, not a direct result of Na+ decrease as has been postulated for a long time.
After the transient response, the cells reach a steady state. Figures 3C–E shows the steady-state cell volume, intracellular pH, and intracellular ion concentration of each species as a function of the permeability coefficient of NHE, αNHE. The results can be interpreted as different levels of NHE inhibition. For example, as NHE is progressively inhibited, the cell volume decreases continuously, corresponds to increased net water efflux. This result is consistent with NHE inhibition during cell migration that the cell speed decreases progressively as NHE is inhibited with increasing concentration of EIPA (Stroka et al., 2014) or HOE642 (Stock et al., 2005).
3.3. Implication of NBC on Cell Volume Regulation Upon NHE Inhibition
In the above analysis (Figures 2, 3), we have used a relatively small permeability coefficient of NBC, and the model predicts cell volume decrease upon NHE inhibition. If we increase the permeability of NBC by 20 folds (or higher), the cell volume does not decrease (Figure 4A). The intracellular ion concentration of each species also remains almost constant upon NHE inhibition (Figure 4B). This is because when the NBC activities increase, it takes place the role of NHE to import Na+, and NHE becomes almost quiescent (compare Figures 3B and 4C). In this case, inhibiting NHE has a minimal effect on the cell volume and intracellular ionic dynamics.
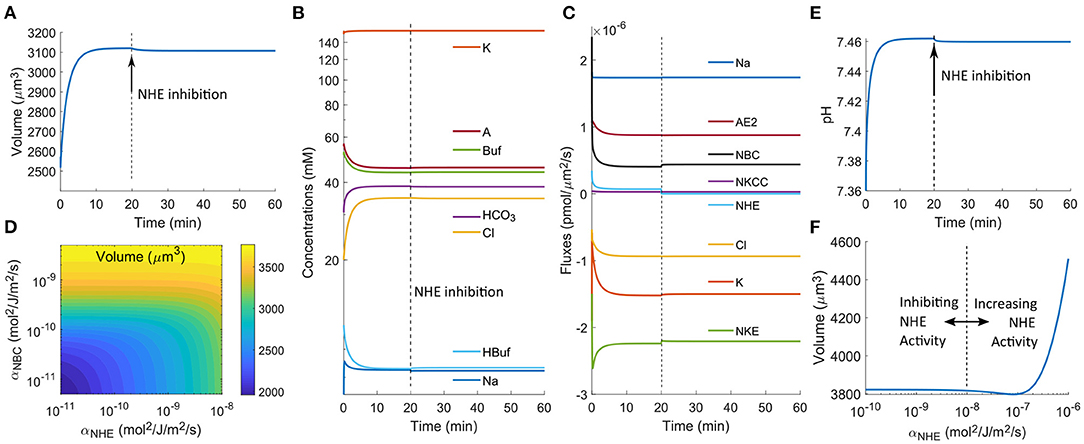
Figure 4. Model predictions of the cellular response upon NHE inhibition at t0 = 20 min. The permeability coefficient of NBC has been increased by 20 times as compared to the value used in Figures 2, 3. (A) Cell volume change upon NHE inhibition. (B) Predicted intracellular ion concentrations over time. (C) Ion fluxes across various channels and transporters over time. (D) Contour plot of the steady-state cell volume as a function of the permeability coefficients of NBC and NHE. (E) Changes in the intracellular pH. (F) Steady-state cell volume as a function of the permeability coefficient of NHE.
The dependence of cell volume on NBC upon NHE inhibition is a continuous function. Figure 4D shows the volume contour as a function of the permeability coefficients of NBC and NHE. When the NBC expression level is low or none, the cell volume is sensitive to NHE inhibition; when the NBC expression level is high or non-trivial, the cell volume is not affected by NHE inhibition. The dependence of the intracellular pH on NBC is the same as that of cell volume when NHE is inhibited: when NBC is present, the cytoplasm is not predicted to acidify when NHE is inhibited (Figure 4E). Our model thus predicts that NBC may serve as a buffering mechanism to both cell volume decrease and cell acidification (Boron and Boulpaep, 1989) upon NHE perturbation. Indeed, similar phenomena have been observed in the literature. For example, human neutrophils express NBCe2, an isoform of NBC (Giambelluca et al., 2014). Inhibition of NHE on suspended human neutrophils has not been found to change cell volume (Grinstein et al., 1986; Rosengren et al., 1994); inhibition of both NHE and NBC has been found to acidify the cells (Giambelluca et al., 2014) (corresponds to Figure 2H). These experimental results can be interpreted by the mechanisms revealed in this work.
Interestingly, migrating, not suspended, human neutrophils have been found to reduce cell volume with NHE inhibition (Rosengren et al., 1994). Migrating neutrophils have larger volumes than suspended neutrophils (Rosengren et al., 1994). On the other hand, migrating cells exhibit a polarized distribution of NHE (Stroka et al., 2014; Li et al., 2020). We thus speculate that migrating cells have a higher expression level of NHE than suspended cells. Our model does predict that when NHE expression increases, the cell volume increases (Figure 4F). In this case, inhibition of NHE is predicted to reduce cell volume because the contribution of NHE takes over that of NBC. This phenomenon has been observed in an experiment where migrating neutrophils reduces cell volume upon NHE inhibition (Rosengren et al., 1994).
3.4. Regulatory Volume Increase by NHE
Here we will briefly discuss the model predictions for one of the most recognized functions of NHE. When cells are transferred from isotonic to hypertonic solutions, cells can (partially) recover their volume, known as regulatory volume increase, and NHE is responsible for this volume recovery (Cala, 1980; Ericson and Spring, 1982; Grinstein et al., 1986; Maeno et al., 2006; Hughes et al., 2010). In the model, we prepare a hypertonic solution by adding 50 mM NaCl to the original extracellular solution. Adding NaCl has been one of the most used methods in the studies of regulatory volume increase (Cala, 1980; Grinstein et al., 1986; Maeno et al., 2006). The model predicts that if the NHE activity remains constant in the entire process, regulatory volume increase does not occur; instead, the cell volume continuously decreases over the transient time, τ (Figure 5A). The regulatory volume increase only happens when NHE is activated upon the initial cell shrink (Figure 5A). In the model, NHE activation is achieved by increasing the permeability coefficient of NHE by three orders of magnitude at the same time as applying the hypertonic solution. Cell shrinkage has been considered to be responsible for this NHE activation; however, the mechanism for this activation remains unclear (Alexander and Grinstein, 2006). In this work, we do not aim to identify the mechanisms for NHE activation; instead, we predict that if this activation occurs, perhaps through other cell signals, regulatory cell volume increase by NHE is observed.
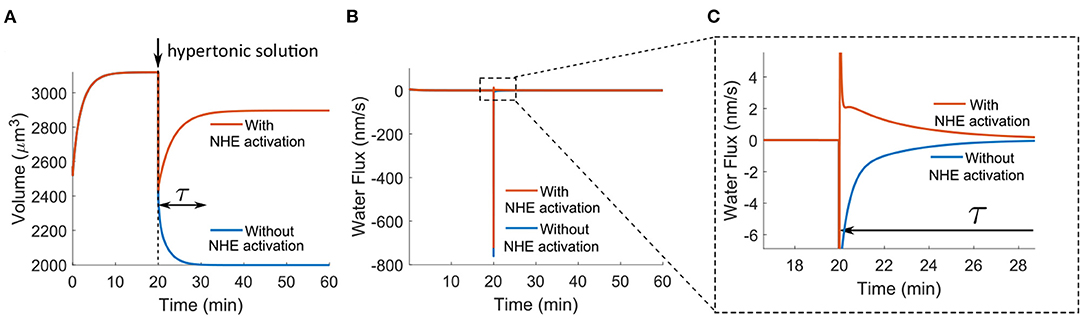
Figure 5. Model predictions of the cell response in the hypertonic solution applied at t0 = 20 min. The hypertonic solution is applied by adding 50 mM NaCl to the isotonic solution. The permeability coefficient of NBC has been increased by 20 times as compared to the value used in Figures 2, 3. (A) Time-dependent response of the cell volume. NHE activation is achieved by increasing the permeability coefficient of NHE by three orders of magnitude at t0 = 20 min. (B) Predicted water flux over time. (C) Zoomed-in profile in B.
Unlike the temporal volume decrease profile under NHE inhibition (Figure 2A), the volume decrease under hypertonic solution is immediate (t ≪ τ) instead of over the transient time τ (Figure 5A). This is because a hypertonic shock leads to an immediate large osmolarity difference and thus an immediate large water outflux (Jwater < 0) two orders of magnitude higher than the flux under NHE inhibition (compare Figures 2B and 5B). On the contrary, the osmolarity difference under NHE inhibition is small (Figure 2E), and the water flux gradually accumulates over the transient time (Figure 2B). When NHE is activated, the large water outflux quickly reverses, and an influx (Jwater > 0) with a small magnitude is predicted (Figure 5C). This influx spans over the transient period of time and the integration of this influx, , determines the amount of volume recovery. In our model, the volume recovery time scale, τ, is about 10 min; this time scale is determined by the permeability coefficients of ion channels, transporters, and pumps used in the model. Fast volume recovery on the order of minutes has been observed from experiments on Amphiuma red blood cells (Ericson and Spring, 1982), human neutrophils (Grinstein et al., 1986), and mouse choroid plexus epithelial cells (Hughes et al., 2010), while slow recovery on the order of 1 h also exists in Necturus gallbladder (Cala, 1980) and HeLa cells (Maeno et al., 2006). Since different cell types express different levels of ion channels, transporters, and pumps, we attribute this time difference to the cell type-specific membrane channel expressions.
3.5. Importance of Bicarbonate Export Under AE2 Inhibition
Equation 2 suggests that and pH are closely related, and thus is also an important ion species to consider whenever H+ changes. Given the interconnection between NHE and AE2, here we discuss the cell response under AE2 inhibition. Under physiological conditions, AE2 exports one and intakes one Cl− at a time. In this model, NBC is a second transporter that transports , and the direction of transport depends on the combined electrochemical potential of and Na+ (Equation 14).
If in the model we only have AE2 but do not include NBC, then from Equation (9) we can see that AE2 is the only transporter that can export . When AE2 is inhibited, is predicted to accumulate in the cytoplasm, and its concentration increases with time without reaching a steady state even at several hours after inhibition (Figure 6A), which leads to continuous volume increase (Figure 6B). This volume increase is significant, and cell lysis can happen if the degree of AE2 inhibition further increases. However, to the best of our knowledge, AE2 inhibition-induced cell swelling and lysis have not been experimentally observed. On the other hand, continuously increasing intracellular will significantly alkalinize the cell, which is also not physiologically favorable. Together, these suggest that cells have additional mechanisms to regulate to prevent its excessive accumulation.
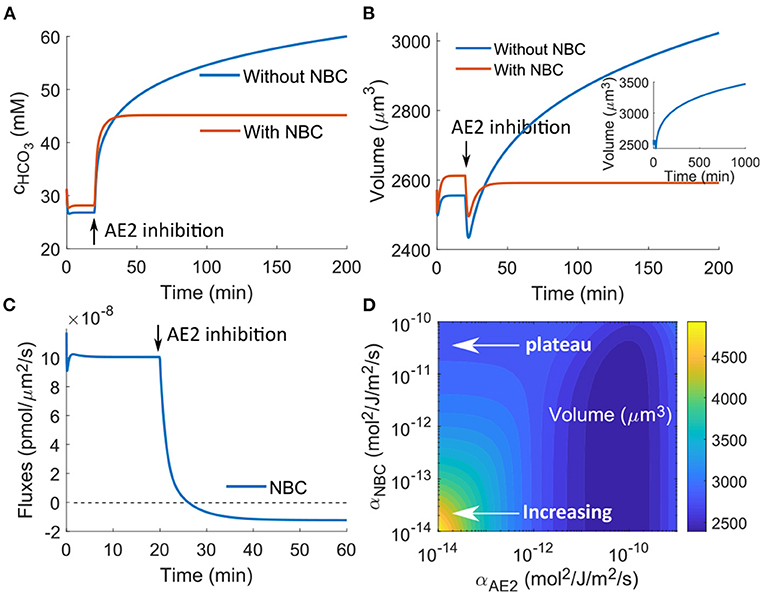
Figure 6. Model predictions of the cellular response upon AE2 inhibition applied at t0 = 20 min by reducing αAE2 by three orders of magnitude. (A) Intracellular concentration change with and without NBC. (B) Model prediction of the cell volume with and without NBC. The insert is a longer time response without NBE, which shows continuous increasing volume in time. (C) NBC flux upon AE2 inhibition. (D) Contour plot of the cell volume as a function of the permeability coefficients of NBC and AE2.
NBC is one of the transporters that can prevent the excessive accumulation of . In the presence of NBC, the concentration of and the cell volume reach steady states around 10 min after the perturbation (Figures 6A,B). This control comes from the export of through the transporter. Before perturbation, the combined electrochemical potential of Na+ and results in an influx of the two ion species (Figure 6C). As accumulates upon AE2 inhibition, the sign of the electrochemical potential reverses, and the NBC begins to export Na+ and . Although the magnitude of the efflux is one order lower than that of the influx before perturbation, when the efflux is integrated over time, it provides sufficient removal. For example, if the efflux is on the order of 10−8 pmol/μm2/s, as predicted by the model (Figure 6C), the amount of ion removal will be on the order of 5 × 10−3 pmol over 10 min for a cell of radius r = 8 μm. This amount corresponds to ~2 mM change in concentration. Therefore, every 10 min, the efflux can remove an equivalent (2nNBC) mM concentration of from the cell, which is sufficient to control the intracellular concentration.
In vivo, the flux through NBC and to what extend this transport can control cell volume depend on the expression level of NBC as well as the degree of AE2 inhibition. We use a contour plot of the steady-state cell volume to show its dependence on the rate constants of NBC and AE2 (Figure 6D). We can see that for small αNBC, equivalent to NBC not being present, the cell volume increases as AE2 is progressively inhibited. The cell volume almost doubles at the small end of αAE2. For large αNBC, equivalent to NBC being present, the cell volume reaches a plateau as αAE2 decreases. In between there exists an improved cell volume control upon AE2 inhibition as αNBC increases. The contour plot also suggests that the cell volume will, depending on the expression level of NBC, increase if the AE2 activity increases. The model predicts that the cell volume is a non-monotonic function of the AE2 activity if NBC is absent and approaches a constant if NBC is present. The exact expressions of AE2 and NBC are likely to be cell-type dependent, and it thus can happen that different cells will respond differently upon perturbation and will have different concentrations of intracellular . On the other hand, if mammalian cells are programmed to maintain constant volume upon reasonable perturbation, the expression level of NBC should be high in all cells. It can be interesting to see from experiments how cell volume modulates when AE2 is inhibited or activated, for both control and NBC-inhibited cells.
3.6. Implication of NBC on Cell Volume Regulation Upon NKE Inhibition
In the previous example, AE2 and NBC are the only two transporters that transport ; therefore, it is relatively easy to provide a physical interpretation of the dynamics of upon AE2 inhibition. When it comes to ions that are transported by multiple channels, transporters, and pumps, such as Na+, the results may not seem to be straightforward. In this section, we will discuss how NBC and are involved in the volume regulation when NKE is inhibited.
As an active pump that transports Na+ and K+ against their electrochemical potential, NKE is known to regulate the intracellular Na+ and K+ concentrations and the membrane potential (Gadsby, 2009). When NKE is inhibited, Na+ accumulates in the cytoplasm, and the K+ concentration starts to reduce, resulting in almost a flip of cytoplasmic concentrations of Na+ and K+ compared to the concentrations in normal conditions (Figure 7A). Meanwhile, the cell membrane is depolarized to ~20 mV (Figure 7B). We do not see a quantitative difference in Na+ and K+ concentrations and the membrane potential with and without NBC (Figures 7A,B); however, NBC helps to stabilize the cell volume to some extend when NKE is inhibited (Figure 7C). The cell is predicted to experience about a 50% volume increase when NBC is absent. But the increase is only about 20% when NBC is present. Of note, the presence of NBC also increases the baseline cell volume due to the additional ions brought by the transporter. We speculate that in wet-lab experiments, 50% volume increase is not expected because although too much ouabain, an NKE inhibitor, will kill cells, a small amount of ouabain (e.g., up to 50 μM for MDA-MB-231) alone has not been found to cause cell lysis (Gould III et al., 2018; Maity et al., 2020). We will next analyze the role of NBC in this process.
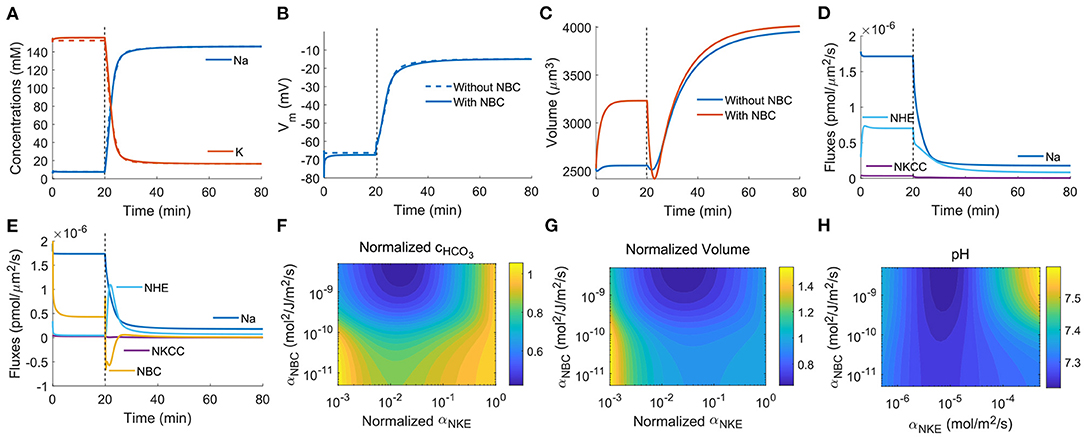
Figure 7. Model predictions of the cellular response upon NKE inhibition applied at t0 = 20 min (indicated by dashed vertical lines) by reducing αNKE by three orders of magnitude. (A) Intracellular Na+ and K+ concentrations. Dashed lines: without NBC. Solid lines: with NBC. (B) Cell membrane potentials. (C) Cell volumes. (D) Fluxes across the channels, transporters, and pumps that transport Na+. NBC is absent. (E) Fluxes across the channels, transporters, and pumps that transport Na+. NBC is present. (F) Contour plot of the steady-state, normalized intracellular concentration as a function of the permeability coefficient of NBC and the normalized permeability coefficient of NKE. αNKE indicates the degree of NKE activity. The concentration of is normalized with respect to the case without NKE inhibition so that the vertical line on the right end of the contour has value 1. (G) Contour plot of the steady-state, normalized cell volume as a function of the permeability coefficient of NBC and the normalized permeability coefficient of NKE. (H) Contour plot of the steady-state intracellular pH as a function of the permeability coefficients of NBC and NKE.
When NBC is absent, passive Na+ channel, NHE, and NKCC are the three channels/transporters that transport Na+ in addition to the NKE that is inhibited. The direction of the fluxes through the three channels/transporters is determined by the gradient of the electrochemical potentials of the relevant ion species. Therefore, each of the three channels/transporters has the possibility to reverse its direction of transport. Although the intracellular Na+ concentration significantly increases upon NKE inhibition, it is not large enough to reverse the direction of the passive Na+ channel, NHE, or NKCC (Figure 7D). When NBC is present, the fluxes through the passive Na+ channel and NKCC do not change compared to the case without NBC, but the flux through NHE is different (Figure 7E). We first notice that the direction of flux through NBC is reversed right after NKE inhibition. This is due to the sudden increase of the intracellular Na+ concentration (Figure 7A), which leads to a reversed gradient of the combined potential of Na+ and across the cell membrane. The reversal of NBC leads to an efflux of , with a factor of nNBC more than the flux of Na+. This efflux acidifies the cell, which activates NHE, as seen by a large peak of the NHE flux following NHE inhibition (Figure 7E). The activation of NHE also brings in Na+, which explains why the concentration of Na+ is unchanged compared to the case with NBC (Figure 7A) even if NBC can export Na+.
The model thus predicts that the presence of NBC has a significant effect on the cytoplasmic . Figure 7F is a contour of the steady-state, normalized intracellular concentration as a function of the permeability coefficient of NBC and the normalized permeability coefficient of NKE. The normalized αNKE indicates the degree of NKE inhibition; the smaller it is, the more inhibited the pump is. The concentration of is normalized with respect to the case without NKE inhibition so that the normalized concentration on the vertical line on the right end of the contour has value 1. When αNBC is large (on the same order of α0), corresponds NBC being present, the concentration of decreases with NKE inhibition, same as the analysis from Figure 7E. This concentration decrease helps to prevent significant cell volume increase (Figure 7C). When αNBC is small (≪α0), corresponds NBC being absent, the concentration of initially decreases and then increases back to the original value as NKE is further inhibited. Here we plot the normalized volume with respect to the volume without NKE inhibition to show the relative volume change. The original concentration of without inhibition in the presence of the NBC is higher than that without NBC.
The normalized cell volume follows the same pattern as the normalized intracellular concentration (compare Figures 7G,F). The original cell volume is also larger when NBC is present compared to that when NBC is absent. This result shows that the size homeostasis of the cell depends on the expression levels of ion channels and transporters. Our work thus suggests that the volume difference across different cell types maybe is the result of their expression levels of ion transporters, in addition to possible differences in protein content.
The model also predicts that with slight NKE inhibition (a 10−1 or 10−2 change in expression), the cell volume will decrease instead of increasing (compare Figure 7G). This result can be model-dependent as it is possible that including additional channels, transporters, and pumps may change the results. But on the other hand, it is also possible that NKE has a duel effect on cell volume depending on its activities. Of note, when NKE permeability is further reduced beyond the range plotted in Figure 7G, the cell volume will continue to increase, implying that excessive inhibition of NKE eventually causes cell lysis, which is consistent with the fact that complete inhibition of NKE leads to cell death (Pchejetski et al., 2003; Valente et al., 2003; Chou et al., 2018).
Although NKE itself does not involve H+ or , its inhibition has an impact on the intracellular pH through NHE (Gatti and Christen, 1985). Our model predicts the same phenomenon. Since the presence of NBC tends to reduce the intracellular concentration upon NKE inhibition, it also acidifies the cell as a result (compare Figure 7H). The model thus provides generic mechanisms that describe the dynamics among different ion species and their implications on both cell volume and pH.
3.7. Predictions of Cell Type-Dependent Cell Properties
In this last section, we provide an example of how different cell types can respond differently upon perturbations of ion channels, transporters, and pumps. The following three common breast cell types will be studied: MCF-10A, normal breast cell line; MCF-7, weakly malignant breast cancer cell line; MDA-MB-231, highly malignant, metastatic breast cancer cell line. These three breast cell lines are known to have varying expression levels of different ion channels, transporters, and pumps, including NHE (Amith and Fliegel, 2013; Boedtkjer et al., 2013), NBC (Boedtkjer et al., 2013; Alka and Casey, 2014), AE2 (Hwang et al., 2019), and NKE (Khajah et al., 2018). These variations provide the qualitative basis for the cell type-dependent parameters used in the model (Table 2). We also adjust the permeation coefficient of the passive sodium channel so that the predicted membrane potential of the three cell types (Figure 8A) matches with experimental measurement (Marino et al., 1994; Yu et al., 2017). Since our model considers a subset of ion channels, transporters, and pumps that are present in cells, parameters used here for the three cell types are not meant to be exact, but rather a qualitative representation of different cell properties.
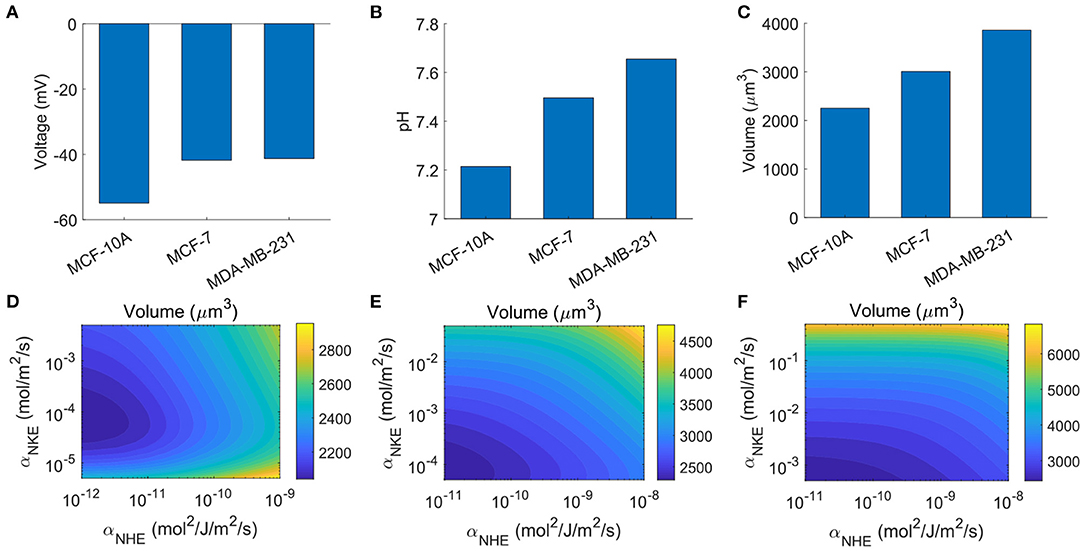
Figure 8. Examples of cell type-dependent cell properties. (A) Computed cell membrane potentials. (B) Model prediction on the intracellular pHs. (C) Model prediction on the cell volume of the three cell types, assuming the cell protein contents are identical. (D–F) The contour of cell volumes for MCF-10A, MCF-7, and MDA-MB-23, respectively, as functions of NKE and NHE activities. The variation of NKE and NHE activities ranges from 10−2to10 folds based on the values listed in Table 2.
With the above setup, the model predicts higher intracellular pH in breast cancer cells than that in the normal breast cell (Figure 8B). This prediction is consistent with the fact that there is an alkalinization of the cytoplasm in breast cancer cells due to the elevated activities of NHE1 (Amith and Fliegel, 2013) and NBCn1 (Alka and Casey, 2014). The model also predicts that the rest cell volume increases progressively with the malignancy level (Figure 8C). The trend of cell volume is consistent with the trend of pH. This is because, as discussed in the above sections, the concentration of bicarbonate increases with increasing pH, which leads to increased cell volume. We note that the cell protein content, or NA, is assumed to be the same. In reality, the cell protein content could be different, but there is currently no data on this.
Based on the analysis so far, it is expected that the three cells will show different cell volume variation patterns when their ion channels, transporters, or pumps are perturbed. Indeed, if we allow NKE and NHE expression levels to vary based on the values listed in Table 2, the three cells exhibits different cell volume changes (Figure 8D, MCF-10A; Figure 8E, MCF-7; and Figure 8F, MDA-MB-231). The model predicts that all three cell types respond to NKE and NHE. The volume of MDA-MB-231 is more sensitive to NKE while the volume of MCF-10A is more sensitive to NHE. These predictions may be different if more ion channels, transporters, and pumps are included in the model. A comprehensive study of cell type-dependent cell properties requires more data on the cell channel composition.
MCF-7 and MDA-MB-231 spheroids indeed have reduced volume when NHE is inhibited (Chang et al., 2014; Rolver et al., 2020), and MCF-7 seems to be more sensitive than MDA-MD-231 on NHE inhibition (Rolver et al., 2020), which is consistent with our model prediction (compare Figures 8E,F). But this tumor volume reduction was probably due to downstream effects of NHE inhibition instead of a direct ion flux change across the cell membrane. We thus leave it as an open question that how expression levels of ion channels, transporters, and pumps affect cell volume in vivo.
3.8. A Few Notes on the Parameters and Alternative Models
We begin with studying the impact of the effective valences of some of the species. The average charge of the non-permeable organic molecules and proteins, i.e., the valence ZA, is a potential variable that can vary across cell types. The model predicts that the cell volume increases with the magnitude of the negative ZA (Figure 9A). The cell also becomes further polarized by several mV per unit ZA change as the proteins carry more negative charges (Figure 9B). The concentrations of intracellular ions will adjust correspondingly. As expected, in general, the negatively charged ions decrease their concentrations with the magnitude of the negative ZA while positively charged ions go in the opposite direction (Figure 9C). The trend of the dependence of various cell responses on ZA is consistent with the model prediction by Kay (2017).
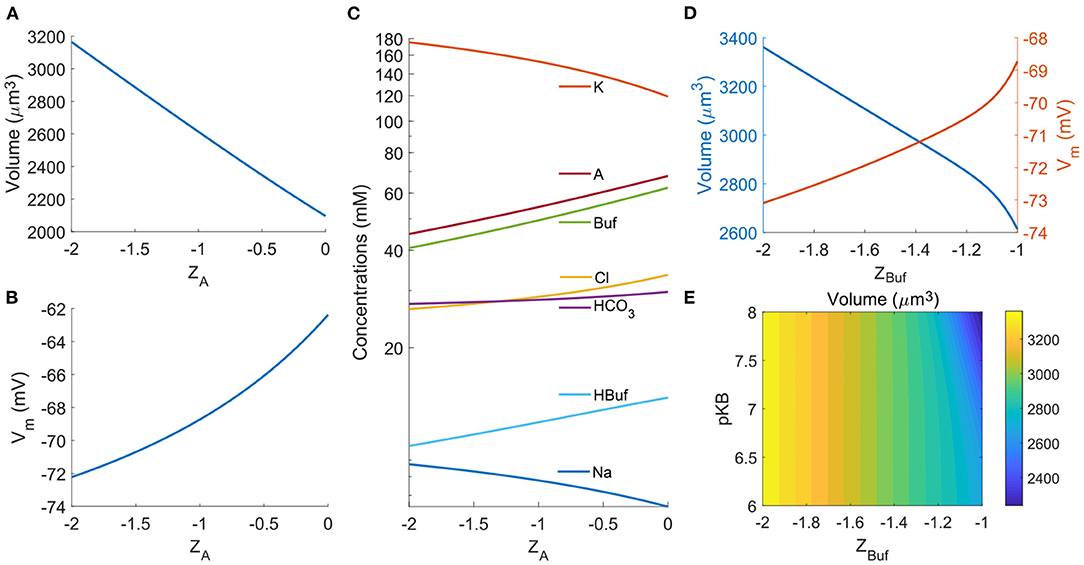
Figure 9. Impact of ZA and ZBuf. (A) Cell volume as a function of ZA. (B) Membrane potential as a function of ZA. (C) Intracellular ion concentrations as function of ZA. (D) Cell volume and Membrane potential as functions of ZBuf. (E) Contour of the cell volume as a function of the effective pKB and ZA.
Different buffer solutions can give rise to different valences of the unprotonated buffers. In the model, we can vary the effective lumped valence of all buffer solutions. Similar to the impacts from the effective valence of the organic molecules and proteins, large |ZBuf| leads to larger cell volume and more polarized cell compared to those from a small |ZBuf| (Figure 9D). Since different buffer solutions will have different reaction equilibrium constant, here we also investigate the effective pKB values on the cell volume. The model predicts that pKB only affects the cell volume when ZBuf is close to −1 (Figure 9E).
In the model, we have assumed a constant cortical tension dominated by the active myosin contractility. Here we briefly examine a model with a more general cortical mechanics. The total cortical stress is
where Em is the cortical elasticity, ηm is the cortical viscosity, and r0 is a reference cortical radius. We re-examine the case of NHE inhibition as shown in Figure 2. With cortical viscosity, the transient time scale increases (Figure 10A). The presence of the cortical elasticity increases the cortical stress and thus reduces the cell volume (Figure 10A). With the increase of the total cortical stress, the intracellular osmotic pressure also increases (Figure 10B). While the cortical elasticity generates positive tensile stress in the cortex, the viscosity generates negative compression stress as the cell shrinks (Figure 10C). We would like to mention that due to the continuous remodeling of the cortex, in reality, there is no defined reference cell radius r0, and thus there does not exist cortical elasticity. The passive cortical mechanics will mostly be the viscous part.
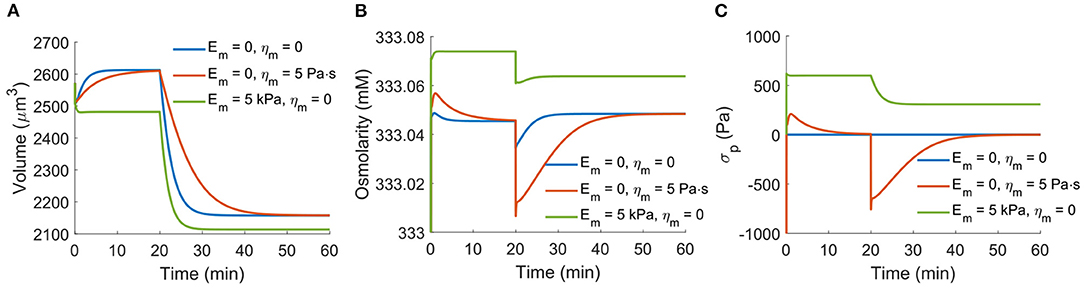
Figure 10. Impact of the cell cortical mechanics on the responses of the cell under NHE inhibition as shown in Figure 2. The data from Em = ηm = 0 is the same as the data in Figure 2. The reference cell volume is taken as r0 = 7.5 μm. (A) Cell volume for different cortical properties. (B) Total intracellular osmolarity for different cortical properties. (C) The passive cortical stress, σp, for different cortical properties.
We have also assumed non-permeable protonated buffer solutions in the model. Since some uncharged buffer solutions can be permeable to the lipid bilayer, such as acetic acid or lactic acid, here we examine the case with permeable protonated buffer solutions, meaning the HBuf moves freely in and out of the cell. The extracellular space is still considered an infinite reservoir with constant properties. In this regard, we prescribe the concentration of HBuf instead of the total amount of intracellular buffer amount, i.e., is given. The unprotonated buffer concentration is determined by the pH, i.e., and . The rest of the modeling framework remains the same. We also keep all the parameters the same with the only change of the extracellular from 35 mM (Table 1) to 25 mM. The 10 mM difference goes to . The extracellular space is adjusted to electroneutral through cA and cG, and the total extracellular osmolarity is kept at 365 mM.
We select the three most informative results and compare these to the original model. Figures 11A–C correspond to Figures 4D, 6D, 7G respectively. Although there is some quantitative difference between the two model choices, the overall trends remain the same. All these results show that the presence of NBC helps to stabilize the cell volume when the cell is under channel/transporter/pump perturbation. Therefore, the conclusion of our model prediction is robust.
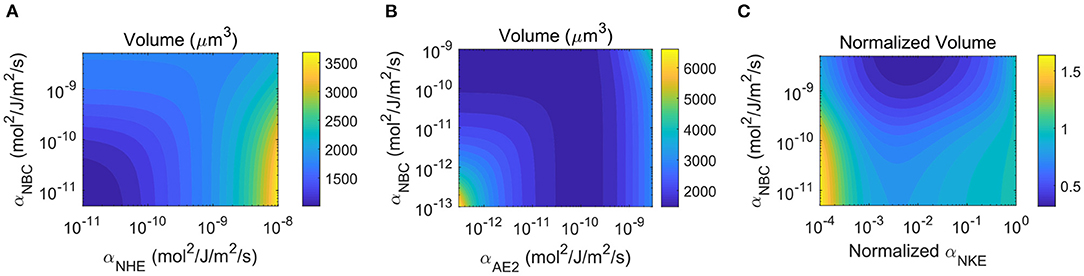
Figure 11. Key model predictions with permeable protonated buffer solution. The predicted trends with permeable protonated buffer solution are the same as a model with non-permeable protonated buffer solution. (A) Contour plot of the cell volume as a function of the permeability coefficient of NBC and NHE. This plot is a counterpart of Figure 4D. (B) Contour plot of the cell volume as a function of the permeability coefficient of NBC and AE2. This plot is a counterpart of Figure 6D. (C) Contour plot of the normalized cell volume as a function of the permeability coefficient of NBC and the normalized permeability coefficient of NKE. This plot is a counterpart of Figure 7G.
4. Discussion and Conclusions
In this work, we performed computational experiments based on a mathematical model to analyze how hydrogen and bicarbonate are involved in cell volume regulation. We included several commonly expressed ion transporters/pumps as well as passive ion channels and focused on generic model predictions on the cell volume and cell osmolyte concentration. For example, at a steady state, the cell volume is tightly correlated with the cell osmolarity, and changes in cell volume result in tiny ion concentration changes (much <1 mM). Therefore, the total intracellular solute concentration remains almost constant regardless of the cell volume. This is consistent with our previous results on cell volume variations as a function of membrane potential (Yellin et al., 2018). In this work, we have focused on a spherical cell. One of the features of a spherical cell is its non-polarity. The trends of volume change predicted by this model still apply to non-polarized cells even if they do not adopt a spherical shape. For adhered cells, the force-balance relationship and the geometry of the cell will be different, but this should only change the results qualitatively. For polarized cells, such as cell migration in confined channels, our model provides information on localized water influx and efflux depending on the membrane protein expression at different spatial locations of the cell membrane.
The model involves a number of parameters (Table 1). Some parameters describe the intrinsic molecular properties of ion channels, transporters, and pumps (e.g., dependence on concentration differences, cortical/membrane tension, pH, and voltage). Other parameters, such as the permeability coefficients of channels, transporters, and pumps (α's), describe the state of ion channel activation as well as the overall expression level and therefore depend on the cell type. We find that the predicted cell response is most sensitive to the permeability coefficients: α's. We noted that these permeability coefficients probably depend strongly on cell signaling and regulatory mechanisms, e.g., post-translational modification and Ca2+ binding. α0 sets the overall cell response time scale to external perturbations. One order of magnitude change in α0 leads to about one order of magnitude change of the transient response time. The activity of NKE plays a major role in controlling the intracellular Na+ concentration and membrane potential. One order of magnitude decrease in αNKE leads to roughly 40 mM increase in intracellular Na+ concentration and 20 mV depolarization. Activities of AE2 and NKE have non-monotonic effects on the cell volume (Figures 6D, 7G) while the effects from NHE and NBC are monotonic (Figures 3F, 6D, 7G). The sensitivity of cell volume to these four permeability coefficients of AE2, NKE, NHE, and NBC depends on their relative ratios. For example, from Figure 6D, we can see that the cell has a larger volume change with the inhibition of AE2 when NBC is absent and vice versa. This is because in this model AE2 and NBC are the only two transporters that can remove from the cell. If one of the transporters is absent, the cell lacks redundant mechanisms for maintaining homeostasis; inhibition of the remaining transporter thus leads to significant cell volume change.
Given the large number of channels and transporters in mammalian cells and significant variations in the expression profiles from cell type to cell type, we do not claim that our work represents a minimal model nor a sufficient model. We aim to develop a model that captures the typical trends of the cellular response under the influence of hydrogen and bicarbonate. Some small variations of the model are also possible. For example, in the model, we have included AE2, which is pH-gated. The two other isoforms of AE2, namely AE1 and AE3, are pH-independent (Sterling and Casey, 1999). Non-pH-gated AEs can be lumped into the model by varying the pH gating parameters if needed. A truly comprehensive model requires concerned effort to generate a consistent set of data. The existence of redundant mechanisms also increases the complexity of a comprehensive model. For example, NBC can be replaced by a combination of other transporters that can remove Na+ and when these two ion species start to accumulate in the cytoplasm. The choice of what and how many ion transporters to include depends on the physical problems to be addressed. In a problem involving pH, the inclusion of NHE, AE2, and NBC is necessary. However, in problems where the variation of pH and is not crucial, these transporters may be left out.
In this model, we did not include Ca2+, which is also an important ion in the cytoplasm. Some channels transport Ca2+ and Na+ and can take the place of NBC if the Na+ dynamics is considered. In addition to channels that directly transport Ca2+, Ca2+ is a second messenger that often regulates the activity of various ion channels and transporters (Mahnensmith and Aronson, 1985; Garty and Palmer, 1997; Ruiz et al., 1999; Shieh et al., 2000). For example, the activity of NHE1 can be modulated by Ca2+ through TRPV4, determining pH-dependent actin polymerization, providing mechanical stability to delineate lamellipodia structure, and defining the efficiency of cell migration (Di Giusto et al., 2020). Ca2+ also affects the structure and dynamics of the cytoskeleton (Oertner and Matus, 2005; Hepler, 2016; Zhao et al., 2019; Maity et al., 2020), which further impacts the distribution and function of ion channel (Levina et al., 1994; Steele and Fedida, 2014; Vallés et al., 2015). The dependence of ion channel activity on Ca2+ and other biochemical signals provides additional regulatory mechanisms for cells to maintain ion homeostasis under environmental perturbation. For example, the contour plot in Figure 7G suggests that the cell volume is a non-monotonic function of the NKE activity for fixed NBC activity. If cells have active control mechanisms that vary NBC activity, cells can also follow a constant volume contour when NHE activity decreases through reducing NBC activity followed by increasing NBC activity. Such active mechanisms remain to be studied.
The active stress generated by cytoskeleton contraction, σa, plays an important role by setting the hydraulic pressure in the cytoplasm. The ionic fluxes in Equations 24–27 are all functions of ion concentrations, and therefore at steady state, it is ion channels, transporters, and pumps that set the overall cell solute concentration, and therefore the total osmolarity difference, ΔΠ. The cell volume is then determined by a ΔΠ and ΔP through force balance. Note that force balance would change depending on the cell surface curvature and cell geometry (Perez-Gonzalez et al., 2019). Therefore, this model could potentially explain how cells sense their size and geometry in different culture conditions, adhesion, substrate stiffness, and extracellular matrix, provided that we understand how cell active contraction is governed in these conditions. Indeed, it is likely that the cell actively controls σa together with ion fluxes and therefore achieves a desired cell volume. By obtaining activity levels of ion channels/transporters/pumps, cytoskeletal motors, and the cell adhesion geometry, we can directly predict the homeostatic cell volume and ultimately explain why different cell types have different volumes.
In this work, we have shown that the expression levels of ion channels, transporters, and pumps determine cells' ability to regulate their volumes. Cells in pathological conditions may alter the expressions or activities of ion channels and transporters compared to physiological conditions (Amith and Fliegel, 2013; Boedtkjer et al., 2013; Alka and Casey, 2014; Gould III et al., 2018; Khajah et al., 2018; Hwang et al., 2019). The ability to alter ion channel activity and expression allows the cell to adapt to environmental changes. The regulation of ion channel activity may be one of the hallmarks of diseases since diseased cells may develop alternative mechanisms for survival and motility. For example, it was shown that ion fluxes may be used by cancer cells to migrate in confined spaces (Stroka et al., 2014). Moreover, cell ionic content can directly influence protein translation and DNA replication (Li et al., 2020). Therefore, the mechanism of cell ionic homeostasis is of central importance in cell biology, and our model has implications for water- and osmosis-driven cell migration, and other biological problems of interest.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
YL and SS developed the model. YL ran the simulations. YL, XZ, and SS wrote the manuscript. All authors contributed to the article and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Alexander, R. T., and Grinstein, S. (2006). Na+/H+ exchangers and the regulation of volume. Acta Physiol. 187, 159–167. doi: 10.1111/j.1748-1716.2006.01558.x
Alka, K., and Casey, J. R. (2014). Bicarbonate transport in health and disease. IUBMB Life 66, 596–615. doi: 10.1002/iub.1315
Amith, S. R., and Fliegel, L. (2013). Regulation of the Na+/H+ exchanger (NHE1) in breast cancer metastasis. Cancer Res. 73, 1259–1264. doi: 10.1158/0008-5472.CAN-12-4031
Bachmann, O., Reichelt, D., Tuo, B., Manns, M. P., and Seidler, U. (2006). Carbachol increases Na+-HCO3- cotransport activity in murine colonic crypts in a , Ca2+/calmodulin-, and PKC-dependent manner. Am. J. Physiol. Gastrointest Liver Physiol. 291, G650–G657. doi: 10.1152/ajpgi.00376.2005
Bahari, S., Davarnejad, R., Bavi, O., and Mohammadi, S. V. (2020). Osmotic water permeability of aquaporin-1 under radial tensile and compressive stimuli. Desalination 492, 114524. doi: 10.1016/j.desal.2020.114524
Baker, P. F., and Willis, J. S. (1972). Inhibition of the sodium pump in squid axons by cardiac glycosides: dependence on extracellular ions and metabolism. J. Physiol. 224, 463–475. doi: 10.1113/jphysiol.1972.sp009905
Ben-Israel, A. (1966). A Newton-Raphson method for the solution of systems of equations. J. Math. Anal. Appl. 15, 243–252. doi: 10.1016/0022-247X(66)90115-6
Bennett, M. R., Farnell, L., and Gibson, W. G. (2008). A quantitative model of cortical spreading depression due to purinergic and gap-junction transmission in astrocyte networks. Biophys. J. 95, 5648–5660. doi: 10.1529/biophysj.108.137190
Blaesse, P., Airaksinen, M. S., Rivera, C., and Kaila, K. (2009). Cation-chloride cotransporters and neuronal function. Neuron 61, 820–838. doi: 10.1016/j.neuron.2009.03.003
Boedtkjer, E., Moreira, J. M. A., Mele, M., Vahl, P., Wielenga, V. T., Christiansen, P. M., et al. (2013). Contribution of Na+, HCO3–cotransport to cellular pH control in human breast cancer: a role for the breast cancer susceptibility locus NBCn1 (SLC4A7). Int. J. Cancer 132, 1288–1299. doi: 10.1002/ijc.27782
Bonar, P. T., and Casey, J. R. (2008). Plasma membrane Cl−/exchangers: structure, mechanism and physiology. Channels 2, 337–345. doi: 10.4161/chan.2.5.6899
Boron, W. F., and Boulpaep, E. L. (1989). The electrogenic Na/HCO3 cotransporter. Kidney Int. 36, 392–402. doi: 10.1038/ki.1989.208
Bueno-Orovio, A., Sánchez, C., Pueyo, E., and Rodriguez, B. (2014). Na/K pump regulation of cardiac repolarization: insights from a systems biology approach. Pflugers Arch. 466, 183–193. doi: 10.1007/s00424-013-1293-1
Burnham, J. A., and Stirling, C. E. (1984a). Quantitative localization of Na-K pump site in frog inner ear dark cells. Hear. Res. 13, 261–268. doi: 10.1016/0378-5955(84)90079-0
Burnham, J. A., and Stirling, C. E. (1984b). Quantitative localization of Na-K pump sites in the frog sacculus. J. Neurocytol. 13, 617–638. doi: 10.1007/BF01148082
Cala, P. M. (1980). Volume regulation by amphiuma red blood cells. the membrane potential and its implications regarding the nature of the ion-flux pathways. J. Gen. Physiol. 76, 683–708. doi: 10.1085/jgp.76.6.683
Casey, J. R., Grinstein, S., and Orlowski, J. (2010). Sensors and regulators of intracellular pH. Nat. Rev. Mol. Cell Biol. 11, 50. doi: 10.1038/nrm2820
Chang, G., Wang, J., Zhang, H., Zhang, Y., Wang, C., Xu, H., et al. (2014). Cd44 targets Na+/H+ exchanger 1 to mediate MDA-MB-231 cells' metastasis via the regulation of ERK1/2. Br. J. Cancer 110, 916–927. doi: 10.1038/bjc.2013.809
Chou, W.-H., Liu, K.-L., Shih, Y.-L., Chuang, Y.-Y., Chou, J., Lu, H.-F., et al. (2018). Ouabain induces apoptotic cell death through caspase-and mitochondria-dependent pathways in human osteosarcoma U-2 OS cells. Anticancer Res. 38, 169–178. doi: 10.21873/anticanres.12205
Di Giusto, G., Pizzoni, A., Rivarola, V., Beltramone, N., White, A., Ford, P., et al. (2020). Aquaporin-2 and Na+/H+ exchanger isoform 1 modulate the efficiency of renal cell migration. J. Cell. Physiol. 235, 4443–4454. doi: 10.1002/jcp.29320
Ericson, A. C., and Spring, K. R. (1982). Volume regulation by necturus gallbladder: apical Na+-H+ and Cl−- exchange. Am. J. Physiol. Cell Physiol. 243, C146–C150. doi: 10.1152/ajpcell.1982.243.3.C146
Gadsby, D. C. (2009). Ion channels versus ion pumps: the principal difference, in principle. Nat. Rev. Mol. Cell. Biol. 10, 344–352. doi: 10.1038/nrm2668
Gadsby, D. C., Kimura, J., and Noma, A. (1985). Voltage dependence of Na/K pump current in isolated heart cells. Nature 315, 63–65. doi: 10.1038/315063a0
Gao, J., Mathias, R. T., Cohen, I. S., and Baldo, G. J. (1995). Two functionally different Na/K pumps in cardiac ventricular myocytes. J. Gen. Physiol. 106, 995–1030. doi: 10.1085/jgp.106.5.995
Garty, H., and Palmer, L. G. (1997). Epithelial sodium channels: function, structure, and regulation. Physiol. Rev. 77, 359–396. doi: 10.1152/physrev.1997.77.2.359
Gatti, J. L., and Christen, R. (1985). Regulation of internal pH of sea urchin sperm. a role for the Na/K pump. J. Biol. Chem. 260, 7599–7602. doi: 10.1016/S0021-9258(17)39650-3
Giambelluca, M. S., Ciancio, M. C., Orlowski, A., Gende, O. A., Pouliot, M., and Aiello, E. A. (2014). Characterization of the Na+/cotransport in human neutrophils. Cell. Physiol. Biochem. 33, 982–990. doi: 10.1159/000358669
Gitlin, I., Carbeck, J. D., and Whitesides, G. M. (2006). Why are proteins charged? networks of charge–charge interactions in proteins measured by charge ladders and capillary electrophoresis. Angew. Chem. Int. Ed. 45, 3022–3060. doi: 10.1002/anie.200502530
Gould III, H. J., Norleans, J., Ward, T. D., Reid, C., and Paul, D. (2018). Selective lysis of breast carcinomas by simultaneous stimulation of sodium channels and blockade of sodium pumps. Oncotarget 9, 15606. doi: 10.18632/oncotarget.24581
Grinstein, S., Furuya, W., and Cragoe Jr, E. J. (1986). Volume changes in activated human neutrophils: the role of Na+/H+ exchange. J. Cell. Physiol. 128, 33–40. doi: 10.1002/jcp.1041280107
Gross, E., Hawkins, K., Abuladze, N., Pushkin, A., Cotton, C. U., Hopfer, U., et al. (2001). The stoichiometry of the electrogenic sodium bicarbonate cotransporter NBC1 is cell-type dependent. J. Physiol. 531, 597–603. doi: 10.1111/j.1469-7793.2001.0597h.x
Hepler, P. K. (2016). The cytoskeleton and its regulation by calcium and protons. Plant Physiol. 170, 3–22. doi: 10.1104/pp.15.01506
Hoffman, J. F. (1969). The interaction between tritiated ouabain and the Na-K pump in red blood cells. J. Gen. Physiol. 54, 343. doi: 10.1085/jgp.54.1.343
Hughes, A. L. H., Pakhomova, A., and Brown, P. D. (2010). Regulatory volume increase in epithelial cells isolated from the mouse fourth ventricle choroid plexus involves Na+–H+ exchange but not Na+–K+–2Cl− cotransport. Brain Res. 1323, 1–10. doi: 10.1016/j.brainres.2009.12.094
Hwang, S., Shin, D. M., and Hong, J. H. (2019). Drug repurposing as an antitumor agent: Disulfiram-mediated carbonic anhydrase 12 and anion exchanger 2 modulation to inhibit cancer cell migration. Molecules 24, 3409. doi: 10.3390/molecules24183409
Jiang, H., and Sun, S. X. (2013). Cellular pressure and volume regulation and implications for cell mechanics. Biophys. J. 105, 609–619. doi: 10.1016/j.bpj.2013.06.021
Karmazyn, M. (2013). NHE-1: still a viable therapeutic target. J. Mol. Cell. Cardiol. 61, 77–82. doi: 10.1016/j.yjmcc.2013.02.006
Kay, A. R. (2017). How cells can control their size by pumping ions. Front. Cell Dev. Biol. 5, 41. doi: 10.3389/fcell.2017.00041
Khajah, M. A., Mathew, P. M., and Luqmani, Y. A. (2018). Na+/K+ ATPase activity promotes invasion of endocrine resistant breast cancer cells. PLoS ONE 13:e0193779. doi: 10.1371/journal.pone.0193779
Klein, M., Seeger, P., Schuricht, B., Alper, S. L., and Schwab, A. (2000). Polarization of Na+/H+ and Cl−/ exchangers in migrating renal epithelial cells. J. Gen. Physiol. 115, 599–608. doi: 10.1085/jgp.115.5.599
Landowne, D., and Ritchie, J. M. (1970). The binding of tritiated ouabain to mammalian non-myelinated nerve fibres. J. Physiol. 207, 529–537. doi: 10.1113/jphysiol.1970.sp009077
Lang, F., Busch, G. L., Ritter, M., Volkl, H., Waldegger, S., Gulbins, E., et al. (1998). Functional significance of cell volume regulatory mechanisms. Physiol. Rev. 78, 247–306. doi: 10.1152/physrev.1998.78.1.247
Lauritzen, G., Stock, C.-M., Lemaire, J., Lund, S. F., Jensen, M. F., Damsgaard, B., et al. (2012). The Na+/H+ exchanger NHE1, but not the Na+, HCO3-cotransporter NBCn1, regulates motility of MCF7 breast cancer cells expressing constitutively active ErbB2. Cancer Lett. 317, 172–183. doi: 10.1016/j.canlet.2011.11.023
Levina, N. N., Lew, R. R., and Heath, I. B. (1994). Cytoskeletal regulation of ion channel distribution in the tip-growing organism saprolegnia ferax. J. Cell Sci. 107, 127–134. doi: 10.1242/jcs.107.1.127
Li, Y., Konstantopoulos, K., Zhao, R., Mori, Y., and Sun, S. X. (2020). The importance of water and hydraulic pressure in cell dynamics. J. Cell Sci. 133, jcs240341. doi: 10.1242/jcs.240341
Li, Y., Mori, Y., and Sun, S. X. (2015). Flow-driven cell migration under external electric fields. Phys. Rev. Lett. 115, 268101. doi: 10.1103/PhysRevLett.115.268101
Li, Y. and Sun, S. X. (2018). Transition from actin-driven to water-driven cell migration depends on external hydraulic resistance. Biophys. J. 114, 2965–2973. doi: 10.1016/j.bpj.2018.04.045
Li, Y., Yao, L., Mori, Y., and Sun, S. X. (2019). On the energy efficiency of cell migration in diverse physical environments. Proc. Natl. Acad. Sci. U.S.A. 116, 23894–23900. doi: 10.1073/pnas.1907625116
Loitto, V.-M., Forslund, T., Sundqvist, T., Magnusson, K.-E., and Gustafsson, M. (2002). Neutrophil leukocyte motility requires directed water influx. J. Leukoc. Biol. 71, 212–222. doi: 10.1189/jlb.71.2.212
Maeno, E., Takahashi, N., and Okada, Y. (2006). Dysfunction of regulatory volume increase is a key component of apoptosis. FEBS Lett. 580, 6513–6517. doi: 10.1016/j.febslet.2006.10.074
Mahnensmith, R. L., and Aronson, P. S. (1985). The plasma membrane sodium-hydrogen exchanger and its role in physiological and pathophysiological processes. Circ. Res. 56, 773–788. doi: 10.1161/01.RES.56.6.773
Maity, D., Bera, K., Li, Y., Ge, Z., Chen, Y., Konstantopoulos, K., et al. (2020). Extracellular hydraulic resistance enhances cell migration. doi: 10.21203/rs.3.rs-108471/v1
Marino, A. A., Iliev, I. G., Schwalke, M. A., Gonzalez, E., Marler, K. C., and Flanagan, C. A. (1994). Association between cell membrane potential and breast cancer. Tumor Biol. 15, 82–89. doi: 10.1159/000217878
Martinac, B. (2004). Mechanosensitive ion channels: molecules of mechanotransduction. J. Cell Sci. 117, 2449–2460. doi: 10.1242/jcs.01232
Mori, Y. (2012). Mathematical properties of pump-leak models of cell volume control and electrolyte balance. J. Math. Biol. 65, 875–918. doi: 10.1007/s00285-011-0483-8
Oertner, T. G., and Matus, A. (2005). Calcium regulation of actin dynamics in dendritic spines. Cell Calcium 37, 477–482. doi: 10.1016/j.ceca.2005.01.016
Ozu, M., Dorr, R. A., Gutiérrez, F., Politi, M. T., and Toriano, R. (2013). Human AQP1 is a constitutively open channel that closes by a membrane-tension-mediated mechanism. Biophys. J. 104, 85–95. doi: 10.1016/j.bpj.2012.11.3818
Pang, V., Counillon, L., Lagadic-Gossmann, D., Poet, M., Lacroix, J., Sergent, O., et al. (2012). On the role of the difference in surface tensions involved in the allosteric regulation of NHE-1 induced by low to mild osmotic pressure, membrane tension and lipid asymmetry. Cell Biochem. Biophys. 63, 47–57. doi: 10.1007/s12013-012-9340-7
Pchejetski, D., Taurin, S., Der Sarkissian, S., Lopina, O. D., Pshezhetsky, A. V., Tremblay, J., et al. (2003). Inhibition of Na+, K+-ATPase by ouabain triggers epithelial cell death independently of inversion of the [Na+]i/[K+]i ratio. Biochem. Biophys. Res. Commun. 301, 735–744. doi: 10.1016/S0006-291X(02)03002-4
Perez-Gonzalez, N. A., Rochman, N. D., Yao, K., Tao, J., Le, M.-T. T., Flanary, S., et al. (2019). YAP and TAZ regulate cell volume. J. Cell Biol. 218, 3472–3488. doi: 10.1083/jcb.201902067
Rolver, M. G., Elingaard-Larsen, L. O., Andersen, A. P., Counillon, L., and Pedersen, S. F. (2020). Pyrazine ring-based Na+/H+ exchanger (NHE) inhibitors potently inhibit cancer cell growth in 3D culture, independent of NHE1. Sci. Rep. 10, 1–17. doi: 10.1038/s41598-020-62430-z
Romero, M. F., Chen, A.-P., Parker, M. D., and Boron, W. F. (2013). The SLC4 family of bicarbonate () transporters. Mol. Aspects Med. 34, 159–182. doi: 10.1016/j.mam.2012.10.008
Rosengren, S., Henson, P. M., and Worthen, G. S. (1994). Migration-associated volume changes in neutrophils facilitate the migratory process in vitro. Am. J. Physiol. Cell Physiol. 267, C1623–C1632. doi: 10.1152/ajpcell.1994.267.6.C1623
Ruiz, O. S., Qiu, Y.-Y., Cardoso, L. R., and Arruda, J. A. L. (1998). Regulation of the renal Na-HCO3 cotransporter: IX. modulation by insulin, epidermal growth factor and carbachol. Regul. Pept. 77, 155–161. doi: 10.1016/S0167-0115(98)00115-3
Ruiz, O. S., Qiu, Y.-Y., Cardoso, L. R., and Arruda, J. A. L. (1999). Regulation of the renal Na-HCO3 cotransporter: X. role of nitric oxide and intracellular calcium. Miner Electrolyte Metab. 25, 171–177. doi: 10.1159/000057441
Ruiz, O. S., Qiu, Y.-Y., Wang, L.-J., and Arruda, J. A. L. (1996). Regulation of the renal Na-HCO3 cotransporter: V. mechanism of the inhibitory effect of parathyroid hormone. Kidney Int. 49, 396–402. doi: 10.1038/ki.1996.58
Russell, J. M. (2000). Sodium-Potassium-Chloride cotransport. Physiol. Rev. 80, 211–276. doi: 10.1152/physrev.2000.80.1.211
Scholz, W., Albus, U., Counillon, L., Gögelein, H., Lang, H.-J., Linz, W., et al. (1995). Protective effects of HOE642, a selective sodium-hydrogen exchange subtype 1 inhibitor, on cardiac ischaemia and reperfusion. Cardiovasc. Res. 29, 260–268. doi: 10.1016/S0008-6363(96)88579-8
Shi, Y. (2013). Common folds and transport mechanisms of secondary active transporters. Annu. Rev. Biophys. 42, 51–72. doi: 10.1146/annurev-biophys-083012-130429
Shieh, C.-C., Coghlan, M., Sullivan, J. P., and Gopalakrishnan, M. (2000). Potassium channels: molecular defects, diseases, and therapeutic opportunities. Pharmacol. Rev. 52, 557–594. Available online at: https://pharmrev.aspetjournals.org/content/52/4/557
Steele, D. F., and Fedida, D. (2014). Cytoskeletal roles in cardiac ion channel expression. Biochim. Biophys. Acta Biomembr. 1838, 665–673. doi: 10.1016/j.bbamem.2013.05.001
Sterling, D., and Casey, J. R. (1999). Transport activity of AE3 chloride/bicarbonate anion-exchange proteins and their regulation by intracellular pH. Biochem. 344, 221–229. doi: 10.1042/bj3440221
Stock, C., Gassner, B., Hauck, C. R., Arnold, H., Mally, S., Eble, J. A., et al. (2005). Migration of human melanoma cells depends on extracellular pH and Na+/H+ exchange. J. Physiol. 567, 225–238. doi: 10.1113/jphysiol.2005.088344
Stroka, K. M., Jiang, H., Chen, S.-H., Tong, Z., Wirtz, D., Sun, S. X., et al. (2014). Water permeation drives tumor cell migration in confined microenvironments. Cell 157, 611–623. doi: 10.1016/j.cell.2014.02.052
Tao, J., Li, Y., Vig, D. K., and Sun, S. X. (2017). Cell mechanics: a dialogue. Rep. Prog. Phys. 80, 036601. doi: 10.1088/1361-6633/aa5282
Thomas, M. R., and O'Shea, E. K. (2005). An intracellular phosphate buffer filters transient fluctuations in extracellular phosphate levels. Proc. Natl. Acad. Sci. U.S.A. 102, 9565–9570. doi: 10.1073/pnas.0501122102
Valente, R. C., Capella, L. S., Monteiro, R. Q., Rumjanek, V. M., Lopes, A. G., and Capella, M. A. M. (2003). Mechanisms of ouabain toxicity. FASEB J. 17, 1700–1702. doi: 10.1096/fj.02-0937fje
Vallés, P. G., Bocanegra, V., Lorenzo, A. G., and Costantino, V. V. (2015). Physiological functions and regulation of the Na+/H+ exchanger NHE1 in renal tubule epithelial cells. Kidney Blood Press. Res. 40, 452–466. doi: 10.1159/000368521
Weinstein, A. M. (1986). A mathematical model of the rat proximal tubule. Am. J. Physiol. Renal Physiol. 250, F860–F873. doi: 10.1152/ajprenal.1986.250.5.F860
Weinstein, A. M. (2013). “Sodium and chloride transport: proximal nephron,” in The Kidney: Physiology and Pathophysiology, 5th Edn, (London; Waltham, MA; San Diego, CA: Academic Press). 1081–1141. doi: 10.1016/B978-0-12-381462-3.00033-1
Yamada, H., Seki, G., Taniguchi, S., Uwatoko, S., Nosaka, K., Suzuki, K., et al. (1996). Roles of Ca2+ and PKC in regulation of acid/base transport in isolated proximal tubules. Am. J. Physiol. Renal Physiol. 271, F1068–F1076. doi: 10.1152/ajprenal.1996.271.5.F1068
Yellin, F., Li, Y., Sreenivasan, V. K. A., Farrell, B., Johny, M., Yue, D., et al. (2018). Electromechanics and volume dynamics in non-excitable tissue cells. Biophys. J. 114, 2231–2242. doi: 10.1016/j.bpj.2018.03.033
Yu, H.-G., McLaughlin, S., Newman, M., Brundage, K., Ammer, A., Martin, K., et al. (2017). Altering calcium influx for selective destruction of breast tumor. BMC Cancer 17, 169. doi: 10.1186/s12885-017-3168-x
Keywords: cell volume regulation, pH, hydrogen, bicarbonate, sodium-hydrogen exchanger, chloride-bicarbonate exchanger, sodium-bicarbonate cotransporter, sodium-potassium exchanger
Citation: Li Y, Zhou X and Sun SX (2021) Hydrogen, Bicarbonate, and Their Associated Exchangers in Cell Volume Regulation. Front. Cell Dev. Biol. 9:683686. doi: 10.3389/fcell.2021.683686
Received: 21 March 2021; Accepted: 31 May 2021;
Published: 24 June 2021.
Edited by:
Biao Kong, Fudan University, ChinaReviewed by:
Ira Kurtz, University of California, Los Angeles, United StatesYoshitaka Nakayama, Victor Chang Cardiac Research Institute, Australia
Ricardo Dorr, Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Argentina
Copyright © 2021 Li, Zhou and Sun. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yizeng Li, eWxpNTRAa2VubmVzYXcuZWR1; Sean X. Sun, c3N1bkBqaHUuZWR1
 Yizeng Li
Yizeng Li Xiaohan Zhou
Xiaohan Zhou Sean X. Sun
Sean X. Sun