Cellular Membranes, a Versatile Adaptive Composite Material

Cellular membranes belong to the most vital yet least understood biomaterials of live matter. For instance, its biomechanical requirements substantially vary across species and subcellular sites, raising the question how membranes manage to adjust to such dramatic changes. Central to its adaptability at the cell surface is the interplay between the plasma membrane and the adjacent cell cortex, forming an adaptive composite material that dynamically adjusts its mechanical properties. Using a hypothetical composite material, we identify core challenges, and discuss how cellular membranes solved these tasks. We further muse how pathological changes in material properties affect membrane mechanics and cell function, before closing with open questions and future challenges arising when studying cellular membranes.

Introduction

The cellular membrane is one of the most vital and complex biomaterials in live matter. It is therefore not surprising that it has over the last decades been the subject of extensive studies, giving insights into a fascinating world of regulatory processes that control localization and activity of proteins and lipids in cellular membranes (Singer and Nicolson, 1972; Edidin et al., 1991; Eggeling et al., 2009). These studies established that biomechanical requirements vary across species and subcellular sites, indicative of tremendous diversity and adaptability (Vasanji et al., 2004; van Meer et al., 2008). Yet, despite substantial advancements over the last few decades, we are still lacking a comprehensive understanding of membrane mechanics at the cell surface.

Individual lipids spontaneously self-assemble into a bilayer that is then subject to thermal fluctuations (Faucon et al., 1989), changes in local lipid composition (Estep et al., 1979), and sustained membrane deformations (Baumgart et al., 2003). Besides lipids, cellular membranes further contain proteins that not only influence the local lipid environment (Contreras et al., 2011; Laganowsky et al., 2014) and mechanical membrane properties (Shi et al., 2018), but also render the membrane transmissive to incoming stimuli. These signals can alter, among many others things, membrane potential (Nernst, 1889), shape (Chen et al., 2016; Graber et al., 2017) and lipid composition (Sugimoto et al., 1984). Importantly, signal-induced changes also affect localization and activity of membrane-bound (Carpenter et al., 1978) and cytosolic (Hancock et al., 1989) proteins. One principal target for such signals is the membrane-associated cortical cytoskeleton (Svitkina, 2020). Possibly the most striking of its many features is the ability of the cytoskeleton to generate mechanical push and pull forces (Peskin et al., 1993; Huxley and Simmons, 1971). Hence, by coupling membranes to the adjacent cell cortex yields a composite material that is equally able to sense and respond to external stimuli.

In this review, we will explore the intricate mechanical properties of this adaptive composite material. Readers interested in learning more on signaling across cellular membranes or cytoskeletal mechanics, we refer to the many excellent reviews written elsewhere (Huber et al., 2013; Lundberg and Borner, 2019; Svitkina, 2020). We begin by defining core mechanical terms, before investigating the material properties of the cell membrane. Next, we show how these properties are affected by its manifold interaction with the cell cortex under physiological and pathophysiological conditions. We conclude by pointing out future challenges toward understanding the mechanical properties of this exciting biomaterial.

Fundamental Cell Mechanics

The plasma membrane and the cortical cytoskeleton jointly form a composite material with unique biomechanical features (Nicolson, 2014). To fully appreciate this elaborate structure, we first need to introduce a number of terms that will repeatedly show up over the following pages. Let’s begin by answering what a composite material actually is. This term – originating from manufacturing engineering – depicts two or more connected materials, where the resulting compound exhibits properties that neither of the individual components by itself possesses (Westkämper and Warnecke, 2011). The material properties of the composite are a function of the individual material properties of its components, their geometry and its interface (i.e., the way those materials are connected). Therefore, by changing one of those parameters the overall properties of the composite will be affected. If this happens by design, for instance in response to a stimulus, the material is referred to as an adaptive composite material. For biological membranes, the main components of this composite material are the plasma membrane (PM) that encapsulates the cell, the cell cortex lining the cytosolic site of the PM, and the membrane-cortex-attachment (MCA) that describes the interface connecting PM and cell cortex. In the following, we refer to the composite material emerging from the combination of PM, MCA and cell cortex as “cell surface.”

Having introduced the basic terms, we next need to recapitulate the essential material properties. For small strains, any membrane deformation can be regarded as the superposition of three basic types of deformation: pure stretch, shear and bending (Figure 1A). A membrane subject to a force acting normal to its edges will experience an extensional stress and an area stretch. The resistance against this stretch is called the stretch modulus K_e. Similarly, a membrane that is subject to forces acting parallel to its edges will experience shear stress, whereby the resistance against the shear deformation is given by the shear modulus K_s. While stretch and shear modulus relate strain to a certain stress, the bending stiffness K_B relates a curvature to a bending moment (i.e., the energy necessary to bend the membrane to its current state). The deformations described so far are purely elastic, and therefore not time dependent. However, biomaterials often exhibit fluid-like behavior, including time dependent plastic deformation. Therefore, we need to introduce a fourth material property, the viscosity η (Figure 1A, right). It depicts the resistance of a fluid against shear stress at a specific shear velocity $\frac{du}{dy}$. In contrast to the shear modulus, the viscosity does not relate stress to strain, but to the rate of deformation. By changing one or a combination of these four essential material properties mechanical adaptation can be achieved. Readers interested in learning more about this topic, we refer to work written elsewhere (Kamm and Grodzinsky, 2015).

FIGURE 1

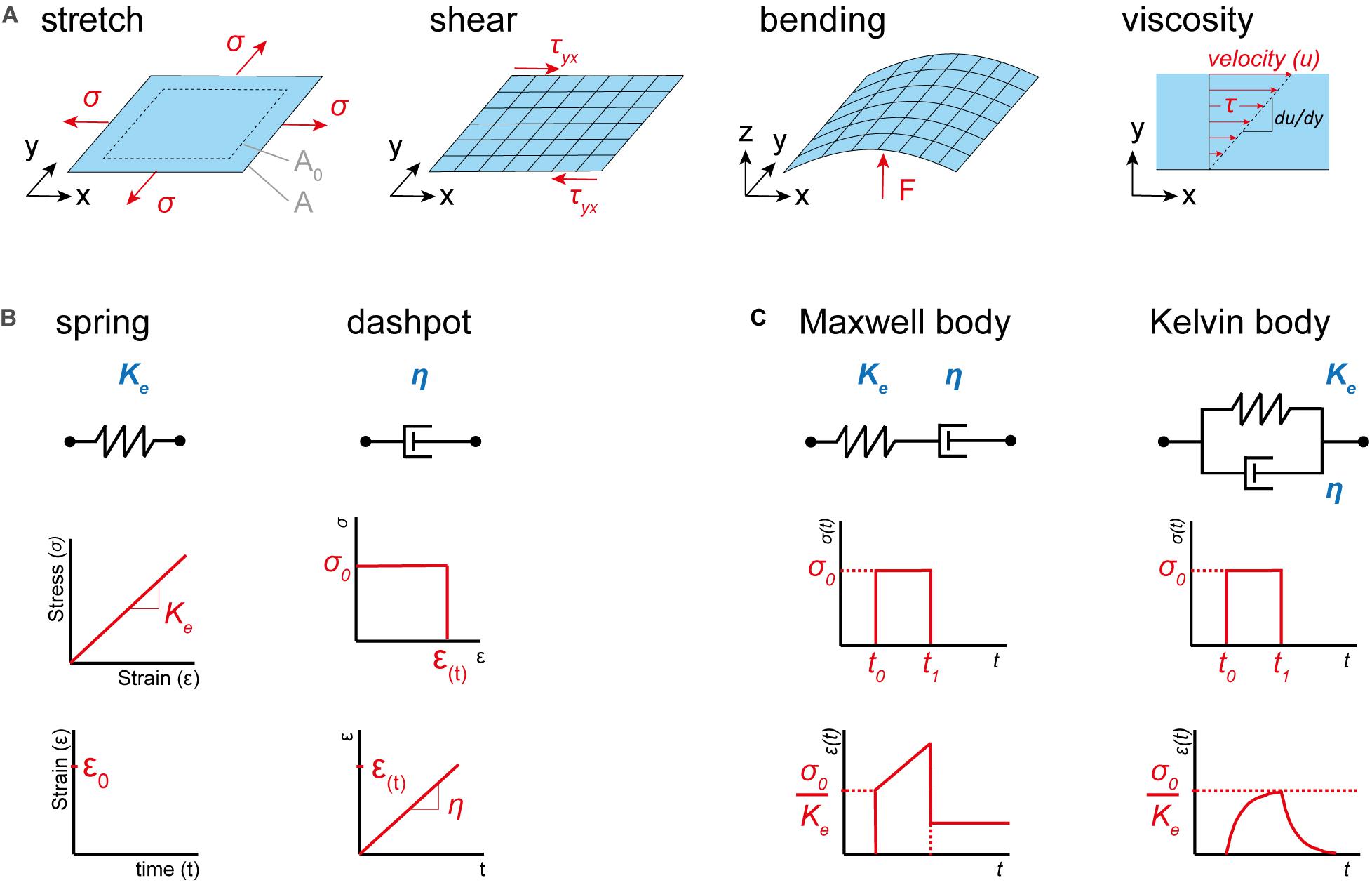
Figure 1. Basic material properties and deformation types. (A) From left to right, membrane exposed to uniform extensional stress σ, which is acting normal to its edges, causes an increase of the area (from A₀ to A). Membrane exposed to forces acting parallel to its surface inducing shear stress τ_yx. Membrane exposed to a point load (F) acting perpendicular to its surface, which is inducing curvature and therefore a bending moment. Viscosity η, the resistance of a fluid against shear stress τ given at a specific shear velocity $\frac{du}{dy}$. (B) Basic properties of a purely elastic (spring, left) and viscous (dashpot, right) material. A purely elastic material always returns to its original state after deformation and exhibits a linear relationship between stress and strain, while a purely viscous material exhibits plastic (permanent) deformations and a linear relationship between stress and shear velocity. (C) Models of viscoelastic materials. Maxwell body (left) consisting of a dashpot and a spring in series displays, like a viscoelastic fluid, permanent deformation after the load is removed. Kelvin body (right) returns, like a viscoelastic solid, to its original state when the load is removed. Images adapted from Seidel et al. (2009) and Kamm and Grodzinsky (2015).

Finally, let’s recapitulate the types of deformations a material can experience. The properties of a material determine its response to a mechanical stimulus. In its most basic form, such a response can be purely elastic or viscous. An elastic material returns to its original shape upon distortion, while a viscous material stays distorted after the load is released. This behavior can be envisioned as a spring (elastic) or dashpot (viscous), respectively (Figure 1B). However, many materials display a viscoelastic response, where viscous and elastic properties are coupled. Basic models for such a behavior are the Maxwell and the Kelvin body (Figure 1C). In a Maxwell body, elastic and viscous elements are paired in series, thus leading to an elastic response for fast distortions, while slowly applied load is captured in a plastic manner. In contrast, the Kelvin body displays elastic and viscous elements in parallel. Hence, under stress the deformation will over time approach the strain response of the elastic component, whereby it is slowed down by the viscous element. Consequently, the Maxwell body is capable of plastic deformation (i.e., viscoelastic fluid), while the Kelvin body will always return to its original shape when the load is released (i.e., viscoelastic solid). As above, we refer readers interested in this topic to work written elsewhere (Meyers and Chawla, 2010).

Engineering a Hypothetical Biomimetic Membrane

Inspired by the famous quote “what I cannot create, I do not understand” from Richard Feynman, we will attempt on the following pages to conceive a hypothetical biomimetic membrane with the following features: It should reliably separates internal from external space. The boundary should further be flexible, tunable, and able to transiently change its material properties in response to incoming signals. For simplicity and didactic reasons, we designed this as an engineering challenge (Supplementary Figure S1 and Supplementary Material), sequentially expanding the number of requirements (i.e., requested functions) of the hypothetical material. In each section, we begin by musing how such a biomimetic structure could be designed, before exploring in detail how this has been accomplished in biological systems.

The Lipid Bilayer, the Core Module of Cellular Membranes

The most fundamental function of our biomimetic material is to reliably separate the interior from the external environment. To achieve such a continuous barrier in an aqueous solution, a biomimetic material must be able to oppose differences in osmotic and hydrostatic pressure without leakage. Ideally, the material would spontaneously assemble, thus limiting the need for energy and control systems.

In cellular membranes, amphipathic lipids spontaneously self-assemble into a 5–7 nm thick lipid bilayer, with the hydrophobic carbohydrate chains facing toward the inside (Huang and Thompson, 1965). This occurs to minimize the free energy of water arising from continuous formation and disassembly of hydrogen bonds (Figure 2A, right). Pure lipid bilayers are reported to have a stretch modulus K_e in the range of 100 to 1000 mN/m (Waugh and Evans, 1979), with a value of ∼200 mN/m as most widely accepted (Rawicz et al., 2000). Considering a pure lipid bilayer with a possible areal stretch of 5% (Hallett et al., 1993), and neglecting thermal fluctuation (Evans and Rawicz, 1990), Eq. 2.5 in Box 1 gives us a rupture tension of 10 mN/m. This value is in accordance to published reports that measured a rupture tensions of 3 to 10 mN/m, depending on the lipid composition of the bilayer (Olbrich et al., 2000). Following Laplace’s law.

FIGURE 2

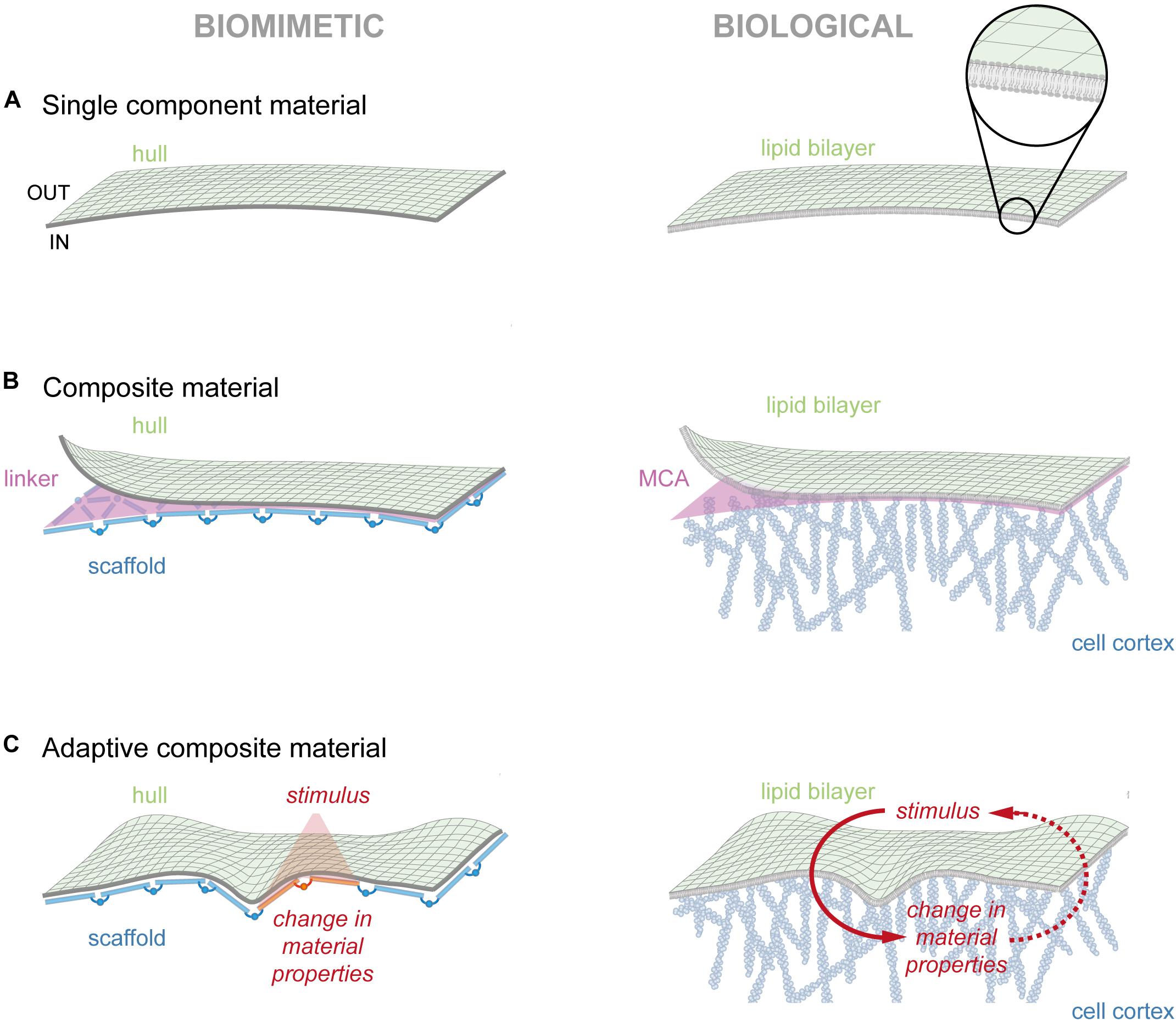
Figure 2. Modules of cellular membrane. (A) To the left, hypothetical biomimetic membrane that separates the inside from outside. To the right, the lipid bilayer presents the outermost structure of the cell membrane. Magnification depicts the 5–7 nm thick bilayer composed of individual lipids. (B) To the left, hypothetical composite material composed of a flexible hull associated to a rigid scaffold. To the right, the plasma membrane is tightly coupled to the cell cortex, creating a composite material. Individual actin proteins assemble into filaments that are facing the cell membrane with the growing end. (C) To the left, hypothetical adaptive composite material that changes material properties upon an external stimulus (red). To the right, the membrane/cortex continuum readily responds to external stimuli (red), reminiscent of an adaptive composite material. Note that changes in actin dynamics can also serve as signal (red, dotted line).

Box 1. Physics at the Cell Surface.

In the following, we consider the cell surface as a plate or shell encapsulating the cytoplasm, following the description by Kamm and Grodzinsky (2015). In general, any deformation can be envisioned as the superposition of three fundamental types of deformation: stretch, bending and shear. Surface tension is defined as the derivation of energy with respect to area, meaning the energy needed to stretch the plate by a certain amount is given by.

$$N=\mathrm{\sigma }h=\frac{Eh}{1-\mathrm{\nu }}\mathrm{\epsilon }=\frac{Eh}{2(1-\mathrm{\nu })}\frac{\mathrm{\Delta }A}{A_0}=K_e\frac{\mathrm{\Delta }A}{A_0},(2.1)$$

where σ depicts the uniform normal stress, N the in plane tension in force per unit length (N/m), E the elastic modulus (Young’s modulus), ν the Poisson ratio, h the plate thickness, ε the strain and K_e the area stretch modulus defined as K_e = $\frac{Eh}{2(1-\mathrm{\nu })}$. The energy needed to bend a plate of the thickness h in one dimension given by

$$M_x=E_{bend}=-\frac{E{h}^3}{12(1-{\mathrm{\nu }}^2)}\frac{{\mathrm{\delta }}^2{u}_z}{\mathrm{\delta }{x}^2}=-K_B\frac{{\mathrm{\delta }}^2{u}_z}{\mathrm{\delta }{x}^2},(2.2)$$

where $\frac{{\mathrm{\delta }}^2{u}_z}{\mathrm{\delta }{x}^2}$ depicts the deflection of the plate in z direction and K_B the bending stiffness defined as $K_B=\frac{E{h}^3}{12(1-{\mathrm{\nu }}^2)}$. Elastic materials exhibit resistance against shear deformation arising when the lateral surfaces of the plate are exposed to two different surface tensions. This resistance is given by the shear modulus K_s, with the unit N/m, relating the arising shear force per unit length N_xy to the amount of shear deformation, the strain ε_xy. The shear force per unit length is the product of the shear stress τ_xy times the plate thickness h, which can also be described by the shear modulus G and the shear deformation ε_xy. Corresponding to Eq. 2.2 the shear modulus can be expressed by Young’s modulus E and the Poisson ratio υ:

$${\mathrm{\sigma }}_{xy}={\mathrm{\tau }}_{xy}h=2G{\mathrm{\epsilon }}_{xy}=\frac{E}{1+\mathrm{\nu }}{\mathrm{\epsilon }}_{xy}=K_s{\mathrm{\epsilon }}_{xy},(2.3)$$

Considering the cells surrounding, we must apply for thermal fluctuation by adding a random force term ξ(t) and, for the damping of membrane movement by the extracellular fluid, we add a term in form of ${\mathrm{\eta }}_e\frac{\mathrm{\delta }{u}_z}{\mathrm{\delta }(t)}$ with the effective viscosity of the surrounding fluid η_e dissipating its energy. Adding thermal fluctuation and energy dissipation due to external fluid damping, neglecting shear stress, yields

$$\mathrm{\Delta }p+\xi (t)=K_B\left(\frac{{\mathrm{\delta }}^4{u}_z}{\mathrm{\delta }{x}^4}+2\frac{{\mathrm{\delta }}^4{u}_z}{\mathrm{\delta }{x}^2\mathrm{\delta }{y}^2}+\frac{{\mathrm{\delta }}^4{u}_z}{\mathrm{\delta }{y}^4}\right)-N\left(\frac{{\mathrm{\delta }}^2{u}_z}{\mathrm{\delta }{x}^2}+\frac{{\mathrm{\delta }}^2{u}_z}{\mathrm{\delta }{y}^2}\right)+{\mathrm{\eta }}_e\frac{\mathrm{\delta }{u}_z}{\mathrm{\delta }t},(2.4)$$

which is giving us a more complete picture of the cell membrane behavior. Note that the principle of superposition is only valid for small strains, where linearization is appropriate (e.g., small discretization of time and space). Neglecting all terms except of pressure and surface tension – as it can be appropriate for small curvatures, Eq. 2.4 gives rise to the famous Laplace equation.

$$\mathrm{\Delta }p=-N\left(\frac{{\mathrm{\delta }}^2{u}_z}{\mathrm{\delta }{x}^2}+\frac{{\mathrm{\delta }}^2{u}_z}{\mathrm{\delta }{y}^2}\right)\cong N\left(\frac{1}{R_1}+\frac{1}{R_2}\right).(2.5)$$

Biomaterials often exhibit viscoelastic properties. Therefore, we also have to consider the materials viscosity η. In contrast to the elastic modulus E, the viscosity relates the stress not to the deformation of the material but to the rate of change of the deformation $\frac{d\mathrm{\epsilon }(t)}{dt}$. One way to describe the properties of a viscoelastic solid is the Kelvin-Voigt model (see Figure 2C), which can be envisioned by an elastic spring and a viscous damper connected in parallel. The elastic properties of the material are given by the elastic modulus E, and the viscous properties by the viscosity η. The experienced stress σ is then given by

$$\mathrm{\sigma }(t)=E\mathrm{\epsilon }(t)+\mathrm{\eta }\frac{d\mathrm{\epsilon }(t)}{dt}.(2.6)$$

However, the cell surface exhibits the ability of plastic deformation and therefore behaves more like a fluid. Regarding the cell cortex this property arises from the turnover rate of the linking proteins. In contrast to a viscoelastic solid, a viscoelastic fluid can be modeled by a Maxwell body, which can be envisioned by an elastic spring and viscous damper connected in series (see Figure 2C). The experienced stress σ is here given by

$$\mathrm{\sigma }(\text{t})+\frac{\mathrm{\eta }}{E}\frac{\mathrm{\sigma }(\text{t})}{\text{dt}}=\mathrm{\eta }\frac{d\mathrm{\epsilon }(t)}{dt}.(2.7)$$

$$\mathrm{\Delta }p=\frac{2N}{R},(1.1)$$

where N depicts the surface tension and R the principal radius of curvature, we find that the PM can therefore withstand a pressure difference Δp of up to 0.2 bar or 20 kPa assuming a radius of 1 μm before ripping, a remarkable performance given its thickness of only 5–7 nm.

With respect to the material properties mentioned at the beginning of the section, the lipid bilayer already provides excellent stretch resistance. However, it is readily deformed in the presence of forces within the plane (i.e., low shear resistance K_s) or perpendicular to it (i.e., low bending rigidity K_B). Hence, to strengthen the structural integrity of the boundary, and render it tunable, additional support is required.

The Membrane-Cortex Interface Forms a Composite Material

For our hypothetical biomimetic material, the mechanical properties of the hull could be further improved by combining it with a self-assembling scaffold that binds with high affinity to the flexible hull to form a tri-partite composite: hull, supporting scaffold and the connecting glue (Figure 2B, left). As one can easily imagine, size, density and rigidity of the scaffold units will directly affect the material properties of the composite. However, these properties equally rely on the assembly pattern of the scaffold along the hull. For instance, scaffolds formed from elongated structures that align along a pre-defined axis will yield polarized (i.e., different) bending moduli along the principal curvatures. In contrast, an omnidirectional assembly of the same structures will produce isotropic mechanical properties. Besides the form of the supporting structure, the spacing between individual subunits also influences the bending stiffness (Naghieh et al., 2018). One such example is agarose gel, which exhibits substantially higher resistance to shear stresses than its primary component water. Hence, by wisely designing the geometry of a supporting structure, or the composition of matrix particles, materials with very diverse mechanical properties may emerge.

A lipid bilayer substantially differs from the cell surface, which is not only stiffer but also displays slower lateral diffusion (Edidin et al., 1991; Shi et al., 2018). This clearly posits the presence of an additional supportive material that interacts with the lipid bilayer. In cells, this composite material is formed through the interaction of the plasma membrane with the cell cortex (Figure 2B, right). The cell cortex consist of straight and branched actin filaments that are crosslinked among each other (Mullins et al., 1998), forming a 100–200 nm thick layer at the inner side of the PM (Chugh and Paluch, 2018). In addition to actin, the cell cortex contains, to a lesser degree, intermediate filaments and microtubules (Koning et al., 2008; Singh et al., 2018), providing the ability to exert mechanical forces and change local material properties. Membrane association of the cell cortex is achieved through a specialized protein group, the FERM domain proteins (named after its founding members 4.1 protein, ezrin, radixin, and moesin), which simultaneously bind to lipids and proteins (Chishti et al., 1998). This dynamic interface, also termed membrane-cortex-attachment (Diz-Muñoz et al., 2010), transforms the two separate structures into one composite material. From Eq. 2.2 in Box 1, we learn that the energy to buckle a material scales with the thickness cubed. Consequentially, the energy to bend a 200 nm thick cell cortex is orders of magnitude higher than for a 5–7 nm thin lipid bilayer. Hence, the contribution of the lipid bilayer to the overall cell surface stiffness can be neglected for shape changes at cellular length scales. Intriguingly, the high frequency regime of the fluctuation spectrum of membrane fluctuation assays seems to depend to a large extent on the mechanical properties of the PM (Gárate et al., 2015), suggesting that the membrane is at least partly able to swing freely at small length-scales. Similar high fluctuation modes at the scale of dozens of nanometers were also observed in vesicles (Betz and Sykes, 2012). Thus, the bending stiffness of the cell surface (see Figure 1A) is likely dominated by the cell cortex on the cellular level and by a partly unattached PM on sub-micron length scales (Salbreux et al., 2012).

The connection from cell cortex to membrane also affects surface tension (Chugh et al., 2017). The cell membrane is attached to the cortex via linker proteins, which in turn are put under tension by the cortical surface tension N_cor, yielding.

$$N_{cor}\frac{2}{R}={\mathrm{\rho }}_{link}{F}_{link},(1.2)$$

where ρ_link depicts the linker protein density and F_link the force applied by each linker. Using Laplace law (see also Box 1, Eq. 2.5), we find.

$$\mathrm{\Delta }p=N_{PM}\frac{2}{R}+{\mathrm{\rho }}_{link}{F}_{link}=\left(N_{PM}+N_{cor}\right)\frac{2}{R},(1.3)$$

which means that cell surface tension N_cell is the sum of membrane tension N_PM and cortical tension N_cor (Sens and Plastino, 2015). Let’s have a closer look at membrane tension. In a lipid bilayer, local gradients in membrane tension (e.g., induced by rapidly pulling on a tether) equalize over the rest of the membrane in a matter of milliseconds (Shi and Baumgart, 2015), which is reminiscent of a fluid lacking shear stress. This, however, changes as soon as the PM is attached to the cellular cortex. Roughly one quarter of the total PM area is occupied by transmembrane proteins, half of which are connected to the cellular cortex (Bussell et al., 1995). These proteins, if attached to the cell cortex, serve as obstacles that limit membrane flow (u).

$$u=\frac{k}{{\mathrm{\eta }}_{lipid}}\nabla N,(1.4)$$

with Darcy permeability k of a porous medium (i.e., the array of obstacles) and lipid viscosity η_lipid (Shi et al., 2018). The lateral permeability k can be described as a function of the area fraction ϕ occupied by the integral proteins and their radius a (Happel, 1959).

$$k\approx -\frac{a^2(1+\ln (\mathrm{\varphi }))}{8\mathrm{\varphi }}.(1.5)$$

Hence, if confined into two dimensions, the flow resistance decreases logarithmically with the distance to the obstacle (rather than exponential). Since the logarithmic function diverges for large distances, the effect will be noticeable no matter how far away from the obstacle we evaluate the system - a phenomenon called the Stokes paradox. The same study further noted that the surface tension of a PM attached to the cell cortex propagate over time in a diffusive manner, given by.

$$\frac{\mathrm{\delta }N}{\mathrm{\delta }t}=\frac{Ek}{{\mathrm{\eta }}_{lipid}}{\nabla }^{2}N,(1.6)$$

where E depicts the elastic modulus of the PM and η_lipid the viscosity of the lipids (i.e., the fluid’s viscosity flowing through these obstacles). Note that Eq. 1.6 exhibits a striking similarity to Fick’s second law of diffusion. In their elegant study, Shi and Cohen defined a tension diffusion coefficient D_N

$$D_N=\frac{Ek}{{\mathrm{\eta }}_{lipid}},(1.7)$$

yielding

$$\frac{\mathrm{\delta }N}{\mathrm{\delta }t}=D_N{\nabla }^{2}N.(1.8)$$

Consequently, the cortex bound integral proteins cause local and long lived gradients of membrane tension. It is plausible to envision that cells may locally alter the tension diffusion coefficient through MCA-induced changes in number and position of transmembrane obstacles (i.e., change ϕ). Consistently, recent work showed a positive correlation between membrane-proximal actin density and membrane tension (Bisaria et al., 2020). If and how membrane tension gradients influence cortical tension N_cor, and in consequence cell tension N_cell, remains elusive.

Finally, let’s consider membrane viscosity. PM viscosity differs from the viscosity of a pure lipid bilayer due to the embedded integral membrane proteins (IMPs). For a suspension with no interparticle interactions (i.e., low concentration), the effective viscosity of such a suspension can be approximated by.

$${\mathrm{\mu }}_e={\mathrm{\mu }}_0(1+B\mathrm{\varphi }),(1.9)$$

where μ₀ is the viscosity of the suspending liquid, ϕ volume fraction of the embedded particles and B a coefficient depending on the particle shape (e.g., spheres, cylinders, disks) (Bird et al., 2007). Hence, it is possible that the attachment, and therefore immobilization of IMPs, may also affect PM viscosity. Despite the existence of some approximations on the effective viscosity (Larson and Higdon, 1986, 1987; Kolodziej, 1988), this complex topic remains unresolved and is beyond the scope of this review (see also Supplementary Material). Importantly, the sole plasma membrane exhibits viscous material properties. Attachment of to the PM to the cell cortex (i.e., the cell surface), however, displays a combination of viscous and elastic properties on the cellular length scale (Bausch et al., 1998). This means that on short time scales (i.e., ∼1 s) the cell surface responds like an elastic material, while it shows properties of a viscous material on longer time scales (i.e., 10–100 s). Considering that the cortex consist of interlinked actin filaments, which are subject to continuous turnover of cross-linking proteins and actin filaments, the cell cortex is able to perform plastic deformation reminiscent of a viscoelastic fluid. This behavior can, in its simplest form, be modeled as a Maxwell body (Begemann et al., 2019) described by Eq. 2.7 in Box 1 (see also Figure 1C).

In conclusion, our short survey demonstrates how interactions of membranes with the cell cortex alter the mechanical properties of the PM itself as well as of the cell surface. Yet, despite the versatility in material properties that can be achieved, the resulting composite material at this point still lacks the ability to readily respond to changes from the environment (i.e., adaptive response).

The Cell Surface Is an Adaptive Composite Material

In the form described this far, the composite material will always thrive to adopt the minimal energy state. Strikingly, mechanical properties of membrane and cortex can be separately tuned with high spatial and temporal accuracy, providing the possibility to turn the passive composite into an active material. In our hypothetical composite material, such adaptivity could be achieved by rendering its components sensitive to a transient stimulus (e.g., light, temperature). The response to such a stimulus, which triggers local changes in one (or a combination) of the four essential material properties (Figure 1A), yields an adaptive composite material (Figure 2C, left).

Following, we will discuss how stimulus-induced transient changes in mechanical properties of membrane or cortex yield an adaptive composite material. We begin with tension. As mentioned above in Eq. 1.3, the tension of the cell surface is the sum of the PM tension and cortex tension, and therefore a function of the density of linker proteins ρ_link and the stretch moduli of the plasma membrane $K_e^{PM}$ and cell cortex $K_e^{cor}$. These parameters, in turn, rely on the respective elastic moduli E, thickness h, and the Poisson ratio ν (Eq. 2.1, Box 1). Hence, signal-induced changes to any of those properties will necessarily influence the cells surface stretch modulus $K_e^{cell}$. The stretch resistance of the lipid bilayer $K_e^{PM}$, for instance, arises from energy penalty caused by exposure of the hydrophobic core to the surrounding aqueous solution. It could therefore, in theory, be tuned by changing the membrane lipid composition, which may also effect the membrane thickness h. However, with a modulus of ∼200 mN/m (Rawicz et al., 2000), the lipid bilayer is not a strongly extendable structure, and thus not well suited. Note that most values in literature describe the apparent stretch modulus of the PM, which integrate large scale changes in membrane area originating from membrane undulation, membrane folds, vesicle fusion, the smoothening of membrane fluctuations and other sources (Le Roux et al., 2019). Complementing membrane-based tension, cortex-based tension can be modulated by signal-dependent changes in actin cross-linker density, the MCA (i.e., density of PM-cortex linker proteins ρ_link) and cortical myosin (Stewart et al., 2011). In particular, the latter renders the composite material suitable to adaptation on physiological timescales (i.e., order of seconds), whereby lipid composition as well as the cortex geometry (e.g., mesh size) will affect the respective elastic moduli.

Bending Stiffness

As membrane and cortical stiffness critically depend on the length scale, we will consider their contribution separately. The bending stiffness of the PM, which is relevant in the sub-micron regime, depends on the composition of the lipid bilayer (Helfrich, 1973). By changing length and saturation of individual carbohydrate chains, the lipid bilayer thickness, and thereby the bending energy, can be modulated (see Eq. 2.2 in Box 1). Adding hydrophobic heads with varying size further renders lipids curvature-sensitive, while differences in charge will influence protein-lipid interactions with peripheral cytosolic proteins (Ebrahimkutty and Galic, 2019; Bassereau et al., 2018). The bending stiffness of the cell cortex, which is relevant in the μm regime, can be influenced by changes to the actin mesh size (depicted by the density of cortex linker proteins) or the thickness of the cortex itself. In addition, signals that change the elastic moduli of both materials (discussed above) will also influence their respective bending rigidities $K_B^{PM}$ and $K_B^{cor}$ (see Eq. 2.2 in Box 1).

Shear Resistance and Viscosity

Pure lipid bilayers behave like a fluid void of shear stress (Mofrad and Kamm, 2006). This is not always the case in cellular membranes (Shi et al., 2018). From Eq. 2.3 in Box 1, we deduce that all cellular stimuli that influence the shear modulus (and therefore Young’s modulus E as well as the Poisson’s ratio υ, as discussed above) will also affect the elastic shear stress response of both materials, and therefore also of the cell surface. As the cell cortex as well as the attached PM both exhibit viscoelastic properties, we further have to consider the control variables of the respective viscosities. In case of the cortex, the dominating control variable (i.e., target for adaptive stimuli) are the relative turnover rates of actin and its cross-linkers, as well as the relative mesh size of the cell cortex (Boulbitch et al., 2000; Kasas et al., 2005). Regarding the PM, and recalling the description of Stokes paradox from the previous paragraph, viscosity of the PM could be modulated by signal-induced changes to the total concentration of integral proteins, its spatial distribution (e.g., clustering), and the fraction of cortex bound units.

The findings summarized in this section highlight the manifold strategies for signal-induced changes in individual material properties that render the cell surface an adaptive composite material. How these material properties are changed under pathophysiological conditions is the topic of the following chapter.

Faulty Material Properties Cause Disease

In any engineered structure, incorporation of faulty materials yields catastrophic consequences for the over-all stability of the object. In cells, such faulty materials manifest as disease. Following, we survey disease arising from individual materials, the resulting composite and its adaptive features, respectively.

As described in the previous section, changes in relative lipid levels within the membrane may not only deplete components involved in signaling, but could also alter its material properties. Mounting evidence exist for changes in lipid balance [e.g., (cholesterol)↑, (sphingomyelin)↑ and (phosphatidylinositol)↓] during aging, but also in lipidosis such as Niemann-Pick disease types A and C (Karten et al., 2002; Arroyo et al., 2014), establishing how mechanical properties of the membrane may be altered in disease.

Intriguingly, faulty materials that lead to disease can also be found in cell cortex proteins. For instance, mutations in smooth muscle α-actin (ACTA2), which alter interactions between actin and myosin (Lu et al., 2015), cause vascular disease and stroke (Guo et al., 2009). Mutations in ACTB, the gene encoding cytoplasmic β-actin, change actin polymerization dynamics (Hundt et al., 2014), resulting in deafness, cancer and developmental disorders (Procaccio et al., 2006). Mutations in the gene encoding α-actinin-4 (ACTN4), an actin cross-linking protein, cause proteinuric kidney disease (Kaplan et al., 2000). Collectively, these few examples illustrate how changes in material properties of cell cortex components yield substantial physiological effects.

Disease can further be traced back to errors of the composite material. As described above, lipid composition determines rigidity and fluidity of membranes. Strikingly, some of these lipids form highly dynamic and heterogeneous membrane nanodomains (Head et al., 2014; Sechi and Wehland, 2000), which can be stabilized to form larger signaling platforms that are associated with actin filaments (Oliferenko et al., 1999; Galic et al., 2012; Begemann et al., 2019). As lipid availability or dynamics is changed in certain disease, the resulting mechanical properties of the membrane-cortex composite are likely altered in such conditions.

Finally, mutations can also affect the adaptability of the composite. One major family of disease originates from mutations in receptor proteins, which disturb signal-induced changes in material properties of the composite. One such example are G-protein coupled receptors (GPCRs), which alter among others the material properties of the cell cortex (Bhattacharya et al., 2004). Here, mutations cause aberrant signaling by disrupting surface expression (Ward et al., 2012), basal activity (Seifert and Wenzel-Seifert, 2002), or ligand binding (Venkatakrishnan et al., 2013). Furthermore, GPCRs directly interact with lipids, which means that changes in membrane composition or mutations in the lipid-recognition motifs can alter GPCR signaling by changing its stability, subcellular localization or activity (Keri and Barth, 2018; Pucadyil and Chattopadhyay, 2006). Importantly, errors in signal-induced changes in material properties can also be traced back to other receptor families (Jiang and Gonen, 2012; Fruman et al., 2017; Zakany et al., 2020), giving rise to an ever-growing family of membrane-related disease. A second major family of disease that influences the adaptability of the composite material relies on membrane curvature. Here, transiently deformed membrane sections trigger recruitment of curvature-sensitive proteins (Peter et al., 2004) and lipids (Wang et al., 2007; James et al., 2010). Notably, many of the more than 100 known curvature-sensing molecules identified in cells directly alter actin polymerization, thus changing mechanical forces applied to the PM. This dual ability of selected molecules to sense and modify actin-induced PM curvature is important, as it posits the core properties of an adaptive composite material. Consistently, defects of individual force-regulatory feedback loops (e.g., OPHN1 and SRGAP2) result in very specific diseases (Billuart et al., 1998; Charrier et al., 2012).

While by far not complete, these selected examples illustrate how the material properties of individual components critically influence the overall mechanical state of the cell surface – both, in health and disease. How the mechanical properties of this versatile adaptive composite material are measured will be discussed in the next section.

Measuring Material Properties in Cellular Membranes

The picture drawn this far depicts the importance of a functioning interplay between cortex, membrane and MCA. Considering its small scale, separating cell cortex from membranes in living cells is a challenging task (Diz-Muñoz et al., 2018). To gain insights into membrane tension, previous studies have taken advantage of pipets and optical tweezers to measure the force needed to extract a membrane tether from the cell surface (Raucher and Sheetz, 2000). Another approach relies on time-resolved membrane fluctuation spectroscopy (Betz and Sykes, 2012). Here, an optical tweezer is being used to measure membrane deformations rather than to pull tethers. In such measurements, the power spectral density of low-frequency fluctuations drops as tension increases (Betz and Sykes, 2012). Notably, fluctuation spectroscopy can also be used to gain insights into bending rigidity and viscosity of the material (Betz and Sykes, 2012). Quantitative measurements on membrane viscosity can also be acquired using high-throughput single molecule tracking or fluorescence correlation spectroscopy (Barbotin et al., 2019).

Yet, as mentioned above, changes in cortex bound protein spacing will affect membrane fluidity (Cohen and Shi, 2020). Hence, measurements from tether pulling and membrane fluctuation present a convolute of membrane and cell cortex properties (Shi et al., 2018). Thus, while each of these approaches allows exciting novel insights into the mechanical properties of cell membranes, it remains a challenging task to unequivocally dissect the contribution of the individual components of the composite material.

Conclusion and Outlook

Seminal work one pure lipid bilayers, which are the topic of other reviews in this special issue, have substantially contributed to our current understanding of membrane mechanics. Yet recent studies argue that some cellular membranes should be considered an adaptive composite material (Shi et al., 2018; Cohen and Shi, 2020). In this review, we used a hypothetical biomimetic material to elucidate the astounding versatility of cellular membranes. We discussed how small changes in the mechanical properties of individual core modules allow the material to readily adapt its properties, thus fulfilling highly diverse functions, while relying on the same building materials. Strikingly, the composite nature of the cell surface not only allows cellular membranes to rapidly adjust its mechanical properties to the given situation, but also provides explanations to disease and some seemingly contradicting properties of the cell surface. One such example is the need for efficient transport of large objects across the cell cortex, while maintaining structural integrity at all times (Wollman and Meyer, 2012). As mentioned above, the lipid-cortex interface largely relies on non-covalent interactions. In consequence, the cytoskeleton continuously de- and reattaches from the lipid bilayer. These transient detachments not only open up the possibility to readily adjust interactions, but also the ability to transport and fuse vesicles (i.e., large objects) without permanent detachment of the plasma membrane from the underlying cortex.

Using the analogy of a hypothetical biomimetic material we realize that man-made materials still lag far behind its biological counterparts. It is encouraging, however, that this opportunity has been recognized, nucleating a rapidly growing research field (Amaral and Pasparakis, 2019; Chen and Li, 2020). Future advancements into bioinspired and biomimetic material will likely benefit from computational approaches (Sun et al., 2018; Schroer et al., 2020), which allow rapid advancement of theoretical and experimental data of membrane-MCA-cortex dynamics at an ever-increasing spatio-temporal resolution.

Author Contributions

Both authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Funding

This work was supported by funds from the DFG (EXC-1003, CRC1348/A06) and the Faculty of Medicine of the University of Muenster to MG (IMF IGA-121610).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank members of the Galic lab for critical feedback and discussion.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fcell.2020.00684/full#supplementary-material

References

Amaral, A. J. R., and Pasparakis, G. (2019). Cell membrane engineering with synthetic materials: applications in cell spheroids, cellular glues and microtissue formation. Acta Biomater. 90, 21–36. doi: 10.1016/j.actbio.2019.04.013

PubMed Abstract | CrossRef Full Text | Google Scholar

Arroyo, A. I., Camoletto, P. G., Morando, L., Sassoe-Pognetto, M., Giustetto, M., van Veldhoven, P. P., et al. (2014). Pharmacological reversion of sphingomyelin-induced dendritic spine anomalies in a Niemann Pick disease type A mouse model. EMBO Mol. Med. 6, 398–413. doi: 10.1002/emmm.201302649

PubMed Abstract | CrossRef Full Text | Google Scholar

Barbotin, A., Galiani, S., Urbanèiè, I., Eggeling, C., and Booth, M. J. (2019). Adaptive optics allows STED-FCS measurements in the cytoplasm of living cells. Opt. Express 27, 23378–23395. doi: 10.1364/OE.27.023378

PubMed Abstract | CrossRef Full Text | Google Scholar

Bassereau, P., Jin, R., Baumgart, T., Deserno, M., Dimova, R., Frolov, V. A., et al. (2018). The 2018 biomembrane curvature and remodeling roadmap. J. Phys. D Appl. Phys. 51:343001. doi: 10.1088/1361-6463/aacb98

PubMed Abstract | CrossRef Full Text | Google Scholar

Baumgart, T., Hess, S. T., and Webb, W. W. (2003). Imaging coexisting fluid domains in biomembrane models coupling curvature and line tension. Nature 425, 821–824. doi: 10.1038/nature02013

PubMed Abstract | CrossRef Full Text | Google Scholar

Bausch, A. R., Ziemann, F., Boulbitch, A. A., Jacobson, K., and Sackmann, E. (1998). Local measurements of viscoelastic parameters of adherent cell surfaces by magnetic bead microrheometry. Biophys. J. 75, 2038–2049. doi: 10.1016/S0006-3495(98)77646-5

CrossRef Full Text | Google Scholar

Begemann, I., Saha, T., Lamparter, L., Rathmann, I., Grill, D., Golbach, L., et al. (2019). Mechanochemical self-organization determines search pattern in migratory cells. Nat. Phys. 15, 848–857. doi: 10.1038/s41567-019-0505-9

CrossRef Full Text | Google Scholar

Betz, T., and Sykes, C. (2012). Time resolved membrane fluctuation spectroscopy. Soft Matter 8, 5317–5326. doi: 10.1039/C2SM00001F

CrossRef Full Text | Google Scholar

Bhattacharya, M., Babwah, A. V., and Ferguson, S. S. G. (2004). Small GTP-binding protein-coupled receptors. Biochem. Soc. Trans. 32(Pt 6), 1040–1044. doi: 10.1042/BST0321040

PubMed Abstract | CrossRef Full Text | Google Scholar

Billuart, P., Bienvenu, T., Ronce, N., Des Portes, V., Vinet, M. C., Zemni, R., et al. (1998). Oligophrenin-1 encodes a rhoGAP protein involved in X-linked mental retardation. Nature 392, 923–926. doi: 10.1038/31940

PubMed Abstract | CrossRef Full Text | Google Scholar

Bird, R. B., Stewart, W. E., and Lightfoot, E. N. (2007). Transport Phenomena (Rev. 2. ed.). Hoboken, NJ: Wiley.

Google Scholar

Bisaria, A., Hayer, A., Garbett, D., Cohen, D., and Meyer, T. (2020). Membrane-proximal F-actin restricts local membrane protrusions and directs cell migration. Science 368, 1205–1210. doi: 10.1126/science.aay7794

PubMed Abstract | CrossRef Full Text | Google Scholar

Boulbitch, A., Simson, R., Simson, D. A., Merkel, R., Häckl, W., Bärmann, M., et al. (2000). Shape instability of a biomembrane driven by a local softening of the underlying actin cortex. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 62(3 Pt B), 3974–3985. doi: 10.1103/physreve.62.3974

PubMed Abstract | CrossRef Full Text | Google Scholar

Bussell, S. J., Koch, D. L., and Hammer, D. A. (1995). Effect of hydrodynamic interactions on the diffusion of integral membrane proteins: tracer diffusion in organelle and reconstituted membranes. Biophys. J. 68, 1828–1835. doi: 10.1016/S0006-3495(95)80359-0

CrossRef Full Text | Google Scholar

Carpenter, G., King, L., and Cohen, S. (1978). Epidermal growth factor stimulates phosphorylation in membrane preparations in vitro. Nature 276, 409–410. doi: 10.1038/276409a0

PubMed Abstract | CrossRef Full Text | Google Scholar

Charrier, C., Joshi, K., Coutinho-Budd, J., Kim, J.-E., Lambert, N., Marchena, J., et al. (2012). Inhibition of SRGAP2 function by its human-specific paralogs induces neoteny during spine maturation. Cell 149, 923–935. doi: 10.1016/j.cell.2012.03.034

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., and Li, J. (2020). Bioinspired by cell membranes: functional polymeric materials for biomedical applications. Mater. Chem. Front. 4, 750–774. doi: 10.1039/C9QM00717B

CrossRef Full Text | Google Scholar

Chen, Z., Atefi, E., and Baumgart, T. (2016). Membrane shape instability induced by protein crowding. Biophys. J. 111, 1823–1826. doi: 10.1016/j.bpj.2016.09.039

PubMed Abstract | CrossRef Full Text | Google Scholar

Chishti, A. H., Kim, A. C., Marfatia, S. M., Lutchman, M., Hanspal, M., Jindal, H., et al. (1998). The FERM domain: a unique module involved in the linkage of cytoplasmic proteins to the membrane. Trends Biochem. Sci. 23, 281–282. doi: 10.1016/S0968-0004(98)01237-7

CrossRef Full Text | Google Scholar

Chugh, P., Clark, A. G., Smith, M. B., Cassani, D. A. D., Dierkes, K., Ragab, A., et al. (2017). Actin cortex architecture regulates cell surface tension. Nat. Cell Biol. 19, 689–697. doi: 10.1038/ncb3525

PubMed Abstract | CrossRef Full Text | Google Scholar

Chugh, P., and Paluch, E. K. (2018). The actin cortex at a glance. J. Cell Sci. 131:jcs186254. doi: 10.1242/jcs.186254

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohen, A. E., and Shi, Z. (2020). Do cell membranes flow like honey or jiggle like jello? BioEssays 42:e1900142. doi: 10.1002/bies.201900142

PubMed Abstract | CrossRef Full Text | Google Scholar

Contreras, F.-X., Ernst, A. M., Wieland, F., and Brügger, B. (2011). Specificity of intramembrane protein-lipid interactions. Cold Spring Harb. Perspect. Biol. 3:a004705. doi: 10.1101/cshperspect.a004705

PubMed Abstract | CrossRef Full Text | Google Scholar

Diz-Muñoz, A., Krieg, M., Bergert, M., Ibarlucea-Benitez, I., Muller, D. J., Paluch, E., et al. (2010). Control of directed cell migration in vivo by membrane-to-cortex attachment. PLoS Biol. 8:e1000544. doi: 10.1371/journal.pbio.1000544

PubMed Abstract | CrossRef Full Text | Google Scholar

Diz-Muñoz, A., Weiner, O. D., and Fletcher, D. A. (2018). In pursuit of the mechanics that shape cell surfaces. Nat. Phys. 14, 648–652. doi: 10.1038/s41567-018-0187-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Ebrahimkutty, M. P., and Galic, M. (2019). Receptor-free signaling at curved cellular membranes. BioEssays 41:e1900068. doi: 10.1002/bies.201900068

PubMed Abstract | CrossRef Full Text | Google Scholar

Edidin, M., Kuo, S. C., and Sheetz, M. P. (1991). Lateral movements of membrane glycoproteins restricted by dynamic cytoplasmic barriers. Science 254, 1379–1382. doi: 10.1126/science.1835798

PubMed Abstract | CrossRef Full Text | Google Scholar

Eggeling, C., Ringemann, C., Medda, R., Schwarzmann, G., Sandhoff, K., Polyakova, S., et al. (2009). Direct observation of the nanoscale dynamics of membrane lipids in a living cell. Nature 457, 1159–1162. doi: 10.1038/nature07596

PubMed Abstract | CrossRef Full Text | Google Scholar

Estep, T. N., Mountcastle, D. B., Barenholz, Y., Biltonen, R. L., and Thompson, T. E. (1979). Thermal behavior of synthetic sphingomyelin-cholesterol dispersions. Biochemistry 18, 2112–2117. doi: 10.1021/bi00577a042

PubMed Abstract | CrossRef Full Text | Google Scholar

Evans, E., and Rawicz, W. (1990). Entropy-driven tension and bending elasticity in condensed-fluid membranes. Phys. Rev. Lett. 64, 2094–2097. doi: 10.1103/PhysRevLett.64.2094

PubMed Abstract | CrossRef Full Text | Google Scholar

Faucon, J. F., Mitov, M. D., Méléard, P., Bivas, I., and Bothorel, P. (1989). Bending elasticity and thermal fluctuations of lipid membranes. Theoretical and experimental requirements. J. Phys. 50, 2389–2414. doi: 10.1051/jphys:0198900500170238900

CrossRef Full Text | Google Scholar

Fruman, D. A., Chiu, H., Hopkins, B. D., Bagrodia, S., Cantley, L. C., and Abraham, R. T. (2017). The PI3K pathway in human disease. Cell 170, 605–635. doi: 10.1016/j.cell.2017.07.029

PubMed Abstract | CrossRef Full Text | Google Scholar

Galic, M., Jeong, S., Tsai, F.-C., Joubert, L.-M., Wu, Y. I, Hahn, K. M., et al. (2012). External push and internal pull forces recruit curvature-sensing N-BAR domain proteins to the plasma membrane. Nat. Cell Biol. 14, 874–881. doi: 10.1038/ncb2533

PubMed Abstract | CrossRef Full Text | Google Scholar

Gárate, F., Betz, T., Pertusa, M., and Bernal, R. (2015). Time-resolved neurite mechanics by thermal fluctuation assessments. Phys. Biol. 12:66020. doi: 10.1088/1478-3975/12/6/066020

CrossRef Full Text | Google Scholar

Graber, Z. T., Shi, Z., and Baumgart, T. (2017). Cations induce shape remodeling of negatively charged phospholipid membranes. Phys. Chem. Chem. Phys. 19, 15285–15295. doi: 10.1039/c7cp00718c

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, D.-C., Papke, C. L., van Tran-Fadulu Regalado, E. S., Avidan, N., Johnson, R. J., Kim, D. H., et al. (2009). Mutations in smooth muscle alpha-actin (ACTA2) cause coronary artery disease, stroke, and Moyamoya disease, along with thoracic aortic disease. Am. J. Hum. Genet. 84, 617–627. doi: 10.1016/j.ajhg.2009.04.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Hallett, F. R., Marsh, J., Nickel, B. G., and Wood, J. M. (1993). Mechanical properties of vesicles. II. A model for osmotic swelling and lysis. Biophys. J. 64, 435–442. doi: 10.1016/S0006-3495(93)81384-5

CrossRef Full Text | Google Scholar

Hancock, J. F., Magee, A. I., Childs, J. E., and Marshall, C. J. (1989). All ras proteins are polyisoprenylated but only some are palmitoylated. Cell 57, 1167–1177. doi: 10.1016/0092-8674(89)90054-8

CrossRef Full Text | Google Scholar

Happel, J. (1959). Viscous flow relative to arrays of cylinders. AIChE J. 5, 174–177. doi: 10.1002/aic.690050211

CrossRef Full Text | Google Scholar

Head, B. P., Patel, H. H., and Insel, P. A. (2014). Interaction of membrane/lipid rafts with the cytoskeleton: impact on signaling and function: membrane/lipid rafts, mediators of cytoskeletal arrangement and cell signaling. Biochim. Biophys. Acta 1838, 532–545. doi: 10.1016/j.bbamem.2013.07.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Helfrich, W. (1973). Elastic properties of lipid bilayers: theory and possible experiments. Z. Nat. Teil C Biochem. Biophys. Biol. Virol. 28, 693–703. doi: 10.1515/znc-1973-11-1209

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, C., and Thompson, T. E. (1965). Properties of lipid bilayer membranes separating two aqueous phases: determination of membrane thickness. J. Mol. Biol. 13, 183–193. doi: 10.1016/S0022-2836(65)80088-2

CrossRef Full Text | Google Scholar

Huber, F., Schnauß, J., Rönicke, S., Rauch, P., Müller, K., Fütterer, C., et al. (2013). Emergent complexity of the cytoskeleton: from single filaments to tissue. Adv. Phys. 62, 1–112. doi: 10.1080/00018732.2013.771509

PubMed Abstract | CrossRef Full Text | Google Scholar

Hundt, N., Preller, M., Swolski, O., Ang, A. M., Mannherz, H. G., Manstein, D. J., et al. (2014). Molecular mechanisms of disease-related human β-actin mutations p.R183w and p.E364k. FEBS J. 281, 5279–5291. doi: 10.1111/febs.13068

PubMed Abstract | CrossRef Full Text | Google Scholar

Huxley, A. F., and Simmons, R. M. (1971). Proposed mechanism of force generation in striated muscle. Nature 233, 533–538. doi: 10.1038/233533a0

PubMed Abstract | CrossRef Full Text | Google Scholar

James, D. J., Khodthong, C., Kowalchyk, J. A., and Martin, T. F. J. (2010). Phosphatidylinositol 4,5-bisphosphate regulation of SNARE function in membrane fusion mediated by CAPS. Adv. Enzyme Regul. 50, 62–70. doi: 10.1016/j.advenzreg.2009.10.012

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, Q.-X., and Gonen, T. (2012). The influence of lipids on voltage-gated ion channels. Curr. Opin. Struct. Biol. 22, 529–536. doi: 10.1016/j.sbi.2012.03.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Kamm, R., and Grodzinsky, A. (2015). Molecular, Cellular, and Tissue Biomechanics. Cambridge, MA: Massachusetts Institute of Technology.

Google Scholar

Kaplan, J. M., Kim, S. H., North, K. N., Rennke, H., Correia, L. A., Tong, H. Q., et al. (2000). Mutations in ACTN4, encoding alpha-actinin-4, cause familial focal segmental glomerulosclerosis. Nat. Genet. 24, 251–256. doi: 10.1038/73456

PubMed Abstract | CrossRef Full Text | Google Scholar

Karten, B., Vance, D. E., Campenot, R. B., and Vance, J. E. (2002). Cholesterol accumulates in cell bodies, but is decreased in distal axons, of Niemann-Pick C1-deficient neurons. J. Neurochem. 83, 1154–1163. doi: 10.1046/j.1471-4159.2002.01220.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Kasas, S., Wang, X., Hirling, H., Marsault, R., Huni, B., Yersin, A., et al. (2005). Superficial and deep changes of cellular mechanical properties following cytoskeleton disassembly. Cell Motil. Cytoskeleton 62, 124–132. doi: 10.1002/cm.20086

PubMed Abstract | CrossRef Full Text | Google Scholar

Keri, D., and Barth, P. (2018). Reprogramming G protein coupled receptor structure and function. Curr. Opin. Struct. Biol. 51, 187–194. doi: 10.1016/j.sbi.2018.07.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Kolodziej, J. A. (1988). Influence of the porosity of a porous medium on the effective viscosity in Brinkman’s filtration equation. Acta Mech. 75, 241–254. doi: 10.1007/BF01174638

CrossRef Full Text | Google Scholar

Koning, R. I., Zovko, S., Bárcena, M., Oostergetel, G. T., Koerten, H. K., Galjart, N., et al. (2008). Cryo electron tomography of vitrified fibroblasts: microtubule plus ends in situ. J. Struct. Biol. 161, 459–468. doi: 10.1016/j.jsb.2007.08.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Laganowsky, A., Reading, E., Allison, T. M., Ulmschneider, M. B., Degiacomi, M. T., Baldwin, A. J., et al. (2014). Membrane proteins bind lipids selectively to modulate their structure and function. Nature 510, 172–175. doi: 10.1038/nature13419

PubMed Abstract | CrossRef Full Text | Google Scholar

Larson, R. E., and Higdon, J. J. L. (1986). Microscopic flow near the surface of two-dimensional porous media. Part 1. Axial flow. J. Fluid Mech. 166, 449–472. doi: 10.1017/S0022112086000228

CrossRef Full Text | Google Scholar

Larson, R. E., and Higdon, J. J. L. (1987). Microscopic flow near the surface of two-dimensional porous media. Part 2. Transverse flow. J. Fluid Mech. 178, 119–136. doi: 10.1017/S0022112087001149

CrossRef Full Text | Google Scholar

Le Roux, A.-L., Quiroga, X., Walani, N., Arroyo, M., and Roca-Cusachs, P. (2019). The plasma membrane as a mechanochemical transducer. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 374:20180221. doi: 10.1098/rstb.2018.0221

PubMed Abstract | CrossRef Full Text | Google Scholar

Lu, H., Fagnant, P. M., Bookwalter, C. S., Joel, P., and Trybus, K. M. (2015). Vascular disease-causing mutation R258C in ACTA2 disrupts actin dynamics and interaction with myosin. Proc. Natl. Acad. Sci. U.S.A. 112, E4168–E4177. doi: 10.1073/pnas.1507587112

PubMed Abstract | CrossRef Full Text | Google Scholar

Lundberg, E., and Borner, G. H. H. (2019). Spatial proteomics: a powerful discovery tool for cell biology. Nat. Rev. Mol. Cell Biol. 20, 285–302. doi: 10.1038/s41580-018-0094-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Meyers, M. A., and Chawla, K. K. (2010). Mechanical Behavior of Materials, 2nd Edn. Cambridge, MA: Cambridge University Press.

Google Scholar

Mofrad, M. R. K., and Kamm, R. D. (2006). Cytoskeletal Mechanics: Models and Measurements in Cell Mechanics. Cambridge Texts in Biomedical Engineering. Cambridge, MA: Cambridge University Press.

Google Scholar

Mullins, R. D., Heuser, J. A., and Pollard, T. D. (1998). The interaction of Arp2/3 complex with actin: nucleation, high affinity pointed end capping, and formation of branching networks of filaments. Proc. Natl. Acad. Sci. U.S.A. 95, 6181–6186. doi: 10.1073/pnas.95.11.6181

PubMed Abstract | CrossRef Full Text | Google Scholar

Naghieh, S., Sarker, M., Karamooz-Ravari, M., McInnes, A., and Chen, X. (2018). Modeling of the mechanical behavior of 3d bioplotted scaffolds considering the penetration in interlocked strands. Appl. Sci. 8:1422. doi: 10.3390/app8091422

CrossRef Full Text | Google Scholar

Nernst, W. H. (1889). The Electromotoric Effectiveness of Ions. Habilitation Thesis, University of Tübingen, Tübingen.

Google Scholar

Nicolson, G. L. (2014). The fluid-mosaic model of membrane structure: still relevant to understanding the structure, function and dynamics of biological membranes after more than 40 years. Biochim. Biophys. Acta 1838, 1451–1466. doi: 10.1016/j.bbamem.2013.10.019

PubMed Abstract | CrossRef Full Text | Google Scholar

Olbrich, K., Rawicz, W., Needham, D., and Evans, E. (2000). Water permeability and mechanical strength of polyunsaturated lipid bilayers. Biophys. J. 79, 321–327. doi: 10.1016/S0006-3495(00)76294-1

CrossRef Full Text | Google Scholar

Oliferenko, S., Paiha, K., Harder, T., Gerke, V., Schwärzler, C., Schwarz, H., et al. (1999). Analysis of Cd44-containing lipid rafts: recruitment of annexin II and stabilization by the actin cytoskeleton. J. Cell Biol. 146, 843–854.

Google Scholar

Peskin, C. S., Odell, G. M., and Oster, G. F. (1993). Cellular motions and thermal fluctuations: the Brownian ratchet. Biophys. J. 65, 316–324. doi: 10.1016/S0006-3495(93)81035-X

CrossRef Full Text | Google Scholar

Peter, B. J., Kent, H. M., Mills, I. G., Vallis, Y., Butler, P. J. G., Evans, P. R., et al. (2004). Bar domains as sensors of membrane curvature: the amphiphysin BAR structure. Science 303, 495–499. doi: 10.1126/science.1092586

PubMed Abstract | CrossRef Full Text | Google Scholar

Procaccio, V., Salazar, G., Ono, S., Styers, M. L., Gearing, M., Davila, A., et al. (2006). A mutation of beta -actin that alters depolymerization dynamics is associated with autosomal dominant developmental malformations, deafness, and dystonia. Am. J. Hum. Genet. 78, 947–960. doi: 10.1086/504271

PubMed Abstract | CrossRef Full Text | Google Scholar

Pucadyil, T. J., and Chattopadhyay, A. (2006). Role of cholesterol in the function and organization of G-protein coupled receptors. Prog. Lipid Res. 45, 295–333. doi: 10.1016/j.plipres.2006.02.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Raucher, D., and Sheetz, M. P. (2000). Cell spreading and lamellipodial extension rate is regulated by membrane tension. J. Cell Biol. 148, 127–136. doi: 10.1083/jcb.148.1.127

PubMed Abstract | CrossRef Full Text | Google Scholar

Rawicz, W., Olbrich, K. C., McIntosh, T., Needham, D., and Evans, E. (2000). Effect of chain length and unsaturation on elasticity of lipid bilayers. Biophys. J. 79, 328–339.

Google Scholar

Salbreux, G., Charras, G., and Paluch, E. (2012). Actin cortex mechanics and cellular morphogenesis. Trends Cell Biol. 22, 536–545. doi: 10.1016/j.tcb.2012.07.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Schroer, C. F. E., Baldauf, L., van Buren, L., Wassenaar, T. A., Melo, M. N., Koenderink, G. H., et al. (2020). Charge-dependent interactions of monomeric and filamentous actin with lipid bilayers. Proc. Natl. Acad. Sci. U.S.A. 117, 5861–5872. doi: 10.1073/pnas.1914884117

PubMed Abstract | CrossRef Full Text | Google Scholar

Sechi, A. S., and Wehland, J. (2000). The actin cytoskeleton and plasma membrane connection: ptdins(4,5)P(2) influences cytoskeletal protein activity at the plasma membrane. J. Cell Sci. 113(Pt 21), 3685–3695.

Google Scholar

Seidel, A., Lepenies, I., Engler, T., Cherif, C., and Zastrau, B. W. (2009). Aspects of creep behavior of textile reinforcements for composite materials. Open Mater. Sci. J. 3, 67–79. doi: 10.2174/1874088X00903010067

CrossRef Full Text | Google Scholar

Seifert, R., and Wenzel-Seifert, K. (2002). Constitutive activity of G-protein-coupled receptors: cause of disease and common property of wild-type receptors. Naunyn Schmiedeberg’s Arch. Pharmacol. 366, 381–416. doi: 10.1007/s00210-002-0588-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Sens, P., and Plastino, J. (2015). Membrane tension and cytoskeleton organization in cell motility. J. Phys. 27:273103. doi: 10.1088/0953-8984/27/27/273103

CrossRef Full Text | Google Scholar

Shi, Z., and Baumgart, T. (2015). Membrane tension and peripheral protein density mediate membrane shape transitions. Nat. Commun. 6:5974. doi: 10.1038/ncomms6974

PubMed Abstract | CrossRef Full Text | Google Scholar

Shi, Z., Graber, Z. T., Baumgart, T., Stone, H. A., and Cohen, A. E. (2018). Cell membranes resist flow. Cell 175, 1769.e13–1779.e13. doi: 10.1016/j.cell.2018.09.054

PubMed Abstract | CrossRef Full Text | Google Scholar

Singer, S. J., and Nicolson, G. L. (1972). The fluid mosaic model of the structure of cell membranes. Science 175, 720–731. doi: 10.1126/science.175.4023.720

PubMed Abstract | CrossRef Full Text | Google Scholar

Singh, A., Saha, T., Begemann, I., Ricker, A., Nüsse, H., Thorn-Seshold, O., et al. (2018). Polarized microtubule dynamics directs cell mechanics and coordinates forces during epithelial morphogenesis. Nat. Cell Biol. 20, 1126–1133. doi: 10.1038/s41556-018-0193-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Stewart, M. P., Helenius, J., Toyoda, Y., Ramanathan, S. P., Muller, D. J., and Hyman, A. A. (2011). Hydrostatic pressure and the actomyosin cortex drive mitotic cell rounding. Nature 469, 226–230. doi: 10.1038/nature09642

PubMed Abstract | CrossRef Full Text | Google Scholar

Sugimoto, Y., Whitman, M., Cantley, L. C., and Erikson, R. L. (1984). Evidence that the Rous sarcoma virus transforming gene product phosphorylates phosphatidylinositol and diacylglycerol. Proc. Natl. Acad. Sci. U.S.A. 81, 2117–2121. doi: 10.1073/pnas.81.7.2117

PubMed Abstract | CrossRef Full Text | Google Scholar

Sun, F., Schroer, C. F. E., Xu, L., Yin, H., Marrink, S. J., and Luo, S.-Z. (2018). Molecular dynamics of the association of L-selectin and FERM regulated by PIP2. Biophys. J. 114, 1858–1868. doi: 10.1016/j.bpj.2018.02.034

PubMed Abstract | CrossRef Full Text | Google Scholar

Svitkina, T. M. (2020). Actin cell cortex: structure and molecular organization. Trends Cell Biol. 30, 556–565. doi: 10.1016/j.tcb.2020.03.005

PubMed Abstract | CrossRef Full Text | Google Scholar

van Meer, G., Voelker, D. R., and Feigenson, G. W. (2008). Membrane lipids: where they are and how they behave. Nat. Rev. Mol. Cell Biol. 9, 112–124. doi: 10.1038/nrm2330

PubMed Abstract | CrossRef Full Text | Google Scholar

Vasanji, A., Ghosh, P. K., Graham, L. M., Eppell, S. J., and Fox, P. L. (2004). Polarization of plasma membrane microviscosity during endothelial cell migration. Dev. Cell 6, 29–41. doi: 10.1016/s1534-5807(03)00397-6

CrossRef Full Text | Google Scholar

Venkatakrishnan, A. J., Deupi, X., Lebon, G., Tate, C. G., Schertler, G. F., and Babu, M. M. (2013). Molecular signatures of G-protein-coupled receptors. Nature 494, 185–194. doi: 10.1038/nature11896

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, W., Yang, L., and Huang, H. W. (2007). Evidence of cholesterol accumulated in high curvature regions: implication to the curvature elastic energy for lipid mixtures. Biophys. J. 92, 2819–2830. doi: 10.1529/biophysj.106.097923

PubMed Abstract | CrossRef Full Text | Google Scholar

Ward, N.-A., Hirst, S., Williams, J., and Findlay, J. B. C. (2012). Pharmacological chaperones increase the cell-surface expression of intracellularly retained mutants of the melanocortin 4 receptor with unique rescuing efficacy profiles. Biochem. Soc. Trans. 40, 717–720. doi: 10.1042/BST20110764

PubMed Abstract | CrossRef Full Text | Google Scholar

Waugh, R., and Evans, E. A. (1979). Thermoelasticity of red blood cell membrane. Biophys. J. 26, 115–131. doi: 10.1016/S0006-3495(79)85239-X

CrossRef Full Text | Google Scholar

Westkämper, E., and Warnecke, H.-J. (2011). Einführung in die Fertigungstechnik (8., aktualis. u. erw. Aufl., korr. Nachdr). Cham: Vieweg + Teubner.

Google Scholar

Wollman, R., and Meyer, T. (2012). Coordinated oscillations in cortical actin and Ca2+ correlate with cycles of vesicle secretion. Nat. Cell Biol. 14, 1261–1269. doi: 10.1038/ncb2614

PubMed Abstract | CrossRef Full Text | Google Scholar

Zakany, F., Kovacs, T., Panyi, G., and Varga, Z. (2020). Direct and indirect cholesterol effects on membrane proteins with special focus on potassium channels. Biochim. Biophys. Acta Mol. Cell Biol. Lipids 1865:158706. doi: 10.1016/j.bbalip.2020.158706

PubMed Abstract | CrossRef Full Text | Google Scholar