Modelling complex molecular interactions in catalytic materials for energy storage and conversion in nuclear magnetic resonance

Nuclear magnetic resonance (NMR) is a non-destructive and atom-specific specific tool that has become a burgeoning analytic method for understanding the detailed molecular interactions in catalysis and energy storage materials. However, the observation of diverse chemical shifts arising from complex molecular interactions makes the interpretation of NMR spectroscopy increasingly challenging, in particular for a novel system without standards for comparison. Density functional theory-NMR (DFT-NMR) is an indispensable tool to mitigate these challenges and provide detailed 3D molecular structures that relate materials and reaction intermediate structures, and information about chemical interactions, dynamics, and reaction mechanisms. This review provides a fundamental background in DFT-NMR relating to theory development, critical parameters for calculating NMR properties, computational accuracy, and the current capabilities. A variety of practical examples from the fields of catalysis and energy storage, including CO₂ capture, are summarized to illustrate the capabilities of DFT-NMR application to date. Last but not least, cautionary notes on the application of these strategies are presented for researchers modeling their own systems.

1 Introduction

Heterogeneous catalysis is indispensable for the sustainable production of fuels, valorized chemicals, and energy conversion technologies (Corma et al., 2007). Discerning the nature of heterogeneous catalysis in terms of surfaces and molecular structures, adsorption species identity and geometry, reaction intermediates, kinetics, and reaction mechanism is critical for gaining scientific and practical insight into the chemical conversion processes that are essential for meeting the needs of the global population. Solid-state magic angle spinning (MAS) NMR spectroscopy, with its non-destructive features, is rapidly being recognized as a potent tool for accessing heterogeneous catalysis by offering atomic-level insights into the structure, interaction, and dynamics of molecules (Bell, 1994; Qi et al., 2021).

The origin of the NMR signal arrives from noting the excitation energy of an atom’s nucleus. Nuclei with non-zero spin properties will distribute to discrete and contrasting spin states when exposed to external magnetic field. Such spin states are present in a relative abundance determined by thermodynamics (Boltzmann distribution). NMR utilizes radio wave frequencies to excite those nuclei in equilibrium from a lower energy spin state to a distribution which more expresses the excited state. The excitation energy is equal to Larmor frequency of nuclei’s precession in the specific external magnetic field and is modified slightly by the electronic environment of the nucleus from bond coordination or other short-range electronic effects. After excitation and removal of radio frequency stimulation, the excess excited nuclei relax to ground state and impart a free induction decay (FID) at energies which correspond to the energy of the nucleus. This gives rise to the NMR signal. The electron density surrounding nucleus modulates the energy of such signals. Thus, the electron density, which is dependent on chemical environment, gives rise to changes in the NMR frequencies (ppm signal). If the electron density is relatively low (high), nuclei are deshielded (shielded), which cause chemical shifts downfield (upfield). As such, NMR is known as a local structure probe (Duer, 2008; Farrar and Becker, 2012).

As a local structure probe, solid state NMR (SSNMR) provides element specific information. However, correct signal assignment and a concrete understanding of the relationship between the chemical shift and molecular structure can be quite difficult. In particular for catalytic applications or energy storage systems with complex mixtures of substrates and surface molecular structures, SSNMR spectra can be complicated and difficult to interpret due to the bonding interactions on the catalyst surface that alter the chemical shielding of chemical species and can induce significant differences in the observed NMR signals relative to either bulk or isolated chemicals. The complex molecular interactions between reactants, products, intermediates, spectator species, and catalyst surfaces can also vary with temperature and pressure, rending interpretation under non-idealized conditions very challenging (Jiang et al., 2011). Moreover, conducting in situ experiments development introduces new complications due to tuned gaseous and liquid environments and some signals being temperature dependent, necessitating a more in-depth interpretation of chemical shifts and interactions (Jaegers et al., 2017a; Jaegers et al., 2020a; Jaegers et al., 2020b).

The rise of in situ NMR techniques subjects these already unclear systems to new chemical environments, exaggerating the challenge to precisely decipher the spectra (Jaegers et al., 2017a; Jaegers et al., 2020a; Jaegers et al., 2020b). Characterization of catalytic materials in operando allows researchers to observe and comprehend catalytic systems under more relevant environments through observing the resonance under a given set of conditions or tracking reaction intermediate formation and surface species in operando conditions. With in situ/operando SSNMR techniques offering a key approach for the study of catalytic reaction mechanisms under controlled conditions, NMR is regarded as an excellent tool to offer information pertaining to surface structure, adsorption species, reaction intermediates, kinetics, and reaction mechanism (Jaegers et al., 2017a; Jaegers et al., 2020b).

Relative to bulk or isolated molecules, those adsorbed onto a catalyst typically exhibit chemical shifts upfield or downfield during in situ solid-state experiments due to the perturbation of the electronic configuration imparted by bonding interactions. These new peak locations lack the standards typically employed to evaluate the data for the spectral assignment. In organometallics or ligand chemistry, for example, sophisticated structures typically make it difficult to distinctly assign discovered peaks that would further disclose interaction details between ligand and metals (Schrecken bach and Ziegler, 1995; Huynh et al., 2009; Pazderski et al., 2009; Akhdar et al., 2021). ³¹P MAS NMR of phosphorous-containing probe molecules, for example, can yield multi-peaks in a range from -80 to 20 with trimethylphosphine (TMP) and 40 to 80 with trimethylphosphine oxide (TMPO) when adsorbing on Lewis acid sites on TiO₂ facets, zeolites, and other catalysts (Zheng et al., 2011). These peaks, typically overlapped, require not only accurate deconvolution to be properly interpreted, but also a strict sense of what such minor or severe downfield/upfield shifts mean physically and molecularly (Zheng et al., 2008a; Zheng et al., 2008b; Peng et al., 2017). The spatial proximity and synergistic effect of acid sites on the adsorbed TMPO can be observed in NMR acidity characterization by the generation of new chemical species which manifest as new peaks in the NMR spectrum. It is impossible to identify specific structures of visualized pictures with molecular interactions directly from experimentally observed peaks (Li et al., 2007a; Yu et al., 2012) Therefore, theoretical simulations can be exploited in conjunction with experimental SSNMR studies to validate the structure−activity correlations of the catalytic system.

Investigation of novel systems continually necessitates new physical pictures to depict the resonance peaks discovered in experiments. Increasingly more catalytic systems are currently being explored in diverse applications, such as metal oxide facet engineering of TiO₂ (101) and (001) by utilizing ¹⁷O NMR (Li et al., 2017), a relatively less studied nucleus due to its low natural abundance and low gyromagnetic ratio (0.038% and –36*10⁶ rad s⁻¹ T⁻¹). The precise interpretation of observed peaks is challenging due to a lack of published references, giving rise to a significant potential advantage for gaining insight by combining theoretical predictions of these structures. Such applications are increasingly being expanded to other challenging nuclei with quadrupole and low sensitivity such as ⁸⁹Y, ¹⁰⁹Ag, ⁴⁵Sc, ⁹⁵Mo (Hanna and Smith, 2010).

To promote the relevance of spectra that are challenging to collect, interpreting the observed NMR chemical shifts is a key goal in analyzing experimental results. From this end, providing support from a computational modeling perspective is an attractive option due to the flexibility to model a desired system. In particular, DFT-NMR, serves as an important tool to aid the description of chemical phenomena and directly interpret observed experimental chemical shifts (Bagno and Saielli, 2015). Quantum chemical calculations, generally based on DFT, provide a trustworthy framework to predict relevant parameters such as chemical shift tensors and coupling constants, generally involving ¹H and ¹³C with notable accuracy (Bagno and Saielli, 2015). In such complex catalytic systems, an accurate prediction of NMR chemical shifts at an affordable computational cost is crucial for discerning different types of structural assignments in experimental studies.

In this review, we will first provide a general background of computational theory for NMR. Practical examples will be offered to demonstrate the application of DFT in SSNMR spectra interpretation for catalysis and energy storage. Finally, relevant cautionary notes and pitfalls that researchers frequently encounter while using DFT-NMR calculations will also be discussed to help expand the use of such techniques.

2 DFT-NMR calculation background

In this section, a general background introduction will be provided including the historical development of DFT-NMR perspectives, essential NMR parameters that can be calculated, the improvements in calculation accuracy, and expansion capabilities of NMR theoretical calculations.

A common difficulty in calculating magnetic properties in the early 1970s was that the wave functions depended on the position of molecules and required basis sets with the inclusion of notably large angular momentum terms. A landmark theory calculation was established for NMR chemical shielding by Ditchfield (Ditchfield). He introduced local gauge origins at the center of mass for each atomic orbital to define the external magnetic field. The method is called gauge-invariant atomic orbitals (GIAO) where the wavefunctions are dictated by self-consistent field (SCF) perturbation theory. Carbon and hydrogen chemical shifts calculated using this method are in good agreement with experimental results. GIAO produces accurate simulation results, but the proposed implementations of the GIAO method required high computational costs when even small or medium-sized molecules were considered. Some modified approaches improve the computational efficiency of GIAO calculations by applying the gauge factors to localized molecular orbitals instead of every atomic orbital in the individual gauge localized orbital (IGLO) method by Schindler and Kutzelnigg (Kutzelnigg, 1980; Schindler and Kutzelnigg, 1982), and the localized orbital/local origin (LORG) method by Hansen and Bouman (Hansen and Bouman, 1985; Hansen and Bouman, 1989). Localized theories, on the other hand, are predicted to encounter issues with delocalized electron structure (certain electron-deficient compounds, conductors, or inorganic molecules) and consequently, significant ring currents. As a result, the GIAO method is still considered as the most widely accepted strategy after boosting the efficiency using modern techniques inspired by analytical derivative methods. The improved GIAO method converges faster than the localized theories and provides the same accuracy with a smaller basis, particularly for the individual tensor components (Wolinski et al., 1990). The establishment of variants of the coupled Hartree-Fock (CHF) method with various gauge origins e.g., the IGLO and GIAO approaches, has been a breakthrough in the field of NMR chemical shift calculations, as systems of chemically significant size became accessible to quantitative treatment. Powerful post-Hartree-Fock approaches for the inclusion of electron correlation in chemical shift calculations were established, although calculation costs limit their widespread applicability as this approach coupled with extended basis sets becomes a lengthy computationally expensive task (Gauss and Stanton, 1996).

Later, a novel strategy for the calculation of NMR shielding tensors under the framework of DFT was introduced. Friedrich et al. (1990) were the first to integrate GIAO with DFT, albeit with restricted by the use of X_α approximation exchange-correlation (XC) functional and minimum basis sets. Malkin et al. (1994) pioneered the work by combining IGLO and DFT to derive spin-spin coupling constants with a large number of molecules. Georg et al. (Schrecken bach and Ziegler, 1995) further improved the methods by applying nonlocal XC functionals and larger basis sets on GIAO with DFT. The calculated shielding constants and tensors from such an approach are in good agreement with experiments. GIAO SCF calculations of NMR shielding neglect the electron correlation and are more time-consuming than the calculation of the energy by a factor of 2-3. An efficient alternative to traditional correlation theories is DFT which shows a considerable computational improvement compared to traditional SCF theory, especially for large molecules (Rauhut et al., 1996). With these advances, DFT-based methods have become key to the investigation of NMR properties for diverse compounds, as no other quantum-chemical method presently available allows for the necessary inclusion of electron correlation at manageable computational costs (Bühl et al., 1999).

NMR calculations demand the computation of numerous pieces of information. The chemical shielding anisotropy tensor(σ), a 3 × 3 matrix of real values corresponding to chemical shielding components in various combinations of the Cartesian directions in Equation 1. By Equation 2, we can convert chemical shielding to chemical shift. Using these primary axes, the isotropic chemical shift (δ_iso) is defined as the average of the three diagonal components of this matrix and is provided by Equation 3. Chemical shift anisotropy (CSA) is a measure of the largest deviation in a chemical shift from the isotropic value. If the biggest chemical shift deviation occurred along the Z-principal axis (δ_ZZ > δ_XX or δ_YY), the CSA would be labeled δ_CSA and supplied by Equation 4. Quadrupole nuclei, with spin number >½, have an electronic quadrupole moment interacting with electric field gradient (EFG) generated by asymmetric charge distribution. Quadrupole coupling constant (C_Q) is the product of EFG and quadrupole moment and can be used as a descriptor of the nucleus for structural purposes. The parameter also manifests itself as perturbations to the signal distribution on the NMR spectrum. These parameters are of great importance in quadrupole nuclei NMR properties in experiments and calculations (Florian et al., 2012; See et al., 2014). Despite the range of signal descriptors and their use in DFT-NMR calculations to describe systems of interest, in this review paper we primarily focus on isotropic and anisotropic chemical shift calculations.

$\mathit{ \sigma }=\left[\begin{array}{c}{\sigma }_{xx }{\sigma }_{xy }{\sigma }_{xz }\\ {\sigma }_{yx }{\sigma }_{yy }{\sigma }_{yz }\\ {\sigma }_{zx }{\sigma }_{zy }{\sigma }_{zz }\end{array}\right](1)$

$\mathit{\delta }=({\mathit{\sigma }}_{\mathit{reference}}-{\mathit{\sigma }}_{\mathit{sample}})\mathit{\ast }{10}^6(2)$

${\mathit{\delta }}_{\mathit{iso}}=\frac{{\mathit{\delta }}_{\mathit{xx}}+{\mathit{\delta }}_{\mathit{yy}}+{\mathit{\delta }}_{\mathit{zz}}}{3}(3)$

${\mathit{\delta }}_{\mathit{CSA}}={\mathit{\delta }}_{\mathit{zz}}-{\mathit{\delta }}_{\mathit{iso}}(4)$

With respect to DFT applied to NMR calculations, a plethora of improved DFT approaches were developed to improve the accuracy of the calculations and improve computational efficiency to make the method more accessible to a wider array of challenging problems. At the root, selection of an exchange-correlation functional that accurately predicts the electronic structure is of great importance to accurately predicting the NMR properties. Generally speaking, the accuracy increases from local density approximation (LDA), to generalized gradient approximation (GGA), to meta-GGA, and hybrid as the functionals become more physically consistent, though computational demands also generally increase. The reader is cautioned that the selection depends strongly on the system and application and that the sourcing of appropriate benchmarking studies for their system is necessary. More precisely, Poater et al. (2003) proposed an orbital-dependent Kohn–Sham exchange-correlation potential (statistical average potential) to improve the accuracy of DFT-NMR calculations. The distinguishing feature of this new potential is that it incorporates physically well-motivated features in both the asymptotic region and the valence and core regions. Results show considerable improvement with respect to previous potentials, like VWN or BP86, at least for the carbon, nitrogen, oxygen, and fluorine chemical shifts. This improvement is attributed to a better description of the gap between the highest occupied and lowest unoccupied orbitals. Keal et al. developed KT1 and KT2 exchange-correlation functionals using GIAO scheme. The calculated isotropic shieldings are 2-3 times more accurate than the conventional generalized gradient approximation Becke–Lee–Yang–Parr (GGA BLYP) functional (Keal et al., 2004). The BP86 gradient-corrected functional has a high agreement with experimental isotropic shifts and is further strengthened by the addition of Hartree-Fock exchange in hybrid functionals (Hrobárik et al., 2007). The shielding tensors were examined using a newly developed approach for decomposing spin-orbit DFT findings into contributions from spin-free localized orbitals. (Autschbach and Zheng, 2008). In addition to exchange-correlation functionals, the basis set is another area to consider with respect to considering all electrons in the calculations (computationally more expensive) or using a frozen core approximation. While generally, the results for DFT-NMR calculations will not differ greatly when using the frozen core approximation, when the reference calculation also employs such treatment there are systems in which this will yield less accurate results. The reader is encouraged to consider both options.

The accuracy of calculated chemical shifts is a major concern in NMR-DFT computations. Theoretical NMR calculations are capable of predicting proton NMR isotropic shieldings and shielding anisotropies with the quantitative agreement with experiments for small, isolated molecules (Kupka et al., 1999). To expand upon this, multinuclear magnetic resonance isotropic nuclear shieldings and their principal components for glucose and several related compounds were calculated at the DFT/6–31+GŁ level of theory using the B3PW91 density functional. The DFT technique performed well in predicting GIAO NMR values for simple sugars (Kupka et al., 1999). Dave Grant’s group has conducted a thorough foundational investigation and demonstrated great agreement within 0.5 ppm between experimental work and calculations (Facelli et al., 1994; Hu et al., 1998). Though successful in the described instance, the choice of models and methodologies has a significant impact on the accuracy of DFT projected chemical shifts. Kolganov et al. found that the predicted chemical shifts deviate by up to 0.8 ppm from the experimental value of 59 ppm due to the varied confinement of the methoxide species at different zeolite sites when considering different configurations of surface intermediates and their location inside the ZSM-5 pores (model accuracy). With an array of exchange-correlation functionals, uncertainty was obtained up to ±1.5 ppm for ¹³C nuclei. They indicate that the full geometry optimization of a cluster model at the PBE0-D3/6–311G (d,p) level of theory followed by GIAO/PBE0-D3/aug-cc-pVDZ calculations is the most suitable approach for the calculation of ¹³C chemical shifts of zeolite surface intermediates (Kolganov et al., 2020a). A number of carefully constructed prior reports demonstrate excellent agreement between theoretical calculations and experimental data (Facelli et al., 1994; Hu et al., 1998; Kupka et al., 1999; Kolganov et al., 2020a) which instills confidence in NMR-DFT’s ability to link experimental observations to a reasonable physical interpretation.

Increasingly computationally demanding DFT-NMR calculations may now be performed due to the rapid expansion of processing power. Unlike the closed-shell NMR shielding tensor, and many other NMR and EPR parameters, paramagnetic NMR (PNMR) shielding is an intrinsically statistical property, defined only as an ensemble average. Calculations of the PNMR shielding, therefore, requires knowledge of magnetic parameters for thermally accessible excited states. Due to these advances, PNMR shielding calculations are now feasible (Moon and Patchkovskii, 2004). A DFT-based method for computing the electron paramagnetic resonance hyperfine coupling tensors, using second-order perturbation theory, and the relativistic zeroth-order regular approximation (ZORA) Hamiltonian, has been developed and verified for radicals with few atoms and for three Ru(III) complexes (Autschbach et al., 2011). These advances have also enabled calculations on larger clusters and periodic structures. In oxide-based catalyst computations, cluster models of about 300 atoms can be calculated with all-electron basis sets to confirm the properties of surface species on the TiO₂ surface (Jaegers et al., 2019). Luong et al. (Luong et al., 2015) utilized DFT NMR to probe the molecular dynamics of polyoxometalate catalytic systems. ³¹P Diffusion Ordered NMR SpectroscopY (DOSY) was used to study bis(4-nitrophenyl) phosphate hydrolysis on Zr-substituted Keggin polyoxometalate (ZrK 2:2). They found that ZrK1:1 is in fast equilibrium with ZrK2:2 in an aqueous solution and ZrK1:1 form as the potentially active species by theoretical calculations. Periodic calculations are extensively discussed recently (Sebastiani et al., 2002; Brouwer et al., 2010; Skachkov et al., 2010; Szeleszczuk et al., 2018). Periodic and cluster calculations are both popular in NMR theoretical simulations. A comparison between periodic and cluster-based approaches for modeling solid-state interactions demonstrates that cluster-based approaches are suited for predicting NMR parameters such as magnetic/chemical-shielding and quadrupolar-coupling tensors of quadrupolar nuclei, applying to ⁹⁵Mo, ²³Na, ⁴³Ca, etc (Johnson et al., 2005; Cuny et al., 2009; Holmes et al., 2017). NMR calculations depend on local structure surrounding the interested element within three to four bonds distances. As long as the cluster system is large enough to maintain an accurate local structure near the site of interest, the results will approach those obtained from periodic calculations. This can be demonstrated by progressively increasing the size of the cluster until the calculated shift of interest approaches a stable value. From this point of view, both periodic and cluster systems are accurate enough to describe the environment of interested nuclei. A periodic structure does represent the real optimized global geometry of a given material more accurately. However, periodic calculations have their own challenges of ensuring accurate dipole and quadrupole corrections in addition to overcoming any screening challenges with charged species.

3 Practical examples

The above section is a general background introduction including historical development of DFT-NMR perspective, essential NMR parameters that can be calculated, the improvement of calculations accuracy, and expansion capabilities of NMR theoretical calculations. In this section, specific examples of the DFT-NMR approach will be described for catalysis and energy storage applications to illustrate the capabilities of DFT-NMR application to date. For catalysis, DFT-NMR can examine catalyst structures, reaction intermediates, and reaction mechanisms. For energy storage, electrodes and electrolytes in batteries are fundamentally studied by DFT-NMR to impart new insights into the structure and bonding relationships among constituent components. The practical examples provided below were selected due to the nucleis’ accessibility in experimental NMR measurement and ability to combine with comprehensive DFT analysis. Those examples are also relevant to catalysis and energy storage applications and pertain to structures, reactants adsorption, reactions mechanisms and characterization. Table 1 summarized selected examples of DFT-NMR calculations in catalysis and energy storage, providing experimental and theoretical chemical shift values, which will be comprehensively discussed in the later text.

TABLE 1

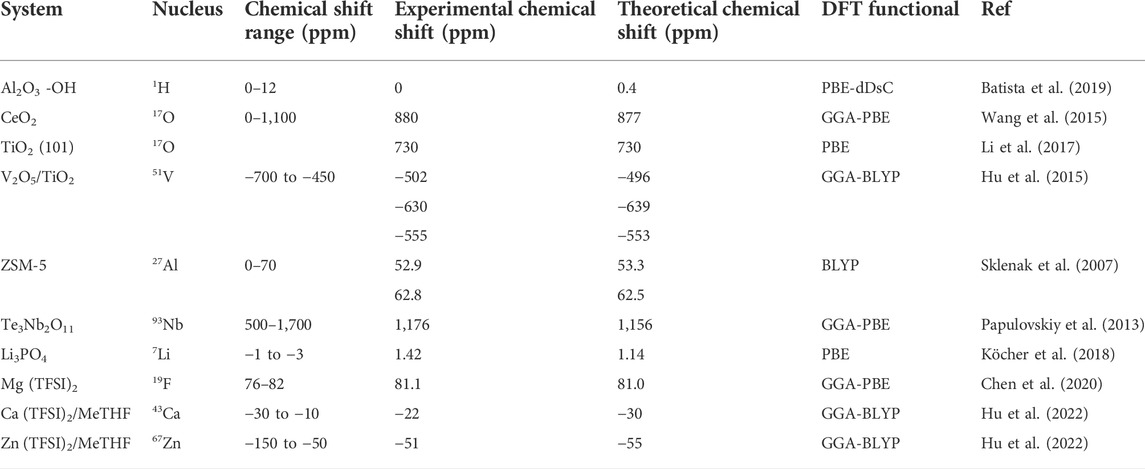
TABLE 1. Selected examples of different nuclei with comparison of experimental and calculated chemical shifts.

3.1 Catalysis

3.1.1 Catalysts structures

Identifying the structure of catalysts is critical for explaining structure-activity relationships. NMR allows for atomic-level insight into the local environment of given nuclei in catalysts. Accurate calculations can aid in cross-validating the structure of catalyst proposed based on experimental spectroscopy, which gives researchers confidence in determining the structure of catalysts. Herein, we will start with a detailed description of most common types of calculations, such as ¹H, ¹³C, ¹⁷O, ²⁷Al, ²⁹Si (Cheng et al., 2017) to more exotic nuclei that are not extensively studied by both experimental and DFT calculations, such as ^47,49Ti (Iijima et al., 2019), ⁵¹V (Pap ulovskiy et al., 2021), ³⁵Cl (Blaakmeer et al., 2016), ⁹⁵Mo ⁸⁹Y, etc.

3.1.1.1 ¹H and ¹³C

¹H NMR is important in characterizing catalytic system constituents which contain protons. In the context of catalytic structures, typically ¹H NMR is employed to study OH groups of catalysts, which play a vital role in reaction mechanisms (Xiao et al., 2020; Lin et al., 2021). Different materials show different ¹H chemical shifts of OH group and DFT NMR has been used to confirm the assignments of these important catalytic surface species. In zeolites and other metal oxides, chemical shifts below 3 ppm are typically ascribed to terminal silanol. AlOH, bridging -OH (Brønsted sites), are in the range of 3.6 ppm–5 ppm. Signals at 6.3–8.7 ppm are explained by hydrogen bonded internal silanol groups (Hunger et al., 1996). In a typical assignment for -OH of y-Al₂O₃, terminal μ₁-Al_IV OH group is observed at around 0 ppm. Bridging μ₂-(Al_V–Al_V) and μ₂-(Al_IV–Al_V) is found at 3 ppm and bridging μ₃-(Al_IV–Al_VI–Al_VI) is found at 4 ppm and 5–11 ppm with hydrogen bonding (Delgado et al., 2011), in good agreement with previous NMR calculations on aluminosilicates done at the molecular level with B3LYP and triple-ς basis sets (Xue and Kanzaki, 2007). Batista et al. (Batista et al., 2019) proposed the surface -OH on Al₂O₃ by DFT calculations combined with high field ¹H MAS NMR (Figure 1A). They found that the sharp peak at 0 ppm is consistent with models of µ1-OH located on the edges and intersection of (110) and (100) that are isolated and devoid of hydrogen bonding, which proposed a refined assignment of OH on Al₂O₃ compared to the prior empirical assignment, although -OH assignment is still under debate (Taoufik et al., 2014). ¹H NMR allows to characterize Metal-Organic Framework (MOF) materials with extraordinary structural complexity. With the help of DFT, Kobera et al. (Kobera et al., 2017) discovered the coexistence of contrasting types of unit cells in zinc boron imidazolate MOF with 80% of zinc boron imidazolate framework (ZBIF) and 20% of zinc imidazolate framework (ZIF). Based on ¹H–¹³C heteronuclear correlation (HETCOR) MAS NMR measurements in combination with gauge-including projector-augmented wave (GIPAW) DFT calculations, the ¹³C peaks were assigned to ZIF and ZBIF correspondingly with mutual interactions between two units. In homogeneous catalysis, ¹³C NMR with the aid of DFT allows for extraction of interaction information. For example, solutions of the [RhCl(C₉H₆NC(nbyl)) (Ph₂PO) (Hpz)] complex exhibit an equilibrium between trigonal bipyramid and a square-planar pyramid with OH groups interacting with phosphoryl and NH. Such a confident assignment of the ¹³C NMR shifts was possible due to the exploitation of DFT ¹³C NMR calculations (Azpeitia et al., 2021).

FIGURE 1

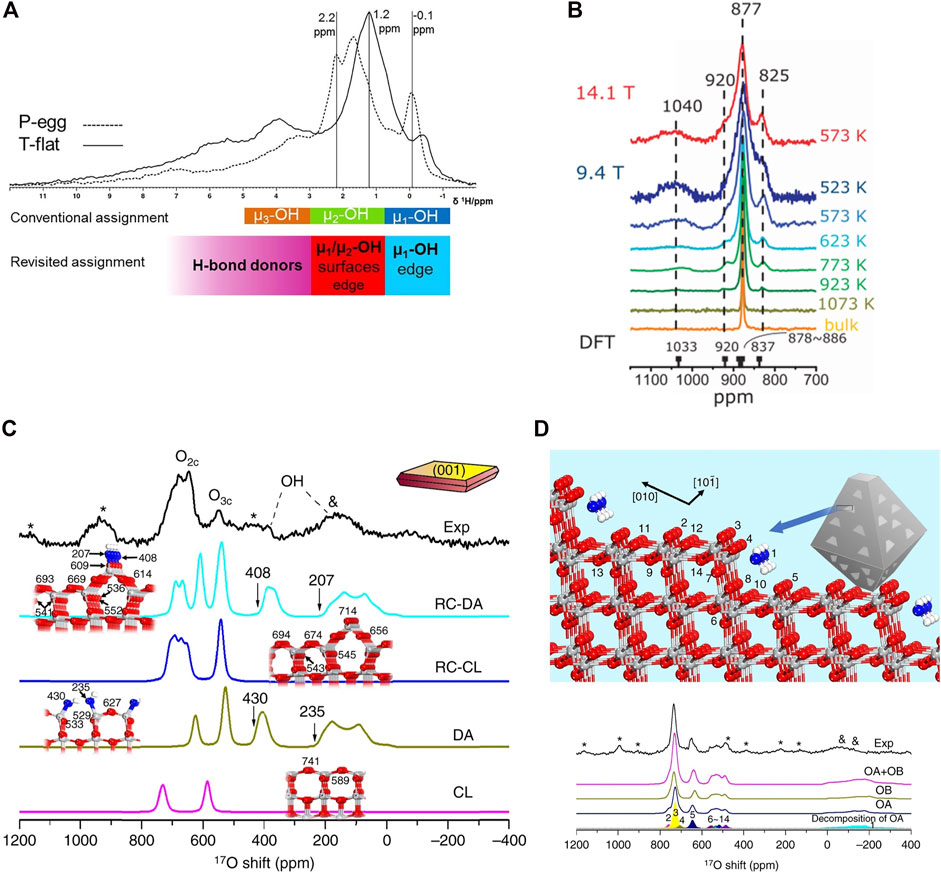
FIGURE 1. (A) ¹H MAS NMR spectra of two different aluminas showing conventional and revisited peak assignments. Reprinted with permission from ref (Batista et al., 2019) (with permission from Elsevier); (B) ¹⁷O NMR spectra for ceria nanoparticles enriched at different temperatures and acquired at different external fields compared with the ¹⁷O NMR spectra of micrometer-sized ceria (bulk ceria). Reprinted from open access from ref (Wang et al., 2015) (C) Simulated and Experimental ¹⁷O NMR spectra of isotopically labeled TiO₂. Simulated TiO₂ is defined as follows: un-reconstructed clean (001) anatase (CL), hydrated (001) anatase with ½ monolayer water coverage (DA), 1 × 4—reconstructed clean (001) anatase (RC-CL), and hydrated 1 × 4—reconstructed (001) anatase (RC-DA); (D) Structure model of TiO₂ (134) for DFT calculations with (101) step planes coupled with simulated and experimental ¹⁷O NMR spectra showing water adsorption modes (OA and OB). Reprinted from open access from ref (Li et al., 2017).

3.1.1.2 ¹⁷O

Though a relatively experimentally challenging nucleus owning to its low natural abundance and sensitivity, ¹⁷O NMR has become increasingly critical in metal oxide catalysts characterization. The combination of ¹⁷O NMR and DFT provides a route for characterizing faceted nanocrystalline oxides and related materials. ¹⁷O NMR spectra of thermally treated nanosized ceria clearly show distinct oxygen species interconvert at elevated temperatures. The oxygen ions in the center layers (fourth to ninth layers) of the model exhibit similar calculated chemical shifts of ∼880 ppm. This value approximates the experimental chemical shift of oxygen ions in bulk ceria (877 ppm), shown in Figure 1B. For the top and bottom three layers, however, different chemical shifts at about 1033, 921, and 837 ppm (with modest C_Q values less than 0.14 MHz) were computed for oxygen ions at the first, second, and third layers of the slab, respectively. These chemical shift values are remarkably similar to those of the three additional peaks observed in NMR spectra of the ceria nanoparticles (about 10 ppm difference) (Wang et al., 2015; Li et al., 2017). employed ¹⁷O solid-state NMR spectroscopy, in combination with DFT calculations, to distinguish anatase TiO₂ nanocrystals with varied exposed facets, which is widely used in photocatalysis and acid-base catalysis. With the modelling of DFT, they showed that there are distinct ¹⁷O NMR shifts from contrastingly-coordinated oxygen on the exposed (001) and (101) facets of anatase nanocrystals. As shown in Figures 1C,D, on the (001), surface reconstruction is responsible for O_2C and O_3C detected in (001) facets while on (101) only step-edge defect site O of DFT calculations can be compatible with experimental observation at 730 ppm.

In addition to bulk and surface ¹⁷O atoms in metal oxides, ¹⁷O atoms those constitute Brønsted bases are of particular interest for catalyst site characterization. Peng et al. (2005) utilized ¹⁷O NMR to discern oxygen directly coupled with Brønsted acid site in zeolites. ¹⁷O–¹H double-resonance NMR experiments are used to prove unequivocally that the ¹⁷O signal is generated by ¹⁷O near ¹H atoms. A large quadrupolar coupling constant and local distortion of 6.6 MHz are determined for this site, which is similar to that obtained in ab initio calculations of zeolite HY-like clusters and is noticeably larger than those of the oxygen atoms in Si–O–Si or Si–O–Al linkages. ¹⁷O NMR can also probe the interaction between silica and supported metals. Detailed ¹⁷O 1D and 2D MQ and HMQC MAS NMR studies show that signals in the Si−OH, Si−O−Si, and Si−O−metal regions are highly sensitive to local structural modifications. With the aid of DFT calculations, using a higher Dunning’s correlation consistent basis set cc-PVTZ for the oxygen atoms with GIAO method, mono-grafted and bi-grafted organometallic species were proposed to illustrate the interaction between support and grafted species (Merle et al., 2012).

3.1.1.3 ⁵¹V

Vanadium is increasingly attracting attention in catalysis. In our prior work, ⁵¹V SSNMR was utilized to describe the structure of supported V₂O₅ catalyst employed in redox processes, such as NOx selective catalytic reduction (SCR) and alcohol oxidative dehydrogenation. These experiments were supported by DFT-NMR calculations to explicate the specific structures in these materials. Quantum chemistry simulations of the ⁵¹V NMR chemical shifts on predicted surface structures were used as an aid in comprehending potential surface vanadium oxide species on the silica support. The results point to the formation of isolated surface VO₄ units for the dehydrated catalysts with the possibility of dimer and cyclic trimer presence for a relatively unreactive, high surface area support (SiO₂) (Jaegers et al., 2017b). It was also found that on titania supports, monomeric V species are prevalent at low vanadium loadings with two ⁵¹V NMR peaks observed at about −502 and −529 ppm for tetrahedral- and square-pyramidal-like structures, respectively. VOx dimers with two bridged oxygens result in a peak at about −555 ppm. The resonance of vanadate dimers and polyvanadates joined by one bridging oxygen atom between two neighboring V atoms is around 630 ppm, as seen in the image (Hu et al., 2015). It was found that the progressive addition of vanadia to TiO₂ forms oligomeric vanadia structures. Tungsten promoters assist the formation of oligomers of VOx. It is indicated that oligomers of VOx are active sites for SCR due to a proportional relationship of SCR reaction rate to [surface VOx concentration]². In the DFT cluster calculations, scalar relativistic effects were accounted for using the zero-order regular approximation. Triple- ζ, two-polarization function (TZ2P) was used as the basis set was used as the basis set and a cluster of about 300 atoms was optimized. Subsequent optimization of the cluster model surface can be expedited by freezing bottom rows of the titania slab (Figure 2B) (Jaegers et al., 2019).

FIGURE 2

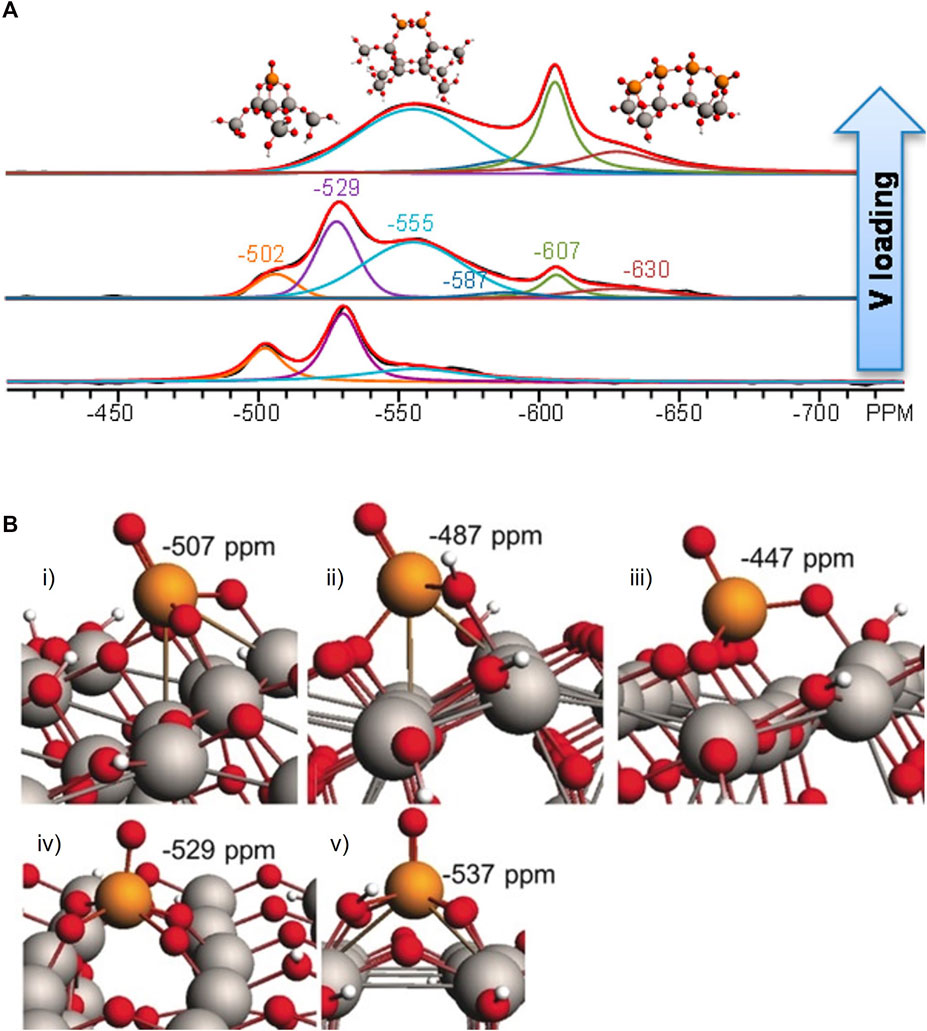
FIGURE 2. (A) ⁵¹V MAS NMR deconvolutions showing different vanadate species that are possible on VOx/TiO₂ and changes in their relative concentrations as V loading increases. Reprinted with permission from ref (Hu et al., 2015). Copyright 2015 American Chemical Society.; (B) DFT cluster models of VO₄ on TiO₂ including distorted VO₄ (i), distorted VO₄ with bridge protonation (ii), distorted VO₄ using O from TiO₂ (iii), distorted square pyramidal (iv), and distorted square pyramidal with bridge protonation (v) along with calculated chemical shifts. Reprinted with perimission from ref (Jaegers et al., 2019) © 2019 Wiley-VCH Verlag GmbH and Co. KGaA, Weinheim.

3.1.1.4 ²⁷Al

²⁷Al NMR spectroscopy is important in characterizing earth-abundant Al-containing materials with tetra-, penta-, octa-coordination environments. Zhao et al. (2017) employed ²⁷Al NMR, ³¹P NMR and DFT to correlate the Al distribution and Brønsted acidity of Beta zeolite. Three varieties of Brønsted acid strengths corresponding to distinct particular Al T-sites were proposed, shown in Figure 3A. They witnessed that the removal of one framework Al in the five-member ring (5 MR) 2-2Al (T1, T5) and 6MR-2Al (T6, T6) sites led to an increasing Brönsted acid strength of dealuminated H-Beta, which serves as a guide to directly manipulate acid strength by modulating the Al distribution. The distribution of catalytically active sites over crystallographic positions in zeolites is not random but determined by synthesis thermodynamics. For differently synthesized ZSM-5 samples, discrete ²⁷Al resonances have been identified by NMR spectroscopy. Shift calculations by DFT using finite cluster models BLYP functional (Lee et al., 1988) with a TZVP basis set (Schäfer et al., 1994) show that the observed resonances belong to Al in different crystallographic sites (Figure 3B) (Sklenak et al., 2007). An experimental and computational variation of −3 ppm of the ²⁷Al isotropic chemical shift is achieved for the substitution of one Al by one Si in the second coordination sphere of a central Al atom. ²⁹Si and ²⁷Al isotropic chemical shifts are shown to be sensitive primarily to short-range structural variations but the ²⁷Al quadrupolar coupling constant (C_Q) exhibits a more complicated behavior connected to the adjacent presence of Loewenstein-violating pairs. The periodic DFT calculations used Perdew−Burke−Ernzerhof (PBE) GGA models and GIPAW (Florian et al., 2012). A thorough analysis was carried out using high-field (19.9 T) ²⁷Al MAS NMR on three specially prepared aluminum oxide samples where the γ-, δ-, and θ-Al₂O₃ phases are dominantly expressed through careful management of the synthesis conditions. Further DFT calculations are undergoing to corroborate the proposed Al sites in different phase of Al₂O₃ (Xu et al., 2021). Ma et al. studied the guest (Mo)-zeolite interactions through ²⁷Al NMR, and two-dimensional ²⁷Al MQ MAS NMR and DFT. They found that following impregnation with molybdenum, an additional species F (Figure 3C) was generated with a large second-order quadrupolar effect (6.2 MHz) which was confirmed by DFT to be ascribed to a distorted tetrahedral framework species bonded with Mo. Mo bound with Al through two bridged oxygen perturbed the tetrahedral environment of Al leading to AlO₄ geometry from T_d to C_2v (Figure 3D). If this interaction is strong enough, Al would be extracted out of lattice by Mo, forming non-framework Al₂(MoO₄)₃ species E in the signal (Ma et al., 2002). This highlights the ability of DFT NMR to use parameters other than isotropic chemical shift to interpret experimental NMR observations.

FIGURE 3

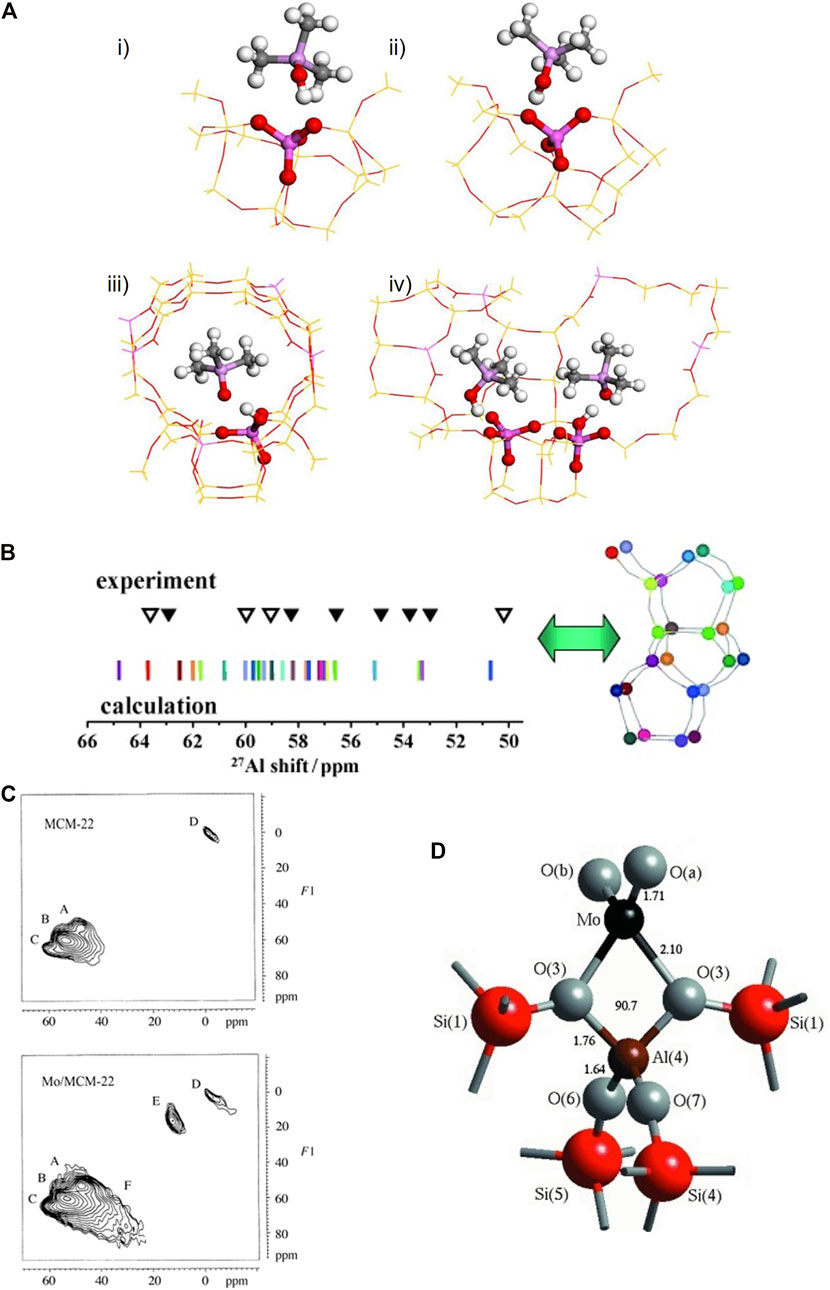
FIGURE 3. (A) Models of TMPO adsorbed onto different T sites: (i) T1, (ii) T9, (iii) 6MR-2AL (T6, T6), (iv) 5MR2-2AL (T1,T5). Al–pink, O–red, P–purple, C–black, H–white. Reprinted with permission from ref (Zhao et al., 2017). Copyright 2017 American Chemical Society; (B) Comparison of calculated and experimental resonances corresponding to Al in different crystallographic sites. Reprinted with permission from ref (Sklenak et al., 2007) © 2007 Wiley-VCH Verlag GmbH and Co. KGaA, Weinheim; (C) 2D Al Mq MAS Spectra of Mo/MCM-22 show three tetrahedral framework alumina (A,B,C) and one octahedral alumna (D) along with Mo loading signals (E,F); (D) Coordination of Mo to the framework of ZSM-5. Reprinted with permission from ref (Ma et al., 2002) © 2002 Wiley-VCH Verlag GmbH and Co. KGaA, Weinheim.

3.1.1.5 ⁸⁹Y, ⁹¹Zr, and ⁹³Nb

Chemical shift anisotropy, which provides three times more information than the isotropic chemical shift value, can also be exploited to interpret chemical systems. Liu et al. studied ⁸⁹Y NMR CSA of layered yttrium hydroxides Y₂(OH)₅X·nH₂O (X = monovalent anions), a useful material for various applications, such as catalyst supports and directly as the catalyst for epoxidation and condensation reactions. DFT calculations demonstrate that a lateral displacement only 28% of the ionic radius of Cl can result in experimentally observable ⁸⁹Y CSA differences. The variation range of ⁸⁹Y CSA is significantly greater than that of ⁸⁹Y isotropic CS, rendering examination beyond isotropic CS of great importance for systems. The effects of substituting hydroxide layers on CSA are greater than those of translating anions. These replacement strategies can greatly affect the properties of layered yttrium hydroxides, which will be response in various applications (Liu et al., 2021).

The structure and local Zr environment of MIL-140A⁹¹Zr in MOF were analyzed by ⁹¹Zr NMR. A calculated C_Q (⁹¹Zr) of 39.8 MHz which incorporated geometry optimization matched well with the observed value (35.0 MHz). It was revealed that ⁹¹Zr SSNMR was more sensitive to the Zr local structure compared to powder XRD, which could be utilized to refine the Metal-centered secondary building units geometry in the Zr-based MOFs (He et al., 2014).

As stated previously, DFT NMR can be used to bridge the gaps of experimental standards, but it can also be used to construct a set of standards for which to compare both computed and experimental chemical shifts. Ab initio DFT calculations for ⁹³Nb NMR over fifty individual compounds were used with experimental data to establish several patterns for generating guidelines in interpreting NMR spectra of complex niobium oxide systems, such as amorphous and multicomponent heterogeneous Nb based catalysts. New experimental and calculated ⁹³Nb NMR data were acquired for numerous compounds of special relevance for catalysis, including AlNbO₄, VNb₉O₂₅, K₈Nb₆O₁₉ and Cs₃NbO₈. The chemical shielding span tends to increase with the coordination. Knowing these broad tendencies is useful while researching multicomponent and frequently amorphous niobium oxide catalytic systems. It became obvious that the GIPAW computational results are often beneficial for correct interpretation and analysis of complex ⁹³Nb NMR spectra due to the profusion of unique niobium sites in a given or among different crystal structures (Papulovskiy et al., 2013).

3.1.2 Adsorbates

3.1.2.1 ³¹P

Aside from direct characterization of catalysts by NMR to offer structure information, characterizing adsorbed molecules to gain insight into the catalyst structure, reaction intermediates, chemical kinetics, and reaction mechanisms offers an alternative avenue to understand systems. These options have become increasingly accessible to catalysis with the emergence of in situ solid state NMR spectroscopy under batch type and continuous flow conditions (Hunger and Horvath, 1995; Zhang et al., 2012). One method of providing structural information about the catalyst is to use probe molecules to characterize the surface (Yang et al., 2005; Li et al., 2007b). Characterizing acid properties of catalysts, for example, is of great significance in acid catalysis. NMR can contribute to this direction with various probe molecules and theory calculations (Zheng et al., 2016). Deuterated pyridine (pyridine-D₅) is one of the most widely used NMR probe molecules. Zheng et al. predicted the pyridine adsorption structure as well as the ¹H chemical shift using an 8T zeolite model with varying Si–H bond lengths to reflect the Brønsted acidic sites with different strengths (from weak to strong to superacid). According to the theoretical calculations, a smaller ¹H chemical shift of the pyridinium ions on the solid acids indicates a stronger acid strength (Zheng et al., 2007). ³¹P MAS NMR investigation characterizing catalyst acidity is suitable as it has a high natural abundance (100%), a nuclear spin of 1/2, and a large gyromagnetic ratio making it a sensitive nucleus. ³¹P MAS NMR of trimethylphosphine (TMP) and trimethylphosphine oxide (TMPO) adsorption on TS-1 or H-Beta zeolites revealed a variety of Brønsted and Lewis acidic sites on the surface, and DFT theoretical calculations further provided the exact assignments of these sites. Two kinds of Brønsted acids were identified by TMPO on H-Beta validated by DFT. The down-field signal at 71.3 ppm can be attributed to TMPO adsorption on either the Al₁–OH–Si₃ or Al₆–OH–Si₄ site, whereas the signal at 67.3 ppm was caused by TMPO attached to the Al₈–OH–Si₃ site. Two types of Lewis acids were identified at −32.0 and −47.0 ppm with TMP adsorbed on H-Beta, attributed to the extra-lattice oxo-AlOH²⁺ species and the three-fold coordinated lattice-Al, extra-framework Al(OH)₃, oxoAlO⁺ species, respectively (Yang et al., 2008; Gu an et al., 2009). According to DFT calculations based on a modeled 8T zeolite cluster model, it was revealed that the ³¹P NMR chemical shifts of various adsorbed trialkylphosphine oxides adsorbed on solid acid catalysts exhibit a linear correlation with the proton affinity (PA), which was used as a measure of Brønsted acid strength. Accordingly, an averaged downfield offset of roughly 8 ppm was found between the ³¹P chemical shifts of adsorbed TEPO, TBPO, and TOPO compared to that observed for TMPO (Zheng et al., 2008a). Concerns have been raised, however, relating the assignment of P containing probe molecules (Bornes et al., 2019; Pires and Fraile, 2020). ³¹P NMR resonances usually assigned to TMPO molecules interacting with Brønsted sites/Lewis sites of varying acid strength instead result from both confinement effects at zeolites channel system and the formation of protonated TMPO dimers. AIMD-based calculations demonstrate that even at modest loadings, certain molecules form (TMPO)₂H⁺ dimers (³¹P resonances in the 40–60 ppm range). (Bornes et al., 2021).

3.1.2.2 ¹³C, ¹⁷O, ¹⁵N, and ¹H

Using CO₂ as an adsorbate, ¹³C and ¹⁷O NMR can investigate the direct CO₂ capture mechanisms and basicity of catalysts (Wang et al., 2014a; Lund et al., 2022). When a CO₂ molecule is adsorbed onto a specific site, the ¹³C chemical shift value of CO₂ will be different compared with that in bulk CO₂ gas phase. That can provide critical information for cross validating the molecular interaction models that are important for designing materials for direct air capture. Lund et al. (Lund et al., 2022) discovered that various CO₂ capture sites with mono- and bidentate carbonates at the Mg−O sites with adjacent Al and bicarbonates at Mg−OH sites without adjacent Al by combining NMR and DFT. Figure 4A summarizes our recent results obtained from the studies of model ionic liquid [P₆₆₆₁₄][Triz]. Pure CO₂ gas generates a single ¹³C NMR peak located at 125 ppm. When a CO₂ molecule interacts with a triazole anion, a C-N bond is formed with a bond distance of 1.629 Å, suggesting a very strong bonding. When a CO₂ molecule is adsorbed onto the ionic liquid, there are two possibilities for adsorption with one forming a strong C-N bond of 1.499 Å and the other one forming a C-N bond of 2.817 Å. The latter is more energetically favorable by 9.8 kcal/mol. These two cases are distinctly different in their ¹³C NMR spectra, i.e., with CO₂ peak positions differing by 26.2 ppm and triazole by -9 ppm, respectively. As for basicity, ¹⁷O NMR can detect CO₂ adsorption sites on MgO. Two 3-coordinated bare surface oxygen sites, resonating at 39 and 42 ppm, are found, although only the latter is involved in CO₂ adsorption. Double resonance NMR and DFT calculation results prove that the difference between the two species is the close proximity to hydrogens, and CO₂ does not bind to the oxygen ions with a shorter O-H distance, shown in Figure 4B. Spin-polarized DFT calculations were carried out using VASP with PAW method. To account for electronic exchange and correlation, the PBE functional was employed. The oxygen-terminated MgO (111) surface was used to study CO₂ adsorptions (Du et al., 2022).

FIGURE 4

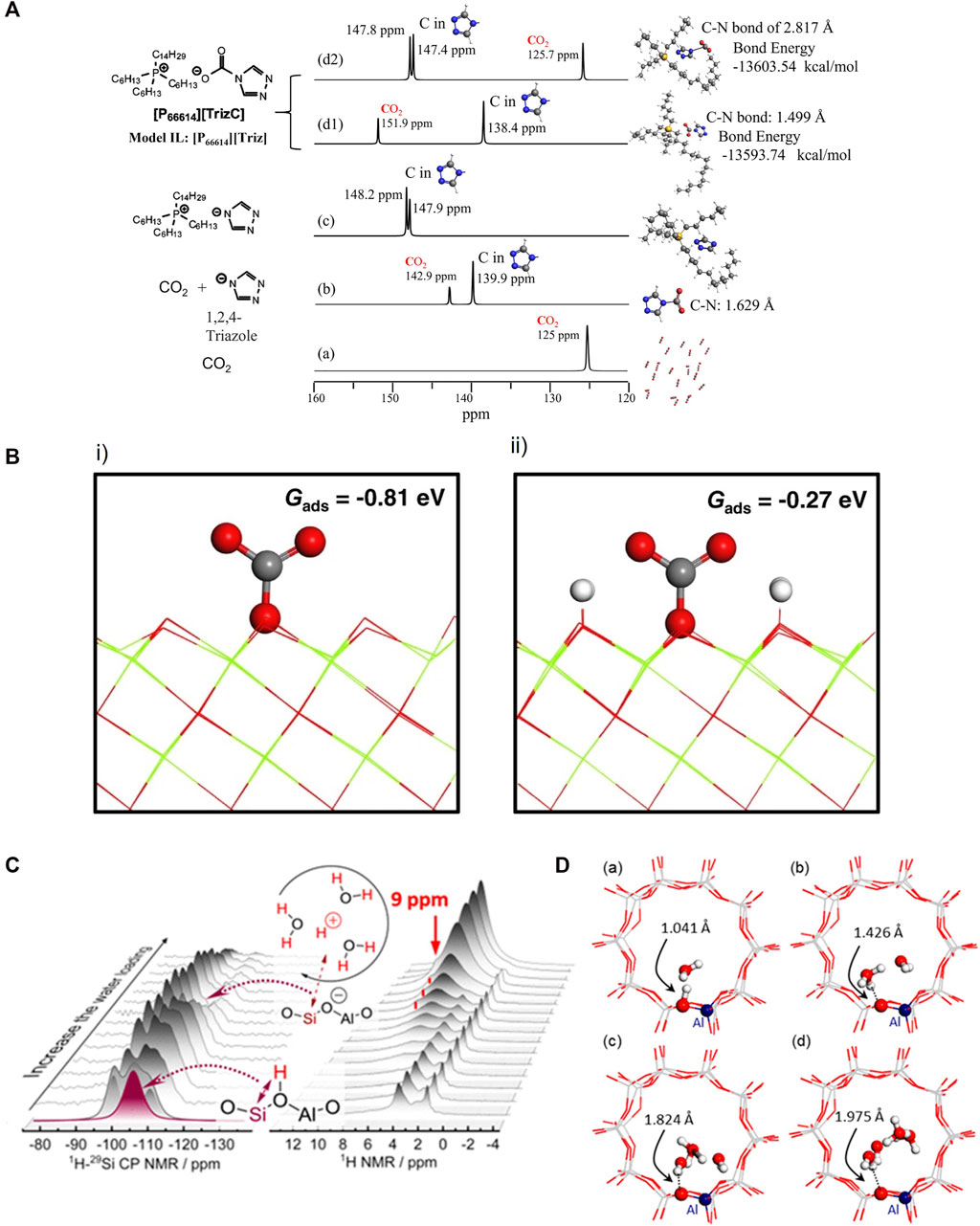
FIGURE 4. (A) DFT-NMR predicted ¹³C NMR spectra of CO₂ and triazole in various cases of model ionic liquids [P₆₆₆₁₄][Triz]. (a) Pure CO₂ gas; (b) CO₂ molecule interacts with a triazole anion. (c) The two carbons associated with trizole in [P₆₆₆₁₄][Triz]; (d) When a CO₂ molecule is absorbed onto IL of [P₆₆₆₁₄][Triz], there are two possibilities of absorptions with one forming a strong C-N bonding of 1.499 Å (d1) and the other one forming a loose C-N bond of 2.817 Å (d2). (B) Molecular CO₂ adsorption on modeled (i) MgO (111) and (ii) MgO(111)-4H. Reprinted from open access from ref (Du et al., 2022). (C) ¹H-²⁹Si CP NMR and ¹H NMR with increasing amount of water loading. (D) Structures modeling with increasing numbers of water molecules optimized by DFT cluster calculations in ZSM-5 channels. Reprinted with permission from ref (Wang et al., 2019) Copyright 2019 American Chemical Society.

Surface adsorbed species of ammonia on zeolites may also be discovered using ¹⁵N NMR. In situ EPR and solid-state NMR spectroscopies combined with DFT calculations allowed the identification of NH⁴⁺ [Cu(NH₃)₅]²⁺ [Cu(O_f)₂(NH₃)₂]²⁺ [Cu(NH₃)₂]⁺, and [CuO_f(NH₃)]⁺ (O_f being framework oxygen) The findings demonstrate that ammonia is able to reduce Cu²⁺ to Cu⁺ and elucidate the species generated in Cu-SSZ-13, which has major implications for the elucidating the SCR reaction mechanism. Periodic DFT was conducted with the GGA and PAW formalisms (Moreno-González et al., 2015).

¹H NMR can be utilized to elucidate water interactions resulting in zeolite Brønsted acid sites converting to hydrated hydronium ions. With rising water chemical potential, a signal at 9 ppm was recorded at loadings of 2–9 water molecules per Brønsted acid site and is ascribed to hydrated hydronium ions on the basis of the evolution of the signal, shown in Figure 4C. The intensity of ¹H−²⁹Si cross-polarization signal grew at first and then gradually declined (Figure 4C). This indicates that hydrogen bonds between water molecules and the tetrahedrally coordinated aluminum in the zeolite lattice weaken with the formation of hydronium ion−water clusters and increase proton mobility. DFT-based ab initio molecular dynamics studies at various temperatures and water concentrations agree well with this interpretation. For chemical shielding calculations, modeling shows in Figure 4D, GGA:BLYP-D was used for geometry optimization, the TZ2P Slater-type basis set was employed (Wang et al., 2019). H-ZSM5 clusters containing 58 T atoms were obtained from a periodic structure previously used as a theoretical model and was terminated by H atoms (Si−H bond lengths fixed at 1.455 Å) to substitute terminal O atoms while maintaining peripheral charge neutrality was shown to be an acceptable approximation for calculating NMR parameters at sites several bonds from the Si-H modeled sites (Jones et al., 2014).

3.1.3 Intermediates/reaction mechanism/dynamics

NMR paired with DFT can also give vital information regarding intermediates, dynamics and reaction mechanisms, all of which are critical to catalysis understanding and hence catalyst design.

3.1.3.1 ¹³C

With the aid of DFT, ¹³C NMR can identify reaction intermediates and spectators of carbon containing chemical processes and offer information on the reaction mechanisms. On ZSM-5 methanol-to-olefins (MTO) occurs through a hydrocarbon-pool process. SSNMR spectroscopy and DFT calculations were used to help discover three types of cyclopentenyl cations and a pentamethylbenzenium ion, which are thought to interact to generate propene via a paring process (Wang et al., 2014b). DFT and ¹³C SSNMR were used to examine the adsorption behaviors of methanol in 8-membered ring cage-type molecular sieves DNL-6 and SAPO-42. As presented in Figure 5A, the chemical shifts of methanol with lta orientation in DNL-6 (51.4 and 51.2 ppm for site O1 and O2) are similar to that adsorbed in the lta cavity of SAPO-42 (51.6 ppm), whereas the chemical shifts of D8R orientation (52.1 and 52.4 ppm for O1 and O2) are roughly 1.0 ppm higher than that of lta orientation, which coincides with the ¹³C NMR experiment. It is concluded that the confined space of double 8-membered rings in DNL-6 promotes the methanol adsorption accompanied by the methyl groups orienting to D8R space and the hydroxyl groups of methanol anchored by Brønsted acid sites (Lou et al., 2021). Methane selective conversion is essential in C1 chemistry. ¹³C SSNMR and DFT may be used to investigate methane interactions and intermediates with Cu/H-ZSM-5. Three distinct surface methoxy-like species (−O–CH₃) was observed: methanol adsorbed on two djacent Cu sites (Cu–(HOCH₃)–Cu, 62.6 ppm), methanol adsorbed on zeolite Brønsted acid sites (52.9 ppm), and lattice-bound methoxy groups (Si–O(CH₃)–Al, 58.6 ppm). NMR and DFT combined results suggested that methane activation by Cu/H-ZSM-5 can be aided by both mononuclear and multinuclear Cu species trapped inside the zeolite (Kolganov et al., 2020b).

FIGURE 5

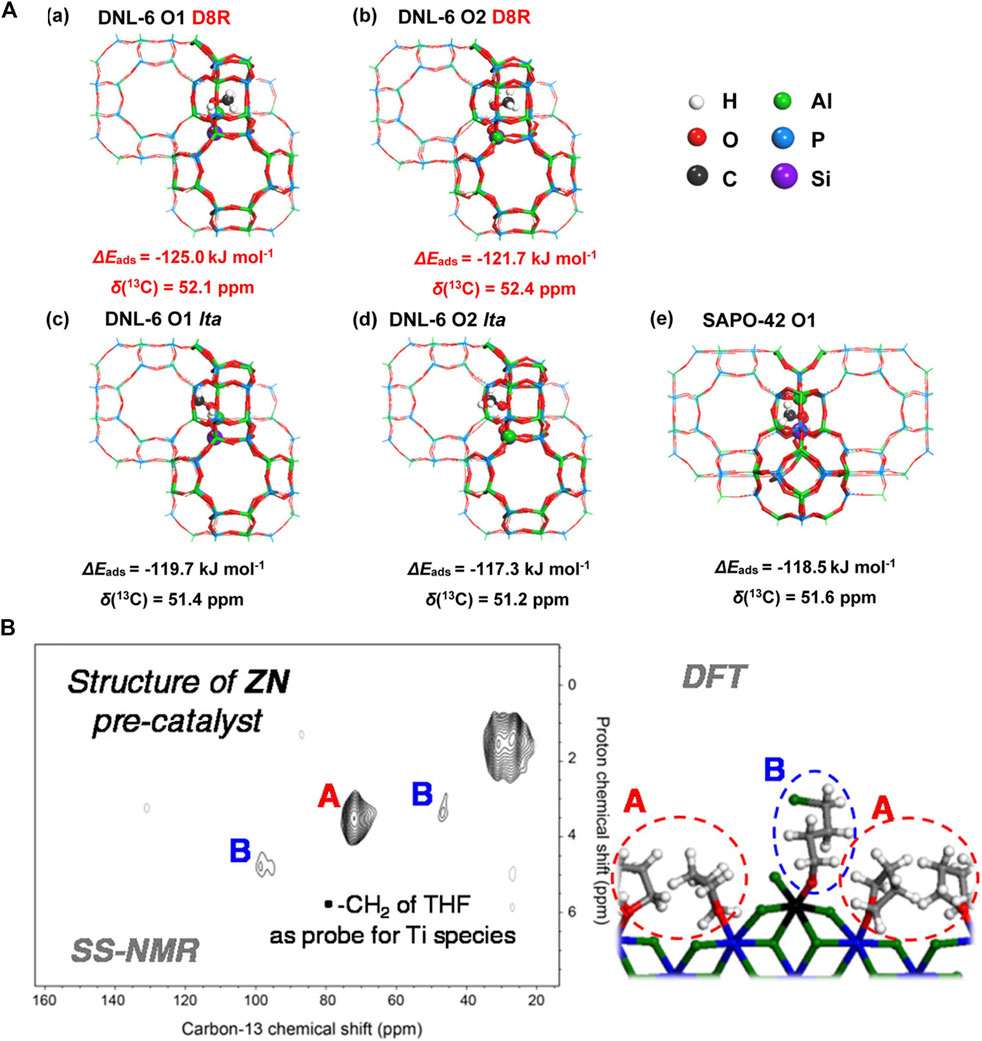
FIGURE 5. (A) Optimized geometries of the methanol adsorbed DNL-6 (a–d) and SAPO-42 zeolites: (a) adsorbed on O1 site with D8R orientation, (b) adsorbed on O2 site with D8R orientation, (c) adsorbed on O1 site with lta cage orientation, (d) adsorbed on O2 site with lta cage orientation, (e) adsorbed on the O1 site of SAPO-42. Reprinted with permission from ref (Lou et al., 2021). © 2020 Wiley-VCH Verlag GmbH (B) 2D 1H-13C HETCOR ssNMR of MgCl2/TiCl4/THF Ziegler-Natta Precatalsyt coupled with DFT calculated adsorption modes for THF. Reprinted with permission from ref (Grau et al., 2012). Copyright 2012 American Chemical Society.

In addition to detecting intermediates on zeolites, coupling high-resolution ¹³C solid-state NMR spectroscopy with periodic DFT calculations, it was demonstrated that the major surface species in the Ziegler-Natta (ZN) precatalyst corresponds to an Ti 4-chlorobutoxy species, which results from the ring-opening of tetrahydrofuran (THF) on a cationic Ti(IV) species (species B in Figure 5B) surrounded by THF coordinated to nearby Mg (A species in Figure 5B) (Grau et al., 2012). Carbocations are relevant to acid-catalyzed reactions although they are difficult to observe in heterogeneous catalysis owning to their relatively short lifetimes. By combining DFT calculations with ¹H and ¹³C MAS NMR spectroscopy, the tert-butyl cation was successfully identified on zeolite H-ZSM-5 upon conversion to isobutene by trapping this intermediate with ammonia (Dai et al., 2015). Surface methoxy can be detected by combinatorial DFT and experimental techniques. The predicted value deviates by up to 0.8 ppm from the experimental value of 59 ppm due to the variable confinement of the methoxide species at different zeolite sites (model accuracy). The selection of the exchange–correlation functional (method accuracy) introduces ±1.5 ppm uncertainty in the computed chemical shifts (Kolganov et al., 2020a). Philippou et al. utilized ¹³C NMR conjunction with DFT to identify different methoxy species on SAPO-34. They discovered that type 1 bridging methoxy is the primary species in the methylation process and results from methanol reaction on a Brønsted acid site, whereas type 2 linear methoxy is produced by interacting with terminal -OH of Al-OH (Philippou et al., 1998). Methoxy species were also examined in Keggin 12-H₃PW₁₂O₄₀ in photocatalysis. Rotational Echo Double Resonance (REDOR) NMR experiments combined with quantum chemical DFT calculations revealed that the two matching methyl groups lie on the O_c and O_d atoms of the Keggin anion, generating the surface O_cCH₃ and O_dCH₃ species, both of which are photochemically reactive. It was revealed that the O_eCH3 species was substantially more reactive (Zhang et al., 2008). Nicholas et al. attempted to examine the existence of the isopropyl cation in isopropanol dehydration reactions on zeolites. With B3LYP as DFT functional and DZVP2 basis set, it was revealed that π-bonded precursor and the covalently bound surface isopropoxy is the active intermediate while the isopropyl cation is not involved in the reaction. In contrast, complete label scrambling does occur for isopropyl bromide on superacids such as SbF₅ and AlBr₃, proving the presence of isopropyl cation (Nicholas et al., 1998).

Molecular dynamics can be investigated by the DFT-NMR combination as well. The molecular dynamics of a range of organometallic complexes attached to silica surface was investigated by NMR and DFT. Differential dynamics features based on dipolar coupling constants are observed through residual ¹H-¹³C dipolar couplings and ¹³C chemical shift anisotropies in a variety of alkylidene-based surface organometallic catalysts. Dynamic behaviors are thought to be related to the presence of bulky ligands and/or to the 4d or 5d nature of the metals. The motion is not isotropic and might consist of either leaps between two locations or confined vibrational movements (Blanc et al., 2008).

To conclude, NMR spectroscopy combined with DFT can provide a wealth of information on catalyst structure, reactant adsorption, reaction intermediate and mechanisms, providing an enabling method for us to better understand catalysis fundamentals. We have shown that when DFT is combined with ¹H, ¹³C, ¹⁷O, ²⁷Al, ⁵¹V, ⁸⁹Y, ⁹¹Zr, and ⁹³Nb NMR, insights into the structure of -OH groups of metal oxides, MOF, Al-containing zeolites, supported vanadium oxide, yttrium hydroxides, niobium oxide, and other materials can be provided. Furthermore, by investigating adsorbates on catalyst surface using ³¹P, ¹⁷O, ¹⁵N, ¹H, and ¹³C, etc., the catalyst acidity, basicity, adsorption species, hydronium ions formation, reaction intermediates and mechanisms and molecular dynamics can be clearly detected.

3.2 Energy storage

In situ and ex situ NMR spectroscopies have also made major contributions to the field of energy storage and suffer from similar spectral interpretations challenges as catalysis applications. With the use of DFT simulations, NMR can provide extensive molecular level information about electrolytes, separators, and electrodes (Hu et al., 2018a).

3.2.1 Electrodes

3.2.1.1 ⁷Li

Electrodes are cathodes and anodes, which are electrical conductors for reduction and oxidation, respectively. These components are necessary materials for the operation of a battery and are commonly comprised of metals. Li is a ubiquitous electrode, especially for Li ion battery applications, but the speciation of Li on the electrode is both diverse and not fully understood. By developing a reference scale of a collection of diamagnetic compounds for Li SSNMR, such as Li₃N, LiCl, etc., the accuracy and dependability of theoretical modeling methodologies of Li chemical shielding values are benchmarked. Geometry, ionic mobility, and relativistic effects are all discussed and examined. The proposed strategy was first examined for simple lithium salts and subsequently with lithium titanate (Li-ion electrode). The selection of XC-functionals has minimal effect on chemical shift while geometry optimization has significant effect on chemical shift and spectrum lineshape. It demonstrated that accurate and dependable computations need an accurate crystal structure (Köcher et al., 2018).

See et al. (See et al., 2014) also employed in situ ⁷Li NMR to explore the low capacity and poor cycling of Li batteries. Both the experiment and the DFT revealed that the sole solid product generated in the cell is Li₂S. Concurrent with the development of a solid component (Li₂S), S is reduced to soluble polysulfide species. During the discharge, soluble Li⁺ species are also found, which has an adverse effect on capacity retention. In theory, the PBE XC-functional was used and electric field gradients were calculated to obtain the quadrupolar coupling constant C_Q.

Defect locations are critical in electrode materials. ⁷Li NMR can also investigate the impact of defect sites on LiVPO₄F material and the resulting local electronic structure. Based on the PAW method, authors substituted one fluoride ion by an oxygen associated with a lithium vacancy. The highest agreement between theory and experimental one was achieved if a lithium vacancy is associated with the O defect, thus creating 2 V⁴⁺ ions around O local electronic structure. The spin transfer mechanisms from V³⁺ or V⁴⁺ ions to the Li nuclei are also investigated (Bamine et al., 2017).

3.2.1.2 ¹⁷O

In addition to Li NMR, ¹⁷O NMR may be used to characterize metal oxides for these types of systems. Five resonances with considerable ¹⁷O shifts were identified in the Li₂MnO₃ cathode, which were attributed to the Fermi contact interaction with directly bound Mn⁴⁺ ions. Utilizing first-principles calculations, the five peaks were divided into two groups by shifts at 1,600–1,950 ppm and 2,100–2,450 ppm, which were ascribed to the ¹⁷O shifts of environments corresponding to the 4i and 8j sites in pure Li₂MnO₃, respectively (Seymour et al., 2016).

3.2.1.3 ²³Na

Additives to carbon-based electrodes are also of a topic of interest with a wide variety of research objectives (Forse et al., 2015; Griffin et al., 2016; Deringer et al., 2018; Cervini et al., 2019; Wang et al., 2021). Morita et al., for example, examined Na state in a hard carbon (HC) electrode with ²³Na NMR. They demonstrated that the sodium components are allocated to Na in electrolyte, reversible ionic Na components, irreversible Na components assigned to SEI or non-extractable sodium ions in HC, and degraded Na compounds. Using DFT calculations, it was shown in geometry optimization that the Na₃ triangle clusters stand perpendicular to the carbon surface, whereas Li₂ and Li₄ clusters lying on the pore surface mutually interact more readily, which elucidates why the adequate heat-treatment temperature of Na HC is needed to achieve large sodium storage, a temperature that exceeds the heat treatment temperature for lithium storage (Dahn et al., 1995; Morita et al., 2016).

3.2.2 Electrolyte

3.2.2.1 ¹H

The electrolyte carries ions during the oxidation and the reduction process as ions are stripped from or intercalated onto the electrode surfaces. Electrolyte dynamics are important in electrochemistry, as we saw with molecular dynamics in the preceding catalysis section. Two types of molecular movements were discovered using ¹H NMR linewidths: isotropic rotation with molecular diffusion and axial rotation with axis fluctuation. The rapid diffusion of crown ether–cation complex intercalates is beneficial for electrochemical and chemical intercalation and deintercalation (Gotoh et al., 2018).

3.2.2.2 ¹⁹F, ¹³C, and ²⁵Mg

Chen et al. studied Mg (TFSI)₂·dimethoxyethane (DME) adduct as an electrolyte component with ¹⁹F NMR and DFT calculations. Such fundamental insight is critical to improve electrolyte design. 45% of adduct TFSI⁻ stays in the crystalline region maintaining the trans conformer, while 55% of the TFSI remains in the disordered region undergoing conformational exchange between cis and trans conformations. DFT simulations provide ¹⁹F chemical shift values that are compatible with cis/trans conformer assignment, and the activation energy estimate for the cis-trans transition (21.1 kJ/mol) accords well with the experimental isomerization rate finding (Chen et al., 2020). Hu et al. previously studied adsorption and decomposition of electrolytes Mg (TFSI)₂ in diglyme on MgO nanoparticles Quantum chemistry calculations confirm methoxy groups on the MgO Surface decomposed from pure diglyme (G2) using ¹³C and ¹H-¹³C cross polarization NMR and quantum chemistry. As shown in Figure 6A, they found that at high Mg (TFSI)₂ salt concentrations, contact ion pairs between Mg and TFSI are formed extensively in the solution with the first solvation shell containing one pair of Mg-TFSI and two G2 molecules and the second solvation shell containing up to six G2 molecules, namely, MgTFSI(G2)₂ (G2)₆⁺, adsorbing onto the MgO surface. At 180°C, the MgO surface promotes desolvation, transforming MgTFSI(G2)₂(G2)₆⁺ to MgTFSI(G2)₂⁺ and releasing G2 molecules from the second solvation shell of the MgTFSI(G2)₂ (G2)₆⁺ cluster into the solution, observed by ¹H–¹³C CP/MAS experiments and supported by DFT (Hu et al., 2019). Hu et al. investigated solvation structures and dynamics of Mg(BH₄)₂ and Mg (TFSI)₂ in G2 using ²⁵Mg NMR and quantum chemistry calculations. It has been proven that TFSI⁻ is entirely separated from Mg²⁺ in dilute concentrations of ordinary Mg (TFSI)₂ in DGM electrolyte. Mg²⁺ and TFSI⁻ are only partially separated at increasing concentrations as the contact ion pair develops. At saturated concentration of Mg(BH₄)₂ in DGM, the first solvation shell of a Mg²⁺ ion consists of two BH₄⁻ anions and one DGM molecule, whereas the second solvation shell contains five to six DGM molecules (Hu et al., 2018b).

FIGURE 6

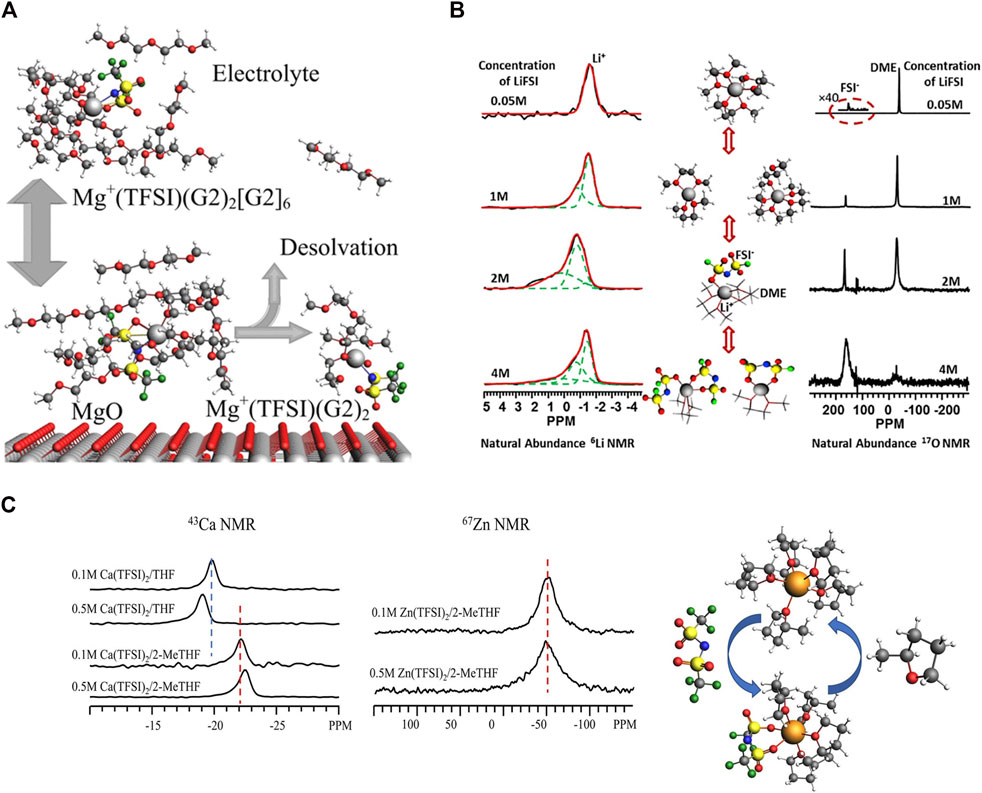
FIGURE 6. (A) Scheme of Mg (TFSI) and G2 adsorption and decomposition on MgO. Reprinted with permission from ref (Hu et al., 2019). Copyright 2019 American Chemical Society; (B) ⁶Li and ¹⁷O NMR Spectra at different LiFSI concentrations showing changes in solvation structures and relevant ppms. Reprinted with permission from ref (Wan et al., 2016). Copyright © 2015 Published by Elsevier (B)V; (C) ⁴³Ca NMR (left) of Ca (TFSI)₂ in THF and 2-MeTHF and ⁶⁷Zn NMR (right) of Zn (TFSI)₂ in THF. Reprinted with permission from ref (Hu et al., 1998). ^© 2022 Battelle Memorial Institute Published by American Chemical Society.

3.2.2.3 ¹⁷O

Wan et al. examined the solvation structure of lithium bis(fluorosulfonyl)imide (LiFSI) in DME liquid electrolyte using ⁶Li and ¹⁷O NMR shown in Figure 6B. They found in dilute concentrations (<1M), the bulk of solvates present as Li⁺(DME)₃ with a minimal contribution from LiFSI(DME)₂. As LiFSI salt concentration surpasses 2 M, the LiFSI(DME) takes over solvate. Increased salt concentration to 4 M gives rise to substantial population of Li⁺(FSI⁻)₂DME solvates. DFT computations are used to validate proposed solvation structures. Molecular dynamics simulations demonstrated that with increasing concentration, the association between DME and Li⁺ decreases, and the coordinated number of FSI increases, which is consistent with the DFT results (Wan et al., 2016). The composition of the solid electrolyte interphase using LiFSI−DME electrolytes are investigated by Wan et al. using multinuclear MAS NMR and DFT. The SEI layer associated with higher concentration (4 M) of LiFSI−DME contains a relatively smaller amount of “dead” metallic Li than the cases with dilute electrolytes (1 M LiFSI−DME and 3M LiTFSI−DME). A considerable quantity of LiF, which exhibits superior mechanical strength and high Li⁺ ionic conductivity, is observed in the SEI layer formed in the concentrated 4 M LiFSI−DME and 3 M LiTFSI−DME systems but not in the diluted 1 M LiFSI−DME system (Wan et al., 2017).

Natural abundance ¹⁷O NMR data combined with computational modeling were used to explore the solvation structures of LiTFSI in several solvents: ethylene carbonate (EC), propylene carbonate (PC), and ethyl methyl carbonate (EMC). The Li ion is coordinated with four double bond oxygen atoms from EC, PC, EMC and TFSI anion. At high LiTFSI concentrations, in particular at saturated concentrations (LiTFSI)₂(PC)₄ for LiTFSI in PC, and (LiTFSI)₂ (EMC)₃ for LiTFSI in EMC are the optimum structures (Deng et al., 2015).

3.2.2.4 ⁴³Zn and ⁶⁷Ca

Recently, our group also conducted a thorough multinuclear NMR investigation (⁴³Zn, ⁶⁷Ca, and ¹⁷O) with quantum chemistry DFT to offer precise insights into solvation structures in electrolytes comprising Ca (TFSI)₂ or Zn (TFSI)₂ in cyclic ether solvents of THF and 2-MeTHF. The cation size impact is highlighted, with Zn bonding stronger with solvent than Ca, which is decreased by the presence of a methyl group in the THF ring, shown in Figure 6C. Anion-containing solvation shells are energetically preferred in all of the electrolytes examined, resulting in significant numbers of contact ion pairs and, as a result, neutrally charged clusters (Hu et al., 2022).

To recapitulate, NMR spectroscopy conjugated with DFT can offer atomic level understanding of electrodes, electrolytes and interface in terms of detailed molecular structures, decomposition, and reaction process. By combining DFT with ⁷Li, ¹⁷O, ²³Na NMR, the structures of Li and Na battery electrodes, defects, phases, and decomposed species can be obtained. Fundamental studies in electrolyte solvation structures, decomposition mechanism on electrode surface, electrolyte dynamics can be accomplished through utilizing ¹⁹F, ¹³C, ²⁵Mg, ⁴³Zn, ⁶⁷Ca, ¹H and ¹⁷O NMR combined DFT.

4 Cautionary notes/pitfalls in modelling

Although the previous sections have detailed detailed myriad use-cases for DFT-NMR, cautionary notes must be provided here for calculations.

A general challenge with DFT is potential disparities between the optimized geometric configuration and those present in a physical system. This could impact the direct calculation of chemical shifts (Szeleszczuk et al., 2018). Finding the appropriate local minimum is important for accurate nuclear properties calculations especially in cluster optimization since DFT-NMR calculations are performed on optimized geometries. We present an example to demonstrate the influence of geometry configuration in this section (Hu et al., 2022). Consider calculating ⁴³Ca chemical shielding with the specific number of H₂O molecules with different initial geometry configurations. The obtained different ⁴³Ca chemical shielding highlights the impact of initial geometry setups, due to the possibility of landing at a local energy minimum for geometry optimization and the chemical shielding (Hu et al., 2022). However, extrapolating the statistical data to an infinite number of water molecules yields a value of 1093.3 ± 2.7 ppm because of the same converged optimized structures. That is, if an infinite number of water molecules surrounds the interested elements, then the optimized geometry should be representative of a physical system and give rise correct and reliable calculated chemical shifts.

In addition to explicit solvent definition, the Conductor-like Screening Model (COSMO) is a generally accepted method to approximate molecules in solution rather than a single molecule in gas phase. The treatment in COSMO can have an impact on the obtained results. To simulate the situation with an infinite number of H₂O molecules, the proper radius and dielectric must be supplied to COSMO for accurate results. Our findings revealed a⁴³Ca chemical shielding of 1094.5 ppm, which is consistent with the extrapolation to complete solvation estimated from the cluster model (Hu et al., 2022). An explicit solvent model may be more accessible to a general audience, at least in most cases, but adds more computational demand and the need to ensure a sufficient number of solvent molecules. For a continuum model, the results are sensitive to the dielectric and radial treatment. If these can be accurately accounted for, the continuum model should also agree with experimental results and will be less computationally demanding.

Choosing appropriate reference materials is of great important to obtain precise calculation results. The reference compound should ideally exhibit similar properties to the structures being studied. It directly determines the accuracy of the chemical shift value, but not the magnitude of the change. For example, when determining ⁴³Ca reference for liquid electrolyte solutions of Ca (TFSI)₂ NMR calculations, an isolated Ca²⁺ ion or one with just a few H₂O molecules around Ca ion are a poor reference point for solvated Ca cations due to local structures which are not directed by the bulk solution (Hu et al., 2022). Either using the sufficient number of H₂O molecules surroundings or extrapolating to infinite number of H₂O are more appropriate methods of gauging ⁴³Ca reference chemical shifts. However, choosing references presenting similar properties allows for consistent and reliable reference chemical shifts. An example for solids comes from the surface structures of vanadium oxide supported on other oxide surfaces which can be effectively referenced to V₂O₅ models (which is the secondary NMR chemical shift reference), or other similar compounds such as the vanadium-containing silsesquioxane. Table 2 shows the agreement between the experimental values for these two compounds when referenced to models of VOCl₃, the generally-accepted experimental ⁵¹V NMR reference which is toxic and volatile so often avoided in practice (Jaegers et al., 2017b).

TABLE 2

TABLE 2. Comparison of experimental and calculated vanadium chemical shifts of model compounds.

Relativistic effects should also be considered, especially for heavy nuclei, which are sensitive to such effects. In general, the relativistic effect is divided into a scalar relativistic (correction of kinetic and potential energy) and a spin–orbit coupling (the electron spin and angular momentum for heavy nuclei and light nuclei next to them) contribution (Kaupp et al., 1997). Thus, the inclusion of either scalar or spin-orbit corrections is vital to be incorporated in order to analyze nuclear properties for either heavy metals or any light atoms proximal to heavy metals (Komorov ský et al., 2008). The relativistic correction for CO/Pt adsorption energy is as high as 70% at the scalar relativistic level and 55% when spin-orbit coupling is involved, emphasizing the need of their inclusion for an accurate description of electron density. Furthermore, relativity changes the preferred adsorption location for CO/Pt from the hollow site to top (Philipsen et al., 1997). Relativistic corrections are required for compounds containing heavy elements when special relativity becomes prominent, resulting in a contraction of bond lengths and a significant change in bond energy (Autschbach, 1981). Despite strong solvent effects, relativistic DFT calculations were shown to effectively predict ¹⁸³W chemical shifts, allowing us to investigate spectra with peak spacings as small as 5 ppm (Bagno et al., 2006). Computational theorists also investigated the effect of frozen-core approximation in order to understand relativistic effects on shielding. They concluded that the frozen-core approximation can lower the number of electrons that are treated in a variational manner. Therefore, the frozen-core approximation can conserve computer resources, in particular for heavy atoms with large cores, without significantly reducing simulation accuracy (Schreckenbach and Ziegler, 1996). The shielding is subject to two types of relativistic effects: direct and geometric. Geometric effects in this context are changes in the shielding caused by relativistic-induced changes to the local minimum energy geometries, i.e., relativistic bond contraction. Direct effects are relativistic effects that confer distinct qualities at a fixed geometry. The electron density and orbital energies will alter as a result of relativity, which will have an effect on shielding. Because DFT NMR calculations rely on precise electron density to estimate the influence of electron density on nuclear shielding, scalar relativity or spin-orbital coupling must be incorporated to calculate heavy transition metals and ligands directly bound to those heavy metals (Schreckenbach and Ziegler, 1997; Wolff and Ziegler, 1998).

5 Conclusion and outlooks

This review offers discussion on the fundamental basis of DFT-NMR theory development, essential parameters, computational accuracy, and capabilities. A variety of practical examples from the fields of catalysis and energy storage are summarized to illustrate the capabilities of DFT-NMR application. It was demonstrated that DFT-NMR combination enables for offering atomic-level experiments evidence and theoretical interpretation to tackle the complexity of chemical shifts or shielding as related to the detailed molecular interaction, in particular for a novel system without standards for comparing. In the last section, cautionary considerations on the implementation of these strategies are presented for researchers modeling their own systems. As computational power continues to improve, future DFT-NMR will most likely be able to better account for quick molecular exchange, i.e., conducting (quantum molecular dynamics) QMD and then NMR calculations and weighting them based on ensemble averages (Heine et al., 2000; Whittemore et al., 2004). Such procedures are becoming more popular as computers become more powerful, but they are still not commonplace and have the potential to provide in-depth molecular dynamics information to understand catalysis and energy storage mechanisms including CO₂ capture. Furthermore, paramagnetic calculations could be given greater attention in the near future. Currently this is an underdeveloped area despite the abundance of paramagnetic nuclei. Another promising direction for future DFT-NMR optimization that is rapidly experiencing more prominence is the use of machine learning algorithms and neural networks. Machine learning is a rising tool for accelerating NMR in silico calculations with more complex systems (Paruzzo et al., 2018; Chaker et al., 2019). Cuny et al. (Cuny et al., 2016) employed a high-dimensional neural-network representation of NMR parameters using an ab initio formalism for large systems. They applied a neural-network NMR (NN-NMR) method to predict the ¹⁷O and ²⁹Si quadrupolar coupling constant and chemical shift parameters of various crystalline silica polymorphs and silica glasses to show the ability to predict NMR parameters of very large systems. Liu et al. (Liu et al., 2019) have developed a deep learning algorithm, based on multiresolution spatial data representation, where each resolution level and atom type are formulated as an independent channel of a deep learning architecture, for chemical shift prediction for atoms in molecular crystals. They obtained satisfying agreement for ¹³C, ¹⁵N, and ¹⁷O chemical shifts when compared to ab initio quantum chemistry methods. Gaumard et al. (Gaumard et al., 2022) utilized machine learning regression methods to obtain DFT isotropic chemical shielding values for a variety of zeolites structures with mean errors within 0.6 ppm. Significant advances in computational methods that allow for such a diverse pool of applications to be investigated more thoroughly could be expected.

Author contributions

WH summarized relevant literature, drafted the manuscript, coordinated the completion and revised the manuscript. NJ constructed the topical outline, provided technical insight, and revised the manuscript. AW surveyed the literature. SM assembled figures, captions, and copyright permissions and helped revise the manuscript language. KM and YW revised the manuscript. JH contributed to the preliminary CO₂ capture studies, directed the writing process, guided the content and revised the manuscript.

Funding

The review on catalysts was supported by the U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences (BES), Division of Chemical Sciences, Geosciences (FWP 47319). The preliminary studies on CO₂ capture were supported by Materials and Chemical Sciences for Direct Air Capture (DAC) of Carbon Dioxide sponsored by the Office of Basic Energy Sciences (FWP 78781). The review on energy storage was supported by the Joint Center for Energy Storage Research (JCESR), an Energy Innovation Hub funded by the United States Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences (BES) (FWP 63076).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akhdar, A., Andanson, J.-M., Faure, S., Traïkia, M., and Gautier, A. (2021). Application of quantitative 1H and 19F NMR to organometallics. J. Organomet. Chem. 950, 121991. doi:10.1016/j.jorganchem.2021.121991

CrossRef Full Text | Google Scholar

Autschbach, J., and Zheng, S. (2008). Analyzing Pt chemical shifts calculated from relativistic density functional theory using localized orbitals: the role of Pt 5d lone pairs. Magn. Reson. Chem. 46 Suppl 1 (Suppl. 1), S45–S55. doi:10.1002/mrc.2289

PubMed Abstract | CrossRef Full Text | Google Scholar

Autschbach, J., Patchkovskii, S., and Pritchard, B. (2011). Calculation of hyperfine tensors and paramagnetic NMR shifts using the relativistic zeroth-order regular approximation and density functional theory. J. Chem. Theory Comput. 7 (7), 2175–2188. doi:10.1021/ct200143w

PubMed Abstract | CrossRef Full Text | Google Scholar

Autschbach, J. (1981). Perspective: Relativistic effects. J. Chem. Phys. 136 (15), 150902. doi:10.1063/1.3702628

CrossRef Full Text | Google Scholar

Azpeitia, S., Mendicute-Fierro, C., Huertos, M. A., Rodríguez-Diéguez, A., Seco, J. M., Mota, A. J., et al. (2021). Experimental and DFT studies on hexacoordinated acyl(alkyl)and pentacooordinated hydroxyalkyl(phosphinite)erhodium(III). Catalytic hydrolysis of ammonia borane. Eur. J. Inorg. Chem. 2021 (9), 879–891. doi:10.1002/ejic.202001028

CrossRef Full Text | Google Scholar

Bagno, A., and Saielli, G. (2015). Addressing the stereochemistry of complex organic molecules by density functional theory-NMR. WIREs Comput. Mol. Sci. 5 (2), 228–240. doi:10.1002/wcms.1214

CrossRef Full Text | Google Scholar

Bagno, A., Bonchio, M., and Autschbach, J. (2006). Computational modeling of polyoxotungstates by relativistic DFT calculations of (183)W NMR chemical shifts. Chem. Eur. J. 12 (33), 8460–8471. doi:10.1002/chem.200600488

PubMed Abstract | CrossRef Full Text | Google Scholar

Bamine, T., Boivin, E., Boucher, F., Messinger, R. J., Salager, E., Deschamps, M., et al. (2017). Understanding local defects in Li-ion battery electrodes through combined DFT/NMR studies: Application to LiVPO4F. J. Phys. Chem. C 121 (6), 3219–3227. doi:10.1021/acs.jpcc.6b11747

CrossRef Full Text | Google Scholar

Batista, A. T. F., Wisser, D., Pigeon, T., Gajan, D., Diehl, F., Rivallan, M., et al. (2019). Beyond γ-Al2O3 crystallite surfaces: The hidden features of edges revealed by solid-state 1H NMR and DFT calculations. J. Catal. 378, 140–143. doi:10.1016/j.jcat.2019.08.009

CrossRef Full Text | Google Scholar

Bell, A. T. (1994). NMR techniques in catalysis. New York, NY: Taylor & Francis.

Google Scholar

Blaakmeer, E. S., Antinucci, G., Busico, V., van Eck, E. R. H., and Kentgens, A. P. M. (2016). Solid-state NMR investigations of MgCl2 catalyst support. J. Phys. Chem. C 120 (11), 6063–6074. doi:10.1021/acs.jpcc.5b12606

CrossRef Full Text | Google Scholar

Blanc, F., Basset, J.-M., Copéret, C., Sinha, A., Tonzetich, Z. J., Schrock, R. R., et al. (2008). Dynamics of silica-supported catalysts determined by combining solid-state NMR spectroscopy and DFT calculations. J. Am. Chem. Soc. 130 (18), 5886–5900. doi:10.1021/ja077749v

PubMed Abstract | CrossRef Full Text | Google Scholar

Bornes, C., Sardo, M., Lin, Z., Amelse, J., Fernandes, A., Ribeiro, M. F., et al. (2019). 1H-31P HETCOR NMR elucidates the nature of acid sites in zeolite HZSM-5 probed with trimethylphosphine oxide. Chem. Commun. 55 (84), 12635–12638. doi:10.1039/c9cc06763a

PubMed Abstract | CrossRef Full Text | Google Scholar

Bornes, C., Fischer, M., Amelse, J. A., Geraldes, C. F. G. C., Rocha, J., and Mafra, L. (2021). What is being measured with P-bearing NMR probe molecules adsorbed on zeolites? J. Am. Chem. Soc. 143 (34), 13616–13623. doi:10.1021/jacs.1c05014

PubMed Abstract | CrossRef Full Text | Google Scholar

Brouwer, D. H., Moudrakovski, I. L., Darton, R. J., and Morris, R. E. (2010). Comparing quantum-chemical calculation methods for structural investigation of zeolite crystal structures by solid-state NMR spectroscopy. Magn. Reson. Chem. 48 Suppl 1 (Suppl. 1), S113–S121. doi:10.1002/mrc.2642

PubMed Abstract | CrossRef Full Text | Google Scholar

Bühl, M., Kaupp, M., Malkina, O. L., and Malkin, V. G. (1999). The DFT route to NMR chemical shifts. J. Comput. Chem. 20 (1), 91–105.

CrossRef Full Text | Google Scholar

Cervini, L., Lynes, O. D., Akien, G. R., Kerridge, A., Barrow, N. S., and Griffin, J. M. (2019). Factors affecting the nucleus-independent chemical shift in NMR studies of microporous carbon electrode materials. Energy Storage Mater. 21, 335–346. doi:10.1016/j.ensm.2019.05.010

CrossRef Full Text | Google Scholar

Chaker, Z., Salanne, M., Delaye, J.-M., and Charpentier, T. (2019). NMR shifts in aluminosilicate glasses via machine learning. Phys. Chem. Chem. Phys. 21 (39), 21709–21725. doi:10.1039/c9cp02803j

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Y., Jaegers, N. R., Han, K. S., Wang, H., Young, R. P., Agarwal, G., et al. (2020). Probing conformational evolution and associated dynamics of Mg(N(SO2CF3)2)2·Dimethoxyethane adduct using solid-state 19F and 1H NMR. J. Phys. Chem. C 124 (9), 4999–5008. doi:10.1021/acs.jpcc.9b10212

CrossRef Full Text | Google Scholar

Cheng, R., Liu, X., Fang, Y., Terano, M., and Liu, B. (2017). High-resolution 29 Si CP/MAS solid state NMR spectroscopy and DFT investigation on the role of geminal and single silanols in grafting chromium species over Phillips Cr/silica catalyst. Appl. Catal. A General 543, 26–33. doi:10.1016/j.apcata.2017.05.011

CrossRef Full Text | Google Scholar

Corma, A., Iborra, S., and Velty, A. (2007). Chemical routes for the transformation of biomass into chemicals. Chem. Rev. 107 (6), 2411–2502. doi:10.1021/cr050989d

PubMed Abstract | CrossRef Full Text | Google Scholar

Cuny, J. r. m., Furet, E., Gautier, R. g., Le Pollès, L., Pickard, C. J., and d'Espinose de Lacaillerie, J.-B. (2009). Density functional theory calculations of 95Mo NMR parameters in solid-state compounds. Chemphyschem 10 (18), 3320–3329. doi:10.1002/cphc.200900586

PubMed Abstract | CrossRef Full Text | Google Scholar

Cuny, J., Xie, Y., Pickard, C. J., and Hassanali, A. A. (2016). Ab initio quality NMR parameters in solid-state materials using a high-dimensional neural-network representation. J. Chem. Theory Comput. 12 (2), 765–773. doi:10.1021/acs.jctc.5b01006

PubMed Abstract | CrossRef Full Text | Google Scholar

Dahn, J. R., Zheng, T., Liu, Y., and Xue, J. S. (1995). Mechanisms for lithium insertion in carbonaceous materials. Science 270 (5236), 590–593. doi:10.1126/science.270.5236.590

CrossRef Full Text | Google Scholar

Dai, W., Wang, C., Yi, X., Zheng, A., Li, L., Wu, G., et al. (2015). Identification of tert-butyl cations in zeolite H-ZSM-5: Evidence from NMR spectroscopy and DFT calculations. Angew. Chem. Int. Ed. 54 (30), 8783–8786. doi:10.1002/anie.201502748

PubMed Abstract | CrossRef Full Text | Google Scholar

Das, N., Eckert, H., Hu, H., Wachs, I. E., Walzer, J. F., and Feher, F. J. (1993). Bonding states of surface vanadium(V) oxide phases on silica: structural characterization by vanadium-51 NMR and Raman spectroscopy. J. Phys. Chem. 97 (31), 8240–8243. doi:10.1021/j100133a020

CrossRef Full Text | Google Scholar

Delgado, M., Delbecq, F., Santini, C. C., Lefebvre, F., Norsic, S., Putaj, P., et al. (2011). Evolution of structure and of grafting properties of γ-alumina with pretreatment temperature. J. Phys. Chem. C 116 (1), 834–843. doi:10.1021/jp208709x

CrossRef Full Text | Google Scholar

Deng, X., Hu, M. Y., Wei, X., Wang, W., Chen, Z., Liu, J., et al. (2015). Natural abundance 17O nuclear magnetic resonance and computational modeling studies of lithium based liquid electrolytes. J. Power Sources 285, 146–155. doi:10.1016/j.jpowsour.2015.03.091

CrossRef Full Text | Google Scholar

Deringer, V. L., Merlet, C., Hu, Y., Lee, T. H., Kattirtzi, J. A., Pecher, O., et al. (2018). Towards an atomistic understanding of disordered carbon electrode materials. Chem. Commun. 54 (47), 5988–5991. doi:10.1039/c8cc01388h

PubMed Abstract | CrossRef Full Text | Google Scholar

Ditchfield, R. (1974). Self-consistent perturbation theory of diamagnetism. Mol. Phys. 27 (4), 789–807. doi:10.1080/00268977400100711

CrossRef Full Text | Google Scholar

Du, J.-H., Chen, L., Zhang, B., Chen, K., Wang, M., Wang, Y., et al. (2022). Identification of CO2 adsorption sites on MgO nanosheets by solid-state nuclear magnetic resonance spectroscopy. Nat. Commun. 13 (1), 707. doi:10.1038/s41467-022-28405-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Duer, M. J. (2008). Solid state NMR spectroscopy: principles and applications. Hoboken, New Jersey: John Wiley & Sons.

Google Scholar

Facelli, J. C., Hu, J. Z., Orendt, A. M., Arif, A. M., Pugmire, R. J., and Grant, D. M. (1994). Solid-state 13C NMR, X-ray, and quantum mechanical studies of the carbon chemical shifts tensors of p-tolyl ether. J. Phys. Chem. 98 (47), 12186–12190. doi:10.1021/j100098a011

CrossRef Full Text | Google Scholar

Farrar, T. C., and Becker, E. D. (2012). Pulse and fourier transform NMR: introduction to theory and methods. Cambridge, MA: Elsevier.

Google Scholar

Florian, P., Veron, E., Green, T. F. G., Yates, J. R., and Massiot, D. (2012). Elucidation of the Al/Si ordering in gehlenite Ca2Al2SiO7 by combined 29Si and 27Al NMR spectroscopy/quantum chemical calculations. Chem. Mater. 24 (21), 4068–4079. doi:10.1021/cm3016935

CrossRef Full Text | Google Scholar

Forse, A. C., Griffin, J. M., Merlet, C., Bayley, P. M., Wang, H., Simon, P., et al. (2015). NMR study of ion dynamics and charge storage in ionic liquid supercapacitors. J. Am. Chem. Soc. 137 (22), 7231–7242. doi:10.1021/jacs.5b03958

PubMed Abstract | CrossRef Full Text | Google Scholar

Friedrich, K., Seifert, G., and Großmann, G. (1990). Nuclear magnetic shielding in molecules. The application of GIAO's in LCAO-Xα-calculations. Z Phys D - Atoms, Mol. Clust. 17 (1), 45–46. doi:10.1007/bf01437495

CrossRef Full Text | Google Scholar

Gaumard, R., Dragún, D., Pedroza-Montero, J. N., Alonso, B., Guesmi, H., Malkin Ondík, I., et al. (2022). Regression machine learning models used to predict DFT-computed NMR parameters of zeolites. Computation 10 (5), 74. doi:10.3390/computation10050074

CrossRef Full Text | Google Scholar

Gauss, J., and Stanton, J. F. (1996). Perturbative treatment of triple excitations in coupled-cluster calculations of nuclear magnetic shielding constants. J. Chem. Phys. 104 (7), 2574–2583. doi:10.1063/1.471005

CrossRef Full Text | Google Scholar

Gotoh, K., Kunimitsu, S., Zhang, H., Lerner, M. M., Miyakubo, K., Ueda, T., et al. (2018). Structure and dynamic behavior of the Na-crown ether complex in the graphite layers studied by DFT and 1H NMR. J. Phys. Chem. C 122 (20), 10963–10970. doi:10.1021/acs.jpcc.8b02965

CrossRef Full Text | Google Scholar

Grau, E., Lesage, A., Norsic, S., Copéret, C., Monteil, V., and Sautet, P. (2012). Tetrahydrofuran in TiCl4/THF/MgCl2: a non-innocent ligand for supported ziegler–natta polymerization catalysts. ACS Catal. 3 (1), 52–56. doi:10.1021/cs300764h

CrossRef Full Text | Google Scholar

Griffin, J. M., Forse, A. C., and Grey, C. P. (2016). Solid-state NMR studies of supercapacitors. Solid State Nucl. Magn. Reson. 74-75, 16–35. doi:10.1016/j.ssnmr.2016.03.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Guan, J., Li, X., Yang, G., Zhang, W., Liu, X., Han, X., et al. (2009). Interactions of phosphorous molecules with the acid sites of H-Beta zeolite: Insights from solid-state NMR techniques and theoretical calculations. J. Mol. Catal. A Chem. 310 (1-2), 113–120. doi:10.1016/j.molcata.2009.06.005

CrossRef Full Text | Google Scholar

Hanna, J. V., and Smith, M. E. (2010). Recent technique developments and applications of solid state NMR in characterising inorganic materials. Solid State Nucl. Magn. Reson. 38 (1), 1–18. doi:10.1016/j.ssnmr.2010.05.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Hansen, A. E., and Bouman, T. D. (1985). Localized orbital/local origin method for calculation and analysis of NMR shieldings. Applications to13C shielding tensors. J. Chem. Phys. 82 (11), 5035–5047. doi:10.1063/1.448625

CrossRef Full Text | Google Scholar

Hansen, A. E., and Bouman, T. D. (1989). Calculation, display, and analysis of the nature of nonsymmetric nuclear magnetic resonance shielding tensors: Application to three-membered rings. J. Chem. Phys. 91 (6), 3552–3560. doi:10.1063/1.456887

CrossRef Full Text | Google Scholar

He, P., Lucier, B. E. G., Terskikh, V. V., Shi, Q., Dong, J., Chu, Y., et al. (2014). Spies within metal-organic frameworks: Investigating metal centers using solid-state NMR. J. Phys. Chem. C 118 (41), 23728–23744. doi:10.1021/jp5063868

CrossRef Full Text | Google Scholar

Heine, T., Zerbetto, F., Seifert, G., and Fowler, P. W. (2000). 13C NMR patterns of odd-numbered C119 fullerenes. J. Phys. Chem. A 104 (17), 3865–3868. doi:10.1021/jp9940349

CrossRef Full Text | Google Scholar

Holmes, S. T., Bai, S., Iuliucci, R. J., Mueller, K. T., and Dybowski, C. (2017). Calculations of solid-state (43) Ca NMR parameters: A comparison of periodic and cluster approaches and an evaluation of DFT functionals. J. Comput. Chem. 38 (13), 949–956. doi:10.1002/jcc.24763

PubMed Abstract | CrossRef Full Text | Google Scholar

Hrobárik, P., Reviakine, R., Arbuznikov, A. V., Malkina, O. L., Malkin, V. G., Köhler, F. H., et al. (2007). Density functional calculations of NMR shielding tensors for paramagnetic systems with arbitrary spin multiplicity: validation on 3d metallocenes. J. Chem. Phys. 126 (2), 024107. doi:10.1063/1.2423003

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, J. Z., Facelli, J. C., Alderman, D. W., Pugmire, R. J., and Grant, D. M. (1998). 15N chemical shift tensors in nucleic acid bases. J. Am. Chem. Soc. 120 (38), 9863–9869. doi:10.1021/ja9816786

CrossRef Full Text | Google Scholar

Hu, J. Z., Xu, S., Li, W.-Z., Hu, M. Y., Deng, X., Dixon, D. A., et al. (2015). Investigation of the structure and active sites of TiO2 nanorod supported VOx catalysts by high-field and fast-spinning 51V MAS NMR. ACS Catal. 5 (7), 3945–3952. doi:10.1021/acscatal.5b00286

CrossRef Full Text | Google Scholar

Hu, J. Z., Jaegers, N. R., Hu, M. Y., and Mueller, K. T. (2018). In situ and ex situ NMR for battery research. J. Phys. Condens Matter 30 (46), 463001. doi:10.1088/1361-648X/aae5b8

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, J. Z., Rajput, N. N., Wan, C., Shao, Y., Deng, X., Jaegers, N. R., et al. (2018). 25Mg NMR and computational modeling studies of the solvation structures and molecular dynamics in magnesium based liquid electrolytes. Nano Energy 46, 436–446. doi:10.1016/j.nanoen.2018.01.051

CrossRef Full Text | Google Scholar

Hu, J. Z., Jaegers, N. R., Chen, Y., Han, K. S., Wang, H., Murugesan, V., et al. (2019). Adsorption and thermal decomposition of electrolytes on nanometer magnesium oxide: An in situ C-13 MAS NMR study. ACS Appl. Mater. Interfaces 11 (42), 38689–38696. doi:10.1021/acsami.9b11888

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, J. Z., Jaegers, N. R., Hahn, N. T., Hu, W., Han, K. S., Chen, Y., et al. (2022). Understanding the solvation-dependent properties of cyclic ether multivalent electrolytes using high-field NMR and quantum chemistry. JACS Au 2 (4), 917–932. doi:10.1021/jacsau.2c00046

PubMed Abstract | CrossRef Full Text | Google Scholar

Hunger, M., and Horvath, T. (1995). A new MAS NMR probe for in situ investigations of hydrocarbon conversion on solid catalysts under continuous-flow conditions. J. Chem. Soc. Chem. Commun., 1423–1424. doi:10.1039/c39950001423

CrossRef Full Text | Google Scholar

Hunger, M., Ernst, S., Steuernagel, S., and Weitkamp, J. (1996). High-field 1H MAS NMR investigations of acidic and non-acidic hydroxyl groups in zeolites H-Beta, H-ZSM-5, H-ZSM-58 and H-MCM-22. Microporous Mater 6 (5), 349–353. doi:10.1016/0927-6513(96)00043-0

CrossRef Full Text | Google Scholar

Huynh, H. V., Han, Y., Jothibasu, R., and Yang, J. A. (2009). 13C NMR spectroscopic determination of ligand donor strengths using N-heterocyclic carbene complexes of palladium(II). Organometallics 28 (18), 5395–5404. doi:10.1021/om900667d

CrossRef Full Text | Google Scholar

Iijima, T., Shimizu, T., Goto, A., Deguchi, K., Nakai, T., Ohashi, R., et al. (2019). 47,49Ti solid-state NMR and DFT study of Ziegler-Natta catalyst: Adsorption of TiCl4 molecule onto the surface of MgCl2. J. Phys. Chem. Solids 135, 109088. doi:10.1016/j.jpcs.2019.109088

CrossRef Full Text | Google Scholar

Jaegers, N. R., Hu, M. Y., Hoyt, D. W., Wang, Y., and Hu, J. Z. (2017). “Development and application of in situ high-temperature, high-pressure magic angle spinning NMR,” in Modern magnetic resonance, 1–19. doi:10.1007/978-3-319-28275-6_93-1

CrossRef Full Text | Google Scholar

Jaegers, N. R., Wan, C., Hu, M. Y., Vasiliu, M., Dixon, D. A., Walter, E., et al. (2017). Investigation of silica-supported vanadium oxide catalysts by high-field 51V magic-angle spinning NMR. J. Phys. Chem. C 121 (11), 6246–6254. doi:10.1021/acs.jpcc.7b01658

CrossRef Full Text | Google Scholar

Jaegers, N. R., Lai, J. K., He, Y., Walter, E., Dixon, D. A., Vasiliu, M., et al. (2019). Mechanism by which tungsten oxide promotes the activity of supported V2 O5/TiO2 catalysts for NOX abatement: Structural effects revealed by (51) V MAS NMR spectroscopy. Angew. Chem. Int. Ed. 58 (36), 12609–12616. doi:10.1002/anie.201904503

PubMed Abstract | CrossRef Full Text | Google Scholar

Jaegers, N. R., Hu, W., Wang, Y., and Hu, J. Z. (2020). High-temperature and high-pressure in situ magic angle spinning nuclear magnetic resonance spectroscopy. J. Vis. Exp. (164), e61794. doi:10.3791/61794

CrossRef Full Text | Google Scholar

Jaegers, N. R., Mueller, K. T., Wang, Y., and Hu, J. Z. (2020). Variable temperature and pressure operando MAS NMR for catalysis science and related materials. Acc. Chem. Res. 53 (3), 611–619. doi:10.1021/acs.accounts.9b00557

PubMed Abstract | CrossRef Full Text | Google Scholar

Jiang, Y., Huang, J., Dai, W., and Hunger, M. (2011). Solid-state nuclear magnetic resonance investigations of the nature, property, and activity of acid sites on solid catalysts. Solid State Nucl. Magn. reson. 39 (3-4), 116–141. doi:10.1016/j.ssnmr.2011.03.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Johnson, C., Moore, E. A., and Mortimer, M. (2005). Periodic ab initio calculation of nuclear quadrupole parameters as an assignment tool in solid-state NMR spectroscopy: applications to 23Na NMR spectra of crystalline materials. Solid State Nucl. Magn. Reson. 27 (3), 155–164. doi:10.1016/j.ssnmr.2004.08.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Jones, A. J., Carr, R. T., Zones, S. I., and Iglesia, E. (2014). Acid strength and solvation in catalysis by MFI zeolites and effects of the identity, concentration and location of framework heteroatoms. J. Catal. 312, 58–68. doi:10.1016/j.jcat.2014.01.007

CrossRef Full Text | Google Scholar

Kaupp, M., Malkin, O. L., and Malkin, V. G. (1997). Interpretation of 13C NMR chemical shifts in halomethyl cations. On the importance of spin-orbit coupling and electron correlation. Chem. Phys. Lett. 265 (1), 55–59. doi:10.1016/s0009-2614(96)01425-x

CrossRef Full Text | Google Scholar

Keal, T. W., Tozer, D. J., and Helgaker, T. (2004). GIAO shielding constants and indirect spin–spin coupling constants: performance of density functional methods. Chem. Phys. Lett. 391 (4-6), 374–379. doi:10.1016/j.cplett.2004.04.108

CrossRef Full Text | Google Scholar

Kobera, L., Rohlicek, J., Czernek, J., Abbrent, S., Streckova, M., Sopcak, T., et al. (2017). Unexpected crystallization patterns of zinc boron imidazolate framework ZBIF-1: NMR crystallography of integrated metal-organic frameworks. Chemphyschem 18 (24), 3576–3582. doi:10.1002/cphc.201701063

PubMed Abstract | CrossRef Full Text | Google Scholar

Köcher, S. S., Schleker, P. P. M., Graf, M. F., Eichel, R.-A., Reuter, K., Granwehr, J., et al. (2018). Chemical shift reference scale for Li solid state NMR derived by first-principles DFT calculations. J. Magnetic Reson. 297, 33–41. doi:10.1016/j.jmr.2018.10.003

CrossRef Full Text | Google Scholar

Kolganov, A. A., Gabrienko, A. A., Chernyshov, I. Y., Stepanov, A. G., and Pidko, E. A. (2020). The accuracy challenge of the DFT-based molecular assignment of 13C MAS NMR characterization of surface intermediates in zeolite catalysis. Phys. Chem. Chem. Phys. 22 (41), 24004–24013. doi:10.1039/d0cp04439c

PubMed Abstract | CrossRef Full Text | Google Scholar

Kolganov, A. A., Gabrienko, A. A., Yashnik, S. A., Pidko, E. A., and Stepanov, A. G. (2020). Nature of the surface intermediates formed from methane on Cu-ZSM-5 zeolite: A combined solid-state nuclear magnetic resonance and density functional theory study. J. Phys. Chem. C 124 (11), 6242–6252. doi:10.1021/acs.jpcc.0c00311

CrossRef Full Text | Google Scholar

Komorovský, S., Repiský, M., Malkina, O. L., Malkin, V. G., Malkin Ondík, I., and Kaupp, M. (2008). A fully relativistic method for calculation of nuclear magnetic shielding tensors with a restricted magnetically balanced basis in the framework of the matrix Dirac–Kohn–Sham equation. J. Chem. Phys. 128 (10), 104101.

PubMed Abstract | Google Scholar

Kupka, T., Pasterna, G., Lodowski, P., and Szeja, W. (1999). GIAO-DFT prediction of accurate NMR parameters in selected glucose derivatives. Magn. Reson. Chem. 37, 421–426. doi:10.1002/(sici)1097-458x(199906)37:6<421::aid-mrc479>3.0.co;2-w

CrossRef Full Text | Google Scholar

Kutzelnigg, W. (1980). Theory of magnetic susceptibilities and NMR chemical shifts in terms of localized quantities. Isr. J. Chem. 19 (1-4), 193–200. doi:10.1002/ijch.198000020

CrossRef Full Text | Google Scholar

Lee, C., Yang, W., and Parr, R. G. (1988). Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 37 (2), 785–789. doi:10.1103/physrevb.37.785

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, S., Zheng, A., Su, Y., Zhang, H., Chen, L., Yang, J., et al. (2007). Brønsted/lewis acid synergy in dealuminated HY zeolite: A combined solid-state NMR and theoretical calculation study. J. Am. Chem. Soc. 129, 11161–11171. doi:10.1021/ja072767y

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, S., Zheng, A., Su, Y., Zhang, H., Chen, L., Yang, J., et al. (2007). Brønsted/lewis acid synergy in dealuminated HY zeolite: A combined solid-state NMR and theoretical calculation study. J. Am. Chem. Soc. 129 (36), 11161–11171. doi:10.1021/ja072767y

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, Y., Wu, X.-P., Jiang, N., Lin, M., Shen, L., Sun, H., et al. (2017). Distinguishing faceted oxide nanocrystals with (17)O solid-state NMR spectroscopy. Nat. Commun. 8 (1), 581. doi:10.1038/s41467-017-00603-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, F., Wang, H., Zhao, Y., Fu, J., Mei, D., Jaegers, N. R., et al. (2021). Elucidation of active sites in aldol condensation of acetone over single-facet dominant anatase TiO₂ (101) and (001) catalysts. JACS Au 1 (1), 41–52. doi:10.1021/jacsau.0c00028

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, S., Li, J., Bennett, K. C., Ganoe, B., Stauch, T., Head-Gordon, M., et al. (2019). Multiresolution 3D-DenseNet for chemical shift prediction in NMR crystallography. J. Phys. Chem. Lett. 10 (16), 4558–4565. doi:10.1021/acs.jpclett.9b01570

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, Z., Liang, L., Xiao, D., Ji, Y., Zhao, Z., Xu, J., et al. (2021). ⁸⁹Y chemical shift anisotropy: a sensitive structural probe of layered yttrium hydroxides revealed by solid-state NMR spectroscopy and DFT calculations. Phys. Chem. Chem. Phys. 23 (48), 27244–27252. doi:10.1039/d1cp04247e

PubMed Abstract | CrossRef Full Text | Google Scholar

Lou, C., Zhang, W., Ma, C., Fan, B., Xu, S., Gao, S., et al. (2021). Revealing the specific spatial confinement in 8-membered ring cage-type molecular sieves via solid-state NMR and theoretical calculations. ChemCatChem 13 (5), 1299–1305. doi:10.1002/cctc.202001682

CrossRef Full Text | Google Scholar

Lund, A., Manohara, G. V., Song, A.-Y., Jablonka, K. M., Ireland, C. P., Cheah, L. A., et al. (2022). Characterization of chemisorbed species and active adsorption sites in Mg-Al mixed metal oxides for high-temperature CO2 capture. Chem. Mater. 34 (9), 3893–3901. doi:10.1021/acs.chemmater.1c03101

PubMed Abstract | CrossRef Full Text | Google Scholar

Luong, T. K. N., Shestakova, P., Mihaylov, T. T., Absillis, G., Pierloot, K., and Parac-Vogt, T. N. (2015). Multinuclear diffusion NMR spectroscopy and DFT modeling: a powerful combination for unraveling the mechanism of phosphoester bond hydrolysis catalyzed by metal-substituted polyoxometalates. Chem. Eur. J. 21 (11), 4428–4439. doi:10.1002/chem.201405810

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, D., Han, X., Zhou, D., Yan, Z., Fu, R., Xu, Y., et al. (2002). Towards guest-zeolite interactions: An NMR spectroscopic approach. Chem. Eur. J. 8 (19), 4557–4561. doi:10.1002/1521-3765(20021004)8:19<4557::aid-chem4557>3.0.co;2-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Malkin, V. G., Malkina, O. L., and Salahub, D. R. (1994). Calculation of spin—spin coupling constants using density functional theory. Chem. Phys. Lett. 221 (1), 91–99. doi:10.1016/0009-2614(94)87023-3

CrossRef Full Text | Google Scholar

Merle, N., Trébosc, J., Baudouin, A., Rosal, I. D., Maron, L., Szeto, K., et al. (2012). 17O NMR gives unprecedented insights into the structure of supported catalysts and their interaction with the silica carrier. J. Am. Chem. Soc. 134 (22), 9263–9275. doi:10.1021/ja301085m

PubMed Abstract | CrossRef Full Text | Google Scholar

Moon, S., and Patchkovskii, S. (2004). “First-principles calculations of paramagnetic NMR shifts,” in Calculation of NMR and EPR parameters, 325–338. doi:10.1002/3527601678.ch20

CrossRef Full Text | Google Scholar

Moreno-González, M., Hueso, B., Boronat, M., Blasco, T., and Corma, A. (2015). Ammonia-containing species formed in Cu-chabazite as per in situ EPR, solid-state NMR, and DFT calculations. J. Phys. Chem. Lett. 6 (6), 1011–1017. doi:10.1021/acs.jpclett.5b00069

PubMed Abstract | CrossRef Full Text | Google Scholar

Morita, R., Gotoh, K., Fukunishi, M., Kubota, K., Komaba, S., Nishimura, N., et al. (2016). Combination of solid state NMR and DFT calculation to elucidate the state of sodium in hard carbon electrodes. J. Mater. Chem. A 4 (34), 13183–13193. doi:10.1039/c6ta04273b

CrossRef Full Text | Google Scholar

Nicholas, J. B., Xu, T., and Haw, J. F. (1998). NMR and theoretical studies of solid acids: super and otherwise. Top. Catal. 6 (1), 141–149. doi:10.1023/a:1019178725784

CrossRef Full Text | Google Scholar

Papulovskiy, E., Shubin, A. A., and Lapina, O. B. (2021). Investigation of vanadia-alumina catalysts with solid-state NMR spectroscopy and DFT. Phys. Chem. Chem. Phys. 23 (35), 19352–19363. doi:10.1039/d1cp03297f

PubMed Abstract | CrossRef Full Text | Google Scholar

Papulovskiy, E., Shubin, A. A., Terskikh, V. V., Pickard, C. J., and Lapina, O. B. (2013). Theoretical and experimental insights into applicability of solid-state 93Nb NMR in catalysis. Phys. Chem. Chem. Phys. 15 (14), 5115–5131. doi:10.1039/c3cp44016h

PubMed Abstract | CrossRef Full Text | Google Scholar

Paruzzo, F. M., Hofstetter, A., Musil, F., De, S., Ceriotti, M., and Emsley, L. (2018). Chemical shifts in molecular solids by machine learning. Nat. Commun. 9 (1), 4501. doi:10.1038/s41467-018-06972-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Pazderski, L., Pawlak, T., Sitkowski, J., Kozerski, L., and Szłyk, E. (2009). 1H,13C,15N and195Pt NMR studies of Au(III) and Pt(II) chloride organometallics with 2-phenylpyridine. Magn. Reson. Chem. 47 (11), 932–941. doi:10.1002/mrc.2491

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, L., Liu, Y., Kim, N., Readman, J. E., and Grey, C. P. (2005). Detection of Brønsted acid sites in zeolite HY with high-field 17O-MAS-NMR techniques. Nat. Mater 4 (3), 216–219. doi:10.1038/nmat1332

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, Y.-K., Hu, Y., Chou, H.-L., Fu, Y., Teixeira, I. F., Zhang, L., et al. (2017). Mapping surface-modified titania nanoparticles with implications for activity and facet control. Nat. Commun. 8 (1), 675. doi:10.1038/s41467-017-00619-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Philippou, A., Salehirad, F., Luigi, D.-P., and Anderson, M. W. M. (1998). Investigation of surface methoxy groups on SAPO-34 A combined magic-angle turning NMR experimental approach with theoretical studies. Faraday Trans. 94 (18), 2851–2856. doi:10.1039/a803881c

CrossRef Full Text | Google Scholar

Philipsen, P. H. T., van Lenthe, E., Snijders, J. G., and Baerends, E. J. (1997). Relativistic calculations on the adsorption of CO on the (111) surfaces of Ni, Pd, and Pt within the zeroth-order regular approximation. Phys. Rev. B 56 (20), 13556–13562. doi:10.1103/physrevb.56.13556

CrossRef Full Text | Google Scholar

Pires, E., and Fraile, J. M. (2020). Study of interactions between brønsted acids and triethylphosphine oxide in solution by 31P NMR: evidence for 2 : 1 species. Phys. Chem. Chem. Phys. 22 (42), 24351–24358. doi:10.1039/d0cp03812a

PubMed Abstract | CrossRef Full Text | Google Scholar

Poater, J., van Lenthe, E., and Baerends, E. J. (2003). Nuclear magnetic resonance chemical shifts with the statistical average of orbital-dependent model potentials in Kohn-Sham density functional theory. J. Chem. Phys. 118 (19), 8584–8593. doi:10.1063/1.1567252

CrossRef Full Text | Google Scholar

Qi, G., Wang, Q., Xu, J., and Deng, F. (2021). Solid-state NMR studies of internuclear correlations for characterizing catalytic materials. Chem. Soc. Rev. 50 (15), 8382–8399. doi:10.1039/d0cs01130d

PubMed Abstract | CrossRef Full Text | Google Scholar

Rauhut, G., Puyear, S., Wolinski, K., and Pulay, P. (1996). Comparison of NMR shieldings calculated from Hartree−Fock and density functional wave functions using gauge-including atomic orbitals. J. Phys. Chem. 100 (15), 6310–6316. doi:10.1021/jp9529127

CrossRef Full Text | Google Scholar

Schäfer, A., Huber, C., and Ahlrichs, R. (1994). Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 100 (8), 5829–5835.

Google Scholar

Schindler, M., and Kutzelnigg, W. (1982). Theory of magnetic susceptibilities and NMR chemical shifts in terms of localized quantities. II. Application to some simple molecules. J. Chem. Phys. 76 (4), 1919–1933. doi:10.1063/1.443165

CrossRef Full Text | Google Scholar

Schreckenbach, G., and Ziegler, T. (1995). Calculation of NMR shielding tensors using gauge-including atomic orbitals and modern density functional theory. J. Phys. Chem. 99 (2), 606–611. doi:10.1021/j100002a024

CrossRef Full Text | Google Scholar

Schreckenbach, G., and Ziegler, T. (1996). The calculation of NMR shielding tensors based on density functional theory and the frozen-core approximation. Int. J. Quantum Chem. 60 (3), 753–766. doi:10.1002/(sici)1097-461x(1996)60:3<753::aid-qua4>3.0.co;2-w

CrossRef Full Text | Google Scholar

Schreckenbach, G., and Ziegler, T. (1997). Calculation of NMR shielding tensors based on density functional theory and a scalar relativistic Pauli-type Hamiltonian. The application to transition metal complexes. Int. J. Quant. Chem. 61 (6), 899–918. doi:10.1002/(sici)1097-461x(1997)61:6<899::aid-qua3>3.0.co;2-r

CrossRef Full Text | Google Scholar

Sebastiani, D., Goward, G., Schnell, I., and Parrinello, M. (2002). NMR chemical shifts in periodic systems from first principles. Comput. Phys. Commun. 147 (1), 707–710. doi:10.1016/s0010-4655(02)00378-8

CrossRef Full Text | Google Scholar

See, K. A., Leskes, M., Griffin, J. M., Britto, S., Matthews, P. D., Emly, A., et al. (2014). Ab initio structure search and in situ 7Li NMR studies of discharge products in the Li-S battery system. J. Am. Chem. Soc. 136 (46), 16368–16377. doi:10.1021/ja508982p

PubMed Abstract | CrossRef Full Text | Google Scholar

Seymour, I. D., Middlemiss, D. S., Halat, D. M., Trease, N. M., Pell, A. J., and Grey, C. P. (2016). Characterizing oxygen local environments in paramagnetic battery materials via (17)O NMR and DFT calculations. J. Am. Chem. Soc. 138 (30), 9405–9408. doi:10.1021/jacs.6b05747

PubMed Abstract | CrossRef Full Text | Google Scholar

Skachkov, D., Krykunov, M., Kadantsev, E., and Ziegler, T. (2010). The calculation of NMR chemical shifts in periodic systems based on gauge including atomic orbitals and density functional theory. J. Chem. Theory Comput. 6 (5), 1650–1659. doi:10.1021/ct100046a

PubMed Abstract | CrossRef Full Text | Google Scholar

Sklenak, S., Dědeček, J., Li, C., Wichterlová, B., Gábová, V., Sierka, M., et al. (2007). Aluminum siting in silicon-rich zeolite frameworks: a combined high-resolution (27)Al NMR spectroscopy and quantum mechanics/molecular mechanics study of ZSM-5. Angew. Chem. Int. Ed. 46 (38), 7286–7289. doi:10.1002/anie.200702628

PubMed Abstract | CrossRef Full Text | Google Scholar

Szeleszczuk, Ł., Pisklak, D. M., and Zielińska-Pisklak, M. (2018). Does the choice of the crystal structure influence the results of the periodic DFT calculations? A case of glycine alpha polymorph GIPAW NMR parameters computations. J. Comput. Chem. 39 (14), 853–861. doi:10.1002/jcc.25161

PubMed Abstract | CrossRef Full Text | Google Scholar

Taoufik, M., Szeto, K. C., Merle, N., Rosal, I. D., Maron, L., Trébosc, J., et al. (2014). Heteronuclear NMR spectroscopy as a surface-selective technique: A unique look at the hydroxyl groups of γ-alumina. Chem. Eur. J. 20 (14), 4038–4046. doi:10.1002/chem.201304883

PubMed Abstract | CrossRef Full Text | Google Scholar

Wan, C., Hu, M. Y., Borodin, O., Qian, J., Qin, Z., Zhang, J.-G., et al. (2016). Natural abundance 17O, 6Li NMR and molecular modeling studies of the solvation structures of lithium bis(fluorosulfonyl)imide/1,2-dimethoxyethane liquid electrolytes. J. Power Sources 307, 231–243. doi:10.1016/j.jpowsour.2015.12.120

CrossRef Full Text | Google Scholar

Wan, C., Xu, S., Hu, M. Y., Cao, R., Qian, J., Qin, Z., et al. (2017). Multinuclear NMR study of the solid electrolyte interface formed in lithium metal batteries. ACS Appl. Mater. Interfaces 9 (17), 14741–14748. doi:10.1021/acsami.6b15383

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, W. D., Lucier, B. E. G., Terskikh, V. V., Wang, W., and Huang, Y. (2014). Wobbling and hopping: Studying dynamics of CO2 adsorbed in metal-organic frameworks via (17)O solid-state NMR. J. Phys. Chem. Lett. 5 (19), 3360–3365. doi:10.1021/jz501729d

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, C., Chu, Y., Zheng, A., Xu, J., Wang, Q., Gao, P., et al. (2014). New insight into the hydrocarbon-pool chemistry of the methanol-to-olefins conversion over zeolite H-ZSM-5 from GC-MS, solid-state NMR spectroscopy, and DFT calculations. Chem. Eur. J. 20 (39), 12432–12443. doi:10.1002/chem.201403972

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, M., Wu, X. P., Zheng, S., Zhao, L., Li, L., Shen, L., et al. (2015). Identification of different oxygen species in oxide nanostructures with (17)O solid-state NMR spectroscopy. Sci. Adv. 1 (1), e1400133. doi:10.1126/sciadv.1400133

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, M., Jaegers, N. R., Lee, M.-S., Wan, C., Hu, J. Z., Shi, H., et al. (2019). Genesis and stability of hydronium ions in zeolite channels. J. Am. Chem. Soc. 141 (8), 3444–3455. doi:10.1021/jacs.8b07969

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Z.-F., Yi, Z., Ahmad, A., Xie, L., Chen, J.-P., Kong, Q., et al. (2021). Combined DFT and experiment: Stabilizing the electrochemical interfaces via boron Lewis acids. J. Energy Chem. 59, 100–107. doi:10.1016/j.jechem.2020.10.041

CrossRef Full Text | Google Scholar

Whittemore, N. A., Welch, K. T., Cox, J. R., Dougall, D. K., and Baker, D. C. (2004). A quenched molecular Dynamics−Rotating frame overhauser spectroscopy study of a series of semibiosynthetically monoacylated anthocyanins. J. Org. Chem. 69 (5), 1663–1669. doi:10.1021/jo035380w

PubMed Abstract | CrossRef Full Text | Google Scholar

Wolff, S. K., and Ziegler, T. (1998). Calculation of DFT-GIAO NMR shifts with the inclusion of spin-orbit coupling. J. Chem. Phys. 109 (3), 895–905. doi:10.1063/1.476630

CrossRef Full Text | Google Scholar

Wolinski, K., Hinton, J. F., and Pulay, P. (1990). Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc. 112 (23), 8251–8260. doi:10.1021/ja00179a005

CrossRef Full Text | Google Scholar

Xiao, S.-T., Wu, S.-M., Dong, Y., Liu, J.-W., Wang, L.-Y., Wu, L., et al. (2020). Rich surface hydroxyl design for nanostructured TiO₂ and its hole-trapping effect. Chem. Eng. J. 400, 125909. doi:10.1016/j.cej.2020.125909

CrossRef Full Text | Google Scholar

Xu, S., Jaegers, N. R., Hu, W., Kwak, J. H., Bao, X., Sun, J., et al. (2021). High-field one-dimensional and two-dimensional (27)Al magic-angle spinning nuclear magnetic resonance study of theta-, delta-, and gamma-Al2O3 dominated aluminum oxides: Toward understanding the Al sites in gamma-Al2O3. ACS Omega 6 (5), 4090–4099. doi:10.1021/acsomega.0c06163

PubMed Abstract | CrossRef Full Text | Google Scholar

Xue, X., and Kanzaki, M. (2007). Al coordination and water speciation in hydrous aluminosilicate glasses: direct evidence from high-resolution heteronuclear 1H-27Al correlation NMR. Solid State Nucl. Magn. Reson. 31 (1), 10–27. doi:10.1016/j.ssnmr.2006.11.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, J., Janik, M. J., Ma, D., Zheng, A., Zhang, M., Neurock, M., et al. (2005). Location, acid strength, and mobility of the acidic protons in Keggin 12-H3PW12O40: A combined solid-state NMR spectroscopy and DFT quantum chemical calculation study. J. Am. Chem. Soc. 127 (51), 18274–18280. doi:10.1021/ja055925z

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, G., Zhuang, J., Ma, D., Lan, X., Zhou, L., Liu, X., et al. (2008). A joint experimental–theoretical study on trimethylphosphine adsorption on the Lewis acidic sites present in TS-1 zeolite. J. Mol. Struct. 882 (1-3), 24–29. doi:10.1016/j.molstruc.2007.09.005

CrossRef Full Text | Google Scholar

Yu, Z., Wang, Q., Chen, L., and Deng, F. (2012). Brønsted/lewis acid sites synergy in H-MCM-22 zeolite studied by 1H and 27Al DQ-MAS NMR spectroscopy. Chin. J. Catal. 33 (1), 129–139. doi:10.1016/s1872-2067(10)60287-2

CrossRef Full Text | Google Scholar

Zhang, H., Zheng, A., Yu, H., Li, S., Lu, X., and Deng, F. (2008). Formation, location, and photocatalytic reactivity of methoxy species on Keggin 12-H3PW12O40: A Joint solid-state NMR spectroscopy and DFT calculation study. J. Phys. Chem. C 112 (40), 15765–15770. doi:10.1021/jp806588q

CrossRef Full Text | Google Scholar

Zhang, W., Xu, S., Han, X., and Bao, X. (2012). In situsolid-state NMR for heterogeneous catalysis: a joint experimental and theoretical approach. Chem. Soc. Rev. 41 (1), 192–210. doi:10.1039/c1cs15009j

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, R., Zhao, Z., Li, S., and Zhang, W. (2017). Insights into the correlation of aluminum distribution and brönsted acidity in H-Beta zeolites from solid-state NMR spectroscopy and DFT calculations. J. Phys. Chem. Lett. 8 (10), 2323–2327. doi:10.1021/acs.jpclett.7b00711

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, A., Zhang, H., Chen, L., Yue, Y., Ye, C., and Deng, F. (2007). Relationship between 1H chemical shifts of deuterated pyridinium ions and brønsted acid strength of solid acids. J. Phys. Chem. B 111 (12), 3085–3089. doi:10.1021/jp067340c

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, A., Huang, S.-J., Chen, W.-H., Wu, P.-H., Zhang, H., Lee, H.-K., et al. (2008). 31P chemical shift of adsorbed trialkylphosphine oxides for acidity characterization of solid acids catalysts. J. Phys. Chem. A 112 (32), 7349–7356. doi:10.1021/jp8027319

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, A., Zhang, H., Lu, X., Liu, S.-B., and Deng, F. (2008). Theoretical predictions of 31P NMR chemical shift threshold of trimethylphosphine oxide absorbed on solid acid catalysts. J. Phys. Chem. B 112 (15), 4496–4505. doi:10.1021/jp709739v

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, A., Huang, S.-J., Liu, S.-B., and Deng, F. (2011). Acid properties of solid acid catalysts characterized by solid-state 31P NMR of adsorbed phosphorous probe molecules. Phys. Chem. Chem. Phys. 13 (33), 14889–14901. doi:10.1039/c1cp20417c

PubMed Abstract | CrossRef Full Text | Google Scholar

Zheng, A., Li, S., Liu, S.-B., and Deng, F. (2016). Acidic properties and structure-activity correlations of solid acid catalysts revealed by solid-state NMR spectroscopy. Acc. Chem. Res. 49 (4), 655–663. doi:10.1021/acs.accounts.6b00007

PubMed Abstract | CrossRef Full Text | Google Scholar