Diamond growth dynamics in a constrained system

Single crystal diamond (SCD) is the most promising future semiconductor. However, it has not been able to make much inroad into the microelectronics industry due to its major disadvantage of the wafer size. Among a few contender technologies, epitaxial lateral outgrowth (ELO) using microwave plasma-assisted chemical vapor deposition (MPACVD) has shown early promise toward lateral area gain during epitaxial growth. While promising, significant wafer area enhancement remains challenging. This study explores the growth dynamics of SCD in a constrained system—a pocket holder—whose effect is twofold: linear dimension and area enhancement and polycrystalline diamond (PCD) edge rim suppression. A series of pocket-type holder designs were introduced that demonstrated that the depth and substrate-to-wall distance are the major means for optimizing and enhancing lateral outgrowth while still suppressing the PCD rim. When taken together with reactor modeling, the pocket effect on the extent of ELO could be understood as directly manipulating and perturbing methyl radical flux near the growing diamond surface, thereby directly manipulating gas-to-solid phase transformation kinetics. Because it was further discovered that simple box-like pockets limit the ELO process to an exponential-decay scenario, a new generation of angled pockets was proposed that allowed boosting ELO to its fullest extent where a constant rate, linear, outgrowth was found. Our results indicate that ELO by MPACVD could become an industrial means of producing SCD at scale.

1 Introduction

The advent of modern technologies such as microwave wireless communication, electrified transportation, renewable power grid, and quantum information has sustained interest in novel electronic materials. While most modern technologies are supported by traditional semiconductor materials like Si or A3B5, new wide bandgap materials are being developed to further enhance electronic and electrical systems capabilities (Tsao et al., 2018). Among existing wide bandgap semiconductors, diamond has the highest electronic, optical, and thermal figures of merit (Burns et al., 2009; Geis et al., 2018) and hence could disrupt communication, energy, and transportation infrastructure and computing. However, the practical implementation of diamond requires significant advances in crystal wafer quality and size as well as overall production yield.

Toward these goals, experiments with low pressure synthesis started already in the 1960s. Eversole (1961) reported diamond homoepitaxial synthesis by a CVD technique with the use of carbon-containing gases at pressures of less than 1 atmosphere and temperatures of around 800 °C–1,000 °C. Eversole had actually succeeded in late 1952, even before the results of HPHT techniques were published. This technique, however, was not very effective since large amounts of graphite were co-deposited with diamond, and growth rates were extremely low. Eversole’s work was followed up by Angus et al. (1968), who provided evidence of the use of atomic hydrogen as an effective technique for graphite removal, making diamond production much more effective. Since that time, the chemical vapor deposition (CVD) method was rolled out and widely and successfully applied to synthesizing diamond. Its variation, microwave plasma-assisted CVD (MPACVD) (Kamo et al., 1983), is the most potent for realizing large area high-quality diamond substrates and epi-layers. Recent progress in MPACVD homo- and heteroepitaxy, allowing for large-area (1–3 inches) and high-quality (dislocation density ≤10³ cm^-2) diamond crystal growth, has opened significant opportunities for diamond. Among existing epitaxy techniques, the (homo)epitaxial layer outgrowth (ELO) technique is a simple and effective sequential single-substrate process. ELO requires special pocket designs helping to impede a parasitic effect called polycrystalline diamond (PCD) rim formation that produces a net negative effect on the resulting useful lateral area of epi-layers (Mokuno et al., 2005/11; Nad et al., 2015; Charris et al., 2017; Nad et al., 2016). Hence, PCD rim suppression allows for lateral single crystal outgrowth.

This research further explores the design and optimization of the pocket holder and reactor configuration to achieve the highest lateral area gain. New insights into substrate holder–plasma interactions in two reactor types were cross-examined. An exponential decay lateral outgrowth regime was discovered and parametrized, and new modifications to the substrate holder were introduced to help attain linear lateral outgrowth.

2 Materials and methods

Figure 1 schematically illustrates the typical setup of the MSU reactor B configuration (A, B) and the temporal evolution of diamond shape and size within the pocket (C, D, E). A gas mixture of methane (CH₄) and hydrogen (H₂) was used as a precursor gas. As the chamber was pressurized, a 2.45-GHz microwave signal was used to ignite and sustain the plasma, which provided CH₃ and H as the main precursor species for diamond growth (Goodwin and Butler, 2018). Samples are held in a pocket holder inside the quartz dome designed to separate the plasma-containing reaction zone inside otherwise ambient air pressurized electromagnetic cavity.

Figure 1

Figure 1. (A) Diamond reactor and (B) schematic diagram of the chamber showing components of the system, wherein the sample stage containing the diamond is positioned at the center of the chamber beneath the plasma. Samples are placed in the pocket and shown without (C) and with plasma (D). After growth is concluded, the grown SCD sample fills the pocket being surrounded by graphitic polycrystalline diamond on the holder surface, as shown in (E).

2.1 Reactor conditions

Diamond growths under sample ID prefixes AI used reactor type B configuration, while SB and ACH prefixes used type C configurations (Lu et al., 2013); process conditions are listed in Table 1. Both reactors were tuned to reduce the reflected power to a minimum value, achieving the desired deposition results, including growth uniformity. In reactor C, depositions were carried out at substrate temperatures of 980 °C with an emission coefficient of 0.1, measured using the optical pyrometer technique described by Nad (2016). Substrate temperatures in reactor B have been recorded with an emission factor of 0.6, meaning that the reported temperatures are about 180 °C–200 °C lower than with an emission coefficient of 0.1. Thus, the targeted temperatures of 760 °C–800 °C are similar to those in reactor type C geometry. All samples were grown under 240 Torr with 400 sccm H₂ 20 sccm CH₄. Input microwave power levels were between 2 and 3 kW. Growth rates for SB diamond depositions were controlled to approximately 25 μm/hour in the vertical direction. ACH samples were also grown in reactor C geometry with substrate temperatures of 1,020 °C. In all cases, the substrate holder was actively water-cooled to regulate and maintain the substrate temperature during growth.

Table 1

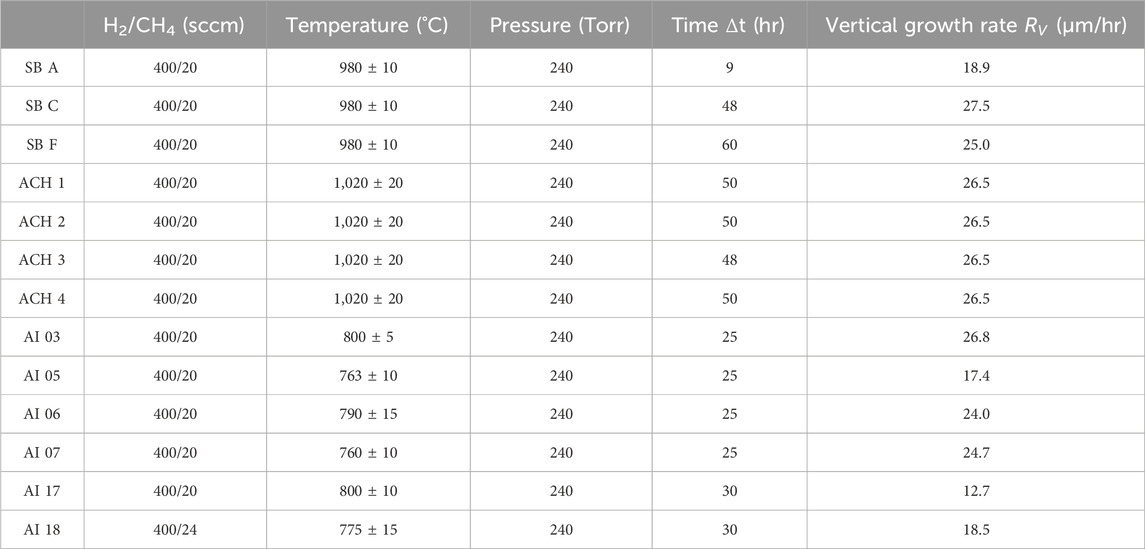
Table 1. Nominal growth conditions for samples grown in Reactors B and C. SB and ACH samples are grown in reactor C [12], which uses a hybrid mode of TM₀₀₁/TM_01n. AI samples are grown in Reactor B [12], which uses a hybrid mode of TM₀₁₃/TEM₀₀₁.

2.2 Preparation and growth

Diamond seeds (type Ib high pressure high temperature (HPHT)) were cleaned with a sequence of acids and solvents including sulfuric, nitric, and hydrochloric acids and acetone, methanol, and isopropyl alcohol to remove contaminants and impurities before loading into the CVD chamber. Seeds were then carefully positioned in the designated conditioned pocket holder and loaded to the CVD chamber. The CVD chamber was held under constant vacuum at base pressure (∼10⁻⁵ Torr) for at least 12 h before deposition. An initial etch was performed at the start of growth using 2.8 kW microwave plasma at 400 sccm H₂ flow and 950 °C substrate temperature for 10 min to 1 h to obtain a clean and fresh surface of the substrates. Epitaxial growths were performed over a range of times from 3 h to 60 h according to pocket holder size (Table 2) under conditioned listed in Table 1.

Table 2

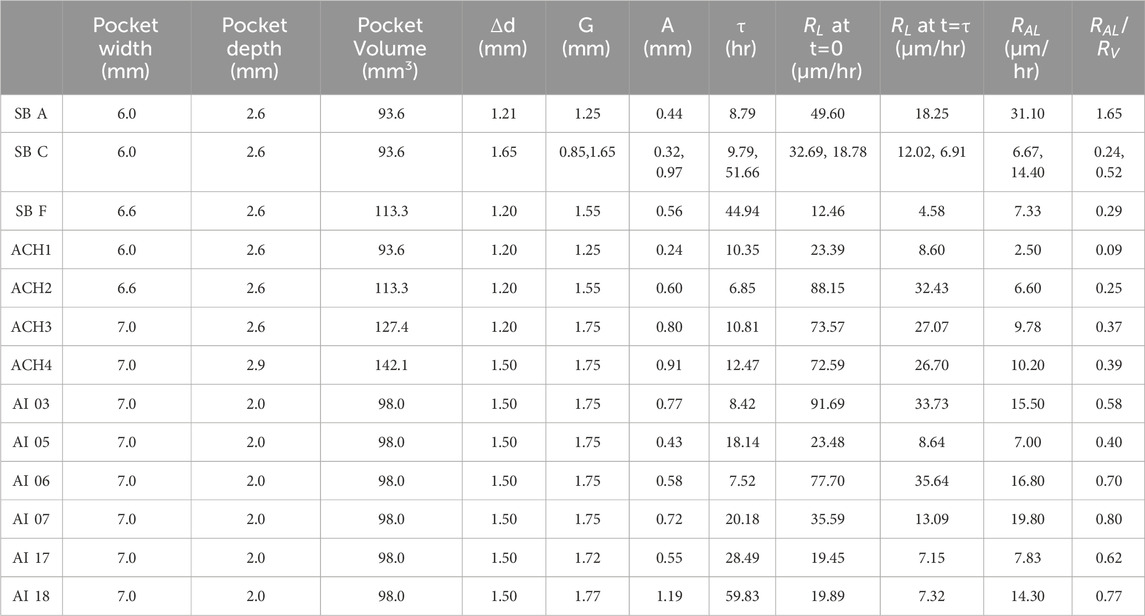
Table 2. Dimensions of pocket holders for samples grown in Reactor B and C. Gap distance (G) is determined based on a standard 3.5 × 3.5 mm diamond substrate size. A calculated lateral growth rate based on the data is $R_L$ =A/τ⋅exp (-t/τ). Average lateral growth rate is calculated as $R_{AL}$ = (L_f-L_i)/2Δt.

3 Results and discussion

3.1 ELO in traditional pocket holder and exponential decay growth

A total of 13 samples were grown in two different reactors to examine the reproducibility of the outgrowth when substrate-to-pocket constraints were manipulated to vary the constrained system parameters. All samples are classified and summarized in Tables 1, 2. The principal characterization metrics are average vertical and lateral growth rates $R_V$ and $R_{AL}$, respectively. SB A and SB F are symmetrically grown; SB C is asymmetrically grown (Figure 2A). Representative pictures of top and side views of SB F and SB C are shown in Figure 2B. AI samples AI 07 and AI 17 top and side views are presented in Figure 2C. In all cases, as shown in Table 2, the initial gap between the substrate edge and pocket wall were different, resulting in different lateral outgrowths.

Figure 2

Figure 2. Schematic of sample placement in pocket holder and growth outcomes for SB and AI samples. (A) SB F was performed with HPHT substrates placed at the center of the pocket, creating conditions for symmetric ELO of the diamond from the four edges and corners of the substrate. SB C growth was placed asymmetrically in the pocket to test ELO behavior as a function of position. The results of ELO (B) demonstrate asymmetric placement results in asymmetric ELO profiles, with the right side of SB C showing a nearly linear outward expansion compared to SB F. (C) Symmetric placement results in AI07 and AI17 ELO profiles.

Because the useful area of a diamond typically shrinks during vertical growth (Yamada et al., 2011), the outgrowth is deemed an unusual effect. A qualitative computational study was thus performed to elucidate the process at stake. Reactor B was modeled in COMSOL in terms of its basic discharge properties—electron concentration and temperature and gas temperature. The basic COMSOL model formulation can be found in Nikhar and Baryshev (2023). The standard operating point of 240 Torr pressure, CH₄/H₂ flow of 20/400 sccm, 2 kW power, and 2.45 GHz frequency was considered. The substrate temperature solved for self-consistency is at 850 °C. The model proceeds with calculating 3D (2D with rotation symmetry) methyl radical distributions. Ionization, electronic and vibrational state excitation of H₂, and dissociation cross-sections of H₂ and CH₄ were taken using databases assembled from Mankelevich et al. (2008), Yoon et al. (2008), and Hassouni et al. (2010). The steady-state CH₃ distributions at the beginning of growth and after the thickness of the growing film quadrupled (equivalent to 60 h of growth) are highlighted. One can clearly see that in the former case, the process begins with the standard out-of-plane/vertical growth as the methyl radical flux (green in Figure 3) is uniformly suspended over the substrate in the pocket (dashed arrows in Figure 3A). As the growing SCD thickens, it perturbs the methyl incoming flux that now comes at an angle (dashed arrows in Figure 3B), enabling the gas-to-solid transformation resulting in ELO. Using gas dynamics simulations, Yamada et al. also indicated that a box pocket design can be proposed where gas flow can be redirected toward the growing SCD corners, making it additionally useful for ELO (Yamada et al., 2006).

Figure 3

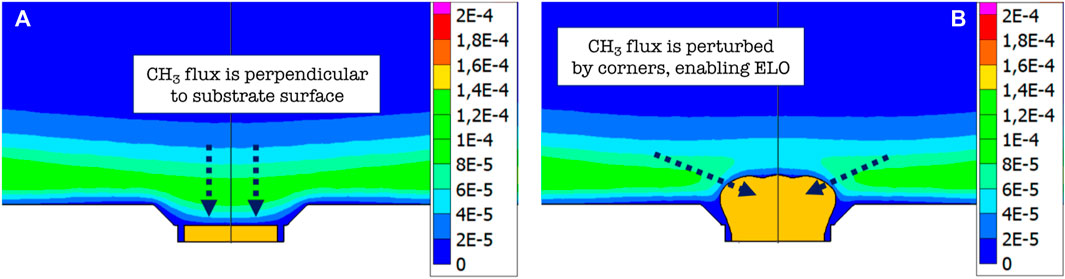
Figure 3. Computational demonstration of the ELO process: (A) 5-mm substrate is recessed in the angled pocket and (B) the substrate is homoepitaxially overgrown by a thick epilayer. The color contours are the spatial distribution of the methyl-to-methane ratio, and color bars represent corresponding values.

From this modeling result, it is possible to parametrize the reactor/substrate within the classical phase change kinetics framework using the equation of Avrami (1940) describing the gas-to-solid phase transformation through temporal lateral gain function L(t) as

$L\left(t\right)=A\left(1-e^{-t/\tau }\right),(1)$

when boundary conditions are set for the simple straight box pocket holder design (Figure 4A). Here, A is the max lateral gain (measured in mm) and τ is the characteristic time (measured in hours). Eq. (1) is a trivial case of first-order exponential decay growth. The lateral gain rate slows exponentially as distance G between the growing CVD crystal and the pocket side wall reduces. Eq. (1) perfectly captures the resulting growth in both symmetric and asymmetric cases in both reactors. The most striking results are shown in Figures 2 and 4, where results for the SB sample series are shown and fitted. The right side of SB C clearly gained more than its left side, and SB F gained literally the same amount on both sides. When taken together with the modeling, it is clear that the wider initial gap allowed more lateral gain because it permitted a larger influx of the methyl radical. Experimental growth dynamics for all of samples parametrized with Eq. (1) (yielding $G$, $A$, and τ) are summarized in Table 2 alongside experimental data ($R_{AL}$, R_L and R_V).

Figure 4

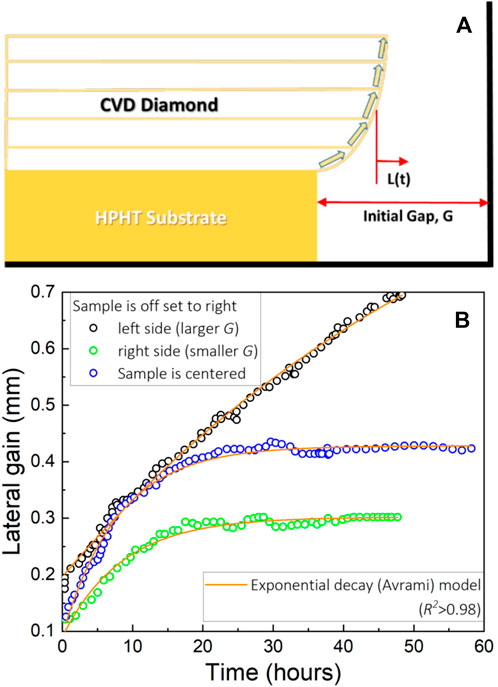
Figure 4. (A) Step-like schematic of the ELO process resulting in the exponential decay mode. (B) Lateral gain experimental data fitted by Eq. 1 for samples SB F (green and black open circles) and SB C (blue open circles).

Early work by Nad et al. (2016) and Charris et al. (2017) indicated that increasing width dimensions in a pocket mode will lead to better outgrowth performance; however, pockets that are too wide cannot suppress PCD growth. Thus, the relationship between the coefficients of the Avrami equation, lateral growth rates, and pocket dimensions should be interrogated. In reactor B, pocket holder dimensions were held fixed for AI samples (see Table 2). A clear positive correlation is observed between the lateral and vertical growth rates at different temperatures, with the ratio of $R_{AL}$/ $R_V$ ranging 0.4–0.8. In reactor C, growth times are longer than in reactor B since holders are deeper, but lateral growth had the same exponential decay regime. The ratio of $R_{AL}$/ $R_V$ for SB A is the greatest at 1.65 since the growth time was the shortest at 9 h and lateral outgrowth was most accelerated. In the same sample series, the larger the growth time, the smaller the $R_{AL}$/ $R_V$ ratio. For the ACH series, the holder dimensions were set with wider and/or deeper pockets. From ACH 1 to ACH 4, the wider the holder, the faster the average lateral growth rate $R_{AL}$, and the larger ratio of $R_{AL}$/ $R_V$. When the optimal pocket depth is found (2.5–3 mm in our case), gap G is the most useful variable to optimize for the best ELO gain. Summarizing the results from SB, ACH, and AI growths performed in the legacy pocket holder configurations, the wider pocket allows wider lateral size and, correspondingly, longer decay time τ. Generally, a set-up with gap distance of 1.5–1.75 mm allowed CVD diamond to gain up 1 mm on a single (100) edge after 48 h at a vertical growth rate of around 25–28 μm/hr.

3.2 ELO in novel pocket holder and steady-state lateral outgrowth mode

Engineering the gap appeared to be the main means of attaining a substantial but still constrained outgrowth using the traditional pocket configuration. The next question is whether the holder–substrate system can be further manipulated to lessen the constraint, such as achieving a best-case scenario where lateral outgrowth does not decay but remains constant. Thus, an angled pocket holder with fixed angle α was introduced (Figure 5A). For reference, α was equal to 90° in the legacy design. Considering the actual experimental situation in the chamber, PCD or graphite was always deposited to the pocket slope, thereby perturbing the initial α. It was hypothesized that PCD/graphite would not influence the growth behavior of the CVD diamond so long as α was between 0° (no pocket) and 90° (vertical wall pocket) and the CVD diamond could show a linear undecayed ELO profile. Importantly, α here becomes the major optimization variable to attain the hypothesized constant rate, linear, outgrowth.

Figure 5

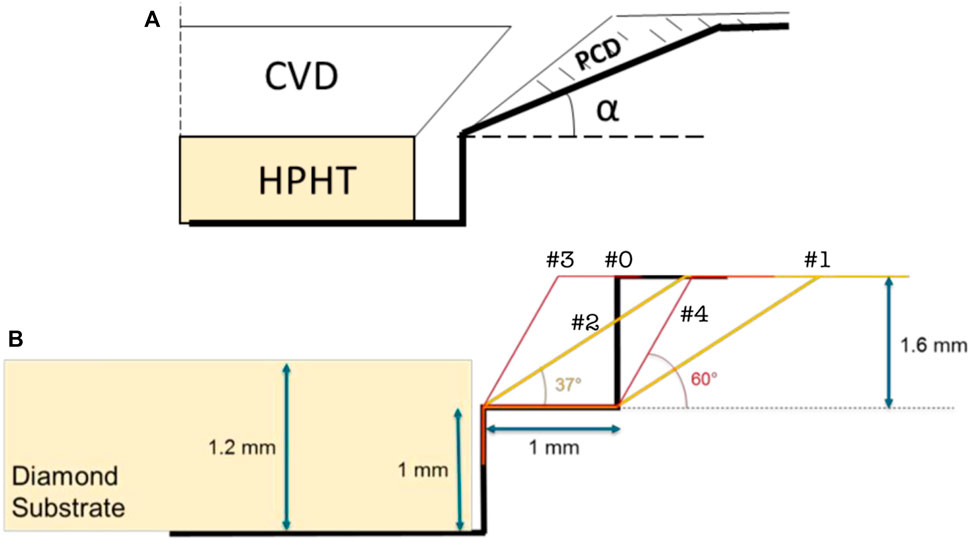
Figure 5. (A) Conceptual design of the new angled pocket holder. (B) Angled holder geometries interrogated in this work.

A series of designs were fabricated where different combinations of inner and outer pocket width, step length, inner and total pocket depth, inner and outer slope ends, and α were considered. As shown in Figure 5B, the inner pocket depth was fixed at 1 mm to expose the top 200–400 μm of the substrate to couple with the methyl radical flux; the inner pocket width was fixed at around 4 mm to keep the substrate at the center; the step length was 1 mm (if the holder design contained one, like designs #0, #1 and #4). The purpose of #0 was to introduce the strongest constraint. The other pockets #1-#4 were designed with different angles (37° versus 60°) with or without a step. The two angle choices are intuitively clear: the angle must be between 0° and 90°, or near to 45°.

All CVD growths were done in reactor C at 980 °C at otherwise identical preparation conditions to those discussed above. The upper pocket depth was 1.6 mm, and the vertical growth rate was typically around 25 μm/hr, making the upper growth time limit of approximately 1.6 mm/25 μm/hr = 64 h. All samples were grown for 50–60 h except for the sample in pocket #1, where growth was stopped after 24 h. The resulting growths are shown in Figure 6A. Optical side view profiles can be summarized as follows.

1) Pocket #0, closest to the traditional pocket described in Section 3.1, yields smooth growth but very limited outgrowth driven by the exponential decay kinetics. Pocket #3, having no step and a large angle of 60°, demonstrated the most severe constraining regime where no ELO was attained. Instead, inward/shrinking growth was found.

2) Pocket #1, combining a step and a small angle of 37°—having the least constraint—appeared too large and allowed the PCD rim to form. Growth was stopped after 24 h because PCD was aggressively growing.

3) Pockets #2 and 4, providing similar effective in-pocket spacing, allowed for the largest lateral gains. Figure 6B compares #2 and #4 pocket holders, where #2 shows the perfect hypothesized relationship; in the inset, one can see a nearly linear relationship between the lateral gain and time, indicating the constant growth rate. Because the pockets are now semi-open, some PCD deposition is expected to form that would cause the gap in #2 to close from 37° (or corner between the step and 60° in #4) toward 45°, thereby inducing quasi-linear ELO. Figure 6B clearly demonstrates that it is possible to maintain equal vertical and lateral gains such that the ratio $R_{AL}$/ $R_V$ is equal to 1. With this demonstration, the linear size of the homoepitaxially grown CVD crystals can be doubled and the area can be quadrupled.

Figure 6

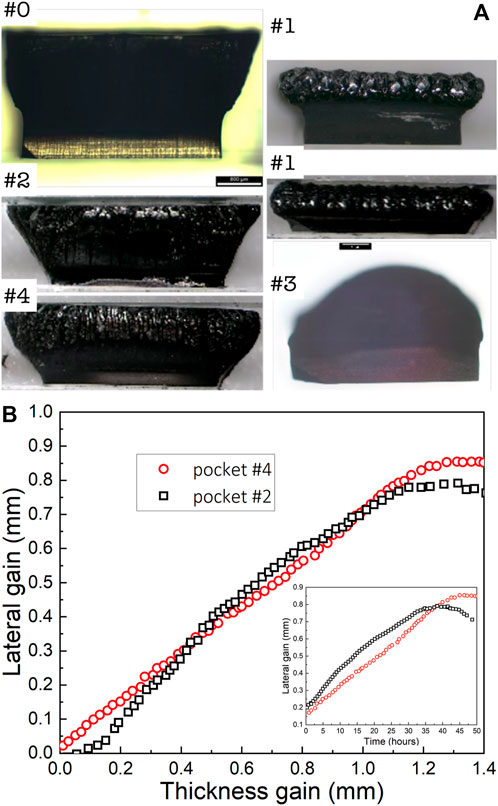
Figure 6. (A) Side view pictures of diamond grown in angled holders. (B) Comparison between pockets #2 and #4 both leading to nearly linear ELO profiles during MPACVD.

4 Conclusion

An extensive experimental interrogation of substrate holder designs was conducted. Based on the traditional rectangular wall pocket design (yielding self-constrained exponential decay mode), it was demonstrated that pocket geometry can be manipulated to attain a constant growth rate ELO. A smooth angled pocket was designed that yielded a “perfect” SCD growth, where the vertical (thickness) to lateral gain ratio was 1 such that the lateral size was doubled and the area was quadrupled. Our results indicate that ELO homoepitaxy, being a simple sequential single-substrate process, could become a self-replicating industrial process for 1–2 inch SCD wafer manufacturing.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

SB: conceptualization, data curation, formal analysis, investigation, methodology, software, visualization, writing–original draft, and writing–review and editing. RD: conceptualization, investigation, methodology, software, and writing–review and editing. MM: conceptualization, formal analysis, investigation, project administration, and writing–review and editing. EG: conceptualization, formal analysis, funding acquisition, investigation, methodology, project administration, resources, supervision, validation, visualization, and writing–review and editing. SVB: project administration, resources, supervision, validation, visualization, and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported in part by the NSF through the College of Engineering, Michigan State University, and Fraunhofer USA, Inc., under Award 2036737 (including a supplemental INTERN Award); and in part by the DOE Basic Energy Science under Award DE-SC0020671.

Acknowledgments

The authors would like to thank Karl Deutscher and Yun Hsiung for the integral contributions to data collection.

Conflict of interest

Authors MM and EG were employed by Fraunhofer USA, Inc., Center Midwest.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor SB is currently organizing a research topic with author SVB.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Angus, J. C., Will, H. A., and Stanko, W. S. (1968). Growth of diamond seed crystals by vapor deposition. J. Appl. Phys. 39 (6), 2915–2922. doi:10.1063/1.1656693

CrossRef Full Text | Google Scholar

Avrami, M. (1940). Kinetics of phase change. II transformation-time relations for random distribution of nuclei. J. Chem. Phys. 8 (2), 212–224. doi:10.1063/1.1750631

CrossRef Full Text | Google Scholar

Burns, R. C., Chumakov, A. I., Connell, S. H., Dube, D., Godfried, H. P., Hansen, J. O., et al. (2009). HPHT growth and x-ray characterization of high-quality type IIa diamond. J. Phys. Condens. Matter 21 (36), 364224. doi:10.1088/0953-8984/21/36/364224

PubMed Abstract | CrossRef Full Text | Google Scholar

Charris, A., Nad, S., and Asmussen, J. (2017). Exploring constant substrate temperature and constant high pressure SCD growth using variable pocket holder depths. Diam. Relat. Mater. 76, 58–67. doi:10.1016/j.diamond.2017.04.010

CrossRef Full Text | Google Scholar

Eversole, W. G. (1961) Synthesis of diamond. USA: to Union Carbide Corporation.

Google Scholar

Geis, M. W., Wade, T. C., Wuorio, C. H., Fedynyshyn, T. H., Duncan, B., Plaut, M. E., et al. (2018). Progress toward diamond power field-effect transistors. Phys. status solidi (a) 215 (22), 1800681. doi:10.1002/pssa.201800681

CrossRef Full Text | Google Scholar

Goodwin, D. G., and Butler, J. E. (2018) “Theory of diamond chemical vapor deposition,” in Handbook of industrial diamonds and diamond films. United States: CRC Press, 527–581.

CrossRef Full Text | Google Scholar

Hassouni, K., Silva, F., and Gicquel, A. (2010). Modelling of diamond deposition microwave cavity generated plasmas. J. Phys. D Appl. Phys. 43 (15), 153001. doi:10.1088/0022-3727/43/15/153001

CrossRef Full Text | Google Scholar

Kamo, M., Sato, Y., Matsumoto, S., and Setaka, N. (1983). Diamond synthesis from gas phase in microwave plasma. J. Cryst. growth 62 (3), 642–644. doi:10.1016/0022-0248(83)90411-6

CrossRef Full Text | Google Scholar

Lu, J., Gu, Y., Grotjohn, T., Schuelke, T., and Asmussen, J. (2013). Experimentally defining the safe and efficient, high pressure microwave plasma assisted CVD operating regime for single crystal diamond synthesis. Diam. Relat. Mater. 37, 17–28. doi:10.1016/j.diamond.2013.04.007

CrossRef Full Text | Google Scholar

Mankelevich, Y. A., Ashfold, M. N., and Ma, J. (2008). Plasma-chemical processes in microwave plasma-enhanced chemical vapor deposition reactors operating with C/H/Ar gas mixtures. J. Appl. Phys. 104 (11). doi:10.1063/1.3035850

CrossRef Full Text | Google Scholar

Mokuno, Y., Chayahara, A., Soda, Y., Horino, Y., and Fujimori, N. (2005/11/01/, 2005). Synthesizing single-crystal diamond by repetition of high rate homoepitaxial growth by microwave plasma CVD. Diam. Relat. Mater. 14 (11), 1743–1746. doi:10.1016/j.diamond.2005.09.020

CrossRef Full Text | Google Scholar

Nad, S. (2016) Growth and characterization of large, high quality single crystal diamond substrates via microwave plasma assisted chemical vapor deposition. East Lansing, Michigan: Michigan State University.

Google Scholar

Nad, S., Charris, A., and Asmussen, J. (2016). MPACVD growth of single crystalline diamond substrates with PCD rimless and expanding surfaces. Appl. Phys. Lett. 109 (16). doi:10.1063/1.4965025

CrossRef Full Text | Google Scholar

Nad, S., Gu, Y., and Asmussen, J. (2015). Growth strategies for large and high quality single crystal diamond substrates. Diam. Relat. Mater. 60, 26–34. doi:10.1016/j.diamond.2015.09.018

CrossRef Full Text | Google Scholar

Nikhar, T., and Baryshev, S. V. (2024). Evidence of gas phase nucleation of nano diamond in microwave plasma assisted chemical vapor deposition. AIP Advances, 14, 045334. doi:10.1063/5.0192057

CrossRef Full Text | Google Scholar

Tsao, J. Y., Chowdhury, S., Hollis, M. A., Jena, D., Johnson, N. M., Jones, K. A., et al. (2018). Ultrawide-bandgap semiconductors: research opportunities and challenges. Adv. Electron. Mater. 4 (1), 1600501. doi:10.1002/aelm.201600501

CrossRef Full Text | Google Scholar

Yamada, H., Chayahara, A., Mokuno, Y., Horino, Y., and Shikata, S. (2006). Simulation of temperature and gas flow distributions in region close to a diamond substrate with finite thickness. Diam. Relat. Mater. 15 (10), 1738–1742. doi:10.1016/j.diamond.2006.03.001

CrossRef Full Text | Google Scholar

Yamada, H., Chayahara, A., Mokuno, Y., Tsubouchi, N., Shikata, S.-i., and Fujimori, N. (2011). Developments of elemental technologies to produce inch-size single-crystal diamond wafers. Diam. Relat. Mater. 20 (4), 616–619. doi:10.1016/j.diamond.2011.01.001

CrossRef Full Text | Google Scholar

Yoon, J.-S., Song, M.-Y., Han, J.-M., Hwang, S. H., Chang, W.-S., Lee, B., et al. (2008). Cross sections for electron collisions with hydrogen molecules. J. Phys. Chem. Reference Data 37 (2), 913–931. doi:10.1063/1.2838023

CrossRef Full Text | Google Scholar