Quasi-one-dimensional carbon-based fractal lattices

Fractal systems are now considered alternative routes for engineering physical properties on the nanoscale. In particular, stable annular quantum corrals have been demonstrated in distinct synthesis procedures and can provide interesting localized and resonant states. We here present a theoretical description of effective fractal lattices, mainly composed of annular Koch geometries based on carbon atoms, and of more complex organic molecules described by triangular Sierpinski geometries. A single band tight-binding approach is considered to derive electronic and transport properties. Fractal molecular linear chains composed of fractal Koch quantum corrals are proposed, and their electronic transport is discussed based on the complexity of the neighboring hopping. The spatial charge distributions at different energies highlight the contribution of the composing metallic and carbons atoms in the quantum corral features, serving as a guide to new functionalization applications based on the symmetry and fractal peculiarities of the proposed nanostructured lattices.

1 Introduction

A crucial size parameter for determining the physical properties of a system is its dimensions. For example, in quasi-1D nanostructured systems such as extensively studied graphene nanoribbons (Castro Neto et al., 2009; Wakabayashi et al., 2010; Berdonces-Layunta et al., 2022), the electron confinement is characterized by 1D-like Van Hove singularities in the density of states (DOS). Quantum corrals are also important nanosystems for studying localized states and have been explored since their first synthesis in 1993 (Crommie et al., 1993). More recently, covalently linked large-sized organic quantum corrals were made possible through bottom-up growth processes with atomic precision, revealing a high degree of controlling localization and resonant states (Peng et al., 2021). Usually, the localized states are highly degenerated and exhibit a set of flat bands of increasing interest to condensed matter physics (Freeney et al., 2022; Kempkes et al., 2019).

On the other hand, fractals are fascinating natural objects and have been extensively investigated within mathematical and theoretical frameworks, taking into account the different focuses for discussing fractal geometries. Advances and future challenges of fractal materials have been discussed recently by Gowrisankar and Banerjee (2021), with advanced research proposing the application of fractal features to the dynamics of highly nonlinear complex systems. A very good overview of fractal origins and applications is also available in the classical book by Mandelbot (1983). The advance of experimental techniques in synthesizing finite fractal molecules, such as self-assembly (Shang et al., 2015), electrostatic attraction (Dai et al., 2023), have allowed a better comprehension of the particles interacting within fractal lattices; this lies in non-integer dimensions known as “Hausdorff dimensions”. Carbon-nanotube-based networks have been successfully designed to work as neural sensor devices (Browning et al., 2021), among other interesting fractal hierarchical investigations of single-walled carbon nanotube films (De Nicola et al., 2015) and other graphite systems (Zhou et al., 2016). Electrons and photons (Xu et al., 2021) moving through such lattices undergo the fractional dimension of the structures, revealing self-similar patterns on the corresponding band structures, density of states (DOS), and electronic conductance. Molecular chains based on carbon Sierpinski triangle architectures have been recently reported (Zhang Y., et al. 2020; Lage and Latgé,2022), exhibiting the manifestation of different spatial charge distribution which may be explored in functional nanodevices (de Laissardie‘re et al., 2010).

Here, we present a fractal version of a Koch snowflake-like quantum corral in two symmetries: the triangular and square Koch corrals. A topological description of the systems is depicted in Figure 1: triangular and square Koch rings, named “TK-G (n)” and “SK-G (n)”, respectively. The decorated rings are obtained by particular rotations in the Koch lines, resulting in C_3v and C_4v symmetries, respectively. The Koch chain dimension is calculated from D = log(N)/log(L), with N being the number of lines between each corner and L the proportional length-fraction of each line compared with the first order G (0), giving D = log(4)/log(3) = log(16)/log(9) = log(64)/log(27) ≈ 1.26, respectively, for the 1^st, 2^nd, and 3^th generations. As expected, this dimension applies also for the TK and SK snowflakes.

FIGURE 1

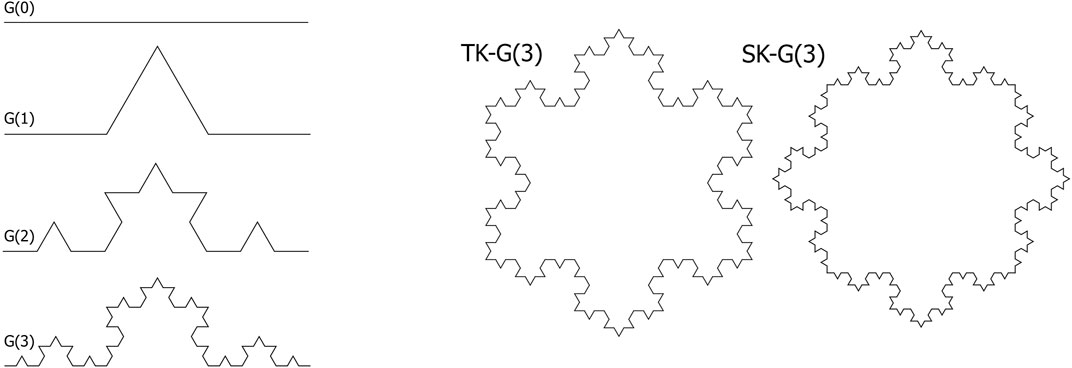
FIGURE 1. Left chart: Koch lines generations 0, 1, 2, and 3 from top to bottom, respectively. Right chart: triangular Koch TK-G (3) and square Koch SK-G (3).

Such quasi-one-dimensional fractal geometries with triangular, square, pentagonal, and hexagonal symmetries were experimentally probed through chemical routes, in which nitrogen bases are connected between metallic atoms (Ru, Fe, and Co) to construct quantum-corral molecular architectures with trapped electrons (Wang et al., 2018; Jiang et al., 2017; Zhang Z. et al., 2020.) With the actual engineering facilities of varying molecular geometries mainly assembled by carbon based composites (Peng et al., 2021), quantum corrals have become ideal systems for studying electronic wave resonances, electronic confinement, and other rich quantum responses. In this work, we explore a variety of localized states in annular geometries, considering both triangular and square Koch symmetries. We investigate electronic properties such as transmission, band structure, and the spatial distributions of the electronic states through density of states on molecular chains that may be compared with STM images. The systems are described within a tight binding framework in which the lattice is included in a microscopy point of view, and not following continuum models (El-Nabulsi and Anukool, 2021; El-Nabulsi and Anukool, 2023). The theoretical approach is used to describe synthesized chemical molecules and to prescribe possible smart routes for application in selective transport nanodevices.

2 Theoretical model

A single-orbital tight-binding (TB) Hamiltonian is used to describe the proposed Koch systems, given by:

$H={\displaystyle \sum _i}{\epsilon }_i{c}_i^{†}{c}_i+{\displaystyle \sum _{⟨ij⟩}}{t}_{ij}{c}_i^{†}{c}_j+{\displaystyle \sum _{⟨⟨ij⟩⟩}}{t}_{ij}^{\prime }{c}_i^{†}{c}_j+h.c.(1)$

with ɛ_i being the on-site energy for an atom located at site i, $c_i^{†}$ (c_i) being the creation (annihilation) operator of an electron on site i, and t_i,j and $t_{i,j}^{\prime }$ being the hopping energies for nearest neighbors (1N) and second-nearest neighboring (2NN) atoms, respectively. We discuss below the effects of considering both first and second neighboring atoms in the Hamiltonian. For the corral lattices, we discuss here, via fractal Koch curves, the urgency of including second and/or further neighboring interactions which will be dictated by the real system to be described, and by a proper comparison with the experimental data, if available (STM images and dI/dV curves, for instance), and with first principle calculations.

The electronic properties of the studied corrals are derived via the eigenfunctions ψ_n and eigenenergies λ_n determination, with n being the number of sites. The local density of states (LDOS) is obtained using a Lorentzian function to better adjust the electronic states as following:

$LDOS\left(E,r_0\right)=\frac{1}{2\pi }{\displaystyle \sum _n}|{\psi }_n\left(r_0\right){|}^2\frac{\mathrm{\Gamma }}{{\left(E-{\lambda }_n\right)}^2+0.25{\mathrm{\Gamma }}^2},(2)$

where r₀ are the site positions. The total density of states (DOS) is calculated by summing LDOS(E, r₀) over all sites.

Transport properties are calculated using the Landauer approach (Data, 1995), in which the system is decoupled into three parts: central conductor, and right and left leads (Felix et al., 2022; Santos et al., 2020; Chico et al., 2015). We consider semi-infinite Koch chains as leads, perfectly matching the central scattering region. Following the Green function formalism, we can also obtain local DOS. The central advanced (a) and retarded (r) Green functions are given as

$G_c^{a,r}\left(E\right)={\left[\omega -H_c-{\mathrm{\Sigma }}_L^{a,r}\left(E\right)-{\mathrm{\Sigma }}_R^{a,r}\left(E\right)\right]}^{-1},(3)$

with ω = E ± iη, η being an infinitesimal energy value and H_c being the Hamiltonian of the central part. ${\mathrm{\Sigma }}_{L,R}^{a,r}(E)$ correspond to left and right self-energies, given by the related surface Green functions, from which the coupling matrices are obtained via ${\mathrm{\Gamma }}^{L,R}(E)=i({\mathrm{\Sigma }}_{L,R}^r(E)-{\mathrm{\Sigma }}_{L,R}^a(E))$. Finally, to derive the electronic conductance in Koch chains, G (E)=$2e^2/h\mathcal{T}(E)$, we calculate the energy-dependent transmission given by

$\mathcal{T}\left(E\right)=\mathrm{T}\mathrm{r}\left[{\mathbf{\Gamma }}^L{\mathit{G}}_c^r{\mathbf{\Gamma }}^R{\mathit{G}}_c^a\right].(4)$

3 Results and discussions

3.1 Koch quantum corrals

We now explore square and triangular geometries, using the Koch fractal, as basic units that comprise molecular systems. Figures 2A, B presents a comparison between the eigenenergies of TK and SK-second generation corrals, respectively, considering first (red curves) and second (blue curves) neighbors, with the second hopping given by t′ = 0.5t. This particular value of hopping energy may be overestimated compared to the smaller intensity parameter usually adopted for graphene-based lattices (t′ = 0.1t). It was chosen considering an inverse linear dependence with atomic distance. Smaller values that should also be considered reduce the changes on the electronic features compared to the single first-neighbor model. However, as we want to highlight how changes may be induced by considering the NN2, we consider stronger coupling limits. It is clear from the results in Figure 2 that the two fractal arrangements (triangular and square) have similar energy spectra for both first and second neighbor models, although they have different numbers of atoms. The corresponding Fermi energies are depicted for both cases in blue and red horizontal dashed lines. While there are available energy states crossing the Fermi level for the 2NN model, the Fermi level is marked by an energy gap E_gap = t for the 1N description, revealing a semiconducting-like feature for that model. A simple comparison between the G (2)-TK and SK eigenvalue results for first neighbors shows a 6- and 12-order degeneracy for the state E = −t, respectively, which is responsible for the sharp peak in the corresponding electronic density of states (red curve) in the bottom of Figure 3A.

FIGURE 2

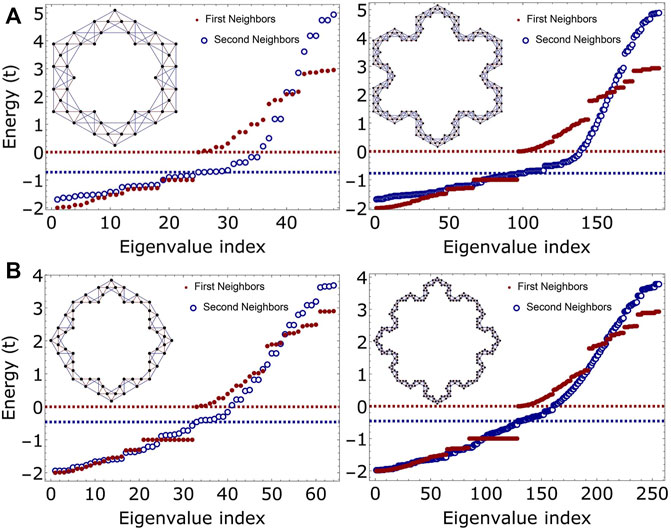
FIGURE 2. Comparison between the energy spectra of (A) triangular and (B) square Koch corrals of second (left) and third (right) generations, G (2) and G (3), respectively. Fermi levels are marked by dashed lines.

FIGURE 3

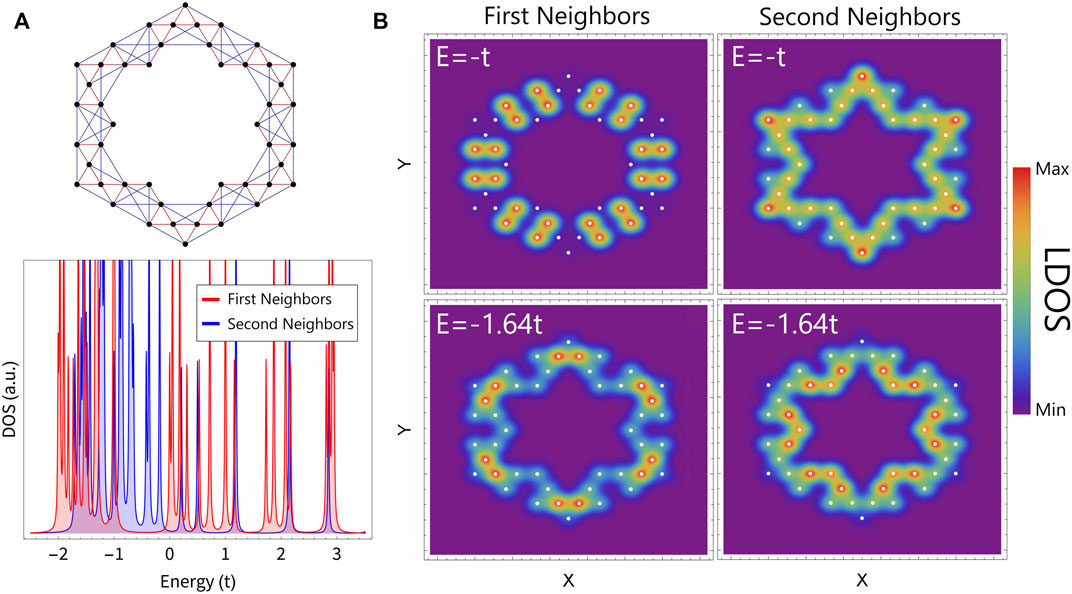
FIGURE 3. Results for a G (2)-TK using first (red curve) and second neighbors (blue curve) TB models. (A) Schematic view of the triangular corral (top) and DOS (bottom). (B) LDOS comparison at energy values equal to E = −t and E = −1.64t, available for both cases. Parameters: t′ = 0.5t and ɛ = 0.

By comparing the LDOS for both first- and second-neighbor results at E = −t (Figure 3B), we note that the electronic density is localized in a dimer-like charge distribution or displayed mostly around all the corral sites, respectively. This difference occurs due to the degeneracy lift and the subsequent formation of a bounding state, caused by the inclusion of second-neighbor interactions that are responsible for spreading the charges through the annular corral. At E = −1.64t, the dimmer-like feature is preserved for the case of the 1N model, although rotated spatially relative to the E = −t example, and preferring the external ST positions. In contrast, the charge for the 2NN case is more pronounced at the internal sites of the corral (see bottom part of Figure 3B). It is important to emphasize that, although triangular and square Koch corrals exhibit similar eigenspectra, as shown in 2, the charges are distributed as expected around the sites according to each symmetry. The charge distribution effects are also preserved in molecular Koch-corral chains, as discussed next.

3.2 Molecular Koch-corral chains

As previously reported (Zhang Z. et al., 2020), the synthesized corrals are usually displayed in lines very close to each other, or sometimes physically connected (Dai et al., 2023). Therefore, in this section we propose a TB model connecting the Koch corrals in order to create a kind of molecular chain with periodic boundary conditions along one single direction. Usually, the fractal dimension in a perfectly symmetrical system promotes energy spectra with fractal characteristics and exhibiting infinite band gaps in the thermodynamic limit. Such characteristic features are verified by comparing electronic band structures or the density of electronic states of different fractal generations revealing the self-similar aspects in energies (Lage and Latgé,2022; Pedersen, 2020). The results for the electronic structures for three successive generations G (2), G (3), and G (4) are shown in Figure 4 using the 1N model. It is possible to see the occurrence of self-similarity allusions between the band structures, highlighted by the shadow regions (blue and yellow) in the figure, at narrower energy ranges as we move to higher orders of Koch-corral structures. This is a fundamental aspect of the fractal nature emerging from the electronic properties of such systems. It is important to note that real self-similarity patterns should require perfect fractal geometries, as presented, for instance, in triangular Sierpinski lattices (Domany et al., 1983; Wang, 1995; Pedersen, 2020). In the construction of the proposed TK chains, the presence of the interfaces between the fractal units breaks the ideal fractal symmetry of the single flakes. In the absence of such perfect self-similarity features, we have not explored the localization nature of the involved wavefunctions.

FIGURE 4

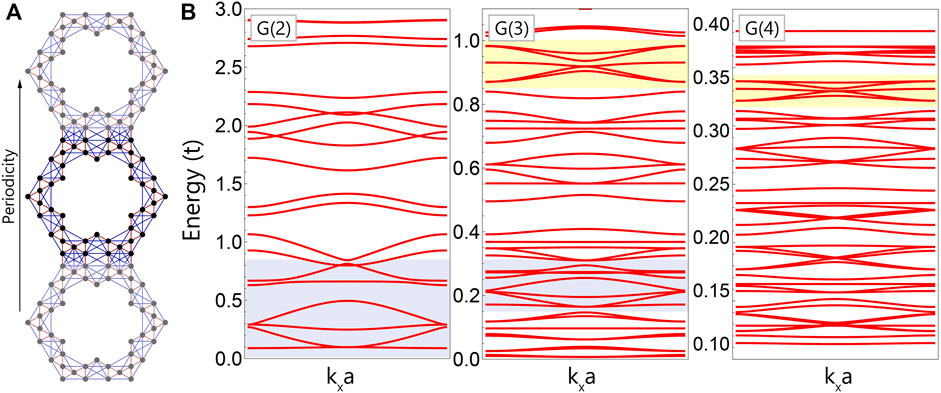
FIGURE 4. (A) G (2)-TK chain illustration with first (red lines) and second (blue lines) neighbors; (B) Corresponding G (2), G (3), and G (3)-TK electronic bands considering only first neighbors and ɛ = 0.

Figure 5A compares the electronic structure of the TK-G2 discussed in Figure 4, considering 1N (red curves) and 2NN (blue curves) models. Remarkably, the negative energy spectrum for the 1N model exhibits almost flat bands—that is, without dispersion, a manifestation of high localized states. For the 2NN approach, however, the spectrum is more dispersed. The electronic conductance results for TK-G (2) chains described by both models are shown in Figure 5B. As expected from the electronic bands relative to the 1N model, the transport response is mostly null for the considered negative energy range. In a more realistic model, up to second neighborhood, the number of available channels increases—marked by the blue conductance in the same energy range—due to the non-zero electronic group velocities in the energy interval from −1.2t to zero.

FIGURE 5

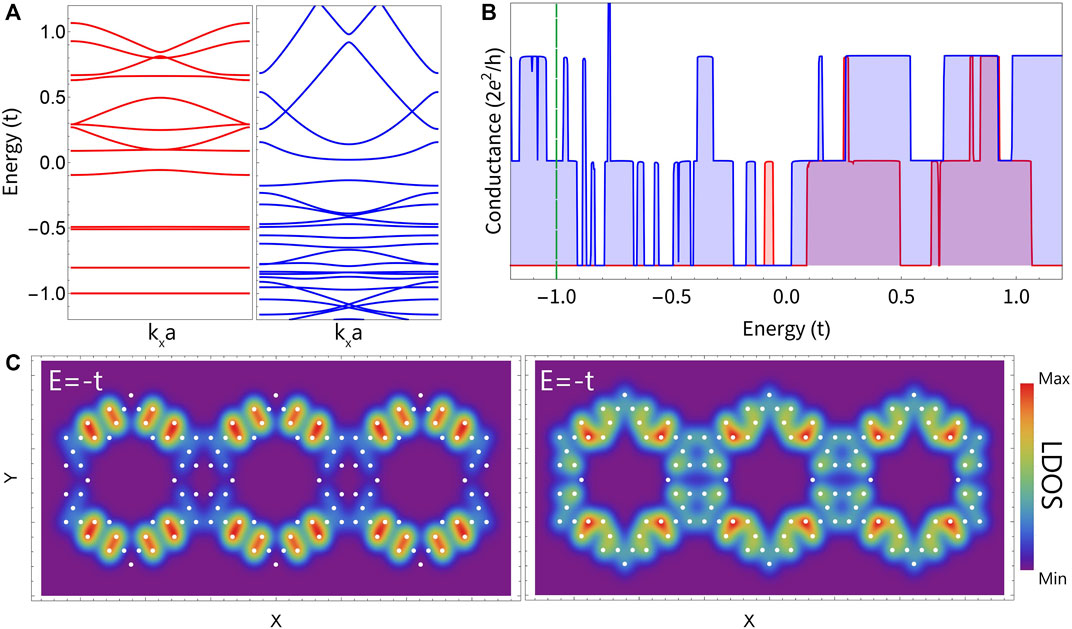
FIGURE 5. TK-G2 chain results considering first (red) and up to second (blue) neighbors, respectively. (A) Electronic bands, (B) electronic conductance, and (C) local density of states at E = −t.

Concerning to the charge distribution at E = −t (Figure 5C), it is clear that, for the 1N model, the charges are concentrated around particular sites that resemble the localized states for the same geometry in the single corral (Figure 3). The wavefunction of such states does not spread along the neighboring unit cells of the molecular chain (Koch corrals), resulting in high localized states and suppression of the transport response at this energy. The situation is completely different within the 2NN model, as shown in the results of the corresponding LDOS (right panel in Figure 3C), highlighting the delocalization of the state through the chain.

3.3 Effective molecular quantum corrals

As mentioned in the introduction, with recent experimental advances in the synthesis and fabrication of carbon nanocomposites, new possible geometries can be explored that take into account the interplay between fractal structures and regular geometries. Here, we propose a quantum corral based on hexagonal symmetries similar to the previously reported hexagram (Zhang Z. et al., 2020) and hexagonal gasket (Newkome et al., 2006). However, in our suggested TB framework, the systems can be considered hexagonal triangular Sierpinski corrals of different orders (HTS). They are generated by repeating Sierpinski triangles connected to form self-similar objects like Koch corrals, as depicted in the G (1–4) sequence (Figure 6A). For the sake of simplicity, we first consider the nanostructures composed of equal atoms, represented by the black dot in all the 4^th first generations G (1–4). In particular, we have taken all on-site energies in the Hamiltonian ϵ_i = 0 representing the carbon lattices. The fractal dimension D of the proposed system can be calculated through the relation (Foroutan-pour et al., 1999):

$D={\displaystyle \underset{r\to 0}{\lim }}\frac{Log\left[N\left(r\right)\right]}{Log\left[r^{-1}\right]}(5)$

with N® being the number of squares as a function of the size r delimited by the image size. The box counting method (Kaurov, 2012) was used to estimate the fractal dimension, where it can be obtained by the linear regression of the values as illustrated in the right-hand chart in Figure 6B. The dimension estimated for the nanostructured system proposed here is D ≈ 1.63, which is consistent with the reported version with hexagonal units instead of Sierpinski triangles (Devaney, 2004), where D = log(6)/log(3) ≈ 1.63.The energy spectrum for the first G (1–4) generations is depicted in the diagram shown in the right-hand panel of Figure 6B. The corresponding degeneracy of the states is coded by the brightness of the colored bars in a direct correspondence. For example, at E = −2t there are 6, 42, 258, and 1,554 degenerate states in the sequence of G (1–4), respectively, and also at E = −t for G (2–4).

FIGURE 6

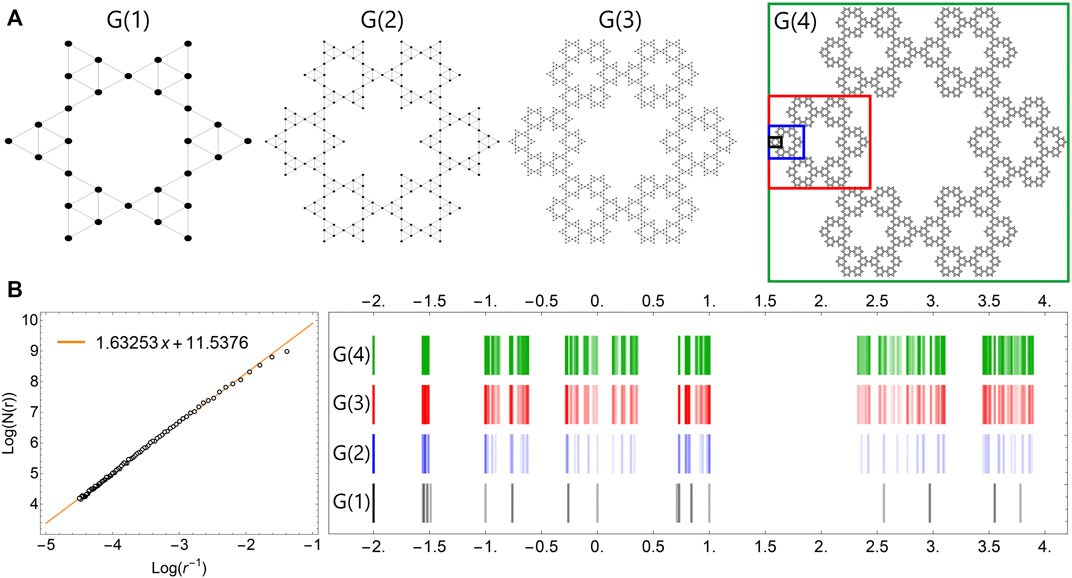
FIGURE 6. (A) From left to right: schematic view of G (1–4) fractal corral structures. For G (4), the colored squares distinguish G (1–4) generations. (B) Left: numerical results for energy spectra in G (1–4); colored bar bright is directly proportional to the degeneracy order of states. Right: box counting linear fit result.

Returning to the molecular synthesized structures, due to the presence of chemical elements in the systems other than carbon atoms, we have chosen different on-site energies in the numerical calculations: ɛ_C = 0.25t, ɛ_Fe = −0.25t, and ɛ_Ru = −0.35t.We have also investigated (not shown here) cases in which ɛ_Ru > ɛ_Fe, which did not produce significantly changes in the present results. The set of different atomic site symmetries in the effective lattice is denoted by circles of different colors, as illustrated in the right-hand chart in Figure 7A. Note that other non-equivalent sites are also marked in the figure with dashed black circles that represent sites very similar to those marked by purple and red circles. The LDOS corresponding to the four non-equivalent colored sites are shown in Figure 7B. The total density of states (averaged over the total number of atoms) is also displayed in shaded grey curves. Special charge densities over the quantum corral sites are depicted in Figure 7C for different states marked in the eigenenergy spectrum diagram. The spatial LDOS for the energies E = −0.3t and 0, next to the Fermi level (E_F = −0.3t), and also for E = 1.1t, show that the main contributions comes from Fe and C sites located in the internal hexagonal. On the other hand, for E = −1.3t, the highest LDOS values come from the Ru atom positions. The charge density panels are consistent with the previous results of the LDOS versus energy presented in Figure 7B, which highlight the charge distribution weight at the individual atomic corral sites. The construction of higher generation lattices would help to identify possible self-similarity manifestations on the electronic properties. Also important is the incorporation of spin-orbit coupling, mainly at the metallic sites, and hybridized-orbital models to allow more realistic description of the metal organic fractal structures (Canellas Núnez et al., 2023). Such analysis can help in engineering the electronic responses of the quantum Triangle Sierpinski corrals and propose appropriate functionalization of the molecules.

FIGURE 7

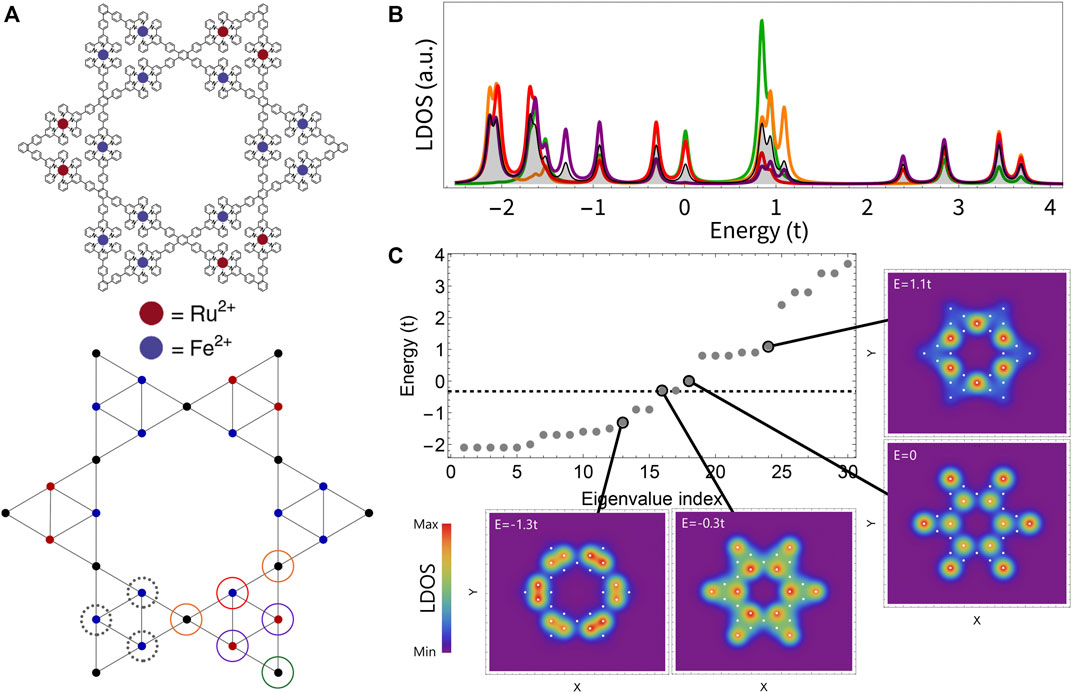
FIGURE 7. (A) Top: chemical molecule illustration synthesized experimentally (adapted from Zhang Z. et al. 2020)). Bottom: proposed tight-binding effective quantum corral, with colored dots denoting C (black), Fe (blue), and Ru (red) atoms. (B) LDOS of the corresponding sites marked by colored circles in the TB corral and total averaged DOS (gray curve). (C) Energy spectrum with the electronic charge distribution for E = −1.3t, −0.3t, 0, and 1.1t. TB parameters: ɛ_C = 0.25t, ɛ_I = −0.25t, and ɛ_Ru = −0.35t.

4 Conclusion

This research has explored the nature of localized states in quantum corrals created by fractal structures, based on C atoms, such as Koch lines and Sierpinski triangles. Annular triangular and square Koch structures were proposed within a first- and up to second-neighbor tight-binding framework. Comparison between the two approaches reveals the existence of spreading electronic states around the corrals, favoring the 2NN description for possible transport applications. The emergence of conducting channels is revealed for the proposed corral chains, similar to what had been previously verified for other organic molecular fractal chains (Lage and Latgé,2022). Furthermore, quantum corral architectures based on triangular Sierpinski units were proposed to effectively describe synthesized organic molecular corrals. The results revealed rich features on the electronic properties and good agreement with STM images of the experimental data (Zhang Y. et al., 2020). Higher order fractal structures can be envisaged that allow investigation of self-similarity responses. Also, more sophisticated descriptions within the same tight-binding approach, incorporating many-body correlation terms (spin-orbit couplings at the metallic sites and electron-electron correlations), may be extended to better describe complex molecular systems with transition metals. We believe that the present research can be used to guide the synthesis of a variety of real fractal molecular nanostructures, highlighting the particular symmetries and possibilities of new functionalization procedures.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

LLL: conceptualization, investigation, methodology, software, visualization, writing–original draft, writing–review and editing. AL: conceptualization, funding acquisition, investigation, methodology, project administration, supervision, validation, visualization, writing–original draft, writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was financed by Brazilian Agencies CNPq and FAPERJ within grant E-26/200.569/2023.

Acknowledgments

The authors would like to thank the INCT de Nanomateriais de Carbono for providing support on the computational infrastructure. LLL thanks the CNPq scholarship.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, editors, and reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Berdonces-Layunta, A., Schulz, F., Aguilar-Galindo, F., Lawrence, J., Mohammed, M. S. G., Muntwiler, M., et al. (2021). Order from a mess: the growth of 5-armchairgraphene nanoribbons. ACS Nano 15, 16552–16561. doi:10.1021/acsnano.1c06226

PubMed Abstract | CrossRef Full Text | Google Scholar

Browning, L. A., Watterson, W., Happe, E., Silva, S., Abril Valenzuela, R., Smith, J., et al. (2021). Investigation of fractal carbon nanotube networks for biophilic neural sensing applications. Nanomaterials 11, 636. doi:10.3390/nano11030636

PubMed Abstract | CrossRef Full Text | Google Scholar

Canellas Núnez, R., Liu, C., Arouca, R., Eek, L., and Yin, Y. (2023). Topological edge and corner states in bi fractals on insb. arxiv-2309.09860.

Google Scholar

Castro Neto, A., Guinea, F., Peres, N. M. R., Novoselov, K. S., and Geim, A. (2009). The electronic properties of graphene. Rev. Mod. Phys. 81, 109–162. doi:10.1103/RevModPhys.81.109

CrossRef Full Text | Google Scholar

Chico, L., Latgé, A., and Brey, L. (2015). Symmetries of quantum transport with rashba spin–orbit: graphene spintronics. Phys. Chem. Chem. Phys. 17, 16469–16475. doi:10.1039/C5CP01637A

PubMed Abstract | CrossRef Full Text | Google Scholar

Crommie, M. F., Lutz, C. P., and Eigler, D. M. (1993). Confinement of electrons to quantum corrals on a metal surface. Science 262, 218–220. doi:10.1126/science.262.5131.218

PubMed Abstract | CrossRef Full Text | Google Scholar

Dai, J., Zhao, X., Peng, Z., Li, J., Lin, Y., Wen, X., et al. (2023). Assembling surface molecular sierpiński triangle fractals via K⁺-Invoked electrostatic interaction. J. Am. Chem. Soc. 145 (25), 13531–13536. doi:10.1021/jacs.3c03691

PubMed Abstract | CrossRef Full Text | Google Scholar

Data, S. (1995). Electronic transport in mesoscopic sysytems. United Kindgom: Cambridge University Press.

Google Scholar

De Nicola, F., Castrucci, P., Scarselli, M., Nanni, F., Cacciotti, I., and De Crescenzi, M. (2015). Multi-fractal hierarchy of single-walled carbon nanotube hydrophobic coatings. Sci. Rep. 5, 8583. doi:10.1038/srep08583

PubMed Abstract | CrossRef Full Text | Google Scholar

Devaney, R. L. (2004). Chaos rules!. Math. Horizons 12(2), 11–13. doi:10.1080/10724117.2004.12023675

CrossRef Full Text | Google Scholar

Domany, E., Alexander, S., Bensimon, D., and Kadanoff, L. P. (1983). Solutions to the Schrödinger equation on some fractal lattices. Phys. Rev. B 28, 3110–3123. doi:10.1103/PhysRevB.28.3110

CrossRef Full Text | Google Scholar

El-Nabulsi, R. A., and Anukool, W. (2021). Quantum dots and cuboid quantum wells in fractal dimensions with position-dependent masses. Appl. Phys. A 127, 856. doi:10.1007/s00339-021-04989-6

CrossRef Full Text | Google Scholar

El-Nabulsi, R. A., and Anukool, W. (2023). Analysis of quantum effects in metal oxide semiconductor field effect transistor in fractal dimensions. MRS Commun. 13, 233–239. doi:10.1557/s43579-023-00334-5

CrossRef Full Text | Google Scholar

Felix, A. B., Pacheco, M., Orellana, P., and Latgé, A. (2022). Vertical and in-plane electronic transport of graphene nanoribbon/nanotube heterostructures. Nanomaterials 12, 3475–34759. doi:10.3390/nano12193475

PubMed Abstract | CrossRef Full Text | Google Scholar

Foroutan-pour, K., Dutilleul, P., and Smith, D. (1999). Advances in the implementation of the box-counting method of fractal dimension estimation. Appl. Math. Comput. 105, 195–210. doi:10.1016/S0096-3003(98)10096-6

CrossRef Full Text | Google Scholar

Freeney, S. E., Slot, M. R., Gardenier, T. S., Swart, I., and Vanmaekelbergh, D. (2022). Electronic quantum materials simulated with artificial model lattices. ACS Nanosci. Au 2, 198–224. doi:10.1021/acsnanoscienceau.1c00054

PubMed Abstract | CrossRef Full Text | Google Scholar

Gowrisankar, A., and Banerjee, S. (2021). Frontiers of fractals for complex systems: recent advances and future challenges. Eur. Phys. J. Special Top. 230, 3743–3745. doi:10.1140/epjs/s11734-021-00376-7

CrossRef Full Text | Google Scholar

Jiang, Z., Li, Y., Wang, M., Song, B., Wang, K., Sun, M., et al. (2017). Self-assembly of a supramolecular hexagram and a supramolecular pentagram. Nat. Commun. 8, 15476–154788. doi:10.1038/ncomms15476

PubMed Abstract | CrossRef Full Text | Google Scholar

Kaurov, V. (2012). Measuring fractal dimension of natural object from digital images. Math. Stack Exch. 2012.

Google Scholar

Kempkes, S. N., Slot, M. R., Freeney, S. E., Zevenhuizen, S. J. M., Vanmaekelbergh, D., Swart, I., et al. (2019). Design and characterization of electrons in a fractal geometry. Nat. Phys. 15, 127–131. doi:10.1038/s41567-018-0328-0

PubMed Abstract | CrossRef Full Text | Google Scholar

L Lage, L., and Latgé, A. (2022). Electronic fractal patterns in building Sierpinski-triangle molecular systems. Phys. Chem. Chem. Phys. 24, 19576–19583. doi:10.1039/d2cp02426h

PubMed Abstract | CrossRef Full Text | Google Scholar

Mandelbot, B. B. (1983). The fractal geometry of nature. 3 edn. New York: Henry Holt and Company.

Google Scholar

Newkome, G. R., Wang, P., Moorefield, C. N., Cho, T. J., Mohapatra, P. P., Li, S., et al. (2006). Nanoassembly of a fractal polymer: a molecular “Sierpinski hexagonal gasket ”. Science 312, 1782–1785. doi:10.1126/science.1125894

PubMed Abstract | CrossRef Full Text | Google Scholar

Pedersen, T. G. (2020). Graphene fractals: energy gap and spin polarization. Phys. Rev. B 101, 235427. doi:10.1103/PhysRevB.101.235427

CrossRef Full Text | Google Scholar

Peng, X., Mahalingam, H., Dong, S., Mutombo, P., Su, J., Telychko, M., et al. (2021). Visualizing designer quantum states in stable macrocycle quantum corrals. Nat. Commun. 12, 5895. doi:10.1038/s41467-021-26198-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Santos, H., Latgé, A., Brey, L., and Chico, L. (2020). Spin-polarized currents in corrugated graphene nanoribbons. Carbon 168, 1–11. doi:10.1016/j.carbon.2020.05.054

CrossRef Full Text | Google Scholar

Shang, J., Wang, Y., Chen, M., Dai, J., Zhou, X., Kuttner, J., et al. (2015). Assembling molecular Sierpiński triangle fractals. Nat. Chem. 7 (5), 389–393. doi:10.1038/nchem.2211

PubMed Abstract | CrossRef Full Text | Google Scholar

Trambly de Laissardière, G., Mayou, D., and Magaud, L. (2010). Localization of Dirac electrons in rotated graphene bilayers. Nano Lett. 10, 804–808. doi:10.1021/nl902948m

PubMed Abstract | CrossRef Full Text | Google Scholar

Wakabayashi, K., Sasaki, K. I., Nakanishi, T., and Enoki, T. (2010). Electronic states of graphene nanoribbons and analytical solutions. Sci. Technol. Adv. Mater. 11, 054504. doi:10.1088/1468-6996/11/5/054504

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, L., Liu, R., Gu, J., Song, B., Wang, H., Jiang, X., et al. (2018). Self-assembly of supramolecular fractals from generation 1 to 5. J. Am. Chem. Soc. 140, 14087–14096. doi:10.1021/jacs.8b05530

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, X. R. (1995). Localization in fractal spaces: exact results on the Sierpinski gasket. Phys. Rev. B 51, 9310–9313. doi:10.1103/PhysRevB.51.9310

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, X. Y., Wang, X. W., Chen, D. Y., Smith, C. M., and Jin, X. M. (2021). Quantum transport in fractal networks. Nat. Phot. 15, 703–710. doi:10.1038/s41566-021-00845-4

CrossRef Full Text | Google Scholar

Zhang, Y., Zhang, X., Li, Y., Zhao, S., Hou, S., Wu, K., et al. (2020a). Packing sierpiński triangles into two-dimensional crystals. J. Am. Chem. Soc. 142, 17928–17932. doi:10.1021/jacs.0c08979

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Z., Li, Y., Song, B., Zhang, Y., Jiang, X., Wang, M., et al. (2020b). Intra- and intermolecular self-assembly of a 20-nm-wide supramolecular hexagonal grid. Nat. Chem. 12, 468–474. doi:10.1038/s41557-020-0454-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhou, Z., Bouwman, W. G., Schut, H., Desert, S., Jestin, J., Hartmann, S., et al. (2016). From nanopores to macropores: fractal morphology of graphite. Carbon 96, 541–547. doi:10.1016/j.carbon.2015.09.069

CrossRef Full Text | Google Scholar