Cyclic soil-structure interaction of integral railway bridges

Integral bridges with larger spans experience increased cyclic interaction with their backfill, particularly due to seasonal temperature changes. This can result in a continuous increase of earth pressure (during the summer positions) as well as an accumulation of settlements in the granular backfill over the bridge’s lifespan. While the soil stresses must be accounted for in the structural design through appropriate calculation methods, the settlements negatively impact the serviceability and the maintenance demands of the railway track and can only be accepted to a very limited extent. Therefore, this paper presents a detailed numerical investigation on the cyclic interaction behavior of integral railway bridges. For this purpose, an elastoplastic soil material model (DeltaSand), which has been calibrated based on a comprehensive experimental program for a well-graded gravel backfill material, and validated 2D and 3D FE models are used. Extensive parametric studies are conducted with varying bridge geometries (lengths, heights), as well as abutment, backfill, and foundation stiffnesses. The numerical results for both, the lateral stress loading and the bending moment of the abutment are compared to analytical design approaches used in Germany, Austria and United Kingdom. Lateral stresses on the abutment and settlements of the backfill show a clear increase with cycles and bridge lengths. The stiffness of both the backfill material and the underground soil highly influences the earth pressure mobilization and its distribution on the abutment. The study also highlights that existing design approaches are not conservative in all cases and should be adjusted.

1 Introduction

Integral bridges, due to the absence of joints and bearings, offer numerous advantages over conventionally supported bridges, see, e.g., (Burke and Martin, 2009; Liu et al., 2022c). Within the DB InfraGO AG network, single- and multi-span reinforced concrete frames with a total span of up to 25 m represent the standard construction method and account for approximately 65% of new bridge constructions over the past 10 years. In the past two decades, also an increasing number of integral railway bridges with medium and long spans of up to 170 m have been constructed, e.g., (Marx and Seidl, 2011; Wenner et al., 2019; Stastny et al., 2022; Granitzer et al., 2024). For the planning and construction of these jointless and bearing-free designs, the DB guideline Ril 804.4501 (2021) was recently introduced as the first official DB regulation. It is based on the design guide for integral road bridges RE-ING (2023). Also in Austria, a new standard (RVS 15.02.12, 2019) for the design of integral bridges has been published. Despite the recent updates, there is still a need for further research, particularly regarding the cyclic interaction between the monolithic structures, their typical foundations and their railway-specific backfills.

The complex cyclic soil-structure interaction (SSI) of integral bridges features two main mechanisms, see Figure 1A: Firstly, primarily due to seasonal thermal deformations of the structure, integral abutments experience recurring increases in earth pressure during summer and decreases during winter. Secondly, the cyclic temperature-induced deformations of the structure lead to repeated compaction of granular backfills, resulting in growing settlements (“ratcheting”) over the bridge’s design lifetime of 100 years (in Germany). These effects intensify significantly with the length of the structure and, consequently, the magnitude of horizontal displacements at the deck’s end. More details are summarized in Section 2. The cyclic increase in earth pressure must be adequately accounted for in the structural design of the bridge, while the accumulation of settlements impacts the serviceability. These settlements must not become too large, as they could affect the railway track alignment and lead to increased maintenance expenses. Especially for ballastless tracks - although not the primary focus of this study - this is highly relevant, since strict standards must be met regarding track alignment and only minimal adjustments to the track can be made after construction.

Figure 1

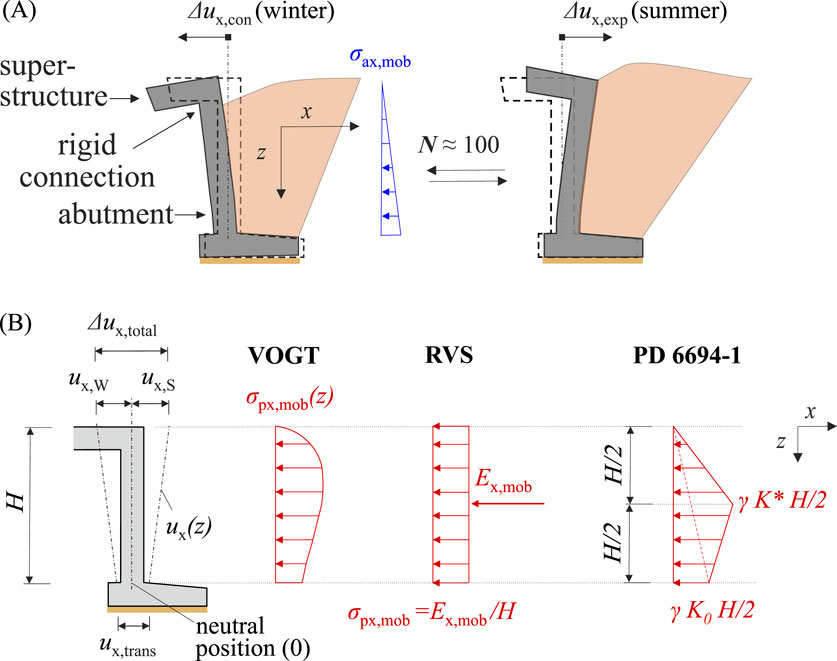
Figure 1. (A) Scheme of the soil-structure interaction of an integral bridge and its backfill, (B) Profile of analytical design approaches by Vogt (1984), RVS 15.02.12 (2019) and PD6694-1 (2020) for the lateral earth pressure on integral abutments in summer.

For traditional coarse-grained backfills, various earth pressure models exist, see, e.g., (RE-ING, 2023; RVS 15.02.12, 2019; PD6694-1, 2020; Kerokoski, 2006; Mass. DOT, 2024). These design approaches vary considerably and are often proposed based on experiments (Vogt, 1984; Springman et al., 1996; England et al., 2000; Tapper and Lehane, 2005) that have limitations, such as boundary effects or simplified abutment deformation (e.g., rigid “foot-point” rotation). Furthermore, they are predominantly derived using poorly-graded (fine) sands. In general, research on the SSI, both with experimental and/or numerical strategies, has focused on integral road bridges and poorly-graded materials, see Section 2. However, no studies are available that consider railway specifics, such as additional track (and traffic) loads, or railway-specific backfill designs. For example, according to DB guideline Ril 836 (2023), only well-graded sand-gravel mixtures are approved as backfill materials. As shown, e.g., in Stastny et al. (2024a) well-graded coarse-grained backfill material mobilizes significantly higher lateral stresses compared to uniformly-graded (fine) sands. Due to these shortcomings (and assumptions), further research is necessary and existing earth pressure approaches need to be carefully checked and improved if required.

Therefore, this study aims to quantify the various influences on the cyclic SSI behavior of integral railway bridges and compares the results to different analytical design approaches for the passive lateral stress mobilization from Germany, Austria and the United Kingdom (RE-ING, 2023; RVS 15.02.12, 2019; PD6694-1, 2020). It focuses on typical integral railway bridges in Germany with full height abutments on spread footings, either with or without additional support of concrete bored piles. Cyclic 2D and 3D finite element (FE) studies are conducted using practice-oriented bridge lengths of $L=$20–140 m and heights of $H=$3–8 m with varying abutment stiffnesses and foundations. The numerical model was validated through preliminary studies. The direct application of temperature loading on the structure allows a realistic simulation of the SSI behavior. The backfill behavior is described by the elastoplastic material model DeltaSand (Galavi, 2021), which was developed for cyclic loading applications. It was calibrated in Stastny et al. (2024b) for a representative well-graded gravel backfill material based on a comprehensive experimental program and tested against other advanced soil models in design case studies on the cyclic SSI of integral bridges. The present investigation further explores the influence of backfill stiffness, comparing it to Karlsruhe fine sand at various relative densities. Subsequently, also the influence of different typical deep foundation designs and underground soil stiffnesses are examined. The study focuses not only on the lateral stress development but also on the abutment’s internal bending forces and the settlement accumulation in the backfill.

The following research questions will be addressed in the in this work:

• What are the main drivers of the cyclic SSI?

• Which lateral stress profile is adequate for well-graded granular backfills, especially for longer integral railway bridges?

• What settlement accumulation in the backfill can be expected due to the horizontal SSI?

Based on the findings, recommendations are formulated for future structural design of integral (railway) bridges.

2 Review on the SSI of integral bridges

Integral abutments are subjected to cyclic variations in earth pressure primarily due to seasonal thermal expansions and contractions of the bridge deck. During warmer months, earth pressure behind the abutment increases, while it decreases during colder periods. These cyclic deformations also cause repeated compaction of granular backfills, leading to settlement accumulation, a phenomenon commonly referred to as “ratcheting” (England et al., 2000; Lehane, 2011; Morley et al., 2024). Scaled experiments and centrifuge tests (see below) have demonstrated that cyclic loading induces a continuous increase in earth pressures and progressive settlement accumulation during a bridge’s life. These effects are more pronounced in longer structures, as the magnitude of thermal deck displacements grows with length. The cyclic increase of stresses and settlements is influenced by various geotechnical and structural factors such as: geometry (length, height, skew, orientation) as well as stiffness of the bridge and abutment, temperature loading (daily, seasonal), abutment movements (magnitude, shape), backfill (material, density, moisture), foundation type and underground stiffness, site-specific conditions (Banks and Bloodworth, 2018; Abdel-Fattah et al., 2018; Hassan et al., 2024). This large number of influencing factors makes it challenging to accurately account for the SSI in design codes and to capture it numerically. The following sections provide a brief review of research on experimental testing and numerical analysis related to the SSI of integral bridges. Field monitoring or special transition zone designs, e.g., transition slabs (Dreier et al., 2011) or the inclusion of compressible material behind the abutment (Sigdel et al., 2023) will not be covered.

2.1 Laboratory testing

Numerous researchers, e.g., (Vogt, 1984; Springman et al., 1996; England et al., 2000; Lehane, 2011; Tapper and Lehane, 2005; Havinga et al., 2017; Walter et al., 2018; Grabe et al., 2019; Liu et al., 2022b; Luo et al., 2023; Alqarawi et al., 2024; Morley et al., 2024), have carried out experimental 1$g$ and/or centrifuge (n$g$) tests to investigate the cyclic SSI behavior of integral (road) bridges. These tests either investigate geotechnical problems at small (er)-scale under normal gravity (1$g$) or in the centrifuge, where the gravitational field is artificially increased to $\mathrm{n}\cdot g$ allowing a small model to replicate the stress and strain conditions of a much larger prototype in the field. The tests, conducted predominantly on poorly-graded fine sands, consistently showed that cyclic loading causes a progressive increase in lateral forces at the abutments during the bridge’s summer expansion. The largest stress increases typically occur during the first 5–20 thermal cycles, but often continue over more than 100 cycles. Additionally, the cyclic loading induces continuous settlement accumulation at the backfill surface. The main reasons for the cyclic increases are addressed as changes in the soil behavior due to: a) cyclic loading amplitude, b) rearrangement of particles (especially upon reloading after the active winter phase), c) densification and increase of particle contacts, e.g., (England et al., 2000; Clayton et al., 2006; Lehane, 2011; Hassan et al., 2024).

Vogt (1984) conducted 1$g$ tests on a 4 m high and 9 m long concrete wall with minimal foot movement. The displacements were applied on the top and the wall showed significant bending (during passive loading) due to its low flexural rigidity. In three test series the wall was pushed (at the top) $N=$140 times with varying amplitudes ($\pm \mathrm{\Delta }/H=$0.05%–0.2%) against a fine sand filling ($C_u=$2.5, $D_r=$45%–76%, moisture content MC = 5–6%). 45 pressure cells and 9 load cells were used to capture the reaction of the soil. Vogt’s tests showed negligible cyclic earth pressure increases after the first cycles. Vogt derived a parabolic function to describe the passive mobilization of earth pressure with respect to the abutment horizontal deformation. This equation is still used for the design of integral bridges in Germany (RE-ING, 2023; Ril 804.4501, 2021), see Section 4.

Franke (1989) derived an equation for the monotonic (active and) passive earth pressure mobilization based on mechanical models. No cyclic experiments were involved. Nevertheless, the equation, as part of ÖNorm B 4434 (1993), is now used in the Austrian guide for integral bridges RVS 15.02.12 (2019) to cover the cyclic passive earth pressure mobilization. Bartl (2004) conducted additional small-scale 1$g$ tests (as well as centrifuge tests) with different monotonic wall movements to determine the passive earth pressure mobilization and proposed adjustments to Franke’s equation.

Small-scale 1$g$ tests by England et al. (2000) and Cosgrove and Lehane (2003) explored stiff abutments with foot point rotations in fine sand, revealing that relative density $D_r$ of the sand significantly influences the mobilization of stresses. Denser materials ($D_r=$94%) exhibited rapid lateral stress increases, with a more moderate growth after a few cycles, while looser materials ($D_r=$21%) continued to increase stresses towards passive levels. Centrifuge tests (spread base and embedded abutments/fine sand) by Springman et al. (1996) found that small cyclic movements cause minimal stress changes, but larger cycles led to significant increases, particularly in the early stages. This was later confirmed by Tapper and Lehane (2005) and Lehane (2011) by means of n$g$ tests (pinned base abutment/fine sand). In their research, stresses in sand increase approximately linearly with cycles on a logarithmic scale, and show increases for up to 1,000 cycles. Contrary to Clayton et al. (2006), particle shape was not found to be a major factor influencing the maximum lateral stresses on integral abutments. The test results of England et al. (2000), Springman et al. (1996), Tapper and Lehane (2005) and Lehane (2011) have been used to develop the analytical earth pressure design guidelines PD6694-1 (2020) in United Kingdom, see Section 4 and Denton et al. (2011).

Xu et al. (2007) and Bloodworth et al. (2012) used cyclic triaxial tests with radial strain-control, showing that (fine) sands exhibit greater lateral stress buildup under cyclic loads compared to stiff clays. Havinga et al. (2017), Walter et al. (2018) and Liu et al. (2022b) conducted mid-scale 1$g$ tests in rigid boxes with fill heights of 1 to 1.25 m on poorly-graded sands or gravels considering 10 to 30 seasonal cycles. Several of these tests allowed to simulate a small translation of the stiff front plate (abutment). Havinga et al. (2017) reported a linear increase of lateral stress with seasonal cycles plotted on a logarithmic scale. Liu et al. (2022b) found that as the abutment’s translational movement increase, horizontal earth pressures behind the abutment decrease. Settlements continued to increase throughout the considered 30 seasonal cycles. Morley et al. (2024) further explored the effects of abutment stiffness and backfill density using centrifuge tests on a 150 m long integral bridge with spread footing in fine sand. Flexible abutments tended to accumulate more settlements than stiff abutments. The tests revealed exponential decay trends of the cyclic lateral earth pressure increase, with dense sand showing significantly higher values compared to loose sand. Additionally, for stiff abutments, peak lateral stresses were observed in the upper half of the abutment, as opposed to mid-height.

2.2 Numerical analysis

Most numerical studies on the SSI of integral bridges use the finite element method with focus on the structural behavior, e.g., (Dicleli, 2005; Civjan et al., 2007; Ooi et al., 2010; Zordan et al., 2011; David et al., 2014; LaFave et al., 2016; Quinn and Civjan, 2017; Della Pietra et al., 2019). In these studies, the soil behavior is often simplified by means of linear-elastic perfect-plastic soil models or (nonlinear) soil springs. Several FE studies, e.g., (Kerokoski, 2006; Efretuei, 2013; Abdel-Fattah et al., 2018; Sandberg et al., 2020; Liu et al., 2023; Silva et al., 2023; Abdullah and El Naggar, 2023), used the elastoplastic Hardening Soil model (Schanz et al., 1999). Only a few researcher conducted studies on the SSI using finite-difference methods (Wood, 2004; Bloodworth et al., 2012; Banks and Bloodworth, 2018; Liu et al., 2022a) or discrete element methods (Zorzi et al., 2017; Xu and Guo, 2021).

Abdel-Fattah and Abdel-Fattah (2019) conducted 2D FE analyses ($H=$6 m, $L=$20–260 m) using the Hardening Soil model to simulate the SSI of integral bridges with piled and shallow foundations and a sandy backfill over four seasonal cycles. They observed that earth pressure increases with both bridge length and the number of cycles. Additionally, they found that the location of the earth pressure resultant also dependes on these two factors. With increasing stiffness of the backfill, the earth pressures due to cyclic loading also rose (except for the lower quarter of the wall).

Bloodworth et al. (2012) and Banks and Bloodworth (2018) conducted cyclic 2D FE simulations to examine earth pressure mobilization behind frame bridges on spread footings ($H=$4 m, $L=$15–100 m). They used a soil model, derived from triaxial test results (Xu, 2005) on Leighton Buzzard sand. The lateral stress development for a total of 120 seasonal cycles (with temperature deformations of 1 year and 120 years return period) was simulated and compared against the current United Kingdom design guidelines PD6694-1 (2020), see Equation 3 in Section 4. The research confirmed that Equation 3 is satisfactory for bridges up to $L=$60 m. Additional calculations with daily temperature cycles, in addition to annual summer-winter variations, showed increased stresses by approximately 10%.

Stastny et al. (2024a) and Stastny et al. (2024b) performed cyclic SSI studies using 2D FE models with three advanced elastoplastic [DeltaSand by Galavi (2021), Sanisand-MS by Liu et al. (2019)] or hypoplastic [Hypo+IGS by Wolffersdorff (1996); Niemunis and Herle (1997)] soil models for cyclic loading. All models were calibrated based on laboratory tests for a well-graded gravel backfill material. Two soil models proved to be capable of capturing the main mechanisms of the cyclic SSI, at least for the considered 20 seasonal cycles. Further studies demonstrated that the cyclic mobilization of earth pressure (in the summer position) is highly influenced by the actual displacement pattern of the abutment. The analyses also exhibited significantly higher cyclic earth pressures for well-graded gravels compared to poorly-graded sands. The SSI behavior for all materials was primarily governed by the “overall” stiffness of the soil model, including the small-strain stiffness.

2.3 Dynamic vertical interaction

This research focuses on the horizontal cyclic SSI due to seasonal temperature deformation of the integral bridge deck. However, it has to be noted that this interaction mechanism is superposed by the vertical dynamic interaction of train, track and backfill. Transition zones of railway bridges with granular backfills are characterized by sharp changes of stiffness (from structure to backfill) as well as differential settlements (in the ballasted track) due to traffic loads. The appearance of settlements may start a deterioration loop, leading to amplified vertical dynamic track loads and accelerations, the development of “hanging sleepers” and further expansion of settlement troughs, compare, e.g., Wang and Markine (2019) and Paixão et al. (2016), Paixão et al. (2021). This, in turn, can accelerate track degradation and increase maintenance costs. Paixão et al. (2016) found that both the settlement amplitude and profile strongly influence this process. The horizontal SSI of longer integral bridges adds additional settlement accumulation to the system, which may intensify and speed up the degradation described above. The acceptability of backfill settlements due to the horizontal cyclic SSI of integral bridges therefore cannot be judged independently of the vertical dynamic train-track interaction. The DB guideline for integral railway bridges Ril 804.4501 (2021) in Germany requires the use of a special transition zone design, such as approach slabs, when horizontal seasonal deck deformations exceed 20 mm. This corresponds to a concrete deck length of approximately 50 m. The requirement is primarily based on experience and repeated evaluation of track measurement data from existing integral railway bridges with or without approach slabs. However, until today, no research has focused on the combined effects of the horizontal cyclic and the vertical dynamic interaction in the transition zones of long integral railway bridges. Although it is not the focus of this study, it remains a significant question for future research.

3 Objects of study

3.1 Bridge geometries and variations

In this investigation, reference structural models of integral railway bridges are used to study the cyclic soil-structure interaction. The geometries are taken from real life projects and are adjusted for easier parametrization. Typically, in Germany integral railway bridges are constructed with full height abutments on a spread footing, either with or without additional support of concrete bored piles. Other forms of embedded wall abutments or bank pad abutments on piles (PD6694-1, 2020) are less common. The same can be said for any form of steel pile profiles, which are popular, e.g., in the United States (Liu et al., 2022c), but rarely used in Germany.

The reference models consist of concrete deck superstructures ($h=$1 m) with total lengths of $L=$20 – 40 – 60 – 80 – 100 – 120 – 140 m, at single spans of $l=$20 m and a slenderness of $l/h=$20, see Figure 3A. Its abutments (width $w=1\mathrm{m}$) with heights of $H=$3 – 5 – 8 m are founded on spread footings. Subsequently, also abutments on deep foundations with either one or two rows of concrete bored piles are studied.

The influence of the following variations on the cyclic SSI of integral bridges is investigated:

• Bridge lengths

• Abutment heights

• Abutment stiffnesses

• Backfill stiffnesses

• Foundation and underground stiffnesses

3.2 Backfill materials

According to the DB guideline Ril 836 (2023), railway bridge backfills must use well-graded sands or gravels, containing no more than 5% fine particles smaller than 0.063 mm. These materials are compacted in situ to 100% Proctor density in 30 cm layers. To ensure appropriate grading and compaction, the material must have a uniformity coefficient $C_u\ge$ 6.

The gravel analyzed in this study is a representative, well-graded material suitable for bridge backfills. Its grain size distribution includes a mean grain size of $d_{50}=$4 mm and a maximum grain size of $d_{100}=$16 mm, with a high uniformity coefficient of $C_u=24$, see Figure 2. The gravel consists of smooth, subrounded grains. An extensive laboratory program (Stastny et al., 2024a) has been conducted to capture the monotonic and cyclic behavior of the gravel backfill and to allow a systematic calibration of advanced soil models for cyclic loading. The experimental investigation comprised oedometer tests with repeated loading and unloading cycles, along with monotonic and cyclic triaxial tests conducted under both drained and undrained conditions. Furthermore, cyclic triaxial tests incorporating bender elements and local strain measurements were performed for small strain measurements. All test series were performed on highly compacted specimens, matching the modified Proctor density, in order to reproduce in situ conditions. Moreover, the stress and loading conditions applied in the tests represent those encountered in backfills of integral bridges, ensuring realistic simulation of field conditions. Further details on the tested material, the experimental program and its test conditions are available in Stastny et al. (2024b).

Figure 2

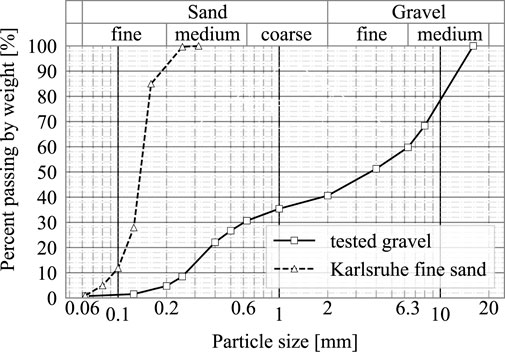
Figure 2. Grain size distribution of the tested well-graded gravel (Stastny et al., 2024a) and of Karlsruhe fine sand (Wichtmann and Triantafyllidis, 2016).

In addition to gravel, the well-known Karlsruhe fine sand (Wichtmann and Triantafyllidis, 2016) is considered in this investigation for comparison reasons. Due to its poor grading, this sand is typically not applicable for backfills of bridges, see Stastny et al. (2024a). However, many experimental as well as numerical studies on cyclic SSI behavior of integral bridges have been focused on poorly-graded (fine) sand, see Section 2. The Karlsruhe fine sand in Wichtmann and Triantafyllidis (2016) has a subangular shape with a mean grain size $d_{50}=$0.14 mm and a uniformity coefficient $C_u=$1.5. Its grain size distribution curve is also shown in Figure 2. Calibrated parameter sets of several material models exist for this sand, including the soil model DeltaSand (Galavi, 2021), which will be incorporated in this investigation.

4 Analytical methods for the mobilized earth pressure

In this contribution, analytical design approaches from Germany, Austria and Great Britain (Vogt, 1984; RVS 15.02.12, 2019; PD6694-1, 2020) are compared against the numerical simulations. In the following, the different approaches will be briefly summarized:

In Germany, for both integral road (RE-ING, 2023) and railway (Ril 804.4501, 2021) bridges the mobilization of passive earth pressure on the abutment (in its summer position) is determined according to Vogt (1984). Based on large-scale 1$g$ tests on uniformly-graded sand, Vogt proposed Equation 1 which describes a parabolic earth pressure profile (see Figure 1B) as a function of the abutment wall displacement $u_x(z)$ and the corresponding depth coordinate $z$:

$K_{\text{px,mob}}\left(z\right)=K_0+\left(K_p-K_0\right)\cdot \frac{\frac{u_x\left(z\right)}{z}}{a+\frac{u_x\left(z\right)}{z}}(1)$

For the discussed studies, the passive earth pressure coefficient $K_p=11.8$ is determined according to DIN 4085 (2018) with a drained soil weight $\gamma =$19 kN/m³, a wall friction of $2/3\phi$ and the mean peak friction angle $\phi =$45.4° obtained from drained triaxial tests on the gravel specimens discussed in Section 3.2. The earth pressure coefficient at rest $K_0=$0.5 was chosen in accordance with the numerical results for the initial “backfilling” phase to allow a fair comparison. In this context, it has to be noted that due to the simulated construction process, $K_0$ does not equal the at-rest earth pressure coefficient for normally consolidated soil $K_0^{\text{NC}}$. The backfill’s relative density can be considered with the factor $a=$0.01–0.1. For (very) dense backfill materials RE-ING (2023) recommends selecting $a=$0.02. The free temperature deformation of the deck is calculated based on DIN EN 1991-1-5/NA (2010) for a constant temperature change with a return period of 50 years, as explained in Section 5.3. RE-ING specifies to apply only the lateral deformation $u_{\text{x,S}}$ (see Figure 1B) of the abutment from its neutral rest position (0) to the summer position (S). However, some researchers, e.g., Szczyrba (2013) and Tue et al. (2021), lately have suggested to apply the full moving range of the abutment $u_{\text{x,total}}=u_{\text{x,W}}+u_{\text{x,S}}$ from winter (W) to summer (S) to allow a more conservative design and also cover potential rearrangements and densification effects of the soil in the winter positions. This proposal will be later examined in Section 6 drawing on the findings from the presented numerical investigations.

In Austria, the guideline for the design of integral bridges RVS 15.02.12 (2019) provides a deformation-dependent earth pressure approach based on ÖNorm B 4434 (1993) and Franke (1989). Here, the earth pressure resultant $E_{\text{mob}}$ is calculated using Equation 2. The equation considers both rotational and translational movement. For simplicity, RVS 15.02.12 suggests applying the resulting earth pressure in a rectangular distribution on the abutment, compare Figure 1B:

$\begin{array}{ll}\hfill E_{\text{x,mob}}& =E_0+\left(E_p-E_0\right)\cdot \hfill \\ \hfill & {\left[1-{\left(1-\frac{u_{\text{x,total}}}{\frac{u_{\text{x,trans}}}{u_{\text{x,total}}}\cdot u_{\text{b,trans}}+\left(1-\frac{u_{\text{x,trans}}}{u_{\text{x,total}}}\cdot u_{\text{b,rot}}\right)}\right)}^2\right]}^{0.7}\le E_p\hfill \end{array}(2)$

Equation 2 contains the soil stress resultants $E_0$ and $E_p$, calculated from $K_0=$0.5 and $K_p=$11.8, as explained above. RVS.15.02.12 suggests taking into account the full moving range of the abutment $u_{\text{x,total}}(z)$ from winter (W) to summer (S) as well as the translational movement of the abutment $u_{\text{x,trans}}$, see Figure 1B. The factors $u_{\text{b,trans}}$ and $u_{\text{b,rot}}$ control the displacements to reach $E_p$ depending on the relative density and type of movement. For dense materials, it is recommended to use $u_{\text{b,trans}}=0.05H$ and $u_{\text{b,rot}}=0.1H$ (RVS 15.02.12, 2019). Recent research by Della Pietra et al. (2019), based on a structural bridge model with springs to represent the soil, concluded that this simplified rectangular earth pressure profile specified in RVS 15.02.12 (2019), leads to similar stresses and bending moments at the frame corner as the approach by Vogt (1984). Therefore, they advise practical engineers to apply the simplification for design purposes.

In the United Kingdom, PD6694-1 (2020) regulates the design of integral bridges. A summary on the development of PD 6694–1 and its previous versions can be found, e.g., in Morley et al. (2024). The United Kingdom approach (Equation 3) is also used in a similar manner by other countries, such as Switzerland (ASTRA 12004, 2011) and Ireland (Place et al., 2006). Up to a maximum thermal deformation criteria of 40 mm, the earth pressure on integral abutments is mainly assessed using the limit equilibrium method. Based on this, for full height frame abutments on spread footings, PD 6694–1 proposes a bilinear profile for the cyclic lateral earth pressure that develops during the design life. It is defined by a peak value of ${\sigma }_{\text{x,mob}}=\gamma K*H/2$ in the middle and ${\sigma }_0$ at the foot of the abutment, see Figure 1B. The coefficient $K*$ can be calculated with Equation 3:

$K^{*}=K_0+{\left(\frac{C{d}_k^{\prime }}{H}\right)}^{0.6}\cdot K_{\text{p;t}}(3)$

Here again $K_0=$0.5 was assumed and the horizontal passive pressure coefficient $K_{\text{p;t}}=$12.57 from PD6694-1 (Table 7). The factor $C$ regulates the soil stiffness below the foundation level. It was determined as $C=$30 based on triaxial test results, as explained in PD 6694–1. Similar to RVS 15.02.12 (2019), PD 6694–1 considers the full movement range of the bridge deck from maximum contraction to maximum expansion. The characteristic value of the horizontal total deck movement $d_k$ is equal to $u_{\text{x,total}}$. The wall deflection in the middle of the abutment $d_k^{\prime }$ at $H/2$ can be determined from a (structural) model or conservatively estimated as $d_k^{\prime }=0.5d_k$. In the present study $d_k^{\prime }$ was taken from the numerical calculations summarized in Section 5. For comparison purposes, the partial factor for thermal effects was not applied to $d_k$ and the partial factor for soil weight was not considered for $K*$. It’s worth noting that this approach does only focus on a thermal movement of the abutment by rotation and/or bending, and does not take additional translation into account. For integral bridges with significant translation shares, i.e., frame abutments on a single row of piles or embedded wall abutments, PD 6694–1 clause 9.4.5 (incl. Annex A) requires soil–structure interaction analysis. Examples can be found, e.g., in Banks and Bloodworth (2018) and Sandberg et al. (2020). The present numerical investigation can also be regarded as such an SSI analysis.

5 2D and 3D finite element analyses

5.1 Constitutive model for cyclic loading

In this investigation, an elastoplastic, state-dependent material model for sand called DeltaSand is employed to simulate the cyclic loading behavior. It was developed by Galavi (2021) and has demonstrated to capture the essential characteristics of small strain and cyclic loading behavior both on element test level and in boundary value problems (Fetrati et al., 2024; Galavi and Martinelli, 2024; Stastny et al., 2024b). The model defines the behavior of sand using a single set of 16 parameters that represent the soil’s intrinsic properties. The current void ratio (i.e., the relative density) and effective stress serve as the primary state variables, influencing key soil characteristics such as stiffness, strength, dilation, and compressibility. The model incorporates distinct yield surfaces for deviatoric, volumetric, and tensile stresses within the effective principal stress space. The deviatoric yield surface, shaped like a cone, includes one isotropic and two kinematic hardening surfaces. The isotropic surface governs monotonic loading, while the kinematic surfaces handle cyclic shear behavior. Elastic behavior is modeled within the kinematic surfaces, taking into account small strain stiffness. To accurately represent soil stiffness during cyclic loading, the extended Masing rule (Vucetic, 1990) is applied. The volumetric yield surface, or “cap,” expands isotropically but does not account for cyclic behavior during volumetric compression. Depending on the stress state, the model activates one of these surfaces, allowing it to predict soil response under different loading conditions. In this study, the Mohr-Coulomb yield surface was selected to define the cone-shaped failure criteria.

The material model has been thoroughly calibrated for the tested gravel material (see Section 3.2) in Stastny et al. (2024a). In Stastny et al. (2024b), DeltaSand has also been compared to other advanced soil models, both on element test level and in a 2D FE design case study of an integral bridge. DeltaSand successfully captured the key mechanisms of cyclic soil-structure interaction, including the cyclic increase of earth pressure on the abutment during summer and the progressive accumulation of settlements in the backfill, particularly over the first 10 seasonal cycles. Additionally, DeltaSand predicted the highest earth pressures, thus making it the most conservative material model choice for the parametric study in the present investigation. Further details on the soil model and its calibration for Karlsruhe fine sand and the tested gravel material can be found in Galavi (2021) and Stastny et al. (2024a).

5.2 Numerical model description

In the following, the 2D and 3D FE models for the cyclic soil-structure interaction analysis of integral railway bridges are described. They represent the bridge geometries and the variations of the abutment, backfill and foundation stiffnesses summarized in Section 3. The aim is to quantify the various influences on the cyclic SSI behavior of typical integral bridges and compare the results to different analytical design approaches for the passive lateral stress mobilization. The FE modelling approach (in combination with the DeltaSand material set) was validated based on extensive preliminary studies including mesh sensitivity and boundary studies, interface examinations [e.g., in Stastny and Tschuchnigg (2023)], back analysis of 1$g$ tests [e.g., in Stastny and Tschuchnigg (2022)] and of long-term monitoring results from a 50 m long integral bridge [e.g., in Stastny et al. (2022)].

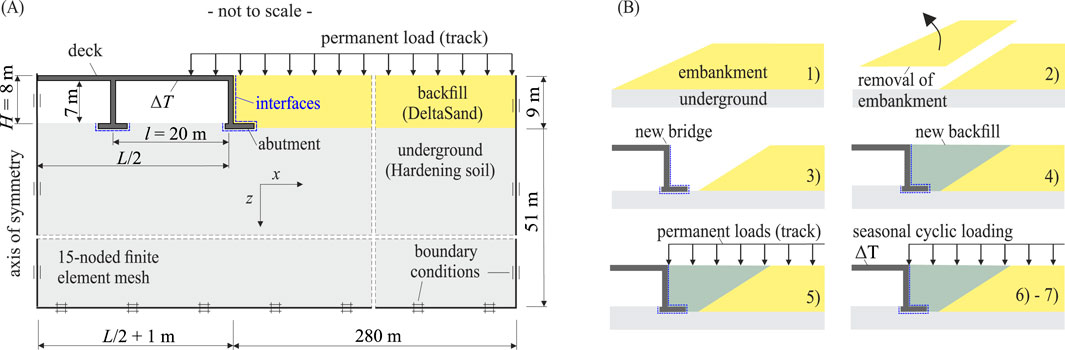
Bridges on spread footing were simulated by means of plane strain FE models in Plaxis 2D version V23.2 (Bentley Systems, 2023) with total dimensions of at least 300 m (length) and 60 m (height) to minimize the effects of boundary conditions. Due to the symmetrical built of the reference bridges, only half of the bridge and its surrounding soil had to be computed, see Figure 3A. The FE mesh was discretized using 15-noded elements ($4^{th}$ order shape function), and the mesh density was gradually refined as it approached the abutment. Drained conditions were assumed. The concrete superstructure and the abutment, both 1 m thick, were simulated using linear elastic continuum elements ($E=$30.5 GPa, $\nu =$0.2). Zero-thickness interface elements were introduced around the abutment contact zones to account for the reduced strength in this region and to allow relative movement between the abutment and the surrounding soil. An interface strength reduction factor of $R_{\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r},\phi }=\tan ({\phi }_{\text{inter}})/\tan ({\phi }_{\text{soil}})=$0.7–0.9 was chosen. Following the recommendations in Stastny and Tschuchnigg (2023), the normal stiffness of the interfaces was set significantly higher than standard settings to prevent interpenetration effects. The backfill behavior was simulated with the material model DeltaSand employing the calibrated parameter sets for the tested gravel material as well as Karlsruhe fine sand as explained in Section 3.2 and 5.1. The initial relative density was set at $D_{\text{r0}}=$80% to reflect the high in situ compaction, comparable to 100% Proctor density. To investigate the effect of relative density, additional analyses were carried out with a lower value of $D_{\text{r0}}=$50%. The underground soil layer was modeled with the elastoplastic Hardening Soil model (Schanz et al., 1999), with stiffness parameters of $E_{50}^{\text{ref}}=E_{\text{oed}}^{\text{ref}}=1/3E_{\text{ur}}^{\text{ref}}=$45 MPa, $p_{\text{ref}}=$100 kPa and the power exponent $m=$0.55 as well as strength constants of $\phi =$40° and $c=$0 kPa. This parameter set represents a subsoil with good bearing capacity suitable for a spread foundation:

Figure 3

Figure 3. (A) 2D FE model with focus on the SSI of an integral bridge, (B) Calculation phases.

Figure 3B illustrates the progression of the simulation phases. In the initial stage, an existing embankment was considered. The initial stress state was established through a gravity loading procedure, which calculates vertical stresses by applying gravitational loads $({\sigma }_y=\gamma \cdot z)$ and allowing the soil to reach equilibrium. Horizontal stresses $({\sigma }_x)$ are not predefined using an earth pressure coefficient $(K_0)$, but determined iteratively by ensuring equilibrium under gravitational body forces and the given boundary conditions. Subsequent phases (2–5) simulated the removal of the embankment and the incremental construction of the new bridge along with backfill, progressively creating a realistic stress state in preparation for cyclic loading. In phase 5, vertical line loads were placed on top of the superstructure and backfill surface to account for the permanent loads of the railway track. Starting from phase 6 the seasonal deformations of the superstructure were simulated by means of direct temperature loads for both summer and winter conditions. In alternating winter and summer phases, constant temperature changes of $\mathrm{\Delta }T=(-)$55 K were applied to the bridge deck. More details on the temperature loading are given in Section 5.3. The direct application of temperature allows to investigate the influence of backfill restraint on the free expansion of the deck. In total, the first and most critical 10 seasonal cycles were simulated with consecutive summer and winter phases. This number of cycles already allows a robust qualitative and quantitative comparison of the main influences on the cyclic SSI behavior, especially since a temperature profile with 50 years return period is considered, see Section 5.3. A similar approach was chosen, e.g., by Abdel-Fattah et al. (2018). Additionally, maintenance cycles on ballasted tracks are shorter, typically in the range of 4 to 5 years, depending on the track velocity and yearly traffic loads. After the tamping process, the influences of backfill settlements on the track alignment is corrected to a certain extent.

The SSI calculations of integral bridges with deep foundation were conducted in Plaxis 3D (version V23.2). To take advantage of the bridge’s symmetry, only half of the structure and the adjacent soil were modeled, see Figure 4. The mesh was generated using quadratic tetrahedral elements (shape function of $2^{nd}$ order), with a refinement level comparable to the 2D simulations. The model properties were chosen according to the 2D FE studies. As shown in Figure 4B the box abutment was modeled with full sized wings oriented parallel to the track direction. It has a clear width of 10 m between the wings, which is typical for a double-track railway. To study the influence of the foundation on the SSI behavior, calculations with varying foundations and varying underground stiffnesses were performed. Thus, a spread footing with underground stiffnesses of $E_{50}^{\text{ref}}=$20 and 45 MPa was simulated. Additionally, foundations with one, respectively, two rows of 6, respectively 5 concrete bored piles (Figure 4) were created assuming an underground stiffness of $E_{50}^{\text{ref}}=$8 MPa. The piles measure 20 m in length at a diameter of 1 m. They were modeled as volume piles with linear elastic continuum elements ($E=$30.5 GPa, $\nu =$0.2) and zero-thickness interfaces. In the 3D FEA the seasonal temperature deformations of the superstructure were idealized by means of horizontal line prescribed displacements at the end of the model bridge deck (Figure 4A) using values from Table 1.

Figure 4

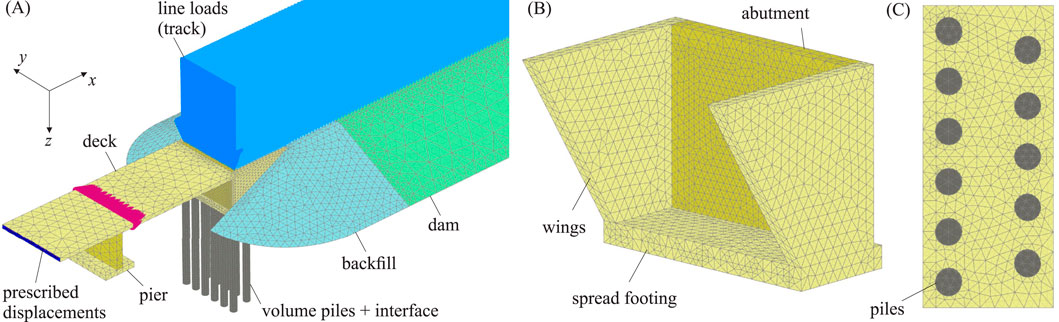
Figure 4. (A) 3D FE model, (B) View of box abutment on spread footing, (C) Top view of foundation with pile layout (two rows).

Table 1

Table 1. Free horizontal temperature deformation $u_{\text{x,free}}$ of a concrete bridge deck calculated based on DIN EN 1991-1-5/NA (2010).

5.3 Temperature loading

As explained in Section 2 the main driver of the cyclic SSI is the seasonal temperature deformation of the integral bridge deck. The corresponding temperature profile was taken from DIN EN 1991-1-5/NA (2010) for concrete bridges. Therefore, a characteristic constant temperature change with a return period of 50 years with $\mathrm{\Delta }{T}_{\text{N,exp}}=$29 K and $\mathrm{\Delta }{T}_{\text{N,con}}=-$ 26 K was considered. Note that also PD6694-1 (2020) requires a 50-year return period for the determination of the thermal deck movement in Equation 3. Consequently, many SSI studies, e.g., Abdel-Fattah et al. (2018), Banks and Bloodworth (2018) and Sandberg et al. (2020), use such long return periods. For simplicity, the total temperature magnitude $\mathrm{\Delta }T=$55 K was divided by two to allow the simulation of equal deformation of $\mathrm{\Delta }T=\pm$27.5 K for summer and winter phases. Based on this, the free seasonal temperature deformation $u_{\text{x,free}}$ of a symmetrical integral bridge can be calculated from $u_{\text{x,free}}=L/2\cdot \mathrm{\Delta }T\cdot {\alpha }_T$ with a thermal expansion coefficient ${\alpha }_T=1\cdot 10^{-5}$ 1/K for concrete. Table 1 summarizes the resulting free deformation $u_{\text{x,free}}$ of the deck for the various total bridge lengths $L$. It must be emphasized that the considered thermal loading exceeds average yearly temperature ranges and thus overestimates most real seasonal deformations. This can be seen, e.g., based on the significantly smaller free deformation for a return period of 2 years with $\mathrm{\Delta }T=$35 K, see Table 1. However, the simplified temperature profile does not account for superimposed daily temperature cycles or creep and shrinkage deformation of the superstructure, which would affect the cyclic thermal loading. For example, numerical investigations by Banks and Bloodworth (2018) demonstrated that incorporating daily cycles superimposed on seasonal behavior can increase stress levels by approximately 10%. In the end, the proposed temperature profile was chosen to allow a conservative estimation of the passive earth pressure mobilization, especially since the present study focuses mainly on the first 10 seasonal cycles of a bridge’s lifetime.

5.4 Numerical model with analytical loading

The differences of the analytical approaches from Section 4 will be compared to the SSI results not only in terms of lateral stresses but also with regard to the abutment’s bending moments. The FE models from Section 5.2 were further used for this purpose. The calculation phases 1 to 5 were computed as described before. In phase 6, the summer temperature change of the bridge deck was simulated also specified above. However, the backfill was deactivated from the top edge of the spread footing up to the ground surface and replaced by a similar vertical line load on the remaining backfill and footing. The line load was calculated by $p=\gamma \cdot H$. Additionally, the analytical loads from Section 4 were applied to the abutment by means of horizontal line loads. The vertical static load of the track was taken into account for both line loads. The bending moments of the abutment (as a consequence of the analytical loading) were evaluated by integrating the results at stress points throughout the area perpendicular to the cross-section line Bentley Systems (2023).

6 Results and discussion

In this section, the results of the numerical SSI parameter studies are discussed and compared against the analytical design approaches from Section 4. The main focus will be on the following quantities:

• lateral stresses ${\sigma }_x$ in the interface behind the abutment

• bending moments $M$ of the abutment

• cyclic settlements $u_z$ of the backfill surface

• horizontal deformations $u_x$ of the abutment

6.1 Influence of bridge length and abutment height

Figure 5 presents the lateral stress distributions in phase summer S2 and S10 of bridges with length $L=$20 m (left column), 80 m (middle column) and 140 m (right column) for heights $H=$8 m (top row), 5 m (middle row) and 3 m (bottom row). Additionally, the stress profiles for the analytical design approaches of RVS 15.02.12 (2019), Vogt (1984) - with temperature deformation from rest to summer (0–S) and winter to summer (W–S) position - and PD6694-1 (2020) are printed. Note that for visual appearance, the stress profiles have been moderately smoothened using an exponentially weighted moving average (EWMA) with a window size of 3, which has no influence on the general trends. As expected, the stresses increase with growing bridge lengths, i.e., growing thermal deformation of the deck. For the first 2 summer cycles (S1 and S2), the stress profile shows a peak approximately in the middle of the abutment. In phase summer 10 (S10) a strong stress increase can be observed for $L=$80 and 140 m which predominantly occurs in the upper part/half of the abutment. The stress profiles from all analytical approaches fail to match the numerical stress distribution. This is particularly relevant for abutments with lower heights. The approaches of Vogt and PD6694-1 show the maximum stresses approximately in the middle of the abutment for $H=$8 m, while Vogt predicts the maximum stress for low abutment heights $H=$3 m to be at the abutment bottom. PD6694-1 is used for comparison only in calculations with $H=$8 m, as its inherent assumption of pure rotation around the base can only be justified for tall abutments (see discussion later). The high stress concentrations of the SSI calculations in the upper part of the abutment can be explained by the additional track surface load and the high stiffness of the tested gravel backfill material. This will be demonstrated when comparing the results to the much softer behavior of Karlsruhe fine sand in Section 6.2, which shows stress peaks roughly at mid-height of the abutment. In centrifuge tests, Morley et al. (2024) also observed that for stiff abutments, the peak lateral stresses occurred in the upper half of the abutment rather than in the middle. Therefore, the high stiffness of the abutment on the spread footing used in the present study might also contribute to the numerical stress profile.

Figure 5

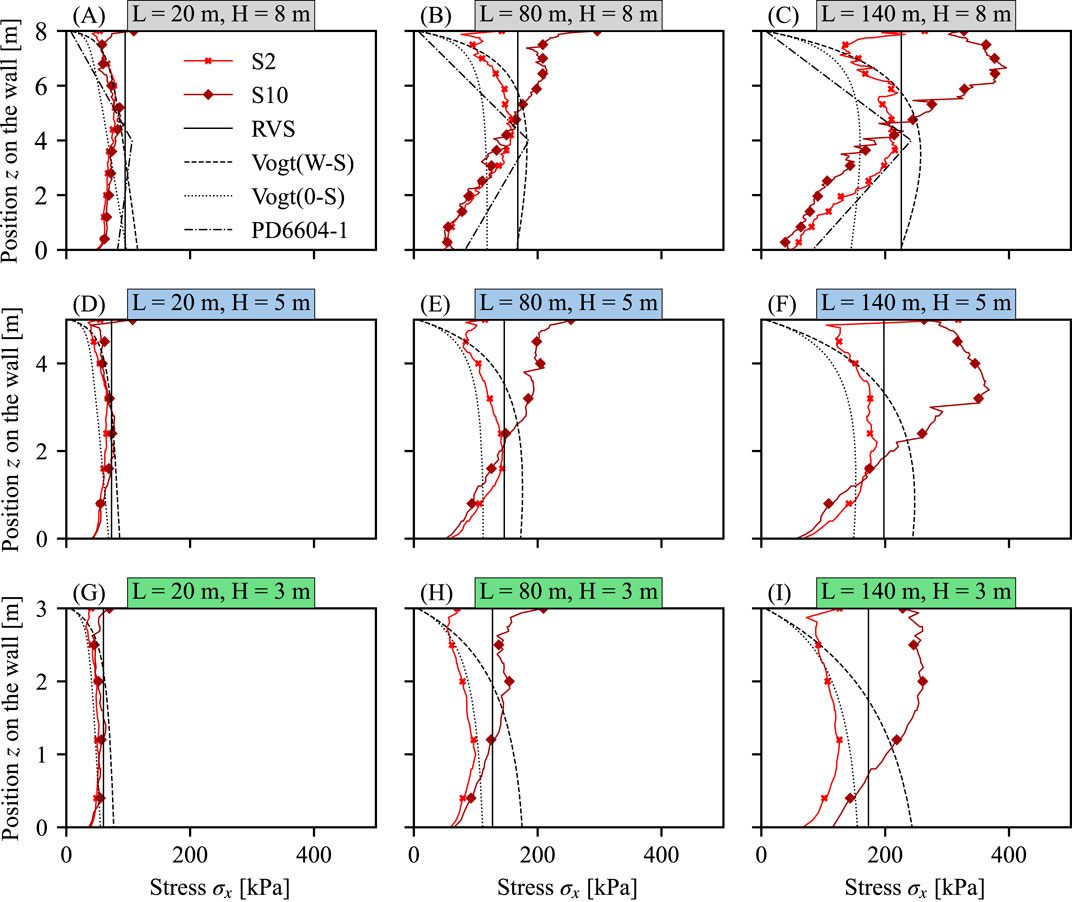
Figure 5. Lateral stress distribution ${\sigma }_x$ over the abutment wall (position $z=$ 0 is located at the abutment foot) in calculation phases summer S2 and S10 compared against the stress distribution from the analytical methods: (A–C) Height $H=$ 8 m, (D–F) $H=$ 5 m, (G–I) $H=$ 3 m.

Figures 6A–C illustrates the development of the total lateral earth pressure forces $F_x$ on the abutments with $H=$3 – 5 – 8 m as the number of cycles $N$ increases (evaluated in summer S1, 2, 5 and 10). The forces are represented by the normalized lateral force $K_{\text{mob}}=2F_x/(\gamma \cdot H^2)$. A nearly linear increase of $K_{\text{mob}}$ with bridge length $L$ can be observed for all abutment heights $H$. While almost no cyclic increase of $K_{\text{mob}}$ appears for short bridges ($L=$20 m), a clear cyclic growth is visible for longer bridge decks. The most pronounced increases occur during the first 5 cycles, but smaller advances are also visible from cycle 5 to 10. This is consistent with experimental data on sand, see, e.g., (England et al., 2000; Lehane, 2011; Havinga et al., 2017). The comparison to the analytical curves highlights that the design approaches may not provide conservative estimations of the passive stress mobilization for all cases. This is particularly true, as the numerical calculations in this study focus solely on the first (most influential) 10 seasonal cycles of a bridge’s lifespan. The approach by Vogt (0–S) significantly underestimates the earth pressures for all investigated bridge geometries. Its adjustment Vogt (W–S) performs much better and can predict slightly higher lateral forces compared to the numerical SSI calculations for most of the considered bridge geometries. The same can be said for the RVS solution, which matches Vogt (W–S)’s trends well and produces only slightly higher $K_{\text{mob}}$ values. However, for longer integral bridges with short(er) abutments of $H=$3 or 5 m both methods underestimate the numerical earth pressure. PD6694-1 can only cover the earth pressure mobilization for small bridges with $L\le$ 40 m in Figure 6A. This corresponds to findings by Banks and Bloodworth (2018), who state that a length limit of 60 m seems appropriate for Equation 3. In PD6694-1 soil-structure interaction analysis is required for (longer) integral bridges with significant translation movement of the abutment. Based on the findings of this study, this should also be considered (in Germany and Austria) for long integral bridges with short abutment heights to secure a safe (and economical) lateral stress profile for the structural bridge design. Alternatively, an increase of the analytical results by a factor $>$ 1 should be considered. The positions $z/H_{\text{abut}}$ of the earth pressure resultant are depicted for both SSI and analytical calculations in Figures 6D–F. $H_{\text{abut}}=H-1$ m refers to the clear abutment height underneath the superstructure. The comparison validates the qualitative observation made in Figure 5: The numerical earth pressure resultant lies in the upper part of the abutment and moves further upwards with both increasing deck length $L$ and increasing (summer) cycles. It is positioned considerably higher compared to the analytical approaches, which all locate the lateral resultant in the middle of the abutment or slightly below.

Figure 6

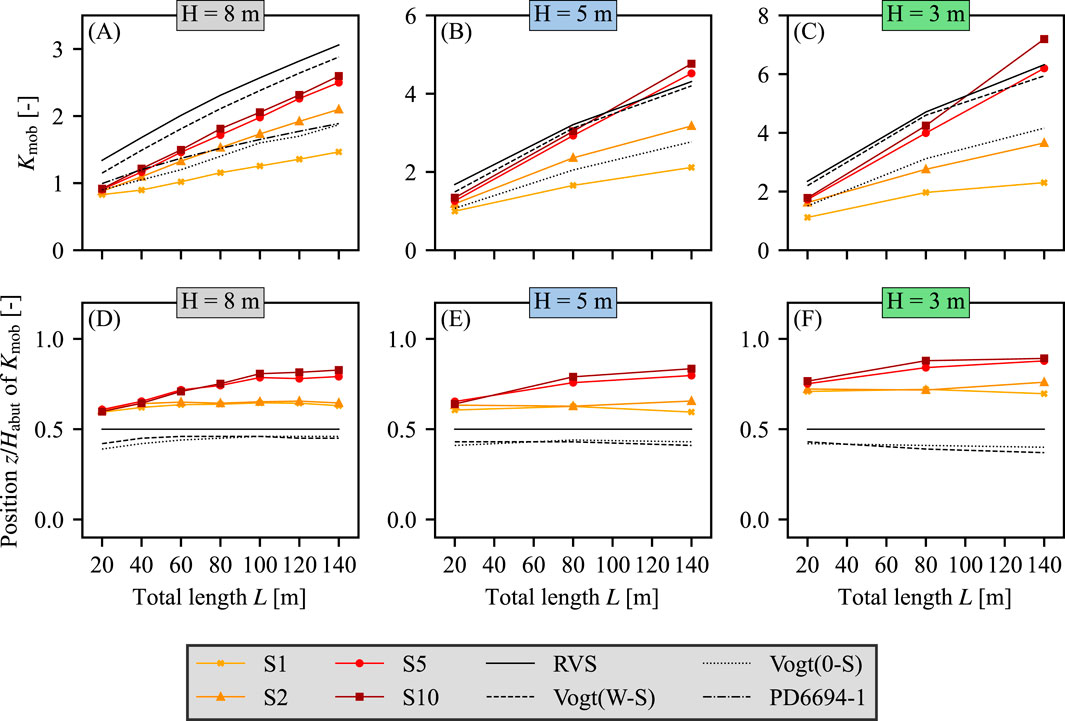
Figure 6. (A–C) Normalized lateral forces $K_{\text{mob}}=2F_x/(\gamma \cdot H^2)$ in the abutment’s summer positions S1, S2, S5 and S10 compared against results from the analytical methods, (D–F) Position $z/H_{\text{abut}}$ of $K_{\text{mob}}$

In Figure 7 the abutment’s bending moments from cyclic loading (i.e., without bending moments from the initial phases) in summer 2 are displayed for $H=$8 m and $L=$20 – 80 – 140 m. In contrast to the comparison of $K_{\text{mob}}$ results, the analytical approaches yield significantly larger bending moments compared to the numerical solutions. The main reason for that is the different position of the earth pressure resultant, as shown in Figures 6D–F. The more central position of the resultants in case of the analytical approaches causes higher internal forces. This observation is further confirmed by the results in Figure 8A. It shows the maximum and minimum bending moments $M_{\text{min}}$ and $M_{\text{max}}$ of the SSI calculations for all examined bridge lengths and summer cycles (from cyclic loading, i.e., without the influences of the initial phases). An almost linear increase of $M_{\text{min}}$ and $M_{\text{max}}$ can be observed with deck length $L$ in both, the SSI calculation and the calculation with analytical loading. With few exceptions for Vogt, the SSI bending moments are smaller than the results with analytical loading, especially for longer integral bridges. Based on that, it can be said that the majority of the analytical approaches allow a safe design of the abutment, at least with respect to bending moments at $H=$8 m. Note that the simplified RVS approach as well as the approach by Vogt (W–S) lead to very similar $M_{\text{min}}$ and $M_{\text{max}}$ for all considered bridge lengths, which further solidifies their compatibility. The minimum bending moments $M_{\text{min}}$ appear in the frame corner and the maximum bending moments $M_{\text{max}}$ roughly in the middle of the abutment, see also Figure 7. This is the case for both, SSI calculations and calculations with analytical loading. As depicted in Figure 8B these positions $z/H_{\text{abut}}$ of $M_{\text{min}}$ and $M_{\text{max}}$ do not vary substantially with bridge lengths.

Figure 7

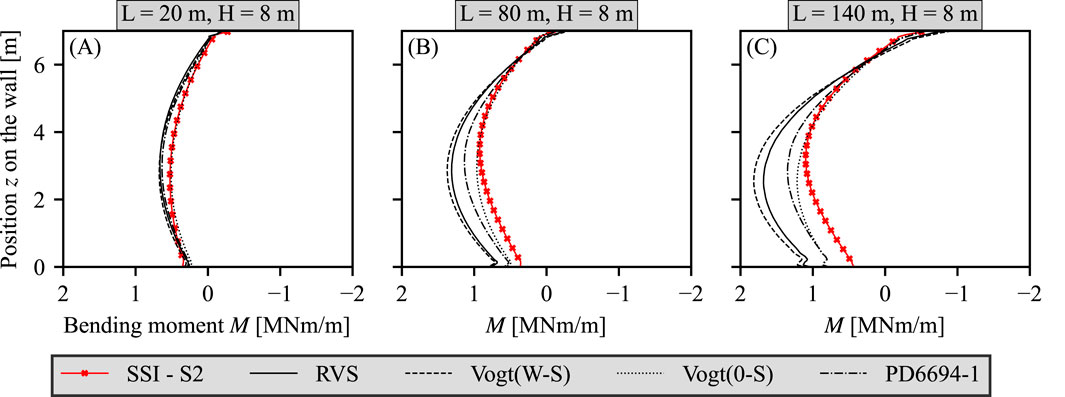
Figure 7. Bending moments of the abutment from cyclic loading in calculation phases summer S2 and winter W2 compared against the results from the analytical methods: (A) Height $H=$ 8 m and total lengths $L=$ 20 m, (B) $L=$ 80 m, (C) $L=$ 140 m.

Figure 8

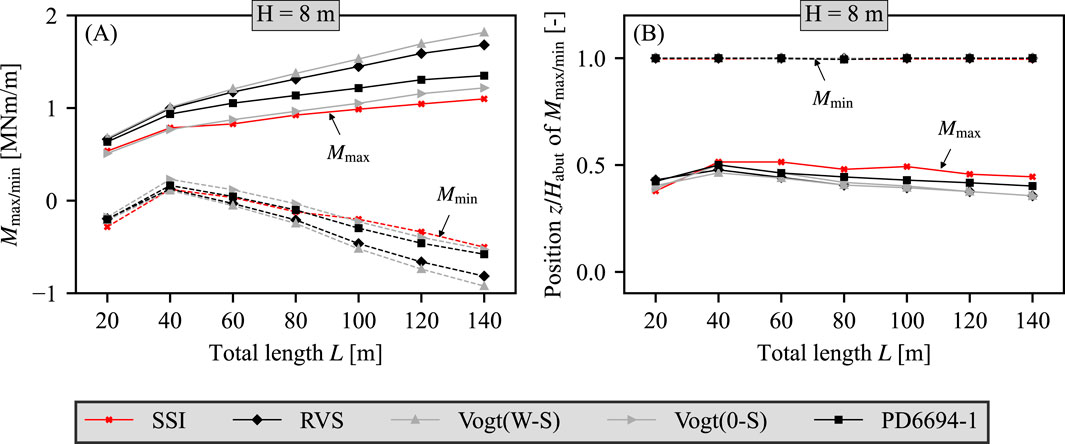
Figure 8. (A) Minimum and maximum bending moment $M_{\text{min}}$ and $M_{\text{max}}$ of the abutment compared against results from the analytical methods, (B) Corresponding position $z/H_{\text{abut}}$ of $M_{\text{min}}$ and $M_{\text{max}}$.

One big advantage of the 2D FE model with direct temperature loading on the bridge deck is its ability to simulate the reaction of both structure and soil during the successive thermal loading steps in each calculation phase. This allows to determine how strongly the abutment’s temperature deformation is restricted by the backfill. For this reason, the ratio of the horizontal top deformation $u_{\text{x,top}}$ and the theoretical free thermal expansion $u_{\text{x,free}}$ of the deck (see Section 5.3) is evaluated in Figure 9. For short bridges, a ratio of almost 1 is found, which means the deck can expand without relevant resistance. For longer bridges, the ratio reduces slightly, leading to a restricted movement of 10% to 12% at $L=$140 m for all heights $H$. Consequently, the simplified assumption of a free thermal expansion of the bridge deck in the structural design can be justified for most integral railway bridges (with comparable properties as in this study). Corresponding findings are reported, e.g., by Della Pietra et al. (2019). Also, a ratio of the horizontal deformation of the abutment foot $u_{\text{x,foot}}$ and the theoretical free thermal expansion $u_{\text{x,free}}$ of the deck can be derived. The dashed lines in Figure 9 display the ratio for the phases summer 2 and winter 2. Based on this, tall abutments with $H=$8 m experience relatively small foot point displacements of ca. 20% in summer, which could justify the common assumption of a foot point rotation for the abutment, e.g., in RE-ING (2023) and PD6694-1 (2020). However, this assumption should be employed with care: Numerical studies by Stastny et al. (2024b) highlight that the lateral earth pressure and its cyclic increase significantly depends on the abutment movement. The assumption of a point rotation might overestimate the passive earth pressure and its cyclic increase substantially. A realistic representation of the abutment deformation in structural design for the determination of the lateral stress mobilization is therefore crucial. This is especially relevant for shorter abutments of $H=$3 m, which almost show a full translation of the abutment in the present study, compare Figure 9C.

Figure 9

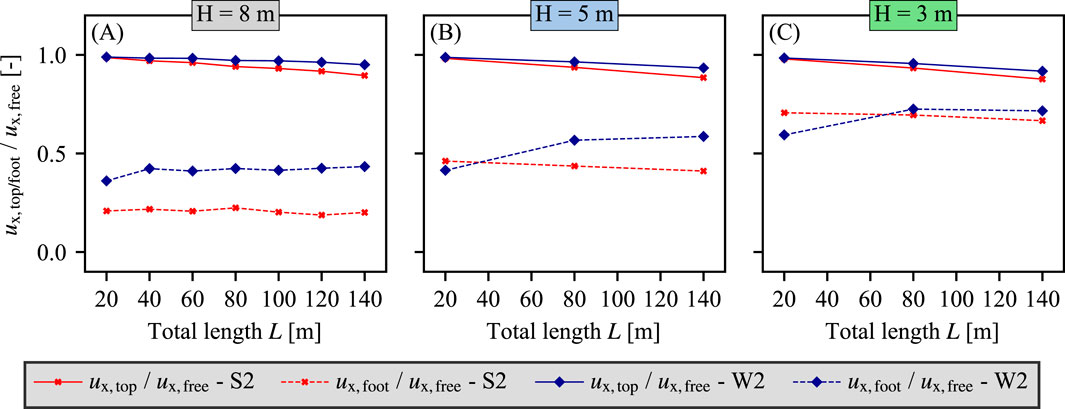
Figure 9. Normalized horizontal displacements of the abutment top $u_{\text{x,top}}/u_{\text{x,free}}$ and foot $u_{\text{x,foot}}/u_{\text{x,free}}$ in calculation phases summer S2 and winter W2. for abutment height (A) H = 8 m, (B) H = 5 m and (C) H = 3 m.

Finally, the development of settlements $u_z$ on the backfill surface is illustrated in Figure 10 for $H=$8 m. A clear growth of settlements with increasing bridge length $L$ can be observed. The maximum settlements appear directly behind the abutment. The settlement shape qualitatively corresponds to results from experimental research with fine sands, e.g., in England et al. (2000) and Morley et al. (2024). These 1$g$ and n$g$ tests on the SSI of integral bridges display a cyclic increase of settlements with a decreasing settlement rate. Also in the present study a moderate increase of settlements can be found from winter 2 to winter 10, which “deepens” the settlement trough in the first 2 m behind the abutment. For bridges with $L=$60 m, settlements of $u_{\text{z,max}}=$ 15 mm and 21 mm are observed in winters 2 and 10, respectively, while for $L=$140 m, settlements of $u_{\text{z,max}}=$37 mm and 46 mm are computed for the same periods. An assessment of the corresponding cyclic changes in void ratio reveals a slight densification of the backfill, especially for longer deck lengths. For shorter abutment heights, similar effects are detected but with (much) smaller absolute settlement values, see Figure 11. For a height of $H=$3 m, the settlement maxima cannot be found directly behind the abutment but at a distance of 2 to 5 m from it. This is related to the stronger translational movement of integral bridges with short abutments.

Figure 10

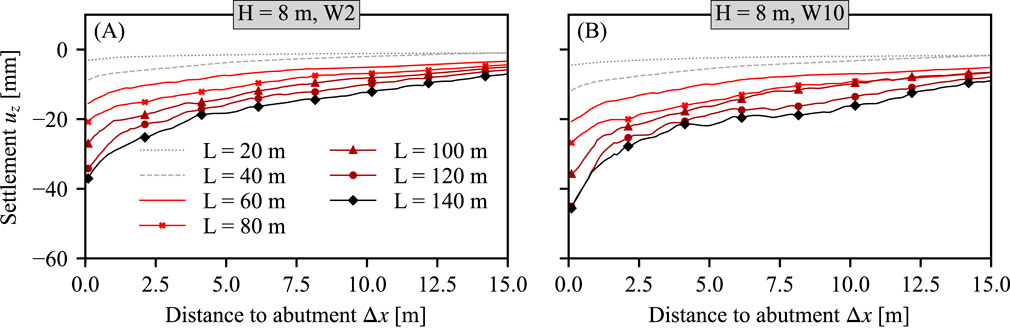
Figure 10. Settlement accumulation for abutment heights $H=$ 8 m in calculation phase (A) winter W2 and (B) winter W10.

Figure 11

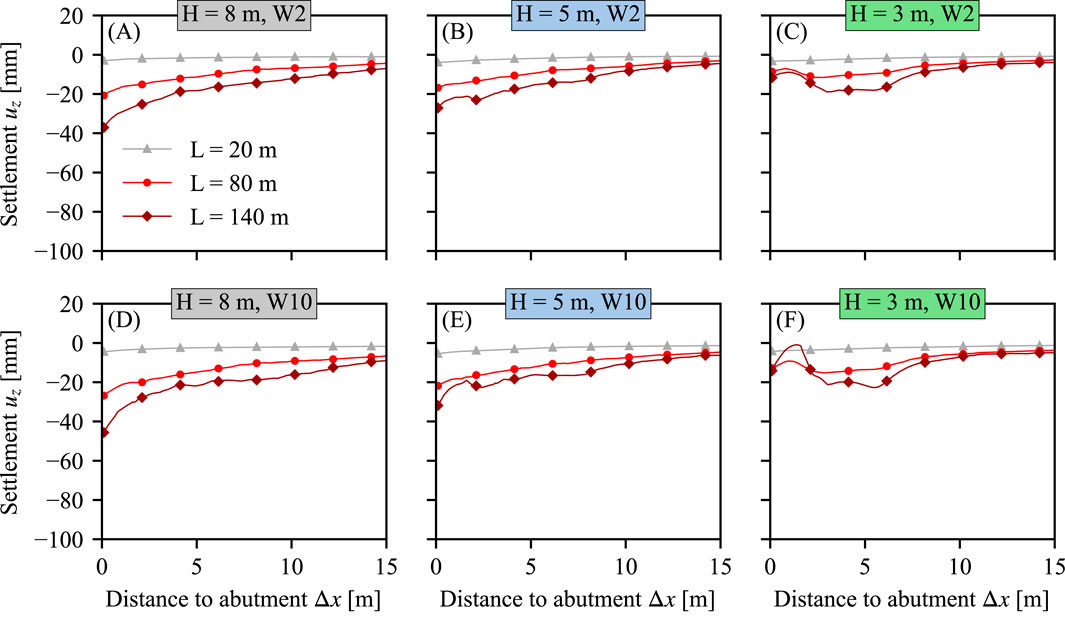
Figure 11. Settlement accumulation for abutment heights $H=$ 3 –5 – 8 m in calculation phase winter W2 (A–C) and winter W10 (D–F).

However, as summarized in Section 2.3, the acceptability of backfill settlements due to the horizontal cyclic SSI of integral bridges cannot be judged independently of the vertical dynamic train-track interaction. Research by Paixão et al. (2016) and Wang and Markine (2019) suggests that for such settlements profiles much higher dynamic vertical track loads and accelerations are likely to occur and will be accompanied by hanging sleepers, i.e., sleepers that lose the direct contact with the ballast in its unloaded position. These effects are clear indicators for a rapid deterioration of the ballast track condition in the transition zone, which leads to a bad track alignment and increased maintenance. Clearly, more research is needed on the combined effects of the horizontal cyclic and the vertical dynamic interaction in the transition zones of longer integral railway bridges. The results of the present study may be a good starting point, as they allow quantifying the isolated effect of the horizontal SSI on the settlement accumulation of integral bridges depending on their deck length. In the absence of further research, the authors recommend implementing specialized transition zone designs, i.e., approach slabs, for seasonal deck deformations beyond 20 mm based on the specifications in DB guideline Ril 804.4501 (2021), compare Section 2.3.

6.2 Influence of abutment and backfill stiffness

The influence of the abutment stiffness has been studied in additional calculations with a 2 m thick uncracked and a 1 m thick cracked abutment. To approximately account for the cracking, the abutment stiffness was reduced to 60% in accordance with DIN EN 1992-2 (2010). The $K_{\text{mob}}$ results for different deck lengths $L$ and abutment heights $H$ are summarized in Figure 12. Based on this comparison, the abutment stiffness has only a limited influence on the cyclic SSI. The stiffer, 2 m thick abutment leads to slightly higher earth pressures, especially for long bridges with short abutments.

Figure 12

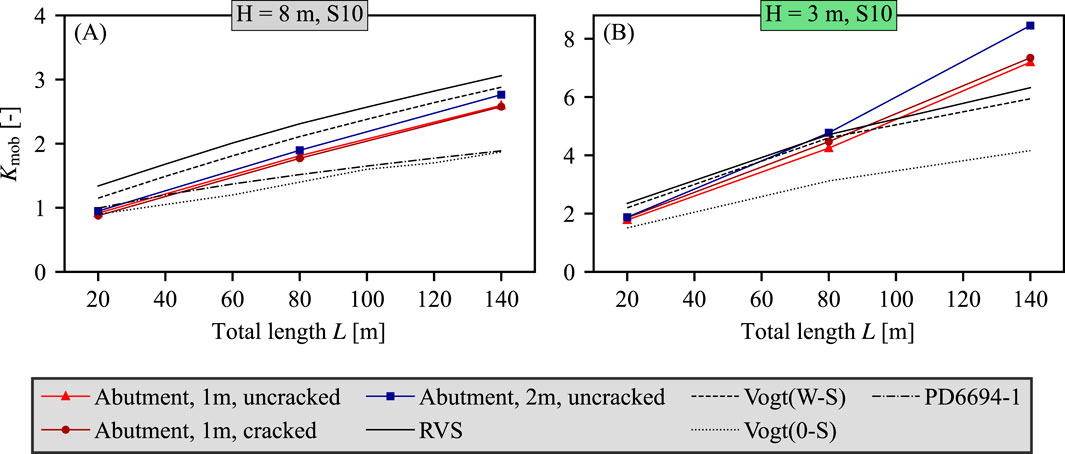
Figure 12. (A–B) Normalized lateral forces $K_{\text{mob}}$ in the abutment’s summer positions S10 for calculations with different abutment stiffnesses.

To evaluate the influence of backfill material on the cyclic SSI two different backfill materials, the well-graded gravel and the poorly-graded Karlsruhe fine sand from Section 3.2, are studied with varying initial relative densities $D_{\text{r0}}=$50% and 80%. It has to be pointed out that in situ relative densities $D_{\text{r0}}\ge$ 80% can be expected after the compaction to 100% Proctor density, while $D_{\text{r0}}$ = 50% is too low for practical purposes. In Figures 13A–D the lateral stress profiles of the different backfill soils are presented exemplarily for SSI calculations of an integral bridge with $L=$140 m and $H=$8 m. Results for both winter and summer positions with increasing cycles 1, 2, 5 and 10 are depicted. As expected, the earth pressure drops to the active limit in the winter positions in all calculations. In the summer positions, the fine sand mobilizes significantly lower lateral stresses compared to the gravel material. The sand shows peak stresses roughly at mid-height, whereas the gravel exhibits stress peaks in the upper part of the abutment. However, also for the fine sand the cyclic increase from cycle S2 to S10 exclusively manifests in the upper half. The stress profile of the fine sand corresponds well to experimental and numerical research from literature, e.g., (England et al., 2000; Lehane, 2011; Abdel-Fattah et al., 2018; Banks and Bloodworth, 2018). The sand stress profiles are also covered much better by the tested analytical approaches. In Figure 13E the associated development of the lateral force $K_{\text{mob}}$ with increasing number of summer cycles is displayed. A continuous cyclic increase of $K_{\text{mob}}$ can be observed for all backfill materials. It is strongest for the first 2 to 5 cycles, after which the growth rate gradually decreases. Based on this comparison, the gravel backfill mobilizes approximately 48% higher earth pressures compared to the fine sand after $N=$10 cycles. Similar findings are reported in Stastny et al. (2024a) based on numerical SSI calculations with several calibrated poorly-graded (fine) sands and well-graded gravel materials. They demonstrate that the differences can be traced back to the higher stiffness at small and large strains of the gravel materials. Also Abdel-Fattah et al. (2018) found significantly higher lateral stresses and an upward shift of the stress peak in FE calculations with increased backfill stiffnesses (and strengths). The comparison in Figure 13E further shows that with a lower relative density, lower $K_{\text{mob}}$ values develop, especially for the gravel material. Recent centrifuge tests by Morley et al. (2024) also confirm that dense sand shows significantly higher lateral stresses compared to loose sand.

Figure 13

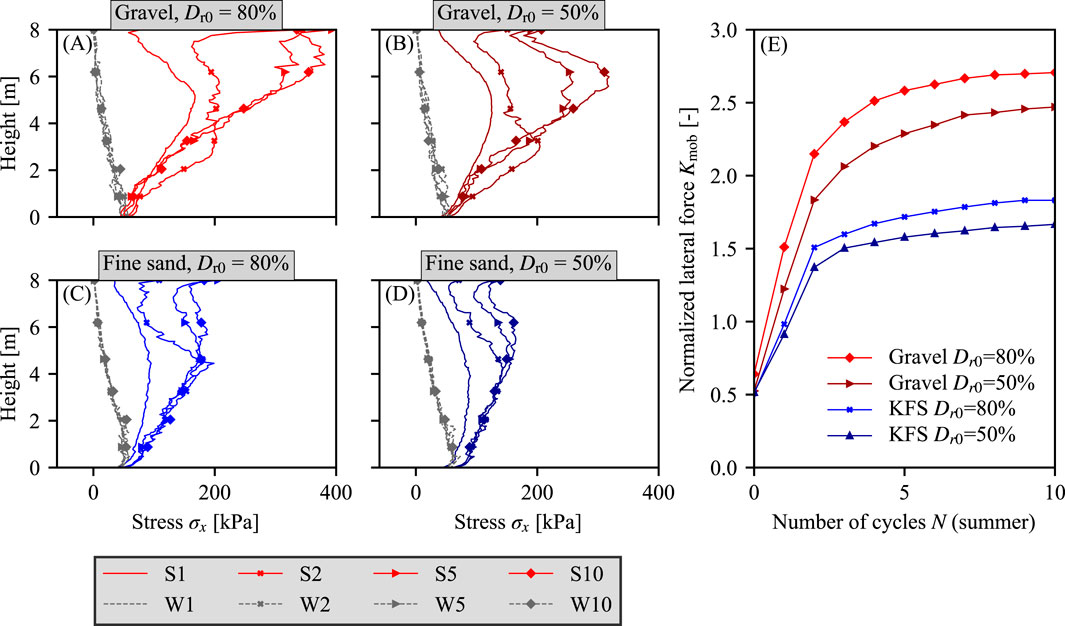
Figure 13. (A–D) Cyclic lateral stress distribution ${\sigma }_x$ over the abutment height $H$ in winter (W) and summer (S) positions for calculations ($L=$ 140 m, $H=$ 8 m) with different backfills - gravel and Karlsruhe fine sand at initial relative densities of $D_{\text{r0}}=$ 50% and 80%, (E) Corresponding cyclic development of normalized lateral forces $K_{\text{mob}}$ in the abutment’s summer positions.

The described trends also occur for different bridge lengths $L$ and abutment heights $H$, see Figure 14. In Figures 14A, B a linear increase of $K_{\text{mob}}$ is visible with increasing $L$ for all backfill materials and densities. The differences between sand and gravel are consistent for all considered bridge geometries, although the difference appears smaller for short bridges with $L=$20 m. All analytical earth pressure approaches, including Vogt (0–S), show higher $K_{\text{mob}}$ values compared to the sand material. This seems reasonable, as the approaches mostly have been derived from experiments on poorly-graded (fine) sands. Interestingly, all backfill materials cause very similar minimum and maximum bending moments in the abutment, see Figures 14C, D. Analogously to the discussion in Section 6.1, this can be explained by the different positions $z/H_{\text{abut}}$ of the earth pressure resultant for the sand and the gravel material. The more central position of the sand resultant causes higher internal forces, although it mobilizes lower earth pressures in total compared to the gravel material.

Figure 14

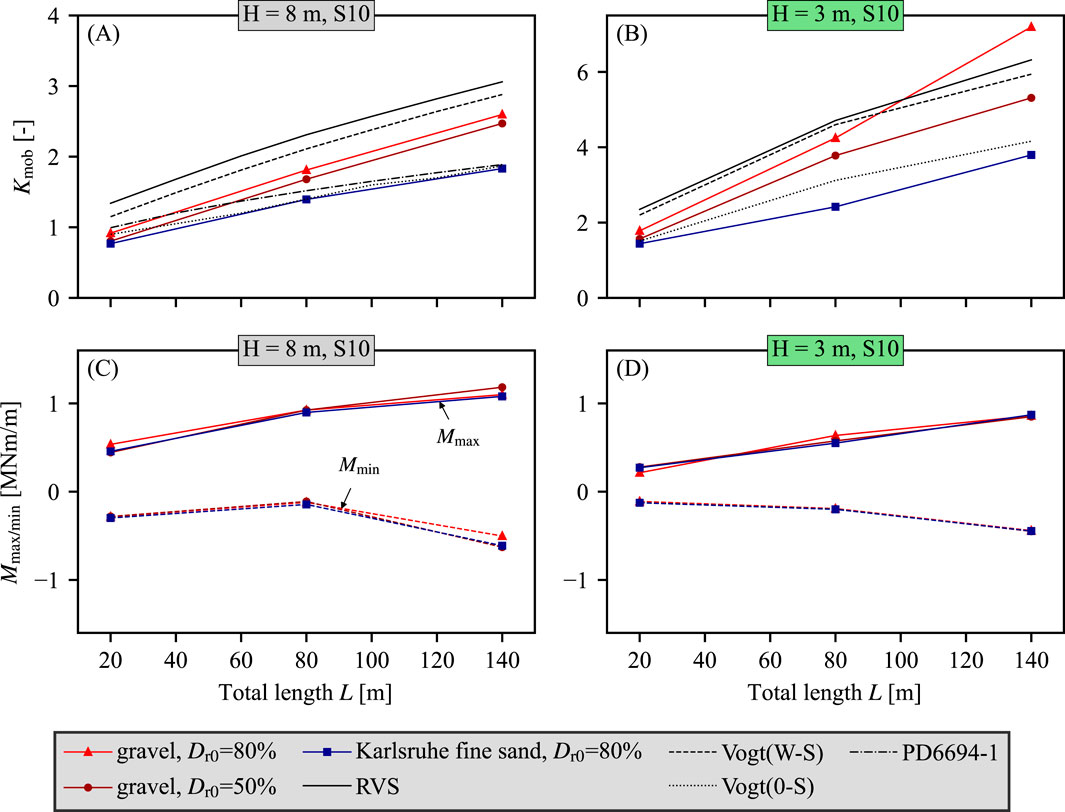
Figure 14. (A–B) Normalized lateral forces $K_{\text{mob}}$ in the abutment’s summer position S10 for calculations with gravel ($D_{\text{r0}}=$ 80%) and Karlsruhe fine sand ($D_{\text{r0}}=$ 50% and 80%) compared against results from the analytical methods, (C–D) Corresponding maximum bending moment $M_{\text{max}}$ of the abutment.

In summary, the use of poorly-graded fine sands in numerical or experimental studies on the cyclic SSI of integral bridges could lead to an underestimation of the cyclic lateral earth pressures. Future numerical and experimental studies on the cyclic SSI should include representative, well-graded backfill materials.

6.3 Influence of foundation and underground stiffness

At last, the influence of the foundation type and underground stiffness was investigated using 3D FE models described in Section 5.2. The lateral stresses were evaluated in the interface at the middle of the abutment (in the axis of symmetry). The resulting $K_{\text{mob}}$ values for various deck lengths $(L)$ and abutment heights $(H)$ are presented in Figure 15. The comparison highlights that the earth pressure on the abutment is significantly influenced by the stiffness of the underground soil. The highest earth pressures are mobilised for the spread foundation with stiff underground ($E_{50}^{\text{ref}}=$45 MPa). For the spread footing with softer underground ($E_{50}^{\text{ref}}=$20 MPa) smaller earth pressures are calculated. The models with a piled foundation and very soft underground ($E_{50}^{\text{ref}}=$8 MPa) show the smallest earth pressures. Almost no difference was found between calculations with one, respectively two pile rows. Additionally, a very similar foot point translation was detected (not shown). These results suggest that the pile behaviour in this study has a rather small influence on the horizontal earth pressures (and its mobilization). Therefore, mainly the lower stiffness of the underground soil is responsible for the significantly lower lateral stresses on the abutment. All 3D calculations for abutment height $H=$8 m do not exceed the analytically calculated earth pressures. This is not the case for some of the 3D models with $H=$3 m and spread footing, see Figure 15B. The 3D calculations also compute slightly higher earth pressures compared to the 2D calculations in Figure 6. This may be related to the fact that the temperature loading in 3D was applied by prescribed displacements, assuming a free deck displacement, see Section 5.2. Thus, slightly higher lateral displacement were applied in comparison to the 2D calculations with direct temperature loading and the corresponding partly restricted movement of the deck, see Section 6.

Figure 15

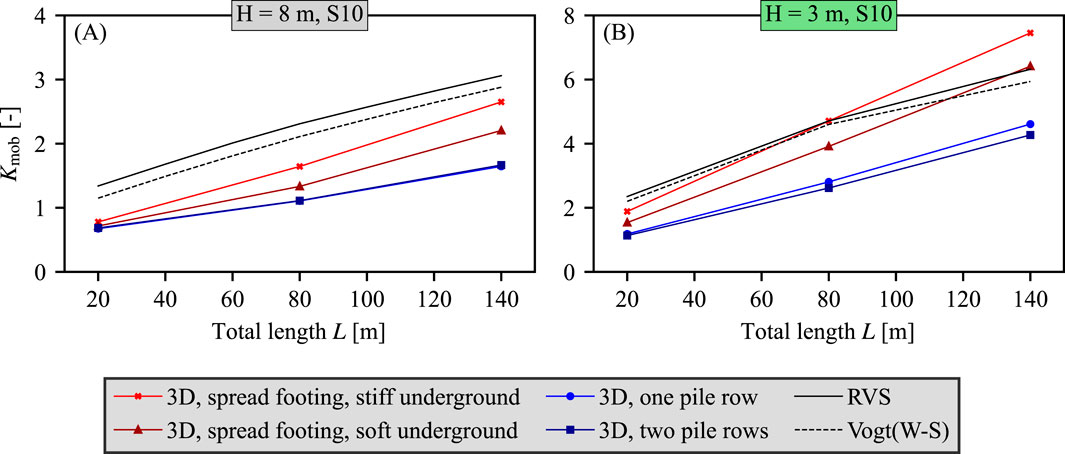
Figure 15. Normalized lateral forces $K_{\text{mob}}$ in the abutment’s summer position S10 for calculations with different foundation systems and underground stiffnesses compared against results from the analytical methods: (A) abutment height H = 8 m, (B) H = 3 m.

7 Conclusion

In this contribution, a comprehensive numerical investigation on the cyclic SSI behavior of integral railway bridges was conducted. A series of parametric studies were performed, examining the effects of varying bridge geometries (lengths $L=$20–140 m and heights $H=$3–8 m), as well as stiffness properties of the structure, backfill and foundation. The primary objective was to quantify the key factors influencing the cyclic SSI behavior of integral railway bridges. The study focuses on typical designs found in Germany, particularly those featuring full-height abutments on spread footings, with or without supplementary support from concrete bored piles. The main advantages of the studies are a) the application of the verified material model DeltaSand for cyclic loading, b) the use of a calibrated parameter set for a representative well-graded gravel backfill material, c) the use of realistic FE models with direct temperature loading which also allows to determine internal forces of the abutment. The numerical SSI results were compared to analytical design approaches for the cyclic mobilization of lateral earth pressure from Germany, Austria and United Kingdom.

The key findings of this research are.

• The cyclic SSI, specifically the passive mobilization of earth pressure, is strongly determined by the bridge length, abutment height, as well as the backfill and foundation/underground stiffness. The abutment stiffness only has a minor influence in this study.

• With increasing deck length $L$, i.e., growing seasonal deformations, significantly higher earth pressures as well as stronger cyclic stress increases are observed. The increase of the abutment height $H$ caused higher peak stresses.

• For tall abutments of $H\ge$ 8 m a foot point translation of ca. 20% can be expected. At shorter heights, the abutment movement is characterized by a significant amount of translation, reaching up to 72%. This emphasizes that the abutment deformation should be evaluated carefully for each (longer) integral bridge in the structural design to determine the lateral stress mobilization and should not be simplified by the (common) assumption of a foot point rotation.

• The backfill material strongly influences the cyclic earth pressure mobilization. Higher stresses are mobilized with the well-graded gravel compared to the poorly-graded fine sand. The increase of the relative density also leads to (slightly) higher earth pressures.

• The stiff gravel material experiences peak stresses and cyclic stress increases predominantly in the upper half of the abutment. This is particularly noticeable for long bridges with short(er) abutments. The stress profiles of the analytical design approaches do not match this distribution, predicting peak stresses at mid-height or below. The FEA with fine sand showed peak stresses in the middle of the abutment.

• Despite the higher earth pressures, gravel materials cause no greater bending moments in the abutment compared to fine sand. This is due to the higher position $z/H_{\text{abut}}$ of the resultant earth pressure on the abutment. For the same reason, the analytical approaches (in most cases) cause higher bending moments compared to the gravel materials, at least for $H=$8 m.

• The study results indicate that current design approaches may not always be conservative, especially since only 10 seasonal cycles have been simulated. Particularly, for long bridges with shorter abutments, deficits in the current design approaches have been found. Similar to the recommendation in PD6694-1 (2020), numerical SSI analysis should be considered for longer integral bridges with significant translation movement of the abutment, e.g., bridges with short heights.

• For the future use of the approach by Vogt (1984), the full thermal movement range of the bridge deck from the winter to the summer position (W–S) should be considered to allow a safe design.

• The simplified rectangular stress profile of RVS 15.02.12 (2019) approximates the effects of Vogt’s parabolic approach (W–S) well and could constitute an easy-to-use method for the structural design of bridges.

• The approach of PD6694-1 (2020) is (only) appropriate for bridge length up to 40 m (based on the evaluation of $K_{\text{mob}}$) in case well-graded gravel materials are used for backfilling.

• Backfill settlements increase with the number of cycles and bridge length. More research is needed to evaluate its influence on the vertical dynamic train-track interaction. Consequently, at this stage, for deck deformations beyond 20 mm, the implementation of approach slabs in accordance with Ril 804.4501 (2021) is recommended.

Future research will focus on the SSI behavior of integral bridges with different typical transition zone designs, such as wedge-shaped cemented granular mixtures or transition slabs. Additionally, more research should be conducted with regard to material models and its calibration for the cyclic SSI, which would allow to simulate all seasonal and potentially even daily cycles during a bridge’s lifetime. Experimental large scale 1$g$ and n$g$ tests (for calibration) should include representative, well-graded materials. Finally, future research, both experimental and numerical, should focus on the combined effects of horizontal cyclic soil-structure interaction (due to thermal deck expansion) and vertical dynamic train-track interaction. The investigation should also account for SSI resulting from the horizontal braking and acceleration forces of trains, as well as the associated abutment displacements. This topic is highly significant for understanding and optimizing track-bridge interaction.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

AS: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Supervision, Validation, Visualization, Writing–original draft, Writing–review and editing. AE: Formal Analysis, Visualization, Writing–review and editing. VG: Resources, Software, Writing–review and editing. FT: Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The first author is employed by DB InfraGO AG. The second author received support from DB InfraGO AG for his master’s thesis. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Acknowledgments

We gratefully acknowledge the financial support from the TU Graz Open Access Publishing Fund for providing the open access funding.

Conflict of interest

Author AS was employed by DB InfraGO AG. Author VG was employed by Witteveen+Bos.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdel-Fattah, M., and Abdel-Fattah, T. (2019). Behavior of integral frame abutment bridges due to cyclic thermal loading: nonlinear finite-element analysis. J. Bridge Eng. 24, 04019031. doi:10.1061/(ASCE)BE.1943-5592.0001394

CrossRef Full Text | Google Scholar

Abdel-Fattah, M., Abdel-Fattah, T., and Hemada, A. (2018). Nonlinear finite-element analysis of integral abutment bridges due to cyclic thermal changes. J. Bridge Eng. 23, 04017134. doi:10.1061/(ASCE)BE.1943-5592.0001183

CrossRef Full Text | Google Scholar

Abdullah, A., and El Naggar, H. (2023). Soil-structure interaction of integral abutments. Transp. Geotech. 38, 100900. doi:10.1016/j.trgeo.2022.100900

CrossRef Full Text | Google Scholar

Alqarawi, A., Leo, C., Liyanapathirana, D., and Hu, P. (2024). Soil-structure interaction issues in integral abutment bridges. Transp. Geotech. 48, 101296. doi:10.1016/j.trgeo.2024.101296

CrossRef Full Text | Google Scholar

ASTRA 12004 (2011). Guideline on structural details of bridges: chapter 3: bridge ends (in German). Bern, Switzerland: ASTRA.

Google Scholar

Banks, J., and Bloodworth, A. (2018). Lateral stress profiles on integral bridge abutments. Proc. Institution Civ. Eng. - Bridge Eng. 171, 155–168. doi:10.1680/jbren.17.00017

CrossRef Full Text | Google Scholar

Bartl, U. (2004). On the mobilization of passive earth pressure in cohesionless soil (in German). Dissertation. Dresden, Germany: Technische Universität Dresden.

Google Scholar

Bentley Systems (2023). Plaxis connect edition V23.2 manual. Exton, USA: Bentley Systems.

Google Scholar

Bloodworth, A., Xu, M., Banks, J., and Clayton, C. (2012). Predicting the earth pressure on integral bridge abutments. J. Bridge Eng. 17, 371–381. doi:10.1061/(asce)be.1943-5592.0000263

CrossRef Full Text | Google Scholar

Burke, J., and Martin, P. (2009). Integral and semi-integral bridges. Oxford, UK: John Wiley and Sons.

Google Scholar

Civjan, S., Bonczar, C., Brena, S., DeJong, J., and Crovo, D. (2007). Integral abutment bridge behavior: parametric analysis of a Massachusetts bridge. J. Bridge Eng. 12, 64–71. doi:10.1061/(ASCE)1084-0702(2007)12:1(64)

CrossRef Full Text | Google Scholar

Clayton, C., Xu, M., and Bloodworth, A. (2006). A laboratory study of the development of earth pressure behind integral bridge abutments. Géotechnique 56, 561–571. doi:10.1680/geot.2006.56.8.561

CrossRef Full Text | Google Scholar

Cosgrove, E., and Lehane, B. (2003). Cyclic loading of loose backfill placed adjacent to integral bridge abutments. Int. J. Phys. Model. Geotechnics 3, 09–16. doi:10.1680/ijpmg.2003.030302

CrossRef Full Text | Google Scholar

David, T., Forth, J., and Ye, J. (2014). Superstructure behavior of a stub-type integral abutment bridge. J. Bridge Eng. 19, 04014012. doi:10.1061/(ASCE)BE.1943-5592.0000583

CrossRef Full Text | Google Scholar

Della Pietra, R., Oberwalder, S., and Tue, N. V. (2019). Key aspects in the design of integral bridges (in German). Beton- und Stahlbetonbau 114, 683–691. doi:10.1002/best.201900030

CrossRef Full Text | Google Scholar

Denton, S., Riches, O., Christie, T., and Kidd, A. (2011). “Developments in integral bridge design,” in Bridge design to eurocodes: UK implementation. Editor S. Denton (London, UK: ICE Publishing), 463–480.

Google Scholar

Dicleli, M. (2005). Integral abutment-backfill behavior on sand soil-pushover analysis approach. J. Bridge Eng. 10, 354–364. doi:10.1061/(ASCE)1084-0702(2005)10:3(354)

CrossRef Full Text | Google Scholar

DIN 4085 (2018). Subsoil. Calculation of earth pressure (in German). Berlin, Germany: DIN.

Google Scholar

DIN EN 1991-1-5/NA (2010). Germany National Annex to Eurocode 1: actions on structures – Part 1–5: general actions – thermal actions. Berlin, Germany: DIN.

Google Scholar

DIN EN 1992-2 (2010). Eurocode 2: design of concrete structures - Part 2: concrete bridges. Berlin, Germany: DIN.

Google Scholar

Dreier, D., Burdet, O., and Muttoni, A. (2011). Transition slabs of integral abutment bridges. Struct. Eng. Int. 21, 144–150. doi:10.2749/101686611X12994961034174

CrossRef Full Text | Google Scholar

Efretuei, E. (2013). Thermal impact on soil-structure interaction for integral bridges. PhD thesis, Leeds, United Kingdom. University of Leeds.

Google Scholar

England, G., Tsang, N., and Bush, D. (2000). Integral bridges: a fundamental approach to the time-temperature loading problem. London, UK: Telford.

Google Scholar

Fetrati, M., Galavi, V., Goodarzi, M., Mörz, T., and Kreiter, S. (2024). Simulation of cone penetrometer tests in sand using three advanced constitutive models: a comparative study. Comput. Geotechnics 176, 106683. doi:10.1016/j.compgeo.2024.106683

CrossRef Full Text | Google Scholar

Franke, D. (1989). Calculation of retaining walls using various mechanical models (in German). Dresden, Germany: Ohde Kolloquium.

Google Scholar

Galavi, V. (2021). DeltaSand: a state dependent double hardening elasto-plastic model for sand: formulation and validation. Comput. Geotechnics 129, 103844. doi:10.1016/j.compgeo.2020.103844

CrossRef Full Text | Google Scholar

Galavi, V., and Martinelli, M. (2024). MPM simulation of the installation of an impact-driven pile in dry sand and subsequent axial bearing capacity. J. Geotechnical Geoenvironmental Eng. 150, 04024019. doi:10.1061/JGGEFK.GTENG-11592

CrossRef Full Text | Google Scholar

Grabe, J., Vogel, P., and Rombach, G. (2019). “Investigation of the soil structure interaction of integral bridges,” in Advances in engineering materials, structures and systems: innovations, mechanics and applications. Editor A. Zingoni (Cape Town, South Africa: ImprintCRC Press), 1–5. doi:10.1201/9780429426506

CrossRef Full Text | Google Scholar

Granitzer, A., Felic, H., Leo, J., Stastny, A., and Tschuchnigg, F. (2024). Numerical investigation of pile foundation systems employing an enhanced embedded finite element. Front. Built Environ. 10, 1454266 doi:10.3389/fbuil.2024.1454266

CrossRef Full Text | Google Scholar

Hassan, M., Liyanapathirana, D., Fuentes, W., Leo, C., and Hu, P. (2024). A review of soil deformation and lateral pressure ratcheting phenomena in integral abutment bridges. Transp. Geotech. 49, 101388. doi:10.1016/j.trgeo.2024.101388

CrossRef Full Text | Google Scholar

Havinga, M., Tschuchnigg, F., Marte, R., and Schweiger, H. (2017). Small scale experiments and numerical analysis of integral bridge abutments. Proc. ICSMGE 2017, 753–756.

Google Scholar

Kerokoski, O. (2006). Soil-structure interaction of long jointless bridges with integral abutments. Phd thesis Tampere, Finland: Tampere University of Technology.

Google Scholar

LaFave, J., Riddle, J., Jarrett, M., Wright, B., Svatora, J., An, H., et al. (2016). Numerical simulations of steel integral abutment bridges under thermal loading. J. Bridge Eng. 21, 04016061. doi:10.1061/(ASCE)BE.1943-5592.0000919

CrossRef Full Text | Google Scholar

Lehane, B. (2011). Lateral soil stiffness adjacent to deep integral bridge abutments. Géotechnique 61, 593–603. doi:10.1680/geot.9.P.135

CrossRef Full Text | Google Scholar

Liu, H., Abell, J., Diambra, A., and Pisanò, F. (2019). Modelling the cyclic ratcheting of sands through memory-enhanced bounding surface plasticity. Géotechnique 69, 783–800. doi:10.1680/jgeot.17.P.307

CrossRef Full Text | Google Scholar

Liu, H., Han, J., and Parsons, R. (2022a). Effects of seasonal temperature change-induced abutment movements on backfill surface settlements behind integral bridge abutments–numerical analysis. Comput. Geotechnics 149, 104884. doi:10.1016/j.compgeo.2022.104884

CrossRef Full Text | Google Scholar

Liu, H., Han, J., and Parsons, R. (2022b). Settlement and horizontal earth pressure behind model integral bridge abutment induced by simulated seasonal temperature change. J. Geotechnical Geoenvironmental Eng. 148, 04022043. doi:10.1061/(ASCE)GT.1943-5606.0002812

CrossRef Full Text | Google Scholar

Liu, H., Han, J., and Parsons, R. (2023). Numerical analysis of geosynthetics to mitigate seasonal temperature change-induced problems for integral bridge abutment. Acta Geotech. 18, 673–693. doi:10.1007/s11440-022-01614-5

CrossRef Full Text | Google Scholar

Liu, H., Han, J., and Parsons, R. L. (2022c). Integral bridge abutments in response to seasonal temperature changes: state of knowledge and recent advances. Front. Built Environ. 8. doi:10.3389/fbuil.2022.916782

CrossRef Full Text | Google Scholar

Luo, S., Huang, Z., Asia, Y., De Luca, F., De Risi, R., Harkness, J., et al. (2023). Physical and numerical investigation of integral bridge abutment stiffness due to seasonal thermal loading. Transp. Geotech. 42, 101064. doi:10.1016/j.trgeo.2023.101064

CrossRef Full Text | Google Scholar

Marx, S., and Seidl, G. (2011). Integral railway bridges in Germany. Struct. Eng. Int. 21, 332–340. doi:10.2749/101686611X12994961034534

CrossRef Full Text | Google Scholar

Mass. DOT (2024). Bridge manual. Boston, MA, United States. Highway Division, Massachusetts Department of Transportation.

Google Scholar

Morley, D., Madabhushi, G., Sakufiwa, D., and Thusyanthan, I. (2024). Investigation into soil ratcheting behind integral bridges using centrifuge modelling. Proc. Institution Civ. Eng. - Bridge Eng., 1–17. doi:10.1680/jbren.23.00046

CrossRef Full Text | Google Scholar

Niemunis, A., and Herle, I. (1997). Hypoplastic model for cohesionless soils with elastic strain range. Mech. Cohesive-frictional Mater. 2, 279–299. doi:10.1002/(SICI)1099-1484(199710)2:4<279::AID-CFM29>3.0.CO;2-8

CrossRef Full Text | Google Scholar

ÖNorm B 4434 (1993). Earth pressure calculations (in German). Vienna, Austria: Österreichisches Normungsinstitut.

Google Scholar

Ooi, P., Lin, X., and Hamada, H. (2010). Numerical study of an integral abutment bridge supported on drilled shafts. J. Bridge Eng. 15, 19–31. doi:10.1061/(ASCE)BE.1943-5592.0000037

CrossRef Full Text | Google Scholar

Paixão, A., Fortunato, E., and Calçada, R. (2016). A numerical study on the influence of backfill settlements in the train/track interaction at transition zones to railway bridges. Proc. Institution Mech. Eng. Part F J. Rail Rapid Transit 230, 866–878. doi:10.1177/0954409715573289

CrossRef Full Text | Google Scholar

Paixão, A., Varandas, J., and Fortunato, E. (2021). Dynamic behavior in transition zones and long-term railway track performance. Front. Built Environ. 7, 658909. doi:10.3389/fbuil.2021.658909

CrossRef Full Text | Google Scholar

PD6694-1 (2020). Recommendations for the design of structures subject to traffic loading to BS EN 1997-1:2004. London, UK: BSI.

Google Scholar

Place, D., Farooq, I., and Tang, V. (2006). “Integral bridges with frame abutments,” in Proceedings of the 1st international Conference on Advances in bridge engineering (London, UK), 26–28.

Google Scholar

Quinn, B., and Civjan, S. (2017). Parametric study on effects of pile orientation in integral abutment bridges. J. Bridge Eng. 22, 04016132. doi:10.1061/(ASCE)BE.1943-5592.0000952

CrossRef Full Text | Google Scholar

RE-ING (2023). Guideline for the design, structural configuration, and equipment of civil engineering structures (in German). Bergisch Gladbach, Germany: BAST.

Google Scholar

Ril 804.4501 (2021). Standard for planning, construction, and maintenance of railway bridges and other civil engineering structures. Integral and semi-integral bridges (in German). Frankfurt am Main, Germany: DB Netz AG.

Google Scholar

Ril 836 (2023). Standard for planning, construction, and maintenance of earthworks and other geotechnical structures (in German). Frankfurt am Main, Germany: DB Netz AG.

Google Scholar

RVS 15.02.12 (2019). Design and construction of integral bridges (in German). Vienna, Austria: Österreichische Forschungsgesellschaft Strasse-Schiene-Verkehr FSV.

Google Scholar

Sandberg, J., Magnino, L., Nowak, P., Wiechecki, M., and Thusyanthan, I. (2020). The integral bridge design concept for the third runway at heathrow, UK. Proc. Institution Civ. Eng. - Bridge Eng. 173, 112–120. doi:10.1680/jbren.19.00044

CrossRef Full Text | Google Scholar

Schanz, T., Vermeer, P., and Bonnier, P. (1999). “The hardening soil model: formulation and verification,” in Beyond 2000 in computational geotechnics (London, United Kingdom: Routledge), 281–296.

CrossRef Full Text | Google Scholar

Sigdel, L., Lu, M., Al-qarawi, A., Leo, C., Liyanapathirana, S., and Hu, P. (2023). Application of engineered compressible inclusions to mitigating soil-structure interaction issues in integral bridge abutments. J. Rock Mech. Geotechnical Eng. 15, 2132–2146. doi:10.1016/j.jrmge.2022.12.033

CrossRef Full Text | Google Scholar

Silva, P., Costa, Y., Walter, J., Kouchaki, B., Zornberg, J., and Costa, C. (2023). Numerical evaluation of a semi-integral bridge abutment under cyclic thermal movements. Transp. Geotech. 39, 100938. doi:10.1016/j.trgeo.2023.100938

CrossRef Full Text | Google Scholar

Springman, S., Norish, A., and Ng, C. (1996). TRL Report 146: cyclic loading of sand behind integral bridge abutments. Berkshire, UK: Highways Agency - Transport Research Laboratory.

Google Scholar

Stastny, A., Knittel, L., Meier, T., and Tschuchnigg, F. (2024a). Experimental determination of hypoplastic parameters and cyclic numerical analysis for railway bridge backfills. Acta Geotech. 19, 6899–6916. doi:10.1007/s11440-024-02312-0

CrossRef Full Text | Google Scholar

Stastny, A., Medicus, G., Galavi, V., Tafili, M., and Tschuchnigg, F. (2024b). Evaluation of advanced soil models for the cyclic soil-structure interaction of integral bridges. Acta Geotechn. (accepted).

Google Scholar

Stastny, A., Stein, R., and Tschuchnigg, F. (2022). “Long-term monitoring of the transition zone of an integral railway bridge in Germany,” in Proc. 11th international symposium on field monitoring in geomechanics (United Kingdom: Imperial College London), 1–7.

Google Scholar

Stastny, A., and Tschuchnigg, F. (2022). “Numerical studies on soil structure interaction of integral railway bridges with different backfills,” in Proc. 16th IACMAG conference (Torino, Italy), 338–345.

Google Scholar

Stastny, A., and Tschuchnigg, F. (2023). “Numerical studies on the use of zero thickness interfaces in cyclic soil structure interaction analysis,” in Proc. 10th NUMGE conference (Imperial College London, United Kingdom), 1–6.

Google Scholar

Szczyrba, S. (2013). Settlement-minimizing construction of the backfill area of bridge abutments (in German). Dissertation. Freiberg, Germany: Technische Universität Bergakademie Freiberg.

Google Scholar

Tapper, L., and Lehane, B. (2005). “Lateral stress development on integral bridge abutments,” in Developments in mechanics and structures of material. Editors A. Deeks, and H. Hao (CRC Press), 2, 1069–1075.

Google Scholar

Tue, N. V., Della Pietra, R., and Mayer, M. (2021). “Integral bridges – structural behavior and suggestions for design, including existing bridges (in German),” in Beton-kalender 2021. Editors K. Bergmeister, F. Fingerloos, and J.-D. Wörner (Berlin: Ernst and Sohn).

Google Scholar

Vogt, N. (1984). Determination of earth resistance during monotonic and cyclic wall movements in sand. (in German). Dissertation. Stuttgart, Germany: Universität Stuttgart.

Google Scholar

Vucetic, M. (1990). Normalized behavior of clay under irregular cyclic loading. Can. Geotechnical J. 27, 29–46. doi:10.1139/t90-004

CrossRef Full Text | Google Scholar

Walter, J., Morsy, A., and Zornberg, J. (2018). “Experimental and numerical investigation of lateral earth pressures generated from repeated loading,” in IFCEE 2018 (American society of civil engineers), 158–168. doi:10.1061/9780784481608.016

CrossRef Full Text | Google Scholar

Wang, H., and Markine, V. (2019). Dynamic behaviour of the track in transitions zones considering the differential settlement. J. Sound Vib. 459, 114863. doi:10.1016/j.jsv.2019.114863

CrossRef Full Text | Google Scholar

Wenner, M., Seidl, G., Garn, R., and Marx, S. (2019). Long-term behavior of a 170-meter-long integral railway bridge (in German). Bautechnik 96, 120–132. doi:10.1002/bate.201800068

CrossRef Full Text | Google Scholar

Wichtmann, T., and Triantafyllidis, T. (2016). An experimental database for the development, calibration and verification of constitutive models for sand with focus to cyclic loading: part i—tests with monotonic loading and stress cycles. Acta Geotech. 11, 739–761. doi:10.1007/s11440-015-0402-z

CrossRef Full Text | Google Scholar

Wolffersdorff, P.-A. v. (1996). A hypoplastic relation for granular materials with a predefined limit state surface. Mech. Cohesive–frictional Mater. 1, 251–271. doi:10.1002/(SICI)1099-1484(199607)1:3<251::AID-CFM13>3.0.CO;2-3

CrossRef Full Text | Google Scholar

Wood, D. (2004). Geotechnical modelling. London, UK: CRC Press.

Google Scholar

Xu, M. (2005). The behaviour of soil behind full-height integral abutments. PhD thesis. Southampton, United Kingdom: University of Southampton.

Google Scholar

Xu, M., Bloodworth, A., and Clayton, C. (2007). Behavior of a stiff clay behind embedded integral abutments. J. geotechnical geoenvironmental Eng. 133, 721–730. doi:10.1061/(ASCE)1090-0241(2007)133:6(721)

CrossRef Full Text | Google Scholar

Xu, M., and Guo, J. (2021). DEM study on the development of the earth pressure of granular materials subjected to lateral cyclic loading. Comput. Geotechnics 130, 103915. doi:10.1016/j.compgeo.2020.103915

CrossRef Full Text | Google Scholar

Zordan, T., Briseghella, B., and Lan, C. (2011). Parametric and pushover analyses on integral abutment bridge. Eng. Struct. 33, 502–515. doi:10.1016/j.engstruct.2010.11.009

CrossRef Full Text | Google Scholar

Zorzi, G., Artoni, R., and Gabrieli, F. (2017). Experiments and DEM simulations of granular ratcheting. EPJ Web Conf., EPJ Web Conf. EDP Sci. 140, 03061, doi:10.1051/epjconf/201714003061

CrossRef Full Text | Google Scholar