An approach to improve the numerical simulation of crushed salt compaction behavior

Crushed salt as backfill material in a repository for high-level nuclear waste is aimed to act as a long-term barrier. The sealing effect of crushed salt evolves with ongoing compaction and therefore reduction in porosity and permeability. For a reliable prognosis of the compaction behavior in the long-term, constitutive models are crucial that capture the experimentally observed processes and credibly extrapolate these processes outside the range they were calibrated in. Up to now there is still no constitutive model for crushed salt which is validated against all factors/processes influencing compaction and/or the whole porosity range (especially $\phi$ < 5%). The constitutive model for crushed salt compaction available in CODE_BRIGHT has been used in the field of repository research for several years. It has been applied in recent research projects on crushed salt compaction, where shortcomings in the modelling of compaction behaviour in dependence on mean stress and deviatoric stress variations are identified. Based on this discovered potential for improvement an approach for the modification of the constitutive model is proposed within this paper. It addresses the assumption of an idealized geometry and network of grains which is introduced by mathematically constraint functions dependent on void ratio. The proposed approach aims to give more flexibility in the handling of geometry dependence. The paper comprises an introduction into the use of crushed salt in the context of nuclear waste repository. The description of the constitutive model for crushed salt available in CODE_BRIGHT is given, as well as, the proposal for improvement and its application. It is finished with a sensitivity study for the new approach followed by a summary and outlook.

1 Introduction

Rock salt is considered as a potential host rock formation for the deep geological disposal of high-level nuclear waste (HLW) in several countries, like Germany (Bundesgesellschaft für Endlagerung, 2020), the Netherlands (Bartol and Vuorio, 2022), and the United States (Sandia National Laboratories, 2014). The safety concept is based on a multi-barrier system comprising rock salt as the geological barrier, sealing elements and backfill as geotechnical barriers, and the waste canisters as technical barriers. Upon terminating the operational phase of the repository, the sealing function is intended to be provided by the waste matrix, waste canisters and the geotechnical barriers (Figure 1). The rock salt and the backfill material are intended to provide the sealing function in the long-term (Bertrams et al., 2020).

Figure 1

Figure 1. Evolution of important barriers’ sealing effectiveness in the post closure phase of a repository. The color intensity represents the degree of sealing effectiveness (Bollingerfehr et al., 2018).

Backfilling of open cavities, drifts and shafts will be realized with crushed salt. Crushed salt is not only a long-term stable and easily available material (mined-off material) but most important it guarantees a maximum compatibility with the host rock. Creep of the rock salt causes convergence of the open cavities, and, in turn, the natural compaction of crushed salt backfill with time (Figure 2). It is expected that porosity and permeability of the crushed salt backfill will decrease during compaction down to barrier properties comparable to undisturbed rock salt (porosity $\phi$ ≤ 1%).

Figure 2

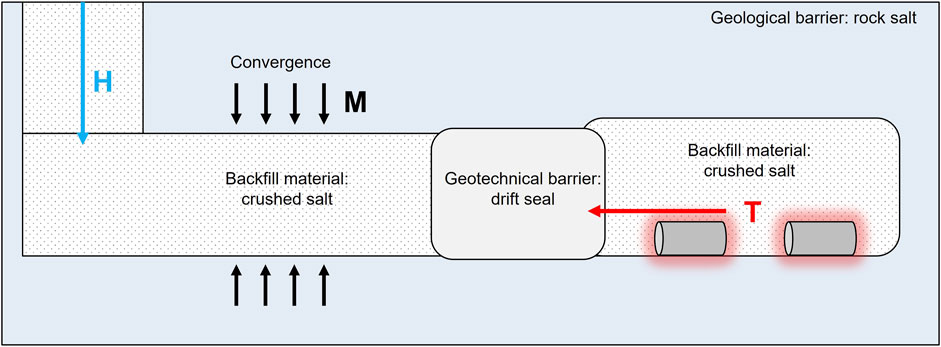
Figure 2. Schematic repository for high-level nuclear waste in rock salt (modified after Friedenberg et al. (2023)).

In order to give a qualified prognosis of the long-term behavior of crushed salt as a barrier, numerical simulations are needed. The constitutive models for crushed salt need to capture the observed phenomena and credibly extrapolate the compaction process outside the range they were calibrated in. The most important metrics to predict for crushed salt in the context of a nuclear waste repository are the evolutions of porosity and permeability with time, since they are determining possible pathways for radionuclide release. The sealing effect of crushed salt against radionuclide migration evolves with decreasing porosity/permeability. Therefore, the point in time when barrier properties are reached is the most important information for long-term safety considerations. Thus, the numerical prediction of the sealing function evolution of crushed salt is crucial for the proof of the long-term safety of a repository in rock salt.

The evolution of porosity and permeability is determined by the compaction process. Crushed salt compaction is influenced by internal material properties (e.g., mineralogy, grain size distribution, initial water content), environmental conditions (e.g., temperature) and stress state (e.g., convergence rate) (Hansen et al., 2014; Kröhn et al., 2017). Therefore, several thermal-hydraulic-mechanical (THM) coupled processes must be considered when investigating the compaction behavior of crushed salt.

In the current state, uncertainties with respect to database and process understanding still remain, especially for the calibration of constitutive models and the numerical simulation of crushed salt with respect to the prognosis of its long-term behavior.

With respect to the current requirements on the long-term safety of a high-level waste repository, the understanding of the process of crushed salt compaction has some important gaps. There is no code/constitutive model available which is validated against (1) the whole porosity range for crushed salt compaction, especially for the low porosity range ($\phi$ < 5%), and (2) all factors and processes influencing the compaction. The measurement of porosities and permeabilities lower than $\phi$ = 5% is still challenging and suitable techniques are currently under development. Additionally, the numerical modelling capability needs to be extended and validated, since only a few models consider the influence of moisture on the compaction. Only a few constitutive models consider the influence of moisture on the creep compaction and few experimental studies on the influence of deviatoric stress on crushed salt are available, thus, it lacks on calibration and validation. Various microstructural processes interact during crushed salt compaction, which are hard to separate, but nevertheless considered in constitutive model formulations. There is the need for a better understanding and investigation of these microstructural processes building the basis for constitutive models (Friedenberg et al., 2024; Wieczorek et al., 2017).

This paper presents an approach aiming at the improvement of the numerical simulation of crushed salt compaction using CODE_BRIGHT. Recent results on a model verification for the long-term compaction behavior of crushed salt will be presented. The work is performed based on experimental data generated in the international KOMPASS projects dealing with the compaction of crushed salt for safe containment (Czaikowski et al., 2020; Friedenberg et al., 2024).

2 Numerical approach

The numerical simulations are performed using the finite element (FEM) code CODE_BRIGHT with the implemented mechanical constitutive model for crushed salt. The mechanical model has been used in the field of repository research for several years and is extensively tested for its performance and validated against experimental data as shown in Olivella et al. (1993), Olivella (1994), Bechthold et al. (1999), Olivella and Gens (2002) and Bechthold et al. (2004).

The model formulation is kept in terms of strain rates and composed of an additive approach (Olivella and Gens, 2002). Several deformation mechanisms account for Equation 1: linear elasticity (EL), grain rearrangement (GR), fluid assisted diffusional transfer (FADT) and dislocation creep (DC). With the combination of these four mechanisms, the relevant deformations for repository conditions are captured (Bechthold et al., 2004).

$\dot{\mathit{\epsilon }}={\dot{\mathit{\epsilon }}}_{\mathit{E}\mathit{L}}+{\dot{\mathit{\epsilon }}}_{\mathit{F}\mathit{A}\mathit{D}\mathit{T}}+{\dot{\mathit{\epsilon }}}_{\mathit{D}\mathit{C}}+{\dot{\mathit{\epsilon }}}_{\mathit{G}\mathit{R}}(1)$

The general stress definitions are presented in the Equations 2–6. Compression is counted positive and tension is counted negative. Attention should be paid to individual definitions of deviatoric stress in the DC and the GR models.

${\mathit{\sigma }}^{\prime }=\mathit{\sigma }-{\mathit{P}}_{\mathit{f}}(2)$

${\mathit{P}}_{\mathit{f}}=\mathbf{max}\left({\mathit{P}}_{\mathit{g}},{\mathit{P}}_{\mathit{l}}\right)(3)$

$\mathit{p}=\frac{{\mathit{\sigma }}_{\mathbf{1}}+\mathbf{2}{\mathit{\sigma }}_{\mathbf{3}}}{\mathbf{3}}(4)$

${\mathit{p}}^{\prime }=\mathit{p}-{\mathit{P}}_{\mathit{f}}(5)$

$\mathit{q}={\mathit{\sigma }}_{\mathbf{1}}-{\mathit{\sigma }}_{\mathbf{3}}(6)$

where ${\sigma }^{\prime }$ is effective stress, $\sigma$ is total stress, $P_g$ and $P_l$ are gas and liquid pressure, respectively, $p$ is total mean stress, $p^{\prime }$ is effective mean stress, $q$ is deviatoric stress, ${\sigma }_1$ is axial stress and ${\sigma }_3$ is radial stress.

The mechanical creep models (FADT and DC) are based on microstructural observations on granular salt materials and therefore cover an idealized geometry forming a regular arrangement of polyhedrons (Olivella and Gens, 2002). Characteristic sizes are specified, and relations derived as shown in Figure 3.

Figure 3

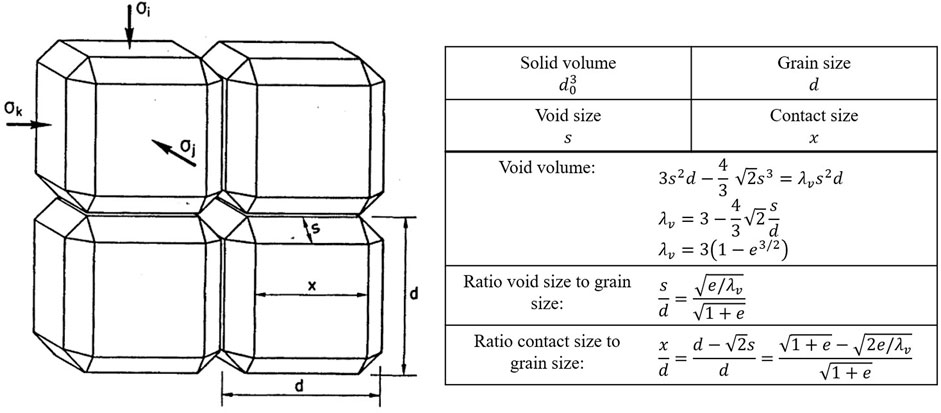
Figure 3. Idealized geometry and characteristic sizes as a basis for the constitutive creep models for crushed salt in CODE_BRIGHT (modified after Olivella and Gens (2002)).

2.1 Linear elasticity

The linear elastic behavior of crushed salt is meant to play a minor role in the compaction process. However, its formulation is essential for the computational framework. The increase in stiffness with ongoing compaction is described by a generalized Hook’s law (Equation 7). Young’s modulus and Poisson’s ratio are applied as elastic constants. The isotropic linear elastic model is formulated in combination with a porosity dependent evolution of Young’s modulus (Olivella et al., 2023). By applying Equation 8, the Young’s modulus is increasing by decreasing porosity, simulating the material’s stiffness increase with ongoing compaction. The change of Young’s modulus with the change of porosity ($dE/d\phi$) is considered to be a constant parameter. In the case of decreasing Young’s modulus with increasing porosity, the minimum value for Young’s modulus limits its decrease.

${\dot{\mathit{\epsilon }}}_{\mathit{E}\mathit{L}}={\mathit{C}}^{\mathit{e}}\dot{\mathit{\sigma }}(7)$

$\mathit{E}={\mathit{E}}_{\mathbf{0}}+\left(\mathit{\phi }-{\mathit{\phi }}_{\mathbf{0}}\right)\frac{\mathit{d}\mathit{E}}{\mathit{d}\mathit{\phi }}\ge {\mathit{E}}_{\mathit{min}}(8)$

where $C^e$ is the elastic compliance matrix, $E$ is the Young’s modulus, $E_0$ is the reference value for Young’s modulus evolution, $\phi$ is the current porosity, ${\phi }_0$ is the reference porosity, $dE/d\phi$ is the variation of Young’s Modulus with porosity and $E_{\mathit{min}}$ is the minimum value for Young’s modulus.

2.2 Fluid assisted diffusional transfer (FADT)

The fluid assisted diffusional transfer mechanism describes the humidity creep of crushed salt, depending on the influence of moisture and dominating in areas of low stresses and low temperatures. Dissolution of salt will take place in areas of high stress concentration; the salt will then migrates through the liquid phase and precipitates in areas of lower stress. The FADT model is based on extensive studies by Schutjens (1991), Spiers et al. (1986), Spiers et al. (1989) and Spiers and Brzesowsky (1993).

The model formulation is derived on basis of the idealized geometry (Figure 3) and the assumptions of dissolution of salt in grain contacts, diffusive flux of salt through the liquid phase driven by a chemical potential gradient and precipitation of salt in pore space. The detailed derivation of the strain rate formulation in Equation 9 is to be found in Olivella and Gens (2002). The strain rate is decomposed in a volumetric and a deviatoric part, labeled by v and d, respectively. Equation 10 and Equation 11 are called the volumetric and deviatoric viscosities, respecitvely. They compile the dependencies on temperature $T$, solid volume $d_0^3$, the material parameter $B$ (Equation 12) and liquid saturation $S_l$. The auxilliary functions $g_{FADT}^v$ (Equation 13) and $g_{FADT}^d$, (Equation 14) as well as the functions $g$ and $f$ are geometry dependent. The functions $g$ and $f$ are derived directly from the idealized geometry in Figure 3, where $g$ is the relative stress concentration and $f$ express the relative pore size (Olivella, 1994).

${\dot{\mathit{\epsilon }}}_{\mathit{F}\mathit{A}\mathit{D}\mathit{T}}=\frac{\mathbf{1}}{\mathbf{2}{\mathit{\eta }}_{\mathit{F}\mathit{A}\mathit{D}\mathit{T}}^{\mathit{d}}}\left({\mathit{\sigma }}^{\prime }-{\mathit{p}}^{\prime }\mathit{I}\right)+\frac{\mathbf{1}}{\mathbf{3}{\mathit{\eta }}_{\mathit{F}\mathit{A}\mathit{D}\mathit{T}}^{\mathit{v}}}{\mathit{p}}^{\prime }\mathit{I}(9)$

$\frac{\mathbf{1}}{{\mathit{\eta }}_{\mathit{F}\mathit{A}\mathit{D}\mathit{T}}^{\mathit{v}}}=\frac{\mathbf{16}\mathit{B}\left(\mathit{T}\right)\sqrt{{\mathit{S}}_{\mathit{l}}}}{{\mathit{d}}_{\mathbf{0}}^{\mathbf{3}}}{\mathit{g}}_{\mathit{F}\mathit{A}\mathit{D}\mathit{T}}^{\mathit{v}}\left(\mathit{e}\right)(10)$

$\frac{\mathbf{1}}{{\mathbf{2}\mathit{\eta }}_{\mathit{F}\mathit{A}\mathit{D}\mathit{T}}^{\mathit{d}}}=\frac{\mathbf{16}\mathit{B}\left(\mathit{T}\right)\sqrt{{\mathit{S}}_{\mathit{l}}}}{{\mathit{d}}_{\mathbf{0}}^{\mathbf{3}}}{\mathit{g}}_{\mathit{F}\mathit{A}\mathit{D}\mathit{T}}^{\mathit{d}}\left(\mathit{e}\right)(11)$

$\mathit{B}\left(\mathit{T}\right)=\frac{{\mathit{A}}_{\mathit{B}}}{\mathit{R}\mathit{T}}\mathit{exp}\left(\frac{{-\mathit{Q}}_{\mathit{B}}}{\mathit{R}\mathit{T}}\right)(12)$

${\mathit{g}}_{\mathit{F}\mathit{A}\mathit{D}\mathit{T}}^{\mathit{v}}\left(\mathit{e}\right)=\frac{{\mathit{g}}^{\mathbf{2}}}{\left(\mathbf{1}+\mathit{e}\right)}(13)$

${\mathit{g}}_{\mathit{F}\mathit{A}\mathit{D}\mathit{T}}^{\mathit{d}}\left(\mathit{e}\right)=\frac{\mathbf{3}{\mathit{g}}^{\mathbf{2}}{\mathit{e}}^{\mathbf{3}/\mathbf{2}}}{\left(\mathbf{1}+\mathit{e}\right)}(14)$

$\mathit{g}=\frac{\mathbf{1}}{{\left(\mathbf{1}-\mathit{f}\right)}^{\mathbf{2}}}=\frac{{\mathit{d}}^{\mathbf{2}}}{{\mathit{x}}^{\mathbf{2}}}(15)$

$\mathit{f}=\sqrt{\frac{\mathbf{2}\mathit{e}}{\mathbf{3}\left(\mathbf{1}-{\mathit{e}}^{\mathbf{3}/\mathbf{2}}\right)}}=\frac{\mathit{s}\sqrt{\mathbf{2}}}{\mathit{d}}(16)$

where $I$ is the identity matrix, $S_l$ is liquid saturation, $d_0$ is characteristic grain size, $T$ is temperature, $A_B$ is a pre-exponential parameter, $Q_B$ is the activation energy, $R$ is the gas constant and $e$ the void ratio.

2.3 Dislocation creep (DC)

The dislocation creep mechanism captures deformations like dislocation glide and climb. It refers to the intracrystalline mechanisms (Olivella, 1994). These mechanisms can be described by power law terms and therefore are grouped here. The model is based on the rock salt power law and combined with a geometrical derivation of a volumetric strain rate and a deviatoric strain rate formulation. It is generalized by the use of a viscoplastic approach including a flow rule and a viscosity parameter. $G$ and $F$ in Equation 18 are formulated as functions of stress invariants. The viscosities in Equations 21, 22 compile geometrical and material properties. The fuctions $g$ and $f$ are the same as defined in Equations 15, 16 (Olivella and Gens, 2002).

${\dot{\mathit{\epsilon }}}_{\mathit{D}\mathit{C}}=\frac{\mathbf{1}}{{\mathit{\eta }}_{\mathit{D}\mathit{C}}^{\mathit{d}}}{\mathit{\Phi }}_{\mathit{D}\mathit{C}}\left({\mathit{F}}_{\mathit{D}\mathit{C}}\right)\frac{\mathit{\partial }{\mathit{G}}_{\mathit{D}\mathit{C}}}{\mathit{\partial }{\mathit{\sigma }}^{\prime }}(17)$

${\mathit{F}}_{\mathit{D}\mathit{C}}={\mathit{G}}_{\mathit{D}\mathit{C}}=\sqrt{{\mathit{q}}_{\mathit{D}\mathit{C}}^{\mathbf{2}}+{\left(\frac{-\mathit{p}}{{\mathit{\alpha }}_{\mathit{p}}}\right)}^{\mathbf{2}}}(18)$

${\mathit{\Phi }}_{\mathit{D}\mathit{C}}\left({\mathit{F}}_{\mathit{D}\mathit{C}}\right)={\mathit{F}}_{\mathit{D}\mathit{C}}^{\mathit{n}}(19)$

${\mathit{\alpha }}_{\mathit{p}}={\left(\frac{{\mathit{\eta }}_{\mathit{D}\mathit{C}}^{\mathit{v}}}{{\mathit{\eta }}_{\mathit{D}\mathit{C}}^{\mathit{d}}}\right)}^{\frac{\mathbf{1}}{\mathbf{1}+\mathit{n}}}(20)$

$\frac{\mathbf{1}}{{\mathit{\eta }}_{\mathit{D}\mathit{C}}^{\mathit{v}}}=\mathit{A}\left(\mathit{T}\right){\mathit{g}}_{\mathit{D}\mathit{C}}^{\mathit{v}}\left(\mathit{e}\right)(21)$

$\frac{\mathbf{1}}{{\mathit{\eta }}_{\mathit{D}\mathit{C}}^{\mathit{d}}}=\mathit{A}\left(\mathit{T}\right){\mathit{g}}_{\mathit{D}\mathit{C}}^{\mathit{d}}\left(\mathit{e}\right)(22)$

${\mathit{g}}_{\mathit{D}\mathit{C}}^{\mathit{v}}\left(\mathit{e}\right)=\mathbf{3}{\left(\mathit{g}-\mathbf{1}\right)}^{\mathit{n}}\mathit{f}(23)$

${\mathit{g}}_{\mathit{D}\mathit{C}}^{\mathit{d}}\left(\mathit{e}\right)={\left(\frac{\sqrt{\mathbf{1}+\mathit{g}+{\mathit{g}}^{\mathbf{2}}}}{\mathbf{3}}\right)}^{\mathit{n}-\mathbf{1}}\left(\frac{\mathbf{2}\mathit{g}+\mathbf{1}}{\mathbf{3}}\right)\mathit{f}+\frac{\mathbf{1}}{\sqrt{\mathit{g}}}(24)$

$\mathit{A}\left(\mathit{T}\right)={\mathit{A}}_{\mathit{A}}\mathbf{exp}\left(-\frac{{\mathit{Q}}_{\mathit{A}}}{\mathit{R}\mathit{T}}\right)(25)$

where $F_{DC}$ is the stress function, $G_{DC}$ is the flow rule, ${\mathrm{\Phi }}_{DC}$ is a scalar function, $n$ is the scaling exponent of the rock salt power law, $g_{DC}^v$ and $g_{DC}^d$ are non-linear functions of void ratio, $A_A$ is a pre-exponential parameter and $Q_A$ is the activation energy. The deviatoric stress $q_{DC}$ is defined as:

${\mathit{q}}_{\mathit{D}\mathit{C}}={\left(\mathbf{3}{\mathbf{J}}_{\mathbf{2}}\right)}^{\mathbf{0.5}}(26)$

with ${\mathrm{J}}_2$ the second invariant of the deviatoric part of the stress tensor.

2.4 Grain rearrangement

The term for grain rearrangement was added for simulating the irreversible processes of grain displacement during compaction taking place mainly at high porosities and under fast loads. This part is added to describe the behaviour of crushed salt as loose aggregate. In its loose state crushed salt is assumed to behave sand-like. Such material behaviour is described by a critical state approach which is based on a yield surface. Due to expansion of the yield surface, bond creation and densification of the crushed salt material is modelled. An important feature is that the hardening of the crushed salt is mainly driven by creep deformations (Equations 27–33) (Olivella and Gens, 2002). The basic equations are the following (Equations 27–33) (Olivella et al., 2023):

${\dot{\mathit{\epsilon }}}_{\mathit{G}\mathit{R}}=\mathit{\Gamma }〈{\mathit{\Phi }}_{\mathit{G}\mathit{R}}\left({\mathit{F}}_{\mathit{G}\mathit{R}}\right)〉\frac{\mathit{\partial }{\mathit{G}}_{\mathit{G}\mathit{R}}}{\mathit{\partial }\mathit{\sigma }}(27)$

$\mathit{\Phi }\left({\mathit{F}}_{\mathit{G}\mathit{R}}\right)={\mathit{F}}_{\mathit{G}\mathit{R}}^{\mathit{m}}(28)$

$\mathit{G}=\mathit{F}=\sqrt{{\mathit{q}}_{\mathit{G}\mathit{R}}^{\mathbf{2}}-{\mathit{\delta }}^{\mathbf{2}}\left({\mathit{p}}_{\mathbf{0}}{\mathit{p}}^{\prime }-{{\mathit{p}}^{\prime }}^{\mathbf{2}}\right)}(29)$

$\mathit{\Gamma }={\mathit{\Gamma }}_{\mathbf{0}}\mathbf{exp}\left(\frac{-{\mathit{Q}}_{\mathit{G}\mathit{R}}}{\mathit{R}\mathit{T}}\right)(30)$

$\mathit{\delta }=\frac{\mathbf{6}\mathbf{sin}\left({\mathit{\varphi }}^{\prime }\right)}{\mathbf{3}-\mathbf{sin}\left({\mathit{\varphi }}^{\prime }\right)}(31)$

$\mathit{d}{\mathit{p}}_{\mathbf{0}}={\mathit{p}}_{\mathbf{0}}\frac{\mathbf{1}+\mathit{e}}{\mathit{{\rm X}}}\mathit{d}{\mathit{\epsilon }}_{\mathit{v}\mathit{o}\mathit{l}}(32)$

where ${\mathrm{\Phi }}_{GR}$ is the stress function, $F_{GR}$ is the viscoplastic yield function, $〈〉$ are Macauley brackets, $G_{GR}$ is the flow potential, $\mathrm{\Gamma }$ is the fluidity, $m$ is the stress exponent, $\delta$ is the slope of the critical state line, $p_0$ is a hardening parameter, ${\mathrm{\Gamma }}_0$ is the initial value of the fluidity, $Q_{GR}$ is the activation energy, ${\epsilon }_v$ is the volumetric strain, $\mathrm{{\rm X}}$ is a parameter in the hardening law, and the invariant $q_{GR}$ is described in terms of octahedral stress:

$\begin{array}{ll}\hfill {\mathit{q}}_{\mathit{G}\mathit{R}}& =\frac{\mathbf{3}}{\sqrt{\mathbf{2}}}{\mathit{\tau }}_{\mathit{o}\mathit{c}\mathit{t}}\hfill \\ \hfill & =\frac{\mathbf{1}}{\sqrt{\mathbf{2}}}\sqrt{{\left({\mathit{\sigma }}_{\mathit{x}}-{\mathit{\sigma }}_{\mathit{y}}\right)}^{\mathbf{2}}+{\left({\mathit{\sigma }}_{\mathit{y}}+{\mathit{\sigma }}_{\mathit{z}}\right)}^{\mathbf{2}}+{\left({\mathit{\sigma }}_{\mathit{z}}+{\mathit{\sigma }}_{\mathit{x}}\right)}^{\mathbf{2}}+\mathbf{6}\left({\mathit{\tau }}_{\mathit{x}\mathit{y}}^{\mathbf{2}}+{\mathit{\tau }}_{\mathit{y}\mathit{z}}^{\mathbf{2}}+{\mathit{\tau }}_{\mathit{z}\mathit{x}}^{\mathbf{2}}\right)}\hfill \end{array}(33)$

3 Improvement approach

3.1 Problem formulation

For developing a crushed salt constitutive model, it is a common approach to derive an idealized geometry and deformation mechanisms from microstructural observations (Olivella, 1994). This approach lacks some generality since grains deform in a non-regular way during the compaction and a constantly regular arrangement cannot be expected. Deformation mechanisms like dislocation creep (grain breakage, plastic deformations) and humidity creep (dissolution and precipitation) dominate under different conditions and act not uniform on a grain (Hansen et al., 2014).

The creep models in CODE_BRIGHT for FADT and DC are based on a geometry dependent formulation, expressed in terms of void ratio (Olivella, 1994). The functions $g$ and $f$ (Equations 15, 16) are related to the characteristic sizes derived from the idealized geometry (Figure 3) and yield the auxiliary functions $g_{FADT}^v,g_{FADT}^d,g_{DC}^v$ and $g_{DC}^d$. These functions can be plotted for their dependence on void ratio as shown in Figure 4.

Figure 4

Figure 4. Auxiliary functions for DC and FADT mechanisms. v = volumetric, d = deviatoric. Modified after Olivella and Gens (2002).

Within the KOMPASS projects, benchmark calculations of long-term triaxial compaction tests on crushed salt were performed using the model implemented in CODE_BRIGHT and presented above. The reproduction of compaction was not satisfactory for both volumetric and deviatoric deformation, as well as their deformation rates (Friedenberg et al., 2023; Friedenberg and Olivella, 2024). Especially, for the creep contribution, which is the most important process in the long-term for porosity and permeability reduction, the accordance between numerical results and experimental data is weak. The example is shown in Section 4.1. Based on this work an idea for the modification of the crushed salt model in CODE_BRIGHT is developed aiming to improve the numerical simulation of crushed salt compaction.

3.2 Modification

The modification approach addresses the prescription of an idealized geometry for the creep models. To give some flexibility in the handling of the geometrical basis, it is proposed to formulate $g_{DC}^v$ and $g_{DC}^d$ in terms of phenomenological functions. The combination of a microstructural basis with phenomenological functions allows the inclusion of both microstructural observations and experimental experiences from triaxial compaction tests.

Since the long-term compaction tests considered in the recent work of the KOMPASS projects were executed on dry crushed salt, the FADT mechanism is assumed to have no or at least a minor effect on the compaction behavior. Therefore, this modification approach focuses on the dislocation creep mechanism.

From the shape of $g_{DC}^v$ and $g_{DC}^d$ as implemented in CODE_BRIGHT, an exponential formulation was found to build the basis for the phenomenological functions:

${\mathit{g}}_{\mathit{D}\mathit{C}}^{\mathit{v}}=\mathit{exp}\left(\mathit{a}*{\mathit{e}}^{\mathit{b}}\right)-\mathbf{1}(34)$

${\mathit{g}}_{\mathit{D}\mathit{C}}^{\mathit{d}}=\mathit{exp}\left(\mathit{c}*{\mathit{e}}^{\mathit{d}}\right)(35)$

where $e$ is the void ratio and $a,b,c$ and $d$ are parameters.

The parameters $a,b,c$ and $d$ do not have a specific physical meaning and cannot be measured during experiments. However, experimental data from standard triaxial compaction tests can be used to calibrate the proposed phenomenological functions and determine the parameters $a,b,c$ and $d$. Therefore, measured volumetric and deviatoric strain rates must be considered, respectively. An example for the calibration process is shown in the following section.

4 Application

The modification of $g_{DC}^v$ and $g_{DC}^d$ in the dislocation creep model was applied in a simulation of a triaxial long-term compaction test and compared to an initial simulation without this modification.

The triaxial compaction test considered here is the TUC-V2 that was executed in framework of the KOMPASS projects and comprises various level of mean stress, deviatoric load cycles and temperature changes (Friedenberg et al., 2024). The tested salt is the lately defined KOMPASS reference material (Czaikowski et al., 2020) representing a bedded Zechstein formation in the middle of Germany. The crushed salt sample had an initial water content of 0.5 w.-% and an initial porosity of 0.167. Figure 5A presents the load history lasting about 750 days and Figure 5B shows the axisymmetric numerical model.

Figure 5

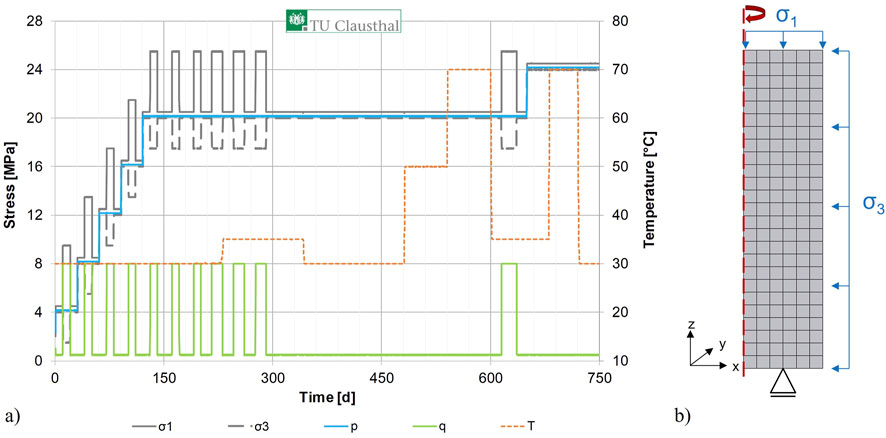
Figure 5. Triaxial long-term compaction test TUC-V2. (A) Loading history. (B) Numerical model and grid (Friedenberg and Olivella, 2024).

In a first step, the available constitutive model is applied, and the parameters are calibrated against the experimental data. The second step includes the modification of the constitutive model and again the simulation of the long-term compaction test. The results of both simulations are compared and discussed.

4.1 Initial simulation

Initially, the available model was calibrated against the experimental data. The simulation was executed in a THM-coupled approach following the stress history given in Figure 5. Thermal processes are based on Fourier’s law, for the hydraulics one phase flow with a constant gas pressure of $P_g$ = 0.1 MPa is assumed and the mechanics are based on the crushed salt model described before. Based on an existing parameter set, the calibration process was performed in combination with a parameter sensitivity to identify the most suitable parameter combination for the simulation of the TUC-V2 test. Detailed information on the sensitivity and calibration procedure can be found in Czaikowski et al. (2020) and Friedenberg et al. (2024). Table 1 gives an overview of the parameters elaborated during calibration. The majority of the parameters are physically based and can be derived from the material itself. Crushed salt is studied for several decades. The significant parameters in the calibration process are part of the dislocation creep (parameter $A_A$) and the grain rearrangement (parameters ${\mathrm{\Gamma }}_0,p_0,\mathrm{{\rm X}}$) models. Due to the lately definition of the KOMPASS reference material and the consequent limited experimental database, the derivation of material specific model parameters is still in progress. Therefore, the calibration process was applied with the aim to keep the parameters in a realistic and meaningful range. This means for parameters with physical meaning to vary them within observed ranges for crushed salt material (e.g., the pre-exponential parameter $A_A$ describes the creep ability, therefore values for different salt formations are available) and for the other parameters to vary them with respect to the conceptual idea and their dependences. The parameter dependences of various combinations are investigated by performing the sensitivity analysis.

Table 1

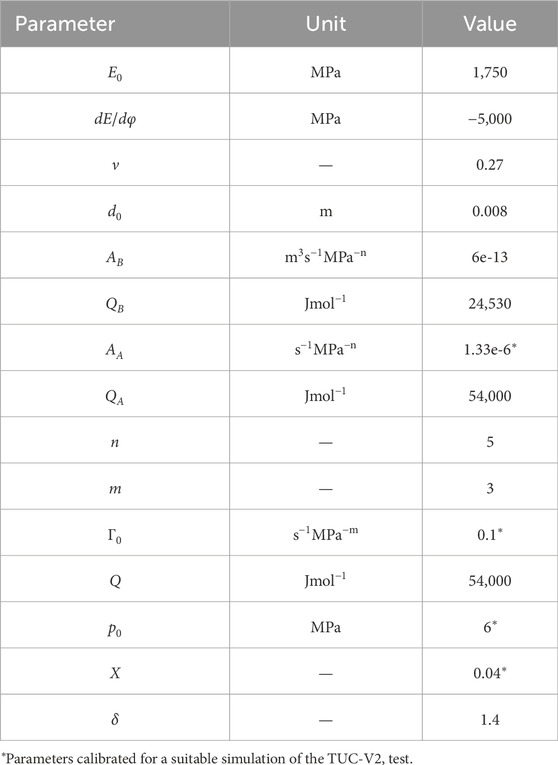
Table 1. Parameters for the simulation of triaxial compaction test TUC-V2 (Friedenberg et al., 2024).

The comparison in Figure 6 shows clear differences between the experimental data and the numerical results. The volumetric compaction is strongly underestimated by the simulation, especially the compaction under the constant mean stress of 20 MPa. The final values for volumetric compaction differ by 3.5%. In contrast, the deviatoric strain is overestimated. The model response to the increase and decrease of deviatoric stress is higher compared to the experimental data. However, the final values for deviatoric strain just differ by 1%.

Figure 6

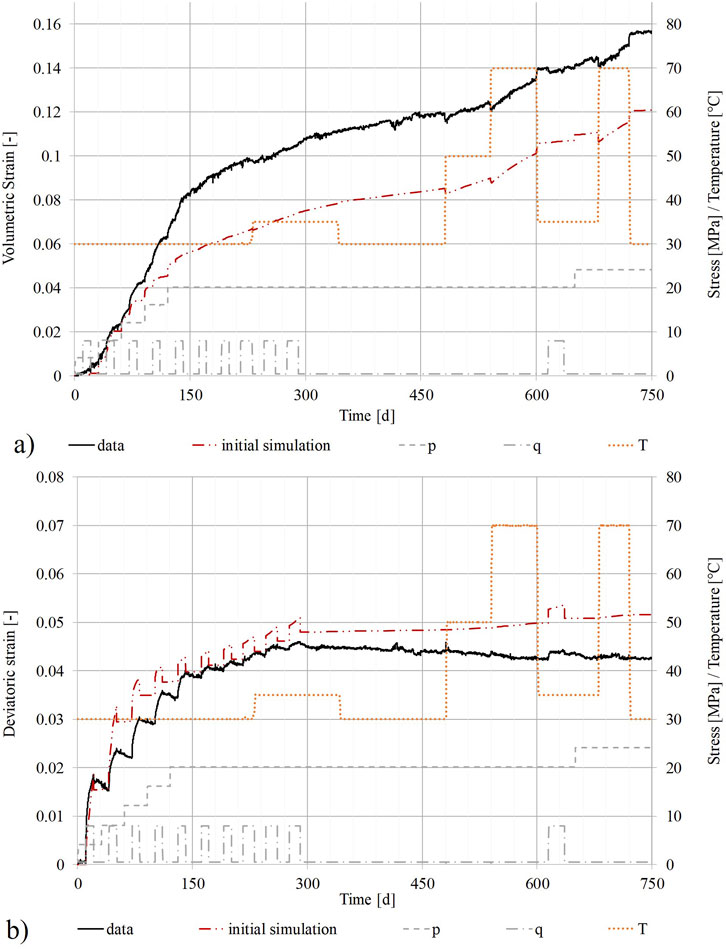
Figure 6. Comparison of measurements for TUC-V2 versus the initial simulation results. (A) volumetric strain. (B) deviatoric strain.

An improvement due to a broader calibration with reasonable parameter ranges could not be achieved, thus the modification approach was developed.

4.2 Modified simulation

The modified approach was developed in the way that Equations 34, 35 can be calibrated against experimental data by using the experimental strain rate data transformed to be comparable with the function values of the $g_{DC}^v$ and $g_{DC}^d$ functions. As a first attempt the volumetric equation $g_{DC}^v$ was calibrated. Considering the experimental data in Figure 7A the trend can be approximated by the choice of parameters $a$ and $b$. For the deviatoric function $g_{DC}^d$ calibration was not performed in this first step and default values are taken (Figure 7B). The corresponding values for the parameters $a,b,c$ and $d$ are shown in Table 2.

Figure 7

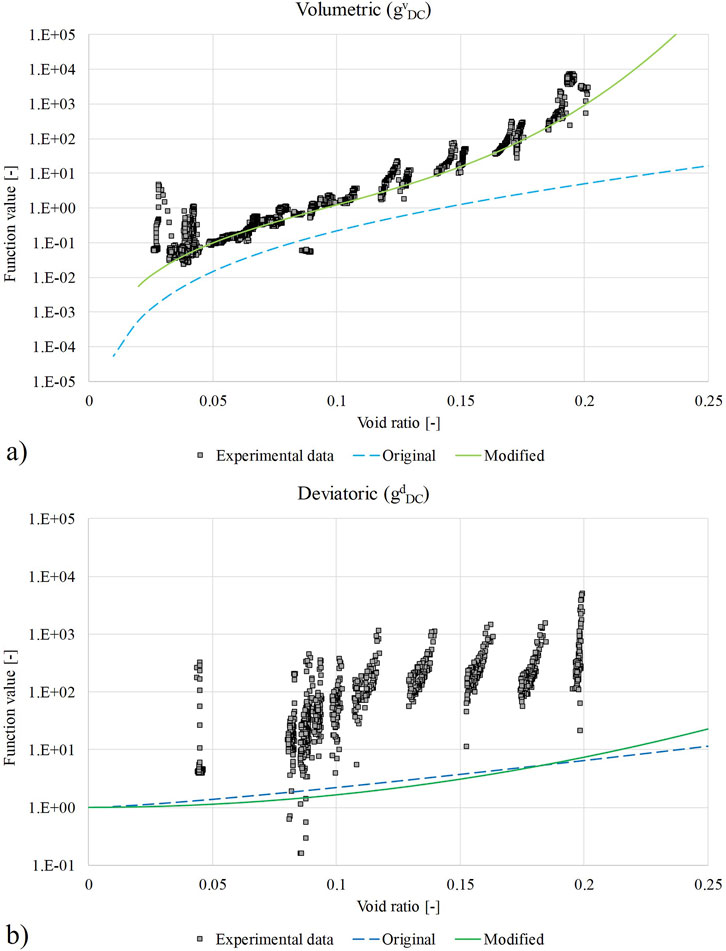
Figure 7. Modified and original functions and experimental data for the geometrical dependencies. (A) Volumetric function $g_{DC}^v$, modified function calibrated against experimental data. (B) Deviatoric function $g_{DC}^d$, default modified function.

Table 2

Table 2. Values for the parameters $a,b,c$ and $d$.

A new simulation with the modified functions and parameters as shown in Table 2 was performed. Due to the calibration of the modified function $g_{DC}^v$ against the experimental data an overall improvement of the numerical results is achieved (Figure 8). The evolution of volumetric strain is reproduced satisfactorily. Now the compaction due to the high mean stress of 20 MPa is captured and the whole volumetric compaction evolution is simulated well. The reproduction of the deviatoric strain evolution shows also improvements. The final value for deviatoric strain is met well. However, the response in deviatoric strain to deviatoric load changes is still overestimated by the model.

Figure 8

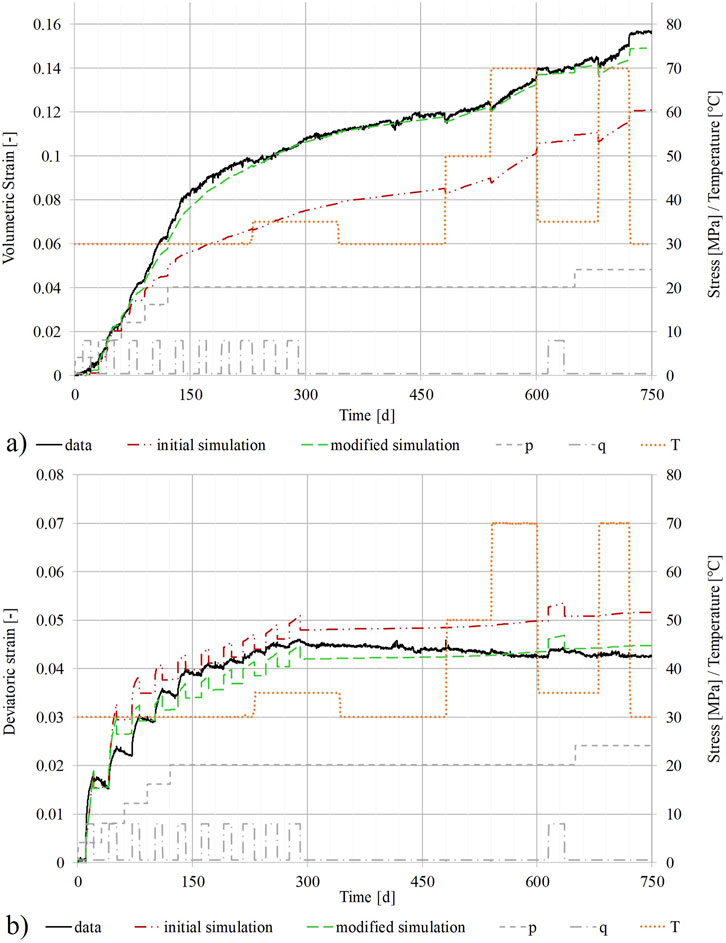
Figure 8. Comparison of experimental data for the TUC-V2 test versus numerical results for the initial simulation and the simulation with the modified functions. (A) Volumetric strain. (B) Deviatoric strain.

A further quantification can be realized by considering the strain rates. Figure 9A show the volumetric strain rates for both simulations, the initial and the modified, compared to the experimental data. The modified simulation shows an improved accordance for the volumetric strain rates during the rapid load changes in the beginning of the test. Up to 300 days the numerical strain rates hardly differ from each other. Figure 9B show the deviatoric strain rates. Only slight differences in the numerical results can be observed for the first 300 days, along with a higher accordance of the modified rates with the data. In both simulations, the strain rates are strongly overestimated at the start of the test. From 300 days on no significant difference between the trend of the numerical results is identifiable.

Figure 9

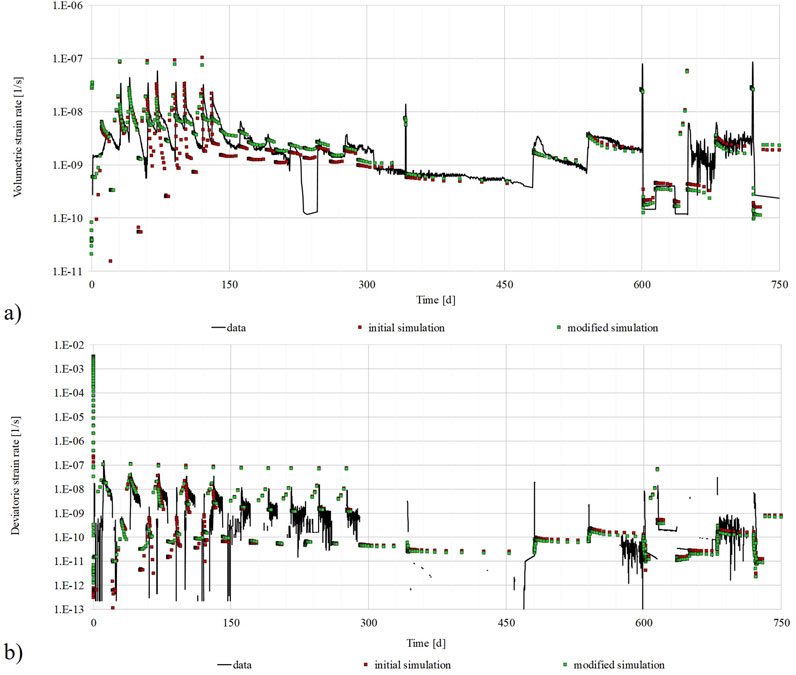
Figure 9. Comparison of experimental data for the TUC-V2 test versus numerical results for the initial simulation and the modifed simulation. (A) Volumetric strain rate, (B) Deviatoric strain rate.

4.3 Discussion

In general, the results show an improvement for the simulation of crushed salt compaction by using the modified functions $g_{DC}^v$ and $g_{DC}^d$. Already with the calibration of the volumetric part, the volumetric compaction is simulated in an adequate manner and the deviatoric strain is reasonably reproduced in its magnitude.

The calibration for the deviatoric part provides some open questions. The experimental data for deviatoric strain shows a large scattering over the function values, leading to difficulties in the calibration process (Figure 7B). The data trend is not straight forward as it is for the volumetric strain. Reasons might be traced back to the execution of the test with short durations of deviatoric stress (10 days) and therefore a wide range of strain rates due to the rapid load changes.

5 Sensitivity

For the new approach sensitivity studies are performed. First, a one-factor-at-a-time sensitivity is presented to show the influence of the newly implemented parameters c and d on deviatoric strain. Then the Morris method is applied to investigate the influence of the individual parameters a, b, c and d on volumetric and deviatoric strain. In the last step, a coupled parameter sensitivity is shown for the influence of the main parameters on volumetric strain and deviatoric strain, respectively.

5.1 One-factor-at-a-time sensitivity for the deviatoric part

Figure 10 presents simple one-factor-at-a-time variations of $c$ and $d$. By choosing $c$ = 200 (Figure 10A) a good calibration of the modified $g_{DC}^d$ function on experimental data is achieved. However, the corresponding model response in Figure 10C shows a rapid increase in deviatoric strain and a complete overestimation. Setting $d$ = 1.5 the function $g_{DC}^d$ is calibrated against the lower bound of the experimental data (Figure 10B). Here, the model response also shows an overestimation of the deviatoric strain. All in all, the default values ($c$ = 50, $d$ = 2) yield the best reproduction of the deviatoric strain in comparison to the measurements (Figure 10D).

Figure 10

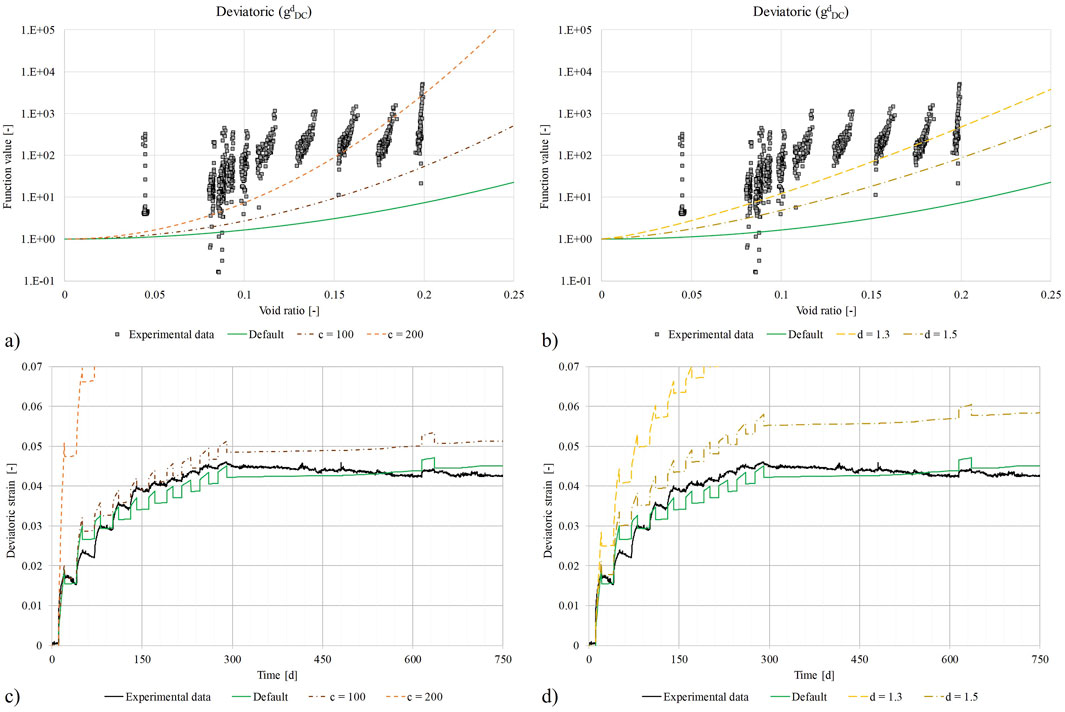
Figure 10. One-factor-at-a-time variations of the parameters $c$ and $d$. (A) Calibration for parameter $c$ against experimental data. (B) Calibration of parameter $d$ against experimental data. (C) Measurements vs. simulations with two values for $c$. (D) Measurements vs. simulations with two values for $d$.

In general, the model response to changes in deviatoric stress is strongly overestimated (Figures 10C, D). In former research work, deviatoric stress and strain represented a minor part. They predominantly focused on mean stress and isotropic compaction conditions (Kröhn et al., 2017). However, in recent crushed salt projects, the need for the investigation of deviatoric stress influence on the compaction was highlighted (Friedenberg et al., 2024).

The presented simulation results indicate an overall need to focus on the simulation of deviatoric stresses with the constitutive model available in CODE_BRIGHT. The consistent strain overestimation in response to the deviatoric load changes might be a general issue but is not part of this modification approach.

5.2 Morris method

The Morris method (Morris, 1991) was used to determine which of the input parameters may have the largest effect within the simulation of the triaxial compaction test TUC-V2. The idea was to use a factor’s screening method to determine the weighted effect of changes in the parameter values. Therefore, the Morris method is based on a “one-factor-at-a-time” approach yielding the global sensitivity by performing a series of local changes at different points in a predefined parametric state-space (Saltelli et al., 2004).

The analysis was carried out by using the Julia programming language (Bezanson et al., 2017). Julia’s in-built capabilities for distributed computing were used to conduct the Morris sensitivity analysis with a simple Monte-Carlo sampling strategy on various workers in parallel. The sampling was performed within the deterministic predefined parametric state-space ($a$ in [100, 1,500], $b$ in [3, 5], $c$ in [50, 200] and $d$ in [2, 5]) and the Morris means are calculated for each parameter. To derive the weighted effect of each parameter, the respective Morris means are divided by the sum of the means.

As indicators for the performance evaluation, the volumetric strain (${\epsilon }_{vol}$) and deviatoric strain (${\epsilon }_{dev}$) are chosen (Figure 11). The results of these analyses show a high influence of the exponent $b$ on the volumetric strain followed by the pre-exponent parameter $a$. For the deviatoric strain, the evolution depends strongly on the exponent $d$ and on the pre-exponential parameter $c$. There is a small influence of the two deviatoric parameter $c$ and $d$ on the volumetric strain and the two volumetric parameters on the deviatoric strain resulting from the formulation of the dislocation creep law (Equations 17–26).

Figure 11

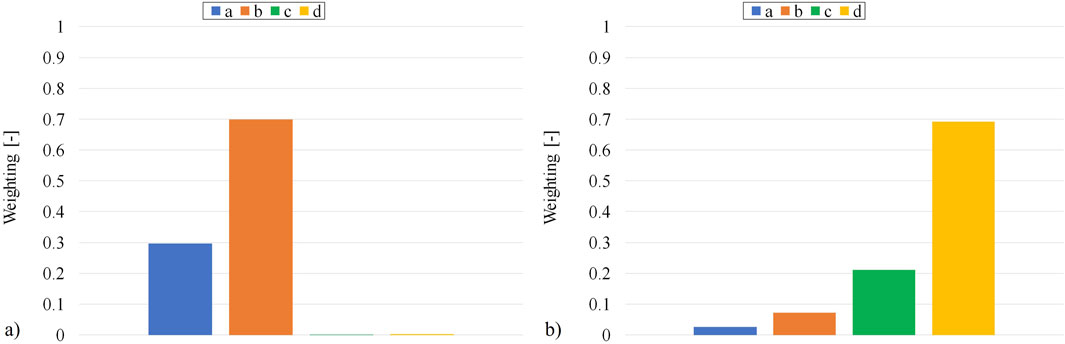
Figure 11. Morris sensitivity for the parameters of the modified approach. (A) Sensitivity for the volumetric strain. (B) Sensitivity for the deviatoric strain.

5.3 Coupled parameter sensitivity

In this analysis, the influence of the main parameters on the respective output quantity is investigated. As shown in the previous section with the Morris method, the volumetric strain output is primarily influenced by the parameters $a$ and $b$ (Equation 34) and the deviatoric strain output is primarily influenced by the parameters $c$ and $d$ (Equation 35).

The analysis was conducted by using an adaptive sparse-grid collocation method (see, e.g., Gates and Bittens (2015)) implemented by the open-source project DistributedSparseGrids.jl (Bittens and Gates, 2023) in the Julia programming language. Hereby, a hierarchical Lagrangian basis enables the adaptive refinement of the parametric model in areas with high effect on the output quantity.

The influence on the volumetric strain for $a$ in [100, 1,500] and $b$ in [2, 5] is shown in Figure 12A. Increasing the exponent $b$ leads to a decrease in the volumetric strain (less compaction), thus the material response is stiffer. The pre-exponential parameter a has a small effect on the volumetric strain output, however, with increasing value of an increase in volumetric strain is observed.

Figure 12

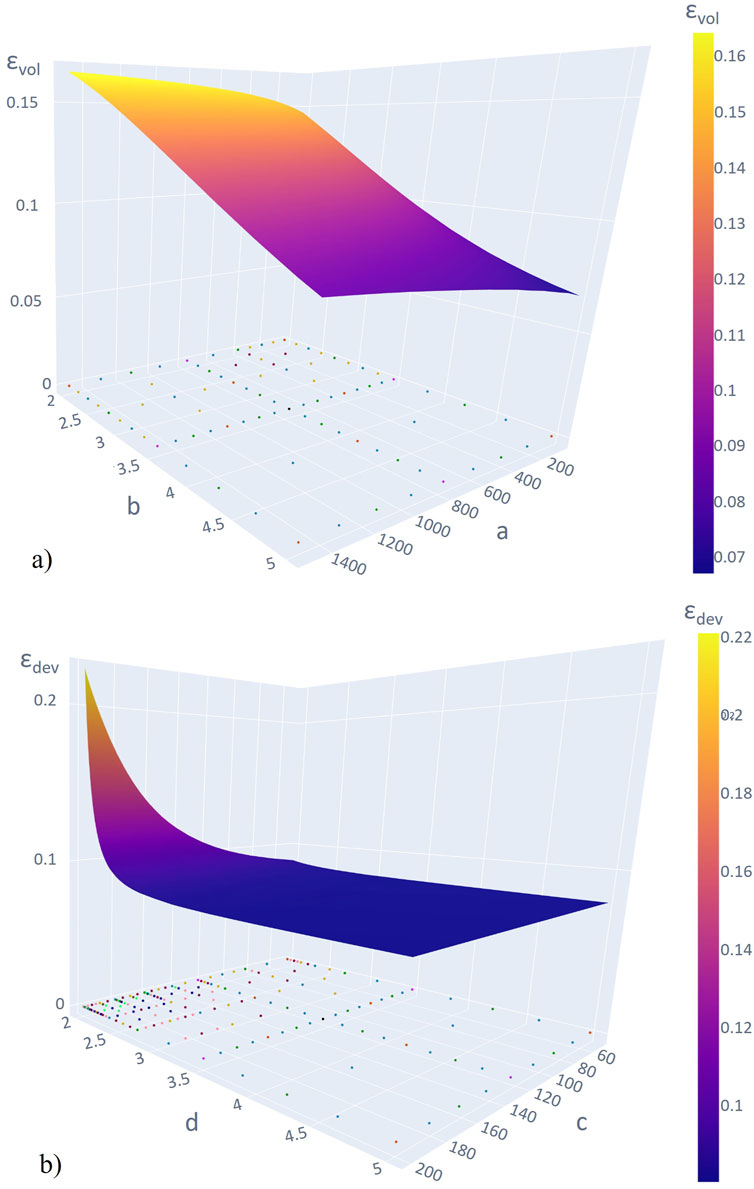
Figure 12. Coupled parameter sensitivity. (A) Sensitivity of parameters $a$ and $b$ on the volumetric strain. (B) Sensitivity of the parameters $c$ and $d$ on the deviatoric strain. The dots show the sampling.

The response of deviatoric strain for $c$ in [50, 200] and $d$ in [2, 3] is shown in Figure 12B. The plot shows nearly no change in deviatoric strain over a wide range of parameters. Only a small number of parameter combinations in the left corner of the plot leads to a sensitive response of the deviatoric strain. The boundaries for this sensitive area can be defined by $c$ > 100 and $d$ < 2.5.

Table 3 presents absolute values for volumetric and deviatoric strains for the interval boundary parameter combinations.

Table 3

Table 3. Output values for different parameter combinations.

6 Conclusion and outlook

This paper presents an approach for the modification of the dislocation creep law in CODE_BRIGHT with the aim of improving the numerical reproduction of crushed salt compaction processes. The approach addresses the stiff geometrical basis of the constitutive model and aims at a more flexible formulation. The two non-linear functions $g_{DC}^v$ and $g_{DC}^d$ which are derived from the idealized geometry assumption are re-formulated to be calibrated against experimental data available from triaxial long-term compaction tests.

Up to date there is no complete consensus on formulating constitutive models. The newly proposed combination of a microstructural basis with phenomenological functions shows an improvement in the numerical simulation of crushed salt compaction by simulating the triaxial long-term compaction test TUC-V2. The volumetric compaction was reproduced adequately both in the absolute values as well as in the volumetric strain rates. An enhancement in results was also achieved for the deviatoric strain and deviatoric strain rates.

Sensitivity approaches are presented to verify the new implementation. By applying the Morris method for parameter screening the sensitivities of the volumetric and deviatoric strain output to the parameters are shown. The result confirms the original idea of the modification approach and confirms the correct implementation of the parameters. Due to the coupled parameter sensitivity the evolution of the respective strain output within a defined parameter space is shown. This analysis gives an idea about the ideal parameter combination.

However, some open questions still occur. The calibration of the modified deviatoric function $g_{DC}^d$ against the experimental data does not lead to an improvement in the numerical results, other than the calibration for the volumetric function. In this course, a general question occurred regarding the simulation of deviatoric strains. The response to deviatoric load changes is permanently overestimated. It has to be mentioned that deviatoric strains in crushed salt are rarely investigated and not much experimental data is available. Future research will focus on the handling of deviatoric stresses in laboratory and on the implementation of deviatoric strains in the constitutive model. In ongoing research, the presented approach will be continuously analyzed for its advantages and shortcomings, calibrated to a greater extent of experimental data and compared to other constitutive models for crushed salt.

All in all, the presented approach builds a basis for improving the numerical simulation of crushed salt compaction processes. These improvements will help to reduce uncertainties and will strengthen the prognosis quality for the long-term safety analysis of a repository in rock salt by predicting the barrier properties of the crushed salt.

Data availability statement

Publicly available datasets were analyzed in this study. This data can be found here: https://www.grs.de/de/aktuelles/publikationen/grs-751.

Author contributions

LF: Investigation, Project Administration, Visualization, Writing–original draft, Writing–review and editing. SO: Methodology, Software, Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The publication of this article is supported by the MEASURES project (FKZ 02E12214A-D) funded by the German Federal Ministry for Environment, Natural Conservation, Nuclear Safety and Consumer Protection (BMUV).

Acknowledgments

The authors would like to thank the KOMPASS family for fruitful discussions and providing the input, and Prof. Uwe Düsterloh for his support. Special thanks go to Maximilian Bittens for the supportive collaboration with the sensitivity evaluation.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Author Disclaimer

The work presented in this paper received scientific support (e.g., experimental data) from the KOMPASS-II project (FKZ 02E11951A-D) and the follow-up MEASURES project (FKZ 02E12214A-D), both funded by the German Federal Ministry for Environment, Natural Conservation, Nuclear Safety and Consumer Protection (BMUV). There is no financial dependence of the work presented on the KOMPASS projects and their follow-up MEASURES.

References

Bartol, J., and Vuorio, M. (2022). “Disposal of radioactive waste in rock salt: long-term research programme,” in The mechanical behavior of salt X: proceedings of the 10th conference on the mechanical behvaior of salt (SaltMech X), utrecht, The Netherlands, 06 - 08 july 2022. Editors J. de Bresser, M. R. Drury, P. A. Fokker, M. Gazzani, S. Hangx, A. R. Niemeijeret al. (London: CRC Press), 236–241.

CrossRef Full Text | Google Scholar

Bechthold, W., Rothfuchs, T., Poley, A., Ghoreychi, M., Heusermann, S., Gens, A., et al. (1999). Backfilling and sealing of underground repositories for radioactive waste in salt (BAMBUS project): final report. EUR Proj. Rep. - Nucl. Sci. Technol. EUR-19124-EN. Available at: http://bookshop.europa.eu/en/-pbCGNA19124/.

Google Scholar

Bechthold, W., Smailos, E., Heusermann, S., Bollingerfehr, W., Bazargan Sabet, B., Rothfuchs, T., et al. (2004). Backfilling and sealing of underground repositories for radioactive waste in salt (BAMBUS II project): final report, Europäische Kommission. EUR Nucl. Sci. Technol. Proj. Rep. EUR-20621-EN. Available at: http://bookshop.europa.eu/en/-pbKINA20621/.

Google Scholar

Bertrams, N., Bollingerfehr, W., Eickemeier, R., Fahland, S., Flügge, J., Frenzel, B., et al. (2020). RESUS - Grundlagen zur Bewertung eines Endlagersystems in flach lagernden Salzformationen. Ges. für Anlagen- Reakt. (GRS) gGmbH, GRS.

Google Scholar

Bezanson, J., Edelman, A., Karpinski, S., and Shah, V. B. (2017). Julia: a fresh approach to numerical computing. SIAM Rev. 59 (1), 65–98. doi:10.1137/141000671

CrossRef Full Text | Google Scholar

Bittens, M., and Gates, R. L. (2023). DistributedSparseGrids.jl: a Julia library implementing an Adaptive Sparse Grid collocation method. J. Open Source Softw. 8 (83), 5003. doi:10.21105/joss.05003

CrossRef Full Text | Google Scholar

Bollingerfehr, W., Bertrams, N., Buhmann, D., Eickemeier, R., Fahland, S., Filbert, W., et al. (2018). KOSINA: concept developments for a generic repository for heat-generating waste in bedded salt formations in Germany. BGE TECHNOLOGY GmbH. Available at: https://www.bge-technology.de/fileadmin/user_upload/FuE_Berichte/KOSINA-Project_Concept-developments-for-a-generic-repository-for-heat-generating-waste-in-bedded-salt-formations.pdf.

Google Scholar

Bundesgesellschaft für Endlagerung (2020). Sub-areas interim report pursuant to section 13 StandAG. Available at: https://www.bge.de/fileadmin/user_upload/Standortsuche/Wesentliche_Unterlagen/Zwischenbericht_Teilgebiete/Summary_Sub-areas_Interim_Report_barrierefrei.pdf (Accessed September 28, 2020).

Google Scholar

Czaikowski, O., Friedenberg, L., Wieczorek, K., Müller-Hoeppe, N., Lerch, C., Eickemeier, R., et al. (2020). KOMPASS: compaction of crushed salt for the safe containment. Ges. für Anlagen- Reakt. (GRS) gGmbH GRS-608.

Google Scholar

Friedenberg, L., Bartol, J., Bean, J., Beese, S., Bresser, J. H. B. de, Coulibaly, J. B., et al. (2024). KOMPASS-II, Compaction of crushed salt for safe containment—phase 2. GRS.Köln: Gesellschaft für Anlagen-und Reaktorsicherheit (GRS) gGmbH.

Google Scholar

Friedenberg, L., and Olivella, S. (2024). “Modification in the numerical modelling of crushed salt compaction processes, ” in Department of Civil and Environmental Engineering, UPC-Barcelona Tech, CIMNE (Eds.): Workshop of CODE_BRIGHT Users, Barcelona, May 24, 2024.

Google Scholar

Friedenberg, L., Olivella, S., and Düsterloh, U. (2023). Numerical analysis for the simulation of crushed salt compaction behavior: ARMA23-0341. 57th U.S. Rock Mechanics/Geomechanics Symposium: Atlanta.

Google Scholar

Gates, R. L., and Bittens, M. R. (2015). A multilevel adaptive sparse grid stochastic collocation approach to the non-smooth forward propagation of uncertainty in discretized problems. doi:10.48550/arXiv.1509.01462

CrossRef Full Text | Google Scholar

Hansen, F. D., Popp, T., Wieczorek, K., and Stührenberg, D. (2014). Granular salt summary: granular salt summary: reconsolidation principles and applications: fuel cycle research and development. Sandia National Laboratories. Available at: https://www.osti.gov/biblio/1164616.

Google Scholar

Kröhn, K.-P., Stührenberg, D., Jobmann, M., Heemann, U., Czaikowski, O., Wieczorek, K., et al. (2017). Mechanical and hydraulic behaviour of compacting crushed salt backfill at low porosities: project REPOPERM - phase 2, GRS- 450. Available at: http://www.grs.de/publikation/grs-450.

Google Scholar

Morris, M. D. (1991). Factorial sampling plans for preliminary computational experiments. Technometrics 33 (2), 161–174. doi:10.2307/1269043

CrossRef Full Text | Google Scholar

Olivella, S. (1994). Nonisothermal multiphase flow of brine and gas through saline media. Barcelona: Universitat Politècnica de Catalunya. Dissertation.

Google Scholar

Olivella, S., and Gens, A. (2002). 'A constitutive model for crushed salt. Int. J. Numer. Anal. Methods Geomechanics 26 (7), 719–746. doi:10.1002/nag.220

CrossRef Full Text | Google Scholar

Olivella, S., Gens, A., Carrera, J., and Alonso, E. E. (1993). “Behaviour of porous salt aggregates. Constitutive and field equations for a coupled deformation, brine, gas and heat transport model,” in Mechanical behavior of salt: 3rd conference; ecole Polytechnique, palaiseau - France, september 14 - 16, 1993. Editor M. Ghoreychi (Clausthal-Zellerfeld: TTP Trans Tech Publ), 255–269.

Google Scholar

Olivella, S., Vaunat, J., and Rodriguez-Dono, A. (2023). CODE_BRIGHT: user's guide (CODE_BRIGHT 2023_12)

Google Scholar

Saltelli, A., Tarantola, S., Campolongo, F., and Ratto, M. (2004). Sensitivity analysis in practice: a guide to assessing scientific models. Eur. EUR-20859-EN. Available at: http://www.loc.gov/catdir/description/wiley041/2003021209.html.

Google Scholar

Sandia National Laboratories (2014). Evaluation of options for permanent geological disposal of spent nuclear fuel and high-level radioactive waste: in support of a comprehensive national nuclear fuel cycle strategy. U.S. Department of Energy. Available at: https://www.energy.gov/sites/prod/files/2014/04/f15/DOE%20DispOptions%20R1%20Volume1%20Apr15.pdf.

Google Scholar

Schutjens, P. M. T. M. (1991). Intergranular pressure solution in halite aggregates and quartz sands: An experimental investigation = Intergranulaire drukoplossing in halietaggregaten en kwartszanden. Zugl. Utrecht, Rijksuniv. Diss. 1991. Available at: https://dspace.library.uu.nl/handle/1874/238558.

Google Scholar

Spiers, C. J., and Brzesowsky, R. H. (1993). “Densification behaviour of wet granular salt: theory versus experiment,” in Seventh symposium on salt. Editor H. Kakihana (Amsterdam: Elsevier), 83–92.

Google Scholar

Spiers, C. J., Peach, C. J., Brzesowsky, R. H., Schutjens, P. M. T. M., Liezenberg, J. L., and Zwart, H. J. (1989). Long-term rheological and transport properties of dry and wet salt rocks: final report. Nucl. Sci. Technol. EUR-11848-EN. Available at: https://publications.europa.eu/s/cYD1.

Google Scholar

Spiers, C. J., Urai, J. L., Lister, G. S., Boland, J. N., and Zwart, H. J. (1986). The influence of fluid-rock interaction on the rheology of salt rock: final report, Nuclear science and technology EUR 10399 EN. Available at: http://bookshop.europa.eu/en/-pbCDNA10399/.

Google Scholar

Wieczorek, K., Düsterloh, U., Heemann, U., Lerch, C., Lüdeling, C., Müller-Hoeppe, N., et al. (2017). Reconsolidation of crushed salt backfill - review of existing experimental database and constitutive models and need for future R&D work: DAEF statement.

Google Scholar

Nomenclature

$\mathit{a}$ parameter in the modification of $g_{DC}^v$ [-]

${\mathit{A}}_{\mathit{A}}$ pre-exponential parameter in DC [s^-1MPa^-n]

${\mathit{A}}_{\mathit{B}}$ pre-exponential parameter in FADT [m³/(s*MPa)]

$\mathit{b}$ exponent in the modification of $g_{DC}^v$ [-]

$\mathit{c}$ parameter in the modification of $g_{DC}^d$ [-]

${\mathit{C}}^{\mathit{e}}$ elastic compliance matrix [1/MPa]

$\mathit{d}$ exponent in the modification of $g_{DC}^d$ [-]

${\mathit{d}}_{\mathbf{0}}$ characteristic grain size [mm]

${\mathit{d}}_{\mathbf{0}}^{\mathbf{3}}$ solid volume [mm³]

$\mathit{e}$ void ratio [-]

$\mathit{E}$ Young’s modulus [MPa]

$\mathit{f},\mathit{g}$ functions of void ratio [-]

${\mathit{F}}_{\mathit{D}\mathit{C}}$ stress function in the DC model

${\mathit{F}}_{\mathit{G}\mathit{R}}$ viscoplastic yield function in the GR model

${\mathit{G}}_{\mathit{D}\mathit{C}}$ flow rule in the DC model

${\mathit{G}}_{\mathit{G}\mathit{R}}$ flow rule in the GR model

$\mathit{I}$ identity matrix [-]

${\mathbf{J}}_{\mathbf{2}}$ second invariant of the deviatoric stress tensor [MPa]

$\mathit{m}$ stress exponent in GR [-]

$\mathit{n}$ stress power in DC [-]

$\mathit{p},{\mathit{p}}^{\prime }$ mean stress (total and effective) [MPa]

${\mathit{p}}_{\mathbf{0}}$ hardening parameter in GR [MPa]

${\mathit{P}}_{\mathit{f}},{\mathit{P}}_{\mathit{l}},{\mathit{P}}_{\mathit{g}}$ fluid pressure, liquid pressure, gas pressure [MPa]

$\mathit{q}$ deviatoric stress [MPa]

${\mathit{q}}_{\mathit{D}\mathit{C}}$ deviatoric stress in DC [MPa]

${\mathit{q}}_{\mathit{G}\mathit{R}}$ deviatoric stress in GR [MPa]

${\mathit{Q}}_{\mathit{A}}$ activation energy in DC [J/mol]

${\mathit{Q}}_{\mathit{B}}$ activation energy in FADT [J/mol]

${\mathit{Q}}_{\mathit{G}\mathit{R}}$ activation energy in GR [J/mol]

$\mathit{R}$ ideal gas constant [J/(mol*K)]

$\mathit{s}$ void size [mm]

${\mathit{S}}_{\mathit{l}}$ liquid saturation [-]

$\mathit{T}$ temperature [K]

$\mathit{x}$ contact size [mm]

$\mathbf{\Gamma }$ fluidity [s^-1MPa^-m]

$\mathit{\delta }$ slope of the critical state line in GR [-]

${\mathit{\epsilon }}_{\mathit{d}\mathit{e}\mathit{v}}$ deviatoric strain [-]

${\mathit{\epsilon }}_{\mathit{v}\mathit{o}\mathit{l}}$ volumetric strain [-]

$\dot{\mathit{\epsilon }}$ strain rate [1/s]

${\dot{\mathit{\epsilon }}}_{\mathit{E}\mathit{L}}$ strain rate for contribution of EL [1/s]

${\dot{\mathit{\epsilon }}}_{\mathit{F}\mathit{A}\mathit{D}\mathit{T}}$ strain rate for contribution of FADT [1/s]

${\dot{\mathit{\epsilon }}}_{\mathit{D}\mathit{C}}$ strain rate for contribution of DC [1/s]

${\dot{\mathit{\epsilon }}}_{\mathit{G}\mathit{R}}$ strain rate for contribution of GR [1/s]

$\mathit{\phi }$ porosity [-]

$\mathit{\varphi }$ fiction angle [°]

${\mathbf{\Phi }}_{\mathit{D}\mathit{C}}$ scalar function for DC

${\mathbf{\Phi }}_{\mathit{G}\mathit{R}}$ stress function of GR

$\mathit{\sigma },{\mathit{\sigma }}^{\prime }$ stress (total and effective) [MPa]

${\mathit{\sigma }}_{\mathbf{1}}$ axial stress [MPa]

${\mathit{\sigma }}_{\mathbf{3}}$ radial stress [MPa]

$\mathit{\tau }$ shear stress [MPa]

$\mathit{{\rm X}}$ hardening parameter in GR [-]