Numerical modeling of wave-induced liquefaction around a gravity-based structure

Residual liquefaction, a significant issue in marine engineering, results from accumulated pore-water pressure in the seabed due to cyclic shear stresses, which compromises soil stability. This study aims to investigate residual liquefaction around gravity-based marine structures by means of a 2D numerical model. The model employs a two-step procedure: First, the stresses in the soil domain are determined via solving Biot equations, and subsequently the generation and diffusion of accumulated pore pressure in the soil is simulated by means of a pressure diffusion equation with a source term. The model was first validated against analytical solution for pore pressure buildup in the seabed under progressive waves, and against experimental data for residual liquefaction around a buried submarine pipeline. The results showed that the model can satisfactorily capture pore pressure buildup and residual liquefaction in the seabed around structures. Once validated, the model was utilized to model the pore-water pressure buildup and residual liquefaction potential around a caisson breakwater under the action of standing waves and the wave-induced rocking motion of the caisson, separately and in combination. Spatial distribution of liquefaction potential was determined in the seabed soil around the caisson with and without a bedding layer on the seabed. The model results revealed the critical role of the bedding layer in reducing liquefaction susceptibility under standing waves and rocking motion, and highlighted that the rocking motion alone poses a significant risk of inducing residual liquefaction in the seabed around the caisson.

1 Introduction

Gravity-based structures are a major type of structures in coastal and offshore engineering. These structures, such as caissons and block-type structures, are not only used for berthing purposes, but can also be utilized as breakwaters, especially when rock is not feasibly available for using as rubble-mound, or when the construction depth is too large for a sloped structure (Tsinker, 2012). In such conditions, caissons are viable alternatives to sloped breakwaters. However, seabed-structure interaction issues induced by waves and current, such as liquefaction and scour, can lead to failure of caisson structures (Sumer and Fredsøe, 2002). There are two types of mechanisms associated with wave-induced liquefaction: (1) momentary liquefaction, and (2) residual liquefaction. Momentary liquefaction is caused by the temporary upward-directed pressure gradient in the seabed soil under wave trough, and it can only affect a limited depth of the soil close to the midline (Sumer, 2014, Chp. 4). Residual liquefaction, on the other hand, occurs as a result of pore-water pressure buildup caused by re-arrangement of soil grains at the expense of pore volume, due to the cyclic shear deformations under wave loading (Sumer, 2014, Chp. 3). This paper focuses on residual liquefaction, where the soil loses its bearing capacity and behaves like a fluid mixture of soil and water. Momentary liquefaction is left out of the scope of the present study.

Residual liquefaction can result in catastrophic consequences. Buried marine structures such as sea mines, pipelines or cables may either sink into the seabed or float to the midline, causing total failure of these structures (Sumer et al., 1999; Damgaard et al., 2006b; Sumer et al., 2006a; Kirca, 2013; Sumer and Kirca, 2022). Likewise, gravity-based structures like caissons can tilt and/or sink into the seabed when the surrounding seabed soil is liquefied (De Groot et al., 2006b). As a remarkable example, Puzrin et al. (2010) reported that caissons of size $O(20m)$ had sunken into the seabed as deep as 7 m, and horizontally displaced as much as 5 m towards the offshore direction in Barcelona Harbor due to residual liquefaction. Another example where the last author acted as a consultant in the aftermath of the incident is that, during a storm event, seven caissons (originally planned to form the berth of a container terminal) placed temporarily about 700 m offshore, acting as a Mulberry harbor, were displaced seaward and embedded in the seabed (the average displacement being 22 m horizontally, and 4.5 m vertically), apparently due to wave-induced residual seabed liquefaction. Liquefaction related failures of marine structures, induced by waves (Sumer, 2006; Damgaard et al., 2006a; Sumer and Kirca, 2022) or earthquakes (De Groot et al., 2006a; Esfeh and Kaynia, 2019; Ju and Mao, 2024) are also encountered in offshore regions. A thorough coverage of the topic for aspects of both coastal and offshore structures can be found in Sumer (2014).

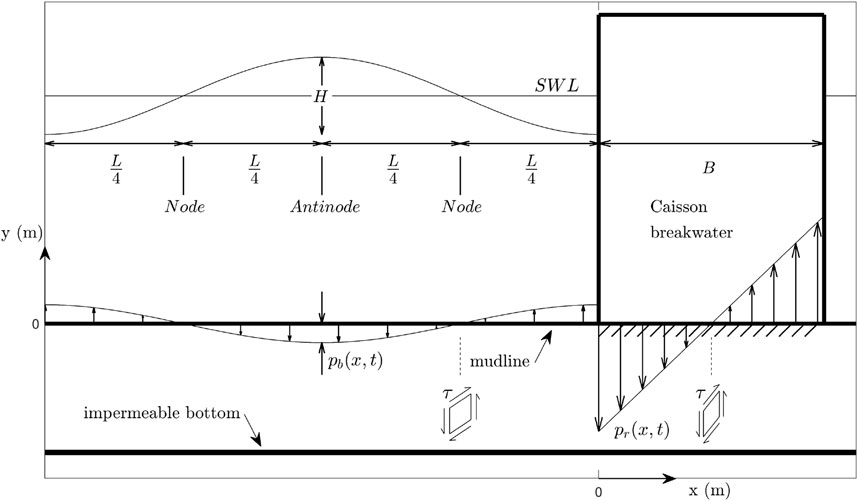
When caissons are subjected to non-breaking waves, the reflected waves from the caisson forms a standing wave profile in front of the caisson. The node location of the standing wave profile (located $L/4$ distance from the caisson edge, where $L$ is the wave length) is a “hotspot” for residual liquefaction since cyclic shear deformations are concentrated at this point (Kirca et al., 2013). Further to the standing waves, the alternating leeward and seaward wave force acting on the caisson under successive wave crests and troughs cause the caisson to rock and to induce cyclic shear deformations underneath the pivotal axis of rocking (Sumer et al., 2008). This additional mechanism causes a second hotspot for residual liquefaction, even more pronounced than the first one (Sumer, 2014, Chp. 8).

Seabed response around caisson breakwaters due to standing waves (Ulker et al., 2010; Duan et al., 2023) and breaking waves (Ulker et al., 2012) were studied in the recent past by means numerical models based on poroelastic behavior of seabed soil. However, the latter studies focused on the momentary liquefaction mechanism, and did not account for the pore-water pressure buildup or rocking of the caisson. For modeling pore-water pressure buildup due to cyclic loading and residual liquefaction, a mathematical model, based on the work of Sumer and Cheng (1999), was described in Sumer (2014), Section 3.2 in detail, which was also validated against experimental data by Sumer et al. (2012). It is to be noted that this model has recently been extended to 3D (Shanmugasundaram et al., 2022) as a part of the NuLIMAS project (a EU-funded research project conducted under the MarTERA programme), and modified so as to simulate the post-liquefaction behavior of seabed soil (Windt et al., 2024). It should also be further noted that here are several other studies in the literature, where the residual liquefaction was numerically modeled by means of a source term similar to that described in (Sumer, 2014, Chp. 3), implemented for 2D (Wang and Gao, 2014; Jeng and Zhao, 2015; Zhao et al., 2016a; Zhao et al., 2016b) and 3D (Li et al., 2011; Zhao et al., 2017; Cui and Jeng, 2021) soil domains.

In this study, the pore-water pressure buildup and residual liquefaction around a caisson breakwater due to standing waves as well as rocking of the caisson was numerically modeled for the first time in the literature. A 2D numerical model was implemented to model the seabed soil. The model has two components: First component solves the Biot equations to calculate the stresses in the soil domain, and the second component calculates the pore-water pressure buildup based on a pressure diffusion equation with a source term for pore-water pressure generation (Sumer, 2014; Section 3.2). First, the model results were validated against the experimental data of Sumer et al. (2006b). Then, the model was used to simulate residual liquefaction around a caisson breakwater due to standing waves, caisson rocking, and co-existence of both mechanisms. Additionally, the influence of a crushed-rock bedding layer placed under the caisson on the seabed in preventing pore-water pressure buildup was also investigated.

2 Materials and methods

2.1 Statement of the problem

The definition sketch is presented in Figure 1.

Figure 1

Figure 1. Definition sketch.

A caisson structure placed on the seabed is exposed to a standing wave. The pressure in excess of hydrostatic pressure acting on the seabed due to standing waves, $p_b(x,t)$, causes shear stresses and shear deformations in the soil, e.g., see the shear stress, $\tau$, and its associated shear deformation at the nodal section illustrated in Figure 1.

The caisson is, at the same time, subjected to rocking due to alternating landward and seaward wave forces, in-phase with the wave crest and troughs on the caisson, respectively, inducing a cyclic pressure on the seabed, $p_r(x,t)$. The latter causes cyclic shear stresses and shear deformations in the soil underneath the caisson (Figure 1).

These two “hotspots” are potential zones of liquefaction (Sumer, 2014, Chp. 8). In this paper, both of these mechanisms will be studied to reveal their potential contributions on the liquefaction potential of the seabed.

2.2 Methodology

The present numerical model comprises a two-step procedure to simulate the pore-water pressure buildup and initiation of residual liquefaction using the finite element method (FEM). In the first step, the stresses in the soil are computed by solving the quasi-static Biot equations, in which the soil is assumed to be a saturated poro-elastic medium (Biot, 1941) with pore-water behavior represented by Darcy’s law, and the inertia terms are neglected. In the second step, the buildup of pore-water pressure is simulated through a pressure diffusion equation with a source term for pore-water pressure generation to obtain the accumulated pore pressures $(\bar{p})$ (Sumer, 2014, Chp. 3). The model will then seek whether liquefaction occurs or not.

The onset of liquefaction is defined as the critical point at which the buildup of pore-water pressure $(\bar{p})$ exceeds the initial mean normal effective stress $({\sigma }_0^{\prime })$. This is expressed by the following liquefaction criterion:

$\text{Liquefaction\hspace{0.17em}criterion:\hspace{0.17em}}\frac{\bar{p}}{{\sigma }_0^{\prime }}\ge 1(1)$

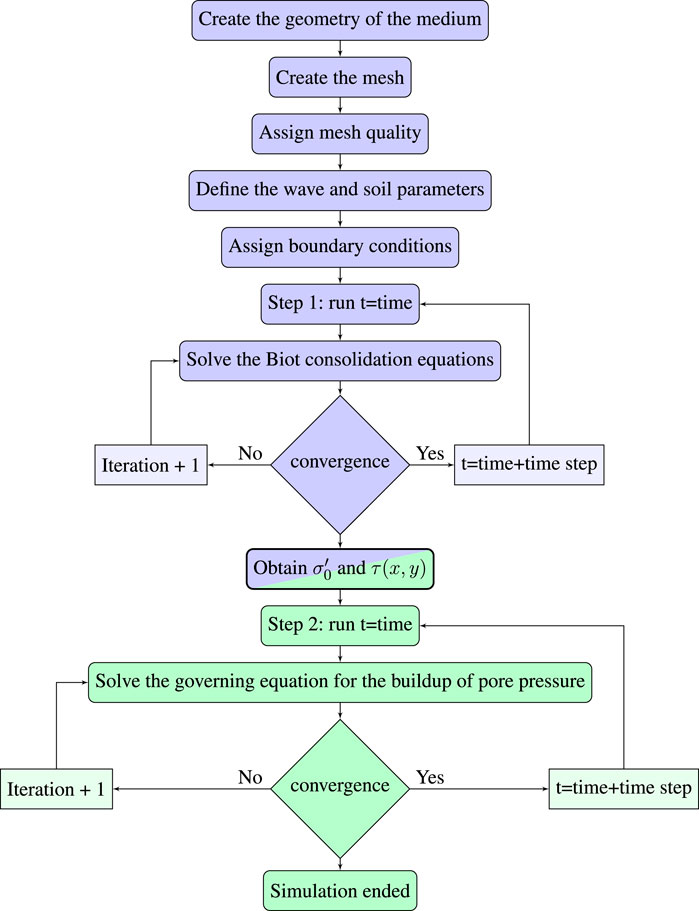
The solution procedure adopted in the model is detailed below.

2.2.1 Step 1

First off, the modeling starts with the initial settlement phase, which involves the placement of soil under static conditions, and waiting for the effective stresses in the soil (due to self-weight of the soil) to be established. Once the system attains to a state of equilibrium in terms of effective stresses after the initial settlement, the overburden due to the caisson is gradually applied and the soil domain is let to stabilize again in terms of additional effective stresses and settlements under to the weight of the caisson. After an equilibrium is reached, the distribution of initial mean normal effective stress across the soil domain, ${\sigma }_0^{\prime }(x,y)$, is calculated as described by Equation 2, ${\sigma }_{y0}^{\prime }$ being the initial vertical effective stress term at the equilibrium condition.

${\sigma }_0^{\prime }={\sigma }_{z_0}^{\prime }\left(\frac{1+2k_0}{3}\right)(2)$

Here, $k_0$ is the coefficient of lateral earth pressure. It should be noted that the initial mean normal effective stress $({\sigma }_0^{\prime })$ for undisturbed seabeds depends only on the self-weight of the soil in terms of submerged specific weight $({\gamma }^{\prime })$ and the soil depth $(z)$, as given by Equation 3 (Sumer, 2014).

${\sigma }_0^{\prime }={\gamma }^{\prime }z\left(\frac{1+2k_0}{3}\right)(3)$

However, to account for the variation in soil stresses generated by structures such as caisson breakwaters, ${\sigma }_0^{\prime }$ needs to be generalized in terms of Equation 2. This modification is applied in all simulated scenarios within the scope of the present study, to maintain consistency. Accordingly, the total effective stress in the soil underneath the caisson would be as given by Equation 4

${\sigma }_0^{\prime }=\left({\gamma }^{\prime }z+{\alpha }_s{p}_c\right)\left(\frac{1+2k_0}{3}\right)(4)$

in which $p_c$ is the static overburden due to the submerged weight of the caisson and ${\alpha }_s$ is a factor related to the spreading of the loaded area with the soil depth (Sumer, 2014, p. 291). It should be re-iterated that the ${\sigma }_0^{\prime }$ is calculated in the numerical model automatically as per the poro-elastic soil constitutive model, prior to the start of the dynamic loading.

Simulation of cyclic loading on the soil begins after the final equilibrium of stresses in the soil under static conditions are reached. As such, standing wave forces governed by $p_b(x,t)$, rocking motion governed by $p_r(x,t)$, or a combination of both is applied on the seabed, depending on the simulated case. When the amplitude of the fluctuations of the forces reaches a steady state at its peak, the amplitude of the cyclic shear stress, $\tau$, is recorded. The amplitude of cyclic shear stress, $\tau$, is calculated from the standard deviation of the time-dependent shear stress on x-y plane, ${\tau }_{xy}(t)$, such as $\tau =\sqrt{2}{\sigma }_{{\tau }_{xy}}$. The initial duration of the loading, where stresses are evolving before reaching a steady-state periodic motion, are not included in the time series used for the calculation. The standard deviation of ${\tau }_{xy}$ is calculated after the point where the mean values of the shear stress reach their maximum.

2.2.2 Step 2

Next, the pore-water pressure buildup is computed. To this end, Equation 5 is solved across the soil domain using the stresses ${\sigma }_0^{\prime }(x,y)$ and $\tau (x,y)$ calculated in Step 1, as described in the preceding paragraphs. Here, $\bar{p}(x,y,t)$ is the period-averaged pore-water pressure in excess of hydrostatic pressure, $c_v$ is the coefficient of consolidation, and $f$ is the pressure generation source term, defined by Equation 6.

$\frac{\partial \bar{p}}{\partial t}=c_v\left(\frac{{\partial }^2\bar{p}}{\partial x^2}+\frac{{\partial }^2\bar{p}}{\partial z^2}\right)+f(5)$

$f=\frac{{\sigma }_0^{\prime }}{N_{l}T}\cdot M\left(\bar{p},{\sigma }_0^{\prime }\right)(6)$

In Equation 6, $T$ is the wave period and $N_l$ is the number of cycles required for liquefaction to occur. $M(\bar{p},{\sigma }_0^{\prime })$ is a step-wise pressure-limiter function used to cap the $\frac{\bar{p}}{{\sigma }_0^{\prime }}$ ratio, as shown in Equation 7.

$M=\left\{\begin{array}{cc}1\hfill & \text{,\hspace{0.17em}if}\frac{\bar{p}}{{\sigma }_0^{\prime }}<1\hfill \\ 0\hfill & \text{,\hspace{0.17em}if}\frac{\bar{p}}{{\sigma }_0^{\prime }}\ge 1\hfill \end{array}\right.(7)$

The role of the pressure-limiter function, $M$ given in Equation 7, can be described as follows: The present model is inherently designed to simulate the pore-water pressure buildup due to cyclic shear strains in the soil, until liquefaction is reached (c.f. Equation 1). Once the soil is liquefied, the soil will change its phase from solid to liquid, and no further accumulated pore pressure is expected to be “generated” in the soil. Therefore, the source term $f$ appearing in Equation 5 should be set to zero whenever $\frac{\bar{p}}{{\sigma }_0^{\prime }}\ge 1$. If the pressure generation within the “liquefied” zones was not limited in the numerical model, accumulated pore pressure would reach “unphysically” high values in the liquefied zones within the soil domain. Therefore, this pressure-limiter, $M$, is used to prevent the source term from producing additional period-averaged pore-water pressure when $\frac{\bar{p}}{{\sigma }_0^{\prime }}$ reaches to 1, and whenever the pore pressure dissipates and the ratio falls below 1, the source term resumes producing pore-water pressure, allowing it to spread.

$N_l$, the number of cycles required for liquefaction, is defined in Equation 8, where $\tau$ is the amplitude of the cyclic shear stress, as explained previously (Peacock and Seed, 1968; De Alba et al., 1976; Sumer, 2014, p. 76 can also be consulted).

$N_l={\left(\frac{1}{\alpha }\frac{\tau }{{\sigma }_0^{\prime }}\right)}^{\frac{1}{\beta }}(8)$

Here, $\alpha$ and $\beta$ are empirical coefficients, defined in Equations 9, 10 respectively, in terms of relative density, $D_r$, as follows.

$\alpha =0.34D_r+0.084(9)$

$\beta =0.37D_r-0.46(10)$

$D_r=\frac{e_{\mathit{max}}-e}{e_{\mathit{max}}-e_{\mathit{min}}}(11)$

Equations 9, 10 are obtained based on the experimental data of De Alba et al. (1976), as described in Sumer et al. (2012). In Equation 11, $e$ is the void ratio, $e_{\mathit{max}}$ and $e_{\mathit{min}}$ are the maximum and minimum void ratio values of the soil, respectively.

The pressure variation on the seabed due to wave action is imposed with respect to the linear wave theory (Dean and Dalrymple, 1991). The time-dependent pressure on the seabed for “progressive waves” and “standing waves” are defined as Equation 12 and Equation 13, respectively (Hsu and Jeng, 1994).

$p_b\left(x,t\right)=\gamma \frac{H_i}{2}\frac{\cos \left(\lambda x-\omega t\right)}{\cosh \left(\lambda h\right)}(12)$

$p_b\left(x,t\right)=\gamma \frac{H_i}{2}\frac{\left[\cos \left(\lambda x-\omega t\right)+\cos \left(-\lambda x-\omega t\right)\right]}{\cosh \left(\lambda h\right)}\text{\hspace{0.17em},\hspace{0.17em}where\hspace{0.17em}}x\le 0(13)$

In the above equations, $k=2\pi /L$ and $\omega =2\pi /L$ are the wave number and angular frequency of the wave, respectively, and $H_i$ is the incident wave height. As such, the height of the standing wave given in Figure 1 becomes two times the incident wave height, $H=2H_i$. The static overburden due to the submerged weight of the caisson is imposed on the seabed by Equation 14.

$p_c\left(x\right)={\gamma }_c\times H_c-\gamma \times h\text{,\hspace{0.17em}where\hspace{0.17em}}0\le x\le B(14)$

in which $H_c$ is the height of the caisson, ${\gamma }_c$ is the overall specific weight of the caisson and $\gamma$ is that for the water.

The pressure imposed on the seabed by the rocking motion of the caisson is calculated via Equation 15. In this equation, $p_{r_{\mathit{amp}}}$ is the amplitude of the rocking pressure (see Figure 1) that is calculated from the overturning moment on the caisson induced by standing waves. The detailed calculation of the overturning moment and $p_{r_{\mathit{amp}}}$ can be found in Sumer (2014), (pp. 283–292). Consequently, the total (static and rocking) pressure load under the caisson, $p_{c_{\mathit{total}}}$, is implemented in the model as shown in Equation 16.

$p_r\left(x,t\right)=p_{r_{\mathit{amp}}}\cdot \frac{\left(x-\frac{B}{2}\right)}{\frac{B}{2}}\cdot \left[-\cos \left(\omega t\right)\right]\text{\hspace{0.17em},\hspace{0.17em}where\hspace{0.17em}}0\le x\le B(15)$

$p_{c_{\mathit{total}}}\left(x,t\right)=p_c\left(x\right)+p_r\left(x,t\right)(16)$

A flowchart describing the implementation of the numerical model is presented in Figure 2. The model described above is implemented in COMSOLE Multiphysics V5.5 A triangular mesh was adopted for the numerical simulations. The finest mesh was described around the structure borders and mesh size was gradually increased with a growth rate of 1.13, which gave the optimum mesh resolution and quality. The finest mesh element size was less than 4 cm. Different mesh sizes were tested, and no meaningful change in model results were seen for finer mesh sizes. Further details regarding numerical modeling are provided in Angin (2023).

Figure 2

Figure 2. The flowchart of the numerical simulations.

2.3 Boundary conditions

The boundary conditions adopted for the numerical model comprise the conditions defined for soil (Biot equations) and the period-averaged pore-water pressure (pressure buildup equation). These conditions applied to the impermeable bottom, lateral boundaries, and the midline of the soil domain, as well as soil-structure boundaries (caisson bottom and pipe walls) are summarized below.

$•$ At the impermeable bottom of the soil deposit $(z=d)$:

     Soil: Fixed boundary, restricts all soil movement; $u=0$, $v=0$. No flux normal to the boundary for the phase-resolved pressure; $\partial p/\partial n=0$.

     Period-averaged pressure: No flux normal to the boundary; $\partial \bar{p}/\partial n=0$.

$•$ At the sides of the model domain:

     Soil: Roller boundary, restricts soil movement normal to the boundary; $u_n=u=0$. No flux normal to the boundary for the phase-resolved pressure; $\partial p/\partial n=0$.

     Period-averaged pressure: No flux normal to the boundary; $\partial \bar{p}/\partial n=0$.

$•$ At the offshore seabed surface (midline, $z=0$):

     Soil: Boundary load governed by wave pressure; ${\sigma }_z=p_b(t,x)$ (Equation 12 or Equation 13).

     Period-averaged pressure: Dirichlet boundary condition with zero pressure; $\bar{p}=0$.

$•$ Underneath the caisson (for the cases with caisson):

     Soil: Boundary load governed by the caisson’s weight and rocking motion; ${\sigma }_z=p_{c_{\mathit{total}}}$ (Equation 16). No flux normal to the boundary for the phase-resolved pressure; $\partial p/\partial n=0$.

     Period-averaged pressure: No flux normal to the boundary; $\partial \bar{p}/\partial n=0$.

$•$ At the onshore seabed surface:

     Soil: Boundary load zero; ${\sigma }_z=0$. Dirichlet boundary condition for the phase-resolved pressure equal to zero; $p=0$.

     Period-averaged pressure: Dirichlet boundary condition with zero pressure; $\bar{p}=0$.

$•$ At the walls of the pipe (for the cases with buried pipeline):

     Soil: Roller boundary, restricts soil movement normal to the boundary; $u_n=0$. No flux normal to the boundary for the phase-resolved pressure; $\partial p/\partial n=0$.

     Period-averaged pressure: No flux normal to the boundary; $\partial \bar{p}/\partial n=0$.

With the numerical model set as described above, two types of simulations were carried out with the implemented model: (1) With progressive waves for model validation, which involves an undisturbed seabed case and a buried pipe case presented in Sections 2, 3 with standing waves and rocking motion of the caisson applied separately and in a combined manner, as presented in Section 4.

3 Results: Progressive waves

For validation of the model, two different cases with progressive waves were tested before the model was used to simulate the liquefaction process around a gravity-based structure induced by standing waves and rocking of the structure. First, the model was run for a residual liquefaction case of undisturbed seabed under progressive waves, and compared with the analytical solution of Sumer (2014). For comparison, the values of wave and soil parameters are taken the same with those defined in the numerical example given in the referenced book of Sumer (2014), (pp. 87–90). The results show a very good agreement between the numerical and analytical model results as far as the buildup of pore water pressure, and the onset of liquefaction processes. The results will not be included here for reasons of space.

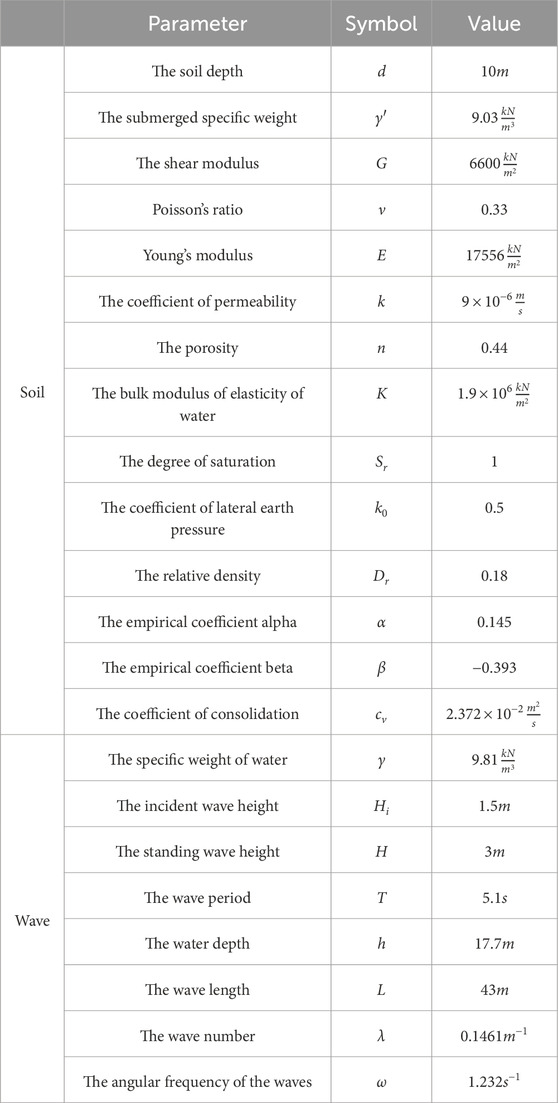
As a second validation case under progressive waves, the experimental study of Sumer et al. (2006b) was simulated with the numerical model. The experiments were conducted in a wave flume with dimensions 0.6 m in width, 0.8 m in depth, and 26.5 m in length. A piston-type wave generator produced regular waves, and a soil pit with dimensions of 17 cm in depth and 90 cm in length was positioned 12 m from the wave generator. A pipe of 8 cm diameter was placed in the soil rigidly, 45 cm from the offshore end of and 2.5 cm from the bottom of the soil pit. The soil and wave properties from the study of Sumer et al. (2006b) are summarized in Table 1.

Table 1

Table 1. The soil and wave properties of the experimental study of Sumer et al. (2006b).

For the numerical model that simulated the experiments of Sumer et al. (2006b), the submerged weight of the pipe along with the self-weight of the soil is considered in the analysis, similar to the caisson scenario. Accumulated pore-water pressure values were measured at three specific locations on the pipeline surface: the bottom (Point 1), the left side facing the incoming wave (Point 2), and the top (Point 3), as shown in Figure 3. As seen in the figure, the numerical model can satisfactorily capture the pore-water pressure buildup, although it appears that the predicted pressures at Point 2 are somewhat larger than the measurements. The predicted maximum pressure attained at Point 2 is, nevertheless, in remarkably good agreement with the experiment.

Figure 3

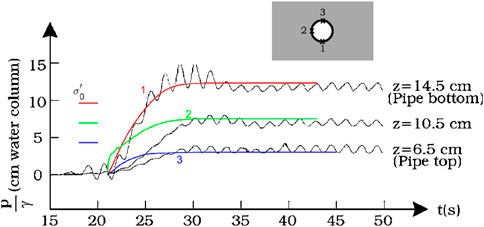
Figure 3. Accumulated pore-water pressure near the pipe. Point 1 is the bottom of the pipe $y=14.5cm$, Point 2 is the left side at the depth of the pipe center $y=10.5cm$, and Point 3 is the top of the pipe $y=6.5cm$. Solid and colored lines: Model results. Fluctuating black lines: Experiment results of Sumer et al. (2006b).

To sum up, the numerical model was shown to satisfactorily capture pore-water pressure buildup and residual liquefaction potential both in the case of undisturbed seabed and around a structure.

4 Results: Standing waves and rocking motion of the caisson

The model runs involving standing wave and rocking motion of the caisson models are performed for the soil and wave parameters defined in Table 2 and for the following dimensions of the caisson: the height of the caisson $H_c=$ 21 m, and the breadth of the caisson $B=$ 17.5 m. (The soil and wave properties and the structure characteristics are selected to be in accord with those reported in Sumer (2014), (pp. 282–293), to facilitate comparison.)

Table 2

Table 2. The soil and wave properties of the seabed in the standing waves and rocking motion cases.

The amplitude of the cyclic overturning moment caused by the 3 m-height standing waves is found as 1,281 kN m/m. The amplitude of the bed pressure underneath the two edges of the caisson is determined as $p_{r_{\mathit{amp}}}=$25.1 kN/${\mathrm{m}}^2$ (Sumer, 2014, pp. 282–293). The properties of the bedding layer under the caisson (formed of crushed rock) used in some of the simulations are given in Table 3. It should be noted that these values of the soil, wave and caisson parameters reflect a realistic design case.

Table 3

Table 3. The soil properties of the bedding layer.

As mentioned above, three different conditions are simulated: the standing-wave-only condition, the rocking-motion-only condition, and the combined condition where both waves and rocking motion affect the seabed.

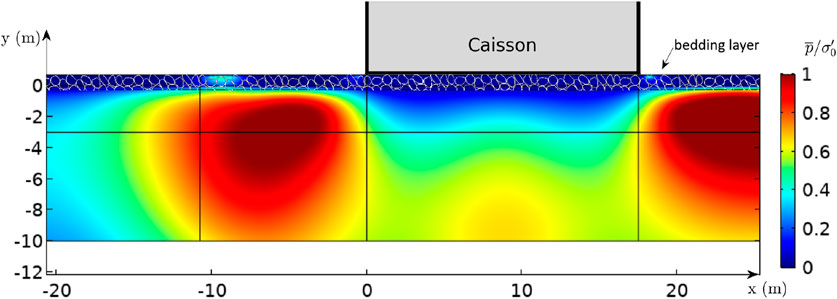
4.1 Standing-wave-only case

In this case, the rocking motion is not considered. The offshore side of the seabed is exposed to the standing wave, while beneath the caisson, only the self-weight of the caisson ($p_c$ given in Equation 14) is applied to the seabed. In this case, the accumulated pore pressure reaches approximately 60$\%$ of the initial mean normal effective stress. As seen in Figure 4, liquefaction susceptibility is observed around the nodes. This finding is consistent with the experimental study of Kirca et al. (2013) and that of Sassa and Sekiguchi (2001). Around $x=0$, the initial normal effective stresses are higher due to the weight of the caisson, which makes this area more liquefaction-resistant than the other anti-nodes. Even without a bedding layer on the surface of the seabed, liquefaction does not occur. Therefore, the standing-wave-only case has not been investigated with a bedding layer on the seabed.

Figure 4

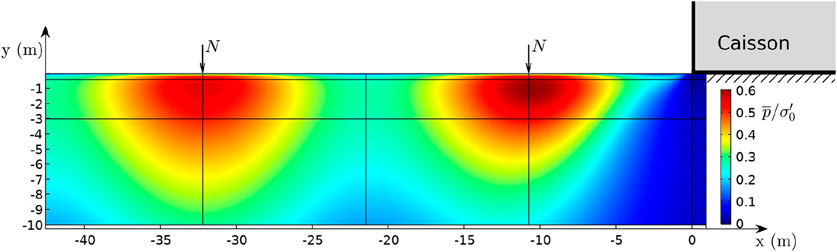
Figure 4. Liquefaction criterion: $\bar{p}/{\sigma }_0^{\prime }$ under the effect of standing waves without a bedding layer on the seabed. Arrows with “N” indicate the nodal sections.

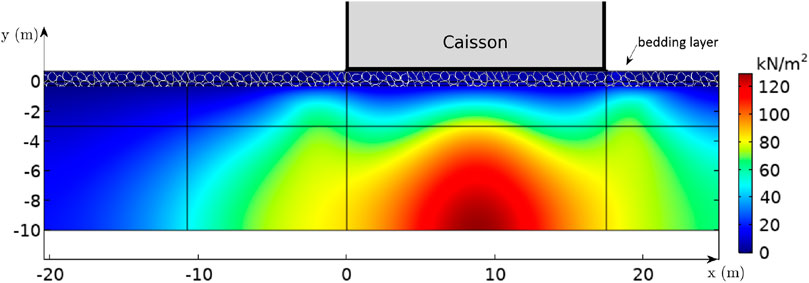
4.2 Rocking-motion-only case

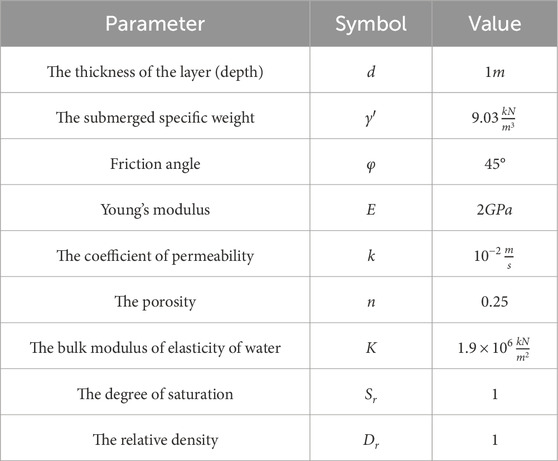
Under the effect of the rocking motion, enormous shear stresses occur. On the other hand, because of the weight of the caisson, the initial normal effective stress values underneath the caisson are also large. For this case, two conditions are simulated: with a bedding layer and without a bedding layer, to understand the effect of the bedding layer, c. f. Figures 5, 6.

Figure 5

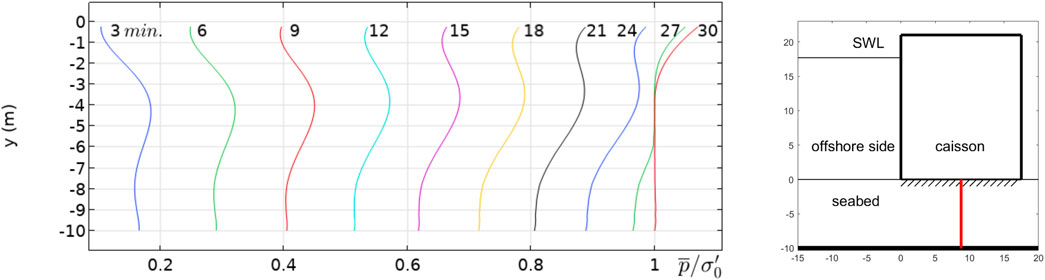
Figure 5. Liquefaction criterion: $\bar{p}/{\sigma }_0^{\prime }$ at different times (in minutes) under the effect of rocking motion only, without a bedding layer on the seabed. The pressures are calculated at the centerline just underneath the caisson, along the red line (see the panel to the right).

Figure 6

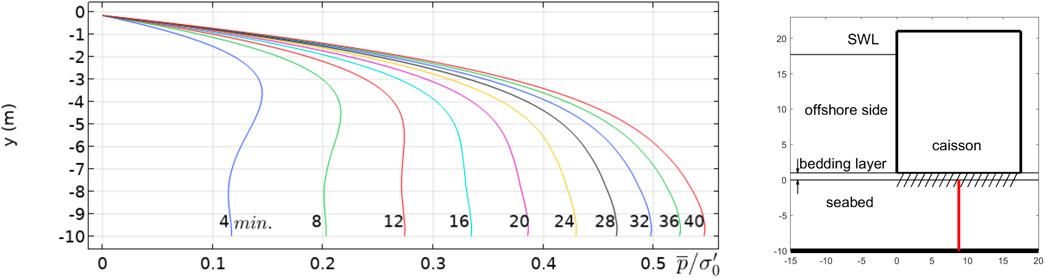
Figure 6. Liquefaction criterion: $\bar{p}/{\sigma }_0^{\prime }$ at different times (in minutes) under the effect of rocking motion only, with a bedding layer on the seabed. The pressures are calculated at the centerline just underneath the caisson, along the red line (see the panel to the right).

Now, Figure 5 shows the time development of the accumulated pore pressure just underneath the caisson (at the center line) in the case where there is no bedding layer. The figure indicates that the central area under the caisson liquefies in less than 30 min.

Figure 6 shows the time development of the accumulated pore pressure, again, just underneath the caisson (at the center line) in the case where there is a bedding layer. With a bedding layer, the central area under the caisson will not liquefy. The ratio between $\bar{p}$ and ${\sigma }_0^{\prime }$ reaches 55$\%$ around 40 min, in Figure 6. Even with sufficient time, it cannot exceed 1. The maximum value stays at approximately 65$\%$ of the critical point.

Placing the caisson directly on the surface of the seabed makes the area highly susceptible to liquefaction, as the excess pore water pressure cannot “escape” because of the sheer presence of the rigid bottom of the caisson. In the case of the bedding layer, however, the bedding layer allows the accumulated pore water to move out, and therefore it hinders the buildup of pore pressure. Also, the presence of the bedding layer reduces the cyclic shear stresses (Sumer et al., 2010).

In Figure 7, the amplitude of the cyclic shear stresses for both conditions, with (Figure 7B) and without (Figure 7A) a bedding layer, are shown on the same scale. As seen in Figure 7A, the amplitude of cyclic shear stress, $\tau$, increases to high values at the points where $p_r$ reaches its maximum value (at the edges of the caisson, see Equation 15), which are the locations where the so-called punching shear failure of the soil may occur. It should be underlined that the assumption of a poro-elastic continuum, i.e. using Biot equations for describing soil constitutive behavior, is not sufficient to simulate such excessive shear failures, and therefore the numerical model results lead to unexpectedly large cyclic shear stress amplitudes at the edges of the caisson, the areas where discontinuity of rocking motion occur. Therefore, the model results showing high-amplitude shear stress areas underneath the edges of the caisson should be treated with care.

Figure 7

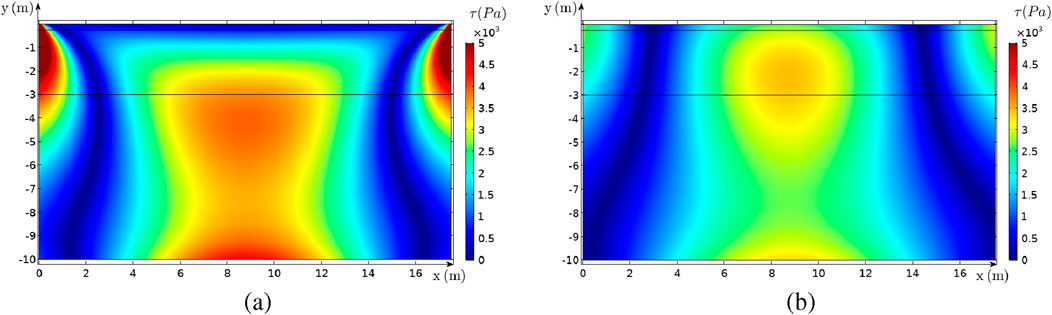
Figure 7. The amplitude of the cyclic shear stress $\tau$ underneath the caisson under the effect of rocking motion only. (A) Without a bedding layer, and (B) with a bedding layer.

For both of the conditions, it is observed that the center line under the caisson is prone to liquefy, as experimentally proven by Sumer et al. (2008). The accumulated pore pressure under the effect of the rocking motion, as seen in Figure 8, reaches its maximum value at the center line under the caisson. However, the high values of the initial mean normal effective stress (Figure 9) prevent the liquefaction at this area. To quantify the liquefaction susceptibility of the seabed due to the rocking of the caisson, Figure 10 shows the variation of liquefaction criterion $(\bar{p}/{\sigma }_0^{\prime })$ around the rocking caisson. As seen in this figure, liquefaction does not occur at the footprint of the caisson, but two liquefaction zones appear at both sides of it. These liquefaction zones horizontally extend outwards from both edges of the caisson up to a distance of approximately $B/2$, and vertically from almost under the bedding layer down to a depth of ca. 6 m.

Figure 8

Figure 8. The initial mean normal effective stress ${\sigma }_0^{\prime }$ under the caisson.

Figure 9

Figure 9. The accumulated pore pressure $(\bar{p})$ under the effect of rocking motion only.

Figure 10

Figure 10. Liquefaction criterion: $\bar{p}/{\sigma }_0^{\prime }$ under the effect of rocking motion only.

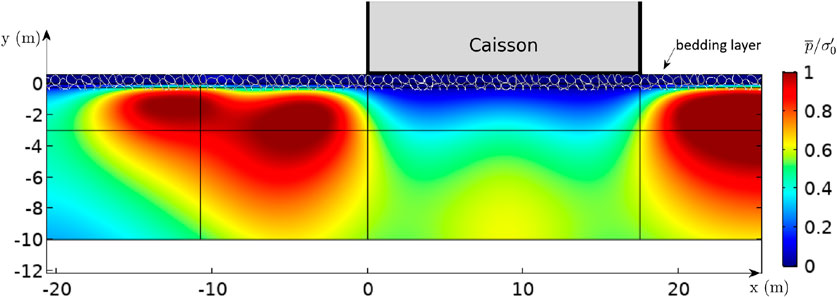
4.3 Both standing waves and rocking motion

In this case, the standing wave is applied in front of the caisson with the caisson undergoing a rocking motion in-phase with the wave (Figure 1). Figure 11 presents the model results showing the liquefaction susceptibility in terms of distribution of $\bar{p}/{\sigma }_0^{\prime }$ in the case of combined loading of the seabed due to standing waves and rocking caisson, while Figure 12 shows the accumulated pore pressure distribution for the same case. When Figures 10, 11 are compared, it can be seen that, with standing waves switched on, accumulated pore pressure in the nodal area in front of the caisson is intensified, as one may expect from Figure 4. However, the liquefaction susceptibility underneath the rocking caisson is not significantly affected from the standing waves, as can be seen from the comparison of Figures 10, 11.

Figure 11

Figure 11. Liquefaction criterion: $\bar{p}/{\sigma }_0^{\prime }$ under the combined effect of rocking motion and standing waves.

Figure 12

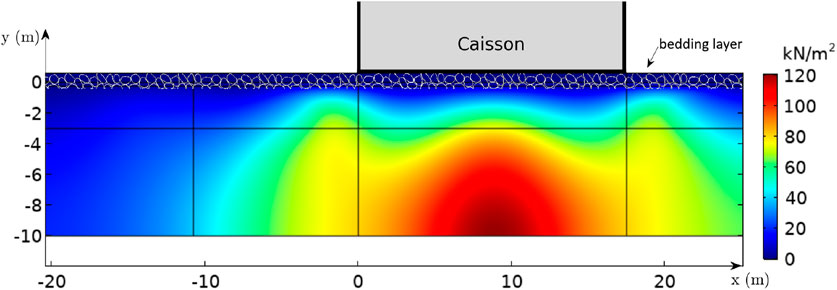
Figure 12. The accumulated pore pressure $(\bar{p})$ under the combined effect of rocking motion and standing waves.

As stated by Kudella et al. (2006), the caisson rocking motion is the primary source of pore pressure beneath the caisson, and the pore pressure generated by waves is negligible in this area. Comparison of Figures 8, 12 shows that the accumulated pore pressure is almost the same beneath the caisson, and liquefaction is not observed in this zone for any of the tested cases. As mentioned above, this is mainly because of the large ${\sigma }_0^{\prime }$ values in this zone due to the weight of the caisson (Figure 9).

When Figure 11 is examined from the stability of caisson point of view, it is evident that the liquefaction zone in front of the caisson extending as far as the nodal point of the standing wave will trigger failure of the caisson foundation, leading to sinking of the caisson into this zone, towards offshore direction. This result clearly explains the sinking and offshore displacement mechanism of the failed caissons in the two case studies referred to in Section 1.

4.4 Discussion of results

With the numerical model results presented above, in this section the findings of the study are discussed in the light of theoretical considerations, and also the limitations of the presented numerical model are discussed along with the modifications envisaged for the future work.

Sumer (2014), (Chp. 7) gave a thorough theoretical background regarding pore-water pressure buildup and residual liquefaction under standing waves, in the light of experimental data. As discussed in the Introduction section, the key feature pointed out by Sumer (2014) was that the cyclic shear stress (and thereby shear deformations leading to the re-arrangement of soil grains) induced by standing waves are concentrated under the node section of the standing wave profile, nearest of which is located at $L/4$ distance from the reflecting wall and others follow with every $L$ distance. However, the pore-water pressure generated under the node sections spreads horizontally towards the anti-nodes due to the diffusion process (Equation 5). When the results of the standing-wave-only case presented in Figure 4 is investigated, it can be seen that the results are in full accord with the theoretical behavior described by Sumer (2014), indicating the model is capable of capturing the physical mechanism of liquefaction under standing waves.

Wave parameters ($H$, $T$, and $L$) play a crucial role in residual liquefaction, directly by inducing pressure variations on the seabed soil, and indirectly by driving the caisson rocking. Although the results for a limited number of wave parameters were presented here due to reasons of space, numerical model results for various cases were tested, which can be found in Angin (2023). Liquefaction susceptibility increases with increasing $H$ and $L$, since both increase the amplitude of wave pressure $(p_b)$ and caisson rocking load $(p_r)$ on the seabed. To give the reader a feel about the sensitivity of liquefaction susceptibility against wave height, the soil would liquefy under standing-wave-only case if the wave height was increased as much as 50%. On the other hand, for a constant pair of $H$ and $L$ values, a smaller $T$ would cause a higher pore-water pressure buildup, given that the source term is inversely proportional with the wave period, $T$. In other words, a faster pace of oscillations would lead to quicker pore-water pressure buildup and residual liquefaction.

Once the rocking of the caisson was introduced in the numerical model, the rocking-induced cyclic shear stress became dominant underneath the caisson leading the intense pore-water pressure buildup at this hotspot (Figure 9) even larger than that induced by standing waves under node section. This result is also in conformity with the theoretical considerations (Sumer, 2014, Section 8.1.2) as well as experimental findings (Sumer et al., 2008).

In the case of combined action of caisson rocking and standing waves, the most applicable scenario to the real life, the results showed that the pore-water pressure buildup around the node caused by the standing waves was enhanced by the caisson rocking so much so that residual liquefaction took place even in the node section (Figure 11). This finding not only agrees with the theoretical considerations (Sumer, 2014; Section 8.1.2), but also can clearly explain the encountered liquefaction-induced caisson failure cases discussed in the Introduction section.

While the presented model was shown to be capable of simulating pore-water pressure buildup induced by waves and structure motion, the model has some limitations. First of all, it should be stated that the poro-elasticity assumption employed in the model, based on Biot’s equations for soil constitutive behavior, may not adequately capture soil responses under extreme displacements of the caisson which would lead to significant shear failures, such as punching shear. Therefore, caution is advised when applying the model to such scenarios involving severe structure displacements. Furthermore, given that the model is designed to simulate pore-water pressure buildup in the seabed soil until it reaches up to the initial mean normal effective stress (c.f. Equation 1), post-liquefaction behavior cannot be simulated by the present model. This means that the model results would be reliable only until the soil is liquefied. Another limitation of the present model is that it is implemented for a 2D problem, whereas 3D effects may be important in a real-life case, especially around the head section of a caisson breakwater. At this juncture, it is to be noted that in a parallel study as part of the NuLIMAS project, a similar model is implemented in OpenFOAM toolbox, which is capable of dealing with 3D geometries and also simulating the post-liquefaction behavior of seabed soil (Windt et al., 2024; Shanmugasundaram et al., 2025) as mentioned in the Introduction section. Future work will focus on modeling the 3D case of seabed liquefaction around a caisson breakwater, including the post-liquefaction behavior.

The results presented above shows that the model can be extended to simulate pore pressure buildup and initiation of seabed liquefaction around various marine structures (e.g., pipelines, cables, anchors, foundations, and rubble-mound breakwaters) in coastal or offshore environments, provided that wave-induced and structure-induced loadings are accurately described.

5 Conclusion

A mathematical model has been developed to study the buildup of pore-water pressure at a gravity-based structure, and to check for liquefaction potential of the seabed under the combined action of (1) standing waves (that form in front of the structure), and (2) the rocking motion of the structure itself induced by the waves.

First, the model was validated for the case of residual liquefaction under progressive waves against analytical results (for an undisturbed seabed case, Sumer (2014), pp. 87–90) and against experimental results (for the case of liquefaction around pipelines, Sumer et al. (2006b)). The results of the validation exercise show that the numerical model can satisfactorily capture pore-water pressure buildup and onset of residual liquefaction.

Once the model was validated, liquefaction susceptibility under standing-waves-only case, rocking-motion-only case, and combined action of standing waves and rocking caisson was investigated, respectively, for a given set of tested values of soil and wave parameters. In the standing-wave-only case, it was seen that the pore-water pressure buildup under the node section reached up to $\bar{p}/{\sigma }_0^{\prime }\approx 0.65$, i.e. no liquefaction occurred. For the rocking-motion-only case, a liquefied zone $(\bar{p}/{\sigma }_0^{\prime }\ge 1)$ was seen extending to a depth of 6 m below the midline at the offshore side of the caisson. For the combined case of standing waves and caisson rocking, the depth of liquefaction zone formed due to caisson rocking did not change, however a second zone of liquefaction appeared due to standing waves, reaching a depth down to 3 m. As expected, these two distinct zones of liquefaction were merged, forming a single zone of liquefaction reaching as far as 15 m offshore from the caisson. This picture agrees well with the observations from the caisson failure cases discussed in the Introduction section, and explains the severe sinking and offshore displacement of the failed caissons.

It is concluded that, for the conditions that can be encountered in practice, the rocking motion of the caisson is the primary source of buildup of pore pressure beneath the caisson, and furthermore, the pore pressure generated by waves is of minor importance. This emphasizes the importance of precise modeling of the dynamic behavior of the caisson when estimating the risk of liquefaction around gravity-based structures.

In terms of reducing the liquefaction susceptibility, the significance of including a bedding layer in the design is demonstrated through a comparison between the scenario where the caisson is placed directly on the seabed and the scenario using a bedding layer to position the caisson. Also, the bedding layer reduces the liquefaction risk by minimizing the punching effect in the model caused by rocking motion and by increasing the initial mean normal effective stresses via the application of overburden pressure.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

VSOK: Conceptualization, Investigation, Methodology, Project administration, Supervision, Validation, Visualization, Writing–review and editing. MA: Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Writing–original draft. BMS: Conceptualization, Formal Analysis, Investigation, Methodology, Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study was funded by (1) the three-year (2020–2023) research program NuLIMAS: Numerical Modelling of Wave-Induced Liquefaction Around Marine Structures, funded through the ERA-NET co-fund MarTERA Program (Grant No. 728053) under EU Horizon 2020 Framework, from the German Federal Ministry for Economic Affairs and Energy (Grant No. 03SX524A), the Scientific and Technological Research Council of Turkey (TUBITAK, Grant No. TEYDEB- 1509/9190068), and the Polish National Center for Research and Development; and (2) the European Union through the Horizon Europe project INF4INiTY under Grant Agreement No. 101136087.

Acknowledgments

Authors acknowledge ITU ARI Teknokent for their ongoing support under the ITU ARI Teknokent Research and Development activities. The authors acknowledge the support of Mr. Selcuk Demirbas on adaptation of the software. The third author, BMS, specially would like to thank Prof. Yakun Guo of University of Bradford, U.K., for the invitation to contribute to what was originally planned a Special Issue on offshore wind energy structures in The Frontiers in Marine Science back in August 2023.

Conflict of interest

Authors VSOK and BMS were founders of BM SUMER Consultancy & Research.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Angin, M. (2023). Numerical modeling of wave-induced liquefaction around a gravity-based structure. Istanbul, Turkiye: Istanbul Technical University, Coastal Sciences and Engineering Program. Master’s thesis.

Google Scholar

Biot, M. A. (1941). General theory of three-dimensional consolidation. J. Appl. Phys. 12, 155–164. doi:10.1063/1.1712886

CrossRef Full Text | Google Scholar

Cui, L., and Jeng, D.-S. (2021). Seabed liquefaction around breakwater heads at a river mouth: an integrated 3d model. Ocean. Eng. 242, 110036. doi:10.1016/j.oceaneng.2021.110036

CrossRef Full Text | Google Scholar

Damgaard, J. S., Sumer, B. M., Teh, T., Palmer, A., Foray, P., and Osorio, D. (2006a). Guidelines for pipeline on-bottom stability on liquefied noncohesive seabeds. J. Waterw. port, Coast. ocean Eng. 132, 300–309. doi:10.1061/(asce)0733-950x(2006)132:4(300)

CrossRef Full Text | Google Scholar

Damgaard, J. S., Sumer, B. M., Teh, T. C., Palmer, A. C., Foray, P., and Osorio, D. (2006b). Guidelines for pipeline on-bottom stability on liquefied noncohesive seabeds. J. Waterw. Port, Coast. Ocean Eng. 132, 300–309. doi:10.1061/(asce)0733-950x(2006)132:4(300)

CrossRef Full Text | Google Scholar

De Alba, P. A., Chan, C. K., and Seed, H. B. (1976). Sand liquefaction in large-scale simple shear tests. J. Geotechnical Eng. Div. 102, 909–927. doi:10.1061/ajgeb6.0000322

CrossRef Full Text | Google Scholar

Dean, R. G., and Dalrymple, R. A. (1991). Water wave mechanics for engineers and scientists, vol. 2. Singapore: world scientific publishing company.

Google Scholar

De Groot, M., Bolton, M., Foray, P., Meijers, P., Palmer, A., Sandven, R., et al. (2006a). Physics of liquefaction phenomena around marine structures. J. Waterw. Port, Coast. Ocean Eng. 132, 227–243. doi:10.1061/(asce)0733-950x(2006)132:4(227)

CrossRef Full Text | Google Scholar

De Groot, M., Kudella, M., Meijers, P., and Oumeraci, H. (2006b). Liquefaction phenomena underneath marine gravity structures subjected to wave loads. J. Waterw. port, Coast. ocean Eng. 132, 325–335. doi:10.1061/(asce)0733-950x(2006)132:4(325)

CrossRef Full Text | Google Scholar

Duan, L., Qin, C., Zhou, J., Tang, G., Wang, D., and Fan, M. (2023). Numerical study of regular wave-induced oscillatory soil response during the caisson installation. Ocean. Eng. 281, 114876. doi:10.1016/j.oceaneng.2023.114876

CrossRef Full Text | Google Scholar

Esfeh, P. K., and Kaynia, A. M. (2019). Numerical modeling of liquefaction and its impact on anchor piles for floating offshore structures. Soil Dyn. Earthq. Eng. 127, 105839. doi:10.1016/j.soildyn.2019.105839

CrossRef Full Text | Google Scholar

Hsu, J. R. C., and Jeng, D. S. (1994). Wave-induced soil response in an unsaturated anisotropic seabed of finite thickness. Int. J. Numer. Anal. Methods Geomechanics 18, 785–807. doi:10.1002/nag.1610181104

CrossRef Full Text | Google Scholar

Jeng, D.-S., and Zhao, H. (2015). Two-dimensional model for accumulation of pore pressure in marine sediments. J. Waterw. Port, Coast. Ocean Eng. 141, 04014042. doi:10.1061/(asce)ww.1943-5460.0000282

CrossRef Full Text | Google Scholar

Ju, S.-H., and Mao, Y.-C. (2024). Research on offshore wind turbine support structures under seismic soil liquefaction. Ocean. Eng. 304, 117750. doi:10.1016/j.oceaneng.2024.117750

CrossRef Full Text | Google Scholar

Kirca, V. S. O. (2013). Sinking of irregular shape blocks into marine seabed under wave-induced liquefaction. Coast. Eng. 75, 40–51. doi:10.1016/j.coastaleng.2013.01.006

CrossRef Full Text | Google Scholar

Kirca, V. S. O., Sumer, B. M., and Fredsøe, J. (2013). Residual liquefaction of seabed under standing waves. J. Waterw. Port, Coast. Ocean Eng. 139, 489–501. doi:10.1061/(asce)ww.1943-5460.0000208

CrossRef Full Text | Google Scholar

Kudella, M., Oumeraci, H., de Groot, M. B., and Meijers, P. (2006). Large-scale experiments on pore pressure generation underneath a caisson breakwater. J. Waterw. Port, Coast. Ocean Eng. 132, 310–324. doi:10.1061/(asce)0733-950x(2006)132:4(310)

CrossRef Full Text | Google Scholar

Li, X.-J., Gao, F.-P., Yang, B., and Zang, J. (2011). Wave-induced pore pressure responses and soil liquefaction around pile foundation. Int. J. Offshore Polar Eng. 21.

Google Scholar

Peacock, W. H., and Seed, H. B. (1968). Sand liquefaction under cyclic loading simple shear conditions. J. Soil Mech. Found. Div. 94, 689–708. doi:10.1061/jsfeaq.0001135

CrossRef Full Text | Google Scholar

Puzrin, A. M., Alonso, E. E., and Pinyol, N. M. (2010). “Caisson failure induced by liquefaction: Barcelona harbour, Spain,” in Geomechanics of failures (Springer Netherlands), 85–148. doi:10.1007/978-90-481-3531-8_5

CrossRef Full Text | Google Scholar

Sassa, S., and Sekiguchi, H. (2001). Analysis of wave-induced liquefaction of sand beds. Géotechnique 51, 115–126. doi:10.1680/geot.2001.51.2.115

CrossRef Full Text | Google Scholar

Shanmugasundaram, R. k., Rusche, H., Windt, C., Kirca, O., Sumer, M., and Goseberg, N. (2022). Towards the numerical modelling of residual seabed liquefaction using openfoam. OpenFOAM® J. 2, 94–115. doi:10.51560/ofj.v2.56

CrossRef Full Text | Google Scholar

Shanmugasundaram, R. K., Rusche, H., Windt, C., Kirca, V. S. O., Sumer, B. M., and Goseberg, N. (2025). Numerical modelling of wave-induced seabed liquefaction: a drift-flux model for liquefied soil. J. Waterw. Port, Coast. Ocean Eng. under Rev.

Google Scholar

Sumer, B. M. (2006). Special issue on liquefaction around marine structures: miscellaneous. J. Waterw. Port, Coast. Ocean Eng. 133, 1–2. doi:10.1061/(ASCE)0733-950X(2007)133:1(1)

CrossRef Full Text | Google Scholar

Sumer, B. M. (2014). Liquefaction around marine structures. Singapore: World Scientific. doi:10.1142/7986

CrossRef Full Text | Google Scholar

Sumer, B. M., and Cheng, N.-S. (1999). “A random-walk model for pore pressure accumulation in marine soils,” in The ninth international Offshore and polar engineering conference (OnePetro).

Google Scholar

Sumer, B. M., Dixen, F. H., and Fredsøe, J. (2010). Cover stones on liquefiable soil bed under waves. Coast. Eng. 57, 864–873. doi:10.1016/j.coastaleng.2010.05.004

CrossRef Full Text | Google Scholar

Sumer, B. M., and Fredsøe, J. (2002). The mechanics of scour in the marine environment. Singapore: World Scientific.

Google Scholar

Sumer, B. M., Fredsøe, J., Christensen, S., and Lind, M. (1999). Sinking/floatation of pipelines and other objects in liquefied soil under waves. Coast. Eng. 38, 53–90. doi:10.1016/s0378-3839(99)00024-1

CrossRef Full Text | Google Scholar

Sumer, B. M., Hatipoglu, F., Fredsøe, J., and Hansen, N.-E. O. (2006a). Critical flotation density of pipelines in soils liquefied by waves and density of liquefied soils. J. Waterw. Port, Coast. Ocean Eng. 132, 252–265. doi:10.1061/(asce)0733-950x(2006)132:4(252)

CrossRef Full Text | Google Scholar

Sumer, B. M., and Kirca, V. S. O. (2022). Scour and liquefaction issues for anchors and other subsea structures in floating offshore wind farms: a review. Water Sci. Eng. 15, 3–14. doi:10.1016/j.wse.2021.11.002

CrossRef Full Text | Google Scholar

Sumer, B. M., Ozgur Kirca, V., and Fredsøe, J. (2012). Experimental validation of a mathematical model for seabed liquefaction under waves. Int. J. Offshore Polar Eng. 22.

Google Scholar

Sumer, B. M., Truelsen, C., and Fredsøe, J. (2006b). Liquefaction around pipelines under waves. J. Waterw. Port, Coast. Ocean Eng. 132, 266–275. doi:10.1061/(asce)0733-950x(2006)132:4(266)

CrossRef Full Text | Google Scholar

Sumer, S., Sumer, B., Dixen, F., and Fredsøe, J. (2008). “Pore pressure buildup in the subsoil under a caisson breakwater,” in Proceedings of the 18. International Offshore (Ocean) and Polar Engineering Conference, Vancouver, British Columbia, Canada, July 6-11, 2008, 664–671.

Google Scholar

Tsinker, G. (2012). Marine structures engineering: specialized applications: specialized applications. Springer Science and Business Media.

Google Scholar

Ulker, M., Rahman, M., and Guddati, M. (2010). Wave-induced dynamic response and instability of seabed around caisson breakwater. Ocean. Eng. 37, 1522–1545. doi:10.1016/j.oceaneng.2010.09.004

CrossRef Full Text | Google Scholar

Ulker, M., Rahman, M., and Guddati, M. (2012). Breaking wave-induced response and instability of seabed around caisson breakwater. Int. J. Numer. Anal. Methods Geomechanics 36, 362–390. doi:10.1002/nag.1073

CrossRef Full Text | Google Scholar

Wang, Y.-F., and Gao, F.-P. (2014). “A numerical model for pore pressure buildup in a porous seabed under the action of combined waves and current,” in ISOPE pacific/asia offshore mechanics symposium (ISOPE) (California, United States: ISOPE).

Google Scholar

Windt, C., Goseberg, N., Schimmels, S., Kudella, M., Shanmugasundaram, R. K., Rusche, H., et al. (2024). Liquefaction around marine structures: development of a numerical modelling Framework in OpenFOAM®. Int. J. Offshore Polar Eng. 34, 182–190. doi:10.17736/ijope.2023.cl24

CrossRef Full Text | Google Scholar

Zhao, H., Jeng, D.-S., Liao, C., and Zhu, J. (2017). Three-dimensional modeling of wave-induced residual seabed response around a mono-pile foundation. Coast. Eng. 128, 1–21. doi:10.1016/j.coastaleng.2017.07.002

CrossRef Full Text | Google Scholar

Zhao, H., Jeng, D.-S., Zhang, H., Zhang, J., and Zhang, H. (2016a). 2-d integrated numerical modeling for the potential of solitary wave-induced residual liquefaction over a sloping porous seabed. J. Ocean Eng. Mar. Energy 2, 1–18. doi:10.1007/s40722-015-0033-3

CrossRef Full Text | Google Scholar

Zhao, H.-Y., Jeng, D.-S., and Liao, C. (2016b). Parametric study of the wave-induced residual liquefaction around an embedded pipeline. Appl. Ocean Res. 55, 163–180. doi:10.1016/j.apor.2015.12.005

CrossRef Full Text | Google Scholar

Nomenclature

$\mathit{\alpha }$ and $\mathit{\beta }$ Empirical coefficients

${\mathit{\alpha }}_{\mathit{s}}$ Factor related to the spreading of the loaded area with the soil depth

$\mathit{B}$ Width of the caisson

${\mathit{c}}_{\mathit{v}}$ Coefficient of vertical consolidation

$\mathit{d}$ Depth of soil domain

${\mathit{D}}_{\mathit{r}}$ Relative density

$\mathit{E}$ Young’s modulus

$\mathit{e}$, ${\mathit{e}}_{\mathit{m}\mathit{i}\mathit{n}}$, ${\mathit{e}}_{\mathit{m}\mathit{a}\mathit{x}}$ Void ratio, minimum and maximum void ratio of the soil

$\mathit{f}$ Source term for pressure buildup per unit time

${\mathit{\phi }}^{\prime }$ Angle of repose of soil

$\mathit{G}$ Shear modulus of elasticity

$\mathit{\gamma }$ Specific weight of water

${\mathit{\gamma }}_{\mathit{c}}$ Specific weight of the caisson

${\mathit{\gamma }}^{\prime }$ Submerged specific weight of soil

$\mathit{h}$ Water depth

${\mathit{h}}_{\mathit{c}}$ Height of the caisson

${\mathit{H}}_{\mathit{i}}$ Incident wave height

$\mathit{H}$ Height of the standing wave

$\mathit{K}$ Bulk modulus of elasticity of water

$\mathit{k}$ Coefficient fo permeability

${\mathit{k}}_{\mathit{0}}$ Coefficient of lateral earth pressure

$\mathit{L}$ Wave length

$\mathit{\lambda }$ Wave number

$\mathit{M}$ Pressure-limiter function for source term

$\mathit{n}$ Porosity of the soil

${\mathit{N}}_{\mathit{l}}$ Number of cycles to cause liquefaction

$\mathit{\nu }$ Poisson’s ratio

$\mathit{\omega }$ Angular frequency of the wave

$\bar{\mathit{p}}$ Accumulated (period averaged) pore pressure

${\mathit{p}}_{\mathit{b}}$ Phase-resolved pore-water pressure

${\mathit{p}}_{\mathit{b}}$ Wave pressure on the seabed

${\mathit{p}}_{\mathit{c}}$ Static overburden on the seabed due to submerged weight of the caisson

${\mathit{p}}_{{\mathit{c}}_{\mathit{t}\mathit{o}\mathit{t}\mathit{a}\mathit{l}}}$ Total load on the seabed due to the caisson

${\mathit{p}}_{\mathit{r}}$ Dynamic load on the seabed due to the rocking of the caisson

${\mathit{p}}_{{\mathit{r}}_{\mathit{a}\mathit{m}\mathit{p}}}$ Amplitude of the load on the seabed due to the rocking of the caisson

${\mathit{S}}_{\mathit{r}}$ Degree of saturation

${\mathit{\sigma }}_{\mathit{0}}^{\prime }$ Initial mean normal effective stress

${\mathit{\sigma }}_{\mathit{z}}$ Total vertical normal effective stress

${\mathit{\sigma }}_{\mathit{z}\mathit{0}}^{\prime }$ Initial vertical normal effective stress

$\mathit{T}$ Wave period

$\mathit{\tau }$ Amplitude of the cyclic shear stresses in soil

${\mathit{\tau }}_{\mathit{x}\mathit{y}}$ Shear stresses in soil

$\mathit{u}$ Horizontal soil displacement

$\mathit{v}$ Vertical soil displacement

${\mathit{u}}_{\mathit{n}}$ Soil displacement normal to the boundary

$\mathit{x}$ Horizontal coordinate

$\mathit{y}$ Vertical coordinate

$\mathit{z}$ Soil depth