Unveiling the seismic sensitivity of the Himalayan tunnels: a comprehensive assessment through analytical and numerical exploration of P-wave dynamics

This study investigated the seismic sensitivity of tunnels in the Jammu Region (JR) of the northwestern Himalayas, a region characterized by significant seismic activity and complex geological conditions. The research combined both analytical and numerical approaches to assess the influence of site conditions, tunnel lining, and reinforcement properties on tunnel resilience. A key objective is to develop a more reliable seismic assessment method by adopting a P-wave-based approach, which is particularly suitable for mountainous tunnels prone to landslides. The study identified three seismic hazard zones, with peak ground accelerations (PGA) ranging from less than 0.3 g to greater than 0.5 g, providing vulnerability aspects. The major outcomes of this study include guidelines for the design and retrofitting of sustainable and resilient underground structures in the Himalayas, with broader implications for global projects in seismically active and geologically complex regions. The methodologies and insights can be applied to infrastructure projects worldwide, enhancing the safety of communities living in vulnerable areas. This work aligns with the United Nations Sustainable Development Goals (SDGs), particularly in promoting resilient infrastructure and sustainable development, contributing to both structural resilience and the geological safety of the Himalayan region.

1 Introduction

Over the past 2 decades, infrastructure development in the Jammu and Kashmir (J&K) has accelerated significantly. However, this progress comes with increased challenges, primarily due to the geological complexities of the Himalayas (Arora et al., 2019; Haider et al., 2023). Located in the northwestern Himalayas, bordering Pakistan, this region has experienced several significant earthquakes, including the devastating 2005 Kashmir earthquake and the 2019 Mirpur earthquake (Shah et al., 2018; Yousuf et al., 2020). Areas such as Rajouri, Ramban, and Poonch are particularly vulnerable to landslides and slope failures, complicating the pursuit of sustainable and resilient transportation infrastructure (Fayaz et al., 2022; Singh et al., 2024). To check seismic sensitivity, analytical methods (Mazaheri et al., 2021) provide a theoretical framework, while numerical simulations (Min et al., 2024) offer detailed insights into how these structures will perform under various seismic scenarios. The importance of this dual-method approach is underscored by global examples where tunnels have sustained significant damage due to strong ground motion events, such as the 1995 Kobe earthquake in Japan (Aldrich, 2011) and the 2008 Wenchuan earthquake in China (Shen et al., 2014). These events highlight the need for thorough seismic assessments to ensure the safety and resilience of underground structures.

This study adopted a P-wave-based approach (Kouretzis et al., 2014), which is more suitable for mountainous tunnels prone to earthquake induced landslides. This method provides a more reliable assessment as the local geology significantly influences overall damage scenarios. This study assessed the seismic sensitivity of tunnels in the Jammu Region (JR) by evaluating the influence of site conditions, tunnel lining, and reinforcement properties. A key strength of this study is its use of both analytical and numerical approaches. Combining these methods is crucial for capturing the complex interaction between seismic waves and tunnel structures, especially in a region with such intricate geological conditions. The maximum ground displacement and settlement were analyzed at the tunnel crown across three proposed seismic hazard zones. For zones A, B, and C, the peak ground acceleration (PGA) was determined to be greater than 0.5 g, between 0.3 and 0.5 g, and less than 0.3 g, respectively. Based on the findings, specific guidelines and recommendations are proposed for designing sustainable and resilient underground structures in the Himalayas, including the retrofitting of existing ones. In the context of the study, major infrastructure projects within the JR are highlighted, with their locations indicated on the study area map presented in Figure 1. This map serves as a visual reference to the key projects assessed for seismic sensitivity, illustrating the geographical distribution of these critical infrastructures within the seismically active and geologically complex region.

Figure 1

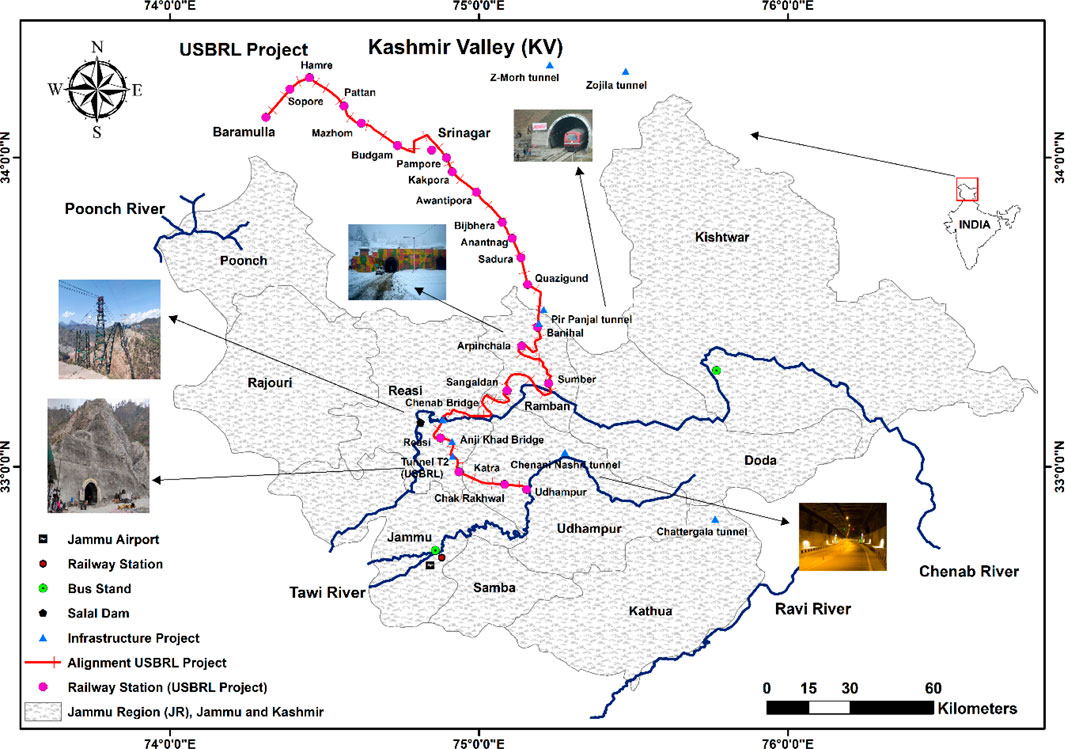
Figure 1. Study area map depicting major tunneling projects in and around the Jammu region, situated in the northwestern part of the Himalayas. The Udhampur-Srinagar-Baramulla Rail Link (USBRL) project is graphically illustrated by a red line, delineating prominent railway stations denoted by distinct pink circles.

The findings from this study have broader implications beyond J&K. The methodologies and insights can be applied to global-level projects, particularly in other seismically active and geologically complex areas. This study offers valuable guidance for creating sustainable and resilient underground structures worldwide. Additionally, the study’s approach can inform the design of underground weapon storage facilities, metro systems, and military safe houses in various global contexts. This work is particularly significant for the safety of people living in Himalayan cities, where the risk of seismic activity and landslides is ever-present. By contributing to the design of safer and more resilient infrastructure, this study directly impacts the wellbeing of these communities, reducing the potential for catastrophic failures during seismic events. Moreover, the study not only advances structural resilience but also contributes to Himalayan geological safety by integrating local geological characteristics into the design process. Moreover, this work aligns with the United Nations Sustainable Development Goals (SDGs), particularly SDG 9 and SDG11, which emphasizes building resilient infrastructure, and promoting sustainable urban expansion. By focusing on sustainable and resilient design in a geologically challenging region, this study contributes to the global effort to enhance infrastructure resilience and safety, ultimately supporting the broader goal of sustainable development. However, detailed site-specific planning and design remain crucial for achieving sustainable and resilient infrastructure under diverse geological conditions.

2 Seismic tunnel damage and performance assessment

2.1 Seismic tunnel damage

Historical earthquakes in various regions worldwide have previously resulted in devastating damage to infrastructure projects such as tunnels, bridges, highways, railway tracks, as well as hydroelectric and nuclear power plants (Uddin et al., 2013; Argyroudis et al., 2019; Proske, 2022). These seismic events have left a trail of destruction and posed significant challenges to the resilience and stability of critical structures. In the seismic annals, notable instances of infrastructure susceptibility to seismic perturbations are discernible through historical seismic events (Blagen et al., 2022). An illustrative manifestation transpired during the 1995 Kobe earthquake in Japan, where the Daikai station, bereft of discernible seismic design considerations, underwent complete structural collapse (Ide et al., 1996; Aldrich, 2011). Another seismic episode of profound consequence materialized during the 1999 Chi-Chi earthquake in Taiwan, wherein 49 of the 57 tunnels incurred damage (Chen et al., 2001; Shou and Wang, 2003). Notably, the tunnel portals exhibited severe impairment, characterized by varying degrees of fissuration and spalling within the tunnel lining (Shen et al., 2014; Zhang et al., 2018; Wen et al., 2021). The ramifications of seismic activity on subterranean structures were further elucidated by Jiang et al. (2010) in an analysis of the Uonuma railway tunnel in Niigata prefecture, Japan, following the seismic convulsions of the 2004 Chuetsu earthquake. Noteworthy was the discernible destabilization of a segment of Nagaoka Station, ostensibly teetering on the precipice of collapse subsequent to an aftershock, albeit eventually resuming operations following a brief suspension. The seismic convulsion of the 2005 Kashmir earthquake precipitated comprehensive deleterious effects upon the state of J&K, extending to both infrastructure and socio-economic domains (Naseer et al., 2010; Nabi, 2014). The unlined northern portal of the Muzaffarabad tunnel succumbed to collapse during this cataclysmic event. The chronicles of seismic-induced infrastructural vulnerabilities persist into the 21st century, exemplified by the 2016 Kumamoto earthquake (Kobayashi et al., 2017). This seismic event, characterized by a substantial magnitude M_w 7.3, underscored the vulnerability of underground structures, notably exemplified by the affliction sustained by the Tawarayama tunnel, situated 22.4 km distant from the epicenter of the principal seismic occurrence (Zhang et al., 2020).

In the European context, akin to the structural compromise witnessed in the Bolu tunnel in Turkey during the seismic upheaval of 1999, a parallel event unfolded with the decimation of the San Bendetto tunnel in Italy, succumbing to the seismic forces unleashed by the Norcia earthquake in 2016 (Callisto and Ricci, 2019). The intrinsic vulnerability of tunnel portals has been underscored, mandating meticulous attention to seismic design considerations to mitigate potential structural degradation. Instances of seismic impact on tunnels, particularly those subjected to substantial magnitude earthquakes, exhibit characteristic patterns of pavement impairment. Notably, manifestations such as uplift, fissuration, and groundwater seepage at construction joints and within concrete linings emerge as prevalent forms of damage (Wei et al., 2023). The nexus between seismic forces and tunnel infrastructure substantiates the imperative for comprehensive seismic design frameworks, particularly safeguarding the inherently susceptible tunnel portals. A noteworthy illustration of seismic-induced tunnel damage is evident in the aftermath of Japan’s 2004 Niigata earthquake, where a preponderance of afflicted tunnels manifested wall deformation (Wang et al., 2009). The structural anomalies were manifestly pronounced, encompassing heaving mechanisms affecting the bottom slab and distortions in the sidewalls (Xia et al., 2008; Kohno et al., 2023). The disparate modes of deformation elucidate the nuanced response of tunnel structures to seismic loading conditions, portraying a spectrum of damage states contingent upon the severity of the seismic environment and the consequential impact on structural integrity.

2.2 Seismic performance assessment

Analytical and numerical modeling methodologies, anchored in the intricate intricacies of S (Shear) and P (Primary) wave propagation dynamics, emerge as indispensable instruments for the assessment of the seismic tunnel performance (Wang 1993; Kouretzis et al., 2014; Zhuang et al., 2021; Bobet et al., 2023; Nie et al., 2024; Sun et al., 2024; Tran et al., 2024 analyzed the seismic stability of circular and rectangular tunnels in cohesive-frictional soils using Mohr-Coulomb criteria and 2D finite element limit analysis. Within the domain of analytical modeling, engineers embark on the formulation of intricate mathematical expressions and equations with the explicit goal of encapsulating the nuanced interplay between seismic waves and the inherent structural complexities of tunnels (Zhong et al., 2022). Specifically, in the context of S and P waves, engineers orchestrate the development of analytical models, wherein the dynamic response of the tunnel is meticulously delineated, incorporating considerations of material properties, geometric configurations, and the perturbing effects of seismic loading (Tsinidis et al., 2016; Mohsenian et al., 2019). This analytical framework equips engineers with a comprehensive comprehension of stress, strain, and displacement distributions permeating the tunnel infrastructure, enabling the discernment of critical points of vulnerability and the identification of potential modes of structural failure. As a corollary, analytical methodologies assume an instrumental role in refining tunnel designs and engendering targeted strategies tailored to fortify these subterranean structures against the vagaries of seismic hazards (Gülkan, 2013; Bela et al., 2023).

Concurrently, numerical modeling, as a complementary facet, engages advanced computational techniques to simulate the intricate behavioral nuances of tunnels subjected to seismic stimuli (Ding et al., 2006; Abate and Massimino, 2017). Predominantly exemplified by the Finite Element Analysis (FEA) methodology, this numerical approach discretizes the tunnel and its surrounding geological milieu into discrete elements, thereby facilitating the meticulous modeling of S and P wave propagation dynamics and their consequential impact on tunnel constituents (Kouretzis et al., 2013; Brodic et al., 2017; Xu et al., 2024). The numerical solution of governing equations proffers quantifiable insights into the seismic response characteristics of tunnels, encompassing stress concentrations, deformations, and prospective loci of structural compromise. This symbiotic amalgamation of analytical and numerical modeling strategies not only amplifies the predictive capacities of engineering endeavors but also expedites the exploration of diverse seismic scenarios, culminating in the optimization of tunnel designs tailored towards elevated seismic resilience (Fabozzi et al., 2018; Huang et al., 2022; Chen et al., 2023).

3 Methodology

3.1 Seismic hazard and zonation

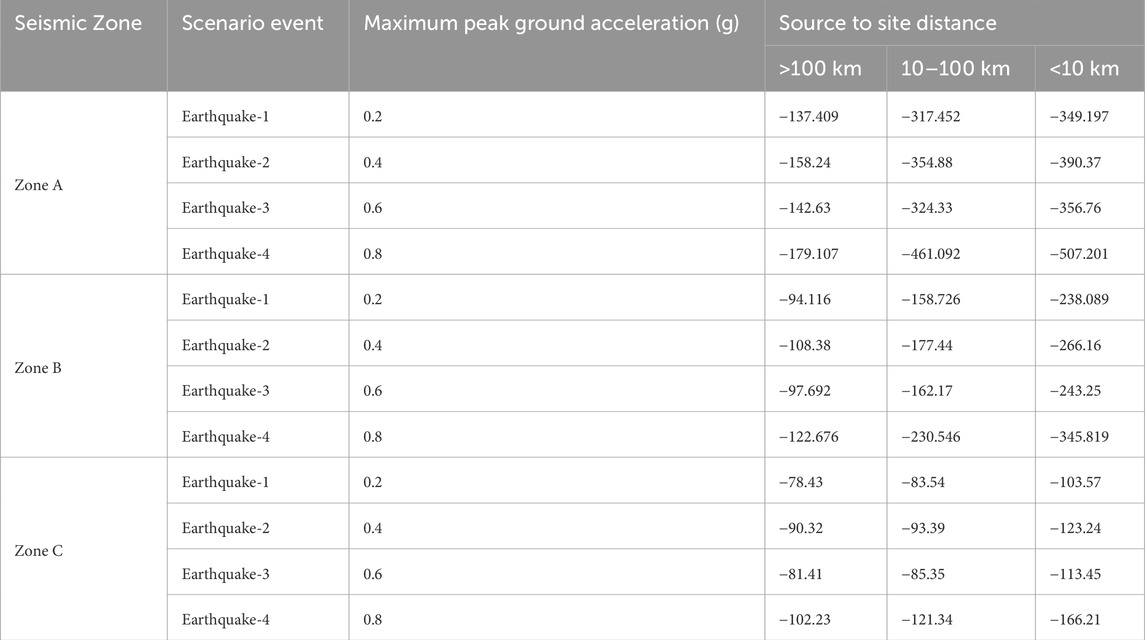
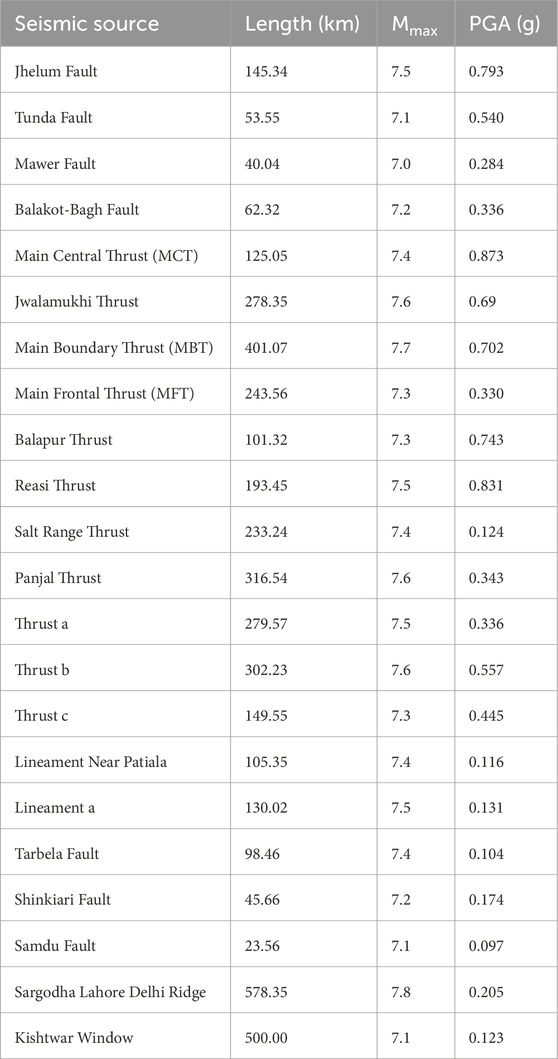
To initiate the seismic sensitivity analysis, the initial step involves delineating seismic zones based on observed peak ground acceleration (PGA) at the bedrock level. This study utilized the seismic sources outlined in Appendix A to evaluate PGA values at the bedrock. As illustrated in Figure 2, the Jammu region (JR) is segmented into three distinct zones, determined by the computed PGA values for selected sites, following the methodologies established by Cornell (1968).

Figure 2

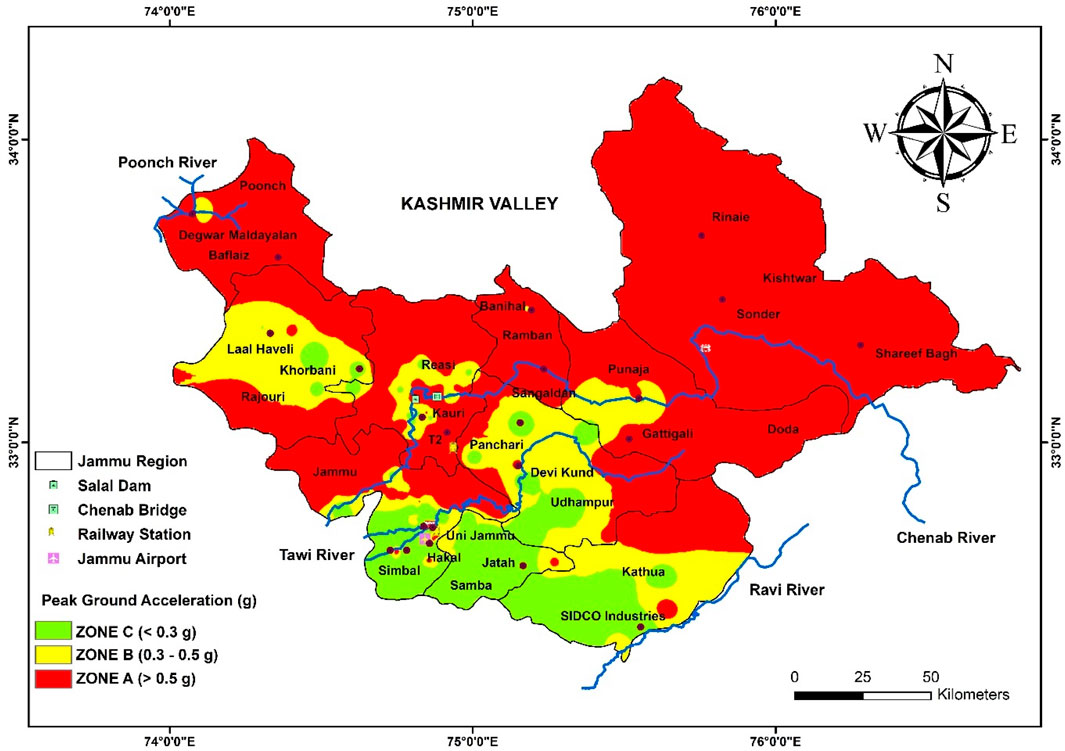
Figure 2. Seismic zones based on hazard level corresponding to 1,000 years return period. This return period refers to the estimated average time interval between occurrences of an earthquake event with the proposed peak ground acceleration (PGA) value that is expected to be experienced approximately once every 1,000 years at any location within study area.

3.2 Model parameters

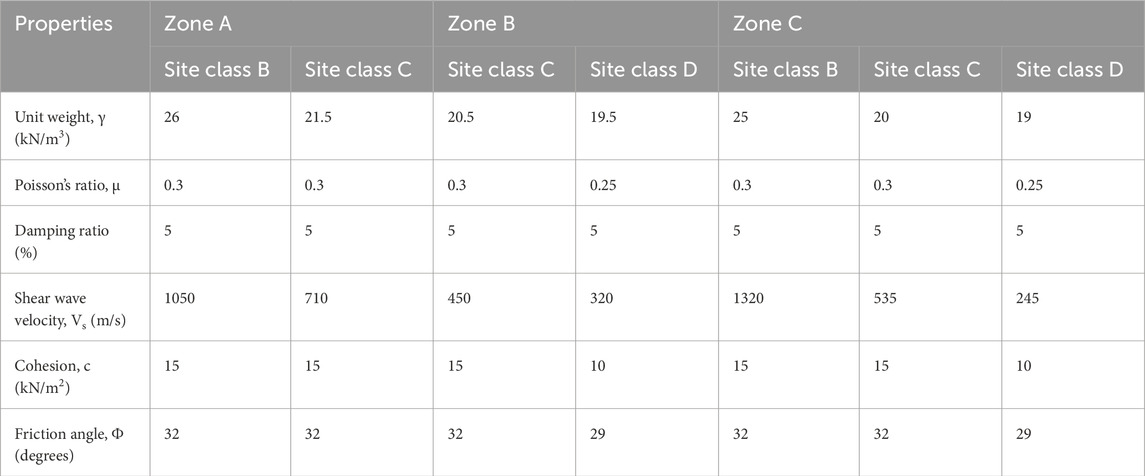
Following the zoning process, the subsequent step involved defining geotechnical and geophysical parameters specific to each zone, tailored to local site conditions (Table 1). These parameters served as input for both analytical and numerical simulations of the surrounding terrain. Observational data indicated that Zones A, B, and C exhibit distinct geotechnical and geophysical characteristics, which significantly influence infrastructure design and seismic response modeling. Zone A sites featured high-density, stiff soils in Site Class B and softer soils in Site Class D, necessitating robust seismic design. Zone B sites presented similar conditions, with a focus on Site Class D (softer soils) requiring additional stability measures. Site belonging to Zone C mirrored these characteristics, emphasizing the need for tailored design strategies across different site classes to address varying soil stiffness and density.

Table 1

Table 1. Zone based geotechnical and geophysical characterisation.

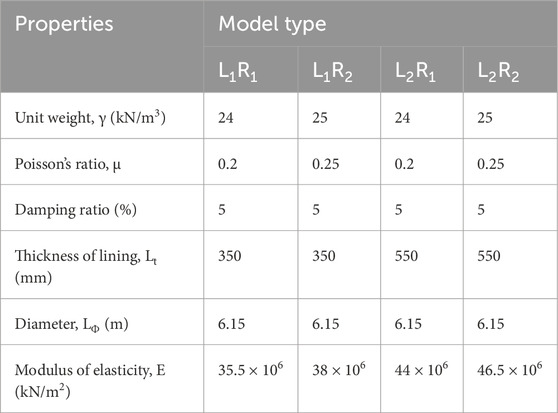
In addition to the properties of the surrounding terrain, the material properties for the assumed tunnel models are also specified. Table 2 outlines specifications for different tunnel models based on their lining and reinforcement properties. All models have almost same unit weight and damping ratio but differ in Poisson’s ratio, lining thickness, and modulus of elasticity. Models with thinner linings and lower moduli of elasticity are contrasted with those featuring thicker linings and higher moduli. These variations in properties affect the tunnel’s structural performance and stability.

Table 2

Table 2. Specification of tunnel model based on lining and reinforcement properties.

3.3 Intensity-response relationship and fragility function

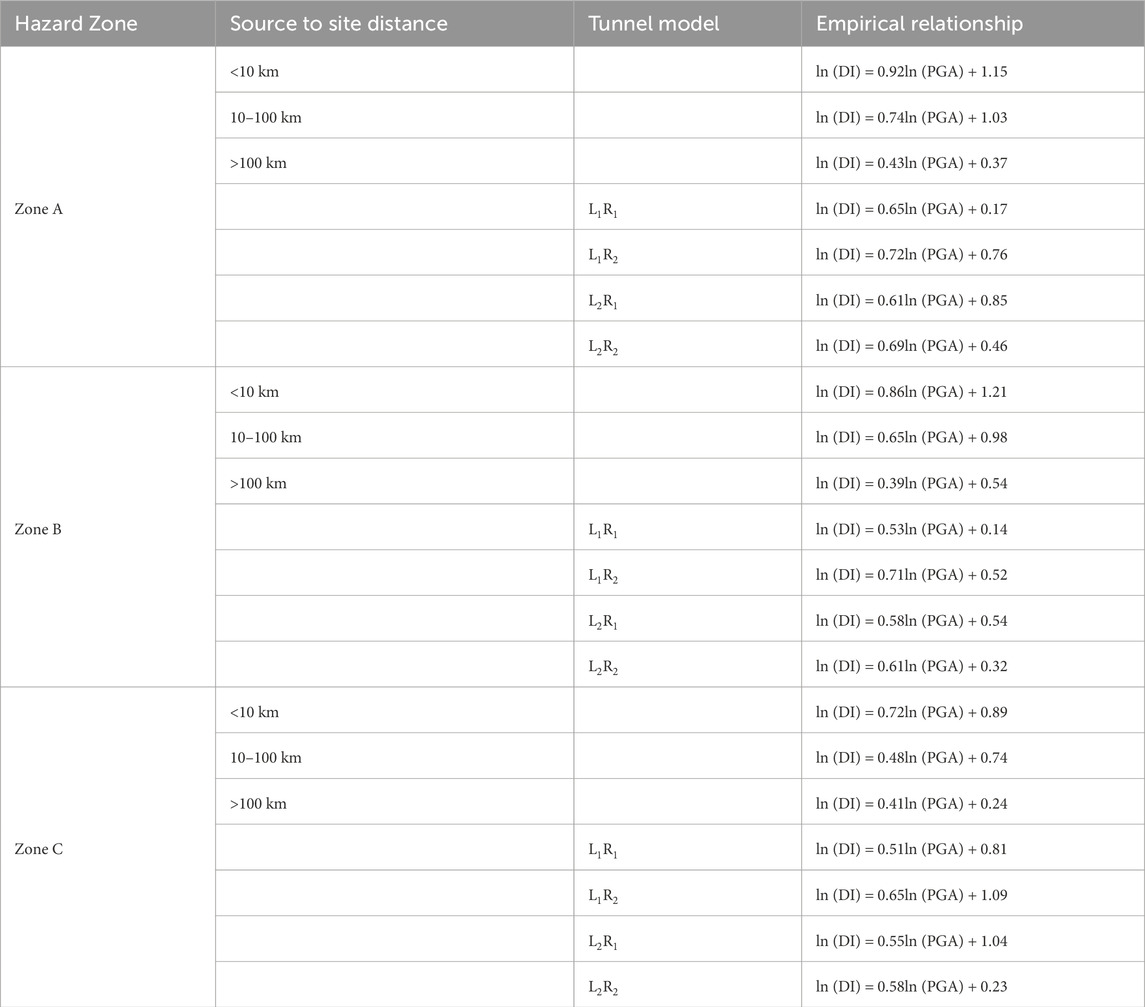
To establish the seismic fragility functions, the intensity-response relationship must be determined for each site associated with a specific tunnel model. To accomplish this, the relationships are developed for all three zones, considering source-to-site distance and the four tunnel models outlined in Table 2. These relationships are captured as empirical equations correlating seismic intensity ($IM$) with PGA (Table 3), following the methodology proposed by Argyroudis and Pitilakis (2012). In Zone A, the sensitivity to PGA is markedly distance-dependent: within 10 km, the slope is steeper, indicating increased responsiveness, whereas beyond 100 km, the slope flattens, signaling reduced sensitivity. Tunnel models L1R1, L1R2, L2R1, and L2R2 exhibited distinct response characteristics, with variations in slope and intercept values that affect their seismic behavior. In Zone C, analogous distance-dependent empirical relationships are observed, with each tunnel model displaying unique intensity-response patterns, underscoring the differential seismic performance across models and zones.

Table 3

Table 3. Seismic intensity-response relationship for defined zones in the present study.

To assess structural vulnerability across various damage states, fragility functions are defined based on selected dominant intensity measures (${IM}_D$), which illustrate the structure’s or system’s response to specific hazard scenarios (Lee et al., 2024). According to Equation 1, these fragility functions are represented by fragility curves that follow a lognormal distribution, assuming that all uncertainty within the database is captured solely by median uncertainty.

$P\left[DS\ge {DS}_i\left|IM\right.\right]=\mathrm{\Phi }\left[\frac{\mathit{ln}IM-\mathit{ln}{IM}_{{DS}_i}}{{\beta }_{total}.{DS}_i}\right](1)$

${\beta }_{total}=\sqrt{{{\beta }_C}^2+{{\beta }_D}^2+{{\beta }_{DS}}^2}(2)$

Within the limit state threshold framework, the Damage State ($DS$) defines specific levels of deterioration in the tunnel lining under seismic loading, reflecting various stages of damage. The standard normal cumulative distribution function (Φ) is used to model the probabilistic nature of damage occurrence. The median threshold value of the seismic intensity measure ($IM$) for each damage state (${IM}_{{DS}_i}$) represents the seismic intensity at which the damage is most likely to occur, serving as a reference for assessing tunnel resilience under varying seismic conditions. This approach is crucial for identifying vulnerability levels and informing design strategies that enhance tunnel safety and performance during seismic events. The rigorous assessment of lognormal standard deviations incorporates the influences of tunnel support capacity (${\beta }_C$), seismic demand (${\beta }_D$), and damage state threshold determination (${\beta }_{DS}$), each recognized as significant sources of uncertainty requiring detailed analysis. Total uncertainty, denoted as ${\beta }_{total}$ is computed using Equation 2. Here, ${\beta }_D$ is estimated based on the maximum bending moment, which reflects the tunnel’s capacity and seismic demand. The intensity-response correlation and fragility cruves for each seismic zone, considering various soil class conditions, are based on the principles outlined in Equation 1. In this study, fragility functions are developed and examined for both analytical and numerical approaches.

4 Analytical approach to seismic sensitivity assessment

This study employed a closed-form analytical solution developed by Kouretzis et al. (2014) to determine the maximum thrust ($T_{\mathit{max}}$) and bending moments ($M_{\mathit{max}}$) within tunnel linings, induced by the deformation resulting from compressional P-wave propagation.

Maximum thrust ($T_{\mathit{max}}$) exerted under conditions of full slippage and no slippage is denoted by Equation 3 and Equation 4 respectively.

$T_{\mathit{max}}=\pm \left[K_3+K_5\right].{\sigma }_{\mathit{max}}.\frac{R_T}{2}(3)$

$T_{\mathit{max}}=\pm \left[K_3+K_4\right].{\sigma }_{\mathit{max}}.\frac{R_T}{2}(4)$

Maximum bending moment ($M_{\mathit{max}}$) exerted under conditions of full slippage and no slippage is denoted by Equations 5 and 6, respectively.

$M_{\mathit{max}}=\pm \left[\left(\frac{\left(1-2{\mu }_{ST}\right)C_R}{6F_R}\right)K_3+K_5\right].{\sigma }_{\mathit{max}}.\frac{{R_T}^2}{2}(5)$

$M_{\mathit{max}}=\pm \left[\left(\frac{\left(1-2{\mu }_{ST}\right)C_R}{6F_R}\right)K_3+1-\frac{K_4}{2}-K_6\right].{\sigma }_{\mathit{max}}.\frac{{R_T}^2}{2}(6)$

The parameters introduced in Equations 5, 6 are further detailed in Equations 7–12:

$K_3=\left(\frac{2\left(1-{\mu }_{ST}\right)}{1+\left(1-2{\mu }_{ST}\right)C_R}\right)(7)$

$K_4=\left(\frac{\left(1-2{\mu }_{ST}\right)\left(1-C_R\right)F_R-\frac{{\left(1-2{\mu }_{ST}\right)}^2{C}_R}{2}+2}{\left[\left(3-2{\mu }_{ST}\right)+\left(1-2{\mu }_{ST}\right)C_R\right]F_R+\left[\frac{5-6{\mu }_{ST}}{2}\right]\left(1-2{\mu }_{ST}\right)C_R+\left(6-8{\mu }_{ST}\right)}\right)(8)$

$K_5=\left(\frac{4\left(1-{\mu }_{ST}\right)}{2F_R+5-6{\mu }_{ST}}\right)(9)$

$K_6=\left(\frac{\left[1+\left(1-2{\mu }_{ST}\right)C_R\right]F_R-\left[\frac{\left(1-2{\mu }_{ST}\right)C_R}{2}\right]-2}{\left[\left(3-2{\mu }_{ST}\right)+\left(1-2{\mu }_{ST}\right)C_R\right]F_R+\left[\frac{5-6{\mu }_{ST}}{2}\right]\left(1-2{\mu }_{ST}\right)C_R+\left(6-8{\mu }_{ST}\right)}\right)(10)$

The mathematical formulations defining the compressibility ratio and flexibility ratio are expounded as follows:

$C_R=\frac{E_{ST}\left(1-{{\mu }_{TL}}^2\right)R_T}{E_{TL}{t}_{TL}\left(1+{\mu }_{ST}\right)\left(1-2{\mu }_{ST}\right)}(11)$

$F_R=\frac{E_{ST}\left(1-{{\mu }_{TL}}^2\right){R_T}^3}{6E_{TL}I\left(1+{\mu }_{ST}\right)}(12)$

Herein, the parameters are defined as follows: $E_{ST}$ signifies the Young’s Modulus of the surrounding terrain, $E_{TL}$ denotes the Young’s Modulus of the tunnel lining material, ${\mu }_{ST}$ represents the Poisson’s ratio of the surrounding terrain, ${\mu }_{TL}$​ indicates the Poisson’s ratio of the tunnel lining material, $t_{TL}$ characterizes the thickness of the tunnel lining, and $I$ stands for the moment of inertia pertaining to the tunnel lining.

The influence of site conditions and lining properties for this approach of analytical investigation is discussed here.

4.1 Influence of site conditions

The analysis indicated that Zone A consistently exhibits the highest thrust, particularly within close proximities (<10 km), where the seismic response is twofold greater than that of Zone B (Table 4). Notably, during the most intense seismic event, Zone A experienced thrust magnitudes exceeding those in Zone C by over threefold, highlighting its elevated seismic susceptibility. Zone B demonstrated a moderate response, with thrust magnitudes approximately half of those in Zone A at equivalent distances, yet still surpassing Zone C, which recorded the lowest thrust across all conditions. The seismic impact on Zone C is substantially less pronounced, with thrust magnitudes being only a fraction of those in Zones A and B, indicating its significantly reduced seismic sensitivity.

Table 4

Table 4. Maximum thrust (in kN) under selected site conditions based on analytical approach.

Zone A exhibited the highest bending moments, particularly for near-field sources, where these values were nearly fivefold greater than those observed for any far field-source (Table 5). For instance, during Earthquake-4, characterized by a PGA of 0.8 g, the bending moment in Zone A peaked at 167.38 kN m, indicating significant structural demands. In contrast, Zone B demonstrated moderate bending moments, typically ranging from 50% to 70% of those in Zone A. At close distances during Earthquake-4, Zone B recorded a bending moment of 114.12 kN m, reflecting a substantial yet comparatively lower impact. Zone C displayed the lowest bending moments across all scenarios, with values generally less than half of those in Zone A. Even under the most intense event at close distances, the bending moment in Zone C reached only 54.85 kN m, underscoring a significantly lower seismic impact. This comparison underscored the escalating seismic risk from Zone C to Zone A, highlighting the necessity for more robust design considerations in the most impacted zones.

Table 5

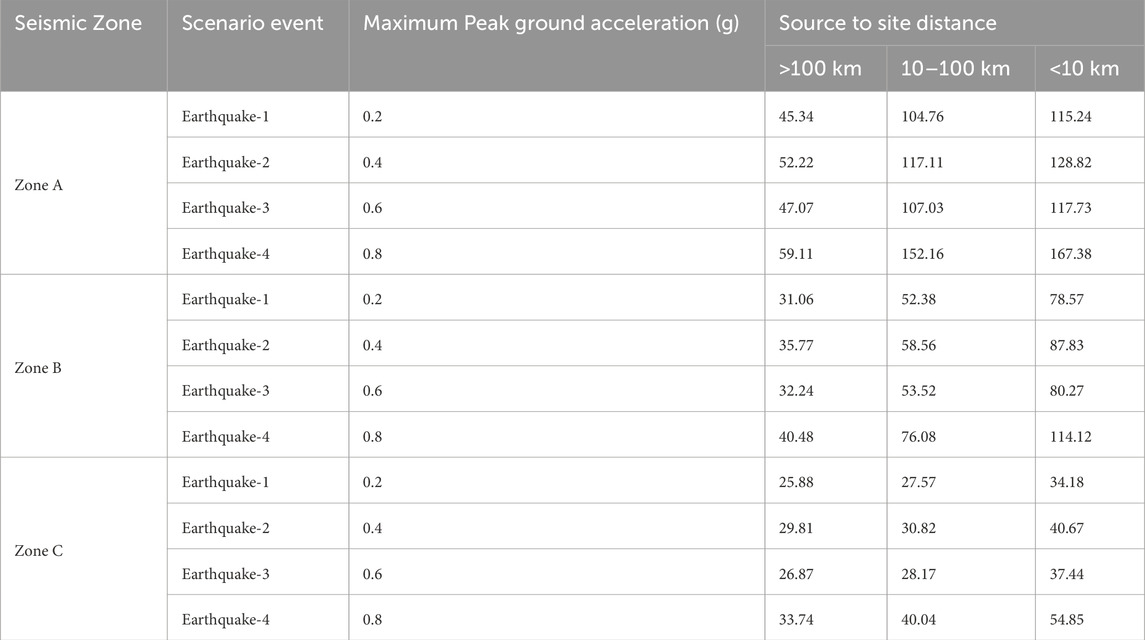
Table 5. Maximum bending moment (in kN m) under selected site conditions based on analytical approach.

4.2 Influence of lining and reinforcement properties

Zone A with impacts during Earthquake-4 (PGA = 0.8g) being approximately three to four times greater than those observed in Zone B and nearly fivefold higher than those in Zone C. For instance, the thrust values in Zone A are markedly elevated compared to Zone B, which exhibits thrust values approximately twice those recorded in Zone C (Table 6). This pattern showed the progressive increase in seismic loads from Zone C to Zone A across the selected tunnel models.

Table 6

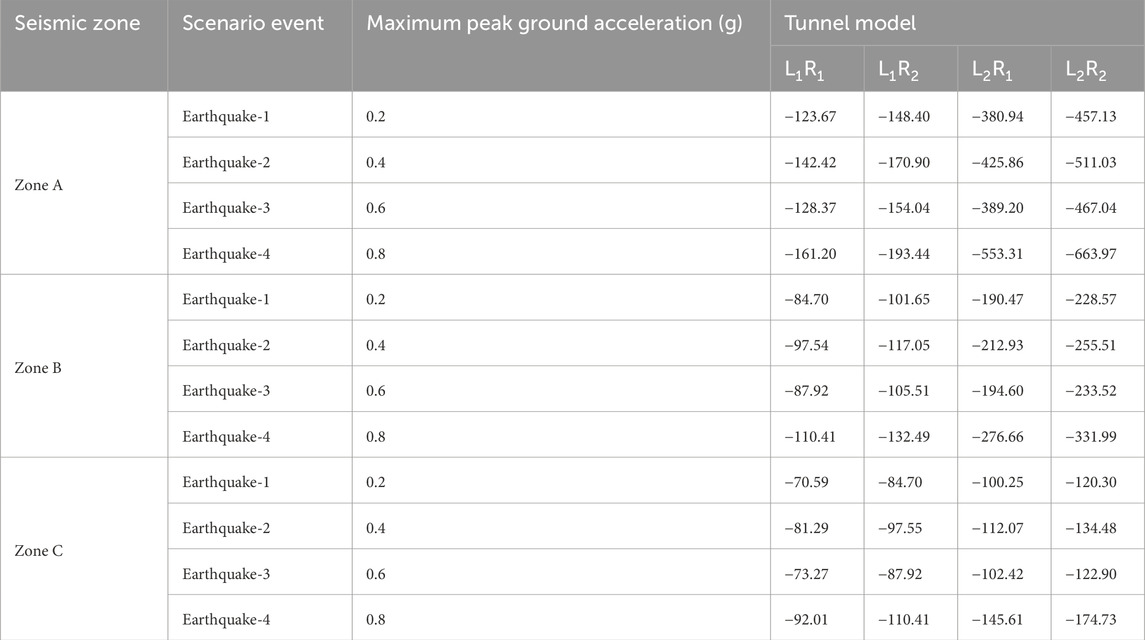
Table 6. Maximum thrust (in kN) under selected lining and reinforcement conditions based on analytical approach.

Table 7 presents a comparative analysis of maximum bending moments ($M_{\mathit{max}}$) across different tunnel models within the three proposed zones. Zone A, characterized by its higher seismic potential, exhibited substantially larger bending moments compared to Zones B and C. During Earthquake-4 (PGA = 0.8g), bending moments in Zone A were up to three to four times greater than those in Zone B and approximately four to five times higher than those in Zone C. For instance, tunnel model L2R2 in Zone A experienced a maximum bending moment of 365.18 kN m, whereas the same model recorded 182.59 kN m in Zone B and only 96.17 kN m in Zone C. In Zone B, while bending moments are notably lower, they remain significant, with values approximately half of those in Zone A, as evidenced by the maximum bending moment of 182.59 kN m for tunnel model L2R2 during the most intense scenario.

Table 7

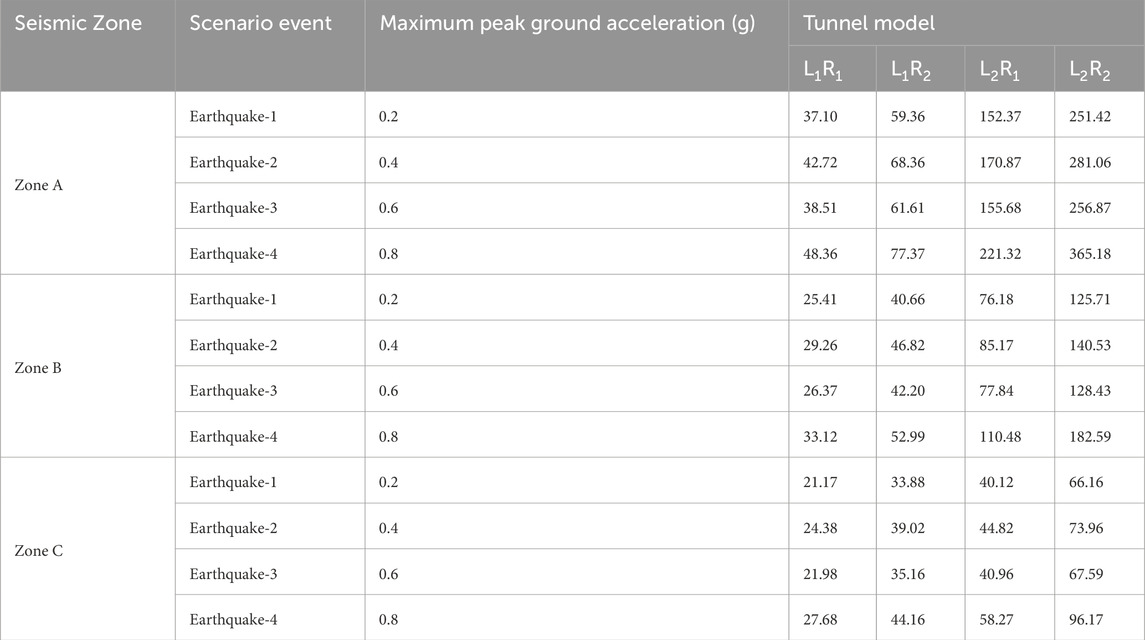
Table 7. Maximum bending moment (in kN m) under selected lining and reinforcement conditions based on analytical approach.

5 Numerical approach to seismic sensitivity assessment

To assess the seismic sensitivity of the proposed tunnel models in various types of surrounding terrain, the study conducted a series of three-dimensional (3D) nonlinear time history analyses using Midas FE software (Midas GTS NX). It is highly suitable for seismic sensitivity analysis of tunnel models, offering advanced capabilities in nonlinear seismic response simulation, soil-structure interaction (SSI) modeling, and adherence to international seismic design standards for accurate and resilient tunnel assessments. These capabilities support sustainable tunnel design by enhancing resilience and reducing the need for extensive retrofitting. The Mohr-Coulomb (MC) constitutive model, specifically chosen for its applicability to isotropic materials is selectd for the analysis in this study. This model describes the elastoplastic behavior, based on plasticity principles, where a material experiences plastic deformation once it reaches a critical state. The critical state is defined by the stress ratio, which represents the ratio of applied shear stress to effective normal stress.

In this investigation, a deliberate enhancement beyond the minimum requirements is evident, as four non-frequent natural ground motions were meticulously selected: North-East India (1986), Uttarkashi (1991), Chamba (1995), and Chamoli (1999) earthquake events.

5.1 Influence of site conditions

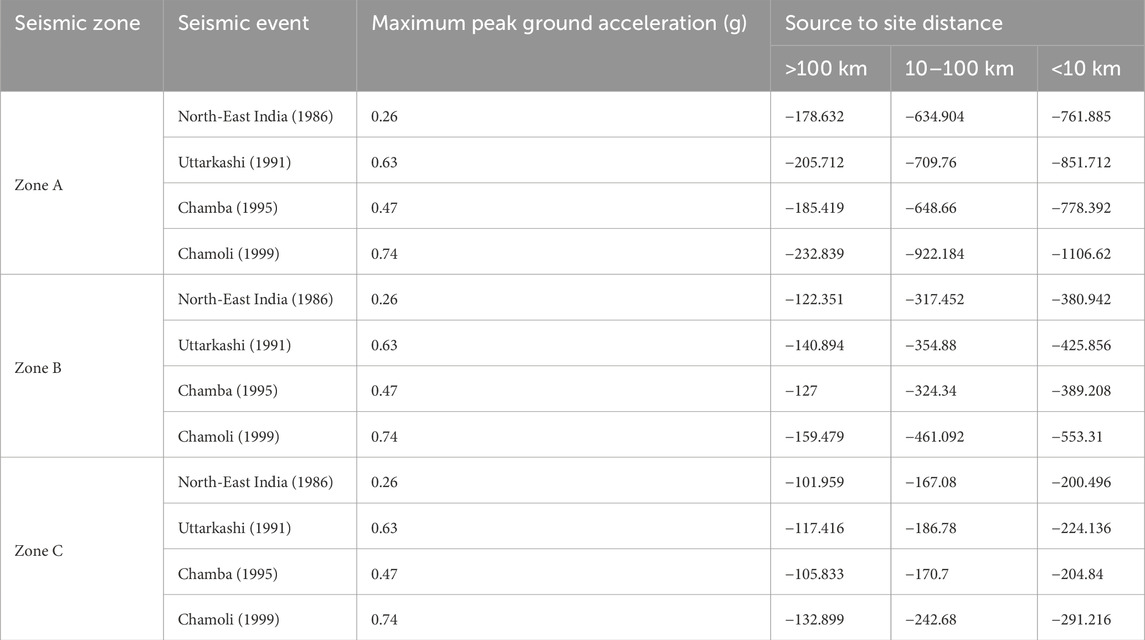
During the Chamoli (1999) event with a PGA of 0.74 g, the thrust at close distances (<10 km) reached approximately 1106.62 kN, which is roughly three times greater than that observed in Zone B and nearly fivefold higher than in Zone C (Table 8). In contrast, Zone B exhibited moderate thrust levels, with a maximum thrust of approximately 553.31 kN during the same event at close distances, reflecting reduced seismic impact relative to Zone A, yet still indicating considerable structural demands. Zone C recorded the lowest thrust values, highlighting a significantly lower seismic force compared to both Zone A and Zone B.

Table 8

Table 8. Maximum thrust (in kN) under selected site conditions based on numerical approach.

During the Uttarkashi (1991) event with a PGA of 0.63 g, the maximum bending moment for Tunnel Model L2R2 in Zone A at close distances (<10 km) was approximately twice as high as those recorded in Zone B and nearly five times greater than in Zone C (Table 9). Zone B exhibited a moderate seismic impact, with bending moments for the same event and distance being about half of those in Zone A, indicating a comparatively reduced level of seismic forces. In contrast, Zone C demonstrated the lowest bending moments, with values during the Uttarkashi (1991) event at close distances being one-third of those in Zone B and about one-fifth of those in Zone A. These differences illustrated the critical need for enhanced lining and reinforcement strategies in higher seismic zones to address varying structural demands and ensure resilience against substantial seismic loading.

Table 9

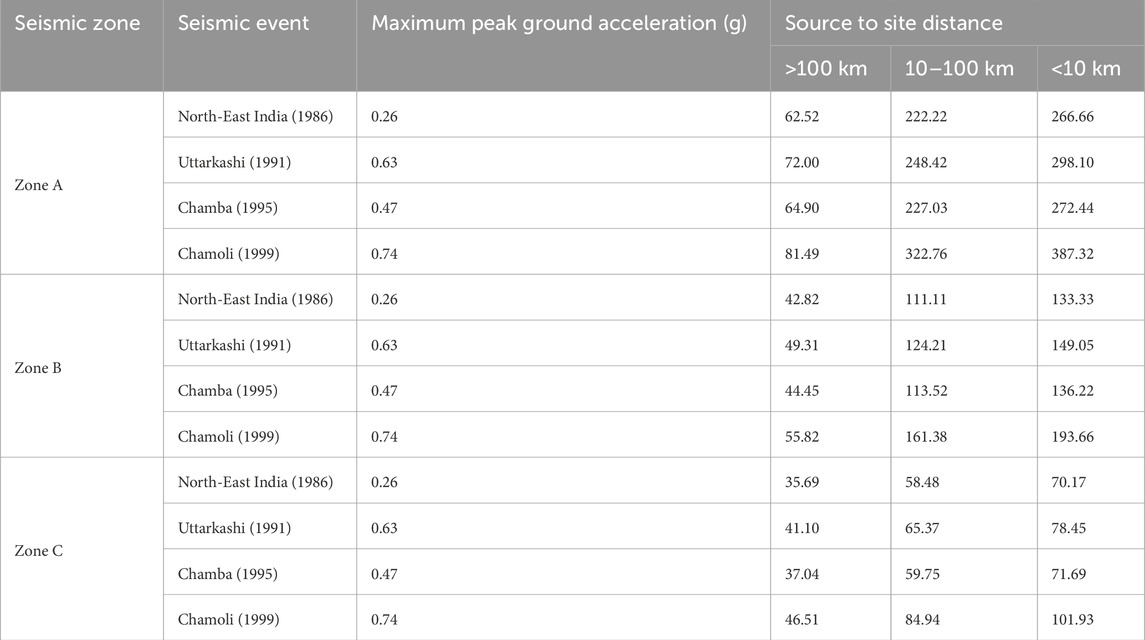
Table 9. Maximum bending moment (in kN m) under selected site conditions based on numerical approach.

5.2 Influence of lining and reinforcement properties

The Chamba (1995) event, with a PGA of 0.6 g, resulted in tunnel model L2R2, which features robust lining and reinforcement, experiencing maximum thrust in Zone A that was four times greater than that observed in Zone B and approximately six times higher than in Zone C (Table 10). For the same event, the thrust in Zone B was half of that recorded in Zone A and about twice the value observed in Zone C. In Zone C, the maximum thrust for tunnel model L2R2 was approximately one-third of the thrust in Zone B and about one-fifth of the values recorded in Zone A.

Table 10

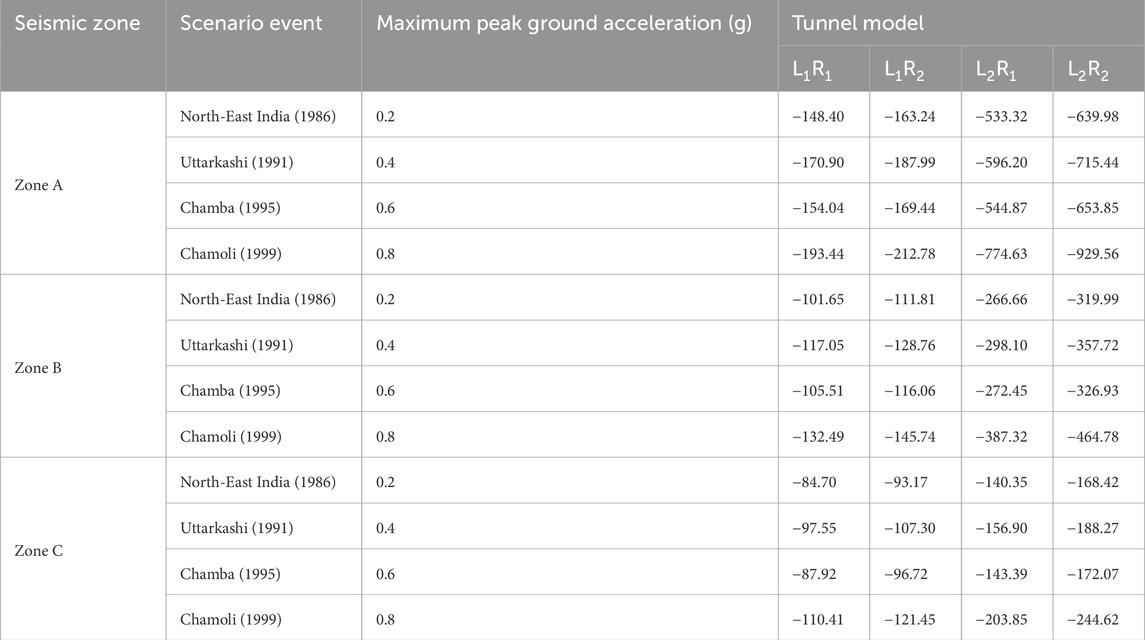
Table 10. Maximum thrust (in kN) under selected lining and reinforcement conditions based on numerical approach.

In Zone A, during the Chamoli (1999) event with a PGA of 0.74 g, tunnel m odel L2R2, featuring robust reinforcement, exhibited bending moments that were approximately three times greater than those recorded in Zone B and five times higher than in Zone C (Table 11). In Zone B, which experienced moderate ground shaking, the bending moments were comparatively reduced. During the North-East India (1986) event with a PGA of 0.26 g, the same tunnel model showed bending moments about double those observed in Zone C and approximately half of those in Zone A. This reduction reflected the decreased seismic demands but still emphasizes the critical role of reinforcement in preserving structural integrity. Tunnel model L1R2 recorded bending moments that were about one-third of those in Zone B and one-fifth of those in Zone A, underscoring the effectiveness of reinforcement in managing bending stresses even under lower seismic forces.

Table 11

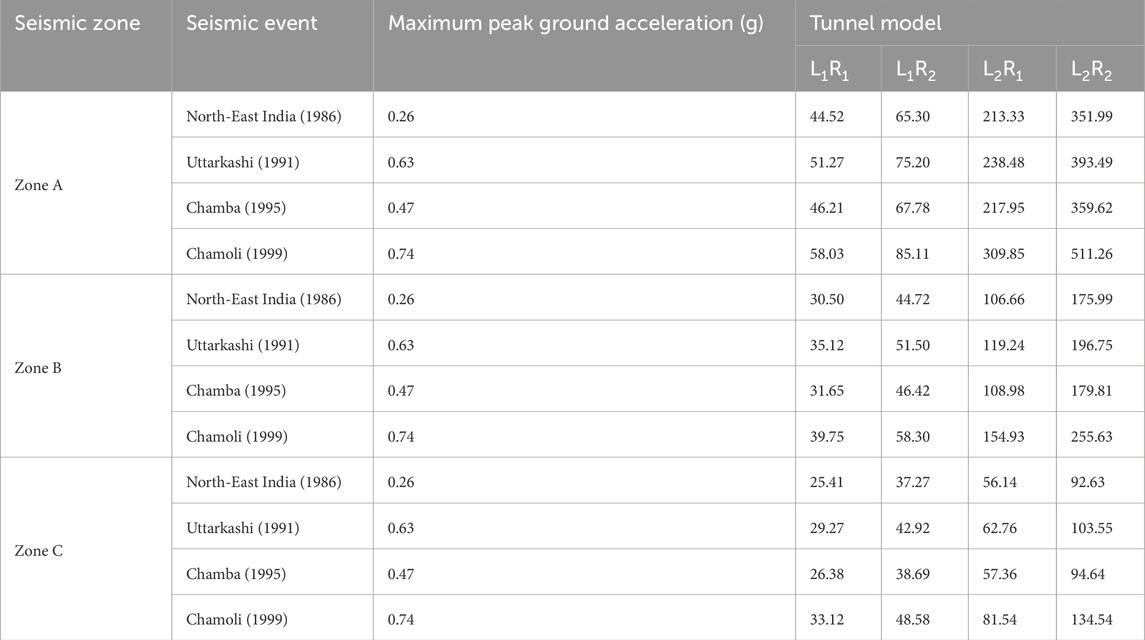
Table 11. Maximum bending moment (in kN m) under selected lining and reinforcement conditions based on numerical approach.

6 Discussion

In this study, fragility functions are developed for various site conditions and tunnel lining properties to assess seismic forces, using both analytical and numerical approaches as detailed in Sections 4 and 5, respectively. It was found that for each 10 km increase in distance, the probability of damage decreases by 21.18% for the analytical approach and 23.04% for the numerical approach. Overall, considering all tunnel model cases, Zone A exhibited 43.34% greater sensitivity to damage compared to Zone B. For each 0.1 g increase in PGA results in a 8.14% increase in probability of damage for the analytical approach, while the numerical analysis showed changes of 10.21%. Additionally, considering the variation in tunnel lining properties as defined in Table 2, the difference in damage probability for each 0.2 g change in PGA is 23.45%, 14.24%, 19.33%, and 32.13% for tunnel models L1R1, L1R2, L2R1, and L2R2 in Zone A. In Zone B, these changes are 56.89%, 19.47%, 18.95%, and 9.57%, respectively. Fragility curves for these findings are illustrated in Figures 3, 4.

Figure 3

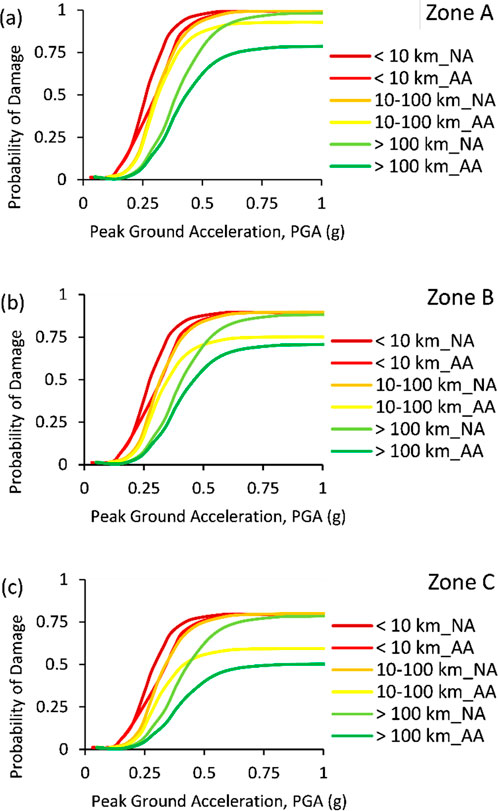
Figure 3. Seismic zone-specific fragility curves tailored to diverse site conditions for: (A) Zone A, (B) Zone B and (C) Zone C.

Figure 4

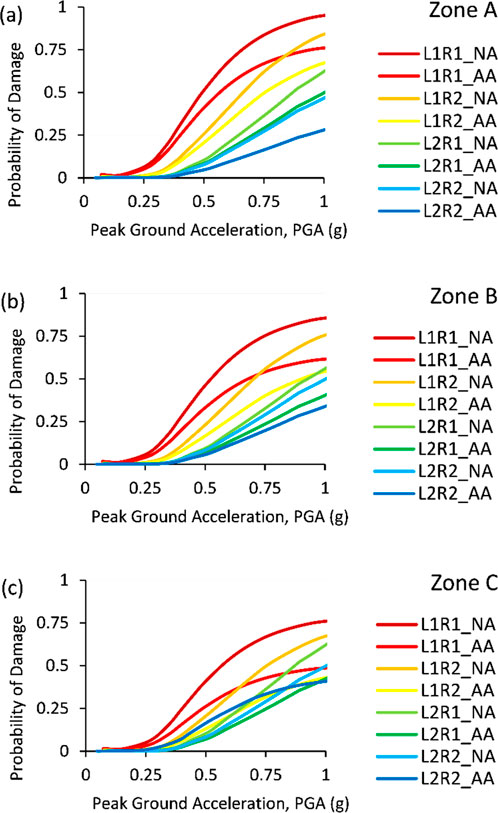
Figure 4. Seismic zone-specific fragility curves tailored to diverse lining and reinforcement conditions for: (A) Zone A, (B) Zone B and (C) Zone C.

For the proposed three seismic zones and four tunnel models, maximum ground displacement and maximum tunnel crown displacement are calculated and compared, as shown in Figure 5. It is observed that ground displacement is nearly identical for tunnel models in Zones B and C. The differences in crown displacement between analytical and numerical outcomes are 34.34%, 43.23%, −11.24%, and 73.04% for models L1R1, L1R2, L2R1, and L2R2, respectively. For tunnel crown settlement, models in Zone A exhibited a 42.28% greater increase in settlement compared to Zones B and C, which show similar patterns across all selected tunnel models.

Figure 5

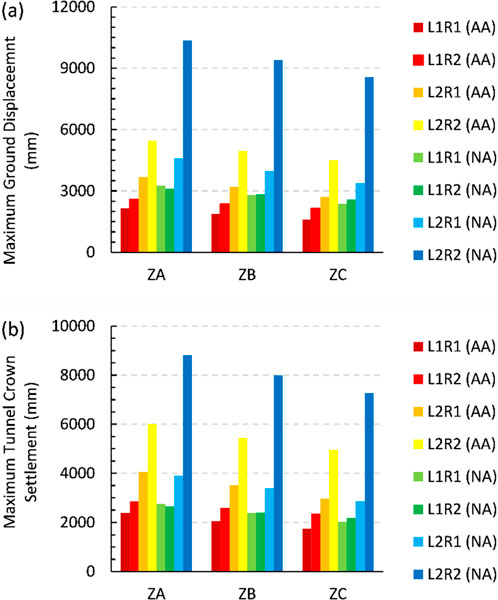
Figure 5. (A) Maximum ground displacement and (B) maximum settlement at tunnel crown for selected lining and reinforcement conditions.

7 Conclusion and future recommendations

In this study, seismic zones within Jammu Region (JR) in the northwestern part of the Himalays were delineated based on peak ground acceleration (PGA) at bedrock, and site-specific geotechnical and geophysical parameters were defined. The study employed both analytical and numerical modeling to assess the seismic performance of tunnels, focusing on P wave dynamics to identify vulnerabilities and inform design enhancements. The analytical approach revealed significant variations in seismic response due to site conditions, with Zone A consistently exhibiting the highest thrust and bending moments, up to threefold greater than in Zone C, indicating the critical need for robust design in this zone. Numerical analysis further demonstrated that robust lining and reinforcement, particularly in tunnel model L2R2, resulted in seismic demands in Zone A up to six times greater than in Zone C. Fragility analysis showed that with each 10 km increase in distance, damage probability decreases by 21.18% and 23.04% for the analytical and numerical approaches, respectively. Zone A exhibited 43.34% greater sensitivity to damage compared to Zone B, with a 0.1g increase in PGA leading to 8.14% and 10.21% rise in damage probability for the analytical and numerical approaches, respectively. Additionally, the study found significant variations in crown displacement across the three seismic zones and four tunnel models, with Zone A showing a 42.28% higher settlement than Zones B and C, emphasizing the critical role of seismic design in managing these vulnerabilities.

Based on the outcomes of the present study, following guidelines are proposed, with broader applicability to global projects in seismically active and geologically complex regions:

7.1 Retrofitting existing structures

(A.1) Prioritize the retrofitting of existing tunnels located in high-risk seismic zones by upgrading lining and reinforcement systems to align with the latest construction standards.

(A.2) Utilize advanced techniques, including fiber-reinforced polymers (FRP) and steel jacketing, to enhance the seismic resilience of older tunnels.

7.2 Sustainability and environmental integration

(B.1) Integrate sustainable practices into tunnel design and construction by utilizing locally sourced, low-impact materials that maintain resilience under seismic stress.

(B.2) Minimize environmental disruption during construction and retrofitting, particularly in ecologically sensitive regions such as the Himalayas.

7.3 Global applicability and knowledge transfer

(C.1) these guidelines to other seismically active and geologically complex regions by accounting for local seismic hazards, geological conditions, and infrastructure requirements.

(C.2) Foster knowledge transfer and collaboration between countries and regions to share best practices, technological advancements, and lessons learned from seismic events.

The limitations for this study include a focus on PGA at bedrock without soil layer amplification, simplified seismic modeling that excludes multi-directional forces, and limited tunnel configurations, which may restrict generalization. Additionally, the site-specific data (Miceli et al., 2024) and regional applicability may not fully represent diverse conditions across the Himalayas, introducing epistemic uncertainties that could affect the accuracy and reliability of the presented numerical model. The work presented in this study aligns with the United Nations Sustainable Development Goals (SDGs), particularly SDG 9 (Industry, Innovation, and Infrastructure) and SDG 11 (Sustainable Cities and Communities), by advancing resilient infrastructure design and sustainable urban expansion in the seismic-prone Himalayan region. Through innovative seismic modeling and robust structural guidelines, it enhances the safety and durability of tunnels, mitigating disaster risks and fostering sustainable urban development. The focus on reducing geological risks and using eco-friendly materials also aligns with environmental sustainability, contributing to the long-term resilience and safety of communities in this geologically complex area.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

AA: Writing–original draft, Writing–review and editing. PM: Funding acquisition, Resources, Writing–review and editing. BM: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research was supported and funded by the Sultan Qaboos University Research Funds (DVC/EMC/24).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abate, G., and Massimino, M. R. (2017). Parametric analysis of the seismic response of coupled tunnel–soil–aboveground building systems by numerical modelling. Bull. Earthq. Eng. 15, 443–467. doi:10.1007/s10518-016-9975-7

CrossRef Full Text | Google Scholar

Aldrich, D. P. (2011). The power of people: social capital’s role in recovery from the 1995 Kobe earthquake. Nat. hazards 56, 595–611. doi:10.1007/s11069-010-9577-7

CrossRef Full Text | Google Scholar

Argyroudis, S. A., Mitoulis, S. Α., Winter, M. G., and Kaynia, A. M. (2019). Fragility of transport assets exposed to multiple hazards: state-of-the-art review toward infrastructural resilience. Reliab. Eng. & Syst. Saf. 191, 106567. doi:10.1016/j.ress.2019.106567

CrossRef Full Text | Google Scholar

Argyroudis, S. A., and Pitilakis, K. D. (2012). Seismic fragility curves of shallow tunnels in alluvial deposits. Soil Dyn. Earthq. Eng. 35, 1–12. doi:10.1016/j.soildyn.2011.11.004

CrossRef Full Text | Google Scholar

Arora, S., Malik, J. N., and Sahoo, S. (2019). Paleoseismic evidence of a major earthquake event (s) along the hinterland faults: pinjore Garden Fault (PGF) and Jhajra Fault (JF) in northwest Himalaya, India. Tectonophysics 757, 108–122. doi:10.1016/j.tecto.2019.01.001

CrossRef Full Text | Google Scholar

Bela, J., Kossobokov, V., and Panza, G. (2023). Seismic Rigoletto: hazards, risks and seismic roulette applications. Front. Earth Sci. 11, 1136472. doi:10.3389/feart.2023.1136472

CrossRef Full Text | Google Scholar

Blagen, J. R., Davies, T. R. H., Wells, A., and Norton, D. A. (2022). Post-seismic aggradation history of the West Coast, South Island, Aotearoa/New Zealand; dendrogeomorphological evidence and disaster recovery implications. Nat. Hazards 114 (3), 2545–2570. doi:10.1007/s11069-022-05479-5

CrossRef Full Text | Google Scholar

Bobet, A., Yu, H., and Tiwari, N. (2023). Seismic response of shallow circular openings to Rayleigh waves. Tunn. Undergr. Space Technol. 135, 105036. doi:10.1016/j.tust.2023.105036

CrossRef Full Text | Google Scholar

Brodic, B., Malehmir, A., and Juhlin, C. (2017). Delineating fracture zones using surface-tunnel-surface seismic data, P-S, and S-P mode conversions. J. Geophys. Res. Solid Earth 122 (7), 5493–5516. doi:10.1002/2017jb014304

CrossRef Full Text | Google Scholar

Callisto, L., and Ricci, C. (2019). Interpretation and back-analysis of the damage observed in a deep tunnel after the 2016 Norcia earthquake in Italy. Tunn. Undergr. space Technol. 89, 238–248. doi:10.1016/j.tust.2019.04.012

CrossRef Full Text | Google Scholar

Chen, R., Lang, Z., Zhang, C., Zhao, N., and Deng, P. (2023). A paradigm for seismic resilience assessment of subway system. Tunn. Undergr. Space Technol. 135, 105061. doi:10.1016/j.tust.2023.105061

CrossRef Full Text | Google Scholar

Chen, Y. G., Chen, W. S., Lee, J. C., Lee, Y. H., Lee, C. T., Chang, H. C., et al. (2001). Surface rupture of 1999 Chi-Chi earthquake yields insights on active tectonics of central Taiwan. Bull. Seismol. Soc. Am. 91 (5), 977–985. doi:10.1785/0120000721

CrossRef Full Text | Google Scholar

Cornell, C. A. (1968). Engineering seismic risk analysis. Bull. Seismol. Soc. Am. 58 (5), 1583–1606. doi:10.1785/BSSA0580051583

CrossRef Full Text | Google Scholar

Ding, J. H., Jin, X. L., Guo, Y. Z., and Li, G. G. (2006). Numerical simulation for large-scale seismic response analysis of immersed tunnel. Eng. Struct. 28 (10), 1367–1377. doi:10.1016/j.engstruct.2006.01.005

CrossRef Full Text | Google Scholar

Fabozzi, S., Bilotta, E., Picozzi, M., and Zollo, A. (2018). Feasibility study of a loss-driven earthquake early warning and rapid response systems for tunnels of the Italian high-speed railway network. Soil Dyn. Earthq. Eng. 112, 232–242. doi:10.1016/j.soildyn.2018.05.019

CrossRef Full Text | Google Scholar

Fayaz, M., Meraj, G., Khader, S. A., and Farooq, M. (2022). ARIMA and SPSS statistics based assessment of landslide occurrence in western Himalayas. Environ. Challenges 9, 100624. doi:10.1016/j.envc.2022.100624

CrossRef Full Text | Google Scholar

Gülkan, P. (2013). A dispassionate view of seismic-hazard assessment. Seismol. Res. Lett. 84 (3), 413–416. doi:10.1785/0220130005

CrossRef Full Text | Google Scholar

Haider, S. A., Hussain, M., Ali, A., Abbasi, M. F., and Wani, S. (2023). Application of UAV photogrammetry and electrical resistivity tomography for characterization of a complex landslide: a case study from northwest Himalayas, Pakistan. Nat. Hazards 117 (3), 3043–3066. doi:10.1007/s11069-023-05977-0

CrossRef Full Text | Google Scholar

Huang, Z., Pitilakis, K., Zhang, D., Tsinidis, G., and Argyroudis, S. (2022). On the effects of salient parameters for an efficient probabilistic seismic loss assessment of tunnels in alluvial soils. Resilient Cities Struct. 1 (3), 24–39. doi:10.1016/j.rcns.2022.10.006

CrossRef Full Text | Google Scholar

Ide, S., Takeo, M., and Yoshida, Y. (1996). Source process of the 1995 Kobe earthquake: determination of spatio-temporal slip distribution by Bayesian modeling. Bull. Seismol. Soc. Am. 86 (3), 547–566. doi:10.1785/bssa0860030547

CrossRef Full Text | Google Scholar

Jiang, Y., Wang, C., and Zhao, X. (2010). Damage assessment of tunnels caused by the 2004 Mid Niigata Prefecture Earthquake using Hayashi’s quantification theory type II. Nat. hazards 53, 425–441. doi:10.1007/s11069-009-9441-9

CrossRef Full Text | Google Scholar

Kobayashi, H., Koketsu, K., and Miyake, H. (2017). Rupture processes of the 2016 Kumamoto earthquake sequence: causes for extreme ground motions. Geophys. Res. Lett. 44 (12), 6002–6010. doi:10.1002/2017gl073857

CrossRef Full Text | Google Scholar

Kohno, M., Higuchi, Y., and Ono, Y. (2023). Evaluating earthquake-induced widespread slope failure hazards using an AHP-GIS combination. Nat. Hazards 116 (2), 1485–1512. doi:10.1007/s11069-022-05725-w

CrossRef Full Text | Google Scholar

Kouretzis, G. P., Andrianopoulos, K. I., Sloan, S. W., and Carter, J. P. (2014). Analysis of circular tunnels due to seismic P-wave propagation, with emphasis on unreinforced concrete liners. Comput. Geotech. 55, 187–194. doi:10.1016/j.compgeo.2013.08.012

CrossRef Full Text | Google Scholar

Kouretzis, G. P., Sloan, S. W., and Carter, J. P. (2013). Effect of interface friction on tunnel liner internal forces due to seismic S-and P-wave propagation. Soil Dyn. Earthq. Eng. 46, 41–51. doi:10.1016/j.soildyn.2012.12.010

CrossRef Full Text | Google Scholar

Lee, J. H., Ansari, A., An, H., and Jeong, J. Y. (2024). Seismic loss and resilience modelling of bridges in soft soils: towards design of sustainable transportation infrastructure facilities. Sus. Resilient Infrastruct. 9 (2), 1–23. doi:10.1080/23789689.2024.2328979

CrossRef Full Text | Google Scholar

Mazaheri, A., Cheraghi Seifabad, M., Mahdavi, S., and Dehghani, B. (2021). Seismic sensitivity analysis of rigidity and thickness of tunnel lining by using Ground_Structure interaction method case study: roudbar lorestan dam. Geotechnical Geol. Eng. 39, 1557–1582. doi:10.1007/s10706-020-01576-z

CrossRef Full Text | Google Scholar

Miceli, E., Gino, D., and Castaldo, P. (2024). Approaches to estimate global safety factors for reliability assessment of RC structures using non-linear numerical analyses. Eng. Struct. 311, 118193. doi:10.1016/j.engstruct.2024.118193

CrossRef Full Text | Google Scholar

Min, A. K., Yue, F., Liao, K., Liu, B., Xiong, S., Jiang, X., et al. (2024). Seismic performance of joints of prefabricated corrugated steel utility tunnels Part (II)–Numerical analysis. J. Constr. Steel Res. 215, 108567. doi:10.1016/j.jcsr.2024.108567

CrossRef Full Text | Google Scholar

Mohsenian, V., Nikkhoo, A., and Hajirasouliha, I. (2019). Estimation of seismic response parameters and capacity of irregular tunnel-form buildings. Bull. Earthq. Eng. 17, 5217–5239. doi:10.1007/s10518-019-00679-0

CrossRef Full Text | Google Scholar

Nabi, P. G. (2014). Coordinating post-disaster humanitarian response: lessons from the 2005 Kashmir earthquake, India. Dev. Pract. 24 (8), 975–988. doi:10.1080/09614524.2014.964187

CrossRef Full Text | Google Scholar

Naseer, A., Khan, A. N., Hussain, Z., and Ali, Q. (2010). Observed seismic behavior of buildings in northern Pakistan during the 2005 Kashmir earthquake. Earthq. Spectra 26 (2), 425–449. doi:10.1193/1.3383119

CrossRef Full Text | Google Scholar

Nie, G. B., Wang, W., Zhang, C. X., Zhi, X. D., and Liu, K. (2024). Seismic evaluation of isolation performance on single layer cylindrical reticulated shells supported along four sides. Eng. Struct. 301, 117279. doi:10.1016/j.engstruct.2023.117279

CrossRef Full Text | Google Scholar

Proske, D. (2022). The collapse frequency of structures. Build. Struct., 89–109. doi:10.1007/978-3-030-97247-9

CrossRef Full Text | Google Scholar

Shah, A. A., Khwaja, S., Shah, B. A., Reduan, Q., and Jawi, Z. (2018). Living with earthquake and flood hazards in Jammu and Kashmir, NW Himalaya. Front. Earth Sci. 6, 179. doi:10.3389/feart.2018.00179

CrossRef Full Text | Google Scholar

Shen, Y., Gao, B., Yang, X., and Tao, S. (2014). Seismic damage mechanism and dynamic deformation characteristic analysis of mountain tunnel after Wenchuan earthquake. Eng. Geol. 180, 85–98. doi:10.1016/j.enggeo.2014.07.017

CrossRef Full Text | Google Scholar

Shou, K. J., and Wang, C. F. (2003). Analysis of the chiufengershan landslide triggered by the 1999 chi-chi earthquake in taiwan. Eng. Geol. 68 (3-4), 237–250. doi:10.1016/s0013-7952(02)00230-2

CrossRef Full Text | Google Scholar

Singh, Y., Ul Haq, A., Bhat, G. M., Johar, S., Chib, S., and Pandita, S. K. (2024). Analysis of February 2023 Thatri landslide in Doda, Jammu and Kashmir: insights from field observations, geotechnical parameters, and GPR survey. J. Geol. Soc. India 100 (1), 9–18. doi:10.17491/jgsi/2024/172978

CrossRef Full Text | Google Scholar

Sun, Q., Hou, M., and Dias, D. (2024). Numerical study on the use of soft material walls to enhance seismic performance of an existing tunnel. Undergr. Space 15, 90–112. doi:10.1016/j.undsp.2023.08.009

CrossRef Full Text | Google Scholar

Tran, D. T., Kumar, D. R., Keawsawasvong, S., Wipulanusat, W., and Jamsawang, P. (2024). Innovative approaches for predicting seismic stability of circular and rectangular tunnels in cohesive-frictional soils using machine learning and finite element limit analysis. Model. Earth Syst. Environ. 10 (4), 5831–5849. doi:10.1007/s40808-024-02080-6

CrossRef Full Text | Google Scholar

Tsinidis, G., Pitilakis, K., and Anagnostopoulos, C. (2016). Circular tunnels in sand: dynamic response and efficiency of seismic analysis methods at extreme lining flexibilities. Bull. Earthq. Eng. 14, 2903–2929. doi:10.1007/s10518-016-9928-1

CrossRef Full Text | Google Scholar

Uddin, W., Hudson, W. R., and Haas, R. (2013). Public infrastructure asset management. McGraw-Hill Education.

Google Scholar

Wang, J. N. (1993). Seismic design of tunnels: a state-of-the-art approach. Monograph 7.

Google Scholar

Wang, Z., Zhao, D., Huang, R., Tang, X., and Mishra, O. P. (2009). Structural heterogeneity in Northeast Japan and its implications for the genesis of the 2004 and 2007 Niigata earthquakes. Bull. Seismol. Soc. Am. 99 (6), 3355–3373. doi:10.1785/0120080281

CrossRef Full Text | Google Scholar

Wei, H., Wu, D., Wu, H., Tang, L., Wang, S., and Sun, H. (2023). Coordinated evolution and mechanism characteristics of the tunnel-landslide system under rainfall conditions. Eng. Fail. Anal. 146, 107118. doi:10.1016/j.engfailanal.2023.107118

CrossRef Full Text | Google Scholar

Wen, Y. M., Xin, C. L., Shen, Y. S., Huang, Z. M., and Gao, B. (2021). The seismic response mechanisms of segmental lining structures applied in fault-crossing mountain tunnel: the numerical investigation and experimental validation. Soil Dyn. Earthq. Eng. 151, 107001. doi:10.1016/j.soildyn.2021.107001

CrossRef Full Text | Google Scholar

Xia, S., Zhao, D., and Qiu, X. (2008). The 2007 Niigata earthquake: effect of arc magma and fluids. Phys. Earth Planet. Interiors 166 (3-4), 153–166. doi:10.1016/j.pepi.2007.12.001

CrossRef Full Text | Google Scholar

Xu, L., Zhu, J., Zhao, G., and Li, S. (2024). Probabilistic seismic capacity models for circular tunnels at different performance levels. Comput. Geotechnics 165, 105906. doi:10.1016/j.compgeo.2023.105906

CrossRef Full Text | Google Scholar

Yousuf, M., Bukhari, S. K., Bhat, G. R., and Ali, A. (2020). Understanding and managing earthquake hazard visa viz disaster mitigation strategies in Kashmir valley, NW Himalaya. Prog. Disaster Sci. 5, 100064. doi:10.1016/j.pdisas.2020.100064

CrossRef Full Text | Google Scholar

Zhang, X., Jiang, Y., and Maegawa, K. (2020). Mountain tunnel under earthquake force: a review of possible causes of damages and restoration methods. J. Rock Mech. Geotechnical Eng. 12 (2), 414–426. doi:10.1016/j.jrmge.2019.11.002

CrossRef Full Text | Google Scholar

Zhang, X., Jiang, Y., and Sugimoto, S. (2018). Seismic damage assessment of mountain tunnel: a case study on the Tawarayama tunnel due to the 2016 Kumamoto Earthquake. Tunn. Undergr. space Technol. 71, 138–148. doi:10.1016/j.tust.2017.07.019

CrossRef Full Text | Google Scholar

Zhong, Z., Shen, Y., Zhao, M., Li, L., and Du, X. (2022). Seismic performance evaluation of two-story and three-span subway station in different engineering sites. J. Earthq. Eng. 26 (14), 7505–7535. doi:10.1080/13632469.2021.1964647

CrossRef Full Text | Google Scholar

Zhuang, H., Yang, J., Chen, S., Dong, Z., and Chen, G. (2021). Statistical numerical method for determining seismic performance and fragility of shallow-buried underground structure. Tunn. Undergr. Space Technol. 116, 104090. doi:10.1016/j.tust.2021.104090

CrossRef Full Text | Google Scholar

Appendix A

TABLE A1

TABLE A1. Seismic sources considered in the present study.