Cyclic behaviours of soft silty clay with long-term traffic loading considering drainage conditions

The traffic loading is a typical cyclic loading with variable confining pressure and always lasts long, and is believed to have a significant effect on the subgrade soil, especially for the subgrade filled with soft clay. However, the mechanics have yet to be fully understood. Given that the duration of traffic loading lasts long enough, the partially drained conditions should be considered for the soft clay under the long-term cyclic loading, rather than the undrained conditions adopted commonly by most previous researches. In this study, 28 cyclic tests were conducted on the remolded saturated soft clay, utilizing both constant confining pressure and variable confining pressure under partially drained and undrained conditions. The effect of cyclic confining pressure and different drainage conditions is analyzed in relation to the evolution of pore pressure and deformation behaviors. Incorporating both the cyclic confining pressure and cyclic stress ratio, a concise pre-diction model of permanent strain is proposed and validated by the experimental results.

1 Introduction

The cyclic behaviors of soils have garnered increasing interest among the researchers in recent times. Owing to advancements in laboratory testing technology, tests involving complex stress paths or prolonged cyclic loading periods can now be precisely controlled and measured. Traffic loading represents a typical cyclic loading, featuring complex stress path and long duration of loading., e.g., an ordinary municipal road may experience at least one million loading cycles within its operational lifetime. And it has been reported that the transportation infrastructures are prone to unexpected settlement or even catastrophic failure after undergoing long-term traffic loading, particularly in cases where the subgrade is composed of clayey soils or soft clays (Chai and Miura, 2002; Wei et al., 2016; Xu et al., 2018; Wu et al., 2022a). The traffic loading exerts a significant impact on subgrade soil, yet the underlying mechanics remain incompletely understood (Sharp and Booker, 1984; Collins and Boulbibane, 2000; Cai et al., 2017; Wu et al., 2022b). Consequently, further investigation into the cyclic behaviors of soils subjected to long-term traffic loading is warranted.

The soft clay, a typical weak soil, is widely distributes in coastal regions, near lakes and along middle and lower rivers courses. These regions are often more developed within a country (Kulkarni et al., 2010; Guo et al., 2017). And often contain a higher density of transportation infrastructures, necessitating increased attention to the settlement of soft subgrades induced by traffic loading. Therefore, investigating the cyclic behavior of saturated soft clay is crucial for understand and predicting the development of subgrade settlement in practical applications. Most researchers posit that during the cyclic loading, pore pressure cannot be effectively discharged from soft clay due to its low permeability in time. As a result, investigations into the cyclic behaviors of soft clays often involve testing under undrained conditions (Diaz-Rodriguez, 1989; Zhou and Gong, 2001; Moses and Rao, 2003; Wang et al., 2019; Khan et al., 2020). However, during prolonged cyclic loading, pore water is eventually able to discharge due to the extended duration of the loading (Hyodo et al., 1992; Guo et al., 2020; Miao et al., 2020; Zhang et al., 2020). Hyodo et al. (1992) and Sakai et al. (2003) were among the first characterize the drainage behavior of low-permeability clay as “partially drained”, and noting that pore water in saturated clay is generated and discharged simultaneously. In light of these previous studies, additional tests on clay subjected to cyclic loading were conducted under partially drained conditions, yielding a number of meaningful results that have been reported and analyzed (Sun et al., 2015a; Chen et al., 2018; Huang et al., 2020). Despite the preponderance of research on the cyclic behaviors of clay under partially drained conditions, there has been a paucity of comparative studies examining the differential behaviors of clay under varying drainage conditions, especially with respect to deformation behaviors.

The variable confining pressure (VCP) has been observed in the stress path of the traffic loading, i.e., the confining pressure of soil elements in the subgrade fluctuates concurrently with variations in axial stress induced by the wheels of vehicle moving (Cai et al., 2012; Gu et al., 2016). Cai et al. (2012) and Sun et al. (2015a), Sun et al. (2015b) have demonstrated that cyclic confining pressure exerts a significant effect on the cyclic behaviors of soft clay under undrained conditions. Gu et al. (2016) and Huang et al. (2020) have conducted stress path analyses that account for the effect of VCP on the saturated soft clay under drained and partially drained conditions. However, their investigations mainly centered on the effect of VCP, with limited comparative analysis of the deformation behaviors between tests under different drainage conditions.

In this study, a total of 28 cyclic experiments were performed on remolded saturated soft clay under partially drained and undrained conditions with both constant and variable confining pressures. The effect of cyclic confining pressure and different drainage conditions is examined with respect to the evolution of pore pressure and deformation behaviors. And considering the cyclic confining pressure and cyclic stress ratio, a concise prediction model of permanent strain is proposed and validated by the test results under both partially drained and undrained conditions.

2 Test materials and preparation

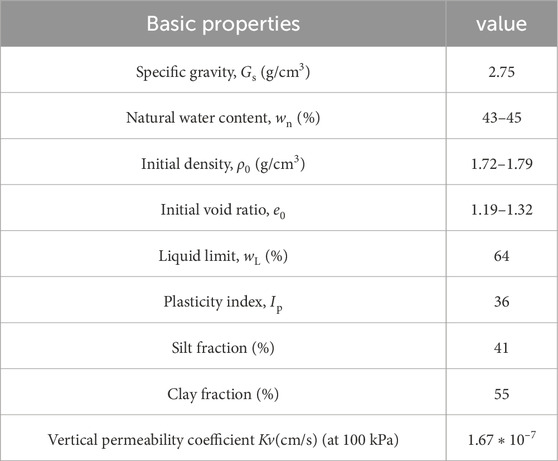
The experimental materials employed in this investigation were originally extracted from Wenzhou, a coastal metropolis in southeast China. Wenzhou clays are a quintessential soft silty clay characterized by elevated water content and diminished permeability. The fundamental physical indices of Wenzhou clays are delineated in Table 1.

Table 1

Table 1. Basic properties of the tested Wenzhou clay.

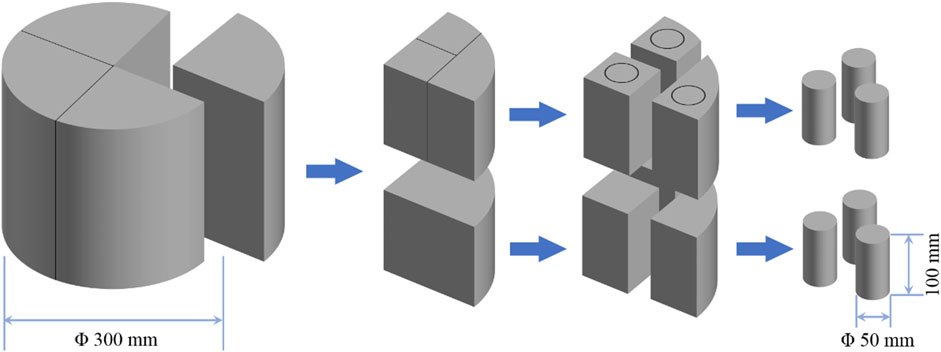
To guarantee the homogeneity of specimens, we implemented a standardized preparing process to obtained the remolded specimens. First, the clay blocks were dried out in the oven and then ground to powder with grinder. Second, the desiccated clay powder was meticulously amalgamated with a predetermined quantity of water (calculated with 1.5 times the liquid limit ${\omega }_L$). The slurry was subsequently pre-consolidated in a large cylindroid consolidation vessel with several loading stages from 12.5 kPa to 50 kPa and lasted for 1 month. The vertical pressure was applied step by step in the following order: gravity pressure (0 kPa), 12.5, 25, 50 kPa. The duration of each step was 24 h. At final, when the vertical strain of clay mud (or specimen) reached a steady value (less than 0.05%/h), the sample was thought to be K0 consolidated completely. After that, the primarily consolidated sample block was partitioned into 24 segments and each part was molded into a cylindrical specimen with a diameter of 50 mm and a height of 100 mm. Sample segmentation as shown in the Figure 1. Ultimately, the specimen was consolidated isotropic in the cyclic triaxial apparatus.

Figure 1

Figure 1. Schematic diagram of soil sample segmentation.

3 Test apparatus and procedures

3.1 Test apparatus

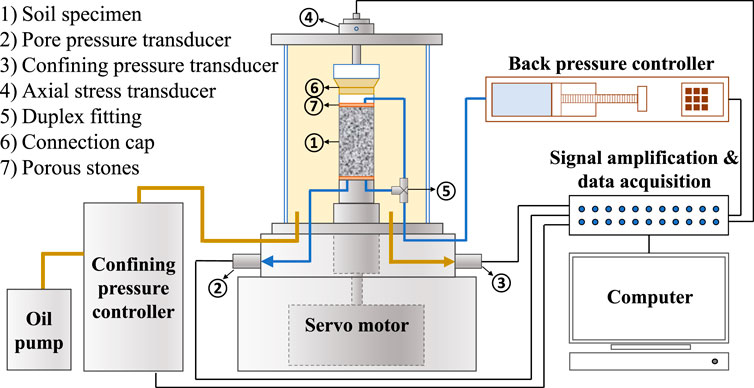
Figure 2 shows apparatus used in this study, it is a two-way dynamic triaxial testing system (DYNTTS) designed and manufactured by GDS Instruments Ltd., United Kingdom. It contents axial vibration exciter, confining pressure and back pressure controller and transducer, an axial displacement transducer, a signal acquisition system and a dynamic control system. This apparatus applies the cyclic deviatoric stress through the servo loading system and the cyclic confining pressure is exerted by means of an oil pressure piston. The term ‘two-way’ signifies that both cyclic deviatoric stress and cyclic confining pressure can be controlled independently, even with user-defined waveforms.

Figure 2

Figure 2. Schematic diagram of the dynamic triaxial testing system.

3.2 Test procedures

All the remolded specimens were positioned on the apparatus base and saturated at a back pressure of 300 kPa with an effective confining pressure of 20 kPa for a minimum of 24 h to ensure B exceeded 0.97. After that, the test specimens were consolidated isotropic under an effective confining pressure of 100 kPa for approximately 36 h to ensure the total volume change of the specimen was less than 60 mm³/h. After consolidation, 28 cyclic tests were conducted with varying confining pressure and drainage conditions.

The test schemes are summarized in Tables 2, 3, the dynamic test were divided into two series, i.e., CCP tests and VCP tests. Different cyclic deviator stress $q^{ampl}$ or cyclic confining pressure ${\sigma }_3^{ampl}$ were applied to the specimens. The loading waveform was compressive and sinusoidal, as shown in Figure 3A, and the frequency for all tests was established at 1 Hz. The stress state of CCP and VCP tests are illustrated in Figures 3B, C, respectively. Each specimen was designed to be loaded up to 50,000 cycles unless it failed prematurely (the failure criteria of axial strain is 10%). Fifty data points (one per 0.02 s) were recorded per cycle.

Table 2

Table 2. The statics triaxial tests schemes.

Table 3

Table 3. The cyclic triaxial tests schemes.

Figure 3

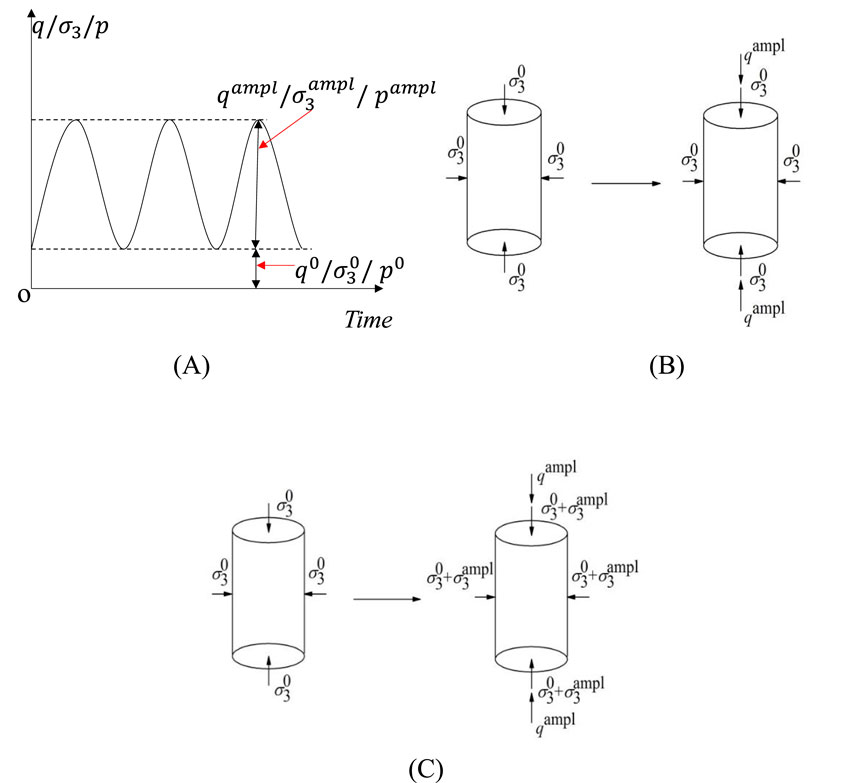
Figure 3. Cyclic triaxial tests: (A) loading waveform of cyclic deviatoric stress or cyclic confining pressure; (B) stress state of the specimen in CCP tests; (C) stress state of the specimen in VCP tests.

3.3 Drainage conditions

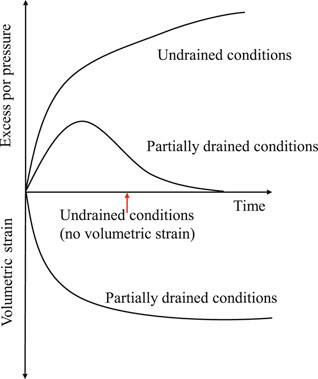
Figure 4 shows, there are three drainage conditions under cyclic loading: undrained, drained, and partially drained. (1) Undrained: The pore water cannot discharge under cyclic loading, resulting in the continuous accumulation of pore water pressure. (2) Drained: It usually exists in the sands and coarse soils. Since the high permeability, the pore water of these soils can discharge quickly during the cyclic loading, and the pore water pressure cannot accumulate. (3) Partially drained: Due to the extremely low permeability of soils, such as the soft clay, the pore water pressure accumulated in the early period of the cyclic test, but it cannot exceed the corresponding value of undrained test under the same loading condition. Hyodo et al. (1992), Sakai et al. (2003), and Cai et al. (2012) verified this result. Yasuhara et al. (1988), and Hyodo and Yasuhara (1988) explained that it is because the pore water pressure generates and dissipates alternately during each cycle, and considered the drainage condition of soils with low permeability as the partially drained situation. Therefore, for the soft silty clay used in this study, the loading condition is partially drained.

Figure 4

Figure 4. Different drained conditions cyclic behavior of soils.

To achieve the partially drained conditions in cyclic loading test, the back pressure was set to be a constant as the same as that during consolidation, and the channel connecting the back pressure is at both the top and bottom of the specimen. Therefore, the pore water pressure induced by the cyclic loading at the boundary of specimen was reduced to zero, leading to the discharge of pore water from the inside of the specimen to the outside. It should be pointed out that, we created the conditions of free drainage for the boundary of specimen, this method of controlling is the same as that for sandy soils in other researches (Cai et al., 2015; Guo et al., 2021). With this method, we can hardly control the degree of partially drained, which mainly depends on the soft clay itself since its low permeability. Sakai et al. (2003), Cai et al. (2012), Sun et al. (2015a), Sun et al. (2015b), and Guo et al. (2020) also conducted partially drained tests with this method.

3.4 Applied stress paths

In cyclic triaxial tests, the amplitudes of axial and the confining pressure are ${\sigma }_1^{ampl}$ and ${\sigma }_3^{ampl}$, respectively. The amplitudes of mean principal stress and deviatoric stress are calculated as follow:

${\mathit{p}}^{\mathit{a}\mathit{m}\mathit{p}\mathit{l}}=\left({\mathit{\sigma }}_{\mathbf{1}}^{\mathit{a}\mathit{m}\mathit{p}\mathit{l}}+\mathbf{2}{\mathit{\sigma }}_{\mathbf{3}}^{\mathit{a}\mathit{m}\mathit{p}\mathit{l}}\right)/\mathbf{3}(1)$

${\mathit{q}}^{\mathit{a}\mathit{m}\mathit{p}\mathit{l}}={\mathit{\sigma }}_{\mathbf{1}}^{\mathit{a}\mathit{m}\mathit{p}\mathit{l}}-{\mathit{\sigma }}_{\mathbf{3}}^{\mathit{a}\mathit{m}\mathit{p}\mathit{l}}(2)$

The ratio of $p^{ampl}$ to $q^{ampl}$ is defined as $\eta$:

$\mathit{\eta }={\mathit{p}}^{\mathit{a}\mathit{m}\mathit{p}\mathit{l}}/{\mathit{q}}^{\mathit{a}\mathit{m}\mathit{p}\mathit{l}}(3)$

In CCP tests, the confining pressure remains constant (${\sigma }_3^{ampl}=0$) $q^{ampl}$. Therefore:

$\mathit{\eta }={\mathit{p}}^{\mathit{a}\mathit{m}\mathit{p}\mathit{l}}/{\mathit{q}}^{\mathit{a}\mathit{m}\mathit{p}\mathit{l}}=\left(\mathbf{1}/\mathbf{3}{\mathit{\sigma }}_{\mathbf{1}}^{\mathit{a}\mathit{m}\mathit{p}\mathit{l}}\right)/{\mathit{\sigma }}_{\mathbf{1}}^{\mathit{a}\mathit{m}\mathit{p}\mathit{l}}=\mathbf{1}/\mathbf{3}(4)$

In VCP tests, the variable confining pressure and deviatoric stress are applied to the specimens simultaneously at the same phase difference. Therefore:

$\mathit{\eta }={\mathit{p}}^{\mathit{a}\mathit{m}\mathit{p}\mathit{l}}/{\mathit{q}}^{\mathit{a}\mathit{m}\mathit{p}\mathit{l}}=\mathbf{1}/\mathbf{3}+{\mathit{\sigma }}_{\mathbf{3}}^{\mathit{a}\mathit{m}\mathit{p}\mathit{l}}/{\mathit{q}}^{\mathit{a}\mathit{m}\mathit{p}\mathit{l}}(5)$

In VCP tests, $\eta$ = 2/3 and 5/6 are adopted in this study. And the cyclic stress ratio (CSR) is defined as the ratio between the cyclic deviator stress $q^{ampl}$ $q_{cyc}$ and the initial effective mean principal stress

$\mathit{C}\mathit{S}\mathit{R}=\frac{{\mathit{q}}^{\mathit{a}\mathit{m}\mathit{p}\mathit{l}}}{\mathbf{2}{\mathit{p}}_{\mathbf{0}}^{\prime }}(6)$

4 Test results

4.1 Pore pressure

The drainage condition is an important factor that directly influences the development of pore pressure, and thereby influences the cyclic behaviors of saturated clay during long-term cyclic loading. Figure 5 shows the typical development of pore pressure with the number of cycles for different tests. In the undrained tests, the pore pressure increases sharply during approximately the first 1,000 cycles, followed by a decreasing growth rate. In the partially drained tests, the development of pore pressure during approximately the first 1,000 cycles are the same as that in the undrained tests, but it is followed by a rapid decrease. At the end of loading period, the average pore pressure even reaches zero. This means that, given enough time, the pore water in the saturated soft silty clay with extremely low permeability is able to discharge during cyclic loading. With different η values, the pore pressure in the undrained tests increases with increasing η, while in partially drained tests, the variation of confining pressure affects the rate of dissipation of pore pressure but has little effect on the final state, and all the average pore pressure eventually become zero. Besides, under undrained conditions, both the amplitudes of pore pressure and the accumulated pore pressure are not linearly related to the level of cyclic confining pressure. However, under partially drained conditions, the amplitudes of pore pressure mainly depend on the CSR and are less influenced by the cyclic confining pressure compared to the undrained tests.

Figure 5

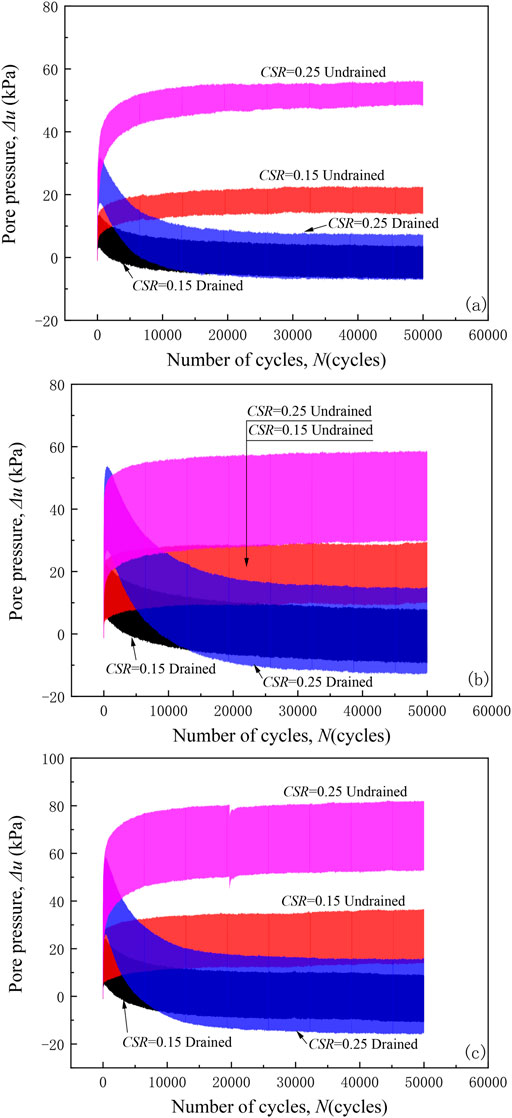
Figure 5. Pore pressure versus number of cycles in cyclic triaxial tests: (A) η = 1/3; (B) η = 2/3; (C) η = 5/6.

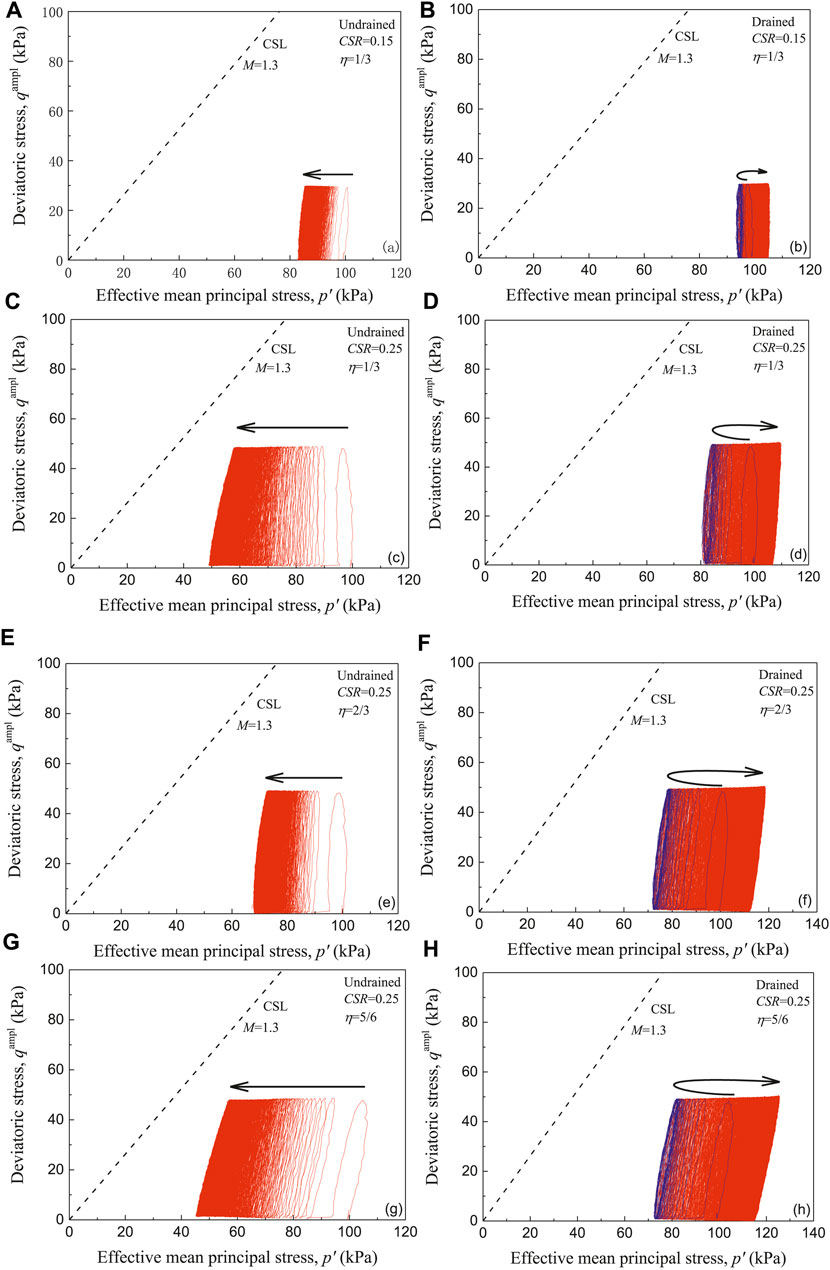
Figure 6 exhibits the typical effective stress path (ESP) for the cyclic triaxial tests under undrained and partially drained conditions. The typical tests with CSR = 0.15 and 0.25 are chosen to be analyzed. The critical state line (CSL) obtained from standard compressive undrained triaxial tests is also marked in Figure 6. In the undrained tests, with the increasing number of cycles, the ESP gradually moves to the left towards the CSL, and the curves all look sparse in the beginning and get denser as the loading goes on. With the same loading numbers, the ESP with higher CSR approaches closer to the CSL, which is consistent with the development of pore pressure mentioned above. For the tests under partially drained condition, the ESP moves toward the CSL in the beginning, but then moves towards the other side, as marked in the figures, which can also be attributed to the changes of pore pressure. Similar to the undrained tests, the leftmost end of ESP for the partially drained test with higher CSR is closer to the CSL. Figures 6C–H present the effects of variable confining pressure on the ESP. For the undrained tests, when η = 2/3, the distance between the stress path and CSL is much greater than in the other two different η value tests, but among the partially drained tests there is no such phenomenon. Besides, the η value also has an effect on the tilt of effective stress loops in undrained tests, as shown in Figures 6C, E, G, but has little effect on the tilt of effective stress loops in partially drained tests, as shown in Figures 6D, F, H. It is consistent with the conclusions on pore pressure mentioned above.

Figure 6

Figure 6. Effective stress paths of monotonic triaxial tests in p'-qplane.

4.2 Axial strain

Before the cyclic test, undrained shear tests were carried out under different confining pressures, and the test results are shown in Figure 7. The critical state line (CSL line) for remolded soft silty clay was obtained in undrained static shear tests, with a slope M of approximately 1.3.

Figure 7

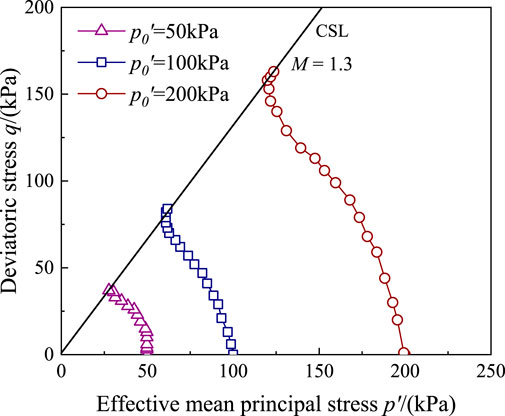
Figure 7. Effective stress path in cyclic triaxial tests: (A)CSR = 0.15, η= 1/3, undrained; (B)CSR = 0.15, η= 1/3, drained; (C)CSR = 0.25, η= 1/3, undrained; (D)CSR = 0.25, η= 1/3, drained; (E)CSR = 0.25, η= 2/3, undrained; (F)CSR = 0.25, η= 2/3, drained; (G)CSR = 0.25, η= 5/6, undrained; (H)CSR = 0.25, η= 5/6, drained.

Axial strain is the most important and concerning cyclic behavior for soils in cyclic triaxial tests. Figure 8 shows the definition of peak strain ε_peak, resilient strain ε_r and permanent strain ε_p induced by cyclic loading. Figure 9 presents the development of axial strain for tests under long-term cyclic loading with different η values, CSR values and the different drainage conditions. The axial strain of 5% was defined as a failure criterion in cyclic triaxial tests since the clay specimen with higher axial strain will no longer be uniform as a specimen in element tests. Figure 8 shows that the permanent strain increases with increasing number of cycles while the growth rate slowly decreases. When the CSR is low, the permanent strain remains at a low value. For example, the axial strain of specimen U03b (CSR = 0.15, η = 2/3, undrained) does not exceed 0.15% from the beginning to the end of the experiment. Its permanent strain only increases 0.0944% for the last 49,000 cycles. When CSR reaches a certain value, the development of strain changes, and the permanent strain increases sharply, while the resilient strain keeps almost unchanged with an increasing number of cycles. Additionally, drainage conditions have a significant effect on the cyclic deformation of clays and this effect varies with different cyclic stress levels. Below a certain stress level, clay has a higher permanent strain under partially drained conditions than under undrained conditions, as seen in the permanent strains of specimen D05b vs. U05b and D04b vs. U04b. However, if the cyclic stress level exceeds a certain value, the results are reversed, as seen in the permanent strains of specimen D07b vs. U07b and D08b vs. U08b. The development of resilient strains follows a different pattern: clay always has a higher resilient strain under undrained conditions than under partially drained conditions, and the cyclic stress level has little effect on this result.

Figure 8

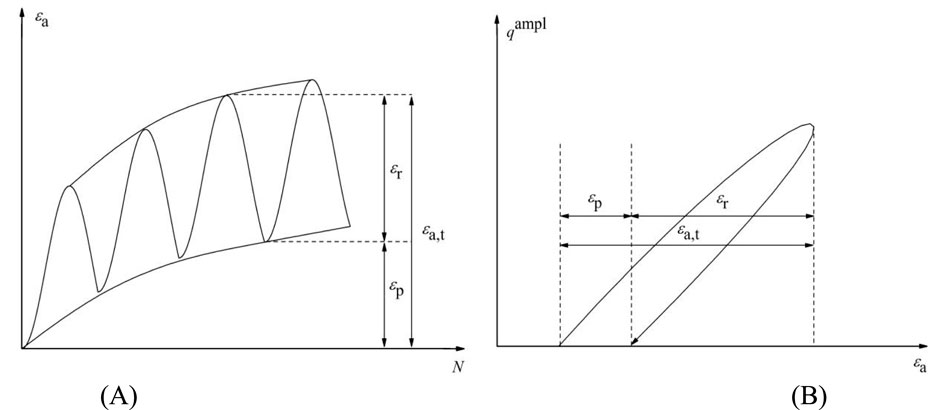
Figure 8. Typical deformation behavior of specimen in cyclic triaxial tests: (A) axial strain versus number of cycles; (B) certain single stress-strain hysteretic loop.

Figure 9

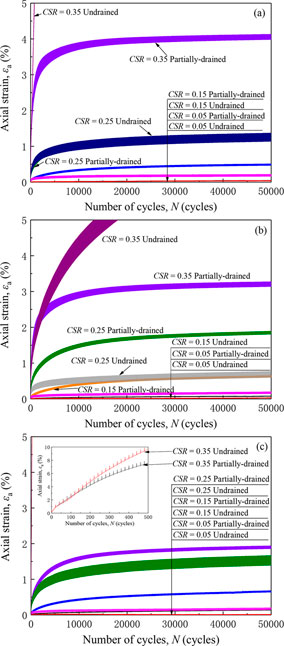
Figure 9. Axial strain versus number of cycles in cyclic triaxial tests: (A) η = 1/3; (B) η = 2/3; (C) η = 5/6.

Furthermore, Figure 9 presents that the cyclic confining pressure obviously accelerates the development of strain for tests under drained conditions. With the same CSR value, the specimen with higher cyclic confining pressure always has higher strain and is less likely to reach stability. For example, when CSR = 0.25, the specimens D04a (η = 1/3, drained), D05b (η = 2/3, drained) and D06b (η = 5/6, drained) have permanent axial strains of 1.12%, 1.69% and 1.78%. However, this ascending trend does not work for tests under undrained conditions. For example, the specimens U04a (η = 1/3, undrained), U05b (η = 2/3, undrained) and U06b (η = 5/6, undrained) have permanent axial strains of 1.13%, 0.56% and 1.18%. The reason for this phenomenon is supposed to be that in undrained tests, the increasing confining pressure accelerates the generation of pore pressure, therefore the specimen becomes weaker, leading to higher strains. While the increasing confining pressure and drainage channel have opposite contributions to the generation of pore pressure in the specimens and therefore decelerate the development of strain.

Figure 10 presents the development of resilient strain versus the number of cycles with typical CSR values (0.05, 0.15, 0.25 and 0.35). The resilient behaviors of soft silty clay under different drainage conditions is quite related to the cyclic stress level. As shown in Figure 10A, with a low cyclic stress level, the resilient strain rises to a stable value within 100 cycles and then remains unchanged until the end of applied cycles. Combining with the development of permanent strain mentioned above, it means that the soft silty clay is likely at the elastic shakedown state (Gu et al., 2019) with this cyclic stress level. And at this state, the cyclic confining pressure has even little effect on the development of resilient strain. Moreover, the drainage conditions have also little effect on the resilient behavior of the soft silty clay, noting that all six curves almost overlap together. Once CSR is greater than 0.05, the development of resilient strains becomes different. For undrained tests, the value of ɛ_r increases nearly linearly before 1,000 cycles, reaches a steady value and then remains this value until the end. However, the resilient strain of tests under partially drained conditions gradually decreases after approximately 1,000 cycles. Also, the cyclic confining pressure has little effect on the resilient behaviors of clay under both partially drained and undrained tests. With increasing CSR, Figure 10C shows the discrepancy between the effect of cyclic confining pressure on the resilient behaviors of clay under different drainage conditions, i.e., the effect of cyclic confining pressure has a significant effect on that of undrained tests but still has little effect on the resilient strain for partially drained tests. When CSR reaches a certain value (CSR = 0.35 in this study), under undrained condition, the resilient strain is positively correlated with cyclic confining pressure (the undrained test with η = 5/6 shows a significant decrease because the specimen has been destroyed and cannot rebound normally), while the partially drained test is just the opposite.

Figure 10

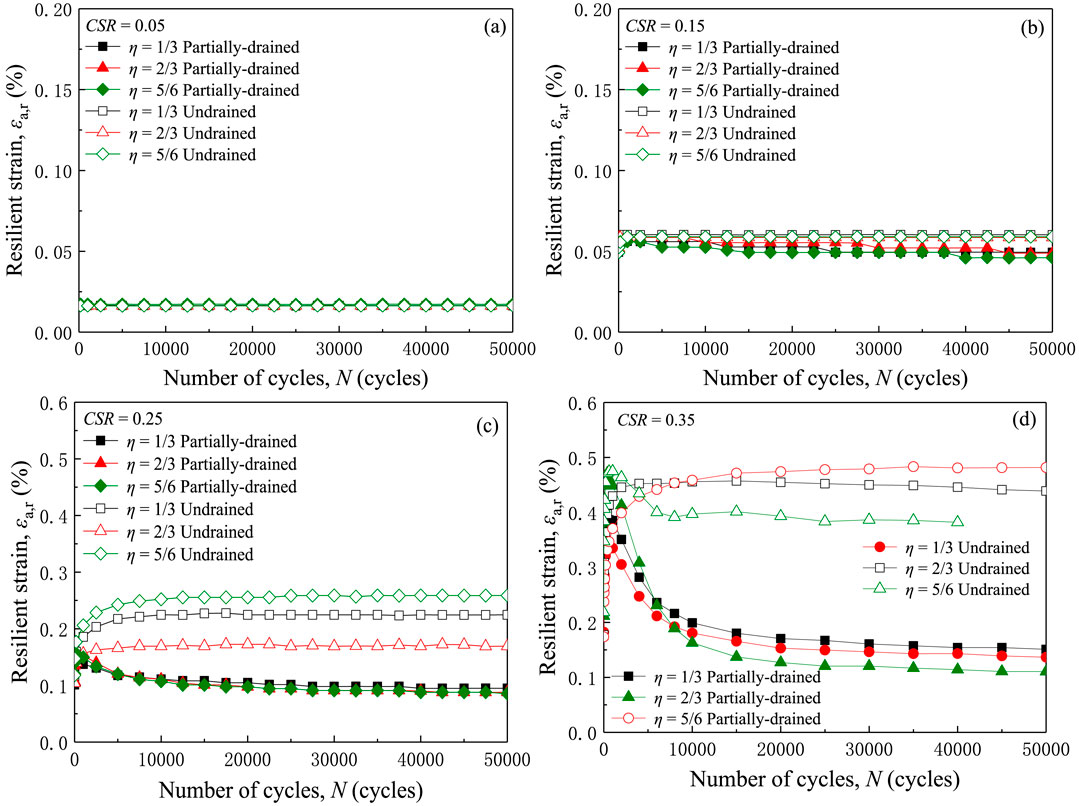
Figure 10. Relationship between resilient strain and number of cycles under different CSRs: (A) CSR = 0.05; (B) CSR = 0.15; (C) CSR = 0.25; (D) CSR = 0.35.

Figure 11 displays the semi-logarithmic relationship between permanent strain and cyclic period with different CSR values. When CSR = 0.05, the permanent strains of specimens are all very tiny (less than 0.15%) during the entire loading period, under three different η values and different drainage conditions. As the CSR increases, the permanent strain gradually increases, and the difference between the permanent strain under different η values becomes more obvious. For example, in a drained experiment at CSR = 0.15, the permanent strain is 0.6377% at η = 5/6, compared to the permanent strain of 0.4647% at η = 1/3, it only increases by 0.1730%. For CSR = 0.35, the permanent strain of η = 5/6 increase of η = 1/3 by 0.6249% after 50,000 cycles. Besides, the difference between the permanent strain in the undrained tests and partially drained tests becomes larger with the increasing CSR and η values. For example, the permanent strain of specimen D08b and U08b (CSR = 0.35, η = 5/6) are the maximum and minimum curves in Figure 11D, respectively. It means that drainage conditions have a significant effect on the plastic or unrecoverable deformation of soils, even on those of soft silty clay with extremely low permeability. And this effect tends to be more profound if with a higher CSR.

Figure 11

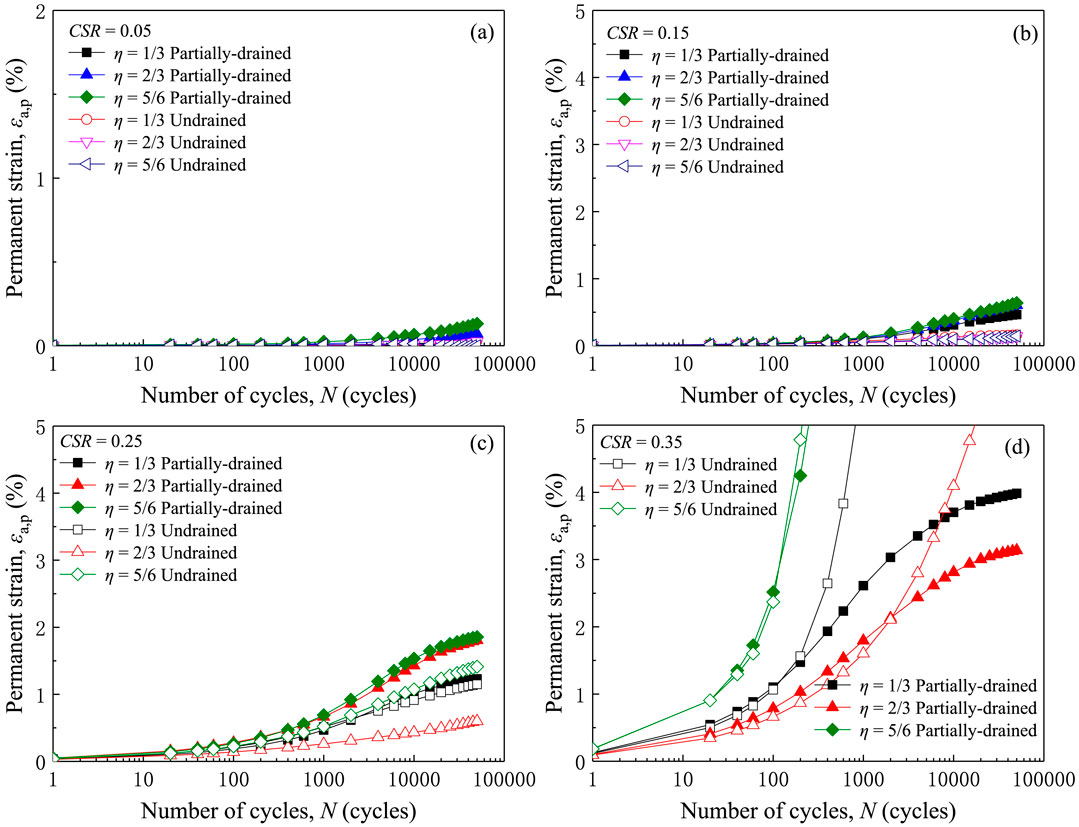
Figure 11. Relationship between permanent strain and number of cycles in a semi-logarithmic plot under different CSRs: (A) CSR = 0.05; (B) CSR = 0.15; (C) CSR = 0.25; (D) CSR = 0.35.

Figure 8 shows the permanent strain after 50,000 cycles, ɛ_p50,000, with different CSR values in CCP tests (Figure 12A) and VCP tests (Figure 12B). When CSR <0.20, the increasing CSR has little effect on the increasing permanent strain of clay, regardless of different drainage conditions and cyclic confining pressures. The curves of permanent strain of undrained and partially drained tests at CSR = 0.05 ∼ 0.25 are flat and almost overlap together. However, when the CSR exceeds 0.25, the permanent strain for the undrained tests is enhanced by the increasing CSR. And the curve of permanent strain of undrained tests shows a much sharper rise with increasing CSR and becomes much higher than that of the partially drained tests. And this discrepancy exists among both the CCP and VCP tests. Moreover, the cyclic confining pressure has a considerable effect on the aggravation caused by the increasing CSR when it exceeds 0.25. But it is the cyclic confining pressure with η = 2/3 that causes the minimum permanent strain under either drainage condition. This phenomenon should be further researched.

Figure 12

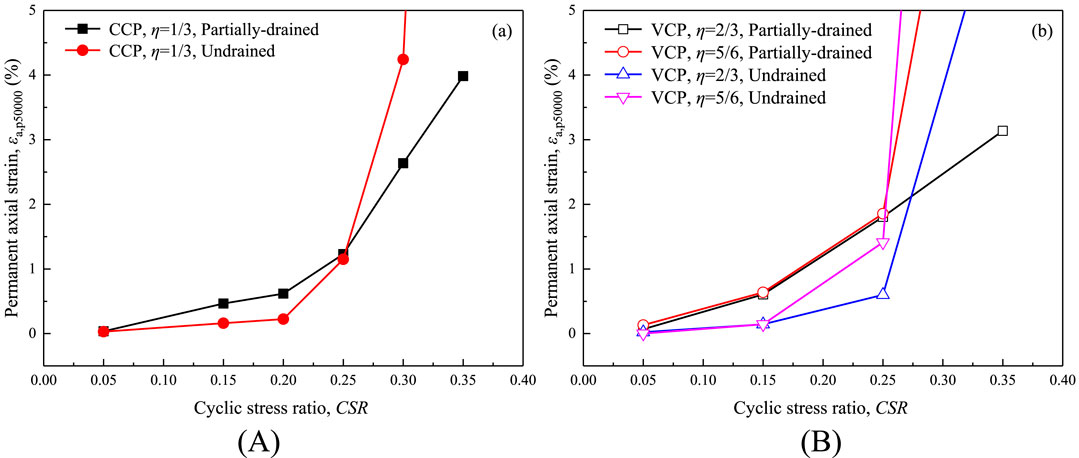
Figure 12. Permanent strain of 50,000th cycle versus CSR in different types of tests: (A) CCP tests; (B) VCP tests.

4.3 Prediction of permanent strain

The prediction of permanent strain for soil under long-term cyclic loading contributes to a more precise prediction of subgrade settlement in actual practices (Lekarp et al., 2000). Therefore, the prediction of permanent strain during cyclic loading has been getting more attention among researchers. Figure 13A, B describe the permanent strain versus the number of cycles in the log-log plot under partially drained and undrained conditions, respectively. Tests with CSR values below 0.25 were chosen for further analysis since higher CSR values are no longer safe for actual practices and are unlikely to exists. Figure 13A shows that the curves between log ɛ_p and log N are generally linear for undrained tests and appear to be two lines with an inflection point at approximately N = 10,000 for partially drained tests. Therefore, the curves for both drainage conditions are linear in a log-log plot after N = 10,000, and an empirical formula for permanent strain can be written as:

${\mathit{\epsilon }}_{\mathit{p}}={\mathit{\epsilon }}_{\mathit{p}\mathbf{10},\mathbf{000}}{\left(\frac{\mathit{N}}{\mathbf{10},\mathbf{000}}\right)}^{\mathit{\alpha }}(7)$

where α is the slope of log ɛ_p and log N, and ɛ_p10,000 is the reference permanent strain, i.e., the permanent strain at cycle No. 10,000 in this study. This power relationship between the permanent strain and the number of cycles has been adopted for soft clay in previous researches (Lekarp et al., 2000; Wang et al., 2013; Wichtmann and Triantafyllidis, 2018). The parameters of Equation 7 are summarized in Table 4.

Figure 13

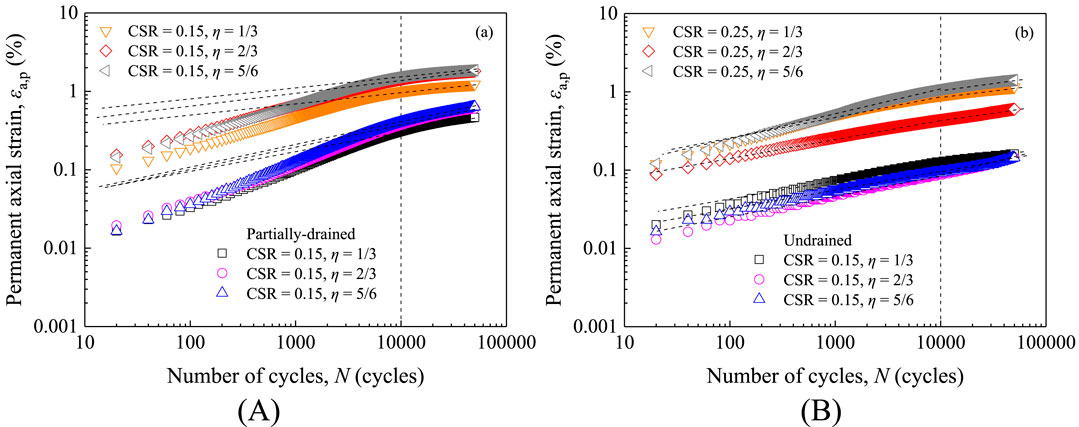
Figure 13. Permanent strain versus cycling numbers in a log-log plot under different drainage conditions: (A) partially drained; (B) undrained.

Table 4

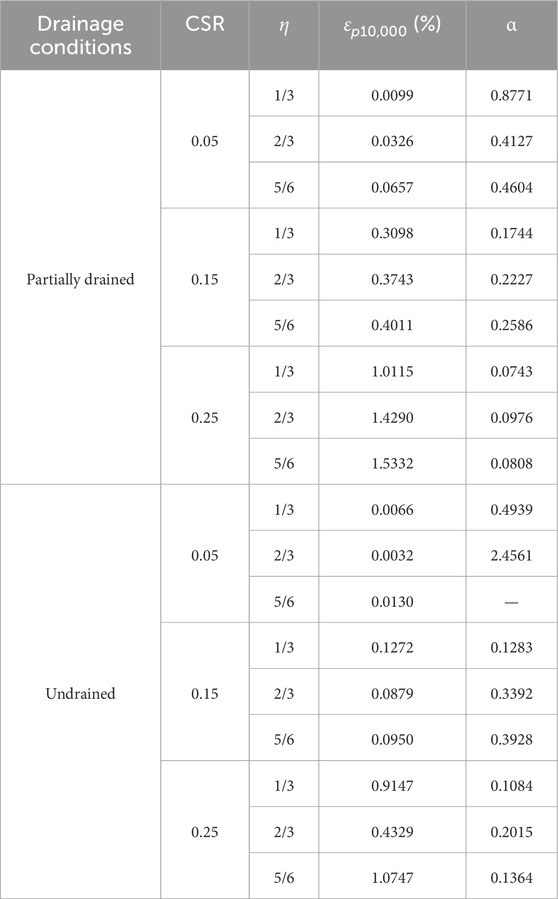
Table 4. Detailed parameters of Equation 7.

Figure 14 presents the relationships between the parameters in Equation 7 and their loading conditions. Comparing these four figures, the reference permanent strain in partially drained conditions is generally higher than those in undrained tests, but the slope of curves in partially drained conditions is generally lower than those in undrained tests. This means the development of strain in partially drained conditions grows higher in the beginning but is more likely to reach the steady value than that in undrained conditions. For partially drained tests, the reference permanent strain increases if either CSR or η increases. While for undrained tests, the reference permanent strain indeed increases with increasing CSR but is hardly affected by the increment of η (this effect only becomes obvious with higher CSR). It is inferred that, in partially drained conditions, the increment of cyclic confining pressures helps discharge pore water in the void of soft silty clay in the early stage of cyclic loading and therefore causes higher strain accumulation. But if it is an undrained test, the total strain remains the same and in the early stage, the increasing trend of radial strains caused by increasing pore pressure is likely to be counteracted by the decreasing trend of radial strains caused an increment of cyclic confining pressures. Therefore, the axial strain tends to be unchanged by increasing η value. However, with more cyclic loading, the increase of axial strain caused by more accumulated pore pressure becomes overwhelming, and that is why the slope of curves for undrained tests is generally higher than those for partially drained tests.

Figure 14

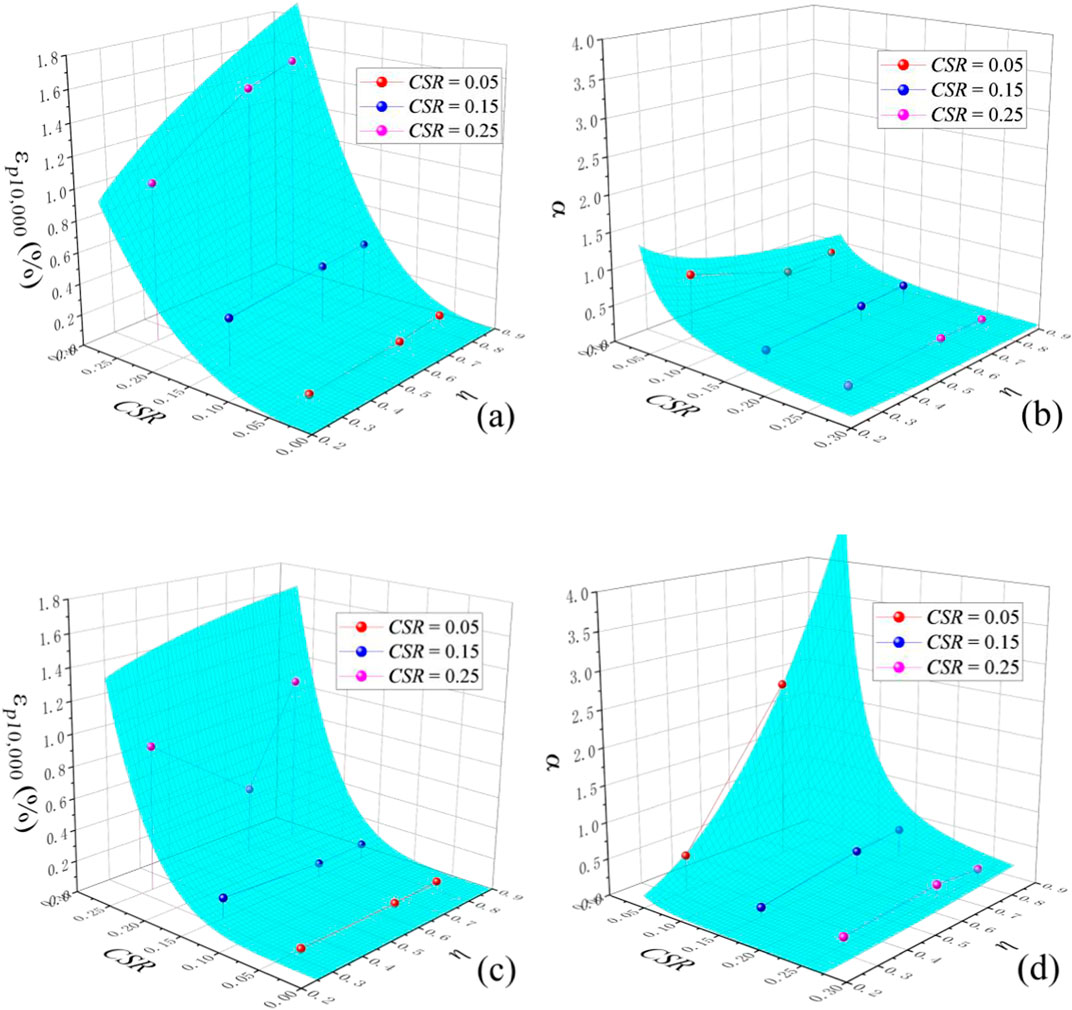
Figure 14. Relationships between the parameters and loading conditions: (A) the reference strain in partially drained tests; (B) α in partially drained tests; (C) the reference strain in undrained tests; (D) α in undrained tests.

As shown in Figure 14, the parameters in Equation 7 can be expressed by the loading conditions as follows:

${\mathit{\epsilon }}_{\mathit{p}\mathbf{10},\mathbf{000}}={\mathit{a}\mathit{C}\mathit{S}\mathit{R}}^{\mathit{b}}{\mathit{\eta }}^{\mathit{c}}(8)$

$\mathit{\alpha }={\mathit{l}\mathit{C}\mathit{S}\mathit{R}}^{\mathit{m}}{\mathit{\eta }}^{\mathit{n}}(9)$

where $a=56.96,b=2.54,c=0.445$ in partially drained tests, $a=552.02,b=4.48,c=0.17$ in undrained tests, $l=0.0145,m=-1.15,n=-0.56$ in partially drained tests, $l=0.0164,m=-1.97,n=2.21$ in undrained tests in this study. Figure 15 shows the permanent strain after 10,000 cycles predicted by the empirical model proposed in this study. The predicted results are in good agreement with the experimental data, which validates the capability and accuracy of this empirical model.

Figure 15

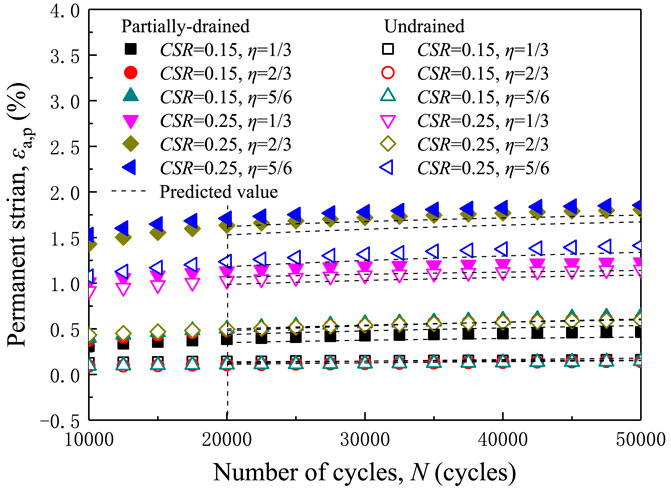
Figure 15. Comparison between experimental results and predicted results by the proposed empirical equation.

5 Conclusion

In this study, 28 cyclic tests were conducted on remolded saturated soft silty clay with both constant confining pressure and variable confining pressure under partially drained and undrained conditions. The effect of cyclic confining pressure and different drainage conditions was analyzed in terms of the development of pore pressure and deformation behaviors. The main conclusions are as follows:

(1) Under undrained conditions, both the amplitudes of pore pressure and the accumulated pore pressure are not linearly related to the level of cyclic confining pressure. While under partially drained conditions, the amplitudes of pore pressure mainly depend on CSR and are less influenced by cyclic confining pressure compared to undrained tests.

(2) Cyclic confining pressure aggravates both the resilient strain and permanent strain of soft silty clay under undrained conditions, and the strains increase more with higher cyclic confining pressure. But under partially drained conditions, both the resilient strain and permanent strain do not increase linearly with cyclic confining pressure, even with relatively higher CSR.

(3) Below a critical value of CSR, 0.25, the permanent strain under different drainage and stress conditions hardly increases with increasing CSR even after long-term cyclic loading. But if CSR is higher than this critical value, the permanent strain will obviously increase, and the permanent strain of undrained tests shows a much sharper rise with increasing CSR and becomes much higher than that of partially drained tests, regardless of the level of cyclic confining pressure.

(4) Considering cyclic confining pressure and cyclic stress ratio, a concise prediction model for permanent strain is proposed and validated by test results under both partially drained and undrained conditions.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

YJ: Writing–original draft, Writing–review and editing. RL: Writing–original draft, Writing–review and editing. FS: Writing–original draft, Writing–review and editing. GC: Writing–original draft, Writing–review and editing. CX: Writing–original draft. JT: Writing–original draft, Writing–review and editing. TW: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The work presented in this study was financially supported by the National Natural Science Foundation of China (No.U2006225), “Zhejiang Key Laboratory of Civil Engineering Structures & Disaster Prevention Mitigation Technology” and “Engineering Research Center of Ministry of Education for Renewable and Energy Infrastructure Construction Technology”. Their support is greatly appreciated.

Conflict of interest

Authors YJ, RL, FS, and GC were employed by Hangzhou Metro Group Co., Ltd of Zhejiang Province.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Cai, Y., Gu, C., Wang, J., Juang, C. H., Xu, C., and Hu, X. (2012). One-way cyclic triaxial behavior of saturated clay: comparison between constant and variable confining pressure. J. Geotechnical Geoenvironmental Eng. 139, 797–809. doi:10.1061/(ASCE)GT.1943-5606.0000760

CrossRef Full Text | Google Scholar

Cai, Y., Guo, L., Jardine, R. J., Yang, Z., and Wang, J. (2017). Stress-strain response of soft clay to traffic loading. Géotechnique 67, 446–451. doi:10.1680/jgeot.15.P.224

CrossRef Full Text | Google Scholar

Cai, Y., Sun, Q., Guo, L., Juang, C. H., and Wang, J. (2015). Permanent deformation characteristics of saturated sand under cyclic loading. Can. Geotech. J. 52, 795–807. doi:10.1139/cgj-2014-0341

CrossRef Full Text | Google Scholar

Chai, J.-C., and Miura, N. (2002). Traffic-load-induced permanent deformation of road on soft subsoil. J. geotechnical geoenvironmental Eng. 128, 907–916. doi:10.1061/(ASCE)1090-0241(2002)128:11(907)

CrossRef Full Text | Google Scholar

Chen, C., Zhou, Z., Zhang, X., and Xu, G. (2018). Behavior of amorphous peaty soil under long-term cyclic loading. Int. J. Geomechanics 18, 04018115. doi:10.1061/(ASCE)GM.1943-5622.0001254

CrossRef Full Text | Google Scholar

Collins, I. F., and Boulbibane, M. (2000). Geomechanical analysis of unbound pavements based on shakedown theory. J. Geotechnical and Geoenvironmental Eng. 126, 50–59. doi:10.1061/(ASCE)1090-0241(2000)126:1(50

CrossRef Full Text | Google Scholar

Diaz-Rodriguez, J. A. (1989). Behavior of Mexico City clay subjected to undrained repeated loading. Can. Geotech. J. 26, 159–162. doi:10.1139/t89-016

CrossRef Full Text | Google Scholar

Gu, C., Wang, J., Cai, Y., Sun, L., Wang, P., and Dong, Q. (2016). Deformation characteristics of overconsolidated clay sheared under constant and variable confining pressure. Soils Found. 56, 427–439. doi:10.1016/j.sandf.2016.04.009

CrossRef Full Text | Google Scholar

Gu, C., Wang, Y., Cui, Y., Cai, Y., and Wang, J. (2019). One-way cyclic behavior of saturated clay in 3D stress state. J. Geotechnical Geoenvironmental Eng. 13. doi:10.1061/(ASCE)GT.1943-5606.0002137

CrossRef Full Text | Google Scholar

Guo, L., Cai, Y., Jardine, R. J., Yang, Z., and Wang, J. (2017). Undrained behaviour of intact soft clay under cyclic paths that match vehicle loading conditions. Can. Geotechnical J. 55, 90–106. doi:10.1139/cgj-2016-0636

CrossRef Full Text | Google Scholar

Guo, L., Fang, Y., Wu, T., Wang, J., Jin, H., and Shi, L. (2021). Cyclic behavior of sand under traffic loading with ‘inclined’ consolidation. KSCE J. Civ. Eng. 25, 1621–1633. doi:10.1007/s12205-021-0892-1

CrossRef Full Text | Google Scholar

Guo, L., Liu, L., Wang, J., Jin, H., and Fang, Y. (2020). Long term cyclic behavior of saturated soft clay under different drainage conditions. Soil Dyn. Earthq. Eng. 139, 106362. doi:10.1016/j.soildyn.2020.106362

CrossRef Full Text | Google Scholar

Huang, J., Chen, J., Lu, Y., Yi, S., Cheng, H., and Cui, L. (2020). Deformation behaviors and dynamic backbone curve model of saturated soft clay under bidirectional cyclic loading. Int. J. Geomechanics 20, 04020016. doi:10.1061/(ASCE)GM.1943-5622.0001628

CrossRef Full Text | Google Scholar

Hyodo, M., and Yasuhara, K. (1988). Analytical procedure for evaluating pore-water pressure and deformation of saturated clay ground subjected to traffic loads. Available at: http://www.sciencedirect.com/science/article/pii/0148906290914198.

Google Scholar

Hyodo, M., Yasuhara, K., and Hirao, K. (1992). Prediction of clay behaviour in undrained and partially drained cyclic triaxial tests. Soils Found. 32, 117–127. doi:10.3208/sandf1972.32.4_117

CrossRef Full Text | Google Scholar

Khan, I., Nakai, K., and Noda, T. (2020). Undrained cyclic shear behavior of clay under drastically changed loading rate. Int. J. GEOMATE 8. doi:10.21660/2020.66.07893

CrossRef Full Text | Google Scholar

Kulkarni, M. P., Patel, A., and Singh, D. N. (2010). Application of shear wave velocity for characterizing clays from coastal regions. KSCE J. Civ. Eng. 14, 307–321. doi:10.1007/s12205-010-0307-1

CrossRef Full Text | Google Scholar

Lekarp, F., Isacsson, U., and Dawson, A. (2000). State of the art. II: permanent strain response of unbound aggregates. J. Transp. Eng. 126, 76–83. doi:10.1061/(ASCE)0733-947X(2000)126:1(76)

CrossRef Full Text | Google Scholar

Miao, Y.-H., Sheng, R.-Y., Yin, J., Zhou, F.-B., and Lu, J.-F. (2020). Dynamic characteristics of saturated soft clays under cyclic loading in drained condition. KSCE J. Civ. Eng. 24, 443–450. doi:10.1007/s12205-020-1539-3

CrossRef Full Text | Google Scholar

Moses, G. G., and Rao, S. N. (2003). Degradation in cemented marine clay subjected to cyclic compressive loading. Mar. Georesources Geotechnol. 21, 37–62. doi:10.1080/10641190306709

CrossRef Full Text | Google Scholar

Sakai, A., Samang, L., and Miura, N. (2003). Partially-drained cyclic behavior and its application to the settlement of a low embankment road on silty-clay. Soils Found. 43, 33–46. doi:10.3208/sandf.43.33

CrossRef Full Text | Google Scholar

Sharp, R. W., and Booker, J. R. (1984). Shakedown of pavements under moving surface loads. J. Transp. Eng. 110, 1–14. doi:10.1061/(asce)0733-947x(1984)110:1(1)

CrossRef Full Text | Google Scholar

Sun, L., Cai, Y., Gu, C., Wang, J., and Guo, L. (2015a). Cyclic deformation behaviour of natural K 0-consolidated soft clay under different stress paths. J. Central South Univ. 22, 4828–4836. doi:10.1007/s11771-015-3034-4

CrossRef Full Text | Google Scholar

Sun, L., Gu, C., and Wang, P. (2015b). Effects of cyclic confining pressure on the deformation characteristics of natural soft clay. Soil Dyn. Earthq. Eng. 78, 99–109. doi:10.1016/j.soildyn.2015.07.010

CrossRef Full Text | Google Scholar

Wang, J., Guo, L., Cai, Y., Xu, C., and Gu, C. (2013). Strain and pore pressure development on soft marine clay in triaxial tests with a large number of cycles. Ocean. Eng. 8, 125–132. doi:10.1016/j.oceaneng.2013.10.005

CrossRef Full Text | Google Scholar

Wang, S., Zhong, Z., Liu, X., and Tu, Y. (2019). Influences of principal stress rotation on the deformation of saturated loess under traffic loading. KSCE J. Civ. Eng. 23, 2036–2048. doi:10.1007/s12205-019-0474-7

CrossRef Full Text | Google Scholar

Wei, X., Wang, G., and Wu, R. (2016). Prediction of traffic loading–induced settlement of low-embankment road on soft subsoil. Int. J. Geomechanics 17, 06016016. doi:10.1061/(ASCE)GM.1943-5622.0000719

CrossRef Full Text | Google Scholar

Wichtmann, T., and Triantafyllidis, T. (2018). Monotonic and cyclic tests on kaolin: a database for the development, calibration and verification of constitutive models for cohesive soils with focus to cyclic loading. Acta Geotech. 26, 1103–1128. doi:10.1007/s11440-017-0588-3

CrossRef Full Text | Google Scholar

Wu, T., Jin, H., Guo, L., Sun, H., Tong, J., Jiang, Y., et al. (2022a). Predicting method on settlement of soft subgrade soil caused by traffic loading involving principal stress rotation and loading frequency. Soil Dyn. Earthq. Eng. 152, 107023. doi:10.1016/j.soildyn.2021.107023

CrossRef Full Text | Google Scholar

Wu, T., Zhang, T., Gu, C., Wang, J., Cai, Y., Sun, H., et al. (2022b). Cyclic behavior of saturated clays in plane strain state. J. Geotechnical Geoenvironmental Eng. 148, 04021172. doi:10.1061/(ASCE)GT.1943-5606.0002721

CrossRef Full Text | Google Scholar

Xu, C., Chen, Q., Luo, W., and Liang, L. (2018). Evaluation of permanent settlement in hangzhou qingchun road crossing-river tunnel under traffic loading. Int. J. Geomechanics 19, 06018037. doi:10.1061/(ASCE)GM.1943-5622.0001338

CrossRef Full Text | Google Scholar

Yasuhara, K., Hirao, K., and Hyodo, M. (1988). Partial-drained behaviour of clay under cyclic loading. Innsbruck, Austria, 659–664.

Google Scholar

Zhang, J., Sun, Y., and Cao, J. (2020). Experimental study on the deformation and strength characteristics of saturated clay under cyclic loading. Adv. Civ. Eng. 2020, 1–9. doi:10.1155/2020/7456596

CrossRef Full Text | Google Scholar

Zhou, J., and Gong, X. (2001). Strain degradation of saturated clay under cyclic loading. Can. Geotechnical J. 38, 208–212. doi:10.1139/t00-062

CrossRef Full Text | Google Scholar