Performance analysis of high temperature thermal energy storage in shallow depth enhanced geothermal system

Introduction: Solar resources are rich in north China and however, solar thermal energy has little contribution to space heating due to the intermittency and instability as well as the lack of seasonal energy storage technology. Although underground thermal energy storage (UTES) can solve the above problems effectively, the existing UTES systems either have low energy storage density and recovery efficiency or have high construction cost.

Methods: Inspired by the enhanced geothermal system (EGS), here a novel scheme of storing high temperature thermal energy into the shallow depth EGS (SDEGS) is proposed. Thermal energy is stored into SDEGS during the non-heating season and is extracted for space heating during the heating season.

Results: The results show the thermal performance of SDEGS always remains stable due to continuous thermal energy injection, and its thermal recovery efficiency is always greater than 90% by storing thermal energy into the tight rocks and circumventing the formation of the natural convection.

Discussion: SDEGS can be constructed in the shallow buried depth rocks having a low requirement about temperature, largely reducing project cost and risk and widening the application range.

1 Introduction

The total district heating area reached to 122.66 × 10⁸ m² in China till 2020 (Wang et al., 2023), and more than 80% utilized coal-based fuel (Han et al., 2022), consuming enormous amounts of energy and releasing vast quantities of fossil carbon into the atmosphere (Wu et al., 2022). Therefore, it is imperative to utilize renewable energy for space heating (Yu et al., 2014; Su et al., 2019).

Solar energy resources are very rich in North China and the average annual radiation is between 930 and 2,330 kWh/m² (Li et al., 2022), having great potential for space heating (163, 2024). However, the total space heating area provided by solar energy in China was only 16.50 × 10⁶ m² up to 2020 due to its instability and intermittency (Rosato et al., 2020), While seasonal thermal energy storage (STES) can overcome the above problems (Yang et al., 2021). Apart from that, STES can take full advantage of solar energy in summer with higher solar radiation (Shah et al., 2018). Underground thermal energy storage (UTES) has been generally acknowledged as the most promising STES technology (Lim et al., 2020). UTES can be sorted into four types ① aquifer thermal energy storage (ATES) (Nilsson and Rohdin, 2019), ② borehole thermal energy storage (BTES) (Fong et al., 2019), ③ tank thermal energy storage (TTES) (Sanner and Knoblich, 1999) and ④ pit thermal energy storage (PTES) (Schmidt et al., 2018). For low temperature ATES (LT-ATES), the temperature of injection water cannot exceed 25°C–30°C (Wesselink et al., 2018), leading to a low energy storage density (Ueckert and Baumann, 2019). While for high temperature ATES (HT-ATES), the recovery efficiency is usually low due to the high heat loss causing by thermal advection (Schout et al., 2014). BTES has much lower energy storage density and higher drilling costs (Xu et al., 2018). TTES and PTES have higher energy density and however, a main drawback of these systems is the remarkable high construction costs (Dahash et al., 2019). In all, the aforementioned four types UTES have obvious disadvantages, limiting their application in solar space heating area. Therefore, it is quite necessary to explore a more appropriate UTES to store solar energy. The most appropriate UTES storing solar energy should have three characteristics at least ① high energy density, ② low construction cost and ③ high recovery efficiency.

On the basis of HT-ATES, we try to find out a proper way to store solar energy in underground space. The research process and performance as well as advantages and disadvantages of HT-ATES is accordingly reviewed below. Lu et al. (2019) evaluated the global potential of ATES considering socio-economic, geo-hydrological, climate, and groundwater factors and ascertained the potential hotspots for its application. Fleuchaus et al. (2018) evaluated the global application status of ATES by operational statistics, and indicated that there are about 2800 ATES systems in operation worldwide, and 99% are LT-ATES. However, LT-ATES is often incompatible with some renewable technologies due to the low storage temperature. Therefore, this study focuses on the HT-ATES owe to having high storage temperature and high storage capacity. HT-ATES faces various challenges and risks impeding its rapid development and deployment. Considering experiences of HT-ATES projects, Fleuchaus et al. (2020) analysed the risks and revealed the main problems encountered. Kabus et al. (2009) reported the energy balances of HT-ATES in Neubrandenburg, which has a thermal recovery efficiency of 46%. Ueckert and Baumann (2019) presented the test results from HT-ATES in Bavarian Molasse Basin, also revealed the thermal recovery efficiency. Schout et al. (2014) carried out an evaluation of the prime influencing factors to recovery efficiency of HT-ATES systems, and concluded that thermal loss caused by natural convection is one key factor. Also, they concluded that the Ra can be used as an indicator of the relative strength of natural convection. Winterleitner et al. (2018) studied the effect of aquifer heterogeneities on thermal recovery efficiency of HT-ATES, and indicated that thermal energy loss mainly occurs due to heterogeneities in the permeability field. By analyzing the effect of injection temperature on thermal recovery efficiency of HT-ATES, Schout et al. (2016) revealed that the injection temperature has a negative effect on thermal recovery efficiency. To improve the thermal recovery efficiency, Lopik et al. (2016) proposed a new method of restraining free thermal convection by increasing salinity of injection water, which can reduce the density difference between injection water and formation water. The simulation results showed that the thermal recovery efficiency is 0.40 for regular HT-ATES, while it increased to 0.69 for the density difference compensation method. It can be concluded according to the analysis above that HT-ATES is a good way to store solar energy if its thermal recovery efficiency can be improved. The major reason for the low thermal recovery efficiency is attributed to natural convection induced by the temperature difference and density difference and therefore, avoiding or limiting natural convection formation is an effective measure to improve the thermal recovery efficiency.

The reserves of heat in hot dry rock (HDR) with depth of 3–10 km exceed 2.52 × 10²⁵ J in China (Hou et al., 2018; Su et al., 2018). To extract thermal energy from HDR, enhanced geothermal system (EGS) is proposed by forming artificial fractures in the tight rocks and circulating fluid between them. For EGS, the circulation water with low temperature is firstly injected into the artificial fractures, and then the heat stored in the tight rocks transfers to the circulation water. For HT-ATES, forming natural convection is easy due to having natural porous and permeability. While for EGS, the thermal energy is stored in the tight rocks, and thus it is very difficult to cause the generation of natural convection due to having low permeability. Therefore, storing thermal energy into tight rocks can prevent the formation of natural convection and thus can increase thermal recovery efficiency compared with HT-ATES. However, at this stage, EGS has high investment and high risk of induced seismicity as well as location problem due to having high requirement to rock temperature (Olasolo et al., 2016; Lu, 2018).

Some of the above problems faced by conventional EGS can be effectively solved if the artificial reservoir can be created in the shallow depth rocks (Bu et al., 2021). Low temperature of rocks in shallow depth is the disadvantage, while changing the function of EGS from electricity generation to space heating is an effective solution to this problem. Inspired by this, we propose a novel scheme of storing high temperature solar thermal energy into the shallow depth EGS (SDEGS) (Bu et al., 2020; He and Bu, 2020). The artificial reservoir is firstly created in the shallow buried depth rocks, which is called shallow depth EGS. The hot water from solar energy enters into the artificial reservoir and transfers thermal energy to surrounding rocks in the non-heating season, realizing thermal energy storage mainly in the rocks rather than in water. In the heating season, cold water is injected into the artificial reservoir and is heated by hot rocks, realizing thermal energy extraction. For SDEGS, the thermal energy is mainly stored in the tight rocks with low porosity and permeability, and the natural conversion is thus difficult to form, leading to an increase in thermal recovery efficiency. Due to having low requirement to temperature, SDEGS can thus be created in the shallow buried depth rocks (limestone, granite and consolidated sandstone and so on), reducing engineering cost and enlarging application range. Storing thermal energy in SDEGS can solve the intermittency and instability of solar energy, and SDEGS can achieve stable thermal energy output due to thermal energy storage. The main function of SDEGS is to store thermal energy for space heating. The major purpose of this study is to demonstrate the feasibility of SDEGS from the thermal performance standpoint by numerical simulation method.

2 Methods

2.1 Physical models

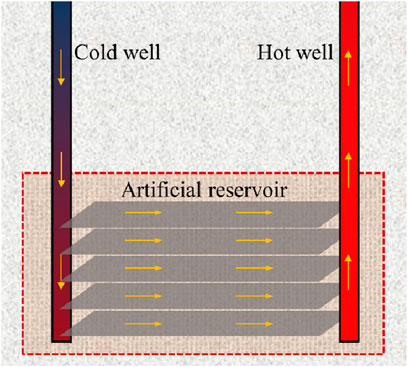
The physical model of SDEGS created in the shallow buried depth rocks is showed in Figure 1, and it is composed mainly of artificial reservoir, cold well and hot well. SDEGS can be applied in hot dry zone composed of sandstone, limestone or granite without underground water. The artificial reservoir is created from 880 m to 1,000 m in depth (shallow depth), and it has five layers of fracture with a layer distance of 30 m in vertical direction. To avoid the mutual interference between two layers of fracture, the vertical distance between two layers of fracture should be set to a reasonable value. The horizontal space between cold well and hot well is 150 m. The length, width, and height of the artificial reservoir are 150 m, 40 m, and 120 m, respectively. At the stage of thermal energy storage, hot water from solar vacuum tube heat collector flows firstly into the hot well and releases its heat to the rocks around the fractures in the artificial reservoir and then flows back to solar heat collector again through the cold well (Figure 2). While at the stage of thermal energy extraction, the cold water enters into the cold well and is heated by the rocks around the fractures and then goes back to the surface through the hot well (Figure 2). The density, specific heat, thermal conductivity and geothermal gradient of rock are respectively 2,900 kg/m³, 705 J/kg/K, 4.5 W/m/K and 30 °C/km, and the inner diameters of cold well and hot well are all 163.98 mm.

Figure 1

Figure 1. Physical model of SDEGS.

Figure 2

Figure 2. System diagram of the hybrid heating system of SDEGS and solar energy.

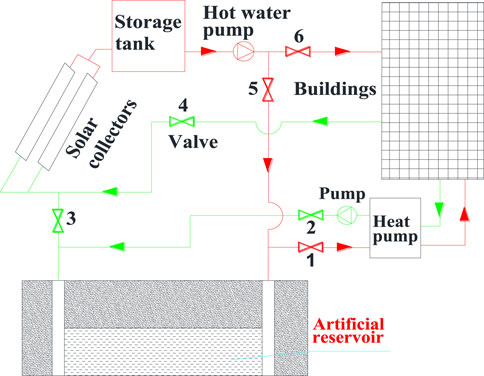
The hybrid heating system of SDEGS and solar energy is shown in Figure 2. Due to having a higher heat collecting efficiency at the temperature range of operation, solar vacuum tube heat collectors are used to generate hot water. To solve the problems of instability and intermittency faced by solar energy, the thermal storage tank on a diurnal basis is constructed on the ground to store short-term heat energy in Figure 2. Once reaching the predetermined temperature, the hot water from the solar vacuum tube heat collectors flows firstly into the storage tank and then it is pumped into the buildings or SDEGS. In non-heating season, valves 3 and 5 are opened and valves 1, 2, 4 and 6 are closed, and the hot water from the storage tank with a temperature of 90°C flows into the hot well and then releases its thermal energy into the SDEGS. In the heating season, valves 1, 2, 4 and 6 are opened and valves 3 and 5 are closed, and the SDEGS and solar energy are combined to provide thermal energy for space heating. The temperatures of supply and return water in the user sides are respectively 40°C and 32°C in the heating season. For the SDEGS, the injection temperature and volume flow rate are respectively 90°C and 50 m³/h in the non-heating season, while they are respectively 10°C and 150 m³/h in the heating season.

2.2 Mathematical models (Huang et al., 2017; Cao et al., 2016)

The assumptions in mathematical model are as follows: (1) the fluid-rock reaction in the artificial reservoir is neglected; (2) the fluid in the artificial reservoir is single-phase flow; (3) the surrounding rocks have uniform porosity and permeability.

2.2.1 Mass conservation equation and momentum equation in the reservoir matrix (rock around the artificial fracture in the artificial reservoir)

The artificial reservoir mainly includes the artificial fracture and the reservoir matrix around the artificial fracture. The reservoir matrix has low porosity and permeability.

Mass conservation equation

$\frac{\partial }{\partial t}\left(\rho \epsilon \right)+\nabla ·\left(\rho \mathrm{u}\right)=-Q_{\mathrm{m}}(1)$

Momentum equation (Darcy’s law)

$\mathrm{u}=-\frac{\kappa }{\mu }\left(\nabla p+\rho \mathrm{g}\nabla \mathrm{Z}\right)(2)$

where, $\rho \mathrm{g}\nabla \mathrm{Z}$ represents the gravity term.

The porosity and permeability for the reservoir matrix are respectively 0.01 and 10^–18 m².

2.2.2 Continuity equation and momentum equation in the fracture (artificial fracture)

Mass conservation equation

$d_{\mathrm{f}}\frac{\partial }{\partial t}\left({\epsilon }_{\mathrm{f}}\rho \right)+{\nabla }_{\mathrm{t}}\cdot \left(\rho u_{\mathrm{f}}{d}_{\mathrm{f}}\right)=d_{\mathrm{f}}{Q}_{\mathrm{m}}(3)$

Momentum equation (Darcy’s law)

${\mathrm{u}}_{\mathrm{f}}=-\frac{{\kappa }_{\mathrm{f}}}{\mu }\left({\nabla }_{\mathrm{t}}p+\rho \mathrm{g}{\nabla }_{t}Z\right)(4)$

κ_f can be calculated by the cubic law equation:

${\kappa }_{\mathrm{f}}=\frac{d_{\mathrm{f}}^2}{12f_{\mathrm{f}}}(5)$

f_f is set to 1 in this paper.

The fracture thickness is set at 1 mm in this study. Of course, the fracture thickness can also be set to other values, we only provide a research approach.

2.2.3 Heat transfer model

Heat transfer equations in reservoir matrix and fracture.

The local thermal equilibrium hypothesis is used to describe the heat transfer in reservoir matrix.

${\left(\rho C_{\mathrm{p}}\right)}_{\text{eff}}\frac{\partial T}{\partial t}+{\rho }_{\mathrm{f}}{C}_{\mathrm{p},\mathrm{f}}\mathrm{u}\cdot \nabla T-\nabla \cdot \left(k_{\text{eff}}\nabla T\right)=-Q(6)$

Energy conservation equation in fractures is expressed as:

$d_{\mathrm{f}}{\left(\rho C_{\mathrm{p}}\right)}_{\text{eff}}\frac{\partial T}{\partial t}+d_{\mathrm{f}}{\rho }_{\mathrm{f}}{C}_{\mathrm{p},\mathrm{f}}{\mathrm{u}}_{\mathrm{f}}\cdot {\nabla }_{\mathrm{t}}T-{\nabla }_{\mathrm{t}}\cdot \left(d_{\mathrm{f}}{k}_{\text{eff}}{\nabla }_{\mathrm{t}}T\right)=d_{\mathrm{f}}Q(7)$

${\left(\rho C_{\mathrm{p}}\right)}_{\text{eff}}=\left(1-\epsilon \right){\rho }_{\mathrm{s}}{C}_{\mathrm{p},\mathrm{s}}+\epsilon {\rho }_{\mathrm{f}}{C}_{\mathrm{p},\mathrm{f}}(8)$

$k_{\text{eff}}=\left(1-\epsilon \right)k_{\mathrm{s}}+\epsilon k_{\mathrm{f}}(9)$

Energy equation in rock

$\rho C_{\mathrm{p}}\frac{\partial T}{\partial t}-\nabla \cdot \left(k\nabla T\right)=Q_{\mathrm{w}}(10)$

2.2.4 Flow and heat transfer model in borehole

Line elements are introduced to represent the pipe and grout inside of the borehole.

The momentum and continuity equations for flow in the pipe are given as follows (Barnard et al., 1966):

$\frac{\partial A_{\mathrm{p}}{\rho }_{\mathrm{f}}}{\partial t}+\nabla \cdot \left(A_{\mathrm{p}}{\rho }_{\mathrm{f}}{\mathrm{u}}_{\mathrm{p}}\right)=0(11)$

${\rho }_{\mathrm{f}}\frac{\partial {\mathrm{u}}_{\mathrm{p}}}{\partial t}+{\rho }_{\mathrm{f}}{\mathrm{u}}_{\mathrm{p}}\cdot \nabla {\mathrm{u}}_{\mathrm{p}}=-\nabla p-f_{\mathrm{D}}\frac{{\rho }_f}{2d_{\mathrm{h}}}{\mathrm{u}}_{\mathrm{p}}\left|{\mathrm{u}}_{\mathrm{p}}\right|+\mathrm{F}(12)$

The Darcy friction factor f_D can be expressed through the Churchill equation (Churchill, 1997):

$f_D=8{\left[{\left(\frac{8}{Re}\right)}^{12}+{\left(A+B\right)}^{-1.5}\right]}^{1/12}(13)$

$A={\left[-2.457\ln \left({\left(\frac{7}{Re}\right)}^{0.9}+0.27\left(e/d_{\mathrm{h}}\right)\right)\right]}^{16},B={\left(\frac{37530}{R\mathrm{e}}\right)}^{16}(14)$

The roughness coefficient of steel pipe is set to e = 0.061 mm.

$\text{Re}=\frac{{\rho }_{\mathrm{f}}{u}_{\mathrm{p}}{d}_{\mathrm{h}}}{\mu }(15)$

Energy equation (Lurie, 2009):

${\rho }_{\mathrm{f}}{A}_{\mathrm{p}}{C}_{\mathrm{p},\mathrm{f}}\frac{\partial T}{\partial t}+{\rho }_{\mathrm{f}}{A}_{\mathrm{p}}{C}_{\mathrm{p},\mathrm{f}}{\mathrm{u}}_{\mathrm{p}}\cdot \nabla T=\nabla \cdot \left(A_{\mathrm{p}}{k}_{\mathrm{f}}\nabla T\right)+f_{\mathrm{D}}\frac{{\rho }_{\mathrm{f}}{A}_{\mathrm{p}}}{2d_{\mathrm{h}}}{\left|{\mathrm{u}}_{\mathrm{p}}\right|}^3+Q_{\text{wall}}(16)$

The second term on the right hand side corresponds to friction heat dissipated due to viscous shear.

$Q_{\text{wall}}={\left(hD\right)}_{\text{eff}}\left(T_{\text{ext}}-T\right)(17)$

${\left(\text{hD}\right)}_{\text{eff}}=\frac{2\pi }{\frac{1}{r_0{h}_{\mathrm{i}}}+\frac{1}{r_{\mathrm{N}}{h}_{\text{ext}}}+{\displaystyle \sum _1^N}\frac{\ln \left(\frac{r_{\mathrm{n}}}{r_{\mathrm{n}-1}}\right)}{k_{\mathrm{n}}}}(18)$

h is given as follow (Gnielinski, 1976).

$h=\text{Nu}\frac{k}{d_{\mathrm{h}}}(19)$

$\text{Nu}=\frac{\left(f_{\mathrm{D}}/8\right)\left(\text{Re}-1000\right)\mathrm{Pr}}{1+12.7{\left(f_{\mathrm{D}}/8\right)}^{1/2}\left({\mathrm{Pr}}^{2/3}-1\right)}(20)$

2.2.5 Mathematical model for solar vacuum tube heat collectors

The thermal efficiency for the solar vacuum tube heat collector is given below (Li et al., 2016):

$TE=0.721-0.89\frac{T_{\mathrm{m}}-T_0}{G}-0.0199\frac{{\left(T_{\mathrm{m}}-T_0\right)}^2}{G}(21)$

G is equal to 750 W/m² for 7 h per day in non-heating season with external average temperature of 21.2°C, and it is 500 W/m² for 5 h per day in heating season with external average temperature of 4.6°C in North China (taking the north China plain as an example).

2.2.6 Boundary and initial conditions

The temperature of surrounding rock keeps constant when it is more than 200 m distance from wells and artificial reservoir. The surface temperature is 15°C and geothermal gradient is 30 °C/km, which can be used to calculate the initial rock temperature. The other parameters set for the well are described in Section 2.1.

2.2.7 Solving method and model verification

The above equations are discretized by finite volume method with the implicit scheme, and solved by Python software using algorithm of TDMA (Tri-diagonal matrix algorithm) together with the initial and boundary conditions (Bu et al., 2021; Bu et al., 2020).

Borehole thermal energy storage (BTES) stores thermal energy mainly into rocks and soil, which has the same principle as SDEGS. Xu et al. (2018) analyzed the performance of BTES located in Chifeng, China by experiment. The BTES experiment consists of 468 boreholes (80 m deep single-U tube heat exchanger). In the non-heating season, the circulated water with a temperature of 75°C flows firstly into the BTES system, and then it flows back to surface with a temperature around 50°C after releasing heat to the soil. The average temperature of inlet and outlet water for U tube is 62.5°C. In the heating season, the thermal recovery efficiency is only 16.4% at the inlet water temperature of 51.9°C, while it rises to 65.9% at the inlet water temperature of 25°C, indicating that the thermal recovery efficiency can be improved by reducing the temperature of inlet water. Given the temperature difference of 5°C in the heat exchanger, the actual temperature of water injecting into the U tube heat exchanger is about 30°C, indicating that there is a temperature difference of 27.5°C between the actual temperature of water injecting into the U tube heat exchanger in the heating season and the average temperature of inlet and outlet water for U tube in the non-heating season.

In this study, the artificial reservoir for SDEGS is created at the depth of about 1,000 m with the rock temperature of about 45°C. In the non-heating season, the temperature of inlet and outlet for SDEGS are respectively 90°C and 31°C with an average temperature of 60.5°C. In the heating season, the inlet temperature for SDEGS is only 10°C, having a temperature difference of 50.5°C between the inlet temperature in the heating season and the average temperature of inlet and outlet water in the non-heating season for SDEGS. Compared with the temperature difference of 27.5°C for BTES reported in the reference (Xu et al., 2018), the greater temperature difference means that more thermal energy can be extracted for SDEGS. In addition, the inlet temperature of 10°C is lower than the initial artificial reservoir temperature of about 45°C, signifying that not only solar thermal energy stored into the SDEGD in the non-heating season can be extracted, but part of the thermal energy originally stored in the rocks can also be extracted due to the comparatively low injection temperature, and thus leading to a high thermal recovery efficiency.

For BTES and SDEGS, storing thermal energy into the rocks or extracting thermal energy from the rocks are mainly through the thermal conduction, which can avoid the generation of natural thermal convection and thus improve the thermal recovery efficiency. It should be emphasized that the thermal recovery efficiency can be further improved by decreasing the injection water temperature for both BTES and SDEGS in the heating season.

3 Results and discussion

The artificial reservoir for SDEGS is created from 880 m to 1,000 m in depth, and five layers of fracture are constructed with a layer distance of 30 m in vertical direction in order to store as much heat energy as possible in the rocks and avoid the mutual thermal interference, as shown in Figure 1. Due to having a higher heat collecting efficiency at the temperature range of operation, solar vacuum tube heat collectors are selected and a daily thermal storage tank is used to overcome the daily fluctuation and instability of solar energy. Solar thermal energy is firstly stored into the SDEGS during the non-heating season and then it is extracted for space heating during the heating season, as shown in Figure 2.

In Figures 3, 6, the symbols T_in and T_out respectively represent the injection and extraction temperature, V_in stands for the volume flow rate, and P, Q and η denote the thermal power, total heat and thermal recovery efficiency, respectively. From Figures 3, 4, all parameters including T_in, T_out, P, Q, η and the temperature field distribution keep basically stable except for the first year. Before the first non-heating season, the rocks are undisturbed and the average rock temperature in the artificial reservoir remains at about 43°C (316.15K), which is higher than that at the end of other heating season, as shown in Figures 4D–F. As a result, T_out for the first non-heating season is greater than that of other non-heating season due to having a higher rock temperature and a small temperature difference between the hot water and the rocks, thus causing a decrease in P and Q for the first thermal storage stage. Taking the 20^th heating season, for example, the yearly average thermal power is 6355.35 kW, which can provide heat for buildings with area of 211,845 m² if the specific heat load is 30 W/m².

Figure 3

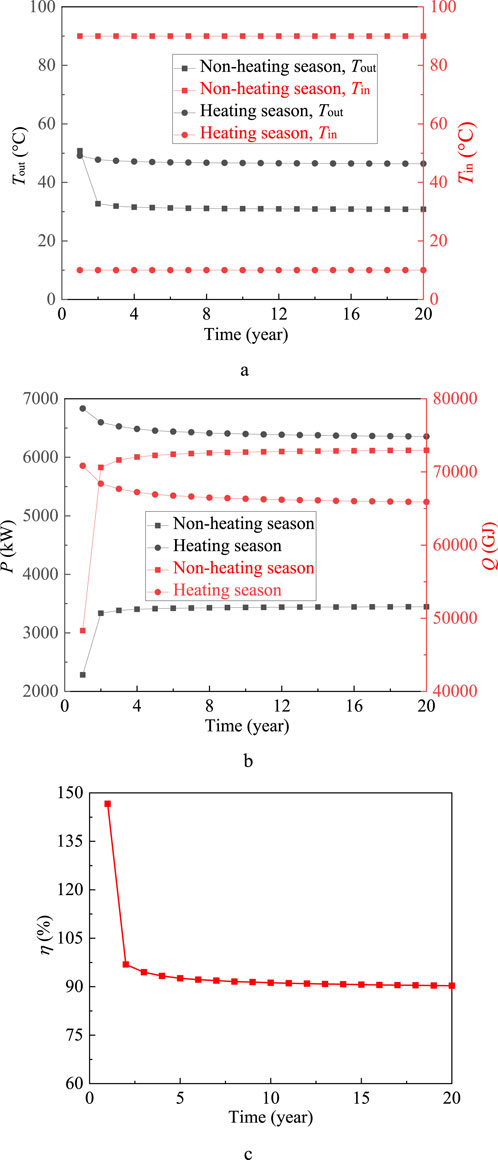
Figure 3. Thermal performance of SDEGS. (A) Injection and extraction temperature; (B) Thermal power and total heat; (C) Thermal recovery efficiency.

Figure 4

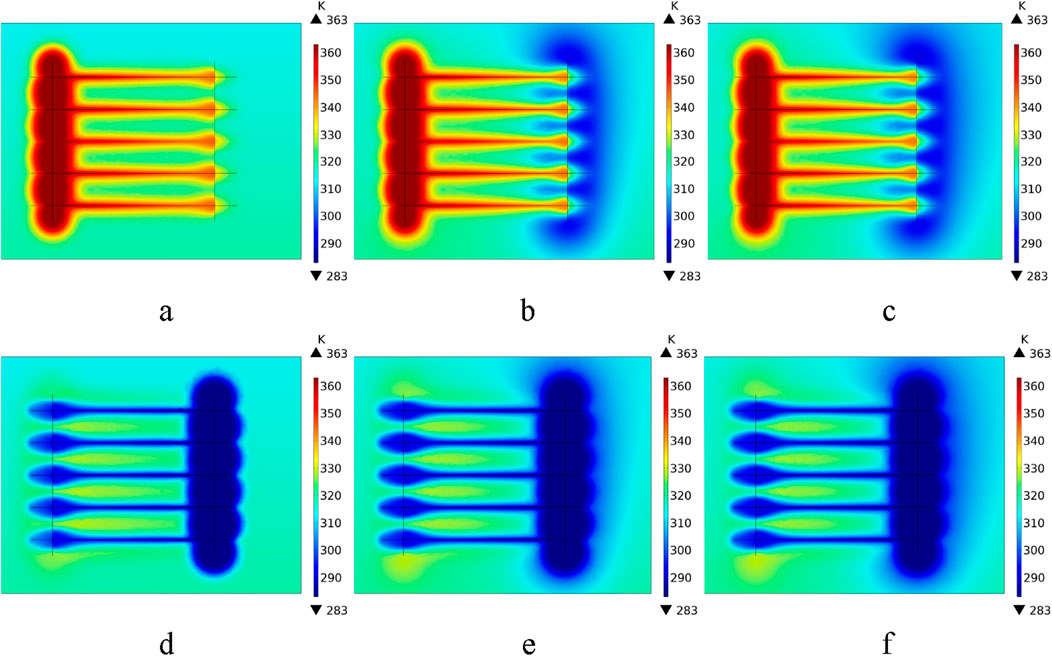
Figure 4. Temperature field distribution around SDEGS (front view). (A) At the beginning of 1^st heating season; (B) At the beginning of 10^th heating season; (C) At the beginning of 20^th heating season; (D) At the end of 1^st heating season; (E) At the end of 10^th heating season; (F) At the end of 20^th heating season.

The thermal recovery efficiency η is defined as the total heat extracted during the heating season divided by the total heat stored during the non-heating season. HT-ATES stores heat energy mainly in the bodies of water, and its thermal recovery efficiency is generally low due to the natural convection induced by density contrasts and higher heat losses to the rocks. While for SDEGS, the thermal energy is stored in the rocks rather in the bodies of water, avoiding the effect of natural convection and thus improving the thermal recovery efficiency. As expected, the thermal recovery efficiency of SDEGS for all heating seasons is greater than 90% as shown in Figure 3C, while it is only 46% for HT-ATES created in Neubrandenburg throughout 3 years of regular operation (Kabus et al., 2009). The working process of storing and extracting thermal energy for SDEGS is described in detail below. During the non-heating season, the water heated by solar energy flows into the artificial reservoir and releases its heat into the rocks around the fractures through convective heat transfer between water and the fracture surface, and then the heat transfers in the rocks from the near-fracture area to the far-fracture area through thermal conduction, realizing thermal energy storage mainly in the rocks rather than in the bodies of water due to the artificial reservoir having a small underground storing space for water storage. During the heating season, the cold water enters into the artificial reservoir and the heat stored in the rocks transfers from the rocks to the cold water due to having temperature difference between the rocks around the fractures and the cold water, completing the heat release process. The process of storing and extracting heating for SDEGS is just like that of spring energy storage and also like a sponge having a high water absorbing and releasing capacity.

Figure 3 shows that T_in, T_out, P, Q and η gradually come to stability with operation time increasing, indicating that SDEGS runs more stable and has a very small performance attenuation for 20 years’ operation under the conditions of constant injection temperature and volume flow rate. Figure 4 demonstrates that the temperature field for the artificial reservoir remains basically unchanged, implying that SDEGS has reached a relatively stable state and can always provide a trustworthy and stable thermal energy throughout its life cycle. The thermal recovery efficiency of SDEGS is always greater than 90% for all heating seasons from Figure 3C, implying that the thermal energy extracted during the heating season is mainly from that stored during the non-heating season. In other words, the thermal performance of SDEGS relies mainly on the thermal energy storage during the non-heating season not on the initial temperature of rocks, indicating that SDEGS can be used for space heating forever and always has a stable thermal output as long as the thermal energy is continually stored into it during the non-heating season. The above analysis also indicates that the artificial reservoir for SDEGS can thus be created in the shallow buried depth rocks without a specific requirement for temperature, thus dramatically reducing the project costs and the risk of hydraulic fracturing as well as widening the range of technology application.

The reason for the high thermal recovery efficiency of SDEGS is briefly analyzed as follows. The thermal influence distance in rocks during the thermal energy storage and extraction stage is firstly determined through the following formula (Alimonti and Soldo, 2016).

$L_S=2\sqrt{{\alpha }_S\tau }=2\sqrt{\frac{{\lambda }_S}{{\rho }_S{C}_S}\tau }(22)$

where, α_S is rock thermal diffusivity, m²/s; τ denotes the operation time, s; L_S stands for the thermal influence distance in rocks, m; ρ_S represents rock density, kg/m³; λ_S is thermal conductivity of rock, W/(m⋅K).

For the non-heating season with an operation time of 245 days, L_S is equal to 13.65 m while it is 9.55 m for the heating season with an operation time of 120 days, thus leading to a loss of the stored thermal energy due to the difference of the thermal influence distance. The thermal recovery efficiency of SDEGS can be further improved if prolonging the extraction heat time during the heating season. The above calculation result also indicates that the vertical distance of 30 m between two layers of fracture is reasonable according to the thermal influence distance. From Figures 4, 5, the thermal influence distance for 20 years’ operation is indeed small. In brief, 10% of the thermal energy collected from solar energy loses in the rocks, which is much smaller than that in HT-ATES. From Figures 4D–F, the temperature of rocks between two layers of fracture at the end of heating season is greater than that at the initial undisturbed state with an average temperature of 43°C, meaning that a few heat stored in the non-heating season cannot be extracted in the heating season. Similarly, the temperature of rocks surrounding the artificial reservoir at the end of heating season from Figures 4D–F and Figure 5B is also greater than the initial undisturbed rock temperature of 43°C, which is the major contributor to the heat loss.

Figure 5

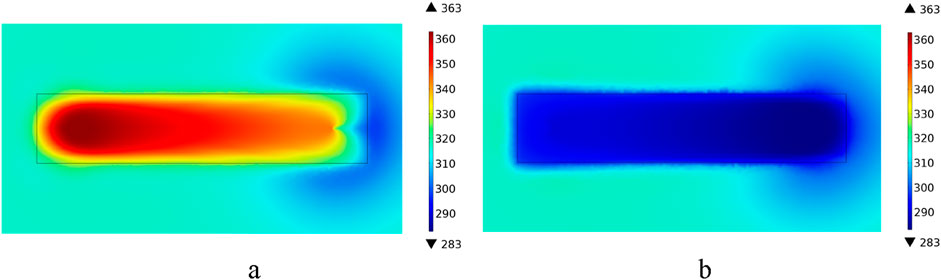
Figure 5. Temperature field distribution around SDEGS (top view). (A) At the beginning of 20^th heating season; (B) At the end of 20^th heating season.

In Figures 4, 5, the size of artificial reservoirs is described in section 2.1. Show that SDEGS has a stable and sustainable thermal output capacity during the heating season at the constant injection temperature and volume flow rate when solar energy is continuously stored into it during the non-heating season. During the heating season, the combined SDEGS and solar energy heating system is used to provide heat for buildings, as shown in Figure 2. To maintain the stable operation of the combined heating system and to accommodate the changes of building heat load, SDEGS should have not only a stable energy output but also should have a flexible adjustment ability due to the instability and intermittency of solar energy. For this, the adjustment ability of thermal output for SDEGS need to be analyzed.

From Figure 3B, the average total heat during the non-heating season is about 72,531.26 GJ, which needs about 25,000 m² solar vacuum tube heat collectors to be installed. By means of the storage and adjustment using the storage tank on a diurnal basis, the daily average thermal power for solar energy during the heating season is 1,629.86 kW. SDEGS has the minimal thermal power of 6355.35 kW at the 20^th heating season for 20 years’ operation. Taking the 20^th heating season as an example, if the heating system is designed according to the heating capacity of 7985.21 kW (6355.35 kW from SDEGS and 1,629.86 kW from solar energy), then the thermal load regulation ability of SDEGS should be higher than the daily average thermal power of solar energy (1,629.86 kW) during the heating season, keeping the heating system stable even if solar energy system does not run for several days. The thermal output capacity of SDEGS can be adjusted by changing the injection temperature and injection volume flow rate during the heating season. Figure 6 shows the adjustment capacity of thermal power for SDEGS. The thermal power of SDEGS during the heating season are respectively 6988.29, 6355.35 and 5805.37 kW at the injection temperature of 5, 10°C and 15°C with a constant volume flow rate of 150 m³/h, and they are respectively 7161.81, 6355.35 and 5291.52 kW at the volume flow rate of 100, 150 and 200 m³/h with a constant injection temperature of 10°C. Compared with the thermal power of 6355.35 kW at the injection temperature of 10°C and volume flow rate of 150 m³/h, the thermal load regulation ability of SDEGS reaches to 632.94 and 806.46 kW respectively by decreasing the injection temperature to 5°C and by increasing the volume flow rate to 200 m³/h. However, the thermal load regulation ability of SDEGS is still less than the daily average thermal power of solar energy (1,629.86 kW). To keep the stable operation of the combined heating system, two measures can be taken to solve the above problem. One is to add an auxiliary heat source with the heat power of about 1,000 kW, and the other is to reduce the heating area. Anyway, the instability and intermittency as well as temporal mismatch faced by solar energy can be effectively solved by storing thermal energy into SDEGS, and the thermal output of the hybrid heating system can also keep stable by adjusting the thermal power of SDEGS or adding an auxiliary heat source with a low thermal power.

Figure 6

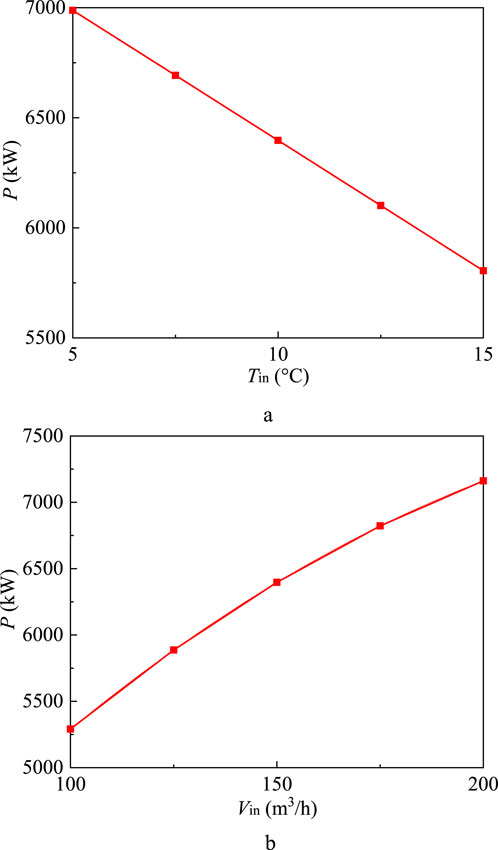
Figure 6. The adjustment capacity of thermal power of SDEGS. (A) Variations of injection temperature at a volume flow rate of 150 m³/h; (B) Variations of volume flow rate at an injection temperature of 10°C.

4 Conclusion

Solar energy has a considerable space heating potential in China and however, intermittency and instability limit its application. Seasonal thermal energy storage (STES), especially underground thermal energy storage (UTES) can effectively solve the above problems faced by solar energy. Enlightened by the enhanced geothermal system (EGS) creating an artificial reservoir in the high temperature rocks, a novel scheme of storing high temperature solar thermal energy into the shallow depth EGS (SDEGS) is proposed. The following conclusions can be drawn.

(1) The thermal performance of SDEGS always keeps stable for 20 years’ operation due to a continuous solar thermal energy storage into the artificial reservoir during the non-heating season, and its thermal recovery efficiency is greater than 90% all long, implying that the thermal performance of SDEGS relies mainly on the solar thermal energy storage during the non-heating season not on the initial temperature of rocks.

(2) The artificial reservoir for SDEGS can be created in the shallow buried depth rocks without a specific requirement for temperature, thus remarkably reducing the project costs and the risk of hydraulic fracturing as well as widening the range of technology application. Therefore, the hybrid heating system of SDEGS and solar energy is a more appropriate technical route for solar space heating.

(3) To further reduce the project cost and avoid the risk of reservoir creation, the abandoned oil and gas fields can be reused as the artificial reservoir.

SDEGS is suitable for use in carbonate rocks and consolidated sandstones as well as granite, while it is difficult to be applied to unconsolidated sandstones due to the lack of the technology of artificial fracture in these areas.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

XB: Conceptualization, Investigation, Methodology, Validation, Writing–original draft. WC: Formal Analysis, Investigation, Methodology, Software, Validation, Writing–review and editing. JD: Funding acquisition, Investigation, Methodology, Writing–review and editing. LW: Investigation, Methodology, Software, Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. Carbon Peak and Carbon Neutralization Science and Technology Innovation Special Fund of Jiangsu Province, China (Grant No. BE2022859).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

163, 2024 163 (2024). GQ1HSOG8053186Z3. Available at: https://www.163.com/dy/article/GQ1HSOG8053186Z3.html.

Google Scholar

Alimonti, C., and Soldo, E. (2016). Study of geothermal power generation from a very deep oil well with a wellbore heat exchanger. Renew. Energy 86, 292–301. doi:10.1016/j.renene.2015.08.031

CrossRef Full Text | Google Scholar

Barnard, A., Hunt, W., Timlake, W., and Varley, E. (1966). A theory of fluid flow in compliant tubes. Biophysical J. 6 (6), 717–724. doi:10.1016/s0006-3495(66)86690-0

CrossRef Full Text | Google Scholar

Bu, X., Guo, Z., and Wang, L. (2021). Performance analysis of shallow depth hydrothermal enhanced geothermal system for building heating. Case Stud. Therm. Eng. 26, 101147. doi:10.1016/j.csite.2021.101147

CrossRef Full Text | Google Scholar

Bu, X., Jiang, K., and He, Y. (2020). Performance analysis of shallow depth hydrothermal enhanced geothermal system for electricity generation. Geothermics 86, 101847. doi:10.1016/j.geothermics.2020.101847

CrossRef Full Text | Google Scholar

Cao, W., Huang, W., and Jiang, F. (2016). A novel thermal–hydraulic–mechanical model for the enhanced geothermal system heat extraction. Int. J. Heat. Mass Tran. 100, 661–671. doi:10.1016/j.ijheatmasstransfer.2016.04.078

CrossRef Full Text | Google Scholar

Churchill, S. (1997). Friction factor equation spans all fluid-flow regimes. Chem. Eng. 84 (24), 91–92.

Google Scholar

Dahash, A., Ochs, F., Janetti, M. B., and Streicher, W. (2019). Advances in seasonal thermal energy storage for solar district heating applications: a critical review on large-scale hot-water tank and pit thermal energy storage systems. Appl. Energy 239, 296–315. doi:10.1016/j.apenergy.2019.01.189

CrossRef Full Text | Google Scholar

Fleuchaus, P., Godschalk, B., Stober, I., and Blum, P. (2018). Worldwide application of aquifer thermal energy storage-A review. Renew. Sustain. Energy Rev. 94, 861–876. doi:10.1016/j.rser.2018.06.057

CrossRef Full Text | Google Scholar

Fleuchaus, P., Schüppler, S., Bloemendal, M., Guglielmetti, L., Opel, O., and Blum, P. (2020). Risk analysis of high-temperature aquifer thermal energy storage (HT-ATES). Renew. Sustain. Energy Rev. 133, 110153. doi:10.1016/j.rser.2020.110153

CrossRef Full Text | Google Scholar

Fong, M., Alzoubi, M., Kurnia, J., and Sasmito, A. (2019). On the performance of ground coupled seasonal thermal energy storage for heating and cooling: a Canadian context. Appl. Energy 250, 593–604. doi:10.1016/j.apenergy.2019.05.002

CrossRef Full Text | Google Scholar

Gnielinski, V. (1976). New equations for heat and mass transfer in turbulent pipe and channel flow. Int. Chem. Eng. 16 (2), 359–368.

Google Scholar

Han, X., Guo, J., and Wei, C. (2022). Residential space-heating energy demand in urban Southern China: an assessment for 2030. Energy and Build. 254, 111598. doi:10.1016/j.enbuild.2021.111598

CrossRef Full Text | Google Scholar

He, Y., and Bu, X. (2020). Performance of hybrid single well enhanced geothermal system and solar energy for buildings heating. Energies 13, 2473. doi:10.3390/en13102473

CrossRef Full Text | Google Scholar

Hou, J., Cao, M., and Liu, P. (2018). Development and utilization of geothermal energy in China: current practices and future strategies. Renew. Energy 125, 401–412. doi:10.1016/j.renene.2018.02.115

CrossRef Full Text | Google Scholar

Huang, W., Cao, W., and Jiang, F. (2017). Heat extraction performance of EGS with heterogeneous reservoir: a numerical evaluation. Int. J. Heat. Mass Tran. 108, 645–657. doi:10.1016/j.ijheatmasstransfer.2016.12.037

CrossRef Full Text | Google Scholar

Kabus, F., Wolfgramm, M., Seibt, A., Richlak, U., and Beuster, H. (2009). “Aquifer thermal energy storage in Neubrandenburg-monitoring throughout three years of regular operation,” in Proceedings, EFFSTOCK Conference, Stockholm, June 14-17, 2009. Available at: https://www.researchgate.net/publication/267257193.

Google Scholar

Li, M., Virguez, E., Shan, R., Tian, J., Gao, S., and Patino-Echeverri, D. (2022). High-resolution data shows China’s wind and solar energy resources are enough to support a 2050 decarbonized electricity system. Appl. Energy 306, 117996. doi:10.1016/j.apenergy.2021.117996

CrossRef Full Text | Google Scholar

Li, P., Li, J., Pei, G., Munir, A., and Ji, J. (2016). A cascade organic Rankine cycle power generation system using hybrid solar energy and liquefied natural gas. Sol. Energy 127, 136–146. doi:10.1016/j.solener.2016.01.029

CrossRef Full Text | Google Scholar

Lim, H., Ok, J., Park, J., Lee, S., Karng, W., and Kang, Y. (2020). Efficiency improvement of energy storage and release by the inlet position control for seasonal thermal energy storage. Int. J. Heat Mass Transf. 151, 119435. doi:10.1016/j.ijheatmasstransfer.2020.119435

CrossRef Full Text | Google Scholar

Lopik, J., Hartog, N., and Zaadnoordijk, W. (2016). The use of salinity contrast for density difference compensation to improve the thermal recovery efficiency in high-temperature aquifer thermal energy storage systems. Hydrogeol. J. 24, 1255–1271. doi:10.1007/s10040-016-1366-2

CrossRef Full Text | Google Scholar

Lu, H., Tian, P., and He, L. (2019). Evaluating the global potential of aquifer thermal energy storage and determining the potential worldwide hotspots driven by socio-economic, geo-hydrologic and climatic conditions. Renew. Sustain. Energy Rev. 112, 788–796. doi:10.1016/j.rser.2019.06.013

CrossRef Full Text | Google Scholar

Lu, S. (2018). A global review of enhanced geothermal system (EGS). Renew. Sustain. Energy Rev. 81, 2902–2921. doi:10.1016/j.rser.2017.06.097

CrossRef Full Text | Google Scholar

Lurie, M. (2009). “Modeling of oil product and gas pipeline transportation,” in Modeling of oil product and gas pipeline transportation (Wiley), 1–214.

CrossRef Full Text | Google Scholar

Nilsson, E., and Rohdin, P. (2019). Performance evaluation of an industrial borehole thermal energy storage (BTES) project-Experiences from the first seven years of operation. Renew. energy 143, 1022–1034. doi:10.1016/j.renene.2019.05.020

CrossRef Full Text | Google Scholar

Olasolo, P., Ju´arez, M., Morales, M., D´Amico, S., and Liarte, I. (2016). Enhanced geothermal systems(EGS): a review. Renew. Sustain. Energy Rev. 56, 133–144. doi:10.1016/j.rser.2015.11.031

CrossRef Full Text | Google Scholar

Rosato, A., Ciervo, A., Ciampi, G., Scorpio, M., Guarino, F., and Sibilio, S. (2020). Energy, environmental and economic dynamic assessment of a solar hybrid heating network operating with a seasonal thermal energy storage serving an Italian small-scale residential district: influence of solar and back-up technologies. Therm. Sci. Eng. Prog. 19, 100591. doi:10.1016/j.tsep.2020.100591

CrossRef Full Text | Google Scholar

Sanner, B., and Knoblich, K. (1999). Advantages and problems of high temperature underground thermal energy storage. Bull. Hydrogeol. 17, 341–348.

Google Scholar

Schmidt, T., Pauschinger, T., Sørensen, P., Snijders, A., Djebbar, R., Boulter, R., et al. (2018). Design aspects for large-scale pit and aquifer thermal energy storage for district heating and cooling. Energy Procedia 149, 585–594. doi:10.1016/j.egypro.2018.08.223

CrossRef Full Text | Google Scholar

Schout, G., Drijver, B., Gutierrez-Neri, M., and Schotting, R. (2014). Analysis of recovery efficiency in high-temperature aquifer thermal energy storage: a Rayleigh-based method. Hydrogeology J. 22 (1), 281–291. doi:10.1007/s10040-013-1050-8

CrossRef Full Text | Google Scholar

Schout, G., Drijver, B., and Schotting, R. (2016). The influence of the injection temperature on the recovery efficiency of high temperature aquifer thermal energy storage: Comment on Jeon et al., 2015. Energy 103, 107–109. doi:10.1016/j.energy.2016.02.122

CrossRef Full Text | Google Scholar

Shah, S., Aye, L., and Rismanchi, B. (2018). Seasonal thermal energy storage system for cold climate zones: a review of recent developments. Renew. Sustain. Energy Rev. 97, 38–49. doi:10.1016/j.rser.2018.08.025

CrossRef Full Text | Google Scholar

Su, C., Madani, H., and Palm, B. (2018). Heating solutions for residential buildings in China: current status and future outlook. Energy Convers. Manag. 177, 493–510. doi:10.1016/j.enconman.2018.10.005

CrossRef Full Text | Google Scholar

Su, C., Madani, H., and Palm, B. (2019). Building heating solutions in China: a spatial techno-economic and environmental analysis. Energy Convers. Manag. 179, 201–218. doi:10.1016/j.enconman.2018.10.062

CrossRef Full Text | Google Scholar

Ueckert, M., and Baumann, T. (2019). Hydrochemical aspects of high-temperature aquifer storage in carbonaceous aquifers: evaluation of a field study. Geotherm. Energy 7 (1), 4–22. doi:10.1186/s40517-019-0120-0

CrossRef Full Text | Google Scholar

Wang, X., Ding, C., Zhou, M., Cai, W., Ma, X., and Yuan, J. (2023). Assessment of space heating consumption efficiency based on a household survey in the hot summer and cold winter climate zone in China. Energy 274, 127381. doi:10.1016/j.energy.2023.127381

CrossRef Full Text | Google Scholar

Wesselink, M., Liu, W., Koornneef, J., and van den Broek, M. (2018). Conceptual market potential framework of high temperature aquifer thermal energy storage - a case study in The Netherlands. Energy 147, 477–489. doi:10.1016/j.energy.2018.01.072

CrossRef Full Text | Google Scholar

Winterleitner, G., Schütz, F., Wenzlaff, C., and Huenges, E. (2018). The impact of reservoir heterogeneities on high-temperature aquifer thermal energy storage systems. A case study from northern Oman. Geothermics 74, 150–162. doi:10.1016/j.geothermics.2018.02.005

CrossRef Full Text | Google Scholar

Wu, C., Chen, Z., Qin, C., Zhang, Y., and Zhang, X. (2022). Exploring the challenges of residential space heating electrification in China: a case study in Jinan and Qingdao. Case Stud. Therm. Eng. 37, 102283. doi:10.1016/j.csite.2022.102283

CrossRef Full Text | Google Scholar

Xu, L., Torrens, J., Guo, F., Yang, X., and Hensen, J. (2018). Application of large underground seasonal thermal energy storage in district heating system: a model-based energy performance assessment of a pilot system in Chifeng, China. Appl. Therm. Eng. 137, 319–328. doi:10.1016/j.applthermaleng.2018.03.047

CrossRef Full Text | Google Scholar

Yang, T., Liu, W., Kramer, G., and Sun, Q. (2021). Seasonal thermal energy storage: a techno-economic literature review. Renew. Sustain. Energy Rev. 139, 110732. doi:10.1016/j.rser.2021.110732

CrossRef Full Text | Google Scholar

Yu, S., Eom, J., Zhou, Y., Evans, M., and Clarke, L. (2014). Scenarios of building energy demand for China with a detailed regional representation. Energy 67, 284–297. doi:10.1016/j.energy.2013.12.072

CrossRef Full Text | Google Scholar

Glossary

A_p is the pipe cross section area of the flow channel, (m²)

C_p,f is the fluid heat capacity at constant pressure, J/(kg·K)

C_p,s is the reservoir matrix heat capacity at contant pressure, J/(kg·K)

d_f is the fracture thickness, m

d_h is the hydraulic diameter, m

D is the pipe wall perimeter, m

e is roughness coefficient, m

f_D is the Darcy friction factor

f_f is roughness factor

F is a volume force term, N/m³

G stands for the solar radiation intensity, W/m²

h is heat transfer coefficient, W/(m²·k)

h_ext is the heat transfer coefficients of outer wall, W/(m²·k)

h_i is the heat transfer coefficients of inner wall, W/(m²·k)

k_eff is effective thermal conductivity, W/(m·K)

k_f is the fluid thermal conductivity, W/(m·K)

k_n is the pipe wall thermal conductivity, W/(m·K)

k_s is the reservoir matrix thermal conductivity, W/(m·K)

p(Pa) is pressure, Q indicates the heat transfer between the reservoir matrix and fractures, W/m³

Q_m is the mass transfer between the reservoir matrix and fractures, kg/(m³·s)

Q_w is the heat source term, W/m³

Q_wall represents external heat exchange through the pipe wall, W/m

r_n is pipe radius, m

Re is Reynolds number

T_ext is the external temperature outside of the pipe, °C

T₀ represents ambient temperature, °C

T_m indicates average outlet and inlet temperature of solar collector, °C

TE denotes thermal efficiency

u is fluid velocities in the reservoir matrix, m/s

u_f is the velocity in fractures, m/s

u_p is the averaged velocity of fluid in pipe, m/s

ρ is the density of the fluid, kg/m³

ρ_f is the fluid density, kg/m³

ρ_s is the reservoir matrix density, kg/m³

ε is the porosity of reservoir matrix, ε_f is the fracture porosity

κ is the permeability of the porous medium, m²

κ_f is the fracture’s permeability, m²

μ is the fluid’s dynamic viscosity, Pa·s

∇_t is the gradient operator restricted to the fracture’s tangential plane

(ρCp)_eff is effective volumetric heat capacity, J/(m³·K)

(hZ)_eff is the total equivalent heat transfer coefficient, W/(m·k)