Simulation study on crack extension law of asphalt pavement under temperature effect

In modern highway construction, asphalt pavement is a widely used structural form, which is easily affected by various external conditions, among which the temperature effect is the most significant. In this paper, the cohesion model is used to simulate the structural cracks of asphalt pavement, the finite element method is used to simulate the asphalt concrete pavement model, and the temperature field simulation model of the pavement is established by using ABAQUS software, with the help of which the spatial distribution of stresses under different temperature conditions is deeply explored, and then the crack extension law during the process of temperature change is systematically investigated, and the effect of the temperature load on the degree of damage to the asphalt pavement is also studied. With the temperature change, the pavement surface layer is affected the most, and the soil base layer is affected the least. The higher the external temperature, the larger the crack expansion width inside the pavement structure, and the faster the corresponding expansion rate. The fatigue damage rate of the pavement structure is accelerated along with the increase of temperature. The research results can provide a theoretical basis for improving the high temperature performance of asphalt pavement.

1 Introduction

As an important part of urban transportation infrastructure, asphalt pavement, in addition to withstanding the repeated effects of various vehicle loads, also has to face the challenges posed by environmental factors such as climate change, seasonal temperature differences, etc. In 1968, Straub provided a theoretical basis for finite element analysis of the pavement temperature field through the actual measurements of sunlight blessing, temperature, and the internal temperature distribution of the asphalt pavement (Heng, 2020). Based on this, Swarna and Reddy (2018) utilized the finite element method to construct a road force model involving the interlayer contact effect, to study the evolution of the road force situation under the action of temperature, and to provide a theoretical basis for road design. Under the action of cyclic low-temperature conditions, changes in the microstructure of concrete occur, porosity increases, and surface damage is exacerbated (He and Lu, 2024). In practical engineering, the road performance of pavement structures is often enhanced by introducing additives. Studies have shown that when thermally expandable polymer microspheres are added to cement mortar, its tensile strength is significantly improved (He et al., 2024). Weiguang et al. (2004) calculated the typical pavement structure and confirmed that there is a huge difference in the magnitude of stress generated in each structural layer under the action of external environment. Shaohua (2019) took asphalt pavement as the research object and used ABAQUS numerical simulation method to study the dynamic response of cracked and non-cracked pavement under different temperatures and different loading conditions. Lili and Xuancang (2011) proposed a meshless method formulation for calculating the transient temperature field and stress field of asphalt pavements by using the variational principle, and the penalty function method was introduced to adjust the boundary conditions in the calculation process. The calculation results are consistent with the field measurement data as well as the finite element analysis results, and the calculation accuracy is better than that of the finite element method. Naiji (2021) constructed a numerical calculation model of asphalt pavement temperature field considering temperature factor according to the real stress state of asphalt pavement, combined with driving load and environmental temperature effect, analyzed the temperature distribution of each layer, and revealed the influence of temperature on the bonding performance of each layer of asphalt pavement. Heidari Rarani based on the double-cantilever beam test comparing the three kinds of VCCT, XFEM and CZM methods to study the delamination expansion, and utilized cohesion model to study the delamination expansion of cracks with higher accuracy (Zhenpeng et al., 2022). Factors such as base modulus attenuation, extent of inundation, and thickness of the surface and base layers can affect the location of pavement fracture in practical engineering applications (Wei et al., 2023). Gan (2020) took the cracks of asphalt pavement as the research object, and through numerical simulation, revealed its main crack morphology and the influencing factors of crack development from the fine level, compared with the test data, and verified the practicality of the established micro crack simulation model.

The aim of this paper is to focus on the temperature field effect of asphalt pavements using advanced numerical simulation techniques to monitor the temperature field distribution of pavement materials under different temperature conditions. Existing studies in simulating the crack expansion behavior of asphalt pavements often set prefabricated cracks on the structure to control the location and size of the generated cracks, etc. In this study, the location of crack expansion of asphalt pavement structures affected by temperature is random, which is more in line with the actual engineering applications. Cracks in asphalt pavement structure are simulated by cohesion model, and the influence mechanism of the crack expansion behavior within the structure under the effect of temperature is explored in detail.

2 Temperature field of pavement structure

2.1 Cohesion model theory

Due to the limitations of traditional contact models, experts on the subject have proposed the use of a cohesion model based on constrained surfaces. This model can fully consider the characteristics of the contact materials and dynamically show the change of the constraint state between layers (Zhenxian, 2022). The cohesion model is used to simulate the internal crack unit of the pavement structure and to establish a three-dimensional structural analysis model of crack-containing asphalt concrete pavement.

2.1.1 Cohesion model (CZM) theory

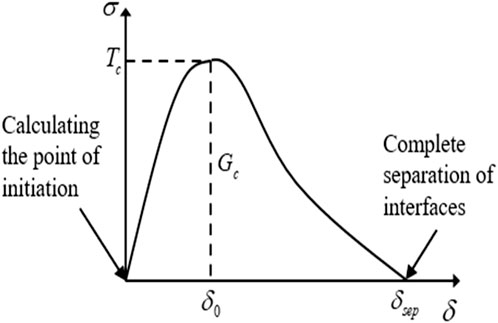
Cohesion model (CZM) was originally proposed by Dugdale, is an important theory in elastic-plastic fracture mechanics, that there is a special cohesion unit in the crack tip region, in which the cohesion unit, the fracture of the structure produces such as a rough variety of damage phenomena (Zixing, 2015), the typical cohesion model force-displacement curves are shown in Figure 1.

Figure 1

Figure 1. Typical cohesion-displacement curves.

In ABAQUS software, the cohesion model contains two types, linear and exponential, which have different damage characteristics when the material reaches its ultimate strength.

The linear type is indicated by Equations 1, 2:

$t=\left\{\begin{array}{l}{T}_C\delta /{\delta }_0,0\le \delta \le {\delta }_0\\ \left(\delta -{\delta }_{sep}\right)\frac{T_C}{{\delta }_0-{\delta }_{sep}},{\delta }_0\le \delta \le {\delta }_{sep}\end{array}\right.(1)$

$G_C=\frac{1}{2}{T}_C{\delta }_{sep}(2)$

Exponential types are denoted by Equations 3, 4:

$t=\exp \left(1\right)\frac{\delta }{{\delta }_0}\exp \left(-\frac{T_C}{{\delta }_0}\right)(3)$

$G_C=\exp \left(1\right)T_C{\delta }_0(4)$

where: T_C is the ultimate strength of the material; δ₀ is the displacement when the material produces damage; δ_sep is the displacement when the material completely separates; G_C is the fracture energy, and the numerical size is equal to the area enclosed by the force-displacement curve.

When using ABAQUS software to simulate the cohesion model, it is clearly proposed that when the material is in the state of no damage, only the linear type can be used to describe the ascending section, and when the material enters the stage of damage evolution, the appropriate model can be selected according to the actual needs. After a series of experimental comparisons, the use of an exponential cohesion model as shown in Figure 2 is more realistic when describing the interlayer damage stress-strain law (Zhenxian, 2022).

Figure 2

Figure 2. Improved cohesion model.

Since there exists a certain degree of slip phenomenon between different interfaces, it is necessary to introduce the corresponding contact theory to analyze the friction problem between the interfaces in order to obtain the final results. In ABAQUS software, in order to satisfy the output target, the damage initial criterion does not affect the cohesive surface, including the maximum stress criterion, the maximum displacement criterion, the quadratic stress criterion and the quadratic displacement criterion. Among them, the quadratic stress criterion is most accurately described with the expression Equation 5:

${\left\{\frac{t_n}{t_n^o}\right\}}^2+{\left\{\frac{t_s}{t_s^o}\right\}}^2+{\left\{\frac{t_t}{t_t^o}\right\}}^2=1(5)$

where: t_n, t_s, t_t denote the nominal stresses in the interface normal, first and second shear directions, respectively.

2.1.2 Cohesive behavior based on contact surfaces

Many researchers have confirmed that the cohesion model is more accurate for modeling those composite structural systems with insufficient interfacial strengths, for example, in revealing certain adhesive contact surfaces, cementation effects, etc., (Rahulkumar et al., 2000; Zhang and Paulino, 2004; Vandenbosch et al., 2005), the cohesion mechanism can effectively portray the stress constraints between the layers within the roadbed structure.

It is worth noting that the cohesive unit region is assumed to be a massless and thicknessless region, in which various nonlinear phenomena can be observed, and these phenomena do not cause damage to other regions except the cohesive region (Minjiang et al., 2020). In response to the damage phenomena of a material or structure, damage modeling is applied to simulate in a nonlinear manner the process of surface cohesion property degradation until failure (Lijuan, 2013; Mingxing et al., 2016). Therefore, it is feasible to apply cohesion models to simulate crack extension behavior.

2.2 Thermal condition analysis

Influenced by solar radiation, the temperature of the atmosphere shows significant differences between daytime and nighttime, and exhibits obvious daily cyclic fluctuations. By analyzing the influence of factors such as the average surface temperature and air temperature difference on the internal temperature gradient of asphalt pavement, the trend of the maximum temperature difference of the surface with time under different weather conditions is derived. Asphalt pavements are periodically affected by solar radiation during the working process, which is generally approximated and described by regularly varying boundary conditions.

For a given asphalt pavement structure (thickness, thermal properties, etc.), the variation of its temperature field is mainly influenced by the following parameters: total daily solar radiation Q, effective sunshine time c, daily maximum temperature $T_a^{\mathit{max}}$, and daily average wind speed $v_w$.

2.2.1 Solar radiation

According to the conclusions of relevant experts, the variation of solar radiation q(t) can be expressed as Equation 6:

$q\left(t\right)=\left\{\begin{array}{l}0,0\le t<12-\frac{c}{2}\\ q_0\cos m\omega \left(t-12\right),12-\frac{c}{2}\le t\le 12+\frac{c}{2}\\ 0,12+\frac{c}{2}<t\le 24\end{array}\right.(6)$

where $q_0$ is the maximum solar radiation, $q_0=0.131mQ$, $m=12/c$; $Q$ is the daily solar radiation $\left(J/m^2\right)$; $c$ is the real daily sunshine duration, $h$; $\omega$ is the angular frequency, $\omega =2\mathrm{\pi }/24,\text{rad}$.

In order to get accurate calculation results, the function needs to be smooth and continuous, and because there will be a certain degree of numerical error in the integration process of the above formula, therefore, based on the relevant theory of Fourier series (Equations 7–9), it can be expanded into the cosine trigonometric form of Fourier series, and the calculation results are more accurate when k reaches 30th order.

$q\left(t\right)=\frac{a_0}{2}+{\displaystyle \sum _{k=1}^{\infty }}{a}_k\cos \frac{k\pi \left(t-12\right)}{12}(7)$

$a_0=\frac{2q_0}{m\pi }(8)$

$a_k=\left\{\begin{array}{l}\frac{q_0}{\pi }\left[\frac{1}{m+k}\sin \left(m+k\right)\frac{\pi }{2m}+\frac{\pi }{2m}\right],k=m\\ \frac{q_0}{\pi }\left[\frac{1}{m+k}\sin \left(m+k\right)\frac{\pi }{2m}+\frac{1}{m-k}\sin \left(m-k\right)\frac{\pi }{2m}\right],k\ne m\end{array}\right.(9)$

2.2.2 Atmospheric temperature and convective heat exchange

Due to the action of solar radiation, the atmospheric temperature shows regular changes. Therefore, the use of linear regression method can transform the time series into corresponding frequency curves or approximate straight lines, so as to realize the prediction and analysis of air temperature. In this process, a single sinusoidal function cannot realize accurate simulation and will produce a large error, so two sinusoidal functions can be used to fit as in Equation 10, and the results obtained are more in line with the actual situation.

$T_a=\overline{T_a}+T_m\left[0.96\sin \omega \left(t-t_0\right)+0.14\sin 2\omega \left(t-t_0\right)\right](10)$

where ${\overline{T}}_a$ is the daily average temperature, °C, ${\overline{T}}_a=0.5\left(T_a^{\mathit{max}}+T_a^{\mathit{min}}\right)$; T_m is the magnitude of the daily temperature change, $T_m=0.5\left(T_a^{\mathit{max}}-T_a^{\mathit{min}}\right)$, and $T_a^{\mathit{max}}$ and $T_a^{\mathit{min}}$ are the daily maximum and minimum temperatures, °C, respectively; and $t_0$ is the initial phase, $t_0=9$.

The coefficient of heat exchange between the road surface and the outside, $h_c$, is mainly determined by the wind speed, $v_{\mathrm{w}}$, and there is a linear connection between $h_c$ and $v_{\mathrm{w}}$ as in Equation 11:

$h_c=3.7v_w+9.4(11)$

where, $h_c$ is the heat exchange coefficient; $v_{\mathrm{w}}$ is the daily average wind speed.

2.2.3 Road surface effective radiation

Due to the different meteorological conditions, the effective radiation of the ground will produce certain differences, which will be affected by the surface temperature, the temperature and humidity of the atmosphere and the combined effect of climatic conditions. The relationship between the three can be expressed as Equation 12:

$q_F=\epsilon \sigma \left[{\left({\left.T_1\right|}_{Z=0}-T_Z\right)}^4-{\left(T_a-T_Z\right)}^4\right](12)$

where, $q_F$ is the effective radiation of the ground; $\epsilon$ is the emissivity of the road surface, and 0.81 is taken for asphalt pavement; σ is the Stefan-Boltzmann constant, $\sigma =5.6697\times {10}^{-8}$, $W/\left(m^2·K^4\right)$; $T_1{|}_{Z=0}$ is the temperature of the road surface; $T_a$ is the temperature of the atmosphere; and $T_Z$ is the value of the absolute zero degree, $-273℃$.

2.3 Fatigue damage evolution equation

The fatigue loading process has an obvious strain rate effect as well as the existence of nonlinear factors in the material itself, which makes the traditional cohesion theory does not describe this phenomenon well. When the cohesion model is used for fatigue analysis, it is found that there is no upper limit to the fatigue life of the cohesive zone under any loading condition. This is due to the fact that there is some degree of strain energy loss within the cohesive zone due to the stress concentration effect, which results in cracks arising at small defects within the zone. Therefore, although the cohesion strength and initial cohesion length in the cohesive zone vary continuously with damage, it is still necessary to construct a cohesion model that reflects the finite life for the accuracy of the calculation results (Viggo, 1990). The problem is difficult to solve because the cohesion model cannot describe the crack extension process inside the material that is affected by stress propagation. When using the cohesion model to predict the trend of fatigue crack expansion, it is also necessary to incorporate the damage accumulation in the case of monotonic loading, in addition to the analysis of the cyclic loading effects. On this basis, a damage variable was introduced in the study. It is defined as the effective surface density of the interface with defects and the damage variable is defined as the ratio of the damaged cross-section to the initial cross-section area, the expression is Equation 13:

$D=\frac{A_D}{A_0}(13)$

According to the theory, the damage variable is added. It can be obtained Equation 14:

$T_{CZ}=\frac{T_{CZ}}{\left(1-D\right)}(14)$

Currently, the current initial normal and tangential cohesive strengths ${\sigma }_{\max ,0}$, ${\tau }_{\max ,0}$ can be used instead of the equivalent initial cohesive strengths ${\sigma }_{\max }$, ${\tau }_{\max }$. Considering the damage variables, the current normal and tangential cohesion are defined and denoted by Equations 15, 16 respectively:

${\sigma }_{\max }=\left(1-D\right){\sigma }_{\max ,0}(15)$

${\tau }_{\max }=\left(1-D\right){\tau }_{\max ,0}(16)$

In order to accurately estimate the damage state of the cohesive zone under each cyclic loading, the damage evolution process must be described in the form of $\dot{D}=\dot{D}\left(T,\Delta u,D\right)$. Several cohesion ontology relationships in common use today do not express the nonlinear coupling between the damage evolution process and the loading history well, so a new cohesion model is needed to represent this interaction process. For cohesion models subjected to cyclic loading, the damage evolution equations need to accurately reflect the damage and destruction occurring in the cohesive zone. The following model integrates the traditional principles of fatigue damage evolution and its characteristics (Kuo, 2022): 1. For conventional structures and materials, damage accumulation occurs only when the deformation exceeds a specific threshold; 2. The rate of damage accumulation is closely related to the magnitude of deformation corresponding to the load level: at high load levels, the damage accumulation is rapid, whereas at low levels, the damage accumulation slows down considerably; 3. When analyzing fatigue problems, there is a clear fatigue life limit value, and the damage accumulation rate is significantly lower than that of the load level. There is a clear fatigue life limit value, when the load level is lower than this value, the material can withstand higher levels of load and damage.

In applying the cohesion model to predict the fatigue crack extension behavior, the damage evolution equation is Equation 17:

${\dot{D}}_m=\frac{\max \left(\Delta {\overline{u}}_t\right)-\max \left(\Delta {\overline{u}}_{t-\Delta t}\right)}{4{\delta }_0},\max \left(\Delta {\overline{u}}_{t-\Delta t}\right)>{\delta }_0(17)$

From the above equation, it is clear that when $\max \left(\Delta {\overline{u}}_t\right)={\delta }_0$, the cohesive zone is undamaged, i.e., ${\dot{D}}_m=0$, and when $\max \left(\Delta {\overline{u}}_t\right)=5{\delta }_0$, the cohesive zone is completely damaged, i.e., ${\dot{D}}_m=1$.

2.4 Pavement structure design

When constructing the 3D finite element structural model, the thickness of the surface layer is selected to be 10 cm, the thickness of the upper base layer is 20 cm, the thickness of the lower base layer is 20 cm, and the thickness of the soil base layer is 200 cm (refer to Table 1 for selection criteria). In the actual engineering application, the roadbed is an infinite half-space body, and it is selected to establish a 3D pavement structural model with a length of 20 m and a width of 6 m, and to use the cohesion unit to simulate the initial crack that penetrates through the upper base layer and has a width of 0 (as shown in Figure 3).

Table 1

Table 1. Thickness range of structural layer of asphalt pavement with inorganic binding material stabilized base course (mm).

Figure 3

Figure 3. Pavement structure modeling.

2.5 Material parameters

Each layer is assumed to be homogeneous, isotropic and elastic. The thermal properties of each layer are listed in Table 2 and, in addition, the mechanical parameters in the pavement structure model are shown in Table 3.

Table 2

Table 2. Table of parameters for pavement temperature field analysis.

Table 3

Table 3. Cracking parameters for pavement structural materials.

The coefficient of thermal expansion of each pavement structure is set in the system and the ambient temperature is defined by a predefined temperature field. As the temperature of the pavement deepens, the temperature at deeper locations within the pavement changes more slowly than at shallower locations, creating a temperature gradient.

In fact, the stability and structural strength of asphalt pavements decrease dramatically with increasing temperature. The higher the temperature, the lower the stiffness modulus and rutting resistance of the asphalt pavement. Under the action of continuous high temperatures, asphalt pavements are exposed to greater distresses due to softening, volume expansion and aging of the asphalt. According to the survey, when the temperature is lower than 30°C, rutting does not occur on asphalt pavements or rutting is limited to a few millimeters. However, when the temperature is higher than 38°C, rutting increases rapidly and severe rutting occurs when the temperature is consistently higher than 40°C. Therefore, three representative temperature cases (10°C, 30°C, and 50°C) were used in the study.

3 Software calculation results and data analysis

3.1 Analysis of temperature field distribution pattern of asphalt pavement

When the asphalt pavement structure was simulated to be heated, the cloud diagrams of temperature stress distribution of its internal structure under the action of three different temperature fields at 10°C, 30°C and 50°C were obtained (shown in Figure 4).

Figure 4

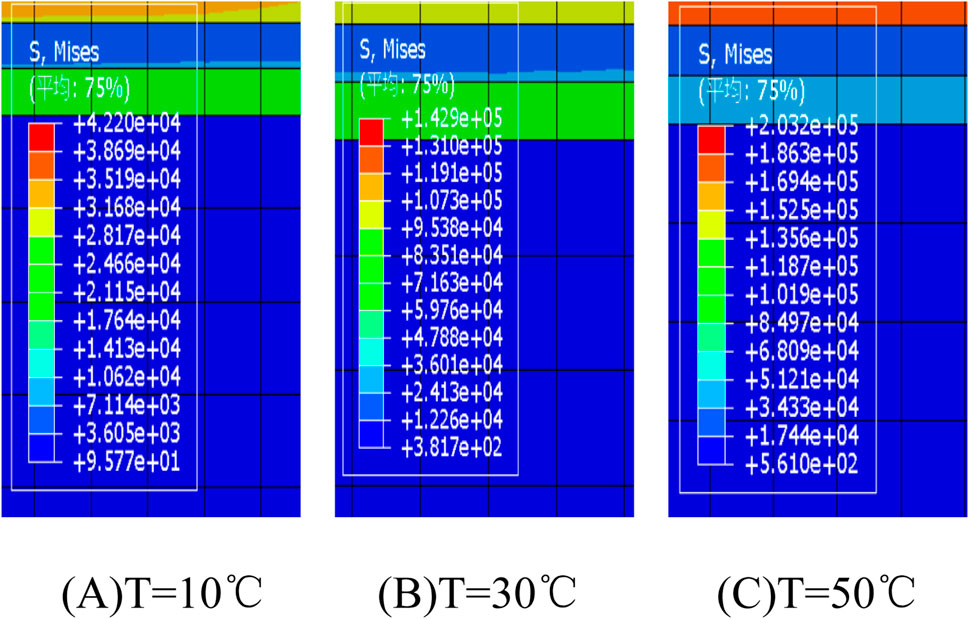
Figure 4. Structural temperature stress distribution cloud for different temperature conditions. (A) T=10°C. (B) T=30°C. (C) T=50°C.

This can be seen through observation:

1) Temperature as the most important factor affecting the change of the properties of asphalt pavement materials, its continuous increase also leads to the asphalt pavement structure by gradually increasing temperature stress, the maximum temperature stress in the center of the surface layer area, and the downward transmission is relatively slow.

2) In the process of heat transfer, due to the influence of transfer speed and reduction effect, the temperature stresses on different structural layers inside the pavement structure show certain hysteresis and weakening effect.

3) When the temperature change occurs externally, the temperature fluctuation inside the pavement structure model is larger than the actual measured value, but the temperature change trend of both is consistent (Litao, 2009). When the temperature reaches 10°C, 30°C, and 50°C, the maximum temperature stresses on the pavement structure are 0.042 MPa, 0.143 MPa, and 0.203°MPa, respectively. In the temperature field simulated by the software, it is assumed that there is no gap between all the pavement structural layers, which indicates that there is no contact thermal resistance, which is very different from the actual engineering applications.

3.2 Analysis of temperature field distribution law of asphalt pavement crack extension process

In investigating the mechanical properties of asphalt pavement structures containing cracks under the influence of temperature loading, the focus is on analyzing how the temperature stresses are distributed in the internal structure of the pavement as the cracks expand. Figure 5 illustrates the trend of tensile stresses on the surface and subgrade of the pavement as the temperature rises, while Figure 6 shows a cloud view of the distribution of temperature stresses during crack expansion.

Figure 5

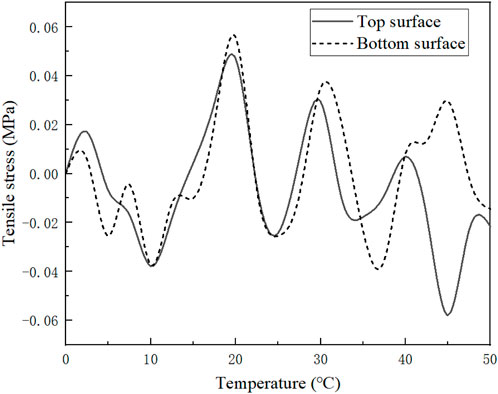
Figure 5. Variation of surface and sub-surface tensile stresses with temperature of the surface layer.

Figure 6

Figure 6. Cloud diagram of temperature stress distribution during crack expansion. (A) T=10°C. (B) T=30°C. (C) T=50°C.

With the application of temperature loads, a large stress concentration occurs near the tip of the crack at the bottom of the face ply, causing damage to the nearby face ply bottom unit, which results in cracking. During this process, the stress concentration propagates, the crack extension behavior increases, and the crack width increases.

As you can tell from the graph:

1) In Figure 5, at the beginning of the warming stage, the surface of the surface layer is subject to temperature loading to produce a small tensile stress, the bottom surface of the tensile stress changes very slowly; when the temperature reaches a certain value, the surface of the surface layer to form the maximum tensile stress, but also at the same time in the bottom surface also produces the maximum tensile stress. As the temperature rises, both the surface and bottom surface tensile stresses of the face layer are changing. In the initial period, the rate of temperature increase at the surface is faster and the tensile stresses at the surface are higher compared to the bottom surface. However, in the subsequent warming process, with the continuous action of the temperature effect, the tensile stress on the surface of the asphalt surface layer gradually weakened and was lower than its counterpart in the bottom layer.

2) When the surface layer and the bottom layer of the pavement are subjected to temperature-induced tensile stresses at the same time and each of them reaches its tensile strength threshold, it will lead to corresponding damage. However, at this stage, macro cracks have not yet appeared, the stress is still in the continuous growth; with the gradual increase in temperature to about 10°C (Figure 6A), the asphalt surface layer of the internal and surface thermal expansion phenomenon, the process gradually formed macro cracks, and ultimately weakened the surface layer of the ability to resist loads.

3) When the temperature load is applied, a large stress will appear near the cracks on the bottom surface of the surface layer, and this concentrated stress may lead to damage to the bottom surface unit of the surface layer near the cracks; when the temperature load is applied to the base layer, the thermal expansion caused by the temperature change will lead to a certain degree of cracking on the bottom surface of the surface layer (Figure 6C). During crack expansion, the maximum temperature stresses on the pavement structure were 2.107 MPa, 2.202 MPa, and 2.358 MPa when the temperature reached 10°C, 30°C, and 50°C, respectively.

3.3 Dynamic response analysis of pavement temperature fatigue cracking

In order to gain a deeper understanding of the mechanical response of the crack-containing pavement structure and the crack extension law under the action of temperature load alone, the stresses on the bottom surface of the pavement structural surface layer in the process of crack extension and the change of the crack width under different temperature conditions were investigated (as shown in Figures 7–9).

Figure 7

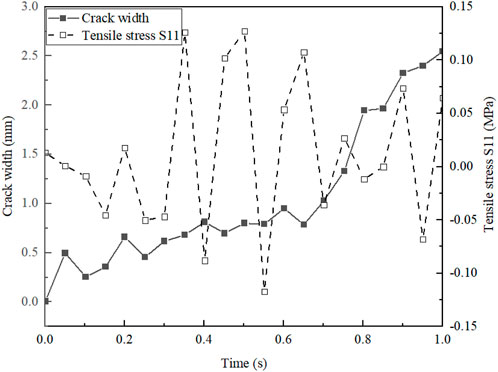
Figure 7. Crack width and tensile stress change in the bottom surface of the surface layer at T = 10°C.

Figure 8

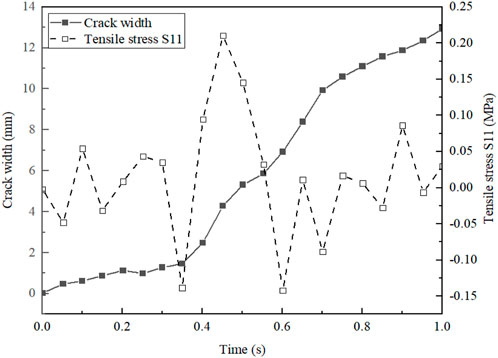
Figure 8. Crack width and tensile stress change in the bottom surface of the surface layer at T = 30°C.

Figure 9

Figure 9. Crack width and tensile stress change in the bottom surface of the surface layer at T = 50°C.

As can be seen from the figure, under different temperatures, the tensile stress on the bottom surface of the surface layer increases and then decreases, with the largest tensile stress occurring at 30°C. In addition, the crack width and rate are also highly dependent on the temperature. In addition, the width and rate of crack expansion are also very much related to the temperature, when the temperature is 10°C, the crack width is only expanded to 2.5°mm, in 30°C and 50°C environment, the crack width is expanded to 12 mm, but when the temperature is 50°C, the crack width is expanded more quickly.

3.4 Crack fatigue damage analysis

In the process of fatigue crack formation, the accumulation of damage is common in the internal structure of the pavement, and those parts of the pavement where fatigue damage accumulates at the fastest rate or where the earliest fatigue damage occurs tend to be the earliest formation of cracks. Figure 10 shows the change of fatigue damage degree of the underside of the structural surface layer of the crack-containing asphalt pavements under the action of different temperature loads.

Figure 10

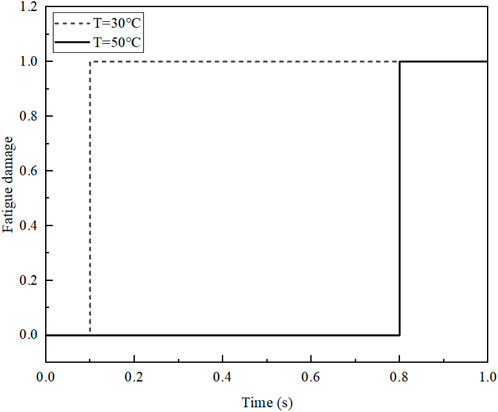
Figure 10. Change curves of damage degree of the bottom surface of the surface layer under the action of different temperatures.

At 30°C, the bottom of the surface layer of the pavement starts damage accumulation from the early stage and maintains a stable accumulation rate, eventually reaching the set damage threshold. When the applied temperature is 50°C, the time of damage accumulation at the bottom of the surface layer is delayed and the accumulation rate is faster. This is due to the fact that the temperature in the transfer process by the resistance of the gas in the gap between the structural layers, has a hysteresis, so that the bottom surface of the surface layer is subjected to a smaller temperature stress, which seriously reduces the rate of damage accumulation.

4 Conclusion

In this paper, the finite element method is used to simulate the asphalt concrete pavement model, and a pavement temperature field model is constructed by using the LOAD module of ABAQUS software, and the stress distribution under different temperature loading conditions is analyzed in detail; next, the crack expansion characteristics under different temperature conditions are explored in detail; then, the effect of temperature loading on the damage of asphalt pavement is studied. Then, the influence of temperature loading on the damage degree of asphalt pavement was investigated. The following conclusions can be drawn:

1) Due to the existence of voids between the internal structural layers of asphalt pavement, the temperature is affected by resistance in the transfer process, resulting in a lag in the temperature change of the internal structure. With the temperature change, the surface layer of the pavement is affected the most, and the soil base layer is affected the least, almost no change.

2) At the initial stage of warming up, the tensile stress does not change much. As the temperature continues to rise, the tensile stress on the bottom surface of the surface layer becomes larger rapidly, which leads to damage and cracking. It takes a long time for the damage to expand from the bottom surface to the surface, and both of them form cracks at the same time.

3) The higher the outside temperature is, the larger the width of crack expansion inside the pavement structure is, and the faster the corresponding expansion rate is. Along with the increase of temperature, the fatigue damage rate of pavement structure will be accelerated.

This paper fails to fully consider the actual situation when establishing the model: when establishing the basic model, it is assumed that all layers of the asphalt pavement structure are isotropic homogeneous materials, which is too idealized and different from the real situation; when analyzing the influence of the temperature field on the expansion of cracks within the asphalt pavement structure, it is assumed that there is no interlayer thermal resistance in the model, whereas the actual pavement structure may affect the temperature transfer due to a number of reasons (e.g., interlayer friction); moreover, the subsequent study needs to deeply explore the crack expansion law under the action of temperature cycling. Temperature transfer; in addition, the crack extension law under the action of temperature cycling needs to be deeply explored in the subsequent research.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JX: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing–original draft. HX: Conceptualization, Formal Analysis, Methodology, Software, Validation, Writing–original draft. TH: Conceptualization, Investigation, Validation, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Gan, L. (2020). Research on crack extension of semi-rigid base asphalt pavement based on cohesion model. Lanzhou, China: Lanzhou Jiaotong University.

Google Scholar

He, R., and Lu, N. L. (2024). Hydration, fresh, mechanical, and freeze-thaw properties of cement mortar incorporated with polymeric microspheres. Adv. Compos. Hybrid Mater. 7, 92. doi:10.1007/s42114-024-00899-2

CrossRef Full Text | Google Scholar

He, R., Nantung, T., and Lu, N. L. (2024). Unraveling microstructural evolution in air-entrained mortar and paste: insights from MIP and micro-CT tomography amid cyclic freezing-thawing damage. J. Build. Eng. 94, 109922. doi:10.1016/j.jobe.2024.109922

CrossRef Full Text | Google Scholar

Heng, L. (2020). Response analysis of asphalt pavement with coupling of vehicle dynamic load, water and temperature. Dalian, China: Dalian University of Technology.

Google Scholar

Kuo, D. (2022). Research on fatigue crack emergence prediction based on cohesion model. Tianjin, China: Tianjin University.

Google Scholar

Lijuan, S. (2013). Thermal stress coupling analysis of semi-rigid base layer asphalt pavement considering interlayer contact. Hangzhou, China: Zhejiang University.

Google Scholar

Lili, Y., and Xuancang, W. (2011). Three-dimensional transient temperature field and vehicle load coupling of asphalt pavement based on meshless method. Highw. Transp. Sci. Technol. 28 (11), 20–26.

Google Scholar

Litao, G. (2009). Calculation of temperature stress and excess pore water pressure in asphalt pavement. Dalian, China: Dalian University of Technology.

Google Scholar

Mingxing, Y., et al. (2016). Application of ABAQUS finite element software in pavement structural analysis. Hangzhou, China: Zhejiang University Press.

Google Scholar

Minjiang, Z., Jiang, Y., and Chao, G. (2020). Numerical simulation of asphalt concrete-inorganic bond interlayer shear test based on cohesion model. Sci. Technol. Eng. 20 (32), 13417–13424.

Google Scholar

Naiji, Z. (2021). Research on fatigue life of asphalt pavement under combined effect of vehicle load and temperature. Chongqing, China: Chongqing Jiaotong University.

Google Scholar

Rahulkumar, P., Jagota, A., Bennison, S. J., and Saigal, S. (2000). Interfacial failures in a compressive shear strength test of glass/polymer laminates. Int. J. Solids Struct. 37 (48-50), 7281–7305. doi:10.1016/s0020-7683(00)00199-2

CrossRef Full Text | Google Scholar

Shaohua, L. (2019). Force analysis of asphalt pavement under temperature-vehicle load coupling. Dalian, China: Dalian University of Technology.

Google Scholar

Swarna, S. T., and Reddy, M. (2018). Analysis of stresses due to traffic and thermal loads in two-lift bonded concrete pavements by finite element method. Adv. Civ. Eng. Mater. 7 (2), 207–222. doi:10.1520/acem20170028

CrossRef Full Text | Google Scholar

Vandenbosch, M. J., Schreurs, P. J. G., and Geers, M. G. D. (2005). An improved description of the exponential Xu and Needleman cohesive zone law for mixed-mode decohesion. Eng. Fract. Mech. 73 (9), 1220–1234. doi:10.1016/j.engfracmech.2005.12.006

CrossRef Full Text | Google Scholar

Viggo, T. (1990). Effect of fibre debonding in a whisker-reinforced meta. Mater. Sci. and Eng. A 125 (2), 203–213.

Google Scholar

Wei, H., Zhou, Y., Huang, W., Wen, P., and Li, J. (2023). Fracture characteristics of a cement concrete pavement plate considering subgrade modulus decay based on a meshless finite block method. Front. Mater. 10, 1157529. doi:10.3389/fmats.2023.1157529

CrossRef Full Text | Google Scholar

Weiguang, L., Aiqin, S., and Yubin, Z. (2004). Temperature stress analysis of semi-rigid materials. J. Chongqing Transp. Inst. (05), 30–34.

Google Scholar

Zhang, Z. J., and Paulino, G. H. (2004). Cohesive zone modeling of dynamic failure in homogeneous and functionally graded materials. Int. J. Plasticity 21 (6), 1195–1254. doi:10.1016/j.ijplas.2004.06.009

CrossRef Full Text | Google Scholar

Zhenpeng, H., Diankai, D., Guofeng, L., et al. (2022). Research on crack extension of composite materials based on cohesion model. Compos. Sci. Eng. (01), 5–12. doi:10.19936/j.cnki.2096-8000.20220128.001

CrossRef Full Text | Google Scholar

Zhenxian, W. (2022). Analysis of interlayer constraint state of asphalt pavement and its effect on structural force. Nanjing, China: Southeast University.

Google Scholar

Zixing, L. (2015). Cohesion modeling of composite interfaces and its application. J. Solid Mech. 36 (S1), 85–94. doi:10.19636/j.cnki.cjsm42-1250/o3.2015.s1.014

CrossRef Full Text | Google Scholar