Recent advances in stability analysis and design of 3D slopes

Slope failures in nature and engineering are typically three-dimensional (3D). The rotational failure mechanism derived from the variational limit equilibrium (LE) method shows superior performance in the stability analysis of the 3D slope. In contrast to the traditional LE methods, it avoids arbitrary kinematical and statical assumptions. Stability charts obtained by the variational LE method are used to derive explicit expression equations of the safety factor, also known as the stability equations, for both 3D reinforced and unreinforced slopes. These equations are highly accurate and can provide a convenient means to assess slope stability in practical engineering. An example of a convex reinforced slope with a turning arc is illustrated in this study to investigate the effect of the 3D effects on the required reinforcement length for design. The results indicate that the 2D method underestimates the required reinforcement length when dealing with a 3D reinforced slope problem. Furthermore, a forensic analysis of the Yeager Airport reinforced slope is conducted within the framework of the variational LE method. The required strength for stability is found to be significantly less than the allowable strength of reinforcements without considering the decrease in soil shear strength. However, the required strength greatly exceeds the allowable strength when the decrease in soil shear strength is considered. The results verify that the decrease in shear strength of the weak layer is responsible for the collapse.

Introduction

In the past decades, the stability analysis of three-dimensional (3D) slopes has attracted significant attention. A majority of the researches (Griffiths and Marquez, 2007; Michalowski and Drescher, 2009; Jiang and Zhou, 2018) indicated that two-dimensional (2D) analysis methods yield a conservative factor of safety, since they overlook 3D effects. The 3D effects stem from the geometry of the slope face and the boundary constraints, such as a filled embankment slope situated in a narrow U- or V-shaped valley, a corner slope constructed for airport expansion, and a concave excavation slope in an open pit mine. Drawing from the above engineering cases, the author and his collaborators have conducted numerous stability analyses of 3D slopes based on variational limit equilibrium (LE) method (Zhang et al., 2016a; Zhang et al., 2016c; Zhang et al., 2018b; Zhang et al., 2023; Zhang et al., 2024) and limit analysis (LA) method (Gao et al., 2013; Gao et al., 2013; Gao et al., 2015; Zhang et al., 2016b; Liu et al., 2023). Even though the numerical analysis method (An et al., 2016; Sun et al., 2017; Shiau et al., 2022) has made great progress, the LE method continues to play a crucial role due to its clear physical meaning and straightforward procedure.

Within the traditional LE method framework (Huang et al., 2002; Jiang et al., 2004; Cheng and Yip, 2007), the geometry of the critical slip surface as well as unknown elements in the LE equations is assumed to render a statically determinate problem. Baker and Garber (1978) combined the variational minimization and LE method to predict the critical slip surface, which was verified to be a log-spiral line. The variational LE method avoids arbitrary kinematical and statical assumptions, except for the Mohr-Coulomb soil failure criterion. Subsequently, Leshchinsky et al. (1985) extended this framework to three-dimensional slopes and a generalized log-spiral surface (Figure 1) failure mechanism was derived from variational extremization. As presented by Leshchinsky and Baker (1986), a central cylinder was inserted into the failure surface to degrade it to a 2D slope as the cylinder tended to be infinitely long. It is noteworthy that the failure mechanism derived from the variational framework is independent of the normal stress on the slip surface. The 3D slip surface shown in Figure 1 is characterized by the sum of the normal stress and frictional force points to the rotational central, and no additional assumptions are required to satisfy a statically determinate problem. The kinematical admissibility of the variationally derived 3D mechanism was validated by Leshchinsky et al. (1985) and Zhang et al. (2016c). They suggested that the variational procedure used in 3D slope stability analysis was equivalent to the upper bound LA method.

Figure 1

Figure 1. Variationally derived 3D failure mechanism for homogeneous slope.

Since the failure mechanism has a clear physical meaning and the LE method has a simple procedure, the variational LE method demonstrates superior performance in analyzing 3D slope stability under complicated conditions. Zhang et al. (2016c) considered a wide range of parameters and adopted an optimization program to yield higher accuracy than the original values reported by Leshchinsky and Baker (1986). Subsequently, the author and his collaborators conducted a series of stability analysis of convex slopes with turning corners (Zhang et al., 2018b) and turning arcs (Zhang et al., 2023) to investigate the 3D effect induced by geometric factors. Adopting the failure mechanism derived from the variational LE framework, the 3D stability of reinforced slopes was examined, and a design procedure for convex reinforced slopes was presented (Zhang et al., 2018a; Zhang et al., 2019; Yang et al., 2020). The results indicated that the 3D effect decreases the required strength of reinforcements, but it yields a longer required length of reinforcements than the 2D analysis methods. Recently, a series of explicit expression equations of the safety factor were obtained by regression analysis to assess the 3D stability of V-shaped fill slopes (Zhang et al., 2024). The stability equations were verified to have excellent accuracy and can be used in practical engineering to calculate the slope safety factor conveniently.

This paper focuses on the variational LE stability analysis method of the 3D slopes. Stability charts obtained by the variational LE method have been used to derive explicit expression equations of the safety factor, also known as the stability equations, for both 3D reinforced and unreinforced slopes. Through an example analysis to investigate the influence of the 3D effects on the required reinforced length for a convex reinforced slope with a turning arc. Finally, a forensic analysis is conducted to explain the cause of failure for the Yeager Airport reinforced slope.

Closed-form solutions for 3D slopes

Stability assessment of 3D slopes is commonly presented as dimensionless charts. Even though the chart provides quick stability assessments, it offers estimates due to the linear interpolation caused by its absence of specific slope conditions. Moreover, it is challenging to be incorporated into the modern digital design workflow. This issue can be mitigated by obtaining closed-form solutions through regression analysis. The charts typically fall into two forms: c/γHF_s versus tanϕ/F_s and F_s/tanϕ versus c/γHtanϕ (c = soil cohesion; γ = soil unit weight; H = slope height; F_s = factor of safety, ϕ = angle of internal friction). Chien and Tsai (2017) and Huang and Ji (2022) adopted the former and latter to obtain closed-form solutions of the 2D slope, respectively. However, the factor of safety in the stability equation of Chien and Tsai (2017) is implicitly expressed and obtained by solving the equation. Consequently, this paper employs the latter form to obtain the closed-form solutions of the 3D slope. The straight finite slope is used as the baseline to conduct regression analysis in this paper. This regression analysis method is innovatively used to obtain the closed-form solutions of reinforced slopes.

Unreinforced slope

Numerous stability charts show the relationship between F_s/tanϕ and c/γHtanϕ is typically a power function when c/γHtanϕ is small and a linear function when c/γHtanϕ is large. Huang and Ji (2022) used a power function (Eq. 1) to address this function for the 2D slope. Both A and B in Eq. 1 are functions of the slope angle β (as shown in Eqs 1, 2). To be consistent with the form of Eqs 2, 3, the expression for “A” is rewritten as a quadratic function. The parameter B is split at c/γHtanϕ = 1 to improve the accuracy while meeting the continuity condition of the equation. For a cohesionless slope, the factor of safety is precisely calculated as tanϕ/tanβ according to the 2D slope model. This conclusion is similarly applied to the 3D slope model. Note that the slope angles β in stability equations in this paper are inputted as degrees (°).

$\frac{F_{\mathrm{s}\_2\mathrm{D}}}{\tan \varphi }=A{\left(\frac{c}{\gamma H\tan \varphi }\right)}^B+\frac{1}{\tan \beta }(1)$

$\mathit{A}=10.5+2.9\times {10}^{-4}{\beta }^2-0.091\beta (2)$

$\mathit{B}=\left\{\begin{array}{l}0.72-3.5\times {10}^{-5}{\beta }^2+0.0032\beta \\ 0.83-2.2\times {10}^{-5}{\beta }^2+0.0026\beta \end{array}\right.(3)$

The solutions of the 2D stability analysis methods are conservative, as they do not account for the 3D end effects. The 3D effects can be interpreted as the difference in F_s/tanϕ for the same c/γHtanϕ and the same slope angle in the stability charts. For a cohesionless slope (i.e., c/γHtanϕ = 0), the factor of safety obtained by both the infinite and 3D slope model is equal to tanϕ/tanβ, resulting in zero 3D effects. On the other hand, the 3D effects increase approximately linearly with c/γHtanϕ. Consequently, the 3D effects can be expressed as a proportional function of c/γHtanϕ with a coefficient of A_3D. The coefficient A_3D is a function of the width-to-height ratio L/H (L = slope width) and the slope angle. The regression analysis revealed that A_3D can be concisely written as a power function of (L/H)sinβ, which captures the geometric feature.

$A_{3\mathrm{D}}=2.29{\left(\frac{L}{H}\sin \beta \right)}^{-1.12}(4)$

Based on the stability equation for the 2D slope obtained by Huang and Ji (2022) and the 3D effects defined by Eq. 4, the stability equation for 3D slopes is expressed as

$\frac{F_{\mathrm{s}}}{\tan \varphi }=A_{3\mathrm{D}}\frac{c}{\gamma H\tan \varphi }+A{\left(\frac{c}{\gamma H\tan \varphi }\right)}^B+\frac{1}{\tan \beta }(5)$

Reinforced slope

In this study, three assumptions are made for the reinforced slope: 1) reinforcements are required to be long enough to avoid compound failure; 2) the filled soil is cohesionless; 3) the vertical spacing between reinforcement layers is constant throughout the structure. Hence, the tensile strength of reinforcement layers can be distributed evenly along the height and width of the slope. If a step-wise layout of reinorcements is adopted, the tensile strength is divide into different evenly distributed sctions (Michalowski, 1997). The dimensionless form, k_u/γHF_s (k_u = nT_ult/H, n = the number of reinforcement layers, T_ult = the ultimate tensile strength of reinforcements), is used to assess the required strength of reinforced slopes. In the limit equilibrium framework, the factor of safety of the reinforced slope is applied to the soil strength and reinforcement strength: ϕ_m = tan⁻¹[tan(ϕ)/F_s], c_m = c/F_s and k_t = k_u/F_s (ϕ_m and c_m are mobilized soil strength, k_t = required reinforcement strength at limit state). Therefore, the stability charts for reinforced slopes can be represented in the form of F_s/tanϕ versus k_u/γHtanϕ. The same regression analysis procedure as the unreinforced slope is conducted to develop the closed-form solutions for reinforced slopes, and the results are as follows:

$\frac{F_{\mathrm{s}}}{\tan \varphi }=A_{3\mathrm{D}\_\mathrm{r}}\frac{k_{\mathrm{u}}}{\gamma H\tan \varphi }+A_{\mathrm{r}}{\left(\frac{k_{\mathrm{u}}}{\gamma H\tan \varphi }\right)}^{B_{\mathrm{r}}}+\frac{1}{\tan \beta }(6)$

$A_{\mathrm{r}}=7.48-1.63\times {10}^{-5}{\beta }^3+0.00316{\beta }^2-0.2\beta (7)$

$B_{\mathrm{r}}=\left\{\begin{array}{l}1.65-3.04\times {10}^{-6}{\beta }^3+6.45\times {10}^{-4}{\beta }^2-0.0461\beta \\ 2.21-2.66\times {10}^{-6}{\beta }^3+6.77\times {10}^{-4}{\beta }^2-0.0567\beta \end{array}\right.(8)$

$A_{3\mathrm{D}\_\mathrm{r}}=0.65{\left(\frac{L}{H}\sin \beta \right)}^{-1.33}(9)$

Both Eqs 5, 6 are concise closed-form solutions consisting of the 2D slope solution (Eqs 8, 9) and the 3D effects (Eq. 7). They can degrade into 2D slope solutions when L/H tends to be infinite. To verify the accuracy, five hundred sets of calculated parameters are randomly generated, and then the factors of safety are calculated with the LE method and closed-form solutions. As shown in Figure 2, the coefficients of determination (R²) approach 1 and the root mean square error (RMSE) is nearly 0, indicating a high level of agreement between the LE methods and closed-form solutions. Though Eqs 6, 7 are developed for straight slopes, the kinds of closed forms can be extended to other geometry slopes (e.g., convex slopes and V-shaped slopes) by simply modifying the coefficient of 3D effects.

Figure 2

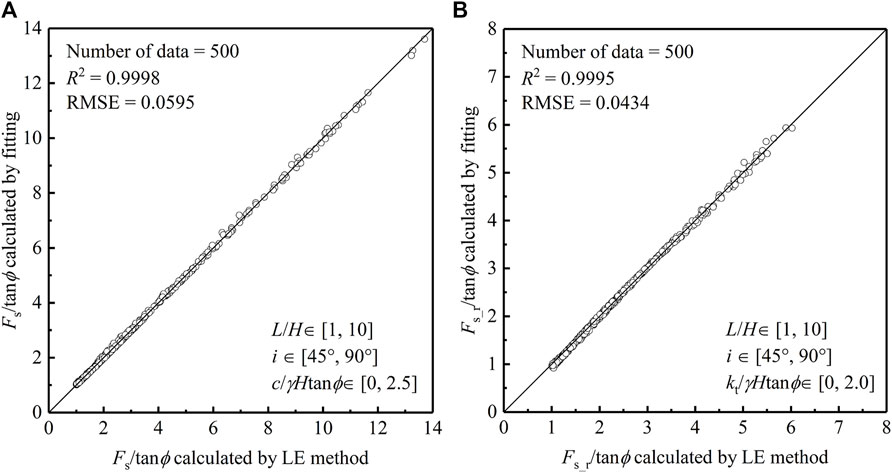
Figure 2. Comparison of safety of factor calculated by the LE method and stability equations: (A) unreinforced slope; (B) reinforced slope.

Required reinforcement length of convex slopes with a turning arc

Convex filled slopes are common in mountainous areas. Zhang et al. (2019) presented a series of design charts of the corner reinforced slope based on the internal stability. The charts provided the required reinforcement length for each layer. This paper presents the design procedure of internal stability for convex slopes with a turning arc. Due to space limitations, the stability charts of reinforced convex slopes with a turning arc are not presented, and the analysis method refers to Yang et al. (2020) and Zhang et al. (2023). An example is illustrated here to illustrate the design procedure. The parameters of the example slope are selected as: soil cohesion c = 0 kPa, soil friction ϕ = 40°, unit weight γ = 20 kN/m³, slope height H = 6 m, slope angle β = 45°, turning angle θ = 90°, bottom curvature radius R = 12 m, reinforcement spacing S_v = 0.6 m, reinforcement layers n = 10. The design safety of factor F_s = 1.5 is used for internal stability. Both the static and dynamic cases (seismic acceleration k_h = 0.3) are assessed. For the given slope, the following steps are needed for internal stability design:

(1) For a required factor of safety of internal stability, F_s, the design angle of internal friction is ϕ_m = tan⁻¹(tanϕ/F_s);

(2) The slip surface is obtained and the required reinforcement strength is determined through the 3D variational LE method. The embedment length within the zone of the slip surface, l_s, is defined as the distance from the corresponding critical slip surface to the slope surface;

(3) The anchorage part must be embedded sufficiently long beyond the slip surface to mobilize the intrinsic tensile resistance, T_max. For a limit state slope, the required embedment length is expressed as Eq. 10.

$l_e=\frac{T_{\max }}{2R_{\mathrm{c}}C\sigma \tan {\varphi }_{\mathrm{m}}}(10)$

where l_e = the required embedment length beyond the slip surface; R_c = the coverage ratio of reinforcement, typically, R_c = 100%; C = an experimental interaction coefficient relating the coefficient for friction at the soil geosynthetic interface; σ = the effective vertical stress acting on the reinforcement at the rear-end of the reinforcement.

(4) Select the maximum total embedment length for each layer, l = l_e + l_s, as the design embedment length.

Figure 3 illustrates the calculated total embedment length of the reinforcement at each layer for both 2D and 3D analysis. On the one hand, the 3D surface is deeper than the 2D surface, requiring a longer reinforcement length in the sliding zone. On the other hand, the 3D analysis results in a shorter embedment length in most layers compared to the 2D analysis due to the smaller required strength, T_max. Generally, in terms of the final result, the 3D analysis yields greater values of the required total length than the 2D analysis. That is, it would be unconservative if using the 2D method to deal with a 3D reinforced slope problem. However, the 2D method is typically conservative for the unreinforced slope.

Figure 3

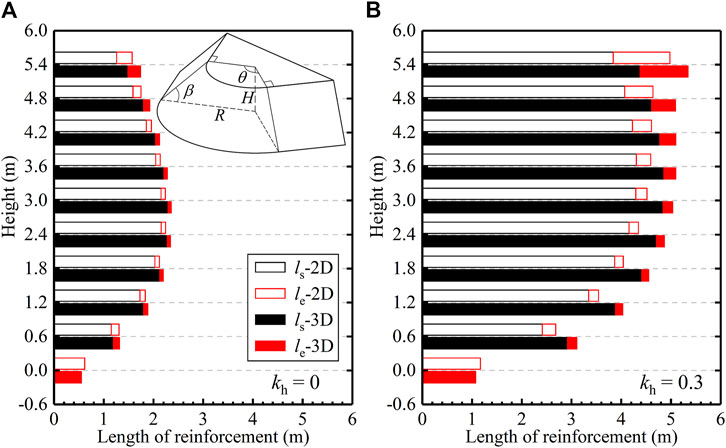
Figure 3. Distribution of the required reinforcement length for the example: (A) k_h = 0; (B) k_h = 0.3.

Forensic analysis of Yeager Airport reinforced slope

A 67-m-tall and 1H:1V reinforced soil slope (RSS) was constructed at Yeager Airport in Charleston to support an extension runway. This RSS structure is a typical example of a convex slope with a turning arc. The design specified a vertical spacing of reinforcement of 46 cm in the lower third of the RSS, and it was increased to 91 cm at higher elevations. It resulted in a total of 85 layers of reinforcements. On 12 March 2015, after a service period of about 8 years, the RSS structure catastrophically collapsed in a compound mode with a distinct 3D failure characteristic. The failure surface sheared through more than 30 layers of reinforcements throughout the exposed head scarp. Only the primary uniaxial geogrids of 20G were used for the failure cross section of the RSS. The broken layers had a manufacturer published minimum average roll value, ultimate strength T_u = 187.8 kN/m and allowable strength T_a = 66.1 kN/m (Berg et al., 2020). However, the tests made by VandenBerge et al. (2021) suggested that their effective strength T_e at the time of the RSS collapse was estimated to be 117.8 kN/m, due to the installation damage and 8-year creep effect. The immediate cause of the failure was the decrease in the shear strength of the soil-rock interface below the reinforced soil. The shear strength decreased from the peak strength toward the fully softened strength during the service period. The strength for the fully softened strength is approximateϕ = 20°, which is much less than the design strength ϕ = 36°.

A forensic analysis of the Yeager Airport slope is conducted using the 3D variational LE method. According to the RSS plan view proposed by Triad Engineering, the RSS is simplified as a convex slope with a 45° turning corner and R/H = 1. Firstly, the stability required reinforcement strength at the limit state is investigated using the design soil strength ϕ = 36° and c = 0 kPa. The result shows that the required strength T_max = 33.1 kN/m is much less than the allowable strength T_a = 66.1 kN/m, which means that the RSS is stable enough if the weak layer does not exist. Then, the fully softened strength (ϕ = 20°) is taken into account for the stability analysis. To simplify the calculation, the fully softened strength is adopted for the entire slip surface. Actually, the simplification will yield a larger value of T_max than the true value, because the soil strength at the upper slip surface is replaced by the fully softened strength. However, it helps to determine the effects of the weak layer on slope stability. Figure 4 illustrates the comparison between the 3D slip surface obtained from the 3D analysis and the observed field, showing a good agreement. The calculated slip volume is approximately 120 thousand cubic meters. According to the results of the 3D analysis, only approximately 60 layers of reinforcements are mobilized. In this situation, the required strength of the upper 60 reinforcement layers is 139.5 kN/m, exceeding the effective strength T_e = 117.8 kN/m. These results verify that the weak layer is the cause of the RSS failure.

Figure 4

Figure 4. View of Yeager Airport slope failure surface: (A) sectional view; (B) 3D view.

Conclusion

This paper introduces the recent advance of the variational LE method on the stability analysis of 3D slopes. The stability equations of 3D reinforced and unreinforced slopes are derived by regression analysis. The equations comprise soil strength and slope geometry, which could facilitate the determination of the safety factor for 3D slopes in practical engineering applications. An example case is analyzed to investigate the 3D effects on the required reinforcement length of convex reinforced slopes with a turning arc. Furthermore, a forensic analysis of the Yeager Airport slope is conducted to explain the cause of the failure. Based on the findings of this study, the following conclusions can be made:

(1) The 3D effects in the stability charts can be expressed as a proportional function of c/γHtanϕ. Based on this, explicit expression equations for the safety factor of unreinforced and reinforced slopes are obtained through regression analysis, and the accuracy of the provided stability equations is verified to be highly reliable.

(2) Although the required strength of 3D analysis is unconservative than that of 2D analysis, the 2D method underestimates the required reinforcement length when dealing with a 3D reinforced slope problem.

(3) The forensic analysis of the Yeager Airport reinforced slope indicates that the slope is stable enough without considering the weak layer. The decrease in shear strength of the weak layer is responsible for the collapse.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

FZ: Writing–original draft, Writing–review and editing. SJ: Writing–original draft, Writing–review and editing. YG: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study was supported by the National Natural Science Foundation of China (Grant No. 52322808) and the Qinglan Project of Jiangsu Province of China.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

An, Y., Wu, Q., Shi, C., and Liu, Q. (2016). Three-dimensional smoothed-particle hydrodynamics simulation of deformation characteristics in slope failure. Géotechnique. 66, 670–680. doi:10.1680/jgeot.15.P.222

CrossRef Full Text | Google Scholar

Baker, R., and Garber, M. (1978). Theoretical analysis of the stability of slopes. Géotechnique 28, 395–411. doi:10.1680/geot.1978.28.4.395

CrossRef Full Text | Google Scholar

Berg, R. R., Collin, J. G., Taylor, T. P., and Watts, C. F. (2020). Case history on failure of a 67 m tall reinforced soil slope. Geotext. Geomembranes 48, 802–811. doi:10.1016/j.geotexmem.2020.06.003

CrossRef Full Text | Google Scholar

Cheng, Y. M., and Yip, C. J. (2007). Three-dimensional asymmetrical slope stability analysis extension of bishop's, janbu's, and morgenstern-price's techniques. J. Geotech. Geoenviron. Eng. 133, 1544–1555. doi:10.1061/(Asce)1090-0241(2007)133:12(1544)

CrossRef Full Text | Google Scholar

Chien, Y. C., and Tsai, C. C. (2017). Immediate estimation of yield acceleration for shallow and deep failures in slope-stability analyses. Int. J. Geomech. 17, 04017009. doi:10.1061/(Asce)Gm.1943-5622.0000884

CrossRef Full Text | Google Scholar

Gao, Y., Zhang, F., Lei, G. H., Li, D., Wu, Y., and Zhang, N. (2013a). Stability charts for 3d failures of homogeneous slopes. J. Geotech. Geoenviron. Eng. 139, 1528–1538. doi:10.1061/(asce)gt.1943-5606.0000866

CrossRef Full Text | Google Scholar

Gao, Y. F., Wu, D., and Zhang, F. (2015). Effects of nonlinear failure criterion on the three-dimensional stability analysis of uniform slopes. Eng. Geol. 198, 87–93. doi:10.1016/j.enggeo.2015.09.010

CrossRef Full Text | Google Scholar

Gao, Y. F., Zhang, F., Lei, G. H., and Li, D. Y. (2013b). An extended limit analysis of three-dimensional slope stability. Géotechnique. 63, 518–524. doi:10.1680/geot.12.T.004

CrossRef Full Text | Google Scholar

Griffiths, D. V., and Marquez, R. M. (2007). Three-dimensional slope stability analysis by elasto-plastic finite elements. Géotechnique. 57, 537–546. doi:10.1680/geot.2007.57.6.537

CrossRef Full Text | Google Scholar

Huang, C. C., Tsai, C. C., and Chen, Y. H. (2002). Generalized method for three-dimensional slope stability analysis. J. Geotech. Geoenviron. Eng. 128, 836–848. doi:10.1061/(Asce)1090-0241(2002)128:10(836)

CrossRef Full Text | Google Scholar

Huang, W., and Ji, J. (2022). Closed-form solutions for regional earthquake–induced landslide prediction: rotational failure mechanism. Landslides 19, 2671–2684. doi:10.1007/s10346-022-01916-5

CrossRef Full Text | Google Scholar

Jiang, J.-C., and Yamagami, T. (2004). Three-dimensional slope stability analysis using an extended spencer method. Soils. Found. 44, 127–135. doi:10.3208/sandf.44.4_127

CrossRef Full Text | Google Scholar

Jiang, Q. H., and Zhou, C. B. (2018). A rigorous method for three-dimensional asymmetrical slope stability analysis. Can. Geotech. J. 55, 495–513. doi:10.1139/cgj-2017-0317

CrossRef Full Text | Google Scholar

Leshchinsky, D., and Baker, R. (1986). Three-dimensional slope stability: end effects. Soils. Found. 26, 98–110. doi:10.3208/sandf1972.26.4_98

CrossRef Full Text | Google Scholar

Leshchinsky, D., Baker, R., and Silver, M. L. (1985). Three dimensional analysis of slope stability. Int. J. Numer. Anal. Metall. 9, 199–223. doi:10.1002/nag.1610090302

CrossRef Full Text | Google Scholar

Liu, Y., Gao, Y., Shu, S., Dai, G., and Zhang, F. (2023). Seismic stability and permanent displacement of 3d slopes with tension cutoff. Int. J. Geomech. 23, 04023158. doi:10.1061/ijgnai.gmeng-8697

CrossRef Full Text | Google Scholar

Michalowski, R. L. (1997). Stability of uniformly reinforced slopes. J. Geotech. Geoenviron. Eng. 123, 546–556. doi:10.1061/(ASCE)1090-0241(1997)123:6(546)

CrossRef Full Text | Google Scholar

Michalowski, R. L., and Drescher, A. (2009). Three-dimensional stability of slopes and excavations. Géotechnique 59, 839–850. doi:10.1680/geot.8.P.136

CrossRef Full Text | Google Scholar

Shiau, J., Lai, V. Q., and Keawsawasvong, S. (2022). Multivariate adaptive regression splines analysis for 3d slope stability in anisotropic and heterogenous clay. J. Rock Mech. Geotechnical Eng. 15, 1052–1064. doi:10.1016/j.jrmge.2022.05.016

CrossRef Full Text | Google Scholar

Sun, C., Chai, J., Xu, Z., and Qin, Y. (2017). 3d stability charts for convex and concave slopes in plan view with homogeneous soil based on the strength-reduction method. Int. J. Geomech. 17, 06016034. doi:10.1061/(asce)gm.1943-5622.0000809

CrossRef Full Text | Google Scholar

VandenBerge, D. R., Valentine, R. J., Brandon, T. L., and Wright, S. G. (2021). Case history: failure of the reinforced soil slope at yeager airport, charleston, West Virginia. J. Geotech. Geoenviron. Eng. 147. doi:10.1061/(asce)gt.1943-5606.0002430

CrossRef Full Text | Google Scholar

Yang, S. C., Gao, Y. F., Leshchinsky, B., Cui, K., and Zhang, F. (2020a). Internal stability analysis of reinforced convex highway embankments considering seismic loading. Geotext. Geomembranes 48, 221–229. doi:10.1016/j.geotexmem.2019.11.001

CrossRef Full Text | Google Scholar

Yang, T., Zou, J. F., and Pan, Q. J. (2020b). Three-dimensional seismic stability of slopes reinforced by soil nails. Comput. Geotech. 127, 103768. doi:10.1016/j.compgeo.2020.103768

CrossRef Full Text | Google Scholar

Zhang, F., Gao, Y. F., Leshchinsky, D., Yang, S. C., and Dai, G. Y. (2018a). 3d effects of turning corner on stability of geosynthetic-reinforced soil structures. Geotext. Geomembranes 46, 367–376. doi:10.1016/j.geotexmem.2018.03.001

CrossRef Full Text | Google Scholar

Zhang, F., Gao, Y. F., Leshchinsky, D., Zhu, D. S., and Lei, G. H. (2016a). Three-dimensional stability of slurry-supported trenches: end effects. Comput. Geotech. 74, 174–187. doi:10.1016/j.compgeo.2016.01.009

CrossRef Full Text | Google Scholar

Zhang, F., Gao, Y. F., Wu, Y. X., Zhang, N., and Qiu, Y. (2016b). Effects of vertical seismic acceleration on 3d slope stability. Earthq. Eng. Eng. Vib. 15, 487–494. doi:10.1007/s11803-016-0338-9

CrossRef Full Text | Google Scholar

Zhang, F., Jia, S., and Shu, S. (2024). Effects of seismic amplification on the 3d stability of fill slopes in v-shaped valleys. Acta Geotech. 19, 3241–3255. doi:10.1007/s11440-023-02167-x

CrossRef Full Text | Google Scholar

Zhang, F., Jia, S. L., Shu, S., Lin, L. Y., and Gao, Y. F. (2023). Stability charts for convex slope with turning arc. Acta Geotech. 19, 2323–2335. doi:10.1007/s11440-023-02086-x

CrossRef Full Text | Google Scholar

Zhang, F., Leshchinsky, D., Baker, R., Gao, Y. F., and Leshchinsky, B. (2016c). Implications of variationally derived 3d failure mechanism. Int. J. Numer. Anal. Metall. 40, 2514–2531. doi:10.1002/nag.2543

CrossRef Full Text | Google Scholar

Zhang, F., Leshchinsky, D., Gao, Y., and Yang, S. (2019). Corner reinforced slopes: required strength and length of reinforcement based on internal stability. Geotext. Geomembranes 47, 408–416. doi:10.1016/j.geotexmem.2019.01.004

CrossRef Full Text | Google Scholar

Zhang, F., Leshchinsky, D., Gao, Y. F., and Yang, S. C. (2018b). Three-dimensional slope stability analysis of convex turning corners. J. Geotech. Geoenviron. Eng. 144, 06018003. doi:10.1061/(Asce)Gt.1943-5606.0001896

CrossRef Full Text | Google Scholar