Seismic evaluation of Site-City interaction effects between city blocks

In urban environments, buildings are often seismically designed with their standalone response, such as isolated structures devoid of surrounding structures. Nonetheless, there is always a chance that a significant seismic interaction between nearby buildings through the underlying soil will occur in big urban areas with high building densities. This paper evaluates the Site-City interaction (SCI) between different city block arrangements under seismic excitation given different parameters of the buildings and centre-to-centre interbuilding distances. A database of strong ground motion records with Far-Field, Near-Field Without Pulse and Near-Field Pulse-Like characteristics are employed. The results suggest that the SCI effects were strongly influenced by the building properties and resonance effects of the soil stratum. Furthermore, as a mean for all the earthquakes considered here, the SCI can amplify or reduce the seismic response of the buildings, depending on the relative position between the city blocks.

1 Introduction

The population of the world has progressively moved from rural to urban areas, as a result of urbanization and modern living. At the moment, 55% of people live in densely populated urban areas, where many of them are located in highly seismic areas. The high building density indicates that there may be a significant seismic interaction between the buildings via the underlying soil, even though it is standard practice to assess a building’s seismic reaction as if it were a separate entity isolated from its surrounding structures. This phenomenon is better known as Structure-Soil-Structure Interaction (SSSI) and can either magnify or attenuate the seismic response of a building (Schwan et al., 2016; Vicencio and Alexander, 2018a; Vicencio and Alexander, 2019; Tombari and Cacciola, 2021; Vicencio and Alexander, 2022; Vicencio et al., 2023). The study of SSSI is a complicated subject with an excessive number of variables, such as the orientation and spatial distribution of buildings, the dynamic properties of the structures and the soil, and the natural characteristics of the earthquakes. So, different approach to analyze this complex problem.

The ability to perform complex analyses that account for intricate geometric arrangements, nonlinearities, and the radiating damping of soil has been made possible by the rapid advancement in computational power and the use of numerical methods. Numerical methods such as Finite Element method (FEM) (Tsogka and Wirgin, 2003; Yahyai et al., 2008; Isbiliroglu et al., 2015; Ghandil and Aldaikh, 2017; Long et al., 2021; Vicencio and Cruz, 2021; Chen et al., 2022; Shabani et al., 2022; Shamsi et al., 2022), boundary element method (BEM) (Kham et al., 2006; Padrón et al., 2011; Han et al., 2020; Zhang and Taciroglu, 2021; Jin and Liang, 2022), and hybrid method (FEM/BEM) (Clouteau et al., 2012; Aji et al., 2022) are some of the most extensively utilized multipurpose tools in earthquake engineering and structural dynamics. The downside of this technics is that their computational complexity due to large number of degrees of freedom (DOF).

Analytical methods are one of the most used technics methods to evaluate the seismic effects in structures. These methods intent to use a limited number of DOF, where the mechanical properties of the system are concentrated in a small number of lumped masses, dashpots, and springs (Mulliken and Karabalis, 1998; Yahyai et al., 2008; Kumar and Narayan, 2019; Cacciola and Tombari, 2020; Zhang et al., 2021; Vicencio et al., 2024). Lu et al. (2018), Lu et al. (2019), Lu et al. (2020) proposed a simple linear model that allows the SSSI between structures, where the dynamic stiffness matrix is formulated based on compliance matrices. Later, the work of Vicencio and Alexander (Vicencio and Alexander, 2021) proposed a linear-elastic numerical model that can include multiple building interactions (allowing only square based buildings), with the seismic excitation in one direction, and considering different heights and interbuilding distances. All these previous studies give a theoretical framework for the study of SSSI with an efficient and straightforward mathematical formulation. However, a gap remains in state-of-the-art knowledge of SSSI when multiple interactions between building clusters in a 3D arrangement are considered.

Physical experimental tests represent an important validation point for all the numerical models presented previously. In the same way, it provides preliminary estimates of the effects of complex interaction problems (Kitada et al., 1999). Examined the coupled interaction between different buildings belonging to nuclear power plants by using forced vibration field tests and shaking table tests. Centrifuge tests have been used to evaluate nonlinear behaviour both on the structures and in the soil (Mason et al., 2013; Trombetta et al., 2013; Trombetta et al., 2015). The results showed that the interaction between the buildings could be beneficial (i.e., reducing the seismic response) or detrimental (i.e., increasing the seismic response), depending on the seismic excitation and the properties of the structures. The work of (Du et al., 2022) investigated the soil-structure-cluster interaction (SSCI) between multiple height structure cluster configurations by using shaking table tests and finite element analysis. The results indicates that the cluster effect affect the ground motion and adjacent high-rise structures enhanced the seismic response of the structure. The disadvantages of this kind of experiment are they are technically challenging to undertake. Nevertheless, shake table and centrifuge tests represent a critical dataset of results to benchmark various computational and theoretical models. This is especially true for the exploration of the complex problem of SSSI for various 3D configurations.

In this study, we extend the previous work on the SSSI (Vicencio and Alexander, 2021) by considering different city blocks arrangements. Note that the interbuilding springs used here were validated by finite element analysis (Aldaikh et al., 2015), shake table tests (Aldaikh et al., 2016), and centrifuge tests (Knappett et al., 2015). The aim of this paper is to answer the following questions,

• Does the presence of multiple buildings affect the seismic response of the complete system?

• Is there evidence to suggest that different types of ground motion (far field, near field without pulse and near field pulse-like) can affect the SSSI behaviour?

• What are the most important parameters that govern this complex problem?

2 Reduced-order model for Site-City interaction effects between structure cluster

2.1 Equation of motion

The reduced-order model consists of a set of $n$ buildings (e.g., a model of a city blocks), distributed over a shared soil stratum, as shown in Figure 1. A known ground displacement field $x_g$ and $y_g$ is applied in the $x$- and $y$- direction respectively, at all foundations. Each superstructure can be modelled as low-order model with translational DOF $x_i$ and $y_i$, and their sway-flexural lateral stiffness $k_{bxi}$ and $k_{byi}$. The wave passage effects, coherence effects, and spatially heterogeneous ground displacements are neglected in the presented work. We only aim to model the important rotational interactions between the buildings.

Figure 1

Figure 1. Idealization model of a city block arrangement.

Each building’s foundation has two orthogonal auto-rotational springs $k_{xi}$ and $k_{yi}$ and various interbuilding-rotational springs defined as a vector ${\mathit{\kappa }}_{ij}=\left[{\kappa }_{xij},{\kappa }_{yij},{\kappa }_{xyij},{\kappa }_{yxij}\right]$ (i.e., the coupling between building $″i^{″}$ and building $″j^{″}$), where ${\kappa }_{xij}$ is the interbuilding-rotational stiffness coefficients in the $x$-direction, ${\kappa }_{yij}$ is the interbuilding-rotational stiffness coefficients in the $y$-direction, and ${\kappa }_{xyij},{\kappa }_{yxij}$ are the cross-coupled terms. Note that the springs $k_{xi}$ , $k_{yi}$ and ${\mathit{\kappa }}_{ij}$ represent the complete dynamic behavior soil stratum, where only rotational DOFs at the foundation level ${\theta }_{xi}$, ${\theta }_{yj}$ are retained. The system geometry and nomenclature used here are described in Figure 2. The kinematic interaction is not considered in the present work, i.e., the transfer function between foundation input motion and free-field motion is one.

Figure 2

Figure 2. Nomenclature of the city block arrangement model.

The potential energy of the complete system is given by Eq. 1 and is calculated by the sum of: (i) the internal work due to auto-rotational springs, and (ii) the internal work due to inter-rotational springs ${\kappa }_{xij}$, ${\kappa }_{yij}$ and the cross-coupled term ${\kappa }_{xyij}$ and ${\kappa }_{yxij}$. The kinetic energy of the complete system is defined by Eq. 2, where each term corresponds to: (i) translational kinetic energy due to sway and foundation rotation of each building’s mass, (ii) the rotational energy of each soil/foundation mass. Note that, in the particular case where the foundation is square, the term collapse to ${\kappa }_{xij}={\kappa }_{xji}$, ${\kappa }_{yij}={\kappa }_{yji}$, and ${\kappa }_{xyij}={\kappa }_{yxij}$.

$U=\frac{1}{2}{\displaystyle \sum _{i=1}^n}\left(k_{xi}{\theta }_{xi}^2+k_{yi}{\theta }_{yi}^2\right)+\frac{1}{2}{\displaystyle \sum _{i=1}^{n-1}}{\displaystyle \sum _{j=i+1}^n}\left({\kappa }_{xij}{\left({\theta }_{xj}-{\theta }_{xi}\right)}^2+{\kappa }_{yij}{\left({\theta }_{yj}-{\theta }_{yi}\right)}^2+{\kappa }_{xyij}{\left({\theta }_{yj}-{\theta }_{xi}\right)}^2+{\kappa }_{yxij}{\left({\theta }_{xj}-{\theta }_{yi}\right)}^2\right)(1)$

$T_E=\frac{1}{2}{\displaystyle \sum _{i=1}^n}\left(m_{bi}{\left({\dot{x}}_i+{\dot{x}}_g-h_i{\theta }_{yi}\right)}^2+m_{bi}{\left({\dot{y}}_i+{\dot{y}}_g-h_i{\theta }_{xi}\right)}^2+m_{bi}{\left({\dot{y}}_i-h_i{\theta }_{xi}\right)}^2+m_{si}{r}_i^2\left({\theta }_{xi}^2+{\theta }_{yi}^2\right)\right)(2)$

where $h_i$ is the height, $m_{bi}$ is the total lumped modal mass of building $i$ and $m_{si}$ is the foundation/soil mass underneath building $i$. $k_{bi}$ is the modal building lateral stiffness and $r_i$ is the soil/foundation mass radius of gyration, and $n$ is the number of buildings. Hence, the Euler-Lagrange equations of motion describing the dynamics of the discretised system of Figure 3 can be derived in the standard way by calculus and is written in matrix form, as follows,

$\mathbf{M}\ddot{\mathbf{x}}+\mathbf{C}\dot{\mathbf{x}}+\mathbf{\text{Kx}}={\mathbf{p}}_{\mathbf{1}}{\ddot{\mathrm{x}}}_g+{\mathbf{p}}_{\mathbf{2}}{\ddot{y}}_g(3)$

where the mass matrix $\mathbf{M}$ (Eqs 4 and 7), the damping matrix $\mathbf{C}$, the stiffness matrix $\mathbf{K}$ (Eq. 8), the force vectors ${\mathbf{p}}_{\mathbf{1}}$, ${\mathbf{p}}_{\mathbf{2}}$ (Eqs 5 and 9) and the DOFs vector $\mathbf{x}$ of the complete system of $n$ buildings are stated as follows,

$\mathbf{M}=\left[\begin{array}{ccccc}{\widehat{\mathbf{M}}}_1& \cdots & 0& \cdots & 0\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ 0& \cdots & {\widehat{\mathbf{M}}}_i& \cdots & 0\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ 0& \cdots & 0& \cdots & {\widehat{\mathbf{M}}}_n\end{array}\right],\mathbf{K}=\left[\begin{array}{ccccc}{\widehat{\mathbf{K}}}_1& \cdots & {\widehat{\mathrm{\kappa }}}_{\mathbf{1}\mathit{i}}& \cdots & {\widehat{\mathrm{\kappa }}}_{\mathbf{1}\mathit{n}}\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ {\widehat{\mathrm{\kappa }}}_{\mathit{i}\mathbf{1}}& \cdots & {\widehat{\mathbf{K}}}_i& \cdots & {\widehat{\mathrm{\kappa }}}_{\mathit{i}\mathit{n}}\\ ⋮& \ddots & ⋮& \ddots & ⋮\\ {\widehat{\mathrm{\kappa }}}_{\mathit{n}\mathbf{1}}& \cdots & {\widehat{\mathrm{\kappa }}}_{\mathit{n}\mathit{i}}& \cdots & {\widehat{\mathbf{K}}}_n\end{array}\right](4)$

$\mathbf{p}={\left[\begin{array}{ccccc}{\widehat{\mathbf{p}}}_1& \cdots & {\widehat{\mathbf{p}}}_i& \cdots & {\widehat{\mathbf{p}}}_n\end{array}\right]}^T,\mathbf{x}={\left[\begin{array}{ccccc}{\widehat{\mathbf{x}}}_1& \cdots & {\widehat{\mathbf{x}}}_i& \cdots & {\widehat{\mathbf{x}}}_n\end{array}\right]}^T,{\widehat{\mathbf{x}}}_i={\left[\begin{array}{cccc}{x}_i& y_i& {\theta }_{yi}& {\theta }_{xi}\end{array}\right]}^{\mathit{T}}(5)$

$\mathbf{C}=\mathbf{M}\left({\displaystyle \sum _{j=1}^{4n}}\frac{2{\xi }_j{\omega }_j}{{\mathbf{\varphi }}_j^T\mathbf{M}{\mathbf{\varphi }}_j}{\mathbf{\varphi }}_j{\mathbf{\varphi }}_j^T\right)\mathbf{M}(6)$

Figure 3

Figure 3. Idealization model of a city block arrangement.

The system’s linear viscous damping matrix $\mathbf{C}$ assumes that each natural mode is damped at ${\xi }_j=0.05$ of the critical damping, ${\mathbf{\varphi }}_j$ is the modal eigenvector of the mode $j$, ${\omega }_j$ are the natural frequencies of the system. Thus, the Caughey orthogonal damping matrix $\mathbf{C}$ can be calculated as (Clough and Penzien, 1993), by Eq. 6. Note that the damping matrix refers to the coupled system. The fundamental frequencies ${\omega }_j$ of the coupled system do not change very much compared to the uncoupled system (Vicencio and Alexander, 2018b), with a maximum of 9% variation in the natural frequencies. Hence, the damping matrix does not vary substantially between the SSSI and SSI systems.

The global mass matrix $\mathbf{M}$ corresponds to a diagonal block matrix, where each different blocks ${\widehat{\mathbf{M}}}_i$ represent the mass matrix for each building $i$.

${\widehat{\mathbf{M}}}_i=\left[\begin{array}{cccc}{m}_{bi}& 0& -m_{bi}{h}_i& 0\\ 0& m_{bi}& 0& -m_{bi}{h}_i\\ -m_{bi}{h}_i& 0& m_{bi}{h}_i^2+m_{si}{r}_i^2& 0\\ 0& -m_{bi}{h}_i& 0& m_{bi}{h}_i^2+m_{si}{r}_i^2\end{array}\right](7)$

The global stiffness matrix $\mathbf{K}$ includes the interaction effects between the buildings (SSSI). Therefore, the diagonal block terms ${\widehat{\mathbf{K}}}_i$ (of the global stiffness matrix $\mathbf{K}$) correspond to the stiffness matrix for each building $i$, including the additional stiffening effect of the adjacent footings. The off-diagonal block terms ${\widehat{\mathit{\kappa }}}_{ij}$ represent the interaction between the buildings $i$ and $j$. Note that all the interaction between buildings are considered.

${\widehat{\mathbf{K}}}_i=\left[\begin{array}{cccc}{k}_{bi}& 0& 0& 0\\ 0& k_{bi}& 0& 0\\ 0& 0& k_{xi}+{\displaystyle \sum _{j=1}^n}\left({\kappa }_{xij}+{\kappa }_{xyij}\right)& 0\\ 0& 0& 0& k_{yi}+{\displaystyle \sum _{j=1}^n}\left({\kappa }_{yij}+{\kappa }_{xyij}\right)\end{array}\right],{\widehat{\mathrm{\kappa }}}_{1i}=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& {-\kappa }_{x1i}& {-\kappa }_{xy1i}\\ 0& 0& {-\kappa }_{xy1i}& {-\kappa }_{y1i}\end{array}\right](8)$

Finally, the global excitation vectors ${\mathbf{p}}_{\mathbf{1}}$, ${\mathbf{p}}_{\mathbf{2}}$ are assembled by the block vector ${\widehat{\mathit{p}}}_i$ of each building $i$ in both directions.

${\widehat{\mathbf{p}}}_{ix}={\left[\begin{array}{cccc}-m_{bi}& 0& -m_{bi}{h}_i& 0\end{array}\right]}^{\mathit{T}},{\widehat{\mathbf{p}}}_{iy}={\left[\begin{array}{cccc}0& -m_{bi}& 0& -m_{bi}{h}_i\end{array}\right]}^{\mathit{T}}(9)$

In this paper, the dynamic properties of each building “$i$”, which is required in the Eq. 3, are deduced according to the following assumptions,

• The fundamental natural period of the structure on a rigid foundation (i.e., with no foundation/soil rotation) can be defined as $T_{xi}=T_{yi}=T_i=c_0{h}_i^{3/4}$. This empirical form is adopted by the approximate empirical relationship proposed by the Euro Code 8 (British Standards Institution, 1996). In this equation the height of the building $h_i$ is taken in meters, and the factor equal to $c_0=0.075$, corresponding for reinforced concrete moment resisting frames.

• Newmark and Rosenblueth consider that the volume of soil mass beneath a square base building is approximately equal to $m_{si}=0.35{\rho }_s{b}_i^3$, where ${\rho }_s$ are the soil density and $b$ the building width.

• The mass of the building can be approximated as $m_{bi}={\rho }_b{b}_i^2{h}_i$, where the average building density can be considered as ${\rho }_b=600\left[kg/m^3\right]$.

• The radius of gyration is calculated according to the Newmark’s empirical expression $r_i=0.33b_i.$

• It has been supported by previous research (Vicencio et al., 2023) the SSSI effects on structures founded on loose soil may exhibit significant interaction, so the soil properties used correspond to loose sand, where the soil density is ${\rho }_s=1300\left[kg/m^3\right]$, the shear wave velocity is $V_s=156\left[m/s\right]$ and the Poisson’s ratio of the soil is ${\nu }_s=0.3$.

• For the case of a singleton building (without any interaction), the rotational stiffness spring coefficient $k_{s\theta }$ is obtained by using the well know empirical formulae $k_{s\theta }=\frac{1}{2}\frac{G_s{b}^3}{1-{\mu }_s}$.

• The two orthogonal auto-rotational springs $k_{xi}$ and $k_{yi}$ and the interbuilding-rotational springs defined as a vector ${\mathit{\kappa }}_{ij}=\left[{\kappa }_{xij},{\kappa }_{yij},{\kappa }_{xyij},{\kappa }_{yxij}\right]$ (i.e., the coupling between building $″i^{″}$ and building $″j^{″}$) are obtained by the methodology presented in (Vicencio and Alexander, 2021), where the springs are determined by an application of an empirical surficial displacement field and inverse system identification using of least-squares. After the calculation of the springs that represent the soil, the complete system is ensembled according to the system matrices described in the dynamic Eq. 3.

2.2 Evaluation of change in power

We are interested in evaluating the change in the response between the coupled (structure-soil-structure interaction SSSI) and the uncoupled (soil-structure interaction, SSI) system. Initially the SSSI solution of Eq. 2 is calculated through time-history analysis. Then, the SSI response of each building is evaluated, where the dynamic analysis is evaluated by setting the inter-rotational springs ${\kappa }_{xij}$, ${\kappa }_{yij}$ and the cross-coupled term ${\kappa }_{xyij}$ and ${\kappa }_{yxij}$ equal to 0. As a measure of change in the response between SSSI and SSI, we will employ the displacement $U_i$ (horizontal sway + rocking, Eq. 10) and the total acceleration $A_i$ (horizontal sway + ground + rocking, Eq. 10) for the top of the building $i$ (in the x-direction), denoted by,

$U_i=x_i-h_i{\theta }_{yi},A_i={\ddot{x}}_i+{\ddot{x}}_g-h_i{\ddot{\theta }}_{yi}(10)$

In addition, it is valuable to characterize the change in total power caused by the multiple SSSI among the buildings. So, the percentage change in total power ${\ddot{\chi }}_i$ for the building $i$, when using the uncoupled SSI analyses rather than coupled SSSI analyses is expressed in terms of the total power spectral densities $E_{PSD}\left(A_i\right)$,

${\chi }_i=100\left\{\frac{{\left[E_{PSD}\left(U_i\right)\right]}_{SSSI}}{{\left[E_{PSD}\left(U_i\right)\right]}_{SSI}}-1\right\},{\ddot{\chi }}_i=100\left\{\frac{{\left[E_{PSD}\left(A_i\right)\right]}_{SSSI}}{{\left[E_{PSD}\left(A_i\right)\right]}_{SSI}}-1\right\}(11)$

where $E_{PSD}\left(U_i\right)$ and $E_{PSD}\left(A_i\right)$ is based on the average of the square Fourier Transform of all data points of the response acceleration time-series $U_i$ and $A_i$. The change of power ${\chi }_i$ and ${\ddot{\chi }}_i$ would be zero if there is no difference in overall response power between SSSI and SSI analyses. Using the Eq. 11 as a comparative metric, delivers a statistical estimate of magnitude that is more robust than employing a single peak of the function (displacement or acceleration).

2.3 Ground motion selection

To determine the effect of SSSI on the system described in Eq. 3 we consider fifty records that are taken from 25 events that occurred between 1971 and 2007 (see Figure 4), from the Pacific Earthquake Engineering Research (PEER-NGA) West database. Nine of records occurred in California (namely, San Fernando, Imperial Valley, Coalinga, Morgan Hill, Hector Mine, Whittier Narrows, Superstition Hills, Loma Prieta, Northridge and Parkfield), and six of them are taken from different places around the world (namely, Kocaeli (Turkey), Chi-Chi (Taiwan), Duzce (Turkey), Irpinia (Italy), Kobe and Chuetsu-oki (Japan)). Each record has two horizontal components. Event magnitudes range from $M_w=6.5$ to $M_w=7.6$ with an average magnitude of $M_w=7.0$. Values of their peak ground accelerations (PGAs) vary from 0.21 g to 0.82 g with a mean value of 0.43 g. All ground motions were recorded on weak soils, which correspond to sites of an average shear wave velocity of less than 180 m/s, i.e., loose sand. Figure 4 displays the elastic response spectrum for all the records and their mean.

Figure 4

Figure 4. Elastic response spectra for all PEER-NGA ground motions.

3 Numerical studies and discussion

3.1 SCI effects on a building cluster with the same height

To evaluate the effect of cluster interaction between the buildings, three types of building cluster with the same building heigh are considered, as shown in Figure 5 (Layout 1: 3 × 3 city blocks of nine equispaced identical buildings, Layout 2: 4 × 4 city blocks of sixteen equispaced identical buildings, Layout 3: 5 × 5 city blocks of twenty-five equispaced identical buildings). The fundamental natural period of the structure on a rigid foundation (i.e., with no foundation/soil rotation) is $T_{xi}=T_{yi}=T_i=0.5\left[s\right]$. The buildings have the same square plan area, with a height to width ratio equal to $h_i/b=1.5$. The centre-to-centre interbuilding distances are equispaced at ${∆}_{xi}={∆}_{yi}=1.2b$. The system is subjected to all earthquake events (fifty in total) in both directions simultaneously (East-West and North-South).

Figure 5

Figure 5. Schematic diagram of the structure cluster layout.

Figure 6 displays the variation of change in power for the displacement on top of the buildings, corresponding to the configuration Layout 1. The results are shown as the mean for Far-Field (FF), Near-Field Without Pulse (NFWP), and Near-Field Pulse Like (NFPL), in order to evaluate the changes depending on the different types of ground motion. The maximum increase in total power response occurred at the centre of the cluster (building 5), with a maximum of ${\chi }_5=12.9\%$, corresponding to the Far-Field records. In addition, there is a reduction in the response for some buildings, with a maximum for building 7 (${\chi }_7=-21.2\%$) to the Near-Field Without Pulse records.

Figure 6

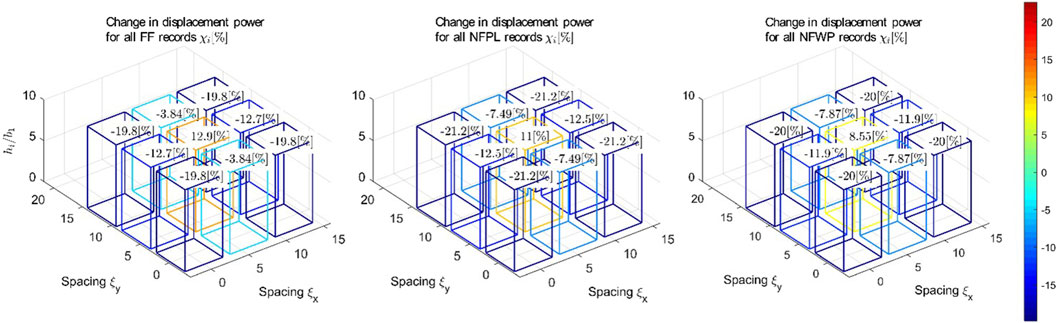
Figure 6. Change in displacement power due to 3D SSSI for a 3 × 3 city blocks of nine equispaced identical buildings and the same height (${\mathit{T}}_{\mathit{i}}=\mathbf{0.5}\left[\mathit{s}\right],{\mathit{h}}_{\mathit{i}}/\mathit{b}=\mathbf{2}$).

Figure 7 shows the variation of change in power for the acceleration on top of the buildings. Similar to the displacement, the maximum increase in total power response occurred at the centre of the cluster (building 5), with a maximum of ${\ddot{\chi }}_5=22.6\%$, corresponding to the Far-Field records. In addition, there is a reduction in the response for some buildings, with a maximum for building 7 (${\ddot{\chi }}_7=-21.2\%$,).

Figure 7

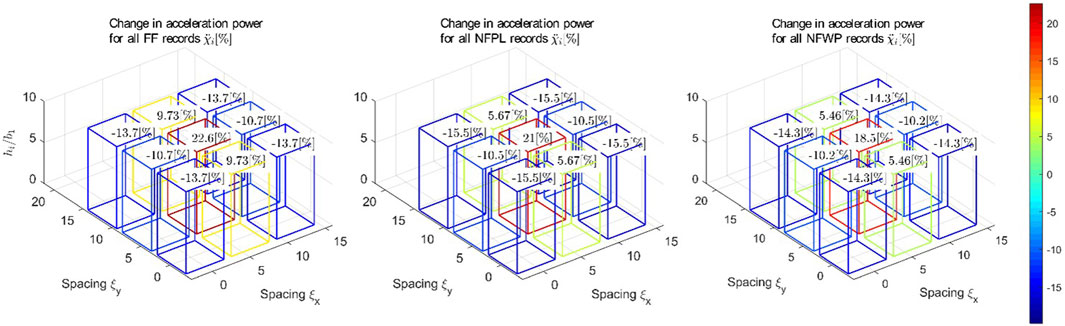
Figure 7. Change in acceleration power due to 3D SSSI for a 3 × 3 city blocks of nine equispaced identical buildings and the same height (${\mathit{T}}_{\mathit{i}}=\mathbf{0.5}\left[\mathit{s}\right],{\mathit{h}}_{\mathit{i}}/\mathit{b}=\mathbf{2}$).

Figures 8A, B show the uncoupled SSI (blue line) and coupled SSSI (red line) response for the top of building 1 and 5, and Figures 8C, D depict the corresponding power spectral density for the total acceleration, considering the Supertition Hill earthquake. Comparing the seismic response, it is clear that building 1 is affected by the surrounding buildings, where the change in power is ${\ddot{\chi }}_1=-23.8\%$. On the other hand, the building 5 (at the center of the city block), there is an amplification of ${\ddot{\chi }}_5=16.9\%$.

Figure 8

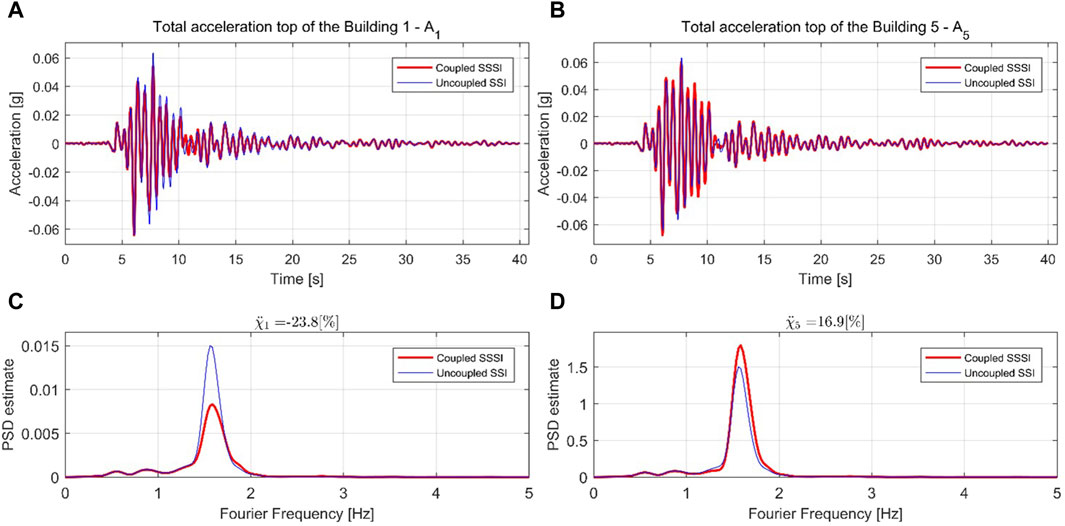
Figure 8. Total acceleration response for (A) building 1, (B) building 5, Power spectral density (C) building 1, (D) building 5.

As we can observe in the previous figure, the amplification/reduction of change in power (displacement and acceleration) between the three different earthquake-type events (FF, NFPL, and NFWP) are similar and follow equivalent trends for maximum values. Therefore, from now on we are plotting the mean of all earthquakes. Figures 9, 10 display the variation of change in power for the displacement ${\chi }_i\left[\%\right]$ and acceleration ${\ddot{\chi }}_i\left[\%\right]$ on top of the buildings, respectively.

Figure 9

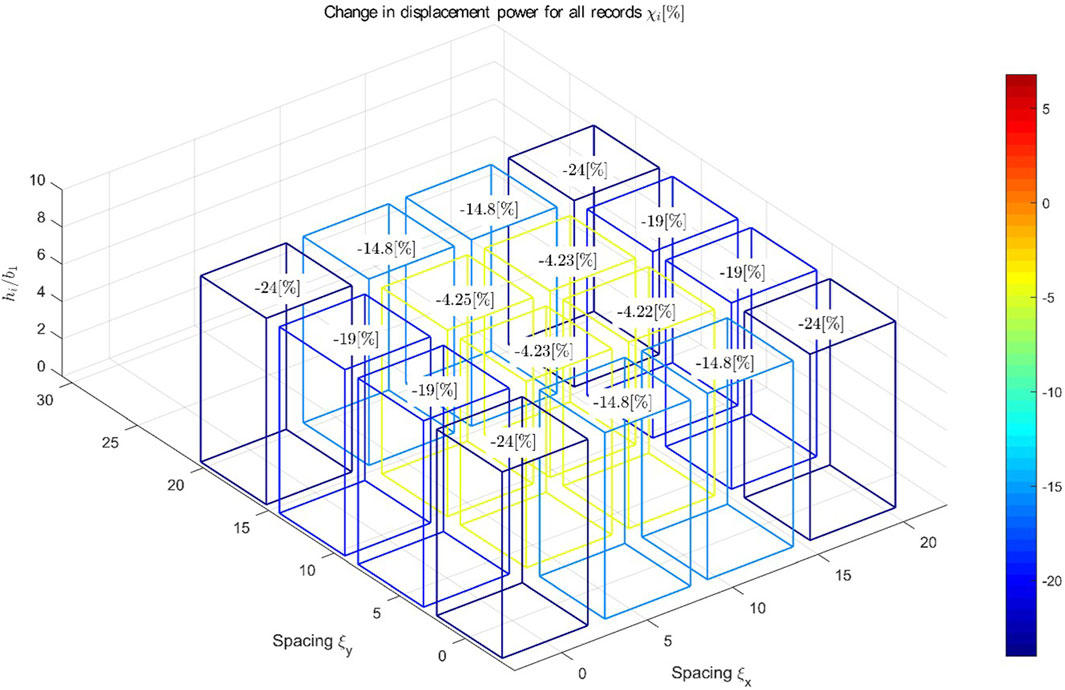
Figure 9. Change in displacement power due to 3D SSSI for a 4 × 4 city blocks of sixteen equispaced identical buildings and the same height, mean for all earthquakes (${\mathit{T}}_{\mathit{i}}=\mathbf{0.5}\left[\mathit{s}\right],{\mathit{h}}_{\mathit{i}}/\mathit{b}=\mathbf{2}$).

Figure 10

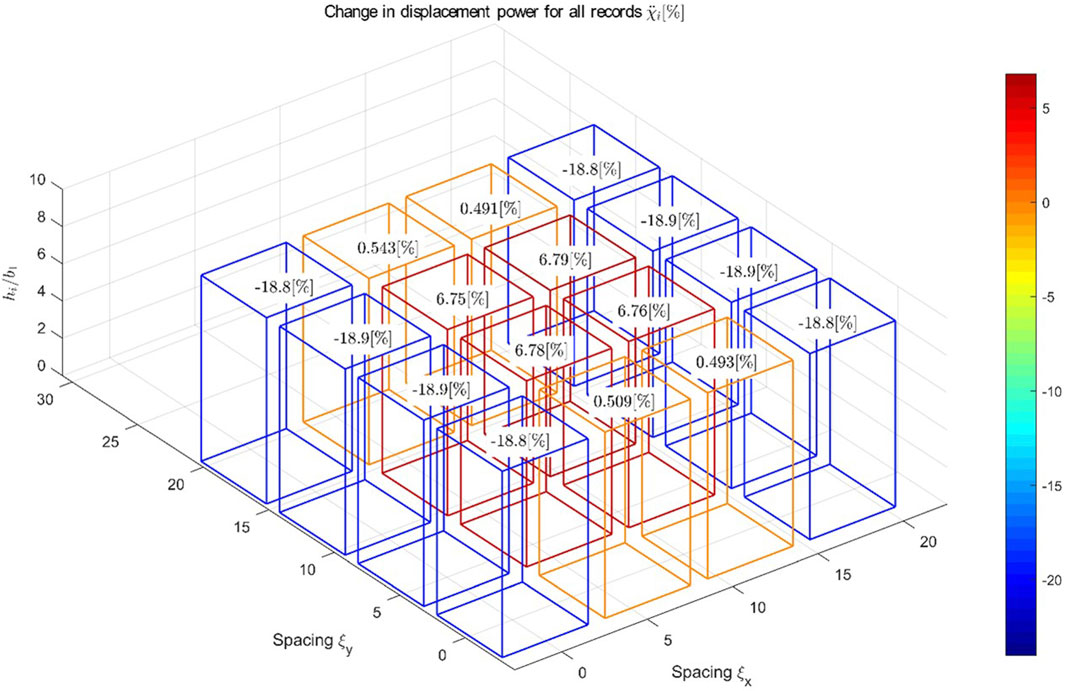
Figure 10. Change in acceleration power due to 3D SSSI for a 4 × 4 city blocks of sixteen equispaced identical buildings and the same height, mean for all earthquakes (${\mathit{T}}_{\mathit{i}}=\mathbf{0.5}\left[\mathit{s}\right],{\mathit{h}}_{\mathit{i}}/\mathit{b}=\mathbf{2}$).

The maximum increase in total power response occurred at the centre of the cluster, with a maximum of ${\ddot{\chi }}_6=6.79\%$ for the acceleration. In the case of the displacement, there is a reduction in the response of ${\chi }_6=-4.25\%$.

Figure 11 shows the variation of change in power for the acceleration ${\ddot{\chi }}_i\left[\%\right]$ on top of the buildings, corresponding to the configuration Layout 3 (5 × 5 city blocks of twenty-five equispaced identical buildings and the same height). In this case, there is an amplification of ${\ddot{\chi }}_{13}=24\%$ at the center of the city block, and a reduction of ${\ddot{\chi }}_{13}=-29\%$ at the corner of the city block. These results are consistent with the transfer functions shown by (Isbiliroglu et al., 2015), where the change in response is calculated in different clusters with variable number of buildings and spacing. As mentioned in the same work, the SCI effects increase as the number of structures increases and the separation between buildings decreases. This is why, in this paper we did not consider larger interbuilding separations (the SCI effects decreases).

Figure 11

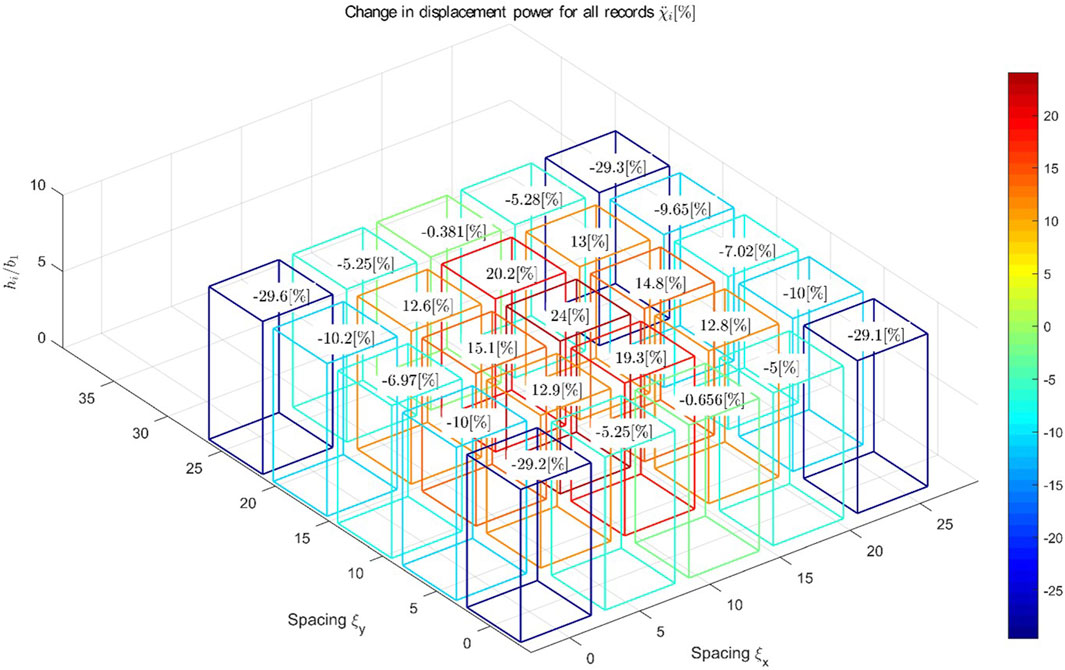
Figure 11. Change in acceleration power due to 3D SSSI for a 5 × 5 city blocks of twenty-five equispaced identical buildings and the same height, mean for all earthquakes (${\mathit{T}}_{\mathit{i}}=\mathbf{0.5}\left[\mathit{s}\right],{\mathit{h}}_{\mathit{i}}/\mathit{b}=\mathbf{2}$).

3.2 SCI effects on a building cluster with different heights

Here we evaluate the effect of cluster interaction between buildings with different height. As before, three types of building cluster are considered (Layout 1: 3 × 3 city blocks of nine equispaced identical buildings, Layout 2: 4 × 4 city blocks of sixteen equispaced identical buildings, Layout 3: 5 × 5 city blocks of twenty-five equispaced identical buildings). The fundamental natural period of the structure on a rigid foundation (i.e., with no foundation/soil rotation) covers a range of $T_{xi}=T_{yi}=\left(0.2\left[s\right]-1.0\left[s\right]\right)$. All the buildings have the same square plan area, therefore the centre-to-centre interbuilding distances are equispaced at ${∆}_{xi}={∆}_{yi}=1.2b$. The system is subjected to all earthquake events (fifty in total) in both directions simultaneously (East-West and North-South).

Figure 12 shows the variation of change in power for the acceleration ${\ddot{\chi }}_i\left[\%\right]$ on top of the buildings, corresponding to the configuration Layout 2 (4 × 4 city blocks of sixteen equispaced identical buildings), where the four central buildings are taller. In this case, due to the differences in height, there is an amplification at the edges of the city blocks, with a maximum of ${\ddot{\chi }}_5=20.1\%$. This highlights the complexity of the interaction, and the need to evaluate the interaction for each particular case, especially when there are important differences between the heights of the buildings.

Figure 12

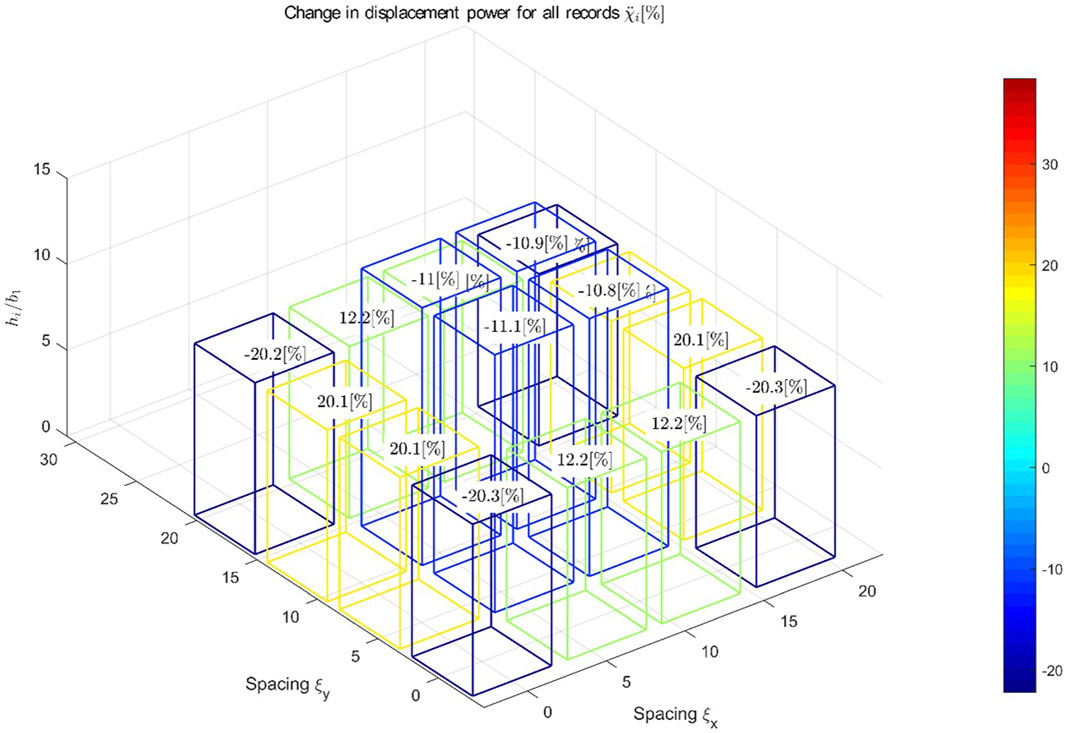
Figure 12. Change in acceleration power due to 3D SSSI for a 4 × 4 city blocks of sixteen equispaced identical buildings with different height. Mean for all earthquakes.

Finally, Figure 13 depicted the variation of change in power for the acceleration ${\ddot{\chi }}_i\left[\%\right]$ on top of the buildings, corresponding to the configuration Layout 3 (5 × 5 city blocks of twenty-five equispaced identical buildings and different height). As the previous discussed, there is a transfer of energy between the taller buildings, to the shorter buildings (${\ddot{\chi }}_7=15.6\%$). These results highlight the relevance of studying the seismic interactions between the buildings and consider the site-city interaction effects, especially in highly dense urban areas. Future studies should consider different buildings configurations, and nonlinear effects. In the same way, data from instrumented buildings are required in order to validate this news numerical simulations.

Figure 13

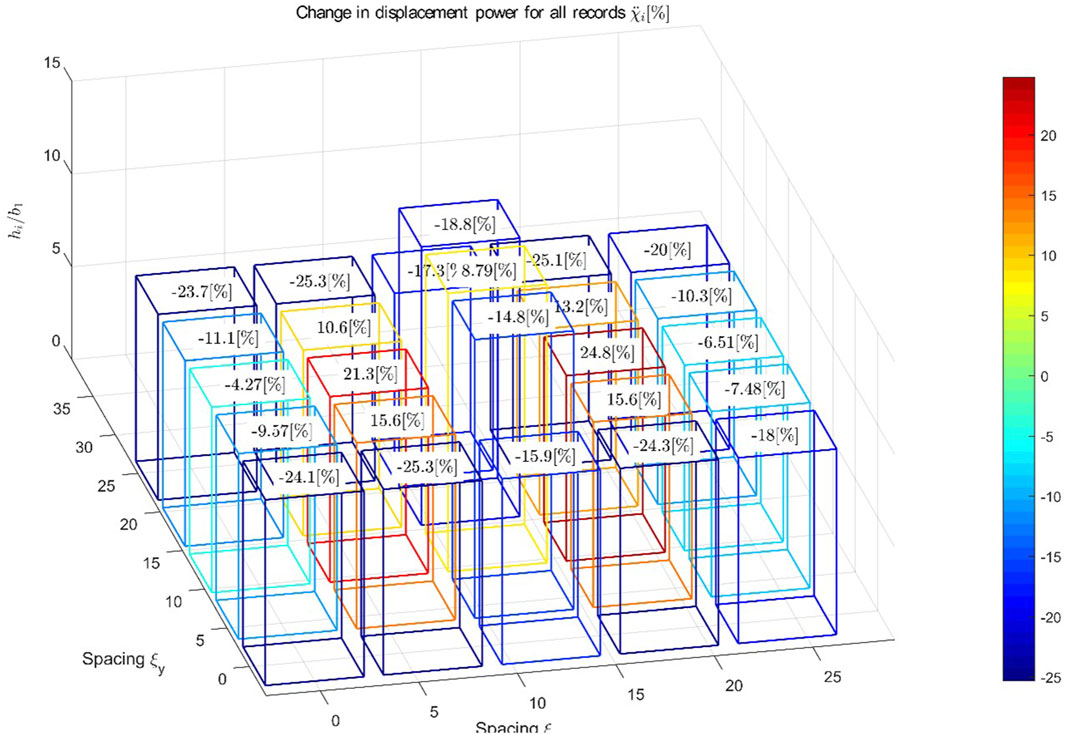
Figure 13. Change in acceleration power due to 3D SSSI for a 5 × 5 city blocks of twenty-five equispaced identical buildings with different height. Mean for all earthquakes.

4 Conclusion

In this paper, we present a theoretical formulation for Structure-Soil-Structure Interaction (SSSI) between adjacent buildings that form a city blocks under earthquake excitation in a 3-dimension arrangement. Different building layout and building properties are considered. A database of strong ground motions records with Far-Field, Near-Field Without Pulse and Near-Field Pulse-Like characteristics are employed. The inter-rotational springs was previously calibrated and validated by (i) finite element analyses (ii) physical experimental test using the University of Bristol’s shaking table and University of Dundee’s centrifuge and (iii) an analytical formulation derived from a Boussinesq deformation field of an elastic half-space. This research has led to the following principal conclusions:

• In most cases, the centre of the city blocks produces the largest amplification when compared with the isolated case (SSI), when the buildings have the same height. The magnitude of the change in the response depends on the dynamic characteristics of the structure adjacent to the building under consideration and the size of the city blocks.

• Regarding of the earthquake event, it is found that there is a reduction in the seismic response at the corner of the city blocks.

• In the case of different building heights, the phenomenon gets more complicated. The SCI effects depend mainly on the relative height ratios between buildings, where the taller buildings’ seismic response is reduced, and the shorter building´s seismic response is increased.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

FV: Conceptualization, Formal Analysis, Methodology, Supervision, Writing–original draft. NA: Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The first author is grateful to the Ministry of Science, Technology, Knowledge and Innovation, Chile and the National Agency of Research and Development (Agencia Nacional de Investigación y Desarrollo, ANID, Chile), for the financial support through FONDECYT Grant No. 11230400.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The handling editor CM-C declared a past collaboration with the authors.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aji, H. D. B., Wuttke, F., and Dineva, P. (2022). 3D structure-soil-structure interaction in an arbitrary layered half-space. Soil Dyn. Earthq. Eng. 159, 107352. doi:10.1016/j.soildyn.2022.107352

CrossRef Full Text | Google Scholar

Aldaikh, H., Alexander, N. A., Ibraim, E., and Knappett, J. (2016). Shake table testing of the dynamic interaction between two and three adjacent buildings (SSSI). Soil Dyn. Earthq. Eng. 89, 219–232. doi:10.1016/j.soildyn.2016.08.012

CrossRef Full Text | Google Scholar

Aldaikh, H., Alexander, N. A., Ibraim, E., and Oddbjornsson, O. (2015). Two dimensional numerical and experimental models for the study of structure-soil-structure interaction involving three buildings. Comput. Struct. 150, 79–91. doi:10.1016/j.compstruc.2015.01.003

CrossRef Full Text | Google Scholar

British Standards Institution (1996). EN 1998-1. Eurocode 8: design of structures for earthquake resistance.

Google Scholar

Cacciola, P., and Tombari, A. (2020). A stochastic ground motion model for the urban environment. Probabilistic Eng. Mech. 59, 103026. doi:10.1016/j.probengmech.2020.103026

CrossRef Full Text | Google Scholar

Chen, S., Liu, Q., Zhai, C., and Wen, W. (2022). Influence of building-site resonance and building properties on site-city interaction: a numerical investigation. Soil Dyn. Earthq. Eng. 158, 107307. doi:10.1016/j.soildyn.2022.107307

CrossRef Full Text | Google Scholar

Clough, R., and Penzien, J. (1993). Dynamics of structures. Second Edition. McGraw-Hill Inc.

Google Scholar

Clouteau, D., Broc, D., Devésa, G., Guyonvarh, V., and Massin, P. (2012). Calculation methods of Structure-Soil-Structure Interaction (3SI) for embedded buildings: application to NUPEC tests. Soil Dyn. Earthq. Eng. 32, 129–142. doi:10.1016/j.soildyn.2011.08.005

CrossRef Full Text | Google Scholar

Du, Z., Guo, T., Wang, J., Yu, S., Liu, J., Liu, X., et al. (2022). Experimental and analytical study on ground motion characteristics under structure cluster disturbance. Earthq. Eng. Struct. Dyn. 51, 2267–2291. doi:10.1002/eqe.3663

CrossRef Full Text | Google Scholar

Ghandil, M., and Aldaikh, H. (2017). Damage-based seismic planar pounding analysis of adjacent symmetric buildings considering inelastic structure–soil–structure interaction. Earthq. Eng. Struct. Dyn. 46, 1141–1159. doi:10.1002/eqe.2848

CrossRef Full Text | Google Scholar

Han, B., Chen, S., and Liang, J. (2020). 2D dynamic structure-soil-structure interaction: a case study of Millikan Library Building. Eng. Anal. Bound Elem. 113, 346–358. doi:10.1016/j.enganabound.2020.01.012

CrossRef Full Text | Google Scholar

Isbiliroglu, Y., Taborda, R., and Bielak, J. (2015). Coupled soil-structure interaction effects of building clusters during earthquakes. Earthq. Spectra 31, 463–500. doi:10.1193/102412EQS315M

CrossRef Full Text | Google Scholar

Jin, L., and Liang, J. (2022). 2D dynamic structure-canyon-structure interaction for the buildings along the urban river-canyon I: incident SH-waves in homogenous half-space. J. Earthq. Eng. 26, 2450–2468. doi:10.1080/13632469.2020.1785587

CrossRef Full Text | Google Scholar

Kham, M., Semblat, J. F., Bard, P. Y., and Dangla, P. (2006). Seismic site-city interaction: main governing phenomena through simplified numerical models. Bull. Seismol. Soc. Am. 96, 1934–1951. doi:10.1785/0120050143

CrossRef Full Text | Google Scholar

Kitada, Y., Hirotani, T., and Iguchi, M. (1999). Models test on dynamic structure–structure interaction of nuclear power plant buildings. Nucl. Eng. Des. 192, 205–216. doi:10.1016/S0029-5493(99)00109-0

CrossRef Full Text | Google Scholar

Knappett, J. A., Madden, P., and Caucis, K. (2015). Seismic structure–soil–structure interaction between pairs of adjacent building structures. Géotechnique 65, 429–441. doi:10.1680/geot.SIP.14.P.059

CrossRef Full Text | Google Scholar

Kumar, N., and Narayan, J. P. (2019). Quantification of fundamental frequencies of 3D basins and structures and site–city interaction effects on responses of structures. Pure Appl. Geophys 176, 4477–4502. doi:10.1007/s00024-019-02158-8

CrossRef Full Text | Google Scholar

Long, H., Wang, Z., Zhang, C., Zhuang, H., Chen, W., and Peng, C. (2021). Nonlinear study on the structure-soil-structure interaction of seismic response among high-rise buildings. Eng. Struct. 242, 112550. doi:10.1016/j.engstruct.2021.112550

CrossRef Full Text | Google Scholar

Lu, X., Cheng, Q., Xu, Z., Xu, Y., and Sun, C. (2019). Real-time city-scale time-history analysis and its application in resilience-oriented earthquake emergency responses. Appl. Sci. 9, 3497. doi:10.3390/app9173497

CrossRef Full Text | Google Scholar

Lu, X., Tian, Y., Wang, G., and Huang, D. (2018). A numerical coupling scheme for nonlinear time history analysis of buildings on a regional scale considering site-city interaction effects. Earthq. Eng. Struct. Dyn. 47, 2708–2725. doi:10.1002/eqe.3108

CrossRef Full Text | Google Scholar

Lu, Y., Li, B., Xiong, F., Ge, Q., Zhao, P., and Liu, Y. (2020). Simple discrete models for dynamic structure-soil-structure interaction analysis. Eng. Struct. 206, 110188. doi:10.1016/j.engstruct.2020.110188

CrossRef Full Text | Google Scholar

Mason, H. B., Trombetta, N. W., Chen, Z., Bray, J. D., Hutchinson, T. C., and Kutter, B. L. (2013). Seismic soil-foundation-structure interaction observed in geotechnical centrifuge experiments. Soil Dyn. Earthq. Eng. 48, 162–174. doi:10.1016/j.soildyn.2013.01.014

CrossRef Full Text | Google Scholar

Mulliken, J. S., and Karabalis, D. L. (1998). Discrete model for dynamic through-the-soil coupling of 3-D foundations and structures. Earthq. Eng. Struct. Dyn. 27, 687–710. doi:10.1002/(SICI)1096-9845(199807)27:7<687::AID-EQE752>3.0.CO;2-O

CrossRef Full Text | Google Scholar

Padrón, L. A., Aznárez, J. J., and Maeso, O. (2011). 3-D boundary element–finite element method for the dynamic analysis of piled buildings. Eng. Anal. Bound Elem. 35, 465–477. doi:10.1016/j.enganabound.2010.09.006

CrossRef Full Text | Google Scholar

Schwan, L., Boutin, C., Padrón, L. A., Dietz, M. S., Bard, P. Y., and Taylor, C. (2016). Site-city interaction: theoretical, numerical and experimental crossed-analysis. Geophys J. Int. 205, 1006–1031. doi:10.1093/gji/ggw049

CrossRef Full Text | Google Scholar

Shabani, M. J., Shamsi, M., and Zakerinejad, M. (2022). Slope topographic impacts on the nonlinear seismic analysis of soil-foundation-structure interaction for similar MRF buildings. Soil Dyn. Earthq. Eng. 160, 107365. doi:10.1016/j.soildyn.2022.107365

CrossRef Full Text | Google Scholar

Shamsi, M., Shabani, M. J., and Vakili, A. H. (2022). Three-Dimensional seismic nonlinear analysis of topography–structure–soil–structure interaction for buildings near slopes. Int. J. Geomechanics 22. doi:10.1061/(asce)gm.1943-5622.0002301

CrossRef Full Text | Google Scholar

Tombari, A., and Cacciola, P. (2021). Toward the definition of a novel response spectrum for the urban environment. Soil Dyn. Earthq. Eng. 143, 106631. doi:10.1016/j.soildyn.2021.106631

CrossRef Full Text | Google Scholar

Trombetta, N. W., Benjamin Mason, H., Hutchinson, T. C., Zupan, J. D., Bray, J. D., and Kutter, B. L. (2015). Nonlinear soil–foundation–structure and structure–soil–structure interaction: engineering demands. J. Struct. Eng. 141, 1–12. doi:10.1061/(asce)st.1943-541x.0001127

CrossRef Full Text | Google Scholar

Trombetta, N. W., Mason, H. B., Chen, Z., Hutchinson, T. C., Bray, J. D., and Kutter, B. L. (2013). Nonlinear dynamic foundation and frame structure response observed in geotechnical centrifuge experiments. Soil Dyn. Earthq. Eng. 50, 117–133. doi:10.1016/j.soildyn.2013.02.010

CrossRef Full Text | Google Scholar

Tsogka, C., and Wirgin, A. (2003). Simulation of seismic response in an idealized city. Soil Dyn. Earthq. Eng. 23, 391–402. doi:10.1016/S0267-7261(03)00017-4

CrossRef Full Text | Google Scholar

Vicencio, F., and Alexander, N. A. (2018a). Dynamic interaction between adjacent buildings through nonlinear soil during earthquakes. Soil Dyn. Earthq. Eng. 108, 130–141. doi:10.1016/j.soildyn.2017.11.031

CrossRef Full Text | Google Scholar

Vicencio, F., and Alexander, N. A. (2018b). Higher mode seismic structure-soil-structure interaction between adjacent building during earthquakes. Eng. Struct. 174, 322–337. doi:10.1016/j.engstruct.2018.07.049

CrossRef Full Text | Google Scholar

Vicencio, F., and Alexander, N. A. (2019). Dynamic Structure-Soil-Structure Interaction in unsymmetrical plan buildings due to seismic excitation. Soil Dyn. Earthq. Eng. 127, 105817. doi:10.1016/j.soildyn.2019.105817

CrossRef Full Text | Google Scholar

Vicencio, F., and Alexander, N. A. (2021). Method to evaluate the dynamic structure-soil-structure interaction of 3-D buildings arrangement due to seismic excitation. Soil Dyn. Earthq. Eng. 141, 106494. doi:10.1016/j.soildyn.2020.106494

CrossRef Full Text | Google Scholar

Vicencio, F., and Alexander, N. A. (2022). Seismic Structure-Soil-Structure Interaction between a pair of buildings with consideration of rotational ground motions effects. Soil Dyn. Earthq. Eng. 163, 107494. doi:10.1016/j.soildyn.2022.107494

CrossRef Full Text | Google Scholar

Vicencio, F., Alexander, N. A., and Málaga-Chuquitaype, C. (2024). Seismic structure-soil-structure interaction between inelastic structures. Earthq. Eng. Struct. Dyn. 53, 1446–1464. doi:10.1002/eqe.4076

CrossRef Full Text | Google Scholar

Vicencio, F., Alexander, N. A., and Saavedra Flores, E. I. (2023). A State-of-the-Art review on Structure-Soil-Structure interaction (SSSI) and Site-City interactions (SCI). Structures 56, 105002. doi:10.1016/j.istruc.2023.105002

CrossRef Full Text | Google Scholar

Vicencio, F., and Cruz, E. F. (2021). A high order nonlinear study to evaluate the seismic response of rotating machines–structure–soil foundation systems. J. Earthq. Eng. 25, 2775–2807. doi:10.1080/13632469.2019.1651422

CrossRef Full Text | Google Scholar

Yahyai, M., Mirtaheri, M., Mahoutian, M., Daryan, A. S., and Assareh, M. A. (2008). Soil structure interaction between two adjacent buildings under earthquake load. Am. J. Eng. Appl. Sci. 1, 121–125. doi:10.3844/ajeassp.2008.121.125

CrossRef Full Text | Google Scholar

Zhang, B., Xiong, F., Lu, Y., Ge, Q., Liu, Y., Mei, Z., et al. (2021). Regional seismic damage analysis considering soil–structure cluster interaction using lumped parameter models: a case study of Sichuan University Wangjiang Campus buildings. Bull. Earthq. Eng. 19, 4289–4310. doi:10.1007/s10518-021-01149-2

CrossRef Full Text | Google Scholar

Zhang, W., and Taciroglu, E. (2021). 3D time-domain nonlinear analysis of soil-structure systems subjected to obliquely incident SV waves in layered soil media. Earthq. Eng. Struct. Dyn. 50, 2156–2173. doi:10.1002/eqe.3443

CrossRef Full Text | Google Scholar