Conditional adaptive time series compensation and control design for multi-axial real-time hybrid simulation

The structural performance of critical infrastructure during extreme events requires testing to understand the complex dynamics. Shake table testing of buildings to evaluate structural integrity is expensive and requires special facilities that can allow for the construction of large-scale test specimens. An attractive alternative is a cyber-physical testing technique known as Real-Time Hybrid Simulation (RTHS), where a large-scale structure is decomposed into physical and numerical substructures. A transfer system creates the interface between physical and numerical substructures. The challenge occurs when using multiple actuators connected with a coupler (i.e., transfer system) to create translation and rotation at the interface. Tracking control strategies aim to reduce time delay errors to create the desired displacements that account for the complex dynamics. This paper proposes two adaptive control methodologies for multi-axial real-time hybrid simulations that improve capabilities for a higher degree of coupling, boundary, complexity, and noise reduction. One control method integrates the feedback proportional derivative integrator (PID) control with a conditional adaptive time series (CATS) compensation and inverse decoupler. The second proposed control method is based on a coupled Model Predictive Control (MPC) with the CATS compensation. The performance of the proposed methods is evaluated using the virtual multi-axial benchmark control problem consisting of a steel frame as the experimental substructure. The transfer system consists of a coupler that connects two hydraulic actuators generating the translation and rotation acting at the joint. Through sensitivity analysis, parameters were tuned for the decoupler components, CATS compensation, and the control design for PID, LQG, and MPC. Comparative results among different control methods are evaluated based on performance criteria, including critical factors such as reduction in the time delay of bothactuators. The research findings in this paper improve the tracking control systems for the multi-axial RTHS of building structures subjected to earthquake loading. It provides insight into the robustness of the proposed tracking control methods in addressing uncertainty and improves the understanding of multiple output controllers that could be used in future cyber-physical testing of civil infrastructure subjected to natural hazards.

1 Introduction

Benchmark control problems provide a baseline for the research community to test control strategies and numerical methodologies to address the challenges presented. In the automotive control engineering community, benchmark control problems often serve as a way to bridge the gap between control theory and control practice. Foundational benchmark problems consist of protecting the built environment with structural control systems and evaluating their effectiveness in reducing damaging effects during extreme events. Spencer Jr et al. (1998) studied the benchmark problem consisting of nonlinear buildings of 3-, 9-, and 20-stories tall equipped with passive, semi-active, and active control devices and evaluating the performance in adapting in real-time during earthquake events. Yang et al. (2004) studied a 76-story highrise building equipped with an active mass damper and subjected to strong wind scenarios. Narasimhan et al. (2006) studied a benchmark problem of an 8-story irregular building equipped with semi-active devices and base isolation systems subjected to earthquake loading. Additional benchmark problems consisted of cable-stayed bridges by Dyke et al. (2003) and highway bridges by Agrawal et al. (2009) equipped with magnetorheological (MR) dampers subjected to seismic events have served the research community in developing strategies for their control. Recently, artificial intelligence and game theory controllers were developed for high-performance mitigation. Their effectiveness in reducing vibrations was evaluated for highrise buildings in Gutierrez Soto and Adeli (2017) and highway bridges in Javadinasab Hormozabad and Gutierrez Soto (2021). While Zambrano et al. (2021) used these benchmark problems to study the vulnerability of structural control systems to cyber attacks. Verification and validation of novel control methods and devices was imperative and this need led to the development of experimental techniques that allowed for flexibility, were cost-effective, and accounted for an accurate representation of the scalability of the proposed systems. One solution that arose is a technique known as hybrid simulation, dynamic substructuring, hardware-in-the-loop, and similar techniques, that combine experimental testing with numerical simulations.

Multiple actuators are needed in hybrid simulation to obtain realistic three-dimensional (3D) behavior of structures. One limitation of prior work in hybrid simulation using multiple actuators is that it is conducted as a pseudo-dynamic test. Pseudo-Dynamic Hybrid Simulation is the process of applying a force slowly to a test specimen to determine how it will react to the forces acting upon it. Recent studies in pseudo-dynamic testing have been used for improving the understanding of buckling-restrained braced frames Mortazavi et al. (2022b); Mojiri et al. (2021) and special concentrically braced frames Mortazavi et al. (2022a). However, pseudo-dynamic tests do not operate in real-time and therefore cannot provide data on how structures will react in an actual time scale of dynamic events. These studies at slow speeds often do not consider the inherent rate-dependent effects. Therefore, it is necessary to evaluate strategies that would account for the rate-dependent effects.

Real-time hybrid simulation (RTHS) is a cyber-physical testing technique that decomposes a large-scale system into numerical and experimental substructures. The experimental substructure, the proof-of-concept specimen in the lab, is selected as the subsystem of unknown performance that is desired to be explored for further studies. Examples of specimens investigated using RTHS are often selected due to the rate dependence of the materials such as rubber bearings by Yuan et al. (2017), structural behavior such as nonlinearities in connections of steel members by Castaneda et al. (2015), rate-dependent damping devices such as MR dampers by Friedman et al. (2015), active inerters by Chen and Chen (2023), or isolation systems such as rolling pendulums in Covarrubias Vargas et al. (2022). To realize the benefits of RTHS, the transfer system that generates the displacement between the numerical and experimental substructures needs to be designed for effective tracking. The tracking capability is given by a controller that satisfies the interface conditions. Therefore, Silva et al. (2020) provided a benchmark control problem consisting of a 3-story frame structure to enable researchers to address challenges in delays caused by a single actuator aiming to create the translation on the floor during seismic events. Fermandois (2019) used model-based compensation to study the accuracy and stability of the actuator using the virtual RTHS benchmark problem. The proposed approach combined feedforward and feedback components. The feedforward allowed for reference tracking while the feedback improved reliability under exogenous noise and a level of uncertainty. Palacio-Betancur and Gutierrez Soto (2023) provides a state-of-the-art review on tracking control techniques used for RTHS in engineering applications, including comparison among techniques proposed for solving the virtual RTHS benchmark control problem.

Multi-axial Real-time Hybrid Simulation (maRTHS) is a type of RTHS that aims to capture the multi-directional dynamic loading acting on a specimen. The interaction between substructures drives the decision on the loading equipment necessary to create the multi-actuator loading assemblies and the corresponding dynamic compensation process. The benchmark problem described in the next section is a virtual maRTHS that allows for the evaluation of control systems design and estimation strategies. This paper aims to fill the research gap in evaluating control methodologies that are best suitable for addressing the challenges of the maRTHS. Method one is composed of decoupling, Proportional-Integral-Derivative (PID) controller, and Conditional Adaptive Time Series (CATS) compensation. Method two consists of an uncoupled Model Predictive Control (MPC) with and without the CATS compensation.

2 Materials and methods

2.1 Problem statement: Description of the benchmark control problem

Condori Uribe et al. (2023) introduce an experimental benchmark control problem focused on multi-axial real-time hybrid simulation (maRTHS). This technique combines numerical and experimental substructures to study the dynamic behavior of complex structures. Specifically, it deals with a type of real-time hybrid simulation that employs multiple hydraulic actuators to accurately represent the response of substructures. The challenges associated with this multi-dimensional or multi-axial RTHS approach include aspects related to control, boundary conditions, computation, nonlinearities, uncertainties, and coupling. Unlike simpler RTHS methods, maRTHS requires multiple-input multiple-output (MIMO) control strategies due to the involvement of more than one hydraulic device actuator. Consequently, additional physical components are necessary to account for the increased degrees of freedom (DOF).

In the benchmark problem introduced by Condori Uribe et al. (2023), a steel frame structure shown in Figure 1 is subjected to seismic base excitation. Compared to earlier scenarios that assumed one actuator RTHS scenarios only, this problem has more complexity and is more realistic since it considers both translational and rotational control objectives. The experimental design, the goals of the problem, the measures of performance, the limitations of the control, the experimental data, finite element models, and state-space models are provided in Condori Uribe et al. (2023). The objective of the maRTHS benchmark is to develop and test control methods that can follow the movement of a plant in both linear and angular directions. The experimental setup (i.e., the partitioned part in Figure 1) consists of a steel frame. The transfer system consists of two hydraulic actuators and a steel coupler that connects the actuators’ length changes and produces the desired motion of the frame node. The control plant is composed of the experimental substructure and transfer system and is shown in Figure 2. The numerical and physical substructures shown in Figure 2 interact by the degrees of freedom (translation in vertical and horizontal directions and rotation) at the common nodes 4 and 7. The subscripts “ns” and “es” refer to numerical substructure and experimental substructure, respectively.

Figure 1

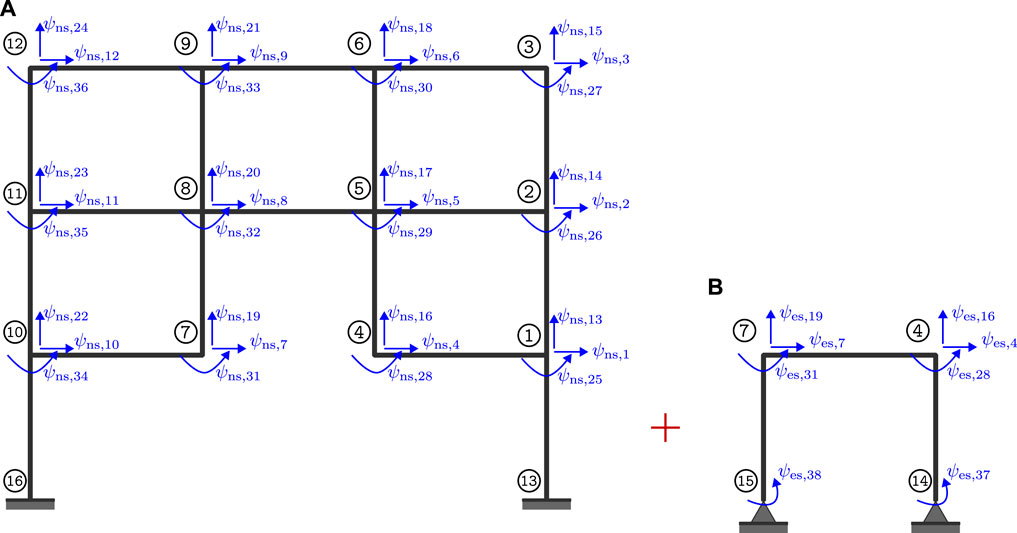
Figure 1. A schematic diagram of how the reference structure is partitioned; (A) Numerical model, and (B) Physical substructure.

Figure 2

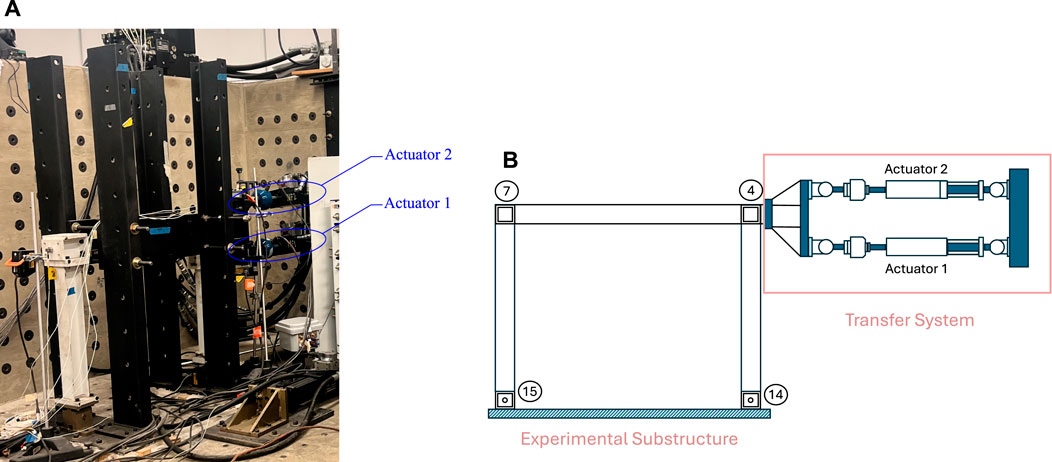
Figure 2. (A) Laboratory setup located at Purdue University and (B) corresponding diagram showing the experimental substructure and transfer system used for the maRTHS benchmark control problem.

This benchmark problem aims to: (1) test, develop, and compare existing or new MIMO control methods, (2) provide a computational tool for exploring different ways of conducting maRTHS, (3) promote the transition from single-actuator RTHS to maRTHS experiments, and (4) offer a challenging problem for new researchers to learn about maRTHS. To move the experimental part in RTHS, a transfer system is required to generate the desired displacements determined in the numerical substructure subjected to dynamic loading. The transfer system will move the actuators to generate the movement in the physical domain. The response from the physical experimental substructure is captured, which will be fed into the numerical domain in real-time. Many factors affect this interaction such as delays, lags that depend on frequency, noise in measurements, how the control and structure interact, how the servo-actuators work, how the multiple actuators and axes are connected in real-time hybrid simulation tests, and the conditions of the environment and lab when testing (Dyke et al., 1995; Phillips and Spencer, 2013; Nakata et al., 2014; Fermandois and Spencer, 2017).

The reference model has to be divided into numerical and experimental segments for the RTHS, as shown in Figure 3. The mass, damping, and stiffness matrices of the divided model are the sum of the numerical and experimental matrices, assuming the frame is linearly elastic:

$\left({\mathbf{M}}_{\text{ns}}+{\mathbf{M}}_{\text{es}}\right)\ddot{\mathbf{\Psi }}+\left({\mathbf{C}}_{\text{ns}}+{\mathbf{C}}_{\text{es}}\right)\dot{\mathbf{\Psi }}+\left({\mathbf{K}}_{\text{ns}}+{\mathbf{K}}_{\text{es}}\right)\mathbf{\Psi }=-\mathbf{M}\mathbf{\Gamma }{\ddot{x}}_g(1)$

where,

$\mathbf{M}={\mathbf{M}}_{\text{ns}}+{\mathbf{M}}_{\text{es}}(2)$

$\mathbf{C}={\mathbf{C}}_{\text{ns}}+{\mathbf{C}}_{\text{es}}(3)$

$\mathbf{K}={\mathbf{K}}_{\text{ns}}+{\mathbf{K}}_{\text{es}}(4)$

Figure 3

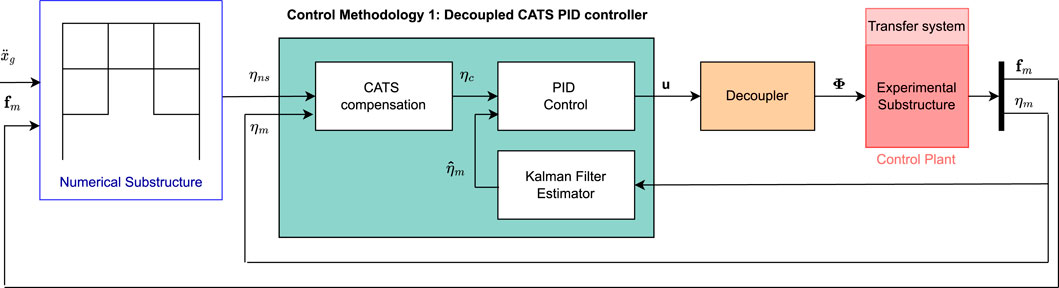
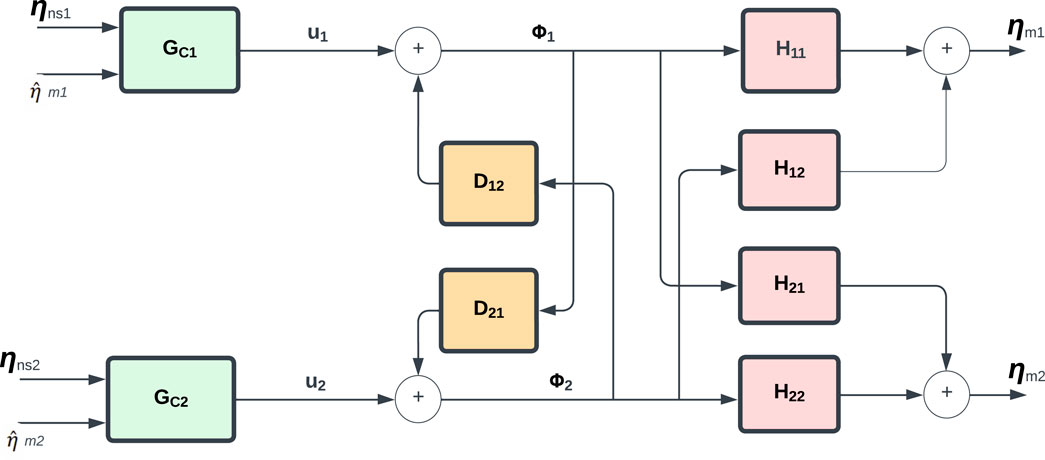
Figure 3. Simplified block diagram of the proposed method 1 Decoupled CATS compensation and PID control design.

To guarantee the quality of the RTHS, the issues that can compromise accuracy and stability must be considered. Hence, a control system that is well-designed and tuned is typically required to handle these issues and accomplish the test objectives. The control system comprises the following three main components: (1) The plant (the system to be controlled) includes the system dynamics (structure) and the transfer system (control action enforcer), (2) The sensing system measures the plant responses using various sensors, (3) The digital controller generates a control action based on a specific control law and uses the measured response of the plant to estimate the states if needed. This digital controller part usually works in a closed loop and has one or more control layers for improving the performance and estimators for producing unmeasured or noisy states.

To achieve the desired displacement, the maRTHS technique aims to adjust the control plant accordingly. The actuators are moved by the controller, which is part of the target system, targeting the displacements coming from the numerical substructure, which is a computer representation of the tested structure. The quality of the tracking and the whole RTHS system is evaluated with criteria related to tracking control, estimation, and global RTHS performance.

The overall performance of the maRTHS is assessed by two types of quantitative evaluations: (1) The tracking control and estimation performance measures the accuracy between the target and measured displacements and (2) the global RTHS experiment performance measures how well the reference structure response and the hybrid system response match. The benchmark uses 10 evaluation criteria for these two types of performance (Table 1). Six criteria are for tracking control performance and four are for global RTHS experiment performance. The criteria are calculated after the RTHS (or virtual RTHS) is finished.

Table 1

Table 1. Assessment of performance for control used in maRTHS benchmark control problem.

As defined earlier, the control plant has two control inputs (i.e., displacement commands) $\mathbf{u}={\left[\begin{array}{cc}\hfill u_1\hfill & \hfill u_2\hfill \end{array}\right]}^T$ and two hydraulic actuator displacements ${\eta }_m={\left[\begin{array}{cc}\hfill {\eta }_{m,1}\hfill & \hfill {\eta }_{m,2}\hfill \end{array}\right]}^T$ as outputs. Subscript 1 is for the bottom actuator and subscript 2 is for the top actuator. A 2 × 2 matrix description of the control plant is functional for this case. The control plant’s transfer function matrix is given by

$\mathbf{H}=\left[\begin{array}{cc}\hfill H_{11}\hfill & \hfill H_{12}\hfill \\ \hfill H_{21}\hfill & \hfill H_{22}\hfill \end{array}\right](5)$

where H_ij is the transfer function from input j to output i. In this matrix, the diagonal terms show how the input and output of each actuator are related and the off-diagonal terms show how one actuator affects the other.

The assumptions made in the benchmark problem study are as follows (Condori Uribe et al., 2023): (1) To simplify the complexity of damping, the study has assumed that the damping matrix is proportional to the sum of the mass and stiffness matrices of the reference system. (2) In the equation describing the motion, which combines the numerical and experimental aspects of partitioned mass, damping, and stiffness matrices, a linear elastic behavior is assumed for the frame (i.e., small deformations and deflections). (3) Joints of the physical frame are assumed to be rigid, i.e., the rotation is small. (4) The coupler is assumed to be rigid and has a high stiffness. Consequently, the deformations are small. (5) The connection between the coupler and joints is rigid. (6) The vertical motion of the nodes is assumed to be negligible.

2.2 Baseline controller: Linear Quadratic Gaussian controller

This paper compares the performance of the two proposed control methodologies with the baseline approach of the conventional control method, the Linear Quadratic Gaussian (LQG) controller. LQG is a close-loop control method that includes two main components: a deterministic LQR and a Kalman Filter. LQR control law requires full state feedback of the dynamic systems, which is provided by the Kalman Filter estimation in case of the existing unmeasured states. The control objective of the LQG is minimizing the tracking error between the measured and desired value of η_c and ${\widehat{\eta }}_m$ respectively. Details of the derivation were presented in the benchmark problem Condori Uribe et al. (2023).

2.3 Proposed methodology 1: Decoupled CATS compensation and PID control design

The first proposed control method shown in Figure 3 consists of a dynamic decoupler to reduce the interaction between actuators, a pair of proportional-integral-derivative (PID) feedback controllers for the decoupled plant (G), and a set of Conditional Adaptive Time Series (CATS) compensators as feed-forward controller to reduce time delay. The components of this methodology are explained in the following subsections.

2.3.1 Decoupler component

The maRTHS benchmark problem involves several measurement and control signals that are coupled together because the actuators are attached to the same steel coupling element, which imposes displacements and rotations on the steel frame. This type of coupling causes difficulties in feedback control design because each control signal affects both measurements. This type of control problem is traditionally solved with a decentralized approach when the interaction between processes is negligible (Garrido et al., 2011). For example, Najafi et al. (2020) studied a decentralized controller for maRTHS of a steel moment frame that has a column as the experimental substructure. The transfer system consists of six actuators connected to a table. A 3-DOF dynamical model composed of two rotational DOF and one DOF for the horizontal translation was used to represent the steel moment frame. However, when the interaction has higher effects, the decentralized approach involves a trade-off in performance between feedback loops, i.e., the designer decides if it is more important to have higher accuracy in some measurements than others. On the other hand, a centralized control approach can handle this interaction.

A centralized controller can be applied in two different ways, purely centralized or a decoupling network combined with single-loop controllers. The former usually involves tuning of multiple processes simultaneously, while the latter uses a decoupler to minimize the interaction between loops, and a set of feedback loops that can be designed separately. For simplicity and practicality, the proposed controller uses a decoupling network with single-loop controllers. In addition, the mentioned decoupling networks can be static for low-frequency processes or dynamic for a wider range of frequencies Liu et al. (2019). This means that a dynamic decoupler is recommended for RTHS because the response of structural systems subjected to seismic loads has a wide frequency content.

The dynamic decoupling of a MIMO system is generally implemented with three approaches: ideal, simplified, and inverted. Ideal decoupling completely reduces the interaction between loops but it is rarely used in practice because it has a complex architecture and high sensibility to model errors, simplified decoupling is easier to implement in practice but it maintains some interaction between loops that complicates controller tuning, and inverted has the same decoupling function as ideal decoupling and the same convenient implementation as simplified decoupling Liu et al. (2019). Therefore, the proposed controller uses an inverted decoupler as shown in Figure 4 to reduce the interaction between actuators.

Figure 4

Figure 4. Diagram of the Decoupler component used in proposed control methodology 1.

The decoupler transfer functions, D₁₂ and D₂₁ are model-based and are taken as Wade (1997):

$D_{12}=-\frac{H_{12}}{H_{11}}(6)$

$D_{21}=-\frac{H_{21}}{H_{22}}(7)$

where the transfer functions H_ij is described in Eq. 5. The decoupling can be expressed in Eqs 8, 9 as follows,

${\eta }_{m1}=H_{11}{\mathrm{\Phi }}_1+H_{12}{\mathrm{\Phi }}_2(8)$

${\eta }_{m2}=H_{21}{\mathrm{\Phi }}_1+H_{22}{\mathrm{\Phi }}_2(9)$

where Φ₁ and Φ₂ are the decoupler components relating to the input of the MIMO system as,

${\mathrm{\Phi }}_1=u_1+D_{12}{\mathrm{\Phi }}_2(10)$

${\mathrm{\Phi }}_2=u_2+D_{21}{\mathrm{\Phi }}_1(11)$

Substituting Eqs 6, 7, 10, 11 into Eqs 8, 9 then,

${\eta }_{m1}=H_{11}{u}_1(12)$

${\eta }_{m2}=H_{22}{u}_2(13)$

Therefore, with the inverted decoupler, the apparent system becomes a pair of single-loop controllers. Nevertheless, this is only possible if the system is realizable, i.e., if the decoupler transfer functions are stable and causal (Liu et al., 2019). Using the transfer function of the system in Eq. 5, the decoupler function D₁₂ has three zeros and four poles, and D₂₁ has four zeros and three poles, therefore, the function D₂₁ is non-causal, and the decoupling is non-realizable. For this particular case, it is possible to force realizability to the system by inserting transfer functions N₁₁ and N₂₂ with stable poles to the input signals of the MIMO system as shown in Figure 5.

Figure 5

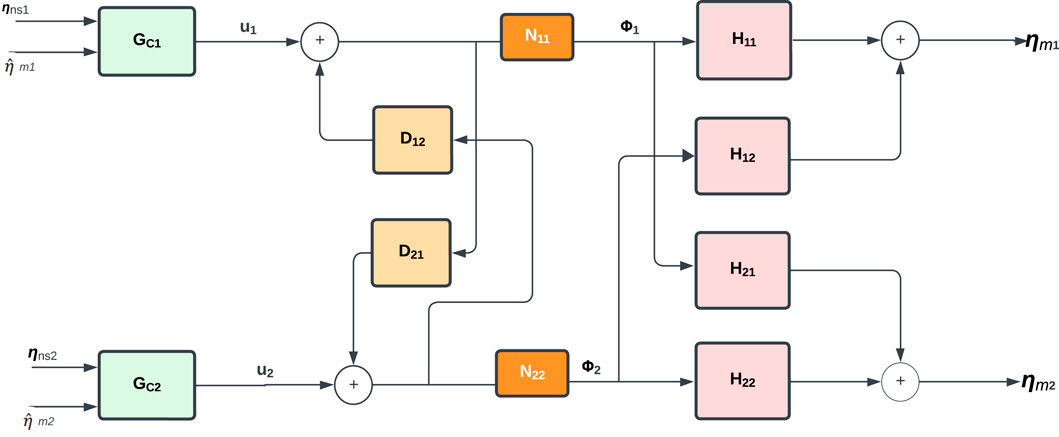
Figure 5. Diagram of the Decoupler component with N₁₁ and N₂₂ used in proposed control methodology 1.

In this case, the decoupler is expressed as:

$D_{12}=-\frac{H_{12}{N}_{22}}{H_{11}{N}_{11}}(14)$

$D_{21}=-\frac{H_{21}{N}_{11}}{H_{22}{N}_{22}}(15)$

where, N₁₁ and N₂₂ are added dynamics. Then, the apparent system takes the following form:

${\eta }_{m1}=H_{11}{N}_{11}{u}_1(16)$

${\eta }_{m2}=H_{22}{N}_{22}{u}_2(17)$

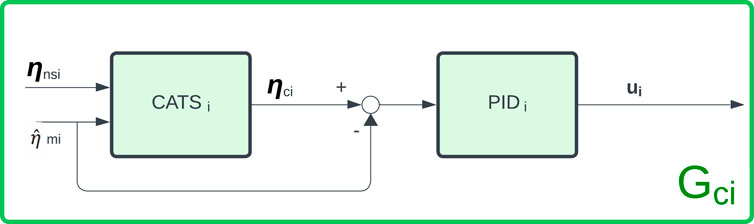
Once this decoupling is implemented it is possible to use any set of feedback/feedforward controllers (G_C1 and G_C2) for each actuator. Hence, it would be possible to use any other single-input single-output (SISO) controller. In this paper, we are proposing the use of the industry standard PID control for each hydraulic actuator, and a previously studied CATS compensator for each actuator.

2.3.2 Proportional–Integral–Derivative controller

The second component of the proposed methodology to solve the maRTHS is the design of a proportional–integral–derivative controller (PID) for the hydraulic actuators. Ogata (2010) defines PID as a conventional feedback control strategy that uses an error value as the difference between the desired value and the measured value. It applies a correction term based on proportional, integral, and derivative values based on the calculated error variable. The block diagram in Figure 6 shows how the PID controller receives the error variable as the difference between the compensated displacement command η_ci and the estimated measured displacement ${\widehat{\eta }}_{mi}$. Due to the decoupler component explained in the previous section, two PID controllers need to be designed for each hydraulic actuator with transfer functions, G₁₁ and G₂₂, formulated as:

$G_{11}=H_{11}{N}_{11}(18)$

$G_{22}=H_{22}{N}_{22}(19)$

where H₁₁ and H₂₂ are the diagonal elements of the transfer function matrix provided by the benchmark, and N₁₁ and N₂₂ are additional dynamics added to the decoupling, respectively.

Figure 6

Figure 6. Block diagram of G_ci composed of the CATS compensator and PID controller for i = 1, 2.

2.3.3 Conditional Adaptive Time Series compensation

The Adaptive Time Series (ATS) compensator was proposed by Chae et al. (2013) and showed that amplitude and time delay errors on the control command signal can be mitigated by using a compensated command displacement as shown in Eq. 20:

${\eta }_{ci}\left(k\right)={\displaystyle \sum _{j=0}^n}{\alpha }_j\frac{d^j{\eta }_{\mathit{nsi}}\left(k\right)}{d{t}^j}(20)$

where k is the time step, α_j for j = 0, 1, …, n are the adaptive compensation parameters, with n as the degree of the compensator, and $\frac{d^j{\eta }_{\mathit{nsi}}(k)}{d{t}^j}$ are time derivative obtained with finite difference method. Palacio-Betancur and Gutierrez Soto (2019) adopted and modified the ATS compensation to solve the benchmark control problem Silva et al. (2020) with a Conditional adaptation to improve tracking for high noise-to-signal ratio, dubbed CATS. The block diagram in Figure 6 shows the integration of the CATS compensator with the PID controller.

2.3.4 Tuning procedure for proposed methodology 1

The proposed methodology one consisted of Decoupling, CATS compensation, and PID control. Sensitivity analysis was conducted to determine the best parameters according to the performance criteria. The proposed methodology has three steps. The first step consisted of tuning the added dynamics of the decoupler (N₁₁, N₂₂). According to the number of poles and zeros of the plant in Eq. 5, if N₁₁ has a relative degree of one, and N₂₂ a relative degree of zero, the decoupler functions in Eqs 14, 15 will become proper with a relative degree of zero. For simplicity and practicality, N₁₁ is chosen with a stable single pole that works as a low-pass filter to avoid high-frequency signals in Φ₁, and N₂₂ as a unity gain. According to the sensitivity analysis, a low pass filter with a cut-off frequency around 20 Hz will not affect earthquake RTHS and will reduce high-frequency signals in inner-loops. Thus, the added dynamics are taken as:

$N_{11}=\frac{33}{s+22}(21)$

$N_{22}=1(22)$

where s is the operator variable in the frequency domain. Following this was step 2 which involved tuning two PID controllers, one PID controller for actuator one with transfer function shown in Eq. 18 and one PID controller for actuator two with transfer function shown in Eq. 19. The process began by using the MATLAB PID tuner application, which would provide the step response plot that can be altered by modifying the response time and transient behavior. Then, the best parameter was selected through an exhaustive search using a range near the values obtained with the tuner application.

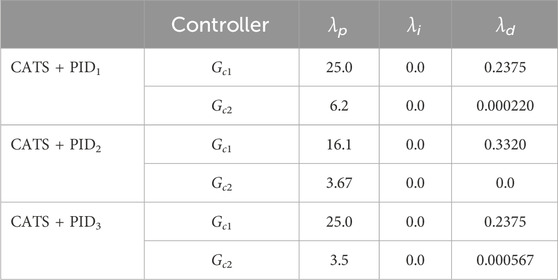
Through this process, it was noticeable that there was not one set of parameters that would generate the overall best performance. For this reason, three sets of controllers were chosen where the first focuses on best performance for actuator 1, the second focuses on best performance for actuator 2, and the third one with overall performance for both actuators. The PID gains for each controller are shown in Table 2, where λ_p, λ_i, and λ_d are the proportional, integral, and derivative gains, respectively.

Table 2

Table 2. Parameters for the decoupled PID controllers in proposed methodology 1

Finally, step three was the tuning of the CATS compensator. Since the maRTHS benchmark has similar system components (e.g., signals and sensors), a first-order CATS compensator with n = 1 is implemented. There were four main values that needed tuning to correct amplitude error and time delay. These include adaptive compensation parameters α₀ and α₁, forgetting factor for Recursive Least Squares (RLS) estimation ξ_RLS, and displacement threshold for conditional adaptation x_tr. The adaptive compensation parameters used for each actuator are shown in Table 3. In addition, x_tr = 0.05 mm, and ξ_RLS = 0.998. For more details about the structure and parameters of the CATS controller see Palacio-Betancur and Gutierrez Soto (2019). In total, the first proposed methodology considers Decoupling, CATS compensator, and PID controllers requiring the determination of 12 variables.

Table 3

Table 3. CATS compensator parameters.

2.4 Proposed methodology 2: CATS optimal control

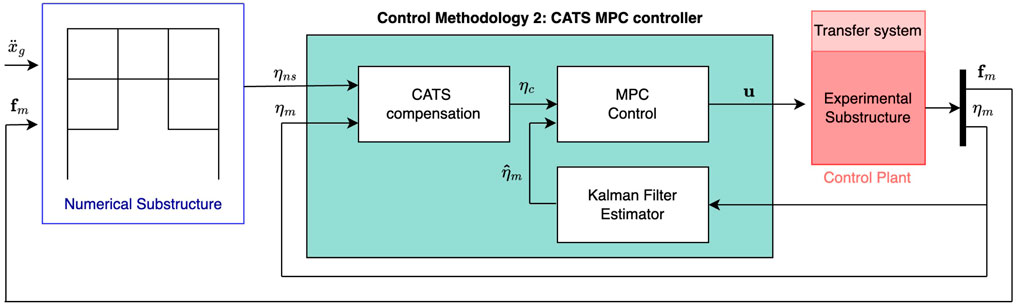
Optimal control methods show the advantages in controller performance, robustness, and flexibility (Stavroulakis et al., 2005). However, the complexity of such controllers’ design sacrifices the computational efficiency. The second proposed methodology combines a set of CATS compensators with two optimal control techniques, which are the LQG controller and the Model Predictive Control (MPC) controller.

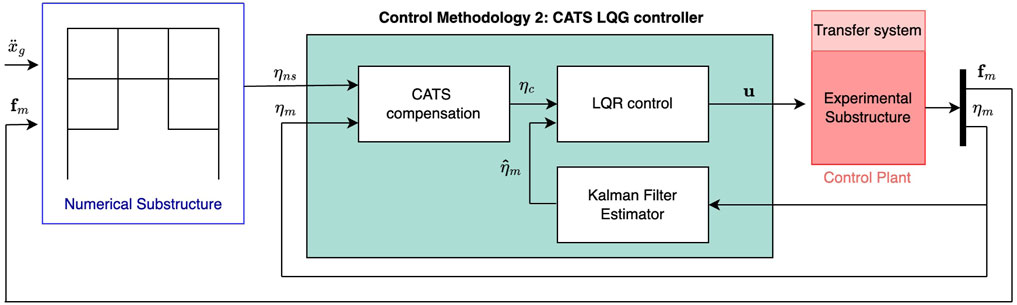
2.4.1 CATS compensator with Linear Quadratic Gaussian control design

The CATS compensator is applied to the baseline controller to reduce the time delays. Figure 7 shows the control framework of CATS + LQG method, which includes a set of the CATS compensators, the LQR controller, and the Kalman filter. The LQR controller design is identical to the baseline controller as discussed in the section 2.2. Kalman filter is used for full state estimation for LQR. The parameters of the CATS compensator are shown in Table Table 3.

Figure 7

Figure 7. Simplified block diagram of the proposed CATS-LQG controller.

2.4.2 CATS compensator with Model Predictive Control design

MPC is an optimization-based control approach that uses a model to dynamically determine the control input. The MPC approach has been effectively used for a variety of applications with promising results, including power systems in (Vazquez et al., 2016; 2014), autonomous vehicles in (Di Cairano et al., 2013; Liu et al., 2017), thermal systems in (Ma et al., 2012; Pangborn et al., 2020), and manufacturing systems in (Balta et al., 2021; Anbarani et al., 2023). MPC has also been used in real-time hybrid simulation. Tsokanas et al. (2022) studied RTHS of a motorcycle by integrating Kalman filtering, MPC and auto-regressive exogenous polynomial algorithm for real-time model identification. Zeng et al. (2023) combined MPC and polynomial-based forward reference for solving the prior virtual RTHS benchmark control problem. One of the advantages of the MPC is its ability to control MIMO systems, which takes into account all the interactions between system input and output variables. MPC can also handle constraints. MPC uses a dynamic model to predict the system behavior over a finite time window, the prediction horizon. Based on these predictions and measured or estimated system states, an optimization program with a defined control cost function and systems constraints is formulated to compute the control inputs for the future finite time steps, which is also known as the control horizon. Only the current control input is implemented.

Figure 8 shows the control framework of CATS-MPC method, which includes a set of the CATS compensators, the MPC controller, and the Kalman filter.

Figure 8

Figure 8. Simplified block diagram of the proposed CATS MPC controller.

CATS + MPC uses the discretized nominal state space model of the system based on the transfer function of Eq. 5. The discrete state space form of the system model can be represented as:

$\mathbf{z}(k+\mathrm{1})=\mathbf{A}\cdot \mathbf{z}(\mathrm{k})+\mathbf{B}\cdot \mathbf{u}(\mathrm{k})(23)$

${\mathit{\eta }}_{\mathrm{m}}(\mathrm{k})=\mathbf{C}\cdot \mathbf{z}(\mathrm{k})+\mathbf{D}\cdot \mathbf{u}(\mathrm{k})(24)$

where A, B, C, and D are the discrete state space matrices; u(k) is the input vector to the system at the time step of k; z(k) is the states of the control plant; and η_m(k) is the output vector. The main control objective of the CATS-MPC is to minimize the error between measured and desired output. Within each prediction horizon, an optimization problem is formulated as

$\begin{array}{cc}\hfill \underset{\mathrm{u}}{\min }& {\displaystyle \sum _{k=1}^{N_p}}{\left({\mathit{\eta }}_{\mathrm{c}}\left(k\right)-{\mathit{\eta }}_{\mathrm{m}}\left(k\right)\right)}^T\mathbf{Q}\left({\mathit{\eta }}_{\mathrm{c}}\left(k\right)-{\mathit{\eta }}_{\mathrm{m}}\left(k\right)\right)\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& \mathbf{z}(\mathrm{k}+\mathrm{1})=\mathbf{A}\cdot \mathbf{z}(\mathrm{k})+\mathbf{B}\cdot \mathbf{u}(\mathrm{k})\hfill \\ \hfill & {\mathit{\eta }}_{\mathrm{m}}(\mathrm{k})=\mathbf{C}\cdot \mathbf{z}(\mathrm{k})+\mathbf{D}\cdot \mathbf{u}(\mathrm{k})\hfill \\ \hfill & {\mathbf{u}}_{\min }\le \mathbf{u}\left(k\right)\le {\mathbf{u}}_{\max },k=1,\dots ,N_p\hfill \end{array}(25)$

where Q is a tuning parameter penalizing the error between desired and predicated system output; η_c(k) is the reference output at time step k; η_m(k) is the predicted output at time step k; u_min, u_max are the minimum and maximum values of the control input for the plant. The optimal control input sequence within the prediction horizon of N_p is calculated by solving the optimization problem of Eq. 25. To initialize the MPC, full state information of the system is required. In maRTHS experiments, only output vector η_m can be measured, while the states z are not available. Therefore, a Kalman Filter is used to estimate the states $\widehat{\mathbf{z}}$.

CATS-MPC was implemented using the MATLAB Model Predictive Control Toolbox. Each control interval is obtained with a sampling frequency of 1,024 Hz. The prediction horizon and control horizon are eight and one respectively. The parameters of the CATS compensator are shown in Table 3.

3 Results

The proposed methods are evaluated using performance criteria corresponding to tracking control performance, estimation performance, and overall global RTHS performance and it is described in Table 1 per Condori Uribe et al. (2023). A total of six controllers, explained in Section 2, were designed. These include the baseline controller (LQG), the baseline controller with time-delay compensation (CATS + LQG), three Decoupled PID controllers with time-delay compensation (CATS + PID₁, CATS + PID₂, CATS + PID₃), and optimal control with time-delay compensation (CATS + MPC). Table 4 shows the performance criteria for all the proposed methodologies. The lower the values of J, the better the performance. It is important to note that the best performance per criterion was not uniform. The bold values show the best results per criterion when compared with other values.

Table 4

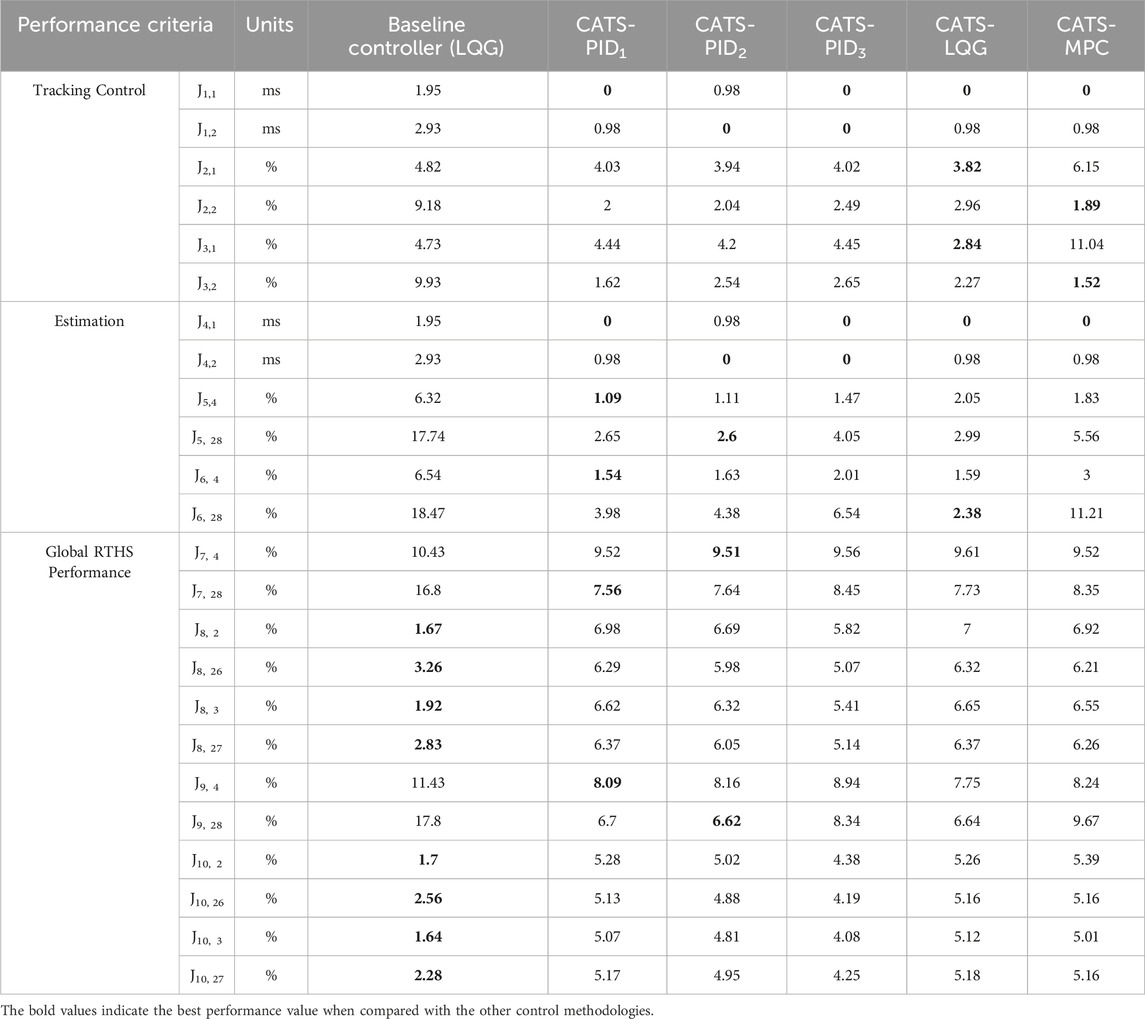
Table 4. Performance criteria of the proposed control methodologies for maRTHS subjected to 0.3 scaled El Centro Earthquake.

All the controllers that used the CATS compensator were able to reduce time delay on both actuators (J₁), however, only CATS + PID₂ and CATS + PID₃ reached zero time delay on actuator 2. Regarding the remaining tracking control criteria, all the proposed controllers reduced the average error (J₂) and peak errors (J₃) compared to the baseline controller. For actuator 2, it went from 9.18% to values around 2%, with the MPC performing the best. For actuator 1, the errors reduced from 4.82% to values around 4% with the exception of the MPC that increased above 6%. This shows that the proposed methodologies have good tracking performance overall, with actuator 2 outperforming actuator 1. Furthermore, the performance criteria for estimation shows that the implementation of time-delay compensation and good feedback control reduced all the errors below 3%, with CATS + PID₁ with the slightly better performance than other controllers. Lastly, the global RTHS performance values shows that the proposed methodologies reduce errors for the response of the interaction node in displacement and rotation (J₇, J₉) compared to LQG, due to the improved tracking performance of the controllers. However, the response on the second and third floor are increased compared to the LQG controller because it seems that the implementation of feed-forward control is creating an overshoot in response on the first story that is exciting the remaining stories of the building in the numerical substructure. More details of these results can be observed in Figures 9–12.

Figure 9

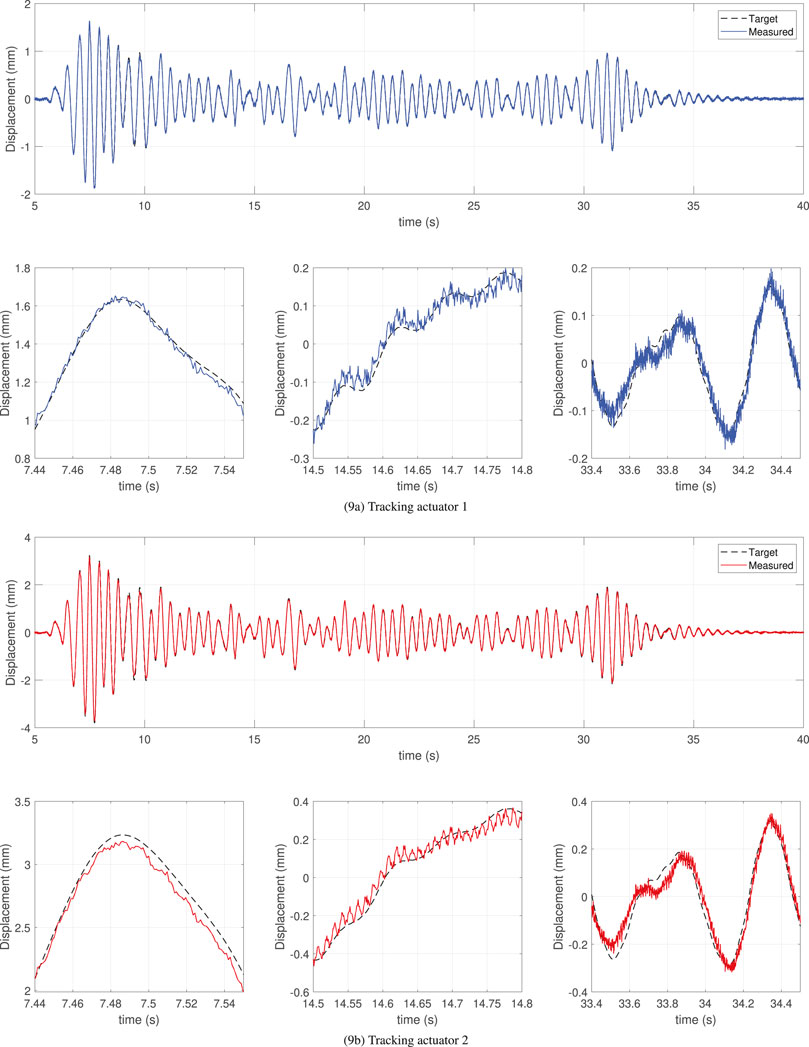
Figure 9. maRTHS tracking performance in actuator coordinates using CATS + LQG controller subjected to 0.3 scaled El Centro earthquake.

Figure 10

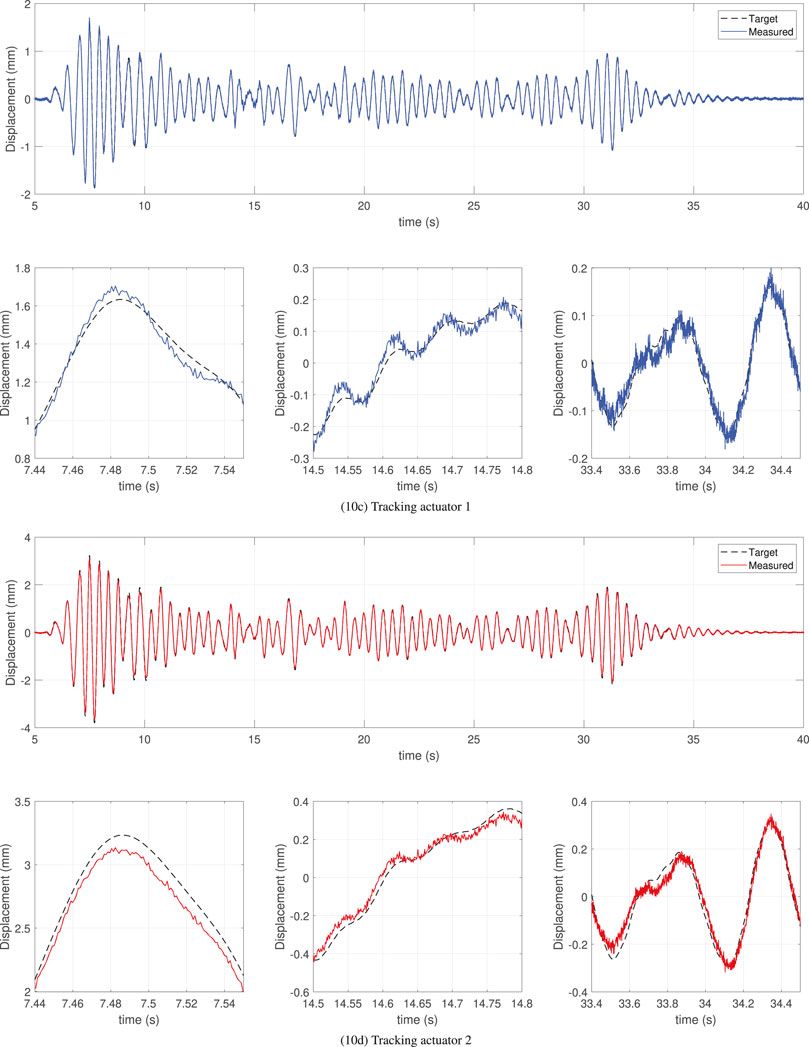
Figure 10. maRTHS tracking performance in actuator coordinates using CATS + PID₃ controller subjected to 0.3 scaled El Centro earthquake.

Figure 11

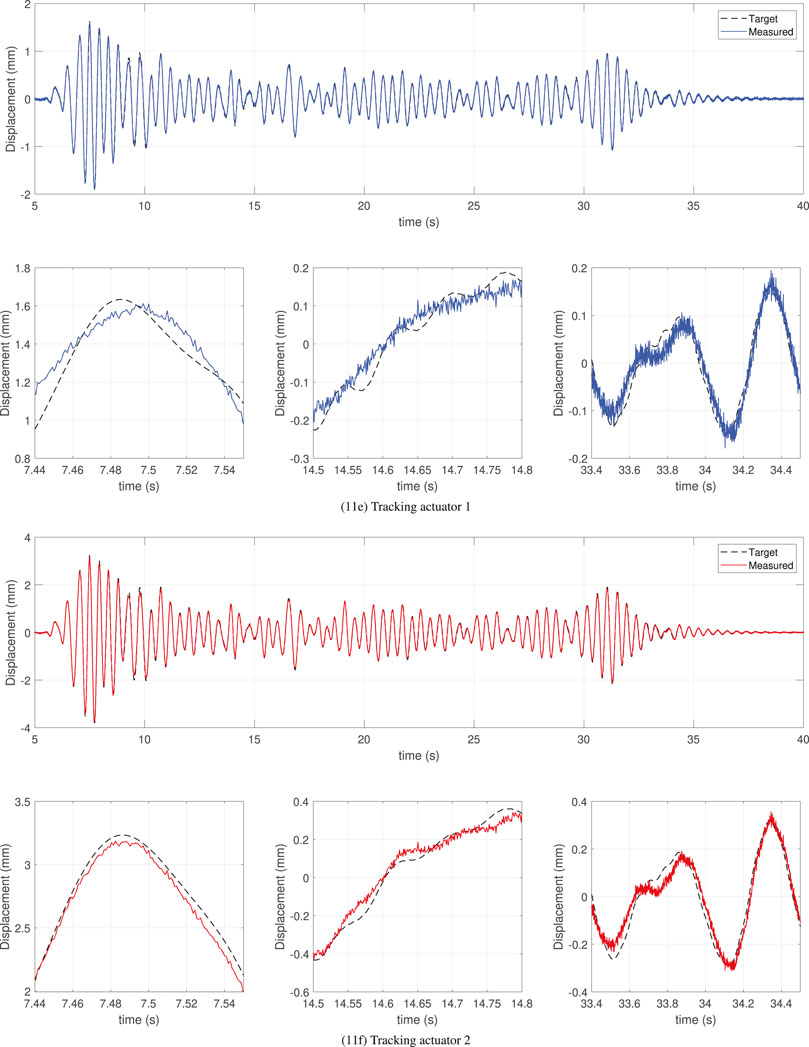
Figure 11. maRTHS tracking performance in actuator coordinates using CATS + MPC controller subjected to 0.3 scaled El Centro earthquake.

Figure 12

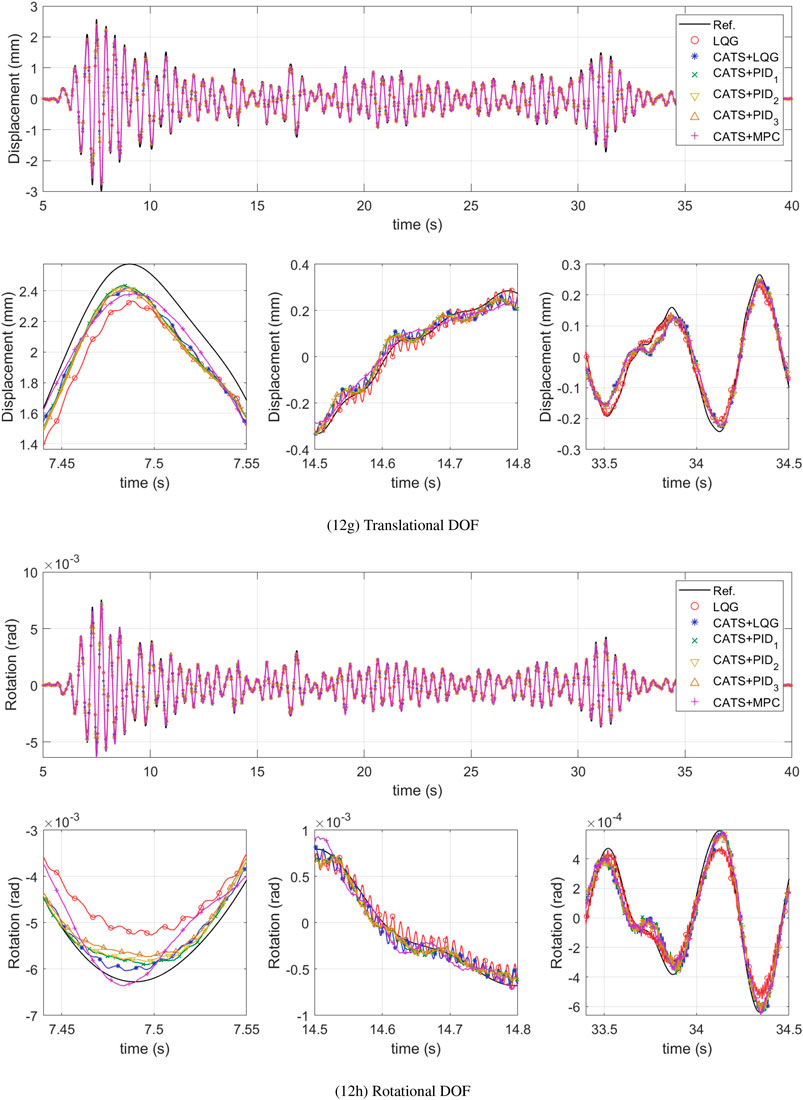
Figure 12. maRTHS global performance at interface node in frame coordinates subjected to 0.3 scaled El Centro earthquake.

Figure 9 shows the time history response of the target displacement (η_ns), and measured displacement (η_m), for each actuator during 0.3 scaled El Centro earthquake using the CATS + LQG response. The bottom figures show the detailed response at a high amplitude, at low amplitude at the middle of the response, and at low amplitudes at the end of the response. Overall, this controller performs well because it closely follows the general tendency of the target displacements for both actuators; however, it contains undesired oscillations generated by sensor noise. These oscillations were also obtained with the LQG controller, which reduces accuracy for both approaches. Similarly, Figure 10 shows the response using CATS + PID₃. The first difference, compared to CATS + LQG, is the increased robustness to disturbances because there are fewer undesired oscillations. The response of CATS + PID₁ and CATS + PID₂ had a similar tendency but CATS + PID₃ outperforms in the global RTHS performance criteria. Note that the measured displacement is closely following the target displacements at low amplitudes but at higher amplitudes, there are noticeable differences. Additionally, actuator 1 has overshoot and undershoot behavior in some instances of the response. For this reason, tracking performance criteria of actuator one are almost double that in actuator two for all CATS + PID controllers.

Figure 11 show the time-history response using the CATS + MPC controller. This approach also demonstrates more robust performance in response to disturbances, as evidenced by less variation in the measured values. The MPC controller, although based on a nominal systems model, effectively mitigates the impact of parametric uncertainties on signal-tracking performance. Instead of using a fixed gain that is calculated offline, the MPC recedingly calculates the control input by solving the optimization problem over the prediction horizon. Similar to the tendencies of the CATS + PID controllers, the CATS + MPC controller has lower tracking performance in actuator one than in actuator two. However, instead of overshoot/undershoots in the measured response of actuator 1, it generates a smoother response that follows the general behavior of the target displacement. This shows why the tracking evaluation criteria of actuator one is almost three times in average response (J₂), and seven times the peak response (J₃), compared with actuator 2.

Finally, Figure 12 shows the time-history global response at the interface node between substructures in frame coordinates, with all the proposed controllers. These figures compare the response of the reference structure without partition with the estimated displacements and rotations during the maRTHS simulation. First note that the LQG and CATS + LQG have the previously mentioned undesired oscillations that are reducing tracking accuracy. This shows why the highest global performance errors at the interface node are generated by LQG. Regardless, the LQG can produce the best global performance criteria on the second and third floor. The proposed CATS + PID controllers have a similar behavior but CATS + PID₃ generated the best global performance between the three. Lastly, the CATS + MPC controller generates a smoother response overall.

Further analysis was conducted using the near-field Kobe earthquake considering the same proposed controllers tuned for the El Centro earthquake. The figures and comparative table are located as Supplementary Material for this paper demonstrating the capability of the proposed control strategies as similar performances to those presented here are observed.

4 Conclusion

Evaluating the structural integrity of different critical infrastructure systems under varying conditions is important to ensure the safety of the structure during extreme events. Benchmark control problem that allows for a virtual Multi-axial Real-time Hybrid simulation allows for simulation testing of large-scale structures in a simulation environment that uses experimental and simulation data. However, it is important to accurately track the difference between the numerical and experimental substructures created by the transfer system. In this paper, two different adaptive control approaches were proposed for the tracking problem in a benchmark example: (1) a Conditional Adaptive Time Series proportional-integral-derivative controller with dynamic decoupling (CATS + PID) and (2) a Conditional Adaptive Time Series optimal controllers (CATS + LQG and CATS + MPC). The results showed that the proposed methods improve different performance criteria for the benchmark control problem. The implementation of time delay compensation improved displacement tracking overall, reaching a time delay of zero or almost zero on one or both actuators. In addition, the CATS + PID and CATS + MPC controllers provided robustness to disturbances to mitigate undesired oscillations. However, the control of actuator one showed to be more challenging than actuator 2. Despite the identical characteristics of the actuation system, the coupling of both actuators with the coupling element and the interaction with the experimental substructure, yield different dynamics for each actuator. According to the amplitude response at low frequencies, actuator 1 has lower responses than actuator 2, which may be the reason for lower performance regardless of the control implementation.

Future work will focus on improving the proposed control strategies, robustness studies considering near-field and far-field earthquakes, and testing them on other types of benchmark studies. Specifically, evaluating whether the proposed control strategies will apply to other civil structures under different extreme conditions. For example, RTHS for floating offshore wind turbines in Sun et al. (2022) and hydrodynamic RTHS for cascading earthquake-tsunami hazard scenarios in Neumann et al. (2023). Future RTHS problems could consider thermomechanical challenges as studied by Montoya et al. (2023) for extraterrestrial habitats. The effects of varying system properties and control tuning parameters on the system performance will be important for different applications and will be studied via simulation and physical case studies. Recent methodologies inspired by machine learning such as deep learning by Canchila et al. (2024) could have critic-actor feedback strategy to determine the control parameters for the methodologies presented. Therefore, it will be important to develop a methodology for identifying the tuning weights for testing different structures and events. In terms of estimation methods to consider in future studies, a nonlinear Bayesian filtering system identification considering unscented Kalman filter, the ensemble Kalman filter, and the particle filters as presented in Erazo et al. (2024).

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://mechs.designsafe-ci.org/resources/projects-data-benchmarks/.

Author contributions

AA: Formal Analysis, Investigation, Software, Visualization, Writing–original draft. HL: Conceptualization, Formal Analysis, Methodology, Software, Writing–original draft. AP-B: Conceptualization, Data curation, Formal Analysis, Methodology, Software, Validation, Visualization, Writing–original draft. KA: Validation, Visualization, Writing–original draft, Writing–review and editing. IK: Funding acquisition, Supervision, Writing–review and editing. MGS: Conceptualization, Funding acquisition, Investigation, Project administration, Resources, Software, Supervision, Visualization, Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The author KA was employed by Schnabel Engineering, Inc.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author MGS declares that she was an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbuil.2024.1384235/full#supplementary-material

References

Agrawal, A., Tan, P., Nagarajaiah, S., and Zhang, J. (2009). Benchmark structural control problem for a seismically excited highway bridge-part i: phase i problem definition. Struct. Control Health Monit. Official J. Int. Assoc. Struct. Control Monit. Eur. Assoc. Control Struct. 16, 509–529. doi:10.1002/stc.301

CrossRef Full Text | Google Scholar

Anbarani, M. T., Balta, E. C., Meira-Góes, R., and Kovalenko, I. (2023). “Risk-averse model predictive control for priced timed automata,” in 2023 American Control Conference (ACC), San Diego, California, 31- June 2 2023 (IEEE), 4332–4338.

CrossRef Full Text | Google Scholar

Balta, E. C., Kovalenko, I., Spiegel, I. A., Tilbury, D. M., and Barton, K. (2021). Model predictive control of priced timed automata encoded with first-order logic. IEEE Trans. Control Syst. Technol. 30, 352–359. doi:10.1109/tcst.2021.3054800

CrossRef Full Text | Google Scholar

Canchila, C., Zhou, S., and Song, W. (2024). Hyperparameter optimization and importance ranking in deep learning–based crack segmentation. J. Comput. Civ. Eng. 38, 04023042. doi:10.1061/jccee5.cpeng-5512

CrossRef Full Text | Google Scholar

Castaneda, N., Gao, X., and Dyke, S. J. (2015). Computational tool for real-time hybrid simulation of seismically excited steel frame structures. J. Comput. Civ. Eng. 29, 04014049. doi:10.1061/(asce)cp.1943-5487.0000341

CrossRef Full Text | Google Scholar

Chae, Y., Kazemibidokhti, K., and Ricles, J. M. (2013). Adaptive time series compensator for delay compensation of servo-hydraulic actuator systems for real-time hybrid simulation. Earthq. Eng. Struct. Dyn. 42, 1697–1715. doi:10.1002/eqe.2294

CrossRef Full Text | Google Scholar

Chen, P.-C., and Chen, P.-C. (2023). Real-time hybrid simulation for seismic control performance evaluation of an active inerter damper system. Eng. Struct. 294, 116760. doi:10.1016/j.engstruct.2023.116760

CrossRef Full Text | Google Scholar

Condori Uribe, J., Salmeron, M., Patino, E., Montoya, H., Dyke, S. J., Silva, C., et al. (2023). Experimental benchmark control problem for multi-axial real-time hybrid simulation. Front. Built Environ. 9, 1270996. doi:10.3389/fbuil.2023.1270996

CrossRef Full Text | Google Scholar

Covarrubias Vargas, B. A., Harvey Jr, P. S., Cao, L., Ricles, J. M., Al-Subaihawi, S., and Villalobos Vega, E. (2022). Characterization and real-time hybrid simulation testing of rolling pendulum isolation bearings with different surface treatments. Earthq. Eng. Struct. Dyn. 51, 2668–2689. doi:10.1002/eqe.3694

CrossRef Full Text | Google Scholar

Di Cairano, S., Bernardini, D., Bemporad, A., and Kolmanovsky, I. V. (2013). Stochastic mpc with learning for driver-predictive vehicle control and its application to hev energy management. IEEE Trans. Control Syst. Technol. 22, 1018–1031. doi:10.1109/tcst.2013.2272179

CrossRef Full Text | Google Scholar

Dyke, S. J., Caicedo, J. M., Turan, G., Bergman, L. A., and Hague, S. (2003). Phase i benchmark control problem for seismic response of cable-stayed bridges. J. Struct. Eng. 129, 857–872. doi:10.1061/(asce)0733-9445(2003)129:7(857)

CrossRef Full Text | Google Scholar

Dyke, S. J., Spencer, B. F., Quast, P., and Sain, M. K. (1995). Role of control-structure interaction in protective system design. J. Eng. Mech. 121, 322–338. doi:10.1061/(ASCE)0733-9399(1995)121:2(322)

CrossRef Full Text | Google Scholar

Erazo, K., Di Matteo, A., and Spanos, P. (2024). Parameter estimation of stochastic fractional dynamic systems using nonlinear bayesian filtering system identification methods. J. Eng. Mech. 150, 04023117. doi:10.1061/jenmdt.emeng-7482

CrossRef Full Text | Google Scholar

Fermandois, G. A. (2019). Application of model-based compensation methods to real-time hybrid simulation benchmark. Mech. Syst. Signal Process. 131, 394–416. doi:10.1016/j.ymssp.2019.05.041

CrossRef Full Text | Google Scholar

Fermandois, G. A., and Spencer, B. F. (2017). Model-based framework for multi-axial real-time hybrid simulation testing. Earthq. Eng. Eng. Vib. 16, 671–691. doi:10.1007/s11803-017-0407-8

CrossRef Full Text | Google Scholar

Friedman, A., Dyke, S. J., Phillips, B., Ahn, R., Dong, B., Chae, Y., et al. (2015). Large-scale real-time hybrid simulation for evaluation of advanced damping system performance. J. Struct. Eng. 141, 04014150. doi:10.1061/(asce)st.1943-541x.0001093

CrossRef Full Text | Google Scholar

Garrido, J., Vázquez, F., Morilla, F., and Hägglund, T. (2011). Practical advantages of inverted decoupling. Proc. Institution Mech. Eng. Part I J. Syst. Control Eng. 225, 977–992. doi:10.1177/2041304110394556

CrossRef Full Text | Google Scholar

Gutierrez Soto, M., and Adeli, H. (2017). Many-objective control optimization of high-rise building structures using replicator dynamics and neural dynamics model. Struct. Multidiscip. Optim. 56, 1521–1537. doi:10.1007/s00158-017-1835-9

CrossRef Full Text | Google Scholar

Javadinasab Hormozabad, S., and Gutierrez Soto, M. (2021). Load balancing and neural dynamic model to optimize replicator dynamics controllers for vibration reduction of highway bridge structures. Eng. Appl. Artif. Intell. 99, 104138. doi:10.1016/j.engappai.2020.104138

CrossRef Full Text | Google Scholar

Liu, C., Lee, S., Varnhagen, S., and Tseng, H. E. (2017). “Path planning for autonomous vehicles using model predictive control,” in 2017 IEEE Intelligent Vehicles Symposium (IV) (IEEE), Los Angeles, California, USA, 11-14 June 2017, 174–179.

CrossRef Full Text | Google Scholar

Liu, L., Tian, S., Xue, D., Zhang, T., Chen, Y., and Zhang, S. (2019). A review of industrial mimo decoupling control. Int. J. Control, Automation Syst. 17, 1246–1254. doi:10.1007/s12555-018-0367-4

CrossRef Full Text | Google Scholar

Ma, Y., Borrelli, F., Hencey, B., Coffey, B., Bengea, S., and Haves, P. (2012). Model predictive control for the operation of building cooling systems. IEEE Trans. control Syst. Technol. 20 (3), 796–803. doi:10.1109/TCST.2011.2124461

CrossRef Full Text | Google Scholar

Mojiri, S., Mortazavi, P., Kwon, O.-S., and Christopoulos, C. (2021). Seismic response evaluation of a five-story buckling-restrained braced frame using multi-element pseudo-dynamic hybrid simulations. Earthq. Eng. Struct. Dyn. 50, 3243–3265. doi:10.1002/eqe.3508

CrossRef Full Text | Google Scholar

Montoya, H., Dyke, S. J., Silva, C. E., Maghareh, A., Park, J., and Ziviani, D. (2023). Thermomechanical real-time hybrid simulation: conceptual framework and control requirements. AIAA J. 61, 2627–2639. doi:10.2514/1.j062857

CrossRef Full Text | Google Scholar

Mortazavi, P., Kwon, O.-S., and Christopoulos, C. (2022a). Four-element pseudodynamic hybrid simulation of a steel frame with cast steel yielding connectors under earthquake excitations. J. Struct. Eng. 148, 04021255. doi:10.1061/(asce)st.1943-541x.0003232

CrossRef Full Text | Google Scholar

Mortazavi, P., Mojiri, S., Kwon, O.-S., and Christopoulos, C. (2022b). Multielement hybrid simulations for performance assessment of multistory special concentrically braced frames. J. Struct. Eng. 148, 04022130. doi:10.1061/(asce)st.1943-541x.0003439

CrossRef Full Text | Google Scholar

Najafi, A., Fermandois, G. A., and Spencer Jr, B. F. (2020). Decoupled model-based real-time hybrid simulation with multi-axial load and boundary condition boxes. Eng. Struct. 219, 110868. doi:10.1016/j.engstruct.2020.110868

CrossRef Full Text | Google Scholar

Nakata, N., Dyke, S. J., Zhang, J., Mosqueda, G., Shao, X., Mahmoud, H., et al. (2014). Hybrid simulation primer and dictionary. Network for earthquake engineering simulation, NEES.

Google Scholar

Narasimhan, S., Nagarajaiah, S., Johnson, E. A., and Gavin, H. P. (2006). Smart base-isolated benchmark building. part i: problem definition. Struct. Control Health Monit. Official J. Int. Assoc. Struct. Control Monit. Eur. Assoc. Control Struct. 13, 573–588. doi:10.1002/stc.99

CrossRef Full Text | Google Scholar

Neumann, C., Simpson, B., Schellenberg, A., Lomonaco, P., and You, S. (2023). Hydrodynamic real-time hybrid simulation demonstrated for cascading seismic and tsunami events. J. Waterw. Port, Coast. Ocean Eng. 149, 04022029. doi:10.1061/(asce)ww.1943-5460.0000733

CrossRef Full Text | Google Scholar

Ogata, K. (2010). Modern control engineering. United Kingdom: Prentice Hall.

Google Scholar

Palacio-Betancur, A., and Gutierrez Soto, M. (2019). Adaptive tracking control for real-time hybrid simulation of structures subjected to seismic loading. Mech. Syst. Signal Process. 134, 106345. doi:10.1016/j.ymssp.2019.106345

CrossRef Full Text | Google Scholar

Palacio-Betancur, A., and Gutierrez Soto, M. (2023). Recent advances in computational methodologies for real-time hybrid simulation of engineering structures. Archives Comput. Methods Eng. 30, 1637–1662. doi:10.1007/s11831-022-09848-y

CrossRef Full Text | Google Scholar

Pangborn, H. C., Laird, C. E., and Alleyne, A. G. (2020). “Hierarchical hybrid mpc for management of distributed phase change thermal energy storage,” in 2020 American Control Conference (ACC) (IEEE), Denver, CO, USA, July 1-3, 2020, 4147–4153.

CrossRef Full Text | Google Scholar

Phillips, B. M., and Spencer, B. F. (2013). Model-based multiactuator control for real-time hybrid simulation. J. Eng. Mech. 139, 219–228. doi:10.1061/(ASCE)EM.1943-7889.0000493

CrossRef Full Text | Google Scholar

Silva, C. E., Gomez, D., Maghareh, A., Dyke, S. J., and Spencer Jr, B. F. (2020). Benchmark control problem for real-time hybrid simulation. Mech. Syst. Signal Process. 135, 106381. doi:10.1016/j.ymssp.2019.106381

CrossRef Full Text | Google Scholar

Spencer, B. F., Christenson, R. E., and Dyke, S. J. (1998). “Next generation benchmark control problem for seismically excited buildings,” in Proceedings of the second world conference on structural control (Kyoto Japan), vol. 2, Kyoto, Japan, June 28 to July 2, 1998, 1135–1360.

Google Scholar

Stavroulakis, G. E., Foutsitzi, G., Hadjigeorgiou, E., Marinova, D., and Baniotopoulos, C. (2005). Design and robust optimal control of smart beams with application on vibrations suppression. Adv. Eng. Softw. 36, 806–813. doi:10.1016/j.advengsoft.2005.03.024

CrossRef Full Text | Google Scholar

Sun, C., Song, W., and Jahangiri, V. (2022). A real-time hybrid simulation framework for floating offshore wind turbines. Ocean. Eng. 265, 112529. doi:10.1016/j.oceaneng.2022.112529

CrossRef Full Text | Google Scholar

Tsokanas, N., Pastorino, R., and Stojadinović, B. (2022). Adaptive model predictive control for actuation dynamics compensation in real-time hybrid simulation. Mech. Mach. Theory 172, 104817. doi:10.1016/j.mechmachtheory.2022.104817

CrossRef Full Text | Google Scholar

Vazquez, S., Leon, J. I., Franquelo, L. G., Rodriguez, J., Young, H. A., Marquez, A., et al. (2014). Model predictive control: a review of its applications in power electronics. IEEE Ind. Electron. Mag. 8, 16–31. doi:10.1109/mie.2013.2290138

CrossRef Full Text | Google Scholar

Vazquez, S., Rodriguez, J., Rivera, M., Franquelo, L. G., and Norambuena, M. (2016). Model predictive control for power converters and drives: advances and trends. IEEE Trans. Industrial Electron. 64, 935–947. doi:10.1109/tie.2016.2625238

CrossRef Full Text | Google Scholar

Wade, H. L. (1997). Inverted decoupling: a neglected technique. ISA Trans. 36, 3–10. doi:10.1016/s0019-0578(97)00008-6

CrossRef Full Text | Google Scholar

Yang, J. N., Agrawal, A. K., Samali, B., and Wu, J.-C. (2004). Benchmark problem for response control of wind-excited tall buildings. J. Eng. Mech. 130, 437–446. doi:10.1061/(asce)0733-9399(2004)130:4(437)

CrossRef Full Text | Google Scholar

Yuan, Y., Wei, W., Igarashi, A., Tan, P., Iemura, H., and Zhu, H. (2017). Experimental and analytical studies of seismic response of highway bridges isolated by rate-dependent rubber bearings. Eng. Struct. 150, 288–299. doi:10.1016/j.engstruct.2017.06.020

CrossRef Full Text | Google Scholar

Zambrano, A., Palacio-Betancur, A., Burbano, L., Niño, A. F., Giraldo, L. F., Gutierrez Soto, M., et al. (2021). “You make me tremble: a first look at attacks against structural control systems,” in Proceedings of the 2021 ACM SIGSAC Conference on Computer and Communications Security, Republic of Korea, November 15-19, 2021, 1320–1337.

CrossRef Full Text | Google Scholar

Zeng, C., Guo, W., and Shao, P. (2023). Performance study of model predictive control with reference prediction for real-time hybrid simulation. J. Vib. Control 30 (7–8), 1659–1673. doi:10.1177/10775463231167251

CrossRef Full Text | Google Scholar