Avni Jain
Andrei V. Metrikine- Faculty of Civil Engineering and Geosciences, Delft University of Technology, Delft, Netherlands
Railway transition zones present a major challenge in railway track design mainly due to abrupt jumps in stiffness and differential settlements that result from crossing stiffer structures such as bridges or culverts. Despite numerous efforts to mitigate these transition effects at both the superstructure and substructure levels, a comprehensive solution remains elusive. Substructure-level interventions have demonstrated some effectiveness but are often cost-prohibitive and challenging to implement in existing operational railway transition zones. In contrast, mitigation measures at the superstructure (rail, sleepers, rail-pads, under-sleeper pads) level can be easily installed but have shown limited improvement in site measurements. This study evaluates the influence of different sleeper configurations in transition zones and reduced sleeper spacings on the operation-driven dynamic amplifications in railway transition zones, employing a recently proposed criterion based on the total strain energy in the track-bed layers (ballast, embankment, and subgrade). In addition to this, the influence of the loss of contact between sleepers and ballast (i.e., hanging sleepers), which typically results from the differential settlement, is studied. The first part of the paper provides useful insights regarding the interventions (and/or initial design) in the sleeper configuration and spacing, whereas the second part of the work highlights the need for interventions to deal with the loss of contact between sleeper and ballast. A 2-dimensional finite element model of an embankment-bridge transition was used for the analysis. The results show that it is not possible to mitigate the transition effects completely using the interventions involving sleeper spacing and configuration.
1 Introduction
Railway transition zones (RTZs) are regions of inhomogeneity in railway tracks where the track crosses stiffer structures, such as bridges or culverts. This inhomogeneity (Jain et al., 2023a) results in an abrupt jump in stiffness experienced by the moving load, causing significant dynamic amplification (Ognibene et al., 2019; Paixão et al., 2021; Charoenwong et al., 2023) and eventually contributing to differential settlement in RTZs. In addition to this, the differential settlement in transition zones is also due to differences in autonomous settlement of the foundations of the stiff and soft parts. Operation-driven dynamic amplifications in RTZs are the subject of this paper. These dynamic amplifications may not be very prominent when considering kinematics but can be clearly seen in terms of the strain energy of the trackbed layers (Jain et al., 2024a). Despite numerous attempts to alleviate these transition effects by gradually increasing stiffness at both the superstructure (rail, rail pads, sleepers, under-sleeper pads) and substructure levels (ballast, sub-ballast, embankment, subgrade), a comprehensive solution remains elusive.
Mitigation measures at the substructure level, including approach slabs (Laco and Borzovič, 2016; Varandas et al., 2016; Heydari-Noghabi et al., 2017a), transition wedges (Paixão et al., 2013; Paixão et al., 2014; Paixão et al., 2015; Ribeiro et al., 2017; Palomo et al., 2021), glued ballast, geotechnical improvements (Hu et al., 2019; Chumyen et al., 2022), etc., have demonstrated some effectiveness; however, their cost-effectiveness ratio is unfavourable. Additionally, these measures are difficult to implement in existing, operational railway transition zones. In contrast, mitigation measures at the superstructure level (Heydari-Noghabi et al., 2017a; Heydari-Noghabi et al., 2017b; Chumyen et al., 2022; Fărăgău et al., 2023) can be easily installed for both old and new transition zones. Although the existing literature involving analytical/numerical evaluations suggests that these measures may be efficient to some extent (Namura and Suzuki, 2007; Jain et al., 2023b), site measurements have not exhibited significant improvements from these interventions (Sañudo et al., 2016; Indraratna et al., 2019).
Common superstructure-level interventions include auxiliary rails (Heydari-Noghabi et al., 2017b; Chumyen et al., 2022; Fărăgău et al., 2023), under-sleeper pads, and large (Shahraki et al., 2015; Shahraki and Witt, 2015; Wilk et al., 2015) or closely spaced sleepers (National Academies of Sciences, Engineering, and Medicine, 2006; Galván Giménez, 2011; Sañudo et al., 2016; Indraratna et al., 2019) made from modified materials (Transit Cooperative Research Program, 2006; Raj et al., 2023). Sleepers are typically constructed from wood or reinforced concrete, with the latter requiring a C50/60 strength class as defined by the Eurocode, which specifies the Elastic modulus of 38 GPa and a Poisson’s ratio of 0.2 (EN 1992-1-1, 2009). Alternative materials, such as plastic, rubber, and composites, have also been utilized in transition zones, with wood proving to be the most effective among them (Nicks, 2009). The average sleeper dimensions are 2.6 m × 0.24 m x 0.24 m, and a standard spacing of 0.6 m (Sañudo Ortega et al., 2021; Sañudo et al., 2022) is commonly employed in railway tracks, including in transition zones. Large (Namura et al., 2004; Shahraki et al., 2015; Shahraki and Witt, 2015) or closely spaced sleepers (Galván Giménez, 2011; Sañudo et al., 2016; Indraratna et al., 2019) have been implemented in transition areas to reduce the abrupt change in track stiffness. These modifications have been effective in decreasing ballast settlement and improving the distribution of the contact force between sleeper and ballast over a larger area, but they have not reduced dynamic load amplification in transition zones. Various sleeper configurations have been analyzed (Sañudo et al., 2017) to evaluate track support separation and to maintain optimal track performance, as assessed by sleeper vertical displacements and stress on ballast. Efforts have also been made to minimize the maximum wheel-rail contact force and stress between the sleeper and foundation, seeking the most efficient distributions of sleeper spacing (Sañudo et al., 2017) adjacent to the transition. However, previous studies have not clearly stated the reasons behind the unsatisfactory performance of these solutions, nor have they assessed the broader implications of these measures on the degradation of ballast, embankment and subgrade. A recent study (Jain et al., 2024a) presents a criterion based on total strain energy in the track bed layers as an indicator of potential irreversible permanent deformations, which can be employed to assess the influence of these solutions on the onset of degradation in different trackbed layers. A detailed analysis of all the track components was performed in (Jain et al., 2024a) by analysing the kinematic responses, stresses, and kinetic and strain energies, concluding that the strain energy is the most comprehensive quantity to evaluate the railway transition as it comprises both distortional and volumetric components of strain energy, while Von Mises stress for instance only captures the distortional component of energy. The details of the criterion can be found in (Jain et al., 2024a) and a valid application of this criterion can be found in a related study (Jain et al., 2023b).
In this paper, the influence of various sleeper configurations and spacing on the dynamic behaviour of railway transition zones are investigated and the need for interventions to mitigate the loss of contact between sleepers and the ballast layer is highlighted, using the recently proposed criterion (Jain et al., 2024a) based on total strain energy in trackbed layers. Firstly, the influence of the specific position of the first sleeper on both sides of the transition interface and the effect of overall and localised (i.e., only in the approach zone) reduced sleeper spacing is studied for the ideal geometric track profile. Secondly, the influence of non-ideal geometry (as a consequence of differential settlement) which entails the loss of contact (Stark and Wilk, 2015; Siahkouhi et al., 2023) between sleepers and ballast on the total strain energy distribution is investigated. The first part of the paper concerns the interventions (and/or design choices) at the superstructure level to avoid dynamic amplifications in transition zones, whereas the second part highlights the need for mitigation measures to deal with the loss of contact.
2 Finite element model of an embankment-bridge transition
A two-dimensional (2-D), plane-strain finite element (FE) model of an embankment-bridge transition was created using ABAQUS, mainly comprising of ballasted track (soft side) of 60 m in length and a ballastless track (stiff side) of 20 m length. The main components of the system under study as shown in Figure 2 namely, rail, railpads, sleepers, under sleeper pads, ballast layer (0.3 m deep), embankment layer (1 m deep), subgrade (1 m deep), and a concrete bridge (2.3 m deep). The sleeper, ballast, embankment, subgrade, and bridge were meshed using linear plane strain quadrilateral elements (CPE4R), and the rail was discretized using two-node linear beam elements (B21). Materials for all components mentioned above were characterized by elastic properties (Elasticity modulus, Poisson’s ratio, density, and Rayleigh damping factors) as tabulated in Table 1 (Jain et al., 2023b). Material properties tabulated in Table 1 have been adopted based on a detailed evaluation and design limits proposed in (Jain et al., 2024b). A static analysis was performed to tune the elastic properties of a thin layer of material under the sleepers referred to as under-sleeper pads (USP) on the stiff side, ensuring the same static vertical rail displacements throughout the track. It is to be noted that these are not conventional under sleeper pads but a way to insure the same static deformations throughout the track in order to study only dynamic effects of the moving load. The key interface and boundary conditions used in the model included vertical springs and dashpots connecting the rail and sleeper midpoint, surface-to-surface tie constraints between the sleeper-ballast, ballast-embankment, and embankment-subgrade, and a hard contact linear penalty method to define the normal behaviour combined with a Coulomb friction model for tangential behaviour at the vertical interface between the ballasted and the ballastless track. Firstly, a static analysis was performed to establish the initial stress state under self-weight, followed by a dynamic analysis (full Newton-Raphson method) for a single moving axle load of 90 kN and a velocity of 144 km/h, using a DLOAD subroutine in ABAQUS (ABAQUS/Standard User’s Manual, 2009). Only one axle load and speed (sub-critical) has been adopted as the main objective of this work is to compare the performance of different configurations (see Section 3) under study and capture the main mechanisms governing the dynamic amplifications under the simplest loading conditions and thus in the cleanest possible manner, to provide insight regarding efficiency or inefficiency of the superstructure level interventions. The effects are expected to be amplified for higher speeds and axle loads. The 2-D model used in this paper has been validated against a 3-D model and the details can be found in (Jain et al., 2024a; Jain et al., 2024b). An ideal geometric track profile is used for evaluation of all the cases as the aim is to study the mechanisms (in isolation of other mechanisms) associated to the initial state of the track subjected to operation-induced loads. The strain energy distribution was found to be very similar in both 2D and 3D models (see Figure 1). For the purpose of this work, 2-D models are used as the cost of computation using the same resources was much higher for one iteration using a 3-D model (approximately 8 h) compared to 2-D models (approximately 40 min). Moreover, the criterion (Jain et al., 2024a) used for evaluation in this work claims to predict the onset of damage in non-linear models based on energy amplification in models with linear elastic materials.
Table 1. Mechanical properties of the track components.
Figure 1. Comparison of the total strain energy in the ballast layer using a 2-D and a 3-D model.
For this study mainly two zones were studied to investigate the dynamic amplifications in railway transition zones (RTZs), namely, the open track (OT) and the approach zone (AZ) on the ballasted track (soft side). Each of these zones is 15 m in length. Figure 2 shows the zone unaffected by the transition effects (open track) and the zone next to the transition interface (approach zone) between the ballasted track and the concrete structure (stiff side), where significant dynamic amplifications are observed. The results studied in this paper are the temporal variation of total strain energy in each of the trackbed layers (ballast, embankment, and subgrade) for the open track and the approach zone. In addition, a percentage increase of the maximum total strain energy in AZ relative to the OT for each case is also presented.
Figure 2. Geometric details of the embankment-bridge transition under study.
3 Results and discussion
This paper investigates six different configurations of the first sleeper on either side of the transition interface (Figure 3) and three different layouts of sleepers with reduced spacing (Figure 5). In the end, the influence of the number of hanging sleepers on the total strain energy amplification is studied. The following sections will describe all these scenarios in detail.
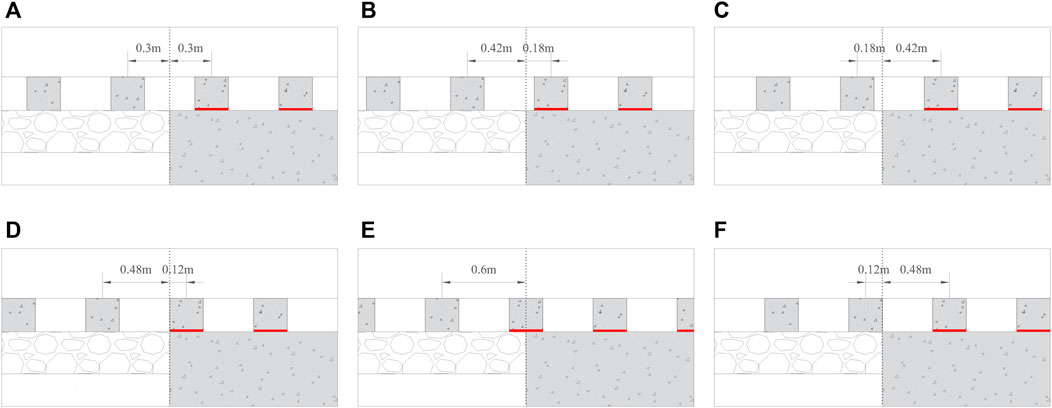
Figure 3. Study cases of different sleeper configurations (A). config 1, (B). config 2, (C). config 3, (D). config 4, (E). config 5, and (F). config 6) around the transition interface (the red layer represents the under-sleeper pads on the stiff side).
3.1 Configuration of sleepers adjacent to the transition interface
The six different sleeper configurations in the proximity of the transition interface as shown in Figure 3 are investigated. The six configurations can be broadly classified into two categories; config.1-3 and config.4-6. Config.1-3 investigate the influence of 3 different spacing configurations of the first sleeper adjacent to the transition interface (on both sides) with respect to the interface, on the total strain energy in AZ compared with that in OT. Config.4-6 analyze the extreme scenarios where the edge/mid-point of the sleeper is located at the transition interface.
Figure 4 shows the time history of total strain energy in ballast (A), embankment (B), and subgrade (C) for the open track and the approach zone, and the percentage increase in the maximum of the total strain energy in the approach zone relative to that in open track for all 6 configurations described above and shown in Figure 3. The results will be investigated in two broad categories of config.1-3 and config.4-6. Figure 4 shows that config.1, 2, and 3 do not exhibit any significant difference in the strain energy variations in ballast, embankment, or subgrade, implying that the position (with respect to the transition interface) of the first sleepers on both sides of the transition interface has negligible influence on the dynamic amplifications in RTZs. However, configurations (config.1–3) involving one of the sleepers being placed right next to the transition interface or on top of it do exhibit significantly larger amplifications in the total strain energy (approx. 5–7 times more than config. 4–6) for all track bed layers, implying that these extreme sleeper configurations must be avoided to achieve better performance of RTZs.
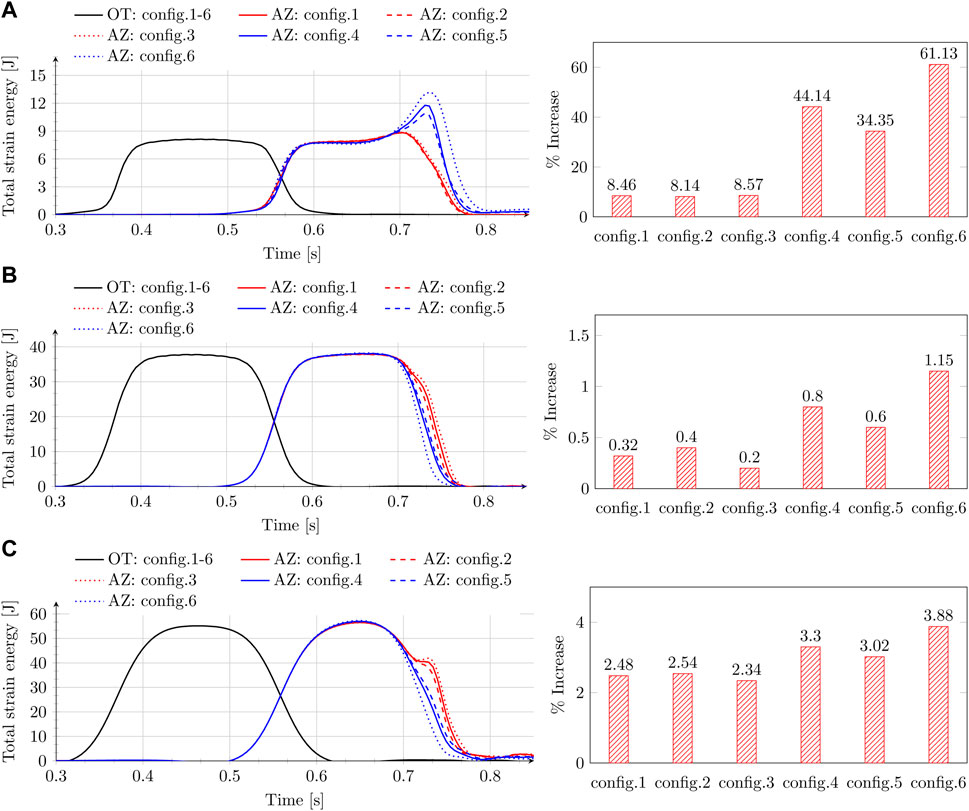
Figure 4. Time history of total strain energy (left) and percentage increase (right) of maximum total strain energy in AZ relative to OT for config.1-6 in ballast (A), embankment (B), and subgrade (C).
3.2 Sleeper layout
Three different sleeper layout (SL) scenarios (Figure 5) were investigated, namely, SL1: standard sleeper spacing of 0.6 m throughout the track (OT and AZ), SL2: reduced sleeper spacing only in the transition zone (approach zone on the stiff and soft side of the track) and SL3: reduced sleeper spacing of 0.3 m throughout the track (OT and AZ).
Figure 5. Sleeper layouts under study: (A) SL1, (B) SL2, (C) SL3.
Figure 6 shows the time history of total strain energy in the ballast (A), embankment (B), and subgrade (C) for the open track and the approach zone, and the percentage increase in maximum total strain energy in the approach zone relative to that in the open track for sleeper layouts described above and shown in Figure 5. On the one hand, some authors (National Academies of Sciences, Engineering, and Medicine, 2006; Galván Giménez, 2011; Sañudo et al., 2016; Indraratna et al., 2019) have associated reduced sleeper spacing in the railway tracks with a reduction in ballast settlement and the results shown in Figure 6A (left) for SL3 (when compared to SL1) can verify this claim for OT. On the other hand, the amplification of maximum total strain energy in AZ relative to OT is higher for SL3 in comparison to SL1 (which is the reference layout). Furthermore, although SL2 shows no amplification of maximum total strain energy in AZ relative to OT in the ballast layer, a significant increase is seen in the embankment layer. This implies that reduced sleeper spacing only in the transition zone is efficient in the reduction of permanent deformations in the ballast layer in the proximity of the transition interface. However, it is not an effective intervention to deal with transition effects in general as it leads to an increased degradation in the embankment layer (no significant change is observed in the behaviour of the subgrade layer for any of the sleeper layouts under study).
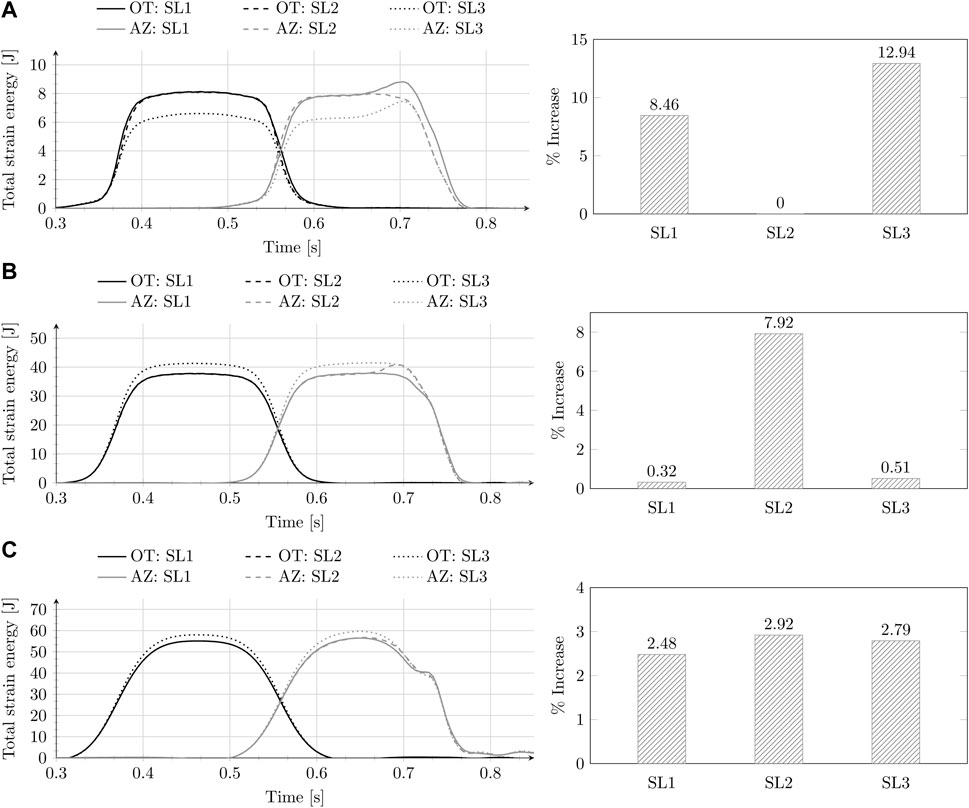
Figure 6. Time history of total strain energy (left) and percentage increase (right) of maximum total strain energy in AZ relative to OT for SL 1-3 in (A) ballast, (B) embankment, and (C) subgrade.
3.3 Loss of contact between sleeper and ballast: Hanging sleepers
In RTZs, the difference in autonomous settlements on the soft and stiff side of the track together with the operation-driven dynamic amplifications lead to non-ideal geometric track configurations. As a consequence of these configurations, one or more sleepers in the vicinity of the transition interface typically lose contact with the ballast layer (Stark and Wilk, 2015; Siahkouhi et al., 2023). Therefore, in this section, the influence of the number (Paixão et al., 2021; Jain et al., 2023a) of hanging sleepers is studied (Figure 7) and compared against the case with no hanging sleepers. No more than 2 hanging sleepers were analyzed as the tracks are necessarily maintained after the occurrence of the second hanging sleeper. It is to be noted that only extreme cases leading to complete loss of contact between the first two sleepers next to the transition interface are investigated.
Figure 7. The embankment-bridge transition under study showing the locations of (A) one hanging sleeper and (B) two hanging sleepers marked in blue.
Figure 8 shows the time history of total strain energy in ballast (A), embankment (B) and subgrade (C) for open track and approach zone, and the percentage increase in the maximum of the total strain energy in the approach zone relative to that in the open track for the embankment-bridge transition with no hanging sleepers, one hanging sleeper and two hanging sleepers, as marked in Figure 8. It can be observed in the results that the occurrence of hanging sleepers affects mostly the top layers (ballast and embankment) and shows a small influence on the subgrade layer (and it does not lead to any amplification). In the embankment layer, one hanging sleeper has no influence, but some amplification in total strain energy can be seen with the occurrence of the second hanging sleeper. In the ballast layer, the presence of a single hanging sleeper in proximity to the transition interface leads to an approximate doubling of the strain energy amplification relative to situations without any hanging sleepers. It is to be noted that the occurrence of a second hanging sleeper has an even more pronounced effect, resulting in an approximately eightfold increase in total strain energy amplification when compared to the situation with no hanging sleepers. Thus, it can be concluded that the impact of hanging sleepers on total strain energy amplification is not merely additive but seemingly exponential, highlighting the need for meticulous monitoring and management of such conditions.
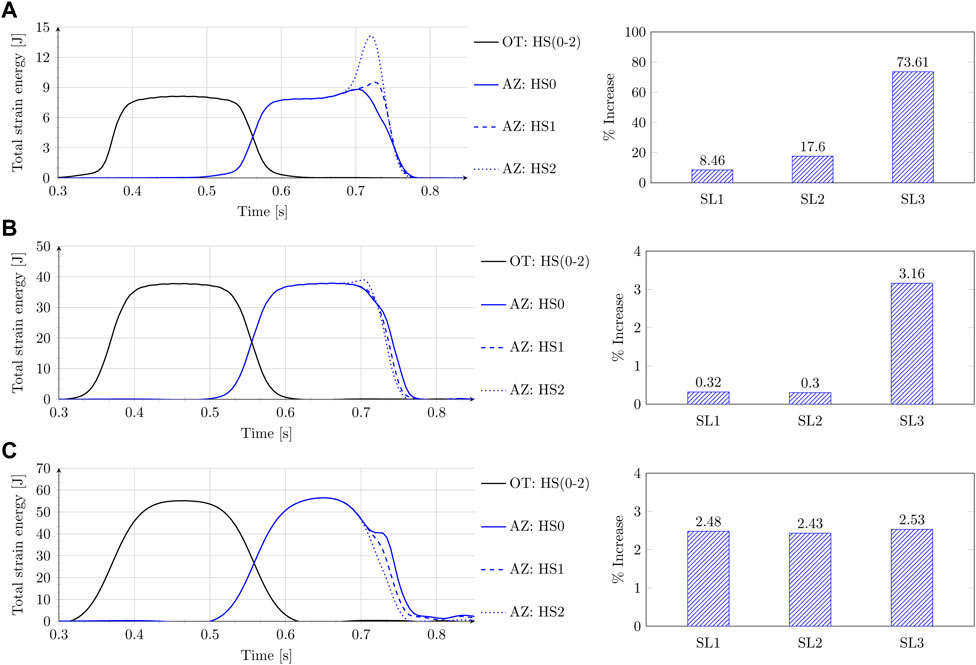
Figure 8. Time history of total strain energy (left) and percentage increase (right) of maximum total strain energy in AZ relative to OT for 0, 1, and 2 number of hanging sleepers next to transition interface for the (A) ballast, (B) embankment and (C) subgrade.
4 Conclusion
Despite certain studies advocating the efficacy of superstructure-based enhancements in railway transition zones (RTZs), site measurements have demonstrated limited efficiency. A recently developed energy-based criterion was used to highlight the potential shortcomings of some of these solutions, thus providing reasoning behind their ineffectiveness. A 2D finite element model was used to analyze the performance of railway transition zones (RTZs) for varying sleeper configuration in the proximity of the transition interface and varying sleeper spacing layouts using a recently developed strain energy-based criterion. Additionally, the loss of contact conditions (hanging sleepers) between the sleeper and ballast layer due to non-ideal geometry was also investigated. Firstly, various sleeper configurations around the transition interface were studied in terms of total strain energy amplifications and it was observed that the positioning of the first sleeper on both sides (soft and stiff) with respect to the transition interface has negligible influence on the performance of the RTZs. However, extreme positions of the sleepers (e.g., sleeper edge resting on the transition interface) must be avoided to limit the strain energy amplification in RTZs. Secondly, the effect of overall reduced sleeper spacing and reduced sleeper spacing only in the approach zones (both on the soft and stiff side) was compared with the standard sleeper spacing configuration (0.6 m). It was observed that even though an overall reduced sleeper spacing leads to lower total strain energy levels in the ballast layer, it does not reduce the strain energy amplification in approach zones with respect to the open track. Moreover, the layout with reduced sleeper spacing only for approach zones led to the mitigation of dynamic amplifications in the ballast layer but eventually resulted in an amplification of the strain energy within the embankment layer. Lastly, the study of the influence of hanging sleepers on the performance of RTZ showed that with an increase in the number of hanging sleepers, an exponential increase in strain energy amplification was observed in the approach zone. This highlights the need for interventions like adjustable sleepers (Wang and Markine, 2018), and wedge-shaped sleepers (Jia et al., 2023) to mitigate the loss of contact between sleepers and the ballast layer. In the end, it was concluded that optimizing the sleeper configuration (overall or in the proximity of the transition interface) does not lead to any significant improvement in the performance of railway transition zones in terms of strain energy amplifications. In addition, some critical configurations (sleeper edge on transition interface) or contact conditions (hanging sleepers) must be avoided or mitigated to prevent extreme strain energy amplifications in railway transition zones.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
AJ: Writing–original draft, Writing–review and editing, Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization. AM: Writing–review and editing, Conceptualization, Methodology, Supervision. MS: Writing–review and editing, Conceptualization, Methodology. KD: Writing–review and editing, Conceptualization, Funding acquisition, Methodology, Project administration, Supervision.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This research is supported by the Dutch Technology Foundation TTW (Project 15968), a part of the Netherlands Organisation for Scientific Research (NWO), and which is partly funded by the Ministry of Economic Affairs.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Charoenwong, C., Connolly, D., Colaço, A., Alves Costa, P., Woodward, P., Romero, A., et al. (2023). Railway slab vs ballasted track: a comparison of track geometry degradation. Constr. Build. Mater. 378, 131121. doi:10.1016/j.conbuildmat.2023.131121
Chumyen, P., Connolly, D., Woodward, P., and Markine, V. (2022). The effect of soil improvement and auxiliary rails at railway track transition zones. Soil Dyn. Earthq. Eng. 155, 107200. doi:10.1016/j.soildyn.2022.107200
Fărăgău, A. B., Jain, A., de Oliveira Barbosa, J., Metrikine, A., and van Dalen, K. (2023). “Auxiliary rails as a mitigation measure for degradation in transition zones,” in Proceedings of the fifth international conference on railway Technology: research, development and maintenance. Editor J. Pombo (Edinburgh: Civil-Comp Press). doi:10.4203/ccc.1.19.4
Galván Giménez, J. M. (2011). Estudio por elementos finitos de la transición vía con balasto-vía en placa.
Heydari-Noghabi, H., Varandas, J. N., Esmaeili, M., and Zakeri, J. (2017b). Investigating the influence of auxiliary rails on dynamic behavior of railway transition zone by a 3d train-track interaction model. Lat. Am. J. Solids Struct. 14, 2000–2018. doi:10.1590/1679-78253906
Heydari-Noghabi, H., Zakeri, J., Esmaeili, M., and Varandas, J. (2017a). Field study using additional rails and an approach slab as a transition zone from slab track to the ballasted track. Proc. Institution Mech. Eng. Part F J. Rail Rapid Transit 232, 970–978. doi:10.1177/0954409717708527
Hu, P., Zhang, C., Wen, S., and Wang, Y. (2019). Dynamic responses of high-speed railway transition zone with various subgrade fillings. Comput. Geotechnics 108, 17–26. doi:10.1016/j.compgeo.2018.12.011
Indraratna, B., Sajjad, M. B., Ngo, T., Correia, A. G., and Kelly, R. (2019). Improved performance of ballasted tracks at transition zones: a review of experimental and modelling approaches. Transp. Geotech. 21, 100260. doi:10.1016/j.trgeo.2019.100260
Jain, A., Marykovskiy, Y., Metrikine, A. V., and van Dalen, K. N. (2024b). Quantifying the impact of stiffness distributions on the dynamic behaviour of railway transition zones. Transp. Geotech. 45, 101211. doi:10.1016/j.trgeo.2024.101211
Jain, A., Metrikine, A., Steenbergen, M., and van Dalen, K. (2023b). Railway transition zones: evaluation of existing transition structures and a newly proposed transition structure. Int. J. Rail Transp, 1–21. doi:10.1080/23248378.2023.2272668
Jain, A., Metrikine, A., Steenbergen, M., and van Dalen, K. (2024a). Design of railway transition zones: a novel energy-based criterion. Transp. Geotech. 46, 101223. doi:10.1016/j.trgeo.2024.101223
Jain, A., van Dalen, K., Metrikine, A., Faragau, A., and Steenbergen, M. (2023a). “Comparative analysis of the dynamic amplifications due to inhomogeneities at railway transition zones,” in Proceedings of the fifth international conference on railway Technology: research, development and maintenance. Editor J. Pombo (Edinburgh: Civil-Comp Press). doi:10.4203/ccc.1.19.1
Jia, W., Markine, V., Carvalho, M., Connolly, D. P., and Guo, Y. (2023). Design of a concept wedge-shaped self-levelling railway sleeper. Constr. Build. Mater. 386, 131524. doi:10.1016/j.conbuildmat.2023.131524
Laco, K., and Borzovič, V. (2016). Reliability of approach slabs and modelling of transition zones of bridges. Appl. Mech. Mater. 821, 741–746.
Namura, A., Kohata, Y., and Miura, S. (2004). Effect of sleeper size on ballasted track settlement. Q. Rep. RTRI 45, 156–161. doi:10.2219/rtriqr.45.156
Namura, A., and Suzuki, T. (2007). Evaluation of countermeasures against differential settlement at track transitions. Q. Rep. RTRI 48, 176–182. doi:10.2219/rtriqr.48.176
National Academies of Sciences, Engineering, and Medicine (2006). Design of track transitions. Washington, DC: The National Academies Press.
Nicks, J. E. (2009). “The bump at the end of the railway bridge,”. Doctoral dissertation (Texas A&M University) Available electronically from https://hdl.handle.net/1969.1/ETD-TAMU-2009-12-7432.
Ognibene, G., Powrie, W., Pen, L. L., and Harkness, J. (2019). “Analysis of a bridge approach: long-term behaviour from short-term response,” in 15th Railway Engineering Conference, Edinburgh, U.K, 1–15.
Paixão, A., Fortunato, E., and Calçada, R. (2013). Design and construction of backfills for railway track transition zones. Proc. Institution Mech. Eng. Part F J. Rail Rapid Transit 229, 58–70. doi:10.1177/0954409713499016
Paixão, A., Fortunato, E., and Calçada, R. (2014). Transition zones to railway bridges: track measurements and numerical modelling. Eng. Struct. 80, 435–443. doi:10.1016/j.engstruct.2014.09.024
Paixão, A., Fortunato, E., and Calçada, R. (2015). A numerical study on the influence of backfill settlements in the train/track interaction at transition zones to railway bridges. Proc. Institution Mech. Eng. Part F J. Rail Rapid Transit 230, 866–878. doi:10.1177/0954409715573289
Paixão, A., Varandas, J. N., and Fortunato, E. (2021). Dynamic behavior in transition zones and long-term railway track performance. Front. Built Environ. 7. doi:10.3389/fbuil.2021.658909
Palomo, M. L., Martínez, J. H. A., Arnoa, A. Z., and Medina, J. J. C. (2021). Structural and vibration performance in different scenarios of a prefabricated wedge for railway transition zones. J. Vib. Eng. & Technol. 9, 1657–1668. doi:10.1007/s42417-021-00319-5
Raj, A., Ngamkhanong, C., Prasittisopin, L., and Kaewunruen, S. (2023). Nonlinear dynamic responses of ballasted railway tracks using concrete sleepers incorporated with reinforced fibres and pre-treated crumb rubber. Nonlinear Eng. 12, 20220320. doi:10.1515/nleng-2022-0320
Ribeiro, C. A., Calçada, R., and Delgado, R. (2017). Calibration and experimental validation of a dynamic model of the train-track system at a culvert transition zone. Struct. Infrastructure Eng. 14, 604–618. doi:10.1080/15732479.2017.1380674
Sañudo, R., Cerrada, M., Alonso, B., and dell’Olio, L. (2017). Analysis of the influence of support positions in transition zones. a numerical analysis. Constr. Build. Mater. 145, 207–217. doi:10.1016/j.conbuildmat.2017.03.204
Sañudo, R., dell’Olio, L., Casado, J., Carrascal, I., and Diego, S. (2016). Track transitions in railways: a review. Constr. Build. Mater. 112, 140–157. doi:10.1016/j.conbuildmat.2016.02.084
Sañudo, R., Miranda, M., Alonso, B., and Markine, V. (2022). Sleepers spacing analysis in railway track infrastructure. Infrastructures 7, 83. doi:10.3390/infrastructures7060083
Sañudo Ortega, R., Pombo, J., Ricci, S., and Miranda, M. (2021). The importance of sleepers spacing in railways. Constr. Build. Mater. 300, 124326. doi:10.1016/j.conbuildmat.2021.124326
Shahraki, M., Warnakulasooriya, C., and Witt, K. J. (2015). Numerical study of transition zone between ballasted and ballastless railway track. Transp. Geotech. 3, 58–67. doi:10.1016/j.trgeo.2015.05.001
Shahraki, M., and Witt, K. J. (2015). 3d modeling of transition zone between ballasted and ballastless high-speed railway track. J. Traffic Transp. Eng. 3. doi:10.17265/2328-2142/2015.04.005
Siahkouhi, M., Wang, J., Han, X., Aela, P., Ni, Y. Q., and Jing, G. (2023). Railway ballast track hanging sleeper defect detection using a smart cnt self-sensing concrete railway sleeper. doi:10.2139/ssrn.4414996
Stark, T. D., and Wilk, S. T. (2015). Root cause of differential movement at bridge transition zones. Proc. Institution Mech. Eng. Part F J. Rail Rapid Transit 230, 1257–1269. doi:10.1177/0954409715589620
Transit Cooperative Research Program (2006). Design of track transitions. Washington, DC: The National Academies Press. doi:10.17226/23228
Varandas, J., Hölscher, P., and Silva, M. (2016). Three-dimensional track-ballast interaction model for the study of a culvert transition. Soil Dyn. Earthq. Eng. 89, 116–127. doi:10.1016/j.soildyn.2016.07.013
Wang, H., and Markine, V. (2018). Corrective countermeasure for track transition zones in railways: adjustable fastener. Eng. Struct. 169, 1–14. doi:10.1016/j.engstruct.2018.05.004
Keywords: mitigation measures, railway transition zones, strain energy amplification, sleeper spacing, hanging sleepers
Citation: Jain A, Metrikine AV, Steenbergen MJMM and van Dalen KN (2024) Dynamic amplifications in railway transition zones: performance evaluation of sleeper configurations using energy criterion. Front. Built Environ. 10:1285131. doi: 10.3389/fbuil.2024.1285131
Received: 29 August 2023; Accepted: 02 April 2024;
Published: 24 April 2024.
Edited by:
Robert Arcos, Universitat Politecnica de Catalunya, SpainReviewed by:
Ana Ramos, University of Porto, PortugalLapyote Prasittisopin, Chulalongkorn University, Thailand
Copyright © 2024 Jain, Metrikine, Steenbergen and van Dalen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Avni Jain, a.jain-1@tudelft.nl