The “direct five-step procedure” for the design of added viscous dampers to be inserted into existing buildings: formulation and case study

This paper introduces an updated formulation of a five-step procedure dealing with the design of fluid viscous dampers for the seismic retrofitting of existing frame buildings. The original design procedure is known as the “direct five-step procedure,” and is articulated into 5 consecutive steps guiding the designer from the identification of the expected seismic performances, to the sizing of the added viscous dampers up to the final verification of the seismic behavior through non-linear dynamic time history analyses. The procedure leads to the full definition of the mechanical characteristics of the commercial non-linear viscous dampers and allows to estimate the maximum dissipative forces acting in the dampers and the internal forces in the frame members. The objective of the design procedure, when applied to a new building, is to size the dampers in order to keep the structural elements within the linear elastic range considering a “rare” earthquake design level. However, when dealing with an existing building, especially if originally designed considering vertical loads only, the insertion of viscous dampers could be not sufficient to keep the structural elements in the elastic range. Thus, it might be necessary to accept local plastic excursion of the structural elements, by taking into account the ductility capacity (albeit probably limited) of the structural members (hysteretic dissipation associated with damage in beams and columns). This latter aspect is explicitly considered in the updated formulation of the “direct five-step procedure” presented here through the introduction of an overall response reduction factor accounting for both the ductility capacity of the structural members and the viscous damping provided by the added dampers. The design procedure is then applied to a 11-storey frame structure case study, which is representative of reinforced concrete buildings designed for vertical loads only. Three different retrofitting design strategies are considered, based on different exploitation of viscous energy dissipation provided by the dampers and hysteretic energy dissipation due to the excursion of the structural members into the inelastic regime.

1 Introduction

Energy dissipation represents a consolidated concept for the mitigation of the seismic effects in building structures (Constantinou et al., 1993; Foti et al., 1998; Christopoulos and Filiatrault, 2006; Liang et al., 2011; Foti, 2014a; Foti, 2014b). Among all possible types of seismic dissipators, fluid viscous dampers have widely proven to be effective in seismic protection of frame structures. However, their application is still limited. This is also due lack of specific code prescriptions and simple design procedures. For instance, the Italian building code (NTC, 2018) does not provide explicit indications for the design of buildings equipped with viscous dampers, while specific design procedures and indications are given for seismic isolation devices.

The applicative guidelines of the Italian building code (hereafter referred to as Circular (C.S.LL.PP. Consiglio Superiore dei Lavori Pubblici, 2019)) distinguish between velocity-dependent dissipation devices and displacement-dependent devices, underlining their common goal of reducing deformations to contain damage and avoid collapse of the structure, and highlighting the importance of a seismic vulnerability analysis for an existing building to be strengthened. Nevertheless, the Circular does not suggest neither pre-dimensioning/design formulas for the different types of dampers, nor practical indications regarding how the ductile capacities of the existing structure could be taken into account.

In the last decades several design procedures for frame buildings equipped with viscous dampers were proposed in the literature (Constantinou et al., 1993; Green, 1987; Constantinou and Symans, 1992; Takewaki, 1997; Pekcan et al., 1999; Shea, 1999; Shukla and Datta, 1999; Takewaki, 2000; Garcia, 2001; Ramirez, 2001; Rami et al., 2002; Singh and Moreschi, 2002; Manual, 2003; Ramirez et al., 2003; Whi et al., 2003; Kasai and Kibayashi, 2004; Levy and Lavan, 2006; Takewaki, 2011; Weng et al., 2012; Landi et al., 2014), including the “five-step procedure” (Trombetti and Silvestri, 2004; Trombetti and Silvestri, 2006; Silvestri et al., 2010; Palermo et al., 2013a; Palermo et al., 2013b; Palermo et al., 2015; Trombetti et al., 2015; Palermo et al., 2017a) and the “direct five-step procedure” (Palermo et al., 2016; Palermo et al., 2017b; Palermo et al., 2018) developed by some of the authors. This latter design procedure consists of 5 consecutive steps and is based on the identification of a target seismic performance to be achieved, such as a target damping ratio. The preliminary design of the dampers and the assessment of the seismic performances of the frame structure is fully developed with analytical formulas, while the final verification of the seismic behavior need to be conducted through non-linear dynamic time-history analyses. The procedure aims at defining the main mechanical characteristics of the commercial fluid viscous dampers which are typically governed by a non-linear force-velocity relationship ($F=c_{NL}\cdot v^{\alpha }$, where $c_{NL}$ indicates the non-linear damping coefficient and α the damping exponent). It also allows to estimate the maximum forces exerted by the dampers and the internal forces in the structural members of the frame building.

In the case of new frame buildings, the main design principle is to keep the structural elements within the linear elastic range for a “rare” earthquake design level. Nevertheless, in the case of existing frame buildings designed for vertical loads only, the introduction of a damper system could be not sufficient to keep the structural elements in the elastic range. Therefore, it might be necessary to accept local plastic excursion of the structural elements, by taking into account the limited ductility capacity of the structural members and the associated hysteretic dissipation resulting from structural damage. The paper proposes a new formulation of the “direct five-step procedure” specifically targeted to existing buildings which accounts for the ductility capacity of the structural members. This new formulation is introduced in Section 2 and then applied in Sections 3 and 4 to a 11-storey Reinforced Concrete (RC) case study building.

The rationale behind the method is general and independent from the specific code while its implementation for practical design requires the reference to a specific building code. Therefore, the current manuscript has been written with reference to the Italian code (NTC, 2018).

2 The “direct five-step procedure” tailored for existing buildings

2.1 Overview of the “direct five-step procedure”

The original “direct five-step procedure” for the design of frame structures equipped with fluid-viscous dampers was proposed by some of the authors (Palermo et al., 2018). The procedure applies to yielding frame structures with a generic along-the-height distribution of inter-storey viscous dampers. It is aimed at guiding the designer through the sizing and verification of both viscous dampers and structural elements.

The design procedure is based on 5 consecutive steps. In STEP 1 the expected seismic performance objectives are identified leading to the evaluation of the total response reduction factor accounting for both the ductility demand and the viscous damping provided by the added dampers, as detailed in Section 2.2. Then, in STEP 2, the linear damping coefficients of the added viscous dampers are computed in order to reduce the structural response according to the selected target damping ratio. Analytical formulas are employed in STEP 3 to estimate the design values of the peak velocities and dissipation forces in the dissipative devices, while an energy criterion is used in STEP 4 to identify the equivalent non-linear damping coefficient of the actual manufactured viscous dampers. Finally, in STEP 5, the internal forces in the structural elements can be estimated through the envelope of two Equivalent Static Analyses (ESA). Non-linear dynamic time history analyses are then carried out to conduct the final verifications.

In particular, for the specific case of inter-storey placement of viscous dampers of equal size, the following direct formulas can be used to estimate both the required damping coefficient and the minimum axial stiffness (fluid + support component) of the commercial non-linear dampers:

$c_{NL}={\overline{\xi }}_{\text{visc}}\cdot \frac{2\pi }{T_1}\cdot \frac{W}{g}\cdot \left(\frac{N+1}{n}\right)\cdot \frac{1}{{\cos }^2\theta }\cdot {\left(0.8\cdot \frac{S_e\left(T_1,{\overline{\eta }}_{\xi }\right)}{2\pi /T_1}\cdot \frac{2}{N+1}\cdot \cos \theta \right)}^{1-\alpha }(1)$

$k_{axial}\ge 10\cdot {\overline{\xi }}_{\text{visc}}\cdot {\left(\frac{2\pi }{T_1}\right)}^2\cdot \frac{W}{g}\cdot \left(\frac{N+1}{n}\right)\cdot \frac{1}{{\cos }^2\theta }(2)$

For existing buildings, the insertion of dampers reduces the deformations and internal forces in the structural elements, and, in the case of structural response beyond the elastic limit, the ductility demand. In the latter case, the available ductility capacity (although probably limited) can be properly considered in the design phase, especially when dealing with old existing buildings designed for vertical loads only (often characterized by reduced seismic capacities). Therefore, in these cases, it might be necessary to partially account for a portion of the available ductility, when designing the added fluid viscous dampers.

In this regard, it is worth pointing out that, in order to consider the coupling of the hysteretic damping provided by the structural elements with the viscous damping provided by the dampers, non-linear dynamic analyses have to be carried out as also recommended by technical codes, such as the Italian code (NTC, 2018). In fact, when dealing with the conventional design based on the response spectrum method, the reduction factor $\eta$ adopted to reduce the ordinates of the elastic design spectra should only account either for the hysteretic damping (through the behavior factor $q$) associated to the ductility and damage of beams and columns or, alternatively, for the viscous damping (through the damping ratio ξ) provided by the added viscous dampers.

In light of this premise, in the next section, a specific focus will be given on STEP 1 of the “direct five-step procedure” with the aim of providing a novel formulation able to combine these two sources of energy dissipation. The reader interested in a more complete understanding of the other steps of the procedure may refer to (Silvestri et al., 2010; Palermo et al., 2017b; Palermo et al., 2018).

2.2 STEP 1: new formulation for existing buildings

In STEP 1, the overall seismic performances are identified and, consequently, the total target reduction factor $\overline{{\eta }_{tot}}$ is evaluated. The overall target seismic performance to be achieved through the insertion of the added dampers is here assumed as the full seismic retrofitting according to the Italian code (NTC, 2018), implying that the seismic capacity of the retrofitted building must be, at least, the same as that of a new building to be designed on the same site of the existing one. Consequently, the total target reduction factor $\overline{{\eta }_{tot}}$ is set equal to the Capacity (C)/Demand (D) ratio between the maximum seismic action that can be withstood by the structure (C) and the seismic action provided by the code for the design of a new building (D):

$\overline{{\eta }_{tot}}=\frac{C}{D}(3)$

Both C and D can be evaluated either considering the global seismic response of the entire structure in terms of base shear ($V_{base}$) vs. roof displacement ($d_{roof}$) capacity curve, or considering the C/D ratios of the single elements (e.g., bending moment, shear force in the most stressed beams and/or columns).

In this work, the focus will be on the global seismic response. For this aim, the capacity C may be evaluated from the results of a non-linear static (e.g., pushover) analysis. In this case, the actual capacity curve can be transformed into an equivalent bilinear curve according to well-known methods (as the N2 method reported in the EC8 (Eurocode 8, 2005) or the equal energy criterion reported in the Italian building code (NTC, 2018)).

For illustrative purposes, Figure 1A provides a qualitative representation of the equivalent bilinear capacity curve of the whole building in terms of $V_{base}$ vs. $d_{roof}$. The capacity C is assumed equal to the yielding base shear $F_y^{*}$. The demand D is assumed equal to the base shear of the equivalent linear structure, $V_{base,LS}$, under the design earthquake. It can be estimated, depending on the desired level of approximation, from different types of seismic analysis, such as the equivalent linear static analysis, the linear dynamic analysis with elastic design response spectrum, or the linear dynamic time-history analysis using a set of earthquake acceleration records compatible with the elastic design spectrum.

FIGURE 1

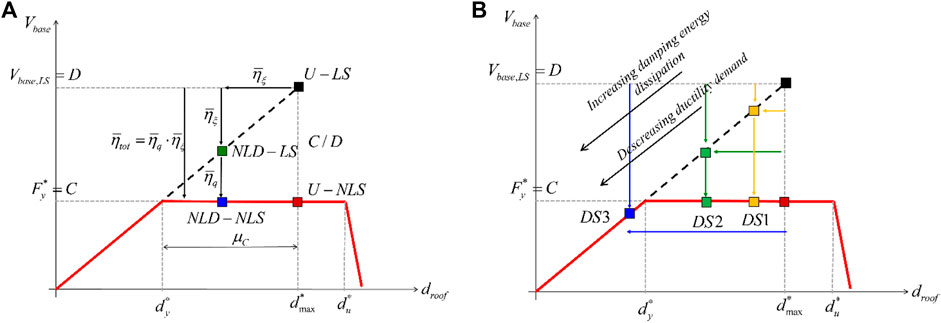
FIGURE 1. (A) Illustration of the target performance point, identified by the blue square (NLD). NL, non-linear response of the existing structure as it is. NLD, non-linear response of the existing structure with dampers. L, response of the equivalent linear structure. LD, response of the equivalent linear structure response with dampers. (B) Illustration of the design strategies, based on different distributions of the reduction factor of the seismic response between viscous dissipation and hysteretic dissipation.

The ductility capacity (${\mu }_C$) is evaluated as the ratio between the ultimate ($d_u^{*}$) and the yielding ($d_y^{*}$) displacements: ${\mu }_C=d_u^{*}/d_y^{*}$. The maximum behavior factor $q_{\max }$ can then be set, by virtue of the equal displacement rule (Chopra, 2012), equal to the ductility capacity: $q_{\max }={\mu }_C$.

Once the total target reduction factor $\overline{{\eta }_{tot}}$ has been determined from the desired target performance, several Design Strategies (DS, as illustrated in Figure 1B) can be adopted by the appropriate combination of the reduction factors due to hysteretic damping (${\overline{\eta }}_q$) and viscous damping (${\overline{\eta }}_{\xi }$) based on the formulation proposed by (Palermo et al., 2013b):

$\overline{{\eta }_{tot}}={\overline{\eta }}_q\cdot {\overline{\eta }}_{\xi }(4)$

If a behaviour factor $q<q_{\max }$ associated to the hysteretic damping is assumed (i.e., ${\overline{\eta }}_q=1/q$), then the target reduction factor due to viscous damping (${\overline{\eta }}_{\xi }$) can be evaluated as follows:

${\overline{\eta }}_{\xi }=\frac{\overline{{\eta }_{tot}}}{{\overline{\eta }}_q}(5)$

The target damping ratio ${\overline{\xi }}_{visc}=\overline{\xi }-{\xi }_{\text{intr}}$ to be obtained with the additional viscous damper system (taking into account the presence of intrinsic damping equal to ${\xi }_{\text{intr}}$ = 5%) is then evaluated by inverting the well-known formulation proposed by Bommer et al. (2000) and adopted by the EC8 (Eurocode 8, 2005) and the Italian code (NTC, 2018):

${\overline{\eta }}_{\xi }=\sqrt{\frac{10}{5+{\xi }_{\mathit{intr}}+{\overline{\xi }}_{visc}}}(6)$

leading to:

${\overline{\xi }}_{visc}=\frac{10\left(1-{{\overline{\eta }}_{\xi }}^2\right)}{{\overline{\eta }}_{\xi }}(7)$

It should be remarked that, since the ductility resources of the existing structure are limited to ${\mu }_C$, in any case, the damper system must be selected such as to provide at least a minimum damping ratio ${\xi }_{\min }$, corresponding to ${\overline{\eta }}_{{\xi }_{\min }}={\overline{\eta }}_{tot}/{\overline{\eta }}_{q_{\max }}$, where ${\overline{\eta }}_{q_{\max }}=1/q_{\max }=1/{\mu }_C$.

If, instead, a target viscous damping ratio (${\overline{\xi }}_{visc}$) (corresponding to a damping reduction factor ${\overline{\eta }}_{\xi }$) is assumed, the inversion of Eq. 4 allows us to obtain an estimation of the ductility demand and thus the target reduction factor due to hysteretic dissipation:

${\overline{\eta }}_q=\frac{\overline{{\eta }_{tot}}}{{\overline{\eta }}_{\xi }}(8)$

In the latter case, the designer should check that the obtained ductility demand is smaller than the ductility capacity, i.e., ${\overline{\eta }}_q\ge {\overline{\eta }}_{q_{\max }}$.

For illustrative purposes, three different design strategies (DS) are represented in Figure 1B, based on three different combinations of hysteretic and viscous dissipation. DS1 is mostly based on hysteretic dissipation, with a reduced amount of viscous damping provided by the added dampers. DS2 is mostly based on viscous damping (e.g., equivalent damping ratio larger than the one related to DS1), with a limited use of hysteretic dissipation, thus limiting structural damages. DS3 is uniquely based on viscous damping (e.g., equivalent damping ratio larger than the one related to DS2), thus completely avoiding structural damages.

3 The case study building

3.1 Building description and Finite Element analysis

The case study here considered is a 11-storey reinforced concrete building located in Bologna (Italy) and designed in the 1970s. The building has a rectangular shape in plan (Figure 2A) with dimensions equal to 44 m (along the longitudinal direction X) and 9.60 m (along the transversal direction Y). It has a total height of 33 m, while the inter-storey height is equal to 3 m. The RC beams have the height contained within the floor thickness, while the columns have different rectangular cross-sections varying both in plan and elevation. The floors are oriented along the longitudinal (X) direction and are assumed to be rigid in their plane, due to the presence of a 5 cm thick concrete slab. Each floor has a total thickness of 25 cm. Class C25/30 concrete and B450C steel are considered. The reinforcement bars are evaluated according to the “simulated design approach” starting from the original design drawings and considering the design rules and code requirements at the time of the design. More in detail, the longitudinal reinforcement bars in the columns were designed to have a cross sectional area larger than 0.5% of the gross area of the concrete section and globally higher than 1%. The longitudinal reinforcement bars in the beams were designed to have a cross a sectional area larger than 0.15% of the gross area of the concrete section, both in the tension side and in the compressed side.

FIGURE 2

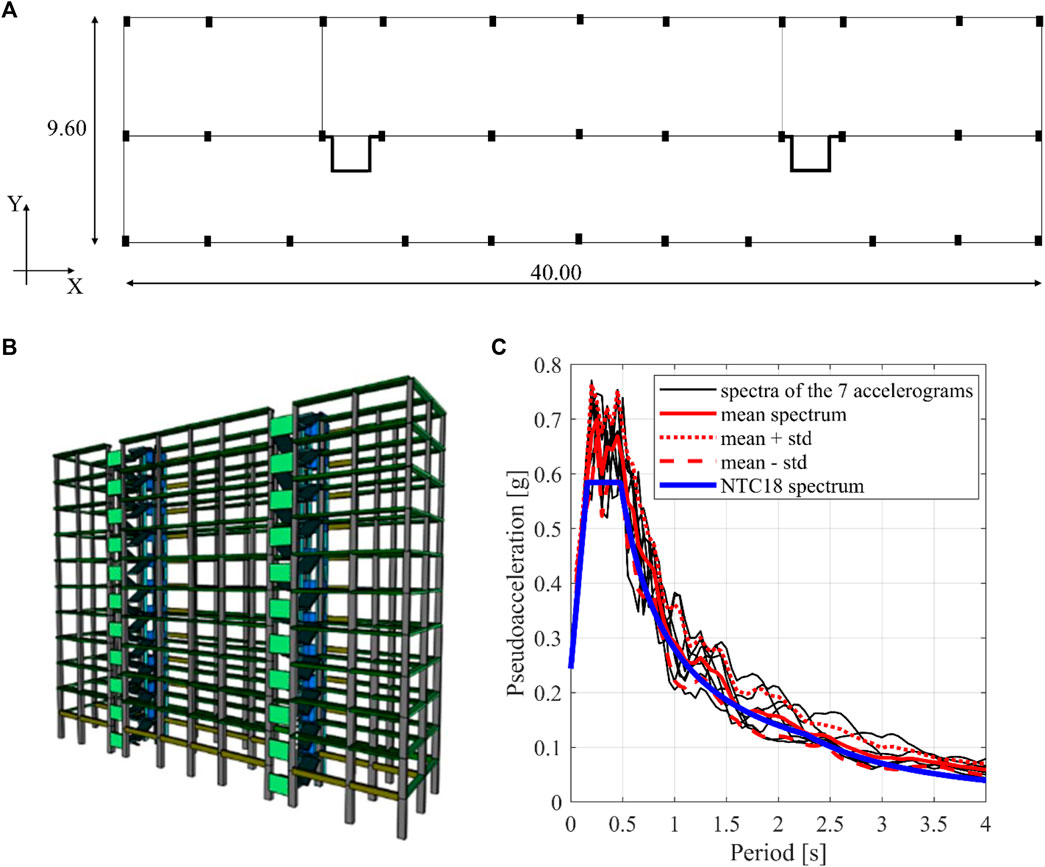
FIGURE 2. (A) Structural building plan. (B) SAP 2000 3D FE model. (C) Pseudoacceleration spectra of the 7 artificial earthquakes compared with the elastic design spectrum of the Italian code (NTC, 2018).

The Finite Element (FE) analyses are carried out using the commercial software SAP2000 NL (Comput. Struct. Inc, 2007). Both linear and non-linear FE models are considered. The non-linear behaviour of the structural elements (i.e., beams and columns) is modeled with flexural plastic hinges placed at both ends of each beam and column. The bending moment–curvature diagram of each plastic hinge has been evaluated on the basis of the actual reinforcement bars and of the axial force corresponding to dead and live loads at their characteristic values, without load partial safety factors (i.e., rare combination at the Serviceability Limit State); isotropic hysteresis type has been assumed. Shear failure has not been considered. The assumption is reasonable in case the shear strength of all the structural elements would be adequately increased by means of localized structural reinforcement interventions (e.g., bands with fiber-reinforced polymeric materials) aimed at: 1) guaranteeing a shear strength higher than the shear force corresponding to the formation of bending plastic hinges (bending capacity suitably increased with overstrength factors), according to the capacity design; 2) increasing the ductility capacity of the cross-section. The viscous dampers, sized to achieve the desired seismic performances, as detailed in Section 4, are modeled using NL-link elements. Both linear (with linear damping coefficient $c_L$) and corresponding non-linear (with non-linear damping coefficient $c_{NL}$ and $\alpha =0.15$) dampers are considered. Clearly, the values of the linear and corresponding non-linear damping coefficient and axial stiffness are computed following the “direct five-step procedure”.

In detail, a total number of 14 different FE models have been developed, including:

• Two undamped (U) models. They are representative of the as-built building without added dampers, namely, an undamped linear model (U-LS) and an undamped non-linear model (U-NLS).

• Six damped (D) models with linear structural elements (LS) and linear or non-linear dampers (LD or NLD). They are representative of the retrofitted building according to the DS1, DS2 and DS3 design strategies.

• Six damped (D) models with non-linear structural elements (NLS) and linear or non-linear dampers (LD or NLD). They are representative of the retrofitted building according to the three different design strategies (DS1, DS2 and DS3) fully detailed in Section 3.3.

The nomenclature adopted to identify the different FE models of the case study building is summarized in Table 1.

TABLE 1

TABLE 1. The nomenclature adopted for all the developed FE models-.

The SAP2000 undamped FE model is represented in Figure 2B.

The linear and non-linear FE models, as listed in Table 1, are used to carry out the FE analyses necessary to verify the seismic performances. Equivalent static analyses and non-linear static analyses are carried out on the U-LS and U-NLS models to evaluate the seismic vulnerability of the as-built building and to compute the C/D ratio.

The linear and non-linear dynamic time-history analyses are conducted on both the undamped models and the damped models. The seismic input consists of a set of 7 artificial accelerograms generated with the software SIMQKE (Vanmarcke et al., 1990), using as Intensity Measure the Peak Ground Acceleration (PGA) and in order to be compatible with the design elastic spectrum associated to the “rare” earthquake design level, according to the Italian code (NTC, 2018). However, within the proposed procedure various and/or vector-valued Intensity Measures (Palermo et al., 2014; Castaldo and Miceli, 2023) and different spectral shapes can be adopted to select natural or artificial ground motions. Figure 2C shows the pseudoacceleration response spectra of the 7 artificial seismic records.

The fundamental periods of vibration are determined through a modal analysis conducted on the U-LS model of the structure. The first mode of vibration has a translational mode shape along the X direction and a period of vibration equal to 1.58 s. The second mode of vibration has a translational mode shape along the Y direction and a period of vibration equal to 2.29 s.

3.2 The seismic vulnerability analysis

The assessment of the seismic vulnerability of the as-built structure has been conducted by performing two sets of non-linear static (e.g., pushover) analyses with the floor horizontal forces applied along the X and Y directions. Two along-the-height distributions of lateral floor forces are considered: 1) uniform and 2) proportional to the fundamental modal shape.

Figure 3A shows the pushover curves (continuous line) along the X and Y direction, for both uniform and first-mode proportional lateral loads distribution, in terms of $V_{base}$ vs. $d_{roof}$ along with their corresponding equivalent bilinear curves (dashed line) with an indication of the obtained values of the base shear capacity (F_y*) and ductility capacity (${\mu }_C$), according to equal energy criterion.

FIGURE 3

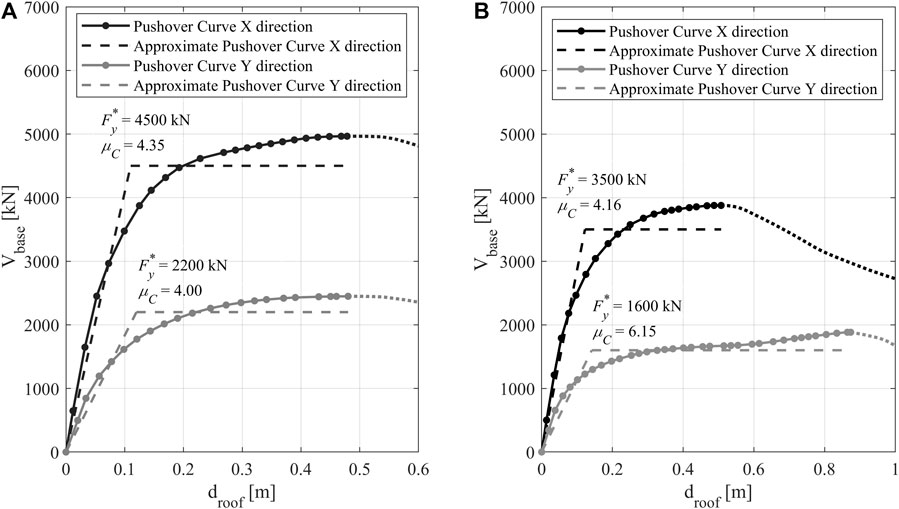
FIGURE 3. Pushover curves as obtained with: (A) uniform distribution of lateral floor forces; (B) lateral forces proportional to the first mode shape.

The base shear demand is evaluated through two equivalent static analyses developed along the X and Y directions. The horizontal floor loads are estimated from the elastic design spectrum ordinate at the fundamental periods ($S_e\left(T_1=1.58s,\eta =1\right)=0.177g$ and $S_e\left(T_1=2.29s,\eta =1\right)=0.121g$ along the X and Y directions, respectively). The seismic weight is associated with the “rare” Serviceability Limit State (SLS) load combination according to the Italian code (NTC, 2018). The resulting total seismic weight of the building is 45,050 kN. The total base shear demand along the X direction is equal to approximately 6,500 kN and, therefore, the C/D ratio of the building in the current state is equal to 0.692. Along the Y direction the total base shear demand is equal to approximately 4,700 kN and, therefore, the C/D ratio of the building in the current state is equal to approximately 0.468.

3.3 Design strategies for the seismic retrofitting

The “direct five-step procedure” adapted to existing buildings, as discussed in Section 2, has been implemented to design the system of added viscous dampers. The damping system configuration is characterized, as shown in Figure 4A, by 16 devices at each storey, 8 of them working along the X direction, while the remaining 8 working along the Y direction.

FIGURE 4

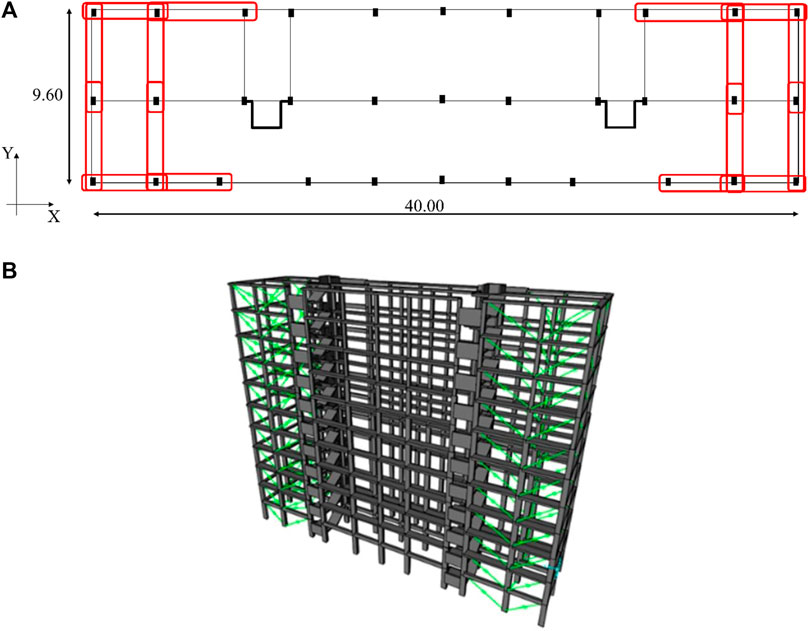
FIGURE 4. (A) Plan view with identification of the spans where the dampers are located. (B) SAP 2000 3D FE model of the building with the added viscous dampers.

The design of the damping system is performed assuming a total target reduction factor (STEP 1) equal to $\overline{{\eta }_{tot}}=0.56$, while the maximum available behavior factor corresponds to the ductility capacity, i.e., $q_{\max }={\mu }_C=4.35$. Based on these initial assumptions, three different design strategies (DS) have been investigated. Each design strategy leads to a different structural response, as qualitatively depicted in Figure 1B, namely, a global elastic structural response when considering the DS3 (based on high viscous damping), an incipient global yielding when considering the DS2 (based on moderate viscous damping), and a limited excursion in the inelastic field when considering the DS1 (based on low viscous damping).

In each DS, a precise value for the equivalent viscous damping ratio (${\overline{\xi }}_{visc}$) is assumed (e.g., ${\overline{\xi }}_{visc}=10\%$ for DS1, ${\overline{\xi }}_{visc}=20\%$ for DS2 and ${\overline{\xi }}_{visc}=30\%$ for DS3) and the corresponding behavior factor q is computed according to the formulation presented in Section 2.2. The computed q value should correspond, assuming the equal displacement rule, to the ductility demand under the design earthquake. Table 2 summarizes the design process (from the left to the right) and the target performances for the three design strategies. For instance, with reference to the DS2, the application of the “direct five-step procedure” leads to the following values of linear and non-linear damping coefficients, equal for all dampers: 8553 kNs/m and 392 kN(s/m)^α along the X direction, while 5352 kNs/m and 252 kN(s/m)^α along the Y direction.

TABLE 2

TABLE 2. Summary of the target performances for the three design strategies.

As already mentioned in Section 2.2, the target reduction factors are evaluated with reference to the global response of the structure (pushover curve). However, in the design phase, also the local response of the structural elements should be checked and the required specific local strengthening interventions must be designed.

4 The verification of the actual seismic performances

The verification of the actual seismic performances of the case study building is carried out through linear and non-linear dynamic time-history analyses, considering the FE models listed in Table 1 and represented in Figure 4B (corresponding to the three design strategies) and the set of the seven artificial seismic records, as described in Section 3.2.

Figure 5 graphically summarizes the main results of the dynamic analyses in terms of $V_{base}$ vs. $d_{roof}$ values along the X and Y directions. Each colored squared mark represents the average values over the 7 seismic responses to the considered earthquake inputs. For the same color class (green, blue, violet and yellow), a color scale from lighter to darker is adopted to distinguish the response associated with the three design strategies, while the black and red marks indicate the response of the linear undamped and damped structures, respectively. The blue marks can be considered as the actual responses since they account for the presence of the non-linear commercial dampers and the non-linear behaviour of the structural elements The pushover capacity curves (continuous black curve) and their corresponding bilinear capacity curves (dashed black curves) are also shown in the figures. It can be noticed that the responses of the three non-linear damped models representative of the different design strategies (blue marks) are close to each other thus indicating that, overall, the three design strategies lead to similar global reductions. In addition, as expected, the DS3 leads to the higher response reduction. This is clearly due to the fact that DS3 is based on a smaller value of total reduction factor ($\overline{{\eta }_{tot}}=0.5$) with respect to the one associated with the other two DSs ($\overline{{\eta }_{tot}}=0.56$).

FIGURE 5

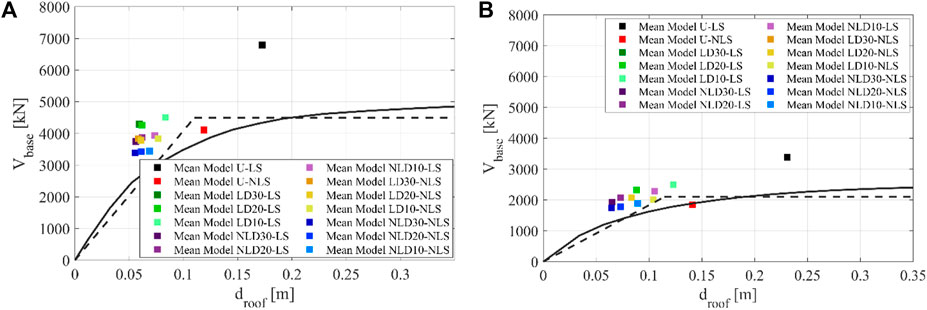
FIGURE 5. (A) Mean structural response along the X direction due to 7 artificial seismic events. (B) Mean structural response along the Y direction due to 7 artificial seismic events.

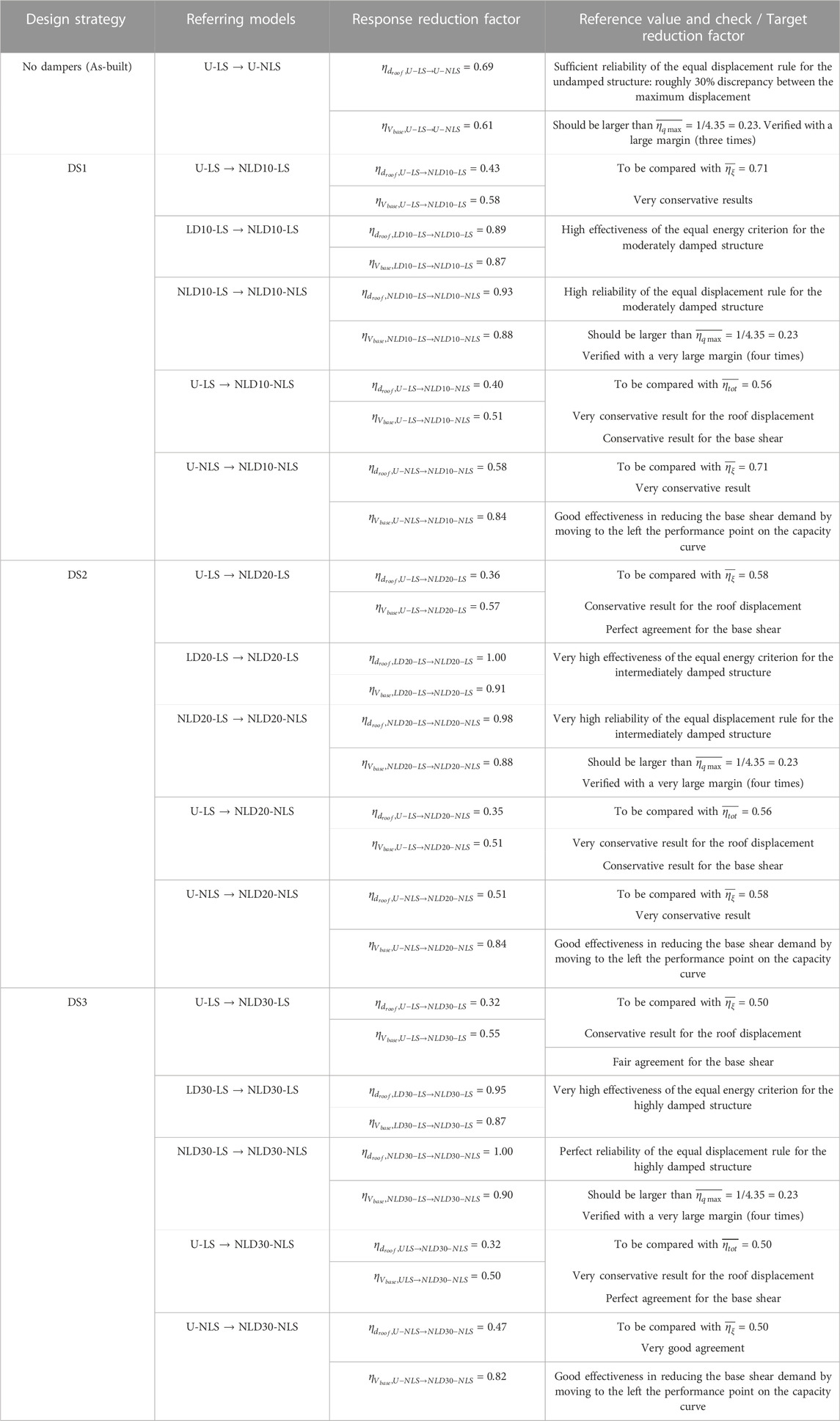
The obtained results can be quantitatively interpreted by introducing several response reduction factors related to the base shear, ${\eta }_{V_{base}}$, and to the peak roof displacement, ${\eta }_{d_{roof}}$, as detailed below:

• The inelastic response due to hysteretic dissipation for the undamped structure. It is quantified by comparing the responses of the U-LS and U-NLS models: ${\eta }_{V_{base},U-LS\to U-NLS}=\frac{V_{base,U-NLS}}{V_{base,U-LS}}$ and ${\eta }_{d_{roof},U-LS\to U-NLS}=\frac{{d_{roof}}_{,U-NLS}}{{d_{roof}}_{,U-LS}}$. The base shear reduction factor should be compared with the reduction factor corresponding to the maximum available behaviour factor $\overline{{\eta }_{q_{\max }}}$, while the roof displacement reduction factor indicates how well the equal displacement rule is satisfied for the undamped structure.

• The viscous energy dissipation due to the dampers. It is quantified by comparing the responses of the U-LS and NLD-LS models: ${\eta }_{V_{base},U-LS\to NLD-LS}=\frac{V_{base,NLD-LS}}{V_{base,U-LS}}$ and ${\eta }_{d_{roof},U-LS\to NLD-LS}=\frac{{d_{roof}}_{,NLD-LS}}{{d_{roof}}_{,U-LS}}$. Both reduction factors should be compared with the target reduction factor $\overline{{\eta }_{\xi }}$.

• The effectiveness of the equivalent energy criterion adopted to dimension the non-linear dampers. It is quantified by comparing the responses of the LD-LS and NLD-LS models: ${\eta }_{V_{base},LD-LS\to NLD-LS}=\frac{V_{base,NLD-LS}}{V_{base,LD-LS}}$ and ${\eta }_{d_{roof},LD-LS\to NLD-LS}=\frac{{d_{roof}}_{,NLD-LS}}{{d_{roof}}_{,LD-LS}}$.

• The inelastic response due to hysteretic dissipation for the damped structure. It is quantified by comparing the responses of the NLD-LS and NLD-NLS models: ${\eta }_{V_{base},NLD-LS\to NLD-NLS}=\frac{{V_{base}}_{,NLD-NLS}}{{V_{base}}_{,NLD-LS}}$ and ${\eta }_{d_{roof},NLD-LS\to NLD-NLS}=\frac{{d_{roof}}_{,NLD-NLS}}{{d_{roof}}_{,NLD-LS}}$. The base shear reduction factor should be compared with the reduction factor corresponding to the maximum available behaviour factor $\overline{{\eta }_{q_{\max }}}$, while the roof displacement reduction factor indicates how well the equal displacement rule is satisfied for the damped structure.

• The theoretical total reduction due to the hysteretic and viscous dissipation. It is quantified by comparing the responses of the U-LS and NLD-NLS models: ${\eta }_{V_{base},U-LS\to NLD-NLS}=\frac{V_{base,NLD-NLS}}{V_{base,U-LS}}$ and ${\eta }_{d_{roof},U-LS\to NLD-NLS}=\frac{{d_{roof}}_{,NLD-NLS}}{{d_{roof}}_{,U-LS}}$. Both response reduction factors should be compared with the total reduction factor $\overline{{\eta }_{tot}}$.

• The actual total reduction due to the hysteretic and viscous dissipation. It is quantified by comparing the responses of the U-NLS and NLD-NLS models: ${\eta }_{V_{base},U-NLS\to NLD-NLS}=\frac{V_{base,NLD-NLS}}{V_{base,U-NLS}}$ and ${\eta }_{d_{roof},U-NLS\to NLD-NLS}=\frac{{d_{roof}}_{,NLD-NLS}}{{d_{roof}}_{,U-NLS}}$. The roof displacement reduction factor should be compared with the reduction factor $\overline{{\eta }_{\xi }}$ due to viscous damping, whilst the base shear reduction factor quantifies the reduction of the excursion of the building into the inelastic range represented by the shift of the performance point to the left of the capacity curve of the structure. Its quantitative value depends, therefore, on two main aspects: the hardening ratio of the capacity curve, the presence or absence of plastic deformations.

Table 3 summarizes the definitions of the response reduction factors and their reference/check values.

TABLE 3

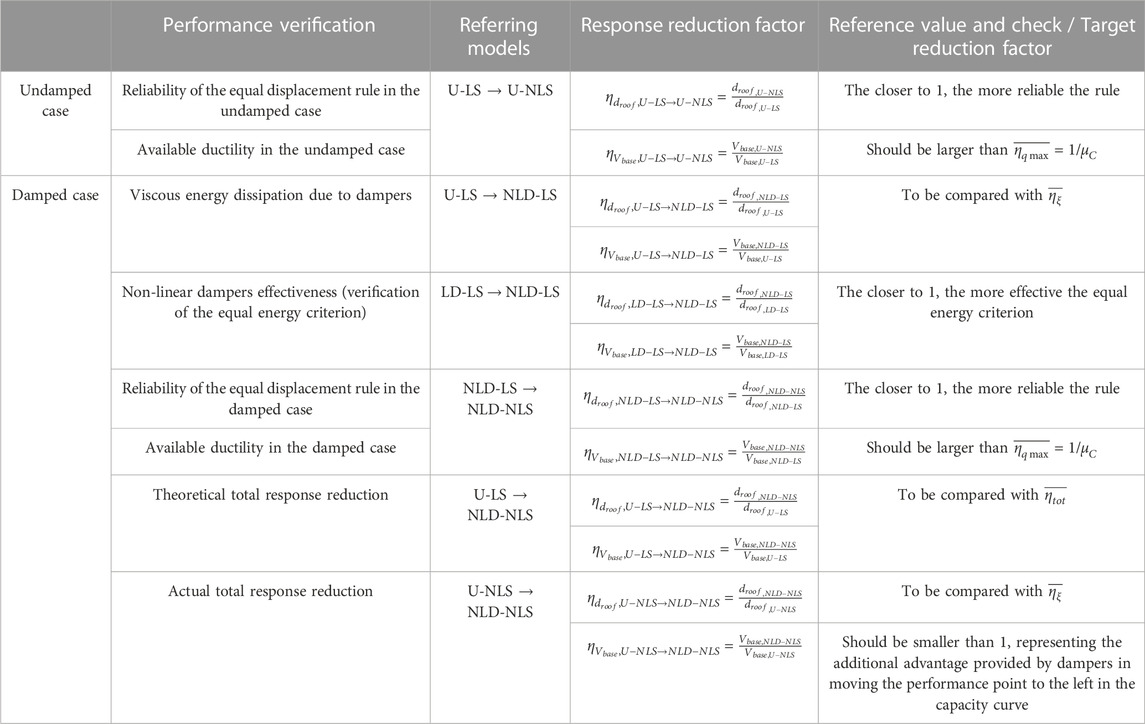
TABLE 3. Summary of the definitions of the response reduction factors and their reference/check values.

For the sake of clearness, Figure 6 provides a graphical representation of the above introduced response reduction factors limited to the DS2. Similar graphs were obtained for the other two design strategies. However, for the sake of conciseness, they are not reported in the paper. The graphical representation of Figure 6 allows us to better appreciate the relationship between the effects of the added dampers and the non-linear structural behaviour on the global structural response and the reduction factors.

FIGURE 6

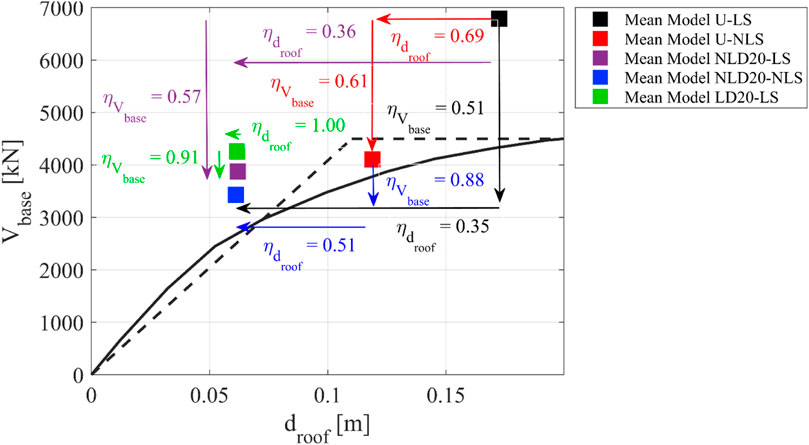
FIGURE 6. Structural response from dynamic time-history analysis of DS2 models with graphical identification of the response reduction factors through arrows.

The values of the response reduction factors obtained for the three considered DS are summarized in Table 4 and compared with the corresponding target values.

TABLE 4

TABLE 4. Values of the response reduction factors obtained for the three design strategies.

The following observations can be made when comparing the performances of undamped linear and non-linear models:

• The actual base shear reduction factor (${\eta }_{V_{base}}=0.61$) is slightly higher than the target one ($\overline{{\eta }_{tot}}=0.56$).

• The obtained value of the roof displacement reduction factor (${\eta }_{d_{roof}}=0.69$) indicates that the non-linear model exhibits a quite reduced peak roof displacement demand with respect to the linear model, thus indicating that the equal displacement rule is not well verified.

The following observations can be made when comparing the performances of the models corresponding to the three different design strategies:

• Overall, the three design strategies lead to a very high energy dissipation capacity (comparison between ${\eta }_{d_{roof},U-LS\to NLD-LS}$ and target damping reduction factor $\overline{{\eta }_{\xi }}$) with actual reduction factors smaller than the target ones. The result indicates that the design procedure leads to conservative estimations.

• Overall, for the three design strategies the damped models with non-linear dampers exhibit a higher effectiveness with respect to the corresponding damped models with linear dampers (both ${\eta }_{d_{roof},LD-LS\to NLD-LS}$ and ${\eta }_{V_{base},LD-LS\to NLD-LS}$ are smaller or equal than 1.00). The higher effectiveness provided by the non-linear dampers was already shown in previous works dealing with the application of the “five-step procedure” for new buildings (Trombetti et al., 2015; Palermo et al., 2018).

• Overall, the three design strategies lead to theoretical global performances (comparison between ${\eta }_{d_{roof},U-LS\to NLD-NLS}$ and total target reduction factors $\overline{{\eta }_{tot}}$) which are higher (+40%–60%) than the corresponding target ones. The result indicates that the design procedure leads to conservative estimations.

• Overall, the three design strategies lead to actual global performances in terms of displacement response (comparison between ${\eta }_{d_{roof},U-LS\to NLD-LS}$ and total target reduction factors $\overline{{\eta }_{tot}}$) which are in line with the corresponding targets.

It should be noted that the obtained numerical results are always affected by model (epistemic) uncertainties that lead to unavoidable discrepancies between the theoretical predictions, either analytical or numerical, and the actual response of the structure (especially in the case of non-linear models (Castaldo et al., 2020)) which hence should be considered in design applications.

5 Conclusion

The paper presented a new formulation of the “direct five-step procedure” for the design of added viscous dampers to be inserted into existing buildings. The main aim of the procedure is to ensure a seismic upgrade through a proper combination of the viscous dissipation provided by the added fluid-viscous dampers together with the hysteretic dissipation associated with the possible excursion of the structural elements into the inelastic regime. The combination of the two sources of energy dissipation leads to the introduction of a total target reduction factor, which can be evaluated as the product of the damping reduction factor (associated with the equivalent viscous damping ratio provided by the added dampers) and the hysteretic reduction factor (corresponding to the inverse of the assumed behavior factor). Clearly, the behavior factor should be selected in order to be compatible with the ductility capacity of the building (i.e., $q<q_{\max }$) as evaluated from the global capacity curve derived through pushover analysis.

The procedure was then applied to an existing reinforced concrete case study building located in Bologna (Italy), by comparing three design strategies based on a different combination of the two sources of energy dissipation. The first strategy is based on a reduced amount of viscous damping with the structure expected to exceed the elastic limit. The second strategy is based on a moderate amount of viscous damping with the structure expected to behave around the yielding point. Finally, the third strategy is based on a high amount of viscous damping which should lead to a full elastic structural response. The seismic performances of the building with the three different damping systems were finally verified through dynamic non-linear time history analyses.

The obtained results indicate that the procedure is capable to achieve the desired target performances in terms of base shear and roof displacement reduction. In fact, for the three analyzed cases, the predictions in terms of base shear and roof displacement were almost in line or conservative with respect to the expectations (i.e., the obtained reduction factors resulted to be smaller than the corresponding target values). This is a desirable property of a design method which is targeted for the preliminary design phase.

In general, higher viscous energy dissipation is observed in the three design strategies leading to higher reductions of the roof displacements with respect to the target ones. This result was already noticed in previous works related to the application of the five-step procedure to new buildings and is mainly attributed to the higher effectiveness of the non-linear dampers with respect to the equivalent linear ones.

The obtained results allow us to state that the method is enough accurate for preliminary design purposes and it is quite effective for a quick comparison between different design strategies. On the other hand, the final design and verifications should, in any case, be conducted by means of dynamic non-linear time history analysis.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

MM: Writing–original draft, Data curation, Investigation, Software, Visualization. MP: Conceptualization, Methodology, Supervision, Writing–review and editing, Validation. SS: Conceptualization, Methodology, Supervision, Writing–review and editing, Funding acquisition, Validation.

Funding

Financial support of Department of Civil Protection (DPC-RELUIS 2019–2021 Grant and DPC-RELUIS 2022–2024 Grant, research line WP15: “Contributi normativi relativi a Isolamento e Dissipazione”) is gratefully acknowledged.

Acknowledgments

The former master students Luca D’Alonzo and Camilla Rita Valente are thanked.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The reviewer DF declared a past co-authorship with the authors MP, SS to the handling editor.

The authors SS and MP declared that they were editorial board members of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bommer, J. J., Elnashai, A. S., and Weir, A. G. (2000). Compatible acceleration and displacement spectra for seismic design codes, Proceedings of the 12th world conference on earthquake engineering, Auckland, New Zealand, January, 2000.

Google Scholar

Castaldo, P., Gino, D., Bertagnoli, G., and Mancini, G. (2020). Resistance model uncertainty in non-linear finite element analyses of cyclically loaded reinforced concrete systems. Eng. Struct. 211, 110496. doi:10.1016/j.engstruct.2020.110496

CrossRef Full Text | Google Scholar

Castaldo, P., and Miceli, E. (2023). Optimal single concave sliding device properties for isolated multi-span continuous deck bridges depending on the ground motion characteristics. Soil Dyn. Earthq. Eng. 173, 108128. doi:10.1016/j.soildyn.2023.108128

CrossRef Full Text | Google Scholar

Chopra, A. K. (2012). Dynamics of Structures. Pearson Education.

Google Scholar

Christopoulos, C., and Filiatrault, A. (2006). Principles of passive supplemental damping and seismic. Pavia, Italy: IUSS Press.

Google Scholar

Comput. Struct. Inc, (2007). SAP2000, “Integrated software for structural analysis & design. Berkeley, CA, USA: Comput. Struct. Inc.

Google Scholar

Constantinou, M. C., and Symans, M. D. (1993). Seismic response of structures with supplemental damping. Struct. Des. Tall Build. 2 (2), 77–92. doi:10.1002/tal.4320020202

CrossRef Full Text | Google Scholar

Constantinou, M. C., and Symans, M. D. (1992). Experimental and analytical investigation of seismic response of structures with supplemental fluid viscous dampers. New York, NY, USA: National Center for earthquake engineering research Buffalo.

Google Scholar

C.S.LL.PP. Consiglio Superiore dei Lavori Pubblici (2019). Circolare n. 7 del 21/01/2019: Istruzioni per l’applicazione dell’«Aggiornamento delle “Norme tecniche per le costruzioni”» di cui al decreto ministeriale 17 gennaio 2018. GU n.35 del 11-2-2019 - Supplemento. Ordinario n. 5. Rome, Italy: Ufficio Pubblicazione Leggi e Decreti - Via Arenula.

Google Scholar

Eurocode 8 (2005). Eurocode 8: design of structures for earthquake resistance-part 1: general rules, seismic actions and rules for buildings. Brussels, Belgium: Brussels Eur. Comm. Stand.

Google Scholar

Foti, D. (2014a). Response of frames seismically protected with passive systems in near-field areas. Int. J. Struct. Eng. 5 (4), 326–345. doi:10.1504/ijstructe.2014.065916

CrossRef Full Text | Google Scholar

Foti, D., Bozzo, L., and Lopez-Almansa, F. (1998). Numerical efficiency assessment of energy dissipators for seismic protection of buildings. Earthq. Eng. Struct. Dyn. 27 (6), 543–556. doi:10.1002/(sici)1096-9845(199806)27:6<543::aid-eqe733>3.0.co;2-9

CrossRef Full Text | Google Scholar

Foti, D. (2014b). On the seismic response of protected and unprotected middle-rise steel frames in far-field and near-field areas. Shock Vib. 2014, 1–11. doi:10.1155/2014/393870

CrossRef Full Text | Google Scholar

Garcia, D. L. (2001). A simple method for the design of optimal damper configurations in MDOF structures. Earthq. spectra 17 (3), 387–398. doi:10.1193/1.1586180

CrossRef Full Text | Google Scholar

Green, N. B. (1987). Earthquake resitant building design and construction. Amsterdam, Netherlands: Elsevier.

Google Scholar

Kasai, K., and Kibayashi, M. (2004). JSSI manual for building passive control technology. PART-1 Man. contents design/analysis methods.

Google Scholar

Landi, L., Pollioa, B., and Diotallevi, P. P. (2014). Effectiveness of different standard and advanced pushover procedures for regular and irregular RC frames. Struct. Eng. Mech. An Int. J. 51 (3), 433–446. doi:10.12989/sem.2014.51.3.433

CrossRef Full Text | Google Scholar

Levy, R., and Lavan, O. (2006). Fully stressed design of passive controllers in framed structures for seismic loadings. Struct. Multidiscip. Optim. 32, 485–498. doi:10.1007/s00158-005-0558-5

CrossRef Full Text | Google Scholar

Liang, Z., Lee, G. C., Dargush, G. F., and Song, J. (2011). Structural damping: applications in seismic response modification, 3. CRC Press.

Google Scholar

Manual, J. (2003). Design and construction manual for passively controlled buildings. Japan: Japan Soc. Seism. Isol. JSSI.

Google Scholar

NTC, (2018). Decreto Ministeriale del 17/01/2018: norme Tecniche per le Costruzioni. Roma, Italy: Ministero delle Infrastrutture.

Google Scholar

Palermo, M., Muscio, S., Silvestri, S., Landi, L., and Trombetti, T. (2013a). On the dimensioning of viscous dampers for the mitigation of the earthquake-induced effects in moment-resisting frame structures. Bull. Earthq. Eng. 11, 2429–2446. doi:10.1007/s10518-013-9474-z

CrossRef Full Text | Google Scholar

Palermo, M., Silvestri, S., Gasparini, G., and Trombetti, T. (2014). A statistical study on the peak ground parameters and amplification factors for an updated design displacement spectrum and a criterion for the selection of recorded ground motions. Eng. Struct. 76, 163–176. doi:10.1016/j.engstruct.2014.06.045

CrossRef Full Text | Google Scholar

Palermo, M., Silvestri, S., Gasparini, G., and Trombetti, T. (2015). Seismic modal contribution factors. Bull. Earthq. Eng. 13, 2867–2891. doi:10.1007/s10518-015-9757-7

CrossRef Full Text | Google Scholar

Palermo, M., Silvestri, S., Gasparini, G., and Trombetti, T. (2017b). Un metodo semplificato per il dimensionamento e l’analisi di strutture equipaggiate con smorzatori viscosi A simplified method for dimensioning and analyzing equipped structures with viscous dampers. Progett. sismica 8 (3), 9–24. doi:10.7414/PS.8.3.9-24

CrossRef Full Text | Google Scholar

Palermo, M., Silvestri, S., Landi, L., Gasparini, G., and Trombetti, T. (2018). A ‘direct five-step procedure’ for the preliminary seismic design of buildings with added viscous dampers. Eng. Struct. 173, 933–950. doi:10.1016/j.engstruct.2018.06.103

CrossRef Full Text | Google Scholar

Palermo, M., Silvestri, S., Landi, L., Gasparini, G., and Trombetti, T. (2016). Peak velocities estimation for a direct five-step design procedure of inter-storey viscous dampers. Bull. Earthq. Eng. 14, 599–619. doi:10.1007/s10518-015-9829-8

CrossRef Full Text | Google Scholar

Palermo, M., Silvestri, S., Trombetti, T., and Landi, L. (2013b). Force reduction factor for building structures equipped with added viscous dampers. Bull. Earthq. Eng. 11, 1661–1681. doi:10.1007/s10518-013-9458-z

CrossRef Full Text | Google Scholar

Palermo, M., Silvestri, S., and Trombetti, T. (2017a). On the peak inter-storey drift and peak inter-storey velocity profiles for frame structures. Soil Dyn. Earthq. Eng. 94, 18–34. doi:10.1016/j.soildyn.2016.12.009

CrossRef Full Text | Google Scholar

Pekcan, G., Mander, J. B., and Chen, S. S. (1999). Fundamental considerations for the design of non-linear viscous dampers. Earthq. Eng. Struct. Dyn. 28 (11), 1405–1425. doi:10.1002/(sici)1096-9845(199911)28:11<1405::aid-eqe875>3.0.co;2-a

CrossRef Full Text | Google Scholar

Ramirez, O. M., Constantinou, M. C., Whittaker, A. S., Kircher, C. A., and Chrysostomou, C. Z. (2002). Elastic and inelastic seismic response of buildings with damping systems. Earthq. Spectra 18 (3), 531–547. doi:10.1193/1.1509762

CrossRef Full Text | Google Scholar

Ramirez, O. M., Constantinou, M. C., Whittaker, A. S., Kircher, C. A., Johnson, M. W., and Chrysostomou, C. Z. (2003). Validation of the 2000 NEHRP provisions’ equivalent lateral force and modal analysis procedures for buildings with damping systems. Earthq. Spectra 19 (4), 981–999. doi:10.1193/1.1622392

CrossRef Full Text | Google Scholar

Ramirez, O. M. (2001). Development and evaluation of simplified procedures for the analysis and design of buildings with passive energy dissipation systems. New York, NY, USA: State University of New York at Buffalo.

Google Scholar

Shea, G. H. (1999). Recommended lateral force requirements and commentary. California, CA, USA: Structural Engineers Association of California.

Google Scholar

Shukla, A. K., and Datta, T. K. (1999). Optimal use of viscoelastic dampers in building frames for seismic force. J. Struct. Eng. 125 (4), 401–409. doi:10.1061/(asce)0733-9445(1999)125:4(401)

CrossRef Full Text | Google Scholar

Silvestri, S., Gasparini, G., and Trombetti, T. (2010). A five-step procedure for the dimensioning of viscous dampers to be inserted in building structures. J. Earthq. Eng. 14 (3), 417–447. doi:10.1080/13632460903093891

CrossRef Full Text | Google Scholar

Singh, M. P., and Moreschi, L. M. (2002). Optimal placement of dampers for passive response control. Earthq. Eng. Struct. Dyn. 31 (4), 955–976. doi:10.1002/eqe.132

CrossRef Full Text | Google Scholar

Takewaki, I. (2011). Building control with passive dampers: optimal performance-based design for earthquakes. Hoboken, New Jersey, United States: John Wiley & Sons.

Google Scholar

Takewaki, I. (2000). Optimal damper placement for critical excitation. Probabilistic Eng. Mech. 15 (4), 317–325. doi:10.1016/s0266-8920(99)00033-8

CrossRef Full Text | Google Scholar

Takewaki, I. (1997). Optimal damper placement for minimum transfer functions. Earthq. Eng. Struct. Dyn. 26 (11), 1113–1124. doi:10.1002/(sici)1096-9845(199711)26:11<1113::aid-eqe696>3.0.co;2-x

CrossRef Full Text | Google Scholar

Trombetti, T., Palermo, M., Dib, A., Gasparini, G., Silvestri, S., and Landi, L. (2015). Application of a direct procedure for the seismic retrofit of a R/C school building equipped with viscous dampers. Front. Built Environ. 1 (14). doi:10.3389/fbuil.2015.00014

CrossRef Full Text | Google Scholar

Trombetti, T., and Silvestri, S. (2004). Added viscous dampers in shear-type structures: the effectiveness of mass proportional damping. J. Earthq. Eng. 8 (02), 275–313. doi:10.1080/13632460409350490

CrossRef Full Text | Google Scholar

Trombetti, T., and Silvestri, S. (2006). On the modal damping ratios of shear-type structures equipped with Rayleigh damping systems. J. Sound. Vib. 292 (1–2), 21–58. doi:10.1016/j.jsv.2005.07.023

CrossRef Full Text | Google Scholar

Vanmarcke, E. H., Cornell, C. A., Gasparini, D. A., and Hou, S. (1990). SIMQKE-I: simulation of earthquake ground motions. Cambridge, MA, USA: Dep. Civ. Eng. Massachusetts Inst. Technol.

Google Scholar

Weng, D. G., Zhang, C., Lu, X. L., Zeng, S., and Zhang, S. M. (2012). A simplified design procedure for seismic retrofit of earthquake-damaged RC frames with viscous dampers. Struct. Eng. Mech. An Int’l J. 44 (5), 611–631. doi:10.12989/sem.2012.44.5.611

CrossRef Full Text | Google Scholar

Whittaker, A. S., Constantinou, M. C., Ramirez, O. M., Johnson, M. W., and Chrysostomou, C. Z. (2003). Equivalent lateral force and modal analysis procedures of the 2000 NEHRP Provisions for buildings with damping systems. Earthq. Spectra 19 (4), 959–980. doi:10.1193/1.1622391

CrossRef Full Text | Google Scholar

Nomenclature