Inelastic response spectra for an integrated displacement and energy-based seismic design (DEBD) of structures

The severe socio-economic impact of recent earthquakes has further highlighted the crucial need for a paradigm shift in performance-based design criteria and objectives towards a low-damage design philosophy, in order to reduce losses in terms of human lives, repair/reconstruction costs, and recovery time (deaths, dollars and downtime). Currently, displacement-based parameters are typically adopted to design/assess the seismic performance of the structures, by limiting the maximum displacement or the maximum interstorey drift ratio (IDR) reached by the structure under different earthquake intensities. However and arguably, displacement-based quantities are characterized by inherent weaknesses, since, for instance, they are not cumulated parameters, thus not able to capture directly the effects of multiple cycles, deterioration and damage cumulation. Therefore, in the last decades, energy-based approaches were investigated and developed in order to establish alternative engineering demand parameters for the assessment of post-event damage through a dynamic energy balance. Towards the main goal of developing an integrated Displacement and Energy-Based Design/assessment procedure (DEBD) for actual use in practice, this research work proposes an innovative approach based on the use of inelastic spectra correlating the energy components with the corresponding maximum displacement response parameters of the structure. In practical terms, the proposal is to further integrate and develop the well-known Direct Displacement-Based Design, by directly adopting the hysteretic energy as an additional design parameter. The energy inelastic spectra are developed through an extensive parametric analysis of Single-Degree-of-Freedom (SDoF) systems, with different nonlinear hysteretic models. In such an approach, the maximum seismic energy demand imparted to a structure can be directly predicted and controlled, whilst distinguishing the various components of the energy balance, including the hysteretic one. The effects of near-field and far-field earthquakes are also investigated. Results show that in the first case the seismic demand is concentrated in the peak of a few large cycles that absorb the demand energy induced by the high component in peak ground velocity in the second case the higher equivalent number of plastic cycles tends to become critical for structures with inadequate structural details and prone to suffer by cumulative cycles and overall plastic fatigue mechanisms.

1 Introduction

In the last decades, the introduction of the Performance-Based Earthquake Engineering (PBEE) concept (SEAOC Vision, 1995; Ghobarah, 2001; Bertero and Bertero, 2002) have led to an innovative seismic design philosophy, in which design objectives for building typologies are identified through the combination of different performance levels of both structural and non-structural components (e.g., fully operational, operational, life safety, and near collapse) and different earthquake intensity levels (e.g., frequent, occasional, rare, and very rare). Currently, three main approaches for the seismic design/assessment of buildings have been developed: i) Force-Based Design (FBD), ii) Displacement-Based Design (DBD), and iii) Energy-Based Design (EBD). The FBD is the most common method, adopted by most of the main international codes such as Standards New Zealand (2004), Standard (2005), ASCE/SEI 7-16 (2017). This method is based on the use 5%-damped elastic spectra, properly scaled by the behavior factors (q), typically selected in line with the typology and characteristics of the building structural skeleton. However, this method presents some criticalities and limits, as pointed out by Priestley (1993). Firstly, the method requires the estimation of the elastic fundamental period T of the equivalent Single-Degree-of-Freedom (SDoF) of the structure and this aspect represents a first critical issue. In fact, the use of the initial stiffness or the cracked stiffness (in many cases by adopting a reduction coefficient equal to 0.5 for the flexural stiffness) for the structural elements can lead to an incorrect estimation of the actual stiffness to be used, namely, the secant stiffness of the force-displacement capacity curve at the yielding point. In fact, as pointed out by Priestley (1998), the stiffness is not constant but proportional to the strength, which is unknown by the definition at the beginning of the design process. Rather, the yielding point (curvature, rotation, displacement) is a constant parameter at a section, member and structural system levels, effectively independent of the strength. Therefore, according to a traditional FBD method a wrong estimation of the fundamental period can affect the seismic design action, potentially leading to an underestimation of the displacement demand. Moreover, the assumption of the Equal Displacement Rule (Muto et al., 1960) represents another main criticism, as potentially (as a cascade effect) affected by the previously mention conceptual mistake associated to the assumption of constant stiffness regardless of strength level, but also due to the fact that it was mostly based on “trends” of an elasto-perfectly plastic hysteresis rule subject to a very limited number (and typology, e.g., far field) of recorded ground motions. Finally, the choice of a Reduction/Behavior factor (R_μ or q) represents another limitation of the method: it is deemed almost impossible to make full use of the behavior factors if the higher values allowed by most of the seismic design codes are adopted and the drift limits are maintained. Consistency with the actual ductility demand of the earthquake and thus of the actual energy dissipation developed by the structural system should be checked to re-evaluate the initially assumed Reduction/Behavior factor.

To overcome the limits of the FDB method, the Direct Displacement-Based Design (DDBD) approach (Priestley, 1998; Priestley et al., 2007) has been developed and proposed since the 1990s. This method is based on the evaluation of secant stiffness to the maximum displacement of the structure (selected by the engineers as a design parameter) for a fixed earthquake intensity, overcoming the issues related to the assumption of the fundamental period (i.e., initial stiffness) value. Then, the design is performed considering an equivalent elastic system (at the design displacement) and the nonlinear behavior is accounted by considering additional viscous damping as a function of the ductility demand, evaluated by assuming the yield displacement of the structure.

In most recent years, the knowledge developed through a DDBD approach, has suggested a compromise solution to “retrofit” the traditional FBD approach, overcoming some key issues and acknowledged limitations. Sporn and Pampanin, 2013 proposed a Corrected-FBD method, which relies upon either an iterative process or a closed-form analytical design method, based on the use of stiffness-strength compatibility domain curves, which also allows to identify the set of compatible and actually useable values of Reduction factors in the design process.

Overall although the DDBD method, as well as the Corrected-FBD method, allow to directly (in the first case) or quasi-indirectly (in the second case) control the maximum design displacement/drift of the structure, not all the limitations of the traditional seismic design approaches based on inherited milestones in the Structural Dynamics and Earthquake Engineering background are eliminated. As an example, the typically adopted equivalent viscous damping value accounts for the (area-based) energy dissipated by the hysteresis rule—related to damage in the case of traditional “monolithic” and ductile structures with discrete plastic hinges—and it is evaluated by empirical relationships with proper correction factors to account for the dynamic response of alternative hysteresis rule (Priestley and Grant, 2005). Therefore, in the DDBD the total hysteretic energy and the cumulated damage to the structure can be controlled but arguably only indirectly using these empirical relationships.

Moreover, the effects of near-field or far-filed earthquakes are considered by adopting different spectral reduction factors to reduce the seismic demand. This is indeed in line with the physic of the problem, since, from an energy point of view, the structure subjected to a near-field earthquake undergoes higher seismic input energy and maximum displacement demand, while it performs fewer cycles to dissipate hysteretic energy (Manfredi et al., 2003; Cheng et al., 2021). However, the approach can be improved as the problem is considered mainly by empirical coefficients to reflect the overall impact on the response for a class of structural systems, without an effective direct control on the relevant energy parameters.

In addition, other limits have been highlighted in the adoption of displacement-based peak quantities only as design parameters. The first one concerns the relationship between the total damage achieved by the structure and the corresponding maximum displacement. Adopting displacement-based peak quantities as sole engineering demand parameters can lead to improper consideration of damage accumulation since, unlike energy-based quantities, they are not cumulative parameters. This issue can be critically emphasized when dealing with mainshock-aftershock earthquake sequences (e.g., Gentile and Galasso, 2021; Pedone et al., 2023).

Substantial research effort has been also devoted to investigating and providing suitable damage parameters to properly evaluate the evolution of damage at both component and structural levels. Towards this scope, a few decades ago the concept of “damage indices” (DIs) has been introduced. When defined in their normalized form, DIs would be typically equal to 1 in the case of failure and equal to 0 in the case of no plastic damage. Conceptually, either displacement-based (e.g., displacement ductility) or energy-based quantities (e.g., hysteresis ductility; Mahin and Bertero, 1981) can be considered to define DIs. Nevertheless, in line with the above discussion, both methods are affected by some limitations.

On one hand, displacement-based quantities are not able to effectively capture the effects of cumulative damage (e.g., repeated cyclic loading and/or the number of plastic excursions), while, on the other hand, characterizing the structural damage by only energy-based quantities may be challenging (e.g., Kazantzi and Vamvatsikos, 2018). Although several studies have proved that designing with energy-based parameters allows for the prediction of displacement-based quantities (e.g., Benavent-Climent, 2011; Morillas and Escolano-Margarit, 2020; Mota-Páez et al., 2021), these methodologies could increase the dispersion of the results in terms of displacement-based quantities from the target (Benavent-Climent and Mota-Páez, 2017), adding further epistemic uncertainties to the inherent and unavoidable aleatory uncertainties associated with the seismic demand. Furthermore, in the latter energy-based approach, displacement-based peak quantities would be assessed only indirectly, whereas a DDBD approach would allow for a direct control of the displacement demand. For this reason, several damage models based on the combination of displacement-based and energy-based quantities have been investigated and proposed in the past (e.g., Banon and Veneziano, 1982; Park and Ang, 1985; Fajfar, 1992; Kunnath et al., 1992; Cosenza et al., 1993). These DIs are typically based on the concept of a low-cycle fatigue failure. Among the others, the DI proposed by Park and Ang. (1985) is arguably the most widely adopted in the literature. In this context, research effort has been also devoted to investigating the relationship between the dissipated energy and displacement ductility (e.g., Akiyama, 1999; Akiyama, 2008; Benavent-Climent et al., 2021). However, some limitations can be highlighted when DIs are considered to characterise structural damage. Among others, one of the most relevant limitations is related to the load history, which can significantly affect the amount of hysteretic energy. Moreover, Cosenza et al. (1993) highlighted that the cycle amplitude is also a relevant parameter, since it has been proved that cycles with limited plastic deformation are less relevant to structural damage than cycles with large plastic deformations. For these reasons, Kappos, 1997 pointed out that DIs should be defined and calibrated considering standardized testing procedures (i.e., with well-defined load history) and a large amount of experimental data. Finally, a performance-based design framework accounting for residual deformation as an additional complementary damage parameter has been proposed by Pampanin et al. (2002), Pampanin et al. (2003), Christopoulos et al. (2003), Christopolous et al. (2004) The above authors highlighted that existing DIs have been typically calibrated to effectively characterize the performance of structures near collapse (i.e., DI = 1), while they seem unable to provide reliable information for lower performance levels (e.g., damage control). Thus, a residual deformation damage index (RDDI) for both structural and non-structural components has been introduced. Moreover, the concept of a residual deformation-based performance matrix has been proposed, which allows identifying different performance levels through a combination of maximum interstory drift and residual deformation. Inelastic residual and residual/maximum displacement spectra were also presented for various hysteresis rules. A further development into a probabilistic framework inclusing maximum and residual displacement for both assessment and design was proposed by Uma et al. (2006).

Based on the above discussion, it is evident that an hybrid and integrated method, capable to combine the latest advances and know-how developed in the earthquake engineering environment and thus starting from a Direct-Displacement Based Design method including residual deformation with integrated features from an Energy-Based Design (EBD) approach could and should be developed and proposed as a more comprehensive and suitable method for the seismic design and assessment of structures under seismic action.

Referring to the original features and latest developments of Energy-based approaches (Figure 1), some of the key advantages could be recognized as: i) the use of scalar cumulative measures (i.e., energy): and ii) the use of complementary and more damage-related information than the sole displacements, such as the number of equivalent cycles. However, as a primary well-known limitation, differently from a displacement-based approach, the energy-based methods still require a better definition of damage state thresholds in terms of hysteretic energy, as well as a well-established design procedure for structures. Thus, research effort is still needed for a reliable implementation of an energy-based approach in seismic engineering. Alternatively and arguably more practically, the combination and integration of the key features of the various method can lead to a powerful and robust design approach.

FIGURE 1

FIGURE 1. Schematic flow chart of FBD (left), DDBD (center) and EBD (right) procedures.

Therefore, this paper aims to investigate the seismic response of different structures from an energy point of view, with particular focus on the development of inelastic input energy spectra and propose an innovative Integrated (Direct) Displacement and Energy-Based Design (DEBD) approach, which offers the advantage of directly measuring/estimating maximum displacements and energy components, using their respective displacement-based and energy-based approaches. In that direction, firstly an extensive parametric analysis of SDoF systems, involving several alternative nonlinear hysteretic models subject to either near-field and far-field recorded ground motions is carried out to develop inelastic input energy spectra. The derived spectra are thus used to predict the maximum seismic input energy demand imparted to a structure and assess the different components of the energy balance. In such a way, the hysteretic energy can be selected at the beginning of the design process for a given earthquake intensity as an additional and complementary design targeted parameter to the maximum (and residual) displacement/drift. An illustrative application of the proposed integrated DEBD approach is thus presented, considering an innovative low-damage (rocking-dissipative) unbonded post-tensioned wall building. A comparison between the proposed DEBD and the more-widely-adopted FDB and DDBD approaches is also carried out. In Section 2 an overview of the key features of energy-based approaches is presented. The inelastic energy spectra are obtained in Section 3, through different parametric analysis of near-field and far-field earthquakes. Subsequently in Section 4 a flowchart shows the application of the proposed integrated Displacement and Energy-Based Design (DEBD) approach, based on inelastic energy spectra illustrated in Section 3. Finally a design example of a DEDB approach is presented and compared with more traditional FBD and advanced DDBD approaches, in order to demonstrate the possibility and reliability to control in the design phase both the maximum (and residual) displacement/drifts as well as the hysteretic energy under seismic action.

2 Origin of the energy approach

Considering, for the sake of simplicity, a SDoF system and applying the definition of work to the force equilibrium equation of motion (1), the energetic-based Equation 3 can be obtained by integrating over the time, $dt$, the product between the equilibrium forces with the instantaneous displacement of the structure $du=\dot{u}dt$ (2) (Akiyama, 1985; Akiyama, 1988). The integration can be carried out either in terms of relative or total displacement of the system with respect to the ground: the two formulations coincide without loss of generality in the periods between T = 0.1 s and T = 4 s (Uang and Bertero, 1988; Uang and Bertero, 1990).

$m\ddot{u}+c\dot{u}+ku=-m{\ddot{u}}_g(1)$

$\int m\ddot{u}\dot{u}dt+\int c{\dot{u}}^{2}dt+\int ku\dot{u}dt=-\int m{\ddot{u}}_g\dot{u}dt(2)$

$E_k+E_d+E_s+E_h=E_i(3)$

In Equation 1, m is the mass of the system, c is the viscous damping coefficient, k is the stiffness of the structure, u is the relative displacement of the structure, $\dot{u}$ is the relative velocity, $\ddot{u}$ is the relative acceleration and ${\ddot{u}}_g$ is the ground acceleration seismic forcing. The first term of Equation 2 E_k represents the Kinetic Energy; E_d is the viscous Damping Energy, accounting for specific phenomena such as friction, microcracking of the structural elements and soil-foundation interaction; the third term of Equation 2 represents the energy absorbed by the structure E_a, composed of the recoverable Elastic Energy E_s and the Hysteretic Energy E_h, representing the energy dissipated by plastic deformations of the structure; finally E_i is the seismic Input Energy, representing the amount of energy imparted to the construction. It is worth noting that the amount of input energy is not fixed for a given earthquake record, and as a result, the same consideration is valid for the hysteretic energy. In fact, input energy depends on the characteristics of the specific structure, e.g., the fundamental period, the damping value and slightly both the force-deformation backbone curve and the cyclic hysteretic behavior (Decanini and Mollaioli, 2001; Pampanin, 2003).

An important parameter in the EBD approach is the ratio between the Hysteretic Energy and the Input Energy $E_{\mathrm{hyst}}/E_{\mathrm{inp}}$. This ratio can be assessed, in a very simplified way, through Equation 4 (Akiyama, 1988).

$\frac{E_{\mathrm{hyst}}}{E_{\mathrm{inp}}}={\left(\frac{1}{1+3\xi +1.2\sqrt{\xi }}\right)}^2(4)$

However, as recently demonstrated by Escolano-Margarit et al., 2023, the Akiyama’s expression should be used for large levels of ductility, but it is inaccurate for low levels of ductility. Other relationships about the $E_{\mathrm{hyst}}/E_{\mathrm{inp}}$ ratio are presented in Decanini and Mollaioli, 2001.

In the approach adopted by the Building Research Institute (2009) for structures with displacement-dependent dampers, the hysteretic energy is directly related to the equivalent velocity V_eq (5):

$V_{eq}=\sqrt{\frac{2E_h}{m}}(5)$

Where V_eq can be assumed to be close to the pseudo-velocity $S_{pv}$ (typically, $S_{pv}$ is an upper-bound of $V_{eq}$); the $S_{pv}$ can be easly obtained from the pseudo-acceleration value (Benavent-Climent et al., 2021).

Past research works in literature investigated the use of energy-based quantities in order to evaluate the seismic performance of buildings. Among many others, an example of the dynamic response of structures over time in terms of energy-based quantities can be found in Pampanin et al. (2001), Pampanin et al. (2003), where a first-in-literature energy term comparison between a recently developed low-damage PRESSS hybrid technology (PREcast Seismic Structural Systems, Priestley et al., 1999), based on jointed ductile connections with unbonded post-tensioned rocking-dissipative mechanisms, and traditional monolithic technology (Reinforced Concrete, RC, buildings or steel structures) was presented. Results show that the kinetic energy of the system oscillates around zero, while the viscous damping energy increases over time, as well as the hysteretic energy after the yielding of the structure. It can be highlighted that the kinetic energy of the hybrid system is higher than a traditional monolithic system due to the higher relative velocity. The energy absorbed $E_a$ in the hybrid system is characterized by more marked oscillations due to the recoverable elastic component. At the end of the ground-motion excitation, after the free oscillations, the kinetic energy is zero and it is possible to observe only the non-recoverable hysteretic energy and the viscous damping energy, which are equal to the seismic input energy imparted to the structure for the energy balance equation (Figure 2A). As noted in those earlier contributions, an energy-based analysis can well explain the actual low-damage mechanisms of a rocking-dissipative unbonded post-tensioned technology, when compared to a traditional (ductility = damage) reinforced concrete solution. The peculiar self-centering and dissipative mechanism of a hybrid system, represented by a flag-shape hysteresis rule, allows to dissipate/release/accommodate the higher input energy motion through a very effective distribution into kinetic motion (forced and then free-oscillation of the rocking system) and an innovative (ductility not equal to damage) hysteresis energy dissipating mechanism. In Christopoulos and Filitrault (2006), the energy balance during an earthquake is explained through a rain flow analogy (Figure 2B). The water entering from the roof of the structure represents the seismic input energy. Thus, the inertia activates the masses kinetic energy and the deformation of the structural elements. Vibration energy is deemed as a continuous transfer of kinetic energy into strain energy and vice versa. During the vibration energy, part of the energy is dissipated by the viscous damping of the structure. If the system is perfectly elastic, the dynamic energy balance would be defined by the energy components mentioned above. Otherwise, when the structural elements overcome their strength capacity, the progressive damage and/or plasticization of the structure causes the increase of hysteretic (plastic) energy.

FIGURE 2

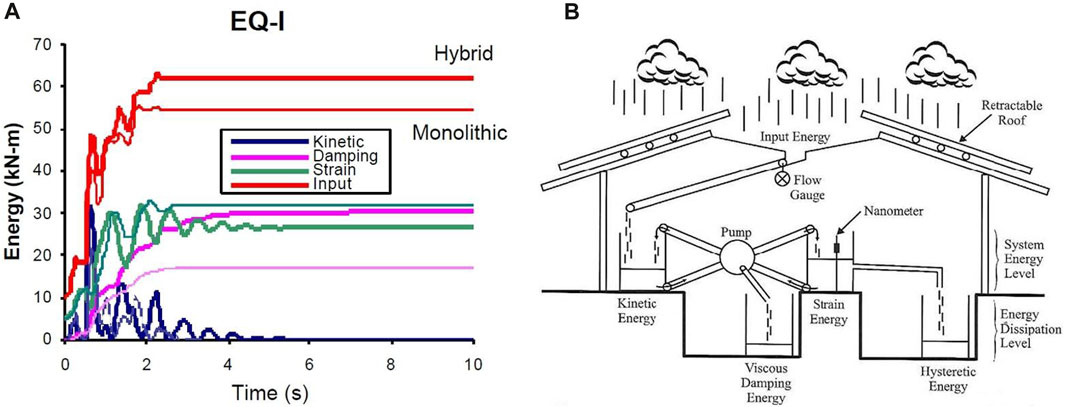
FIGURE 2. Energy-based concept illustrations. (A) Comparison of energy time-history between hybrid and traditional technology (Pampanin, 2003). (B) Rain flow analogy during an earthquake (Christopoulos and Filitrault, 2006).

Decanini and Mollaioli. (2001) and later Mollaioli et al. (2011) studied a methodology for the assessment of the seismic energy demands imposed on structures. In these works, inelastic design energy spectra were developed and the authors pointed out that ductility is a non-negligible parameter in the determination of the inelastic input energy spectrum. Other important parameters are the site-source distance, the characteristics of the soil and the period of vibration. Then it is also observed that the ductility demand strongly affects the hysteretic energy. Specifically, its increase especially occurs for very rigid structures. However the hysteretic cycle model affects much more in the evaluation of the hysteretic energy and seismic input energy ratio (E_hyst/E_inp), rather than only in the evaluation of the seismic input energy.

Many researchers proposed energy-based design methods for different structural systems. Akbas et al. (2001) performed statistical analyses to study energy input and dissipation. The authors emphasized the relationship between the energy input and structural properties, the energy distribution throughout the structure, and the energy dissipation capacity of the structure and the structural elements. Chou and Uang. (2003) investigated the distribution of hysteretic energy and proposed an energy-based design approach. The energy-based design for self-centering concrete frames was studied by Song et al. (2021). They outlined an energy-based design based on a proposed damage model; hysteretic energy demand was introduced as a key design parameter to consider the effects of cumulative damages on structures. In Benavent-Climent et al. (2010) design energy input spectra are presented for moderate-to-high seismicity regions. Approaches concerning the energy-based seismic design methodology were proposed by Leelataviwat et al. (2007) and Donaire-Ávila et al. (2017).

Finally, the equivalent cycles performed by the structures represent another critical damage indicator that can be obtained by adopting an energy-based approach. This quantity provides the number of plastic cycles at the maximum plastic excursion value developed by the structure to dissipate the hysteretic energy induced by the seismic demand. For a perfectly plastic system this value is defined as (Eq. 6):

$n_{eq}=\frac{E_h}{V_y\left({\Delta }_{\mathit{max}}-{\Delta }_y\right)},(6)$

The seismic input energy (seismic demand) is generally related to the PGV, the amplification factor of the velocity and the duration of the earthquake excitation (Manfredi et al., 2003). The highest values of input energy are typically in the zone near the fracture where the earthquake occurs. However, its peak is given by the velocity which rapidly decreases with the distance, while the number of plastic cycles tends to progressively increase by increasing the distance from the fault. The damages caused by the near-field earthquakes are mainly due to the PGV and Incremental Velocity IV (i.e., the area underlying the highest pulse). The ground movement under near-fault leads the structure to absorb a large amount of energy with few plastic cycles. Hence cyclical damage to structures is generally more important for far-field earthquakes, while for near-field earthquakes it governs the response to peak demand. Structures need construction details for the structural and non-structural elements, in order to ensure good cyclic behavior.

3 Inelastic response spectra: parametric analysis

3.1 Description of the case-study structures and modelling approach

In order to develop inelastic design spectra for different typologies of structures, a parametric analysis of the seismic performance of different SDoF systems is performed. The case-study structures are characterized by the same force-displacement monotonic behavior, but different hysteresis rules. Specifically, the geometry of the system is described by the fundamental period T and the spectral acceleration S_a. Constant strength inelastic design spectra for each S_a values are presented (Mahin and Lin, 1983 and Pal et al., 1987), rather than for fixed ductility values (such as in Iwan, 1980; Chopra and Goel, 1999), in order to obtain inelastic spectra more applicable during the structure design phase. To represent the behavior of several structures, 15 different periods are selected with fine discretization for lower values, to simulate different heights and construction technologies. Moreover, six values between 0.05 and 0.5 g are considered for spectral acceleration (S_a). According to Kam et al. (2008) a value of 0.5 g is representative of a moderate level of acceleration, in order to protect the non-structural contents. Strength degradation is not included in the model. Finally, different hysteretic behaviors are considered to account for the different construction technologies, namely: Perfect Elastic (OSC), Elastoplastic (EP), Takeda Thin (TKS), Takeda Fat (TKF), Nonlinear Elastic (EL), and Hybrid (HYB). For each hysteretic behavior, the analysis is carried out considering both no hardening (r = 0) and hardening equal to 5% of the initial elastic stiffness (r = 0.05). The selected values for both the fundamental period and the yielding acceleration S_ay, as well as the considered hysteresis rules, are listed in Figure 3.

FIGURE 3

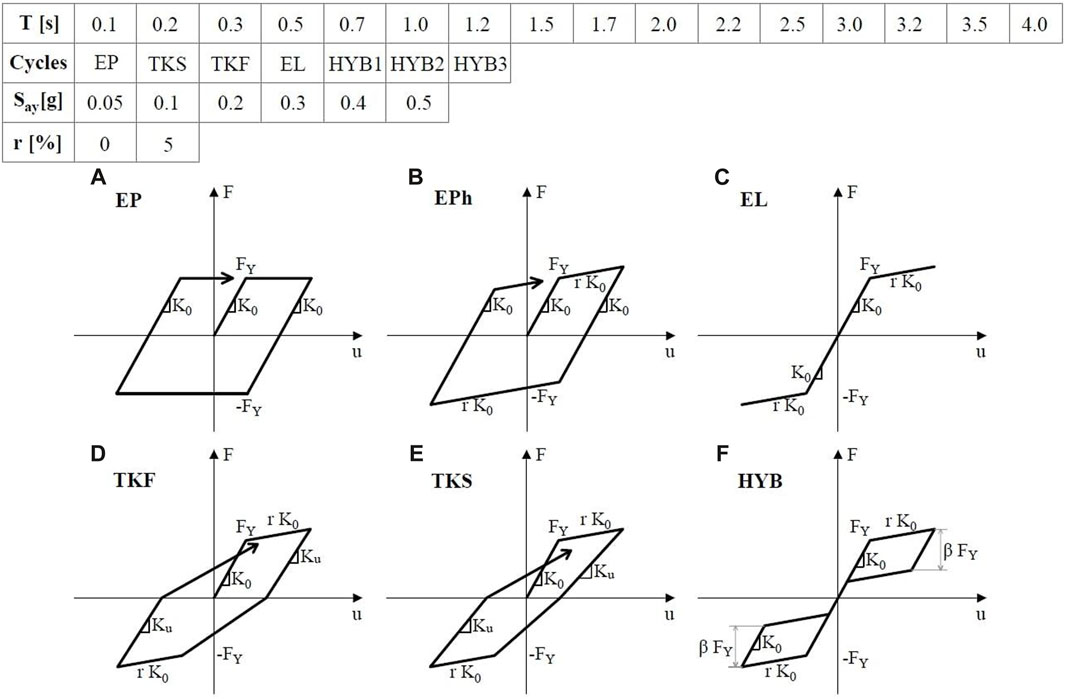
FIGURE 3. Alternative Hysteretic cycles. (A): Perfect Elastoplastic; (B): Elastoplastic with Hardening; (C): Nonlinear Elastic; (D): Takeda Fat; (E): Takeda Thin; (F): Hybrid Self-Centering.

The Elastoplastic rule (EP, Figure 3A, B) is deemed as representative of the cyclic behavior of steel or seismic isolated structures. Concerning the Takeda hysteresis rule (Otani, 1974), this hysteretic model is typically adopted for Reinforced Concrete (RC) structures, since it allows to consider the degradation of stiffness due to cracks and loss of bond. Two main parameters must be defined in the Takeda rule: the unloading stiffness α, the reloading stiffness β. Hence, two alternative behaviors are considered in this study: a Takeda Fat (TKF, Figure 3D), characterized by an unloading stiffness α equal to 0.3 and a reloading stiffness β equal to 0.6, and a Takeda Thin (TKS, Figure 3E) model, with α equal 0.5 and β = 0. The former (TKF) is representative of ductile RC frames (i.e., beam-sway mechanism), while the latter (TKS) is representative of structures with high axial load stress, in which a higher inherent re-centering behavior is observed (Priestley et al., 2007). To represent hybrid low-damage structures such as PRESSS or Pres-Lam technologies, consisting of a combination of a nonlinear elastic behavior to represent the self-centering contribution provided by the unbonded post-tension tendons and an elastoplastic cycle for the energy dissipation contribution of the external hysteretic plug and play, the Flag-Shape hysteretic cycle is selected. This model requires the definition of an additional parameter, namely, β, the contribution ratio (to the total capacity) of the hysteretic dissipation. In this study, three different β values are considered, i.e., 0.2, 0.4, and 0.6 (HYB, Figure 3F). Finally, the Nonlinear Elastic case is also considered in the parametric analysis (EL, Figure 3C), as representative of structures characterized by earthquake-resistant elements with only unbonded post-tension tendons and without supplemental dissipative components.

The analyses are performed using the structural software Ruaumoko2D (Carr, 2007). From a computational point of view, the SDoF system is modelled through a mass on a roller sliding in the horizontal direction and connected by an elastic translational spring; viscous coefficient is modelled considering a Rayleigh damping proportional to the initial stiffness of the system and 5% of critical damping. The length of the spring and the mass are unitary to generalize the results and for this reason the nonlinear yielding forces F_y match with S_ay values.

3.2 Ground-motion selection

To evaluate the nonlinear dynamic behavior of the structures, the suite of unscaled ground motions of the Peer West 2 database (Pacific Earthquake Engineering Research Center, 2000) are used. The site of L’Aquila (Italy) is considered in this study. The acceleration spectrum is carried out according to the Italian building code (D.M. 17/01/2018. Norme Tecniche per le Costruzioni (NTC), 2018), considering a building life equal to 100 years, Importance Level II (usage class) typical or residential buildings, usage coefficient CU equal to 1 and soil type E. All the selected accelerograms are “as recorded,” i.e., not scaled. Ground motion records are selected considering either near-field earthquakes, with a site-source distance less than 10 km and “Pulse—like Records” type specified in the database, and for far-field earthquakes, where the distance is beyond 20 km and the type is described in the database as “NO Pulse—like Records”. The considered range of magnitudes is consistent with the Probabilistic Seismic Hazard Analysis (PSHA) of the site of interest, i.e., between 5 and 7. Overall, 84 near-field earthquakes and 25 far-field earthquakes are adopted (Supplementary Table S1 ). Figure 4 shows the individual acceleration, displacement and velocity spectra of the selected records (for both near-field and far-field earthquakes) and their average spectra.

FIGURE 4

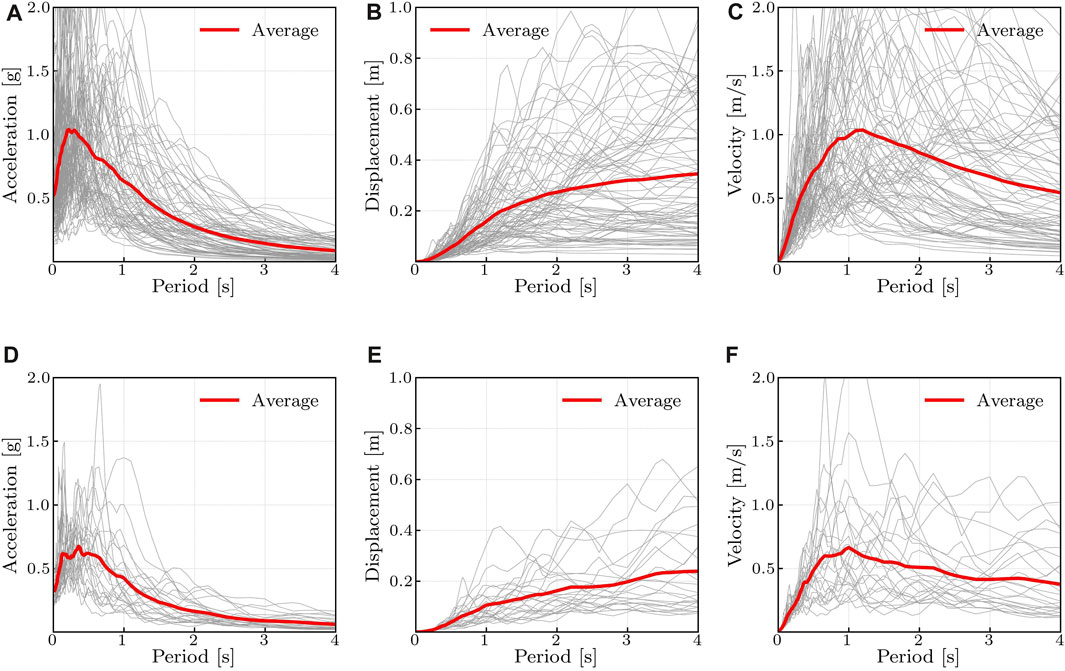
FIGURE 4. Response spectra of the selected ground motions. (A): Near-field absolute acceleration. (B): Near-field displacement. (C): Near-field spectral velocity. (D): Far-field absolute acceleration. (E): Far-field displacement. (F): Far-field spectral velocity.

3.3 Results and discussion

In order to facilitate the discussion, the results of the performed parametric analyses can be grouped into four main blocks.

- Near-field records and SDoF systems with no hardening (r = 0);

- Near-field records and SDoF systems with hardening (r = 5%);

- Far-field records and SDoF systems with no hardening (r = 0);

- Far-field records and SDoF systems with hardening (r = 5%).

For the sake of brevity, only the main obtained results are discussed below, including a full description response spectra of the SDoF systems with zero hardening under near-field records and a comparison between near-field and far-field earthquakes for the self-centering SDoF systems with either r = 0 and r = 0.05.

3.3.1 Near-field records and SDoF systems with no hardening

Concerning the seismic input energy per unit mass, the final cumulative value induced by each earthquake is considered, in order to correlate it with the final hysteretic energy, representing the progressive damage to the structure. Figure 5 shows the seismic input energy demand for each considered hysteresis rule and fixed values of yielding point, espressed in terms of S_ay, in order to define the seismic input energy inelastic spectra.

FIGURE 5

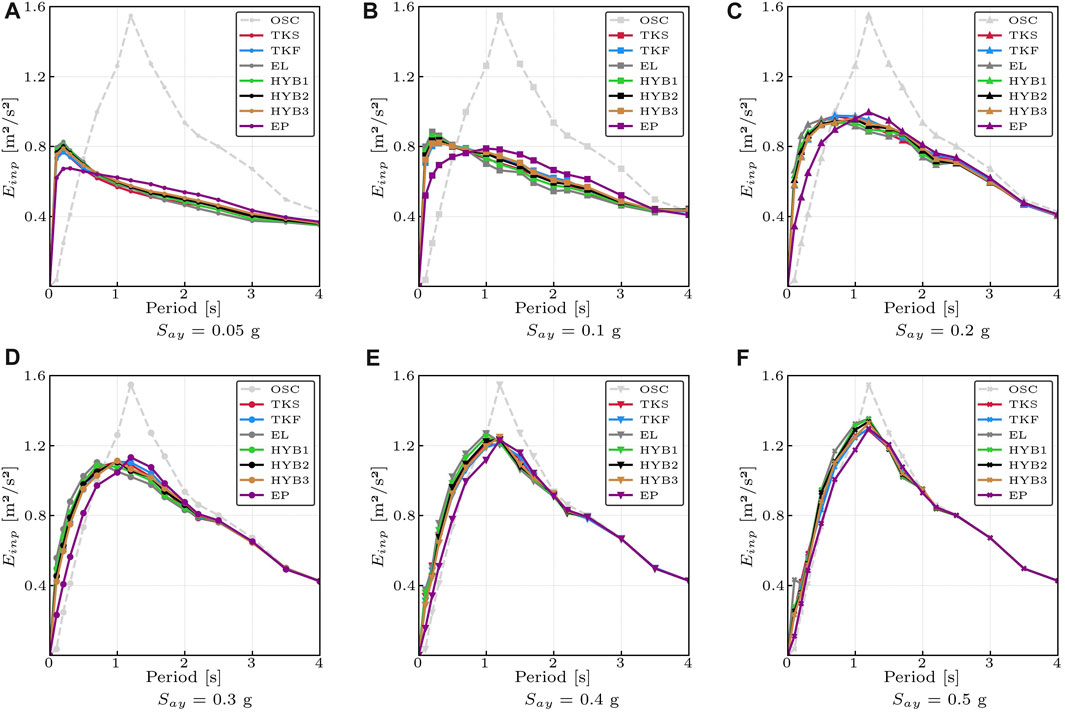
FIGURE 5. Comparison of the average final seismic input energy inelastic spectra varying the yielding acceleration S_ay—Near-field case. Perfect Elastic (OSC), Takeda Thin (TKS), Takeda Fat (TKF), Nonlinear Elastic (EL), Self-Centering Hybrid (HYB), Elastoplastic (EP). (A): S_ay = 0.05 g. (B): S_ay = 0.10 g. (C): S_ay = 0.20 g. (D): S_ay = 0.30 g. (E): S_ay = 0.40 g. (F): S_ay = 0.50 g.

By increasing the yielding acceleration S_ay, the seismic input energy tends to impart the same energy as the elastic oscillator with 5% of critical damping. This result is consistent with the observation of Decanini and Mollaioli. (2001), which concluded that as the ductility decreases, the seismic input energy increases; by increasing the ductility, on the other hand, the peak of the spectrum shifts towards the lower periods. For medium-high values of spectral yielding acceleration S_ay, the seismic input tends to be constant with any hysteretic cycle: For low values of S_ay instead, it can be noted that for very rigid structures, it is the hysteretic cycles with greater re-centering behavior that impart greater input energy (HYB1, HYB2, HYB3 and EL), compared to traditional monolithic technologies (especially elastoplastic EP, where the seismic input energy is about 80% of that low-damage seismic input energy). Finally, for very flexible structures, the seismic input energy tends to be constant for all hysteretic models and for each yield point S_ay.

Results of the hysteretic energy and seismic input energy ratio E_hyst/E_inp inelastic spectra, are shown in Figure 6.

FIGURE 6

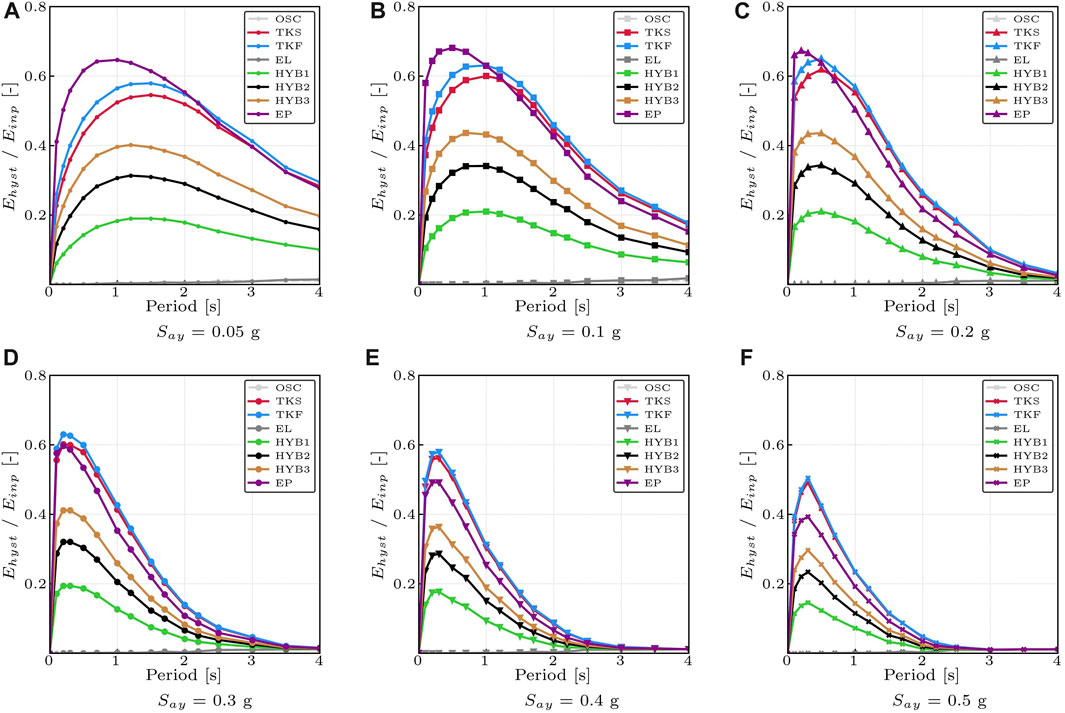
FIGURE 6. Comparison of the average hysteretic energy and seismic input energy ratio E_hyst/E_inp inelastic spectra varying S_ay—Near-field case. (A): S_ay = 0.05 g. (B): S_ay = 0.10 g. (C): S_ay = 0.20 g. (D): S_ay = 0.30 g. (E): S_ay = 0.40 g. (F): S_ay = 0.50 g.

The hysteresis rule is the fundamental parameter governing the amount of energy dissipated by hysteresis. It can be noted that traditional systems (i.e., EP, TKS, and TKF) are characterized by the greatest hysteretic energy contribution regardless of the yielding S_ay values. However, for traditional monolithic structures, this implies important cumulative residual displacement and damage. Increasing the spectral yielding acceleration, less dissipation of hysteretic energy is reached (due to an increase of the re-centering behavior given by the elastic component of strength). By increasing the S_ay value, the peak of the Input Energy spectrum shifts towards period values ​​corresponding to rigid structures, with a lower contribution of the hysteretic ratio, E_hyst/E_inp, and this is consistent with Cheng et al. (2021) and Fajfar and Vidic (1994). For low values of S_ay, the EP cycle has higher values ​​of E_hyst/E_inp ratio, with a maximum values equal to almost 70% (considering period values of lower than 0.5 s). As expected, the TKF hysteresis rule dissipates more hysteretic energy than the TKS, because the latter is used to simulate the axial load of the structures, which allows greater re-centering component. Finally, considering a flag-shape behavior, higher values of the area of the cyclic hysteresis loops (i.e., higher β values) lead to higher hysteresis dissipative contribution; in fact, the third hybrid hysteretic model, namely, HYB3 (with β = 0.6), has the highest hysteretic component. Figure 7 shows some classical inelastic spectra in terms of maximum displacement, absolute acceleration, and velocity for different level of spectral yielding acceleration values S_ay.

FIGURE 7

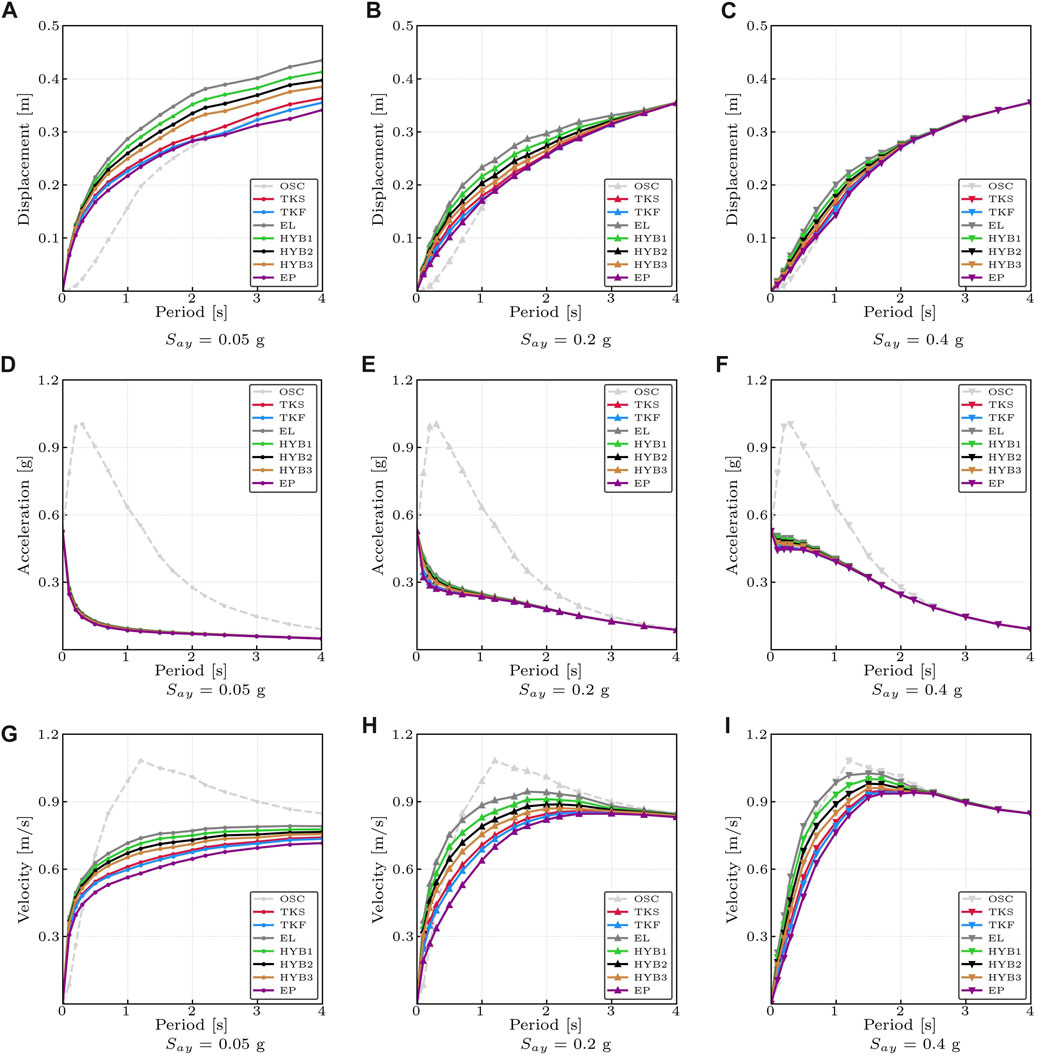
FIGURE 7. Examples of the maximum response inelastic spectra varying S_ay—Near-field case. (A): Maximum Displacement—S_ay = 0.05 g. (B): Maximum Displacement—S_ay = 0.2 g. (C): Maximum Displacement—S_ay = 0.40 g. (D): Acceleration—S_ay = 0.05 g. (E): Acceleration—S_ay = 0.2 g. (F): Acceleration—S_ay = 0.40 g. (G): Velocity—S_ay = 0.05 g. (H): Velocity—S_ay = 0.2 g. (I): Velocity—S_ay = 0.40 g.

Worth reminding that Equal displacement rule (EDR) is typically considered applicable between the elastic and inelastic oscillators for medium-low stiffnesses. For rigid structures, the classical seismic design approaches modify the EDR assumption into an Equal Energy approach by increasing the expected inelastic displacement. In fact, as mostly confirmed in Figures 7A–C, the nonlinear behavior increases the displacement response of more rigid structures. The latter result is further amplified by decreasing the S_ay values, since the strength difference between the inelastic and elastic oscillator increases (Fajfar, 2000). The peak displacement responses are higher for hysteretic cycles which have greater re-centering elastic component (in order: EL, HYB1, HYB2, HYB3), while the more dissipative hysteretic cycles show lower values. Then, it is possible to observe that by increasing the yielding point S_ay, both the absolute acceleration and the relative velocity of the nonlinear oscillators increase. The hysteretic cycle does not affect the inelastic absolute acceleration spectra, except for short periods in which the elastic component amplifies the effect. Nonlinear elastic (EL) or low-damage hybrid (HYB) systems have the highest velocity response: this is confirmed by the higher kinetic and dissipation energy components due to the viscous damping in the dynamic energy balance.

3.3.2 Response spectra of SDoF systems with hardening r = 5%

In this paragraph, a comparison of inelastic spectra (r = 0 and r = 0.05) is reported. For the sake of brevity and without loss of generality, it is decided to report the results of the HYB2 cycle only (which is also used in the worked example in Section 4). Firstly, the effects of near-filed earthquakes are investigated. Figure 8 shows that considering hardening behavior equal to 0.05 (continuous line), in general, a small increase in the seismic input energy demand is observed (Figure 8A). This difference is substantial for lower period values. Regarding the energy ratio E_hyst/E_inp (Figure 8B) hardening behavior has little effect. The maximum displacement decreases due to the modelling of the hardening, especially for low values of the yield point S_ay (Figure 8C). Concerning the absolute acceleration and velocity, both increase if the hardening behavior is included (Figures 8D, E). Finally, the most relevant effect of the hardening behavior is the reduction of the residual displacement at the end of the earthquake and this is showed in Figure 8F for EP cycle, because low-damage systems have negligible residual displacement. The latter results are consistent with Christopoulos et al., 2003, Christopoulos et al., 2004.

FIGURE 8

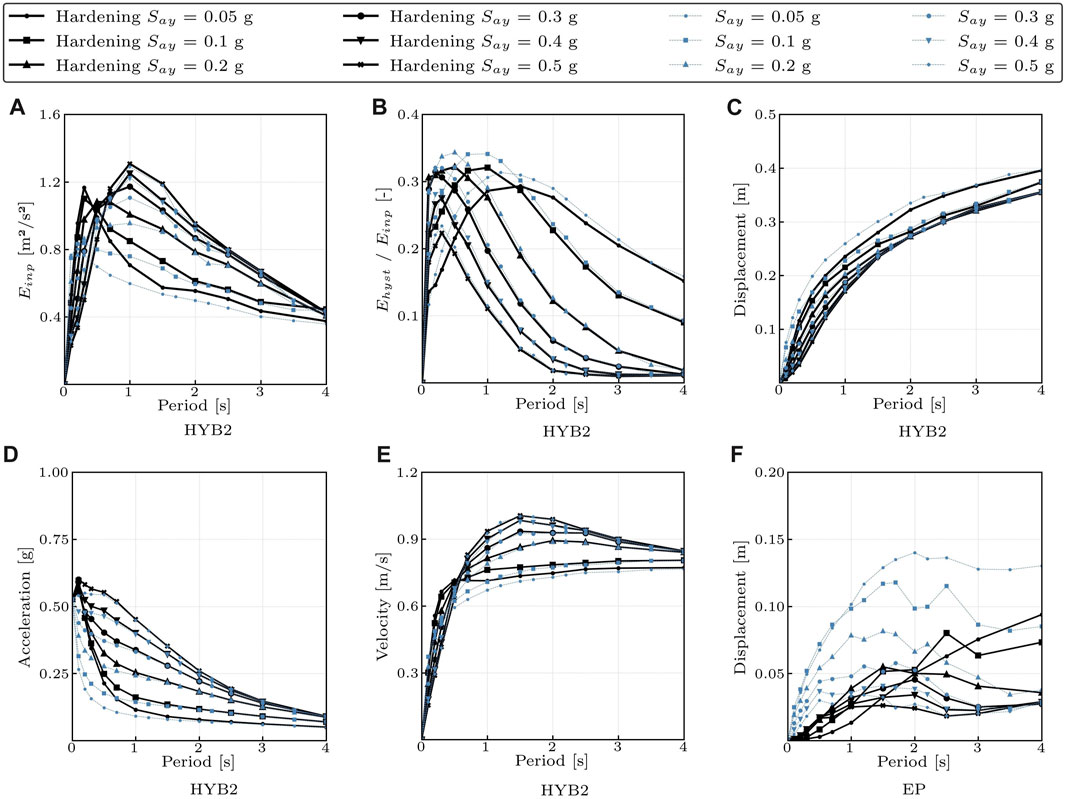
FIGURE 8. Comparison of the HYB2 average inelastic spectra r = 0 vs. r = 0.05—Near-field case. (A): Seismic input energy. (B): E_hyst/E_inp. (C): Maximum Displacement. (D): Absolute acceleration. (E): Relative velocity. (F): Residual displacements of the EP cycle.

Considering far-field earthquake records, the results in terms of response spectra are shown in Figure 9, again for the HYB2 cycle and considering both no hardening (r = 0 with dashed line) and hardening behaviors (r = 0.05 with continuous line). The seismic input energy, for far-field earthquakes, is much lower than for near-field earthquakes (Figure 9A). Considering the hardening of the hysteretic models it is possible to observe a small increase in the seismic input energy demand. This difference is substantial for lower period values. On the other hand, the E_hyst/E_inp ratio is slightly lower in the far-field scenario than in the near-field earthquakes (Figure 9B). Considering the hardening of the hysteretic models (continuous line), it is possible to note a slight decrease in the hysteretic energy. The maximum displacement is lower in the far-field scenario rather than in the near-field scenario, since the seismic energy demand is lower (Figure 9C). The maximum displacement decreases due to the presence of hardening, especially for low values of the yielding point S_ay. Absolute acceleration is not very sensitive between near-field and far-field earthquakes (in the second case it is slightly lower, Figure 9D). However, the same conclusion is not valid for the velocity: as for the seismic input energy, also the relative velocity of the structure (Figure 9E) and, consequently, the kinetic energy dissipated by the viscous damping decrease considering near-field earthquake scenario.

FIGURE 9

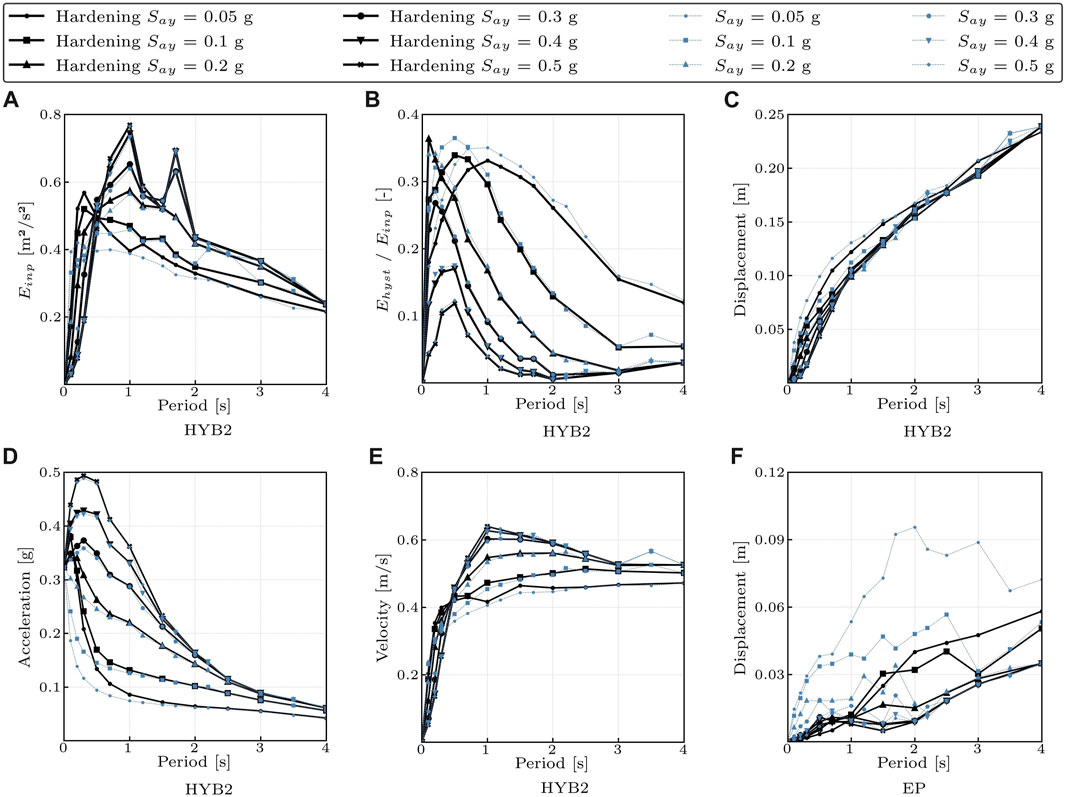
FIGURE 9. Comparison of the HYB2 average inelastic spectra r = 0 vs. r = 0.05—Far-field case. (A): Seismic input energy. (B): E_hyst/E_inp. (C): Maximum Displacement. (D): Absolute acceleration. (E): Relative velocity. (F): Residual displacements of the EP cycle.

3.3.2.1 Number of equivalent plastic cycles

The number of plastic cycles n_eq are higher in the far-field scenario than in the near-field earthquakes. The ground movement under near-fault leads the structure to absorb a large amount of energy with few plastic cycles. Hence cyclical damage to structures is generally more important for far-field earthquakes. Then Figure 10 shows that traditional monolithic structures undergo more plastic cycles than low-damage structure, due to their higher hysteretic energy component. The shape of the curves is in agreement with Cheng et al. (2021).

FIGURE 10

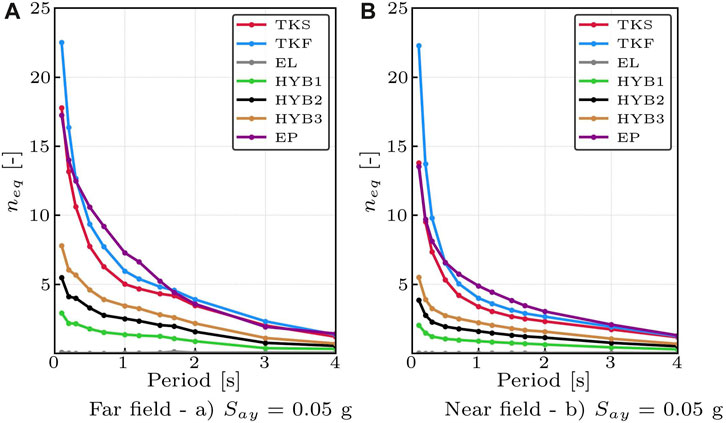
FIGURE 10. Example of the number of equivalent plastic cycles. (A): Far-field earthquakes. (B): Near-field earthquakes.

4 Energy-based design: worked example

This section presents an illustrative application of the displacement/energy-based design using the inelastic spectra r = 0 obtained in the previous Section 3. In this approach, both the hysteretic energy and the maximum displacement are considered as control/target design parameters. Figure 11 shows a conceptual flow chart summarizing the proposed integrated Displacement and Energy-Based Design (DEBD) procedure to define an objective capacity curve for the considered structures.

FIGURE 11

FIGURE 11. Flowchart of the integrated Displacement and Energy-Based Design (DEBD) procedure.

The proposed integrated DEBD design procedure is also compared with the classical design approaches (FBD and DDBD), in order to highlight exclusively a direct control on the design seismic performance parameters.

4.1 Description of the case-study structure

The case-study structure is characterized by a plan dimension of 28 m × 22 m (Figure 12), with an interstorey height of 3.6 m for five floors (18 m in total height). Lateral resistance is provided by two perimeter seismic frames in the longitudinal direction Typo, and two walls in the transversal direction. The wall length is 5.5 m and its thickness is 0.4 m. The total mass is 1,446 tons and it is divided respectively in 298 and 254 tons for each floor and the roof. The energy-based design procedure is applied to a PRESSS hybrid wall with re-centering ratio λ equal to 1.6 (β = 0.4).

FIGURE 12

FIGURE 12. Case study building geometry. (A): Typical floor plan. (B): Geometrical wall elevation.

4.2 Record selection

The performance of the wall is compared using nonlinear time history analyses (NLTHAs), considering different near-field accelerograms (Supplementary Table S2) from those used for the inelastic spectra of Section 3.2. The ultimate life safety (ULS) intensity level is evaluated according to the building code (NTC 2018), considering a building life equal to 100 years, Importance Level II (usage class) typical or residential buildings, usage coefficient CU equal to 1 and soil type E.

4.3 Case-study design

4.3.1 Force-based design

The analysis is performed according to the Italian NTC2018 code. The wall is modelled with lumped masses on the nodes of the structure and with frame elements which have: i) modulus of elasticity equals to 34 GPa; ii) reduction coefficient equal to 0.5 for the flexural stiffness. From the modal analysis the fundamental period of the structure is 0.63 s. A behavior factor q = 4 is selected, based on typical design practice and in line with the NTC2018 miminum requirements. The elastic period of the structure is calculated through modal analysis and the other parameters are evaluated with linear static analysis according to Italian NTC 2018. It is crucial to emphasize that it would be recommended to reduce the behavior factor q, if a traditional monolithic structure design had been carried out in order to reduce the residual damage to the structural elements. A rigorous consistency with the actual ductility demand of the earthquake and thus of the actual energy dissipation developed by the structural system should be checked to re-evaluate the initially assumed behavior factor, making the design process iterative. However, this last step was omitted from the worked example since it is outside the goals of this research work.

4.3.2 Direct displacement-based design

In the DDBD, the maximum lateral displacement achievable under seismic action is fixed at 0.17 m, corresponding to approximately 1.30% of equivalent SDoF interstorey drift. It is has herein chosen not to select a higher interstorey drift value for Life Safety Limit State in order to reduce the deformation demand on the Plug and Play external replacable dissipaters (Pampanin et al., 2010). The yielding displacement of the wall is calculated with the DDBD cantilever formulation (by assuming the yield stress f_y equal to 450 MPa and the steel modulus of elasticity E_s equal to 210 GPa), and it is equal to 0.06 m, that corresponds to a 0.4% of equivalent SDoF interstorey drift. The hysteretic energy is empirically represented by an additional area-based equivalent viscous damping (Eq. 7) as per Priestley et al. (2007). A more rigorous analysis was omitted for this last parameter since it is outside the goals of the research work. Furthermore, by designing for near-field earthquakes, the spectral reduction factor $\eta$ is adjusted by modifying the square root (typical for far-field earthquakes) in a power factor equal to 0.25, i.e., $\eta ={\left(\frac{7}{{\xi }_{eq}+2}\right)}^{0.25}.$

${\xi }_{eq}=5+30\left(\frac{1-\frac{1}{\sqrt{\mu }}}{\lambda +1}\right),\text{Hybrid\hspace{0.17em}systems}(7)$

4.3.3 Displacement and Energy-based design

For PRESSS low-damage technologies, maximizing the hysteretic energy represents a fundamental objective to reduce the seismic input energy demand while avoiding significant structural damage (unlike the traditional monolithic structures). According to Priestley, 1998, the yielding displacement is considered independent of the strength capacity and it is derived as per the DDBD method. A strength capacity S_ay = 0.2 g is considered, in order to maximize the energy ratio E_hyst/E_inp and reach the maximum displacement equal to 0.17 m. In this way the elastic period (secant to the yielding point) of the structure is 0.7 s. The parameters interpolated in the inelastic spectra are shown below (Figure 13), including the seismic input energy demand for unit mass (Figure 13C).

FIGURE 13

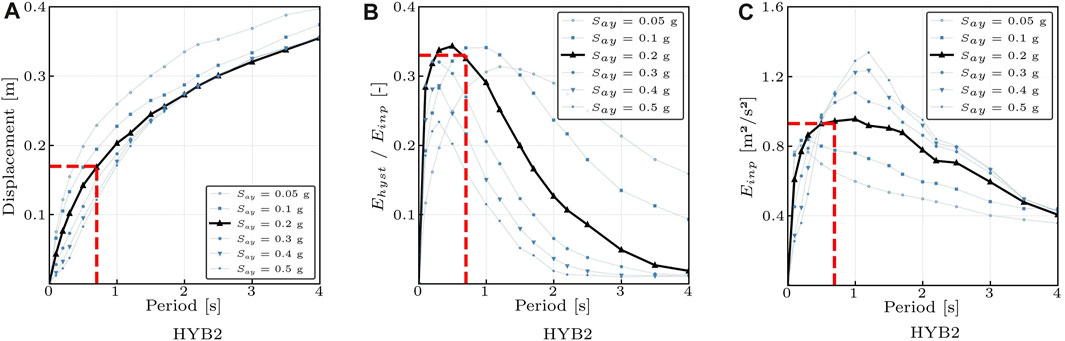
FIGURE 13. Interpolation of design parameters in the inelastic spectra. (A): Maximum Displacement. (B): Hysteretic energy and seismic input energy ratio E_hyst/E_inp. (C): Unitary seismic input energy.

4.4 Comparison between the seismic design methods

The simplified target design pushover curves obtained with DEBD, DDBD and FBD methods are shown in Figure 14. Moreover, for the DEBD only, the overturning moment (OTM) is evaluated and a detailed design of the hybrid connection of the wall is carried out. A comparison between the target design (obtained through the DEBD procedure) and the designed hybrid wall is presented in Figure 14A, while Figure 14B shows the geometrical and reinforcement details of the considered hybrid connection.

FIGURE 14

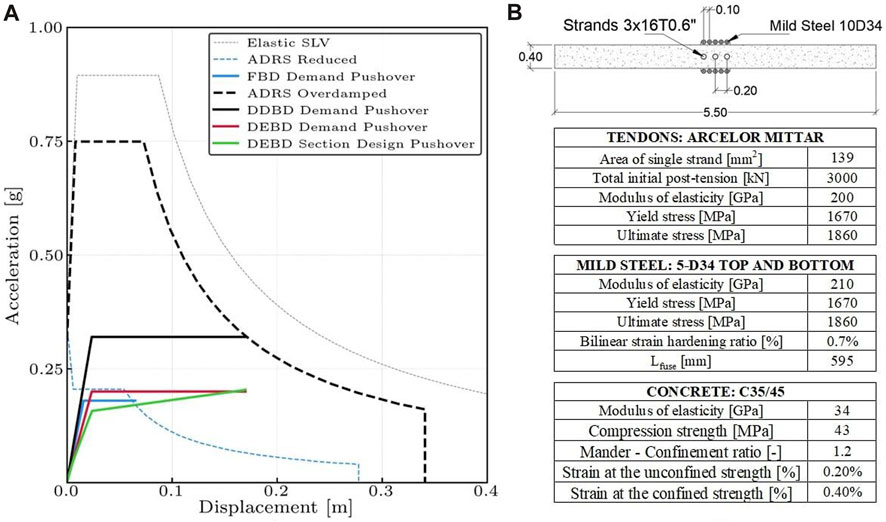
FIGURE 14. Worked example design results. (A): Comparison of alternative pushover target design curves depending on the design methods. (B): Section design data of the PRESSS wall.

In order to investigate the effectiveness of the alternative design methodologies, including the proposed DEBD, NLTHAs are carried out on a Multi-Degree-of-Freedom (MDoF) numerical model implemented in the structural software Ruaumoko. Specifically, masses are concentrated in the nodes of each floor and the nonlinear behavior is concentrated at the base with HYB2 hysteretic cycle modeled as a rotational spring. The viscous coefficient is modelled considering a Rayleigh damping proportional to the initial stiffness of the system and 5% of critical damping.

The results of the performed investigation are resumed in Table 1. Looking at the results of the NLTHAs, it can be observed that, as expected, the closest approach to the energy target predictions showed in Figure 13, it is the Displacement and Energy-Based Design. In fact for the DDBD and FBD methods, only in a second step it is checked if energy NLTHA results are acceptable, while with the DEBD method energy results match with the design parameters. The obtained maximum displacements are very similar between the DEBD and DDBD methods and both methods provide a conservative evaluation with respect to their target design value of 0.17 m. On the other hand, the FBD method significantly underestimates the maximum displacements compared to the design value and this is mainly due to the selected high value of the behavior factor q, which should be in principle double checked and iterated on (Sporn and Pampanin, 2013). Residual displacements evaluated through the NLTHAs are equal to 0.1 mm due to the re-centering behavior of the flag-shape hysteresis cycle. NLTHAs results show a slight increase in absolute acceleration compared to the target values; for the DEBD approach the average is 0.25 g, but this value remains lower than this specific DDBD case and this allows greater protection of the non-structural content (Kam et al., 2008). From the energy point of view, the advantages of adopting a DEBD approach can be recognized, since this approach allows to maximize the average hysteretic energy and to control the seismic input energy demand. It is worth stressing that, for the low-damage PRESSS technology, the hysteretic energy is only expected to reduce the seismic demand without implying significant structural damage, since it is associated to the yielding of the (external re-placeable) Plug and Play devices, rather than to the development of potentially non-repairable plastic hinges in the structural traditional monolithic members. The average results of FBD show the highest hysteretic energy value, but it should be emphasized that the average actual response displacements have exceeded the FBD target value (in other words, the target objectives implied in the FBD have not been respected). Furthermore, the average seismic input energy demand evaluated through NLTHAs is close to the DEBD method target value, which is calculated as the product of the unitary seismic input energy (Figure 13C) with the total floor masses of the structure (1,446 tons). Finally, the NLTHAs of the section design wall show similar results in hysteretic energy and maximum displacements compared to the DEBD method, while the absolute accelerations are lower due to the hardening of the wall connection design.

TABLE 1

TABLE 1. Comparison between NLTHAs response results and the design target parameters.

5 Conclusion

In the present paper, the energy-based seismic behavior of structures has been investigated. The main objective of the presented research work was to highlight and discuss the energy-based seismic performance of structures by directly adopting the hysteretic energy as an additional design parameter, in order to propose an innovative Integrated (Direct) Displacement and Energy-Based Design (DEBD) approach.

Towards this goal, the energy-based approach has been studied on an average set of accelerograms divided into near-field and far-field scenarios. A parametric analysis has been carried out for different nonlinear hysteretic cycles, representative of the cyclic behavior of the structures: Takeda Thin, Takeda Fat, Elastoplastic, Nonlinear Elastic and Flag-Shape. Specifically, the latter is deemed representative of the innovative hybrid re-centering and dissipative low-damage technologies (e.g., PRESSS in concrete or PRES-LAM in timber). For each considered hysteretic rule, constant-strength inelastic response spectra have been derived, thus setting fixed values of the strength capacity (in terms of yielding acceleration point S_ay). The performance has been evaluated through the averaging of nonlinear dynamic analyses concerning: i) final seismic input energy, ii) hysteretic energy and seismic input energy ratio E_hyst/E_inp, iii) maximum displacement, iv) absolute acceleration, v) relative velocity of the structure. The investigation has been carried out also considering either an elastic-perfectly plastic monotonic behavior (r = 0) or hardening behavior (r = 0.05). The latter showed a strong reduction of residual displacements at the end of the earthquake, due to the increase in strength of the oscillator. From the energy point of view, hardening has generally little effect on the reduction of the final hysteretic energy, except for very rigid structures. Furthermore, it was highlighted that under near-fault sources the seismic input energy is higher than for far-fault earthquakes. For these latter earthquakes, the structures are more vulnerable to cyclical fatigue: in fact, the number of plastic cycles is greater. On the other hand, under near-field effects, due to the high-velocity component, structures absorb the seismic demand in fewer larger cycles. Inelastic energy spectra can be used to select the most performing construction technologies accounting for the control of cumulative damage. The introduction of self-centering hybrid structures showed the gradual increase of hysteretic energy when increasing the hysteretic dissipation contribution β, which in turns reduces the seismic input energy demand. In this typology of structures, hysteretic energy is dissipated only through the plasticization of the external replaceable Plug and Play devices, thus without any substantial structural damage in the plastic hinge region as typical of a traditional monolithic solution designed according to capacity design philosophy (Blume et al., 1961; Park and Pauley, 1975).

Finally, a worked DEBD example of a hybrid low-damage PRESSS wall has been presented to highlight the possible benefit of controlling the structural damage using the inelastic energy spectra obtained in this paper, by correlating the energy components with the corresponding maximum displacement response parameters of the structure, in order to obtain an innovative Integrated Displacement&Energy-Based Design approach. Three alternative design approaches have been considered in the investigation, i.e., Force-Based Design (FBD), Direct Displacement-Based Design (DDBD), and Displacement and Energy-Based Design (DEBD). The effectiveness of the design methodologies has been evaluated by performing also NLTHAs of an MDoF model of the structure.

Firstly, it should be noted that discrepancy between the three methods could be larger than expected, since code (FBD) and empirical (DDBD) formulas were used for the traditional approaches, while in the DEBD case design parameters are evaluated through a stricter parametric analysis by using NLTHAs. Either way, results highlighted that the target and predicted energy seismic parameters were closer in the DEBD approach, rather than the DDBD or even more compared to the FBD. In general, FBD has been shown unable to provide adequate control of the design parameters such as maximum displacement and hysteretic energy. Yet, both DDBD and the proposed DEBD methodology allow for a better estimation of the maximum displacement of the structure. Moreover, when compared to the DDBD, the proposed DEBD methodology allows for maximizing the hysteretic energy, which was one of the target objectives in the design phase for the presented illustrative application. Such an approach has a specific benefit when considering disspative self-centering low-damage solution system, as the hysteretic energy does not represent structural cumulative damage as typical of monolithic traditional counterparts.

Yet, when dealing with general typology of structures, future developments should focus on correlating the hysteretic energy levels with the corresponding damage levels, in order to better define the repairability limit state of structures.

In addition, regulatory energy response spectra should be developed, so as to make DEBD more applicable in the professional practice and more comparable with the current seismic design methods.

In this paper, n_eq parameter was investigated for both far-field and the near-field scenarios, however it was not included in the proposed DEBD procedure. The aim was therefore to correlate n_eq with future research, which should also include hysteretic energy and the corresponding damage levels for a more robust EBD procedure.

Finally, an alternative energy dissipation strategy could be developed, using for instance velocity-dependent devices, exploiting the high-velocity component induced by near-field earthquakes, and thus improving the seismic performance of the structure. The design of such devices might be relatively simple through an energy-based approach as it directly distinguishes the energy components of the balance, such as viscous damping energy and absorbed hysteretic energy.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

GP: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Visualization, Writing–original draft, Writing–review and editing. LP: Conceptualization, Validation, Visualization, Writing–review and editing. SD'A: Conceptualization, Validation, Visualization, Writing–review and editing. SP: Conceptualization, Project administration, Supervision, Validation, Writing–review and editing, Methodology.

Funding

The authors declare that no financial support was received for the research, authorship, and/or publication of this article.

Acknowledgments

The authors want to acknowledge the financial support of the Italian Ministry of University and Research (MUR) for funding of the Doctoral Scholarship of GP, LP and SD'A.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbuil.2023.1264033/full#supplementary-material

References

Akbas, B., Shen, J., and Hao, H. (2001). Energy appproach in peformance-based seismic design of steel moment resisting frames for basic safety objective. Struct. Des. Tall Spec. Build. 10 (3), 193–217. doi:10.1002/tal.172

CrossRef Full Text | Google Scholar

Akiyama, H. (1985). Earthquake resistant limit-state design for buildings (English version). Tokyo, Japan: University of Tokyo press.

Google Scholar

Akiyama, H. (1988). “Earthquake resistant design based on the energy concept,” in Proceedings of 9th WCEE (Tokyo, Japan: WCEE), 905–910.

Google Scholar

Akiyama, H. (1999). Earthquake-resistant design method for buildings based on energy balance. Tokyo: Gihodo Shuppan.

Google Scholar

Akiyama, H. (2008). Lecture notes on earthquake resistant limit state design. Japan: IISEE/BRI.

Google Scholar

ASCE/SEI 7-16 (2017). Design loads on buildings and other structures. Reston: American Society of Civil Engineers.

Google Scholar

Banon, H., and Veneziano, D. (1982). Seismic safety of reinforced concrete members and structures. Earthq. Eng. Struct. Dyn. 10 (2), 179–193. doi:10.1002/eqe.4290100202

CrossRef Full Text | Google Scholar

Benavent-Climent, A. (2011). An energy-based method for seismic retrofit of existing frames using hysteretic dampers. Soil Dyn. Earthq. Eng. 31 (10), 1385–1396. doi:10.1016/j.soildyn.2011.05.015

CrossRef Full Text | Google Scholar

Benavent-Climent, A., Donaire-Ávila, J., and Mollaioli, F. (2021). “Key points and pending issues in the energy-based seismic design approach,” in International workshop on energy-based seismic engineering (Cham: Springer), 151–168.

CrossRef Full Text | Google Scholar

Benavent-Climent, A., López-Almansa, F., and Bravo-González, D. A. (2010). Design energy input spectra for moderate-to-high seismicity regions based on Colombian earthquakes. Soil Dyn. Earthq. Eng. 30 (11), 1129–1148. doi:10.1016/j.soildyn.2010.04.022

CrossRef Full Text | Google Scholar

Benavent-Climent, A., and Mota-Páez, S. (2017). Earthquake retrofitting of R/C frames with soft first story using hysteretic dampers: energy-based design method and evaluation. Eng. Struct. 137, 19–32. doi:10.1016/j.engstruct.2017.01.053

CrossRef Full Text | Google Scholar

Bertero, R. D., and Bertero, V. V. (2002). Performance-based seismic engineering: the need for a reliable conceptual comprehensive approach. Earthq. Eng. Struct. Dyn. 31 (3), 627–652. doi:10.1002/eqe.146

CrossRef Full Text | Google Scholar

Blume, J. A., Newmark, N. M., and Corning, L. H. (1961). Design of multistory reinforced concrete buildings for earthquake motions. Chicago: Portland Cement Association.

Google Scholar

Building Research Institute (2009). The building standard Law of Japan. Tokyo (Japan): The Building Center of Japan.

Google Scholar

Carr, A. (2007). RUAUMOKO2D – the maori god of volcanoes and earthquakes. Christchurch, New Zealand: University of Canterbury.

Google Scholar

Cheng, Y., Mollaioli, F., and Donaire-Ávila, J. (2021). Characterization of dissipated energy demand. Soil Dyn. Earthq. Eng. 147, 106725. doi:10.1016/j.soildyn.2021.106725

CrossRef Full Text | Google Scholar

Chopra, A. K., and Goel, R. K. (1999). Capacity-demand-diagram methods based on inelastic design spectrum. Earthq. spectra 15 (4), 637–656. doi:10.1193/1.1586065

CrossRef Full Text | Google Scholar

Chou, C. C., and Uang, C. M. (2003). A procedure for evaluating seismic energy demand of framed structures. Earthq. Eng. Struct. Dyn. 32 (2), 229–244. doi:10.1002/eqe.221

CrossRef Full Text | Google Scholar

Christopoulos, C., and Filiatrault, A. (2006). Principles of passive supplemental damping and seismic. Pavia, Italy: IUSS Press.

Google Scholar

Christopoulos, C., Pampanin, S., and Nigel Priestley, M. J. (2003). Performance-based seismic response of frame structures including residual deformations part I: single-degree of freedom systems. J. Earthq. Eng. 7 (01), 97–118. doi:10.1080/13632460309350443

CrossRef Full Text | Google Scholar

Christopoulos, C., and Pampanin, S. (2004). Towards performance-based design of MDOF structures with explicit consideration of residual deformations. Invit. Pap. ISET J. Earthq. Technol. Special Issue Perform. Based Seismic Des. 41 (1), 53–73.

Google Scholar

Cosenza, E., Manfredi, G., and Ramasco, R. (1993). The use of damage functionals in earthquake engineering: A comparison between different methods. Earthq. Eng. Struct. Dyn. 22, 855–868. doi:10.1002/eqe.4290221003

CrossRef Full Text | Google Scholar

D.M. 17/01/2018. Norme Tecniche per le Costruzioni (NTC) (2018). Gazzetta ufficiale, n. 42 del 20/02/2018, supplemento ordinario n.8 [in Italian], Roma, Italia.

Google Scholar

Decanini, L., and Mollaioli, F. (2001). An energy-based methodology for the assessment of seismic demand. Soil Dyn. Earthq. Eng. 21 (2), 113–137. doi:10.1016/s0267-7261(00)00102-0

CrossRef Full Text | Google Scholar

Donaire-Ávila, J., Benavent-Climent, A., Lucchini, A., and Mollaioli, F. (2017). “Energy-based seismic design methodology: A preliminary approach,” in Proceedings of the 16th world conference on earthquake engineering (Santiago, Chile: WCEE).

Google Scholar

Escolano-Margarit, D., Morillas-Romero, L., and Benavent-Climent, A. (2023). “Experimental assessment of the energy that contributes to damage,” in International workshop on energy-based seismic engineering (Cham: Springer Nature Switzerland), 129–137.

CrossRef Full Text | Google Scholar

Fajfar, P. (2000). A nonlinear analysis method for performance-based seismic design. Earthq. spectra 16 (3), 573–592. doi:10.1193/1.1586128

CrossRef Full Text | Google Scholar

Fajfar, P. (1992). Equivalent ductility factors, taking into account low-cycle fatigue. Earthq. Eng. Struct. Dyn. 21 (10), 837–848. doi:10.1002/eqe.4290211001

CrossRef Full Text | Google Scholar

Fajfar, P., and Vidic, T. (1994). Consistent inelastic design spectra: hysteretic and input energy. Earthq. Eng. Struct. Dyn. 23 (5), 523–537. doi:10.1002/eqe.4290230505

CrossRef Full Text | Google Scholar

Gentile, R., and Galasso, C. (2021). Hysteretic energy-based state-dependent fragility for ground-motion sequences. Earthq. Eng. Struct. Dyn. 50, 1187–1203. doi:10.1002/eqe.3387

CrossRef Full Text | Google Scholar

Ghobarah, A. (2001). Performance-based design in earthquake engineering: state of development. Eng. Struct. 23 (8), 878–884. doi:10.1016/s0141-0296(01)00036-0

CrossRef Full Text | Google Scholar

Iwan, W. D. (1980). Estimating inelastic response spectra from elastic spectra. Earthq. Eng. Struct. Dyn. 8 (4), 375–388. doi:10.1002/eqe.4290080407

CrossRef Full Text | Google Scholar

Kam, W. Y., Pampanin, S., Palermo, A., and Carr, A. (2008). “Design procedure and behaviour of advanced flag-shape (AFS) MDOF systems,” in 2008 New Zealand Society of Earthquake Engineering (NZSEE) Conference, Wairakei, New Zealand, 11–13 April, 2008.

Google Scholar

Kappos, A. J. (1997). Seismic damage indices for RC buildings: evaluation of concepts and procedures. Prog. Struct. Eng. Mater. 1 (1), 78–87. doi:10.1002/pse.2260010113

CrossRef Full Text | Google Scholar

Kazantzi, A. K., and Vamvatsikos, D. (2018). The hysteretic energy as a performance measure in analytical studies. Earthq. Spectra 34, 719–739. doi:10.1193/112816EQS207M

CrossRef Full Text | Google Scholar

Kunnath, S. K., Reinhorn, A. M., and Lobo, R. (1992). IDARC version 3.0: A program for the inelastic damage analysis of reinforced concrete structures. New York: University at Buffalo.

Google Scholar

Leelataviwat, S., Saewon, W., and Goel, S. C. (2007). “An energy-based method for seismic evaluation of structures,” in Proceedings of structural engineers association of California convention SEAOC (Lake Tahoe, California: SEAOC).

Google Scholar

Mahin, S., and Bertero, V. V. (1981). An evaluation of inelastic seismic design spectra. J. Struct. Div. ASCE 107, 1777–1795. doi:10.1061/jsdeag.0005782

CrossRef Full Text | Google Scholar

Mahin, S. A., and Lin, J. (1983). Construction of inelastic response spectra for single-degree-of-freedom systems. Berkeley: Earthquake Engineering Center, University of California.

Google Scholar

Manfredi, G., Polese, M., and Cosenza, E. (2003). Cumulative demand of the earthquake ground motions in the near source. Earthq. Eng. Struct. Dyn. 32 (12), 1853–1865. doi:10.1002/eqe.305

CrossRef Full Text | Google Scholar

Mollaioli, F., Bruno, S., Decanini, L., and Saragoni, R. (2011). Correlations between energy and displacement demands for performance-based seismic engineering. Pure Appl. Geophys. 168 (1-2), 237–259. doi:10.1007/s00024-010-0118-9

CrossRef Full Text | Google Scholar

Morillas, L., and Escolano-Margarit, D. (2020). Estimation of cyclic demand in metallic yielding dampers installed on frame structures. Appl. Sci. 10 (12), 4364. doi:10.3390/app10124364

CrossRef Full Text | Google Scholar

Mota-Páez, S., Escolano-Margarit, D., and Benavent-Climent, A. (2021). Seismic response of RC frames with a soft first story retrofitted with hysteretic dampers under near-fault earthquakes. Appl. Sci. 11 (3), 1290. doi:10.3390/app11031290

CrossRef Full Text | Google Scholar

Muto, K., Decanini, L., and Saragoni, R. (1960). Nonlinear response analyzers and application to earthquake resistant design. Proc. Second World Conf. Earthq. Eng. 2, 649–668.

Google Scholar

Otani, S. (1974). Sake: A computer program for inelastic response of R/C frames to earthquakes. Civil Engineering Studies SRS-413, University of Illinois, Urbana-Champaign.

Google Scholar

Pacific Earthquake Engineering Research Center (2000). PEER strong motion database. Berkeley: PEER, University of California.

Google Scholar

Pal, S., Dasaka, S. S., and Jain, A. K. (1987). Inelastic response spectra. Comput. Struct. 25 (3), 335–344. doi:10.1016/0045-7949(87)90126-x

CrossRef Full Text | Google Scholar

Pampanin, S. (2003). Alternative design philosophies and seismic response of precast concrete buildings. Struct. Concr. 4 (4), 203–211.

Google Scholar

Pampanin, S., Christopoulos, C., and Priestley, M. J. N. (2003). Performance-based seismic response of frame structures including residual deformations. Part I: single-degree of freedom systems. J. Earthq. Eng. 7, 97–118. doi:10.1080/13632460309350443

CrossRef Full Text | Google Scholar

Pampanin, S., Christopoulos, C., and Priestley, M. J. N. (2002). Residual deformations in the performance-based seismic assessment of frame systems, research report ROSE. Pavia: European School on Advanced Studies on Reduction of Seismic Risk, 226.

Google Scholar

Pampanin, S., Marriott, D., and Palermo, A. (2010). PRESSS design handbook. Auckland, NZ: New Zealand Concrete Society.

Google Scholar

Pampanin, S., Priestley, M. J. N., and Sritharan, S. (2001). Analytical modelling of the seismic behaviour of precast concrete frames designed with ductile connections. J. Earthq. Eng. 5, 329–367. doi:10.1080/13632460109350397

CrossRef Full Text | Google Scholar

Park, R., and Paulay, T. (1975). Ductile reinforced concrete frames: some comments on the special provisions for seismic design of ACI 318-71 and on capacity design. Bull. N. Z. Soc. Earthq. Eng. 8 (1), 70–90. doi:10.5459/bnzsee.8.1.70-90

CrossRef Full Text | Google Scholar

Park, Y. J., and Ang, H. S. (1985). Mechanistic seismic damage model for reinforced concrete. J. Struct. Eng. 111, 722–739. doi:10.1061/(asce)0733-9445(1985)111:4(722)

CrossRef Full Text | Google Scholar

Pedone, L., Gentile, R., Galasso, C., and Pampanin, S. (2023). Energy-based procedures for seismic fragility analysis of mainshock-damaged buildings. Front. Built Environ. 9, 1–20. doi:10.3389/fbuil.2023.1183699

CrossRef Full Text | Google Scholar

Priestley, M. J. N., Calvi, G. M., and Kowalsky, M. J. (2007). “ Direct displacement-based seismic design of structures,” in NZSEE conference, Christchurch, NZ, 1–23.

Google Scholar

Priestley, M. J. N. (1998). “Displacement-based approaches to rational limit states design,” in Proceedings of the eleventh European conference on earthquake engineering: 6-11 september 1998 (Paris, France: AA Balkema), 317.

Google Scholar

Priestley, M. J. N., and Grant, D. N. (2005). Viscous damping in seismic design and analysis. J. Earthq. Eng. 9 (2), 229–255. doi:10.1142/s1363246905002365

CrossRef Full Text | Google Scholar

Priestley, M. N. (1993). Myths and fallacies in earthquake engineering: conflicts between design and reality. Bull. N. Z. Soc. Earthq. Eng. 26 (3), 329–341. doi:10.5459/bnzsee.26.3.329-341

CrossRef Full Text | Google Scholar

Priestley, M. N., Sritharan, S., Conley, J. R., and Pampanin, S. (1999). Preliminary results and conclusions from the PRESSS five-story precast concrete test building. PCI J. 44 (6), 42–67. doi:10.15554/pcij.11011999.42.67

CrossRef Full Text | Google Scholar

SEAOC Vision (1995). “Comittee,” in Performance-based seismic engineering (Sacramento: Report prepared by Structural Engineers Assocation of California).

Google Scholar

Song, G., Yang, T. Y., and Zhou, Y. (2021). Energy-based seismic design for self-centering concrete frames. Bull. Earthq. Eng. 19 (12), 5113–5137. doi:10.1007/s10518-021-01157-2

CrossRef Full Text | Google Scholar

Sporn, B., and Pampanin, S. (2013). “A “retrofit” solution for force-based design: eliminating the need for iteration and initial period estimation,” in 2013 NZSEE Conference, Wellington, NZ.

Google Scholar

Standard, B. (2005). Eurocode 8: design of structures for earthquake resistance. Part 1, 1998–2001.

Google Scholar

Standards New Zealand (2004). NZS1170.5 Earthquake actions - New Zealand. Wellington, New Zealand: NZS.

Google Scholar

Uang, C. M., and Bertero, V. V. (1990). Evaluation of seismic energy in structures. Earthq. Eng. Struct. Dyn. 19, 77–90. doi:10.1002/eqe.4290190108

CrossRef Full Text | Google Scholar

Uang, C. M., and Bertero, V. V. (1988). “Use of energy as a design criterion in earthquake resistant design,” in Report no. UCB/EERC-88/18, earthquake engineering research center (Berkeley: University of California at Berkeley).

Google Scholar

Uma, S. R., Pampanin, S., and Christopoulos, C. (2006). “A probabilistic framework to develop performance objectives based on maximum and residual deformations,” in Proceedings of the 1st European conference in earthquake engineering and seismology (ECEES) (Geneva, Switzerland: ECEES), Sept 3–8.

Google Scholar