- 1Department of Civil and Environmental Engineering, Tufts University, Medford, OR, United States
- 2Gavin and Doherty Geosolutions Ltd, Dublin, Ireland
- 3Department of Civil and Environmental Engineering, University of Nevada, Reno, NV, United States
Dynamic models of structural and mechanical systems can be updated to match the measured data through a Bayesian inference process. However, the performance of classical (non-adaptive) Bayesian model updating approaches decreases significantly when the pre-assumed statistical characteristics of the model prediction error are violated. To overcome this issue, this paper presents an adaptive recursive variational Bayesian approach to estimate the statistical characteristics of the prediction error jointly with the unknown model parameters. This approach improves the accuracy and robustness of model updating by including the estimation of model prediction error. The performance of this approach is demonstrated using numerically simulated data obtained from a structural frame with material non-linearity under earthquake excitation. Results show that in the presence of non-stationary noise/error, the non-adaptive approach fails to estimate unknown model parameters, whereas the proposed approach can accurately estimate them.
1 Introduction
Bayesian model updating aims to estimate uncertain model parameters by minimizing the discrepancies between measured and predicted responses (Friswell and Mottershead, 2013). This technique has been extensively used for structural system identification (Behmanesh et al., 2015), parameter estimation (Ching et al., 2006; Astroza et al., 2014), damage identification (Doebling et al., 1996; Yang et al., 2006), and virtual sensing (Wenzel et al., 2007; Nabiyan et al., 2020). However, the performance of Bayesian model updating depends on the quality of prior knowledge about the prediction error, which includes the effects of modeling error and measurement noise (Beck and Yuen, 2004). In classical (non-adaptive) Bayesian model updating methods, the prediction error is assumed as a stationary, zero-mean Gaussian white noise process. However, this is not always the case in practice, and the prediction error can generally be a non-stationary, non-white, and non-Gaussian process due to the effect of modeling error (Sanayei et al., 2001; Law and Stuart, 2012; Nabiyan et al., 2022). The estimation accuracy of non-adaptive Bayesian methods can be adversely affected in practice when the prediction error deviates from stationary Gaussian assumption (Mehra, 1972; Xu et al., 2019).
To mitigate the need for prior knowledge about prediction error in model updating, several methods referred to as adaptive Bayesian model updating methods have been proposed (Akhlaghi et al., 2017; Amini Tehrani et al., 2020; Song et al., 2020b). Most of the adaptive Bayesian model updating methods in the literature consider a zero-mean Gaussian white noise with an unknown covariance matrix for modeling prediction error and estimate the error covariance matrix together with other model parameters or states. Zheng et al. (2018) developed a robust adaptive unscented Kalman filter (UKF) to improve the accuracy and robustness of state estimation of a non-linear system with uncertain noise covariance. In this method, first the states of the non-linear system are estimated using a standard UKF (Wu and Smyth, 2007), and then a covariance-matching method (Mehra, 1972) is utilized to estimate the covariance matrix of process noise and measurement noise. Astroza et al. (2019) used a similar approach to jointly estimate the unknown model parameters along with the diagonal entries of the covariance matrix of the prediction error. Huang et al. (2020) developed a hierarchical Bayesian model by combining sparse Bayesian learning (Tipping, 2001) with dual Kalman filters. Their hierarchical model employs two inference levels, state and parameter estimation and noise–parameter learning. They considered a zero-mean Gaussian distribution for the measurement noise in which the diagonal entries of its covariance matrix were learned solely from the measurement data up to the current time step. Yuen and Kuok (2016) proposed a Bayesian probabilistic algorithm to estimate the noise covariance matrix for the extended Kalman filter using the maximum a posteriori approach. Their method is also applicable for non-stationary noise with a time-variant covariance matrix. Song et al. (2020b) proposed two adaptive Kalman filters formulated based on covariance-matching techniques (Mehra, 1972) to jointly estimate the unknown model parameters along with the full covariance matrix of the prediction error. The validation studies show the superior performance of the presented adaptive filtering methods compared to standard UKF, in which the prediction errors have predefined distributions. The mentioned studies assumed a zero-mean Gaussian white noise for the prediction error. However, the modeling error may cause the prediction error to have non-zero mean (Sanayei et al., 2001). To address this issue, Kontoroupi and Smyth (2016) proposed a Bayesian method to estimate a biased (non-zero mean) prediction error. They assumed that the mean vector and covariance matrix of the prediction error are time-invariant and have Gaussian and inverse-Wishart distributions, respectively. In a previous work, Nabiyan et al., (2022) developed a two-step marginal maximum a posteriori (MAP) estimation approach to find a point estimation of the unknown model parameters and the prediction error statistics, where the mean vector and covariance matrix of the prediction error are considered to be time-variant.
In this paper, we introduce a completely different mathematical approach with better performance, in comparison to our previous work, (Nabiyan et al., 2022) for estimating both the unknown model parameters and statistical characteristics (mean vector and covariance matrix) of the prediction error, as well as approximating their joint posterior distribution. Exact calculation of this high-dimensional joint posterior distribution is intractable, so the process requires approximation (Šmídl and Quinn, 2006). Two approximation schemes can be used: stochastic or sampling methods such as Markov chain Monte Carlo (MCMC) (Bishop and Nasrabadi, 2006) and deterministic or variational frameworks such as variational Bayesian (VB) (Opper and Saad, 2001; Beal, 2003). In comparison to the sampling methods, the VB method is analytically tractable and is computationally less demanding (Beal, 2003). The VB method is used in this work as a tool to segregate the posterior distribution into separate components, which can help in solving the problem analytically. The VB method has been successfully applied for joint state and noise estimation in navigation, target tracking, and control-related applications (Huang et al., 2017; Zhang et al., 2018). In these applications, the adaptive VB Kalman filter method was used to jointly estimate the covariance matrix of a zero-mean prediction error and the state of linear (Sarkka and Nummenmaa, 2009; Sun et al., 2012; Huang et al., 2016; Huang et al., 2017) or non-linear (Sarkka and Hartikainen, 2013; Shi et al., 2018; Sun et al., 2018) state-space models. The VB method assumes that the approximate joint distribution is the product of some single- or multi-variable factors and uses the Kullback–Leibler (KL) divergence to minimize the difference between the approximation and the true posterior. In this paper, we introduce a new adaptive method for non-linear model updating based on the VB method to approximate the joint posterior distribution of the unknown model parameters and statistical characteristics of the prediction error at each time step.
The paper is structured as follows: Section 2 provides the model updating problem statement. Section 3 presents a detailed derivation of the proposed VB method for estimating the joint posterior distribution of unknown model parameters and statistical characteristics of the prediction error. The formulation of the VB method is then compared with that of the two-step marginal MAP estimation method (Nabiyan et al., 2022) in Section 4. In Section 5 and Section 6, the proposed method is verified by two model updating case studies: one with time-variant measurement noise and the other with modeling error. The results are compared to those from the two-step marginal MAP estimation method published in Nabiyan et al., (2022) and a non-adaptive Bayesian model updating method. Finally, the conclusions are presented in Section 7.
2 Model updating problem statement
We consider the measured response of a non-linear (or linear) dynamic system
where
In this paper, we developed a new adaptive recursive Bayesian model updating method. Like other recursive Bayesian model updating algorithms, the proposed method has two steps at each time
In our previous work (Nabiyan et al., 2022), we developed a two-step maximum a posteriori (MAP) estimation method to estimate
To solve this MAP problem, we broke the problem into two iterative MAP estimation problems as
3 Variational Bayesian (VB) method
VB is a method to approximate a joint distribution
where
Using variational calculus to minimize the aforementioned KL divergence with respect to each of
where
The joint distribution
where
Here, we further expanded the terms on the right-hand side of Eq. 8. Based on Eq. 2, the likelihood function
For the second and third terms on the right-hand side of Eq. 8, it is assumed, similar to (Nabiyan et al., 2022), that
where
By substituting Eqs. 9, 10, and 11 into Eq. 8, we obtain
The Gaussian (or normal) distribution and the inverse-Wishart (IW) distribution are proportional to the following expressions:
where
Using Eq. 12 and the definitions of normal and IW distributions in Eq. 13, the term
where
Now, having the expansion of
where
Using Supplementary Appendix Lemma S1 in the Appendix, the expectation term in Eq. 15 can be evaluated as
Now, we consider
It should be noted that in deriving Eq. 17, we use
where
In Eq. 6,
By linearizing
The first exponential term in the right-hand side of Eq. 20 shows a Gaussian distribution for
where
In a similar way, we can evaluate the expectation term in Eq. 7 as follows. Getting the mathematical expectation of Eq. 14 with respect to
where
Now, considering
Based on Eq. 7,
The right-hand side of Eq. 24 includes the product of two Gaussian distributions for
Now having
4 Comparison of the VB method with two-step marginal MAP estimation method
In this section, we compare the proposed variational Bayesian (VB) method with the two-step marginal MAP estimation method that was recently developed by Nabiyan et al. (2022) for joint estimation of unknown model parameters and the mean vector and covariance matrix of the prediction error. The formulations of the two methods are closely similar. There are two main differences between the two methods, as explained as follows. First, in the two-step marginal MAP estimation method, the mode of IW distribution is used as an
In most applications, these two differences have small effects on the results because of the following reasons. First, the difference between the mode and mean of the IW distribution decreases through time as the value of
5 Case study 1: 3-Story 1-bay steel moment frame considering time-variant measurement noise
In this section, the performance of the proposed method is evaluated when applied to a numerical model of a 3-story 1-bay steel moment frame structure under earthquake excitation. The estimation results are compared with those of the two-step marginal MAP estimation method (Nabiyan et al., 2022) and a non-adaptive Bayesian model updating method (Ebrahimian et al., 2015). The story height and the bay width are 3.5 m and 6.0 m, respectively, as shown in Figure 2A. The frame’s geometric and material properties are similar to those used in our previous work (Nabiyan et al., 2022), and more details about the considered case study can be found there.
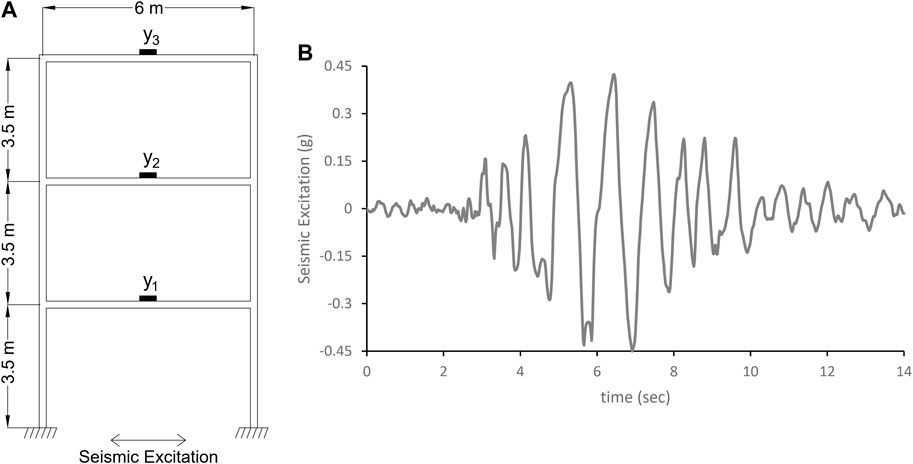
FIGURE 2. (A) 3-story 1-bay steel moment frame and (B) 0° component of ground acceleration time history of the Loma Prieta earthquake recorded at Los Gatos station (Nabiyan et al., 2022).
The numerical model of the frame is developed in OpenSees (McKenna, 2000). For this, force-based beam–column elements with seven integration points are used for columns and beams. A single fiber is used to represent each flange of beam and column cross-sections, while 10 fibers are used to discretize their webs. The uniaxial Giuffre–Menegotto–Pinto (GMP) material model (Filippou et al., 1983) with primary parameters
is used to model the steel fibers and simulate the nominal/true dynamic response of the structure, where
To simulate measurement data, the frame structure is excited by the Loma Prieta earthquake (0° component at Los Gatos station), as shown in Figure 2B. Then, the horizontal absolute acceleration response time histories of each floor (shown by black boxes in Figure 2A) are extracted and contaminated with artificial measurement noise to result in simulated measurement data. The measurement noise is considered a non-stationary Gaussian random process with time-variant mean vector
Our goal is to estimate the unknown model parameters
Now, the proposed VB method is applied to jointly estimate the unknown model parameter vector
The estimated components of the mean vector and covariance matrix of the prediction error (measurement noise in this example) by the three methods (VB, two-step marginal MAP, and the non-adaptive) are compared with their true values in Figure 3 and Figure 4, respectively. The non-adaptive Bayesian model updating method, as mentioned before, does not estimate the mean vector and the covariance matrix of the prediction error, so they remain constant during the estimation process. However, both the VB and the two-step marginal MAP estimation methods can accurately track the trend of the true/nominal mean and covariance of error through time. As can be seen in Figure 4, in comparison to the two-step marginal MAP method, the VB method better estimates the covariance matrix of the prediction error at the early time steps because of the additional term discussed in the previous section.
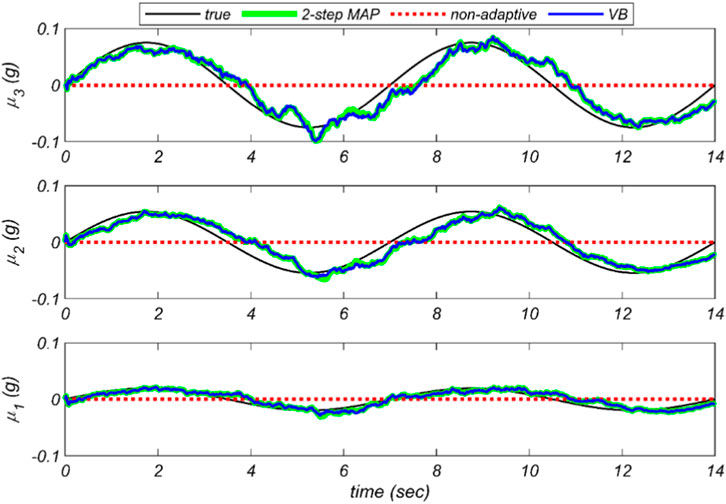
FIGURE 3. Comparison of the estimated components of the mean vector of measurement noise by the three methods (VB, two-step marginal MAP, and the non-adaptive) with the true ones. It should be noted that
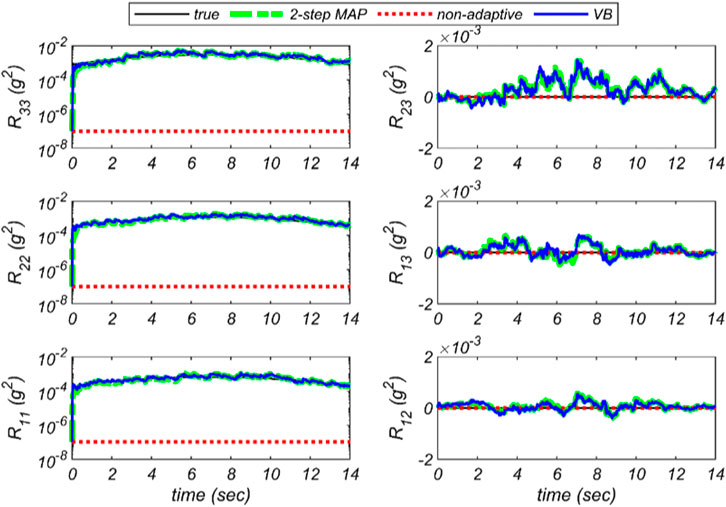
FIGURE 4. Comparison of the estimated components of the covariance matrix of measurement noise by the three methods (VB, two-step marginal MAP, and the non-adaptive) with the true ones. It should be noted that
Figure 5 shows the time histories of the unknown model parameters estimated by all three methods: the proposed VB method, the two-step marginal MAP estimation method, and the non-adaptive Bayesian method. It can be observed that the non-adaptive model updating method converges to incorrect unknown model parameters, or even diverges. However, adaptive methods can estimate unknown model parameters very well. The weakness of the non-adaptive method shows that estimation of the prediction error significantly affects the model updating results when the prediction error has a time-variant non-zero mean and, therefore, should not be ignored. Comparing the VB method with the two-step marginal MAP estimation method, the VB method better estimates the parameter
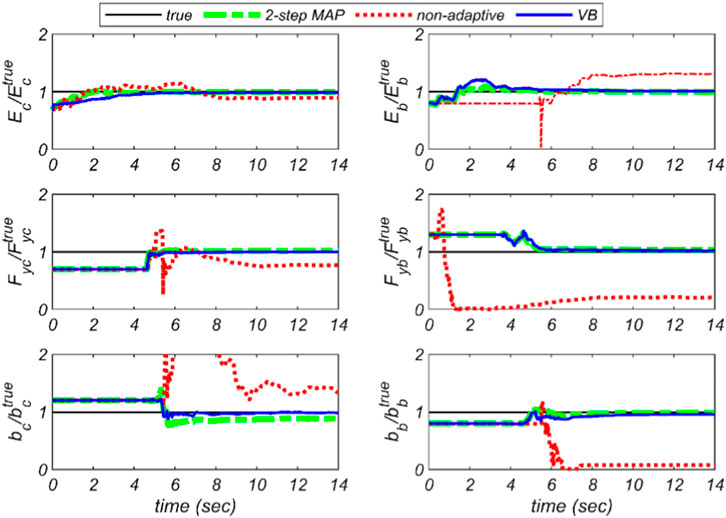
FIGURE 5. Time histories of the estimated model parameters obtained by the three methods: the proposed VB method, the two-step marginal MAP estimation method, and the non-adaptive Bayesian method.
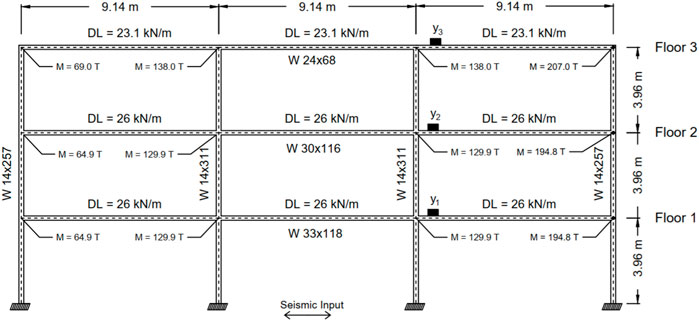
6 Case study 2: 3-Story 3-bay steel moment frame considering modeling error
In this second study, we examine the proposed VB method in the presence of modeling error on a 3-story, 3-bay steel moment frame. The frame is taken from Song et al., (2020a), and the geometry, frame sections, and loads are shown in Figure 6. All beams and columns have wide flange profiles and are modeled with displacement-based beam–column elements. Rayleigh damping with 2% damping of the first and second modes is considered for structural damping. Distributed gravity loads are considered concentrated masses at nodes. The measured data are simulated using the steel constitutive model of Giuffre–Menegotto–Pinto (GMP) for beams and columns, in which their true properties are selected the same as in the previous example. The frame is excited by the Loma Prieta earthquake shown in Figure 2B, and the horizontal absolute acceleration responses at each floor (marked by black boxes in Figure 6) are recorded. Then, 1% RMS NSR Gaussian zero-mean white noise is added to these simulated acceleration responses to be considered measurement data.
While we use the GMP constitutive model Figure 7A to simulate the measurements, a bilinear model (Figure 7B) is used in the estimation process to add explicit modeling error to the model updating process.
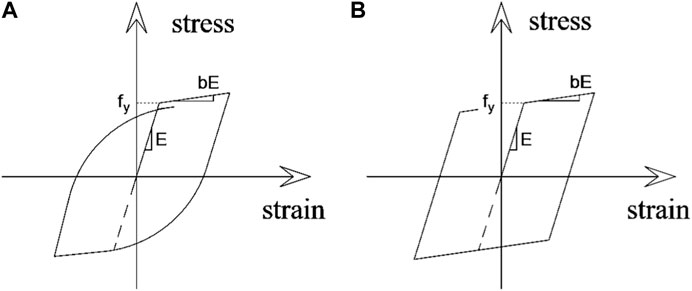
FIGURE 7. Material model (A) GMP used for simulating responses and (B) bilinear used in the estimation process.
For model updating in this example, the material properties of columns and beams are considered unknown model parameters, similar to the previous example. The initial estimate for the unknown model parameters and its covariance matrix are selected as
Figure 8 shows the model updating results for the three methods: the proposed VB method, the two-step marginal MAP estimation method, and the non-adaptive Bayesian method. As can be seen, the non-adaptive method cannot estimate unknown model parameters correctly for all parameters, except
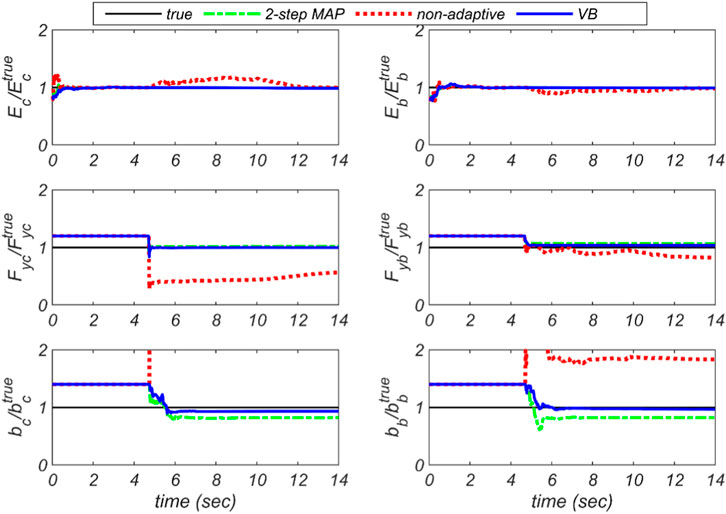
FIGURE 8. Time histories of the estimated model parameters obtained by the three methods: the proposed VB method, two-step marginal MAP estimation method, and the non-adaptive Bayesian method for the second case study.
To investigate the capability of the updated model with material modeling error in predicting the responses, absolute acceleration responses at each floor and moment–curvature response at the base of the first story’s inner column are predicted from the updated model using all three methods and compared with their true counterparts in Figure 9 and Figure 10, respectively. Although, as can be seen in Figure 9, the discrepancies between measured and predicted acceleration responses are minimized, and the estimated parameters are biased for the case of non-adaptive, and to a lesser extent for the two-step MAP method. As can be observed in Figure 10, the response predictions are considerably improved by both adaptive methods, and their predictions agree with the true moment–curvature response. Comparing the proposed VB method with the two-step MAP method, the VB method better predicts the response because of better estimation of unknown model parameters.
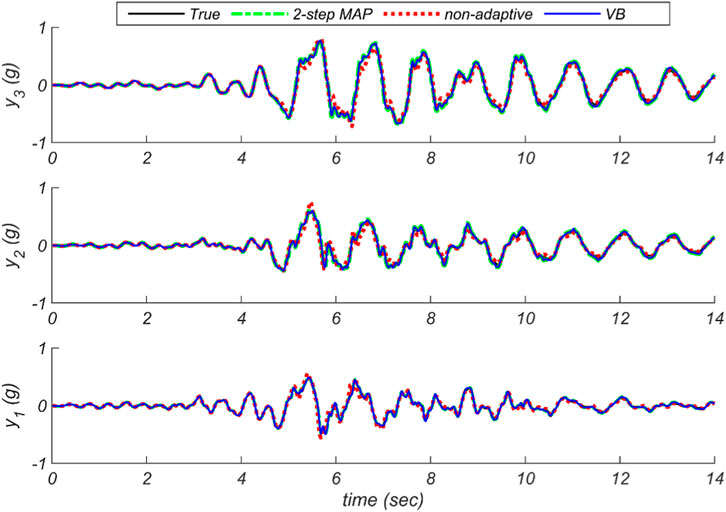
FIGURE 9. Absolute acceleration responses at each floor obtained by the true model and the updated ones using the three methods: the proposed VB method, the two-step marginal MAP estimation method, and the non-adaptive Bayesian method.
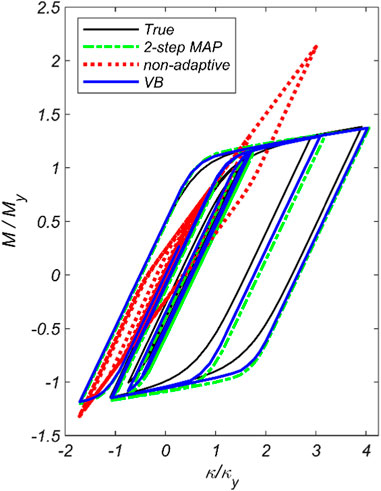
FIGURE 10. Moment–curvature responses at the base of the inner column obtained by the true model and the updated one using the three methods: the proposed VB method, the two-step marginal MAP estimation method, and the non-adaptive Bayesian method.
7 Conclusion
In this paper, we exploited the variational Bayesian (VB) approach and proposed an adaptive variational Bayesian model updating method for joint model and noise identification. A detailed mathematical derivation is provided in the paper. The performance of the proposed method is demonstrated through two numerical case studies. Two non-linear steel moment frames subjected to earthquake excitation were used, in which six parameters characterizing the constitutive models of the steel beams and columns were considered unknown. In the first case study, absolute acceleration responses at each floor contaminated by Gaussian noise with a time-variant mean vector and covariance matrix were considered measurement data. For considering modeling error in the second case study, a steel constitutive model of Giuffre–Menegotto–Pinto (GMP) is used for data simulation, and a bilinear constitutive model is used in the estimation process. The estimation results of both case studies showed that the proposed VB-based method performs well in the presence of time-variant prediction error (measurement noise and modeling error). The proposed VB-based method was also compared to a recently developed two-step marginal MAP estimation method, and the non-adaptive Bayesian model updating method. The results showed that both adaptive methods have comparable performance, while the non-adaptive method resulted in significantly biased estimations due to the adverse effects of non-stationary prediction error. The future scope of this work is to extend the algorithm to estimate the dynamic inputs, which will result in a joint input–parameter–noise estimation, and to validate the algorithm in real-world applications where the modeling errors can result in divergence or significant bias in regular model updating algorithms.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors without undue reservation.
Author contributions
HE and M-SN conceptualized the framework. M-SN and MS derived the formulations. HE and BM verified the derivations. M-SN and MS implemented the formulation and analyzed the results. BM and HE investigated the results. M-SN and MS developed the first draft. HE and BM revised and edited. HE and BM supervised the project.
Acknowledgments
The fourth author acknowledges partial support for this study through the National Science Foundation Grant 1903972. The opinions, findings, and conclusions expressed in this paper are those of the authors and do not necessarily represent the views of the sponsors.
Conflict of interest
Author MS was employed by Gavin and Doherty Geosolutions Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbuil.2023.1143597/full#supplementary-material
References
Akhlaghi, S., Zhou, N., and Huang, Z. (July 2017). Adaptive adjustment of noise covariance in Kalman filter for dynamic state estimation, Proceedings of the 2017 IEEE power and energy society general meeting (IEEE). Chicago, IL, USA. doi:10.1109/PESGM.2017.8273755
Amini Tehrani, H., Bakhshi, A., and Yang, T. T. (2020). Online probabilistic model class selection and joint estimation of structures for post-disaster monitoring. J. Vib. Control 27, 1860–1878. doi:10.1177/1077546320949115
Astroza, R., Alessandri, A., and Conte, J. P. (2019). A dual adaptive filtering approach for nonlinear finite element model updating accounting for modeling uncertainty. Mech. Syst. Signal Process 115, 782–800. doi:10.1016/j.ymssp.2018.06.014
Astroza, R., Ebrahimian, H., and Conte, J. P. (2014). Material parameter identification in distributed plasticity FE models of frame-type structures using nonlinear stochastic filtering. J. Eng. Mech. 141 (5), 4014149. doi:10.1061/(ASCE)EM.1943-7889.0000851
Astroza, R., Ebrahimian, H., and Conte, J. P. (2017). “Batch and recursive bayesian estimation methods for nonlinear structural system identification,” in Risk and reliability analysis: Theory and applications. Springer series in reliability engineering. Editor P. Gardoni (Berlin, Germany: Springer), 341–364. doi:10.1007/978-3-319-52425-2_15
Astroza, R., Ebrahimian, H., and Conte, J. P. (2019b). Performance comparison of Kalman−based filters for nonlinear structural finite element model updating. J. Sound. Vib. 438, 520–542. doi:10.1016/j.jsv.2018.09.023
Beal, M. J. (2003). Variational algorithms for approximate Bayesian inference: Dissertation. University of London, University, London UK.
Beck, J. L., and Yuen, K.-V. (2004). Model selection using response measurements: Bayesian probabilistic approach. J. Eng. Mech. 130 (2), 192–203. doi:10.1061/(asce)0733-9399(2004)130:2(192)
Behmanesh, I., Moaveni, B., Lombaert, G., and Papadimitriou, C. (2015). Hierarchical Bayesian model updating for structural identification. Mech. Syst. Signal Process 64, 360–376. doi:10.1016/j.ymssp.2015.03.026
Bishop, C. M., and Nasrabadi, N. M. (2006). Pattern recognition and machine learning. New York, NY, USA: Springer.
Cesmd, (2019). Center for engineering strong motion data, cesmd- A cooperative effort. https://strongmotioncenter.org.
Ching, J., Beck, J. L., and Porter, K. A. (2006). Bayesian state and parameter estimation of uncertain dynamical systems. Probabilistic Eng. Mech. 21 (1), 81–96. doi:10.1016/j.probengmech.2005.08.003
Deisenroth, M. P., Faisal, A. A., and Ong, C. S. (2020). Mathematics for machine learning. Cambridge University Press, Cambridge, UK.
Doebling, S. W., Farrar, C. R., Prime, M. B., and Shevitz, D. W. (1996). Damage identification and health monitoring of structural and mechanical systems from changes in their vibration characteristics: A literature review. NM, USA: Los Alamos National Lab. doi:10.2172/249299
Ebrahimian, H., Astroza, R., and Conte, J. P. (2015). Extended Kalman filter for material parameter estimation in nonlinear structural finite element models using direct differentiation method. Earthq. Eng. Struct. Dyn. 44 (10), 1495–1522. doi:10.1002/eqe.2532
Filippou, F. C., Popov, E. P., and Bertero, V. V. (1983). Effects of bond deterioration on hysteretic behavior of reinforced concrete joints. EERC 83–19. Earthquake Engineering Research Center. Berkeley, CA, USA: Univ. of California.
Friswell, M., and Mottershead, J. E. (2013). Finite element model updating in structural dynamics. Springer Science and Business Media, Berlin, Germany.
Granström, K., and Orguner, U. (2011). Properties and approximations of some matrix variate probability density functions. Linköping University Electronic Press, Linköping, Sweden.
Huang, Y., Yu, J., Beck, J. L., Zhu, H., and Li, H. (2020). Novel sparseness-inducing dual Kalman filter and its application to tracking time-varying spatially-sparse structural stiffness changes and inputs. Comput. Methods Appl. Mech. Eng. 372, 113411. doi:10.1016/j.cma.2020.113411
Huang, Y., Zhang, Y., Li, N., and Zhao, L. (2016). Design of sigma-point Kalman filter with recursive updated measurement. Int. J. Circuits, Syst. Signal Process. 35 (5), 1767–1782. doi:10.1007/s00034-015-0137-y
Huang, Y., Zhang, Y., Wu, Z., Li, N., and Chambers, J. (2017). A novel adaptive Kalman filter with inaccurate process and measurement noise covariance matrices. IEEE T Autom. Contr 63 (2), 594–601. doi:10.1109/TAC.2017.2730480
Kollo, T., and Von Rosen, D. (2006). Advanced multivariate statistics with matrices. Springer Science and Business Media, Berlin, Germany.
Kontoroupi, T., and Smyth, A. W. (2016). Online noise identification for joint state and parameter estimation of nonlinear systems. ASCE-ASME J. Risk Uncertain. Eng. Syst. A Civ. Eng. 2 (3), B4015006. doi:10.1061/AJRUA6.0000839
Law, K. J., and Stuart, A. M. (2012). Evaluating data assimilation algorithms. Mon. Weather Rev. 140 (11), 3757–3782. doi:10.1175/mwr-d-11-00257.1
McKenna, F., Fenves, G. L., and Scott, M. H. (2000). Open system for earthquake engineering simulation. Berkeley, CA, USA: University of California.
Mehra, R. (1972). Approaches to adaptive filtering. IEEE T Autom. Contr 17 (5), 693–698. doi:10.1109/tac.1972.1100100
Nabiyan, M. S., Ebrahimian, H., Moaveni, B., and Papadimitriou, C. (2022). Adaptive bayesian inference framework for joint model and noise identification. J. Eng. Mech. 148 (3), 4021165. doi:10.1061/(ASCE)EM.1943-7889.0002084
Nabiyan, M. S., Khoshnoudian, F., Moaveni, B., and Ebrahimian, H. (2020). Mechanics-based model updating for identification and virtual sensing of an offshore wind turbine using sparse measurements. Struct. Contr. Health Monit. 28, e2647. doi:10.1002/stc.2647
O'Hagan, A., and Forster, J. J. (2004). Kendall's advanced theory of statistics, 2. 2, Arnold, London, UK.
Opper, M., and Saad, D. (2001). Advanced mean field methods: Theory and practice. MIT Press, Cambridge, MA, USA.
Paolella, M. S. (2018). Linear models and time-series analysis: Regression, ANOVA, ARMA and GARCH. John Wiley and Sons, New York, NY, USA.
Song, M., Behmanesh, I., Moaveni, B., and Papadimitriou, C. (2020). Accounting for modeling errors and inherent structural variability through a hierarchical bayesian model updating approach: An overview. Sensors 20 (14), 3874. doi:10.3390/s20143874
Sanayei, M., Arya, B., Santini, E. M., and Wadia-Fascetti, S. (2001). Significance of modeling error in structural parameter estimation. COMPUT-AIDED Civ. Inf. 16 (1), 12–27. doi:10.1111/0885-9507.00210
Sarkka, S., and Hartikainen, J. (September 2013). Non-linear noise adaptive Kalman filtering via variational Bayes, Proceedings of the 2013 IEEE international workshop on machine learning for signal processing (MLSP), (IEEE), Southampton, UK.
Sarkka, S., and Nummenmaa, A. (2009). Recursive noise adaptive Kalman filtering by variational Bayesian approximations. IEEE T Autom. Contr 54 (3), 596–600. doi:10.1109/TAC.2008.2008348
Shi, Y., Tang, X., Feng, X., Bian, D., and Zhou, X. (2018). Hybrid adaptive cubature Kalman filter with unknown variance of measurement noise. Sensors 18 (12), 4335. doi:10.3390/s18124335
Šmídl, V., and Quinn, A. (2006). The variational Bayes method in signal processing. Springer Science and Business Media, Berlin, Germany.
Song, M., Astroza, R., Ebrahimian, H., Moaveni, B., and Papadimitriou, C. (2020). Adaptive Kalman filters for nonlinear finite element model updating. Mech. Syst. Signal Process 143, 106837. doi:10.1016/j.ymssp.2020.106837
Sun, C., Zhang, Y., Wang, G., and Gao, W. (2018). A new variational Bayesian adaptive extended Kalman filter for cooperative navigation. Sensors 18 (8), 2538. doi:10.3390/s18082538
Sun, J., Zhou, J., and Gu, X. (2012). Variational Bayesian two-stage Kalman filter for systems with unknown inputs. Procedia Eng. 29, 2265–2273. doi:10.1016/j.proeng.2012.01.299
Tzikas, D. G., Likas, A. C., and Galatsanos, N. P. (2008). The variational approximation for Bayesian inference. IEEE Signal Process. Mag. 25 (6), 131–146. doi:10.1109/MSP.2008.929620
Weinstock, R. (1974). Calculus of variations: With applications to physics and engineering. Dover Publications, New York.
Wenzel, T., Burnham, K., Blundell, M., and Williams, R. (2007). Kalman filter as a virtual sensor: Applied to automotive stability systems. Trans. Inst. Meas. Control 29 (2), 95–115. doi:10.1177/0142331207072990
Wu, J. (2005). Some properties of the normal distribution. https://cs.nju.edu.cn/_upload/tpl/00/ed/237/template237/paper/Gaussian.pdf.
Wu, M., and Smyth, A. W. (2007). Application of the unscented Kalman filter for real-time nonlinear structural system identification. Struct. Contr. Health Monit. 14 (7), 971–990. doi:10.1002/stc.186
Xu, D., Wu, Z., and Huang, Y. (2019). A new adaptive Kalman filter with inaccurate noise statistics. Int. J. Circuits, Syst. Signal Process. 38 (9), 4380–4404. doi:10.1007/s00034-019-01053-w
Yang, J. N., Lin, S., Huang, H., and Zhou, L. (2006). An adaptive extended Kalman filter for structural damage identification. Struct. Contr. Health Monit. 13 (4), 849–867. doi:10.1002/stc.84
Yuen, K. V., and Kuok, S. C. (2016). Online updating and uncertainty quantification using nonstationary output-only measurement. Mech. Syst. Signal Process 66, 62–77. doi:10.1016/j.ymssp.2015.05.019
Zhang, Q., Yang, Y., Xiang, Q., He, Q., Zhou, Z., and Yao, Y. (2018). Noise adaptive Kalman filter for joint polarization tracking and channel equalization using cascaded covariance matching. IEEE Photonics J. 10 (1), 1–11. doi:10.1109/JPHOT.2018.2797050
Keywords: adaptive Bayesian model updating, variational Bayesian technique, noise identification, model prediction error, non-stationary noise
Citation: Nabiyan M-S, Sharifi M, Ebrahimian H and Moaveni B (2023) A variational Bayesian inference technique for model updating of structural systems with unknown noise statistics. Front. Built Environ. 9:1143597. doi: 10.3389/fbuil.2023.1143597
Received: 13 January 2023; Accepted: 22 March 2023;
Published: 24 April 2023.
Edited by:
Jian Li, University of Kansas, United StatesReviewed by:
Hua-Ping Wan, Zhejiang University, ChinaYong Huang, Harbin Institute of Technology, China
Copyright © 2023 Nabiyan, Sharifi, Ebrahimian and Moaveni. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Hamed Ebrahimian, aGVicmFoaW1pYW5AdW5yLmVkdQ==
†These authors have contributed equally to this work and share first authorship
 Mansureh-Sadat Nabiyan
Mansureh-Sadat Nabiyan Mahdi Sharifi
Mahdi Sharifi Hamed Ebrahimian
Hamed Ebrahimian Babak Moaveni
Babak Moaveni