
95% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Built Environ. , 16 February 2023
Sec. Computational Methods in Structural Engineering
Volume 9 - 2023 | https://doi.org/10.3389/fbuil.2023.1066525
This article is part of the Research Topic Methods and Applications in Computational Methods in Structural Engineering View all 7 articles
 George Z. Voyiadjis1*
George Z. Voyiadjis1* Peter I. Kattan2
Peter I. Kattan2The development of the theories of undamageable materials and bimodal self-regenerating materials leads directly to four-dimensional materials. Both are types of sought after materials. The authors have established that undamageable materials are the limit of Voyiadjis-Kattan materials of order n as n approaches infinity. Similarly, the authors established also that so called bimodal materials are the limit of self-regenerating materials of order n as n approaches infinity. In this work, a solid link is established between these theories that were developed recently and the new four-dimensional materials to come. It is concluded that both undamageable materials and bimodal materials are prime examples of four-dimensional materials. The conclusion is based on sound mathematical and mechanical principles.
The basic principles of damage mechanics were laid out in the fifities with the pioneering work of Kachanov (1958). More recent work on this topic was made by Lee et al. (1985), Voyiadjis and Kattan (1992, 2005, 2006, 2009), Sidoroff (1981), and Kattan and Voyiadjis (1993, 2001a, 2001b).
Kachanov (1958) developed the fundamental basis of continuum damage mechanics using the concept of effective stress. More recent advancements in this topic were made by Rabotnov (1969) and by others later (Ladeveze and Lemaitre, 1984; Kattan and Voyiadjis, 2001a; 2001b; Voyiadjis and Kattan, 2005; 2006; 2009; 2012a; 2012c). The value of the damage variable ranges between 0 and 1 but usually cannot exceed 0.3. In the two extreme cases of 0 and 1, the material is in the virgin state and totally damaged, respectively.
Many advancements were made in damage mechaics recently (Rice, 1971; Sidoroff, 1981; Ladeveze et al., 1982; Lee et al., 1985; Voyiadjis, 1988; Kattan and Voyiadjis, 1990; 1993; Voyiadjis and Kattan, 1990; 1992; Hansen and Schreyer, 1994; Doghri, 2000; Luccioni and Oller, 2003; Celentano et al., 2004; Lubineau and Ladeveze, 2008; Lubineau, 2010).
Basaran and coworkers develop the theory further to apply it to novel materials (Basaran and Yan, 1998; Basaran and Tang, 2002; Basaran et al., 2003; Basaran and Nie, 2004; 2007). Other theoretical developments appeared later by Sosnovkiy and Sherbakov (2016). A relation has also been made thus far linking damage mechaics to biological systems. For details about the concept of the fourth dimension, check the Appendix.
This work consists of three major sections. In Section 2 the principles of the mechanics of undamageable materials are reviewed. The section starts with a review of higher-order strain energy form. This is followed by a study of the damage variable and the proof that the undamageable material maintains a zero value for the damage variable throughout the process of deformation and damage. Finally, the elastic stiffness equations for undamageable materials are presented.
In Section 3 the principles of the mechanics of self-regenerating materials are presented. First the theoretical formulation is reviewed. This is followed by the elastic stiffness equations and how the elastic stiffness recovers in self-regenerating materials. Finally, the road to bimodal materials is explored by studying self-regenerating materials when the exponent
Finally in the Conclusion it is postulated that both undamageable materials and bimodal materials are types of four-dimensional materials. It is seen that when infinity is reached, a dimension is crossed and we enter into the world of four-dimensional materials.
The original issue in this work is the term “fourth-dimensional material” and its associated conepts. This term has never appeared before in the literature or anywhere else. However, the theories of undamageable materials and bimodal materials have been presented before by the authors and they review them here along with their associated concepts and equations (Voyiadjis and Kattan, 2013a; 2017d). The presentation here is brief and updates the previous work of the authors.
As it was stated in the conclusion this work addresses both the theory of undamageable materials and the theory of self-regenerating materials. In particular both the undamageable material and the proposed bimodal material are of vital interest to the manufacturing world. Both these materials are achieved mathematically as one approaches infinity. It is noted that as infinity is approached a dimension is crossed and one evolves into the four-dimensional materials. This fact was proved mathematically in the authors’ own work on the subject (Voyiadjis and Kattan, 2017c). Thus it is seen that both undamageable materials and bimodular materials are types of four-dimensional materials. This is the true nature of these hypothetical materials.
In this section the mechanics of undamageable materials are reviewed. One starts with the higher-order strain energy forms, then proceeds to a study of the damage variable in these materials, then the elastic stiffness equations are presented.
Higher order strain energy forms are studied and introduced in this section. These new forms are usually linked to non-linear stress-strain relations and are studied in detail in this work These new proposed types of materials are called here Voyiadjis-Kattan materials (Voyiadjis and Kattan, 2013a, 2013b).
One first starts with the linear relation. The linear stress-strain relation
Use will be made of the terminology by Voyiadjis-Kattan material of order
One first starts with the most general from of the stress-strain equation:
One now illustrates the general case using the higher-order strain energy form
Next, one substitutes the general stress-strain relation
Simplifying the above relation, one obtains:
Differentiating both sides of the above equations lead to the following:
The above is the governing differential equation of the system and is solved using the MATLAB Symbolic Math Toolbox. The solution is obtained as follows:
Substituting the above expression into the general constitutive relation
The above solution is obtained after applying the initial condition that the stress is zero when the strain is zero. The above equation is a non-linear stress-strain relationship that governs the behavior of the Voyiadjis-Kattan material of order
For certain selected values of n, the results are shown in Table 1. Other existing materials similar to the Voyiajdis-Kattan material are shown in Table 2. Figure 1 showns a graph of the various stress-strain relations of Table 1. Figure 1 is generated based on Eq. 7 and proper units appear on the figure.

TABLE 1. The proposed higher-order strain energy forms and their corresponding stress-strain relations (constitutive equations for Voyiadjis-Kattan material of order
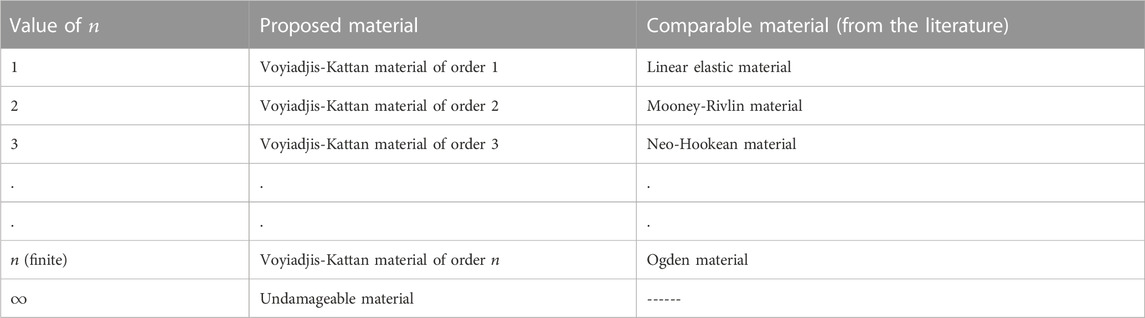
TABLE 2. Comparison between the Voyiadjis-Kattan material of order
One considers a linear elastic material with modulus of elasticity
The scalar damage variable
where
Using the hypothesis of elastic energy equivalence one assumes the complementary elastic strain energy (
Using the hypothesis of elastic energy equivalence and using Eq. 10, one obtains
Postulating a new hypothesis of higher-order energy equivalence in the form
one consequently obtains:
Finally, one obtains the relation
In this case, it is easily shown that using
For the general case and for a general value of n, one obtains:
In this case, it is easily shown that using
Several curves are plotted on the same graph paper to show the relations between the ratio of the stresses
One now explains the above results using the formulas derived for
Therefore one obtains
1. The Voyiadjis-Kattan material of order
2. The undamageable material is the limit of the Voyiadjis-Kattan material of order
3. The linear elastic material is a type of Voyiadjis-Kattan material of order 1.
4. In an undamageable material, the value of the stress will remain equal to zero throughout the deformation process. Also, the damage variable will be equal to zero throughout.
5. The undamageable material has zero strain energy.
6. The undamageable material has non-zero strain values. Thus, the undamageable material is a type of deformable body, not a rigid body.
7. The Voyiadjis-Kattan material of order
In this section, the precise equations governing the elastic stiffness transformation for Voyiadjis-Kattan materials are derived (Voyiadjis and Kattan, 2013a; 2012b; 2012c; 2013b; 2014). For this derivation, use is made of the classical damage variable that is defined in terms of area reduction. In this regard, the effective stress is given by:
where
Utilizing a hypothesis of higher-order energy equivalence in the following form:
and substituting Eq. 14 into Eq. 15, and simplifying, one obtains the following expression for the effective strain:
It should be noted that the stress-strain relationship for the Voyiadjis-Kattan material of order
Substituting for the effective stress from Eq. 14 into Eq. 17, one obtains:
Next, substituting for the stress from Eq. 7 into Eq. 18 and simplifying the resulting equation, one obtains:
and furthermore substituting Eq. 16 into Eq. 19 and simplifying one obtains:
The above relation can be re-written in the following form:
Again, substituting Eq. 16 into Eq. 21 and simplifying, one obtains:
It should be noted that as one approaches infinity, a dimension is crossed and evolves into of four dimensions. Thus undamageable materials are a type of four-dimensional material. Their realization in the manufacturing technology will require work in the fourth dimension. Another type of four-dimensional materials will be the bimodal material of Section 3.3 below where infinity is approached and a dimension is crossed again.
In this section the mechanics of self-regenerating materials are presented. One starts with the scalar formulation then this is followed by the recovery of elastic stiffness in these materials. Finally the extreme case when the exponent
Based on the recent work of the authors (Voyiadjis and Kattan, 2017a; 2017b), one utilizes a new scalar bur non-linear damage variable
It is noted from Figure 4 that both damage variables satisfy the same boundary condition but while
Based on the above equations, one can then write the following relation:
The values of the effective stress are real when the damage variable
The following observations are made regarding Figure 5 and the associated Eq. 7: Note that Figure 5 is generated based on Eq. 24 and appears with proper units.
1. The simple expression shown in Eq. 24, along with Figure 5, clearly describes a damage stage that is followed by a healing stage.
2. The behavior observed in Figure 5 is a characteristic of soft materials, especially for biological tissue.
3. The expression given in Eq. 24 is the basis for a new hypothetical type of material to be called Self-Regenerating Material (SRGM). This material may be developed in the future when the manufacturing technology may address such challenges.
4. The constitutive equations of Self-Regenerating Materials in terms of elastic stiffness are developed in Section 4.
5. Upon loading, the virgin (undamaged) material undergoes damage in the range
6. Upon further loading, beyond
7. The two boundary cases at
Using the hypothesis of elastic strain equivalence, substituting the elastic constitutive relations
Alternatively, using the hypothesis of elastic energy equivalence, substituting Eq. 24 into Eq. 10, and simplifying (while assuming
Finally one obtains the following expression for the elastic stiffness in this case:
The relations of Eqs 27, 25 are plotted in Figure 6. The results of this section are summarized in Table 3.
Further developments of the theory derived in Section 4 for self-regenerating materials are shown in this section especially with the loss of stiffness and its further recovery. These results can be extended to the hypothetical case when
Both Eqs 25, 27 for the elastic stiffness transformation due to damage can be generalized using the following expression:
where
The expression of Eq. 28 is plotted in Figure 7 for several values of the integer exponent
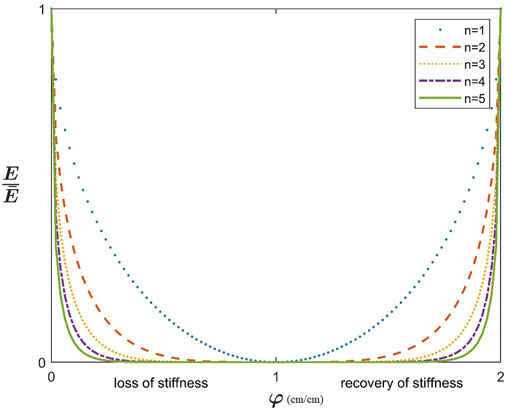
FIGURE 7. Elastic stiffness degradation and recovery for different values of the integer exponent n.
It is very interesting and paramount to observe in this section the strange behavior of the limit material of Figure 8 which naturally exists as biological tissue with its capability to fully heal itself (see Section 4) As shown in Figure 8, the elastic stiffness of this material is zero everywhere except at the two end points, i.e., at
The main characteristics of the postulated bimodal material are summarized below based on Eq. 28 and Figure 8:
1. The bimodal material suffers a sudden drop of its elastic stiffness from
2. The bimodal material breaks down (or its elastic stiffness vanishes completely) upon the start of loading and remains in this vanished state until the end point of loading.
3. The bimodal material undergoes a sudden gain in elastic stiffness from zero to its maximum value of
4. It seems that the elastic stiffness of the bimodal material suddenly disappears upon the start of loading and suddenly re-appears upon the end of loading. This strange behavior gives this material its name.
5. The bimodal material is the limit of the self-regenerating material of order
It should be noted that as one reaches infinity, a dimension is crossed and enters the mathematics of four dimensions. Thus this bimodal material is another type of four-dimensional materials. The first type of four-dimensional material was the undamageable material of Section 2.
This work has been divided into two major parts, existing mainly in Sections 2, 3. In Section 2 the theory of undamageable materials is presented while in Section 3 the theory of self-regenerating materials is presented. In particular both the undamageable material of Section 2 and the bimodal material of Section 3.3 are of vital interest to the manufacturing world. Both these materials are achieved mathematically as one approaches infinity. It is noted that as infinity is approached a dimension is crossed and one evolves into four-dimensional materials. This fact was proved mathematically in the authors’ own work on the subject (Voyiadjis and Kattan, 2017c). Thus it is seen that both undamageable materials and bimodal materials are types of four-dimensional materials. This is the true nature of these hypothetical materials.
As it was stated here this work addresses both the theory of undamageable materials and the theory of self-regenerating materials. In particular both the undamageable material and the proposed bimodal material are of vital interest to the manufacturing world. Both these materials are achieved mathematically as one approaches infinity. It is noted that as infinity is approached a dimension is crossed and one evolves into the four-dimensional materials. This fact was proved mathematically in the authors’ own work on the subject (Voyiadjis and Kattan, 2017c). Thus it is seen that both undamageable materials and bimodular materials are types of four-dimensional materials. This is the true nature of these hypothetical materials.
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Basaran, C., Lin, M., and Ye, H. (2003). A thermodynamic model for electrical current induced damage. Int. J. Solids Struct. 40 (26), 7315–7327. doi:10.1016/j.ijsolstr.2003.08.018
Basaran, C., and Nie, S. (2007). A thermodynamics based damage mechanics model for particulate composites. Int. J. Solids Struct. 44, 1099–1114. doi:10.1016/j.ijsolstr.2006.06.001
Basaran, C., and Nie, S. (2004). An irreversible thermodynamics theory for damage mechanics of solids. Int. J. Damage Mech. 13 (3), 205–223. doi:10.1177/1056789504041058
Basaran, C., and Tang, H. (2002). Implementation of a thermodynamic framework for damage mechanics of solder interconnects in microelectronics packaging. Int. J. Damage Mech. 11 (1), 87–108. doi:10.1106/105678902022259
Basaran, C., and Yan, C. Y. (1998). A thermodynamic framework for damage mechanics of solder joints. Trans. ASME, J. Electron. Packag. 120, 379–384. doi:10.1115/1.2792650
Celentano, D. J., Tapia, P. E., and Chaboche, J-L. (2004). “Experimental and numerical characterization of damage evolution in steels,”. Editors G. Buscaglia, E. Dari, and O. Zamonsky (Argentina: Bariloche), XXIII.Mec. Comput.
Doghri, I. (2000). Mechanics of deformable solids: Linear and nonlinear, analytical and computational aspects. Münster, Germany: Springer-Verlag.
Hansen, N. R., and Schreyer, H. L. (1994). A thermodynamically consistent framework for theories of elastoplasticity coupled with damage. Int. J. Solids Struct. 31 (3), 359–389. doi:10.1016/0020-7683(94)90112-0
Kachanov, L. (1958). On the creep fracture time. Izv. Akad. Nauk. USSR Otd. Tech. 8, 26–31. (in Russian).
Kattan, P. I., and Voyiadjis, G. Z. (1990). A coupled theory of damage mechanics and finite strain elasto-plasticity – Part I: Damage and elastic deformations. Int. J. Eng. Sci. 28 (5), 421–435. doi:10.1016/0020-7225(90)90007-6
Kattan, P. I., and Voyiadjis, G. Z. (1993). A plasticity-damage theory for large deformation of solids – Part II: Applications to finite simple shear. Int. J. Eng. Sci. 31 (1), 183–199. doi:10.1016/0020-7225(93)90075-6
Kattan, P. I., and Voyiadjis, G. Z. (2001b). Damage mechanics with finite elements: Practical applications with computer tools. Munster, Germany: Springer-Verlag.
Kattan, P. I., and Voyiadjis, G. Z. (2001a). Decomposition of damage tensor in continuum damage mechanics. J. Eng. Mech. ASCE 127 (9), 940–944. doi:10.1061/(asce)0733-9399(2001)127:9(940)
Ladeveze, P., and Lemaitre, J. (1984). “Damage effective stress in quasi-unilateral conditions,” in Proceedings of the The 16th International Cogress of Theoretical and Applied Mechanics, Pennsylvania, USA, December 1984 (Denmark: Lyngby).
Ladeveze, P., Poss, M., and Proslier, L. (1982). Damage and fracture of tridirectional composites. Jpn. Soc. Compos. Mater. 1, 649–658.
Lee, H., Peng, K., and Wang, J. (1985). An anisotropic damage criterion for deformation instability and its application to forming limit analysis of metal plates. Eng. Fract. Mech. 21, 1031–1054. doi:10.1016/0013-7944(85)90008-6
Lubineau, G., and Ladeveze, P. (2008). Construction of a micromechanics-based intralaminar mesomodel, and illustrations in ABAQUS/standard. Comput. Mater. Sci. 43 (1), 137–145. doi:10.1016/j.commatsci.2007.07.050
Lubineau, G. (2010). A pyramidal modeling scheme for laminates – identification of transverse cracking. Int. J. Damage Mech. 19 (4), 499–518. doi:10.1177/1056789509102725
Luccioni, B., and Oller, S. (2003). A directional damage model. Comput. Methods Appl. Mech. Eng. 192, 1119–1145. doi:10.1016/s0045-7825(02)00577-7
Rabotnov, Y. (1969). “Creep rupture,” in Proceedings, Twelfth International Congress of Applied Mechanics, Berlin, Germany, October 1969. Editors M. Hetenyi, W. G. Vincenti, and Stanford (Springer-Verlag), 342–349.
Rice, J. R. (1971). Inelastic constitutive relations for solids: An internal variable theory and its application to metal plasticity. J. Mech. Phys. Solids 19, 433–455. doi:10.1016/0022-5096(71)90010-x
Roizen, M. (2014). The healing of injured soft tissues. https://chiro-trust.org/whiplash/healing-injured-soft-tissues-including-neck-back/.
Sidoroff, F. (1981). “Description of anisotropic damage application in elasticity,” in IUTAM colloqium on physical nonlinearities in structural analysis (Berlin, Germany: Springer-Verlag), 237–244.
Sosnovskiy, L. A., and Sherbakov, S. (2016). Mechanothermodynamic entropy and analysis of damage state of complex systems. Entropy 18, 268. doi:10.3390/e18070268
Voyiadjis, G. Z. (1988). Degradation of elastic modulus in elastoplastic coupling with finite strains. Int. J. Plasticity 4, 335–353. doi:10.1016/0749-6419(88)90023-x
Voyiadjis, G. Z., and Kattan, P. I. (2009). A comparative study of damage variables in continuum damage mechanics. Int. J. Damage Mech. 18 (4), 315–340. doi:10.1177/1056789508097546
Voyiadjis, G. Z., and Kattan, P. I. (1990). A coupled theory of damage mechanics and finite strain elasto-plasticity – Part II: Damage and finite strain plasticity. Int. J. Eng. Sci. 28 (6), 505–524. doi:10.1016/0020-7225(90)90053-l
Voyiadjis, G. Z., and Kattan, P. I. (2017c). A generalized hypothesis of elastic energy equivalence in continuum damage mechanics. Eng. Trans. 65 (2), 351–369.
Voyiadjis, G. Z., and Kattan, P. I. (2012b). A new class of damage variables in continuum damage mechanics. ASME J. Eng. Mater. Technol. 134 (2). doi:10.1115/1.4004422
Voyiadjis, G. Z., and Kattan, P. I. (1992). A plasticity-damage theory for large deformation of solids – Part I: Theoretical formulation. Int. J. Eng. Sci. 30 (9), 1089–1108. doi:10.1016/0020-7225(92)90059-p
Voyiadjis, G. Z., and Kattan, P. I. (2017d). A theory of damage and self-regenerating materials. Acta Mech. 228, 4249–4268. doi:10.1007/s00707-017-1928-y
Voyiadjis, G. Z., and Kattan, P. I. (2006). Advances in damage mechanics: Metals and metal matrix composites with an introduction to fabric tensors. Second. Amsterdam, Netherlands: Elsevier.
Voyiadjis, G. Z., and Kattan, P. I., 2005, Damage mechanics, Taylor and Francis (CRC Press).Boca Raton, FL, USA.
Voyiadjis, G. Z., and Kattan, P. I. (2017b). Decomposition of elastic stiffness degradation in continuum damage mechanics. ASME, J. Eng. Mater. Technol. 139 (2). doi:10.1115/1.4035292
Voyiadjis, G. Z., and Kattan, P. I. (2014). Healing and super healing in continuum damage mechanics. Int. J. Damage Mech. 23 (2), 245–260. doi:10.1177/1056789513491773
Voyiadjis, G. Z., and Kattan, P. I. (2013a). Introduction to the mechanics and design of undamageable materials. Int. J. Damage Mech. 22 (3), 323–335. doi:10.1177/1056789512446518
Voyiadjis, G. Z., and Kattan, P. I. (2012a). Mechanics of damage processes in series and in parallel: A conceptual framework. Acta Mech. 223 (9), 1863–1878. doi:10.1007/s00707-012-0678-0
Voyiadjis, G. Z., and Kattan, P. I. (2017a). Mechanics of damage, healing, damageability, and integrity of materials: A conceptual framework. Int. J. Damage Mech. 26 (1), 50–103. doi:10.1177/1056789516635730
Voyiadjis, G. Z., and Kattan, P. I. (2013b). On the theory of elastic undamageable materials. ASME J. Eng. Mater. Technol. 135 (2), 021002–021016. doi:10.1115/1.4023770
Voyiadjis, G. Z., Yousef, M. A., and Kattan, P. I. (2012c). New tensors for anisotropic damage in continuum damage mechanics. ASME J. Eng. Mater. Technol. 134 (2). doi:10.1115/1.4006067
In this Appendix, the authors try to explain the fourth dimension and what they mean by four-dimentional materials.
Consider a point. It has no extensions so the point is zero-dimensional. Now consider a set of n such points arranged horizontally on a straight line. Once the number of points n increases, the points get closer together. They become closer and closer with increasing n until n approaches infinity. When n approaches infinity the points become stuck together and effectively become a straight line. As n approached infinity, the points are no longer zero-dimensional but become a one-dimensional straight line. Thus a dimension is crossed when n approached infinity.
Similarly consider a straight line. It is clearly one-dimensional. Consider n such straight lines arranged in parallel. Let the number of these straight lines be n. Once n increases, the straight lines become closer together. This continues until n approaches infinity when the straight lines become stuck together in a plane. Thus as n approached infinity the straight lines are no longer one-dimensional but become a two-dimensional plane. Thus again a dimension is crossed as n approaches infinity.
The same thing happens when the crossing from a two-dimensional plane to a three-dimensional cube occurs. Consider a number n of two-dimensional planes arranged in parallel. As n increases, the planes get closer together. Once n approaches infinity the planes become stuck together and a three-dimensional cube is formed. In this case, again, a dimension is crossed when n approaches infinity. The planes are no longer two-dimensional planes but have become a three-dimensional cube.
Finally consider a three-dimensional cube. Consider n such three-dimensional cubes arranged in parallel. As the number of cubes n increases, the cubes become closer together. As n approaches infinity, the cubes become stuck into a fourth-dimensional hypercube called a tesseract. Thus as n approached infinity the cubes are no longer three-dimensional but have become a fourth-dimensional hypercube. Again, one notices that a dimension is crossed when n approaches ininity.
The same thing happens with materials. For normal three-dimensional materials everthing is normal as the exponent n is small. But when n becomes large and approaches infinity, a dimension is crossed and one obtains four-dimensional materials. Trying to explain this in terms of damage and healing, one can say that microvoids (zero dimension), microcracks (one dimensional), microflat spaces (two dimensional), microspherical spaces (three dimensional), collapse of spherical spaces into other shapes are fourth dimensional artifacts. Recovery in the same dimension implies closure of microvoids, microcracks, et. (Watson, 2003; Waston, 2006; Bower, 2009; Roizen, 2014).
Keywords: four-dimensional materials, undamageable materials, self-regenerating materials, bimodal materials, damage
Citation: Voyiadjis GZ and Kattan PI (2023) Toward four-dimensional materials: The true nature of undamageable materials and bimodal self-regenerating materials. Front. Built Environ. 9:1066525. doi: 10.3389/fbuil.2023.1066525
Received: 11 October 2022; Accepted: 07 February 2023;
Published: 16 February 2023.
Edited by:
Franco Milicchio, Roma Tre University, ItalyReviewed by:
Rostand Moutou Pitti, Université Clermont Auvergne, FranceCopyright © 2023 Voyiadjis and Kattan. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: George Z. Voyiadjis, dm95aWFkamlzQGVuZy5sc3UuZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.