
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Built Environ., 16 February 2023
Sec. Wind Engineering and Science
Volume 9 - 2023 | https://doi.org/10.3389/fbuil.2023.1005264
This article is part of the Research TopicRecent Advances in Risk and Community Resilience Analysis against WindstormsView all 5 articles
Strong hurricane winds often cause severe infrastructure damage and pose social and economic consequences in coastal communities. In the context of community resilience planning, estimating such impacts can facilitate developing more risk-informed mitigation plans in the community of interest. This study presents a new framework for synthetically simulating scenario-hurricane winds using a parametric wind field model for predicting community-level building damage, direct economic loss, and social consequences. The proposed synthetic scenario approach uses historical hurricane data and adjusts its original trajectory to create synthetic change scenarios and estimates peak gust wind speed at the location of each building. In this research, a stochastic damage simulation algorithm is applied to assess the buildings’ physical damage. The algorithm assigns a damage level to each building using the corresponding damage-based fragility functions, predicted maximum gust speed at the building’s location, and a randomly generated number. The monetary loss to the building inventory due to its physical damage is determined using FEMA’s direct loss ratios and buildings’ replacement costs considering uncertainty. To assess the social impacts of the physical damage exposure, three likely post-disaster social disruptions are measured, including household dislocation, employment disruption, and school closures. The framework is demonstrated by its application to the hurricane-prone community of Onslow County, North Carolina. The novel contribution of the developed framework, aside from the introduced approach for spatial predicting hurricane-induced wind hazards, is its ability to illuminate some aspects of the social consequences of substantial physical damages to the building inventory in a coastal community due to the hurricane-induced winds. These advancements enable community planners and decision-makers to make more risk-informed decisions for improving coastal community resilience.
Hurricanes are multi-hazard events that induce strong winds, storm surge, and heavy rain in coastal communities, as well as flash flooding and riverine flooding in inland communities. Hazard risk maps are effective tools that facilitate risk communication to engineers and community resilience planners. For instance, the national storm surge hazard maps that are generated by National Oceanic and Atmospheric Administration (NOAA) and the National Weather Service (NWS) help communities in hurricane-prone coastal areas along the U.S. East and Gulf Coasts and Puerto Rico to evaluate their risk to the hurricane-induced storm surge hazard. Similarly, Federal Emergency Management Agency (FEMA) has developed flood risk maps that communities use to know which areas have the highest risk of flash and riverine flooding. However, wind speed maps that are provided by building codes such as ASCE-7, despite their relative maturity for design purposes, are not efficient tools for assessing the resilience of a community against hurricane-induced winds. Severe hurricanes (Categories 3–5) have highly non-uniform wind speeds over a given geographical area. Wind risk maps in building codes consider uniform wind speeds (and often constant intensity in small communities) for buildings in the same risk category. Thus, these wind risk maps can significantly overestimate damage and loss due to hurricane-induced winds if applied at the community level.
As hurricanes approach coastlines, they impact large geographic areas. Thus, understanding and evaluating community-level impacts is an effective approach to advancing resilience. Between 1980 and 2021, hurricanes were by far the costliest and deadliest billion-dollar disaster events in the United States with $27.6B annual cost and 160 fatalities per year (Smith 2020). Consequences of such catastrophic events are only expected to rise as a result of climate change and urbanization. Beyond dollar losses and human casualties, hurricanes cause disruptions in the community’s social system, which amplify pre-disaster disparities, including access to healthcare, education, and employment (Enderami et al., 2021). Thus, a comprehensive equity-informed community resilience plan must consider social and economic impacts, alongside the physical impacts of natural hazards. To move toward this goal, community planners need to be provided with tools and actionable frameworks that enable them to demonstrate disparate community level impacts to make equity-informed decisions. The majority of available frameworks in the literature, however, focus on estimating damage and direct economic losses to the built environment at the individual property level and consequently ignore the social impacts of such destructions (e.g., Pinelli et al., 2004; Vickery et al., 2006a; Xu and Brown 2008; Kakareko et al., 2017; Wang et al., 2020; Adhikari et al., 2021). Therefore, we focus the scope of our study on hurricane-induced wind hazards. This paper presents a novel framework for synthetically simulating scenario-hurricane winds using a parametric wind field model for predicting community-level building damage, direct economic loss, and social consequences to help fill the identified gap in knowledge. The framework is illustrated on the Onslow County, North Carolina testbed, and provided to the user community as an open-source Python Jupyter Notebook (Mazumder et al., 2020; https://doi.org/10.17603/ds2-jzcv-he68).
Hurricanes pose multiple hazards to coastal communities, including intense winds, storm surges, heavy rains, and flooding. Strong hurricane winds can cause physical damage to building systems (i.e., interior, exterior, and content losses), and storm surges can cause extensive structural damage in severe cases. In addition, content losses occur due to wind-driven rain and surge heights entering buildings (Baradaranshoraka et al., 2017). Intense winds often lead to severe damage to buildings, and subsequent building functionality loss, leading occupants to leave their houses (Park et al., 2013). The nature of impact due to hurricanes varies significantly from coastline to inland and is very complex to model. Studies focusing on analyzing the combined impact of hurricane winds and storm surges could not properly allocate damages between these hazards (Baradaranshoraka et al., 2017; Nofal et al., 2021). While the combined storm surges and winds often impact buildings near the coastline, buildings in inland are primarily impacted by hurricane winds. While some of the most recent hurricanes that hit the U.S. coastline were primarily flood and storm surge events (e.g., 2016 Hurricane Matthew), some other hurricanes (e.g., 2018 Hurricane Michael) were very intense upon landfall, and hurricane wind caused the most destruction. In this study, we focus on understanding the impact of hurricane wind on coastal buildings at a community scale.
Hurricane wind hazard models have been developed using numerical simulation (Georgiou 1986), probabilistic approach (Simiu and Scanlan 1996), empirical hurricane track models (Vickery et al., 2000a; b; 2006a; 2009a; b), and data-driven techniques (Guo and van de Lindt 2019). Modelling and simulation of hurricane wind has advanced significantly over the last 2 decades (Powell et al., 1998; Vickery et al., 2006a; b; Xu and Brown 2008; Guo and van de Lindt 2019). However, solving non-linear primitive equations for hurricane numerical simulation and risk estimation involves extensive computation analysis. Therefore, researchers investigated parametric models as an alternative to numerical simulation techniques to gain higher computational efficiency. To generate non-uniform wind over a distributed area, several wind field models exist in the literature (e.g., Russell 1969; Schwerdt et al., 1979; Holland 1980; Batts et al., 1984). Among the existing models, Holland’s (1980) wind profile model, which allows estimating spatially distributed wind speeds of a hurricane, is used to generate non-uniform wind at a community level for high computation efficiency. Holland parameter is widely used in past studies for predicting wind hurricane wind speeds (e.g., Vickery et al., 2000a; b; Vickery and Wadhera 2008; Salman and Li 2018; Wang et al., 2020). Besides wind hazard modelling, extensive research has been conducted to characterize hurricane storm surge (Weisberg and Zheng, 2008; Dietrich et al., 2013; Sebastian et al., 2014), surge-induced coastal inundation (Torres et al., 2015; van Berchum et al., 2019), and combined hurricane wind-storm surge behavior (Li et al., 2012; Unnikrishnan and Barbato 2017; Bushra et al., 2019). Despite the fact that hurricane wind modeling matured remarkably over the past 3 decades, wind speed estimation presented in many existing hazard models and in building codes and design standards primarily focus on the performance evaluation of individual buildings or facilities against constant design speed over a large area (Pant and Cha 2018; Adhikari et al., 2021) and do not provide guidelines to account for spatial variation of wind speeds over a large area.
Although hurricanes are widespread destructive events, previous research has mainly focused on estimating damage and loss following such events at the individual facility-level, as opposed to predicting building portfolio performance against spatially-varied hazardous winds at a community scale. Specifically, past research has focused on risk assessment of individual residential buildings (Pinelli et al., 2004; Masoomi et al., 2019; Wang et al., 2020) and infrastructure systems, including electrical power network (Salman and Li 2018), transportation network (Wu et al., 2013), bridges (Snaiki et a. 2020), and evacuation modelling (Blanton et al., 2020; Davidson et al., 2020). Outcomes of hazard models are then used to estimate the performance of buildings using deterministic approaches (Emanuel et al., 2006), probabilistic approaches (Pinelli et al., 2004; Li and Ellingwood 2006), and Bayesian capacity modelling approaches (Mishra et al., 2017; Kakareko et al., 2020). Other studies have focused on analyzing building performance against multiple hazards (Masoomi et al., 2019; Nofal et al., 2021), and subsequent loss estimation (Vickery et al., 2006b; Baradaranshoraka et al., 2017; Kakareko et al., 2017). Previous studies (e.g., Vickery et al., 2006b; Li and Ellingwood 2006; Baradaranshoraka et al., 2017; Kakareko et al., 2017; 2020; Salman and Li 2018; Masoomi et al., 2019; Wang et al., 2020; Nofal et al., 2021) often used fragility functions as reliable tools for estimating the various level of damage probabilities for structures given hurricane-induced hazard intensity. Many of these studies are based on probabilistic approaches and have evaluated damage and losses to residential buildings subject to hurricane wind under stationary conditions (Pinelli et al., 2004; Deierlein et al., 2020; Adhikari et al., 2021). Overall, past studies have contributed to gaining a better understanding of the performance (i.e., damage and loss) of various structures against hurricane hazards as single or combined loads (Huang et al., 2001; Pinelli et al., 2004; Li and Ellingwood 2006; Salman and Li 2018; Bushra et al., 2019). Even still, most of these existing methods for estimating hurricane damage and loss are limited to evaluating individual facility/structure’s performance.
Post-hurricane report (e.g., NIST 2017) addressed research needs and challenges at the community scale to mitigate the risk of natural hazards. To mitigate the impact of future hurricane hazards, the probable damaging effect of a potential hurricane must be quantified considering spatially varied wind intensities at a community scale.
Of the studies that operate at the community-level, a major challenge is capturing hazard-damage-loss relationships accurately (Deierlein et al., 2020). Researchers have developed community-scale loss models for insurance purposes, including private (RMS 2010; AIR 2015) and public (FEMA 2010; Hamid et al., 2010) models for residential buildings. Regional hurricane risk analysis models include event-based simulations (Huang et al., 2001) and probabilistic non-stationary processes (Khajwal and Noshadravan 2020). Other studies performed community-level hurricane risk analysis using distributed computing platforms (Abdelhady et al., 2019; Abdelhady et al., 2020) and data-driven techniques (Guo and van de Lindt 2019). However, these probabilistic approaches are unable to account for the spatial distribution of hurricane intensities as the probabilistic hazard map represents an aggregated effect of numerous hurricane events (Adachi and Ellingwood 2010), limiting their application in community risk-management decision-making. Another challenge is that assessing a large number of buildings in a community following these approaches is computationally extensive, which indicates the need to develop a simple framework to speed up the simulation.
Damages to building and infrastructure systems often result in disruption of functionality, leading to a socioeconomic crisis in severe cases (Masoomi et al., 2020). Besides physical impacts, socioeconomic impacts also shape post-disaster recovery of a community, which is necessary to account for in community risk management (Masterson et al., 2014; van de Lindt et al., 2020). Unfortunately, hurricane risk assessment modules have often been limited to estimating physical damages to the built environment (e.g., Pinelli et al., 2004; Vickery et al., 2006a; Xu and Brown 2008; Kakareko et al., 2017; Wang et al., 2020; Adhikari et al., 2021). Studies used various proxy indicators, including health condition, age, race, gender, poverty, and income, to estimate the social vulnerability of community (Fekete 2009; Bjarnadottir et al., 2010; Abbas and Routray 2014; Rufat et al., 2019; Drakes et al., 2021). Such proxy measures have been used to understand the social impacts of disaster on society, including economic losses, damage to residential households, property loss, displacement, migration, shelter use, public assistance, and mortality (Myers et al., 2008; Burton 2010; Finch et al., 2010; Yoon 2012; Liu and Li 2016; Tate et al., 2016). Few other studies investigated the influence of social connection in their evacuation decision after hurricanes (Collins et al., 2017; 2018; Yabe and Ukkusuri 2020). However, these studies heavily relied on an individual disaster or were limited to geographic context.
Population dislocation is one of the common consequences of disasters and it has become a growing concern in the United States after Hurricane Katrina in 2005 (van de Lindt et al., 2020). When community members have to dislocate from a community, which can even be a neighborhood, their social networks will be interrupted (Erikson, 1978). Population dislocation can happen as a result of direct damages to residential buildings or other disaster impacts including utility outages, physical access disruption, concerns about safety, and loss of community capitals (Sutley and Hamideh 2020; Enderami et al., 2021; Daniel et al., 2022). Disasters also can disrupt community members’ access to their jobs and students’ access to their schools; such disruptions can be caused due to several reasons such as significant damage to the organization’s building, employee loss caused by household dislocation, etc. Hence, this study developed a new approach for estimating disaster impacts on society by evaluating household dislocation, employment disruption, and school closure. Estimating these measures will help decision-makers and stakeholders better plan disaster preparedness and recovery. In addition to estimating physical damage to buildings, the proposed framework also connects building damages with building occupancy data to estimate social impacts (i.e., population dislocation, school closure, and employment disruptions) on the community.
Figure 1 illustrates the proposed framework for assessing community-level building damage and social and economic losses due to hurricane-induced winds. The framework consists of three modules including hazard analysis, vulnerability analysis, and loss estimation. In the hazard analysis module, a hurricane scenario is selected by analyzing the frequency of past hurricanes and risk mitigation objectives. Characteristics of historical hurricanes are obtained from the HURDAT2 database, including path trajectory and wind speed distribution. Then, synthetic hurricane scenarios are generated by adjusting the original event characteristics to estimate probable consequences due to similar events. Building-specific maximum peak gust wind speed is then determined for the selected hurricane scenario following procedures described in Section 3.1. In the vulnerability analysis module, the probability of building damage exceeding four discrete damage levels is determined using fragility functions and estimated peak gust wind speed. Damage level is then assigned to a building stochastically by comparing the maximum peak gust wind speed, probabilities of damage states, and a randomly generated number. Detailed steps of vulnerability analysis are presented in Section 3.2. Finally, in the loss estimation module, direct financial losses resulting from physical damages are evaluated using a building damage ratio and building replacement values. To account for the uncertainty in loss prediction, a coefficient of variation is assumed for damage ratios based on engineering judgment. Social impacts are assessed by estimating the number of dislocated households, potential employment disruption, and the number of students who may lose their access to school. Details of the loss estimation module are described in Section 3.3. To perform the proposed framework efficiently, this study also develops an open-source python tool for future users, described in Section 3.4.
In the context of community resilience research, scenario-based approaches are more common to estimate natural hazard demands. A scenario event (or a portfolio of scenarios) lets researchers more effectively communicate risk to decision-makers and community resilience planners by evaluating what may happen if a certain natural hazard occurs in their community. Scenario-hurricane analysis can be performed based on either selecting the historical hurricane track or simulating a synthetic hurricane (Salman and Li 2018). Due to the shortness of data on past hurricanes, and their often poor quality, the datasets of such events are highly uncertain. Thus, using a historical hurricane model to produce large sets of synthetic hurricane tracks is an alternative strategy. Synthetic scenario models are simplified and fast-to-compute mathematical surrogate models to inform the probabilistic risk of storms in an area. A synthetic scenario modeling approach allows researchers to change the attribute of the scenario event and generate a suite of storms by making realistic but user-driven incremental adjustments in the original storm’s features (Jia et al., 2016; Fereshtehnejad et al., 2021). The framework presented in Figure 1 applies a deterministic synthetic scenario approach and considers a set of plausible hypothetical hurricanes, in addition to the original scenario, to determine the hazard demand. The original scenario is a historical hurricane with a specified strength passing close to the community of interest. To create the hypothetical scenarios, the original hurricane’s track is replicated parallel to the coastline, at interval distances equal to the desired area’s coastline length, with the same central pressure and intensity as the original hurricane. The appropriate historical scenario event for a particular region can be selected based on the frequency of hazard occurrence and the community’s risk perspective (Lin and Wang 2016). Past hurricane characteristics (e.g., hurricane wind speeds, hurricane track) can be retrieved from various sources, such as the National Hurricane Center (NHC) and the Revised Atlantic hurricane database (HURDAT2) prepared by National Oceanic and Atmospheric Administration (NOAA) (Vickery et al., 2009a; NOAA 2021). Original scenario selection, the number of hypothetical scenarios, and replica orientation are tied to the resolution of the desired community’s model and are situation-specific factors that should be determined based on the user’s analysis goal and engineering judgment.
To assess damage to the building inventory of a community, the peak gust wind speed at the location of each building at various time instants within the community needs to be estimated using a hurricane wind field model. The most commonly used hurricane wind speed estimation technique is numerical simulations (e.g., Georgiou 1986; Vickery et al., 2000a) which require solving non-linear primitive equations, and subsequent risk estimation involves extensive computation analysis. Researchers investigated parametric models as an alternative to numerical simulation techniques to gain higher computational efficiency. To generate non-uniform wind over a distributed area, several wind field models exist in the literature (e.g., Russell 1969; Schwerdt et al., 1979; Holland 1980; Batts et al., 1984). Among the existing models, the simplest form of a parametric model for high computational efficiency is Holland (1980) wind profile model (Guo and van de Lindt 2019). Hence, the proposed framework applies the widely adopted Holland (1980) wind profile model for this purpose (see Wang et al., 2020; Guo and van de Lindt 2019; Salman and Li 2018; Vickery and Wadhera 2008; Vickery et al., 2000a for examples).
Holland’s model employs a pressure profile parameter, known as the ‘Holland parameter’, that allows for estimating spatially distributed wind speeds of a hurricane. The strongest hurricane wind occurs at the eye wall; wind intensity decays as the location moves away from the hurricane center (Xu and Brown 2008). Gradient wind speed at building location is estimated using the radial wind profile model provided by Holland (1980) expressed as
where Rmax is the radius of the maximum wind speed, r is the distance from hurricane eye to the building site, B is the Holland pressure profile parameter,
where
The Coriolis parameter is determined by the following expression (Xu and Brown, 2008):
where
To assess the physical vulnerability of the building it is required to convert gradient wind speed to surface wind speed. A conversion factor of 0.83 near the eyewall, reducing to 0.75 away from the eyewall is used to convert gradient wind speed to surface (10 m above ground/water level) wind speed (Batts et al., 1984; Georgiou, 1986; Vickery et al., 2009b). Structural damage during a hurricane is generally associated with peak gust wind speed. Hence, the surface wind speed is further converted to 3-sec gust wind speed, multiplying surface wind speed by a gust wind factor of 1.287 with a standard deviation of 0.02 (Xu and Brown 2008; Salman and Li 2018).
A community’s building portfolio is composed of many different types of structures. To lower the computational cost, it is often desirable to use reduced-order models, such as fragility functions, to approximate a community’s building portfolio. HAZUS fragility functions and defined damage states (FEMA 2012) were adopted in the proposed framework. Four potential damage states, as defined in Figure 2A, are considered for a building subjected to hurricane wind hazards (FEMA 2012). Maximum peak gust wind speed is estimated at the location of each building using Eqs 1–4. The expected damage state is then assigned to the building stochastically based on the control axis value on the fragility curve (i.e., wind speed), and a random number generated on a uniform distribution U[0,1] (Klise et al., 2017; Mazumder et al., 2020). The intersection of x-axis (i.e., wind speed) and y-axis (i.e., random number) indicates the damage state for a particular building for a single realization (Klise et al., 2017), as shown in Figure 2C. Damage ratios represent the percent of the building value required to repair the building and their repair cost typically varies from one building to another. The uncertainty associated with the expected damage ratio for a particular building is modeled assuming a normal distribution with a coefficient of variation of 0.05, as shown in Figure 2D (FEMA 2012). Figure 2D shows random normal distributions of damage ratios corresponding to four damage states (Friedland 2009).
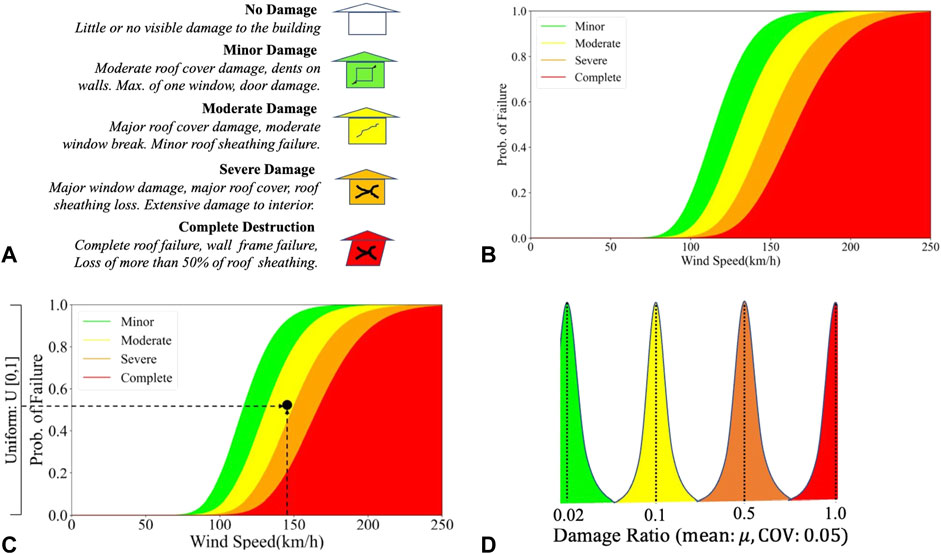
FIGURE 2. (A) Damage States, (B) Generalized fragility curves correspond to damage states, and (C) Stochastic damage simulation, and (D) Distribution of building damage ratio.
Direct financial loss caused by a hurricane is determined as a portion of the building replacement value using damage ratios based on the HAZUS hurricane loss model. Expected damage ratios (mean values) for none, minor, moderate, severe, or complete damage states are assumed as 0%, 2%, 10%, 50%, and 100%, respectively (FEMA 2012, p 7-11). Uncertainty in damage ratio for each building is modeled using a normal distribution with a mean damage ratio and a coefficient of variation (COV) (Lin and Wang 2016). Mean (μ) and COV values of the damage ratio for four damage states are shown in Figure 2D. Total direct financial loss for a community is estimated as
where di and BRVi are damage ratio and building replacement value for i-th building, respectively, and n is the total number of buildings. For each building, di is generated through a Monte Carlo simulation where random normal distribution is used for the corresponding damage state of the building, as shown in Figure 2D.
To measure the social impacts of the disaster on the community, population dislocation, employment disruption, and school closures are taken as proxies for common post-disaster social disruptions (Daniel et al., 2022). It is assumed that the residential buildings experiencing either severe or complete damage states will lose functionality, and occupants living or working in these buildings will be dislocated (Daniel et al., 2022). The number of persons dislocated at the community level can be estimated by multiplying the number of residential units with severe and complete damage by the average size of households, which is 2.72 in the U.S. between 2016–2020 (U.S. Census Bureau Quick Facts., 2022a). Of note, the housing vacancy rate in coastal communities’ housing market is higher than the national average because of the greater number of seasonal properties in these areas. The framework predicts the number of community members likely to face unemployment and the number of students likely to (at least temporarily) lose their access to education based on the number of occupants of the commercial buildings and schools within the community that are severely or completely damaged. The number of occupants is estimated using the occupant count criteria outlined by (U.S. Green Building Council, 2019) and National Fire Protection Association Life Safety Code (NFPA 2021). An overview of the criteria used to estimate the number of occupants in each building type is presented in Table 1.
Hurricane risk simulation at a community scale often requires analyzing building portfolio damage for many buildings, which is computationally extensive. Performing hurricane risk analysis models requires extensive training and expertise and is computationally demanding. Hence, the current study develops an easy-to-use open-source python tool, Scenario-based Hurricane Risk Analysis (SHRA), executable on Jupyter Notebook and other platforms. This tool is relied on commonly used open-source python packages, such as NumPy, Matplotlib, and Pandas, and is designed to simulate the proposed hurricane scenario analysis. This tool is computationally efficient and allows plotting the physical damage outputs interactively on OpenStreetMap and estimating social impacts to support decision-making. This tool’s source codes, and illustrative examples are available on DesignSafe-CI. The analysis can be easily repeated for any testbed using SHRA with reasonable modification of scenario hurricane track characteristics, and fragility curves (Mazumder et al., 2022; https://doi.org/10.17603/ds2-jzcv-he68).
To demonstrate the proposed framework described in Section 2, a case study is performed for the hurricane-prone community of Onslow County, North Carolina. The county is located in the southeastern coastal region of North Carolina, about 190 km east of Raleigh and 80 km north of Wilmington. The county is spread over a terrain of about 2,000 square km with a population of more than 204,000 people, with a median household income of $50,278, and 45.1% of the population is female. The county is home to 64.5% of non-Hispanic White, 15.6% of Black or African American, 13.4% Hispanic Latino, 2.2% Asian, 1.1% American Indian, and 3.2% Other Races (U.S. Census Bureau 2022a). Approximately 12.5% of the county’s population is living below the poverty level, which is less than the national average. An estimated 24.6% of the population is under 18 years of age, whereas 9.6% is 65 years and over (US Census Bureau 2022b; Onslow County 2021). Onslow County has experienced 17 hurricanes in the past 40 years (NOAA 2021), making it an important area for hurricane research, resilience analysis, and adoption of such findings in practice.
Past hurricane events that travelled through a buffer distance of 100 km radius of the Onslow testbed were retrieved from the historical hurricane tracks database (NOAA 2020), as shown in Figure 3. Any hurricane that passes through a 100 km radius of Onslow County would be highly damaging to the area. In total, 50 hurricanes have hit within 100 km of Onslow County between 1857 and 2000, as listed in Supplementary Table S1 and shown in Figure 3B; the majority occurring between August and October. Figure 3D presents the annual frequency and return period for these 50 records, as well as for each hurricane intensity (category). The annual frequency and return period of category 4 hurricanes are estimated as 0.01 and 82 years, respectively.
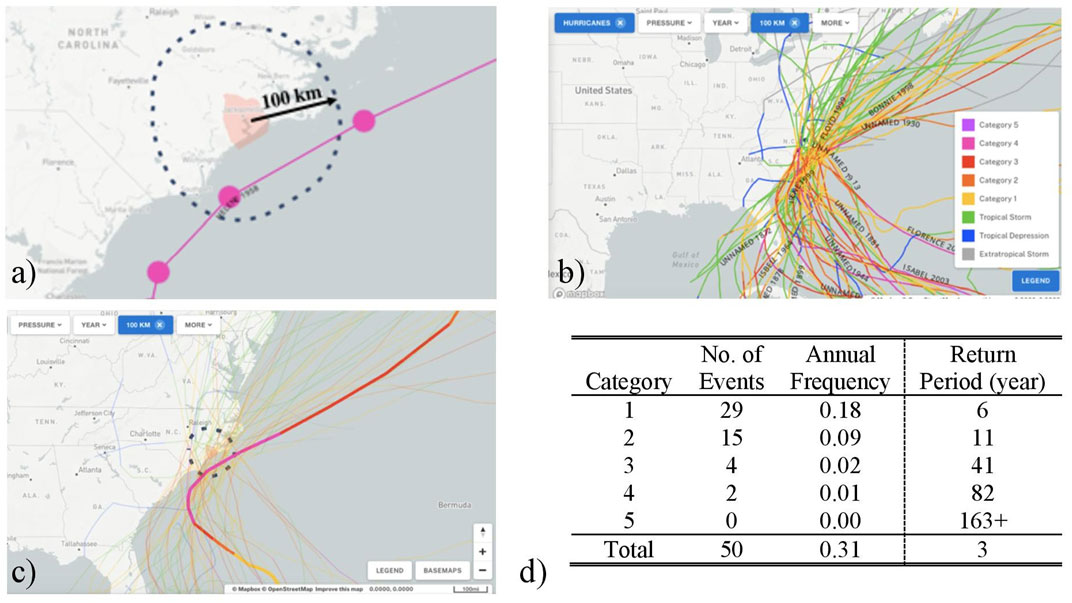
FIGURE 3. (A) Onslow County, (B) Hurricanes passed through within 100 km of the radius of the Onslow County, (NOAA 2020) (C) Helene track (NOAA 2020), and (D) Annual frequency and return periods of hurricanes based on past hurricane events between 1857 and 2020.
Hurricane Helene (1958), the strongest hurricane to pass within 100 km of Onslow County in the past 160 years, is applied here for assessing the potential damage and losses of the Onslow County due to a major hurricane. As shown in Figure 3C, while Helene has been the strongest hurricane in this region, Helene’s trajectory offers an approximate typical path for the history of hurricanes that have passed within 100 km of Onslow County. Since Helene was the strongest hurricane in this region, the objective of this study was limited to examining hurricane scenarios that are closely related to hurricane Helene’s size and angle of approach.
Hurricane Helene made landfall in September 1958 and severely impacted coastline counties of North Carolina including New Hanover County, Brunswick County, Pender County, Onslow County, Carteret County, and Dare County including a widespread power outage and telecommunication disruption (NWS 2021). Due to the mandatory evacuation of coastal islands and beach towns, Hurricane Helene caused no direct fatalities. However, significant property damage was observed within approximately 15 km of the coast. Many small buildings and houses were destroyed by the hurricane winds and resulting in $11 million in 1958 USD economic losses in North Carolina. Hurricane Helene caused greater damage to New Hanover, and Brunswick Counties compared to other counties, resulting in $7.28 and $2.34 millions in 1958 USD, respectively. Significant roof and window damage were observed in many buildings located in Onslow County (NWS 2021). Although Hurricane Helene caused a lesser impact on Onslow County compared to New Hanover and Brunswick Counties, a future reoccurrence of Hurricane Helene or a similar hurricane event with closer proximity to Onslow County is likely to cause severe damage and loss to Onslow County given the urban development since 1958. Hence, this study examined the impact of a reoccurrence of Hurricane Helene following the actual path of Hurricane Helene and five hypothetical (synthetic) paths maintaining the same size and angle of approach. The five synthetic paths are shifted towards Onslow County; the process for generating these five synthetic tracks is described next.
The 24-hour hurricane track, at 6-hr intervals, for Hurricane Helene (1958) was retrieved from the HURDAT2 data that includes peak intensity of hurricanes, as shown in Figure 4A with red dots. A linear interpolation was performed at 30-minute intervals to obtain finer records of the actual hurricane track, as represented by the yellow dots in Figure 4A. Linear interpolation of wind speeds is suggested for HURDAT2 data since non-linear interpolation could incorrectly boost wind data for the interpolated points (RDA 2020). To examine potential hurricane risk scenarios for Onslow County, five synthetic hurricane tracks were projected by offsetting the original track to the northeast at 50 km intervals while maintaining the original central pressures and intensities of Hurricane Helene. Figure 4B mapped the six hurricane tracks, where P1-P5 denote the five synthetic tracks. Ranges of the maximum wind speed radius, central pressure difference, and Holland parameters were found as 36.2–42.0 km, 70.0–83.0 millibars, and 1.27–1.32, respectively, for the synthetic hurricane scenarios. A synthetic track shifted towards Onslow County is expected to produce stronger wind and storm surges in Onslow County due to the counterclockwise rotation of wind forces (Sebastian et al., 2014). Using these six synthetic hurricane tracks, the current study explores a wider range of possible risk scenarios for Onslow County.
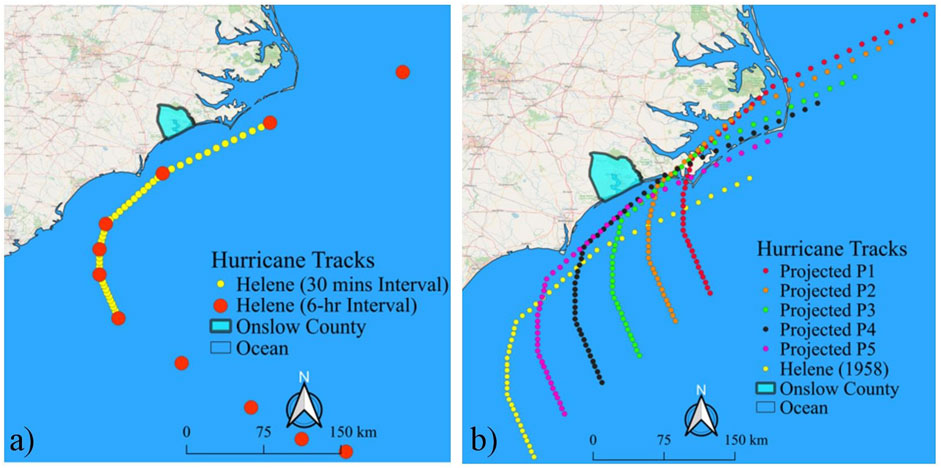
FIGURE 4. (A) Hurricane Helene, and (B) six hurricane scenarios (P1-P5 denote the synthetic tracks).
Hurricane wind intensity estimation for a particular location due to a hurricane scenario can be presented by a generalized vortex shape wind speed hazard curve that provides the gust wind speed given the distance from the hurricane eye to the building site. Figure 5A shows generalized vortex shape wind speed hazard curves estimated for Onslow County due to Hurricane Helene (1958). This curve provides a general trend of wind speed variation given a site distance from the hurricane eye. The maximum wind intensity occurs at the radius of maximum wind, and intensity decays as the hurricane eye moves further away from the location of interest.
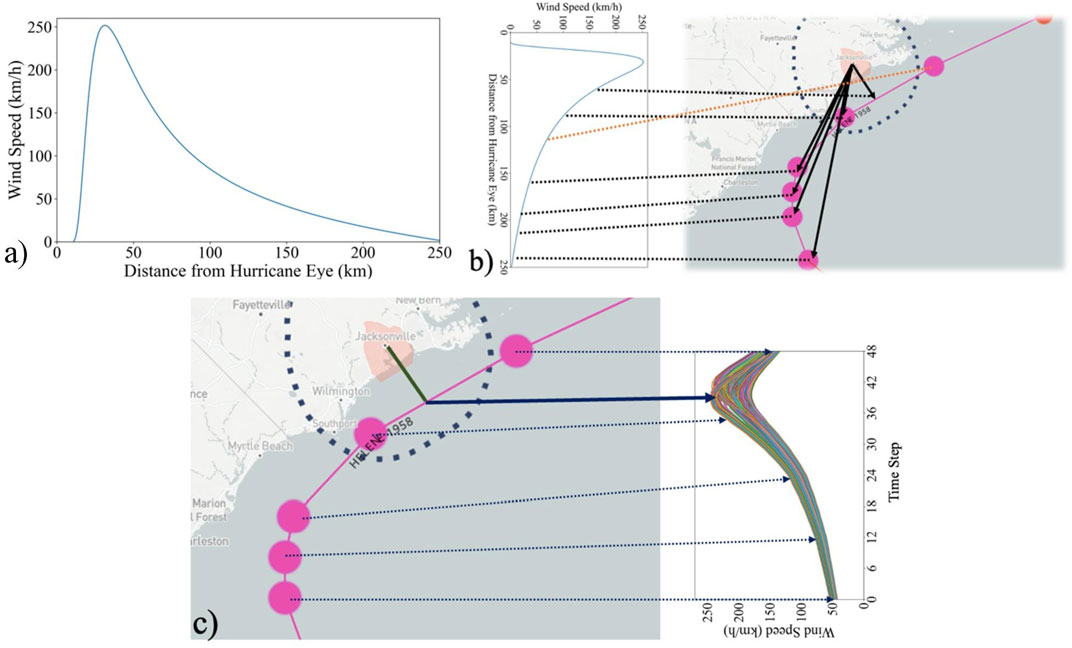
FIGURE 5. (A) Vortex shape for wind speed estimation, (B) Hurricane Helene track and (C) wind speed trajectory measured at 59,692 building sites in Onslow County.
Figure 5 illustrates how buildings in Onslow County experienced wind intensity over 24 h during Hurricane Helene. The time between two dots in Figure 5C represents a 6-hour interval, where linear interpolation was performed to obtain finer records of the hurricane at 30-minute intervals. Each hurricane scenario analysis was performed for 24 h at 30-min intervals, thus using 49-time instants of peak gust wind speed estimates, as shown in Figure 5C. At a given building site, the wind intensity increases as the hurricane eye approaches, with the maximum peak gust wind experienced when the distance between the hurricane eye and the building site is the shortest (represented by a solid arrow). As shown in Figure 5C, while passing by Onslow County, Helene’s track remains parallel to the Onslow coastline. Hence, wind intensity decays as a function of distance to the hurricane eye and distance from the coastline.
The Onslow County building inventory is a collection of geospatial data on existing buildings’ physical characteristics, market values, and corresponding fragility-based vulnerability functions. The information necessary to initiate the inventory was obtained mostly from the open-to-public datasets provided by Onslow County’s government (Onslow County 2021). The retrieved data were cleaned and spatially joined to initiate the intended community-level building inventory. The accuracy of the initiated building inventory was verified through cross-referencing and comparing the mutual attributes with well-known private datasets, including Microsoft Building Footprint that is released as open data and available to download free of charge, and ReferenceUSA (ReferenceUSA 2020) that is available with a subscription. We also used OpenStreetMap (OSM 2020), Google satellite and street view images to visually validate some physical attributes of approximately 1% of randomly selected buildings in the inventory. Collectively, we were able to procure the location, footprint outlines, year built, number of stories, occupancy type, square footage, structural type, exterior wall material, market value, number of households and dwelling type (for residential buildings only) for 59,692 properties in Onslow County.
For the fragility assignment, we estimated the terrain surface roughness as 0.35 m and 0.70 m according to the county topography. Information regarding roof shape, cover material, sheathing, nailing pattern, and wall connection type are also needed to assign the most closely related HAZUS damage function. These types of data often are scarcely available and could not be obtained here. Thus, we adopted the concept of building portfolio to model the different building types within the community. A building a portfolio is a collection of building archetypes with different attributes that are supposed to represent a community’s building stock in a community resilience analysis (Nofal and van de Lindt 2020). In this study, the Onslow building inventory was simplified to 49 building archetypes as described in Supplementary Table S2. Based on the assumption that the most recent building code was used at the time of construction, a mapping algorithm was developed to map each building to its corresponding archetype. The mapping algorithm first specifies the corresponding archetype group for a building based on the building’s occupancy type and structure material. Then, according to the building’s wall type and/or the number of stories, the algorithm identifies all possible archetypes for that particular building and classifies them into three classes based on their year built. The classes are before 1950, between 1950 and 2000, and after 2000. These thresholds were selected since significant evolution occurred in building codes before and after these periods. Subsequently, since more recent codes tend to produce higher quality buildings, the roof sheathing nailing pattern and roof/wall connection are allocated randomly but biased to the building. For instance, based on expert opinions and engineering judgment, the probability of using an 8 days nailing pattern was assumed 80% and 20% if the building’s construction year is after 2000 or before 1950, respectively. Finally, the mapping algorithm randomly assigns the damage model such that all mapped fragility functions are equally likely if more than one archetype could correspond to a particular building. For example, Archetypes A2 and A6, which differ only in roof shape, have an equal chance to be assigned to a building. More details on the mapping algorithm can be found by Enderami et al. (2021). Figure 6 provides the spatial distribution and number of each building archetype within the Onslow building inventory. The colorful dots in Figure 6A represent the centroids of the buildings’ footprints. As evident in Figure 6B, the majority (i.e., 79.6%) of buildings within the study area are residential buildings (Group A archetypes), 9.3% of buildings are manufactured homes (Group B archetypes), 1.7% of buildings are non-engineered hotel/motel or multi-family homes (Group C archetypes) and rest of the buildings are commercial, and industrial buildings. Across all buildings, 76.4% are one-story, 22.9% are two-story, and 0.6% are three-story buildings.
Figures 7A–F plot the peak gust wind speeds estimated at 59,692 building sites at 49-time steps for the six hurricane scenarios. Figures 7A, F show a similar and opposite skew for hurricanes P1 and Helene. The eyes of these two hurricanes are further away from Onslow County compared to P2—P5 trajectories. For hurricanes P2—P5, the hurricane eyes are closer to many buildings than the radius of the maximum wind for a particular period, resulting in wind intensity drops for many buildings, as reflected in Figures 7B–E. This phenomenon is also explained by the vortex shape shown in Figure 5.
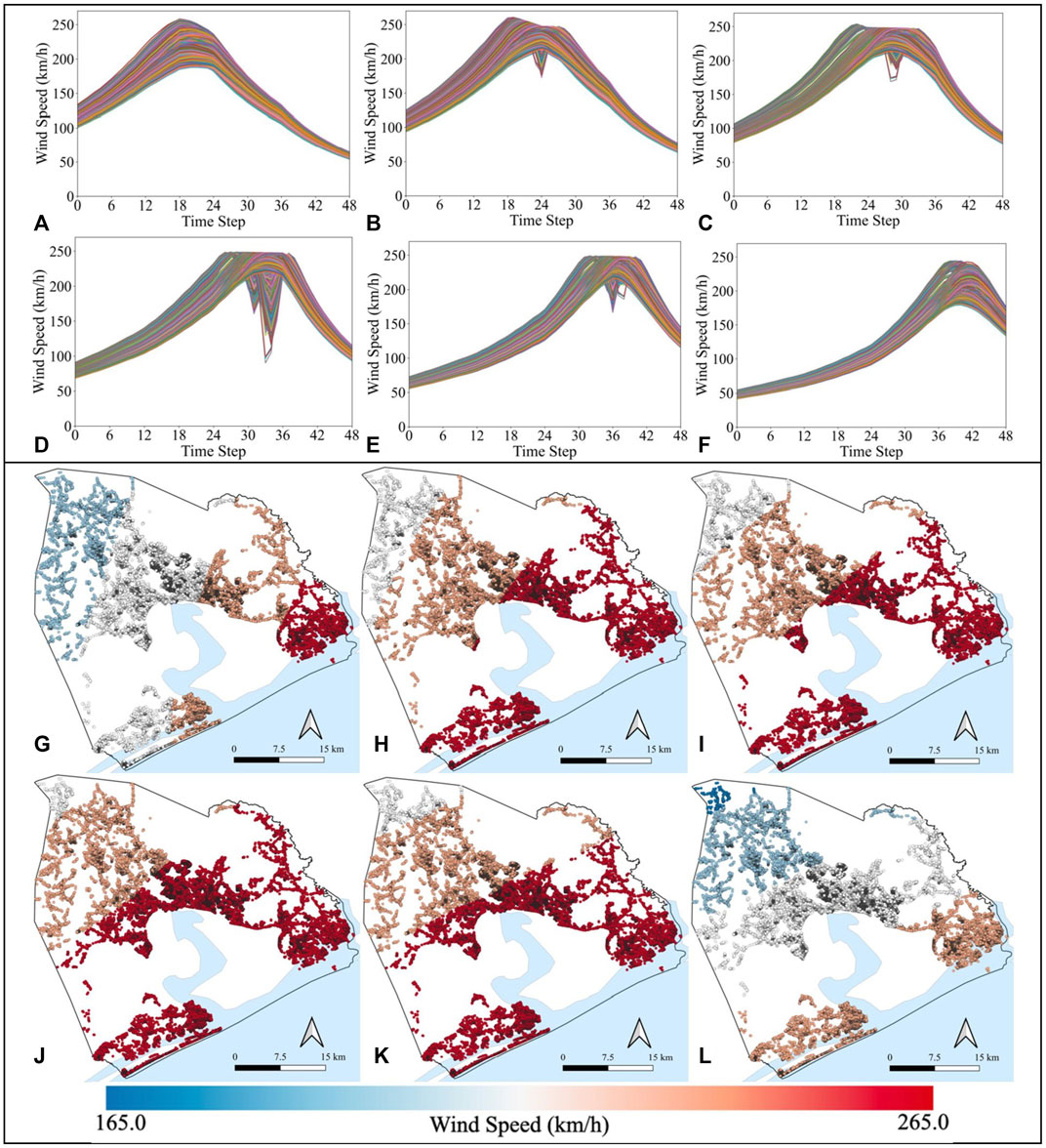
FIGURE 7. Wind speed trajectory for 59,692 buildings due to hurricanes: (A) P1, (B) P2, (C) P3, (D) P4, (E) P5, and (F) Helene, and Maximum peak gust wind speed maps for hurricanes: (G) P1, (H) P2, (I) P3, (J) P4, (K) P5, and (l) Helene.
Figures 7G–I displays the spatial gradient of estimated maximum peak gust wind speeds for the six hurricane scenarios across the Onslow testbed, where dark red is faster wind speeds, and blue is lower wind speeds. Conversion factors 0.83 near the eyewall and 0.75 away from the eyewall to convert gradient wind speed to surface wind speed and a factor 1.287 were used to covert surface wind speed to 3-sec gust wind speed, respectively. Average maximum peak gust wind speeds for the testbed buildings due to hurricanes P1, P2, P3, P4, P5, and Helene are estimated as 211.8, 231.0, 231.6, 233.4, 232.4, and 207.1 km/h, respectively. Standard deviations of the maximum peak gust wind speeds for hurricanes P1, P2, P3, P4, P5, and Helene are found as 14.8, 9.64, 7.13, 4.75, 5.75, and 14.3, respectively. In general, for all six hurricanes, the wind speed gradient is highest at the coast and decays for buildings more inland. Among these hurricane scenarios, wind speed is least dispersed over the testbed area for hurricane P4, whereas wind speed is highly dispersed over the study area for hurricanes P1 and Helene. In general, the wind intensities increase as hurricane tracks move closer to the county and decrease with hurricane tracks moving away from the country, as expected.
Existing fragility functions in HAZUS were used for estimating hurricane wind-induced damage. Figure 8 shows the fragility curves of the four damage states for the 49 building structural archetypes. As shown considering the width of the plotted curves in each subplot of Figure 8, the fragility curves span a range of possible wind speeds associated with hurricanes and thus are capable of capturing the spectrum of performance experience during the hurricane scenarios. Damage state 1, for minor damage, has the shortest wind speed range, at approximately 145–225 km/h at the 50th percentile, whereas damage state 4 for complete damage ranges from approximately 200–250 km/h at the 50th percentile (i.e., uncertainty in damage state assignment increases with damage severity).
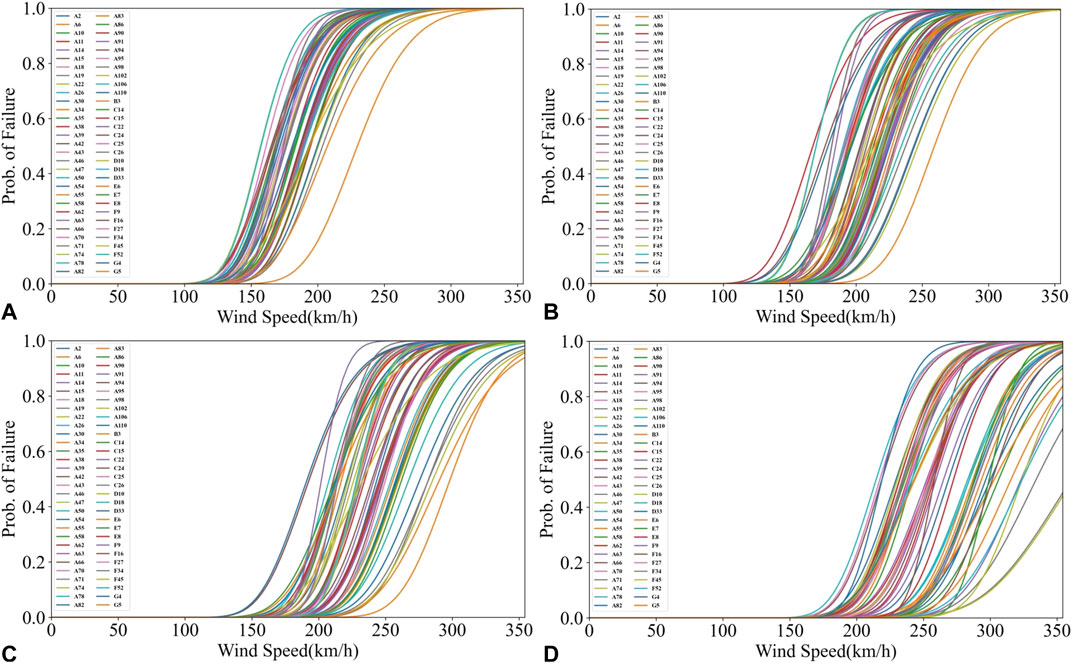
FIGURE 8. Building fragility curves for damage state: (A) minor, (B) moderate, (C) severe, and (D) complete.
Once the maximum peak gust wind speed is determined for a building, damage state probabilities are determined for the building using the appropriate fragility functions provided in Figure 8. Figure 9 shows the estimated probability of exceeding four damage states for the six hurricane scenarios, where dark purple is higher probabilities and green is lower probabilities.
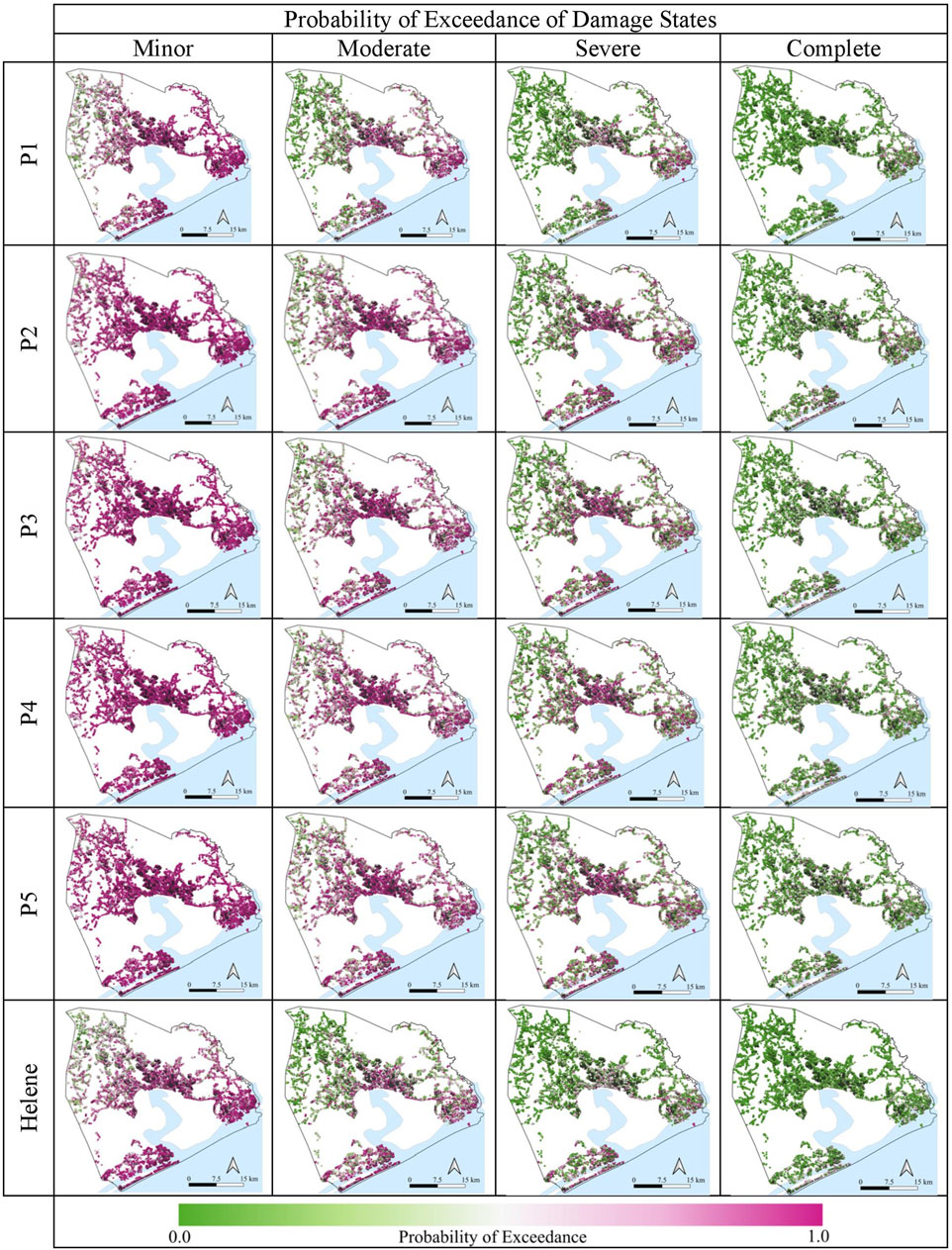
FIGURE 9. Building damage state probability maps for four damage states and six hurricane scenarios in Onslow testbed.
As shown in Figure 9, the probabilities of exceeding four damage states are relatively higher for hurricanes P2-P4 compared with the probabilities of exceeding four damage states for hurricanes P1 and Helene. For hurricane P1, mean probabilities of exceedance for minor, moderate, severe, and complete are 0.75, 0.41, 0.19 and 0.10, respectively. For hurricane P2, mean probabilities of exceedance for minor, moderate, severe, and complete are 0.87, 0.61, 0.36, and 0.19, respectively. For the most severe hurricane P4, the mean probabilities of exceedance for minor, moderate, severe, and complete are 0.90, 0.64, 0.37, and 0.21, respectively. Mean damage state probabilities of other hurricanes P2-P3, and P5 are found to be similar to hurricane P4. After estimating damage state probabilities, the damage state is assigned stochastically to each building using the maximum peak gust wind speed, damage state probabilities, and a random number (as described in Section 3.2). Figures 10A–F show the resulting building damage maps for the six hurricane scenarios. Table 2 summarizes the outcomes of the damage simulation. All six hurricanes caused significant damage to buildings in Onslow. Hurricane P4 is the most severe, resulting in 37.1% of buildings being either severely or completely damaged. A similar level of damaged was observed due to hurricanes P1-P3. Helene’s actual track caused the least damage considering all six scenarios, as expected.
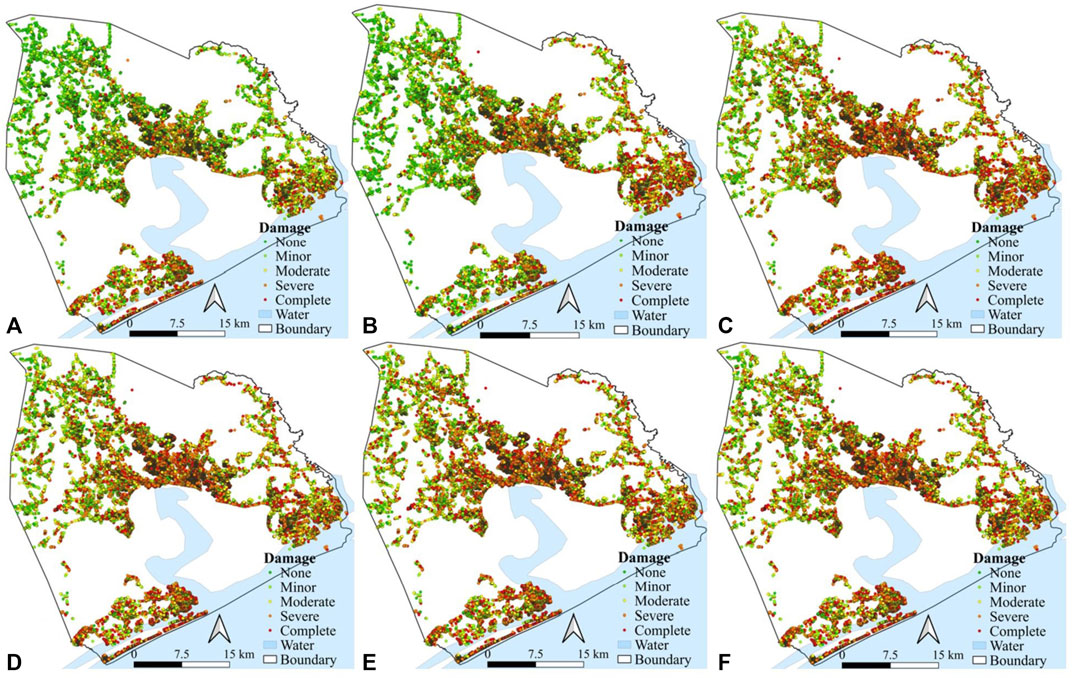
FIGURE 10. Building damage maps for hurricanes: (A) P1, (B) P2, (C) P3, (D) P4, (E) P5 and (F) Helene.
Damage ratio and building value are used to estimate direct financial loss resulting from the building’s physical damage. Building values are estimated using tax parcel data obtained from the Onslow County website (Onslow County, 2021). As discussed in Section 3.2, 2%, 10%, 50%, and 100% are assumed as the mean damage ratios for a building that sustained minor, moderate, severe, and complete damage, respectively. The actual damage ratio is generated for each building through a random sampling in the Monte Carlo Simulation. Figure 11 shows generated damage ratios for the six hurricane scenarios. Using building values and damage ratios, the financial losses are estimated as $5,536, $5,795, $9,338, $9,137, $9,507, and $9,167 million USD for Hurricanes Helene, P1, P2, P3, P4, and P5, respectively. As an overall trend, the reoccurrence of a Category 4 hurricane following any of the six tracks will cause severe physical damage to buildings near the coastline.
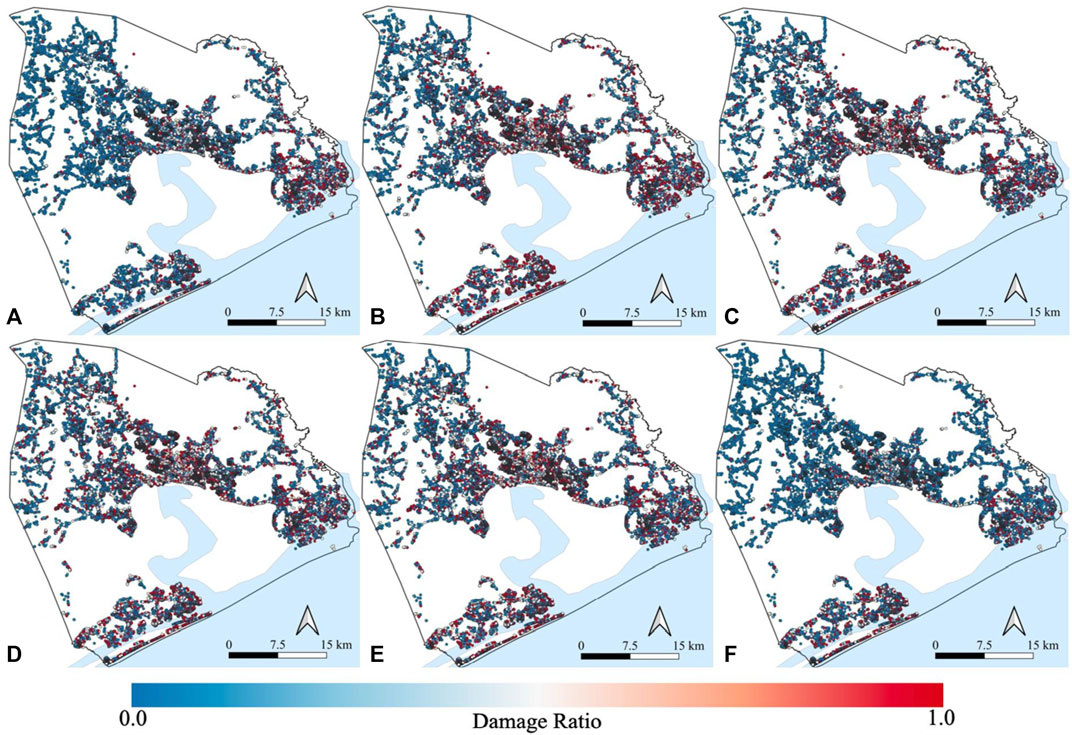
FIGURE 11. Damage ratio maps for hurricanes: (A) P1, (B) P2, (C) P3, (D) P4, (E) P5, and (F) Helene.
Figure 12 provides the spatial distribution of dislocated households for the six hurricane scenarios. Hurricanes Helene and P1 resulted in 15.9% and 19.1% of residential buildings experiencing either severe or complete damage, respectively. Hurricanes P2-P4 resulted in more than 35% of residential buildings experiencing either severe or complete damage. The pattern of damages and dislocation are highly related to hurricane trajectories. Hurricane P1 resulted in most of the damages and dislocation near the coastline. Hurricane P2 resulted in a high dislocation concentration in the county’s north-eastern part. Hurricanes P3-P5 resulted in a similar level of damage and dislocation throughout the county. Although P1 and Helene resulted in a similar level of damage to buildings, due to the difference in hurricane paths, dislocation due to Helene is more dispersed over the county. In general, the dislocation concentration is higher near the coastline area.
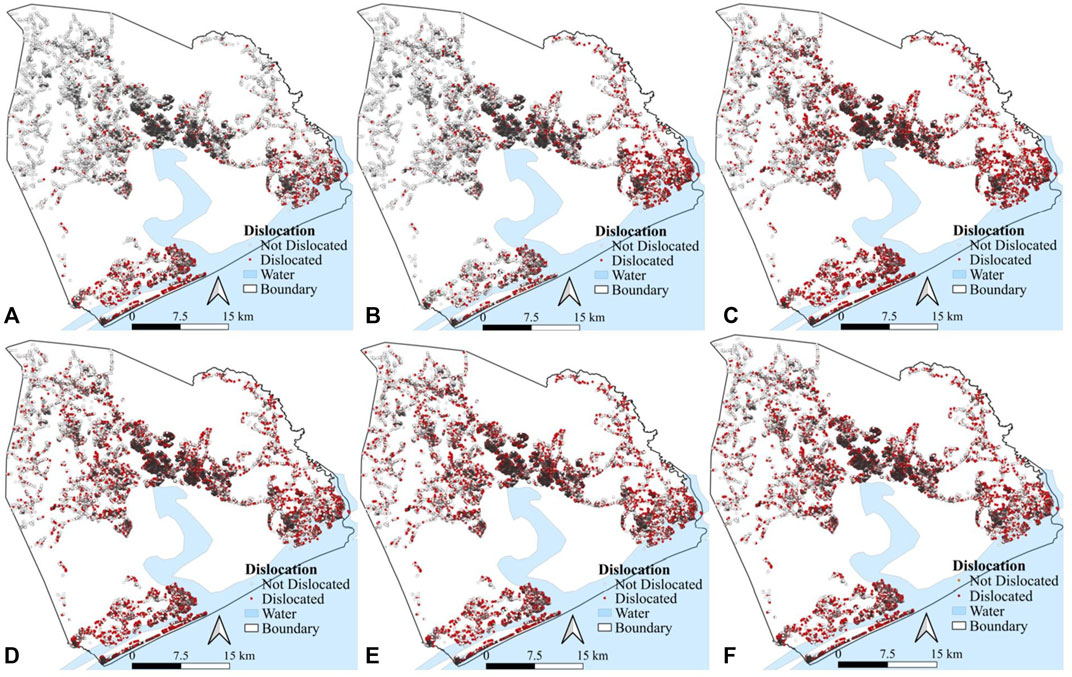
FIGURE 12. Household dislocation map for hurricanes: (A) P1, (B) P2, (C) P3, (D) P4, (E) P5, and (F) Helene.
Onslow building inventory includes 53,840 residential buildings (providing 64,950 housing units), and 5,214 commercial buildings, 440 school affiliated buildings, and 198 other types of buildings. The estimated numbers for potential household dislocations, employment disruptions, and educational interruptions for the six hurricane scenarios are presented in Table 3. To estimate the number of dislocated persons a vacancy rate of 14.3% is randomly assigned to damaged housing units (ACS 2021). Hurricane P4 has the most severe impact on household dislocation by the potential of dislocating approximately 21,262 households (with 57,832 residents) that representing about 28% of the county’s population. In contrast, original Helene is the least disruptive by probably dislocating about 12% of the total population (i.e., about 23,770 persons). Based on Section 3.3.2 procedures, the number of people likely to experience employment disruption and the number of students likely to experience school disruption are estimated in Table 3. As a result of hurricane P4, 45,575 persons experienced employment disruption, and 16,707 students temporarily lost access to school. Helene caused 22,586 employment disruption and resulted in school closure for 5,536 students. About 50% of business buildings are general office/service and retail buildings, and at least 60% of these buildings are damaged due to hurricanes P2-P5. Hurricanes Helene and P1 also resulted in more than 30% of general office/services and retail buildings dislocation. Hence, people working in general office/services and retail are expected to experience significant employment disruption due to these hurricanes.
Thus, a future hurricane with the same central pressures and intensities as Hurricane Helene, but with a likely different trajectory, could cause more severe social impacts on the Onslow County compared to the original Helene.
There is no damage data available from Hurricane Helene to be used for validation of the predicted physical damage and social impacts. Importantly, Hurricane Helene occurred in 1958 and the community’s building inventory and population fabric have changed significantly since 1958 due to urbanization, economic development, building code and regulation changes, among other reasons. Thus, true validation may not be possible for the presented analyses. However, the accuracy of the hazard module in estimating peak gust wind speed was verified by comparing predicted values with recorded wind data during Hurricane Helene. For example, the maximum wind speed due to Helene was recorded 241 km/h (150 mph) for Onslow County; this study simulated a maximum wind speed for Hurricane Helene of 240 km/h. Estimated peak gust wind speeds for two stations (Wilmington airport and Cape Fear, NC) also provided similar outcomes. Simulated and recorded peak gust wind speeds were 212 km/h and 220 km/h, respectively, at Wilmington airport. At Cape Fear station, simulated and recorded peak gust wind speeds were 212 km/h and 220 km/h, respectively (NWS, 2021). Onslow County has a 204,000 population (U.S. Census Bureau 2022a), about 64,000 employments (U.S. Census Bureau 2022b), and about 26,000 students (U.S. News 2022). Using the proposed occupancy counts (as shown in Table 1), we found that 78,904 residents (40% of total residents), 51,173 employees (about 80% of total employees), and 17,087 students (above 65% of total students) would be impacted due to most severe Hurricane P4. These numbers show a reasonable estimate of social impact with respect to damage data and verify a reasonable estimate of the framework’s results.
Community-level portfolio impact assessment is essential for comprehensively addressing future disaster threats and improving resilience. This framework provides two major contributions to the state-of-the-art of hurricane risk analysis by: 1) introducing a simplified procedure to perform synthetic scenario-based hurricane risk analysis for estimating community-level damage and loss to buildings due to strong hurricane winds; 2) connecting and quantifying physical, economic, and social consequences for a community resulting from severe hurricanes. Unlike other models, the approach estimates peak gust wind speeds at building sites considering the spatial variation of wind intensities. The framework is illustrated with a virtual testbed of the hurricane-prone community of Onslow County, North Carolina. The present study describes testbed development procedures, where data was obtained, and the verification and validation process for the hazard and building data.
Regional hurricane analysis revealed that the annual frequency of hurricane categories decreases as hurricane category increases. The most probable hurricane scenario for Onslow County is a Category 1 hurricane. Although the most destructive scenario for Onslow County would be a Category 5 hurricane, this region has not experienced a Category 5 hurricane since 1857. The largest hurricane to pass within 100 km of Onslow County in the past 160 years was selected for analyzing potential risk scenarios. While a reoccurrence of 1958 Hurricane Helene (Category 4) will cause severe damage to buildings, Hurricane Helene’s track shifted towards Onslow County was shown to produce stronger winds, more severe damage to buildings, and more severe social disruption. Five synthetic trajectories were generated by shifting Hurricane Helene’s path northeast at 50 km intervals. The six hurricane scenario analyses greatly improved current understanding of how a future major hurricane event may impact Onslow. These findings can assist decision-makers in shaping future policies to improve community disaster resilience.
Estimated physical damage to buildings and resulting consequence can be utilized for city-wide planning for mitigating the impact of the future hurricane disaster, including resource allocation and distribution disaster response needs; spatial damage distribution may help decision-makers and stakeholders to plan for rehabilitation maintenance planning. Future analysis should account for the effect of hurricane-induced multiple hazards on the buildings.
While the social impacts of hurricanes on the community due to the disruption of utilities and transportation networks are typically significant immediately after a hurricane, including functionality loss of buildings due to utility outages and physical accessibility loss to road networks; however, the recovery of civil infrastructure systems is faster than damaged buildings repair and recovery as individual buildings failure depends on various recovery assistance and funding mechanisms. The scope of the current study was limited to understanding intermediate and long-term social impacts due to the failure of buildings.
For a large urban area, the process of hurricane scenario analysis requires a large number of simulations and can be computationally expensive. The presented study consisted of 49 iterations for 59,692 buildings in six hurricane scenarios. A soft-computing algorithm was required to execute the presented hurricane analyses; this algorithm is provided to interested readers as a python-based program to execute the proposed hurricane analysis (Mazumder et al., 2022; https://doi.org/10.17603/ds2-jzcv-he68).
The datasets generated for this study can be obtained from the corresponding author upon request. The python tool, SHRA, is available on DesignSafe. https://doi.org/10.17603/ds2-jzcv-he68.
RKM: Conceptualization, methodology, modelling, analysis, writing—original draft, python tool development. SAE: Modelling—social impact analysis, building inventory development, writing—review and editing. EJS: Investigation, review of the work critically for important intellectual content, writing—review and editing. All authors contributed to the manuscript reading and approved the submitted version.
This work was supported by the National Science Foundation under Grant No. CMMI 1847373.
The authors acknowledge Meredith Dumler for their work on testbed development.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The views expressed are those of the author(s), and do not necessarily reflect the views of the funding agency.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbuil.2023.1005264/full#supplementary-material
1Note: only hurricane events are considered, and other tropical storms are ignored.
Abbas, H. B., and Routray, J. K. (2014). Vulnerability to flood-induced public health risks in Sudan. Disaster Prev. Manag. 23 (4), 395–419. doi:10.1108/DPM-07-2013-0112
Abdelhady, A. U., Lin, S. Y., Xu, L., Sediek, O. A., Hlynka, A. W., El-Tawil, S., and Menassa, C. (2019). “A distributed computing platform for community resilience estimation,” in Proceeding of the 13th International Conference on Applications of Statistics and Probability in Civil Engineering(ICASP13).
Abdelhady, A. U., Spence, S. M., and McCormick, J. (2020). A framework for the probabilistic quantification of the resilience of communities to hurricane winds. J. Wind Eng. Industrial Aerodynamics 206, 104376. doi:10.1016/j.jweia.2020.104376
ACS (2021). Selected housing characteristics. Survey/Program: American Community Survey, TableID: DP04, Available at: https://data.census.gov/cedsci (Access April 8, 2021).
Adachi, T., and Ellingwood, B. R. (2010). Comparative assessment of civil infrastructure network performance under probabilistic and scenario earthquakes. J. Infrastructure Syst. 16 (1), 1–10. doi:10.1061/(asce)1076-0342(2010)16:1(1)
Adhikari, P., Abdelhafez, M. A., Dong, Y., Guo, Y., Mahmoud, H. N., and Ellingwood, B. R. (2021). Achieving residential coastal communities resilient to tropical cyclones and climate change. Front. Built Environ. 6, 220. doi:10.3389/fbuil.2020.576403
AIR (AIR Worldwide Corporation) (2015). AIR hurricane model for the United States.” Brochure from AIR. Boston: AIR Worldwide Corporation.
Baradaranshoraka, M., Pinelli, J. P., Gurley, K., Peng, X., and Zhao, M. (2017). Hurricane wind versus storm surge damage in the context of a risk prediction model. J. Struct. Eng. 143 (9), 04017103. doi:10.1061/(asce)st.1943-541x.0001824
Batts, M. E., Russell, L. R., and Simiu, E. (1984). Hurricane wind speeds in the United States. National Bureau of Standards Special Publication, 67–88.665
Blanton, B., Dresback, K., Colle, B., Kolar, R., Vergara, H., Hong, Y., et al. (2020). An integrated scenario ensemble-based framework for hurricane evacuation modeling: Part 2—hazard modeling. Risk Anal. 40 (1), 117–133. doi:10.1111/risa.13004
Burton, C. G. (2010). Social vulnerability and hurricane impact modeling. Nat. Hazards Rev. 11 (2), 58–68. doi:10.1061/(asce)1527-6988(2010)11:2(58)
Bushra, N., Trepanier, J. C., and Rohli, R. V. (2019). Joint probability risk modelling of storm surge and cyclone wind along the coast of Bay of Bengal using a statistical copula. Int. J. Climatol. 39 (11), 4206–4217. doi:10.1002/joc.6068
Cha, E. J., and Ellingwood, B. R. (2013). The role of risk aversion in nuclear plant safety decisions. Struct. Saf. 44, 28–36. doi:10.1016/j.strusafe.2013.05.002
Collins, J., Ersing, R., and Polen, A. (2017). Evacuation decision-making during Hurricane Matthew: An assessment of the effects of social connections. Weather, Clim. Soc. 9 (4), 769–776. doi:10.1175/wcas-d-17-0047.1
Collins, J., Ersing, R., Polen, A., Saunders, M., and Senkbeil, J. (2018). The effects of social connections on evacuation decision making during Hurricane Irma. Weather, Clim. Soc. 10 (3), 459–469. doi:10.1175/wcas-d-17-0119.1
County, O. (2021). Onslow County government website. Available at: https://www.onslowcountync.gov/(accessed on 02 03, 2021).
Daniel, L., Mazumder, R. K., Enderami, S. A., Sutley, E. J., and Lequesne, R. D. (2022). Community capitals framework for linking buildings and organizations for enhancing community resilience through the built environment. J. Infrastructure Syst 28 (1), 04021053. doi:10.1061/(ASCE)IS.1943-555X.0000668
Davidson, R. A., Nozick, L. K., Wachtendorf, T., Blanton, B., Colle, B., Kolar, R. L., et al. (2020). An integrated scenario ensemble-based framework for hurricane evacuation modeling: Part 1—decision support system. Risk Anal. 40 (1), 97–116. doi:10.1111/risa.12990
Deierlein, G. G., Mckenna, F., Zsarnóczay, A., Kijewski-Correa, T. L., Kareem, A., Elhaddad, W., et al. (2020). A cloud-enabled application framework for simulating regional-scale impacts of natural hazards on the built environment. Front. Built Environ. 6, 196. doi:10.3389/fbuil.2020.558706
Dietrich, J. C., Dawson, C. N., Proft, J. M., Howard, M. T., Wells, G., Fleming, J. G., et al. (2013). “Real-time forecasting and visualization of hurricane waves and storm surge using SWAN+ ADCIRC and FigureGen,” in Computational challenges in the geosciences (New York, NY: Springer), 49–70.
Emanuel, K., Ravela, S., Vivant, E., and Risi, C. (2006). A statistical deterministic approach to hurricane risk assessment. Bull. Am. Meteorological Soc. 87 (3), 299–314. doi:10.1175/bams-87-3-299
Enderami, S. A., Sutley, E. J., and Hofmeyer, S. L. (2021). Defining organizational functionality for evaluation of post-disaster community resilience. Sustain. Resilient Infrastructure 7, 1–18. doi:10.1080/23789689.2021.1980300
Fekete, A. (2009). Validation of a social vulnerability index in context to river-floods in Germany. Nat. Hazards Earth Syst. Sci. 9 (2), 393–403. doi:10.5194/nhess-9-393-2009
FEMA (2010). HAZUS-MH coastal storm surge methodology. Washington, DC: Federal Emergency Management Agency, Mitigation Division.
Fereshtehnejad, E., Gidaris, I., Rosenheim, N., Tomiczek, T., Padgett, J. E., Cox, D. T., et al. (2021). Probabilistic risk assessment of coupled natural-physical-social systems: Cascading impact of hurricane-induced damages to civil infrastructure in galveston, Texas. Nat. Hazards Rev. 22 (3), 04021013. 202“. doi:10.1061/(ASCE)NH.1527-6996.0000459
Finch, C., Emrich, C. T., and Cutter, S. L. (2010). Disaster disparities and differential recovery in New Orleans. Popul. Environ. 31 (4), 179–202. doi:10.1007/s11111-009-0099-8
Friedland, C. J. (2009). “Residential building damage from hurricane storm surge: Proposed methodologies to describe, assess and model building damage,”. LSU Doctoral Dissertations. 2897.
Georgiou, P. N. (1986). “Design wind speeds in tropical cyclone-prone regions,”. Dissertation (Doctor of Philosophy).
U.S.Green Building Council (2019). Reference guide for building design and construction, LEED v4. Leadership in energy and environmental design.
Guo, Y., and van de Lindt, J. (2019). Simulation of hurricane wind fields for community resilience applications: A data-driven approach using integrated asymmetric Holland models for inner and outer core regions. J. Struct. Eng. 145 (9), 04019089. doi:10.1061/(asce)st.1943-541x.0002366
Holland, G. J. (1980). An analytic model of the wind and pressure profiles in hurricanes. Mon. weather Rev. 108 (8), 1212–1218. doi:10.1175/1520-0493(1980)108<1212:aamotw>2.0.co;2
Huang, Z., Rosowsky, D. V., and Sparks, P. R. (2001). Long-term hurricane risk assessment and expected damage to residential structures. Reliab. Eng. Syst. Saf. 74 (3), 239–249. doi:10.1016/s0951-8320(01)00086-2
Jia, G., Taflanidis, A. A., Nadal-Caraballo, N. C., Melby, J. A., Kennedy, A. B., and Smith, J. M. (2016). Surrogate modeling for peak or time-dependent storm surge prediction over an extended coastal region using an existing database of synthetic storms. Nat. Hazards 81 (2), 909–938. 201“. doi:10.1007/s11069-015-2111-1
Kakareko, G., Jung, S., Mishra, S., and Vanli, O. A. (2020). Bayesian capacity model for hurricane vulnerability estimation. Struct. Infrastructure Eng. 17, 638–648. doi:10.1080/15732479.2020.1760318
Kakareko, G., Jung, S., Vanli, O. A., Tecle, A., Khemici, O., and Khater, M. (2017). Hurricane loss analysis based on the population-weighted index. Front. Built Environ. 3, 46. doi:10.3389/fbuil.2017.00046
Khajwal, A. B., and Noshadravan, A. (2020). Probabilistic hurricane wind-induced loss model for risk assessment on a regional scale. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part A Civ. Eng. 6 (2), 04020020. doi:10.1061/ajrua6.0001062
Klise, K. A., Bynum, M., Moriarty, D., and Murray, R. (2017). A software framework for assessing the resilience of drinking water systems to disasters with an example earthquake case study. Environ. Model. Softw. 95, 420–431. doi:10.1016/j.envsoft.2017.06.022
Li, Y., and Ellingwood, B. R. (2006). Hurricane damage to residential construction in the US: Importance of uncertainty modeling in risk assessment. Eng. Struct. 28 (7), 1009–1018. doi:10.1016/j.engstruct.2005.11.005
Li, Y., van de Lindt, J. W., Dao, T., Bjarnadottir, S., and Ahuja, A. (2012). Loss analysis for combined wind and surge in hurricanes. Nat. hazards Rev. 13 (1), 1–10. doi:10.1061/(asce)nh.1527-6996.0000058
Lin, P., and Wang, N. (2016). Building portfolio fragility functions to support scalable community resilience assessment. Sustain. Resilient Infrastructure 1 (3-4), 108–122. doi:10.1080/23789689.2016.1254997
Liu, D., and Li, Y. (2016). Social vulnerability of rural households to flood hazards in Western mountainous regions of Henan province, China. Nat. Hazards Earth Syst. Sci. 16 (5), 1123–1134. doi:10.5194/nhess-16-1123-2016
Masoomi, H., Burton, H., Tomar, A., and Mosleh, A. (2020). Simulation-based assessment of postearthquake functionality of buildings with disruptions to cross-dependent utility networks. J. Struct. Eng. 146 (5), 04020070. doi:10.1061/(asce)st.1943-541x.0002555
Masoomi, H., van de Lindt, J. W., Ameri, M. R., Do, T. Q., and Webb, B. M. (2019). Combined wind-wave-surge hurricane-induced damage prediction for buildings. J. Struct. Eng. 145 (1), 04018227. doi:10.1061/(asce)st.1943-541x.0002241
Masterson, J. H., Peacock, W. G., Van Zandt, S., Grover, H., Field Schwarz, L., and Cooper, J. (2014). Planning for community resilience: A handbook for reducing vulnerability to disasters. Washington, DC: Island Press.
Mazumder, R. K., Fan, X., Salman, A. M., Li, Y., and Yu, X. (2020). Framework for seismic damage and renewal cost analysis of buried water pipelines. J. Pipeline Syst. Eng. Pract. 11 (4), 04020038. doi:10.1061/(asce)ps.1949-1204.0000487
Mazumder, R. K., Enderami, S. A., and Sutley, E. J. (2022). “Scenario hurricane risk analysis,” in Scenario-based hurricane risk analysis (SHRA) framework (DesignSafe-CI). doi:10.17603/ds2-jzcv-he68
Microsoft (2020). Microsoft building footprint database for the United States. Available at: https://www.microsoft.com/en-us/maps/building-footprints.
Mishra, S., Vanli, O. A., Alduse, B. P., and Jung, S. (2017). Hurricane loss estimation in wood-frame buildings using Bayesian model updating: Assessing uncertainty in fragility and reliability analyses. Eng. Struct. 135, 81–94. doi:10.1016/j.engstruct.2016.12.063
Myers, C. A., Slack, T., and Singelmann, J. (2008). Social vulnerability and migration in the wake of disaster: The case of hurricanes Katrina and rita. Popul. Environ. 29 (6), 271–291. doi:10.1007/s11111-008-0072-y
NDCD (2021). Billion-dollar weather and climate disasters: Events. NOAA's National Climatic Data Center NCDC. Available at: https://www.ncdc.noaa.gov/billions/events.
NIST (2017). Strategic plan for the national windstorm impact reduction program. prepared by the Interagency Coordinating Committee of NWIRPAvailable at: https://www.nist.gov/system/files/documents/2018/09/24/nwirp_strategic_plan.pdf.
NOAA (2020). Historical hurricane tracks. Available at: https://coast.noaa.gov/hurricanes (accessed on Dec 09, 2020).
NOAA (2021). Revised atlantic hurricane database (HURDAT2), atlantic oceanographic and meteorological laboratory. National Oceanic and Atmospheric Administration, Available at: https://www.aoml.noaa.gov/hrd/hurdat/Data_Storm.html (accessed on Jan 08, 2021).
Nofal, O. M., Van De Lindt, J. W., Do, T. Q., Yan, G., Hamideh, S., Cox, D. T., et al. (2021). Methodology for regional multihazard hurricane damage and risk assessment. J. Struct. Eng. 147 (11), 04021185. doi:10.1061/(asce)st.1943-541x.0003144
Nofal, O. M., and van de Lindt, J. W. (2020). High-resolution approach to quantify the impact of building-level flood risk mitigation and adaptation measures on flood losses at the community-level. Int. J. Disaster Risk Reduct. 51, 101903. doi:10.1016/j.ijdrr.2020.101903
NWS (2021). Hurricane Helene: September 27, 1958. National Weather Service, Available at: https://www.weather.gov/ilm/HurricaneHelene (accessed on 07 11, 2020).
OSM (2020). OpenStreetMap. Available at: https://www.openstreetmap.org/(accessed on 09, 2020).
Pant, S., and Cha, E. J. (2018). Effect of climate change on hurricane damage and loss for residential buildings in Miami-Dade County. J. Struct. Eng. 144 (6), 04018057. doi:10.1061/(asce)st.1943-541x.0002038
Park, S., van de Lindt, J. W., and Li, Y. (2013). Application of the hybrid ABV procedure for assessing community risk to hurricanes spatially. Nat. hazards 68 (2), 981–1000. doi:10.1007/s11069-013-0674-2
Pinelli, J. P., Simiu, E., Gurley, K., Subramanian, C., Zhang, L., Cope, A., et al. (2004). Hurricane damage prediction model for residential structures. J. Struct. Eng. 130 (11), 1685–1691. doi:10.1061/(asce)0733-9445(2004)130:11(1685)
Pita, G., Pinelli, J. P., Gurley, K., and Mitrani-Reiser, J. (2015). State of the art of hurricane vulnerability estimation methods: A review. Nat. Hazards Rev. 16 (2), 04014022. doi:10.1061/(asce)nh.1527-6996.0000153
Powell, M. D., Houston, S. H., Amat, L. R., and Morisseau-Leroy, N. (1998). The HRD real-time hurricane wind analysis system. J. Wind Eng. Industrial Aerodynamics 77, 53–64. doi:10.1016/s0167-6105(98)00131-7
RDA (Research Data Achieve) (2020). Data for climate and weather research. University Corporation Atmospheric Research, Available at: https://rda.ucar.edu/datasets/ds824.1/docs/format_hurdat.html (accessed on Aug 9, 2021).
ReferenceUSA, (2020). Available at: http://www.referenceusa.com/(accessed on 05, 2020).
RMS (Risk Management Solutions) (2010). Study of Florida’s windstorm mitigation credits. Newark, CA: Report from RMS.
Rufat, S., Tate, E., Emrich, C. T., and Antolini, F. (2019). How valid are social vulnerability models? Ann. Am. Assoc. Geogr. 109 (4), 1131–1153. doi:10.1080/24694452.2018.1535887
Russell, L. R. (1969). Probability distributions for Texas Gulf coast hurricane effects of engineering interest. Stanford University.
Salman, A. M., and Li, Y. (2018). A framework to investigate the effectiveness of interconnection of power distribution systems subjected to hurricanes. Struct. Infrastructure Eng. 14 (2), 203–217. doi:10.1080/15732479.2017.1345954
Schwerdt, R. W., Ho, F. P., and Watkins, R. R. (1979). Meteorological criteria for standard project hurricane and probable maximum hurricane windfields, Gulf and East Coasts of the United States.
Sebastian, A., Proft, J., Dietrich, J. C., Du, W., Bedient, P. B., and Dawson, C. N. (2014). Characterizing hurricane storm surge behavior in Galveston Bay using the SWAN+ ADCIRC model. Coast. Eng. 88, 171–181. doi:10.1016/j.coastaleng.2014.03.002
Simiu, E., and Scanlan, R. H. (1996). Wind effects on structures: Fundamentals and applications to design.
Smith, A. B. (2020). 2010–2019: A landmark decade of US. Billion-dollar weather and climate disasters. National Oceanic and Atmospheric Administration.
Snaiki, R., Wu, T., Whittaker, A. S., and Atkinson, J. F. (2020). Hurricane wind and storm surge effects on coastal bridges under a changing climate. Transp. Res. Rec. 2674 (6), 23–32. doi:10.1177/0361198120917671
Tate, E., Strong, A., Kraus, T., and Xiong, H. (2016). Flood recovery and property acquisition in Cedar Rapids, Iowa. Nat. Hazards 80 (3), 2055–2079. doi:10.1007/s11069-015-2060-8
Torres, J. M., Bass, B., Irza, N., Fang, Z., Proft, J., Dawson, C., et al. (2015). Characterizing the hydraulic interactions of hurricane storm surge and rainfall–runoff for the Houston–Galveston region. Coast. Eng. 106, 7–19. doi:10.1016/j.coastaleng.2015.09.004
Unnikrishnan, V. U., and Barbato, M. (2017). Multihazard interaction effects on the performance of low-rise wood-frame housing in hurricane-prone regions. J. Struct. Eng. 143 (8), 04017076. doi:10.1061/(asce)st.1943-541x.0001797
US Census Bureau (2022a). US cencus QuickFacts, Onslow county. Available at: https://www.census.gov/quickfacts/onslowcountynorthcarolina.
U.S. Census Bureau (2022b). American community survey B23025: Employment status for the population 16 Years and over. Available at: https://data.census.gov/cedsci/table?q=B23025&t=Employment%3AEmployment%20and%20Labor%20Force%20Status&g=0500000US37133&y=2019&d=ACS%205-Year%20Estimates%20Detailed%20Tables&tid=ACSDT5Y2019.B23025 (accessed on Jun 17, 2022).
U.S. News (2022). Onslow county schools, data. Available at: https://www.usnews.com/education/k12/north-carolina/districts/onslow-county-schools-104152#:∼:text=Onslow%20County%20Schools%20contains%2037,of%20students%20are%20economically%20disadvantaged (accessed on June 17, 2022).
van Berchum, E. C., Mobley, W., Jonkman, S. N., Timmermans, J. S., Kwakkel, J. H., and Brody, S. D. (2019). Evaluation of flood risk reduction strategies through combinations of interventions. J. Flood Risk Manag. 12 (S2), e12506. doi:10.1111/jfr3.12506
van De Lindt, J. W., Peacock, W. G., Mitrani-Reiser, J., Rosenheim, N., Deniz, D., Dillard, M., et al. (2020). Community resilience-focused technical investigation of the 2016 Lumberton, North Carolina, flood: An interdisciplinary approach. Nat. Hazards Rev. 21 (3), 04020029. doi:10.1061/(asce)nh.1527-6996.0000387
Vickery, P. J., Lin, J., Skerlj, P. F., Twisdale, L. A., and Huang, K. (2006a). HAZUS-MH hurricane model methodology. I: Hurricane hazard, terrain, and wind load modeling. Nat. Hazards Rev. 7 (2), 82–93. doi:10.1061/(asce)1527-6988(2006)7:2(82)
Vickery, P. J., Masters, F. J., Powell, M. D., and Wadhera, D. (2009a). Hurricane hazard modeling: The past, present, and future. J. Wind Eng. Industrial Aerodynamics 97 (7-8), 392–405. doi:10.1016/j.jweia.2009.05.005
Vickery, P. J., Skerlj, P. F., Lin, J., Twisdale, L. A., Young, M. A., and Lavelle, F. M. (2006b). HAZUS-MH hurricane model methodology. II: Damage and loss estimation. Nat. Hazards Rev. 7 (2), 94–103. doi:10.1061/(asce)1527-6988(2006)7:2(94)
Vickery, P. J., Skerlj, P. F., Steckley, A. C., and Twisdale, L. A. (2000a). Hurricane wind field model for use in hurricane simulations. J. Struct. Eng. 126 (10), 1203–1221. doi:10.1061/(asce)0733-9445(2000)126:10(1203)
Vickery, P. J., Skerlj, P. F., and Twisdale, L. A. (2000b). Simulation of hurricane risk in the US using empirical track model. J. Struct. Eng. 126 (10), 1222–1237. doi:10.1061/(asce)0733-9445(2000)126:10(1222)
Vickery, P. J., and Wadhera, D. (2008). Statistical models of Holland pressure profile parameter and radius to maximum winds of hurricanes from flight-level pressure and H* Wind data. J. Appl. Meteorology Climatol. 47 (10), 2497–2517. doi:10.1175/2008jamc1837.1
Vickery, P. J., Wadhera, D., Twisdale, L. A., and Lavelle, F. M. (2009b). US hurricane wind speed risk and uncertainty. J. Struct. Eng. 135 (3), 301–320. doi:10.1061/(asce)0733-9445(2009)135:3(301)
Wang, C., Zhang, H., Ellingwood, B. R., Guo, Y., Mahmoud, H., and Li, Q. (2020). Assessing post-hazard damage costs to a community’s residential buildings exposed to tropical cyclones. Struct. Infrastructure Eng. 17, 443–453. doi:10.1080/15732479.2020.1845215
Weisberg, R. H., and Zheng, L. (2008). Hurricane storm surge simulations comparing three-dimensional with two-dimensional formulations based on an Ivan-like storm over the Tampa Bay, Florida region. J. Geophys. Res. Oceans 113 (C12). doi:10.1029/2008jc005115
Wu, Y. J., Hayat, T., Clarens, A., and Smith, B. L. (2013). Climate change effects on transportation infrastructure: Scenario-based risk analysis using geographic information systems. Transp. Res. Rec. 2375 (1), 71–81. doi:10.3141/2375-09
Xu, L., and Brown, R. E. (2008). “A hurricane simulation method for Florida utility damage and risk assessment,” in Proceeding of the 2008 IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century (IEEE), 1–7.
Yabe, T., and Ukkusuri, S. V. (2020). Effects of income inequality on evacuation, reentry and segregation after disasters. Transp. Res. part D Transp. Environ. 82, 102260. doi:10.1016/j.trd.2020.102260
Keywords: hurricane wind fields, scenario analysis, social impacts, damage and loss, equity, community resilience
Citation: Mazumder RK, Enderami SA and Sutley EJ (2023) A novel framework to study community-level social and physical impacts of hurricane-induced winds through synthetic scenario analysis. Front. Built Environ. 9:1005264. doi: 10.3389/fbuil.2023.1005264
Received: 28 July 2022; Accepted: 17 January 2023;
Published: 16 February 2023.
Edited by:
Ahmed U. Abdelhady, Verisk Analytics, United StatesReviewed by:
Reda Snaiki, École de Technologie Supérieure, CanadaCopyright © 2023 Mazumder, Enderami and Sutley. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ram Krishna Mazumder, cmttYXp1bWRlckBrdS5lZHU=, cnhtNTYyQGNhc2UuZWR1
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.