Prediction of fatigue crack propagation in metals based on IBAS-PF

Owing to particle leanness, the standard Particle Filter (PF) algorithm is prone to the problem of reduced prediction accuracy when predicting fatigue crack propagation. An improved particle filter algorithm based on the optimization algorithm of beetle antenna search (IBAS-PF) for fatigue crack propagation in metals is proposed in this paper. The discrete Paris formula was used to establish the state equation of fatigue crack propagation, in which the uncertainty of material and crack propagation process were considered. Meanwhile, the characteristics of Lamb wave signals under different crack lengths were extracted to establish the observation equation. The sampling process of the PF algorithm was optimized based on the beetle antennae search algorithm to improve the particle diversity and the prediction accuracy. Compared with the standard PF algorithm, the improved BASO-PF algorithm has higher accuracy for metal fatigue crack propagation, as well as better state estimation ability.

1 Introduction

Fatigue cracks are regarded as one of the main reasons for the failure of engineering structures. If the crack propagation process cannot be monitored and predicted by effective means, the accumulation of damage to a certain extent can easily cause the sudden failure of the overall structure, which will lead to serious accidents and hazards. Therefore, it is of great significance to accurately predict the fatigue crack growth in metals.

The Paris formula (Paris and Erdogan, 1963) is often used in engineering to predict fatigue crack growth. However, the fatigue crack growth of engineering structures is affected by both the internal material and external environmental factors, and usually shows a certain degree of uncertainty (Yeratapally et al., 2017). The Paris model cannot take this into account, so it is difficult to predict the fatigue crack growth with high accuracy. The data-driven fatigue crack growth prediction method is a current research hotspot. Wang et al. (2016) combined the extended Kalman filter (EKF) and unscented Kalman filter (UKF) algorithms to estimate the parameters m and c in the Paris model, and carried out crack propagation prediction. He et al. (2013) proposed a crack propagation prediction method combining Lamb wave finite element simulation analysis and Bayesian update. Compared with the EKF and UKF algorithms, the particle filter (PF) algorithm has fewer restrictions on the model and wider application range. Orchard and Vachtsevanos (2009) used the PF algorithm to predict the life of planetary gears with cracks, and found that its prediction accuracy was higher than the EKF algorithm. Chen et al. (2016, 2017, 2018, 2019) and Sbarufatti et al. (2016) applied the PF algorithm to fatigue crack growth prediction, and the research results show that this method can effectively improve the prediction accuracy.

However, the optimal number of particles in the PF algorithm is often difficult to choose. In addition, too many particles will reduce the computational efficiency and affect the real-time prediction of crack growth (Yang and Gao, 2019). By introducing intelligent optimization algorithms into the standard PF algorithm, the particles obtained by a priori sampling can move to the region with high a posteriori probability, and the problem of particle leanness can also be overcome. Some researchers combined the particle swarm algorithm (Zhang et al., 2014), the genetic algorithm (Li et al., 2017), and the firefly algorithm (Tian et al., 2019) with the PF algorithm, which has successfully increased the number of effective particles and improved the prediction accuracy of the PF algorithm.

This paper proposes a fatigue crack growth prediction method based on the improved beetle antenna search-particle filter (IBAS-PF) algorithm. The state space model based on the Paris formula is used to characterize the crack growth process, and the observation space equation is established based on the characteristics of the monitoring signals of the Lamb waves. This method uses Lamb waves to online monitor the crack growth, and combines the IBAS-PF algorithm to correct the cumulative error of the Paris model in real time. Finally, the unilateral fatigue crack growth experiment of Q235 steel specimens is used to verify the effectiveness of the method proposed in this paper.

2 Particle filtering

2.1 Standard particle filter algorithm

A discrete-time system is composed of the state equation (Eq. 1) and the observation equation (Eq. 2):

$x_k=g_k\left(x_{k-1},q_k\right)(1)$

$y_k=h_k\left(x_k,r_k\right)(2)$

where x_k and y_k are the state value and observation value of the system at time k respectively, g_k (·) and h_k (·) can be nonlinear functions, q_k and r_k represent the random noise.

Suppose X_k = {x₀, ···, x_k} is the state sequence from time 0 to k, and Y_k = {y₁, ···, y_k} is the observation sequence from time 1 to k. According to the Bayesian filtering theory, the optimal estimated value ${\widehat{x}}_k$ at time k is calculated by Eq 3:

${\widehat{x}}_k={\displaystyle \int x_k}p\left(x_k|Y_k\right)\text{d}{x}_k(3)$

The posterior probability distribution p (x_k|Y_k) can be obtained following the two steps below:

Prediction:

$p\left(x_k|Y_{k-1}\right)={\displaystyle \int p\left(x_k|x_{k-1}\right)p\left(x_{k-1}|Y_{k-1}\right)\text{d}{x}_{k-1}}(4)$

Update:

$p\left(x_k|Y_k\right)=\frac{p\left(y_k|x_k\right)p\left(x_k|Y_{k-1}\right)}{p\left(y_k|Y_{k-1}\right)}(5)$

where p (x_k|Y_k-1) is the prior probability distribution without considering the current measurement value y_k, p (x_k|x_k-1) is the transition function defined by Eq. 1, p (y_k|x_k) is the likelihood function defined by Eq. 2, and p (y_k|Y_k-1) is the normalization constant.

For general systems, it is usually difficult to obtain the analytical solution of a posteriori probability p (x_k|Y_k). The PF algorithm introduces the Monte Carlo sampling to solve the problem, which approximates the posterior probability distribution p (X_k|Y_k) by sampling a series of weighted particles:

$p\left(X_k|Y_k\right)\approx {\displaystyle \sum _{i=1}^N{\tilde{w}}_k^i\delta \left(X_k-X_k^i\right)}(6)$

where ${\tilde{w}}_k^i$ is the normalized weight corresponding to the particle set $X_k^i$, N represents the number of particles, δ (·) is the Dirac function.

However, the true posterior distribution p (X_k|Y_k) is generally unknown. Therefore, $X_k^i$ (i = 1,…, N) is usually sampled from a pre-defined and easy-to-implement reference distribution q (X_k|Y_k) (i.e., the important density function), and the corresponding unnormalized importance weight is defined by:

$w_k^i\propto \frac{p\left(X_k^i|Y_k\right)}{q\left(X_k^i|Y_k\right)}(7)$

If the important density function can be decomposed into q (X_k|Y_k) = q (x_k|x_k-1, y_k)q (X_k-1|Y_k-1), then the importance weight can be further written as:

$w_k^i\propto w_{k-1}^i\frac{p\left(y_k|x_k^i\right)p\left(x_k^i|x_{k-1}^i\right)}{q\left(x_k^i|x_{k-1}^i,y_k\right)}(8)$

Considering the feasibility of the algorithm, $p\left(x_k^i|x_{k-1}^i\right)$ is selected as $q\left(x_k^i|x_{k-1}^i,y_k\right)$ in the standard PF algorithm, and Eq 8 can be simplified as:

$w_k^i\propto w_{k-1}^{i}p\left(y_k|x_k^i\right)(9)$

The normalized importance weight is written as:

${\tilde{w}}_k^i=\frac{w_k^i}{{\displaystyle \sum _{i=1}^N{w}_k^i}}(10)$

However, with the continuous progress of the prediction-update recursion, only a few particles will have large weights while most particles will have small weights, which is known as the phenomenon of particle degradation. Gordon et al. (2002) introduced the resampling step into the PF algorithm to overcome particle degradation, and the commonly used resampling methods are system resampling (Carpenter et al., 1999), random resampling (Kitagawa, 1996), residual resampling (Liu and Chen, 1998), polynomial resampling (Li et al., 2015), etc. However, excessive use of resampling will lead to particle depletion. Since particles with large weights are replicated multiple times, a large number of particles are repeated during the sampling process. When the number of particles is small or the number of recursive steps is large, the prediction accuracy of the particle filter algorithm will decline.

2.2 Improved beetle antenna search-particle filter algorithm

In the standard PF algorithm, the particles are sampled from p (x_k|x_k-1) only according to the a priori knowledge, without considering the influence of the current observation value y_k. In order to optimize the sampling process, we introduce the BAS algorithm into the PF algorithm.

Jiang and Li, 2017a proposed the beetle antenna search algorithm, of which the basic idea is based on the foraging process of longhorn beetles. A longhorn beetle has two antennae. It decides the next search direction based on the intensity of the food smell felt by the antennae on the left and right sides, and then moves toward the side with stronger smell. Even in an unknown environment, longhorn beetles can successfully find food in most cases. Similarly, the fitness function f (·) is analogous to the smell of food. Suppose the location of the longhorn beetle is defined by x^t at time t, the search space of the left and right antennae are defined as:

$\{\begin{array}{l}{x}_l^t=x^t-d^t\overrightarrow{b}\\ x_r^t=x^t+d^t\overrightarrow{b}\end{array}(11)$

where $x_l^t$ and $x_r^t$ represent the locations of the left and right antennae at time t, d^t is the perception length of the antennae, and $\overrightarrow{b}$ is a random unit vector which represents the orientation of the head of the longicorn beetle is random.

The longicorn beetle updates its position according to the odor concentration $f\left(x_l^t\right)$ and $f\left(x_r^t\right)$ at the left and right antennae:

$x^{t+1}=x^t+{\delta }^t\overrightarrow{b}\text{sign}\left(f\left(x_r\right)-f\left(x_l\right)\right)(12)$

where δ^t is the step length at time t, sign (·) is the sign function.

The perception length d^t and the step length δ^t should be set large enough to cover the whole area and avoid falling into the local optimum. As time goes on, the values of the two parameters should be gradually reduced to facilitate high-precision local search. Therefore, the two parameter values are updated as follows:

$d^t=\alpha d^{t-1}+0.01(13)$

${\delta }^t=\beta {\delta }^{t-1}(14)$

To improve the performance of the beetle antennae search optimizer.

The BAS method can be integrated with many other algorithms to promote the efficiency of the optimization. For example, BAS with particle swarm optimization (Lin and Li, 2018; Zhang et al., 2020), artificial bee colony (Cheng et al., 2019), fallback (Wu et al., 2020), and ADAM (Khan et al., 2020). Some researchers have also proposed the improved variants of the BAS algorithm such as beetle swarm antennae search (Mu et al., 2019) and BAS without parameter tuning (Jiang and Li 2017b).

In the present study, the standard PF algorithm is optimized based on the BAS algorithm to improve the particle diversity and the prediction accuracy. The specific steps of the IBAS-PF algorithm proposed in this paper are as follows:

Step 1. Initialization. Generate the particle set ${\left\{x_0^i\right\}}_{i=1}^N$ from the prior distribution p(x₀), set the weights of all particles to 1/N, and then set k = 1.

Step 2. Generate the particles ${\left\{x_k^i\right\}}_{i=1}^N$ from the transition function $p\left(x_k^i|x_{k-1}^i\right)$.

Step 3. Update the locations of the particles using the BAS algorithm according to Eq. 12, where the fitness function f is given by:

$f=\exp \left[-\frac{1}{2R}{\left(y_k^{obs}-y_k^{pre}\right)}^2\right](15)$

where $y_k^{obs}$ is the true observed value at time k, $y_k^{pre}$ is the observed value predicted by the observation equation (Eq. 2), and R is the variance of the observed noise r.

Step 4. Update the weights according to Eq. 9, and then normalize them according to Eq. 10.

Step 5. Resample to obtain the new equally-weighted particle set ${\left\{x_k^i,1/N\right\}}_{i=1}^N$.

Step 6. Obtain the estimated state value using Eq. 3. Set k = k +1, and then return to Step 2.

3 Prediction of fatigue crack propagation in metals based on improved beetle antenna search-particle filter

3.1 State equation based on the paris formula

The classic Paris formula is applied to establish the state equation of fatigue crack growth:

$\frac{\text{d}a}{d{N}_f}=C{\left(\mathrm{\Delta }K\right)}^m(16)$

where a is the crack length, N_f is the number of fatigue cycles, da/dN_f is the crack growth rate per cycle. C and m are material parameters. According to the previous research Qu et al. (2008), it is assumed that C obeys the lognormal distribution, while m is a constant. The stress intensity factor amplitude ∆K can be calculated by Eq. 17:

$\mathrm{\Delta }K=Y\mathrm{\Delta }\sigma \sqrt{\pi a}(17)$

where ∆σ is the stress amplitude, and Y is the geometric shape correction coefficient.

Discretize Eq. 16 and consider the dispersion of materials and the uncertainty of fatigue crack growth process, the state equation is given by:

$\{\begin{array}{l}{a}_t=a_{t-1}+C_{t-1}{\left(\mathrm{\Delta }{K}_{t-1}\right)}^m\mathrm{\Delta }{N}_f+q\\ C_t=C_{t-1}\end{array}(18)$

where a_t-1, C_t-1, ΔK_t-1 are the crack length, material parameter, and stress intensity factor amplitude at time t-1 respectively, ∆N_f is the fatigue cycle period from time t-1 to t, and q is the process noise.

3.2 Observation equation based on the lamb wave signals

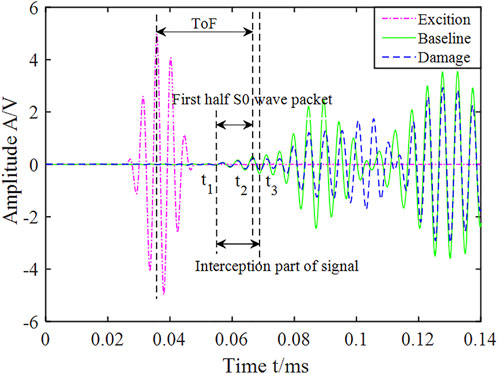
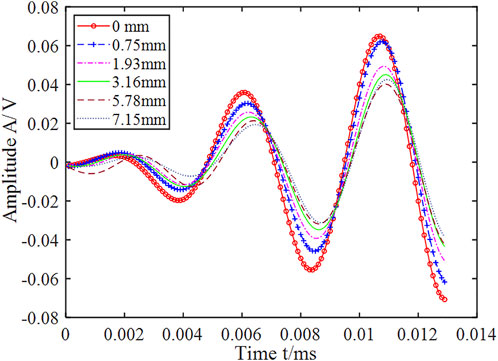
The PZT sensors were mounted on the surface of the test specimen to excite and receive Lamb wave signals. During the fatigue test, the Lamb wave monitoring signals corresponding to different crack lengths were collected. As shown in Figure 1, the S0 wave packet from t₁ to t₃ is intercepted for analysis (Liu et al., 2019). The damage index DI based on the correlation coefficient is used to quantitatively characterize the influence of the crack length on the Lamb wave signals:

$DI=1-\frac{C_{AB}}{{\sigma }_A{\sigma }_B}(19)$

where A is the reference Lamb waves signal, and B is the damage signal obtained under different crack lengths. C_AB and σ_A (σ_B) represent the covariance and the standard deviation of the signals.

FIGURE 1

FIGURE 1. Schematic diagram of the Lamb wave signal extraction.

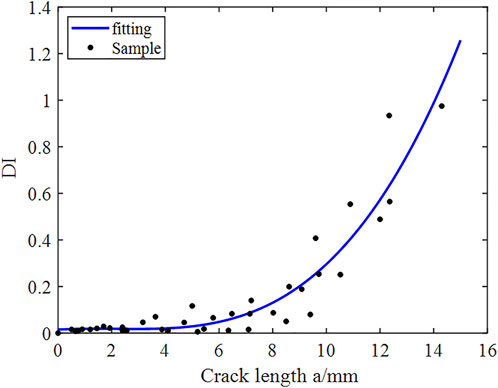
The relationship between DI and the crack length a is obtained by curve fitting, and the observation equation is given by:

$D{I}_t=s\left(a_t\right)+r(20)$

where DI_t is the damage index at time t, s is the fitting function, and r is the observation noise of the Lamb wave signal.

3.3 Process of fatigue crack growth prediction

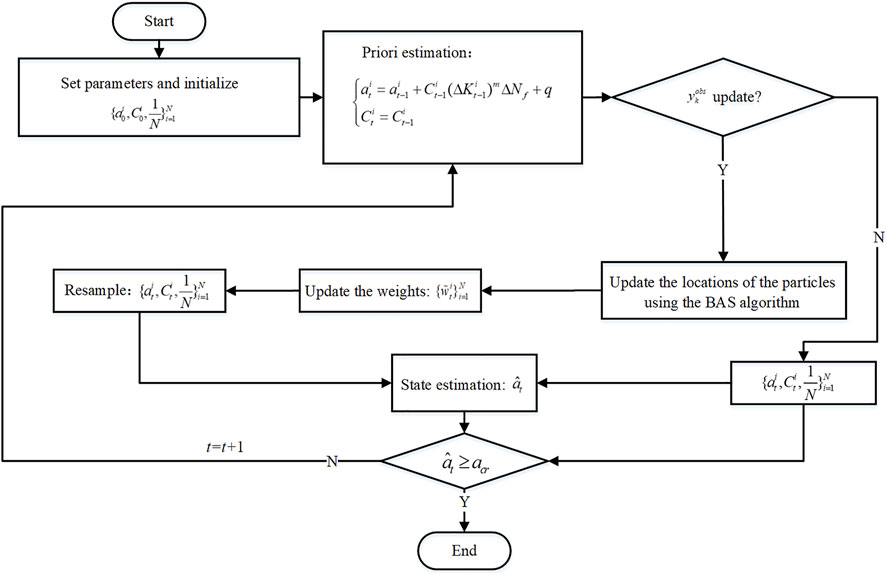
The process of fatigue crack growth prediction based on the IBAS-PF algorithm in Section 2.2 is shown in Figure 2.

FIGURE 2

FIGURE 2. Fatigue crack growth prediction based on IBAS-PF algorithm.

4 Experimental verification

4.1 Experimental setup

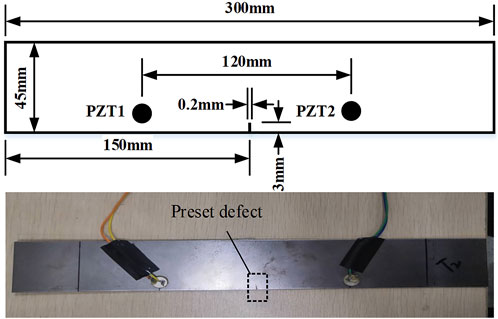
The effectiveness of the proposed prediction method is verified by the unilateral fatigue crack growth experiment of Q235 steel specimens in this section. The experimental setup was similar to that of Chen et al. (2019), and the fatigue test of five specimens was carried out. Nevertheless, a unilateral fatigue crack was cut in the present study instead of machining a through hole. As shown in Figure 3, the size of the test specimen is 300 mm × 45 mm × 2 mm, and the initial vertical defect of 3 mm × 0.2 mm × 2 mm was preset at the midline using wire cutting to control the direction of crack propagation.

FIGURE 3

FIGURE 3. The dimension of the test specimen.

As shown in Figure 4, the experimental system consists of a fatigue testing machine (MTS Landmark), a signal generator (Unit UTG 2025A), a power amplifier (Krohn-Hite 7602M), and a signal receiver (Yokogawa DL350). The PZT piezoelectric ceramic sensor is made of P51 material. The specimen bears a sinusoidal fatigue load with a maximum load of 16 KN, a stress ratio of 0.1, and a loading frequency of 6Hz. Apply an appropriate amount of white correction fluid to the surface near the crack of the test piece to facilitate observation, and the fatigue crack is projected on the laptop screen through a microscope and measured with a ruler.

FIGURE 4

FIGURE 4. The experimental platform for fatigue crack growth monitoring.

4.2 Determination of the state and observation equations

The geometric shape correction coefficient Y can be calculated by the following formula:

$Y=1.12-0.23\frac{a}{b}+10.6{\left(\frac{a}{b}\right)}^2-21.7{\left(\frac{a}{b}\right)}^3+30.4{\left(\frac{a}{b}\right)}^4(21)$

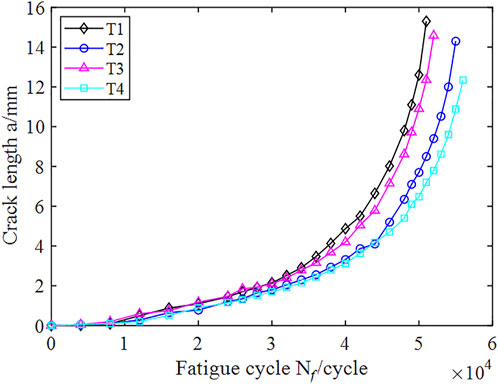
where a is the fatigue crack length and b is the width of the specimen. The a-N_f curves of the four specimens T1-T4 under the same loading condition are plotted in Figure 5. The material parameters C and m in the Paris formula are calculated using the seven-point incremental polynomial method, and the standard deviation of the process noise q is determined by the average maximum crack growth after ∆N_f = 75 cycles, which gives logC₀ ∼ N (−13.07, 0.1377²), m = 3.19, w ∼ N (0, 0.0234²).

FIGURE 5

FIGURE 5. The fatigue cycle versus the crack length.

After each observation of the crack growth length, the measurement signal of Lamb waves is collected. In this experiment, a 5-peak sinusoidal modulation signal with a center frequency of 220 kHz was used as the excitation signal. The voltage amplitude was 10 V, which was amplified by a power amplifier 100 times and applied to PZT1. PZT2 was the signal receiving end. The sampling frequency of the signal receiver is 10 MHz, and the collected signal is passed through a band-pass filter for noise reduction. Figure 6 shows the extracted Lamb wave signals under different crack propagation lengths of the T3 specimen. Extract the Lamb wave signals of the T1 to T4 specimens to calculate the DI curve, and get the relationship between DI and crack length a by curve fitting (Figure 7):

$D{I}_t=6.21\times {10}^{-4}{\left(a_t-3\right)}^3-4.46\times {10}^{-3}{\left(a_t-3\right)}^2+1.08\times {10}^{-2}\left(a_t-3\right)+7.29\times {10}^{-3}+r(22)$

FIGURE 6

FIGURE 6. Signal extraction of the T3 specimen under different crack lengths.

FIGURE 7

FIGURE 7. The DI values corresponding to different crack lengths.

The standard deviation of the observation noise r is taken as the root mean square error obtained by cure fitting, which gives r ∼ N (0, 0.0765²).

4.3 Fatigue crack growth prediction

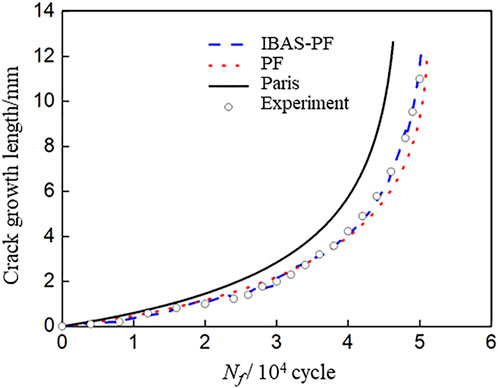
The effectiveness of the fatigue crack growth prediction method based on the IBAS-PF algorithm is verified using the T5 specimen. The number of particles N is set to 500, and the initial values of the perception length d^t and the step length δ^t are set as 0.1 and 0.5 respectively. Both α and β are set as 0.95. The prediction experiment was carried out in Matlab R2016a on a win10 Dell desktop computer with 64-bit 8G memory. The algorithm simulation prediction experiment was performed 20 times, and the average value was taken as the output of the prediction result. The fatigue crack growth can be divided into three stages: unstable crack initiation, stable cracking propagation and final fracture. The comparison between the prediction and experimental data is carried out in the second stage since the Paris law is only valid when the fatigue crack growth is stable. Figure 8 shows the results of fatigue crack growth prediction using the PF and the IBAS-PF algorithm. As the fatigue cycle period continues to increase, the prediction error of the Paris formula is increasing. The filtering algorithms consider the influence of material dispersion and the uncertainty of fatigue crack propagation process, and uses the observed value extracted from the Lamb wave signals to constantly correct the prediction error of the state equation based on Paris formula. Thus the prediction accuracy is significantly improved. However, in the middle and late stages of crack propagation, with the aggravation of particle leanness, the prediction error of the standard PF algorithm increases gradually. After 46,000 fatigue cycles, the relative error and root mean square error of the PF algorithm are −15.1% and 0.385 mm respectively, while the relative error of the IBAS-PF algorithm is 1.8% and the root mean square error is 0.118 mm, indicating that the IBAS-PF algorithm has higher prediction accuracy than the PF algorithm.

FIGURE 8

FIGURE 8. Crack length prediction and the experimental results.

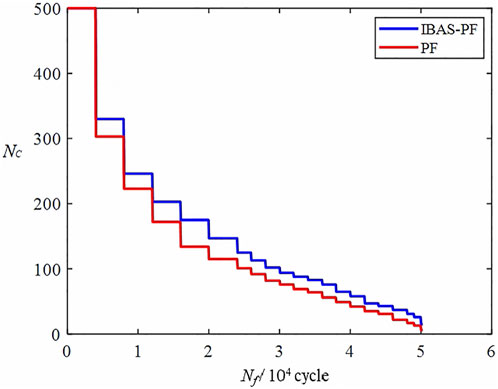
The number of particles of the material parameter C which are not repeated in the prediction experiment, N_C, was used to evaluate the effectiveness of the algorithm in alleviating the lack of particles. As shown in Figure 9, the number of particles in the IBAS-PF algorithms is significantly higher than that of the standard PF algorithms at the same time.

FIGURE 9

FIGURE 9. The N_C values corresponding to different fatigue cycles N_f.

5 Conclusion

In the prediction of metal fatigue crack growth, the standard PF algorithm is prone to the problem of reduced prediction accuracy due to particle leanness. A metal fatigue crack propagation method based on the IBAS-PF algorithm is proposed in the present paper. The discrete Paris formula is used to establish the state equation of the fatigue crack propagation, and the characteristics of Lamb wave signals under different crack lengths are extracted to establish the observation equation. By introducing the latest observed information, the sampling process of the PF algorithm is optimized based on the beetle antenna search algorithm, and the diversity of the particles is improved. The experimental results of the Q235 steel specimens show that compared with the standard PF algorithm, the IBAS-PF algorithm has higher accuracy of crack propagation prediction and stronger ability of state estimation. In principle, the proposed method can also be extended to predict the propagation of multiple fatigue cracks, as well as the crack growth in a real structure with several elements and connections. However, more sensors will be needed to identify the cracks, and the state equation and the observation equation of the IBAS-PF algorithm will be much more complicated. Further studies are required to solve these problems.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SW and XZ participated in conception and design. GZ contributed to the analysis and interpretation of the data, as well as drafted the article. GJ revised the manuscript.

Funding

This research was funded by the science and technology plan of Jiangsu administration for market regulation (KJ196043).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Reference

Carpenter, J., Clifford, P., and Fearnhead, P. (1999). Improved particle filter for nonlinear problems. IEE Proc. Radar Sonar Navig. 146 (1), 2–7. doi:10.1049/ip-rsn:19990255

CrossRef Full Text | Google Scholar

Chen, J., Yuan, S., and Jin, X. (2019). On-Line prognosis of fatigue cracking via a regularized particle filter and guided wave monitoring. Mech. Syst. Signal Process. 131, 1–17. doi:10.1016/j.ymssp.2019.05.022

CrossRef Full Text | Google Scholar

Chen, J., Yuan, S., Qiu, L., Cai, J., and Yang, W. (2016). Research on a Lamb wave and particle filter-based on-line crack propagation prognosis method. Sensors 16, 320. doi:10.3390/s16030320

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, J., Yuan, S., Qiu, L., Wang, H., and Yang, W. (2018). On-Line prognosis of fatigue crack propagation based on Gaussian weight-mixture proposal particle filter. Ultrasonics 82, 134–144. doi:10.1016/j.ultras.2017.07.016

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, J., Yuan, S., and Wang, H. (2017). Mixture proposal particle filtering for guided wave based fatigue crack propagation prognosis. Procedia Eng. 188, 25–32. doi:10.1016/j.proeng.2017.04.453

CrossRef Full Text | Google Scholar

Cheng, L., Yu, M., Yang, J., and Wang, Y. (2019). “An improved artificial bee colony algorithm based on beetle antennae search,” in Chinese control conference (CCC), 2312–2316.

CrossRef Full Text | Google Scholar

Gordon, N. J., Salmond, D. J., and Smith, A. (2002). Novel approach to nonlinear/non-Gaussian bayesian state estimation. IEE Proc. F. Radar Signal Process. UK. 140 (2), 107–113. doi:10.1049/ip-f-2.1993.0015

CrossRef Full Text | Google Scholar

He, J., Guan, X., Peng, T., Liu, Y., Saxena, A., Celaya, J., et al. (2013). A multi-feature integration method for fatigue crack detection and crack length estimation in riveted lap joints using Lamb waves. Smart Mat. Struct. 22 (10), 105007. doi:10.1088/0964-1726/22/10/105007

CrossRef Full Text | Google Scholar

Jiang, X., and Li, S. (2017a). BAS: Beetle antennae search algorithm for optimization problems. Int. J. Robot. Con. 1 (1), 1–3. doi:10.5430/ijrc.v1n1p1

CrossRef Full Text | Google Scholar

Jiang, X., and Li, S. (2017b). Beetle antennae search without parameter tuning (BAS-WPT) for multi-objective optimization. arXiv preprint arXiv:1711.02395.

Google Scholar

Khan, A. H., Cao, X., Li, S., Katsikis, V. N., and Liao, L. (2020). BAS-ADAM: An adam based approach to improve the performance of beetle antennae search optimizer. IEEE/CAA J. Autom. Sin. 7 (2), 461–471. doi:10.1109/jas.2020.1003048

CrossRef Full Text | Google Scholar

Kitagawa, G. (1996). Monte Carlo filter and smoother for non-Gaussian nonlinear state space models. J. Comput. Graph. Stat. 1 (1), 1–25. doi:10.2307/1390750

CrossRef Full Text | Google Scholar

Li, K., Wu, J., Zhang, Q., Su, L., and Chen, P. (2017). New particle filter based on ga for equipment remaining useful life prediction. Sensors 17 (4), 696. doi:10.3390/s17040696

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, T., Bolic, M., and Djuric, P. M. (2015). Resampling methods for particle filtering: Classification, implementation, and strategies. IEEE Signal Process. Mag. 32 (3), 70–86. doi:10.1109/msp.2014.2330626

CrossRef Full Text | Google Scholar

Lin, M. J., and Li, Q. H. (2018). A hybrid optimization method of beetle antennae search algorithm and particle swarm optimization. DEStech Trans. Eng. Technol. Res. 1, 396–401.

CrossRef Full Text | Google Scholar

Liu, J. S., and Chen, R. (1998). Sequential Monte Carlo methods for dynamic systems. J. Am. Stat. Assoc. 93 (443), 1032–1044. doi:10.1080/01621459.1998.10473765

CrossRef Full Text | Google Scholar

Liu, X., Zhang, W., Liu, X., Dai, W., and Fu, G. (2019). A novel RLS-KS method for parameter estimation in particle filtering-based fatigue crack growth prognostics. IEEE Access 7, 156764–156778. doi:10.1109/access.2019.2948291

CrossRef Full Text | Google Scholar

Mu, Y., Li, B., An, D., and Wei, Y. (2019). Three-dimensional route planning based on the beetle swarm optimization algorithm. IEEE Access 7, 117804–117813. doi:10.1109/access.2019.2935835

CrossRef Full Text | Google Scholar

Orchard, M., and Vachtsevanos, G. (2009). A particle-filtering approach for on-line fault diagnosis and failure prognosis. Trans. Inst. Meas. Control 31 (3-4), 221–246. doi:10.1177/0142331208092026

CrossRef Full Text | Google Scholar

Paris, P., and Erdogan, F. (1963). A critical analysis of crack propagation laws. J. Basic Eng. 85 (4), 528–533. doi:10.1115/1.3656900

CrossRef Full Text | Google Scholar

Qu, X., Ma, Y., Cui, H., Zhang, J., and Wang, C. (2008). “Statistical research of material coefficient in Paris law,” in Chinese MTS fracture test symposium, 26–31.

Google Scholar

Sbarufatti, C., Corbetta, M., Manes, A., and Giglio, M. (2016). Sequential monte-carlo sampling based on a committee of artificial neural networks for posterior state estimation and residual lifetime prediction. Int. J. Fatigue 83, 10–23. doi:10.1016/j.ijfatigue.2015.05.017

CrossRef Full Text | Google Scholar

Tian, M., Bo, Y., Chen, Z., Wu, P., and Yue, C. (2019). Multi-target tracking method based on improved firefly algorithm optimized particle filter. Neurocomputing 359, 438–448. doi:10.1016/j.neucom.2019.06.003

CrossRef Full Text | Google Scholar

Wang, Y., Binaud, N., Gogu, C., and Fu, J. (2016). Determination of Paris' law constants and crack length evolution via extended and unscented kalman filter: An application to aircraft fuselage panels. Mech. Syst. Signal Process. 80, 262–281. doi:10.1016/j.ymssp.2016.04.027

CrossRef Full Text | Google Scholar

Wu, Q., Lin, H., Jin, Y., Chen, Z., Li, S., and Chen, D. (2020). A new fallback beetle antennae search algorithm for path planning of mobile robots with collision-free capability. Soft Comput. 24 (3), 2369–2380. doi:10.1007/s00500-019-04067-3

CrossRef Full Text | Google Scholar

Yang, W., and Gao, P. (2019). Lamb wave-minimum sampling variance particle filter-based fatigue crack prognosis. Sensors 19, 1070. doi:10.3390/s19051070

PubMed Abstract | CrossRef Full Text | Google Scholar

Yeratapally, S. R., Glavicic, M. G., Argyrakis, C., and Sangid, M. D. (2017). Bayesian uncertainty quantification and propagation for validation of a microstructure sensitive model for prediction of fatigue crack initiation. Reliab. Eng. Syst. Saf. 164, 110–123. doi:10.1016/j.ress.2017.03.006

CrossRef Full Text | Google Scholar

Zhang, B., Duan, Y., Zhang, Y., and Wang, Y. (2020). “Particle swarm optimization algorithm based on beetle antennae search algorithm to solve path planning problem,” in IEEE 4th information technology, networking, electronic and automation control conference (ITNEC) (IEEE), 1, 1586–1589.

CrossRef Full Text | Google Scholar

Zhang, C. Q., Lei, G. E., and Han, D. (2014). Research on particle swarm particle filter algorithm based on target tracking. Com. Simul. 8, 398–402.

Google Scholar