
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Built Environ., 05 July 2022
Sec. Wind Engineering and Science
Volume 8 - 2022 | https://doi.org/10.3389/fbuil.2022.858067
This article is part of the Research TopicThe Virtual Wind Tunnel for Sustainable and Climate Adaptive Urban and Building DesignView all 5 articles
The construction of a building inevitably changes the microclimate in its vicinity. Many city authorities request comprehensive wind studies before granting a building permit, which can be obtained through Computational Fluid Dynamics (CFD) simulations. Investigating the wind conditions for 12 wind directions has previously been considered sufficient in most literature and the industry. However, the effect of changing the number of simulated wind directions is still not well understood. This article investigates the influence of the number of simulated wind directions on pedestrian wind comfort maps. A neighborhood in Niigata city, Japan, was chosen as a case study. Simulations are performed in OpenFOAM using a Reynolds-averaged Navier-Stokes model and the realizable k-ϵ turbulence model. The inlet profiles form a homogeneous atmospheric boundary layer with neutral stratified conditions and a logarithmic velocity profile. The pedestrian wind comfort maps are converging toward a final map as more wind directions are included. The area of the maps classified with the same comfort as using 64 wind directions is 79% using 4 wind directions, 92% using 8 wind directions, 96% using 16 wind directions, and 99% using 32 wind directions. A greater understanding of the influence of the number of simulated wind directions included may enable more efficient pedestrian wind comfort studies that recognize the associated uncertainties.
The field of computational fluid dynamics (CFD) continues to develop as new and improved numerical methods evolve while computational power becomes more cost-effective and available. A result of this development is that CFD is increasingly applied to solve urban wind engineering problems, such as wind loads on buildings and bridges (Huang et al., 2007; Tamura et al., 2008; Montazeri and Blocken, 2013; Thordal et al., 2019), and pedestrian wind comfort (Blocken and Persoon, 2009; Blocken et al., 2012; Janssen et al., 2013; Blocken and Stathopoulos, 2016; Cheynet et al., 2019). Detailed insight into the wind flow at a given geographic location, including both historical and possible future scenarios, complements numerous applications in urban planning, climate and environmental modeling, and other applications (Blocken, 2014).
Assessing pedestrian wind comfort is a critical consideration for new building developments. Pedestrian wind comfort refers to the mechanical effect of wind on people at the ground level. The wind shear effect caused by bluff bodies commonly present in urban environments, such as buildings and other bulk structures, strongly modifies the local wind conditions. High-rise buildings are especially known for frequently causing high wind velocities at pedestrian level, reducing the pedestrian wind comfort in their vicinity. On some occasions, the strong local wind gusts could even be considered a safety concern.
There is rising concern that uncomfortable and dangerous wind conditions in urban areas will be more common in the future as climate change can cause more frequent extreme weather events (National Academies of Sciences, Engineering, and Medicine and others, 2016). Also, further urbanization through increased high-rise buildings, and a more dense built environment in general, is likely to worsen the wind environment.
These urban wind problems can be addressed by including pedestrian wind comfort studies in city planning processes, and in the design phase before erecting new buildings. In academia and industry, the possible negative effect of new buildings on the local window environment is garnering increased attention. A growing number of city authorities request pedestrian wind comfort studies before granting building permits.
The key component of a pedestrian wind comfort study is the estimation of a pedestrian wind comfort map. The pedestrian wind comfort map illustrates the wind conditions experienced at the ground level by pedestrians at a site in a given period, usually annually or seasonally. These maps are produced by combining detailed wind simulations from multiple wind directions, statistical meteorological data from the location, and a set of defined wind comfort criteria.
The set of wind simulations used as inputs represents the different wind conditions occurring at the location throughout the period, typically a year. The setup of the simulations only differs in the wind direction applied at the inlet, which is evenly distributed in the horizontal plane within the set. Wisse et al. (2002) argue that 12 wind directions are enough for the analysis of pedestrian wind comfort; 12 wind directions with 30° increments are used in most published journal papers, including (Blocken et al., 2004; Blocken and Carmeliet, 2008; Blocken and Persoon, 2009; Blocken et al., 2012; Dhunny et al., 2018). Hågbo et al. (2021) instead used the eight wind directions. City of London Corporation (2019) recommends that 36 equally spaced wind directions should be used in pedestrian-level wind analysis before the erection of buildings taller than 25 m, but specifies that this number is calibrated for the City of London and may not be appropriate for other areas. Similarly, Leeds City Council (2021) recommends the use of a minimum of 36 wind directions for buildings taller than 15 m within the City of Leeds. The substantial discrepancy in the recommended number of wind directions, from 12 to 36, highlights the need to investigate the count’s influence.
This study investigates the influence of the number of simulated wind directions on pedestrian wind comfort maps. Increasing the number of wind directions will likely result in more accurate maps, but will also raise the computational costs. The required number of wind directions needed to reach a satisfactory accuracy is presumably dependent on the complexity of the urban environment and local meteorological conditions. Other associated uncertainties in the production of the maps, such as the local statistical meteorological data or the simulation’s ability to represent the annual local wind conditions, may justify fewer simulated wind directions.
CFD is already used today in urban planning to predict wind velocity levels in urban areas. Regardless of the method’s agreement with experiments, it is valuable to investigate the number of wind directions necessary to simulate to obtain a converged pedestrian wind comfort map. An improved understanding of the influence of the number of simulated wind directions and its associated accuracy in specific cases may help develop more efficient and reliable tools to perform pedestrian wind comfort studies.
Although this study focuses on pedestrian wind discomfort due to high wind speeds, relatively high wind speeds and canopy ventilation can be considered desirable in other aspects of urban environment modeling. These include thermal comfort, pollutant dispersion, and air quality assessment. Therefore, results from this study can also be of value for those applications of urban wind simulations.
This paper begins with a chapter describing the methodology in detail, starting with the computational domain and grid, and the numerical setup of the wind simulations. Then, the process of producing the aggregated pedestrian wind comfort maps is outlined. Finally, the results are presented and discussed.
Poor simulation setup can lead to inaccurate results; therefore, Best practice guidelines (BPGs) have been developed for properly conducting CFD analysis of the wind environment in urban areas. These guidelines are based on the cross-comparison between CFD simulations, wind tunnel experiments, and field measurements on several cases. The BPGs provided by Franke et al. (2007) and Tominaga et al. (2008) were closely followed to set up the simulations. The simulation setup is based on the one presented in Hågbo et al. (2021). It only differs in a few numerical settings, such as the algorithm handling the pressure-velocity coupling and site-specific parameters.
The location chosen for this study is a neighborhood in Niigata city in Japan, a building complex with simple building shapes. This location is used in the Architectural Institute of Japan (AIJ) benchmark case E, and its geometric model and data from wind tunnel experiments are provided at Architectural Institute of Japan, (2021). Other published CFD studies on this location available in the literature include (Tominaga et al., 2005; Mochida and Lun, 2008; Caniot et al., 2011; Tominaga, 2012).
The BPGs have been used as a minimum requirement when sizing the computational domain. The guidelines are based on box-shaped domains. They are only suitable if wind at the inlet has one specific direction, which is inward parallel to the domain’s sidewalls.
A cylindrical domain is used as the intention of this study was to have a flexible mesh suitable for simulating wind from any horizontal direction. Therefore, the recommendations of the BPGs had to be applied and adapted to the cylindrical domain.
The routine of using a cylindrical computational domain when performing urban wind simulations was introduced by Kastner and Dogan, (2020). They reported that a cylindrical domain yielded comparable results to a traditional box-shaped domain in terms of accuracy and convergence behavior. Figure 1 presents the computational domain, and the dimensions are listed on the right side of the figure.
The BPGs suggest that the top of the domain should be 5 Hmax from the top of the tallest building. Hmax, as defined by Franke, (2006), is the height of the tallest building and is essential in sizing the computational domain. Here, Hmax is 60 m. As there is no elevation in the terrain patch, the height of the domain is set to 6 Hmax. Franke et al. (2007) suggest a distance of 15 Hmax downstream of the buildings to the outlet of the domain. As the cylindrical domain is suitable for wind coming in from any direction, the radial distance from the buildings to the domain’s sides is set to 15 Hmax.
The computational grid was developed according to the BPGs, and Figure 2 presents a partial view of the grid structure from the side. The final grid is produced with snappyHexMesh, the hex-dominant unstructured mesh generator of OpenFOAM. snappyHexMesh requires a base mesh and 3D geometry in the form of a triangulated surface, here represented by the building model and the terrain model. Hågbo et al. (2019) concluded that an unstructured mesh generated with snappyHexMesh could be sufficient in urban wind simulations where only the general flow features are of interest.
The base mesh was generated with blockMesh, a meshing utility in OpenFOAM suitable for simple structured meshes with grading and curved edges. The grid is stretched vertically in the base mesh with an overall expansion ratio of three. It means that the height of the top cells is three times the height of the bottom cells.
The grid is refined successively in a 2:1 ratio near the terrain and buildings in the final mesh, with eight grid cells between each refinement level. Two refinement levels are used on the outermost part of the terrain patch, while three levels are used within a radius of 500 m from the center of the patch. Four refinement levels are applied near the buildings.
The grid consists of about 12.1 million cells, and key features of the mesh are listed in Table 1.

TABLE 1. Key features of the mesh used. The reported cell dimensions correspond to the sizes at the surface of the patches. And at ground-level for the height of the cells adjacent to a patch, z, as the mesh is stretched vertically. The cell’s length, x, and width, y, remain constant. Here, the x/y columns do not represent a ratio but the cell size in both horizontal directions as they are identical for each refinement level.
The height of the cells adjacent to the buildings and on the terrain near the buildings is 0.34 m. On the rest of the terrain within the built area, the cell height is 0.68 m, ensuring the elevation height of 2 m to be within a minimum of the third cell from the ground. These cell heights give the average non-dimensional wall distances y+ value of about 7.0 × 103 for the building patch and 9.0 × 103 for the terrain patch in the built region.
These are relatively high values that significantly exceed the recommended values of (30–500) (Franke et al., 2007), meaning that the first cell center is well outside the log-law region. However, standard logarithmic wall functions are typically also used in CFD simulations of atmospheric boundary layer wind flow when y+ is well above the recommended upper limit without reducing the accuracy of the simulated wind velocity field. Examples using y+ values of the same order of magnitude as in this study include the studies cited herein (Blocken et al., 2007; van Hooff and Blocken, 2010a; van Hooff and Blocken, 2010b; van Hooff et al., 2011).
The high Reynolds number flow studied here makes it challenging to be within the log-law region. The most important reason for using these high y+ values is that the recommended range is based on smooth walls and would yield unnecessarily small near-wall cells for our rough terrain wall. It should also be noted that the log-law profile is not necessarily valid given the complex geometry of the terrain.
Apart from the y+-values, the resolution is sufficiently high according to the BPGs, as it satisfies the recommendation of a minimum of 10 cells per building side and in the passage between buildings, as well as at least 3 cells from the ground to the elevation height (Franke et al., 2007; Yoshie et al., 2007; Tominaga et al., 2008). In this study, the elevation height was set to 2 m above ground level, a reasonable height for pedestrian wind comfort evaluation.
An outline of the simulation setup applied is provided at Table 2. The wind simulations were performed by solving the incompressible, three-dimensional steady Reynolds-averaged Navier-Stokes (RANS) equations with the finite volume method. Turbulent closure was provided by the realizable k-ϵ turbulence model developed by Shih et al. (1995) and the SIMPLEC algorithm handled the pressure-velocity coupling ensuring that the continuity equation is satisfied. The realizable k-ϵ turbulence model was chosen, as it is recommended by Blocken et al. (2003) and Blocken et al. (2004) in the application of pedestrian wind environment simulations, as it proved to perform substantially better than the standard k-ϵ model. Second-order discretization schemes were used for the spatial discretization, including the convective terms.
The iterative convergence criteria were that the scaled residuals should drop four orders of magnitude for k (turbulent kinetic energy), ϵ (turbulent kinetic energy dissipation rate), and each Cartesian component of U(velocity), as recommended for all flow variables by the BPGs. The convergence criterion for p (pressure) was relaxed to 5.0 × 10–4. This was done to speed up the simulations, as reaching a residual drop of four orders of magnitude required significantly longer simulation time. The relaxation of the convergence criterion did not impact the wind velocity magnitude at the pedestrian level in the built area investigated in this paper. These criteria were met for all simulations presented.
The simulations were conducted using the OpenFOAM (version 6) toolbox, which is an open-source CFD software package (Weller et al., 1998).
An overview of the boundary conditions (BCs) used is presented in Table 3. Combined inlet/outlet boundary conditions are used on the computational domain’s sides to allow for wind in any direction. The inlet profiles were set to form a homogeneous atmospheric boundary layer (ABL) with neutral stratified conditions and a logarithmic velocity profile, according to the BPGs. The wind speed at a reference height of 10 m, Uref10m, was set to 5 m s−1. Outlet conditions were used with constant pressure and zero gradient for the remaining variables. The direction of the flux automatically determines the inlet and outlet regions.
No-slip conditions with wall functions were used for both the terrain and the buildings layer. The logarithmic law for smooth walls was used for the buildings. A rough wall condition was applied for the terrain (Hargreaves and Wright, 2007). The roughness was set to z0 = 3.00 m to replicate the profiles used in the experiment. The slip condition was applied to the top boundaries.
The instantaneous regional wind conditions at any urban site continuously change with time. They include quantities such as wind velocity and direction, turbulence, humidity, and temperature, and how these parameters vary with height. The varying conditions result from changing external weather patterns, which depend on other factors such as time of day, season, atmospheric stability, formation of low- and high-pressure systems, and many more.
The pedestrian wind comfort maps are produced by combining wind simulations, local statistical meteorological data in the form of a wind rose, and a set of defined comfort criteria. There are numerous sets of wind comfort criteria, and in this study, a version of the Lawson wind comfort criteria (Lawson, 1978) is used, see Table 4. The Lawson criteria classify areas with “comfortable” activity types based on their associated accepted average wind speed intervals and exceedance frequency. The calculation of wind comfort criteria was also considered in Blocken and Carmeliet, (2004), Blocken et al. (2012) and Vita et al. (2020a). Note that only comfort is considered in this work, not pedestrian distress (Vita et al., 2020b).
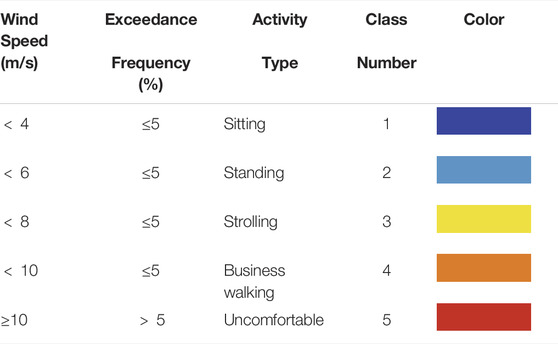
TABLE 4. Pedestrian wind comfort criteria used in the study, based on Lawson wind comfort criteria Lawson (1978).
The number of simulated wind directions used in the production of the pedestrian wind comfort maps in this study is:
1) 4, increments of 90°
2) 8, increments of 45°
3) 16, increments of 22.5°
4) 32, increments of 11.25°
5) 64, increments of 5.625°
Not all wind speeds are simulated. Instead, a representative wind field for each Lawson category is found by a linear scaling of the simulated wind velocity. The maximum value in each wind speed range is used as the scaling factor to be conservative. Linear scaling is justified as the wind is well within the turbulent flow regime for all the wind speed intervals under consideration, and hence similar flow distributions are expected.
The procedure of producing pedestrian wind comfort maps in this study is as follows. First, the wind is simulated from 64 evenly distributed horizontal wind directions. A set of 4, 8, 16, 32, or all 64 simulations of evenly distributed wind directions are used further.
Then, the pedestrian wind comfort is evaluated in all the computational cells using the algorithm outlined in Figure 3.
Since the Lawson criteria are based on exceedance probability, it needs to be determined how often the local wind velocity in each computational cell is above the given criteria. Since we assume equal probabilities for each wind direction and each wind class, the frequency for each wind class is
In general, this frequency would be obtained from the wind rose for the location. Next, we need to find the local velocity of the cell for each wind direction and wind class. We only have a single simulation for each wind direction. For each wind class, we calculate a representative local velocity in each cell for this wind class by doing a linear scaling the simulated wind velocity,
Here, Uref is the reference velocity at 10 m height for the simulated case. For Uclass, we use the upper bound of the class to be conservative. If this local velocity for the wind class exceeds any of the comfort criteria, we accumulate the frequency in this cell by Pclass. After all the wind directions and wind classes have been considered, we determine if the total accumulated frequency has been exceeded for each category in the Lawson criteria, and assign the appropriate comfort value to the cell.
The algorithm assigns a comfort class to all the cells within the computational domain. Finally, a pedestrian wind comfort map is produced by reading the comfort of the cells located 2 m above the terrain level and projecting its representing color onto the terrain patch below.
In this case study, the local wind statistics were arbitrarily chosen such that the wind was to always be 5 m s−1 at 10 m height and that the frequency of each wind sector was identical. In that way, the importance of each wind simulation is equally weighed in the pedestrian comfort maps.
The wind tunnel experiments were conducted at a 1/250 scale (Yoshie et al., 2007). A boundary layer with properties similar to an atmospheric boundary layer was generated in the wind tunnel upstream of the test section of dimensions 1.8 m length, 1.8 m width, and 1.8 m height. The vertical profile of the horizontal wind velocity was developed to follow a function with a power-law exponent of 0.25 when reaching the test section. Scalar wind velocities at 0.008 m above the wind tunnel floor (2 m above the ground surface in real scale) were measured by multi-point thermistor anemometers.
Figure 4 shows the normalized, simulated wind velocity magnitude at 2 m above ground, with the wind from N (0°). The colored dots are located in the same position as the 80 probes in the wind tunnel experiments, and their color represents the wind velocity magnitude difference, ΔUval, between the wind tunnel experiment and the simulation, where ΔUval is:
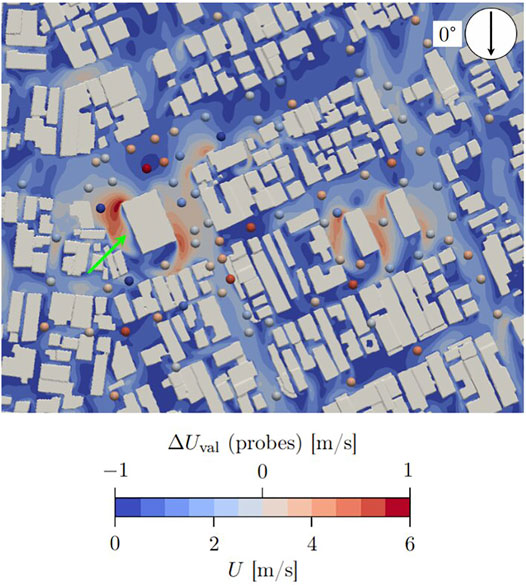
FIGURE 4. Normalized simulated wind speed at 2 m above ground with wind from N (0°). The colored dots represent the wind speed difference, ΔUval, between the wind tunnel experiment and the simulation at the 80 probes. The black arrow indicates the wind direction at the inlet, and the green arrow points to the high-rise building.
Blue-colored dots indicate that the wind velocity magnitude of the simulation is greater than in the wind tunnel experiments, and red-colored dots mean that the wind velocity magnitude of the simulation is lower than in the wind tunnel experiments. The experimental values compared against are averaged over time.
Figure 4 clearly shows the expected speed-up effect at the ground level near the side corners of the high-rise building relative to the overall wind direction. The similarly expected wake regions of low wind velocity magnitudes are seen leeward of the buildings.
When comparing the wind velocity magnitudes at the probes in the simulations to the results from the wind tunnel experiments from 16 wind directions, we see a slight trend that the simulations are overpredicting the effects of the buildings. More specifically, the simulated values in relatively high wind speed areas are generally too high compared to wind tunnel results. Likewise, the simulated values are too low compared to wind tunnel results in low wind speed regions. This trend is slightly noticeable in Figure 4, where red dots are somewhat located in blue low-velocity areas, and blue dots in red high-velocity areas. Note that the calculated differences, represented by the colored dots, are highly sensitive to the location of the probes as they are positioned within regions of high flow gradients.
Similar observations were made on the same benchmark case by Tominaga et al. (2005), Mochida and Lun, (2008), and Caniot et al. (2011). All three studies reported that the CFD simulations generally agree with the wind tunnel experiments, but that the simulations tended to underestimate the wind speed in the wake regions of buildings. Tominaga et al. (2005) note that the disagreement is also seen for other comparable benchmark tests and that it is partly related to differences in the definition of the average wind velocity magnitude in the two methods. While the wind tunnel tests register time averages of the instantaneous scalar velocity, the simulations use the velocity vector’s time averages (Tominaga et al., 2005). Mochida and Lun (2008) argue that it is related to the used turbulence models’ inability to reproduce the vortex shedding from tall buildings. Caniot et al. (2011) emphasize that the points of high relative difference are positioned near the edges of the wakes where high flow gradients occur, making the values highly location-sensitive.
Table 5 lists the average relative difference of wind velocity magnitude, and the Pearson correlation coefficient (PCC) between wind simulations and wind tunnel experiments for 16 wind directions at the 80 probes. The experimental values compared against the simulations are averaged over time. The table quantifies that the wind velocity magnitude of the simulations is overall lower at the ground level than in the wind tunnel experiments. For the 16 wind directions, the average relative difference of wind velocity magnitude is in the range from −1% to −35%, and the Pearson correlation coefficient is in the range 0.71–0.84.
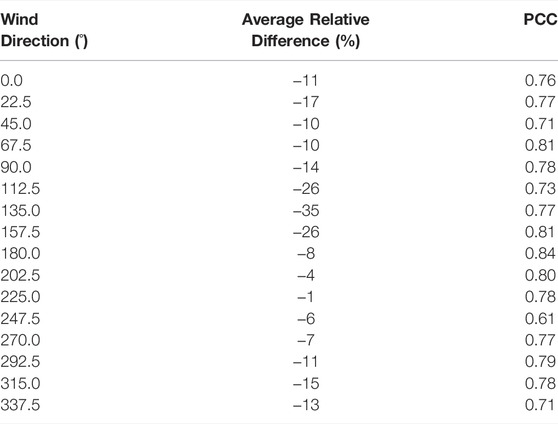
TABLE 5. The average relative difference of wind velocity magnitude, and the Pearson correlation coefficient (PCC), between wind simulations and wind tunnel experiments for 16 wind directions at the 80 probes.
The overprediction of the extent and significance of the wake regions of low wind velocity magnitudes, leeward of the buildings, agrees with other RANS simulations in the literature. Generally, it is because the transient nature of the flow is difficult to fully represent in time-averaged simulations, leading to less turbulent mixing in the simulations. It is also evident in Table 5 where the negative values of the average relative difference of wind velocity magnitude between wind simulations and wind tunnel experiments are because many of the probes are located within the wake regions in the simulations.
Figure 5 presents the wind velocity magnitude at 2 m above ground for 16 simulations representing wind from a 90° wide sector around the reference wind direction N (0°). Notice that there are generally always high wind speeds in the vicinity of any two of the corners in the high-rise building, and which of the corners is affected is highly dependent on the wind direction. For example, the high wind speed corners in the 349° simulation are the West and the North corners, but are the West and the East corners for the 0° simulation, where the wind direction is only shifted by 11°. Similar jumps of high wind velocity areas occur throughout all wind sectors.

FIGURE 5. Wind speed at 2 m above ground. The 16 included simulations represent wind from a 90° wide sector around the reference wind direction N (0°). The compared area is within 100 m in each horizontal direction of the high-rise building and does not include the building footprint area. The black arrow indicates the wind direction at the inlet.
The variance within the set is best viewed in Figure 6. It illustrates the wind velocity magnitude difference within the North sector, ΔUNsec, to reference wind direction simulation at 2 m above ground, where ΔUNsec is:
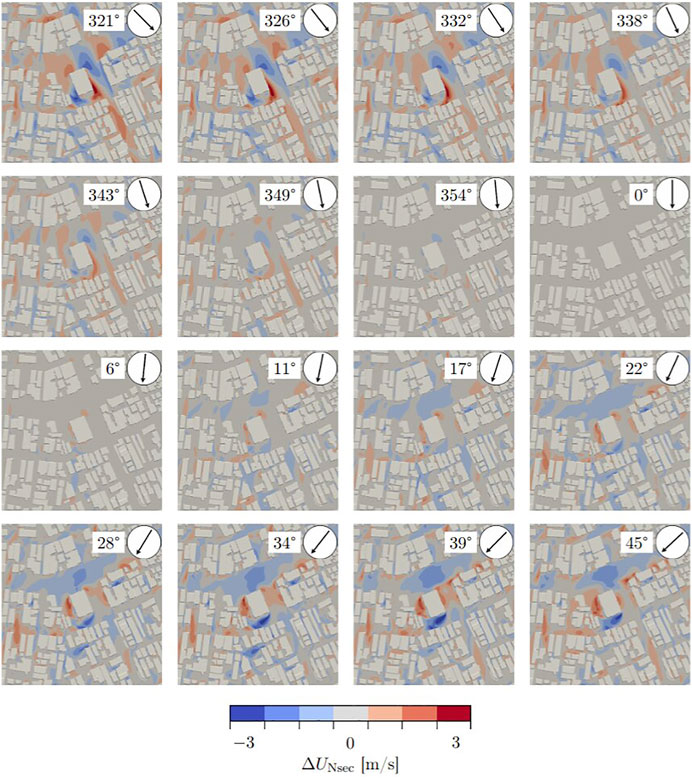
FIGURE 6. Wind speed difference, ΔUNsec, to reference wind direction simulation at 2 m above ground 100 m in each horizontal direction of the high-rise building. The 16 included simulations represent wind from a 90° wide sector around the reference wind direction N (0°). The black arrow indicates the wind direction at the inlet.
Negative values, represented by blue, correspond to areas where the reference case has a lower wind velocity magnitude than the compared case and vice versa. It is clear that the differences to the reference wind direction simulation grow with increasing wind direction shift from it, in terms of both magnitude and spatial extent. The differences are especially pronounced near the corners of the high-rise building. Notice that the difference is represented by alternating signs/colors going around the high-rise building. This alternation is related to the high sensitivity of the location of the “high wind speed corners,” seen in Figure 5. Quantification of the variances seen in Figure 6 is provided in Table 6.
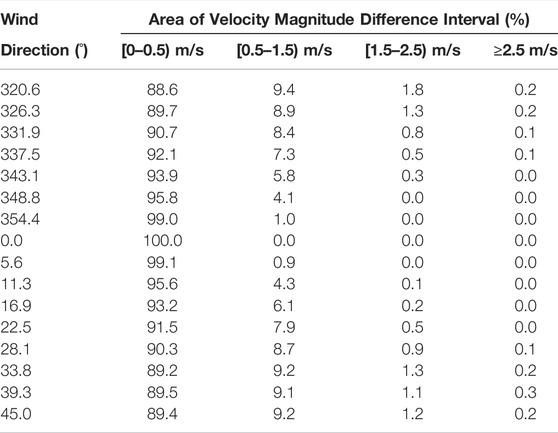
TABLE 6. Area of intervals of wind speed difference to reference wind direction simulation at 2 m above ground. The 16 included simulations represent wind from a 90° wide sector around the reference wind direction N (0°). The compared area is within 100 m in each horizontal direction of the high-rise building and does not include the building footprint area. This table quantifies the observations in Figure 6.
Each wind sector is equally spaced. The width of the sectors depends on the number of wind directions included in the production of the pedestrian wind comfort maps. Therefore, each wind simulation represents a 90° wide sector when 4 wind directions are used. Wind coming from the North sector ranging from 315° (NW) to 45° (NE) is represented by only one wind simulation of wind coming from 0° (N).
Table 6 shows that out of the 16 wind directions simulated in this sector, about a minimum of 88.6% of the area has an absolute value difference in wind velocity magnitude of less than 0.5 m s−1 in the wind simulation with the highest discrepancy to the reference wind simulation. The remaining 11.4% is the maximum area in the reference wind simulation that is more than 0.5 m s−1 off compared to one of the wind direction simulations it represents in the 90° wide sector.
Doubling the number of wind simulations used in the pedestrian wind comfort maps from 4 to 8 reduces the sector width each wind simulation represents to 45°. It reduces the area to 8.5%. Likewise, 16 wind directions further reduce the wind sector increments to 22.5° and the area to 4.4%; 32 wind directions give increments of 11.25° and an area of 1.0%.
Specially detailed information of the wind velocity magnitude distribution at pedestrian-level obtained from wind simulations is essential when producing the pedestrian wind comfort maps. The number of simulated wind directions decides the equally spaced wind sector increments each wind simulation represents. Fewer wind directions causing larger increments are naturally associated with higher variance in wind velocity distribution within this wind sector. This relation is evident in Figures 5, 6 and Table 6.
Figure 7 shows the pedestrian wind comfort maps at 2 m above ground produced using either 4, 8, 16, 32, or 64 evenly distributed horizontal wind directions. Only a section of the computational domain, 100 m in each horizontal direction of the high-rise building is presented.
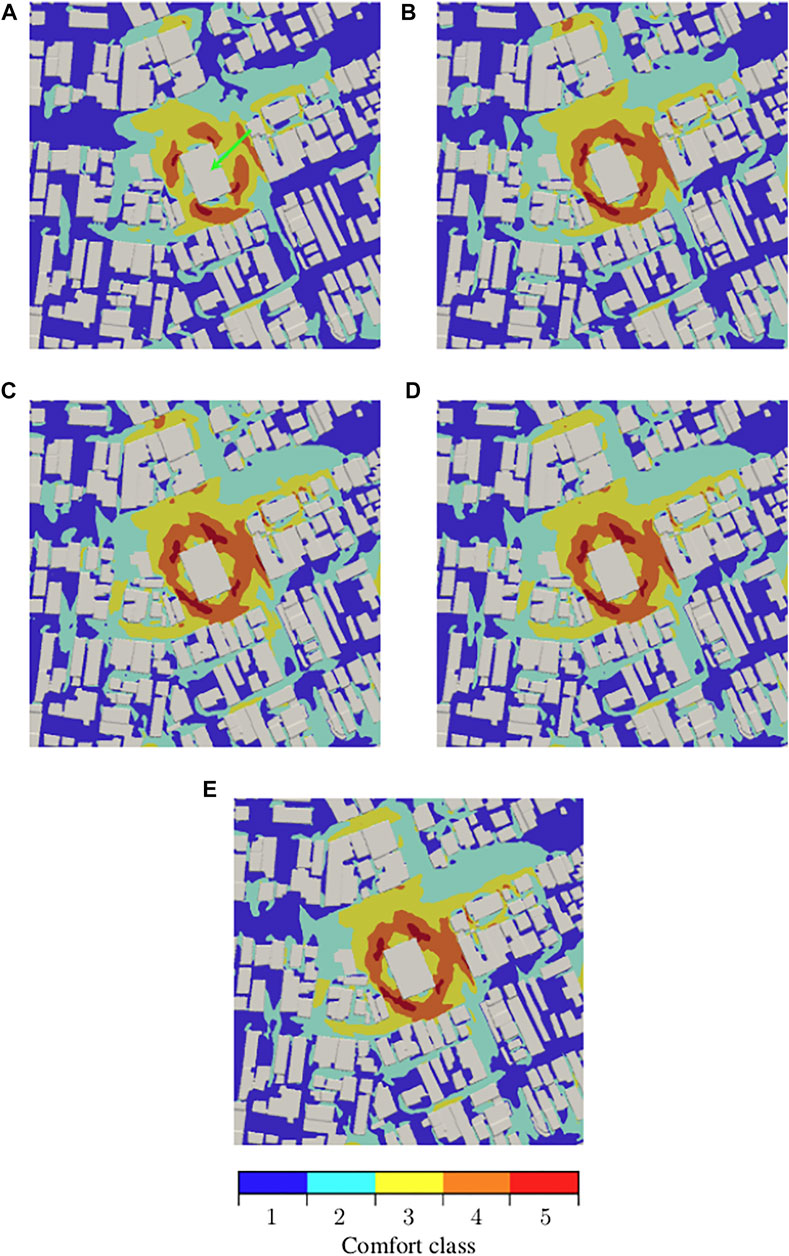
FIGURE 7. Pedestrian wind comfort maps at 2 m above ground 100 m in each horizontal direction of the high-rise building indicated by the green arrow. Generated using (A) 4 (B) 8 (C) 16 (D) 32, and (E) 64 wind directions.
Ground areas in the vicinity of the high-rise building, especially near the corners, are classified with the worst (“uncomfortable”) or the second-worst (“business walking”) wind comfort classification in all the maps. In these areas, the frequent strong wind is caused by a wind pull-down effect often seen near high buildings, particularly ones with sharp corners. The wind is considerably weaker at the ground level close to the other lower buildings. The areas with frequent high wind are more evenly distributed around the high-rise building, as more wind directions are included in the production of the maps, especially compared to the map produced with wind simulations from only 4 wind directions.
The differences in the pedestrian wind comfort maps are best viewed in Figure 8. The figure gives the classification difference to the reference case, ΔC, where:
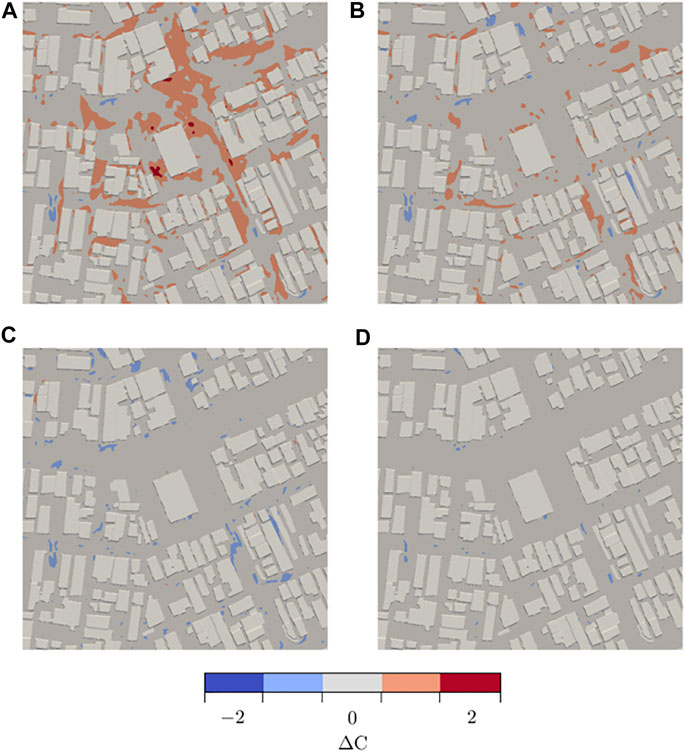
FIGURE 8. Wind comfort classification difference, ΔC, to the map using all 64 wind directions at 2 m above ground 100 m in each horizontal direction of the high-rise building. Compared against using (A) 4 (B) 8 (C) 16, and (D) 32 wind directions.
Ci is the pedestrian wind comfort class of a given location using 64 wind directions. Cj is the classification at the same location using a different number of wind directions. The map produced from the most wind directions, here 64, is likely the most accurate and is used as the reference case.
Negative values, represented by blue, correspond to areas where the reference case has a lower classification number, meaning an improved wind comfort class, than the compared case and vice versa. Notice that there is a relatively large total area in red in Figure 8A. The reference case has a higher classification number in these red areas, meaning a worse wind comfort class, than the case using only 4 wind directions.
Quantification of the differences is provided in Table 7. It shows the percentage of area classified differently compared to maps using all the 64 simulated wind directions. The total area classified differently from the reference map clearly reduces in size as more wind directions are included; 79% of the area within 100 m in each horizontal direction of the high-rise building is classified with the same pedestrian wind comfort class as the map produced using 64 wind directions. This number increases to 92% using 8 wind directions, 96% using 16 wind directions, and finally 99% using 32 wind directions. Similar values were observed when including the whole building area of radius 200 m.
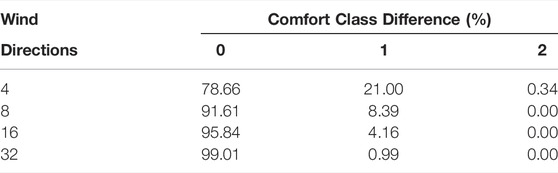
TABLE 7. Area of comfort classification difference, ΔC, to the map using all 64 wind directions at 2 m above ground. The compared area is within 100 m in each horizontal direction of the high-rise building and does not include the building footprint area. This table provides numbers for the areas seen in Figure 8.
This article presents an investigation on the influence of the number of simulated wind directions on pedestrian wind comfort maps. A neighborhood in Niigata city, Japan, was chosen as a case study, as it is a benchmark case with available data for geometry and wind tunnel experiments. The main findings of the analysis include the following:
1) A generally good agreement with experimental results was reported with a reasonable variance for such a complex geometry when validating the simulation setup. There is a trend that the simulations do not introduce enough mixing, causing the simulated velocity in high speed areas to be higher than the measured values, and vice versa in the low wind speed regions. This trend is believed to be due to the RANS modeling not being able to capture the mixing caused by large transient fluctuations caused by the building geometries. This is also suggested in other studies of the same region (Tominaga et al., 2005; Mochida and Lun, 2008; Caniot et al., 2011).
2) The pedestrian wind comfort maps are converging toward a final map as more wind directions are included. Doubling the number of wind directions from 4 to 8 changes the maps significantly, but only a slight variation is observed when doubling the wind direction count from 32 to 64.
The pedestrian comfort criteria used in this work only consider the mean wind speed. Other criteria exist, for instance, using turbulent kinetic energy or gust factors (Vita et al., 2020b). While the results current study give some insight that could be relevant also for other criteria, this could be investigated in more detail.
Transient simulations will likely provide more accurate predictions of the size of the wake regions. This possibility of improved predictions is related to the fact that steady RANS simulations are time-averaged and cannot capture the wind’s dynamic and instantaneous behavior, which LES (large eddy simulation) methods attempt. The superior accuracy of wake predictions of transient simulations over steady simulations is evident in Mochida and Lun, (2008). The study examined and compared data sets of simulation results from nine groups, all simulating wind on a single tall building of geometry 2:1:1 (height, width, length).
Other past studies on pedestrian level wind conditions have proved RANS′ ability to accurately predict the mean wind speed in high wind speed regions when following BPGs, while the performance in low wind speed regions can be poor (Yoshie et al., 2007; Blocken and Carmeliet, 2008; Blocken et al., 2008; Blocken and Stathopoulos, 2016; Blocken, 2018). Blocken and Stathopoulos, (2016) argue that the poor prediction within these low-velocity regions does not compromise the accuracy of the pedestrian wind comfort assessment. The statement can be supported by studying the overall procedure of calculating pedestrian comfort, see Figure 3. The cell is assigned the same velocity class within the whole velocity class range from 0 m s−1 to 4 m s−1. It, therefore, contributes equally to the low-velocity regions of the pedestrian comfort map. Despite LES’s superior accuracy over RANS simulations, RANS is often the practical choice for many applications of urban wind simulations due to the known drawback of LES compared to RANS. These drawbacks include substantially higher computational costs, and that highly resolved experimental data are required to provide the input conditions, which are often not available. Blocken and Stathopoulos, (2016) and Blocken, (2018) argue the continued use of the RANS approach for the pedestrian-level wind studies.
It is reasonable to assume that adding the simulation of more inlet wind directions increases the accuracy of the produced pedestrian wind comfort maps. Increasing the number of wind directions included in the pedestrian wind comfort maps will lead to less pronounced changes, eventually causing the maps to converge to a satisfactory level of accuracy. The number of wind directions needed to reach this point is likely site-dependent on various factors that need further study.
At the same time, more wind directions require more computational costs. Therefore, evaluating the cost-benefit is necessary when deciding the number of wind directions to simulate in a specific case. In this decision process, a clear understanding of the required level of accuracy and the expected accuracy associated with the number of wind directions included for the specific case are essential. Table 7 is the most important result to study in this process. The present results indicate that simulation of 8 wind directions is insufficient to give a sufficiently converged pedestrian comfort map. Using more than 32 wind directions also appears excessive, as the changes in the pedestrian comfort map with more simulated wind directions are too small to influence a decision-making process for building permit purposes.
Future work includes studying the effect of the following:
1) Level of urbanization, meaning the urban area’s geometrical complexity going from rural to hyper-urban.
2) The complexity of the terrain.
3) The local meteorological conditions and their variations with the seasons.
4) Atmospheric thermal stability.
5) Inlet profiles, conventional idealized profiles without wind veer, or fully developed profiles with wind veer. Including wind veer, or “twisted wind profiles,” gave superior results in an Air Ventilation Assessment (Weerasuriya et al., 2018), and will likely affect pedestrian comfort as well.
A greater understanding of the influence of the number of simulated wind directions included and the corresponding factors may enable more efficient pedestrian wind comfort studies that account for potential uncertainties.
The raw data supporting the conclusions of this article will be made available by the authors without undue reservation.
T-OH and KG both employees at the Department of Mechanical and Structural Engineering and Materials Science at the University of Stavanger. Conceptualization: T-OH and KG. Data curation: T-OH and KG. Formal analysis: T-OH and KG. Funding acquisition: Not needed. Investigation: T-OH and KG. Methodology: T-OH and KG. Project administration: T-OH. Resources: T-OH and KG. Software: T-OH and KG. Supervision: KG. Validation: T-OH and KG. Visualization: T-OH. Writing—original draft: T-OH. Writing—review editing: T-OH and KG.
Both authors are employees at the University of Stavanger, which provides salary and covers the expenses of the computational power required to conduct this research. Additionally, this research is part of the Future Energy Hub Project funded by The Norwegian Research Council (project no.: 280458), The University of Stavanger, and local industry partners.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Architectural Institute of Japan (2021). Guidebook for Cfd Predictions of Urban Wind Environment. Available at: https://www.aij.or.jp/jpn/publish/cfdguide/index_e.htm (accessed May, 2021).
Blocken, B. (2014). 50 Years of Computational Wind Engineering: Past, Present and Future. J. Wind Eng. Industrial Aerodynamics 129, 69–102. doi:10.1016/j.jweia.2014.03.008
Blocken, B., and Carmeliet, J. (2004). Pedestrian Wind Environment Around Buildings: Literature Review and Practical Examples. J. Therm. Envelope Build. Sci. 28, 107–159. doi:10.1177/1097196304044396
Blocken, B., and Carmeliet, J. (2008). Pedestrian Wind Conditions at Outdoor Platforms in a High-Rise Apartment Building: Generic Sub-configuration Validation, Wind Comfort Assessment and Uncertainty Issues. Wind Struct. 11, 51–70. doi:10.12989/was.2008.11.1.051
Blocken, B., Janssen, W. D., and van Hooff, T. (2012). Cfd Simulation for Pedestrian Wind Comfort and Wind Safety in Urban Areas: General Decision Framework and Case Study for the Eindhoven University Campus. Environ. Model. Softw. 30, 15–34. doi:10.1016/j.envsoft.2011.11.009
Blocken, B. (2018). Les over Rans in Building Simulation for Outdoor and Indoor Applications: A Foregone Conclusion? Build. Simul. 11, 821–870. doi:10.1007/s12273-018-0459-3
Blocken, B., Moonen, P., Stathopoulos, T., and Carmeliet, J. (2008). Numerical Study on the Existence of the Venturi Effect in Passages Between Perpendicular Buildings. J. Eng. Mech. 134, 1021–1028. doi:10.1061/(asce)0733-9399(2008)134:12(1021)
Blocken, B., and Persoon, J. (2009). Pedestrian Wind Comfort Around a Large Football Stadium in an Urban Environment: Cfd Simulation, Validation and Application of the New Dutch Wind Nuisance Standard. J. Wind Eng. Industrial Aerodynamics 97, 255–270. doi:10.1016/j.jweia.2009.06.007
Blocken, B., Roels, S., and Carmeliet, J. (2004). Modification of Pedestrian Wind Comfort in the Silvertop Tower Passages by an Automatic Control System. J. Wind Eng. Industrial Aerodynamics 92, 849–873. doi:10.1016/j.jweia.2004.04.004
Blocken, B., Roels, S., and Carmeliet, J. (2003). Pedestrian Wind Conditions in Passages through Buildings-Part 1. Numerical Modeling, Sensitivity Analysis and Experimental Verification. Tech. rep., Research Report, Laboratory of Building Physics. Belgium: Catholic University of Leuven.
Blocken, B., and Stathopoulos, J. P. A. J. (2016). Pedestrian-level Wind Conditions Around Buildings: Review of Wind-Tunnel and CFD Techniques and Their Accuracy for Wind Comfort Assessment. Build. Environ. 100, 50–81. doi:10.1016/j.buildenv.2016.02.004
Blocken, B., Stathopoulos, T., and Carmeliet, J. (2007). Cfd Simulation of the Atmospheric Boundary Layer: Wall Function Problems. Atmos. Environ. 41, 238–252. doi:10.1016/j.atmosenv.2006.08.019
Caniot, G., Li, W., and Dupont, G. (2011). “Validations and Applications of a Cfd Tool Dedicated to Wind Assessment in Urban Areas,” in 13th International Conference on Wind Engineering.
Cheynet, E., Jakobsen, J. B., and Snæbjörnsson, J. (2019). Flow Distortion Recorded by Sonic Anemometers on a Long-Span Bridge: towards a Better Modelling of the Dynamic Wind Load in Full-Scale. J. Sound Vib. 450, 214–230. doi:10.1016/j.jsv.2019.03.013
City of London Corporation (2019). Wind Microclimate Guidelines for Developments in the City of London. Available at: https://www.cityoflondon.gov.uk/assets/Services-Environment/wind-microclimate-guidelines.pdf (accessed January, 2022).
Dhunny, A. Z., Samkhaniani, N., Lollchund, M. R., and Rughooputh, S. D. D. V. (2018). Investigation of Multi-Level Wind Flow Characteristics and Pedestrian Comfort in a Tropical City. Urban Clim. 24, 185–204. doi:10.1016/j.uclim.2018.03.002
Franke, J., Hellsten, A., Schlünzen, H., and Carissimo, B. (2007). Cost Action 732-best Practice Guideline for the CFD Simulation of Flows in the Urban Environment. Brussels, COST: Cambridge Environmental Research Consultants.
Franke, J., Mochida, A., Tominaga, Y., and Yoshie, R. (2006). “TA4 CFD Guideline for Pedestrain Wind Environment (Organized Session), Wind Engineers, JAWE,” in 2006 The fourth international symposium on computational wind engineering (Yokohama: JapanCiteseer), 529–536. doi:10.5359/jawe.2006.529
Hågbo, T.-O., Giljarhus, K. E. T., and Hjertager, B. H. (2021). Influence of Geometry Acquisition Method on Pedestrian Wind Simulations. J. Wind Eng. Industrial Aerodynamics 215, 104665. doi:10.1016/j.jweia.2021.104665
Hågbo, T.-O., Giljarhus, K. E. T., Qu, S., and Hjertager, B. H. (2019). The Performance of Structured and Unstructured Grids on Wind Simulations Around a High-Rise Building. IOP Conf. Ser. Mater. Sci. Eng. 700, 012001. doi:10.1088/1757-899x/700/1/012001
Hargreaves, D. M., and Wright, N. G. (2007). On the Use of the K- Model in Commercial CFD Software to Model the Neutral Atmospheric Boundary Layer. J. Wind Eng. Industrial Aerodynamics 95, 355–369. doi:10.1016/j.jweia.2006.08.002
Huang, S., Li, Q. S., and Xu, S. (2007). Numerical Evaluation of Wind Effects on a Tall Steel Building by CFD. J. Constr. Steel Res. 63, 612–627. doi:10.1016/j.jcsr.2006.06.033
Janssen, W. D., Blocken, B., and van Hooff, T. (2013). Pedestrian Wind Comfort Around Buildings: Comparison of Wind Comfort Criteria Based on Whole-Flow Field Data for a Complex Case Study. Build. Environ. 59, 547–562. doi:10.1016/j.buildenv.2012.10.012
Kastner, P., and Dogan, T. (2020). A Cylindrical Meshing Methodology for Annual Urban Computational Fluid Dynamics Simulations. J. Build. Perform. Simul. 13, 59–68. doi:10.1080/19401493.2019.1692906
Lawson, T. V. (1978). The Widn Content of the Built Environment. J. Wind Eng. Industrial Aerodynamics 3, 93–105. doi:10.1016/0167-6105(78)90002-8
Leeds City Council (2021). Draft Wind Micro-climate Toolkit for Leeds. Available at: https://www.leeds.gov.uk/docs/Draft%20wind%20and%20microclimate%20toolkit.pdf (accessed January, 2022).
Mochida, A., and Lun, I. Y. F. (2008). Prediction of Wind Environment and Thermal Comfort at Pedestrian Level in Urban Area. J. wind Eng. industrial aerodynamics 96, 1498–1527. doi:10.1016/j.jweia.2008.02.033
Montazeri, H., and Blocken, B. (2013). CFD Simulation of Wind-Induced Pressure Coefficients on Buildings with and without Balconies: Validation and Sensitivity Analysis. Build. Environ. 60, 137–149. doi:10.1016/j.buildenv.2012.11.012
National Academies of Sciences, Engineering, and Medicine and others (2016). Attribution of Extreme Weather Events in the Context of Climate Change. Washington, D.C: National Academies Press.
Shih, T.-H., Liou, W. W., Shabbir, A., Yang, Z., and Zhu, J. (1995). A New K-ϵ Eddy Viscosity Model for High Reynolds Number Turbulent Flows. Comput. Fluids 24, 227–238. doi:10.1016/0045-7930(94)00032-t
Tamura, T., Nozawa, K., and Kondo, K. (2008). Aij Guide for Numerical Prediction of Wind Loads on Buildings. J. Wind Eng. Industrial Aerodynamics 96, 1974, 1984. doi:10.1016/j.jweia.2008.02.020
Thordal, M. S., Bennetsen, J. C., and Koss, H. H. H. (2019). Review for Practical Application of CFD for the Determination of Wind Load on High-Rise Buildings. J. Wind Eng. Industrial Aerodynamics 186, 155–168. doi:10.1016/j.jweia.2018.12.019
Tominaga, Y., Mochida, A., Yoshie, R., Kataoka, H., Nozu, T., Yoshikawa, M., et al. (2008). Aij Guidelines for Practical Applications of CFD to Pedestrian Wind Environment Around Buildings. J. Wind Eng. Industrial Aerodynamics 96, 1749–1761. doi:10.1016/j.jweia.2008.02.058
Tominaga, Y. (2012). Visualization of City Breathability Based on Cfd Technique: Case Study for Urban Blocks in Niigata City. J. Vis. 15, 269–276. doi:10.1007/s12650-012-0128-z
Tominaga, Y., Yoshie, R., Mochida, A., Kataoka, H., Harimoto, K., and Nozu, T. (2005). Cross Comparisons of Cfd Prediction for Wind Environment at Pedestrian Level Around Buildings. Part 2, 2661–2670.
van Hooff, T., and Blocken, B. (2010a). Coupled Urban Wind Flow and Indoor Natural Ventilation Modelling on a High-Resolution Grid: A Case Study for the Amsterdam Arena Stadium. Environ. Model. Softw. 25, 51–65. doi:10.1016/j.envsoft.2009.07.008
van Hooff, T., and Blocken, B. (2010b). On the Effect of Wind Direction and Urban Surroundings on Natural Ventilation of a Large Semi-enclosed Stadium. Comput. Fluids 39, 1146–1155. doi:10.1016/j.compfluid.2010.02.004
van Hooff, T., Blocken, B., and van Harten, M. (2011). 3d Cfd Simulations of Wind Flow and Wind-Driven Rain Shelter in Sports Stadia: Influence of Stadium Geometry. Build. Environ. 46, 22–37. doi:10.1016/j.buildenv.2010.06.013
Vita, G., Shu, Z., Jesson, M., Quinn, A., Hemida, H., Sterling, M., et al. (2020a). On the Assessment of Pedestrian Distress in Urban Winds. J. Wind Eng. Industrial Aerodynamics 203, 104200. doi:10.1016/j.jweia.2020.104200
Vita, G., Shu, Z., Jesson, M., Quinn, A., Hemida, H., Sterling, M., et al. (2020b). On the Assessment of Pedestrian Distress in Urban Winds. J. Wind Eng. Industrial Aerodynamics 203, 104200. doi:10.1016/j.jweia.2020.104200
Weerasuriya, A. U., Tse, K. T., Zhang, X., and Kwok, K. C. S. (2018). Integrating Twisted Wind Profiles to Air Ventilation Assessment (Ava): The Current Status. Build. Environ. 135, 297–307. doi:10.1016/j.buildenv.2018.03.024
Weller, H. G., Tabor, G., Jasak, H., and Fureby, C. (1998). A Tensorial Approach to Computational Continuum Mechanics Using Object-Oriented Techniques. Comput. Phys. 12, 620–631. doi:10.1063/1.168744
Wisse, J., Krüs, H., and Willemsen, E. (2002). Wind Comfort Assessment by Cfd - Context and Requirements. Nantes, France: Centre Scientifique et Technique du Batiment, 154–163.
Keywords: CFD, RANS, realizable k-ε turbulence model, urban wind, pedestrian comfort, wind environment assessment, wind directions
Citation: Hågbo T-O and Giljarhus KET (2022) Pedestrian Wind Comfort Assessment Using Computational Fluid Dynamics Simulations With Varying Number of Wind Directions. Front. Built Environ. 8:858067. doi: 10.3389/fbuil.2022.858067
Received: 19 January 2022; Accepted: 26 May 2022;
Published: 05 July 2022.
Edited by:
Catherine Gorle, Stanford University, United StatesReviewed by:
Hassan Hemida, University of Birmingham, United KingdomCopyright © 2022 Hågbo and Giljarhus. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Trond-Ola Hågbo, dHJvbmQtb2xhLmhhZ2JvQHVpcy5ubw==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.