Applications of Machine Learning to Wind Engineering

Advances of the analytical, numerical, experimental and field-measurement approaches in wind engineering offers unprecedented volume of data that, together with rapidly evolving learning algorithms and high-performance computational hardware, provide an opportunity for the community to embrace and harness full potential of machine learning (ML). This contribution examines the state of research and practice of ML for its applications to wind engineering. In addition to ML applications to wind climate, terrain/topography, aerodynamics/aeroelasticity and structural dynamics (following traditional Alan G. Davenport Wind Loading Chain), the review also extends to cover wind damage assessment and wind-related hazard mitigation and response (considering emerging performance-based and resilience-based wind design methodologies). This state-of-the-art review suggests to what extend ML has been utilized in each of these topic areas within wind engineering and provides a comprehensive summary to improve understanding how learning algorithms work and when these schemes succeed or fail. Moreover, critical challenges and prospects of ML applications in wind engineering are identified to facilitate future research efforts.

1 Introduction

Wind engineering is an interdisciplinary field to provide rational treatment of interaction between the atmospheric boundary-layer winds and human activities (Cermak 1975). There is a long and significant history for machine learning (ML) applications in several subfields involved in wind engineering, such as fluid mechanics (Brunton et al., 2020), meteorology (Chen et al., 2020) and mechanics of structures (Salehi and Burgueño 2018). The application of statistical learning to turbulence modeling in early 1940s (Kolmogorov 1941) and perceptron learning to structural design in late 1980s (Adeli and Yeh 1989) are representative examples. On the other hand, it seems similar passions have not been shared by researchers in the wind engineering community. Actually, ML-based wind engineering is still in its infancy stage and the full-capacity of ML has not been leveraged yet. However, the exceptional performance of ML to extract hidden informative features from data shows great promise for addressing unresolved complexities and issues originated from first principles investigations in the field of wind engineering. In addition, recent advances in performance-/resilience-based wind engineering have placed new demands on wind characterization, aerodynamics modeling and structural analysis that need powerful simulation tools such as ML to overcome the emerging challenges by simultaneously achieving high computational efficiency and accuracy. It is reasonable to expect the revitalization of ML within the wind engineering field that is fueled by 1) rapidly evolving learning algorithms and high-performance computational hardware, 2) unprecedented volume of data generated with improved wind engineering techniques and methodologies, and 3) urgent needs for more accurate and efficient learning and modeling of complex phenomena in wind-related problems.

As a key subfield of artificial intelligence (AI) [that together with natural intelligence plays a role of the computational part of the ability to achieve goals in the world (McCarthy 2007)], ML develops learning algorithms that use inputs from a sample generator and observations from a system to generate an approximation of its outputs (Cherkassky and Mulier 2007). The evolution of learning algorithms started when McCulloch and Pitts (1943) invented the first mathematical model of a neural network. In 1952, Arthur Samuel from IBM introduced the first self-learning computer program to play the game of checkers (Wiederhold et al., 1990). Then, Rosenblatt (1957) designed the first neural network for computers (the perceptron) that set the foundation of deep neural networks (DNNs). Kelley (1960) presented the method of gradients (or method of steepest descent) in his analytical development of flight performance optimization, which was used to develop the basics of a continuous backpropagation model for training feedforward neural networks (Rumelhart et al., 1986). On the other hand, Hopfield (1982) created a feedback neural network that was considered as the first recurrent neural network (RNN). LeCun et al. (1989) combined convolutional neural network (CNN) and backpropagation algorithm to recognize handwritten digits. Watkins (1989) introduced the concept of Q-learning based on Markov process to significantly enhance the practicability and feasibility of reinforcement learning. Later, Cortes and Vapnik (1995) designed a support-vector network considered as a new learning machine for two-group classification problems with high generalization ability. Hochreiter and Schmidhuber (1997) introduced a long short-term memory cell to address the long-term dependency issue in RNN. To overcome the learning difficulty in DNNs, Hinton et al. (2006) derived a fast, greedy algorithm that can learn deep, directed belief networks one layer at a time and hence facilitate the rapid development of deep learning. Recently, Goodfellow et al. (2014) proposed a generative adversarial network consisting of two models (i.e., generative and discriminative models) that compete with each other in a zero-sum game. The sophisticated ML algorithm needs the help of advanced computational hardware [e.g., graphics processing unit (GPU) and tensor processing unit (TPU)] to unlock its full potential (Berggren et al., 2020). For example, the great success of AlexNet (a deep CNN on GPU) is essentially attributed to its ability to leverage GPU for training (Krizhevsky et al., 2012).

Equipped with both sophisticated algorithms and advanced computational hardware, the learning machine (LM) is driven by data. Both the quantity (data rich and comprehensive) and quality of the training/testing data are important to ensure good performance of ML applications. Wind engineering by nature is a data-rich field (e.g., high spatial and temporal resolution), and it is rapidly becoming a data-comprehensive domain due to recent advances of analytical, numerical, experimental and field-measurement methods (Kareem and Wu 2013; Hangan et al., 2017). The data of spatiotemporally varying wind flows are extended from synoptic events measured by airport wind observation system with traditional anemometers to non-synoptic events measured by several field campaigns with advanced doppler radars and Lidars (Light Detection and Ranging) [e.g., Verification of the Origins of Rotation in Tornadoes Experiment (VORTEX) and Radar Observations of Tornadoes and Thunderstorms Experiment (ROTATE) campaigns for tornado events and Severe Convective OUtflow in Thunderstorms (SCOUT) and Wind Ports and Sea (WPS) campaigns for thunderstorm downburst events]. Massive wind data over complex terrain/topography are collected by continuous-wave short-range WindScanner systems (e.g., Berg et al., 2013). The low Reynolds-number, straight-line-wind, stationary aerodynamics data generated in conventional boundary-layer wind tunnels are extended to 1) high-Reynolds-number aerodynamics data resulting from recently built large-scale facilities [e.g., windstorm simulation facility at Insurance Institute for Business and Home Safety (IBHS), Wall of Wind (WOW) at Florida International University and Wind Engineering Energy and Environment (WindEEE) at Western University], 2) vortex-flow aerodynamics data produced by tornado simulators (e.g., tornado-like vortex simulator at Iowa State University and VorTECH at Texas Tech University), and 3) transient aerodynamics data generated in emerging actively controlled wind tunnels (e.g., individually-controlled multi-fan wind tunnels at Tongji University, University at Buffalo and University of Florida). Also, significant nonlinear and inelastic structural dynamics data under strong winds are being created in laboratories due to advances in performance-based wind design methodology (Abdullah et al., 2020). In addition to the experimental and field-measurement approaches the comprehensive data are further enriched by high-fidelity large-scale simulation tools that are advanced by theoretical developments in wind engineering field (Blocken 2014; Kareem 2020), such as computational fluid dynamics/computational structural dynamics (CFS/CSI)-based hybrid modeling of transient structural response (Hao and Wu 2018) and statistics-based synthesis of nonstationary wind field (Wang and Wu 2021). The Computational Modeling and Simulation Center (SimCenter) of the Natural Hazards Engineering Research Infrastructure (NHERI) program provides an effective way to integrate various simulation tools (Deierlein and Zsarnóczay 2021). Furthermore, novel real-time aerodynamics hybrid simulation techniques are emerging to effectively generate nonlinear and full-scale data in wind engineering by seamlessly stitching the numerical modeling in computer and physical testing in wind tunnel (Wu et al., 2019; Wu and Song 2019). Data quality is essential to facilitate curation and reuse of the diverse and large datasets generated in the field of wind engineering. There are numerous methods and criteria specified by various wind engineering research groups/centers to ensure the high data quality, and the NHERI DesignSafe cyberinfrastructure platform recently suggested the best practices for detailed data quality assessment in terms of metadata quality, data content quality, data completeness and representation and data publications review (Rathje et al., 2017).

The improved understanding concerning the complex nature of wind fields (e.g., nonstationary and non-Gaussian features), the associated structural aerodynamics/aeroelasticity (e.g., transient and nonlinear features) and the resulting load effects (e.g., nonlinear and inelastic structural response), as well as the necessary shift from a prescriptive design approach to performance-based design methodology and further to resilience-based design philosophy (i.e., improving the rapidity, robustness, resourcefulness and redundancy), poses new challenges in wind engineering field. Hence, there is an urgent need of more accurate and efficient learning and modeling tools for effective solutions. The conventional stationary and linear analysis framework for wind-structure interactions established by Robert H. Scanlan (1914–2001) and Alan G. Davenport (1932–2009) has been very successful due to its simplicity and applicability, however, its shortcomings have begun to surface since the underlying complexities associated with many wind engineering problems clearly show a departure from implicit assumptions of stationarity, Gaussianity and linear features. A number of semi-empirical nonlinear reduced-order models have been developed in this context and improvement in their efficiency and robustness is a topic of cutting-edge research in the wind engineering community (Wu 2013). Unfortunately, these reduced-order models do not always have a satisfactory representation of the full nonlinear equations which govern the complex phenomena in wind-related problems. An alternate way is to utilize the CFD techniques, however, their computational effort is too high considering the three-dimensional nature of winds and associated bluff-body aerodynamics. While CFD plays a significant role in generating high-fidelity data of complex wind-structure interactions, its high computational cost makes it not easy to be used either in an informational mode to enhance wind hazard-related planning and development activities (e.g., risk mitigation that needs to quickly run thousands of scenarios at minimal computational expense) or in an operational mode to support emergency management and response associated with a wind hazard (e.g., decision making that needs real-time prediction capability under an uncertain environment). To address the emerging challenges, data-driven machine learning offers a promising approach that is capable of processing big data in wind engineering field as well as modeling associated complex phenomena with high computational efficiency and simulation accuracy.

With the rapid development of ML applications in wind engineering due to the confluence of advanced learning algorithms, high-performance computational hardware and big data, it is believed that a systematic review on this subject is important to suggest to what extend ML has been utilized in each of the topic areas within wind engineering and provide a comprehensive summary to improve understanding how learning algorithms work and when these schemes succeed or fail. Specifically, a total of 65 ML algorithms (Appendix A) are identified for their applications in the five topic areas of wind climate, terrain/topography, aerodynamics/aeroelasticity, structural dynamics and damage assessment, and mitigation and response. This review first presents technical background of typical ML approaches in terms of supervised learning, unsupervised learning, semi-supervised learning and reinforcement learning (RL), followed by the state of research and practice of ML applications to each topic area within wind engineering field, and concluded with critical research gaps and future prospects. While ML can augment the analytical approaches [e.g., data-driven discovery of closure models (Raissi et al., 2019)], numerical schemes [e.g., data-driven turbulence modeling (Duraisamy et al., 2019)], experimental tests [e.g., data-driven active control of transient wind simulation (Li et al., 2021a)] and field measurements [e.g., data-driven sparse sensor placement (Manohar et al., 2018)] in wind engineering, the review only focuses on its role to complement existing methodologies and hence potentially extend/transform current lines of wind engineering research and practice.

2 Background of Machine Learning

Machine learning (ML) is a subclass of artificial intelligence (AI) that extracts the underlying pattern within a set of data (e.g., Murphy 2012; Goodfellow et al., 2016; Mohri et al., 2018). To acquire the hidden pattern and knowledge of a problem, the learning process involves in general five important steps, namely data collection, data preparation, training, evaluation and parameters tuning. Once the learning machine is trained based on the available data (usually retrieved from analytical solutions, numerical simulations, experimental tests or full-scale measurements), it can predict future or unseen events. Based on the data fed into the learning machine, ML algorithms can be classified into four categories, namely supervised learning, unsupervised learning, semi-supervised learning and reinforcement learning (Figure 1).

FIGURE 1

FIGURE 1. Machine learning categories.

To train the algorithm, the supervised learning fully depends on labeled data, the unsupervised learning relies purely on unlabeled data and the semi-supervised learning combines limited labeled data with a large amount of unlabeled data. For reinforcement learning (RL), there is essentially no predefined data. Although RL is occasionally treated as semi-supervised learning considering the agent learns from its own experiences in terms of infrequent and partial rewards, it is classified here into separate category to highlight there is no explicit, external supervisory information provided to the learning agent. It is noted the kriging and polynomial chaos expansions as two widely-used, data-driven statistical interpolation approaches are not reviewed in this study.

2.1 Supervised Learning

Supervised learning models are a set of algorithms that learn the mapping, from given labeled training data, between known inputs and outputs. The trainable parameters of these models are determined based on the minimization of the loss function. Supervised learning models usually require a large amount of reliable and unbiased data for training which might not be always available. These algorithms can be employed for two important tasks, namely regression and classification.

2.1.1 Regression

Regression is a type of supervised learning in which the output is a numeric variable. Among many regression models, feed-forward neural networks (FFNN) are widely utilized in wind engineering field [Figure 2]. They are statistical models inspired by biological learning (McCulloch and Pitts 1943) and characterized by adaptive weights between neurons which are tuned using a learning algorithm from observed training data. For simplicity, the FFNN is also denoted as artificial neural network (ANN) in this study.

FIGURE 2

FIGURE 2. Architecture of a typical FFNN.

Deep neural networks (DNN) are also a type of FFNN characterized by a deep architecture equipped with multiple layers, and hence allows for better generalization and accuracy (Deng and Yu 2014; Pouyanfar et al., 2018). The convolutional neural networks (CNN) is another important FFNN with sparse convolutional matrices that are usually employed for pattern recognition and image classification (Krizhevsky et al., 2012; Goodfellow et al., 2016). Recurrent neural networks (RNN) are a class of feedback neural networks that allow previous outputs to be used as inputs while having hidden states and are suited to model time-dependent regression problems (e.g., Medsker and Jain 1999; Mandic and Chambers 2001). Long short-term memory (LSTM) are an advanced version of RNN to alleviate the gradient vanishing and exploding issue by only keeping necessary past information in future model states (Bengio et al., 1994).

2.1.2 Classification

Classification is another type of supervised learning in which the output is a categorical variable or a class. Support vector machines (SVM) (Scholkopf and Smola 2018) and random forest (RF) (Breiman 2001) are two classical examples of classification algorithms. SVM classifier identifies a hyperplane in a high-dimensional space in which a simple linear classification can be performed. RF classifier, on the other hand, fits a number of decision tree classifiers on various sub-samples of the dataset, then averages the results to improve outcome accuracy [Figure 3].

FIGURE 3

FIGURE 3. Architecture of a typical random forest classifier.

2.2 Unsupervised Learning

Unsupervised learning models draw inferences from datasets to describe hidden structures from unlabeled data based on inherent characteristics (Russell and Norvig 2016). These models usually group instances of input data using a defined similarity index (global criterion). Clustering and dimensionality reduction are two standard examples of unsupervised learning applications.

2.2.1 Clustering

Clustering is an unsupervised learning task used for pattern recognition that automatically discovers natural groups or clusters in data. A cluster refers to a collection of data points aggregated together with similar features (Maulik and Bandyopadhyay 2002). The k-means clustering is one of the simplest unsupervised ML models. It is a centroid-based algorithm that partitions the data into k clusters. Mean-shift clustering is another unsupervised model with a sliding-window-based algorithm to identify dense areas of data points. Other clustering algorithms such as the density-based spatial clustering of applications with noise, the expectation–maximization clustering using gaussian mixture models and the agglomerative hierarchical clustering are also popularly used for statistical data analysis.

2.2.2 Dimensionality Reduction

Dimensionality reduction aims to find the most important features within the dataset by identifying lower-dimensional representations for high-dimensional data. It minimizes the storage space, reduces the computation time and avoids overfitting. The ML-based dimensionality reduction can be divided into linear and nonlinear algorithms. The principal component analysis (PCA) is a commonly used linear technique that can be regarded as a two-layer neural network with a linear activation function. It essentially provides new uncorrelated variables, also denoted as principal components, which maximize the variance. The nonlinear autoencoder is a specific type of FFNN that compresses the initial input space into a reduced dimensional space using the encoder and then decompresses the obtained latent space back to the original input space using the decoder. Accordingly, deep autoencoders have a “bottleneck” architecture designed for extraction of representative features [Figure 4]. The autoencoder algorithm has been attracting attention in fluid mechanics community for efficient development of reduced-order models.

FIGURE 4

FIGURE 4. Architecture of a typical autoencoder model.

2.3 Semi-Supervised Learning

Semi-supervised learning models operate based on limited labeled data with a large amount of unlabeled data. Hence, they can be regarded as combination results of supervised learning and unsupervised learning algorithms. The generative adversarial network (GAN) is a well-known semi-supervised learning algorithm for estimating generative models via an adversarial process. One important feature of semi-supervised learning algorithms is their labelled-data efficiency. To this end, it may be reasonable to consider the physics-informed deep learning (PIDL) as a semi-supervised model that leverages physics-based equations in the augmented loss function to significantly reduce the data demand during training process.

2.3.1 Generative Adversarial Network

The GAN model consists of two competing neural networks, namely the generator and the discriminator (Goodfellow et al., 2014). It generates new data based on a probability distribution that approximately represents the training data (true or labelled data). Specifically, the generator produces fake samples to imitate the distribution of a real dataset, then the discriminator tries to distinguish (through a classification process) between the real samples and fake ones (from the generator). The GAN model is trained such that the new generated samples accurately represent the underlying mechanisms of the studied system. The architecture of a typical GAN model is illustrated in Figure 5.

FIGURE 5

FIGURE 5. Architecture of a typical GAN model.

2.3.2 Physics-Informed Deep Learning

The concept of PIDL models was originally proposed several decades ago (Psichogios and Ungar 1992; Dissanayake and Phan-Thien 1994) in which prior knowledge (in terms of the physics-based governing equations) is integrated within the neural networks to reduce the high-volume of required training data. Typically, a small amount of labelled data along with a large number of unlabeled data that satisfy the underlying physics of the system of interest (also denoted as collocations points) are used to train these models. Hence, self-supervision plays a significant role in PIDL models. Recently, Raissi et al. (2017a, b) advanced the PIDL models by leveraging the automatic differentiation technique to solve partial differential equations. The architecture of a typical PIDL model is presented in Figure 6.

FIGURE 6

FIGURE 6. Architecture of a typical PIDL model.

2.4 Reinforcement Learning

RL algorithm is usually formulated based on Markov decision process (Sutton and Barto, 2018). The core part of RL is its agent that interacts with its environment. Accordingly, the agent learns a policy that maps the states to the actions by maximizing the expected cumulative reward using an automated trial-and-error process (e.g., Mnih et al., 2015; Silver et al., 2017). Typical reinforcement learning models include value-based models (e.g., Q-learning or deep Q-learning) (Watkins and Dayan 1992), policy-based models (e.g., deep deterministic policy gradient) (Lillicrap et al., 2015) and hybrid models (e.g., actor-critic) (Williams 1992). Recently, the deep RL (with DNN-based policy) has been gaining attention in wind engineering community as an efficient way for dynamic control and shape optimization (Li et al., 2021a; 2021b). The architecture of a typical deep RL is depicted in Figure 7.

FIGURE 7

FIGURE 7. Architecture of a typical RL.

3 Applications of Machine Learning to Wind Engineering

This section provides a comprehensive review of the state of research and practice of ML for its applications to wind engineering. In addition to ML applications to wind climate, terrain/topography, aerodynamics/aeroelasticity and structural dynamics (following traditional Alan G. Davenport Wind Loading Chain), the review also extends to cover wind damage assessment and wind-related hazard mitigation and response (considering emerging performance-based and resilience-based wind design methodologies). Considering the overwhelming number of existing research publications, this review is by no means exhaustive. Rather, it attempts to provide a state-of-the-art perspective on ML applications to wind engineering-related fields.

3.1 Wind Climate

The review of ML applications to wind climate is organized by classifying it into classical boundary-layer winds, tropical cyclones and non-synoptic events. By leveraging the increasingly available datasets (e.g., satellite data), ML has become a supporting tool or even a reliable competitor of classical approaches for wind climate modeling (e.g., CFD). Most reviewed articles employed ML algorithms as a regression (e.g., long-term prediction of surface wind speed) or a classification (e.g., downburst occurrence prediction) tool. The selected metrics to evaluate the performance of ML algorithms included the root mean square (RMS), coefficient of correlation, mean squared error (MSE), mean absolute error (MAE), mean absolute percentage error (MAPE), coefficient of determination (R2), among others.

3.1.1 Classical Boundary-Layer Winds

Air movement in the planetary boundary layer plays a fundamental role in current wind design of structures and infrastructure. Although a detailed universal description of flow characteristics in the boundary-layer region has not been possible, the classical boundary-layer winds in gales from large depressions or in monsoons can be well represented by a number of empirical or semi-empirical models [e.g., power-law profile for distribution of mean wind speed (Davenport 1960) and power spectrum for turbulent fluctuations (Panofsky and McCormick 1960)]. The major research efforts have been focused on the accurate estimate of design wind speed in a statistical analysis framework (Simiu and Scanlan 1978). Specifically, long-term wind data from meteorological observations are analyzed based on extreme value theory to obtain the design wind speed at each location. However, the accurate forecast of classical boundary-layer winds is very challenging since it involves a large range of various temporal and spatial scales (e.g., from fractions of a meter to several thousand kilometers for spatial scale and from fractions of seconds to several years for time scales). Usually, the temporal and spatial resolutions from the state-of-the-art weather forecast models [e.g., global forecast system from National Oceanic and Atmospheric Administration (NOAA)] are not sufficient for wind engineering purpose. On the other hand, the unprecedented volumes of data from field measurements (e.g., weather station and satellite) provide a solid foundation to advance ML applications for classical boundary-layer winds.

Table 1 presents the reviewed applications of ML for classical boundary-layer winds, where the ML model, training scheme, input data, output data, data source and performance metric are summarized for each application. The training/testing data were essentially retrieved from field measurements. From Table 1, it can be concluded that most applications used ML as a regression model for prediction of mean wind speed (averaging time ranged from minutes to months), while the short-term prediction of turbulent fluctuations that are very important to structural dynamics is very limited. In many applications, the selection of ML models is simply based on gut feeling or past experience. Although several researchers conducted comparison studies to select good ML models for their specific applications, it might be very challenging to generalize the obtained results to other applications due to a lack of a systematic comparison framework.

TABLE 1

TABLE 1. Summary of ML applications for classical boundary-layer winds.

3.1.2 Tropical Cyclones

Tropical cyclones (TCs), also commonly known as hurricanes in North Atlantic, typhoons in western North Pacific and cyclones in Australia, are low-pressure storms that form over a warm ocean surface (Holton and Hakim 2013). With an average of 90 events reported annually (Zhao et al., 2012), TCs and their cascading hazards (e.g., wind, rain, storm surge and wave) pose a serious threat to public safety, livelihoods and local economies in many coastal regions around the globe. Hence, significant efforts have been made in modeling and predicting TCs and relatively well-established mesoscale numerical weather prediction frameworks [e.g., Weather Research and Forecasting (WRF) model] are available for high-fidelity simulations. However, the high-fidelity computationally expensive models might not be always appropriate for planning activities in an uncertain environment where Monte Carlo simulations are needed or emergency managements where real-time or near-real-time predictions are required. The high demand for a rapid and reliable technique used to assist decision-makers and planers results in many ML models for efficient simulations of key stages in the life cycle of a TC. These ML applications to TCs are fueled by increasingly available remotely-sensed and high-fidelity numerical data. The review in this section is organized following the four important components of full track of a TC, namely genesis, translation, intensity and wind field.

3.1.2.1 Tropical Cyclone Genesis

TC genesis requires several necessary environmental conditions (e.g., existence of low-pressure area and sea surface temperature of at least 26°C), however, the exact mechanisms of TC formation are still not well understood (Gray 1968, 1979; Emanuel 2003; Holton and Hakim 2013). To predict the TC genesis, both numerical and statistical models were developed. The numerical models (e.g., global forecast system) are essentially based on the physical principles and their performance heavily depends on improved understanding of TC genesis mechanism. The statistical models (e.g., Michael 2017; Chen and Duan 2018; Cui and Caracoglia 2019) linearly relate the TC genesis to a few selected environmental factors, and hence show poor interpolation and limited predictability. The lack of a deep understanding of underlying mechanisms stimulated data-driven techniques for TC genesis simulations. As a result, increasing ML applications are available to accurately predict TC genesis. Table 2i presents the reviewed applications of ML for TC genesis, where the ML model, training scheme, input data, output data, data source and performance metric are summarized for each application. The training/testing data were essentially retrieved from satellite measurements along with reanalysis results. It is expected the improved spatial resolution of currently available datasets will further enhance simulation results of ML models. From Table 2i, it can be concluded that most applications used ML as a classification model for either short-term or long-term forecasting of TC genesis. Although more dynamic and thermodynamic environmental factors can be retrieved using advanced remote sensing technologies in recent years, the identification of the most appropriate set of inputs to ML models (predictors) is still very challenging.

TABLE 2

TABLE 2. Summary of ML applications for tropical cyclones.

3.1.2.2 Tropical Cyclone Translation

Numerical forecast models have been successfully applied in forecasting normal TC trajectories, but they are computationally expensive. Although several statistical models were also developed based on a large amount of historical TC path records (e.g., Vickery et al., 2000,2009; Emanuel et al., 2006; Hall and Jewson 2007; Chen and Duan 2018; Snaiki and Wu 2020a; Snaiki and Wu 2020b), their linear nature makes them incapable of capturing the inherent nonlinearities in such a complex dynamic system (Zhang and Nishijima 2012). Both numerical and statistical models or their combinations (statistical-dynamics models) show poor performance in forecasting sudden speed change, recurvature and stagnation in TC movement (Chen et al., 2020). To satisfy both simulation accuracy and efficiency, increasing ML applications emerged for TC path prediction. Table 2ii presents the reviewed applications of ML for TC translation, where the ML model, training scheme, input data, output data, data source and performance metric are summarized for each application. The training/testing data were essentially retrieved from meteorological databases (e.g., satellite data) and reanalysis results. Typically, the TC track information is available only at each 6-h interval. From Table 2ii, it can be concluded that most applications used ML as a regression model for TC path prediction. Since the forecast of TC track can be regarded as a time series prediction problem, the feedback neural networks such as RNNs and LSTMs are preferred and lead to good performance. However, their performance within each 6-h interval is unknown due to the sampling limitation in the training data.

3.1.2.3 Tropical Cyclone Intensity

The TC intensity (over ocean or land) can be measured in terms of central pressure or maximum sustained wind speed. It is impacted by several complicated physical phenomena (e.g., atmosphere-ocean interaction and vertical wind shear), and hence remains one of the most challenging issues in TC forecasting especially for rapid intensification prediction. To avoid the high computational cost of numerical forecast models, both statistics-based (e.g., Vickey et al., 2000; DeMaria et al., 2005; Hall and Jewson 2007; Vickey et al., 2009) and physics-based (e.g., Snaiki and Wu 2020a) tools were developed for fast prediction of TC intensity. However, neither statistical nor physical models guarantee prediction accuracy of TC intensity due essentially to the over-simplification of such a complicated dynamic system. To improve simulation accuracy while keeping a high efficiency, increasing ML applications are available for TC intensity prediction. Table 2iii presents the reviewed applications of ML for TC intensity, where the ML model, training scheme, input data, output data, data source and performance metric are summarized for each application. The training/testing data were essentially retrieved from meteorological databased (e.g., satellite data) and reanalysis results. From Table 2iii, it can be concluded that most applications used ML as a regression (or a classification) model for estimation of intensity time series (or levels). Although encouraging simulation results indicate a good performance of ML models in predicting TC intensity for their specific applications, the selection of the most appropriate set of inputs (including the number of predictors and previous time steps) is still very challenging. In addition, it is not easy to conduct a systematic comparison among reviewed ML models since the used performance metrics differ substantially from one application to another.

3.1.2.4 Tropical Cyclone Wind Field

TC wind hazard is of great significance since it (directly) induces significant damage to life and property and (indirectly) triggers other TC-induced hazards (e.g., storm surge and waves). Substantial research efforts have been made for development of numerical models (e.g., WRF) or analytical models (e.g., Snaiki and Wu 2017a; Snaiki and Wu 2017b; Snaiki and Wu 2018; Snaiki and Wu 2020c; Fang et al., 2018; He et al., 2019) to simulate the boundary-layer wind field. However, none of these models can simultaneously achieve simulation accuracy and efficiency. To address this issue, increasing ML applications emerged for TC boundary-layer wind field simulation. Table 2iv presents the reviewed applications of ML for TC wind field, where the ML model, training scheme, input data, output data, data source and performance metric are summarized for each application. The training/testing data were essentially retrieved from meteorological databases (e.g., satellite data) and high-fidelity simulations. It is expected the improved spatial resolution of currently available datasets will further enhance simulation results of ML models. From Table 2iv, it can be concluded that most applications use ML as a regression model for prediction of surface wind speed. Since these ML models were often trained and fine-tuned to predict the TC wind field at a specific region, it might be very challenging to generalize the obtained results to other locations. It is noted that only wind field at a certain altitude is available in most ML applications due essentially to training data sparsity issue in vertical dimension. The widely-used logarithmic or power-law profiles are typically employed to obtain the TC boundary-layer winds. Accordingly, the supergradient winds that may have significant implications to the wind design of tall buildings is not captured (Snaiki and Wu 2020c).

3.1.3 Non-synoptic Winds

Unlike synoptic winds that are associated with large-scale meteorological systems characterized by horizontal scales of thousands of kilometers and time scales of days, the non-synoptic wind systems are local phenomena (e.g., a horizontal scale of several hundreds of meters) and short lived (e.g., a time scale of a few minutes) (Chowdhury and Wu 2021). Furthermore, the transient nature of non-synoptic winds makes them exhibit time-varying mean wind speeds and nonstationary/non-Gaussian fluctuations. Accordingly, the detection, measurement, and modeling of non-synoptic wind systems lag behind those of synoptic winds. However, numerous studies have demonstrated the importance of the non-synoptic wind events on the structural design (e.g., Holmes 1999; Letchford et al., 2002; Hao and Wu 2017). For example, the design wind speeds with relatively high return periods are usually dominated by the thunderstorm downbursts (Twisdale and Vickery 1992; Solari et al., 2015) and the ASCE 7–22 includes the first-ever criteria for tornado-resistant design (ASCE, 2021). Recently, there is a rapid development of field-measurement networks (e.g., THUNDERR project at University of Genova) and laboratory facilities (e.g., WindEEE at Western University) for improved understanding of non-synoptic wind systems. These advances offer an unprecedented volume of data, and hence provide an opportunity to facilitate ML applications to non-synoptic winds. Although the non-synoptic wind systems can be originated from various mechanisms (e.g., convective storm, gravity wave or negative buoyancy) (Bluestein 2021), the review only focuses on those associated with convective storms. Specifically, ML applications to thunderstorms (subsynoptic-scale weather system) are first presented, followed by detailed reviews of its applications to two important types of non-synoptic wind events associated with thunderstorms, namely downbursts and tornadoes.

3.1.3.1 Thunderstorms

A thunderstorm is short-lived atmospheric weather system accompanied by lightning and thunder, gusty winds, heavy rain, and sometimes hail (Solari 2020). The life cycle of a thunderstorm usually consists of cumulus stage, mature stage and dissipative stage, and it typically lasts around 30 min. Both mesoscale and microscale numerical models have been developed for simulation of thunderstorms (Hawbecker 2021). Mesoscale modeling covers a large-scale computational domain (and hence fully considers physics involved), however, it is limited to a low spatiotemporal resolution. Microscale modeling utilizes a high spatiotemporal resolution (and hence obtains important small-scale features in the simulation of winds), however, it is limited to a relatively small-scale computational domain resulting in insufficiently reliable boundary conditions. To avoid shortcomings of currently available numerical models, ML models may provide a promising approach for efficient and accurate simulation of key stages in the life cycle of a thunderstorm. Table 3i presents the reviewed applications of ML thunderstorms, where the ML model, training scheme, input data, output data, data source and performance metric are summarized for each application. The training/testing data were essentially retrieved from meteorological databases and reanalysis results. From Table 3i, it can be concluded that most applications used ML as either a classification or a regression model for prediction of thunderstorm occurrence. Obviously, there is still room for more comprehensive applications of ML in terms of modeling and forecasting each aspect of the thunderstorm from formation to dissipation. In addition, most ML applications to thunderstorm were limited to simple models with standard algorithms (e.g., ANN with backpropagation).

TABLE 3

TABLE 3. Summary of ML applications for non-synoptic winds.

3.1.3.2 Downbursts

Downbursts are one of the most spectacular and dangerous events resulting from thunderstorms (Solari 2020). Their radial outflows and ring vortices after touchdown produce strong wind gusts very close to the ground and therefore lead to substantial structural damages (e.g., Yang et al., 2018). Downbursts are typically simulated numerically using CFD (e.g., Mason et al., 2009; Aboshosha et al., 2015; Haines and Taylor 2018; Hao and Wu 2018; Oreskovic et al., 2018; Oreskovic and Savory 2018; Iida and Uematsu 2019) or experimentally using wind tunnels (e.g., Jesson et al., 2015; Jubayer et al., 2016; Hoshino et al., 2018; Aboutabikh et al., 2019; Asano et al., 2019; Junayed et al., 2019; Romanic et al., 2019). Both numerical and experimental approaches to obtain wind fields associated with downbursts are very time consuming (either computational expensive or labor intensive). This shortcoming motivated increasing use of ML tools for efficient and accurate simulations of downbursts. Table 3ii presents the reviewed applications of ML for downbursts, where the ML model, training scheme, input data, output data, data source and performance metric are summarized for each application. The training/testing data were essentially retrieved from field measurement. From Table 3ii, it can be concluded that most applications used ML as a classification model for prediction of the occurrence of downburst or probability of damaging wind. There are a very limited number of ML applications for modeling and forecasting the downburst wind field, hence more research efforts are needed in this aspect. It is noted that the reviewed ML applications usually involved a high number of predictors. The employment of relatively high number of input variables may be necessary due to the complexity of downburst prediction. However, it makes the ML models not easy to use since these input variables might not be always available.

3.1.3.3 Tornadoes

Tornadoes are characterized by a rotating column of air descending from supercell thunderstorms lasting from several minutes to few hours. They are the most intense of all non-synoptic wind events, and hence result in significant damage and collapse of structures (Hao and Wu 2016, 2020). Several analytical and empirical models have been developed to simulate the vertical and radial wind profiles of tornado-like vortices (e.g., Wen and Chu 1973; Baker and Sterling 2017). These models are clearly over-simplified. The tornado wind fields are also modeled using CFD simulations (e.g., Kuai et al., 2008; Ishihara et al., 2011; Liu and Ishihara 2015; Eguchi et al., 2018; Gairola and Bitsuamlak 2019; Kawaguchi et al., 2019; Huo et al., 2020; Liu et al., 2021) or laboratory tests (e.g., Sarkar et al., 2006; Refan and Hangan 2016; Razavi and Sarkar 2018; Tang et al., 2018; Ashton et al., 2019; Gillmeier et al., 2019; Hou and Sarkar 2020; Razavi and Sarkar 2021). However, CFD simulations of tornadoes are computational expensive while the laboratory tests are labor intensive. These shortcomings motivated increasing use of ML tools for efficient and accurate modeling of tornadoes. Table 3iii presents the reviewed applications of ML for tornadoes, where the ML model, training scheme, input data, output data, data source and performance metric are summarized for each application. The training/testing data were essentially retrieved from meteorological datasets (e.g., Radio-based data). From Table 3iii, it can be concluded that most applications use ML as a classification or a regression model for prediction of tornado occurrence. Obviously, there is still room for more comprehensive applications of ML in terms of simulation of the full track of a tornado (including its intensity and associated wind field). Just like ML applications to downbursts, a high number of input variables (predictors) were utilized for the reviewed ML models. The identification of the most appropriate set of predictors is still very challenging, and a trail-and error approach was typically employed. In addition, it is not easy to conduct a systematic comparison among reviewed ML models since the used performance metrics differ substantially from one application to another.

3.2 Terrain and Topography

Wind characteristics including mean wind speeds and turbulent fluctuations are much affected by the surrounding terrain and topography. As a consequence, careful consideration of local terrain roughness and topographic features as well as surrounding obstacles is vital to the accurate determination of wind pressures on structures and pedestrian level winds. Wind codes and standards consider the terrain effects corresponding to limited (and simplified) terrain geometries (e.g., escarpment and single hill) through correction factors. To examine the effects of complex terrain condition on wind fields, wind tunnel tests are usually employed with a very small geometric scale (e.g., 1:500). Alternatively, numerical schemes such as the mass-conservation or momentum-conservation model can be used to capture the terrain effects on oncoming wind fields. Although the topographic effects can be well simulated based on momentum-conservation models (e.g., using Reynolds-averaged Navier-Stokes equations), the needed computational time makes it impractical for use as a real-time decision support tool. The mass-conservation model computes wind fields over complex terrain in seconds to a few minutes (Forthofer et al., 2014a; 2014b), but the accuracy of simulation may be poor because nonlinear momentum effects are not considered (Jackson and Hunt 1975). Considering the complex terrain-wind data from high-fidelity CFD simulations, wind tunnel tests and field measurements are increasingly available, ML tools can be utilized (as computationally efficient reduced-order models that possess high simulation accuracy of complex nonlinear systems) to provide rapid estimation of wind flows over various terrain conditions. However, ML development for terrain and topographic considerations is still at an early stage with a limited number of studies reported in the literature. Table 4 presents the reviewed applications of ML for terrain and topography, where the ML model, training scheme, input data, output data, data source and performance metric are summarized for each application. The training/testing data were essentially retrieved from either CFD simulations or wind tunnel tests. From Table 4, it can be concluded that most applications used ML as a regression model for prediction of wind fields over various terrain conditions and topographic configurations. There are a few studies that applied ML techniques to assist in efficient search for a correct layout of passive flow altering devices (e.g., spires and roughness elements) in the boundary-layer wind tunnel. It is noted that the current ML applications to consider topographic effects on wind fields are usually limited to terrain configurations that can be characterized by several parameters, hence, the employed ML models and training schemes are simple and standard (e.g., ANN with backpropagation). However, several advanced ML models such as autoencoder (e.g., Fukami et al., 2019) and GAN (Kim and Lee 2020) have been utilized to assist in the generation of turbulent inflow (as a realistic inlet boundary condition of CFD simulations).

TABLE 4

TABLE 4. Summary of ML applications for terrain and topography.

3.3 Aerodynamics and Aeroelasticity

The bluff-body aerodynamics and aeroelasticity play a critical role in the safe and cost-effective design of wind-sensitive structures, and their considerations rely heavily on boundary-layer wind tunnels. In addition to the Reynolds number effects (due to very small model scales), wind tunnel tests are very time consuming and labor intensive. To this end, CFD techniques have been rapidly developed for simulations of structural aerodynamics (gust-induced effects) and aeroelasticity (motion-induced effects). The purpose is to make CFD simulations serve as a complementary or even alternative approach to wind tunnel tests. Despite significant advances of hardware and algorithms, the reliable CFD simulations of wind-structure interactions are still computationally very expensive due to three-dimensional nature of wakes and intensive flow separations from structures. Hence, a number of reduced-order models have been developed to efficiently model structural aerodynamics and aeroelasticity (Wu and Kareem 2013). Unfortunately, these reduced-order models do not always have a satisfactory representation of the full nonlinear equations that govern the wind-structure interactions. Specifically, modern bridge decks and super tall buildings with unusually geometries all exhibit nonlinear unsteady aerodynamics and aeroelasticity that limit the applicability of the state-of-the-art reduced-order modeling methodologies. On the other hand, the Kolmogorov Neural Network existence theorem offers mathematical foundation for applying multilayer neural networks to approximate arbitrary nonlinear systems with any precision (Huang and Lippmann 1988; Hornik, 1991). With high-fidelity data and advanced algorithms, ML models can simultaneously achieve great simulation efficiency and accuracy. It is noted that there are numerous ML applications to aerodynamics and aeroelasticity of both bluff bodies (e.g., circular cylinder) and streamlined bodies (e.g., airfoil) in fluid mechanics community (e.g., Kutz 2017; Brunton et al., 2020), however, they are not discussed here. The review in this section only covers wind-sensitive structures in civil engineering. The ML applications for bridge aerodynamics and aeroelasticity are first reviewed in Table 5i and then followed by buildings and other structures in Table 5ii, where the ML model, training scheme, input data, output data, data source and performance metric are summarized for each application. The training/testing data were essentially retrieved from either CFD simulations or wind tunnel tests. From Table 5, it can be concluded that most applications used ML as a regression model for prediction of steady-state force coefficients, flutter derivatives and vortex-induced vibrations (VIV) of various bridges and for modeling of wind pressure coefficients of various buildings (as well as estimation of the interference factors for adjacent buildings). The different aerodynamic representations in bridges (mainly using global quantities such as force coefficients) and buildings (mainly using local quantities such as pressure coefficients) are partially due to available data types from wind tunnel tests. Although satisfactory ML simulation results have been obtained (in terms of interpolations), most reviewed applications do not necessarily have good performance in terms of extrapolations outside the training datasets. It is noted that the currently available ML models of aerodynamics and aeroelasticity are developed for the main purpose of being used as preliminary design tools to avoid the high-cost wind tunnel tests in the early design stage. There is a lack of systematic comparison among various ML models, hence, their selection for specific applications is rather rudimentary.

TABLE 5

TABLE 5. Summary of ML applications for aerodynamics and aeroelasticity.

3.4 Structural Dynamics and Damage Assessment

Due to the computational complexity of numerical techniques (e.g., finite element method) for solving wind-induced nonlinear structural response, reduced-order models (e.g., ANN) have been developed to alleviate the computational cost of the high-fidelity models. The ML models have been used for structural dynamics and damage assessment for several decades mainly in the field of earthquake engineering (e.g., Wu et al., 1992; Masri et al., 1993; Jiang and Adeli 2005; Pei et al., 2005; Gholizadeh et al., 2009; Facchini et al., 2014; Derkevorkian et al., 2015; Liang 2019; Wu and Jahanshahi 2019; Yu et al., 2020). However, similar applications have not emerged in wind engineering community until recently due essentially to the linear consideration of the wind-induced structural response [ASCE 7-16 (ASCE, 2017)]. Recent advances of performance-based wind design methodology have placed increasing importance on effective simulations of nonlinear, inelastic structural dynamics response under strong winds. The numerical estimation of wind-induced nonlinear structural response using a high-fidelity finite element model is computationally very expensive due to its small time-step size and long simulation duration. Accordingly, several ML applications to wind-induced structural dynamics have been developed in recent years for simultaneously achieving high simulation accuracy and efficiency. The performance-based (and further resilience-ba sed) wind design philosophies also require accurate damage assessment of structures and infrastructure under extreme storms. The structural damages under winds depend on numerous factors including wind features (e.g., wind speed/direction and topography) and built environment characteristics (e.g., building opening and roof slope), hence its assessment and quantification are extremely challenging. On the other hand, increasingly available field-measurement data characterizing structural damages under strong wind events [e.g., resulting from post-disaster reconnaissance activities such NHERI Natural Hazards Reconnaissance (RAPID) Facility and NSF Structural Extreme Events Reconnaissance (StEER) Network] provide a great opportunity to learn from data by using various ML models. The ML applications for structural dynamics are first reviewed in Table 6i and then followed by damage assessment in Table 6ii, where the ML model, training scheme, input data, output data, data source and performance metric are summarized for each application. The training/testing data were essentially retrieved from numerical simulations, wind tunnel tests and field measurements. From Table 6, it can be concluded that most applications used ML as a regression model for modeling structural dynamics and as a regression or a classification model for structural damage assessment. While many applications employed simple ML models and standard training schemes (e.g., ANN with backpropagation), some advanced schemes such as knowledge-enhanced LSTM have been successfully applied to predict time series of wind-induced nonlinear structural response. It is noted that the selection of the most appropriate set of inputs to ML models for damage assessment (predictors or features) is still very challenging.

TABLE 6

TABLE 6. Summary of ML applications for structural dynamics and damage assessment.

3.5 Mitigation and Response

Both long-term and short-term strategies are needed to enhance resilience of individual structures or communities to withstand wind-related hazards. One important long-term consideration is to mitigate structural response/vibration subjected to winds through structural optimization and/or control. For structural optimization under winds, the shape optimization is probably the most effective approach to reduce aerodynamic loading. For wind-induced vibration control, both aerodynamic and mechanical measures are well recognized in wind engineering community. Although the structural performance evaluation under winds is typically a very complicated task, the corresponding simulations during optimization or (active) control process is required to be efficient and accurate because they need to be conducted either repeatedly for numerous scenarios or in a (near) real-time sense. As noted earlier, the ML models are very promising to simultaneously achieve the high simulation efficiency and accuracy goal. In addition, the RL models that have gained increasing popularity in recent years can be used as very effective optimization or control algorithms compared to conventional approaches (Silver et al., 2017). In the consideration of short-term actions, efficient management strategies are critically important. Although the ML models used in the disaster (including wind-related hazard) management framework (i.e., covering preparedness, response and recovery) have recently been systematically reviewed (e.g., Sun et al., 2020), its applications to social media-informed response are still discussed here since the unprecedentedly abundant data from various powerful communication tools (e.g., Twitter) greatly facilitate the rapid ML model developments in this field. Table 7i,ii respectively present the reviewed applications of ML for mitigation and response, where the ML model, training scheme, input data, output data, data source and performance metric are summarized for each application. The training/testing data were essentially retrieved from CFD simulations and experimental tests for structural mitigation or from social media platforms for disaster response. From Table 7i, it can be concluded that the structural performance evaluations in mitigation applications usually used ML as a regression model while RL was typically utilized as an effective optimization or control algorithm. It is noted that relatively few ML applications for structural optimization and control under winds have been generated compared to those in earthquake engineering community (e.g., Ghaboussi and Joghataie 1995; Adam and Smith 2008; Jiang and Adeli 2008; Yakut and Alli 2011; Subasri et al., 2014; Khodabandehlou et al., 2018; Khalatbarisoltani et al., 2019; Hayashi and Ohsaki 2020). From Table 7ii, it can be concluded that most social media-informed response applications used ML as a classification model for disaster rescue and relief information dissemination. Although these ML applications present promising results in terms of effectively supporting timely decision-making, there is a concern of using information from social media platforms due to a lack of data quality control.

TABLE 7

TABLE 7. Summary of ML applications for mitigation and response.

3.6 Summary

The ML applications in each topical area of wind engineering are summarized in Figure 8. As shown in the figure, ML models are unevenly distributed among these areas. The wind climate area has the most ML applications followed by the aerodynamics and aeroelasticity area, and they are respectively contributed by wind engineering-related fields of meteorology and fluid mechanics. On the other hand, the wind engineering-exclusive field of terrain and topography has the least applications of ML. Although ML models have been instrumental in modern structural design for winds, their developments are in a very preliminary stage and there is still a long way to go before they can complement or even replace existing approaches of wind tunnel tests and CFD simulations. In general, the supervised learning dominates the ML applications in wind engineering with the podium position attributed to simple models with standard algorithms (e.g., ANN with backpropagation). Actually, the selection of various ML models is rather rudimentary since there is a lack of systematic comparison among them (e.g., in terms of model complexity and performance). It is noted that the great potential of semi-supervised learning and unsupervised learning (as well as RL) with little or no labelled data is not leveraged yet. Accordingly, the current ML developments in wind engineering heavily rely on available labelled data. For example, the ML applications to non-synoptic winds are much less than those of synoptic winds due essentially to the difficulty in obtaining the data of local and short-lived storms. On the other hand, the recent emergence of numerous ML applications to social media-informed disaster response is due mainly to the unprecedentedly abundant data from various powerful communication tools. For the reviewed ML applications, the training/testing data are retrieved from several major sources (e.g., field measurements, wind tunnel tests, numerical simulations and social media platforms). In the determination of ML model inputs and outputs, a good understanding of underlying physics of each application is critical to effectively select an appropriate set of predictors (ML inputs) while the output types heavily depend on the needs of traditional analysis procedure in each application (e.g., local wind pressures for building design and global wind forces for bridge design).

FIGURE 8

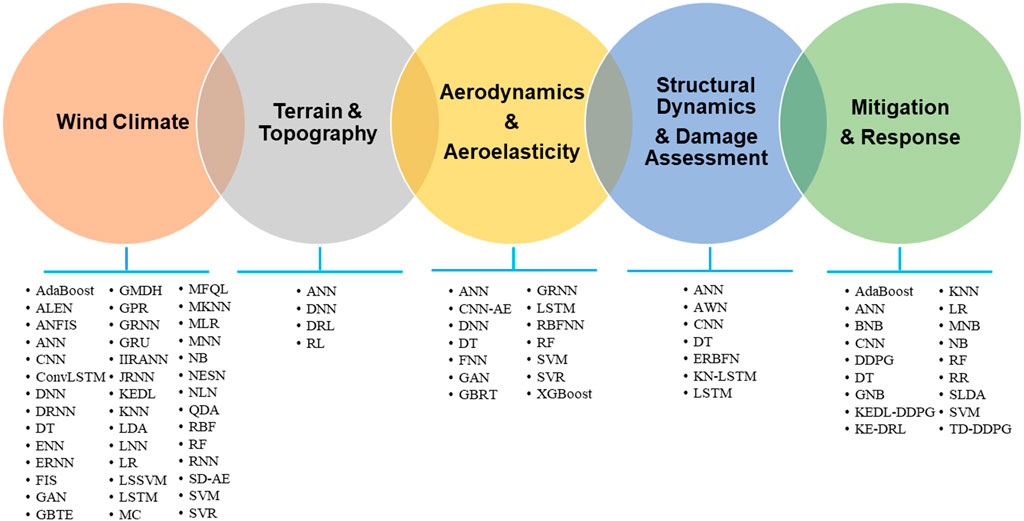
FIGURE 8. Overview of reviewed ML applications in wind engineering (following Alan G. Davenport Wind Loading Chain).

4 Challenges and Prospects

The rapidly increasing ML applications to wind engineering have generated a large volume of datasets associated with a large set of domain-specific algorithms. It is strongly believed that the platforms encouraging open sharing of these datasets and algorithms would greatly benefit the ML research progress in wind engineering. The openly available wind engineering datasets will greatly reduce efforts for their creation/collection and pre-processing, and open-source ML algorithms will save significant time for their re-implementation. The reduced need of time and effort to use the state-of-the-art or latest developed ML tools under such a culture of openness would spur interests among researchers in wind engineering, and hence result in more related ML applications. Moreover, the developed cyberinfrastructure to store and share data usually has a systematic curation procedure to ensure the high quality of its standardized benchmark datasets. Also, the open-source software allows the hidden bugs/tricks of ML algorithms to be easily uncovered and accordingly makes them more robust. In addition to availability, the reproducibility and testability of wind engineering data and domain-specific algorithms due to a culture of openness would also facilitate the adoption of the obtained transparent and trustworthy ML tools in real-world problems. Although the wind engineering community has started to embrace the prevalent openness of ML community (e.g., NHERI DesignSafe platform), the culture of openness is still in its early stage. It is expected that more incentives based on the existing reward system (e.g., a digital object identifier for each dataset or algorithm published by the platform) are needed to motivate the ML wind engineering community towards open science. Given a potential open-science environment with openly available datasets and open-source algorithms (supported by open-access scientific publications), some remaining challenges and future prospects are discussed in terms of data in wind engineering and algorithms in ML. It is noted that both challenge and prospect lists are not exhaustive.

4.1 Challenges and Research Gaps

The reviewed various ML models for a wide range of topics in wind engineering suggests that their cross field has recently attracted much interest. However, there are still numerous challenges to advance ML applications to wind engineering from conception and research into practice. These remaining challenges of data in wind engineering and algorithms in ML are discussed in this sub-section.

4.1.1 Wind Engineering Data Challenges

Wind engineering data could be rich in some dimensions but may be poor in others. For example, a large volume of flow data or pressure data could be obtained by one wind tunnel test (using advanced measurement systems with high resolution in space and high sampling rate in time), however, all these data would be located at a point in the Reynolds number dimension. For structural response under winds, most of the data are located in the linear elastic domain, while very limited nonlinear inelastic data needed to advance implementation of performance-based wind design are available. Another example is that the anemometric monitoring network typically generates abundant data in time dimension but sparse data in space. More importantly, it is usually very challenging or expensive to create extra points in currently data-scarce dimensions. Wind engineering data could be short in time span of their collection. For example, the climate changing impacts are not easy to be considered based on the currently available wind data since their record period is much shorter than the time scale of climate changing. Also, few structural performance data under winds are long enough to take the life-span deterioration behaviors into account. Essentially, the learning machine based on current wind-structure interaction data cannot be used for accurately predicting future long-term behaviors of the same wind-structure system. Wind engineering data could be highly heterogeneous for collaborative or large-scale ML applications. Many complex tasks (e.g., life-cycle performance evaluation of structures under winds) and/or real-world problems (e.g., hurricane resilience assessment of coastal communities) in wind engineering need collaborative efforts and/or large-scale implementations. The datasets generated from these activities may result from various CFD simulation tools or field measurement devices, and they are typically interpreted by different entities before sent to a central processing platform. Accordingly, significant processing efforts (e.g., data cleaning, data aggregation, dimension reduction and data standardization) are needed for these heterogeneous datasets with high variability of data types and formats (e.g., mixtures of structured, semi-structured and unstructured data). In addition, advanced powerful learning machines are necessary to generate new knowledge from large, heterogeneous sets of wind engineering data.

4.1.2 Machine Learning Algorithm Challenges

ML algorithms commonly-used in wind engineering are standard ones designed for solving problems in other fields (e.g., handwriting recognition or computer vision). While these classical algorithms (e.g., ANN with backpropagation) achieved great success for simple wind engineering applications, they are not necessarily concise and efficient. More importantly, the immediate applications of these popular algorithms to modern wind engineering (involving nonstationary and non-Gaussian wind flow, transient and nonlinear aerodynamics, nonlinear and inelastic structural dynamics, or time-variant wind-structure system under a changing climate) may be very challenging. On the other hand, the newly developed ML algorithms (e.g., advanced LSTM and GAN) need to be carefully scrutinized for their applicability to these complex problems. ML algorithms commonly-used in wind engineering are supervised ones that need a significant amount of labelled data. Although the cost of obtaining/collecting the data from various sources (e.g., numerical simulations, wind tunnel tests, or field measurements) is greatly reduced and accordingly unprecedented volume of data are increasingly available, these datasets may be limited to unlabeled due to a lack of sufficient human resources (with expert knowledge) for data labeling. ML algorithms commonly-used in wind engineering are purely data-driven ones that are usually consider as black boxes. Furthermore, currently available ML models usually present a conflict between their advances (and hence performance) and explainability. One important feature of human intelligence is the ability to explain the rationale behind its decisions to others, hence, the explainability of learning machines is often an essential prerequisite for establishing a trust relationship between human intelligence and artificial intelligence. The highly non-transparent nature of ML algorithms may be acceptable for some applications in wind engineering (e.g., a CNN mapping the oncoming winds to pressure fields on or velocity fields around various bridge decks), however, it may be a clear drawback for many high-stake applications (e.g., evacuation planning or transportation infrastructure management under a landfalling hurricane) since any error in prediction may have catastrophic consequences. It is noted that the high-stake applications also place a high demand for quantification of uncertainties involved in ML algorithm selection, training and performance evaluation (along with data collection), whereas the formalization of uncertainty quantification for purely data-driven approaches is very challenging and not well established yet. ML algorithms commonly-used in wind engineering are typically selected based on past experience (or simply by “gut feeling”) and the associated model hyperparameters (e.g., layer and neuron numbers, activation function and learning rate) are usually obtained by extensive trial and error. While the selected ML algorithms present good performance for the particular applications of interest, they are not necessarily an optimal choice. A systematic approach to identify the most appropriate ML model and associated best hyperparameters essentially needs a global optimization within a high dimensional space, and is currently very challenging for wind engineering applications.

4.2 Prospects and Future Directions

The remaining challenges, while not trivial, provide new research opportunities for the development of more effective ML tools. The identified prospects of data in wind engineering and algorithms in ML are discussed in this sub-section.

4.2.1 Wind Engineering Data Prospects

To generate/collect wind engineering data that are scarce in certain dimensions, advanced full-scale/laboratory/numerical tools and technologies need to be utilized or developed. In addition to large-scale facilities (e.g., WindEEE), various high-fidelity and efficient modern CFD techniques (e.g., hybrid large eddy simulation/Reynolds-averaged Navier-Stokes schemes) should be exploited to generate data of high-Reynolds number scenarios. The rational loading protocols for extreme wind performance cyclic testing of deformation-controlled MWFRS (Main Wind Force Resisting System) members need to be designed to generate the wind-induced nonlinear inelastic structural response data. Also, data reconstructions using linear/nonlinear dimensionality reduction techniques (e.g., singular value decomposition/autoencoder) should be employed to enhance spatial resolution of full-scale measurements. To generate/collect wind engineering data that cover sufficiently-long time span of structural behaviors, more reliable long-term structural health monitoring systems should be established in addition to high-fidelity modeling of aging and deterioration of wind-sensitive structures. For the consideration of wind engineering data under a changing climate, synthesized wind fields (resulting from tropical cyclones, extratropical cyclones or local non-synoptic storms) need to be generated by global climate models coupled with accurate and efficient downscaling exercises under projected climate conditions [e.g., various RCP (Representative Concentration Pathway) scenarios]. To effectively learn from heterogeneous data that need to be first unified, they can be efficiently processed by advanced big data analytics. For example, unsupervised or semi-supervised clustering techniques could be used for data cleaning, data fusion techniques of Kalman filters could be used for data aggregation, and linear principal component analysis or nonlinear self-organizing map could be used for dimensional reduction.

4.2.2 ML Algorithm Prospects

To facilitate ML applications to complex wind engineering problems, the state-of-the-art or latest algorithms emerging in ML community could be leveraged. For example, the GAN could be used for effectively generating nonstationary and non-Gaussian wind flow through its two competing sub-networks, the CNN could be employed for efficiently mapping oncoming winds to pressure fields (characterizing transient and nonlinear aerodynamics) on structures with an arbitrary shape because it is particularly good at handling input-output data with a known grid-like topology, the LSTM could be utilized for accurately simulating nonlinear and inelastic structural dynamics since its forget gates ensure a reliable consideration of long-term dependencies (where the structural response at the current time depends on not only the current wind load but also the load history), and the lifelong learning networks should be explored for adaptively modeling time-variant wind-structure system assuming their underlying parameters can be continuously modified to accommodate new data inputs. The direct or immediate applications of the advanced ML algorithms to complex wind engineering problems may not necessarily result in parsimonious models that may need specialized customization for each application. To reduce the demand for labelled data in ML applications to wind engineering, both unsupervised learning and semi-supervised learning (including physics-informed machine learning) are promising alternatives to popularly used supervised learning. In addition, advanced ML algorithms have been emerging (e.g., reservoir computing) for processing information generated by complicated dynamical systems using very small training datasets. To open the ML black box, model explainability and interpretability in wind engineering applications needs to be enhanced. Various general techniques have been developed to improve understanding of the ML model predictions, such as sensitivity analysis and layer-wise relevance propagation. On the other hand, the definitions of explainability and interpretability are typically domain dependent, hence, the domain knowledge in wind engineering should be leveraged for enhanced explainability/interpretability of each ML application. It is expected that the explainability/interpretability analysis (along with uncertain quantification) will likely become a fundamental building block for bounding the overall confidence in ML applications in wind engineering (parallel to verification and validation in CFD simulations). To enable an automatic search of ML model hyperparameters in wind engineering applications, increasingly available optimization schemes with improved efficiency and accuracy (e.g., grid search, random search, Bayesian optimization and population-based training) can be utilized to find the best configuration for each task. On the other hand, it is believed that a practical guide to selection of ML models in wind engineering applications will greatly facilitate their appropriate use. The best practices for model selection in each application are essentially consistent with the principle of Ockham’s razo by first testing simple linear ML models (due to their easy to implement and high model explainability), and then followed by more complex nonlinear models (without data overfitting). Among ML models with similar complexity, a predetermined performance metric is typically used for further model selection. Since iteration is generally needed in a purely performance-driven ML model selection, the domain knowledge is suggested to be utilized for a more effective search process.

4.3 Knowledge-Enhanced Machine Learning

As discussed in preceding sections, domain knowledge could be leveraged for improved selection of ML model and its inputs and outputs in wind engineering applications. Hence, a good understanding of fundamental physics and other types of domain knowledge underlying each subfield of wind engineering would enable more effective use of ML tools. It is noted that the fundamental physics in terms of governing equations is a special type of domain knowledge, and recent studies have demonstrated that the required labelled datasets could be significantly reduced by incorporating the underlying physics into training process (and hence enhancing the regularization mechanism) (e.g., Raissi et al., 2017a; 2017b). Other equation-based domain knowledge such as empirical/semi-empirical formulas were also employed as part of the loss function in deep learning to provide machine-readable prior knowledge that facilitates the effective regularization of the neural networks for simulations of tropical cyclone winds (Snaiki and Wu 2019) and nonlinear structural dynamics (Wang and Wu 2020). In addition, the equation-free domain knowledge has been integrated into a deep RL-based aerodynamic shape optimizer (via the transfer-learning and meta-learning techniques) to remarkably enhance the training efficiency for wind engineering applications (Li et al., 2021a). These emerging successful applications indicate that this novel scheme of knowledge-enhanced machine learning (KEML) could significantly enhance ML applications to wind engineering. To fully embrace the promising potential of KEML, systematic research efforts are needed to efficiently identify knowledge representations (invariances, physics equations, empirical formulas, probabilistic relations, logic rules, simulation results, field observations, human feedback, and others) in various subfields of wind engineering and then to effectively integrate them into each module of machine learning pipeline (data preparation, model selection, model training, and others). While domain knowledge could be employed to enhance purely data-driven ML tools, it is expected that learning machines could be utilized for harnessing data to discover new knowledge in wind engineering (e.g., governing laws characterizing transport of turbulence quantities or optimization of wind-structure system).

5 Concluding Remarks

A total of 65 machine learning (ML) algorithms were reviewed in terms of their applications to each topical area of wind engineering, namely wind climate, terrain/topography, aerodynamics/aeroelasticity, structural dynamics, wind damage assessment and wind-related hazard mitigation and response. The most ML applications were found in wind climate area, while the terrain/topography area had the least applications of ML. Although the ML-based wind engineering is fueled by the unprecedented volume of analytical, numerical, experimental and field-measurement data together with rapidly evolving learning algorithms and high-performance computational hardware, it is still at an early stage of development. Most of wind engineering applications employed supervised learning with standard ML models designed for solving problems in other fields, and the promising unsupervised and semi-supervised learning tools were rarely used to reduce the high demand of labelled data. For the selection of ML models and associated hyperparameters in wind engineering applications, it was typically based on expertise and extensive trial and error. In this review, the culture of openness, explainability/interpretability and uncertainty quantification were identified as important research gaps that need to be addressed in ML-based wind engineering community. Furthermore, the knowledge-enhanced machine learning was considered as a very promising scheme to enhance ML applications to wind engineering.

Author Contributions

All authors contributed to the study conception and design, data collection, analysis and interpretation of results, drafted manuscript preparation, reviewed the results, and approved the final version of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbas, T., Kavrakov, I., Morgenthal, G., and Lahmer, T. (2020). Prediction of Aeroelastic Response of Bridge Decks Using Artificial Neural Networks. Comput. Structures 231, 106198. doi:10.1016/j.compstruc.2020.106198

CrossRef Full Text | Google Scholar

Abdi, D., Levine, S., and Bitsuamlak, G. “Application of an Artificial Neural Network Model for Boundary Layer Wind Tunnel Profile Development,” in Proceedingsof the 11th Americas Conference on Wind Engineering, San Juan, Puerto Rico, June 2009.

Google Scholar

Abdullah, S. A., Aswegan, K., Jaberansari, S., Klemencic, R., and Wallace, J. W. (2020). Performance of Reinforced Concrete Coupling Beams Subjected to Simulated Wind Loading. ACI Struct. J. 117 (3), 283–295. doi:10.14359/51724555

CrossRef Full Text | Google Scholar

Aboshosha, H., Bitsuamlak, G., and El Damatty, A. (2015). Turbulence Characterization of Downbursts Using LES. J. Wind Eng. Ind. Aerodynamics 136, 44–61. doi:10.1016/j.jweia.2014.10.020

CrossRef Full Text | Google Scholar

Aboutabikh, M., Ghazal, T., Chen, J., Elgamal, S., and Aboshosha, H. (2019). Designing a Blade-System to Generate Downburst Outflows at Boundary Layer Wind Tunnel. J. Wind Eng. Ind. Aerodynamics 186, 169–191. doi:10.1016/j.jweia.2019.01.005

CrossRef Full Text | Google Scholar

Adam, B., and Smith, I. F. (2008). Reinforcement Learning for Structural Control. J. Comput. Civ. Eng. 22 (2), 133–139. doi:10.1061/(asce)0887-3801(2008)22:2(133)

CrossRef Full Text | Google Scholar

Adeli, H., and Yeh, C. (1989). Perceptron Learning in Engineering Design. Computer‐Aided Civil Infrastructure Eng. 4 (4), 247–256.

Google Scholar

Adrianto, I., Trafalis, T. B., and Lakshmanan, V. (2009). Support Vector Machines for Spatiotemporal Tornado Prediction. Int. J. Gen. Syst. 38, 759–776. doi:10.1080/03081070601068629

CrossRef Full Text | Google Scholar

Alemany, S., Beltran, J., Perez, A., and Ganzfried, S. (2019). Predicting Hurricane Trajectories Using a Recurrent Neural Network. Aaai 33 (01), 468–475. doi:10.1609/aaai.v33i01.3301468

CrossRef Full Text | Google Scholar

Ali, M. M., Kishtawal, C. M., and Jain, S. (2007). Predicting Cyclone Tracks in the north Indian Ocean: An Artificial Neural Network Approach. Geophys. Res. Lett. 34 (4), L04603. doi:10.1029/2006gl028353

CrossRef Full Text | Google Scholar

American Society of Civil Engineers (2017). Minimum Design Loads and Associated Criteria for Buildings and Other Structures. Reston, VA: Structural Engineering Institute of American Society of Civil Engineers.

Google Scholar

American Society of Civil Engineers (2021). Minimum Design Loads for Buildings and Other Structures. Reston, VA: Structural Engineering Institute of American Society of Civil Engineers.

Google Scholar

Asano, K., Iida, Y., and Uematsu, Y. (2019). Laboratory Study of Wind Loads on a Low-Rise Building in a Downburst Using a Moving Pulsed Jet Simulator and Their Comparison with Other Types of Simulators. J. Wind Eng. Ind. Aerodynamics 184, 313–320. doi:10.1016/j.jweia.2018.11.034

CrossRef Full Text | Google Scholar

Ashktorab, Z., Brown, C., Nandi, M., and Culotta, A. “Tweedr: Mining Twitter to Inform Disaster Response,” in Proceedings of the 11th International ISCRAM Conference, Pennsylvania, USA, May 2014, 269–272.

Google Scholar

Ashton, R., Refan, M., Iungo, G. V., and Hangan, H. (2019). Wandering Corrections from PIV Measurements of Tornado-like Vortices. J. Wind Eng. Ind. Aerodynamics 189, 163–172. doi:10.1016/j.jweia.2019.02.010

CrossRef Full Text | Google Scholar

Baik, J.-J., and Paek, J.-S. (2000). A Neural Network Model for Predicting Typhoon Intensity. J. Meteorol. Soc. Jpn. 78 (6), 857–869. doi:10.2151/jmsj1965.78.6_857

CrossRef Full Text | Google Scholar

Bailey, P. A., and Kwok, K. C. S. (1985). Interference Excitation of Twin Tall Buildings. J. Wind Eng. Ind. Aerodynamics 21 (3), 323–338. doi:10.1016/0167-6105(85)90043-1

CrossRef Full Text | Google Scholar

Baker, C. J., and Sterling, M. (2017). Modelling Wind fields and Debris Flight in Tornadoes. J. Wind Eng. Ind. Aerodynamics 168, 312–321. doi:10.1016/j.jweia.2017.06.017

CrossRef Full Text | Google Scholar

Bani‐Hani, K. A. (2007). Vibration Control of Wind‐induced Response of Tall Buildings with an Active Tuned Mass Damper Using Neural Networks. Struct. Control. Health Monit. 14 (1), 83–108. doi:10.1002/stc.85

CrossRef Full Text | Google Scholar

Barbounis, T. G., Theocharis, J. B., Alexiadis, M. C., and Dokopoulos, P. S. (2006). Long-term Wind Speed and Power Forecasting Using Local Recurrent Neural Network Models. IEEE Trans. Energ. Convers. 21 (1), 273–284. doi:10.1109/tec.2005.847954

CrossRef Full Text | Google Scholar

Bengio, Y., Simard, P., and Frasconi, P. (1994). Learning Long-Term Dependencies with Gradient Descent Is Difficult. IEEE Trans. Neural Netw. 5 (2), 157–166. doi:10.1109/72.279181

PubMed Abstract | CrossRef Full Text | Google Scholar

Berg, J., Mann, J., and Patton, E. G. (2013). Lidar-observed Stress Vectors and Veer in the Atmospheric Boundary Layer. J. Atmos. oceanic Technol. 30 (9), 1961–1969. doi:10.1175/jtech-d-12-00266.1

CrossRef Full Text | Google Scholar

Berggren, K., Xia, Q., Likharev, K. K., Strukov, D. B., Jiang, H., Mikolajick, T., et al. (2020). Roadmap on Emerging Hardware and Technology for Machine Learning. Nanotechnology 32 (1), 012002. doi:10.1088/1361-6528/aba70f

PubMed Abstract | CrossRef Full Text | Google Scholar

Bitsuamlak, G., Stathopoulos, T., and Bedard, C. (2006). Effects of Upstream Two-Dimensional hills on Design Wind Loads: a Computational Approach. Wind and Structures 9 (1), 37–58. doi:10.12989/was.2006.9.1.037

CrossRef Full Text | Google Scholar

Bitsuamlak, G. T., Bédard, C., and Stathopoulos, T. (2007). Modeling the Effect of Topography on Wind Flow Using a Combined Numerical-Neural Network Approach. J. Comput. Civ. Eng. 21 (6), 384–392. doi:10.1061/(asce)0887-3801(2007)21:6(384)

CrossRef Full Text | Google Scholar

Bitsuamlak, G. T. (2004). “Evaluating the Effect of Topographic Elements on Wind Flow: a Combined Numerical Simulation-Neutral Network Approach,” (Montreal, Quebec, Canada: Concordia University). Doctoral dissertation.

Google Scholar

Bitsuamlak, G. T., Stathopoulos, T., and Bédard, C. “Neural Network Predictions of Wind Flow over Complex Terrain,” in 4th Structural Specialty Conf. of the Canadian Society for Civil Engineering, Whistler, BC Canada, May 2002.

Google Scholar

Blessmann, J., and Riera, J. D. (1985). Wind Excitation of Neighbouring Tall Buildings. J. wind Eng. Ind. aerodynamics 18 (1), 91–103. doi:10.1016/0167-6105(85)90076-5

CrossRef Full Text | Google Scholar

Blocken, B. (2014). 50 Years of Computational Wind Engineering: Past, Present and Future. J. Wind Eng. Ind. Aerodynamics 129, 69–102. doi:10.1016/j.jweia.2014.03.008

CrossRef Full Text | Google Scholar

Bluestein, H. B. (2021). “The Types of Non-synoptic Wind Systems,” in The Oxford Handbook of Non-synoptic Wind Storms. Editors H. Hangan, and A. Kareem (Oxford, United Kingdom: Oxford University Press). doi:10.1093/oxfordhb/9780190670252.013.1

CrossRef Full Text | Google Scholar

Bre, F., Gimenez, J. M., and Fachinotti, V. D. (2018). Prediction of Wind Pressure Coefficients on Building Surfaces Using Artificial Neural Networks. Energy and Buildings 158, 1429–1441. doi:10.1016/j.enbuild.2017.11.045

CrossRef Full Text | Google Scholar

Breiman, L. (2001). Random Forests. Mach Learn. 45, 5–32. doi:10.1023/a:1010933404324

CrossRef Full Text | Google Scholar

Brunton, S. L., Noack, B. R., and Koumoutsakos, P. (2020). Machine Learning for Fluid Mechanics. Annu. Rev. Fluid Mech. 52, 477–508. doi:10.1146/annurev-fluid-010719-060214

CrossRef Full Text | Google Scholar

Cermak, J. E. (1975). Applications of Fluid Mechanics to Wind Engineering—A Freeman Scholar Lecture. J. Fluids Eng. 97 (1), 9–38. doi:10.1115/1.3447225

CrossRef Full Text | Google Scholar

Chakrabarty, H., Murthy, C. A., and Gupta, A. D. (2013). Application of Pattern Recognition Techniques to Predict Severe Thunderstorms. Ijcte 5 (6), 850–855. doi:10.7763/ijcte.2013.v5.810

CrossRef Full Text | Google Scholar

Chaudhuri, S., Dutta, D., Goswami, S., and Middey, A. (2013). Intensity Forecast of Tropical Cyclones over North Indian Ocean Using Multilayer Perceptron Model: Skill and Performance Verification. Nat. Hazards 65 (1), 97–113. doi:10.1007/s11069-012-0346-7

CrossRef Full Text | Google Scholar

Chaudhuri, S., and Middey, A. (2011). Adaptive Neuro-Fuzzy Inference System to Forecast Peak Gust Speed during Thunderstorms. Meteorology Atmos. Phys. 114 (3-4), 139. doi:10.1007/s00703-011-0158-4

CrossRef Full Text | Google Scholar

Chen, C. H., Wu, J. C., and Chen, J. H. (2008). Prediction of Flutter Derivatives by Artificial Neural Networks. J. wind Eng. Ind. aerodynamics 96 (10-11), 1925–1937. doi:10.1016/j.jweia.2008.02.044

CrossRef Full Text | Google Scholar

Chen, G., and Lombardo, F. T. (2020). An Automated Classification Method of Thunderstorm and Non-thunderstorm Wind Data Based on a Convolutional Neural Network. J. Wind Eng. Ind. Aerodynamics 207, 104407. doi:10.1016/j.jweia.2020.104407

CrossRef Full Text | Google Scholar

Chen, R., Wang, X., Zhang, W., Zhu, X., Li, A., and Yang, C. (2019). A Hybrid CNN-LSTM Model for Typhoon Formation Forecasting. Geoinformatica 23 (3), 375–396. doi:10.1007/s10707-019-00355-0

CrossRef Full Text | Google Scholar

Chen, R., Zhang, W., and Wang, X. (2020). Machine Learning in Tropical Cyclone Forecast Modeling: A Review. Atmosphere 11 (7), 676. doi:10.3390/atmos11070676

CrossRef Full Text | Google Scholar

Chen, Y., and Duan, Z. (2018). A Statistical Dynamics Track Model of Tropical Cyclones for Assessing Typhoon Wind hazard in the Coast of Southeast China. J. Wind Eng. Ind. Aerodynamics 172, 325–340. doi:10.1016/j.jweia.2017.11.014

CrossRef Full Text | Google Scholar

Chen, Y., Kopp, G. A., and Surry, D. (2002). Interpolation of Wind-Induced Pressure Time Series with an Artificial Neural Network. J. Wind Eng. Ind. Aerodynamics 90 (6), 589–615. doi:10.1016/s0167-6105(02)00155-1

CrossRef Full Text | Google Scholar

Chen, Y., Kopp, G. A., and Surry, D. (2003). Prediction of Pressure Coefficients on Roofs of Low Buildings Using Artificial Neural Networks. J. wind Eng. Ind. aerodynamics 91 (3), 423–441. doi:10.1016/s0167-6105(02)00381-1

CrossRef Full Text | Google Scholar

Chen, Z., Yu, X., Chen, G., and Zhou, J. “Cyclone Intensity Estimation Using Multispectral Imagery from the FY-4 Satellite,” in Proceedings of the 2018 International Conference on Audio, Language and Image Processing (ICALIP), Shanghai, China, July 2018 (Piscataway, New Jersey, United States: IEEE), 46–51.

Google Scholar

Cheng, X. X., Zhao, L., and Ge, Y.-J. (2016). Field Measurements on Flow Past a Circular cylinder in Transcritical Reynolds Number Regime. Acta Phys. Sin. 65 (21), 214701. doi:10.7498/aps.65.214701

CrossRef Full Text | Google Scholar

Cherkassky, V., and Mulier, F. M. (2007). Learning from Data: Concepts, Theory, and Methods. Hoboken, New Jersey, United States: John Wiley & Sons.

Google Scholar

Chitsazan, M. A., Sami Fadali, M., and Trzynadlowski, A. M. (2019). Wind Speed and Wind Direction Forecasting Using echo State Network with Nonlinear Functions. Renew. Energ. 131, 879–889. doi:10.1016/j.renene.2018.07.060

CrossRef Full Text | Google Scholar

Chowdhury, J., and Wu, T. (2021). “Aerodynamic Loading Due to Non-synoptic Wind Systems,” in The Oxford Handbook of Non-synoptic Wind Storms. Editors H. Hangan, and A. Kareem (Oxford, United Kingdom: Oxford University Press), 337.

CrossRef Full Text | Google Scholar

Chung, J., Lee, S. W., Chang, S., and Kim, Y. S. “Estimation of Flutter Derivatives of Various Sections Using Numerical Simulation and Neural Network,” in The 2012 World Congress on Advances in Civil, Environmental, and Materials Research (ACEM’ 12), Seoul, Korea, August 26-30, 2012.

Google Scholar

Coffer, B., Kubacki, M., Wen, Y., Zhang, T., Barajas, C. A., and Gobbert, M. K. (2020). “Using Machine Learning Techniques for Supercell Tornado Prediction with Environmental Sounding Data,” in Tech. Rep. HPCF–2020–18, UMBC High Performance Computing Facility (Baltimore County: University of Maryland).

Google Scholar

Collins, W. G., and Tissot, P. (2016). Thunderstorm Predictions Using Artificial Neural networksArtificial Neural Networks-Models and Applications. London: IntechOpen.

Google Scholar

Collins, W., and Tissot, P. (2015). An Artificial Neural Network Model to Predict Thunderstorms within 400 Km2 South Texas Domains. Met. Apps 22 (3), 650–665. doi:10.1002/met.1499

CrossRef Full Text | Google Scholar

Cortes, C., and Vapnik, V. (1995). Support-vector Networks. Mach Learn. 20 (3), 273–297. doi:10.1007/bf00994018

CrossRef Full Text | Google Scholar

Cui, W., and Caracoglia, L. (2019). A New Stochastic Formulation for Synthetic hurricane Simulation over the north Atlantic Ocean. Eng. Structures 199, 109597. doi:10.1016/j.engstruct.2019.109597

CrossRef Full Text | Google Scholar

Davenport, A. G. (1960). Rationale for Determining Design Wind Velocities. J. Struct. Div. 86 (5), 39–68. doi:10.1061/jsdeag.0000521

CrossRef Full Text | Google Scholar

Deierlein, G. G., and Zsarnóczay, A. (2021). State of the Art in Computational Simulation for Natural Hazards Engineering. Second Edition. Plano, Texas: Center Comput. Modeling Simulation. SimCenter.

Google Scholar

DeMaria, M., Mainelli, M., Shay, L. K., Knaff, J. A., and Kaplan, J. (2005). Further Improvements to the Statistical hurricane Intensity Prediction Scheme (SHIPS). Weather Forecast. 20 (4), 531–543. doi:10.1175/waf862.1

CrossRef Full Text | Google Scholar

Deng, L., and Yu, D. (2014). Deep Learning: Methods and Applications. Foundations Trends. Signal. Processing 7 (3–4), 197–387. doi:10.1561/2000000039

CrossRef Full Text | Google Scholar

Derkevorkian, A., Hernandez-Garcia, M., Yun, H.-B., Masri, S. F., and Li, P. (2015). Nonlinear Data-Driven Computational Models for Response Prediction and Change Detection. Struct. Control. Health Monit. 22 (2), 273–288. doi:10.1002/stc.1673

CrossRef Full Text | Google Scholar

Devaraj, A., Murthy, D., and Dontula, A. (2020). Machine-learning Methods for Identifying Social media-based Requests for Urgent Help during Hurricanes. Int. J. Disaster Risk Reduction 51, 101757. doi:10.1016/j.ijdrr.2020.101757

CrossRef Full Text | Google Scholar

Diaz, J., and Joseph, M. B. (2019). Predicting Property Damage from Tornadoes with Zero-Inflated Neural Networks. Weather Clim. Extremes 25, 100216. doi:10.1016/j.wace.2019.100216

CrossRef Full Text | Google Scholar

Dissanayake, M. W. M. G., and Phan-Thien, N. (1994). Neural-network-based Approximations for Solving Partial Differential Equations. Commun. Numer. Meth. Engng. 10 (3), 195–201. doi:10.1002/cnm.1640100303

CrossRef Full Text | Google Scholar

Duraisamy, K., Iaccarino, G., and Xiao, H. (2019). Turbulence Modeling in the Age of Data. Annu. Rev. Fluid Mech. 51, 357–377. doi:10.1146/annurev-fluid-010518-040547

CrossRef Full Text | Google Scholar

Eguchi, Y., Hattori, Y., Nakao, K., James, D., and Zuo, D. (2018). Numerical Pressure Retrieval from Velocity Measurement of a Turbulent Tornado-like Vortex. J. Wind Eng. Ind. Aerodynamics 174, 61–68. doi:10.1016/j.jweia.2017.12.021

CrossRef Full Text | Google Scholar

Elshaer, A., Bitsuamlak, G., and El Damatty, A. (2017). Enhancing Wind Performance of Tall Buildings Using Corner Aerodynamic Optimization. Eng. Structures 136, 133–148. doi:10.1016/j.engstruct.2017.01.019

CrossRef Full Text | Google Scholar

Elshaer, A., Bitsuamlak, G., and El Damatty, A. “June. Aerodynamic Shape Optimization of Tall Buildings Using Twisting and Corner Modifications,” in Proceedings of the 8th International Colloquium on Bluff Body Aerodynamics and Applications, June 2016Northeastern University. Boston, Massachusetts.

Google Scholar

Emanuel, K., Ravela, S., Vivant, E., and Risi, C. (2006). A Statistical Deterministic Approach to hurricane Risk Assessment. Bull. Amer. Meteorol. Soc. 87 (3), 299–314. doi:10.1175/bams-87-3-299

CrossRef Full Text | Google Scholar

Emanuel, K. (2003). Tropical Cyclones. Annu. Rev. Earth Planet. Sci. 31 (1), 75–104. doi:10.1146/annurev.earth.31.100901.141259

CrossRef Full Text | Google Scholar

English, E. C., and Fricke, F. R. (1999). The Interference index and its Prediction Using a Neural Network Analysis of Wind-Tunnel Data. J. Wind Eng. Ind. Aerodynamics 83 (1-3), 567–575. doi:10.1016/s0167-6105(99)00102-6

CrossRef Full Text | Google Scholar

Everingham, M., Van Gool, L., Williams, C. K. I., Winn, J., and Zisserman, A. (2010). The Pascal Visual Object Classes (Voc) challenge. Int. J. Comput. Vis. 88 (2), 303–338. doi:10.1007/s11263-009-0275-4

CrossRef Full Text | Google Scholar

Facchini, L., Betti, M., and Biagini, P. (2014). Neural Network Based Modal Identification of Structural Systems through Output-Only Measurement. Comput. Structures 138, 183–194. doi:10.1016/j.compstruc.2014.01.013

CrossRef Full Text | Google Scholar

Fahlman, S. E. (1988). “Faster-learning Variations of Back-Propagation: An Empirical Study,” in Proc. 1988 Connectionist Models Summer School. Editors D. Touretzky, G. Hinton, and T. Sejnowski (San Mateo, CA: Morgan Kaufmann), 38–51.

Google Scholar

Fang, G., Zhao, L., Cao, S., Ge, Y., and Pang, W. (2018). A Novel Analytical Model for Wind Field Simulation Under Typhoon Boundary Layer Considering Multi-Field Correlation and Height-Dependency. J. Wind. Eng. Ind. Aerodyn. 175, 77–89.

CrossRef Full Text | Google Scholar

Fan, D., Yang, L., Wang, Z., Triantafyllou, M. S., and Karniadakis, G. E. (2020). Reinforcement Learning for bluff Body Active Flow Control in Experiments and Simulations. Proc. Natl. Acad. Sci. USA 117 (42), 26091–26098. doi:10.1073/pnas.2004939117

PubMed Abstract | CrossRef Full Text | Google Scholar

Fernández-Cabán, P. L., Masters, F. J., and Phillips, B. M. (2018). Predicting Roof Pressures on a Low-Rise Structure from Freestream Turbulence Using Artificial Neural Networks. Front. Built Environ. 4, 68. doi:10.3389/fbuil.2018.00068

CrossRef Full Text | Google Scholar

Forthofer, J. M., Butler, B. W., McHugh, C. W., Finney, M. A., Bradshaw, L. S., Stratton, R. D., et al. (2014b). A Comparison of Three Approaches for Simulating fine-scale Surface Winds in Support of Wildland Fire Management. Part II. An Exploratory Study of the Effect of Simulated Winds on Fire Growth Simulations. Int. J. Wildland Fire 23 (7), 982–994. doi:10.1071/wf12090

CrossRef Full Text | Google Scholar

Forthofer, J. M., Butler, B. W., and Wagenbrenner, N. S. (2014a). A Comparison of Three Approaches for Simulating fine-scale Surface Winds in Support of Wildland Fire Management. Part I. Model Formulation and Comparison against Measurements. Int. J. Wildland Fire 23 (7), 969–981. doi:10.1071/wf12089

CrossRef Full Text | Google Scholar

Fu, J. Y., Li, Q. S., and Xie, Z. N. (2006). Prediction of Wind Loads on a Large Flat Roof Using Fuzzy Neural Networks. Eng. Structures 28 (1), 153–161. doi:10.1016/j.engstruct.2005.08.006

CrossRef Full Text | Google Scholar

Fu, J. Y., Liang, S. G., and Li, Q. S. (2007). Prediction of Wind-Induced Pressures on a Large Gymnasium Roof Using Artificial Neural Networks. Comput. structures 85 (3-4), 179–192. doi:10.1016/j.compstruc.2006.08.070

CrossRef Full Text | Google Scholar

Fukami, K., Nabae, Y., Kawai, K., and Fukagata, K. (2019). Synthetic Turbulent Inflow Generator Using Machine Learning. Phys. Rev. Fluids 4 (6), 064603. doi:10.1103/physrevfluids.4.064603

CrossRef Full Text | Google Scholar

Gairola, A., and Bitsuamlak, G. (2019). Numerical Tornado Modeling for Common Interpretation of Experimental Simulators. J. Wind Eng. Ind. Aerodynamics 186, 32–48. doi:10.1016/j.jweia.2018.12.013

CrossRef Full Text | Google Scholar

Gao, D.-L., Chen, W.-L., Li, H., and Hu, H. (2017). Flow Around a Circular cylinder with Slit. Exp. Therm. Fluid Sci. 82, 287–301. doi:10.1016/j.expthermflusci.2016.11.025

CrossRef Full Text | Google Scholar

Ghaboussi, J., and Joghataie, A. (1995). Active Control of Structures Using Neural Networks. J. Eng. Mech. 121 (4), 555–567. doi:10.1061/(asce)0733-9399(1995)121:4(555)

CrossRef Full Text | Google Scholar

Gholizadeh, S., Salajegheh, J., and Salajegheh, E. (2009). An Intelligent Neural System for Predicting Structural Response Subject to Earthquakes. Adv. Eng. Softw. 40 (8), 630–639. doi:10.1016/j.advengsoft.2008.11.008

CrossRef Full Text | Google Scholar

Giffard-Roisin, S., Yang, M., Charpiat, G., Kumler Bonfanti, C., Kégl, B., and Monteleoni, C. (2020). Tropical Cyclone Track Forecasting Using Fused Deep Learning from Aligned Reanalysis Data. Front. Big Data 3, 1–13. doi:10.3389/fdata.2020.00001

PubMed Abstract | CrossRef Full Text | Google Scholar

Gillmeier, S., Sterling, M., and Hemida, H. (2019). Simulating Tornado-like Flows: the Effect of the Simulator's Geometry. Meccanica 54 (15), 2385–2398. doi:10.1007/s11012-019-01082-4

CrossRef Full Text | Google Scholar

Goodfellow, I., Bengio, Y., and Courville, A. (2016). Deep Learning, 1. Cambridge: MIT press, 2.

Google Scholar

Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., et al. (2014). “Generative Adversarial Nets,” in Advances in Neural Information Processing Systems. Editors M. I. Jordan, Y. LeCun, and S. A. Solla (Cambridge, Massachusetts, United States: MIT Press), 2672–2680.

Google Scholar

Gray, W. M. (1968). Global View of the Origin of Tropical Disturbances and Storms. Mon. Wea. Rev. 96 (10), 669–700. doi:10.1175/1520-0493(1968)096<0669:gvotoo>2.0.co;2

CrossRef Full Text | Google Scholar

Gray, W. M. (1979). “Hurricanes: Their Formation, Structure and Likely Role in the Tropical Circulation. Meteorology over the Tropical Oceans,” in Meteorology over the Tropical Oceans. Editor D. B. Shaw (James Glaisher House, Grenville, Bracknell: Royal Meteorological Society), 155–218.

Google Scholar

Haines, M., and Taylor, I. (2018). Numerical Investigation of the Flow Field Around Low Rise Buildings Due to a Downburst Event Using Large Eddy Simulation. J. Wind Eng. Ind. Aerodynamics 172, 12–30. doi:10.1016/j.jweia.2017.10.028

CrossRef Full Text | Google Scholar

Hall, T. M., and Jewson, S. (2007). Statistical Modelling of North Atlantic Tropical Cyclone Tracks. Tellus A: Dynamic Meteorology and Oceanography 59 (4), 486–498. doi:10.1111/j.1600-0870.2007.00240.x

CrossRef Full Text | Google Scholar

Hangan, H., Refan, M., Jubayer, C., Romanic, D., Parvu, D., LoTufo, J., et al. (2017). Novel Techniques in Wind Engineering. J. Wind Eng. Ind. Aerodynamics 171, 12–33. doi:10.1016/j.jweia.2017.09.010

CrossRef Full Text | Google Scholar

Hao, J., and Wu, T. (2018). Downburst-induced Transient Response of a Long-Span Bridge: A CFD-CSD-Based Hybrid Approach. J. Wind Eng. Ind. Aerodynamics 179, 273–286. doi:10.1016/j.jweia.2018.06.006

CrossRef Full Text | Google Scholar

Hao, J., and Wu, T. (2017). Nonsynoptic Wind-Induced Transient Effects on Linear Bridge Aerodynamics. J. Eng. Mech. 143 (9), 04017092. doi:10.1061/(asce)em.1943-7889.0001313

CrossRef Full Text | Google Scholar

Hao, J., and Wu, T. (2020). Numerical Analysis of a Long-Span Bridge Response to Tornado-like Winds. Wind and Structures 31 (5), 459–472.

Google Scholar

Hao, J., and Wu, T. “Tornado-induced Effects on Aerostatic and Aeroelastic Behaviors of Long-Span Bridge,” in Proceeding of the 2016 World Congress on Advances in Civil Environmental & Materials Research, Jeju, Korea, September 2016.

Google Scholar

Hasegawa, K., Fukami, K., Murata, T., and Fukagata, K. “Data-driven Reduced Order Modeling of Flows Around Two-Dimensional bluff Bodies of Various Shapes,” in Fluids Engineering Division Summer Meeting, American Society of Mechanical Engineers, San Francisco, CA, July 28–August 1, 2019, V002T02A075.

Google Scholar

Hasegawa, K., Fukami, K., Murata, T., and Fukagata, K. (2020). Machine-learning-based Reduced-Order Modeling for Unsteady Flows Around bluff Bodies of Various Shapes. Theor. Comput. Fluid Dyn. 34, 367–383. doi:10.1007/s00162-020-00528-w

CrossRef Full Text | Google Scholar

Hawbecker, P. (2021). “Mesoscale, Microscale, and Numerical Models,” in The Oxford Handbook of Non-synoptic Wind Storms. Editors H. Hangan, and A. Kareem (Oxford, United Kingdom: Oxford University Press), 239.

CrossRef Full Text | Google Scholar

Hayashi, K., and Ohsaki, M. (2020). Reinforcement Learning for Optimum Design of a Plane Frame under Static Loads. Eng. Comput. 37, 1999–2011. doi:10.1007/s00366-019-00926-7

CrossRef Full Text | Google Scholar

He, Y. C., Li, Y. Z., Chan, P. W., Fu, J. Y., Wu, J. R., and Li, Q. S. (2019). A Height-Resolving Model of Tropical Cyclone Pressure Field. J. Wind. Eng. Ind. Aerodyn. 186, 84–93.

CrossRef Full Text | Google Scholar

Hinton, G. E., Osindero, S., and Teh, Y.-W. (2006). A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 18 (7), 1527–1554. doi:10.1162/neco.2006.18.7.1527

PubMed Abstract | CrossRef Full Text | Google Scholar

Hochreiter, S., and Schmidhuber, J. (1997). Long Short-Term Memory. Neural Comput. 9 (8), 1735–1780. doi:10.1162/neco.1997.9.8.1735

PubMed Abstract | CrossRef Full Text | Google Scholar

Holmes, J. D. (1999). “Modeling of Extreme Thunderstorm Winds for Wind Loading of Structures and Risk Assessment,” in Wind Engineering into the 21st Century, Proceedings of the Tenth International Conference on Wind Engineering, Copenhagen, Denmark, 21-24 June 1999. Editor A. Larsen (Boca Raton, Florida, United States: CRC Press), 1409–1415.

Google Scholar

Holton, J. R., and Hakim, G. J. (2013). An Introduction to Dynamic Meteorology. Fifth edition. Amsterdam: Academic Press.

Google Scholar

Hopfield, J. J. (1982). Neural Networks and Physical Systems with Emergent Collective Computational Abilities. Proc. Natl. Acad. Sci. 79 (8), 2554–2558. doi:10.1073/pnas.79.8.2554

PubMed Abstract | CrossRef Full Text | Google Scholar

Hornik, K. (1991). Approximation Capabilities of Multilayer Feedforward Networks. Neural networks 4 (2), 251–257. doi:10.1016/0893-6080(91)90009-t

CrossRef Full Text | Google Scholar

Hoshino, N., Iida, Y., and Uematsu, Y. (2018). Effects of Non-stationarity of Downburst on the Wind Loading of Buildings. J. Wind Eng. 43 (1), 1–13. doi:10.5359/jwe.43.1

CrossRef Full Text | Google Scholar

Hou, F., and Sarkar, P. P. (2020). Aeroelastic Model Tests to Study Tall Building Vibration in Boundary-Layer and Tornado Winds. Eng. Structures 207, 110259. doi:10.1016/j.engstruct.2020.110259

CrossRef Full Text | Google Scholar

Hu, G., and Kwok, K. C. S. (2020). Predicting Wind Pressures Around Circular Cylinders Using Machine Learning Techniques. J. Wind Eng. Ind. Aerodynamics 198, 104099. doi:10.1016/j.jweia.2020.104099

CrossRef Full Text | Google Scholar

Hu, G., Liu, L., Tao, D., Song, J., Tse, K. T., and Kwok, K. C. S. (2020). Deep Learning-Based Investigation of Wind Pressures on Tall Building under Interference Effects. J. Wind Eng. Ind. Aerodynamics 201, 104138. doi:10.1016/j.jweia.2020.104138

CrossRef Full Text | Google Scholar

Huang, D., Shiqing, H., Xuhui, H., and Xue, Z. (2017). Prediction of Wind Loads on High-Rise Building Using a BP Neural Network Combined with POD. J. Wind Eng. Ind. Aerodynamics 170, 1–17. doi:10.1016/j.jweia.2017.07.021

CrossRef Full Text | Google Scholar

Huang, G., He, H., Mehta, K. C., and Liu, X. (2015). Data-based Probabilistic Damage Estimation for Asphalt Shingle Roofing. J. Struct. Eng. 141 (12), 04015065. doi:10.1061/(asce)st.1943-541x.0001300

CrossRef Full Text | Google Scholar

Huang, W. F., and Xu, Y. L. (2013). Prediction of Typhoon Design Wind Speed and Profile over Complex Terrain. Struct. Eng. Mech. 45 (1), 1–18. doi:10.12989/sem.2013.45.1.001

CrossRef Full Text | Google Scholar

Huang, W. Y., and Lippmann, R. P. (1988). “Neural Net and Traditional Classifiers,” in Neural Information Processing Systems. Editor D. Z. Anderson (Berlin/Heidelberg, Germany: Springer Science & Business Media), 387–396.

Google Scholar

Huo, S., Hemida, H., and Sterling, M. (2020). Numerical Study of Debris Flight in a Tornado-like Vortex. J. Fluids Structures 99, 103134. doi:10.1016/j.jfluidstructs.2020.103134

CrossRef Full Text | Google Scholar

Iida, Y., and Uematsu, Y. (2019). Numerical Study of Wind Loads on Buildings Induced by Downbursts. J. Wind Eng. Ind. Aerodynamics 191, 103–116. doi:10.1016/j.jweia.2019.05.018

CrossRef Full Text | Google Scholar

Imran, M., Elbassuoni, S., Castillo, C., Diaz, F., and Meier, P. “Extracting Information Nuggets from Disaster-Related Messages in Social media,” in Proceedings of the 10th International Conference on Information Systems for Crisis Response and Management, Information Systems for Crisis Response and Management, Baden-Baden, Germany, May 2013, 791–801.

Google Scholar

Imran, M., Mitra, P., and Castillo, C. “Twitter as a Lifeline: Human-Annotated Twitter Corpora for NLP of Crisis-Related Messages,” in Proceedings of the Tenth International Conference on Language Resources and Evaluation (LREC 2016), European Language Resources Association (ELRA), Portorož, Slovenia, May 2016.

Google Scholar

Ishihara, T., Oh, S., and Tokuyama, Y. (2011). Numerical Study on Flow fields of Tornado-like Vortices Using the LES Turbulence Model. J. Wind Eng. Ind. Aerodynamics 99 (4), 239–248. doi:10.1016/j.jweia.2011.01.014

CrossRef Full Text | Google Scholar

Jackson, P. S., and Hunt, J. C. R. (1975). Turbulent Wind Flow over a Low hill. Q.J R. Met. Soc. 101 (430), 929–955. doi:10.1002/qj.49710143015

CrossRef Full Text | Google Scholar

Jesson, M., Sterling, M., Letchford, C., and Haines, M. (2015). Aerodynamic Forces on Generic Buildings Subject to Transient, Downburst-type Winds. J. wind Eng. Ind. aerodynamics 137, 58–68. doi:10.1016/j.jweia.2014.12.003

CrossRef Full Text | Google Scholar

Jiang, X., and Adeli, H. (2008). Dynamic Fuzzy Wavelet Neuroemulator for Non-linear Control of Irregular Building Structures. Int. J. Numer. Meth. Engng 74 (7), 1045–1066. doi:10.1002/nme.2195

CrossRef Full Text | Google Scholar

Jiang, X., and Adeli, H. (2005). Dynamic Wavelet Neural Network for Nonlinear Identification of Highrise Buildings. Comp-aided Civil Eng. 20 (5), 316–330. doi:10.1111/j.1467-8667.2005.00399.x

CrossRef Full Text | Google Scholar

Jubayer, C., Elatar, A., and Hangan, H., “Pressure Distributions on a Low-Rise Building in a Laboratory Simulated Downburst.” in Proceedings of the 8th International Colloquium on Bluff Body Aerodynamics and Applications, Boston, Massachusetts, USA. June 2016

Google Scholar

Junayed, C., Jubayer, C., Parvu, D., Romanic, D., and Hangan, H. (2019). Flow Field Dynamics of Large-Scale Experimentally Produced Downburst Flows. J. Wind Eng. Ind. Aerodynamics 188, 61–79. doi:10.1016/j.jweia.2019.02.008

CrossRef Full Text | Google Scholar

Jung, S., Ghaboussi, J., and Kwon, S.-D. (2004). Estimation of Aeroelastic Parameters of Bridge Decks Using Neural Networks. J. Eng. Mech. 130 (11), 1356–1364. doi:10.1061/(asce)0733-9399(2004)130:11(1356)

CrossRef Full Text | Google Scholar

Kamangir, H., Collins, W., Tissot, P., and King, S. A. (2020). Deep‐learning Model Used to Predict Thunderstorms within 400 Km2 of South Texas Domains. Meteorol. Appl. 27 (2), e1905. doi:10.1002/met.1905

CrossRef Full Text | Google Scholar

Kareem, A. (2020). Emerging Frontiers in Wind Engineering: Computing, Stochastics, Machine Learning and beyond. J. Wind Eng. Ind. Aerodynamics 206, 104320. doi:10.1016/j.jweia.2020.104320

CrossRef Full Text | Google Scholar

Kareem, A., and Wu, T. (2013). Wind-induced Effects on bluff Bodies in Turbulent Flows: Nonstationary, Non-gaussian and Nonlinear Features. J. Wind Eng. Ind. Aerodynamics 122, 21–37. doi:10.1016/j.jweia.2013.06.002

CrossRef Full Text | Google Scholar

Kawaguchi, M., Tamura, T., and Kawai, H. (2019). Analysis of Tornado and Near-Ground Turbulence Using a Hybrid Meteorological Model/engineering LES Method. Int. J. Heat Fluid Flow 80, 108464. doi:10.1016/j.ijheatfluidflow.2019.108464

CrossRef Full Text | Google Scholar

Kelley, H. J. (1960). Gradient Theory of Optimal Flight Paths. Ars J. 30 (10), 947–954. doi:10.2514/8.5282

CrossRef Full Text | Google Scholar

Khalatbarisoltani, A., Soleymani, M., and Khodadadi, M. (2019). Online Control of an Active Seismic System via Reinforcement Learning. Struct. Control. Health Monit. 26 (3), e2298. doi:10.1002/stc.2298

CrossRef Full Text | Google Scholar

Khanduri, A. C., Bédard, C., and Stathopoulos, T. (1997). Modelling Wind-Induced Interference Effects Using Backpropagation Neural Networks. J. wind Eng. Ind. aerodynamics 72, 71–79. doi:10.1016/s0167-6105(97)00259-6

CrossRef Full Text | Google Scholar

Khodabandehlou, H., Pekcan, G., Fadali, M. S., and Salem, M. M. A. (2018). Active Neural Predictive Control of Seismically Isolated Structures. Struct. Control. Health Monit. 25 (1), e2061. doi:10.1002/stc.2061

CrossRef Full Text | Google Scholar

Khosravi, A., Koury, R. N. N., Machado, L., and Pabon, J. J. G. (2018b). Prediction of Wind Speed and Wind Direction Using Artificial Neural Network, Support Vector Regression and Adaptive Neuro-Fuzzy Inference System. Sustainable Energ. Tech. Assessments 25, 146–160. doi:10.1016/j.seta.2018.01.001

CrossRef Full Text | Google Scholar

Khosravi, A., Machado, L., and Nunes, R. O. (2018a). Time-series Prediction of Wind Speed Using Machine Learning Algorithms: A Case Study Osorio Wind Farm, Brazil. Appl. Energ. 224, 550–566. doi:10.1016/j.apenergy.2018.05.043

CrossRef Full Text | Google Scholar

Kim, J., and Lee, C. (2020). Deep Unsupervised Learning of Turbulence for Inflow Generation at Various Reynolds Numbers. J. Comput. Phys. 406, 109216. doi:10.1016/j.jcp.2019.109216

CrossRef Full Text | Google Scholar

Kim, M., Park, M.-S., Im, J., Park, S., and Lee, M.-I. (2019). Machine Learning Approaches for Detecting Tropical Cyclone Formation Using Satellite Data. Remote Sensing 11 (10), 1195. doi:10.3390/rs11101195

CrossRef Full Text | Google Scholar

Kim, S., Kim, H., Lee, J., Yoon, S., Kahou, S. E., Kashinath, K., et al. “Deep-hurricane-tracker: Tracking and Forecasting Extreme Climate Events,” in Proceedings of the 2019 IEEE Winter Conference on Applications of Computer Vision (WACV), Waikoloa, HI, USA, January 2019 (Piscataway, New Jersey, United States: IEEE), 1761–1769.

Google Scholar

Kolmogorov, A. N. (1941). The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds Numbers. Cr Acad. Sci. URSS 30, 301–305.

Google Scholar

Križan, J., Gašparac, G., Kozmar, H., Antonić, O., and Grisogono, B. (2015). Designing Laboratory Wind Simulations Using Artificial Neural Networks. Theor. Appl. climatology 120 (3-4), 723–736. doi:10.1007/s00704-014-1201-4

CrossRef Full Text | Google Scholar

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Imagenet Classification with Deep Convolutional Neural Networks. Adv. Neural Inf. Process. Syst. 60, 84–90. doi:10.1145/3065386

CrossRef Full Text | Google Scholar

Kuai, L., Haan, F. L. J., Gallus, W. A. J., and Sarkar, P. P. (2008). CFD Simulations of the Flow Field of a Laboratory-Simulated Tornado for Parameter Sensitivity Studies and Comparison with Field Measurements. Wind and Structures 11 (2), 75–96. doi:10.12989/was.2008.11.2.075

CrossRef Full Text | Google Scholar

Kumar, G., and Malik, H. (2016). Generalized Regression Neural Network Based Wind Speed Prediction Model for Western Region of India. Proced. Comput. Sci. 93, 26–32. doi:10.1016/j.procs.2016.07.177

CrossRef Full Text | Google Scholar

Kutz, J. N. (2017). Deep Learning in Fluid Dynamics. J. Fluid Mech. 814, 1–4. doi:10.1017/jfm.2016.803

CrossRef Full Text | Google Scholar

Lagerquist, R. A., Homeyer, C. R., McGovern, A., Potvin, C. K., Sandmael, T., and Smith, T. M. “Deep Learning for Real-Time Storm-Based Tornado Prediction,” in Proceedings of the 29th Conference on Severe Local Storms, Stowe, VT, October 2018 (Boston, Massachusetts, United States: AMS).

Google Scholar

Lagerquist, R., McGovern, A., Homeyer, C. R., Gagne, D. J., and Smith, T. (2020). Deep Learning on Three-Dimensional Multiscale Data for Next-Hour Tornado Prediction. Monthly Weather Rev. 148, 2837–2861. doi:10.1175/mwr-d-19-0372.1

CrossRef Full Text | Google Scholar

Lagerquist, R., McGovern, A., and Smith, T. (2017). Machine Learning for Real-Time Prediction of Damaging Straight-Line Convective Wind. Weather Forecast. 32 (6), 2175–2193. doi:10.1175/waf-d-17-0038.1

CrossRef Full Text | Google Scholar

Lahouar, A., and Slama, J. B. H. “Wind Speed and Direction Prediction for Wind Farms Using Support Vector Regression.” in Proceedings of the 2014 5th International Renewable Energy Congress (IREC). Hammamet, Tunisia. March 2014 (Piscataway, New Jersey, United States: IEEE), 1–6.

Google Scholar

Lakshmanan, V., Stumpf, G., and Witt, A. “A Neural Network for Detecting and Diagnosing Tornadic Circulations Using the Mesocyclone Detection and Near Storm Environment Algorithms,” in Proceedings of the AI Applications with a Nowcasting Flavor (Joint between the Fourth Conference on Artificial Intelligence and the 21st International Conference on Interactive Information and Processing Systems (IIPS) for Meteorology, Oceanography, and Hydrology), San Diego, CA, USA, January 2005 (Boston, Massachusetts, United States: AMS).

Google Scholar

Le, V., and Caracoglia, L. (2020). A Neural Network Surrogate Model for the Performance Assessment of a Vertical Structure Subjected to Non-stationary, Tornadic Wind Loads. Comput. Structures 231, 106208. doi:10.1016/j.compstruc.2020.106208

CrossRef Full Text | Google Scholar

LeCun, Y., Boser, B., Denker, J. S., Henderson, D., Howard, R. E., Hubbard, W., et al. (1989). Backpropagation Applied to Handwritten Zip Code Recognition. Neural Comput. 1 (4), 541–551. doi:10.1162/neco.1989.1.4.541

CrossRef Full Text | Google Scholar

Letchford, C. W., Mans, C., and Chay, M. T. (2002). Thunderstorms—their Importance in Wind Engineering (A Case for the Next Generation Wind Tunnel). J. Wind Eng. Ind. Aerodynamics 90 (12-15), 1415–1433. doi:10.1016/s0167-6105(02)00262-3

CrossRef Full Text | Google Scholar

Li, G., and Shi, J. (2010). On Comparing Three Artificial Neural Networks for Wind Speed Forecasting. Appl. Energ. 87 (7), 2313–2320. doi:10.1016/j.apenergy.2009.12.013

CrossRef Full Text | Google Scholar

Li, S., Laima, S., and Li, H. (2018). Data-driven Modeling of Vortex-Induced Vibration of a Long-Span Suspension Bridge Using Decision Tree Learning and Support Vector Regression. J. Wind Eng. Ind. Aerodynamics 172, 196–211. doi:10.1016/j.jweia.2017.10.022

CrossRef Full Text | Google Scholar

Li, S., Snaiki, R., and Wu, T. (2021a). A Knowledge‐enhanced Deep Reinforcement Learning‐based Shape Optimizer for Aerodynamic Mitigation of Wind‐sensitive Structures. Computer‐Aided Civil Infrastructure Eng. 36 (6), 733–746. doi:10.1111/mice.12655

CrossRef Full Text | Google Scholar

Li, S., Snaiki, R., and Wu, T. (2021b). Active Simulation of Transient Wind Field in a Multiple-Fan Wind Tunnel via Deep Reinforcement Learning. J. Eng. Mech. 147 (9), 04021056. doi:10.1061/(asce)em.1943-7889.0001967

CrossRef Full Text | Google Scholar

Li, T., Wu, T., and Liu, Z. (2020). Nonlinear Unsteady Bridge Aerodynamics: Reduced-Order Modeling Based on Deep LSTM Networks. J. Wind Eng. Ind. Aerodynamics 198, 104116. doi:10.1016/j.jweia.2020.104116

CrossRef Full Text | Google Scholar

Li, Z., and Li, C. (2018). “Selection of Kernel Function for Least Squares Support Vector Machines in Downburst Wind Speed Forecasting,” in Proceedings of the 2018 11th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China (Piscataway, New Jersey, United States: IEEE), 337–341. doi:10.1109/iscid.2018.10178

CrossRef Full Text | Google Scholar

Liang, X. (2019). Image‐based post‐disaster Inspection of Reinforced concrete Bridge Systems Using Deep Learning with Bayesian Optimization. Computer‐Aided Civil Infrastructure Eng. 34 (5), 415–430. doi:10.1111/mice.12425

CrossRef Full Text | Google Scholar

Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T., Tassa, Y., et al. (2015). Continuous Control with Deep Reinforcement Learning. arXiv. arXiv:1509.02971.

Google Scholar

Lin, T. Y., Goyal, P., Girshick, R., He, K., and Dollár, P. “Focal Loss for Dense Object Detection,” in Proceedings of the IEEE international conference on computer vision, Venice, Italy, October 2017, 2980–2988. doi:10.1109/iccv.2017.324

CrossRef Full Text | Google Scholar

Litta, A. J., Idicula, S. M., and Francis, C. N. (2012). Artificial Neural Network Model for the Prediction of Thunderstorms over kolkata. Int. J. Comput. Appl. 50 (11), 50–55. doi:10.5120/7819-1135

CrossRef Full Text | Google Scholar

Liu, Z., Cao, Y., Cao, J., Wang, Y., and Cao, S. (2021). Numerical Study of Tornado-Borne Debris on a Low-Rise Building through Large Eddy Simulation. J. Fluids Structures 106, 103379. doi:10.1016/j.jfluidstructs.2021.103379

CrossRef Full Text | Google Scholar

Liu, Z., and Ishihara, T. (2015). Numerical Study of Turbulent Flow fields and the Similarity of Tornado Vortices Using Large-Eddy Simulations. J. Wind Eng. Ind. Aerodynamics 145, 42–60. doi:10.1016/j.jweia.2015.05.008

CrossRef Full Text | Google Scholar

López, P., Velo, R., and Maseda, F. (2008). Effect of Direction on Wind Speed Estimation in Complex Terrain Using Neural Networks. Renew. Energ. 33 (10), 2266–2272. doi:10.1016/j.renene.2007.12.020

CrossRef Full Text | Google Scholar

Lute, V., Upadhyay, A., and Singh, K. K. (2009). Support Vector Machine Based Aerodynamic Analysis of cable Stayed Bridges. Adv. Eng. Softw. 40 (9), 830–835. doi:10.1016/j.advengsoft.2009.01.008

CrossRef Full Text | Google Scholar

Mandic, D., and Chambers, J. (2001). Recurrent Neural Networks for Prediction: Learning Algorithms, Architectures and Stability. Hoboken, New Jersey, United States: John Wiley & Sons.

Google Scholar

Manna, S., and Nakai, H. “Effectiveness of Word Embeddings on Classifiers: A Case Study with Tweets,” in Proceedings of the 2019 IEEE 13th International Conference on Semantic Computing (ICSC), Newport Beach, CA, USA, January 2019 (Piscataway, New Jersey, United States: IEEE), 158–161.

Google Scholar

Manohar, K., Brunton, B. W., Kutz, J. N., and Brunton, S. L. (2018). Data-driven Sparse Sensor Placement for Reconstruction: Demonstrating the Benefits of Exploiting Known Patterns. IEEE Control. Syst. Mag. 38 (3), 63–86. doi:10.1109/MCS.2018.2810460

CrossRef Full Text | Google Scholar

Martínez-Vázquez, P., and Rodríguez-Cuevas, N. (2007). Wind Field Reproduction Using Neural Networks and Conditional Simulation. Eng. structures 29 (7), 1442–1449. doi:10.1016/j.engstruct.2006.08.024

CrossRef Full Text | Google Scholar

Marzban, C. (2000). A Neural Network for Tornado Diagnosis: Managing Local Minima. Neural Comput. Appl. 9, 133–141. doi:10.1007/s005210070024

CrossRef Full Text | Google Scholar

Marzban, C., Paik, H., and Stumpf, G. J. (1997). Neural Networks vs. Gaussian Discriminant Analysis. AI Appl. 11 (1), 49–58.

Google Scholar

Marzban, C., and Stumpf, G. J. (1998). A Neural Network for Damaging Wind Prediction. Wea. Forecast. 13, 151–163. doi:10.1175/1520-0434(1998)013<0151:annfdw>2.0.co;2

CrossRef Full Text | Google Scholar

Marzban, C., and Stumpf, G. J. (1996). A Neural Network for Tornado Prediction Based on Doppler Radar-Derived Attributes. J. Appl. Meteorol. 35, 617–626. doi:10.1175/1520-0450(1996)035<0617:annftp>2.0.co;2

CrossRef Full Text | Google Scholar

Maskey, M., Ramachandran, R., Ramasubramanian, M., Gurung, I., Freitag, B., Kaulfus, A., et al. (2020). Deepti: Deep-Learning-Based Tropical Cyclone Intensity Estimation System. IEEE J. Sel. Top. Appl. Earth Observations Remote Sensing 13, 4271–4281. doi:10.1109/jstars.2020.3011907

CrossRef Full Text | Google Scholar

Mason, M. S., Wood, G. S., and Fletcher, D. F. (2009). Numerical Simulation of Downburst Winds. J. Wind Eng. Ind. Aerodynamics 97 (11-12), 523–539. doi:10.1016/j.jweia.2009.07.010

CrossRef Full Text | Google Scholar

Masri, S. F., Chassiakos, A. G., and Caughey, T. K. (1993). Identification of Nonlinear Dynamic Systems Using Neural Networks. J. Appl. Mech. 60 (1), 123–133. doi:10.1115/1.2900734

CrossRef Full Text | Google Scholar

Matsumoto, M., Kobayashi, Y., and Shirato, H. (1996). The Influence of Aerodynamic Derivatives on Flutter. J. Wind Eng. Ind. Aerodynamics 60, 227–239. doi:10.1016/0167-6105(96)00036-0

CrossRef Full Text | Google Scholar

Maulik, U., and Bandyopadhyay, S. (2002). Performance Evaluation of Some Clustering Algorithms and Validity Indices. IEEE Trans. Pattern Anal. Machine Intell. 24 (12), 1650–1654. doi:10.1109/tpami.2002.1114856

CrossRef Full Text | Google Scholar

Mayo, M., Wakes, S., and Anderson, C. “Neural Networks for Predicting the Output of Wind Flow Simulations over Complex Topographies,” in Proceedings of the 2018 IEEE International Conference on Big Knowledge (ICBK), Singapore, November 2018 (Piscataway, New Jersey, United States: IEEE), 184–191.

Google Scholar

McCann, D. W. (1992). A Neural Network Short-Term Forecast of Significant Thunderstorms. Wea. Forecast. 7 (3), 525–534. doi:10.1175/1520-0434(1992)007<0525:annstf>2.0.co;2

CrossRef Full Text | Google Scholar

McCarthy, J. (2007). From Here to Human-Level AI. Artif. Intelligence 171 (18), 1174–1182. doi:10.1016/j.artint.2007.10.009

CrossRef Full Text | Google Scholar

McCulloch, W. S., and Pitts, W. (1943). A Logical Calculus of the Ideas Immanent in Nervous Activity. Bull. Math. Biophys. 5 (4), 115–133. doi:10.1007/bf02478259

CrossRef Full Text | Google Scholar

Medina, B., Carey, L., Amiot, C., Mecikalski, R., Roeder, W., McNamara, T., et al. (2019). A Random forest Method to Forecast Downbursts Based on Dual-Polarization Radar Signatures. Remote Sensing 11 (7), 826. doi:10.3390/rs11070826

CrossRef Full Text | Google Scholar

Medsker, L., and Jain, L. C. (1999). Recurrent Neural Networks: Design and Applications. Boca Raton, Florida, United States: CRC Press.

Google Scholar

Michael, B. (20172017). Tropical Cyclone Genesis Forecasting and Pre-genesis Forecasts Report. Miami, FL, USA: National Hurricane Center.

Google Scholar

Micheli, L., Hong, J., Laflamme, S., and Alipour, A. (2020). Surrogate Models for High Performance Control Systems in Wind-Excited Tall Buildings. Appl. Soft Comput. 90, 106133. doi:10.1016/j.asoc.2020.106133

CrossRef Full Text | Google Scholar

Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., et al. (2015). Human-level Control through Deep Reinforcement Learning. nature 518 (7540), 529–533. doi:10.1038/nature14236

PubMed Abstract | CrossRef Full Text | Google Scholar

Mohandes, M. A., Halawani, T. O., Rehman, S., and Hussain, A. A. (2004). Support Vector Machines for Wind Speed Prediction. Renew. Energ. 29 (6), 939–947. doi:10.1016/j.renene.2003.11.009

CrossRef Full Text | Google Scholar

Mohri, M., Rostamizadeh, A., and Talwalkar, A. (2018). Foundations of Machine Learning. Cambridge, Massachusetts, United States: MIT press.

Google Scholar

Moradi Kordmahalleh, M., Gorji Sefidmazgi, M., and Homaifar, A. (2016). “A Sparse Recurrent Neural Network for Trajectory Prediction of atlantic Hurricanes,” in Proceedings of the Genetic and Evolutionary Computation Conference 2016. Editor F. Neumann (New York, United States: Association for Computing Machinery), 957–964.

CrossRef Full Text | Google Scholar

More, A., and Deo, M. C. (2003). Forecasting Wind with Neural Networks. Mar. structures 16 (1), 35–49. doi:10.1016/s0951-8339(02)00053-9

CrossRef Full Text | Google Scholar

Murphy, K. P. (2012). Machine Learning: A Probabilistic Perspective. Cambridge, Massachusetts, United States: MIT press.

Google Scholar

Nikose, T. J., and Sonparote, R. S. (2020). Computing Dynamic Across-Wind Response of Tall Buildings Using Artificial Neural Network. J. Supercomput 76 (5), 3788–3813. doi:10.1007/s11227-018-2708-8

CrossRef Full Text | Google Scholar

Nikose, T. J., and Sonparote, R. S. (2019a). Dynamic along Wind Response of Tall Buildings Using Artificial Neural Network. Cluster Comput. 22 (2), 3231–3246. doi:10.1007/s10586-018-2027-0

CrossRef Full Text | Google Scholar

Nikose, T. J., and Sonparote, R. S. (2019b). Dynamic Wind Response of Tall Buildings Using Artificial Neural Network. The Struct. Des. Tall Spec. Buildings 28 (13), e1657. doi:10.1002/tal.1657

CrossRef Full Text | Google Scholar

Oh, B. K., Glisic, B., Kim, Y., and Park, H. S. (2019). Convolutional Neural Network-Based Wind Induced Response Estimation Model for Tall Buildings. Comput. Aided Civ. Infrastruct. Eng. 34, 843–858. doi:10.1111/mice.12476

CrossRef Full Text | Google Scholar

Oh, B. K., Kim, K. J., Kim, Y., Park, H. S., and Adeli, H. (2017). Evolutionary Learning Based Sustainable Strain Sensing Model for Structural Health Monitoring of High-Rise Buildings. Appl. Soft Comput. 58, 576–585. doi:10.1016/j.asoc.2017.05.029

CrossRef Full Text | Google Scholar

O’Neal, A., Rodgers, B., Segler, J., Murthy, D., Lakuduva, N., Johnson, M., et al. “Training an Emergency-Response Image Classifier on Signal Data,” in Proceedings of the 2018 17th IEEE International Conference on Machine Learning and Applications (ICMLA), Orlando, FL, USA, December 2018 (Piscataway, New Jersey, United States: IEEE), 751–756.

Google Scholar

Oreskovic, C., Orf, L. G., and Savory, E. (2018). A Parametric Study of Downbursts Using a Full-Scale Cooling Source Model. J. Wind Eng. Ind. Aerodynamics 180, 168–181. doi:10.1016/j.jweia.2018.07.020

CrossRef Full Text | Google Scholar

Oreskovic, C., and Savory, E. (2018). Evolution and Scaling of a Simulated Downburst-Producing Thunderstorm Outflow. Wind and Structures 26 (3), 147–161. doi:10.12989/was.2018.26.3.147

CrossRef Full Text | Google Scholar

Pan, B., Xu, X., and Shi, Z. (2019). Tropical Cyclone Intensity Prediction Based on Recurrent Neural Networks. Electron. Lett. 55 (7), 413–415. doi:10.1049/el.2018.8178

CrossRef Full Text | Google Scholar

Panofsky, H. A., and McCormick, R. A. (1960). The Spectrum of Vertical Velocity Near the Surface. Q.J R. Met. Soc. 86 (370), 495–503. doi:10.1002/qj.49708637006

CrossRef Full Text | Google Scholar

Park, M.-S., Kim, M., Lee, M.-I., Im, J., and Park, S. (2016). Detection of Tropical Cyclone Genesis via Quantitative Satellite Ocean Surface Wind Pattern and Intensity Analyses Using Decision Trees. Remote sensing Environ. 183, 205–214. doi:10.1016/j.rse.2016.06.006

CrossRef Full Text | Google Scholar

Pei, J. S., Wright, J. P., and Smyth, A. W. (2005). Mapping Polynomial Fitting into Feedforward Neural Networks for Modeling Nonlinear Dynamic Systems and beyond. Comput. Methods Appl. Mech. Eng. 194 (42-44), 4481–4505. doi:10.1016/j.cma.2004.12.010

CrossRef Full Text | Google Scholar

Pi, Y., Nath, N. D., and Behzadan, A. H. (2020). Convolutional Neural Networks for Object Detection in Aerial Imagery for Disaster Response and Recovery. Adv. Eng. Inform. 43, 101009. doi:10.1016/j.aei.2019.101009

CrossRef Full Text | Google Scholar

Potter, C. W., and Negnevitsky, M. (2006). Very Short-Term Wind Forecasting for Tasmanian Power Generation. IEEE Trans. Power Syst. 21 (2), 965–972. doi:10.1109/tpwrs.2006.873421

CrossRef Full Text | Google Scholar

Pouyanfar, S., Sadiq, S., Yan, Y., Tian, H., Tao, Y., Reyes, M. P., et al. (2018). A Survey on Deep Learning: Algorithms, Techniques, and Applications. ACM Comput. Surv. (Csur) 51 (5), 1–36. doi:10.1145/3234150

CrossRef Full Text | Google Scholar

Psichogios, D. C., and Ungar, L. H. (1992). A Hybrid Neural Network-First Principles Approach to Process Modeling. Aiche J. 38 (10), 1499–1511. doi:10.1002/aic.690381003

CrossRef Full Text | Google Scholar

Raissi, M., Perdikaris, P., and Karniadakis, G. E. (2017a). Physics Informed Deep Learning (Part I): Data-Driven Solutions of Nonlinear Partial Differential Equations. arXiv preprint. arXiv:1711.10561.

Google Scholar

Raissi, M., Perdikaris, P., and Karniadakis, G. E. (2017b). Physics Informed Deep Learning (Part II): Data-Driven Discovery of Nonlinear Partial Differential Equations. arXiv 1711, 10566.

Google Scholar

Raissi, M., Perdikaris, P., and Karniadakis, G. E. (2019). Physics-informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations. J. Comput. Phys. 378, 686–707. doi:10.1016/j.jcp.2018.10.045

CrossRef Full Text | Google Scholar

Rathje, E. M., Dawson, C., Padgett, J. E., Pinelli, J.-P., Stanzione, D., Adair, A., et al. (2017). DesignSafe: New Cyberinfrastructure for Natural Hazards Engineering. Nat. Hazards Rev. 18 (3), 06017001. doi:10.1061/(asce)nh.1527-6996.0000246

CrossRef Full Text | Google Scholar

Razavi, A., and Sarkar, P. P. (2021). Effects of Roof Geometry on Tornado-Induced Structural Actions of a Low-Rise Building. Eng. structures 226, 111367. doi:10.1016/j.engstruct.2020.111367

CrossRef Full Text | Google Scholar

Razavi, A., and Sarkar, P. P. (2018). Laboratory Study of Topographic Effects on the Near-Surface Tornado Flow Field. Boundary-layer Meteorol. 168 (2), 189–212. doi:10.1007/s10546-018-0347-5

CrossRef Full Text | Google Scholar

Refan, M., and Hangan, H. (2016). Characterization of Tornado-like Flow fields in a New Model Scale Wind Testing Chamber. J. Wind Eng. Ind. Aerodynamics 151, 107–121. doi:10.1016/j.jweia.2016.02.002

CrossRef Full Text | Google Scholar

Richman, M. B., and Leslie, L. M. (2012). Adaptive Machine Learning Approaches to Seasonal Prediction of Tropical Cyclones. Proced. Comput. Sci. 12, 276–281. doi:10.1016/j.procs.2012.09.069

CrossRef Full Text | Google Scholar

Richman, M. B., Leslie, L. M., Ramsay, H. A., and Klotzbach, P. J. (2017). Reducing Tropical Cyclone Prediction Errors Using Machine Learning Approaches. Proced. Comput. Sci. 114, 314–323. doi:10.1016/j.procs.2017.09.048

CrossRef Full Text | Google Scholar

Riedmiller, M., and Braun, H. “A Direct Adaptive Method for Faster Backpropagation Learning: The RPROP Algorithm,” in Proceedings of the IEEE international conference on neural networks, San Francisco, CA, USA, March 1993 (Piscataway, New Jersey, United States: IEEE), 586–591.

Google Scholar

Rizzo, F., and Caracoglia, L. (2020). Artificial Neural Network Model to Predict the Flutter Velocity of Suspension Bridges. Comput. Structures 233, 106236. doi:10.1016/j.compstruc.2020.106236

CrossRef Full Text | Google Scholar

Robertson, B. W., Johnson, M., Murthy, D., Smith, W. R., and Stephens, K. K. (2019). Using a Combination of Human Insights and ‘deep Learning' for Real-Time Disaster Communication. Prog. Disaster Sci. 2, 100030. doi:10.1016/j.pdisas.2019.100030

CrossRef Full Text | Google Scholar

Romanic, D., LoTufo, J., and Hangan, H. (2019). Transient Behavior in Impinging Jets in Crossflow with Application to Downburst Flows. J. Wind Eng. Ind. Aerodynamics 184, 209–227. doi:10.1016/j.jweia.2018.11.020

CrossRef Full Text | Google Scholar

Rosenblatt, F. (1957). The Perceptron, a Perceiving and Recognizing Automaton Project Para. Buffalo, New York, United States: Cornell Aeronautical Laboratory.

Google Scholar

Rumelhart, D. E., Hinton, G. E., and Williams, R. J. (1986). Learning Representations by Back-Propagating Errors. nature 323 (6088), 533–536. doi:10.1038/323533a0

CrossRef Full Text | Google Scholar

Russell, S., and Norvig, P. (2016). Artificial Intelligence: A Modern Approach. London, United Kingdom: Pearson Education Limited.

Google Scholar

Rüttgers, M., Lee, S., Jeon, S., and You, D. (2019). Prediction of a Typhoon Track Using a Generative Adversarial Network and Satellite Images. Sci. Rep. 9 (1), 1–15. doi:10.1038/s41598-019-42339-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Salehi, H., and Burgueño, R. (2018). Emerging Artificial Intelligence Methods in Structural Engineering. Eng. structures 171, 170–189. doi:10.1016/j.engstruct.2018.05.084

CrossRef Full Text | Google Scholar

Santosa, B. (2007). Feature Selection with Support Vector Machines Applied on Tornado Detection. IPTEK J. Technol. Sci. 18 (1). doi:10.12962/j20882033.v18i1.178

CrossRef Full Text | Google Scholar

Sarkar, P. P., Haan, F. L., Balaramudu, V., and Sengupta, A., “Laboratory Simulation of Tornado and Microburst to Assess Wind Loads on Buildings.” in Proceedings of the Structures Congress 2006: Structural Engineering and Public Safety. St. Louis, Missouri, United States. May 2006. 1–10. doi:10.1061/40889(201)11

CrossRef Full Text | Google Scholar

Saunders, J. W., and Melbourne, W. H. (1980). “Buffeting Effects of Upstream Buildings,” in Wind Engineering. Editor J. W. Saunders (Pergamon: Pergamon Press), 593–606. doi:10.1016/b978-1-4832-8367-8.50059-0

CrossRef Full Text | Google Scholar

Scholkopf, B., and Smola, A. J. (2018). Learning with Kernels: Support Vector Machines, Regularization, Optimization, and beyond. Adaptive Computation and Machine Learning Series. Cambridge, Massachusetts, United States: MIT Press.

Google Scholar

Sfetsos, A. (2000). A Comparison of Various Forecasting Techniques Applied to Mean Hourly Wind Speed Time Series. Renew. Energ. 21 (1), 23–35. doi:10.1016/s0960-1481(99)00125-1

CrossRef Full Text | Google Scholar

Sharma, R., Shikhola, T., and Kohli, J. K. (2020). Modified Fuzzy Q-Learning Based Wind Speed Prediction. J. Wind Eng. Ind. Aerodynamics 206, 104361. doi:10.1016/j.jweia.2020.104361

CrossRef Full Text | Google Scholar

Silver, D., Schrittwieser, J., Simonyan, K., Antonoglou, I., Huang, A., Guez, A., et al. (2017). Mastering the Game of Go without Human Knowledge. nature 550 (7676), 354–359. doi:10.1038/nature24270

PubMed Abstract | CrossRef Full Text | Google Scholar

Simiu, E., and Scanlan, R. H. (1978). Wind Effects on Structures. Hoboken, New Jersey, United States: Wiley.

Google Scholar

Smith, T. M., Elmore, K. L., and Dulin, S. A. (2004). A Damaging Downburst Prediction and Detection Algorithm for the WSR-88D. Wea. Forecast. 19 (2), 240–250. doi:10.1175/1520-0434(2004)019<0240:addpad>2.0.co;2

CrossRef Full Text | Google Scholar

Snaiki, R., and Wu, T. (2017b). A Linear Height-Resolving Wind Field Model for Tropical Cyclone Boundary Layer. J. Wind Eng. Ind. Aerodynamics 171, 248–260. doi:10.1016/j.jweia.2017.10.008

CrossRef Full Text | Google Scholar

Snaiki, R., and Wu, T. (2018). A Semi-empirical Model for Mean Wind Velocity Profile of Landfalling hurricane Boundary Layers. J. Wind Eng. Ind. Aerodynamics 180, 249–261. doi:10.1016/j.jweia.2018.08.004

CrossRef Full Text | Google Scholar

Snaiki, R., and Wu, T. (2020c). An Analytical Model for Rapid Estimation of hurricane Supergradient Winds. J. Wind Eng. Ind. Aerodynamics 201, 104175. doi:10.1016/j.jweia.2020.104175

CrossRef Full Text | Google Scholar

Snaiki, R., and Wu, T. (2020b). Hurricane hazard Assessment along the United States Northeastern Coast: Surface Wind and Rain fields under Changing Climate. Front. Built Environ. 6, 573054. doi:10.3389/fbuil.2020.573054

CrossRef Full Text | Google Scholar

Snaiki, R., and Wu, T. (2019). Knowledge-enhanced Deep Learning for Simulation of Tropical Cyclone Boundary-Layer Winds. J. Wind Eng. Ind. Aerodynamics 194, 103983. doi:10.1016/j.jweia.2019.103983

CrossRef Full Text | Google Scholar

Snaiki, R., and Wu, T. (2017a). Modeling Tropical Cyclone Boundary Layer: Height-Resolving Pressure and Wind fields. J. Wind Eng. Ind. Aerodynamics 170, 18–27. doi:10.1016/j.jweia.2017.08.005

CrossRef Full Text | Google Scholar

Snaiki, R., and Wu, T. (2020a). Revisiting hurricane Track Model for Wind Risk Assessment. Struct. Saf. 87, 102003. doi:10.1016/j.strusafe.2020.102003

CrossRef Full Text | Google Scholar

Solari, G., Burlando, M., De Gaetano, P., and Repetto, M. P. (2015). Characteristics of Thunderstorms Relevant to the Wind Loading of Structures. Wind and Structures 20 (6), 763–791. doi:10.12989/was.2015.20.6.763

CrossRef Full Text | Google Scholar

Solari, G. (2020). Thunderstorm Downbursts and Wind Loading of Structures: Progress and prospect. Front. Built Environ. 6, 63. doi:10.3389/fbuil.2020.00063

CrossRef Full Text | Google Scholar

Stiles, B. W., Danielson, R. E., Poulsen, W. L., Brennan, M. J., Hristova-Veleva, S., Tsae-Pyng Shen, T. P., et al. (2014). Optimized Tropical Cyclone Winds from QuikSCAT: A Neural Network Approach. IEEE Trans. Geosci. Remote Sensing 52 (11), 7418–7434. doi:10.1109/tgrs.2014.2312333

CrossRef Full Text | Google Scholar

Subasri, R., Suresh, S., and Natarajan, A. M. (2014). Discrete Direct Adaptive ELM Controller for Active Vibration Control of Nonlinear Base Isolation Buildings. Neurocomputing 129, 246–256. doi:10.1016/j.neucom.2013.09.035

CrossRef Full Text | Google Scholar

Subramanian, D., Salazar, J., Duenas-Osorio, L., and Stein, R. “Constructing and Validating Geographically Refined HAZUS-MH4 hurricane Wind Risk Models: A Machine Learning Approach,” in Proceedings of the Advances in hurricane engineering: Learning from our past, Miami, Florida, United States, October 2013, 1056–1066. doi:10.1061/9780784412626.092

CrossRef Full Text | Google Scholar

Sun, W., Bocchini, P., and Davison, B. D. (2020). Applications of Artificial Intelligence for Disaster Management. Nat. Hazards 103, 2631–2689. doi:10.1007/s11069-020-04124-3

CrossRef Full Text | Google Scholar

Sun, Y., Yang, L., and Wu, Y. “Wind Load Prediction of Large-Span Dry Coal Sheds Based on GRNN and its Application,” in Proceedings of International Structural Engineering and Construction, Valencia, Spain, July, 2017. doi:10.14455/isec.res.2017.189

CrossRef Full Text | Google Scholar

Sutton, R. S., and Barto, A. G. (2018). Reinforcement Learning: An Introduction. Cambridge, Massachusetts, United States: MIT press.

Google Scholar

Tagliaferri, F., Viola, I. M., and Flay, R. G. J. (2015). Wind Direction Forecasting with Artificial Neural Networks and Support Vector Machines. Ocean Eng. 97, 65–73. doi:10.1016/j.oceaneng.2014.12.026

CrossRef Full Text | Google Scholar

Tang, Z., Feng, C., Wu, L., Zuo, D., and James, D. L. (2018). Characteristics of Tornado-like Vortices Simulated in a Large-Scale ward-type Simulator. Boundary-layer Meteorol. 166 (2), 327–350. doi:10.1007/s10546-017-0305-7

CrossRef Full Text | Google Scholar

Taniike, Y., and Inaoka, H. (1988). “Aeroelastic Behavior of Tall Buildings in Wakes,” in Advances in Wind Engineering. Editors C. Kramer, and H. J. Gerhardt (Amsterdam, Netherlands: Elsevier), 317–327. doi:10.1016/b978-0-444-87156-5.50043-6

CrossRef Full Text | Google Scholar

Tian, J., Gurley, K. R., Diaz, M. T., Fernández-Cabán, P. L., Masters, F. J., and Fang, R. (2020). Low-rise Gable Roof Buildings Pressure Prediction Using Deep Neural Networks. J. Wind Eng. Ind. Aerodynamics 196, 104026. doi:10.1016/j.jweia.2019.104026

CrossRef Full Text | Google Scholar

Tian, W., Huang, W., Yi, L., Wu, L., and Wang, C. (2020). A CNN-Based Hybrid Model for Tropical Cyclone Intensity Estimation in Meteorological Industry. IEEE Access 8, 59158–59168. doi:10.1109/access.2020.2982772

CrossRef Full Text | Google Scholar

Tian, Z., Ren, Y., and Wang, G. (2020). An Application of Backtracking Search Optimization-Based Least Squares Support Vector Machine for Prediction of Short-Term Wind Speed. Wind Eng. 44 (3), 266–281. doi:10.1177/0309524x19849843

CrossRef Full Text | Google Scholar

Trafalis, T. B., Adrianto, I., Richman, M. B., and Lakshmivarahan, S. (2014). Machine-learning Classifiers for Imbalanced Tornado Data. Comput. Manag. Sci. 11 (4), 403–418. doi:10.1007/s10287-013-0174-6

CrossRef Full Text | Google Scholar

Turkkan, N., and Srivastava, N. K. (1995). Prediction of Wind Load Distribution for Air-Supported Structures Using Neural Networks. Can. J. Civ. Eng. 22 (3), 453–461. doi:10.1139/l95-053

CrossRef Full Text | Google Scholar

Twisdale, L. A., and Vickery, P. J. (1992). Research on Thunderstorm Wind Design Parameters. J. Wind Eng. Ind. Aerodynamics 41 (1-3), 545–556. doi:10.1016/0167-6105(92)90461-i

CrossRef Full Text | Google Scholar

Uematsu, Y., and Tsuruishi, R. (2008). Wind Load Evaluation System for the Design of Roof Cladding of Spherical Domes. J. wind Eng. Ind. aerodynamics 96 (10-11), 2054–2066. doi:10.1016/j.jweia.2008.02.051

CrossRef Full Text | Google Scholar

Ukkonen, P., Manzato, A., and Mäkelä, A. (2017). Evaluation of Thunderstorm Predictors for Finland Using Reanalyses and Neural Networks. J. Appl. Meteorology Climatology 56 (8), 2335–2352. doi:10.1175/jamc-d-16-0361.1

CrossRef Full Text | Google Scholar

Varshney, K., and Poddar, K. (2012). Prediction of Wind Properties in Urban Environments Using Artificial Neural Network. Theor. Appl. Climatology 107 (3-4), 579–590. doi:10.1007/s00704-011-0506-9

CrossRef Full Text | Google Scholar

Vickery, P. J., Skerlj, P. F., and Twisdale, L. A. (2000). Simulation of Hurricane Risk in the U.S. Using Empirical Track Model. J. Struct. Eng. 126 (10), 1222–1237. doi:10.1061/(asce)0733-9445(2000)126:10(1222)

CrossRef Full Text | Google Scholar

Vickery, P. J., Wadhera, D., Twisdale, L. A., and Lavelle, F. M. (2009). U.S. Hurricane Wind Speed Risk and Uncertainty. J. Struct. Eng. 135 (3), 301–320. doi:10.1061/(asce)0733-9445(2009)135:3(301)

CrossRef Full Text | Google Scholar

Vyavahare, A. Y., Godbole, P. N., and Nikose, T. (2012). Analysis of Tall Building for across Wind Response. Int. J. Civil Struct. Eng. 2 (3), 679–986.

Google Scholar

Wang, H., and Wu, T. (2021). Fast Hilbert-Wavelet Simulation of Nonstationary Wind Field Using Noniterative Simultaneous Matrix Diagonalization. J. Eng. Mech. 147 (3), 04020153. doi:10.1061/(asce)em.1943-7889.0001897

CrossRef Full Text | Google Scholar

Wang, H., and Wu, T. (2020). Knowledge-Enhanced Deep Learning for Wind-Induced Nonlinear Structural Dynamic Analysis. J. Struct. Eng. 146 (11), 04020235. doi:10.1061/(asce)st.1943-541x.0002802

CrossRef Full Text | Google Scholar

Wang, H., Zhang, Y.-M., Mao, J.-X., and Wan, H.-P. (2020). A Probabilistic Approach for Short-Term Prediction of Wind Gust Speed Using Ensemble Learning. J. Wind Eng. Ind. Aerodynamics 202, 104198. doi:10.1016/j.jweia.2020.104198

CrossRef Full Text | Google Scholar

Wang, J., and Cheng, C. M. “Aero-Data Based Wind Resistant Design of Rectangular Shaped Tall Buildings,” in Proceedings of the International Conference on Innovations in Civil and Structural Engineering (ICICSE’15), Istanbul, Turkey, June 2015, 148–154.

Google Scholar

Wang, J., Cheng, C. M., and Chen, C. H. “The Study of Wind Force Coefficient Predictions for Rectangular High-Rise Buildings,” in Proceedings of The eighth Asia-Pacific conference on wind engineering, Chennai, India, December 2013, 10–14.

Google Scholar

Wang, J., and Cheng, C. M. (2017). Formulation of Estimation Models for Wind Force Coefficients of Rectangular Shaped Buildings. J. Appl. Sci. Eng. 20 (1), 55–62. doi:10.6180/jase.2017.20.1.07

CrossRef Full Text | Google Scholar

Wang, Y., Zhang, W., and Fu, W. “Back Propogation (BP)-neural Network for Tropical Cyclone Track Forecast,” in Proceedings of the 2011 19th International Conference on Geoinformatics, Shanghai, China, June 2011 (Piscataway, New Jersey, United States: IEEE), 1–4.

Google Scholar

Watkins, C. J. C. H. (1989). Learning from Delayed Rewards. Cambridge, UK: King's College.

Google Scholar

Watkins, C. J., and Dayan, P. (1992). Q-learning. Machine Learn. 8 (3-4), 279–292. doi:10.1023/a:1022676722315

CrossRef Full Text | Google Scholar

Wei, C.-C. (2015). Forecasting Surface Wind Speeds over Offshore Islands Near Taiwan during Tropical Cyclones: Comparisons of Data-Driven Algorithms and Parametric Wind Representations. J. Geophys. Res. Atmos. 120 (5), 1826–1847. doi:10.1002/2014jd022568

CrossRef Full Text | Google Scholar

Wei, C.-C. (2019). Study on Wind Simulations Using Deep Learning Techniques during Typhoons: a Case Study of Northern Taiwan. Atmosphere 10 (11), 684. doi:10.3390/atmos10110684

CrossRef Full Text | Google Scholar

Wen, Y.-K., and Chu, S.-L. (1973). Tornado Risks and Design Wind Speed. J. Struct. Div. 99 (12), 2409–2421. doi:10.1061/jsdeag.0003666

CrossRef Full Text | Google Scholar

Wiederhold, G., McCarthy, J., and Feigenbaum, E. (1990). Arthur Samuel: pioneer in Machine Learning. Commun. ACM 33 (11), 137–139.

Google Scholar

Wijnands, J. S., Qian, G., and Kuleshov, Y. (2016). Variable Selection for Tropical Cyclogenesis Predictive Modeling. Monthly Weather Rev. 144 (12), 4605–4619. doi:10.1175/mwr-d-16-0166.1

CrossRef Full Text | Google Scholar

Wijnands, J. S., Shelton, K., and Kuleshov, Y. (2014). Improving the Operational Methodology of Tropical Cyclone Seasonal Prediction in the Australian and the South Pacific Ocean Regions. Adv. Meteorology 2014, 838746. doi:10.1155/2014/838746

CrossRef Full Text | Google Scholar

Williams, R. J. (1992). Simple Statistical Gradient-Following Algorithms for Connectionist Reinforcement Learning. Machine Learn. 8 (3-4), 229–256. doi:10.1007/bf00992696

CrossRef Full Text | Google Scholar

Wu, R.-T., and Jahanshahi, M. R. (2019). Deep Convolutional Neural Network for Structural Dynamic Response Estimation and System Identification. J. Eng. Mech. 145 (1), 04018125. doi:10.1061/(asce)em.1943-7889.0001556

CrossRef Full Text | Google Scholar

Wu, T., and Kareem, A. (2013). Bridge Aerodynamics and Aeroelasticity: A Comparison of Modeling Schemes. J. Fluids Structures 43, 347–370. doi:10.1016/j.jfluidstructs.2013.09.015

CrossRef Full Text | Google Scholar

Wu, T., and Kareem, A. (2011). Modeling Hysteretic Nonlinear Behavior of Bridge Aerodynamics via Cellular Automata Nested Neural Network. J. Wind Eng. Ind. Aerodynamics 99 (4), 378–388. doi:10.1016/j.jweia.2010.12.011

CrossRef Full Text | Google Scholar

Wu, T., Li, S., and Sivaselvan, M. (2019). Real-time Aerodynamics Hybrid Simulation: a Novel Wind-Tunnel Model for Flexible Bridges. J. Eng. Mech. 145 (9), 04019061. doi:10.1061/(asce)em.1943-7889.0001649

CrossRef Full Text | Google Scholar

Wu, T. (2013). “Nonlinear bluff-body Aerodynamics,” (Indiana, USA: University of Notre Dame). Doctoral dissertation.

Google Scholar

Wu, T., and Song, W. (2019). Real-time Aerodynamics Hybrid Simulation: Wind-Induced Effects on a Reduced-Scale Building Equipped with Full-Scale Dampers. J. Wind Eng. Ind. Aerodynamics 190, 1–9. doi:10.1016/j.jweia.2019.04.005

CrossRef Full Text | Google Scholar

Wu, X., Ghaboussi, J., and Garrett, J. H. (1992). Use of Neural Networks in Detection of Structural Damage. Comput. Structures 42 (4), 649–659. doi:10.1016/0045-7949(92)90132-j

CrossRef Full Text | Google Scholar

Yakut, O., and Alli, H. (2011). Neural Based Sliding-Mode Control with Moving Sliding Surface for the Seismic Isolation of Structures. J. Vibration Control. 17 (14), 2103–2116. doi:10.1177/1077546310395964

CrossRef Full Text | Google Scholar

Yang, Q., Gao, R., Bai, F., Li, T., and Tamura, Y. (2018). Damage to Buildings and Structures Due to Recent Devastating Wind Hazards in East Asia. Nat. Hazards 92 (3), 1321–1353. doi:10.1007/s11069-018-3253-8

CrossRef Full Text | Google Scholar

Yasen, M. Z. Y., Al-Jundi, R. A. S., and Al-Madi, N. S. A. “Optimized ANN-ABC for Thunderstorms Prediction,” in Proceedings of the 2017 International Conference on New Trends in Computing Sciences (ICTCS), Amman, Jordan, October 2017 (Piscataway, New Jersey, United States: IEEE), 98–103.

Google Scholar

Yu, C., Li, Y., Xiang, H., and Zhang, M. (2018). Data Mining-Assisted Short-Term Wind Speed Forecasting by Wavelet Packet Decomposition and Elman Neural Network. J. Wind Eng. Ind. Aerodynamics 175, 136–143. doi:10.1016/j.jweia.2018.01.020

CrossRef Full Text | Google Scholar

Yu, M., Huang, Q., Qin, H., Scheele, C., and Yang, C. (2019). Deep Learning for Real-Time Social media Text Classification for Situation Awareness - Using Hurricanes Sandy, Harvey, and Irma as Case Studies. Int. J. Digital Earth 12 (11), 1230–1247. doi:10.1080/17538947.2019.1574316

CrossRef Full Text | Google Scholar

Yu, Y., Yao, H., and Liu, Y. (2020). Structural Dynamics Simulation Using a Novel Physics-Guided Machine Learning Method. Eng. Appl. Artif. Intelligence 96, 103947. doi:10.1016/j.engappai.2020.103947

CrossRef Full Text | Google Scholar

Zambrano, T. G., and Peterka, J. A. (1978). Wind Load Interaction on an Adjacent Building. CER 77, 78–26.

Google Scholar

Zhang, A., and Zhang, L. (2004). RBF Neural Networks for the Prediction of Building Interference Effects. Comput. Structures 82 (27), 2333–2339. doi:10.1016/j.compstruc.2004.05.014

CrossRef Full Text | Google Scholar

Zhang, C., Dai, L., Ma, L., Qian, J., and Yang, B. (2017). Objective Estimation of Tropical Cyclone Innercore Surface Wind Structure Using Infrared Satellite Images. J. Appl. Remote Sensing 11 (4), 046030. doi:10.1117/1.jrs.11.046030

CrossRef Full Text | Google Scholar

Zhang, S., and Nishijima, K. “Statistics-based Investigation on Typhoon Transition Modeling,” in Proceedingsof the Seventh International Colloquium on Bluff Body Aerodynamics and Application, Shanghai, China, September 2012, 364–373.

Google Scholar

Zhang, T., Lin, W., Lin, Y., Zhang, M., Yu, H., Cao, K., et al. (2019). Prediction of Tropical Cyclone Genesis from Mesoscale Convective Systems Using Machine Learning. Weather Forecast. 34 (4), 1035–1049. doi:10.1175/waf-d-18-0201.1

CrossRef Full Text | Google Scholar

Zhang, W., Fu, B., Peng, M. S., and Li, T. (2015). Discriminating Developing versus Nondeveloping Tropical Disturbances in the Western North Pacific through Decision Tree Analysis. Weather Forecast. 30 (2), 446–454. doi:10.1175/waf-d-14-00023.1

CrossRef Full Text | Google Scholar

Zhang, Y., Chandra, R., and Gao, J. “Cyclone Track Prediction with Matrix Neural Networks,” in Proceedings of the 2018 International Joint Conference on Neural Networks (IJCNN), Rio de Janeiro, Brazil, July 2018 (Piscataway, New Jersey, United States: IEEE), 1–8.

Google Scholar

Zhao, M., Held, I. M., and Lin, S.-J. (2012). Some Counterintuitive Dependencies of Tropical Cyclone Frequency on Parameters in a GCM. J. Atmos. Sci. 69 (7), 2272–2283. doi:10.1175/jas-d-11-0238.1

CrossRef Full Text | Google Scholar

Zhu, J., and Zhang, W. (2018). Probabilistic Fatigue Damage Assessment of Coastal Slender Bridges under Coupled Dynamic Loads. Eng. Structures 166, 274–285. doi:10.1016/j.engstruct.2018.03.073

CrossRef Full Text | Google Scholar

Appendix A: List of reviewed machine learning algorithms (Note: Acronyms with * represent those reviewed in this contribution).

A2C advantage actor critic

AdaBoost* adaptive boosting

AE* autoencoder

ALEN* adaptive linear element network

ANFIS* adaptive neuro-fuzzy inference system

ANN* artificial neural network

AWN* adaptive wavelet network

BNB* Bernoulli naive Bayes

BNN* Bayesian neural network

CGAN conditional GAN

CNN* convolutional neural network

CNN-AE* convolutional neural network-based autoencoder

ConvLSTM* convolutional Long Short-Term Memory

DCGAN deep convolutional GAN

DDPG* deep deterministic policy gradient

DDQN double deep Q-network

DNN* deep neural network

DQN deep Q-network

DRL* deep reinforcement learning

DRNN* diagonal recurrent neural networks

DT* decision tree

ENN* Elman neural network

ERBFN* radial basis function neural network

ERNN* Elman recurrent neural networks

FIS* fuzzy inference system

FNN* fuzzy neural network

GAN* generative adversarial network

GBRT* gradient boosted regression trees

GBTE* gradient-boosted tree ensembles

GMDH* group method of data handling

GNB* gaussian naïve Bayes

GPR* gaussian process regression

GRU* gated recurrent unit network

GRNN* generalized regression neural network

ICA independent component analysis

IIRANN* infinite impulse response artificial neural network

JRNN* Jordan recurrent neural networks

KEDL* knowledge-enhanced deep learning

KE-DRL* knowledge-enhanced deep reinforcement learning

KE-LSTM* knowledge enhanced long short-term memory

KM k-means

KNN* k-nearest neighbors

LAFMN* local activation feedback multilayer network

LDA* linear discriminant analysis

LNN* linear neural network

LR* logistic regression

LSSVM* least squares support vector machine

LSTM* long short-term memory

MC* multiple correlation

MFQL* modified fuzzy Q-learning

MLR* multiple linear regression

MNB* multinomial naive Bayes

MNN* matrix neural network

MSC mean-shift clustering

NB* naïve Bayes

NESN* nonlinear echo state networks

NLN* neural logic network

OLR* ordinary linear regression

PCA principal component analysis

PI* Physics-informed

PPO proximal policy optimization

QDA* quadratic discriminant analysis

QL* Q-learning

RBF* radial basis function

RBFNN* radial basis function neural network

RF* random forest

RL* reinforcement learning

RNN* recurrent neural networks

RR* ridge regression

SC spectral clustering

SD-AE* stacked denoising autoencoder

SLDA* supervised latent Dirichlet Allocation

SGD* stochastic gradient descent

SVM* support vector machines

SVR* support vector regression

TRPO trust region policy optimization

WGAN Wasserstein GAN

XGBoost* extreme gradient boosting