Experimental investigation of shear-extension coupling effect in anisotropic reinforced concrete membrane elements

Performance based analysis under seismic loads using the finite element method for wall-type reinforced concrete (RC) members in buildings and in important structures like liquid retaining structures, nuclear containment structures, offshore concrete gravity structures etc., necessitates the understanding of the non-linear behaviour of the constituent membrane elements. The current orthotropic formulation of the softened membrane model (SMM) can be strictly used only when the reinforcement is symmetric to the principal axes of applied stresses. When the reinforcement is asymmetric, shear strain is generated due to the normal stresses in the principal axes of applied stresses, which is referred to as shear-extension coupling. An anisotropic formulation is required to capture the generated shear strain. The current study quantifies the shear strain due to asymmetry in reinforcement, by testing panels under biaxial tension-compression using a large-scale panel testing facility. A model for the shear strain is proposed based on the tests data. The paper presents the experimental programme, important test results and the modelling of shear strain. Expression developed for the shear strain can be incorporated in the solution algorithm of the SMM for improved prediction of the shear behaviour of a membrane element. This further aids in accurate prediction of the seismic performance of the important structures mentioned earlier.

1 Introduction

Shear walls in buildings and other wall-type members in liquid retaining structures, nuclear containment structures, offshore concrete gravity structures (CGS) are a part of the lateral load resisting system of the structure (Figure 1). They withstand loads generated due to wind, earthquakes and sea waves (for CGS). When these extreme loads act on the structure, the members may be stressed beyond their linear response. A performance based analysis using the finite element method (FEM) is used to analyse such a structure. Thus, modelling the non-linear behaviour of the wall-type members is necessary to generate the system response in the analysis of the structure.

FIGURE 1

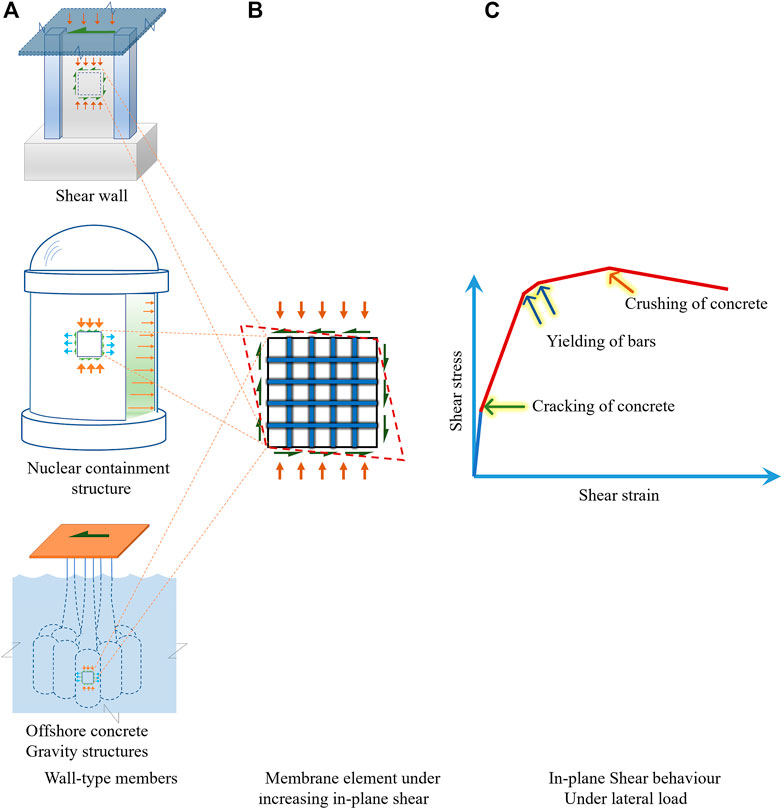
FIGURE 1. Shear behaviour in reinforced concrete structures. (A) Wall type members. (B) Membrane element under increasing in planeshear (C) In plane Shear behaviour under lateral load.

Two-dimensional (2D) membrane elements can be used to create a finite element computational model of a wall (Hsu, 1991). Establishing the post-cracking non-linear in-plane shear stress versus shear strain behaviour of a membrane element under lateral loads (Figure 1), in presence of in-plane normal stresses at the edges, can help in predicting the behaviour of the assemblage of the elements. The behaviour of a membrane element under increasing shear strain has three distinct stages: 1) initiation of cracking of concrete, 2) yielding of the reinforcing bars (rebar) in the two orthogonal directions and 3) initiation of crushing of the concrete. The Modified Compression Field Theory (MCFT) (Vecchio and Collins, 1986) and Softened Membrane Model (SMM) (Hsu and Zhu, 2002) can be used to accurately predict the response of an RC membrane element under increasing in-plane shear strain. The present study is based on the formulation of SMM.

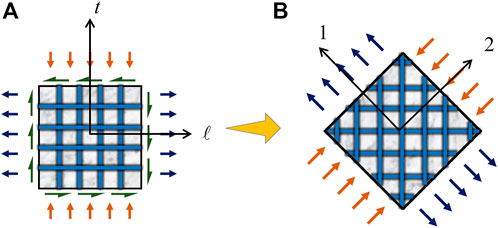
Although after cracking, RC becomes discontinuous and heterogenous, it is treated as a continuous homogenous material with smeared properties, across the length of a membrane element. Two coordinate systems are defined to express the equations, as shown in Figure 2. First is the ℓ-t system, which represents the longitudinal (ℓ-) and transverse (t-) directions of the bars in the membrane element (Pang and Hsu, 1996). The stresses and strains in the formulation are expressed in this system. The applied normal stresses under service condition are ${\sigma }_l$ and ${\sigma }_t$ . The applied shear stress (equivalent static load for the effect of an earthquake) is denoted as ${\tau }_{lt}$ . Thus, the ℓ-t system is selected as the reference axes system to model the behaviour under shear.

FIGURE 2

FIGURE 2. Membrane element (A) Applied stresses, (B) Principal stresses.

Second is the two to one system which represents the principal axes of in-plane stresses applied to the membrane element. The stresses and strains in cracked concrete are expressed in this system. In the presence of increasing in-plane shear in a membrane element, the state of principal stresses becomes biaxial tensile−compressive. To give importance to compression carried by concrete after cracking, the axis of compression (2-) is considered to be the leading axis with respect to the axis of tension (ℓ-). The inclination of the two to one system with respect to the ℓ-t system is denoted by ${\alpha }_2$ .

The SMM uses an orthotropic formulation to quantify the generated 2D strains. This is used to estimate the additional tensile strain generated due to compression in the orthogonal direction. This is analogous to the Poisson’s effect in a linear elastic element (Zhu 2000; Zhu and Hsu 2002). The orthotropic formulation necessities the assumption that the reinforcement grid be symmetric with respect to the principal axes of applied in-plane stresses. This particular assumption will be satisfied only when the reinforcement grid is aligned along the axes or is inclined at an angle 45°, with equal amount of reinforcement in the two directions (Hsu 1993; Hsu and Mo, 2010). However, if the reinforcement is placed asymmetric with respect to the principal axes of stresses (2–1), the axes do not remain as principal axes for the generated strains with increasing shear stress. Shear strain (${\gamma }_{21}$) is generated in addition to normal strains in the two to one system. This generation of additional shear strain is termed as shear—extension coupling.

Though the SMM accurately predicts the response of symmetric elements, the shear strain (${\gamma }_{\mathrm{l}\mathrm{t}}$) is underestimated for elements with asymmetry in reinforcement, especially after the yielding of the bars. The current orthotropic formulation of the SMM estimates the additional shear strain (${\gamma }_{21}$) by a trial-and-error based procedure. It does not calculate it rationally based on mechanics.

In the present study, a 2D anisotropic formulation is introduced to quantify and subsequently model ${\gamma }_{21}$ (Kosuru and Sengupta, 2018). In the following sections, first, an overview of the SMM is presented. Next, cases of asymmetry of reinforcement are elucidated and the anisotropic formulation is introduced. The experimental programme is explained, and the important test results are presented. A model for ${\gamma }_{21}$ is proposed based on the tests results.

2 Research significance

The formulation of SMM was generalised to incorporate the effect of shear‒extension coupling in a membrane element with asymmetry in reinforcement. An experimental programme was undertaken to quantify the effect of shear‒extension coupling in RC panels with asymmetry in reinforcement and tested under biaxial tension‒compression. Based on the tests, expression for ${\gamma }_{21}$ was developed. The solution algorithm of SMM was modified to incorporate the mechanics-based expression for ${\gamma }_{21}$ in place of the trial-and-error based procedure. The generalisation was corroborated against test results from the literature. Thus, the generalised formulation of SMM can be subsequently used in a finite element analysis of a wall-type member.

3 Softened membrane model

The SMM satisfies the principle of RC mechanics of equilibrium of forces and compatibility of strains in concrete and rebar. A summary of the equilibrium and compatibility equations, the constitutive models and the model for Poisson’s effect is provided for ready reference (Hsu and Zhu, 2002).

3.1 Equilibrium equations

The applied stresses in the ℓ-t coordinate system, ${\sigma }_l,{\sigma }_t$ and ${\tau }_{lt}$ are in equilibrium with the average internal stresses in the rebar (f_l and f_t) and in the concrete (${\sigma }_2^c,{\sigma }_1^c$ and ${\tau }_{21}^c$). Based on 2D stress transformation, the following equations were developed.

${\sigma }_l={\sigma }_2^c{\cos }^2{\alpha }_2+{\sigma }_1^c{\sin }^2{\alpha }_2+{\tau }_{21}^{c}2\sin {\alpha }_2\cos {\alpha }_2+{\rho }_l{f}_l(\mathrm{1a})$

${\sigma }_t={{\sigma }_2^c{\sin }^2{\alpha }_2+\sigma }_1^c{\cos }^2{\alpha }_2-{\tau }_{21}^{c}2\sin {\alpha }_2\cos {\alpha }_2+{\rho }_t{f}_t(\mathrm{1b})$

${\tau }_{lt}=\left(-{\sigma }_2^c+{\sigma }_1^c\right)\sin {\alpha }_2\cos {\alpha }_2+{\tau }_{21}^c\left({\cos }^2{\alpha }_2-{\sin }^2{\alpha }_2\right)(\mathrm{1c})$

Here, ${\sigma }_2^c,{\sigma }_1^c$ and ${\tau }_{21}^c$ are the normal and shear stresses in concrete in the two to one coordinate system, respectively. ${\rho }_l$ and ${\rho }_t$ are the reinforcement ratios in the ℓ- and t-directions, respectively.

3.2 Compatibility equations

The strains in the ℓ-$t$ coordinate system (${\epsilon }_l,{\epsilon }_t$ and ${\gamma }_{lt}$) are expressed in terms of the strains in the two to one coordinate system (${\epsilon }_2,{\epsilon }_1$ and ${\gamma }_{21}$) based on 2D strain transformation.

${\epsilon }_l={\epsilon }_2{\cos }^2{\alpha }_2+{\epsilon }_1{\sin }^2{\alpha }_2+\frac{{\gamma }_{21}}{2}2\sin {\alpha }_2\cos {\alpha }_2(\mathrm{2a})$

${\epsilon }_t={\epsilon }_2{\sin }^2{\alpha }_2+{\epsilon }_1{\cos }^2{\alpha }_2-\frac{{\gamma }_{21}}{2}2\sin {\alpha }_2\cos {\alpha }_2(\mathrm{2b})$

$\frac{{\gamma }_{lt}}{2}=\left({-\epsilon }_2+{\epsilon }_1\right)\sin {\alpha }_2\cos {\alpha }_2+\frac{{\gamma }_{21}}{2}\left({\cos }^2{\alpha }_2-{\sin }^2{\alpha }_2\right)(\mathrm{2c})$

It is to be noted that ${\gamma }_{21}$ generates due to the shear-extension coupling in an anisotropic element. This leads to an increase in γ_lt.

3.3 Constitutive models

Based on extensive tests of panels under biaxial tension-compression, the following relationships were developed.

1) Concrete under compression (Belarbi (1991); Belarbi and Hsu (1995))

For ${\epsilon }_{2u}/\zeta {\epsilon }_0\le 1$,

${\sigma }_2^c=\zeta f_c^{/}\left[2\left(\frac{{\epsilon }_{2u}}{\zeta {\epsilon }_0}\right)-{\left(\frac{{\epsilon }_{2u}}{\zeta {\epsilon }_0}\right)}^2\right](\mathrm{3a})$

For ${\epsilon }_{2u}/\zeta {\epsilon }_0>1$,

${\sigma }_2^c=\zeta f_c^{/}\left[1-{\left(\frac{\left({\epsilon }_{2u}/\zeta {\epsilon }_0\right)-1}{\left(4/\zeta \right)-1}\right)}^2\right](\mathrm{3b})$

Here, ${\epsilon }_{2u}$ and ${\epsilon }_0$ are the uniaxial component of compressive strain, and compressive strain corresponding to peak stress in a concrete cylinder, respectively. The symbol $f_c^{/}.$ represents the compressive strength of concrete cylinder. The compressive strength of concrete in the panel is represented as $\zeta f_c^{/}$. The softening of concrete under compression due to orthogonal tensile strain is quantified by the coefficient ζ, which is defined as follows (Zhang and Hsu, 1998).

$\zeta =\frac{0.9}{\sqrt{1+\frac{{\epsilon }_{1u}}{{\eta }^{/}}}}(4)$

${\eta }^{/}$ is taken as $\eta$ or reciprocal of $\eta$ whichever is less than 1.0. $\eta$ is the ratio of the capacities of the rebar along the transverse and longitudinal directions (${\rho }_t{f}_{yt}/{\rho }_l{f}_{yl}$). This is a measure of asymmetry in the reinforcement grid.

2) Concrete under tension (Belarbi and Hsu, 1994)

For ${\epsilon }_{1u}\le {\epsilon }_{cr}$,

${\sigma }_1^c=E_c{\epsilon }_{1u}(\mathrm{5a})$

For ${\epsilon }_{1u}>{\epsilon }_{cr}$,

${\sigma }_1^c=f_{cr}{\left(\frac{{\epsilon }_{cr}}{{\epsilon }_{1u}}\right)}^{0.4}(\mathrm{5b})$

Here, $f_{cr}$, ${\epsilon }_{cr}$, ε_1u and $E_c$ are the cracking stress, cracking strain, uniaxial component of tensile strain and the elastic modulus of concrete in uniaxial tension, respectively. For the post-cracking analysis, only Eq. 5B is required.

3) Concrete under shear (Zhu et al., 2001)

${\tau }_{21}^c=\frac{{\sigma }_1^c-{\sigma }_2^c}{2\left({\epsilon }_1-{\epsilon }_2\right)}{\gamma }_{21}(6)$

The shear stress and strain in concrete are related through the normal stresses and strains so as to use the previous constitutive relationships and avoid an empirical shear modulus.

4) Rebar under tension (Belarbi and Hsu, 1994)

The following expressions are in generic notations which are applicable for the bars along the ℓ- and t-directions.

For ${\epsilon }_{su}\le {\epsilon }_n^{\ast }$,

$f_s=E_s{\epsilon }_{su}(\mathrm{7a})$

For ${\epsilon }_{su}>{\epsilon }_n^{\ast }$,

$f_s=\left(0.91-2B\right)f_y+\left(0.02+0.25B\right)E_s{\epsilon }_{su}=f_n^{\ast }+E_p{\epsilon }_{su}(\mathrm{7b})$

Here, $f_s$ and ${\epsilon }_{su}$ are the stress and strain in the bars, respectively. ${\epsilon }_n^{\ast }=\left(0.91-2B\right){\epsilon }_y$ approximates the apparent yield strain. ${\epsilon }_y$ and $f_y$ are the yield strain and the yield stress of a bare bar coupon, respectively. $f_n^{\ast }$ is the apparent yield stress of the rebar embedded in concrete. $B=\left(1/\rho \right){\left(f_{cr}/f_y\right)}^{1.5}$ is a measure of tensile strength of concrete with respect to the yield stress of rebar. Eqs. 7A,7B are termed as uniaxial relationships, as they were developed by testing panels under uniaxial tension.

3.4 Poisson’s effect

As mentioned before, in the SMM, the Poisson’s effect is considered through an orthotropic formulation of 2D strains in the two to one coordinate system. The uniaxial components of the strains (${\epsilon }_{1u}$ and ${\epsilon }_{2u}$) are related to the total strains (${\epsilon }_1$ and ${\epsilon }_2$) in terms of apparent Poisson’s ratios (Hsu/Zhu ratios) ( ${\nu }_{12}$ and ${\nu }_{21}$) as follows (Sengupta and Belarbi (2001); Bavukkatt (2008)).

$\left\{\begin{array}{c}{\epsilon }_2\\ {\epsilon }_1\end{array}\right\}=\left[\begin{array}{cc}1& -{\nu }_{21}\\ -{\nu }_{12}& 1\end{array}\right]\left\{\begin{array}{c}{\epsilon }_{2u}\\ {\epsilon }_{1u}\end{array}\right\}(\mathrm{8a})$

Considering ${\nu }_{21}=0$ (based on tests it was found that the effect of tension on compressive strain is negligible), the strains are expressed as shown in Eqs. 8B, 8C. The uniaxial strains ${\epsilon }_{1u}$ and ${\epsilon }_{2u}$ are denoted as ${\overline{\epsilon }}_1$ and ${\overline{\epsilon }}_2$ in the reference.

${\epsilon }_2={\epsilon }_{2u}(\mathrm{8b})$

${\epsilon }_1={\epsilon }_{1u}-{\nu }_{12}{\epsilon }_{2u}(\mathrm{8c})$

The Hsu/Zhu ratio ${\nu }_{12}$ is defined as follows (Eqs. 9A, 9B).

For ${\epsilon }_{sf}\le {\epsilon }_y$,

${\nu }_{12}=0.2+850{\epsilon }_{sf}(\mathrm{9a})$

For ${\epsilon }_{sf}>{\epsilon }_y$,

${\nu }_{12}=1.9(\mathrm{9b})$

Here, ${\epsilon }_{sf}$ is the average tensile strain of bars along the ℓ- and t-directions that yield first.

The above equations are solved simultaneously to develop the shear stress versus strain behaviour of a membrane element.

4 Cases of asymmetry in membrane elements

In an orthotropic material, the principal axes of applied stresses coincide with the principal axes of generated strains. This is referred to as the principle of coaxiality. When the reinforcement is not symmetric, the principle of coaxiality is violated. Asymmetry of reinforcement can occur in two cases as demonstrated in Figure 3. Here, the principal axes of applied stresses (loading axes) (2–1) are shown as vertical and horizontal axes as is represented for a panel specimen under test. The reinforcement grid is shown inclined to the loading axes.

FIGURE 3

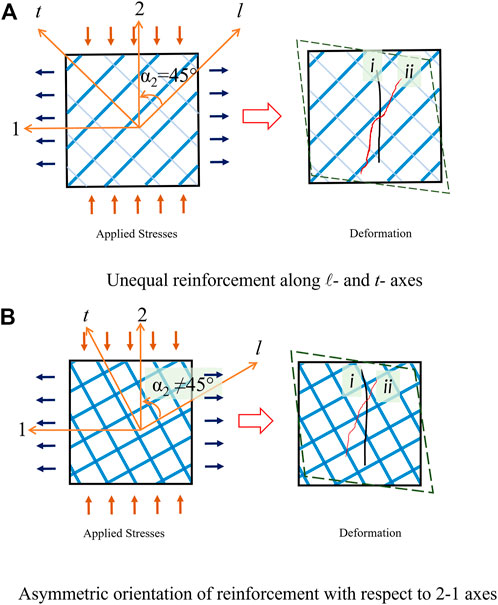
FIGURE 3. Cases of asymmetry in membrane elements. (A) Unequal reinforcement along ℓ- and t-axes. (B) Asymmetric orientation of reinforcement with respect to 2-1 axes.

Case 1) ${\rho }_l>{\rho }_t$ with ${\alpha }_2=45°$

Here, the longitudinal (ℓ-) and transverse (t-) bars are inclined at 45° to the directions of loading. However, when the amount of reinforcement along λ-axis is more than that along t-axis (${\rho }_l>{\rho }_t$), the crack which initially forms perpendicular to one- axis (marked as i in Figure 3A) tends to rotate clockwise and becomes perpendicular to the t-axis (marked as ii in Figure 3A), especially after the yielding of the transverse bars. This generates shear strain (${\gamma }_{21}$) along the principal stress axes 2–1. Similarly, if ${\rho }_l<{\rho }_t$ then the cracks will rotate anti-clockwise, generating ${\gamma }_{21}$ of opposite sign. After the yielding of the bars, the capacities of the bars in the two directions expressed as ${\rho }_l{f}_{yl}$ and ${\rho }_t{f}_{yt}$ are the relevant quantities for comparison.

Case 2) ${\rho }_l={\rho }_t$ with ${\alpha }_2\ne 45°$

Here, the reinforcements along the ℓ- and t-directions are equal. However, when the reinforcement is asymmetrically inclined to the loading axes (with an angle other than 45°, within the range between 0° and 90°), the crack which initially forms along i tends to rotate and bisect the angle between the bars (marked as ii in Figure 3B).

The above two cases can occur either separately or simultaneously.

5 Model for shear-extension coupling

The limitation of SMM can be rectified by extending the orthotropic formulation to a generalised formulation of 2D strains. Kosuru and Sengupta (2018) proposed a 2D anisotropic formulation for an RC membrane element incorporating shear‒extension coupling coefficients, similar to that used in linear elastic composite materials (Robert, 1999).

Maintaining the convention of coordinate system of SMM (2- and one- are the leading and trailing axes, respectively) and noting that ${\tau }_{21}=0$ (no shear stress in two to one axes system) and ${\nu }_{21}=0$, the 2D anisotropic model can be written as in Eq. 10.

$\left\{\begin{array}{c}{\epsilon }_2\\ {\epsilon }_1\\ {\gamma }_{21}\end{array}\right\}=\left(\begin{array}{cc}1& 0\\ -{\nu }_{21}& 1\\ {\eta }_{\mathrm{21,2}}& {\eta }_{\mathrm{21,1}}\end{array}\right)\left\{\begin{array}{c}{\epsilon }_{2u}\\ {\epsilon }_{1u}\end{array}\right\}(10)$

Here, ${\epsilon }_{2u}$ and ${\epsilon }_{1u}$ represent the uniaxial strains due to applied compressive and tensile stresses, respectively. The apparent shear–extension coupling coefficients are denoted as ${\eta }_{\mathrm{21,1}}$ and ${\eta }_{\mathrm{21,2}}$. These quantities are not intrinsic material properties, but they are analogous to smeared properties for an RC membrane element after cracking of concrete or yielding of the bars. Their values change with increasing loading due to the non-linear behaviour of concrete and rebar. The generated shear strain in the two to one axes system due to lack of symmetry of the reinforcement, is expressed in Eq. 11.

${\gamma }_{21}={\eta }_{\mathrm{21,2}}{\epsilon }_{2u}+{\eta }_{\mathrm{21,1}}{\epsilon }_{1u}(11)$

The coefficients are defined as ratios of average strains, as follows.

${\eta }_{\mathrm{21,2}}=\frac{{\gamma }_{21,{\sigma }_2}}{{\epsilon }_{2u}}(\mathrm{12a})$

${\eta }_{\mathrm{21,1}}=\frac{{\gamma }_{21,{\sigma }_1}}{{\epsilon }_{1u}}(\mathrm{12b})$

To model the behaviour of an asymmetric membrane element precisely, ${\eta }_{\mathrm{21,1}}$ and ${\eta }_{\mathrm{21,2}}$ needs to be quantified. This requires modelling of ${\gamma }_{21,{\sigma }_2}$ and ${\gamma }_{21,{\sigma }_1}$ only, as ${\epsilon }_{2u}$ and ${\epsilon }_{1u}$ can be estimated from the applied stresses ${\sigma }_2$ and ${\sigma }_1$, respectively (using the uniaxial constitutive relationships). However, it is to be noted that ${\eta }_{\mathrm{21,1}}$ and ${\eta }_{\mathrm{21,2}}$ are ratios of small strains and hence, their estimates based on tests are prone to error. Instead of modelling ${\eta }_{\mathrm{21,1}}$ and ${\eta }_{\mathrm{21,2}}$, ${\gamma }_{21}$ is directly modelled based on the tests described next.

6 Experimental programme

An experimental programme was undertaken to evaluate the shear strain (${\gamma }_{21})$ by testing panels under biaxial tension–compression (Kosuru and Sengupta, 2020). The instantaneous shear strain generated due to asymmetric reinforcement in the membrane element is hypothesized to be influenced by four parameters, as follows.

• Measures of nonlinearity based on instantaneous material stresses:

    - Tensile stress in the bars, specifically the transition from pre-yield to post-yield condition. The normalised stress of the transverse bars whose amount is lower, is expressed as $R\left(f_t\right)=f_t/f_{yt}^{\ast }$.

    - Compressive stress in concrete till crushing. The normalised stress is expressed as $S\left({\sigma }_2^c\right)={\sigma }_2^c/\zeta f_c^{/}$.

• Measures of asymmetry of reinforcement:

    - Difference in the amounts and grades of reinforcement in the two directions. This is expressed as the amount asymmetry index ($H={\rho }_l{f}_{yl}/{\rho }_t{f}_{yt}$). H is a measure of Case (a) type of asymmetry of the reinforcement. It is the inverse of η mentioned earlier, to have the values greater than 1.0 when the amount of longitudinal reinforcement is more. For consistency, this index is considered the same in both the pre-yield and post-yield regimes.

    - Angle of inclination of the rebar grid with respect to the principal axes of applied stresses (${\alpha }_2$) is the inclination asymmetry index. It is a measure of Case (b) type of asymmetry of the reinforcement.

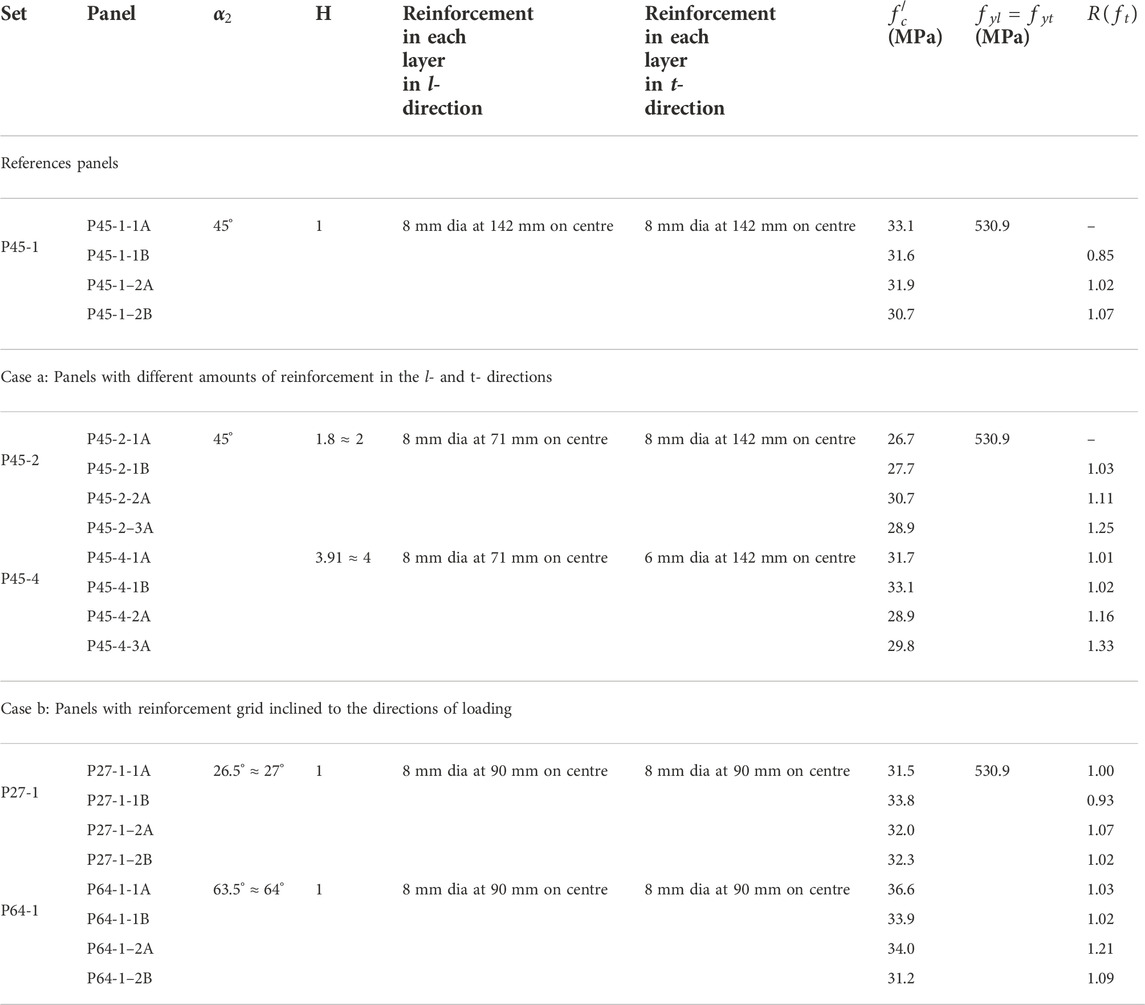
20 panels were tested to quantify ${\gamma }_{21}$ with respect to the identified parameters. The details of the panels tested are given in Table 1. The panels were divided into five sets, with each set consisting of four panels. Out of the four, the values of tension applied in two panels corresponded to pre-yield and those in the other two corresponded to post-yield condition of the bars. To check repeatability, two panels were tested under a certain condition.

TABLE 1

TABLE 1. - Details of test programme.

Orthotropic panels:

1) With reinforcement symmetric with respect to the axes of loading (equal amounts of reinforcement in the two directions and grid inclined at 45° to the axes). These formed the reference cases. (P45-1 set)

Anisotropic panels with unequal amounts of reinforcement in the two directions (grid inclined at 45°):

2) With ratios of amounts of reinforcement along λ- and t-directions approximately equal to 2.0. (P45-2 set)

3) With ratios of reinforcement in the two directions approximately equal to 4.0. (P45-4 set)

Anisotropic panels with grid inclined other than 45° (equal amounts of reinforcement in the two directions): Two cases were selected as follows.

4) With grid inclined at 27°. (P27-1 set)

5) With grid inclined at 64°. (P64-1 set)

Further tests can be conducted for panels with intermediate values of ${\alpha }_2$ .

6.1 Test setup

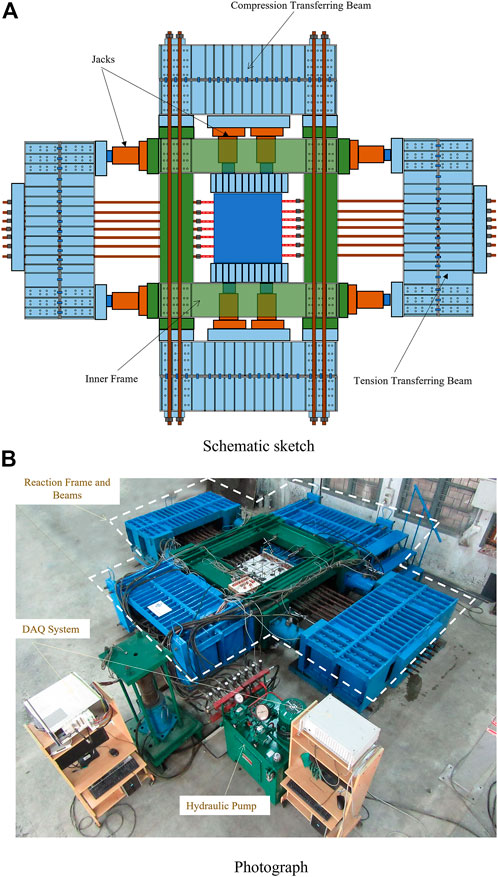
A biaxial panel testing facility is available at the Structural Engineering Laboratory of Indian Institute of Technology Madras to test RC panels under in-plane loading. Originally the facility was used to test prestressed panels under biaxial tension (Achyutha et al., 2000). This was subsequently reconfigured to conduct biaxial tension-compression tests (Sengupta et al., 2005). The facility consists of a horizontal self-equilibrating system made of frames and beams, supported on a fiber reinforced concrete floor. Loading of capacity 2000 kN can be applied in each horizontal direction. A schematic sketch of the setup is shown in Figure 4A. The components are:

1) Two stiff built-up beams and high strength tie rods of 32 mm diameter, for transferring tension. The beams are placed on heavy duty sliding bearings.

2) Two stiff reaction beams and high strength tie rods for self-equilibration, along the compression direction.

3) Eight load controlled hydraulic jacks, a set of four jacks in each direction, for applying compression or tension.

FIGURE 4

FIGURE 4. Test setup. (A) Schematic sketch. (B) Photograph.

The two sets of jacks are operated separately by two pumps, and two pairs of distribution blocks. The oil pressure from each pump is controlled by a hand operated lever. Each distribution block maintains approximately equal pressure in the four jacks connected to it. A view of the test setup is shown in Figure 4B.

6.2 Loading protocol

To investigate the effect of the chosen parameters, panel specimens were tested under sequential tension–compression. Although, increasing shear corresponds to proportional increase of tension and compression, a sequential tension–compression load path was selected to segregate the effects of tension (in terms of $\left.R\left(f_t\right)\right)$ and compression (in terms $\left.S\left({\sigma }_2^c\right)\right)$ on the shear strain ${\gamma }_{21}$. Initially, tension was applied along the 1-direction up to a predetermined level based on $R\left(f_t\right)$. It was maintained constant during the subsequent compression phase. The compression was applied along the 2-direction up to the crushing of concrete $\left(S\left({\sigma }_2^c\right)=1.0\right)$.

6.3 Test specimens

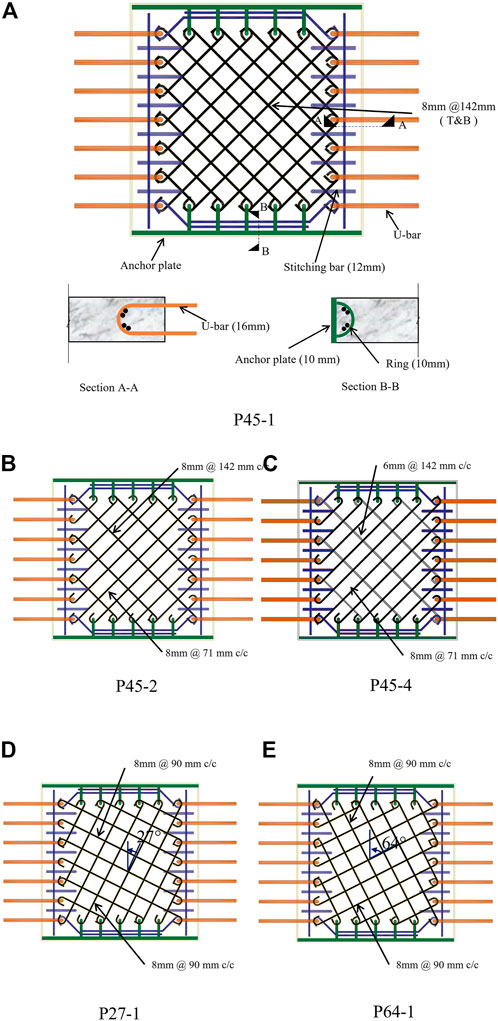
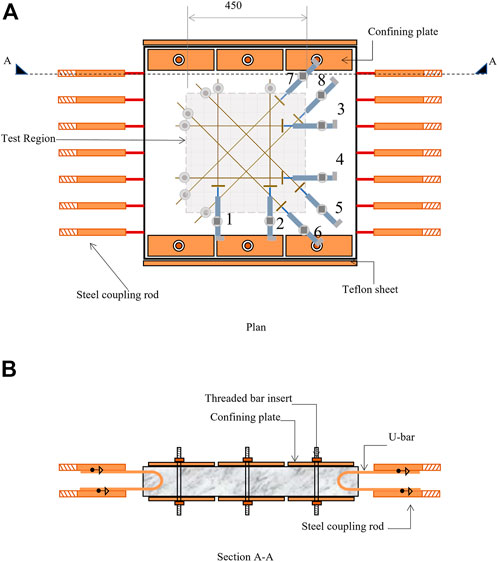
All the panel specimens were of dimensions 800 mm × 800 mm × 100 mm. The horizontal dimensions were fixed based on the requirement that a minimum of three to four cracks form along the direction of tension within the test region. The thickness of 100 mm was selected such that the capacity of a panel with normal strength concrete, when tested under uniaxial compression, was less than the capacity of the testing facility i.e., 2000 kN. The reinforcement was provided in two layers and details are shown in Figure 5.

FIGURE 5

FIGURE 5. Reinforcement details of panel series. (A) P45-1 (B) P45-2 (C) P45-4 (D) P27-1 (E) P64-1.

The following features were added to avoid premature failures.

1) Stitching reinforcement was provided along the tension edges of the panel to avoid premature cracking of the edges.

2) A panel consisted of an anchorage plate along each compression edge for adequate anchorage of bars during the application of tension load.

3) The compression edges were also strengthened by placing confining steel plates along the edges, to avoid premature crushing of the edges during the application of compression.

4) Teflon sheets were placed at the compression edges to reduce friction.

6.4 Instrumentation

Load cells of capacity 500 kN were used to measure the tension load applied by the hydraulic jacks. As there was no gap to place load cells on the compression side, a hydraulic jack connected in series to the compression jacks was placed in a separate reaction standalone frame outside the panel tester, to measure the compression load.

Deformations were measured using linear variable differential transducers (LVDTs). LVDTs were fixed only on the top face of the panel. As the bottom face was inaccessible, no LVDT was placed below the panel. The average strains were calculated from the measured deformations. Arrangement of the LVDTs is shown in Figure 6. LVDTs one and two were used to record deformation along the compression direction (ε₂). LVDTs three and four recorded the deformation along tension direction (ε₁). LVDTs five to eight recorded the deformations along the diagonals to quantify the average shear strain (γ₂₁).

FIGURE 6

FIGURE 6. Instrumentation and additional features. (A) Plan. (B) Section A A.

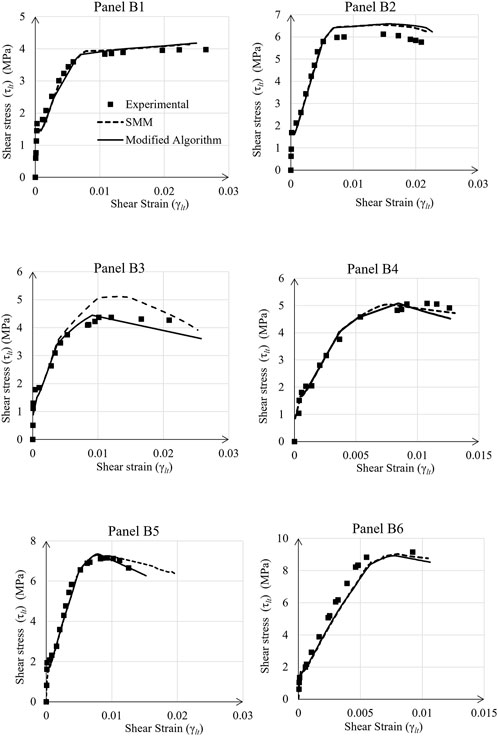
7 Test results

7.1 Measurement of shear strain ${\mathit{\gamma }}_{\mathit{21}}$

Figure 7 shows a typical cracked specimen at different stages of the loading during the test. Panel P45-4-2 A is chosen for demonstration. It can be observed from the figure that the cracks which started to form perpendicular to the direction of tension rotate gradually to become parallel to the λ-direction with increasing load. This can be attributed to the higher stiffness in the λ-direction due to the presence of higher amount of reinforcement along the λ-axes.

FIGURE 7

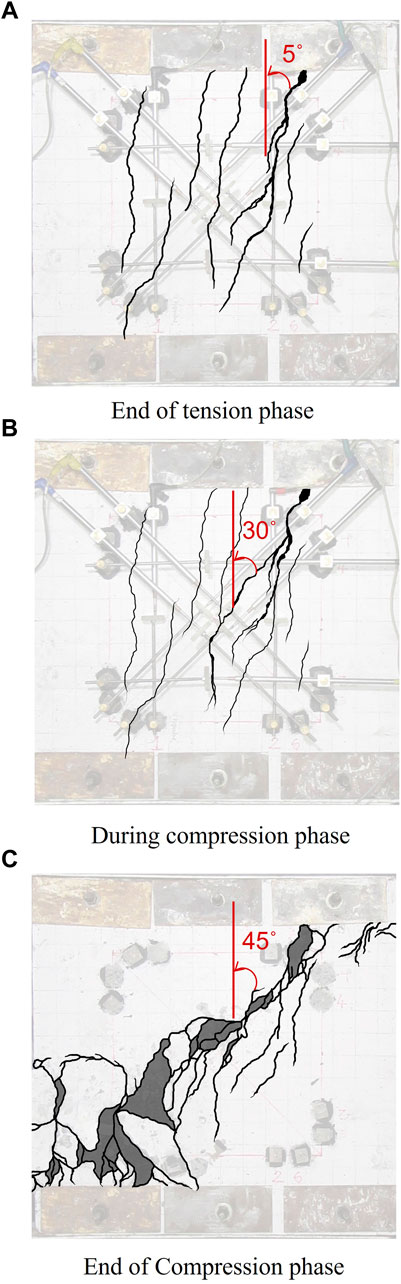
FIGURE 7. Panel P45-4-2 A at different stages of loading. (A) End of tension phase. (B) During compression phase. (C) End of Compression phase.

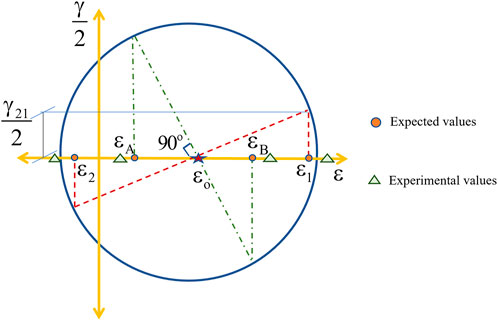
Shear strain ${\gamma }_{21}$ can be computed from three measured strains from a rosette, using 2D strain transformation equations. Since four strains were measured along 1-, 2-, A- and B- directions, as shown in Figure 8A, first 2D Mohr’s compatibility condition was checked with the measured strains. Figure 8B shows the Mohr’s circle for measured strains. The compatibility condition ${\epsilon }_1+{\epsilon }_2={\epsilon }_A+{\epsilon }_B$ for P45-4 series panels is demonstrated in Figure 8C. It can be noted from the plot that the measured strains are consistent and satisfy the criteria during the initial phase of loading. However, the equality slightly deviates with increase in load. This can be attributed to the substantial cracking which occurred due to the application of tension close to the yield load. Thus, a shear strain value calculated from three measured strains may not be consistent. This is demonstrated in Figure 9. If the compatibility is maintained, all the strains would have fallen on the points marked as “Expected values”. As the experimental values do not coincide with the expected values, a unique Mohr’s circle cannot be drawn considering all the four points. A best fit Mohr’s circle can be drawn by calculating the root mean square (RMS) value of ${\gamma }_{21}$ given by the following equation.

$\frac{{\gamma }_{21}}{2}=\sqrt{\frac{{\left({\epsilon }_0-{\epsilon }_A\right)}^2+{\left({\epsilon }_0-{\epsilon }_B\right)}^2}{2}}(\mathrm{13a})$

Here, ${\epsilon }_0$ is the average location of the centre of the circle and is given by the following expression.

${\epsilon }_0=\frac{{\epsilon }_1+{\epsilon }_2+{\epsilon }_A+{\epsilon }_B}{4}(\mathrm{13b})$

FIGURE 8

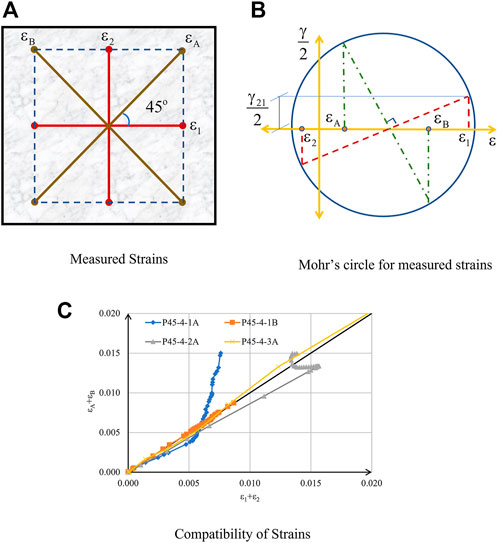
FIGURE 8. Mohr’s Compatibility check. (A) Measured Strains (B) Mohr’s circle for measured strains (C) Compatibility of Strains.

FIGURE 9

FIGURE 9. Schematic representation of best fit Mohr’s circle with RMS value of ${\gamma }_{21}$

7.2 Modelling of shear strain ${\mathit{\gamma }}_{\mathit{21}}$

Based on the method of separation of variables, ${\gamma }_{21}$ was modelled as a function of the identified parameters as shown in Eq. 7. Although, sequential tests were conducted, the effects of the two parameters causing the non-linear variation of the response, R(f_t) and S (${\sigma }_2^c$), act simultaneously under proportional loading (Figure 12). Therefore, ${\gamma }_{21}$ was expressed as the product of two functions $F_1\left[S\left({\sigma }_2^c\right)\right]$ and $F_2\left[R\left(f_t\right)\right].$

The other two parameters $H$ and ${\alpha }_2$ affect the magnitude of ${\gamma }_{21}$ . The maximum value of ${\gamma }_{21}$ in panels with difference in amounts of reinforcement is modelled by $F_3\left[H\right]$. The maximum value of ${\gamma }_{21}$ in panels with rebar grid inclined at angle other than 45° is modelled by $F_4\left[{\alpha }_2\right]$. Since a membrane element can have both cases of asymmetry simultaneously, additive functions were selected.

${\gamma }_{21}=F_1\left[S\left({\sigma }_2^c\right)\right]F_2\left[R\left(f_t\right)\right]\left(F_3\left[H\right]+F_4\left[{\alpha }_2\right]\right)(14)$

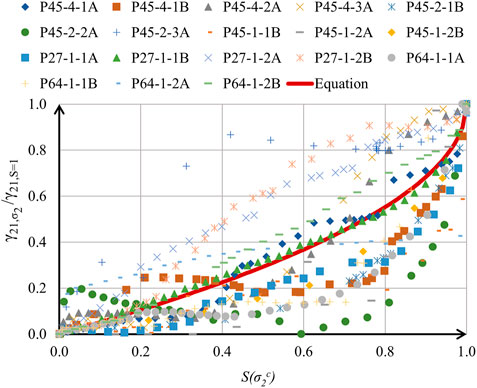
7.2.1 Variation of shear strain with compressive stress in concrete

Figure 10 shows the variation of normalised ${\gamma }_{21}$ versus S (${\sigma }_2^c$) in concrete. The values of ${\gamma }_{21}$ are normalised by the maximum value attained at the end of compression phase (${\gamma }_{21,S=1}$ at S (${\sigma }_2^c$) = 1). Based on the trend of the variation, a best fit second order polynomial was selected, as shown in Eq. 15. The equation satisfies the condition that ${\gamma }_{21}/{\gamma }_{21,S=1}=1$ and the slope of the curve is vertical at $S\left({\sigma }_2^c\right)=1$.

FIGURE 10

FIGURE 10. Normalised shear strain versus normalised compressive stress.

For $0<S\left({\sigma }_2^c\right)\le 1$,

$\frac{{\gamma }_{21}}{{\gamma }_{21,S=1}}=F_1\left[S\left({\sigma }_2^c\right)\right]=1-\sqrt{1-S\left({\sigma }_2^c\right)}(15)$

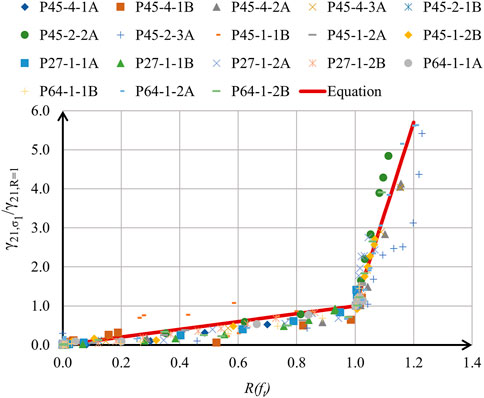
7.2.2 Variation of shear strain with tensile stress in reinforcement

The variation of normalised ${\gamma }_{21}$ with respect to at $R\left(f_t\right)$ is modelled as a bilinear curve as shown in Figure 11. The values of ${\gamma }_{21}$ are normalised by the value attained at yielding of the bars (${\gamma }_{21,R=1}$ at $R\left(f_t\right)=1.0$). For a panel where the bars did not yield, the value was scaled to correspond to $R\left(f_t\right)=1.0$. It is observed that before yielding, ${\gamma }_{21}$ increases gradually. However, after yielding, ${\gamma }_{21}$ increases rapidly. The equations satisfy the condition that ${\gamma }_{21}/{\gamma }_{21,R=1}=1$ at $R\left(f_t\right)=1$.

FIGURE 11

FIGURE 11. Normalised shear strain versus normalised tensile stress.

For $\left(f_t\right)\le 1$,

$\frac{{\gamma }_{21}}{{\gamma }_{21,R=1}}=F_2\left[R\left(f_t\right)\right]=R\left(f_t\right)(\mathrm{16a})$

For $1\le R\left(f_t\right)\le 1.2$

$\frac{{\gamma }_{21}}{{\gamma }_{21,R=1}}=F_2\left[R\left(f_t\right)\right]=23.5R\left(f_t\right)-22.5(\mathrm{16b})$

The maximum value of $R\left(f_t\right)=1.2$ is based on the ultimate stress that could be applied.

7.2.3 Variation of shear strain with asymmetry in reinforcement

The magnitude of ${\gamma }_{21}$ for a panel is the sum of the values at the ends of tension phase and compression phase.

${\gamma }_{21,\mathit{max}}={\gamma }_{21|\sigma 1,R=1}+{\gamma }_{21,|\sigma 2,S=1}(17)$

The assumption is that there is no effect of load path, sequential or proportional. This is demonstrated in Figure 12.

FIGURE 12

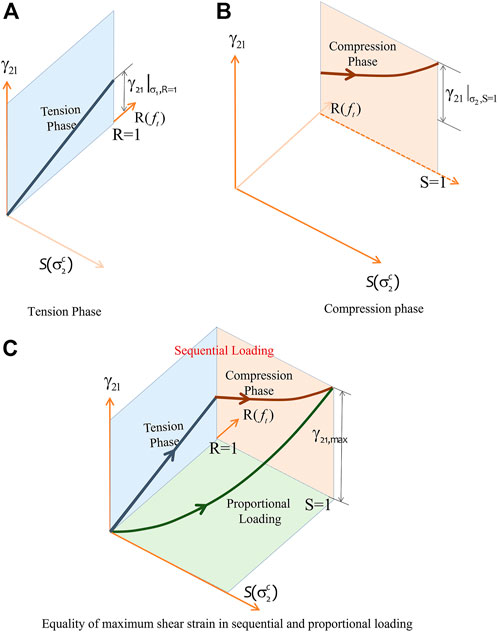
FIGURE 12. Schematic sketches showing maximum shear strain in load path. (A) Tension Phase. (B) Compression phase. (C) Equality of maximum shear strain in sequential and proportional loading.

Variation of the numerical value of ${\gamma }_{21,\mathit{max}}$ with respect to H is plotted for panels with ${\alpha }_2=45°\left(F_4=0\right)$ in Figure 13A. It shows an increasing trend which is lower than a linear variation. Thus, F3 [H] is expressed as follows.

FIGURE 13

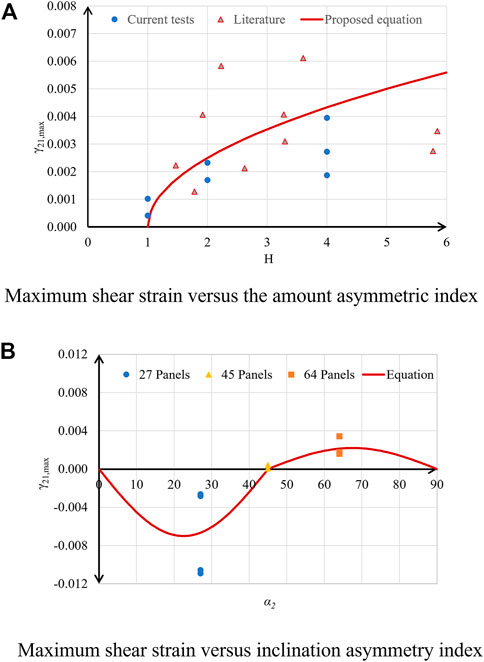
FIGURE 13. Maximum shear strain versus asymmetry. (A) Maximum shear strain versus the amount asymmetric index. (B) Maximum shear strain versus inclination asymmetry index.

For $\ge 1$,

$F_3\left[H\right]={\gamma }_{21,\max |{\alpha }_2=45°}=-0.0025\sqrt{H-1}(18)$

In Figure 13A, maximum shear strain values for B-series panels (Pang and Hsu, 1995) and VB-series panels (Zhang and Hsu, 1998) are also shown along with panels from the present experimental programme. Though the panels from literature were tested under proportional loading, it can be seen that the equation proposed above predicts fairly for all the panels. This validates that sequential and proportional loading produce comparable values of maximum shear strain.

Variation of ${\gamma }_{21,\mathit{max}}$ with respect to ${\alpha }_2$ (Figure 13B) can be modelled as a sinusoidal variation as the sign of ${\gamma }_{21}$ in panels with ${\alpha }_2$ = 27°is opposite to those in panels with ${\alpha }_2=$ 64°. However, the amplitude of ${\gamma }_{21,\mathit{max}}$ is less for ${\alpha }_2=$ 64° due to increased dowel action of the bars across a crack. The function F4 [α₂] is modelled as follows.

For $0°\le {\alpha }_2\le 45°$

$F_4\left[{\alpha }_2\right]={\gamma }_{21,\max |H=1}=-0.007\sin \left(4{\alpha }_2\right)(\mathrm{19a})$

For $0°\le {\alpha }_2\le 90°$

${F_4\left[{\alpha }_2\right]=\gamma }_{21,\mathit{max}|H=1}=-0.0022\sin \left(4{\alpha }_2\right)(\mathrm{19b})$

The above equations can be substantiated by testing panels with intermediate values of ${\alpha }_2$ .

Equations 15–19 form a complete model for estimation of ${\gamma }_{21}$ in SMM. A modified solution algorithm was proposed to incorporate the mechanics-based expression for ${\gamma }_{21}$ (Kosuru and Sengupta, 2022). This algorithm was used to predict the behaviour of the B-series panels from literature mentioned earlier (Figure 14). It can be seen that the shear behaviour curves could be estimated with reasonable accuracy. The behaviour of a panel was predicted beyond the peak load using an extrapolation of Eq. 15. However, this needs to be substantiated by testing panels under deformation-controlled loading.

FIGURE 14

FIGURE 14. Shear stress (t_lt) versus shear strain (γ_lt) of B series panels (Pang and Hsu,1995).

8 Conclusion

The conclusions from the present study are as follows.

1) The SMM utilises an orthotropic formulation of 2D strains to incorporate the Poisson’s effect in an RC membrane element. This does not consider rationally the shear strain generated in the principal axes of applied stresses (${\gamma }_{21}$) for an element with reinforcement asymmetric to the loading. An anisotropic formulation is proposed to generalise the applicability of SMM by incorporating the effect of shear−extension coupling.

2) Two cases of asymmetry were investigated: a) the amounts of reinforcement in the longitudinal and transverse directions are not equal, but the reinforcement grid is inclined at 45° to the principal axes of loading, b) the amounts of reinforcement are equal in both the directions, but the grid is not inclined at 45°.

3) The shear strain ${\gamma }_{21}$ is modelled in terms of four parameters. These are the instantaneous tensile stress in reinforcement, instantaneous compressive stress in concrete, amount asymmetric index and the inclination asymmetry index.

4) A total of 20 panels were tested under biaxial tension-compression to quantify ${\gamma }_{21}$. The panels were divided into five sets for studying the effects of the parameters. A model to estimate ${\gamma }_{21}$ is proposed based on the identified parameters. This was corroborated against test results from the literature.

5) The proposed model for ${\gamma }_{21}$ can be used with the modified algorithm of SMM to estimate the shear stress versus shear strain behaviour of the membrane elements. This can further be used in a performance based analysis of a structure with wall-type members, with an implementation in the finite element method (Zhu et al., 2001; Kosuru and Sengupta, 2021).

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

Conceptualization, AS and RK; methodology, AS and RK; Experimental investigation, RK; analysis, AS and RK; writing—original draft preparation and editing, RK; writing—review, AS; visualization, RK; supervision, AS; project administration, AS. All authors have read and agreed to the published version of the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Achyutha, H., Paramasivam, V., Hari, K., Harsha, K. S., Koteswara Rao, P. C., and Sivathanu Pillai, C. (2000). An experimental test facility to carry out biaxial tension test on concrete panels. J. Struct. Eng. CSIR ‒ Struct. Eng. Res. Centre 27 (3), 165–168.

Google Scholar

Bavukkatt, R. (2008). Modelling the deformation characteristics of reinforced concrete panels under biaxial tension-compression. PhD dissertation, Chennai, India: Department of Civil Engineering.

Google Scholar

Belarbi, A., and Hsu, T. T. C. (1994). Constitutive laws of concrete in tension and reinforcing bars stiffened by concrete. Struct. J. Am. Concr. Inst. 91 (4), 465–474.

Google Scholar

Belarbi, A., and Hsu, T. T. C. (1995). Constitutive laws of softened concrete in biaxial tension-compression. Struct. J. Am. Concr. Inst. 92 (5), 562–573.

Google Scholar

Belarbi, A. (1991). Material laws of reinforced concrete in biaxial tension-compression. PhD dissertation, Houston: Department of Civil and Environmental Engineering.

Google Scholar

Hsu, T. T. C., and Mo, Y. L. (2010). Unified theory of concrete structures. West Sussex, U.K: Wiley.

Google Scholar

Hsu, T. T. C. (1991). Nonlinear analysis of concrete membrane elements. Struct. J. Am. Concr. Inst. 88 (5), 552–561.

Google Scholar

Hsu, T. T. C. (1993). Unified theory of reinforced concrete. Boca Raton, FL: CRC Press, 329.

Google Scholar

Hsu, T. T. C., and Zhu, R. R. H. (2002). Softened membrane model for reinforced concrete elements in shear. ACI Struct. J. Am. Concr. Inst. 99 (4), 460–469.

Google Scholar

Kosuru, R. S., and Sengupta, (2021). Effect of shear—extension coupling in a membrane element with asymmetry of reinforcement”, Proceedings of the, 17th world conference in earthquake engineering, organised by Japan Association for Earthquake Engineering (17WCEE), Sendai, Japan. 21 October 2021.

Google Scholar

Kosuru, R. S., and Sengupta, A. K. (2018). Proceedings 11^th structural engineering convention. Kolkata: Jadavpur University. 19.

Google Scholar

Kosuru, R. S., and Sengupta, A. K. (2022). Incorporation of Shear−Extension coupling in softened membrane model. Journal of structural engineering. 12. 1-10.

Google Scholar

Pang, X. B., and Hsu, T. T. C. (1995). Behaviour of reinforced concrete membrane elements in shear. Struct. J. ACI 92 (6), 665–679.

Google Scholar

Pang, X. B., and Hsu, T. T. C. (1996). Fixed-angle softened-truss model for reinforced concrete. Struct. J. Am. Concr. Inst. 93 (2), 197–207.

Google Scholar

Robert, M. J. (1999). Mechanics of composite materials. Philadelphia: Taylor & Francis, 519.

Google Scholar

Sengupta, A. K., and Belarbi, A. (2001). Modeling effect of biaxial stresses on average stress-strain relationship of reinforcing bar in reinforced concrete panels. Struct. J. Am. Concr. Inst. 98 (5), 629–637.

Google Scholar

Sengupta, A. K., Perla, R. M. R., and Jacob, B. (2005). Testing RC panels under in-plane biaxial loads. Indian Concr. J. 79 (6), 51–56.

Google Scholar

Vecchio, F. J., and Collins, M. P. (1986). The modified compression-field theory for reinforced concrete elements subjected to shear. ACI Struct. J. 83 (2), 219–231.

Google Scholar

Zhang, L. X., and Hsu, T. T. C. (1998). Behavior and analysis of 100 MPa concrete membrane elements. J. Struct. Eng. (N. Y. N. Y). 124 (1), 24–34. doi:10.1061/(asce)0733-9445(1998)124:1(24)

CrossRef Full Text | Google Scholar

Zhu, R. R. H., Hsu, T. T. C., and Lee, J. Y. (2001). Rational shear modulus for smeared crack analysis of reinforced concrete. Struct. J. Am. Concr. Inst. 98 (4), 443–450.

Google Scholar

Zhu, R. R. H., and Hsu, T. T. C. (2002). Poisson effect in reinforced concrete membrane elements. Struct. J. Am. Concr. Inst. 99 (5), 631–640.

Google Scholar

Zhu, R. R. H. (2000). Softened membrane model for reinforced concrete elements considering Poisson effect. PhD dissertation, Houston, TX: Department of Civil and Environmental Engineering.