Comprehensive Review on the Dynamic and Seismic Behavior of Flat-Bottom Cylindrical Silos Filled With Granular Material

The seismic design of industrial flat-bottom ground-supported silos filled with granular material still presents several challenges to be addressed. They are related to the main aspects which differentiate silo structures containing granular material from other civil structural typologies: 1) the relatively low silo structure mass as compared to the ensiled content mass; 2) the granular nature of the ensiled material. Indeed, the internal actions in the structural members are governed by the complex dynamic interactions along the interfaces between granular content and silo wall or base, or even the internal interaction between particles. More in detail, even though the scientific interest in such complex interactions dates back to the middle of the 19th century, several issues are still unclear such as the dependency of the fundamental dynamic properties (period of vibration and damping ratio) on the characteristics of the dynamic excitation (intensity, frequency content, duration) or the amount of ensiled material mass activated during a seismic excitation and provoking extra pressures on the wall (effective mass). Therefore, most of current seismic code provisions for silos are grounded on rather approximate and simplified assumptions leading to often over-conservative evaluations. The present paper intends to provide a comprehensive summary of the mainly acknowledged experimental and theoretical advances in the dynamic and seismic behavior of silos, supporting the potential researcher in the field to understand the real differences between the code assumptions and recommendations and the actual conditions, as well as illustrating the open issues to be still further investigated.

Introduction

Storage containers of bulk material are known as bins (or grain bins), silos or even bunkers. Although there is no globally accepted definition for each of the previous terms, “bins” or “bunkers” are commonly used to refer to squat containers with a shallow filling condition of a variety of material like coal, ore, gravel and crushed stones, while slender containers of food supplies (e.g., wheat, corn …) and cement are usually called “silos” (Li, 1994). The European design provisions EN 1991-4:2006, EN 1998-4:2006 and EN 1993-4:2007 (European Committee for Standardization, 2006a; European Committee for Standardization, 2006b; European Committee for Standardization, 2007) adopt the term “silo” as an inclusive term for all structures for the storage of granular solid, whilst the term “bin” is common in the north American countries (ANSI-ASAE S433.1: 2019). Flat-bottom ground-supported silos, typically made of steel or reinforced concrete (r.c.), are storage structures that are directly placed on a r.c. plate foundation. Typically, cast in-situ r.c. silos present circular hollow section with uniform thickness; while steel silos are made up either of isotropic flat wall or orthotropic corrugated cold-formed wall with variable thicknesses, usually supported with bolted C- or open hat-shaped vertical stiffeners.

The type of granular material (wheat, corn, rice, sugar, soya beans, maize, barley, …) has to be clearly specified in the design phase, since its mechanical properties (which can substantially change from a product to another one, as per the Table E.1 of Annex E of EN 1991-4:2006) strongly affect both the static and the dynamic behavior of the filled silo system and the choice of the more appropriate wall section (e.g., flat-walled section is commonly used for powder content, whist corrugated-walled section is preferred for bulk solids).

Steel silos are thin-walled structures which are very sensitive to human made mistakes and construction errors, as well as to damages occurred during shipment and transportation. Moreover, special care should be paid during the first filling procedure, considering even the adjacent silos (i.e., the whole silo battery), since specific filling programs on different steps should be envisaged to guarantee the stability of the whole silo battery without causing any differential settlements leading eventually to structural defects that might also affect the dynamic response of silos during seismic events.

Several earthquakes, that occurred in the last decades, had catastrophic consequences on storage facilities and mainly silos. Description of damages and main causes of collapses can be found in the in-situ post-earthquake surveys reports (Dogangun et al., 2009; Fierro et al., 2011; Uckan et al., 2015). In December 1988, Northern Armenia was hit by a M6.8 earthquake with devastating consequences on several industrial facilities including silos mainly due to construction imperfections accompanied by inadequate inspections (Arze, 1992, Arze, 1993; Griffin et al., 1995). Another interesting case was noticed after the M6.3 L’Aquila (Central Italy) earthquake, where the failure was reported of three adjacent tall steel silos in a chemical facility near L’Aquila city due to the collision with a close r.c. structure (Grimaz, 2014). During the M8.8 2010 Chile earthquake, extensive damages and collapses stroke many silos in an industrial facility in the city of Concepción, where two rows of silos collapsed due to the failure of the base connections (Villalobos and Mendoza. 2011). In addition, several silo failures occurred across the region, where some fully filled silos up to 5,000 tons capacity showed different failure modes, including global overturning and buckling mechanisms due to the lack of stiffening elements (Grossi et al., 2010). In May 2012, Emilia-Romagna region (Northern Italy) was hit by two M5.8 earthquakes and several metal silos collapsed in various ways, including plastic hinge development near the silo base (Augenti et al., 2013; Gioncu and Mazzolani, 2014). In general, most of the reported failures were associated with brittle behavior in the absence of structural redundancy and alternative resisting mechanisms, which represents an inherent common deficiency due to the structural configuration of silos. Finally, the majority of the reported silo failures (85%) are related to incorrect adopted design concepts, or executive construction problems (Arze, 1992). Figure 1 schematically represents the most common failure mechanisms during earthquake events.

FIGURE 1

FIGURE 1. Common failure mechanisms of flat-bottom filled silo systems during earthquake events.

It is thus clear that the proper evaluation of the forces transmitted by the stored material to the silo structure, during both filling and discharging phases or in the event of an earthquake ground-motion, is of fundamental importance. This task is particularly complex since the granular nature of the ensiled content triggers off a highly non-linear behaviour strongly affecting the highly vulnerable thin cylindrical wall (especially, in empty conditions or asymmetric discharging conditions). Specific additional loading cases accounting for the potential eccentric pipe flow phenomenon (e.g., when side discharging is required), and empty conditions loading combinations (at least one for wind and one for seismic loads) must be considered since it might lead to buckling problems or deformations with a strong impact on the filled silo system behavior during the seismic event. In this respect, specific design recommendations for silo structures can be found in several international building codes, including the Eurocode provisions (EN 1991-4: 2006; EN 1993-4: 2006; EN 1998-4: 2006), U.S. building codes FEMA P-750 (ASCE-7, 2005; UBC, 1994; American Concrete Institute, 1997), and the Japanese building code (Architectural Institute of Japan (AIJ), 2010). Nevertheless, most of the mentioned design provisions are based on rather approximate and over-conservative assumptions which reflect the current state of knowledge regarding the dynamic behavior and complex interaction of the granular solid with the silo structure.

In light of this (Seismic Design of Silos: Main Issues and Current Provisions), this work intends to present a comprehensive overview of the available research works on the dynamic behavior of filled silo systems. The experimental works aimed at characterizing the dynamic properties of the granular materials and the dynamic response of small- and full-scaled silos are summarized (Dynamic Experimental Tests on Granular Media, Empty and Filled Silo Systems), as well as the main theoretical studies and numerical investigations to develop predictive models (Theoretical Studies and Numerical Modelling on the Dynamic Behavior of Filled Silo Systems). The final objective is to identify the main challenges for future research (Future Research Challenges).

Seismic Design of Silos: Main Issues and Current Provisions

The structural response of storage units filled with granular solid, in static but particularly in dynamic conditions, is strongly affected by the not fully understood interaction between the structural elements and the stored content particles. This aspect is especially important for steel silos characterized by a very low self-weight with respect to the stored material. In this respect, the essential matters far from being fully understood might be outlined in two points:

• the effective mass, or the portion of the overall particulate material interacting with the silo structure wall under seismic conditions and provoking additional dynamic overpressures onto the shell wall of the silo;

• the fundamental period (or, equivalently, the fundamental frequency) corresponding to the first mode of vibration of the filled silo system, due to uncertainties concerning both the above-mentioned effective mass and the lateral stiffness provided by the ensiled material.

Both aspects are of central importance for the evaluation of the earthquake actions since, in practice, the seismic design of silos is generally conducted by means of equivalent static analysis. In detail, the static horizontal forces are usually given in terms of dynamic overpressures (additional horizontal pressures with respect to the static ones) generated by the stored material onto the wall of the silo and are related to the effective mass. The ensiled content, pushing on the silo wall, tends to lean against the wall due to the particle-wall friction, exerting non-negligible actions, as reported by numerous theoretical studies and experimental research works since the end of the 19th century (Janssen, 1895; Naito, 1988; Nielsen, 1998; Vanel and Clément, 1999; Ovarlez et al., 2003; Rotter, 2008; Qadir et al., 2010; Silvestri et al., 2012; Pieraccini et al., 2015; Qadir et al., 2016; Silvestri et al., 2016; Silvestri et al., 2021). A brief review of the current provisions in standards is presented hereafter with specific reference to the two above-mentioned issues.

UBC (Uniform Building Code, 1994) provisions recommend to design ground-supported silos using the procedures for rigid structures (defined by a fundamental period of vibration smaller than 0.06 s), considering a seismic force resulting from an effective mass composed by the total mass of the silo structure and the whole content material.

ACI 313-97 (American Concrete Institute, 1997) provisions suggest that the effective mass should be estimated at 80% of the actual mass of the stored material in order to calculate the lateral seismic inertia forces. Lateral force reduction is permitted due to energy loss caused by intergranular motion and internal frictional conditions in the ensiled solid, as found by both Chandrasekaran and Jain (1968) and Harris and Von Nad (1985), which the standard expressly refers to. Moreover, the provisions highlight the necessity of rational method to evaluate the period of vibration.

EN 1998-4 (European Committee for Standardization, 2006b) provisions provide general principles and practical application rules for the earthquake design of elevated and ground-supported silos. They refer to: 1) the evaluation of the extra horizontal pressures during a seismic event onto the wall height; 2) seismic analysis methods; 3) numerical modelling of silos for seismic analysis. Silo structures are supposed to operate in the elastic field; thus, the elastic analysis of the silo shell wall is to be considered. In the absence of more accurate evaluations, global seismic response should be evaluated modelling the particulate material as an effective mass with related rotational inertia located at the center of mass based on the assumption that particulate contents move in unison with the wall. Barring a more accurate evaluation, 80% of the stored material can be assumed as activated effective mass. If the dynamic response and the mechanical properties of the particulate material are not explicitly represented and accurately considered in the analysis (by adopting adequate modelling techniques to reproduce its dynamic response and mechanical properties), the effect on the silo wall of the solid particulate’s response to the horizontal component of the seismic input may be summarized in additional horizontal pressures onto the wall (leading to normal radial and tangential circumferential components). The provisions recommend structural damping ratio of 5% and contents damping ratio of 10% (in the absence of specific information). The provisions of EN 1998-4: 2006 are mainly based on: 1) the theoretical formulation by Trahair et al. (1983) proposing the dynamic overpressure exerted by the stored material under seismic excitation onto the wall and 2) the numerical study findings of Rotter and Hull (1989).

FEMA P-750 (NEHRP, 2009) provisions classify silos as “non-building structures not similar to buildings”. They provide guidelines on the evaluation of: 1) the global horizontal seismic action on the silo, and 2) the distribution of overpressures acting on the silo wall. Only the impulsive type of global lateral seismic forces is considered due to the fundamental period of vibration of the silo itself, which is considered to be noticeably short, corresponding to the highest acceleration value from the design spectral response (in the plateau area of the spectrum). Global lateral seismic forces should be determined on the basis of an effective mass equal to the total volume weight of the filled material reduced by two multiplication factors: effective mass and density factors, where the product of those two factors should not be less than 0.5, in addition to the self-weight of the silo. Concerning the forces distribution on the silo wall and foundation, the standard suggests using the formula proposed by Trahair et al. (1983) according to the filling aspect ratio, that results in significant reductions in the effective mass for the squat silo case.

ASCE 7-10 (2010) provisions provide guidelines regarding the evaluation of: 1) the global lateral actions applied on a silo and 2) the distribution of these forces on the shell wall and foundation. The horizontal forces applied on silos are to be evaluated using a short period structure acceleration value. The effective mass is introduced as the fraction of the total stored material interacting with the silo shell during the seismic event and should be used for the evaluation of the total inertial shear force as well as the overturning moment at the base level of the silo. It is also reported that the effective mass is affected by: 1) the physical and mechanical properties of stored solids; 2) the silo filling aspect ratio; 3) the intensity of the earthquake ground motion. The shear force portion transferred to the base by the inter-granular behavior (friction) of the stored material should be considered when evaluating the value of the effective mass. However, the standard does not provide any formulae to estimate the effective mass.

Architectural Institute of Japan (AIJ) (2010) provisions mainly refer to the impulsive mass (i.e., the effective mass) that interacts with the silo wall at the structure’s base. Owing to loss of energy triggered by the friction between the silo wall and particles as well as by the internal friction within the granular material itself, the impulsive mass is smaller than the total ensiled mass. Nevertheless, it should be considered not lower than 80% of the whole mass. Design seismic loads evaluation for the ground-supported storage silos can be performed by two methods: 1) the “modified seismic coefficient method” and 2) the classical modal analysis. The former uses the “Equivalent Lateral Force” method, assuming a value of 0.60 s for the first period of the filled silo system (if unknown), to evaluate horizontal design acceleration. The latter models the filled silo system as a cantilever beam with different point masses (lumped masses model) to evaluate the actions exerted on the structure. The standard does not provide a specific value of the damping ratio on which the parameters necessary for the two aforementioned methods are based on (S_aj: design acceleration response spectrum corresponding to the first natural period, D_h: coefficient determined by the radiation damping of the silo basement and depending on the area of the silo foundation).

Table 1 compares the afore-mentioned provisions highlighting the main shortcomings. In detail, for each code, Table 1 shows: 1) the effective mass (m_eff) expressed as a percentage of the total mass; 2) the presence of specific formulae to estimate the horizontal overpressures (Δp) exerted on the silo wall; 3) suggested values for the fundamental period of vibration (T); 4) the proposed seismic analysis methods.

TABLE 1

TABLE 1. Summary of the provisions in current standards.

As concluding remarks on the code provisions, it is generally acknowledged that the building seismic standards are not directly applicable to agricultural/industrial facilities and storage units (Arze, 1992), such as silos. Indeed, the absence of a widely accepted theoretical framework on the dynamic response of filled silo systems highlights significant shortcomings in the existing provisions for seismic design (Brown and Nielsen, 1998; Holler and Meskouris 2006; Carson and Craig 2015). Consequently, significant scientific progress is required for a wider understanding of the topic, as acknowledged by some of the most pre-eminent researchers (Dowrick, 1988; Ayuga et al., 2001; Ayuga et al., 2005; Holler and Meskouris, 2006; Rotter, 2008) and experienced professionals (Carson and Craig, 2015) in the field.

Figure 2 conceptually summarises the differences between the state-of-art of the scientific knowledge for the filled silos systems and the frame structures. The graphical representation takes inspiration from the set theory; the idea is that the size of the oval is somehow proportional to the extent of the knowledge or the accuracy of the code provisions. The knowledge is still limited for silos and consequently the code provisions are far to be accurate and comprehensive, in contrast to the case of frame structures.

FIGURE 2

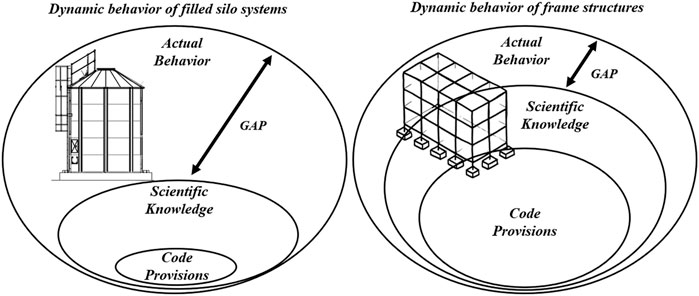
FIGURE 2. Code provisions vs. scientific knowledge vs. actual behavior: filled silo systems vs. frame structures.

Dynamic Experimental Tests on Granular Media, Empty and Filled Silo Systems

This section provides a summary of the essential results from experimental investigations on the dynamic and seismic response of granular material and of cylindrical flat-bottom ground-supported silos.

Experimental Dynamic Tests on the Granular Solid

Granular material state [jammed, glassy or fluid (Raihane et al., 2009)] is highly affected by the seismic input nature and the physical/mechanical properties of the particles. Several experimental studies were developed trying to investigate the transition limits between such states in both qualitative and quantitative ways. These tests were usually conducted by imposing a harmonic motion (characterized by a certain frequency content f with a maximum acceleration amplitude a, commonly indicated in units of gravity acceleration g) at the base of a rectangular box containing granular material (Figure 3).

FIGURE 3

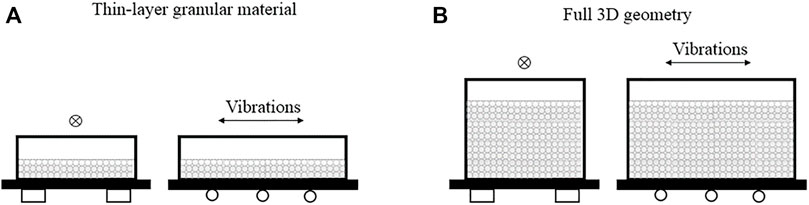
FIGURE 3. General setup for the shaking bed test of granular material: (A) thin-layer; (B) full 3D geometry.

Ristow et al. (1997) tried to understand the dynamic behavior of granular solid, by studying the response of a thin 20-mm layer of Ballottini glass (with a small average diameter 0.5–0.6 mm) using a horizontal shaking apparatus (Figure 3A). Particles do not move at low frequencies; they begin to move as the frequency increases. Then, the granular solid showed a complete transition into a fluidized phase beyond a critical value of the frequency.

Metcalfe et al. (2002) performed an experimental study on the transition limits of the granular material under the effect of horizontal shaking (sand, glass beads). Analysis of the system evolution involved keeping the frequency constant while gradually increasing the acceleration a. A critical value of a (0.40–0.60 g) results in a loose behavior characterized by dilatation response and strong sloshing of the solid at the surface level as particles exceed friction, including a small number of “sliders” (free particles) at the surface level that move for any a value. For frequencies between 2 and 8 Hz, fluid state appears at a critical acceleration value a_cu. a_cu seemingly depends on the material’s physical properties and increases for rougher particles.

Raihane et al. (2009) studied the impact of the vibrations induced by a harmonic sinusoidal input on a 3-dimensional sand granular medium (as in Figure 3B). The container base was subjected to widely variable frequency content range (from 20 up to 300 Hz) sinusoidal vibrations with an acceleration amplitude between 0.10 and 8.00 g. Particles movement during vibrations was monitored using ultra-fast acquisition video recording. At a given acceleration value (around 0.40 g, similar to that found in other studies), the state of granular media changes from uniformly rigid to multi state layered over the depth, with fluidized particles at the top surface.

Dynamic Tests on Cylindrical Flat-Bottom Ground-Supported Silos

Various experimental tests were performed starting from the second half of the last century to study the dynamic behavior of ground-supported cylindrical silos and comprehend the complex interaction of shell wall and particulate material under seismic excitation. Shaking table tests were used in almost all the investigations. Different types of dynamic inputs have been commonly used: 1) white noise “random input” signals (referred to as WN), 2) impulsive loads (IL), 3) stationary “sinusoidal” harmonic signals (HS), and 4) earthquake recorded signals (EQK). Scientific literature also reports on some free vibration tests (FV).

Chandrasekaran and Jain (1968) performed the first vibrating motion tests on cylindrical containers filled with granular material. Two silos of steel and perspex were equipped with vibration transducers and strain gauges. The silos were tested in empty and different filling conditions, where the corresponding aspect ratio in the maximum filling condition h_c/d_c (h_c: filling height, d_c: silo diameter) was close to 10. Silo specimens were filled with different materials, like sand, cement and wheat. The silos were excited by means of the sudden releasing of the silo after forcing an initial displacement, allowing for free vibrations (FV) to be developed. Later, the effective mass was evaluated using a theoretical formula proposed by Chandrasekaran and Saini (1969). The effective mass values, evaluated for 25 different configurations, were found to be significantly lower than the unity (barely exceeding 50%).

Lee (1981) conducted an experimental shaking table campaign on a scaled lucite cylindrical silo (h = 1,500 mm as “silo height”, d_c = 300 mm) specimen filled with sand at different filling heights (h_c). The specimen was equipped with 6 accelerometers over the wall height and several longitudinal and circumferential strain gauges. The test included free vibration tests (FV) and sinusoidal inputs (HS) to investigate: the profile of the horizontal accelerations (related to dynamic amplification) over the wall height, the equivalent damping ratio, the fundamental period of vibration, as well as the stresses experienced by the wall. It was found that the fundamental frequency of vibration decreases as the filling height increases, while the damping ratio varies with input frequency till reaching a maximum value at the resonance frequency.

Yokota et al. (1983) performed a series of shaking table tests on a scaled acrylic resin cylindrical silo (h = d_c = 1,500 mm) filled with coal and instrumented with different accelerometers either on the wall or within the filled material, in addition to strain gauges and earth pressure sensors. Different configurations were considered including empty and fully filled conditions, and with/without lid/roof too. The testing program encompassed free vibration (FV) tests on the empty silo and random white noise vibration (WN) tests on the filled silo systems. The main objective of the campaign was to identify the natural frequencies, the modal shapes, the damping ratios of the silo, and the differences in the measured values of horizontal accelerations between the wall and the ensiled material. In fully filled conditions, the damping ratio was four times larger than the one obtained in the empty silo case, while the dynamic amplification factor at the top level was around 3.0 under HS excitation.

Shimamoto et al. (1984) studied the response of a silo filled with coal system through shaking table tests on four scaled PVC and steel silos (h = 1,600 mm, d_c = 1,500 mm). The specimens were instrumented with accelerometers on the wall (along the input direction) and in the middle of the filled material. The testing program was performed considering stationary sinusoidal waves (HS) and real seismic records (EQK). Under HS excitation, rigid body motion occurs for input with a much lower frequency than the fundamental one of the filled silo system and acceleration amplitude a≤0.20 g. Noticeable differences were observed in the vertical profiles (over the silo height) of the horizontal acceleration of the filled material near the wall and along the central line when the input frequency content was close to the first or the second natural silo frequencies. By introducing the real seismic records (EQK), the maximum response of the acceleration amplitude value measured from all controlled points (either on the wall or inside the filled material) was registered at the same time instant at which the maximum peak table acceleration happened; the highest dynamic amplifications noticed at the silo wall upper part were around 1–4; dynamic amplifications inside the granular material increased from the base to the solid surface, reaching an amplification factor of around 2–5.

Harris and von Nad (1985) performed shaking tests on two very slender steel silos (h = 3,050 mm, d_c = 457 and h = 1,520 mm, d_c = 203 mm) filled with sand and wheat. The silo base was welded to an elastic support frame, and a hydraulic actuator was used to apply horizontal harmonic excitation (HS). Displacement measurements at the base and at the top of the silo were registered. The tests were performed with the purpose of determining the effective mass, as the unknown quantity of the dynamic equilibrium equations with known displacements (coinciding with the recorded ones) assuming flexible bending silo response and considering the rotational and translational flexibility of the support frame. The obtained results from their approach supported the 80% effective mass rule as suggested by some standards in that period.

Sasaki and Yoshimura (1984) conducted shaking table tests on a scaled uniform mortar cylindrical silo filled with brown rice. They used a stave-silo (h = 2030 mm, d_c = 1,020 mm) constructed with blocks of mortar and confined by steel hoops, and they filled it with various materials. Empty and filled conditions of the silo model were tested. Both harmonic (HS) and seismic (EQK) tests were performed. In general, it was noticed that 1) the stored materials produced distinct changes in the vibration characteristics of the silo system, where the resonant frequency gets lowered by filling the silo; 2) the interaction between the silo wall and granular solid during a seismic event can be different due to the variation of the filled material; and 3) the maximum registered horizontal dynamic overpressure distribution was quasi uniform over the entire height, except for an unexpected peak which was observed near the base.

Sasaki and Yoshimura (1988) performed tests on two scaled silos (h = 1985mm, d_c = 820 mm): a stave silo model obtained with mortar blocks and circumferential steel hoops, in addition to another silo model realized as a continuous uniform mortar model, in order to study the structural discontinuity effect on the actual earthquake response of the silo model. The silo specimens were filled with rice and equipped with different instrumentation: strain gauges, accelerometers, lateral pressure sensors. The tests were performed by using both sinusoidal inputs (HS) and real recorded earthquakes (EQK) (Tokachu-oki 1968 and Nemurohanto-oki 1973) in empty and full conditions. Under harmonic excitation, the presence of the ensiled material reduced the fundamental resonance frequency of the stave silo model where the effect of the joints of staves produced the degradation of stiffness. Moreover, a gradual decrease of acceleration response (amplification) factor was noticed with the increase of the peak table acceleration.

Naito (1988) reported on shaking table tests (Kawazoe et al., 1983 in Japanese) performed on a scaled steel coal silo (h = d_c = 1,500 mm). The silo was equipped with accelerometers positioned over the height along the center vertical line inside the stored material, while the silo wall was instrumented by strain gauges. The base plate and silo wall rested on two different load cells to measure the global shear force at the wall base level and at the table level. Sinusoidal inputs (HS) were used to provoke and investigate resonance response of the granular material. It was found that the resonance frequency and response magnification at resonance frequency decrease with increasing excitation. Moreover, the response decreases at frequencies above the first resonance and with increasing frequency, which becomes less steep with the increment of frequency.

Holler and Meskouris (2006) reported some results of shaking table tests (performed at Saclay in France) on a scaled steel silo (h = 1,100 mm, d_c = 1,000 mm) filled with sand. The silo wall was equipped with three pressure sensors and one accelerometer placed on the table. The experimental results were used to calibrate a representative Finite Element (FE) model in order to verify load assumptions stipulated in current European standards.

Tatko and Kobielak (2008) excited a scaled flat-bottom slender silo (h = 1,200 mm, d_c = 400 mm) filled with sand with horizontal impulsive loads (IL). The silo was supported by a spring system to simulate different soil stiffness, since the main objective was to analyze the dynamic interaction between the silo structure and the soil. The specimen was instrumented by horizontal pressure sensors placed at different heights of the silo wall. Dynamic inputs were generated using a ballistic pendulum in the form of a single pulse applied horizontally to the bottom plate. Fundamental frequencies, horizontal time-pressure variation and radial overpressure vertical profiles were measured. The dynamic overpressures over the silo height are influenced by subsoil stiffness. Moreover, the distribution of the maximum dynamic pressures over wall height is nonlinear, while the overpressure value changes depending on the direction. Nonetheless, the relationship between the average lateral dynamic pressure exerted by the ensiled solid and the maximum acceleration amplitude of subsoil is nonlinear.

Silvestri et al. (2016) conducted shaking table tests on two scaled polycarbonate silos (h = 1,500 mm, d_c = 1200 mm) filled with Ballottini glass beads and equipped with an upper stiffening ring. Three different configurations were tested to account for two wall friction conditions and two aspect ratios (0.5 and 1.0). The silos were instrumented with accelerometers (on the wall along the input direction at various heights, and over three vertical lines inside the granular solid), strain gauges over the wall height and around the circumference to evaluate the internal actions in the wall and a Linear Variable Displacement Transducer to measure the lateral displacements of the upper stiffening ring. The silos were subjected to: 1) white noise (WN) excitation; 2) harmonic excitation (HS), and 3) recorded earthquakes (EQK). Natural frequencies were evaluated from WN tests. The main purpose of the tests was to experimentally verify the analytical model proposed by Silvestri et al. (2012) for the estimation of the peak global forces at the silo base (shear force and overturning moment). The findings showed that the particle-wall friction influences the wall base overturning moment and the effective mass for the squat silo is considerably lower than 80%.

Recently, Silvestri et al. (2021) performed a large experimental campaign of shaking table tests on a full-scale flat-bottom steel manufactured silo (h = 5,500 mm, d_c = 3,640 mm) characterized by a horizontally corrugated wall profile, open C hat-shaped vertical stiffeners and a paneled conically shaped roof. The filling material was soft wheat achieving an aspect ratio of around 0.9, corresponding to a squat silo case according to EN 1991-4:2006 classification. The filled silo system was tested under two base conditions: fixed and seismically isolated (Figure 4). The testing program included white noise signals (WN), low-frequency (0.5 and 1 Hz) sinusoidal signals (HS), and three earthquake records (EQK): an artificial earthquake record, a real “far-from-resonance frequency content” input, and a second real “close-to-resonance frequency content” input. The main findings are summarized hereafter: “The damping ratio increases with increasing acceleration (enhanced frictional dissipative mechanisms associated to relative sliding of granular particles) … [omissis] … The resonance frequency … [omissis] … slightly decreases with increasing acceleration (increasing of damping ratio and larger effective mass) and it slightly increases with increasing compaction (higher stiffness provided by the granular material). No significant dynamic amplification was observed for the whole filled silo system (both the silo wall and the ensiled granular material) for low-frequency sinusoidal inputs. For the most demanding earthquake input (in terms of close-to resonance frequency content), the dynamic amplification factor increased along the silo wall height up to values around 1.4 at the top surface of the solid content [omissis] … The measured dynamic overpressures seemed to increase slightly more than linearly with depth from the top to the bottom.”

FIGURE 4

FIGURE 4. The tested flat-bottom steel silo of the SERA-SILOS project (Silvestri et al., 2021): (A) fully restrained and (B) seismically isolated.

General Observations

The previous section introduced the main available experimental studies (see Table 2 for a detailed comparison of their main findings) on the dynamic behavior of filled silo systems in the literature. It can be noticed that the majority of the experimental campaign was conducted during the 1980s. After then, the rate of interest became less mainly due to the technical difficulties and the expensive costs, even if the academic focus on this field could not give definite answers leaving various open issues. Nevertheless, the main remarks from the above summarized experimental works are:

1- The nature of the dynamic base excitation, the frequency content and the peak acceleration values have a strong impact on the dynamic response of the filled silo system. This is caused by the non-steady state of the stored granular material depending on the input properties (e.g., a granular material characterized by high intergranular friction properties and high particle-wall friction coefficient typically leads to a relatively high damping ratio and a high activated portion of the stored material as an effective mass) that leads to a non-linear response of the filled silo system.

2- The effective mass was evaluated using different methods, which might affect the reliability of the results (analysis of the variation of the frequency between empty and filled silos, or interpretation of the dynamic overpressure measurements, or global assessment evaluation of the overturning bending moment at the silo base). Moreover, it resulted to be influenced by the input properties. For instance, a high effective mass was always obtained as a result of the application of an input with a frequency content close the resonance of the filled silo system.

3- The acceleration measurements recorded by the accelerometers placed along the centerline of the stored material showed higher amplification factors than those recorded from the monitored points over the silo wall height.

4- In most cases, the small size of the adopted scaled silo models was not suitable to account for the role of the vertical stiffeners. In addition, the effect of the silo roof on the silo system response was included only in few works.

TABLE 2

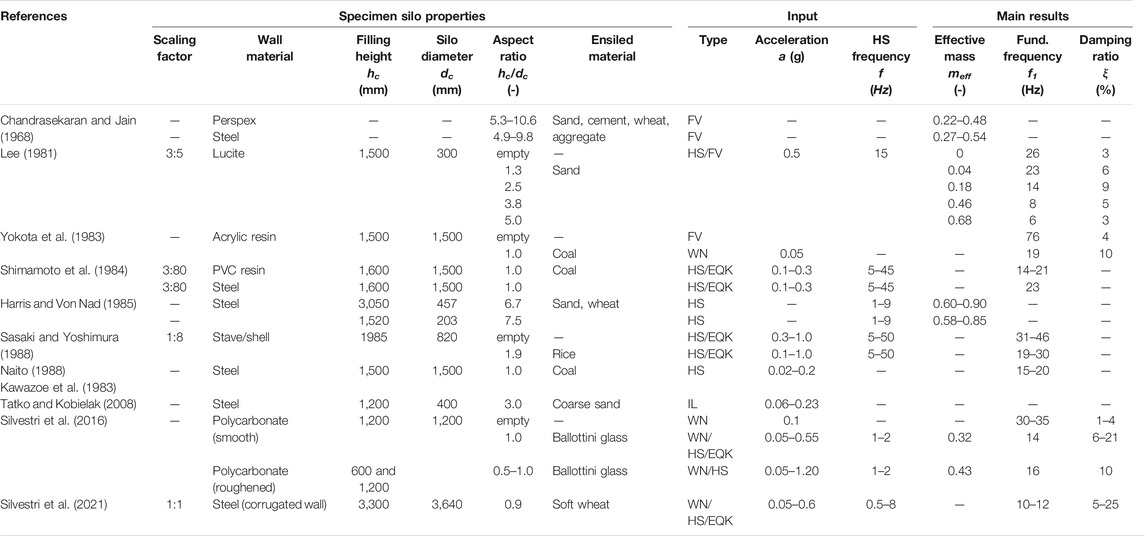
TABLE 2. Summary of the main experimental results of dynamic tests on filled silo systems found in the scientific literature.

Theoretical Studies and Numerical Modelling on the Dynamic Behavior of Filled Silo Systems

This section provides a summary of the theoretical studies and numerical modelling techniques presented in the scientific literature for the estimation of the dynamic behavior of ground supported cylindrical silos.

Analytical Models

Yang (1976) and Haroun (1980) studied the dynamic behavior of a liquid-filled cylindrical shell. Although focusing on liquid storage containers, the works provided a novel analytical method for evaluating the fundamental period of cylindrical storage tanks. The tank wall was modelled as a uniform linear-elastic cantilever beam, considering both shear and flexural deformations when determining the vibration properties of the liquid-filled shell system. The entire liquid mass was considered rigidly attached to the tank wall to determine the fundamental period of vibration.

Lee (1981) proposed an analytical model to estimate the effective mass of ground-supported cylindrical silos subjected to harmonic base excitation. More specifically, the effective mass is obtained from the variation of the fundamental frequency of vibration in empty and full conditions. The analytical framework includes the following hypotheses: 1) the stored material does not provide any additional stiffness to the equivalent system; 2) the participating mass of the equivalent system in the motion consists of the wall mass plus the activated portion of stored material under seismic excitation; 3) the filled silo system behaves like a uniform flexible cantilever beam in terms of the distribution of mass, inertia and material. The analytical framework is based on the works by Chandrasekaran and Saini (1969) and Chandrasekaran and Jain (1968).

Trahair et al. (1983) proposed the first analytical simple formulae to estimate the distribution of the dynamic overpressures (additional with respect to the static pressures) depending on the filling height of the content; two categories of ground-supported structures were identified (squat and slender) depending on the aspect ratio. The analytical model was first proposed for the rectangular silo and then extended to the case of the circular one. A uniform static horizontal body force corresponding to a time-constant acceleration was considered. For the slender silo, the model assumes a total mass participation, reflected in a uniform overpressure profile along the height of the silo wall. For the squat silo, the activated mass is lower than the total one depending on the filling height. The formulation does not account for the shear stresses developed along the particle-wall interface (Rotter and Hull 1989).

Younan and Veletsos (1998) and Veletsos and Younan (1998) investigated the response of cylindrical containers characterized by both rigid and flexible vertical walls, and filled with homogeneous, linear, viscoelastic media under dynamic excitation, with the following fundamental assumptions: 1) the container with the filled material is modelled by a cantilever shear-beam (identified with a natural frequency); 2) the entire mass of the viscoelastic material dynamically interacts with the cylinder shell; 3) the sliding of the contained material with respect to the base is not allowed. The dynamic response of the filled container system was described in terms of vertical and radial modes. The fundamental circular frequency of the system depends on the stored material physical and mechanical properties, wall roughness, frictional interfaces conditions and slenderness ratio of the silo. The natural frequencies of the equivalent model are not affected by the wall mechanical properties. “For liquid-containing flexible tanks, the effective mass is effectively equal to or only somewhat smaller than that for the corresponding rigid tanks, whereas the amplification factor AF may be substantially larger than the unit value appropriate for rigid tanks. By contrast, for solid-containing flexible tanks, not only is the effective mass significantly smaller than for the corresponding rigid tanks, but the AF, … [omissis] …, is of the same order of magnitude as, or substantially higher than, for the corresponding rigid tanks”. Due to these opposite effects regarding effective mass and amplification factor, “the critical responses of the solid-containing systems may be higher than, equal to, or lower than those induced in tanks of the same dimensions by liquids of the same density”.

Silvestri et al. (2012) extended the Janssen (1895) and Koenen (1896) static model to derive analytical formulae for the additional dynamic overpressures provoked by the stored material on the wall of flat-bottom silos. The first analytical theory, later refined by Pieraccini et al. (2015), was developed for “an idealized system of a cylindrical silo filled with an incompressible compacted material under idealized dynamic conditions such as a time-constant acceleration input”. The proposed theoretical model considers the particle-wall friction coefficient, as well as the potential sliding of the contained material with respect to the base. The model subdivides the filled material into a central portion transfering its inertial forces directly to the ground by means of base friction, and an effective mass interacting with the silo wall. For shallow filled silo systems (commonly classified as “squat”), the model predicts a noticeably smaller activated portion of the material than the entire mass.

Durmuş and Livaoglu (2015) presented analytical formulae to estimate the fundamental period of vibration of a filled silo system. The formulae are derived assuming an equivalent Single-Degree-Of-Freedom (SDOF) model as an inverted pendulum fixed at the bottom with a top lumped mass, corresponding to a cantilever beam with flexural response. The stored material is treated as an elastic homogeneous medium. The overall mass of the model accounts for the self-weight of the silo and 2/3 of the entire solid weight (reduced according to the ACI 371R-98). The equivalent lateral stiffness of the model is provided by the silo wall section (flexural stiffness) and the interacting portion of the confined granular particles.

Numerical Simulations

Yokota et al. (1983) built a linear Finite Element (FE) representative model of the silo specimen in empty and filled-with-coal conditions, to interpret the experimental results of the tests described in Dynamic Tests on Cylindrical Flat-Bottom Ground-Supported Silos. The empty container was modeled as a shell structure with cylindrical shape using 26 linear elements, while the filled one consisted of 253 triangular-shaped axisymmetric elements. The stored material was modeled as a multi-layered element with different elastic moduli (Young’s modulus decreases going from the bottom to the top surface) to consider the effects of the corresponding confining pressure and strain level at each elevation as resulted from dynamic triaxial tests. On one hand, the first natural frequency obtained from the analytical results of the empty silo case moderately exceeded the experimental value, whilst the analytical and experimental frequency values resulted closer for the higher modes. On the other hand, the filled model gave close frequency values for the first two modes of vibration, whilst the gap was larger for the higher modes.

Shimamoto et al. (1984) developed a FE model of the tested silos using shell elements with a conical shape. The stored coal was modelled using non-linear asymmetric solid elements. Cyclic triaxial tests were performed on coal samples for the experimental assessment of the mechanical properties (shear modulus) of the coal material. The dependency of the coal’s dynamic properties on the experimental strain was considered through the application of the equivalent linear analysis method, which was originally developed by Schanable et al. (1972). Numerically simulated and experimental results were compared for two peak acceleration values (a = 0.03 and 0.10 g). The developed model was able to well capture the resonance frequency in both cases, and also to reproduce the dynamic amplification effects for the lower acceleration value, but not for the higher acceleration value, due to particles sliding phenomena that occurred after exceeding an acceleration limit.

Naito (1988) studied numerically the non-linear behavior of filled silo systems under dynamic conditions. Solid axisymmetric elements were used to build the FE model for both the cylindrical wall and the silo content. The mechanical properties of the stored material (coal) were selected on the basis of elastic wave velocity diagnosing method for different confining pressure conditions. The proposed numerical model was verified by comparing the obtained results with shaking table results.

Rotter and Hull (1989) simulated the seismic response of a cylindrical silo filled with granular material in shallow filling condition corresponding to a “squat” aspect ratio. The FE model considered an axisymmetric body assuming the elastic response of both the cylindrical silo wall and the particulate material under dynamic excitations. The dynamic input consisted of a uniform lateral acceleration without accounting for any amplification over the height. The simulation assumed no vertical slipping phenomena between the silo wall and adjacent particles and replicated their synchronized movement. The roof was ignored because it provided negligible effects in containing the wall upper part displacements. The base of the silo wall was fixed, and the particle-wall interface was ideally rough. The membrane stresses in the wall were examined by performing a parametric study accounting for the variation in different geometrical aspects and material properties. The findings indicated that stresses increase with increasing filling condition from “squat” to “slender” (with a stable value in case of slender silos) and with increasing radius-to-wall thickness ratio.

Sasaki and Yoshimura (1992) reproduced numerically the dynamic testing conditions of a 1:8 scaled model (h_c/d_c ≈ 2.0) of a stave-silo reported in previous research works (Sasaki and Yoshimura, 1984; Sasaki et al., 1986; Sasaki and Yoshimura, 1988), i.e., a rice-filled silo characterized by structural discontinuities. The silo wall was modelled using a so-called “stave silo element”, using the shell element theory to account for the stiffness provided from the shell. The participation of the granular material in the seismic interaction was assured by using a “fictitious mass density” giving an effective mass of 0.70 to fit the resonance curves from the experimental tests.

Holler and Meskouris (2006) developed a numerical model to study the dynamic behavior of filled silo systems based on the assemblage of the filled material, the wall of the silo, the wall-particle friction interface, the silo foundation, as well as the surrounding soil to consider Soil-Structure-Interaction effects. Elastic shell elements were adopted to model the silo wall. The filled material nonlinearity was considered by assigning a hypoplastic behavior to the representative solid elements. The frictional interface of the material particles with the wall was modelled by means of contact elements preserving the essential geometrical compatibility between the structure and content. The model was calibrated on the basis of reported results of shaking table test, so that it was able to capture the dynamic overpressure profile exerted by the stored material. The modelling approach was applied to the cases of steel slender and squat silos and allowed the comparison of the obtained radial and circumferential dynamic overpressures with the theoretical predictions suggested by prEN 1998-4 (CEN 2003b). The numerical findings highlighted that, for the squat case, the inertia force corresponding to a considerable fraction of the total filled material is transmitted directly to the ground by means of the particle-base friction, resulting in the theoretical overestimation of the dynamic overpressure by the European standard for this slenderness category.

Lately and due to the lack of the experimental comparable results for full-scale models, the research trend was drifted towards the numerical investigation of the filled silo system behavior. Different shell and solid elements were implemented to simulate the container and the content behavior in linear and non-linear conditions, and different techniques were applied to model the friction interface between the main granular solid and silo flat wall (Nateghi and Yakhchalian, 2011; Nateghi and Yakhchalian, 2012; Jagtap et al., 2015; Livaoğlu and Durmus, 2015; Guo et al., 2016; Livaoğlu and Durmuş, 2016; Katsanos et al., 2018). The differences of the modelling techniques and assumptions have strong impact on the outcomes of these works.

General Observations

The theoretical studies, either accompanied or not by experimental validation, aim usually at investigating the suitability of the Single Degree Of Freedom model to approximate the dynamic behavior of the filled/empty silo system. Furthermore, a clear effort was devoted to the effect of the filling aspect ratio on the seismic behavior (Trahair et al., 1983; Silvestri et al., 2012; Pieraccini et al., 2015); in this respect, the reduction of the effective mass was identified for squat silos. In addition, various numerical modelling attempts were performed to reproduce the real silos conditions which showed some promising results despite the strong assumptions on the granular solid behavior and the various interfaces conditions. The main shortcomings of these works can be associated with neglecting the effect of the intergranular friction through modelling the granular solid as a solid layer, beside neglecting the effect of the possible sliding of the particles over the base when exceeding a certain input magnitude limit (acceleration) corresponding to the friction coefficient of the stored particles with base material. Moreover, the adopted numerical models considered always simple silos with a flat wall section in order to reduce the computation cost, which leaves many uncertainties by not accounting for the effect of the vertical stiffeners and the connection details (e.g., base plate connections, roof details, sheet overlapping areas and the bolted connection between the sheets and the stiffeners) on the system response or even the variant corrugated wall sections as well.

Table 3 shows a summary of the essential characteristics of the previously introduced numerical research works.

TABLE 3

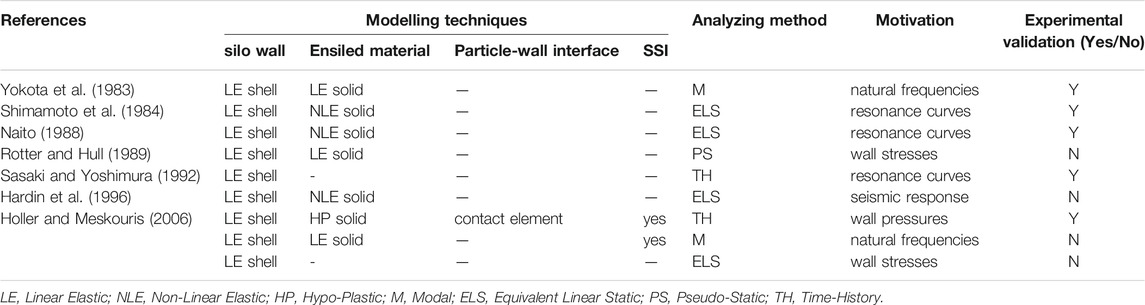
TABLE 3. Summary of the main characteristics in the cited numerical studies found in scientific literature.

Future Research Challenges

The dynamic response of filled silo systems is different from the one of any other type of structures due to the complicated nature of the components and the potential interaction conditions varying in accordance with filling aspect ratios, and physical and mechanical properties of the stored material. Therefore, a careful planning for future research is indeed necessary, especially for the experimental studies which are fundamental to verify analytical and numerical models. Many unexpected problems may arise either related to the testing conditions or to the functionality of the instrumentations (the technical difficulties may increase with the use of corrugated walls, vertical stiffeners and paneled roof). Advancements in the analytical models are still necessary to fill the gap concerning reliable formulae for the estimation of the fundamental frequency and the effective mass. Finally, numerical results are very sensitive to the modelling techniques and input parameters, where it is very hard to develop a representative model capable of giving trustworthy results. Thus, potential developments in the future should consider different aspects as detailed below, either experimentally or theoretically.

In the experimental field:

1- The frictional properties of the ensiled granular material may change from static conditions (silo at rest) to dynamic conditions (seismic excitation, filling and discharging). Different friction coefficients may lead to considerably different overpressures.

2- The effects of the wall corrugation on the particle-wall effective friction coefficient and on the global dynamic and seismic response of the filled silo system have to be still fully understood. Furthermore, the loads transferred by means of the vertical stiffeners to the ground should be assessed. That would allow to expand the current knowledge on the effects of the flat and corrugated wall sections, in terms of captured vertical forces, from the static to the seismic conditions.

3- The actual after-filling conditions on the dynamic response should be better considered, mainly in terms of the obtained eccentricity of the top pile, since the current standards account for it in static conditions only after exceeding a certain limit.

4- The difference in terms of dynamic amplification captured in the granular material between the centerline of the whole granular volume and the near-wall position should be understood. It is thus suggested monitoring those locations carefully by using 3-axial accelerometers and pressure cells, in order to understand the relationships between the measured accelerations and the provoked dynamic overpressures.

5- A critical point is also represented by the full understanding of the dependence of the overpressure distribution and effective mass on the different filling heights and thus on different aspect ratios.

6- The effect of the base roughness should be considered, to understand the possible movement of the granular mass as solid mass under high magnitude seismic input conditions.

7- The effect of the vertical component of the seismic input should be also accounted for in future studies.

In the theoretical field:

1- An overall theoretical framework is still missing which accounts for the effects of frictional properties of the granular material, the aspect ratios, the input acceleration level, etc.

2- The local distribution of the dynamic overpressure components along the section circumference and over the silo height should be further assessed, allowing for more robust design formula since the majority of the analytical studies assume uniform distribution of overpressures and the majority of the standards do not approach this problem.

3- A reliable formula for the prediction of the fundamental frequency of the filled silo system is needed, in which the effective mass would play a fundamental role as well as the effect of the additional stiffness provided by the granular material. Although this issue was already faced in some previous works, major differences were noticed in terms of the considered behavior of the equivalent SDOF model assumed for the filled silo system.

In conclusion, research advances in the field are urgently needed. Otherwise, in the lack of a full understanding, the solution would be represented by a design-oriented approach which must consider larger safety factors, as suggested by Carson (2001).

Conclusion

This paper reviews the main steps of the historical developments of research work in the field of the dynamic and seismic behavior of flat-bottom filled silo systems. A comprehensive summary of the essential experimental, theoretical and numerical studies since the 1960s has been reported, highlighting the main findings along with the open issues still to be investigated.

The challenging side of such a topic is deeply related to the nonlinear behavior of the granular material due to the non-stable friction conditions varying with the input type and pressure level, as well as the complicated interaction with the silo structure considering different possible interfaces (flat or corrugated wall section).

Despite the considerable number of the performed experimental works in the last decades, it is not surprising that the main outputs helped only underlining the main aspects of the system behavior, treating some topics like the dynamic overpressure qualitatively and leaving the quantitative assessment as an unresolved matter. However, the experimental findings related to the fundamental frequency and the corresponding equivalent damping ratio are of a great importance. Furthermore, many theoretical studies were developed in parallel with the experimental ones looking for a more mature understanding of the problem.

Finally, it must be highlighted that the performed research studies are not capable of providing definite answers yet. That is reflected through the absence of a universally accepted theoretical framework to predict the seismic response of the filled silo system, hence the lack of design formulae in almost all the standards. Thus, additional research is necessary to address the unresolved issues by proposing efficient analytical models, mainly related to the estimation of the fundamental frequency and the effective mass of the filled silo system.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication. Collection of Data: LP and SM. Writing–Original Draft: LP, MP, and SM. Visualization: LP, MP, and SM. Writing–Reviewing and Editing: SM, SS, and GG. Resources: DF and SS. Supervision: TT and SS.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

American Concrete Institute (ACI) (1997). Standard Practice for Design and Construction of concrete Silos and Stacking Tubes for Storing Granular Materials and Commentary. Farmington Hills, MI: American Concrete Institute. ACI 313-97/313-R97.

Google Scholar

ANSI/ASAE S433.1 (2019). Loads Exerted by Free-Flowing Grain on Bins. Available at: https://www.scribd.com/document/365669904/ANSI-ASAE-EP433-Loads-Exerted-by-Free-Flowing-Grain-on-Bins.

Google Scholar

Architectural Institute of Japan (AIJ) (2010). Design Recommendation for Storage Tanks and Their Supports with Emphasis on Seismic Design. Tokyo, Japan: AIJ.

Google Scholar

Arze, E. (1992). “Seismic Deisgn Practices of Industries,” in Earthquake Engineering, Proceedings of the Tenth World Conference. Editor A. Bernal (Rotterdam: Balkema), 5019–5023.

Google Scholar

Arze, E. (1993). Seismic Design of Industrial Facilities. Tectonophysics 218, 23–41. doi:10.1016/0040-1951(93)90257-K

CrossRef Full Text | Google Scholar

ASCE-7 (2005). Chapter 15. Seismic Design Requirements for Nonbuilding Structures. Reston, VA: ASCE Library. doi:10.1061/9780784408094

CrossRef Full Text | Google Scholar

Augenti, N., Nanni, A., and Parisi, F. (2013). Construction Failures and Innovative Retrofitting. Buildings 3 (1), 100–121. doi:10.3390/buildings3010100

CrossRef Full Text | Google Scholar

Ayuga, F., Aguado, P., Gallego, E., and Ramírez, Á. (2005). New Steps towards the Knowledge of Silos Behaviour. Int. Agrophysics 19 (1), 7–17.

Google Scholar

Ayuga, F., Guaita, M., and Aguado, P. (2001). SE-structures and Environment. J. Agric. Eng. Res. 78 (3), 299–308. doi:10.1006/jaer.2000.0640

CrossRef Full Text | Google Scholar

Brown, C. J., and Nielsen, J. (1998). Silos: Fundamentals of Theory, Behavior and Design. Florida, United States: CRC Press.

Google Scholar

Carson, J., and Craig, D. (2015). Silo Design Codes: Their Limits and Inconsistencies. Proced. Eng. 102, 647–656. doi:10.1016/j.proeng.2015.01.157

CrossRef Full Text | Google Scholar

Carson, J. W. (2001). Silo Failures: Case Histories and Lessons Learned. Handb. Powder Technol. 10, 153–166. doi:10.1016/S0167-3785(01)80017-8

CrossRef Full Text | Google Scholar

Chandrasekaran, A. R., and Jain, P. C. (1968). Effective Live Load of Storage Materials under Dynamic Conditions. Indian Concrete J. 42 (9), 364–365.

Google Scholar

Chandrasekaran, A. R., and Saini, S. S. (1969). Live Load Effect on Dynamic Response of Structures. J. Struct. Div. 95 (4), 649–660. doi:10.1061/JSDEAG.0002243

CrossRef Full Text | Google Scholar

Dogangun, A., Karaca, Z., Durmus, A., and Sezen, H. (2009). Cause of Damage and Failures in Silo Structures. J. Perform. Constr. Facil. 23 (2), 65–71. doi:10.1061/(asce)0887-3828(2009)23:2(65)

CrossRef Full Text | Google Scholar

Dowrick, D. J. (1988). Edgecumbe Earthquake. Bnzsee 21 (3), 198–203. doi:10.5459/bnzsee.21.3.198-203

CrossRef Full Text | Google Scholar

Durmuş, A., and Livaoglu, R. (2015). A Simplified 3 D.O.F. Model of A FEM Model for Seismic Analysis of a Silo Containing Elastic Material Accounting for Soil-Structure Interaction. Soil Dyn. Earthquake Eng. 77, 1–14. doi:10.1016/j.soildyn.2015.04.015

CrossRef Full Text | Google Scholar

European Committee for Standardization (2006a). EN 1991-4 Eurocode 1. Actions on Structures, Part 4 -Silos, Tanks and Pipelines. Brussels: CEN.

Google Scholar

European Committee for Standardization (2007). EN 1993-4 Eurocode 3. Design of Steel Structures - Part 4-1: Silos. Brussels: CEN.

Google Scholar

European Committee for Standardization (2006b). EN 1998-4 Eurocode 8. Design of Structures for Earthquake Resistance, Part 4 -Silos, Tanks and Pipelines. Brussels: CEN.

Google Scholar

Fierro, E., Miranda, E., and Perry, C. “Behavior of Nonstructural Components in Recent Earthquakes,” in Proceedings of the Architectural Engineering Conference (AEI), Oakland, California, United States, March-April 2011, 235–243. doi:10.1061/41168(399)44

CrossRef Full Text | Google Scholar

Gioncu, V., and Mazzolani, F. M. (2014). Seismic Design of Steel Structures. Florida, United States: CRC Press. ISBN 9781138075375.

Google Scholar

Griffin, M. J., Bragagnolo, L. J., and Yanev, P. I. (1995). The December 7,1988 Armenia Earthquake Effects on Selected Power, Industrial and Commercial Facilities. Available at: https://inis.iaea.org/collection/NCLCollectionStore/_Public/30/052/30052386.pdf.

Google Scholar

Grimaz, S. (2014). Can Earthquakes Trigger Serious Industrial Accidents in Italy? Some Considerations Following the Experiences of 2009 L’Aquila (Italy) and 2012 Emilia (Italy) Earthquakes. Boll. di Geofis. Teor. Ed. Appl. 55 (1), 227–237. doi:10.4430/bgta0116

CrossRef Full Text | Google Scholar

Grossi, P., Williams, C., Cabrera, C., Tabucchi, T., Sarabandi, P., Rodríguez, A., et al. (2010). The 2010 Maule, Chile Earthquake: Lessons and Future Challenges. Newark, California, United States: Risk Managed. Solutions. Inc., 1–46.

Google Scholar

Guo, K., Zhou, C., Meng, L., and Zhang, X. (2016). Seismic Vulnerability Assessment of Reinforced concrete Silo Considering Granular Material-Structure Interaction. Struct. Des. Tall Spec. Build 25 (18), 1011–1030. doi:10.1002/tal.1295

CrossRef Full Text | Google Scholar

Hardin, B. O., Bucklin, R. A., and Ross, I. J. (1996). Shear-Beam Analysis for Seismic Response of Metal Wheat Bins. Transact. ASAE 39 (2), 677–687. doi:10.13031/2013.27552

CrossRef Full Text | Google Scholar

Haroun, M. (1980). “Dynamic Analysis of Liquid Storage Tanks - EERL,”. Report, 80-04 (Pasadena, CA: California Institute of Technology). doi:10.7907/1JZR-HK48

CrossRef Full Text | Google Scholar

Harris, E. C., and von Nad, J. D. (1985). Experimental Determination of Effective Weight of Stored Material for Use in Seismic Design of Silos. ACI J. Proc. 82 (6), 828–833.

Google Scholar

Holler, S., and Meskouris, K. (2006). Granular Material Silos under Dynamic Excitation: Numerical Simulation and Experimental Validation. J. Struct. Eng. 132 (10), 1573–1579. doi:10.1061/(asce)0733-9445(2006)132:10(1573)

CrossRef Full Text | Google Scholar

Jagtap, P., Chakraborty, T., and Matsagar, V. (2015). Nonlinear Dynamic Behavior of Granular Materials in Base Excited Silos. Mech. Adv. Mater. Structures 22 (4), 313–323. doi:10.1080/15376494.2014.947821

CrossRef Full Text | Google Scholar

Janssen, H. A. (1895). Versucheübergetreidedruck in Silozellen. Z. Ver. Dtsch. Ing. 39 (35), 1045–1049.

Google Scholar

Katsanos, E. I., Tuska, M., and Latini, C. “Ida-based Definition of Damage States for Rc Silo Subjected to Seismic Excitations,” in Proceedings of the 16th European Conference on Earthquake Engineering, Thessaloniki, Greece, June 2018, 1–12.

Google Scholar

Kawazoe, H., et al. (1983). Shaking Table Tests and Simulation of a Coal Silo. Ann. Rep. Kajima Instit. Construct. Technol. 31, 127–134.

Google Scholar

Koenen, M. (1896). Berechnung des Seiten-und Bodendrucks in Silozellen. Centralblatt der Bauverwaltung 16, 446–449.

Google Scholar

Lee, S. J. (1981). “Experimental Study of Cylindrical Silos Subject to Seismic Excitation,”. PhD thesis (Ohio: The Ohio State University).

Google Scholar

Li, H. (1994). “Analysis of Steel Silo Structures on Discrete Supports,”. PhD thesis (Edinburgh: The University of Edinburgh). Available at: http://hdl.handle.net/1842/289.

Google Scholar

Livaoglu, R., and Durmuş, A. (2016). A Simplified Approximation for Seismic Analysis of Silo-Bulk Material System. Bull. Earthquake Eng. 14 (3), 863–887. doi:10.1007/s10518-015-9851-x

CrossRef Full Text | Google Scholar

Livaoğlu, R., and Durmuş, A. (2015). Investigation of wall Flexibility Effects on Seismic Behavior of Cylindrical Silos. Struct. Eng. Mech. 53 (1), 000. doi:10.12989/sem.2015.53.1.159

CrossRef Full Text | Google Scholar

Metcalfe, G., Tennakoon, S. G. K., Kondic, L., Schaeffer, D. G., and Behringer, R. P. (2002). Granular Friction, Coulomb Failure, and the Fluid-Solid Transition for Horizontally Shaken Granular Materials. Phys. Rev. E 65 (3), 1–15. doi:10.1103/PhysRevE.65.031302

CrossRef Full Text | Google Scholar

Naito, Y. “Equivalent Linear Technique in the Finite Element Method Applied to Deformation with Volume Change and to an Axisymmetric Body under an Unaxisymmetric Load,” in Proceedings of the 9th World Conference on Earthquake Engineering, Tokyo-Kyoto, Japan, August 1988, 133–138.3

Google Scholar

Nateghi, F., and Yakhchalian, M. (2011). Seismic Behavior of Reinforced concrete Silos Considering Granular Material-Structure Interaction. Proced. Eng. 14, 3050–3058. doi:10.1016/j.proeng.2011.07.384

CrossRef Full Text | Google Scholar

Nateghi, F., and Yakhchalian, M. (2012). Seismic Behavior of Silos with Different Height to Diameter Ratios Considering Granular Material-Structure Interaction. Ije 25, 25–35. doi:10.5829/idosi.ije.2012.25.01b.04

CrossRef Full Text | Google Scholar

NEHRP (2009). Recommended Seismic Provisions for New Buildings and Other Structures. Washington D.C: FEMA P750.

Google Scholar

Nielsen, J. (1998). Pressures from Flowing Granular Solids in Silos. Philos. Trans. R. Soc. Lond. Ser. A: Math. Phys. Eng. Sci. 356, 2667–2684. doi:10.1098/rsta.1998.0292

CrossRef Full Text | Google Scholar

Ovarlez, G., Fond, C., and Clément, E. (2003). Overshoot Effect in the Janssen Granular Column: A Crucial Test for Granular Mechanics. Phys. Rev. E 67 (6), 060302/1–060302/4. doi:10.1103/PhysRevE.67.060302

CrossRef Full Text | Google Scholar

Pieraccini, L., Silvestri, S., and Trombetti, T. (2015). Refinements to the Silvestri's Theory for the Evaluation of the Seismic Actions in Flat-Bottom Silos Containing Grain-like Material. Bull. Earthquake Eng. 13 (11), 3493–3525. doi:10.1007/s10518-015-9786-2

CrossRef Full Text | Google Scholar

Qadir, A., Guo, H., Liang, X., Shi, Q., and Sun, G. (2010). Effect of the Ratios of Diameter of Silo to Bead on the Pressure Screening in Granular Columns. Eur. Phys. J. E 31 (3), 311–314. doi:10.1140/epje/i2010-10581-7

CrossRef Full Text | Google Scholar

Qadir, A., Ispalove, N., Ali, A., Chand, R., Shah, M. A., Khan, A., et al. (2016). Experimental and Numerical Determination of Apparent Mass Variation of Granular media Confined in Silo Geometry. Acta Phys. Pol. A. 129 (3), 378–382. doi:10.12693/APhysPolA.129.378

CrossRef Full Text | Google Scholar

Raihane, A., Bonnefoy, O., Gelet, J.-L., Chaix, J.-M., and Thomas, G. (2009). Experimental Study of a 3D Dry Granular Medium Submitted to Horizontal Shaking. Powder Technol. 190 (1), 252–257. doi:10.1016/j.powtec.2008.04.068

CrossRef Full Text | Google Scholar

Ristow, G. H., Straßburger, G., and Rehberg, I. (1997). Phase Diagram and Scaling of Granular Materials under Horizontal Vibrations. Phys. Rev. Lett. 79 (5), 833–836. doi:10.1103/PhysRevLett.79.833

CrossRef Full Text | Google Scholar

Rotter, J. M., and Hull, T. S. (1989). Wall Loads in Squat Steel Silos during Earthquakes. Eng. Structures 11 (3), 139–147. doi:10.1016/0141-0296(89)90002-3

CrossRef Full Text | Google Scholar

Rotter, J. (2008). “Structures, Stability, Silos and Granular Solids,” in Structures, Stability, Silos and Granular Solids: A Personal Adventure Structures and Granular Solids: From Scientific Principles to Engineering Applications. Editors J. F. Chen, and J. G. Teng (Florida, United States: CRC PRESS-TAYLOR and FRANCIS GROUP), 1–17. doi:10.1201/9780203884447.ch1

CrossRef Full Text | Google Scholar

Sasaki, Y., and Yoshimura, J. (1984). “Dynamic Behavior of concrete Stave Silos,” in Proceedings of the 8th World Conference on Earthquake Engineering (Hoboken, New Jersey, United States: Prentice-Hall).

Google Scholar

Sasaki, Y., and Yoshimura, J. (1992). “Dynamic Discrete Modeling and Computer Simulation of Seismic Response of concrete Stave Silos with Structural Discontinuity,” in Earthquake Engineering, Proceedings of the Tenth World Conference (Rotterdam: Balkema), 5065–6070.

Google Scholar

Sasaki, Y., and Yoshimura, J. “Seismic Response of Concrete Stave Silos with Structural Discontinuity,” in Proceedings of the Ninth World Conference on Earthquake Engineering, Tokyo-Kyoto, Japan, August 1988.

Google Scholar

Sasaki, Y., Yoshimura, J., and Dohkoshi, J. (1986). Experimental Studies of the Earthquake Response Characteristics of Concrete Stave Silos. Nogyo Shisetsu 17 (2), 24–33. doi:10.11449/sasj1971.17.2_24

CrossRef Full Text | Google Scholar

Schanable, P. B., Lysmer, J., and Seed, H. B. (1972). “SHAKE: A Computer Program for Earthquake Response Analysis of Horizontally Layered Sites,”. Report No. EERC, 72-12 (Berkeley: Earthquake Engineering Research Center, University of California).

Google Scholar

Shimamoto, A., Kodama, M., and Yamamura, M. (1984). “Vibration Tests for Scale Model of Cylindrical Coal Storing Silo,” in Proceedings of the 8th World Conference on Earthquake Engineering (Hoboken, New Jersey, United States: Prentice-Hall), 5, 287–294.

Google Scholar

Silvestri, S., Gasparini, G., Trombetti, T., and Foti, D. (2012). On the Evaluation of the Horizontal Forces Produced by Grain-like Material inside Silos during Earthquakes. Bull. Earthquake Eng. 10 (5), 1535–1560. doi:10.1007/s10518-012-9370-y

CrossRef Full Text | Google Scholar

Silvestri, S., Ivorra, S., Chiacchio, L. D., Trombetti, T., Foti, D., Gasparini, G., et al. (2016). Shaking-table Tests of Flat-Bottom Circular Silos Containing Grain-like Material. Earthquake Engng Struct. Dyn. 45 (1), 69–89. doi:10.1002/eqe.2617

CrossRef Full Text | Google Scholar

Silvestri, S., Mansour, S., Marra, M., Distl, J., Furinghetti, M., Lanese, I., et al. (20212022). Shaking Table Tests of a Full‐scale Flat‐bottom Manufactured Steel Silo Filled with Wheat: Main Results on the Fixed‐base Configuration. Earthquake Engng Struct. Dyn. 51, 169–190. doi:10.1002/eqe.3561

CrossRef Full Text | Google Scholar

Tatko, R., and Kobielak, S. (2008). Horizontal Bulk Material Pressure in Silo Subjected to Impulsive Load. Shock and Vibration 15 (5), 543–550. doi:10.1155/2008/289317

CrossRef Full Text | Google Scholar

Trahair, N. S., Abel, A., Ansourian, P., Irvine, H. M., and Rotter, J. M. (1983). Structural Design of Steel Bins for Bulk Solids. Sydney, Australia: Australian Institute of Steel Construction, 30. ISBN 0909945357.

Google Scholar

UBC “Uniform Building Code. Structural Engineering Design Provisions,” in Proceedings of the International Conference of Building Officials, Whittier, May 1994, 492.

Google Scholar

Uckan, E., Akbas, B., Shen, J., Wen, R., Turandar, K., and Erdik, M. (2015). Seismic Performance of Elevated Steel Silos during Van Earthquake, October 23, 2011. Nat. Hazards 75 (1), 265–287. doi:10.1007/s11069-014-1319-9

CrossRef Full Text | Google Scholar

Vanel, L., and Clément, E. (1999). Pressure Screening and Fluctuations at the Bottom of a Granular Column. Eur. Phys. J. B 11 (3), 525–533. doi:10.1007/s100510050965

CrossRef Full Text | Google Scholar

Veletsos, A. S., and Younan, A. H. (1998). Dynamics of Solid-Containing Tanks. II: Flexible Tanks. J. Struct. Eng. 124 (1), 62–70. doi:10.1061/(asce)0733-9445(1998)124:1(62)

CrossRef Full Text | Google Scholar

Villalobos, F., and Mendoza, M. “Damages Observed in the 2010 Concepción Earthquake Related to Soil Phenomena,” in Proceedings of the 5th International Conference on Earthquake Geotechnical Engineering, Santiago, Chile, January 2011.

Google Scholar

Yang, J. Y. (1976). “Dynamic Behavior of Fluid-Tank Systems,” Ph.D.Thesis. Houston, TX: Rice University.

Google Scholar

Yokota, H., Sugita, M., and Mita, I. (1983). “Vibration Tests and Analyses of Coal-Silo Model,” in Proc., 2nd Int. Conf. On the Design of Silos for Strength and Flow (Stratford-upon-Avon: Powder Advisory Centre), 107–116.

Google Scholar

Younan, A. H., and Veletsos, A. S. (1998). Dynamics of Solid-Containing Tanks. I: Rigid Tanks. J. Struct. Eng. 124 (1), 52–61. doi:10.1061/(asce)0733-9445(1998)124:1(52)

CrossRef Full Text | Google Scholar