- Department of Civil and Environmental Engineering, University of Michigan, Ann Arbor, MI, United States
Over the past decade, significant research efforts have been dedicated to the development of performance-based wind engineering (PBWE). Notwithstanding these efforts, frameworks that integrate the damage assessment of the structural and envelope system are still lacking. In response to this need, the authors have recently proposed a PBWE framework that holistically treats envelope and structural damages through progressive multi-demand fragility models that capture the inherent coupling in the demands and damages. Similar to other PBWE methodologies, this framework is based on describing the hurricane hazard through a nominal straight and stationary wind event with constant rainfall and one-hour duration. This study aims to develop a PBWE framework based on a full description of the hurricane hazard in which the entire evolution of the storm track and time-dependent wind/rain fields is simulated. Hurricane-induced pressures impacting the building envelope are captured through the introduction of a non-stationary/-straight/-Gaussian wind pressure model. Time-dependent wind-driven rain is modeled through a computational fluid dynamics Eulerian multiphase framework with interpolation schemes for the rapid computation of wind-driven rain intensities over the building surface. Through the development of a conditional stochastic simulation algorithm, the envelope performance is efficiently characterized through probabilistic metrics associated with rare events of design interest. The framework is demonstrated through analyzing a 45-story archetype building located in Miami, FL, for which the envelope performance is estimated in terms of a suite of probabilistic damage and loss metrics. A comparative study is carried out in order to provide insights into the differences that can occur due to the use of nominal hurricane models.
1 Introduction
Performance-based design (PBD) has been widely accepted as a rational way of assessing risks to engineered facilities subjected to natural hazards (Porter, 2003). Over the past decade, significant research efforts have been placed on the development of frameworks for the performance-based assessment of wind-excited buildings (Ciampoli et al., 2011; Smith and Caracoglia, 2011; Petrini and Ciampoli, 2012; Barbato et al., 2013; Bernardini et al., 2015; Pita et al., 2016; Chuang and Spence, 2017; Cui and Caracoglia, 2018; Ierimonti et al., 2019; Micheli et al., 2019; Ouyang and Spence, 2019; Cui and Caracoglia, 2020; Ouyang and Spence, 2020; Ouyang and Spence, 2021). Most frameworks developed to date assess damage and loss to the building system based on demands estimated exclusively from the structural response (e.g., peak interstory drifts, accelerations) notwithstanding how a significant portion of envelope damage is generated from local dynamic wind pressure. In an attempt to address this, the authors have recently introduced a PBWE framework where damage is estimated through a progressive analysis in which coupled structural response and wind pressure demands are considered as input to a multi-demand fragility analysis that captures damage state interdependency (Ouyang and Spence, 2019, 2020, 2021). Similar to existing PBWE methodologies, this framework adopted a nominal hurricane hazard based on the assumption of a straight (i.e., constant wind direction) and stationary wind event of one-hour duration. The intensity of the wind event was characterized through the maximum mean hourly wind speed to occur at the building top. Likewise, the intensity of the concurrent rain event was characterized through the maximum horizontal rainfall to occur during the hurricane at the site of interest. While this nominal hurricane setting simplifies subsequent damage and loss analysis, the relative accuracy of performance assessments based on nominal hurricanes, as compared to those carried out considering the full non-straight/-stationary nature of hurricane winds and concurrent rainfall, remains unknown.
To fill this knowledge gap, this work develops a PBWE framework for the performance assessment of envelope systems based on describing the full evolution of the hurricane event through parametric hurricane models for both the wind and concurrent rainfall fields. In particular, hurricane tracks are described through the probabilistic parametric models outlined by Vickery and Twisdale (1995a); Vickery et al. (2000b); and Cui et al. (2021), while the associated wind fields are described through the two-dimensional wind field model outlined by Vickery and Twisdale (1995b); Vickery et al. (2000a); and Jakobsen and Madsen (2004). These models are subsequently combined with parametric precipitation models (e.g., Lonfat et al., 2007; Grieser and Jewson, 2012; Geoghegan et al., 2018; Snaiki and Wu, 2018; Brackins and Kalyanapu, 2020) that use as input a subset of the hurricane model parameters therefore enabling a probabilistic description of concurrent horizontal rainfall intensity. The consideration of continuously time-varying hurricane inputs (i.e., evolving storm track and horizontal rainfall intensity) requires a new set of models for the simulation of the aerodynamic loads and wind-driven rain. To this end, a novel wind-tunnel-informed non-straight/-stationary/-Gaussian wind pressure simulation framework is introduced. For the wind-driven rain, the Eulerian multiphase computational fluid dynamics (CFD) model outlined by Kubilay et al. (2013, 2015) is adopted with an interpolation scheme within the space of the wind speed and direction therefore allowing for the efficient estimation of the instantaneous rainwater deposition on the building envelope in terms of the continually varying wind speed and direction.
To demonstrate the applicability of the framework, a 45-story archetype building located in Miami, FL, is studied in terms of probabilistic performance metrics associated with envelope damages, monetary losses, and water ingress. A comprehensive comparison of the results with those obtained by considering a nominal hurricane setting is also carried out with the aim of better understanding the feasibility of using classic hurricane hazard models in the PBWE of engineered building systems.
2 The Performance-Based Wind Engineering Setting
Pioneered by the Pacific Earthquake Engineering Research (PEER) center (Porter, 2003), frameworks for probabilistic performance-based earthquake engineering have been widely adopted as the basis for developing frameworks for PBWE. The current work is developed based on the recently proposed PBWE framework outlined by Ouyang and Spence (2020), the implementation of which enables the estimation of probabilistic building envelope performance metrics of interest to stakeholders (e.g., expected repair costs, expected water ingress) based on a nominal description of the hurricane hazard. In particular, as detailed in Ouyang and Spence (2020), the framework is based on characterizing performance through solving the following probabilistic integral:
where G(x|y) is the conditional complementary cumulative distribution function (CCDF) of random variable x given y, sm is the system measure variables (e.g., number of damaged components and amount of water ingress), Rh is the mean hourly rainfall intensity, αH is the wind direction,
For the hurricane framework proposed in this study, Eq. 1 cannot be directly adopted as the hurricane inputs of wind speed (
where λe is the annual recurrence rate of hurricanes of engineering interest while G(Θ) is the CCDF of Θ. It is important to observe that inherent to estimating the term G(sm|Θ) is not only the time-dependent nature of
where
1) Hurricane hazard analysis, in which the terms
2) Response analysis, in which the structural and aerodynamic responses are simulated based on the hurricane parameter vector Θ to estimate G(sm|Θ);
3) Loss and consequence analysis, in which the estimates of sm are translated into probabilistic measures of monetary losses and volumes of water ingress through the term G(dv|sm).
This study is focused on developing a methodology for estimating the performance of envelope systems of engineered buildings through solving Eq. 3. As compared to the frameworks outlined in Ouyang and Spence (2019, 2020, 2021), which are based on a classic straight/stationary hurricane model of nominal one-hour duration, appropriate hurricane track and wind field models need to be identified (Section 3) for subsequent use as input to new stochastic aerodynamic models that are capable of capturing the non-stationary/-straight/-Gaussian wind pressures of full hurricanes (Section 4.1). Additionally, the stochastic simulation scheme outlined in Ouyang and Spence (2020, 2021) requires reformulating in terms of the parameter vector Θ for enabling rare event simulation in the space of full hurricanes (Section 7). Through these advances, new knowledge on the envelope performance of engineered buildings during full hurricanes will be created through application to an archetype case study (Section 8). To ensure a straightforward comparison of the results of this study with those reported by Ouyang and Spence (2019, 2020, 2021), the same case study building will be considered.
3 Hurricane Hazard Analysis
3.1 Hurricane Representations
Given a site and reference height, H, of interest, the following definitions of hurricane event will be adopted in this work:
• Nominal Hurricane: a site-specific stationary (constant time-averaged wind speed
• Full Hurricane: a site-specific non-stationary (time-varying average wind speed
From the above definitions, it is clear that for a given full hurricane, the parameters of the corresponding nominal hurricane are defined as follows:
It is important to observe that the straight and stationary nature of the nominal hurricane enables existing models to be used for representing the stochastic wind pressures on the building envelope, e.g., those outlined in Ouyang and Spence (2020). However, these models cannot be used to represent the stochastic wind pressures in full hurricanes due to their non-stationary and non-straight nature. To overcome this, Section 4.1 will introduce a novel non-straight/-stationary/-Gaussian stochastic wind pressure model. The remainder of this section will focus on identifying appropriate parametric models for representing the storm track, wind field, and hazard curve of full hurricanes.
3.2 Full Hurricane Model
3.2.1 Storm Track Model
The storm track model outlined by Vickery and Twisdale (1995a) and Vickery et al. (2000b) is adopted to simulate hurricanes making landfall at a site of interest. In this model, a hurricane risk region is first formed through a circular subregion centered at a location of interest (e.g., building location). Hurricane tracks are subsequently modeled as straight lines crossing the subregion. Within this context, the hurricane lifetime begins when the hurricane center enters the subregion and ends when it leaves the subregion. In this model, the distance vector between the site of interest and the hurricane center, rs, at any given time t during the hurricane event is defined as:
where dmin is the minimum distance between the hurricane center and the site of interest (taken positive if the site of interest sits to the left of the hurricane track and negative otherwise), Rs is the diameter of the subregion centered at the site of interest, θ is the angle between the storm track and the north direction, and e and n are the unit vectors pointing towards East and North.
3.2.2 Wind Field Model
The parametric model proposed by Jakobsen and Madsen (2004) is adopted to model the hurricane wind velocity field. The choice of this model was made as it represents a parametric solution to the wind field model outlined by Vickery et al. (2000a) that has been carefully validated and used as the basis of the ASCE 7 wind maps. The implementation of this wind field model is coupled with the hurricane track input vector Θ through the initial central pressure difference (Δp0) and the radius of the maximum wind (rM). In this model, the mean hourly hurricane wind field at 500 m at time t is solved for the tangential and radial velocity components as:
where vc is the tangential component of the velocity field; uc is the radial component of the velocity field; B is the Holland number; h is the boundary layer thickness; f is the Coriolis parameter; (r, β) are the polar coordinates of a reference system centered at the eye of the hurricane with β = 0 when r points in the positive direction of e; Cd ( ∼0.0015) is a drag coefficient related to the boundary layer average velocity; K is the diffusion coefficient; r′ = r/rM; vM is the maximum tangential velocity given by:
where ρa is the air density, e is the base of the natural logarithmic function, and λ is a coefficient related to the advective, diffusive, and frictional drag terms in the momentum equations defined as
Based on Eqs. 5, 6, the wind field vector vs at time t can be written as:
where rG ( ∼ 500 km) is the environmental length scale defining the extent to which the translation speed of the hurricane, c, decays in the radial direction. Based on the above definitions, the mean hourly wind speed at a location and height of interest can be estimated through the following transformation:
where H is the height of interest height (e.g., building height), z0 is the terrain roughness length at the site of interest, z01 is the roughness length at 10 m in open terrain, 0.1171 is a dimensionless coefficient related to transforming wind speeds from 500 to 10 m in open terrain, and βs is the angle in polar coordinates between the eye of the storm and the site of interest.
As the hurricane moves along its track, the wind speed,
3.2.3 Filling-Rate Model
Once hurricanes make landfall, the central pressure difference (Δp) will in general decay resulting in a reduction in the wind field and hence the wind speed at the site of interest. To simulate this phenomenon, the following filling-rate model is adopted (Vickery and Twisdale, 1995b):
where an exponential decay is used to model the dissipation of the hurricane central pressure deficit once landfall is made. To include uncertainties in the decay rate, the following probabilistic filling constant af, dependent on the initial central pressure difference Δp0, is considered:
where ϵf is a zero-mean normally distributed error term with standard deviation σϵ while the parameters a1 and a2 are site-specific and model the expected decay. Suggested values for various locations for a1, a2, and σϵ can be found in the study by Vickery and Twisdale (1995b). The parameters a0, a1, and ϵf are included in the hurricane input parameter vector Θ.
3.2.4 Precipitation Model
To model the concurrent rainfall, the IPET (Interagency Performance Evaluation Task) parametric precipitation model, developed based on the National Aeronautics and Space Administration’s Tropical Rainfall Measuring Mission database, is adopted (Lonfat et al., 2004; Chen et al., 2006). Comparative studies have suggested this model is superior to other commonly used parametric rainfall models (Lonfat et al., 2004; Brackins and Kalyanapu, 2020). From the IPET model, the evolution of the mean hourly horizontal rainfall, Rh(t), can be estimated at the site of interest directly from the hurricane parameters Δp(t), rs(t), and rM at any given time, t, through the following expression:
where Δp is in millibars, Rh is in h/mm, and rs(t) and rM are in kilometers. The value calculated by Eq. 13 provides the symmetric component of the rainfall field. To estimate the asymmetric component, Rh(t) can be multiplied by a factor of 1.5 if the site of interest is in the northern hemisphere and to the right of the hurricane track (0.5 if it is to the left).
3.3 Hazard Curve of the Full Hurricane Model
The intensity of each hurricane is measured through the maximum mean hourly wind speed,
Following this definition, the performance assessment of envelope systems through Eq. 3 relies on an accurate estimation of the hazard curve
where the components of Θ are the initial central pressure difference Δp0, translation speed c, size of the hurricane rM, approach angle θ, shortest distance dmin between site of interest and hurricane track, and the coefficients a0, a1, and ϵf of the filling-rate model,
where λe is the mean annual recurrence rate of hurricanes of engineering interest.
4 Response Analysis: Envelope Actions
4.1 Non-stationary/-straight/-Gaussian External Pressure
4.1.1 Overview
Based on the straight and stationary wind pressure simulation model outlined by Ouyang and Spence (2020), a non-stationary/-straight wind pressure model is developed to capture the effects on the aerodynamic pressures of the continuously varying wind speed and direction associated with full hurricanes. The main steps of the model are outlined in the conceptual flowchart of Figure 1. The model is calibrated to data in the form of vectors of model-scale surface pressure coefficients Cp,e,M(tM), with tM the model-scale time, collected in wind tunnel tests where stationary/straight but non-Gaussian pressures are measured at a grid of sensors on the model surface for a discrete set of wind directions (e.g., {10°, 20°, …, 360°}). To reconcile the discrete wind directions of the wind tunnel data with the continuously varying wind directions of the hurricane track, these last are transformed into a piece-wise discrete representation, as illustrated in step (I) of Figure 1, where a set of segments with constant wind directions are defined. In step (II), model-scale stationary/straight but non-Gaussian wind pressure coefficient vector processes,
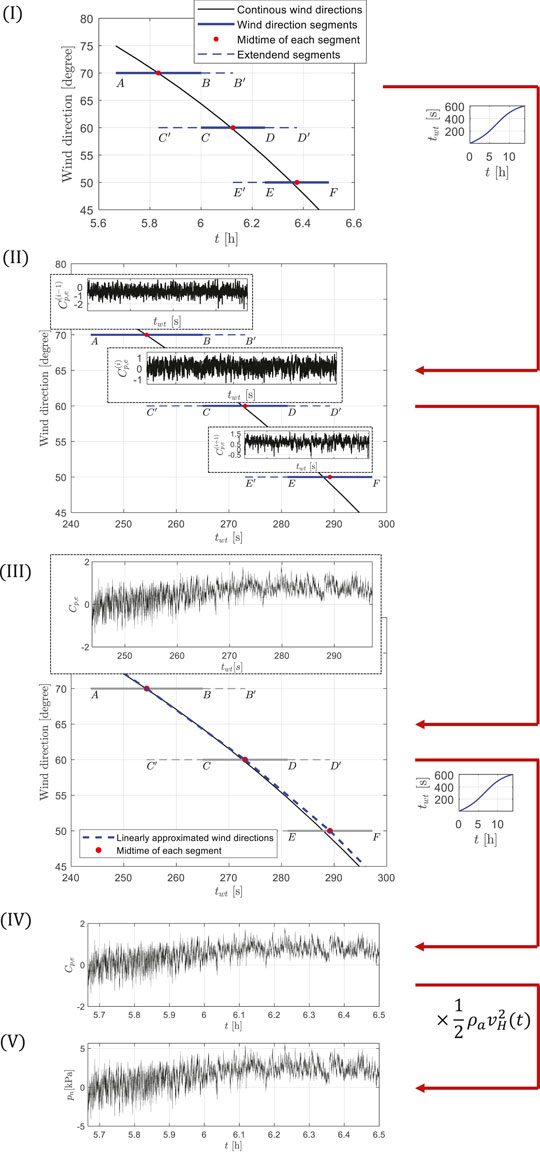
FIGURE 1. Conceptual flowchart of the non-stationary/-straight/-Gaussian stochastic wind pressure simulation model.
4.1.2 Procedure
In the following, further details of each step of the model outlined in Figure 1 are provided.
Step I
The continuous wind direction history, αH(t), is first discretized into a set of segments with each segment representing a straight wind event. This discretization can be expressed as:
where
Step II
In this step, a wind pressure coefficient vector process,
where γH is the ratio of the model to full-scale height and
where
Through Eq. 18, the duration of each extended segment is calculated and used to simulate the stationary/straight but non-Gaussian wind pressure coefficient vector processes,
Step III
From the stationary wind pressure coefficient vector processes
The following linear ramping-based filter is then applied to each time-averaged component:
where
To merge the fluctuation components,
By iterating over all segments, with special boundary consideration for i = 1 and i = Nseq,
Through the transition model outlined above, the merged wind pressure vector process will have second-order statistics (auto- and cross-correlation functions) that vary following a near-linear relationship between the wind directions in which wind tunnel data are available. Inherent to this transition model is the capture of non-Gaussianity in Cp,e,M(tM) that matches those observed in the wind tunnel for the discrete wind directions at which wind tunnel tests were performed.
Step IV
To generate the wind pressure vector process at a building-scale with a target constant sampling frequency, the model-scale wind pressure coefficient vector process needs to be sampled with a nonuniform sampling frequency due to the continuously varying wind speed –vH(t). This nonuniform sampling is achieved through a model-scale interpolation scheme, where the uniform time samples tl, with l ∈ (1, 2, …, Nl) and Nl the total number of uniform samples at a building-scale, are mapped to the model-scale through Eq. 17. This leads to a nonuniform space of model-scale time samples tM(tl) that are evaluated through interpolation. The discrete representation of the building-scale non-stationary/-straight/-Gaussian pressure coefficient vector process, Cp,e(tl), is defined as:
Step V
From the pressure coefficient processes of Eq. 24, the non-stationary/-straight/-Gaussian external pressures can be estimated as:
where pe is the vector of the non-stationary/-straight/-Gaussian pressure processes at the sensor grid locations at full scale. To estimate the pressure processes at a location, identified by the coordinate ξxyz, on the building envelope where direct measurements were not carried out, 2D interpolation with extrapolation can be used (Ouyang and Spence, 2019, 2020).
4.2 Wind-driven Rain
The simulation of the time-dependent wind-driven rain is developed through the extension of the nominal wind-driven rain model outlined by Ouyang and Spence (2020). For the nominal hurricane, constant wind-driven rain is simulated through the 3D steady Reyolds-averaged Navier-Stokes (RANS) equations-based Eulerian multiphase (EM) model proposed by (Huang and Li (2012); Kubilay et al., (2013, 2017). The implementation of this framework consists of two steps: 1) the RANS equations with a realizable k-ϵ turbulence model are solved for the steady-state wind field around the building; and 2) based on the steady-state solution from the first step, the EM model is implemented with the k − ϵ turbulence model to solve for wind-dispersed rain phases. In particular, each rain phase represents a phase flow problem for a group of raindrops with diameters in a predefined range. The solution of the EM model gives a vector of normalized specific catch ratios,
To model the time-dependency of the wind-driven rain due to the continuously varying wind speed and direction, the specific catch ratios would need to be continuously solved in time. This poses a significant computational issue as this would in general imply the need to solve RANS-based EM models for a sequence of wind speeds and directions for each storm track of interest. To overcome this issue, an interpolation-based approach is adopted, where the specific catch ratios at each envelope point of interest,
where Φ(t) is a weighting vector whose kth component is defined as:
where Δdk is the raindrop diameter range of the kth rain phase, dk is the median raindrop diameter in the kth rain phase, and fh is the PDF of the raindrop diameter distribution.
5 Response Analysis: System Analysis
Based on the envelope actions, demands in terms of dynamic story drifts and local net dynamic pressures can be estimated through the adoption of the models outlined by Ouyang and Spence (2020). Based on these demands, system measures, sm, associated with the final damage states of each vulnerable envelope component and subsequent water ingress can be evaluated. As will be briefly outlined below, the use of the models outlined by Ouyang and Spence (2020) enables not only the capture of the interdependencies between demands and damages but also the progressive nature of wind-induced damage.
5.1 Demands
5.1.1 Structural Response
Based on the results reported by Ouyang and Spence (2021), the structural system is assumed to respond elastically. The dynamic response of the structural system can therefore be estimated through solving the following modal equations:
where qi,
where ϕi is the ith mode shape; M is the structural mass matrix; and
From the solution of Eq. 28, the dynamic structural response can be approximated from the first Nm modes as:
Dynamic story drift, Dr(t), at any location of interest can then be directly estimated through a linear combination of the appropriate components of x(t).
5.1.2 Net Dynamic Pressure
The net pressure demands at an envelope location ξxyz of interest, pn(t, ξxyz), are evaluated as:
where e(t, ξxyz) is the external pressure estimated through the models of Section 4.1 at ξxyz while pi(t, ξxyz) is the corresponding internal pressures. To estimate the dynamic internal pressures pi(t, ξxyz), the interior of the building is modeled as a system of interconnected compartments. Initially, the building is considered enclosed with negligible internal pressurization. During the hurricane, openings can be created in the envelope due to component damages, which allows air to flow into or out of the building triggering dynamic internal pressures in all compartments that are connected through an internal opening. To solve the transient air flows, the internal pressure model outlined by Ouyang and Spence (2019) is adopted, in which the air velocity at each opening is described through the unsteady-isentropic form of the Bernoulli equation (Vickery and Bloxham, 1992; Yu et al., 2008; Guha et al., 2011). To treat the time dependency of
It is important to observe that in solving for pi(t, ξxyz), the current drift-induced damage state of each envelope component must be considered. This couples not only the structural and pressure demands (e.g., a drift-induced damage to the envelope can cause air flow therefore affecting the internal pressure) but also the demand and damage analysis (e.g., the occurrence of a drift- or pressure-induced damage state can affect internal pressures). It should also be observed that damage to the envelope is progressive in nature as it accumulates over the duration of the event.
5.2 System Measures
5.2.1 Component Damages
To model the damage susceptibility of the ith envelope component to
5.2.2 Water Ingress
The concurrent rainfall leads to the deposition of rainwater on the envelope. Damage to the envelope can then lead to water ingress. To estimate the volume of water ingress, the flow rate at each opening can be estimated directly from Rwdr(ξxyz, t), estimated through the models of Section 4.2, and the steady-state water runoff solution derived by Ouyang and Spence (2019). From the flow rate at each opening, the total volume of water entering through an opening at a given time,
6 Loss and Consequence Analysis
To translate the final damage states of each envelope component into repair costs and actions, the concept of unit loss function (ULF), as defined by Federal Emergency Management Agency (FEMA) (2012), is adopted. Specifically, the ULF defines the repair cost as a monotonically decreasing function with respect to the total number of components in a given damage state. To consider economies of scale, a minimum quantity, Qmin, is defined as the lower limit below which economies of scale do not take effect. Likewise, a maximum quantity, Qmax, is defined as the upper limit after which economies of scale no longer occur. To include uncertainty in the loss estimation, the value given by the ULF is taken as the expected value of a lognormal random variable with assigned dispersion. This dispersion accounts, to a certain extent, for the many complexities involved in estimating repair cost and time following a hurricane, e.g., administrative backlogs, demand surge, lack of materials, and shortage of labor. Through ULFs, each envelope damage state can be converted to estimates of the repair cost (or time). The evaluation of the total system level repair cost, i.e., the decision variable (dv), can then be evaluated by summing all envelope component repair costs. This scheme can also be used to estimate downtimes associated with repair actions. Similarly, the system-level consequence of envelope damage related to total volume of water ingress can be assessed by summing the volumes of water ingress at each damaged envelope component. Additionally, the information provided by the framework on water ingress would support the use of models for estimating damage to the interior components and contents by providing detailed information on the water paths and flow rates at each damaged envelope component.
7 Simulation Strategy
The evaluation of the envelope system performance relies on the possibility of efficiently solving Eq. 3. Because the failure rates of interest to this work are small, i.e., related to rare events, and the models used to characterize performance are computational intense, direct Monte Carlo (MC) methods are generally intractable. To overcome this, a conditional stochastic simulation scheme that integrates subset simulation (Au and Beck, 2001) is developed. The approach is based on using
where
To evaluate Eq. 32 through the approach outlined above, subset simulation is first used to estimate the hazard curve,
8 Case Study
8.1 Building System
To illustrate the proposed framework while also studying the differences between performance assessments carried out using nominal as opposed to full hurricane hazard models, the archetype building outlined in (Ouyang and Spence, 2020) with location Miami, FL, is considered. As shown in Figure 2, the building is a rectangular 45-story steel structure with central core and symmetric X-bracing. The total height of the structure is 180 m with a constant floor height of 4 m. The structural system was designed to satisfy typical serviceability and life safety requirements. The first 10 vibration modes were considered adequate for representing the dynamic response. The first three natural frequencies were 1.30, 1.67, and 2.70 rad/s, respectively. The damageable components considered in the case study are the dual-pane laminated glazing units of size of 1.2 × 2 m2. The thickness of each laminated pane is taken as 6 mm. Each floor has 180 units with 60 units on the south (north) face and 30 units on the east (west) face, which results in a total of 8,100 units for the entire building. To calibrate the damage model of Section 5.2.1, two drift-induced damages states (defined as hairline cracking,
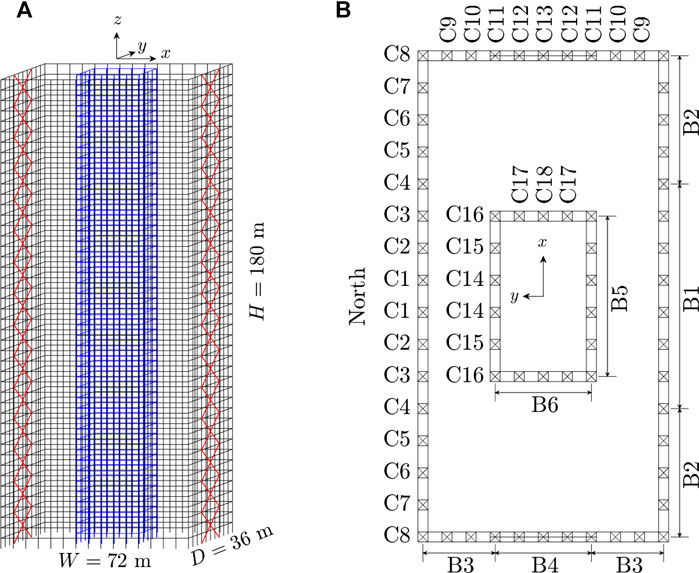
FIGURE 2. (A) Three-dimensional illustration of the 45-story structure; (B) plan view indicating the floor member layout (B = beam and C = column) and North.
8.2 Hurricane Hazard
To calibrate the parametric hurricane model of Section 3.2.1, and therefore the vector Θ to Miami, a subregion diameter of Rs = 500 km was considered while the probabilistic characteristics of the components of Θ followed those suggested by Vickery and Twisdale (1995a). In converting mean hourly wind speeds at 500 m to H = 180 m (i.e., building top) through Eq. 10, values of z0 = 1.28 m and z01 = 0.03 m were considered. The aerodynamic model of Section 4.1.2 was calibrated to a data set of the Tokyo Polytechnic University (TPU) wind tunnel pressure database (Tokyo Polytechnic University, 2008). These data are used to calibrate the stationary/straight but non-Gaussian wind pressure coefficient processes, Cp,e,M(tM), at model-scale. For the data set considered, the ratio of tunnel model height to building height, γH, was 1:360 while the mean wind speed at model height during the wind tunnel tests was
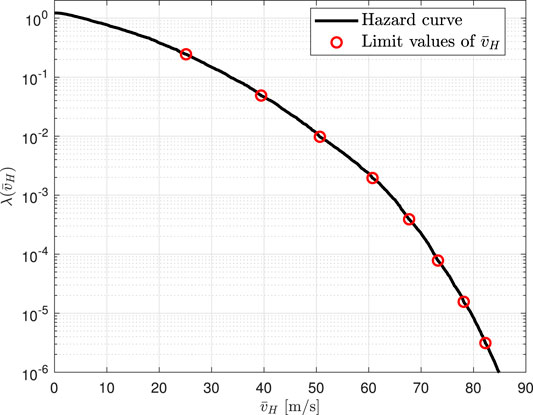
As defined in Section 3.2.1, each sample of Θ uniquely determines the hurricane track of a full hurricane. To estimate the hazard curve through subset simulation, an intermediate probability of Ps = 0.2 was chosen together with
8.3 Results
8.3.1 Preamble
To enable the comparison between the full hurricane model of this work and a classic nominal hurricane setting, for each full hurricane sample, a nominal hurricane is also generated based on the maximum wind speed
8.3.2 Discussion on a Single Event
To illustrate and discuss the evolution of damage during a full hurricane event, a single hurricane event is analyzed in detail in this section. The event corresponds to a category five hurricane on the Saffir-Simpson scale (Taylor et al., 2010), with a maximum mean hourly wind speed at the building top of 67.7 m/s. The time evolution of mean hourly wind speed
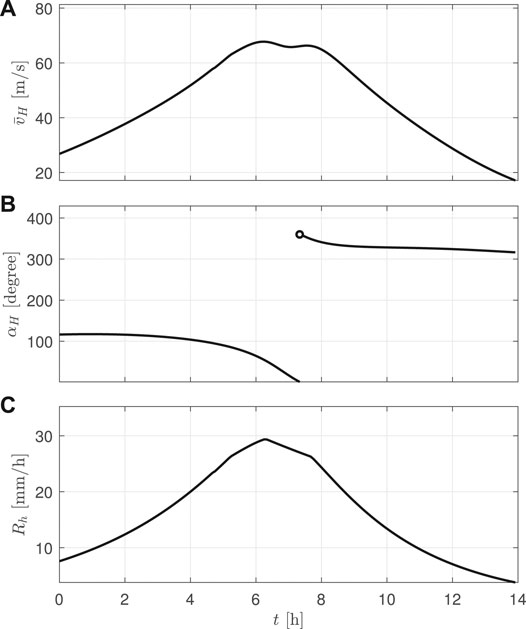
FIGURE 4. The simulated category V hurricane in Saffir-Simpson scale measured at the building site: (A) evolution of the mean hourly wind speed; (B) wind direction; and (C) mean hourly rainfall intensity.
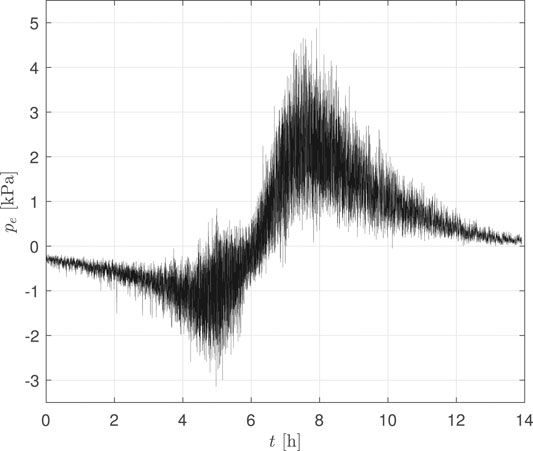
FIGURE 5. An example of the non-stationary/-straight/-Gaussian external wind pressure process for an envelope component located at the upper-left corner of the south face of the building.
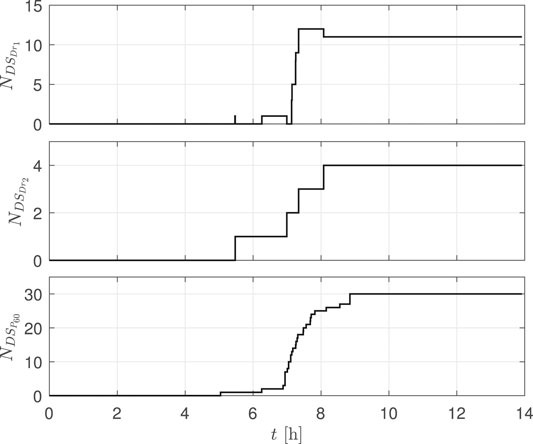
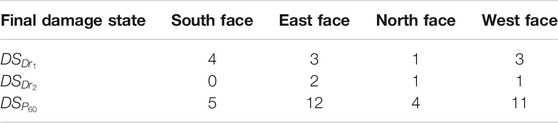
Figure 6 reports the accumulation of damage over the duration of the hurricane in terms of the total number of envelope components assuming
8.3.3 Probabilistic Performance Metrics
The mean annual rate of each envelope component assuming as a final damage state
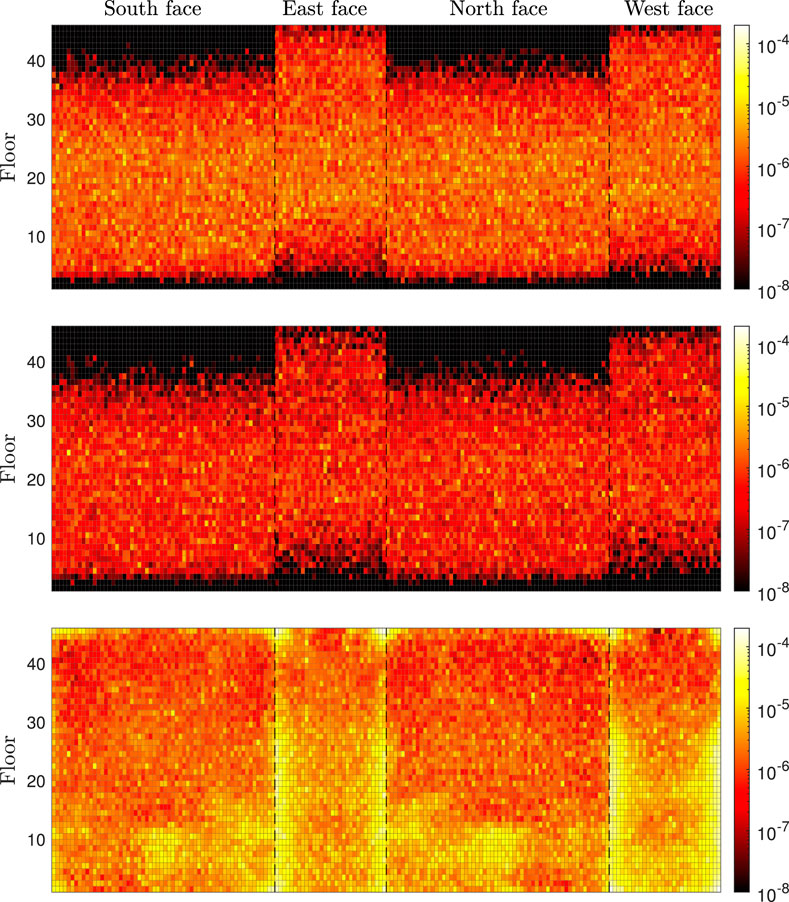
FIGURE 8. Mean annual rate of each envelope component assuming as a final damage state
To evaluate the system-level envelope performance for both the nominal and full hurricanes, Figure 9 reports the damage curves for both scenarios in terms of the mean annual rate of exceeding a total number of components assuming as a final damage state
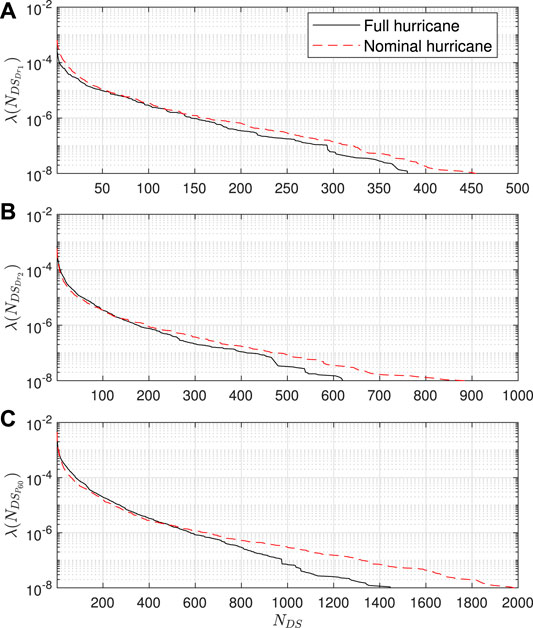
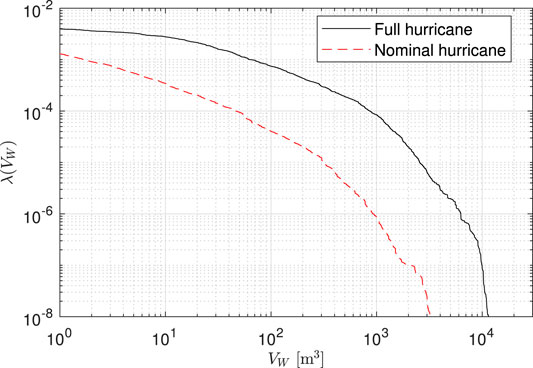
FIGURE 9. Mean annual rate of exceeding a total number of envelope components assuming as a final damage state: (A)
To investigate this, the distribution of maximum wind speed duration is analyzed for all hurricane samples in hazard intervals three to nine, where the first two intervals are not considered as the value of
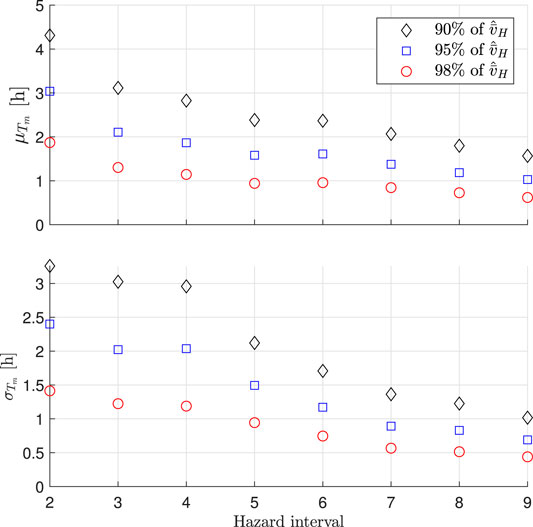
FIGURE 10. Mean,
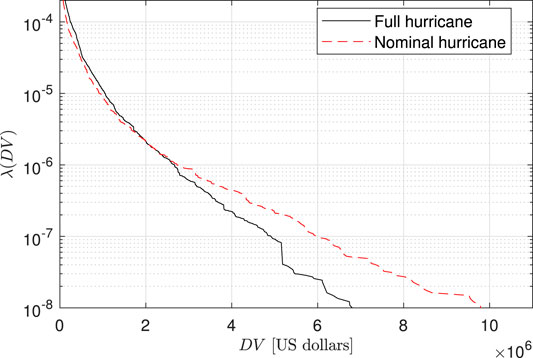
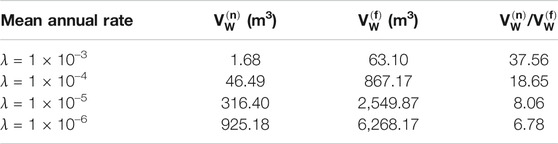
The loss curves associated with repair costs are reported in Figure 11. The relative magnitude of total repair cost between the nominal and full hurricanes is similar to the damage curves of Figure 9C, which implies that the pressure-induced damages dominate the total repair cost associated with the envelope components. Figure 12 reports the exceedance rates associated with the consequence metric of total volume of water ingress VW. From the comparison of the water ingress curves, the nominal hurricane significantly underestimates the total amount of water ingress as compared to the full hurricane. To quantify this underestimation, Table 3 reports the total water ingress at different exceedance rates for the nominal and full hurricanes. As can be seen, a near 40-fold underestimation of water ingress can be seen for exceedance rates of 1 × 10–3. The root of this difference can be traced back to how the nominal hurricane neglects the water that can enter the building due to rainfall after the peak wind speeds have occurred. As the exceedance rates decrease, the underestimation of total water ingress from the nominal hurricane also decreases. This is due to how as the hurricane events become more extreme, the majority of damage will occur at the beginning of the nominal hurricane event therefore increasing the duration in which water can ingress.
9 Summary and Conclusion
A framework is outlined for the performance assessment of the envelope system of engineered buildings subject to a full representation of the hurricane hazard. A new wind-tunnel-informed non-stationary/-straight/-Gaussian wind pressure stochastic simulation model is introduced to support full hurricane event simulation. Through the development of a conditional stochastic simulation framework, efficient estimation of probabilistic metrics associated with the performance of the envelope system in rare events is made possible. The framework was illustrated through a case study consisting of a 45-story archetype building located in Miami, FL. Performance metrics associated with the total number of damaged envelope components, monetary loss, and total water ingress were evaluated. The comparison of the performance metrics with those estimated for a classic nominal representation of the hurricane hazard showed that performance assessments made with the nominal hurricane representation will generate similar amounts of damages and losses for a mean annual rate greater than 2 × 10–6. For events with smaller rates than 2 × 10–6, the nominal hurricanes significantly overestimated (up to 50%) the damages and losses. In terms of the water ingress, a full hurricane representation will generate a much larger volume of water ingress, over 30-fold larger for rates of 1 × 10–3, than seen for simulations using a nominal hurricane representation. This underestimation was seen to decrease with the reduction of the exceedance rates.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, and further inquiries can be directed to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
The research effort was supported in part by the United States (US) National Science Foundation (NSF) under Grant No. CMMI-1562388 and CMMI-1750339. This support is gratefully acknowledged.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Au, S.-K., and Beck, J. L. (2001). Estimation of Small Failure Probabilities in High Dimensions by Subset Simulation. Probabilistic Eng. Mech. 16, 263–277. doi:10.1016/s0266-8920(01)00019-4
Barbato, M., Petrini, F., Unnikrishnan, V. U., and Ciampoli, M. (2013). Performance-based hurricane Engineering (PBHE) Framework. Struct. Saf. 45, 24–35. doi:10.1016/j.strusafe.2013.07.002
Bernardini, E., Spence, S. M. J., Kwon, D.-K., and Kareem, A. (2015). Performance-based Design of High-Rise Buildings for Occupant comfort. J. Struct. Eng. 141, 1–14. doi:10.1061/(asce)st.1943-541x.0001223
Brackins, J. T., and Kalyanapu, A. J. (2020). Evaluation of Parametric Precipitation Models in Reproducing Tropical Cyclone Rainfall Patterns. J. Hydrol. 580, 124255. doi:10.1016/j.jhydrol.2019.124255
Chen, S. S., Knaff, J. A., and Marks, F. D. (2006). Effects of Vertical Wind Shear and Storm Motion on Tropical Cyclone Rainfall Asymmetries Deduced from TRMM. Monthly Weather Rev. 134, 3190–3208. doi:10.1175/mwr3245.1
Chuang, W.-C., and Spence, S. M. J. (2017). A Performance-Based Design Framework for the Integrated Collapse and Non-collapse Assessment of Wind Excited Buildings. Eng. Structures 150, 746–758. doi:10.1016/j.engstruct.2017.07.030
Ciampoli, M., Petrini, F., and Augusti, G. (2011). Performance-based Wind Engineering: Towards a General Procedure. Struct. Saf. 33, 367–378. doi:10.1016/j.strusafe.2011.07.001
Cui, W., and Caracoglia, L. (2018). A Unified Framework for Performance-Based Wind Engineering of Tall Buildings in hurricane-prone Regions Based on Lifetime Intervention-Cost Estimation. Struct. Saf. 73, 75–86. doi:10.1016/j.strusafe.2018.02.003
Cui, W., and Caracoglia, L. (2020). Performance-based Wind Engineering of Tall Buildings Examining Life-Cycle Downtime and Multisource Wind Damage. J. Struct. Eng. 146, 04019179. doi:10.1061/(asce)st.1943-541x.0002479
Cui, W., Zhao, L., Cao, S., and Ge, Y. (2021). Bayesian Optimization of Typhoon Full-Track Simulation on the Northwestern pacific Segmented by Quadtree Decomposition. J. Wind Eng. Ind. Aerodynamics 208, 104428. doi:10.1016/j.jweia.2020.104428
Federal Emergency Management Agency (FEMA) (2012). Seismic Performance Assessment of Buildings, Volume 1 - Methodology (FEMA Publication P-58-2). Washington, D.C: Tech. rep..
Geoghegan, K. M., Fitzpatrick, P., Kolar, R. L., and Dresback, K. M. (2018). Evaluation of a Synthetic Rainfall Model, P-Cliper, for Use in Coastal Flood Modeling. Nat. Hazards 92, 699–726. doi:10.1007/s11069-018-3220-4
Grieser, J., and Jewson, S. (2012). The Rms Tc-Rain Model. Meteorologische Z. 21, 79–88. doi:10.1127/0941-2948/2012/0265
Guha, T. K., Sharma, R. N., and Richards, P. J. (2011). Internal Pressure Dynamics of a Leaky Building with a Dominant Opening. J. Wind Eng. Ind. Aerodynamics 99, 1151–1161. doi:10.1016/j.jweia.2011.09.002
Huang, S. H., and Li, Q. S. (2012). Large Eddy Simulations of Wind-Driven Rain on Tall Building Facades. J. Struct. Eng. 138, 967–983. doi:10.1061/(asce)st.1943-541x.0000516
Ierimonti, L., Venanzi, I., Caracoglia, L., and Materazzi, A. L. (2019). Cost-based Design of Nonstructural Elements for Tall Buildings under Extreme Wind Environments. J. Aerosp. Eng. 32, 04019020. doi:10.1061/(asce)as.1943-5525.0001008
Jakobsen, F., and Madsen, H. (2004). Comparison and Further Development of Parametric Tropical Cyclone Models for Storm Surge Modelling. J. Wind Eng. Ind. Aerodynamics 92, 375–391. doi:10.1016/j.jweia.2004.01.003
Kubilay, A., Derome, D., Blocken, B., and Carmeliet, J. (2013). CFD Simulation and Validation of Wind-Driven Rain on a Building Facade with an Eulerian Multiphase Model. Building Environ. 61, 69–81. doi:10.1016/j.buildenv.2012.12.005
Kubilay, A., Derome, D., Blocken, B., and Carmeliet, J. (2015). Numerical Modeling of Turbulent Dispersion for Wind-Driven Rain on Building Facades. Environ. Fluid Mech. 15, 109–133. doi:10.1007/s10652-014-9363-2
Kubilay, A., Derome, D., and Carmeliet, J. (2017). Analysis of Time-Resolved Wind-Driven Rain on an Array of Low-Rise Cubic Buildings Using Large Eddy Simulation and an Eulerian Multiphase Model. Building Environ. 114, 68–81. doi:10.1016/j.buildenv.2016.12.004
Lonfat, M., Marks, F. D., and Chen, S. S. (2004). Precipitation Distribution in Tropical Cyclones Using the Tropical Rainfall Measuring mission (TRMM) Microwave Imager: A Global Perspective. Mon. Wea. Rev. 132, 1645–1660. doi:10.1175/1520-0493(2004)132<1645:pditcu>2.0.co;2
Lonfat, M., Rogers, R., Marchok, T., and Marks, F. D. (2007). A Parametric Model for Predicting hurricane Rainfall. Monthly Weather Rev. 135, 3086–3097. doi:10.1175/mwr3433.1
Micheli, L., Alipour, A., Laflamme, S., and Sarkar, P. (2019). Performance-based Design with Life-Cycle Cost Assessment for Damping Systems Integrated in Wind Excited Tall Buildings. Eng. Structures 195, 438–451. doi:10.1016/j.engstruct.2019.04.009
Ouyang, Z., and Spence, S. M. J. (2019). A Performance-Based Damage Estimation Framework for the Building Envelope of Wind-Excited Engineered Structures. J. Wind Eng. Ind. Aerodynamics 186, 139–154. doi:10.1016/j.jweia.2019.01.001
Ouyang, Z., and Spence, S. M. J. (2020). A Performance-Based Wind Engineering Framework for Envelope Systems of Engineered Buildings Subject to Directional Wind and Rain Hazards. J. Struct. Eng. 146, 04020049. doi:10.1061/(asce)st.1943-541x.0002568
Ouyang, Z., and Spence, S. M. J. (2021). Performance-based Wind-Induced Structural and Envelope Damage Assessment of Engineered Buildings through Nonlinear Dynamic Analysis. J. Wind Eng. Ind. Aerodynamics 208, 104452. doi:10.1016/j.jweia.2020.104452
Petrini, F., and Ciampoli, M. (2012). Performance-based Wind Design of Tall Buildings. Struct. Infrastructure Eng. 8, 954–966. doi:10.1080/15732479.2011.574815
Pita, G. L., Pinelli, J.-P., Gurley, K., Weekes, J., and Cocke, S. (2016). Hurricane Vulnerability Model for Mid/high-Rise Residential Buildings. Wind and Structures 23, 449–464. doi:10.12989/was.2016.23.5.449
Porter, K. A. (2003). “An Overview of PEER’s Performance-Based Earthquake Engineering Methodology,” in Proc. Ninth International Conference on Applications of Statistics and Probability in Civil Engineering (ICASP9), July 6–9 (Rotterdam, Netherlands: Millpress).
Smith, M. A., and Caracoglia, L. (2011). A Monte Carlo Based Method for the Dynamic “Fragility Analysis” of Tall Buildings under Turbulent Wind Loading. Eng. Structures 33, 410–420. doi:10.1016/j.engstruct.2010.10.024
Snaiki, R., and Wu, T. (2018). An Analytical Framework for Rapid Estimate of Rain Rate during Tropical Cyclones. J. Wind Eng. Ind. Aerodynamics 174, 50–60. doi:10.1016/j.jweia.2017.12.014
Taylor, H. T., Ward, B., Willis, M., and Zaleski, W. (2010). The Saffir-simpson hurricane Wind Scale. Washington, DC, USA: Atmospheric Administration.
[Dataset] Tokyo Polytechnic University (2008). TPU Wind Pressure Database. Tokyo, Japan: Tokyo Polytechnic University.
Vickery, B. J., and Bloxham, C. (1992). Internal Pressure Dynamics with a Dominant Opening. J. Wind Eng. Ind. Aerodynamics 41, 193–204. doi:10.1016/0167-6105(92)90409-4
Vickery, P. J., Skerlj, P. F., and Twisdale, L. A. (2000b). Simulation of hurricane Risk in the Us Using Empirical Track Model. J. Struct. Eng. 126, 1222–1237. doi:10.1061/(asce)0733-9445(2000)126:10(1222)
Vickery, P. J., Skerlj, P., Steckley, A. C., and Twisdale, L. A. (2000a). Hurricane Wind Field Model for Use in hurricane Simulations. J. Struct. Eng. 126, 1203–1221. doi:10.1061/(asce)0733-9445(2000)126:10(1203)
Vickery, P. J., and Twisdale, L. A. (1995a). Prediction of hurricane Wind Speeds in the united states. J. Struct. Eng. 121, 1691–1699. doi:10.1061/(asce)0733-9445(1995)121:11(1691)
Vickery, P. J., and Twisdale, L. A. (1995b). Wind-field and Filling Models for hurricane Wind-Speed Predictions. J. Struct. Eng. 121, 1700–1709. doi:10.1061/(asce)0733-9445(1995)121:11(1700)
Yu, S., Lou, W., and Sun, B. (2008). Wind-induced Internal Pressure Response for Structure with Single Windward Opening and Background Leakage. J. Zhejiang University-SCIENCE A 9, 313–321. doi:10.1631/jzus.a071271
Appendix
Structural System
The layout of the structural system is shown in Figure 2 with beams and columns grouped in plan as shown in Figure 2B. Groups of beams and columns extend three consecutive floors. The diagonal braces are grouped as pairs over the height of the building. The beams and bracing elements are assigned sections from the W24 AISC (American Institute for Steel Construction) family while the columns are box sections with wall thickness taken as 1/20 of the mid-line width of the section. The floors are considered rigid in their plane with a mass density of 0.38 t/m2. The damping ratio for each vibration mode was taken as a lognormal random variable of mean 0.014 and coefficient of variation 0.3. The structural system was designed to meet: 1) 1/400 story drift ratios under 50-year mean recurrence interval (MRI) wind blowing down the x or y directions; and 2) demand to capacity ratios of less than one for 1700-year MRI wind blowing down the x or y directions. The resulting member sizes are reported in Table 4.
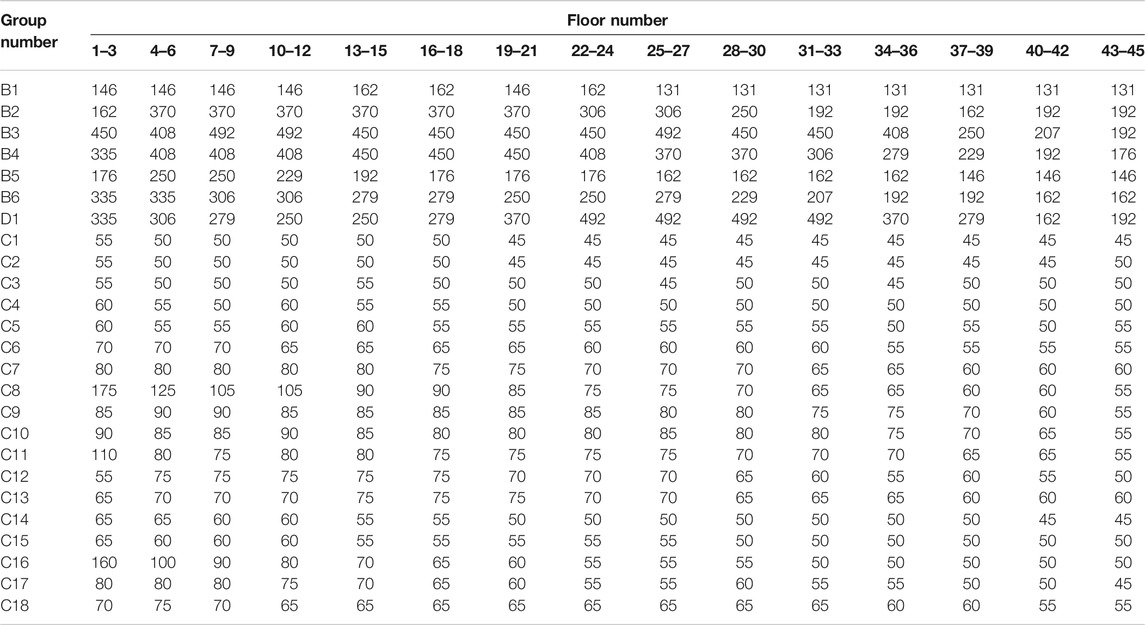
TABLE 4. Member sizes for the structural system. D1 indicates diagonals while W24 sections are identified through their weight per unit length using imperial units. Box sections are identified in terms of their mid-line width in cm.
Envelop System
Each glass panel was mounted 0.5 m from the upper floor and 1.5 m from the lower floor. The cladding system was considered not to provide lateral stiffness. The equivalent net pressure demand was defined as follows:
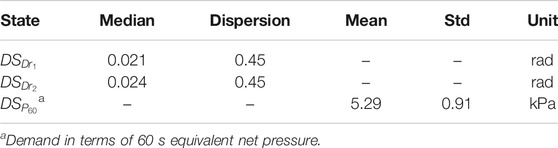
with teq = 60 s and s = 16. The damage state
Wind-Driven Rain Simulation
The normalized specific catch ratios necessary for calibrating the interpolation-based scheme of Section 4.2 were estimated in OpenFOAM 4.1. Three computational domains were considered for wind angles of αH = 0°, αH = 45°, and αH = 90°. Each domain extended, at full scale, 900 m upwind/laterally and 2,700 m downwind of the building. Each domain had a total of 139,500 rectangular elements in a structured mesh. Seventeen rain phases were considered with raindrop diameters ranging from 0.3 to 2.4 mm with a 0.3 mm increment and from 2.4 to 6 mm with an increment of 0.4 mm. Through symmetry, the simulation results were extended to wind directions of 135°, 180°, 225°, 270°, and 315°. Solutions were estimated for the wind speeds defining the boundaries of the nine conditional failure events used in deriving the hazard curve of Section 8.2.
Keywords: performance-based wind engineering, hurricanes, building envelopes, probabilistic damage and loss modeling, extreme winds
Citation: Ouyang Z and Spence SM (2021) A Performance-Based Wind Engineering Framework for Engineered Building Systems Subject to Hurricanes. Front. Built Environ. 7:720764. doi: 10.3389/fbuil.2021.720764
Received: 04 June 2021; Accepted: 30 September 2021;
Published: 24 November 2021.
Edited by:
Brian M Phillips, University of Florida, United StatesReviewed by:
Swamy Selvi Rajan, NeXHS Renewables Private Limited, IndiaJean-Paul Pinelli, Florida Institute of Technology, United States
Copyright © 2021 Ouyang and Spence. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Seymour M.J. Spence, c21qc0B1bWljaC5lZHU=
 Zhicheng Ouyang
Zhicheng Ouyang Seymour M.J. Spence
Seymour M.J. Spence