
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Built Environ., 03 May 2021
Sec. Earthquake Engineering
Volume 7 - 2021 | https://doi.org/10.3389/fbuil.2021.631360
This article is part of the Research TopicAdvances in Seismic Performance and Risk Estimation of Precast Concrete BuildingsView all 11 articles
Following the empirical observation of widespread collapses of cladding panel connections of precast industrial buildings under recent seismic events, new design solutions have been developed in the framework of the European project SAFECLADDING, including isostatic systems effectively decoupling the seismic response of frame structure and cladding panels. The present paper is aimed at evaluating the seismic response and vulnerability of precast frame structures employing pendulum, cantilever, and rocking cladding connection systems. Within the framework of the research project RINTC–Implicit seismic risk of code-conforming structures funded by the Italian Civil Protection Department within the ReLUIS program, the seismic performance of a typical precast industrial building has been assessed with a probabilistic approach based on the results of static and multi-stripe dynamic non-linear analyses. The seismic vulnerability assessment of each structural system has been carried out with reference to life safety and damage limit states considering three sites of increasing seismic hazard in Italy. The effect of distributed panel mass modeling vs. more common lumped mass modeling has been analyzed and critically commented based on the results of demand over capacity (D/C) ratios. Moreover, biaxial seismic D/C ratios have been evaluated for realistic strong hinge connections for cladding panels.
Since the end of World War II, precast buildings have been widely constructed in Europe and other world regions as industrial and commercial frame buildings and residential panel/block buildings. The typical modern industrial single-story precast frame structure consists of cantilever tall columns restrained at the base with pocket foundations and connected at the top to hinged prestressed beams supporting different typologies of prestressed roof elements. Vertical or horizontal precast concrete panels are connected to load bearing frame elements as perimeter cladding. The cladding-to-structure connections may play a crucial role under seismic action (Biondini et al., 2013). The traditional design approach for the precast structure is based on a bare frame model where peripheral cladding panels are considered as masses only, without any in-plane stiffening contribution. Panels have been often connected to the structure with fixed fastenings proportioned for out-of-plane horizontal actions related to the local mass of single panels, neglecting any in-plane possible interaction with the frame. Different earthquakes that recently occurred in Southern Europe have shown that this approach is not adequate. Frame structures properly designed and detailed for seismic actions performed satisfactorily (Biondini and Toniolo, 2009), while many cladding panels collapsed after failure of their connections (Toniolo and Colombo, 2012; Belleri et al., 2015a). Surveys from areas where the frame structures were not conceived for seismic strength (Belleri et al., 2015b, 2017), and did not perform satisfactorily, also reported extensive failures of cladding panels and their connections (Bournas et al., 2013; Magliulo et al., 2014; Savoia et al., 2017; Batalha et al., 2019). The SAFECLADDING project was funded by the European Commission to tackle this issue. The project analyzed innovative design solutions to improve the performance of both existing and new precast buildings. Three different cladding connection arrangements were investigated: Isostatic, Integrated, and Dissipative (Biondini et al., 2013; Dal Lago et al., 2018). The cladding solution analyzed in this project is made of external precast concrete panels connected with mechanical devices, which represent since many decades the standard solution for precast buildings. However, it is worth noting that this solution is not representative of the existing heritage of precast structures, since many of them are cladded with infill walls made of masonry or precast concrete stacked panels. In this case, the seismic behavior of the global structural assembly and of the local cladding wall is remarkably different from the case of external panels, with the stiffening effect and the strength being much larger, where the failure mode is usually related to the in-plane-out-of-plane interaction on the cladding wall rather than on its mechanical connections (Asteris et al., 2017; Pasca et al., 2017; Mazza, 2019; Di Domenico et al., 2021).
In this paper, Isostatic systems aimed at decoupling the motion of frame structure and external panels have been addressed. Three different connection arrangements for vertical cladding panels have been considered in the present study: (1) Pendulum, (2) Cantilever, and (3) Rocking. Details about each arrangement and numerical modeling strategies can be found in Dal Lago (2019). Each of these arrangements was previously subjected to seismic testing on full-scale prototype within the SAFECLADDING project (Negro and Lamperti Tornaghi, 2017; Toniolo and Dal Lago, 2017; Dal Lago and Molina, 2018). This paper is aimed at providing indications on the seismic behavior of precast industrial frame structures with Isostatic cladding connection arrangements based on probabilistic seismic vulnerability assessment. The work has been carried out in the framework of the Italian research project RINTC–Implicit seismic risk of code-conforming structures, as part of a wider project conducted by ReLUIS (Italian Laboratories University Network of Earthquake Engineering) and funded by the Italian Department of Civil Protection.
The considered case-study buildings consist of a reference geometry with Pendulum, Cantilever, and Rocking cladding-to-structure designed for soil type C for three sites in L'Aquila (AQ), Naples (Napoli, NA), and Milan (Milano, MI) with high to low hazard levels, respectively. The Cantilever solution has been investigated both including and neglecting the effect of friction induced by out-of-plane loading during the in-plane sliding of the connection. The considered case-study building reflects a common type of precast industrial buildings across Europe.
Figure 1A shows the 3D view of the frame structure without cladding panels (the same frame arrangement has been previously modeled by Magliulo et al., 2018). Figure 1B shows the structural cross section of the building and the schematic plan view of the considered building, with one 15-m-wide bay in the transversal direction (i.e., the X direction) and four 6-m-wide bays in the longitudinal direction (i.e., the Z-direction), the building being cladded by 2.2-m-wide and 6.85-m-tall vertical cladding panels with soft corners (Figure 1C).
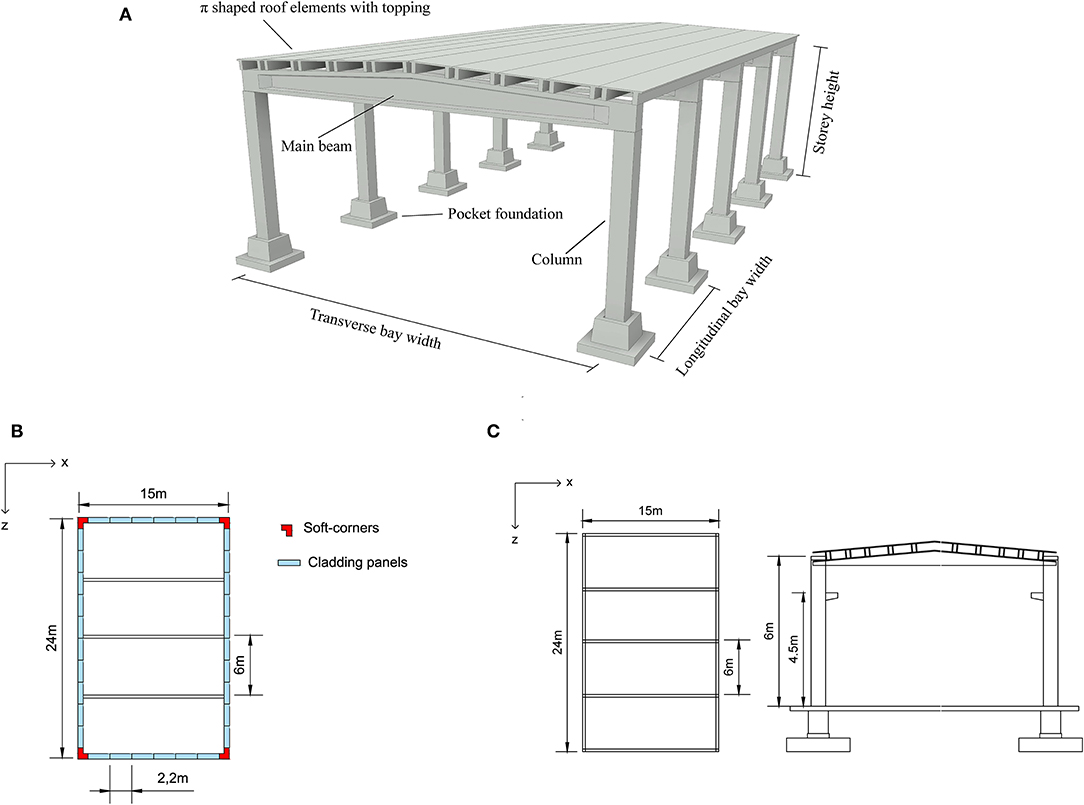
Figure 1. (A) 3D view of the frame structure without cladding panels, (B) plan view, and (C) transversal cross section of the building.
Each considered case-study building consists of squared section precast columns fixed at the base with isolated pocket foundations. The columns are connected by means of double dowels to the main precast prestressed beam having a variable depth cross section in the longitudinal direction, and by means of bolted connections to the girders having a rectangular cross section, in the longitudinal direction. The roof element consists of the double T section connected with each other through mechanical connections and topped with cast-in-situ reinforced concrete slab. The rigid diaphragm effect is hence considered for the case-study buildings, although the roof slab of precast industrial structures is often not topped, which would require its explicit modeling to account for the deformability of roof elements and their connections (Dal Lago et al., 2017, 2019; Dal Lago and Ferrara, 2018). The cladding system consists of vertical precast panels with specific weight of 4 kN/m2, connected to the roof peripheral beams via different connection arrangements (Pendulum, Cantilever, and Rocking system). The structural elements for the considered case studies are designed (Ercolino et al., 2018; Magliulo et al., 2018) according to the Italian building code NTC08 (MIT (Ministero delle Infrastrutture e dei Trasporti), 2008), which is very similar to Eurocode 8 (CEN, 2005) for soil type C for the three investigated sites. Dowel connections have been designed according to the Italian technical specifications CNR 10025/98 (2000), taken as typical reference for designers. More thorough information on structural details is available in Magliulo et al. (2018).
All the case studies have been modeled in OpenSees (Mazzoni et al., 2006) to perform non-linear static and multi-stripe dynamic analysis. Figure 2A shows the 3D view of the numerical model.
The columns are modeled with elastic elements characterized by lumped plasticity at the base. In the OpenSees software, the plastic hinge is implemented with a non-linear spring element characterized by the “Modified Ibarra–Medina–Krawinkler deterioration model with peak-oriented hysteretic response” whose behavior is described by a trilinear backbone curve, which accounts for history-dependent strength and stiffness deterioration based on energy dissipation (Ibarra et al., 2005).
The beams and girder elements are modeled with elastic elements as well; the main double-tapered beams are modeled with a simplified constant cross section, which is characterized by the mean values of site-dependent height and width of the cross sections. This simplification should not result in large modeling errors, since all the horizontal elements are not part of the lateral load-bearing system of the building assembly. The roof elements are not modeled, and rigid diaphragm constraint is applied at the roof level in correspondence to the location of the mean center of gravity of the beams.
The connections between beams and columns are perfectly hinged due to bolted connections. The top column joint, where main and peripheral beams are converging, is modeled such that the main beam can rotate in the transversal plane at its base with respect to the column (Figure 2B). As a result, the building is slightly more flexible in the direction of the peripheral beams (z-axis). The geometrical eccentricities (Figures 2C,D) of structural elements have been modeled by rigid elements based on the model developed by Ercolino et al. (2018).
The isostatic cladding-to-structure connections (Pendulum, Cantilever, and Rocking) are modeled with following strategies for three considered sites (L'Aquila, Napoli, and Milano).
Concerning the pendulum arrangement, the total mass of structural elements as well as panels is lumped to the master node at the center of the roof, where the identification number 1111 in Figure 3 represents the master node. The lumped masses assigned to the master node were 404.27 tons for both Milano and Napoli buildings, and 408.67 for L'Aquila building. This assumption of null in-plane neither out-of-plane stiffening contribution reflects the kinematics of truss-like panels hinged at both base and top beam. The mass associated to the frame structure was set to 258.29 tons for both Milano and Napoli buildings, and to 262.68 tons for L'Aquila building. The masses associated to the cladding panels in X and Z directions, respectively, were set to 89.83 tons and 56.15 tons for all buildings.
In the cantilever arrangement, relative horizontal in-plane sliding occurs between the structure and the cladding panel under seismic action, with panels not moving in-plane and rigidly tilting in the out-of-plane direction. Thus, the connector is subjected to multiaxial actions, and horizontal sliding may be hampered by friction (Figure 4A). The cantilever arrangement has been modeled with two different strategies, either considering or neglecting the friction forces in the cladding-to-structure connections.
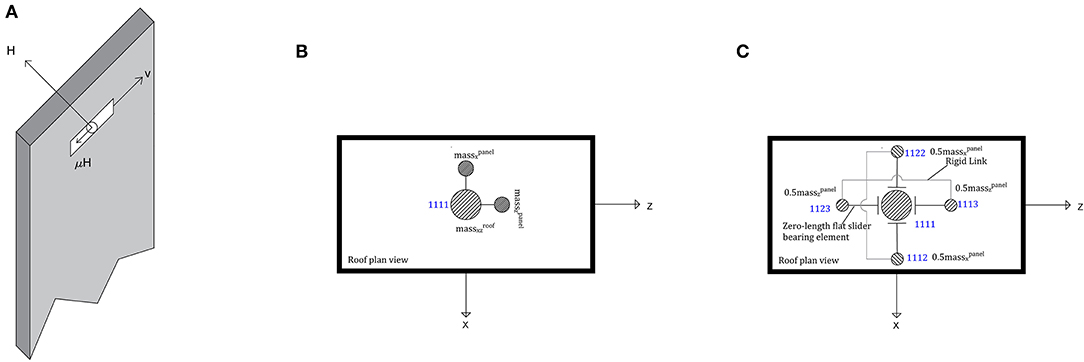
Figure 4. (A) Schematic friction mechanism occurring in the cantilever panels when subjected to multi-axial seismic excitation. (B) Cantilever model without friction forces. (C) Cantilever model with friction forces.
The cantilever model without friction has been developed by modifying the lumped masses at the master node. As shown in Figure 4B, two different masses in both directions have been assigned, i.e., in the X direction, the total assigned mass is massxz,roof + massx,panel and in the Z direction massxz,roof + massz,panel.
The cantilever model accounting for friction effects has been modified as illustrated in Figure 4C. The lumped mass in the master node is referred to the frame structure in both directions, while the mass of the panels has been assigned to two independent nodes in each horizontal direction. To model the friction between the frame structure and panels, the axially rigid zero-length “flat slider bearing” element has been used in OpenSees. In order to account for such effect, a constant dynamic friction coefficient equal to 0.22 has been set in the model based on the test results obtained by Dal Lago and Lamperti Tornaghi (2018) on a cladding-to-structure sliding connection subjected to multi-axial loading.
In the rocking arrangement, the panels brace the structure up to a lateral load associated with the scenario in which the overturning moment overcomes the stabilizing one provided by the panel self-weight (Figure 5A). After this phenomenon occurs, the panels rigidly rotate providing a restoring force that is slightly decreasing with the displacement due to second-order effects associated with the reduction of the lever arm from the center of mass of the panel to the rotation center located at one of its corners (Figure 5B). The lumped mass in the master node is the same as the pendulum case, and the building model has been modified as described in Figure 5C.

Figure 5. Rocking panel: (A) geometry and loads, (B) non-linear force–displacement relationship, and (C) schematic view of the numerical model assumptions for the Rocking arrangement.
Two fixed non-linear springs representing the mechanical behavior of the panels (Figure 5B) are linked to the master node. Due to progressive contact of the vertical sliders with the channel lips after random tolerance positioning, an initial tolerance gap δtol = 2 mm is considered in the model covered by a linear branch, which is calibrated following experimental observations reported in Toniolo and Dal Lago (2017), Negro and Lamperti Tornaghi (2017). The shear stiffness of the springs is null. Friction may provide additional actions under seismic motion, but it has been disregarded, supposedly being much less than the restoring force of the panel.
Finally, it is to be remarked that the strongly non-linear idealized behavior of Figure 5B is not associated with any dissipation of energy, being the multilinear hysteresis completely elastic.
Non-linear static analyses are performed in both of the horizontal X and Z directions for all considered case studies, i.e., three isostatic panel arrangements at each investigated site. Figure 6 shows the pushover curves for all case studies.
For the examined structural typology, pushover curves depend on the mechanical behavior of frame columns under lateral loading conditions. Consequently, when cross-section design and construction detailing of columns depend on non-seismic actions (e.g., wind forces) and code minimum requirements, pushover curves and roof lateral displacement capacities may match for different case studies, even if they are characterized by different seismic hazard levels.
The pushover curves for each structural typology shown in Figure 6 are adopted to define the structural capacity threshold for the collapse limit state, to be presented in the following section.
The limit states are defined according to performance-based design criteria and refer to specific Engineering Demand Parameters (EDPs) of seismic performance, related to global and/or local seismic response of the structural and non-structural elements. Therefore, appropriate EDPs are selected to describe the structural demand and compared with threshold values representative of the structural capacity for specific limit states. Demand-over-Capacity (D/C) ratios have been evaluated with respect to the Damage Limit States (DLSs) and Collapse Limit States (CLSs) to carry out seismic response and vulnerability assessment.
This limit state corresponds to the failure of structural elements, which corresponds to the failure of the structure. Two limits state have been considered as CLS: Global Failure Limit State (GFLS) and Local Failure Limit State (LFLS).
The engineering demand parameter for GFLS representing the global failure of the structure in terms of lateral load resisting behavior is the maximum roof displacement. The corresponding top displacement capacity is evaluated via non-linear pushover analyses (Figure 6). The EDP threshold is identified along the softening branch of the pushover curve as the post-peak displacement corresponding to a 50% reduction in base shear, in accordance with the general RiNTC project criteria (Iervolino et al., 2018). Table 1 shows the displacement capacity threshold for all considered cases.
LFLS is defined by the shear failure of the beam-column dowel connection. The shear strength of the dowel connection has been evaluated with a more recent formulation, outcome of a large experimental program carried out in the framework of the Safecast project, as the minimum of those actions associated with ductile failure of the dowel bars and crushing of surrounding concrete (EUR 27935 EN, 2016). The steel failure resulted critical for the considered joints, where the dowel strength has been computed on the safe side assuming the unconfined concrete strength. The shear strength values of the connections of the different buildings considered are 79.5 kN, 153.4 kN, and 232.0 kN for Milano, Napoli, and L'Aquila, respectively. Details on this calculation and on comparisons with formulas provided by other authors, including Vintzeleou and Tassios (1987) and Zoubek et al. (2015), are available in Cimmino et al. (2020).
This limit state corresponds to damage prevention of the non-structural elements, i.e., cladding panels. DLS is relevant in terms of the economic losses, and it causes building use interruption for the repair. Two limit states have been considered as DLS, namely, Standard Damage Limit State (SDLS) and Panel Failure Limit State (PFLS).
The adopted EDP for SDLS is the roof displacement, and the capacity threshold value is set to 1% of inter-story drift in accordance with the provisions of NTC2008 and Eurocode 8. It is to be noted that past studies carried out by Babič and Dolšek (2016) show that at roof displacement of 1% of column height, 50% of traditional panel-to-structure connections fail. These results have been obtained on traditional connections which are characterized by a small displacement capacity (Zoubek et al., 2016), which is however not depending on the height of the building. The limit of 1% of column height to attain DLS is practically too tolerant for traditional cladding connections, and too strict for the innovative panel connections considered in this work, since the latter can easily accommodate much larger displacements.
Despite being a potential source of casualties, the collapse of the cladding panels associated with the failure of their connections with the structure is herein framed as an intermediate damage condition in accordance with the general RiNTC project criteria (Iervolino et al., 2018), since this event does not lead to global failure or jeopardy of the global structural system. The functional limit displacement for each panel arrangement depends on their aspect ratio and has been set to 250 mm for all arrangements, based on attainment of collision for pendulum and rocking arrangements and on the exhaustion of the slider stroke for cantilever arrangement.
The time-history response of the case study buildings depends on the intensity measure of the seismic event, e.g., peak ground acceleration PGA or spectral acceleration at first natural period Sa(T1). Seismic assessment has been carried out by means of multi-stripe analyses (Jalayer and Cornell, 2003; Jalayer, 2013) at 10 intensity levels associated with the return periods collected in Cimmino et al. (2020) for subsoil type C (not reported here for the sake of brevity). A set of 20 records is selected at each intensity level for the three sites. The ground motion records have been selected based on the conditional mean spectrum approach selecting as reference intensity measure the spectral acceleration at period of 2.0 s (Shome and Cornell, 1999; Jayaram et al., 2011; Lin et al., 2013).
Figure 7 shows the comparison of displacement time-history for the investigated panel arrangements under one of the selected ground motions at the L'Aquila site. The maximum top displacement has been reduced in the rocking system due to the restoring forces provided by the self-weight of the cladding panels. Residual drift after the earthquake is almost zero. The response of the simplified cantilever shows a similar trend to the pendulum system in terms of maximum top displacement and shear. The addition of the friction forces does not introduce a relevant difference in this case either.
The mean values of the D/C ratio for CLS are similar among the investigated panel arrangements. For the sake of brevity, only the D/C curves related to the pendulum arrangement are reported in Figure 8. Circle markers are associated with global collapse condition, while square markers refer to local collapse conditions. Structures designed according to different hazard levels are differentiated by the markers' color: Milano in red, Napoli in blue, and L'Aquila in black. The D/C ratios in terms of the shear force in the beam-to-column connections associated with LFLS are always larger than those in terms of the roof displacements associated with GFLS. Only in the case of the L'Aquila site has attainment of the failure limit reached the largest considered return period of 100,000 years, whereas it is never attained in the case of Milano and Napoli. This indicates that the seismic vulnerability to the seismic action of the panel arrangements is significantly lower than the one assumed for design with a reference return period of TR = 475 years. Therefore, this shows that the Italian building code, which follows the approach of Eurocode 8, overestimates the necessary capacity requirements for these case studies. With reference to another ultimate limit state according to the Italian building code which is the “near collapse limit state” (i.e., SLC) associated with a return period of 975 years, the D/C ratio is still significantly lower than 1. It is important to note that the mean D/C ratios increase with the hazard level at each site, showing that the code provisions do not guarantee uniform average safety with respect to the collapse limit state.
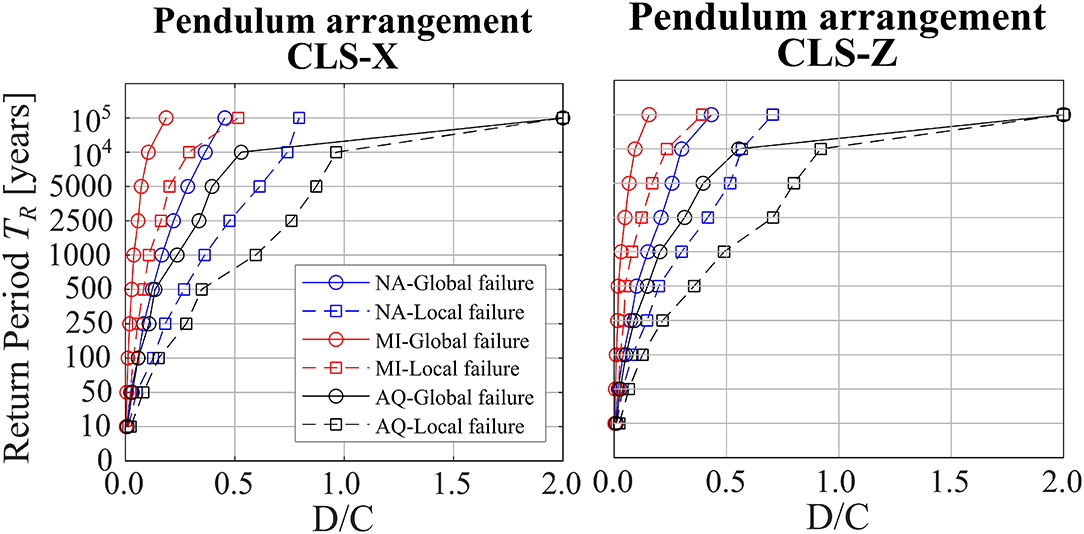
Figure 8. The mean value of D/C ratio with reference to Collapse Limit State for all considered panel arrangement at three considered sites.
Concerning DLS, Figure 9 shows the comparison of the mean value of the D/C ratio for both Damage limit states with a marker layout similar to the one proposed in Figure 8. In general, the D/C ratios for DLS are much larger than those at CLS, mainly due to the intrinsic flexibility of precast industrial frames composed by cantilever columns only acting as a lateral load-resisting system.
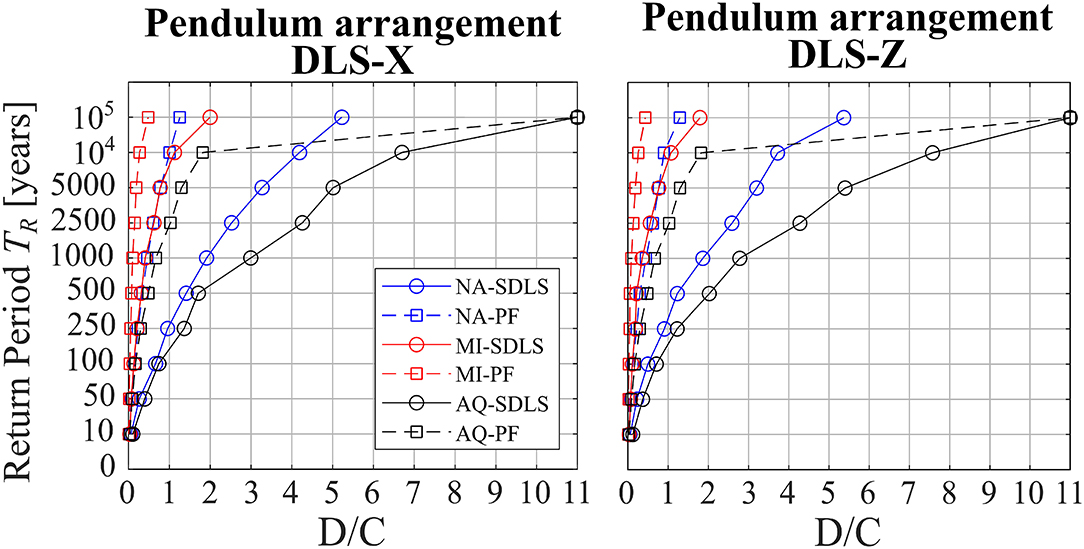
Figure 9. The mean value of D/C ratio with reference to Damage Limit State for all considered panel arrangement at three considered sites.
According to the Italian build code, design at DLS is referred to a return period of the TR = 50 year. In L'Aquila (high hazard) and Napoli (medium hazard), the mean Standard DLS is attained at a return period of 250 years. As mentioned in the previous section, the standard limit associated with SDLS is severe for the panel arrangements designed with modern connections, as they could easily accommodate small displacements without failure. The second considered damage limit state, the mean Panel DLS is attained at TR = 2500 year in the case of L'Aquila, TR = 10,000 years in Napoli, and never attained in Milano. As in the case of the Collapse limit state, the D/C ratio increases as the hazard level increases for the same return period. The results conclude that the above-cited codes do not guarantee a uniform distance from the attainment of a damage limit state when varying the seismic hazard. The results of the “Panel Failure limit state” show the effectiveness of the considered panel arrangements.
Even though the mean value of the Demand/Capacity ratio looks similar for different panel arrangements, the maximum response of each panel arrangement differs from each other. Figure 10 shows the ratio of the maximum value of EDPs at each intensity level of cantilever with friction/cantilever without the friction/Rocking system to that of the Pendulum system.

Figure 10. Performance ratio of the other panel connection systems over the pendulum system: (A) displacement and (B) local shear.
Figure 10 shows the relevant reduction of the displacement and the shear forces in the rocking system due to the restoring forces which added non-linear elastic hysteresis. This effect is more evident in a weaker frame of a low seismic hazard site, e.g., Milano. The response of the cantilever system is similar to that of the pendulum system.
Upgraded models have been set to investigate the influence of the simplifying assumption of lumped panel mass instead of a more realistic distribution of masses. To this aim, only the pendulum arrangement has been considered. The numerical model has been modified model as described in Figure 11, removing the amount of lumped mass associated with the cladding panels from the master node of the roof and implementing two vertical beam elements collecting the spread mass and stiffness of the full lines of panels. The stiffness of a single panel has been modeled which has been assimilated to the one of a 12-cm-thick solid concrete panel, equivalent of typical sandwich panels with the outer suspended layer. The elastic beam elements have been restrained at their base with a flexural hinge with prevented torsion. The element is linked to the master node at its height, enforcing a portion of the panel to behave as a cantilever beyond such location.
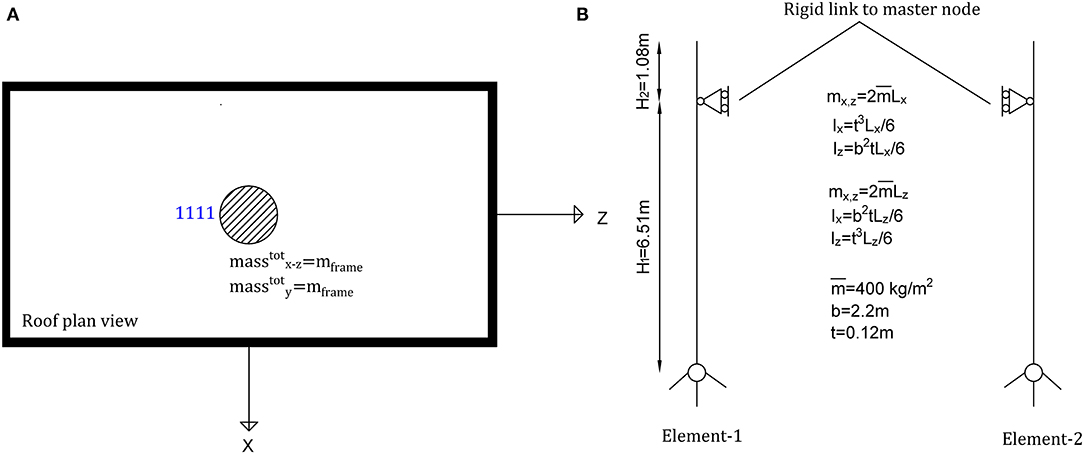
Figure 11. Details of mass modeling: (A) lumped frame mass, (B) spread mass over elastic beam elements.
In such a model, the single element tilts during the seismic motion in both horizontal directions. Nonetheless, their rotational inertia is taken into consideration with this modeling technique, while it has been disregarded with the simplified assumptions of lumped mass. The theoretical values of the natural periods associated with the main vibration modes in each translational direction are reported in Table 2 and have been computed according to Foti et al. (2018). The results of the numerical model confirm with remarkable precision the theoretical values (Table 2), with differences originating only from numerical rounding. A comparison with the periods from the models with lumped mass is also provided in Table 2. The results show that the more realistic spread mass distribution leads to a decrease of the fundamental periods of the order of 6–10%.

Table 2. Fundamental periods calculated in each main direction: comparison with model results for both spread and lumped panel mass assumptions.
The full set of non-linear dynamic analyses previously carried out on the lumped mass model has been repeated with the spread mass model. Figure 12 represents the statistical description of the ratio between maximum measured displacements (i.e., EDP for GFLS and SDLS) for spread mass models vs. lumped mass models. Sample mean values and standard deviations for such ratios are obtained for each stripe based on the time-history analyses of the 20 ground motions. A large dispersion of ratios can be observed, meaning that the dynamic behavior is remarkably modified by the panel mass modeling technique. Furthermore, the mean ratios highlight an increase of about 10% of the maximum displacements, quantifying the error on the unsafe side made when adopting the simplified assumption of lumped mass distribution.
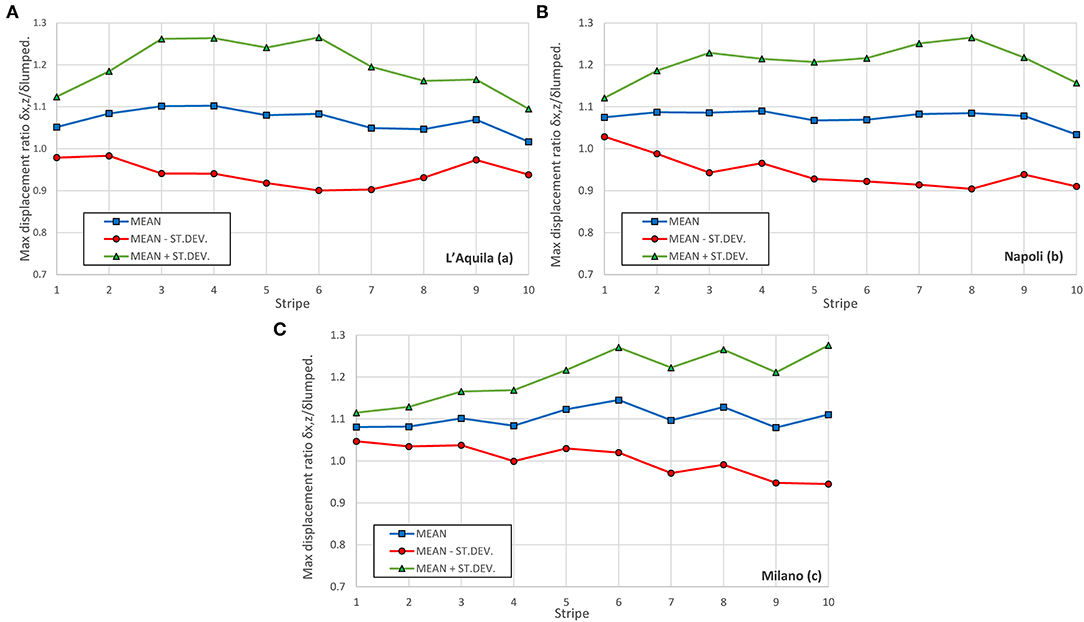
Figure 12. Maximum displacement ratio of results from model with spread panel mass and lumped panel mass for the site: (A) Milano, (B) Napoli, and (C) L'Aquila.
Within the spread mass model, the in-plane and out-of-plane forces in the panel connections have been recorded as the concentrated horizontal shear actions on the beam elements simulating the panels in correspondence of the link with the roof master node. Considering the shear key connector successfully used in the experimentation related to both pendulum and rocking systems in the Safecladding test program (Negro and Lamperti Tornaghi, 2017; Toniolo and Dal Lago, 2017; Dal Lago and Molina, 2018), whose structural behavior under simple shear and combined shear-axial forces is described in Figure 13, the D/C ratios and failure rates could be evaluated. The results, collected in Figure 14, show peculiarly low D/C ratios apart from the higher stripes of the L'Aquila site. This is attributable not only to the large strength of the device but also to the low accelerations transmitted by the more flexible frame structures designed at Milano and Napoli sites.
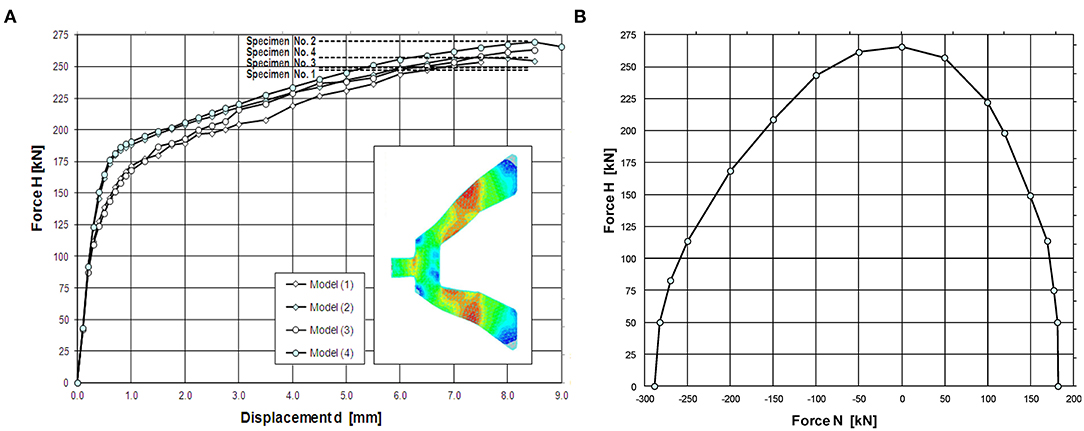
Figure 13. Cladding shear key connection considered: (A) numerical shear pushover curves vs. experimental strength and (B) shear-axial interaction domain.
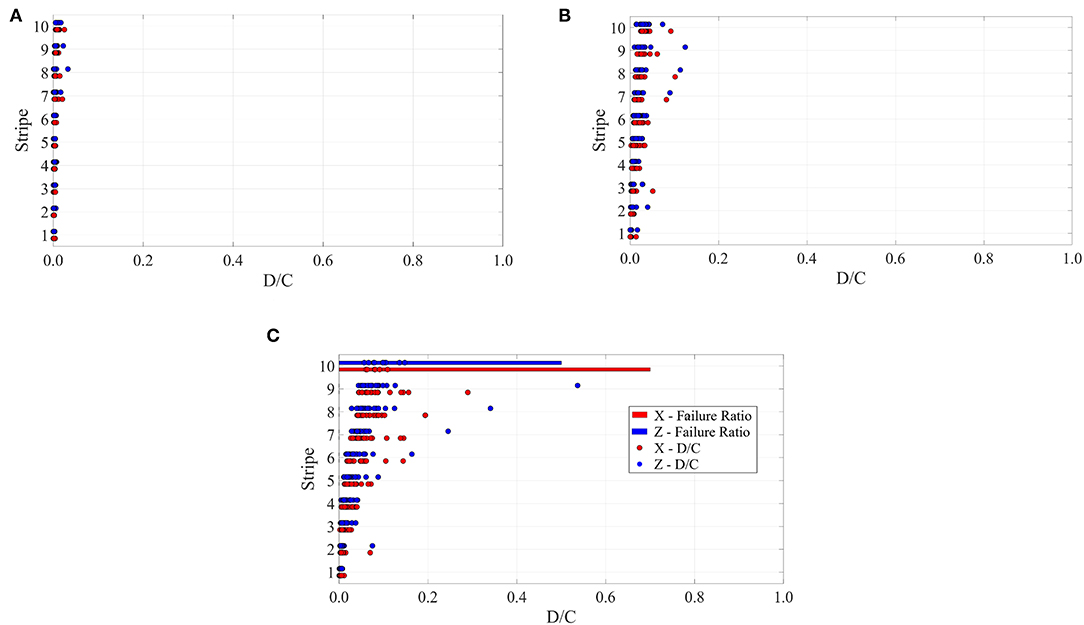
Figure 14. Cladding connection D/C and failure ratios for the site of: (A) Milano, (B) Napoli, and (C) L'Aquila.
The D/C ratio curves obtained in this work indicate a low vulnerability of well-detailed modern precast industrial frame structures provided with decoupling cladding connections, with combined global/local collapses recorded only for the higher return period of 105 years in the site of high seismic hazard of L'Aquila. The seismic behavior of this structural typology is characterized by large deformability and displacement capacity, with the global collapse condition being associated with the leaning of the structure due to second-order effect. However, this behavior makes the structural assembly less performant toward the damage limit state, since the standard damage limitation conditions are overcome with high probability for large return periods in all the considered sites.
The adoption of innovative cladding connections leading to an effective decoupling of the frame structure motion from the lateral stiffness of the cladding panels of precast industrial buildings leads to relevant enhancement in their seismic behavior, with displacement being associated with the failure of these connections about one order of magnitude larger than that associated with more traditional fixed channel connections. The performance in the damage limit state appears to be much better if adopting specific engineering demand parameters related to the failure of the cladding panel connections considered, for instance the no-collision condition for tilting panels (pendulum and rocking arrangements) or the exhaustion of the available stroke for sliding connections typical of the cantilever arrangement.
The rocking arrangement provides the lower maximum drifts, due to the recentering effect provided by the self-weight of the cladding panels, which is more pronounced for weaker frame structures, hence for low seismic hazard areas. The adoption of the common assumption of lumped mass of the cladding panels in the centroid of the roof involving a percentage of the total panel mass related to its tributary area proved not to be fully on the safe side, since the comparison with new models involving a spread panel mass shows that the lumped models provide higher fundamental periods (associated in general with lower accelerations) and systematically lower seismic displacements, with around 10% being the increase in displacement demand when considering spread cladding mass. Moreover, spreading the mass by introducing the panel rotational inertia severely affects the dynamic behavior of the structural system. The maximum loads on one real typology of strong hinged panel-to-structure connection considered are fully compatible with the device strength for all intensity measure levels for the sites of Milano (low hazard) and Napoli (medium hazard), while the demand overcomes the capacity only in the higher-intensity measure level for the site of L'Aquila (high hazard).
The D/C curves computed are more severe for sites with a higher seismic hazard. This result highlights that the current code provisions for the Italian territory do not ensure uniform safety with respect to both collapse and damage limit states as the seismic hazard varies, the safety margin lowering with the hazard. Ongoing developments are concerning the vulnerability analysis of both new and existing buildings with flexible diaphragm and with sophisticated constitutive laws for the existing roof slab and cladding panel connections, also considering the effect of the vertical acceleration. Further developments should also aim to address the seismic risk of structures and systems of structures with a probabilistic life-cycle perspective based on probabilistic frameworks involving performance metrics such as resilience (Capacci and Biondini, 2020; Capacci et al., 2020) as well as economic user cost indicators (Messore et al., 2020).
The raw data supporting the conclusions of this article will be made available by the authors upon request.
KG developed the numerical model, arranged the pre-processing, and carried out post-processing of the results. BDL provided guidance for the underlying modeling assumptions of the considered precast structures and drafted the paper. LC provided guidance for the implementation of the structural model and the development of the multi-stripe seismic risk analyses. FB supervised and coordinated the activities. All authors contributed to the article and approved the submitted version.
This research study was funded by the Italian Department of Civil Protection within the framework of the national project DPC/ReLUIS 2019-2021.
BDL is partner—and KG is collaborator—of DLC Consulting srl of Milan, Italy, a Structural Engineering consultant company active in different fields, among which precast concrete structures. The consultant holds several patents, including some concerning cladding panel connections which may be employed to make some of the arrangements investigated in the paper.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The other members of the working group on precast concrete buildings within the project DPC/ReLUIS 2019-2021, including Andrea Belleri, Davide Bellotti, Gennaro Magliulo, Roberto Nascimbene, and Paolo Riva, are gratefully acknowledged for their cooperation.
Asteris, P. G., Cavaleri, L., Di Trapani, F., and Tsaris, A. K. (2017). Numerical modelling of out-of-plane response of infilled frames: state of the art and future challenges for the equivalent strut macromodels. Eng. Struct. 132, 110–122. doi: 10.1016/j.engstruct.2016.10.012
Babič, A., and Dolšek, M. (2016). Seismic fragility functions of industrial precast building classes. Eng. Struct. 118, 357–370. doi: 10.1016/j.engstruct.2016.03.069
Batalha, N., Rodrigues, H., and Varum, H. (2019). Seismic performance of RC precast industrial buildings—learning with the past earthquakes. Inn. Infrastruct. Solut. 4:4. doi: 10.1007/s41062-018-0191-y
Belleri, A., Brunesi, E., Nascimbene, R., Pagani, M., and Riva, P. (2015a). Seismic performance of precast industrial facilities following major earthquakes in the italian territory. ASCE J. Perf. Constr. Fac. 29:04014135. doi: 10.1061/(ASCE)CF.1943-5509.0000617
Belleri, A., Labò, S., Marini, A., and Riva, P. (2017). The influence of overhead cranes in the seismic performance of industrial buildings. Front. Built Environ. 3:64. doi: 10.3389/fbuil.2017.00064
Belleri, A., Torquati, M., Riva, P., and Nascimbene, R. (2015b). Vulnerability assessment and retrofit solutions of precast industrial structures. Earthq. Struct. 8, 801–820. doi: 10.12989/eas.2015.8.3.801
Biondini, F., Dal Lago, B., and Toniolo, G. (2013). Role of wall panel connections on the seismic performance of precast structures. Bull. Earthq. Eng. 11, 1061–1081. doi: 10.1007/s10518-012-9418-z
Biondini, F., and Toniolo, G. (2009). Probabilistic calibration and experimental validation of the seismic design criteria for one-story concrete frames. J. Earthq. Eng. 13, 426–462. doi: 10.1080/13632460802598610
Bournas, D., Negro, P., and Taucer, F. (2013). Performance of industrial buildings during the Emilia earthquakes in Northern Italy and recommendations for their strengthening. Bull. Earthq. Eng. 12, 2383–2404. doi: 10.1007/s10518-013-9466-z
Capacci, L., and Biondini, F. (2020). Probabilistic life-cycle seismic resilience assessment of aging bridge networks considering infrastructure upgrading. Struct. Infrastruct. Eng. 16, 659–675. doi: 10.1080/15732479.2020.1716258
Capacci, L., Biondini, F., and Titi, A. (2020). Lifetime seismic resilience of aging bridges and road networks. Struct. Infrastruct. Eng. 16, 266–286. doi: 10.1080/15732479.2019.1653937
CEN, (2005). Eurocode 8: Design of Structures for Earthquake Resistance-Part 1: General Rules, Seismic Actions and Rules for Buildings. Dublin: National Standards Authority of Ireland.
Cimmino, M., Magliulo, G., and Manfredi, G. (2020). Seismic collapse assessment of new European single-story RC precast buildings with weak connections. Bull. Earthq. Eng. 18, 6661–6686. doi: 10.1007/s10518-020-00952-7
CNR 10025/98 (2000). Istruzioni per il progetto, l'esecuzione ed il controllo delle strutture prefabbricate in calcestruzzo: CNR 10025/98(in Italian). Roma : Consiglio nazionale delle ricerche.
Dal Lago, B. (2019). Numerical simulation of seismic tests on precast concrete structures with various arrangements of cladding panels. Comput. Concr. 23, 81–95. doi: 10.12989/cac.2019.23.2.081
Dal Lago, B., Bianchi, S., and Biondini, F. (2019). Diaphragm effectiveness of precast concrete structures with cladding panels under seismic action. Bull. Earthq. Eng. 17, 473–495. doi: 10.1007/s10518-018-0452-3
Dal Lago, B., Biondini, F., and Toniolo, G. (2018). Seismic performance of precast concrete structures with energy dissipating cladding panel connection systems. Struct. Concr. 19, 1908–1926. doi: 10.1002/suco.201700233
Dal Lago, B., and Ferrara, L. (2018). Efficacy of roof-to-beam mechanical connections on the diaphragm behaviour of precast decks with spaced roof elements. Eng. Struct. 176, 681–696. doi: 10.1016/j.engstruct.2018.09.027
Dal Lago, B., and Lamperti Tornaghi, M. (2018). Sliding channel cladding connections for precast structures subjected to earthquake action. Bull. Earthq. Eng. 16, 5621–5646. doi: 10.1007/s10518-018-0410-0
Dal Lago, B., and Molina, F. J. (2018). Assessment of a capacity spectrum design approach against cyclic and seismic experiments on full-scale precast RC structures. Earthq. Eng. Struct. Dyn. 47, 1591–1609. doi: 10.1002/eqe.3030
Dal Lago, B., Toniolo, G., Felicetti, R., and Lamperti Tornaghi, M. (2017). End support connection of precast roof elements by bolted steel angles. Struct. Concr. 18, 755–767. doi: 10.1002/suco.201600218
Di Domenico, M., De Risi, M. T., Ricci, P., Verderame, G. M., and Manfredi, G. (2021). Empirical prediction of the in-plane/out-of-plane interaction effects in clay brick unreinforced masonry infill walls. Eng. Struct. 227:111438. doi: 10.1016/j.engstruct.2020.111438
Ercolino, M., Bellotti, D., Magliulo, G., and Nascimbene, R. (2018). Vulnerability analysis of industrial RC precast buildings designed according to modern seismic codes. Eng. Struct. 158, 67–78. doi: 10.1016/j.engstruct.2017.12.005
EUR 27935 EN (2016). “Design guidelines for wall panel connections,” in SAFECLADDING (Grant agreement n° 314122. Year 2012), eds A. Colombo, P. Negro, G. Toniolo, and M. Lamperti Tornaghi (Luxembourg: Publications Office of the European Union), 1–150.
Foti, F., Dal Lago, B., and Martinelli, L. (2018). “Sull'interazione sismica fuori piano tra telai prefabbricati e pannelli di tamponamento/on the seismic out-of-plane interaction between precast frames structures and cladding panels,” in Italian Concrete Days 2018 (ICD2018), Milano/Lecco, Italy, 15th-18th June, Paper No. 42 (Milano/Lecco).
Ibarra, L. F., Medina, R. A., and Krawinkler, H. (2005). Hysteretic models that incorporate strength and stiffness deterioration. Earthq. Eng. Struct. Dyn. 34, 1489–1511. doi: 10.1002/eqe.495
Iervolino, I., Spillatura, A., and Bazzurro, P. (2018). Seismic reliability of code-conforming Italian buildings. J. Earthq. Eng. 22, 5–27. doi: 10.1080/13632469.2018.1540372
Jalayer, F. (2013). Direct probabilistic seismic analysis: implementing non-linear dynamic assessments (Ph.D. thesis dissertation). Stanford University, Stanford, CA, United States.
Jalayer, F., and Cornell, C. A. (2003). A special application of non-linear dynamic analysis procedures in probability-based seismic assessments in the region of global dynamic instability. Appl. Stat. Probab. Civ. Eng. 1–2.
Jayaram, N., Lin, T., and Baker, J. W. (2011). A computationally efficient ground-motion selection algorithm for matching a target response spectrum mean and variance. Earthq. Spectra 27, 797–815. doi: 10.1193/1.3608002
Lin, T., Haselton, C. B., and Baker, J. W. (2013). Conditional spectrum-based ground motion selection. Part I: hazard consistency for risk-based assessments. Earthq. Eng. Struct. Dyn. 42, 1847–1865. doi: 10.1002/eqe.2301
Magliulo, G., Bellotti, D., Cimmino, M., and Nascimbene, R. (2018). Modeling and seismic response analysis of RC precast Italian code-conforming buildings. J. Earthq. Eng. 22, 140–167. doi: 10.1080/13632469.2018.1531093
Magliulo, G., Ercolino, M., Petrone, C., Coppola, O., and Manfredi, G. (2014). Emilia earthquake: the sesmic performance of precast RC buildings. Earthq. Spectra 30, 891–912. doi: 10.1193/091012EQS285M
Mazza, F. (2019). In-plane-out-of-plane non-linear model of masonry infills in the seismic analysis of r.c.-framed buildings. Earthq. Eng. Struct. Dyn. 48, 432–453. doi: 10.1002/eqe.3143
Mazzoni, S., McKenna, F., Scott, M. H., and Fenves, G. L. (2006). Open System for Earthquake Engineering Simulation (OpenSEES) User Command-Language Manual. Pacific Earthq. Eng. Res. Cent. 465.
Messore, M. M., Capacci, L., and Biondini, F. (2020). Life-cycle cost-based risk assessment of aging bridge networks. Struct. Infrastruct. Eng. 17, 515–533. doi: 10.1080/15732479.2020.1845752
MIT (Ministero delle Infrastrutture e dei Trasporti) (2008). D.M. 14/01/2008–Norme Tecniche per le Costruzioni. Rome: MIT.
Negro, P., and Lamperti Tornaghi, M. (2017). Seismic response of precast structures with vertical cladding panels: the SAFECLADDING experimental campaign. Eng. Struct. 132, 205–228. doi: 10.1016/j.engstruct.2016.11.020
Pasca, M., Liberatore, L., and Masiani, R. (2017). Reliability of analytical models for the prediction of out-of-plane capacity of masonry infills. Struct. Eng. Mech. 64, 765–781. doi: 10.12989/sem.2017.64.6.765
Savoia, M., Buratti, N., and Vincenzi, L. (2017). Damage and collapses in industrial precast buildings after the 2012 Emilia earthquake. Eng. Struct. 137, 162–180. doi: 10.1016/j.engstruct.2017.01.059
Shome, N., and Cornell, C. A. (1999). Probabilistic Seismic Demand Analysis of Non-linear Structures. Technical Report. Stanford University.
Toniolo, G., and Colombo, A. (2012). Precast concrete structures: the lessons learned from the L'Aquila earthquake. Struct. Concr. 13, 73–83. doi: 10.1002/suco.201100052
Toniolo, G., and Dal Lago, B. (2017). Conceptual design and full-scale experimentation of cladding panel connection systems of precast buildings. Earthq. Eng. Struct. Dyn. 46, 2565–2586. doi: 10.1002/eqe.2918
Vintzeleou, E. N., and Tassios, T. P. (1987). Behavior of dowels under cyclic deformations. ACI Struct. J. 84, 18–30. doi: 10.14359/2749
Zoubek, B., Fischinger, M., and Isaković, T. (2015). Estimation of the cyclic capacity of beam-to-column dowel connections in precast industrial buildings. Bull. Earthq. Eng. 13, 2145–2168. doi: 10.1007/s10518-014-9711-0
Keywords: seismic vulnerability, precast structures, industrial buildings, probabilistic assessment, panel connection systems, multi-stripe analysis, pushover analysis
Citation: Gajera K, Dal Lago B, Capacci L and Biondini F (2021) Multi-Stripe Seismic Assessment of Precast Industrial Buildings With Cladding Panels. Front. Built Environ. 7:631360. doi: 10.3389/fbuil.2021.631360
Received: 19 November 2020; Accepted: 22 February 2021;
Published: 03 May 2021.
Edited by:
Massimo Latour, University of Salerno, ItalyReviewed by:
Saverio Spadea, University of Dundee, United KingdomCopyright © 2021 Gajera, Dal Lago, Capacci and Biondini. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bruno Dal Lago, YnJ1bm8uZGFsbGFnb0B1bmluc3VicmlhLml0
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.