
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Built Environ., 12 February 2021
Sec. Earthquake Engineering
Volume 7 - 2021 | https://doi.org/10.3389/fbuil.2021.627546
This article is part of the Research TopicAdvances in Seismic Performance and Risk Estimation of Precast Concrete BuildingsView all 11 articles
As widely known, connections performance under seismic loads can significantly affect the structural response of RC precast buildings. Within the scientific community, an increasing number of studies has been carried out on this topic, in the light of the recent earthquake aftermaths all over Europe. Indeed, connections turned out to be the weakest part of the precast structures and their failure often provoked the global collapse of the whole building. The present study aims at assessing the seismic behavior of a single-story RC precast building in terms of global collapse implementing two different models of the beam-to-column connection, a simplified and a refined one. A lumped plasticity approach is used to simulate the structural nonlinear behavior at the column base. In order to assess the refined connection model, a preliminary scheme with an isolated single dowel is validated by comparing the pushover outcomes with experimental results from literature. Nonlinear static and dynamic analyses are performed on two models of a 3D single-story RC precast building, one implementing the simple beam-to-column connection model and the other one implementing the refined mode. The comparison clearly shows that the differences are negligible if the global collapse limit state is considered.
Recent earthquakes in Europe stressed the importance of adequate seismic design as well as vulnerability assessment approaches for precast industrial structures (Sezen et al., 2000; Toniolo and Colombo, 2012; Magliulo et al., 2014b; Ozden et al., 2014; Belleri et al., 2015). The experience of such seismic events pointed out the weakness of connection systems for both structural elements and nonstructural components. The most catastrophic failures were caused by the presence of frictional connections (i.e., without any mechanical devices), which had a very low strength under horizontal loads. Moreover, some damaged structures showed also the deficiencies of some mechanical connections because of inadequate design details, such as in the case of dowel beam-to-column connections. Such connections consist of one or more steel threaded bars (dowels) cast at the column top and inserted in the beam by means of holes filled with mortar. In some applications the dowels can be fastened at the top of the beam to enhance the connection stability during the construction phase (Figure 1).
In the last decades, several research studies have been performed to investigate the vulnerability of modern (new) structures with mechanical connections under seismic actions (Vintzeleou and Tassios, 1987; Safecast, 2012; Zoubek et al., 2013; Magliulo et al., 2014a; Kremmyda et al., 2014; Brunesi et al., 2015; Zoubek et al., 2015; Dal Lago et al., 2018; Bressanelli et al., 2019; Cimmino et al., 2020; Sousa et al., 2020). Vintzeleou and Tassios (1987) conducted an experimental investigation in order to detect the main failure mechanisms of dry connections provided with dowels under cyclic loads. Tests pointed out two different failure modes: failure mode I and failure mode II, depending on the size of the concrete cover. If the concrete cover is greater than 6–7 times the diameter of the dowel, the yielding of the dowels and the consequent crashing of the concrete around them are observed (failure mode I). Otherwise, if the concrete cover is smaller than this value, the connection fails due to the splitting of the concrete cover in one of the two horizontal principal directions (failure mode II). The former mechanism is defined as a ductile collapse, whereas the latter provides a fragile failure. The same authors proposed relationships to calculate the dowel connection strength for both the failure modes under monotonic as well as cyclic loads. More recent studies confirmed these results (Psycharis and Mouzakis, 2012a; Psycharis and Mouzakis, 2012b). The research project “SAFECAST—Performance of innovative mechanical connections in precast building structures under seismic conditions”—(Safecast, 2012) developed a vast experimental campaign to analyze the behavior of different connections typologies as well as to define new design approaches and/or provisions. Several experimental tests were performed on the dowel beam-to-column connection and design formulas were also proposed. However, such investigated dowel systems had peculiar features, typically adopted in Slovenian buildings, such as the use of a steel tube around the dowel in the beam. Therefore, those results have some limitations of applicability and they need further investigation. Zoubek et al. (2013) assessed the dowel connection by means of a numerical model in ABAQUS FEA software (DSS Corp., 2010), which was validated on both the monotonic and cyclic tests of the SAFECAST framework. A key aspect of the model was the contact surface between the dowel and the concrete/grout in the direction of the dowel axis as well as in the orthogonal axis, as already highlighted in Maitra et al. (2009) and Guezouli and Lachal (2012). The failure mode in both the experimental test and the numerical model was a ductile mechanism, i.e., with the yielding of the dowel and simultaneous crashing of the surrounding concrete (Vintzeleou and Tassios, 1987). It was found that the resistance of the dowel increases with the plastic hinge depth. Furthermore, large rotations at the base of the columns can reduce the dowel strength since the steel bars undergo also tensile stresses along with the shear strains. In the framework of the SAFECAST project, Kremmyda et al. (2014) developed a numerical model in ABAQUS (DSS Corp., 2010) to detect the ductile failure mechanism as well as to identify the plastic hinges in the dowel and to measure the dissipated energy. The model was validated with experimental results under both cyclic and monotonic loads. Some research studies dealt with the fragile failure mechanism. Magliulo et al. (2014a) performed monotonic tests on a dowel connection, designed according to Italian codes and construction methodologies. The failure of this connection involved the splitting of the lateral concrete cover in the column because of its inadequate dimension. A numerical model in ABAQUS was also developed by the same authors (Magliulo et al., 2014a) which was capable to reproduce the experimental evidence. A parametric study was then performed to assess the influence of some main geometrical features on the connection response (dowel diameter, frontal cover, and lateral cover). Zoubek et al. (2015) studied the design formulas of the connection strength, for both the ductile and fragile failure mechanism. In particular, the strength of the ductile mechanisms can be calculated by using the already available formulas in the literature, which were extensively validated by both numerical model and evidence. However, if a fragile mechanism occurs, the available formulas were found inadequate in evaluating the connection capacity because of the neglected contribution of the stirrups in the connection. The authors proposed a new equation for this mechanism and showed a good agreement with past experimental results. Brunesi et al. (2015) carried out an experimental campaign on two planar three-story frames, in order to assess the effectiveness of beam-to-column dowel connections and panel-to-structure links. A ¾ scaled bare frame, designed for a medium to high seismicity, was considered to study the dowel connection response. The frame underwent quasi-static cyclic roof displacements, applied by actuators located at each slab level. The structural collapse was dictated by connection failure; indeed, dowels failed in shear, after yielding, when the structure was still in the elastic field. The observed poor seismic performance has led the authors to discourage the use of this structural type of building in high seismic areas. Bressanelli et al. (2019) performed a wide investigation on the modeling assumption reliability in reproducing the real seismic response of RC precast buildings. The assessed issues mainly concern the mass distribution, the influence of the higher vibrational modes, and the dowel connection implementation. A detailed numerical model for the connections is introduced in the structural scheme, instead of the usual perfect hinge constraint; however, given the variation of several parameters, it is not easy to understand how the change of the connection model affects the results of the dynamic analyses. Cimmino et al. (2020) dealt with the seismic assessment of a precast industrial building designed according to the modern codes. Since the last seismic events showed the inadequacy of some pinned connections, whose failure prevented the development of plastic hinges at the columns base, structural capacity was evaluated with both a global and a local approach; the global failure mode was related to the attainment of the ultimate rotation of the plastic hinges, whereas the local collapse considered the connections breakdown. Furthermore, for both the connections failure modes (ductile and fragile), a comparison between all the available formulations was made. As concerns the ductile failure, expressions by CNR 10025/1984 (CNR 10025/84, 1984), Vintzeleou and Tassios (1987) monotonic and cyclic, EOTA (TR045, 2013) monotonic and cyclic, and Safecast (2012) were applied for the calculation of connections shear strength and it is found that, neglecting the case of Vintzeleou and Tassios—cyclic, which is proved to be too conservative (Magliulo et al., 2015), SAFECAST formula provided the lowest strength. Sousa et al. (2020) developed a very accurate dowel connection model, accounting for the deformability of the neoprene pad, the friction at the concrete-neoprene interface, and the dowels response under horizontal loads. The model is experimentally validated, confirming its goodness in catching connection failure mode and maximum strength. A parametric analysis of the components geometrical and mechanical properties shows the possibility to generalize the application of the proposed model.
The results of nonlinear dynamic and static analyses of a new RC precast building under seismic actions are reported in the manuscript. For the same structure, two models of the dowel connections are compared at the global collapse limit state: 1) a perfect hinge constraint between the beam and the column and 2) a degrading hysteretic model that can simulate a more actual behavior of the connection under horizontal loads. The model of the beam-to-column connection is the only modified parameter of the performed analyses, allowing for a clear identification of the effects of such a modification. Other studies implemented refined beam-to-column dowel connection models, but, to the authors’ knowledge, none of them showed the equivalence in terms of building global collapse between a refined model and a very simple approach based on the connection strength monitoring.
The analyzed structure is a single-story RC precast industrial building, located in Central Italy (L’Aquila) on soil type C (180 m/s ≤ Vs,30 ≤ 360 m/s), according to EC8 (CEN, 2005). The structure consists of four 6 m long spans in the longitudinal direction (Z direction in Figure 2) and one 15 m long span in the transversal direction (X direction in Figure 2). The total height of the columns is equal to 9 m with a crane bracket at 7.5 m from the base. The structure is designed according to the recent Italian seismic code (NTC 2008). The roof has prestressed RC elements connected by means of both mechanical devices and a cast in situ concrete slab. The connection between the roof and the principal beams is obtained by means of dowel connections. The main beams are located along the transversal direction; their peculiar shape is illustrated in Figure 3. Dowel connections, made by 2ϕ24 mm threaded bars, are used between the main beams and the columns. They are designed with horizontal forces provided by the capacity design, i.e., as the minimum between the column base resisting moment/column height ratio by the factor γRd = 1.20 and the value given by the seismic analysis assuming the behavior factor q = 1. The diameter and the number of the dowels are designed according to Italian guidelines (CNR 10025/84, 1984), which provide the following formula for the connection horizontal strength:
where n = 2 is the number of dowels, α = 1.6 is a coefficient taking into account the confinement provided by the beam-column mutual pressure, db is the dowel resistant diameter, fyd = fy/γS = 564 N/mm2 is the steel design yielding strength, and fcd = αcc fck/γc = 25.87 N/mm2 is the concrete design strength. The secondary beams have a U-shaped section and they are connected to the columns by dowel connections. The columns are precast elements with a square shaped cross-section (Figure 4), connected to a socket foundation at the base. As concerns the structural materials, concrete with characteristic compressive strength equal to 45 N/mm2 and steel with characteristic yielding strength equal to 450 N/mm2 are considered in the design stage. Further details about the design steps and results can be found in Ercolino et al. (2018).
A 3D nonlinear model of the structure is developed in OpenSees (PEER, 2007). Columns are fixed at the base, while secondary beams are hinged to the columns. Columns and beams are modeled as elastic elements and a lumped plasticity approach is used to model the nonlinear behavior of the structure with plastic hinges at the columns base. Geometrical nonlinearities are taken into account for columns according to a PDelta coordinate transformation, which adds the second-order bending moments at the element ends. The eccentricities between the longitudinal axes of the structural elements are considered as rigid links at the beam-to-column connection in both the transversal and the longitudinal direction of the building (Figure 5). The roof elements are not modeled in the structure and a rigid diaphragm can be assumed at the top of the beams because of the stiffness of the cast in situ concrete slab. Thus, all the seismic mass, equal to 543 t, is lumped in the barycenter of the deck. The cladding panels are not modeled and their contribution to the global stiffness of the structure is neglected.
The monotonic moment-rotation envelope curve assigned at the column base consists of three branches: the first branch defines the postcracking response of the column by means of a secant stiffness up to the yielding point; the second branch is characterized by a hardening response until the maximum strength (capping point); and the third branch shows a softening behavior up to the ultimate rotation (postcapping point). It is provided according to Fischinger et al. (2008), where an ideal backbone curve is proposed for precast cantilever columns (i.e., with large shear span ratio) designed according to modern codes, by comparing experimental results with literature formulas. In particular, the suggested envelope consists of 1) the yielding rotation by Fardis and Biskinis (2003); 2) the capping rotation, the capping moment, and the ultimate rotation by Haselton (2006); 3) the yielding moment as the value corresponding to the yielding of the steel reinforcement or the crushing of the concrete in the cover. In Figure 6 the monotonic backbones for both corner and lateral columns are plotted; the difference is due to the different values of axial loads acting on them (333 kN for the corner columns and 456 kN for the lateral columns). The hysteretic model is assigned according to Ibarra et al. (2005), taking into account the cyclic degradation based on energy dissipation criteria.
In the modeling phase, mean mechanical characteristics of the structural materials are considered: mean compressive strength equal to 59.7 N/mm2 for the concrete and mean yielding strength equal to 490 N/mm2 for the steel reinforcement.
The connection between the main beams and the columns is modeled with two different approaches: 1) as a hinge constraint and 2) with a more accurate model providing the actual hysteretic force-displacement behavior, as presented in this section. The latter model is analyzed with a preliminary study as a single connection. Then, it is added to the 3D nonlinear model of the structure to assess how it affects the overall response under earthquake actions.
The refined model is calibrated on the experimental results of the Safecast (2012) project. In particular, the model is based on the outcomes of eleven monotonic tests performed at the Laboratory of the National Technical University of Athens by Kremmyda et al. (2014) and provides the backbone curve shown in Figure 7.
The maximum strength of the connection is assumed according to the Safecast (2012) formula:
where fy and fc are the mean steel yielding strength and the mean concrete compressive strength, respectively, and α is a coefficient taking into account the possible presence of axial stress in the dowel, which is assumed equal to zero. The Safecast (2012) formula was chosen for the sake of safety, since it gives the minimum value of strength with respect to the other formulas available in the literature (Cimmino et al., 2020). In particular, it provides a value of the connection strength lower than the value provided by the design Eq. 1, if in the two formulas the same values of the concrete and steel strength, respectively, are used.
The yielding displacement is evaluated as
where Fy is the connection strength (VRd) and λ is determined according to Ferreira and El Debs (2000). The capping point is defined by the displacement equal to 0.5ϕ (where ϕ is the diameter of the dowels) and the shear force equal to the connection strength (VRd). Finally, the residual strength of the connection is assumed equal to zero at a displacement equal to 1.5ϕ. Table 1 shows the values of the forces and displacements of the connection model, assuming the same behavior along the positive and the negative horizontal direction. In order to implement the connection cycling response, the OpenSees model “uniaxial Material ModIMKPeakOriented” (PEER, 2007) was applied to the zero-length element representing the dowel connection along the x direction, which provides a degrading hysteretic behavior in terms of force-displacement.
A single dowel connection is modeled (Figure 6A) and a nonlinear static analysis is performed in order to verify the efficiency of the proposed modeling approach. The model consists of two nodes, connected by a stiff elastic one-dimensional element. The connection model is assigned between the two nodes in the horizontal direction (X in Figure 8A). A pushover analysis is performed in X direction and the results are presented in Figure 8B with a green solid line. The results of the analysis demonstrate the capability of the numerical model to simulate the expected behavior of the connection.
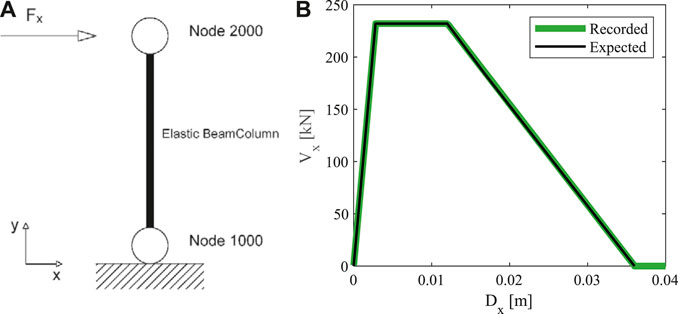
FIGURE 8. (A) Single dowel connection modeling scheme. (B) Comparison between the expected and the recorded pushover curves.
Nonlinear static (pushover) analyses are performed on two different structural models in order to evaluate how the dowel connection modeling affects the structural capacity in terms of global collapse. In the first model the main beam-to-column dowel connection is assumed as perfect hinge and the collapse is reached when the horizontal force in the hinge equals the connection horizontal strength, i.e., 232 kN. Assuming that all connections contemporaneously reach their maximum strength due to the in-plane rigidity of the roof including the main beams, the total horizontal force at the beam-to-column connection is equal to 2320 kN (Figure 9A). The second model takes into account the actual mechanical properties of the dowel connection by means of the above presented refined model. This latter model is assigned to all main beam-to-column connections along the X direction.
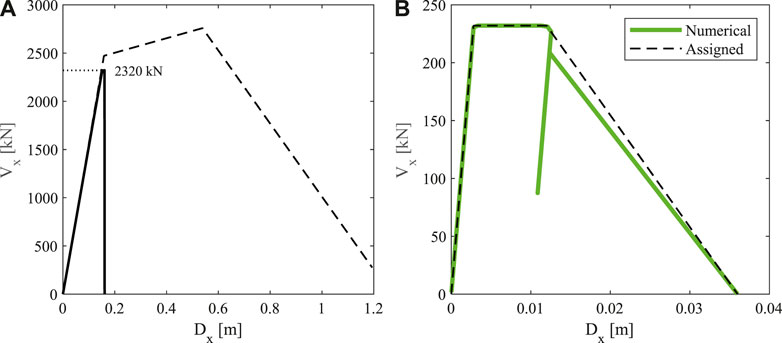
FIGURE 9. (A) Pushover curves along X direction for both the models and (B) force-displacement curve in a single dowel connection. Results of the multistripe analyses.
The analysis outcomes are presented in Figure 9. In particular, in Figure 9A the pushover results are reported in terms of base shear-top displacement for both models. The thick line shows the results of the refined model, where, at the reaching of the connection maximum strength, a quick drop is observed, denoting the failure of all connections and the global collapse of the building. For the assessed building, the kinematics under seismic actions (Brunesi et al., 2015) does not determine any additional constraint at the connection level, since the beams never come in contact with the columns and the corbels. In the first model the global collapse reaching is pointed out by the dotted horizontal line at 2320 kN. The pushover first branches of the two models are coincident until the attainment of the base shear value equal to 2320 kN, denoting the conventional collapse of the first model and the observed collapse of the second model. It can be concluded that nonlinear static analyses of the two models provide the same results in terms of global collapse of the building.
Figure 9 shows some insights too. The dashed line in Figure 9A plots the pushover curve in the case of main beam-to-column connections without strength limitation (Kramar et al., 2010; Magliulo et al., 2018). In this case, the global pushover curve follows the behavior of the plastic hinge at the column base, covering a postcracking, a postyielding, and, finally, a postcapping branch. It is worth noting that the failure of the connections and the consequent global collapse of the building precede the yielding at the column base, which should never happen if the capacity design is implemented for the connection design. Indeed, the observed behavior is due to the different formulas referenced for the design of the connections (Eq. 1) and for their assessment (Eq. 2). The latter one, which is an outcome of the recent research, provides a strength significantly lower than the former one, which is extensively used in Italy being provided by technical guidelines (Cimmino et al., 2020). Figure 9B shows the force-displacement curve recorded in the refined model of the connection during the nonlinear static analysis. It is evident that the refined model is well functioning, because the force-displacement relationship well follows the assigned model, except for a local numerical instability in the softening branch, which did not affect the analyses.
Multistripe nonlinear dynamic analyses are performed in order to compare the performance of the two models described in the previous sections in terms of global collapse. Ten increasing intensity levels (IM) are defined through an accurate hazard analysis (Iervolino et al., 2017) and, for each IM, twenty accelerograms are selected by means of the Conditional Spectrum Method (Lin et al., 2013a; Lin et al., 2013b). The Conditional Spectrum Method was applied by defining the target spectrum with an assigned value of pseudo-acceleration at the fundamental period of the structure (T1 equal to 2.0 s). The selected acceleration records belong to both the Italian accelerometric archive (Itaca) and the NGwest database. Both the horizontal components are used in the analyses along the X and Z directions of the structure (Figure 2). The spectrum-compatibility procedure was carried out on the component with the maximum value of PGA, which is then applied in the transversal direction (X). Table 2 shows the considered intensity levels and the conditioned spectral pseudo-acceleration at each return period.
The structural collapse is achieved when the seismic demand (D) exceeds the corresponding capacity value (C) in the X direction of the building. The failure criteria already defined for nonlinear static analyses are implemented in order to assess the structural vulnerability of the case study under nonlinear dynamic analyses: i. the reaching of the horizontal strength of the main beam-to-column connection when it is modeled as an internal hinge (internal hinge case); ii. the reaching of the maximum strength (flat branch of the backbone curve) of the main beam-to-column connection refined model (refined force parameter); iii. the ultimate displacement of the main beam-to-column connection refined model, i.e., the displacement corresponding to the connection strength equal to zero (refined displacement parameter). The corresponding demand parameters are as follows: i. the global horizontal force at the main beam-to-column connection level; ii. the force recorded in the main beam-to-column connection refined model; iii. the displacement recorded in the main beam-to-column connection refined model.
The results of the multistripe analyses are presented in Figure 10 as demand/capacity ratios for the internal hinge case (A), the refined force parameter (B), and the refined displacement parameter (C). Obviously, all the attainments of the collapse are identified as D/C = 1. Figure 11 provides the recorded collapses in all cases for each ground motion. The plots show that the refined model of the connection does not modify the results in terms of global collapse of the building, when it is reported in terms of forces and displacements. The differences evidenced by the three plots shown in Figure 10 are only related to the different parameters representing the demand/capacity ratio. The obtained result is due to the large stiffness of the connection and to its limited ductility (Figure 7), which are not able to modify the global building deformability and ductility.
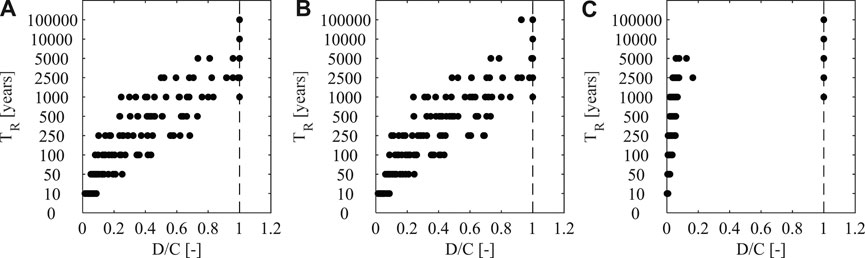
FIGURE 10. Demand/capacity ratios for each ground motion at each return period: (A) internal hinge case, (B) refined force parameter, (C) refined displacement parameter.
In the presented study a refined trilinear model of the main beam-to-column dowel connection of single-story RC precast buildings is proposed, based on literature experimental results. Nonlinear static analyses are performed on both the single connection model and the 3D case study provided with the proposed dowel connection model. Nonlinear dynamic analyses, namely, multistripe analyses, are also performed. Ten stripes, corresponding to ten increasing intensity levels, are considered, and, for each of them, twenty ground motions are selected, resulting in two-hundred time history analyses. The numerical study gave the outcomes and conclusions presented below.
(1) The refined model is able to well simulate the behavior of the dowel beam-to-column connection, as detected in past experimental studies.
(2) Pushover analyses show that the global collapse occurs when the maximum strength of the connections is attained. Such failure occurs before the yielding at the column base. The recorded collapse is due to the simultaneous failure of all connections, because of both the rigid floor at the roof level and symmetry of the building.
(3) The failure criterion of the beam-to-column connection refined model can be defined equivalently as the attainment of either the maximum resistance or the ultimate displacement.
(4) The refined model of the connection does not affect the global response of the building in terms of collapse and, consequently, does not offer an improved accuracy of the results. Indeed, nonlinear dynamic analyses outcomes show that the global collapses, detected monitoring the proposed connection model capacity, are 73 out of 200, as the ones detected considering the connections as internal hinges and monitoring the reaching of their horizontal strength. Therefore, nonlinear time history analyses of single-story RC precast buildings can be carried out using a simple model of the beam-to-column connection (internal hinge), requesting a lower numerical analysis effort.
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
GM contributed to conception or design of the work, critical revision of the article, and final approval of the version to be published. CDS contributed to data collection, data analysis and interpretation, and drafting the article. ME contributed to conception or design of the work, critical revision of the article, and the final approval of the version to be published.
This research study has been funded by the Italian Department of Civil Protection, in the framework of the national project DPC-ReLUIS-EUCENTRE RINTC 2019–2021. During the article writing phase the author CDS has been funded by the Ph.D. scholarship of the University of Parthenope “Fenomeni e rischi ambientali––FERIA”, tutor prof. Nicola Caterino.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The contribution of Michele Cirillo for some numerical analyses is gratefully acknowledged.
Belleri, A., Brunesi, E., Nascimbene, R., Pagani, M., and Riva, P. (2015). Seismic performance of precast industrial facilities following major earthquakes in the Italian territory. J. Perform. Constr. Facil. 29, 04014135. doi:10.1061/(asce)cf.1943-5509.0000617
Bressanelli, M., Belleri, A., Riva, P., Magliulo, G., Bellotti, D., and Dal Lago, B. (2019). Effects of modeling assumption on the evaluation of the local seismic response for RC precast industrial buildings. COMPDYN 2019-7th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, 1–14. Crete, Greece. 24-26 June 2019.
Brunesi, E., Nascimbene, R., Bolognini, D., and Bellotti, D. (2015). Experimental investigation of the cyclic response of reinforced precast concrete framed structures. Pcij 60, 57–79. doi:10.15554/pcij.03012015.57.79
CEN (2005). Eurocode 8: design of structures for earthquake resistance - Part 3: assessment and retrofitting of buildings. Brussels, Belgium:CEN.
Cimmino, M., Magliulo, G., and Manfredi, G. (2020). Seismic collapse assessment of new European single-story RC precast buildings with weak connections. Bull. Earthq. Eng. 18, 1–26. doi:10.1007/s10518-020-00952-7
CNR 10025/84 (1984). “Istruzioni per il progetto, l'esecuzione ed il controllo delle strutture prefabbricate in conglomerato cementizio e per le strutture construite con sistemi industrializzati (in Italian)”. Bollettino Ufficiale del CNR. Rome, Italy:CNR.
Dal Lago, B., Negro, P., and Dal Lago, A. (2018). Seismic design and performance of dry-assembled precast structures with adaptable joints. Soil Dynam. Earthq. Eng. 106, 182–195. doi:10.1016/j.soildyn.2017.12.016
Ercolino, M., Bellotti, D., Magliulo, G., and Nascimbene, R. (2018). Vulnerability analysis of industrial RC precast buildings designed according to modern seismic codes. Eng. Struct. 158, 67–78. doi:10.1016/j.engstruct.2017.12.005
Fardis, M. N., and Biskinis, D. (2003). Deformation capacity of RC members, as controlled by flexure or shear. Editor S.H.E.P.-B.E.F.E.R.R.C.S.a.V.H.S.O. Kabeyasawa T (Tokyo, Japan: University of Tokyo).
Ferreira, A., and El Debs, M. (2000). Deformability of beam-column connection with elastomeric cushion and dowel bar to beam axial force. 2nd international symposium on prefabrication.
Fischinger, M., Kramar, M., and Isaković, T. (2008). Cyclic response of slender RC columns typical of precast industrial buildings. Bull. Earthq. Eng. 6, 519–534. doi:10.1007/s10518-008-9064-7
Guezouli, S., and Lachal, A. (2012). Numerical analysis of frictional contact effects in push-out tests. Eng. Struct. 40, 39–50. doi:10.1016/j.engstruct.2012.02.025
Haselton, C. (2006). Assessing seismic collapse safety of modern reinforced concrete moment-frame Buildings. Editor P. Report (Chico: Department of Civil Engineering California State University).
Ibarra, L. F., Medina, R. A., and Krawinkler, H. (2005). Hysteretic models that incorporate strength and stiffness deterioration. Earthq. Eng. Struct. Dynam. 34, 1489–1511. doi:10.1002/eqe.495
Iervolino, I., Spillatura, A., and Bazzurro, P. (2017). “RINTC Project - assessing the (implicit) seismic risk of code-conforming structures in Italy COMPDYN 2017,”. Editors M. Papadrakakis, and M. Fragiadakis6th ECCOMAS Thematic Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, 15–17 June. Rhodes Island, Greece. 15-17 June 2017.
Kramar, M., Isaković, T., and Fischinger, M. (2010). Seismic collapse risk of precast industrial buildings with strong connections. Earthq. Eng. Struct. Dynam. 39, 847–868. doi:10.1002/eqe.970
Kremmyda, G. D., Fahjan, Y. M., and Tsoukantas, S. G. (2014). Nonlinear FE analysis of precast RC pinned beam-to-column connections under monotonic and cyclic shear loading. Bull. Earthq. Eng. 12, 1615–1638. doi:10.1007/s10518-013-9560-2
Lin, T., Haselton, C. B., and Baker, J. W. (2013a). Conditional spectrum-based ground motion selection. Part I: hazard consistency for risk-based assessments. Earthq. Eng. Struct. Dynam. 42, 1847–1865. doi:10.1002/eqe.2301
Lin, T., Haselton, C. B., and Baker, J. W. (2013b). Conditional spectrum-based ground motion selection. Part II: intensity-based assessments and evaluation of alternative target spectra. Earthq. Eng. Struct. Dynam. 42, 1867–1884. doi:10.1002/eqe.2303
Magliulo, G., Bellotti, D., Cimmino, M., and Nascimbene, R. (2018). Modeling and seismic response analysis of RC precast Italian code-conforming buildings. J. Earthq. Eng. 22, 140–167. doi:10.1080/13632469.2018.1531093
Magliulo, G., Ercolino, M., Cimmino, M., Capozzi, V., and Manfredi, G. (2015). Cyclic shear test on a dowel beam-to-column connection of precast buildings. Earthq. Struct. 9, 541–562. doi:10.12989/eas.2015.9.3.541
Magliulo, G., Ercolino, M., Cimmino, M., Capozzi, V., and Manfredi, G. (2014a). FEM analysis of the strength of RC beam-to-column dowel connections under monotonic actions. Construct. Build. Mater. 69, 271–284. doi:10.1016/j.conbuildmat.2014.07.036
Magliulo, G., Ercolino, M., Petrone, C., Coppola, O., and Manfredi, G. (2014b). The Emilia earthquake: seismic performance of precast reinforced concrete buildings. Earthq. Spectra. 30, 891–912. doi:10.1193/091012eqs285m
Maitra, S. R., Reddy, K. S., and Ramachandra, L. S. (2009). Load transfer characteristics of dowel bar system in jointed concrete pavement. J. Transport. Eng. 135, 813–821. doi:10.1061/(asce)te.1943-5436.0000065
Ozden, S., Akpinar, E., Erdogan, H., and Atalay, H. M. (2014). Performance of precast concrete structures in October 2011 Van earthquake, Turkey. Mag. Concr. Res. 66, 543–552. doi:10.1680/macr.13.00097
Psycharis, I. N., and Mouzakis, H. P. (2012a). Assessment of the seismic design of precast frames with pinned connections from shaking table tests. Bull. Earthq. Eng. 10, 1795–1817. doi:10.1007/s10518-012-9372-9
Psycharis, I. N., and Mouzakis, H. P. (2012b). Shear resistance of pinned connections of precast members to monotonic and cyclic loading. Eng. Struct. 41, 413–427. doi:10.1016/j.engstruct.2012.03.051
Safecast (2012). Design guidelines for connections of precast structures under seismic actions. Editor J.R.C.O.E. Commission (Luxembourg).
Sezen, H., Elwood, K., Whittaker, A., Mosalam, K., Wallace, J., and Stanton, J. (2000). “Structural engineering reconnaissance of the August 17, 1999, Kocaeli (Izmit), Turkey earthquake”.
Sousa, R., Batalha, N., and Rodrigues, H. (2020). Numerical simulation of beam-to-column connections in precast reinforced concrete buildings using fibre-based frame models. Eng. Struct. 203, 109845. doi:10.1016/j.engstruct.2019.109845
Toniolo, G., and Colombo, A. (2012). Precast concrete structures: the lessons learned from the L'Aquila earthquake. Struct. Concr. 13, 73–83. doi:10.1002/suco.201100052
TR045 (2013). Design of metal anchors for use in concrete under seismic actions. Brussels, Belgium: EOTA.
Vintzeleou, E. N., and Tassios, T. P. (1987). Behavior of dowels under cyclic deformations. ACI Struct. J. 84, 18–30. doi:10.14359/2749
Zoubek, B., Fischinger, M., and Isakovic, T. (2015). Estimation of the cyclic capacity of beam-to-column dowel connections in precast industrial buildings. Bull. Earthq. Eng. 13, 2145–2168. doi:10.1007/s10518-014-9711-0
Keywords: precast structures, dowel connection, nonlinear model, pushover analysis, multistripe analysis
Citation: Magliulo G, Di Salvatore C and Ercolino M (2021) Modeling of the Beam-To-Column Dowel Connection for a Single-Story RC Precast Building. Front. Built Environ. 7:627546. doi: 10.3389/fbuil.2021.627546
Received: 09 November 2020; Accepted: 08 January 2021;
Published: 12 February 2021.
Edited by:
Andrea Belleri, University of Bergamo, ItalyReviewed by:
Emanuele Brunesi, Fondazione Eucentre, ItalyCopyright © 2021 Magliulo, Di Salvatore and Ercolino. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Gennaro Magliulo, Z21hZ2xpdWxAdW5pbmEuaXQ=
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.