Modeling of the Tensile Behavior FRCM Systems for Repair and Strengthening Interventions of Masonry Structures

Fiber Reinforced Cementitious Matrix (FRCM) systems are an innovative solution for strengthening interventions of existing masonry and concrete constructions. The current literature provides interesting experimental and numerical studies which underline the potentialities of FRCMs and their specific features. Direct tensile tests are generally used for characterizing the behavior of FRCM strengthening systems. These tests particularly underline the occurrence of both matrix cracking and debonding of the reinforcement from the matrix, phenomena which particularly influence the performance of FRCM systems. The present paper aims at numerically analyzing the response of FRCM strengthening systems during tensile tests carried out throughout different setup configurations. To this end, a simple model carried out from literature and opportunely modified is presented in the paper and validated with reference to experimental case studies. Moreover, the obtained results are critically examined to emphasize the role of the proposed model for the interpretation of the results carried out from standard tensile tests.

Introduction

The current literature contains a relevant number of studies concerning the use of composite material for strengthening interventions of constructions. The majority are based on the use of Fiber Reinforced Polymers, FRP (Bertolesi et al., 2017a; Fabbrocino et al., 2019) and, only in recent years natural materials for the reinforcement (Formisano et al., 2017a, b) or inorganic materials for the matrix have been introduced.

Indeed, strengthening systems based on the use of fabric reinforced cementitious matrix (FRCM) have been recently introduced for the repair and rehabilitation of structures. This system is composed of inorganic matrices (in lieu of epoxy matrices), incorporating a reinforcement with a grid configuration.

The current literature contains studies specifically concerning this type of strengthening system. They concern both experimental issues (Arboleda, 2014; de Felice et al., 2014; Carozzi F. G. et al., 2014; D’Antino et al., 2015a, b; Donnini et al., 2015; Grande et al., 2015; Caggegi et al., 2017; Carozzi et al., 2017; DeSantis et al., 2017; Leone et al., 2017; Lignola et al., 2017) and theoretical and numerical models (D’Ambrisi et al., 2012, 2013; Bertolesi et al., 2014, 2017b; Carozzi and Poggi, 2015; Grande et al., 2015, 2017; Ombres et al., 2016; Grande and Milani, 2018; Malena et al., 2019).

The majority of experimental tests concerns both shear-lap tests, mainly finalized to examine the local bond behavior of FRCMs applied to masonry and concrete supports and, tensile tests, recently introduced for experimentally characterizing FRCM strengthening systems (ACI434,2016).

Regarding shear-lap bond tests, they underline the occurrence of the following phenomena (Valluzzi et al., 2012): cohesive failure of the substrate; de-bonding at the reinforcement/substrate interface; de-bonding at the textile/matrix interface; sliding of the textile within the reinforcement thickness; tensile failure of the textile in the un-bonded portion and tensile failure of the textile within the mortar.

On the other hand, important properties influenced by the damage of the matrix (cracking) and the damage of the reinforcement-matrix interface (debonding) are derived by performing direct tensile tests. Although different setup devices (particularly in terms of gripping mechanisms) are available in literature for carrying out tensile tests on FRCM specimens (Contamine et al., 2011), the most common ones are the clamping gripping and clevis gripping configurations. The clamping configuration is characterized by clamping with a significant lateral pressure steel or aluminum plates to the specimen ends and connecting the plates to the machine (Figure 1). Differently, according to the Annex A of AC434, the clevis-grip setup is carried out by bonding steel or aluminum plates to the specimen ends by high-strength epoxy glue (Figure 2).

FIGURE 1

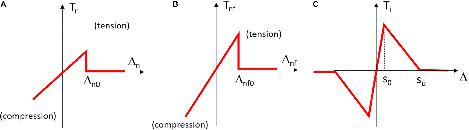
Figure 1. Clamping setup configuration: (A) setup scheme; (B) scheme accounted for the modeling phase (reproduced from Grande and Milani, 2020).

FIGURE 2

Figure 2. Clevis setup configuration: (A) setup scheme; (B) scheme accounted for the modeling phase.

In this paper the response of FRCM specimens subjected to tensile tests carried out by both clamping and clevis gripping setups is numerically analyzed. In particular, a simple model is used for simulating the experimental response and to capture both the phenomena related to the tensile response of the matrix and the ones depending on the bond between the reinforcement and the matrix. The main feature of the proposed model is its simplicity consisting of using spring-elements for reproducing the behavior of the components of the specimen (matrix and reinforcement) and their interaction at the level of the reinforcement-matrix interface. The constitutive laws introduced in the model for simulating the behavior of each component are indeed directly derived from standard tests on bare materials (in particular tensile tests involving matrix and reinforcement specimens) and shear lap tests devoted to investigated the interaction between the reinforcement and the matrix. This allows to analyze the role of each component on the tensile global response of the specimen by considering the occurrence of the different failure phenomena experimentally observed. Then, the proposed model results a simple but valid support tool for the design of FRCM strengthening systems.

After the presentation of the model by underlying its main features concerning the two accounted setup configurations, the results of the numerical analyses are discussed in detail. The comparison with the experimental results is then reported for validating the proposed modeling approach and to better understand the role of the setup configuration.

Spring-Model Approach

The proposed modeling approach for the simulation of the tensile behavior of FRCM specimens is based on the work carried out by Grande et al. (2019) by introducing some important modifications for considering the different setup configurations here accounted. The model consists of a simple 1D-schematization of the reinforcement-interface-matrix system obtained throughout the assemblage of translational non-linear springs (Figure 3). Each element E composing the mesh of the specimen is characterized by six nodes, and then, by six translational degrees of freedom along the direction of the reinforcement:

FIGURE 3

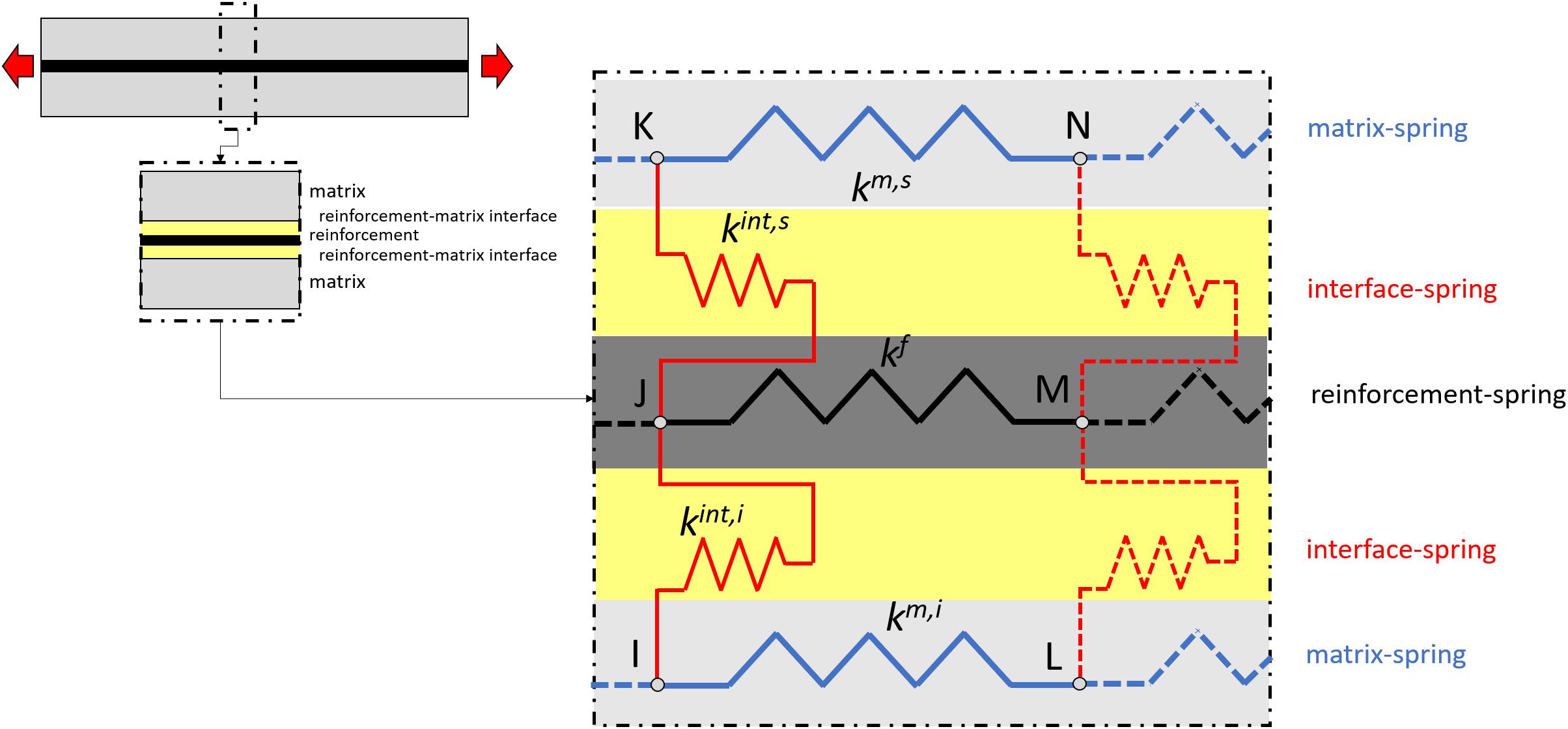
Figure 3. Spring-model for the study of the tensile behavior of FRCM specimens (Grande and Milani, 2020).

$${\underset{¯}{U}}^E={\left[\begin{array}{cccccc}{u}_I\hfill & u_J\hfill & u_K\hfill & u_L\hfill & u_M\hfill & u_N\hfill \end{array}\right]}^T(1)$$

The stiffness coefficients of the springs connecting among them the nodes of the matrix and the nodes of the reinforcement, k^m,i(ΔU^m,i), k^m,e(ΔU^m,e), k^f(ΔU^f), are dependent on the axial deformation of these components of the specimen: ΔU^m,i = u_L-u_I; ΔU^m,e = u_N-u_K; ΔU^f = u_M-u_J. On the contrary, the stiffness coefficients of the two zero-length non-linear springs, k^int,i(ΔU^int,i) and k^int,e(ΔU^int,e), depend on the values of the relative displacements between the strengthening and the matrix: ΔU^int,i = u_J-u_I; ΔU^int,e = u_J-u_K.

The constitutive laws of the springs composing the model are carried out on the basis of the experimental behavior of the bare materials (mainly tensile tests on matrix and reinforcement specimens) and, also considering the experimental outcomes emerging from shear-lap tests. Indeed, according to the model proposed in Grande et al. (2019), different non-linear constitutive laws are introduced for simulating the behavior of the springs with the main goal to account for the cracking of the matrix and the debonding of the reinforcement within the matrix (Figure 4).

FIGURE 4

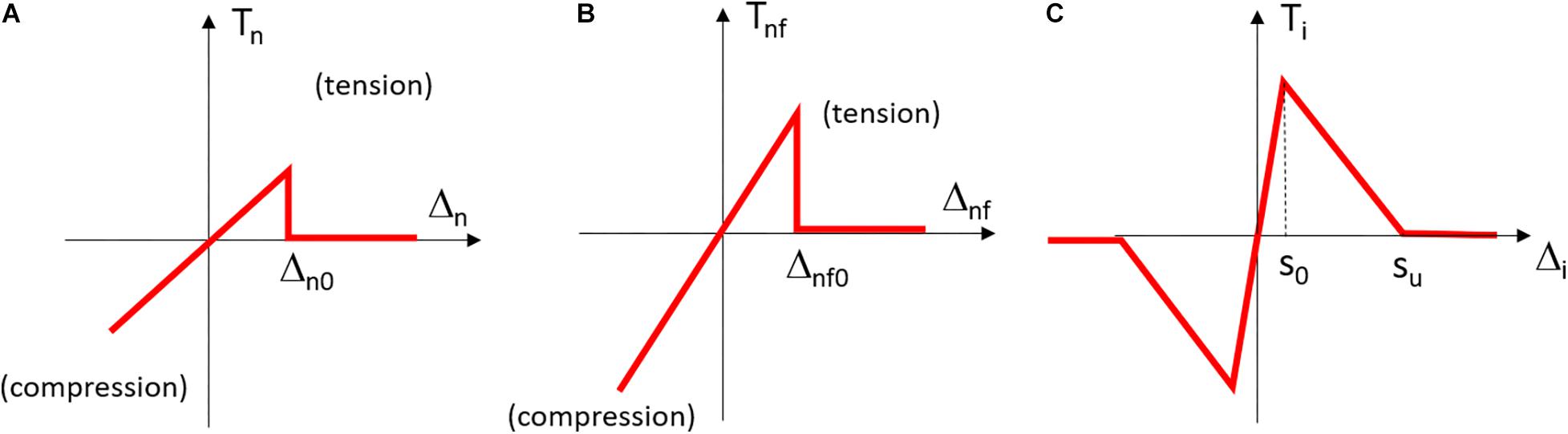
Figure 4. Constitutive laws introduced for the springs: (A) matrix-spring; (B) reinforcement-spring; (C) reinforcement-matrix spring.

The whole model has been implemented in The Mathworks Inc. Matlab Version (2018) by considering an iterative procedure based on the classic Newton-Raphson algorithm.

Clamping Gripping Case

Regarding the clamping setup configuration, according to the model proposed by Grande et al. (2019), the effect of the steel plates of the setup has been introduced by imposing the same displacement at the end joints of both matrix-springs and reinforcement-matrix interface spring. Indeed, thanks to the pressure imposed by the plates, the zones of the specimen covered by these plates are not affected by either the cracking of the matrix (the pressure imposed by the plates opposes to axial deformations of matrix) nor the slipping of the reinforcement from the matrix (Figure 1). These effects also emerge from the experimental evidences: after the cracking of the matrix zone not covered by the steel plates, the response of the specimen is governed by the axial response of the reinforcement fixed at the zones covered by the steel plates (Arboleda et al., 2016; Malena et al., 2019).

Clevis Gripping Configuration

In the case of the clevis gripping configuration it is very important to account for the contribution of the two end regions of the specimen covered by steel plates, since in these regions the two layers of matrix behave as confined by the steel plates of the setup. Indeed, as underlined in Arboleda et al. (2016), the slipping of the reinforcement inside these zones of the specimen leads to phenomena similar to the ones developing in case of a pullout test. On the contrary, in the remaining zone of the specimen not covered by steel plates, the slipping of the reinforcement occurs together with the cracking of the matrix, similarly to the case of the clamping configuration.

Taking into account these considerations, in the present paper the model proposed in Grande and Milani (2020) referring to the clamping configuration, has been opportunely modified to consider the effects developing at the ends of the specimen in case of the clevis configuration.

Indeed, as shown in Figure 2, at the end of the model it has been provided an additional element characterized by:

– Matrix springs with a linear behavior.

– Interface springs characterized by a greater value of the bond strength respect to the interface springs composing the remaining zone of the specimen.

The first assumption is finalized to avoid the damage of the end zone of the matrix for simulating the presence of the steel plates. The second assumption is aimed at considering in a simplified way the bond overstrength due to the confining effect of the setup steel plates covering the matrix.

Analyses and Obtained Results

Numerical analyses are performed with reference to the tensile tests carried out in DeSantis et al. (2018), where specimens made of a reinforcement composed of Ultra High Tensile Stress Steel (UHTSS) cords embedded into two layers of mineral-NHL mortar were tested by using two different setup configurations: clamping configuration and clevis configuration.

Regarding the tests carried out by using the clamping configuration, they involved prismatic specimens characterized by: length L = 600 mm; width of matrix b_c = 40 mm; thickness of matrix t_c = 10 mm; textile with a nominal width b_p = 31.75 mm (corresponding to a cross-section area of 2.67 mm²). Two steel plates clamped to the matrix for a length equal to 78 mm were provided for carrying out the tests.

On the other hand, the tests performed by using the clevis gripping configuration concerned coupons characterized by: length L = 500 mm; width of matrix b_c = 50 mm; thickness of the matrix t_c = 13 mm. In this case eight cords composed the textile embedded in matrix. The steel plates of the setup bonded to the matrix surfaces were characterized by a length of 250 mm.

In a recent work carried out by Malena et al. (2019), it has been proposed a finite element simulation of the specimens tested in DeSantis et al. (2018), by modeling both the regions of the specimens, i.e., the one not covered by steel plates and the one covered by steel plates, and also modeling the steel plates bonded to the exterior surface of the matrix.

In this paper, the model proposed for both the setup configurations only considers the zone of the specimen not covered by the setup steel plates. In particular, as explained in the previous paragraphs, while in the case of the clamping setup the zones covered by the steel plates are accounted in terms of boundary conditions (the same displacement is imposed to the last sections of both matrix and reinforcement), in the case of the clevis configuration these zones are accounted by opportunely modifying the constitutive laws of additional finite elements added at the ends of the specimen. In particular, taking into account the parameters reported in Malena et al. (2019) (see Table 1), the bond strength of the additional end elements of the clevis scheme has been deduced in order to obtain a similar value of the experimental peak force: this has leads to a bond strength value of these elements equal to twenty times the bond strength of the elements in the zone not covered by steel plates.

TABLE 1

Table 1. Parameters characterizing the accounted specimens.

The results obtained from the numerical analyses are reported in Figure 5 for the clamping case and in Figure 6 for the clevis case in terms of stress-strain curves. In the same figures is also reported the envelop of the experimental curves. From both the figures it emerges a good approximation of the experimental global response, particularly in the case of the clamping case where the second branch of the numerical curve is into the envelope region. In the case of the clevis configuration an overestimation of the global response is observed although the numerical curve well reproduces the stages of the global response. Indeed, in this case the introduction of the additional end elements characterized by a greater bond strength is essential for capturing the occurrence of the post-peak phase of the reinforcement-matrix interface in the zone of the specimen not covered by the setup steel plates. Indeed, in case of these elements are not introduced in the model, the obtained numerical curve is not able to reproduce the phase influenced by the debonding of the reinforcement from the matrix as shown in Figure 7.

FIGURE 5

Figure 5. Comparison between numerical and experimental stress-strain curves: clamping case.

FIGURE 6

Figure 6. Comparison between numerical and experimental stress-strain curves: clevis case.

FIGURE 7

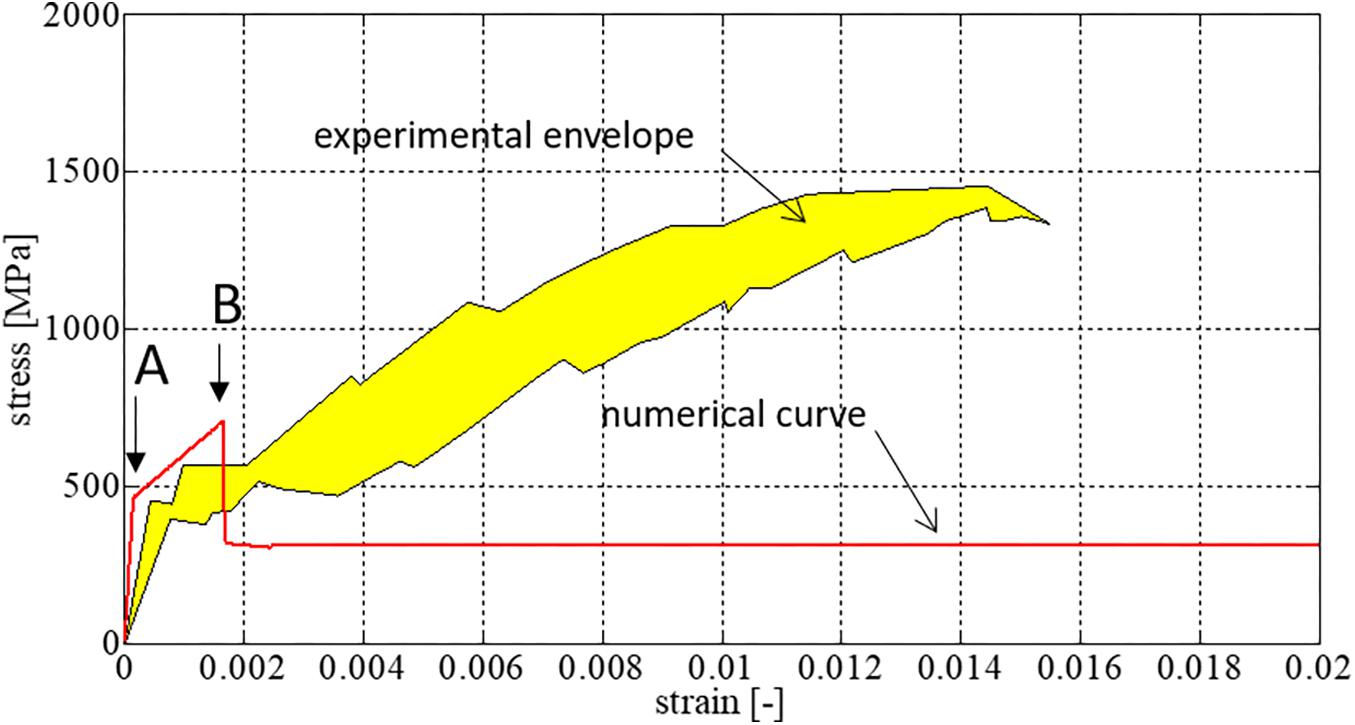
Figure 7. Comparison between numerical and experimental stress-strain curves: clevis case modeled without the additional end elements.

This feature can be observed by also examining the damage status of the components of the model at different load steps, reported in Figure 8 for one half of the specimen and where green color indicates the pre-peak stage and red color indicates the post-peak stage. From this figure it emerges that in the case of the clamping scheme only the damage of the matrix due to the attainment of the tensile strength occurs; differently, in the case of the clevis scheme equipped with the additional end elements, after the damage of the matrix (step A), also the damage of the interface at the loaded end occurs (step B). In the case of the clevis model without the additional end elements, it is evident that the model is not able to reproduce the phase where the damage of the interface occurs.

FIGURE 8

Figure 8. Damage status of the components of the model (one half specimen): undamaged (green); damaged (red), ^∗model with the additional end elements, ^∗∗model without additional end elements.

On the basis of the obtained results it is then evident the ability of the simple proposed approach to simulate the tensile behavior of FRCM specimens by opportunely set both the constitutive laws of the material components and the boundary conditions characterizing the test setup. Regarding the first ones, the authors have selected the same constitutive laws introduced by Malena et al. (2019) in a more sophisticated FE model, deduced on the basis of experimental outcomes. At the same time, the test setup configuration represents a further important aspect accounted in the modeling phase. Indeed, the analyses here performed have underlined that the influence of the different failure phenomena (cracking and reinforcement-matrix debonding) on the global response of the specimen particularly depends on the setup configuration and, then, on its numerical schematization. Indeed, in the case of the clevis setup configuration, it has been essential to introduce specific elements in the model for reproducing the behavior of the regions of the specimen inside the steel plates of the setup.

Remarks and Conclusion

The characterization of FRCM specimens throughout direct tensile tests is a technique nowadays recognized and suggested by standard codes. Information derived from this type of tests are indeed particularly useful for understanding the interaction mechanisms between the matrix and the reinforcement, which are the main responsible for the global response of the strengthening system. Nevertheless, the configuration of the tensile test influences the development of some of these phenomena during the test.

In this paper it has been presented a simple modeling approach for simulating the response of FRCM specimens during a tensile test conducted throughout two different setup configurations: clamping and clevis setup.

Particular attention has been devoted to the clevis configuration where the authors have here proposed the introduction of additional end elements for reproducing the experimental behavior of the regions of specimen covered by the steel plates of the setup. Indeed, it has been underlined that the behavior of these regions influences the global response of the specimen and, in particular, the damage process of the uncovered region. The confining effect of the steel plates leads to an increase of the shear strength at the reinforcement-matrix interface and, then, a different bond behavior along the length of the specimen. In the paper, this increase has been set on the basis of the experimental response. Future improvements will concern the development of simple formula for estimating this effect, whose effectiveness can be assessed just by using the proposed modeling approach.

The numerical analyses performed with reference to case studies derived from the current literature have allowed to assess the reliability of the proposed model (together with the introduced assumptions) and, moreover, to investigate the phenomena related to the damage of matrix material (cracking) and the debonding of the reinforcement from the matrix.

It is evident that the proposed model is based on a 1D-schematization which does not allow to capture the distribution of stresses along the transverse direction: an effect which could be emphasized by the grid configuration of the reinforcement. Moreover, although scarcely observed, the model does not account for the debonding phenomenon at the matrix-support interface.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

ACI434 (2016). ACI 434. Acceptance Criteria for Masonry and Concrete Strengthening Using Fabric-Reinforced Cementitious Matrix (FRCM) and Steel Reinforced Grout (SRG) Composite Systems. Naples, FL: ACI.

Google Scholar

Arboleda, D. (2014). Fabric Reinforced Cementitious Matrix (FRCM) Composites for Infrastructure Strengthening and Rehabilitation: Characterization Methods. PhD Thesis University of Miami Coral Gables, FL..

Google Scholar

Arboleda, D., Carozzi, F. G., Nanni, A., and Poggi, C. (2016). Testing procedures for the uniaxial tensile characterization of fabric-reinforced cementitious matrix composites. J. Compos. Constr. 20:04015063. doi: 10.1061/(ASCE)CC.1943-5614.0000626

CrossRef Full Text | Google Scholar

Bertolesi, E., Carozzi, F. G., Milani, G., and Poggi, C. (2014). Numerical modeling of fabric reinforce cementitious matrix composites (FRCM) in tension. Constr. Build. Mater. 70, 531–548. doi: 10.1016/j.conbuildmat.2014.08.006

CrossRef Full Text | Google Scholar

Bertolesi, E., Fabbrocino, F., Formisano, A., Grande, E., and Milani, G. (2017a). FRP-strengthening of curved masonry structures: local bond behavior and global response. Key Eng. Mater. 747, 134–141.

Google Scholar

Bertolesi, E., Milani, G., Ghiassi, B., and Poggi, C. (2017b). Simple numerical homogenization model for FRCM reinforced masonry panels subjected to out-of-plane loads. Key Eng. Mater. 747, 234–241.

Google Scholar

Caggegi, C., Carozzi, F. G., De Santis, S., Fabbrocino, F., Focacci, F., and Hojdys, Ł., et al. (2017). Experimental analysis on tensile and bond properties of PBO and aramid fabric reinforced cementitious matrix for strengthening masonry structures. Compos. Part B Eng. 127, 175–195. doi: 10.1016/j.compositesb.2017.05.048

CrossRef Full Text | Google Scholar

Carozzi, F. G., Bellini, A., D’Antino, T., de Felice, G., Focacci, F., and Hojdys, Ł., et al. (2017). Experimental investigation of tensile and bond properties of Carbon-FRCM composites for strengthening masonry elements. Compos. Part B Eng. 128, 100–119. doi: 10.1016/j.compositesb.2017.06.018

CrossRef Full Text | Google Scholar

Carozzi, F. G., Milani, G., and Poggi, C. (2014). Mechanical properties and numerical modeling of fabric reinforced cementitious matrix (FRCM) systems for strengthening of masonry structures. Compos. Struct. 107, 711–725. doi: 10.1016/j.compstruct.2013.08.026

CrossRef Full Text | Google Scholar

Carozzi, F. G., and Poggi, C. (2015). Mechanical properties and debonding strength of fabric reinforced cementitious matrix (FRCM) systems for masonry strengthening. Compos. Part B Eng. 70, 215–230. doi: 10.1016/j.compositesb.2014.10.056

CrossRef Full Text | Google Scholar

Contamine, R., Si Larbi, A., and Hamelin, P. (2011). Contribution to direct tensile testing of textile reinforced concrete (TRC) composites. Mater. Sci. Eng. A 528, 8589–8598. doi: 10.1016/j.msea.2011.08.009

CrossRef Full Text | Google Scholar

D’Ambrisi, A., Feo, L., and Focacci, F. (2012). Bond-slip relations for PBO-FRCM materials externally bonded to concrete. Compos. Part B Eng. 43, 2938–2949. doi: 10.1016/j.compositesb.2012.06.002

PubMed Abstract | CrossRef Full Text | Google Scholar

D’Ambrisi, A., Feo, L., and Focacci, F. (2013). Experimental and analytical investigation on bond between Carbon-FRCM materials and masonry. Compos. Part B Eng. 46, 15–20. doi: 10.1016/j.compositesb.2012.10.018

CrossRef Full Text | Google Scholar

D’Antino, T., Pellegrino, C., Carloni, C., Sneed, L. H., and Giacomin, G. (2015a). Experimental analysis of the bond behavior of glass, carbon, and steel FRCM composites. Key Eng. Mater. 624, 371–378.

Google Scholar

D’Antino, T., Sneed, L. H., Carloni, C., and Pellegrino, C. (2015b). Influence of the substrate characteristics on the bond behavior of PBO FRCM-concrete joints. Constr. Build. Mater. 101, 838–850. doi: 10.1016/j.conbuildmat.2015.10.045

CrossRef Full Text | Google Scholar

de Felice, G., De Santis, S., Garmendia, L., Ghiassi, B., Larrinaga, P., Lourenço, P. B., et al. (2014). Mortar-based systems for externally bonded strengthening of masonry. Mater. Struct. Constr. 47 2021–2037. doi: 10.1617/s11527-014-0360-1

PubMed Abstract | CrossRef Full Text | Google Scholar

DeSantis, S., Carozzi, F. G., de Felice, G., and Poggi, C. (2017). Test methods for textile reinforced mortar systems. Compos. Part B Eng. 127, 121–132. doi: 10.1016/j.compositesb.2017.03.016

CrossRef Full Text | Google Scholar

DeSantis, S., Hadad, H. A., De Caso, Y., Basalo, F., De Felice, G., and Nanni, A. (2018). Acceptance criteria for tensile characterization of fabric-reinforced cementitious matrix systems for concrete and masonry repair. J. Compos. Constr. 2:04018048. doi: 10.1061/(ASCE)CC.1943-5614.0000886

CrossRef Full Text | Google Scholar

Donnini, J., Corinaldesi, V., and Nanni, A. (2015). FRCM mechanical properties using carbon fabrics with different coating treatments. Ame. Concr. Inst.Special Publ. 305, 8.1–8.12. doi: 10.1016/j.compositesb.2015.11.012

CrossRef Full Text | Google Scholar

Fabbrocino, F., Formisano, A., Grande, E., and Milani, G. (2019). Bond mechanism of FRPs externally applied to curved masonry structures: experimental outcomes and numerical modeling. Key Eng. Mater. 817, 105–111.

Google Scholar

Formisano, A., Dessì, E., and Landolfo, R. (2017a). “Mechanical-physical experimental tests on lime mortars and bricks reinforced with hemp,” in AIP Conference Proceedings, Thessalonki.

Google Scholar

Formisano, A., Fabbrocino, F., Dessi, E., and Chiumiento, G. (2017b). “Experimental shear tests on tuff blocks triplets with hemp fibres reinforced lime mortar. in AIMETA 2017,” in Proceedings of the 23rd Conference of the Italian Association of Theoretical and Applied Mechanics, Salerno.

Google Scholar

Grande, E., Imbimbo, M., Marfia, S., and Sacco, E. (2019). Numerical simulation of the de-bonding phenomenon of FRCM strengthening systems. Frat. Integr. Strutt. 13, 321–333. doi: 10.3221/IGF-ESIS.47.24

CrossRef Full Text | Google Scholar

Grande, E., Imbimbo, M., and Sacco, E. (2015). Investigation on the bond behavior of clay bricks reinforced with SRP and SRG strengthening systems. Mater. Struct. Constr. 48, 3755–3770. doi: 10.1617/s11527-014-0437-x

CrossRef Full Text | Google Scholar

Grande, E., and Milani, G. (2018). Interface modeling approach for the study of the bond behavior of FRCM strengthening systems. Compos. Part B Eng. 141, 221–233. doi: 10.1016/j.compositesb.2017.12.052

CrossRef Full Text | Google Scholar

Grande, E., Imbimbo, M., and Sacco, E. (2017). Local bond behavior of frcm strengthening systems: some considerations about modeling and response. Key Eng. Mat. 747, 101–107. doi: 10.4028/www.scientific.net/KEM.747.101

CrossRef Full Text | Google Scholar

Grande, E., and Milani, G. (2020). Numerical simulation of the tensile behavior of FRCM strengthening systems. Composites Part B Eng. 189. doi: 10.1016/j.compositesb.2020.107886

CrossRef Full Text | Google Scholar

Leone, M., Aiello, M. A., Balsamo, A., Carozzi, F. G., Ceroni, F., Corradi, M., et al. (2017). Glass fabric reinforced cementitious matrix: tensile properties and bond performance on masonry substrate. Compos. Part B Eng. 127, 196–214. doi: 10.1016/j.compositesb.2017.06.028

CrossRef Full Text | Google Scholar

Lignola, G. P., Caggegi, C., Ceroni, F., De Santis, S., Krajewski, P., Lourenço, P. B., et al. (2017). Performance assessment of basalt FRCM for retrofit applications on masonry. Compos. Part B Eng. 128, 1–18. doi: 10.1016/j.compositesb.2017.05.003

CrossRef Full Text | Google Scholar

Malena, M., Sangirardi, M., and de Felice, G. (2019). Steel Reinforced Grout under uniaxial load: experimental evidences and numerical modelling. Constr. Build. Mater. 227:116808. doi: 10.1016/j.conbuildmat.2019.116808

CrossRef Full Text | Google Scholar

Ombres, L., Mazzuca, S., and Verre, S. (2016). Analysis of the bond between fabric reinforced cementitious mortar (FRCM) strengthening systems and masonry. Rehabend 69, 418–426. doi: 10.1016/j.compositesb.2014.10.027

CrossRef Full Text | Google Scholar

The Mathworks Inc. Matlab Version. (R2018b). MATLAB - MathWorks - MATLAB. Available online at: https://nl.mathworks.com/products/matlab.html (accessed August 28, 2018).

Google Scholar

Valluzzi, M. R., Oliveira, D. V., Caratelli, A., Castori, G., Corradi, M., De Felice, G., et al. (2012). Round robin test for composite-to-brick shear bond characterization. Mater. Struct. Constr. 45, 1761–1791. doi: 10.1617/s11527-012-9883-5

CrossRef Full Text | Google Scholar