
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Built Environ. , 22 November 2019
Sec. Earthquake Engineering
Volume 5 - 2019 | https://doi.org/10.3389/fbuil.2019.00139
Performance-based earthquake engineering has created the need for practical ways to assess the response of non-structural components (NSCs), which may be affected by deformation and/or acceleration demands of the superstructure. In the research study detailed in this paper, peak floor accelerations (PFAs) and floor response spectra (FRS) are computed using non-linear time history analysis (NTHA) for a comprehensive suite of 30 steel moment-resisting frame (MRF) archetypes, designed in accordance to Eurocode 8, considering different levels of non-linear seismic demand. The mean trends observed were compared with the most recent approaches proposed in the literature for prediction of acceleration demands. It was found that for PFAs, the available methods provide accurate predictions of the actual structural response under elastic and inelastic demands. However, the estimation procedures for the FRS yielded relevant differences in comparison to the observed elastic and inelastic responses, which entails the need for further development of such methods. It was also concluded that the existing PFA and FRS estimation methodologies present in several guidelines for seismic design and/or assessment do not provide reliable estimates of the acceleration demands incurred by the building. This highlights the very important need for an improvement of these codified procedures for a more reliable prediction of the seismic structural response.
Under seismic excitations, the dynamic response of a building's superstructure is expected to impose demands (deformation, velocity, acceleration) on building components of both structural (SCs) and non-structural (NSCs) nature. This process may, in turn, incur the non-linear response and consequent damage of SCs and NSCs. Regarding the latter, NSCs may comprise a significant percentage of the building's economic value (e.g., 65–85% for commercial buildings, possibly higher for structures of higher importance such has nuclear plants as hospitals; Miranda and Taghavi, 2003). Therefore, earthquake-induced damage to NSCs, prompted by excessive displacement, velocity, and/or acceleration demands, can be a major source of economic and social disruption. In particular, several authors have reported the significant contribution of damage to acceleration-sensitive components in major seismic events of a recent past [e.g., Northridge, 1994 (Villaverde, 1997); Chile, 2010 (Miranda et al., 2012); Darfield, 2010 (Dhakal, 2010)].
For the aforementioned reasons, the topic of seismic design and assessment of NSCs has experienced increased popularity in recent years, with existing codified procedures shown to be particularly unreliable (Sullivan et al., 2013). Although a significant amount of research on the response of secondary systems was conducted in the late 90's, the majority of the literature focused on the estimate of the response of piping and equipment in critical facilities (e.g., nuclear power plants). However, these proposals entail excessive levels of complexity for application in the design of NSCs for ordinary buildings (Taghavi and Miranda, 2005a). In a later period, however, several research studies focused on the simplified estimation of earthquake-induced horizontal floor acceleration demands in buildings (Rodriguez et al., 2002; Sankaranarayanan and Medina, 2007; Moghaddasi et al., 2008). An important contribution to the understanding of lateral peak floor acceleration (PFA) demands was developed by Taghavi and Miranda (2005a,b), who performed extensive analyses of idealized elastic structures to assess the influence of different parameters (e.g., mass and lateral stiffness distribution) on the PFA demands. Afterwards, Taghavi and Miranda (2012) extended the previously referred work to account for the non-linear behavior on multi degree of freedom (MDOF) systems. More recently, simplified methodologies, based on a modal superposition approach, have been proposed to estimate floor acceleration demands in elastic single degree of freedom (SDOF) systems (Sullivan et al., 2013), elastic MDOFs (Sullivan and Calvi, 2014), and inelastic MDOFs (Welch and Sullivan, 2017). In the case of the latter, a modification was proposed to account for the non-linear structural response, as well as a set of equations to compute the floor response spectra (FRS). This methodology was evaluated for two case studies, demonstrating a good agreement between the proposal and the results of non-linear time-history analyses. Finally, it is important to highlight the work of Vukobratovic and Fajfar (2016, 2017), in which the authors also proposed a methodology for the estimation of floor acceleration demands in inelastic MDOF systems. The method is likewise based on a modal superposition approach, modified to account for the inelastic response of the structure.
The aforementioned research contributions allow for a vast background of information regarding the expected acceleration demands on NSCs located in buildings. Notwithstanding, the proposed methodologies were generally individually validated via a limited number of idealized archetypes. It is thus pertinent to assess their effectiveness for a more comprehensive suite of case study buildings, whilst also employing more detailed numerical simulation approaches. Moreover, it is also important to conduct a direct comparison between the acceleration demand estimates provided by the different methods available in the literature, an evaluation that has not been conducted yet. With this in mind, this research study aims to evaluate the expected levels of floor acceleration demands considering 30 steel moment-resisting frames (MRFs) under seismic excitation. The scope encompasses the comparison of peak floor accelerations (PFAs) and FRS, obtained through non-linear time-history analyses, against the most recent simplified estimation approaches (Vukobratovic and Fajfar, 2017; Welch and Sullivan, 2017). Finally, the accuracy of codified methodologies in existing seismic design and assessment guidelines is also evaluated.
A number of recent research proposals have delved into the development of procedures for the estimation of floor acceleration demands (Vukobratovic and Fajfar, 2017; Welch and Sullivan, 2017), being based on the application of modal superposition approaches. As shown in Figure 1, this process revolves around an eigenvalue analysis of the superstructure, determining its modal characteristics (i.e., mode shapes and periods of vibration). With this information, the spectral accelerations for each mode can be computed using an elastic acceleration response spectrum. Such spectrum can be based on existing prescriptions in seismic design guidelines or, in turn, on a specific ground motion excitation. Next, the contributions of spectral acceleration of each of the modes of interest are computed in proportion to the mode shape and, finally, the resulting responses for several frequencies of the NSC are combined via modal combination rules (e.g., square root of the sum of the squares, SRSS, or complete quadratic combination CQC). Because all mode shape ordinates are null at the base, no peak floor acceleration demands can be computed at this position. Instead, explicit assignment of the peak ground acceleration (PGA) to the ground floor should be adopted. To account for inelastic structural response, the common approach of both studies discussed above is to introduce a reduction factor, R, within the calculation procedure to account for the level of ductility demand. In the case of Vukobratovic and Fajfar (2017) the use of the non-linear first mode shape obtained from a pushover analysis is proposed to compute the response.
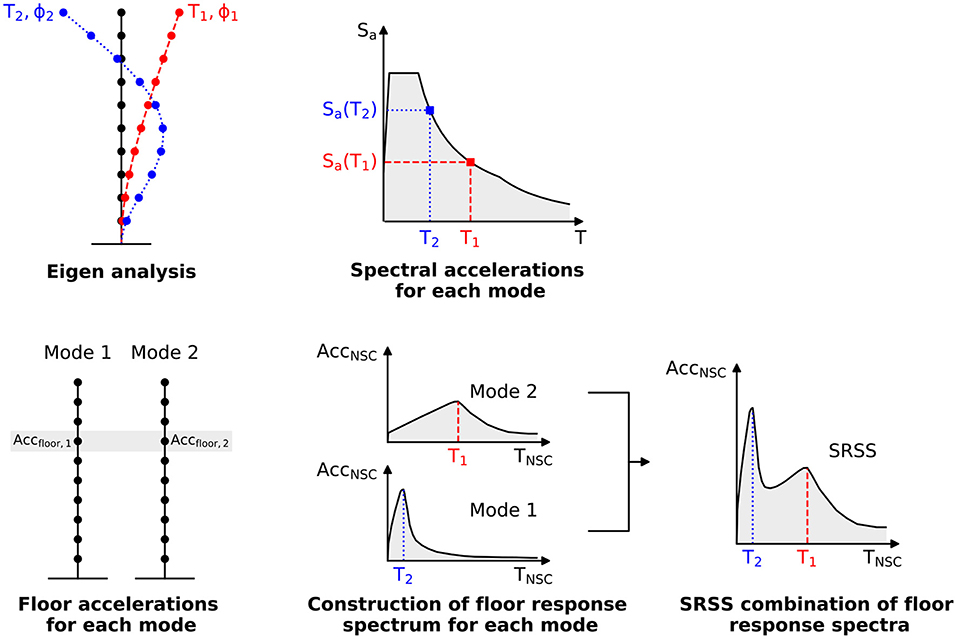
Figure 1. Modal superposition methodology for the computation of floor acceleration demands (adapted from Sullivan and Calvi, 2014).
The expression to compute the PFAs associated with each mode follows Equation (1). In this expression, PFAij is the peak floor acceleration in floor j due to vibration mode i, Γi is the modal participation factor of mode i, φij is the coordinate of mode shape i at floor j, Sa(Ti,ξ) is the damped spectral acceleration, obtained from the elastic response spectrum, for mode i and damping ratio ξ, and R is the reduction factor to account for non-linear behavior. As one may infer from the expression, its formulation is identical to classical equations from structural dynamics to compute the elastic force vector in a MDOF system, with the inclusion of the R factor to account for non-linearity in the response. This parameter should be computed with Equation (2) or Equation (3), as per Vukobratovic and Fajfar (2017) and Welch and Sullivan (2017), respectively. In Equation (2), Tp is the fundamental period of the superstructure, and Tc the second corner period defined in the acceleration response spectrum of Eurocode 8 (CEN, 2005a).
From the equations shown before, one may infer that whilst, Vukobratovic and Fajfar (2017) propose a single reduction factor that is applied only to the 1st mode of vibration, the approach of Welch and Sullivan (2017) is more complex. In the latter, the authors define different factors for steel moment frames and reinforced concrete walls, and, furthermore, different values for the fundamental period of the superstructure and the higher modes of vibration.
To what pertains the computation of the floor response spectrum (FRS), which conveys the relationship between the acceleration demand of the floor and a NSC connected to the floor with a given period, Sullivan and Calvi (2014) and Vukobratovic and Fajfar (2017) have proposed different sets of equations to approximate the response of every mode separately, which are then combined using a modal combination rule. For simplicity purposes, these procedures are not replicated herein, and the reader is referred to the respective papers for further details.
As discussed in the Introduction, the aim of this research study is to assess the accuracy of existing procedures for the estimation of earthquake-induced floor acceleration demands in steel MRFs. To this end, a comprehensive population of steel building archetypes were obtained from existing literature (Macedo et al., 2019), being representative of the current building stock in Portugal, a country facing different levels of seismic intensity. A total of six different building configurations were evaluated with different number of bays and span lengths (see Table 1). Furthermore, different building heights (2, 3, 4, 5, and 8 stories), corresponding to low- and medium-rise buildings, were considered. In total, 30 steel MRF archetypes were adopted in this study. All buildings were assumed to be located in Porto, a low-seismicity city in mainland Portugal and the considered soil was type B, according to the classification of Eurocode 8 (CEN, 2005a). shows the elevation and plan views of one of the building configurations, with the analyzed frame highlighted in shaded red.
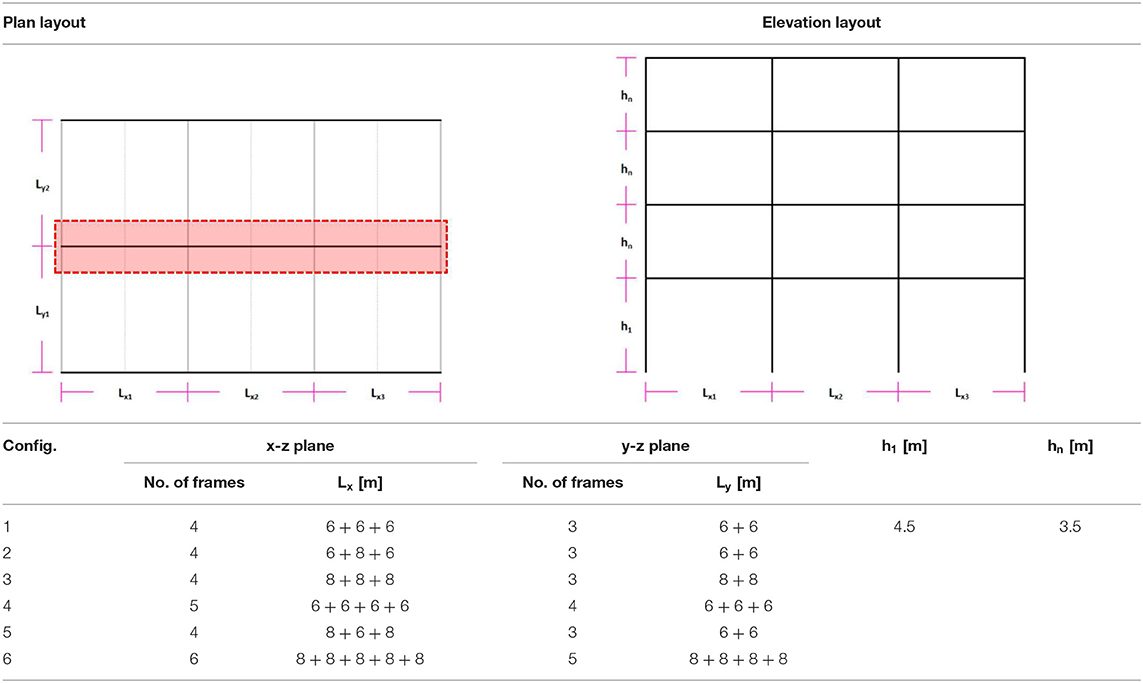
Table 1. Building configurations and geometrical properties (Macedo et al., 2019).
Seismic resistance in the longitudinal (x) direction was considered to be provided by a lateral load resisting system composed of steel MRFs, whilst a braced frame system was assumed in the transverse (y) direction. For this study, only the internal longitudinal frames were analyzed. The steel MRFs were initially designed for gravity loads in accordance with the provisions of Eurocode 3 (CEN, 2005b) for cross-sectional resistance, stability checks, and deflection limits. Seismic design was performed in accordance with the provisions of Eurocode 8 (CEN, 2005a), considering medium ductility class level (DCM), corresponding to a reference behavior factor of 4. In the application of the European seismic design requirements, the serviceability inter-story drift ratio was limited to 1% and the stability coefficient, θ, was limited to 0.2. Capacity design of the non-dissipative members was conducted according to the requirements of the code, in conjunction with the modifications proposed by Elghazouli and Castro (2009). The EC8 capacity design requirements at beam-column joints were also considered in the design of all frames, by imposing a minimum ratio of flexural capacities of the members framing the joint, as per the weak beam-strong column criterion of the code. S275 steel grade was adopted for all structural members and seismic design was based on the equivalent lateral force method proposed by the European code. Gravity loads were assumed to be transferred to the beams of the MRFs via point loads at the position of the primary and secondary transversal beams (see Table 1) and seismic masses were computed based on the combination of the full dead load and 30% of the live load adopted, using the relevant tributary areas. The seismic design of the structures was mostly controlled by stiffness requirements related with the control of P-Delta effects, as denoted by Macedo et al. (2019).
To simulate the code-recommended seismic demand for the assumed low-seismicity location of the archetypes, a suite of recorded ground motion records was selected. This selection was performed based on disaggregation results and average shear wave velocity for the first 30 meters of soil, vs30, in agreement with the requirements of the European code. A suite of 40 ground motion records was selected and scaled in order to obtain an appropriate matching between the median spectrum of the suite and the EC8 elastic response spectrum defined for the case-study location, for a wide range of fundamental periods (between 0.05 and 4 s). The ground motion record selection was conducted using SelEQ (Macedo and Castro, 2017), for a damping level of 2%, typical of steel building structures (Bernal et al., 2015). Figure 2 shows the mean and median acceleration response spectra of the selected ground motion suite for the site location under study, as well as the EC8 elastic response spectrum for a probability of exceedance of 10% in 50 years. As shown in the figure, a fairly good agreement between the mean and median acceleration response spectrum of the suite and the code-prescribed spectrum was guaranteed by the ground motion record set.
The assessment of the structures was carried out based on response-history analyses conducted with the non-linear finite element analysis framework OpenSees (PEER, 2006). The simulation models were constructed based on the work of Chopra and McKenna (2015). These models consider material inelasticity through a distributed plasticity approach for both beams and columns, with members being simulated through a single force-based inelastic finite element. Five Gauss-Lobatto integration points were adopted for each finite element, with section discretization being attained via a total of 30 steel fibers. A bilinear stress-strain relationship was assumed for the material constitutive model, with a yield strength of 275 MPa, an elastic modulus of 210 GPa, and a strain hardening ratio of 0.5%. As mentioned earlier, only the response of internal critical 2D frames of the archetype buildings was considered. Furthermore, beams and columns were simulated using centerline-to-centerline lengths, without explicit simulation of the panel zone regions. Therefore, no considerations were made regarding the simulation of the behavior of the joints as full continuity between beams and columns was assumed. Seismic masses on each floor level were equally distributed across the main beam-column intersection nodes associated with a given floor level, and all horizontal degrees-of-freedom at each floor level were constrained to move together. Columns at the ground floor were assumed to be fully constrained at the base, and second order effects were considered through P-Delta transformation. The periods of vibration associated with the suite of archetype MRFs, resulting from the numerical modeling approach detailed before, are summarized in Figure 3.
For what concerns the damping model adopted, this aspect has been the subject of several studies within the literature. A reference analysis of the consequences of Rayleigh (mass and stiffness-proportional) damping is discussed by Charney (2008) whereas an experimental verification was conducted by Petrini et al. (2008). In both examples, the shortcomings of using initial-stiffness-based viscous damping was demonstrated. Recently, Chopra and McKenna (2015) proposed a damping modeling approach based on superposition of modal damping matrices and, at the same time, highlighted the convenience of using distributed plasticity models over lumped plasticity ones to avoid “spurious” damping forces in the non-linear range. The authors concluded, however, that using either a mass and tangent-stiffness proportional Rayleigh damping or superposition-based damping models yield very similar results. One should note as well that both the floor acceleration demand estimation procedures under assessment herein also employ such damping modeling approach. For these reasons, the numerical models developed in the research detailed in this paper employed a Rayleigh damping model with mass and tangent stiffness proportional coefficients. A damping ratio of 2% was assigned on the 1st and the kth vibration periods of the archetype under study, with k being the minimum between 3 and the total number of stories of the archetype.
In the context of this research study, floor acceleration demands under both elastic and inelastic structural response were assessed. Hence, the reference seismic demand reflected by the median response spectrum of the ground motion suite was scaled to induce different target ductility demands. This process was attained on the basis of underlying assumptions of Eurocode 8. According to the code, with the use of the prescribed elastic response spectrum associated to a given seismic location, an elastic base shear demand, Vel, can be calculated. The code then allows the designer to employ a behavior factor, q, to reduce this elastic demand to a design value, Vd, whilst accepting that the structure will respond inelastically. However, to comply with the entirety of the seismic design framework (e.g., limitation of lateral deformations to control global stability effects), it might occur that the first plastic hinge is formed for a base shear demand well above Vd, due to overstrength, Ω. Furthermore, the first plastic hinge might occur for deformation levels lower than that associated with the peak lateral strength of the building, as denoted by the αu/α1 parameter of the code. This is related to the redistribution characteristics and redundancy of the building.
In the context of this study, the αu/α1 parameters associated with each of the archetypes, illustrated in Figure 3, were estimated based on non-linear static pushover analyses employing the numerical models detailed previously, in line with methodologies used by Macedo et al. (2019). Considering the aforementioned aspects, it is possible to estimate the required shear demand to induce inelastic structural response. Assuming an idealized force-deformation relationship, the shear demand associated with a given elastic response spectrum (e.g., median of a ground motion suite) can be scaled to target ductility demands, μtarget. This is attained by the factor . This factor was applied to the record ensemble when running dynamic analyses for a specific target ductility demand. For an expected elastic response of the structure, a μtarget factor below 1 should be adopted, whilst values above 1 would entail inelastic response.
In order to compare the accuracy of different floor acceleration demand estimation approaches, the total difference and the normalized root mean square error, NRMSE, metrics were adopted, defined, respectively, by Equations (4) and (5). The EDP parameter in both equations can stand for peak floor acceleration or for floor spectral acceleration, whereas the n parameter in Equation (4) can stand for the number of stories of the frame or the total number of periods for which the FRS is calculated.
According to Taghavi and Miranda (2005a), adjusting the damping value of the 2nd vibration mode (in order to be consistent with the Rayleigh damping assigned to the models) can be an important step toward the appropriate estimation of PFAs. This recommendation was devised from simplified lumped mass models and its significance to more complex structural systems was not investigated by the authors. As such, a sensitivity study was conducted to assess the influence of the aforementioned damping modeling adjustment for steel MRFs, as summarized in Figure 4 for elastic demand. In the figure, the mean (across the record suite) PFAs of all 30 MRFs, calculated with an adjusted damping (AD) for the 2nd mode and a simplified approach where a single damping ratio is assigned to all modes (CD), are directly compared. The PFAs shown in the figure were calculated via the superposition of the contributions of the minimum between 3 and the number of stories of the MRF, and are expressed as a function of the floor position along the height of the frame, as per the h/H ratio shown in the plots.
As seen in Figure 4, the modification of the damping ratio for the second mode does not lead to a significant difference in relation to the PFAs computed through a constant damping model for the majority of archetypes assessed. The results indicate some differences between the CD and AD approaches in some 8-story MRFs, with buildings up to 4-stories showing no appreciable influence of the damping “model” used in the PFA estimation procedure. Since the latter (i.e., AD) is a much less practical procedure, the more simplified alternative (i.e., CD) was adopted for the PFA estimation of the frames in this study. Further investigations should be conducted to assess the influence of these damping “models” in more detail, perhaps considering the influence of the ductility demand on the PFAs estimated with constant or adjusted damping approaches.
Taghavi and Miranda (2005a) and Vukobratovic and Fajfar (2016) recommend the use of three modes of vibration to properly estimate the response of PFAs of buildings. This recommendation, however, stems from the analyses of the dynamic response of simplified lumped mass models. In the context of this study, the appropriateness of this criterion to steel MRFs was investigated, by comparing the PFA estimates employing different number of modes with the structural responses coming from NLTHA. As shown in Figure 5, the results obtained for an 8-story archetype indicate that the mismatch between the estimated and measured PFAs is lessened with the inclusion of more modal contributions. However, for the archetype in question, the inclusion of three modes still yields an estimated PFA profile that somewhat deviates from the structural response observed through NLTHA. In order to conclude upon the appropriate number of modes to consider whilst estimating PFAs, the NLTHA results associated with the population of archetypes considered in this study were compared with the PFA estimates employing different number of modes. This analysis is summarized in Figure 6, by means of the NRMSE associated with every frame for a given number of considered modes.
The analysis of the results in Figure 6 allows inferring about the relationship between the accuracy of the PFA estimation method and the number of modes included in the calculation procedure. Generally speaking, the use of more modes resulted in lower NRMSEs, with the best comparisons being associated with the use of the number of modes equal to the number of stories of the frame. Although this can be comfortably achieved for low-rise archetypes, the same approach applied to medium- to high-rise structures can be impractical. This is because the contribution of each of the modes needs to be superimposed in the estimation procedure. For this reason, Welch and Sullivan (2017) propose the inclusion of up to four modes of vibration for buildings below 8 stories (implicitly using less modes for three and two story buildings), and including five modes for higher frames. As shown in Figure 6, the increase in accuracy seems to continue up to the 5th mode of vibration, for the 5- and 8-story frames, after which the NRMSE trends become approximately stable. Based on this observation, it was considered that the minimum number of modes to employ in the PFA estimation procedure should be the lesser of 5 or the number of stories of the frame. This criterion was applied in the results presented in the remaining sections of this paper.
The first accuracy assessment conducted in this study is related to the response of case-study structures within the linear elastic domain range. To attain this, a target ductility demand of 1 was considered, employing the procedure described in section Target Ductility Demands and Comparison Metrics and using a multiplier of 0.5·Ω/q. The comparisons of the PFA distributions, between the mean response-history results of the ground motion suite and the modal superposition procedure explained in section Review of Estimation Procedures for Floor Acceleration Demands in Buildings, are shown in Figure 7 for some of the considered archetypes. The prediction associated with the existing estimation design procedure of Eurocode 8 is also included in the figures for comparison purposes.
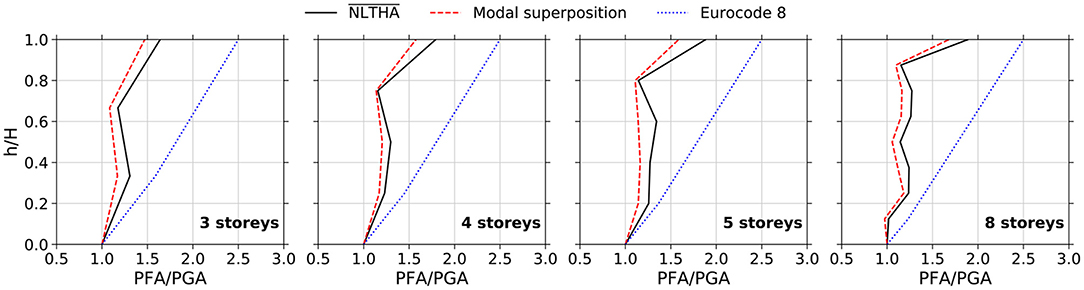
Figure 7. Example of PFA comparisons between mean response-history analyses and estimation procedures (with targeted elastic ductility demands, archetypes of building config. 1).
As one may infer from the results shown in Figure 7, the modal superposition-based PFA estimation procedures agree fairly well with the mean response-history results obtained from the numerical analyses. The estimated PFA distributions along the height of the frames were consistently below mean response-history results, with relevant differences in the comparisons for different building heights. It is important to note, however, that the EC8-based methodology was found to provide overconservative, completely erroneous estimates of peak floor acceleration demands. These findings are aligned with those of Sullivan et al. (2013), who highlighted the unreliability of existing codified procedures to estimate PFA demands in buildings. In order to have a more general overview of the comparisons across the whole set of archetypes, Figure 8 summarizes the NRMSE values, computed for every floor of every MRF, against the normalized position of the floor along the height of the archetype.
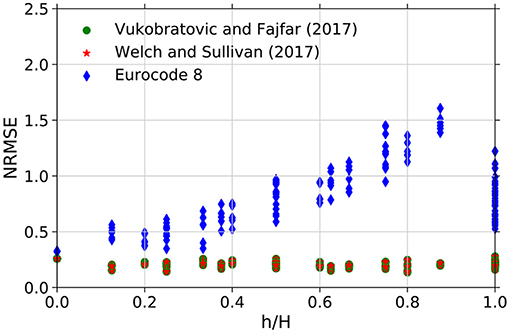
Figure 8. Overview of PFA estimation accuracy assessment, with targeted elastic demands (μ = 0.5) across all archetypes.
As shown in Figure 8, the results associated with the PFA estimate procedures proposed by Vukobratovic and Fajfar (2017) and Welch and Sullivan (2017) lead to identical comparisons to the actual dynamic responses coming from NLTHA. This is due to the fact that for elastic structural demands, the same underlying modal-superposition-based approach is adopted in both proposals. To what pertains the NRMSE values, the results obtained in this study show no significant relation of the error against the normalized frame height, with similar values across all archetypes. Furthermore, NRMSE levels associated with the EC8-based methodology were much higher than those associated with the aforementioned literature procedures. A careful inspection of the prediction approach given in the code allows concluding about the limited number of parameters that are considered, such as the fundamental period of vibration of the building, the design PGA and the height at which the floor is located. Important aspects are thus neglected, such as the mode shapes of the building or the occurrence of nonlinearity in the response of the superstructure. These aspects have been recognized in recent studies (Vukobratovic and Fajfar, 2017; Welch and Sullivan, 2017) as being extremely relevant to an appropriate estimation of floor acceleration demands in buildings. Therefore, and in the particular case of the results shown in Figure 8, the relevant differences associated with the use of the EC8-method are attributed to the non-consideration of the mode shapes of the buildings. As such, the results obtained in this study demonstrate that the European approach may not be suitable for an accurate estimation of PFAs in buildings subjected to earthquakes, especially for higher stories.
In addition to the comparisons made for elastic ductility demands, it is also important to evaluate how the existing PFA estimation procedure performs when an inelastic structural response is incurred. As outlined by Rodriguez et al. (2002), the amplification of PFAs relative to the PGA is reduced when structures are subjected to non-linear demands. This was confirmed across the analyses conducted in this research work (see Figure 9). According to the aforementioned authors, this reduction has a great effect on the 1st vibration mode which, given its important contribution to the resultant PFA response across-multiple modes, entails generally higher reductions as one moves along the building height. This observation was also validated in the case-study buildings considered herein through comparison of mean NLTHA results for different ductility demands, with the roof level generally displaying the largest reductions of PFA/PGA across all floor levels (see Figure 9). It is important to note that, as shown in the figure, the current approach of the European seismic design code does not reflect this PFA/PGA reduction for higher ductility demands. Instead, even though the code acknowledges that higher seismic intensities entail higher floor acceleration demands, the same ratio PFA/PGA is kept constant regardless of the seismic demand. As previously discussed in section Review of Estimation Procedures for Floor Acceleration Demands in Buildings, the most recent approaches to compute the peak floor acceleration responses of MDOF systems introduce a reduction factor to account for the non-linear structural behavior. The PFA estimates resulting from the application of these procedures to inelastic demands are exemplified in Figure 10 for a set of structural archetypes.
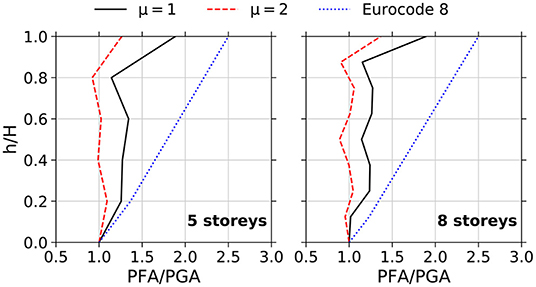
Figure 9. Example of PFA to PGA across multiple ductility demands (archetypes of building config. 1).
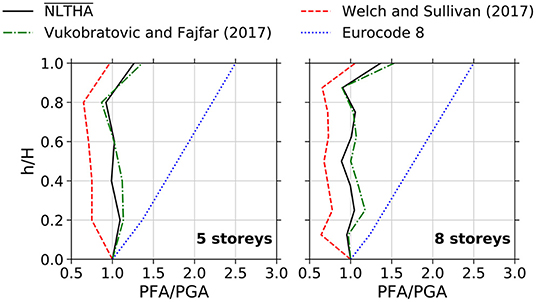
Figure 10. Example of PFA comparisons between mean response-history analyses and estimation procedures (with targeted inelastic ductility demands μ = 2, archetypes of building config. 1).
As one may observe from Figure 10, the approach by Vukobratovic and Fajfar (2017) provides PFA estimates closer to the response-history results, when compared to the alternative methodology proposed by Welch and Sullivan (2017). A closer look on both estimation procedures shows that the reduction factor associated with the former methodology is applied to the first mode of vibration only. On the other hand, the proposal of Welch and Sullivan (2017) reduces the response for the higher modes as well, as denoted by Equation (3). This difference between the two methods is the main factor behind the different accuracy levels observed. In a similar fashion to the results with elastic demands shown before, the EC8-based estimates were generally very distant from the numerical results obtained, once again demonstrating the inaccuracy of the existing methodology of the European code for the estimation of PFAs under inelastic ductility demands of the superstructure. By performing the same computations exemplified in Figure 10 across all case study steel MRFs, the NRMSE can be computed across the archetype suite, as summarized in Figure 11. Only the results associated with an elastic seismic demand factored by 2·Ω·(αu/α1)/q, which means a ductility demand of μ = 2 for the frames, was assessed in this process.
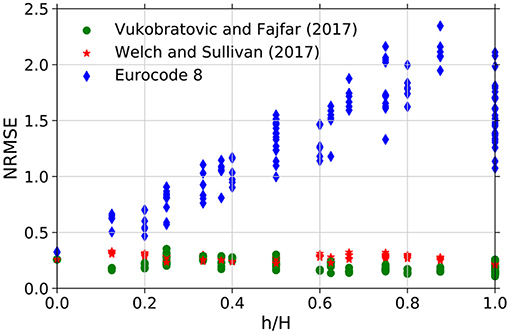
Figure 11. Overview of PFA estimation accuracy assessment, with targeted inelastic ductility demands (μ = 2) across all archetypes.
The results from Figure 11 suggest that the approach of Vukobratovic and Fajfar (2017) for non-linear demands produces more accurate predictions of PFAs in comparison to the methodology by Welch and Sullivan (2017). Furthermore, the results also show that, once again, the estimation of PFAs with the EC8 approach does not properly reflect responses obtained through non-linear time-history analyses. It is important to point out that although the computation of PFAs is an important step toward the prediction of the demand of acceleration-sensitive non-structural components (NSCs), it is so for a specific vibration period (i.e., associated with a rigid NSC). Therefore, it is also important to assess the accuracy of the considered floor acceleration demand estimation methodologies in terms of the floor response spectrum, which takes into account the amplification/reduction of the PFA for a given period of vibration of the NSC, as detailed in the next section.
As discussed in section Review of Estimation Procedures for Floor Acceleration Demands in Buildings, the floor response spectrum is highly affected by parameters such as damping of superstructure and NSCs. For consistency purposes, and considering that this research study focuses on a comparative assessment of PFA and FRS estimation procedures, the damping ratio adopted for the NSCs was assumed the same as that of the building archetypes (i.e., 2%). The number of modes of the superstructure factored into the computation of the FRS was taken as the lesser of 5 or the number of stories of the structure, according what discussed in section On the Influence of Number of Modes Considered to Estimate PFAs. A wide range of vibration periods of the NSC was considered for the creation of the FRS, namely up to 2.5 s with steps of 0.01 s. An example of the resulting FRS is shown in Figure 12 for several floor levels of a single archetype MRF. In the figure, the mean results associated with the NLTH analyses are compared with those obtained with the proposals of Vukobratovic and Fajfar (2017) and Welch and Sullivan (2017), as well as with the codified-methodologies of Eurocode 8, the American code ASCE7-10 (ASCE7-10, 2010) and the New-Zealand guidelines NZS 1170.5 (NZS1170.5, 2004).
As shown in Figure 12, the effect of higher modes is present across the floor levels shown in the left side of the figure, with a particular influence in the bottom and upper levels, as denoted by the FRS peaks observed in the FRS at low periods of the NSC. On the other hand, the influence on the FRS related to the first mode of vibration contributes more to the uppermost floor, while it has a very slight effect on the bottom floors of the MRF. Regarding the comparison with the considered FRS estimation approaches, the procedure of Vukobratovic and Fajfar (2017) was found to be more accurate in overall terms, whilst the approach by Welch and Sullivan (2017) seemed to provide closer estimates to the peak values of the FRS. Nonetheless, both methods agreed fairly well with the numerical results obtained. However, the same cannot be said about the FRS computed through the methodologies present in the considered seismic design and assessment codes. As shown in the figure, both the general shape and maximum amplitude was not captured by any of the codes under evaluation herein. Following the results shown regarding the PFA estimates, the observations detailed in this section continue to demonstrate the apparent unreliability of existing guidelines to estimate floor acceleration demands in buildings.
In order to summarize the FRS comparison across all floor levels of all archetypes, the difference between the mean FRS obtained through NLTHA and with each estimation procedure was computed for every floor of every archetype. From this process, the results obtained for a select number of MRFs are summarized in Figure 13. In the figure the FRS differences for the 3-, 5-, and 8-story archetypes are shown at three floor positions along the building height, namely the 1st floor, a middle floor and the top floor. The FRS differences observed across the set of archetypes with the same number of stories (i.e., across the six different in-plan configurations) are shown via their median value and 16th and 84th percentiles. Furthermore, in order to evaluate the FRS differences in a global sense, a more general comparison was carried out for all floor levels of the entire archetype suite considered in this study, namely through the computation of the NRMSE metric associated with the observed and estimated FRS. The main results obtained in this process are presented in Figure 13.
The analysis of the results shown in Figure 13 allow concluding that, in an overall sense, the FRS estimation procedure proposed by Vukobratovic and Fajfar (2017) agrees better with the FRS observed through NLTHA. This observation was generally evident regardless of building height and the position of the floor along the height of the MRF. Although the matching between the observed and estimated FRS was not perfect, with Sa,NSC differences as high as ±50%, they were normally much lower than those associated with the methodology of Welch and Sullivan (2017), with peak differences close to 300%. Furthermore, it is also important to note that, whilst the latter procedure generally provided higher estimates of Sa,NSC, the former often entailed unconservative levels of Sa,NSC, in particular for the bottom floors shown in the figure. These observations can be confirmed through the examination of Figure 13, where the approach by Vukobratovic and Fajfar (2017) is shown to provide better FRS estimates (i.e., lower NRMSEs) than the method proposed by Welch and Sullivan (2017).
In addition to the observed and estimated FRS comparisons for a targeted elastic ductility shown in the previous section, it is also important to evaluate how the FRS estimation procedures fare under inelastic ductility demands of the superstructure. In this context, a single non-linearity level was considered, characterized by a ductility factor μ of 2. Similar observations to those inferred from Figure 12 were obtained for this non-linearity level, namely: (i) an important effect of higher modes of the superstructure can be observed in the FRS peaks, whilst the importance of the 1st mode becomes negligible at the bottom stories; and (ii) the considered code-based procedures to estimate the FRS lead very different FRS results when compared to the those observed through NLTHA. However, one key difference to the results shown in Figure 12 can be observed under inelastic ductility demands: the procedures of Vukobratovic and Fajfar (2017) and Welch and Sullivan (2017) provide very similar estimates of the FRS shape and peaks, with a generally closer matching to the FRS observed via NLTHA. This important observation suggests that, although the proposal by Welch and Sullivan (2017) may lead to relevant FRS differences in comparison to the observed values under elastic ductility demands of the superstructure, the accuracy of the method seems to greatly improve when the MRF behaves non-linearly.
By evaluating the FRS comparisons for a ductility factor μ of 2 across a wider range of floor levels and archetypes, the results shown in Figure 14 were obtained. In general, the Sa,NSC comparisons with the NLTHA results allows concluding that the accuracy of the considered literature FRS estimation procedures fluctuates in relation to the results discussed in the previous section of this paper. As shown in the figures, whilst the procedure of Vukobratovic and Fajfar (2017) becomes less accurate for inelastic ductility demand of the MRF, the accuracy of the Welch and Sullivan (Welch and Sullivan, 2017) proposal increases. Furthermore, as shown in Figure 14, whilst the former approach still provides generally unconservative FRS estimates, the latter tends to overestimate the acceleration demands imposed on the NSCs. In a global sense, however, the median error levels (i.e., median NRMSE shown in Figure 14) of both methods were very similar, despite a much greater error dispersion of the Welch and Sullivan (2017) procedure.
The research study reported in this paper provided a critical assessment of state-of-the-art methods to estimate earthquake-induced floor acceleration demands in buildings. By comparing the estimates against the responses observed through NLTHA, considering both elastic and inelastic ductility demands of a comprehensive suite of steel MRF archetype buildings, the level of accuracy entailed by the use of the procedure by Vukobratovic and Fajfar (2017) and Welch and Sullivan (2017) to estimate PFA and FRS was assessed. Furthermore, the estimates resulting from existing methodologies prescribed in several seismic design and/or assessment guidelines were also compared against the observed structural responses. From the set of analyses conducted in the present study, a number of concluding remarks can be made:
• Floor acceleration demands obtained through NLTHA are very sensitive to the way damping is considered. Despite several research studies focusing on the most appropriate damping modeling approach for seismic response simulation, the topic still remains an issue of extensive debate in the Earthquake Engineering community. Further research is required on the topic, preferably using experimental validation to determine which damping model better conveys the actual structural behavior;
• The number of modes employed for the estimation of floor acceleration demands through the superposition of modal contributions plays a major role on the final results obtained. It was found that using the lesser of 5 modes or the number of stories of the structures yields acceptable results for the large number of regular steel MRFs analyzed in this work;
• For the estimation of PFA demands, both estimation procedures considered in this study (Vukobratovic and Fajfar, 2017; Welch and Sullivan, 2017) yielded identical results when the structure was subjected to elastic demands. This is due to the similar formulations behind each method when the structure is expected to behave elastically. However, for inelastic demand, the method by Vukobratovic and Fajfar (2017) provides better PFA estimates than the approach by Welch and Sullivan (2017). This is due to the underlying differences between the inelastic reduction factors proposed in both procedures. Furthermore, regardless of the ductility demand of the superstructure, the PFAs estimated from the recommendations of Eurocode 8 were found to deviate significantly from the demands observed through NLTHA;
• For the estimation of FRS under elastic ductility demands, the approach by Vukobratovic and Fajfar (2017) was found to be a better predictor of the acceleration demands on NSCs. On the other hand, the procedure by Welch and Sullivan (2017) generally overestimates the FRS. Under inelastic demand, the accuracy of the Welch and Sullivan (2017) method improved, though the methodology by Vukobratovic and Fajfar (2017) still yielded the best comparison with NLTHA. To what pertains the FRS estimates provided by Eurocode 8, ASCE 7–10 and NZS 1170.5, it was found that the comparisons with the NLTHA results yield substantial differences, regardless of the ductility demand of the MRF.
The datasets generated for this study are available on request to the corresponding author.
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
IG gratefully acknowledges the support of the ReLUIS Consortium for this research via Line 7 of the ReLUIS/DPC 2014-2018.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
ASCE7-10 (2010). Minimum Design Loads for Buildings and Other Structures Commentary. Reston, VA: American Society of Civil Engineers.
Bernal, D., Döhler, M., Kojidi, S. M., Kwan, K., and Liu, Y. (2015). First mode damping ratios for buildings. Earthq. Spectra 31, 367–381. doi: 10.1193/101812E.Q.S.311M
CEN (2005a). EN 1998-1, Eurocode 8: Design of structures for earthquake resistance - Part 1: General Rules, Seismic Actions and Rules for Buildings. Brussels: European Committee for Standarization.
CEN (2005b). EN 1993-1-1, Eurocode 3: Design of steel structures - Part 1.1: General Rules for Buildings. Brussels: European Committee for Standarization.
Charney, F. A. (2008). Unintended consequences of modeling damping in structures. ASCE J. Struct. Eng. 134, 581–592. doi: 10.1061/(ASCE)0733-9445(2008)134:4(581)
Chopra, A. K., and McKenna, F. (2015). Modeling viscous damping in nonlinear response history analysis of buildings for earthquake excitation. Earthq. Eng. Struct. Dyn. 45, 193–211. doi: 10.1002/eqe.2622
Dhakal, R. P. (2010). Damage to non-structural components and contents in the 2010 Darfield earthquake. Bull. N. Z. Soc. Earthq. Eng. 4, 404–411. doi: 10.5459/bnzsee.43.4.404-411
Elghazouli, A. Y., and Castro, J. M. (2009). Design of Steel Structures, Seismic Design of Buildings to Eurocode 8. Boca Raton, FL: CRC Press, 158–189.
Macedo, L., and Castro, J. (2017). SelEQ: An advanced ground motion record selection and scaling framework. Adv. Eng. Softw. 114, 32–47. doi: 10.1016/j.advengsoft.2017.05.005
Macedo, L., Silva, A., and Castro, J. M. (2019). A more rational selection of the behavior factor for seismic design according to Eurocode 8. Eng. Struct. 188, 69–86. doi: 10.1016/j.engstruct.2019.03.007
Miranda, E., Mosqueda, G., Retamales, R., and Pekcan, G. (2012). Performance of nonstructural components during the 27 february 2010 Chile earthquake. Earthq. Spectra 1, 453–471. doi: 10.1193/1.4000032
Miranda, E., and Taghavi, S. (2003). “Estimation of seismic demands on acceleration-sensitive nonstructural components in critical facilities,” in Proceedings of the Seminar on Seismic Design, Performance, and Retrofit of Nonstructural Components in Critical Facilities, ATC 29-2 (Newport Beach, CA), 347–360
Moghaddasi, K. M., Pampanin, S., and Chase, J. G. (2008). “Simplified method for performance-based design of non-structural components,” in The 14th World Conference on Earthquake Engineering (Beijing).
NZS1170.5 (2004). Structural Design Actions. Part5: Earthquake Actions - New Zealand - Commentary. Wellington: Standard New Zealand.
PEER (2006). OpenSees: Open System for Earthquake Engineering Simulation. Berkeley, CA: Pacific Earthquake Engineering Research Center; University of California.
Petrini, L., Maggi, C., Priestley, N., and Calvi, M. (2008). Experimental verification of viscous damping modeling for inelastic time history analyzes. J. Earthq. Eng. 12, 125–145. doi: 10.1080/13632460801925822
Rodriguez, M. E., Restrepo, J. I., and Carr, A. J. (2002). Earthquake-induced floor horizontal accelerations in buildings. Earthq. Eng. Struct. Dyn. 31, 693–718. doi: 10.1002/eqe.149
Sankaranarayanan, R., and Medina, R. A. (2007). Acceleration response modification factors for non-structural components attached to inelastic moment-resisting frame structures. Earthq. Eng. Struct. Dyn. 36, 2189–2210. doi: 10.1002/eqe.724
Sullivan, T. J., and Calvi, P. M. (2014). Estimating floor spectra in multiple degree of freedom systems. Earthq. Struct. 7, 17–38. doi: 10.12989/eas.2014.7.1.017
Sullivan, T. J., Calvi, P. M., and Nascimbene, R. (2013). Towards improved floor spectra estimates for seismic design. Earthq. Struct. 4, 109–132. doi: 10.12989/eas.2013.4.1.109
Taghavi, S., and Miranda, E. (2005a). Approximate floor acceleration demands in multistory buildings. I Formulation. ASCE J. Struct. Eng. 131, 203–211. doi: 10.1061/(ASCE)0733-9445(2005)131:2(203)
Taghavi, S., and Miranda, E. (2005b). Approximate floor acceleration demands in multistory buildings. II: Application. ASCE J. Struct. Eng. 131, 212–220. doi: 10.1061/(ASCE)0733-9445(2005)131:2(212)
Taghavi, S., and Miranda, E. (2012). Probabilistic Study of Peak Floor Acceleration Demands in Nonlinear Structures. Lisbon: WCEE.
Villaverde, R. (1997). Seismic design of secondary structures: state of the art. ASCE J. Struct. Eng. 123, 1011–1019. doi: 10.1061/(ASCE)0733-9445(1997)123:8(1011)
Vukobratovic, V., and Fajfar, P. (2016). A method for the direct estimation of floor acceleration spectra for elastic and inelastic MDOF structures. Earthq. Eng. Struct. Dyn. 45, 2495–2511. doi: 10.1002/eqe.2779
Vukobratovic, V., and Fajfar, P. (2017). Code-oriented floor acceleration spectra for building structures. Bull. Earthq. Eng. 15, 3013–3026. doi: 10.1007/s10518-016-0076-4
Keywords: steel moment-resisting frames, OpenSees, modal superposition, peak floor acceleration, floor response spectrum
Citation: González I, Silva A, Macedo L, Monteiro R and Castro JM (2019) Critical Assessment of Estimation Procedures for Floor Acceleration Demands in Steel Moment-Resisting Frames. Front. Built Environ. 5:139. doi: 10.3389/fbuil.2019.00139
Received: 05 July 2019; Accepted: 08 November 2019;
Published: 22 November 2019.
Edited by:
Panagiotis Mergos, City University of London, United KingdomReviewed by:
Emanuele Brunesi, Fondazione Eucentre, ItalyCopyright © 2019 González, Silva, Macedo, Monteiro and Castro. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: José Miguel Castro, bWlndWVsLmNhc3Ryb0BmZS51cC5wdA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.