Mitigation of Traffic Induced Vibration Using Geocell Inclusions

This paper describes the potential use of geocell reinforcement in mitigating the traffic induced vibration. The vibration caused by the vehicular movement was simulated over the unreinforced and geocell reinforced sections using a mechanical oscillator. The displacement amplitude and peak particle velocity were measured to understand the vibration mitigation efficacy of geocell. The effect of depth of placement of geocell on the mitigation of vibration parameters was studied. The inclusion of geocell was found effective in reducing the induced vibration based on the experimental results. The vibration mitigation efficacy of geocell was improved significantly at the shallow depth of placement of geocell mattress. The improvement in elasticity of the subgrade was observed maximum when the geocell was placed at a depth of 0.1B from the ground surface. Further, analytical and numerical approaches were used to predict the displacement amplitude vs. frequency response of reinforced soil sections. FLAC3D was used for performing the numerical investigation. The geocell was modeled according to its honeycomb shape to acquire the accurate response of geocell reinforced section. Whereas, mass spring dashpot analogy was followed for the analytical evaluation. In overall, the amplitude response predicted from the numerical and analytical studies were found to be in good agreement with the experimental results.

Introduction

The mitigation of intense levels of ground vibration generated by the rail and road networks is a common concern in urban areas. These vibrations can possibly exhibit adverse effects on the nearby structures, sensitive equipment, technical processes, and inhabitants (Murillo et al., 2009). The intensity of vibration is majorly influenced by both traffic and rail or road performance. The vehicle weight and speed are the major traffic characteristics. Structure/subgrade stability and roughness are the performance parameters. The frequency of vibration emanated from different vehicles is summarized in Table 1.

TABLE 1

Table 1. Frequency of vibration induced by different vehicles (Barneich, 1985).

The vibration energy emanated from the traffic is transmitted through the ground in the form of surface and body waves (Woods, 1968; Ujjawal et al., 2019). In an elastic half space, surface waves are exclusively propagate along the surface, and body waves propagate in the form of spherical wave front in all directions. As a result, the body waves attenuate earlier than the surface waves. Miller and Pursey (1955) reported the distribution of total induced energy as 67% Rayleigh waves, 26% shear waves, and 7% compression waves. DIN 4150 (1999) recommended the tolerance limits of vehicle induced vibration for safeguarding the structures and human beings. Similarly, various studies reported the problems associated with the traffic induced vibration. Paolucci et al. (2003) observed the level of discomfort caused by the train induced vibration by comparing the field measurements with the limits suggested in DIN 4150 (1999). The train generated vibrations was found to reach the limits from “troublesome to persons” to the “severe to persons” occasionally.

Various studies reported that the amplitude of vibration is a function of speed of the vehicle and irregularity of the road (Watts and Krylov, 2000; Crispino and D'apuzzo, 2001; D'Apuzzo, 2007). In addition, heavy vehicles was found to produce the most of perceptible levels of vibrations. On the other hand, several methods have been recommended for attenuating the amplitude of induced vibration. The open trench approach was found the first and efficient approach for the mitigation of vibration in active and passive methods (Woods, 1968). However, to prevent the instability of sidewalls of an open trench, it was filled with different geo-materials (Thompson et al., 2016). The bentonite, water, concrete, soil and bentonite mixture, and EPS (expanded polystyrene) geofoam were the examples of such materials.

Alzawi and El Naggar (2011) studied the vibration mitigation efficacy of open and soft-filled trenches through field studies. Çelebi et al. (2009) reported the performance of concrete filled trench based on field measurements. Kim et al. (2000) highlighted the isolation behavior of rubber chips filled open trench. Massarsch (2005) reported the brief review about the screening efficacy of gas cushions. Various researchers evaluated amplitude reduction ratio (ARR) to quantify the screening efficacy of open and infilled trenches (Woods, 1968). The ARR is the ratio between displacement amplitude observed in the presence of barrier system to the displacement amplitude of without barrier system. Similarly, threshold limits were proposed to assess the level of damage experienced by different buildings due to traffic vibration. The threshold limits of ground vibration intensity for different buildings is listed in Table 2. Amick and Gendreau (2000) reported the standard criteria for the safe operation of buildings based on field recordings of train induced vibration. It was also stated that the building damage criteria does not essentially indicate that the structure is free from trifling turbulences. Wiss (1981) observed that the threshold range of vibration based on human perception gets “disturbing” at 7 mm/s and “very disturbing” at 25 mm/s. Thus, the ideal vibration mitigation system is aimed to attenuate the vibration levels in order to satisfy two different criteria namely, human discomfort and damage to the buildings.

TABLE 2

Table 2. Threshold limits of PPV for different structures due to traffic vibrations (Amick and Gendreau, 2000).

On the other hand, trench systems are expensive and not a viable approach to protect the structures located in the close proximity to the vibration source. In such cases, subgrade stiffening is an alternative approach of mitigating the ground induced vibration. Few researchers suggested that the subgrade stiffening not only mitigate the traffic vibration but also reduces the track settlement and deflections (Ekanayake et al., 2014; Thompson et al., 2015). The techniques adopted for stiffening the subgrade are vibro-compaction, jet grouting, vibro-replacement, excavation and replacement, stabilization, and reinforced earth (Thompson et al., 2015; Venkateswarlu et al., 2018a). Coulier et al. (2015) investigated the efficacy of jet grout columns in mitigating the rail induced vibration through the field and numerical investigation. Various studies reported the benefits of changing the soil profile of the foundation bed in reducing the amplitude of machine vibration (Baidya and Rathi, 2004; Baidya et al., 2006; Mandal et al., 2012). In addition, the significant improvement in natural frequency of the foundation bed was observed in the presence of stiff layer nearer to the surface footing. Few studies evaluated the reduction in ground vibration by the stabilization of soil bed (Mitchell, 1981; Baker, 1982; Welsh, 1986; Saride and Dutta, 2016).

Currently, the reinforced earth technique being popularly used for strengthening the subgrade in order to support the static and cyclic loads (Hegde, 2017). Boominathan et al. (1991) and Haldar and Sivakumar Babu (2009) studied the potential benefits of this method in reducing the vibration induced by industrial machines. In addition, the use of geosynthetics was well-studied for strengthening the track performance (Biabani and Indraratna, 2015; Biabani et al., 2016; Nimbalkar and Indraratna, 2016). However, limited studies have been addressed the vibration isolation ability of geosynthetics reinforced foundation beds. Hegde and Sitharam (2016) reported that the geocell reinforcement enhances the elastic response and natural frequency of the foundation bed. The numerical evaluation of Azzam (2015) found that the presence of confined cell could effectively mitigate the amplitude of vibration through increasing the damping of a subgrade. Venkateswarlu et al. (2018a) reported that increase in elastic response of foundation bed due to the inclusion of geocells. Few studies reported the potential using the geocell in mitigating the lateral spreading of machine induced vibration (Venkateswarlu and Hegde, 2018; Venkateswarlu et al., 2018b).

Based on existing literature, the vibration mitigation efficacy of geocell reinforced subgrade system is not completely understood. The present study is aimed to demonstrate the geocell potential in mitigating the traffic induced vibration. The vibration caused by vehicular movement was generated using oscillator assembly. The influence of depth of placement of geocell on the vibration mitigation efficacy of geocell reinforced subgrade has been investigated. In addition, numerical and analytical approaches have been demonstrated for predicting the amplitude vs. frequency response of different subgrade sections.

Materials

Subgrade Soil

The particle size distribution of the soil used for the preparation of different subgrade sections is shown in Figure 1A. It consists of 84% coarse fraction and 16% fines content followed by the silt and clay compositions are 11 and 5%, respectively. As per Unified Soil Classification System, soil was classified as silty sand having the group symbol SM. The experimentally determined physical and mechanical properties of SM are listed in Table 3.

FIGURE 1

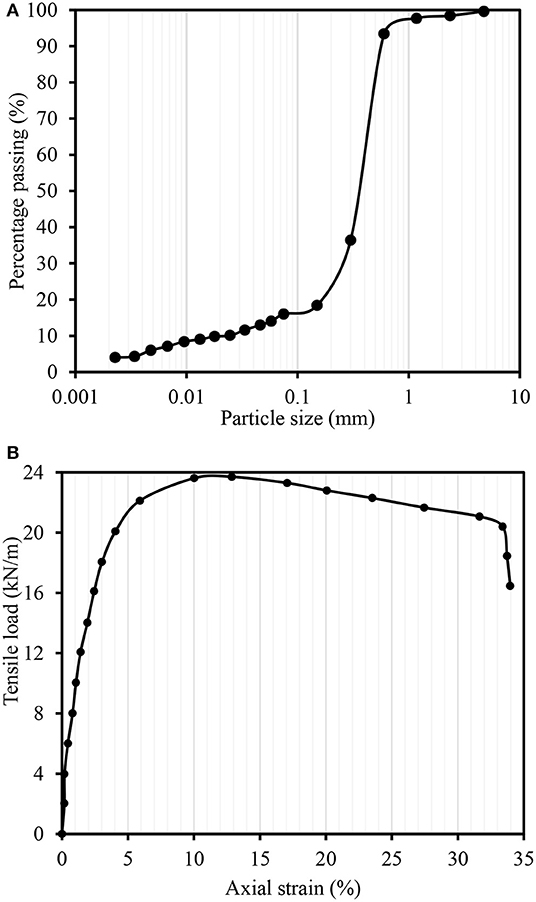
Figure 1. Characterization of materials: (A) particle size distribution of subgrade soil; and (B) stress vs. strain response of geocell reinforcement.

TABLE 3

Table 3. Properties of different materials used in the present study.

Geocell

In this study, the NPA (Novel Polymeric Alloy) geocell mattress with cell pocket having equivalent diameter 250 mm was used. The cell walls were perforated and textured with rhomboidal shape indentation to mobilize friction with infill soil. The maximum tensile load capacity of geocell was determined from the stress vs. strain response as shown in Figure 1B. The ultimate load and failure strain were observed as 23.8 kN/m and 12.1%, respectively. The test was performed in accordance with ISO, E. 10319 (2015). The other properties of the geocell reinforcement are listed in Table 3.

Experimental Investigation

Experimental Setup

The test setup for inducing the traffic vibration over subgrade sections is shown in Figure 2. During the test, sinusoidal dynamic excitation replicating the traffic vibration was generated using mechanical oscillator. It was mounted over the loading plate. The loading plate helps to transfer the induced vibration from the oscillator to the subgrade section. It was made up of concrete and having the dimensions of 600 mm² and 200 mm thickness. The combined assembly of plate and oscillator was placed at the center of reinforced section. The 6 HP capacity DC motor was attached with the oscillator to induce the vibration at a required frequency. The frequency was adjusted and measured using speed control device with the use of speed measuring sensor. The maximum resolution of the sensor was 10,000 RPM. The vibration response was measured in terms of displacement amplitude and peak particle velocity. To record the amplitude of vibration, vibration meter with accelerometer assembly was used. This assembly was designed for the continuous measurement of displacement amplitude. The accelerometer used in this study can measure the acceleration corresponding to vertical mode. The 3D geophone was used to measure the peak particle velocity (PPV) of the applied excitation. The measured PPV is the sum of the particle velocities measured in three orthogonal directions. To record the measurements of geophone, vibration monitoring terminal was used.

FIGURE 2

Figure 2. Arrangement of the test setup.

Preparation of Subgrade Sections

Two different subgrade sections, namely, unreinforced and geocell reinforced subjected to traffic induced vibration were studied. Both the sections were prepared with the dimensions of 2 m (length) × 2 m (width) × 0.5 m (depth) at the field. The test sections were prepared in five numbers of layers with thickness of each layer equal to 100 mm. To do so, manual compaction mode was followed using a rammer of 12 kg. The subgrade soil was compacted at optimum moisture content (OMC) pertaining to the standard proctor as per IRC: 37 (2012). Before using the soil for compaction, it was mixed with OMC and allowed to reach the state of maturation. To establish uniform condition of the sections, predetermined amount of blows were applied over the each layer using the height of fall of 500 mm. The number of blows were determined in accordance with the compaction energy of standard proctor. The specifications of IS 2720-29 (1975) were followed to study the dry density variation along the longitudinal and lateral directions of the sections. Total, 9 numbers of soil samples were collected from left (L), center (O), and right (R) locations of the subgrade as shown in Figure 3a. Figures 3b,c shows the variation of dry density and water content at various locations of the sections. The dry unit weight of the subgrade was found to vary between 17.26 and 17.44 kN/m³. Similarly, the variation in optimum moisture content was found in the range of variation was 12.1 ± 4%.

FIGURE 3

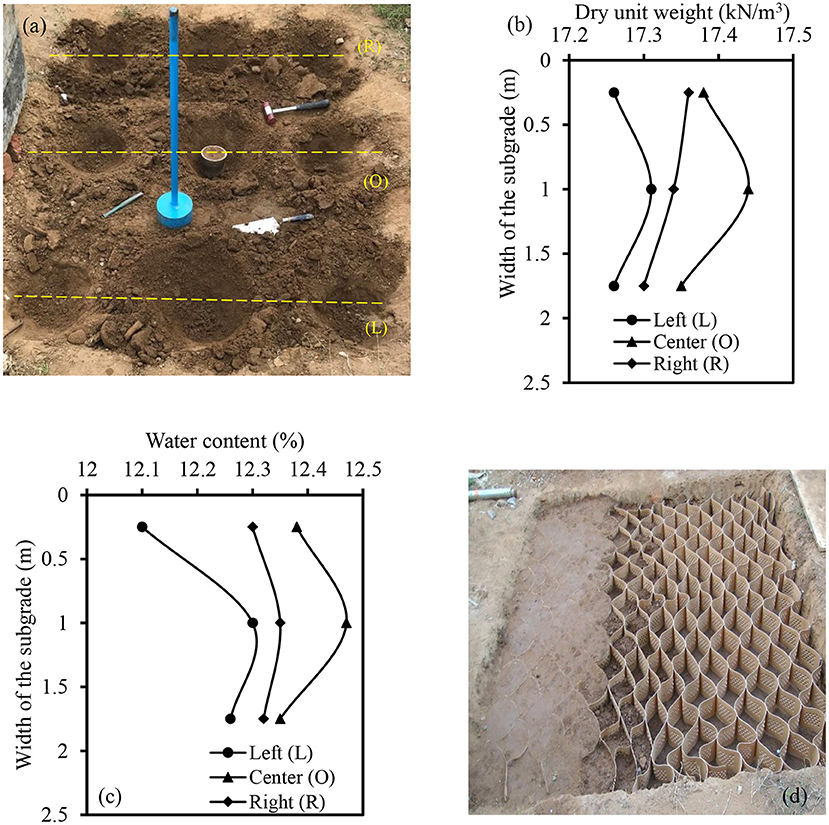
Figure 3. Preparation of different subgrade sections: (a) collection of soil samples; (b) dry unit weight distribution; (c) OMC variation; and (d) partially filled geocell mattress.

The aforementioned procedure was followed up to the placement of geocell in the preparation of geocell reinforced subgrade section. Over the compacted surface, geocell mattress was positioned and expanded using metallic stacks. Each pocket of geocell was filled using SM material. The total height of geocell was compacted in three layers with the help of tamping rod. In addition, the suitable precautions were followed to protect the cell walls from bending and distortion as reported by Biswas and Krishna (2017) and Hegde (2017). After compacting all the geocell pockets, soil cover with the thickness equal to the depth of placement of geocell was provided. The test section with the partially filled geocell mattress is shown in Figure 3d. The dynamic excitation was applied over the test sections corresponding to the frequency of 30 Hz. It replicates the vibration caused by different vehicles as listed in Table 1.

Experimental Results

Primarily, the displacement amplitude and PPV were measured up to the distance of 5 m from the vibration source. Total, 10 monitoring points were selected at an interval of 0.5 m. The efficacy of geocell in controlling the displacement amplitude of vibration was quantified in terms of amplitude reduction ratio (ARR). It is defined as the ratio between amplitude of vibration observed in the reinforced case to the amplitude of unreinforced case. The minimum ARR is generally recommended for better screening of the ground vibration. The ARR vs. normalized distance is shown in Figure 4. The normalized distance is obtained by dividing the distance from the vibration source (d) with the width of loading plate (B). The ARR was significantly diminished with the decrease in depth of placement of geocell mattress (U) from the surface of subgrade. The increase in U resulted in the amplification of ARR. Moreover, ARR found to decrease with the increase in normalized distance regardless of the depth of placement of geocell. The increase in ARR was observed beyond the d/B ratio of 5 in all the cases. The variation in soil conditions at the subgrade section and away from the subgrade might be the cause for the amplification of ARR.

FIGURE 4

Figure 4. Variation of ARR with the normalized distance.

The effect of d/B and U on the PPV is shown in Figure 5. The efficacy of geocell in attenuating the PPV of the foundation bed was decreased with the increase in depth of placement. The maximum attenuation of PPV was observed more than 48% at the depth of placement of 0.1B. Thus, the presence of geocell nearer to the surface is more beneficial for the effective attenuation of vibration. In general, the subgrade performance under the transit loading conditions is majorly depends on two parameters namely, dynamic shear modulus and elasticity of the bed. Increase in modulus enriches the stiffness of the bed. Whereas, the elasticity controls the deformation of the subgrade under the continuous action of cyclic stresses. Thus, the change in these parameters with the increase in U/B was studied. The elasticity of the bed was quantified using elastic uniform compression (C_u). It was estimated by,

$\begin{array}{ll}{C}_u=K\times A& (1)\end{array}$

$\begin{array}{ll}{f}_r=\frac{1}{2\pi }\sqrt{\frac{Kg}{W}}& (2)\end{array}$

where K is the stiffness of the subgrade, A is the contact area between the loading plate and surface of the subgrade, f_r is the resonant frequency of a system, W is the total weight of vibrating mass, and g is the acceleration due to gravitational force. To measure the f_r, variation in displacement amplitude was observed for unreinforced and geocell reinforced cases by varying the frequency from 0 to 45 Hz. The displacement amplitude becomes maximum at the f_r. The observed resonance parameters of different subgrade sections are listed in Table 4.

FIGURE 5

Figure 5. Change in PPV with the normalized distance and depth of placement of geocell.

TABLE 4

Table 4. Variation of resonance parameters.

Based on f_r, K and C_u were evaluated. Similarly, the shear modulus (G) was determined using the following relation as suggested by Timoshenko and Goodier (1970).

$\begin{array}{ll}K=\frac{4G{r}_0}{1-\vartheta }& (3)\end{array}$

where r₀ is the equivalent radius of the loading plate. The value of Poisson's ratio (ϑ) was considered as 0.3 while determining the shear modulus (G). The variation of G and C_u for different cases is shown in Figure 6. The maximum improvement in both the parameters was observed when the geocell located at the placement of 0.1B. It was attributed due to the increase in natural frequency of the subgrade system by the additional confinement offered by geocell. Hegde and Sitharam (2016) also reported the improvement in elastic response in the presence of geocell based on the results of cyclic plate load test. Further, the displacement amplitude vs. frequency response of different reinforced sections was studied through the numerical and analytical methods. The description about both the approaches are explained in the subsequent sections.

FIGURE 6

Figure 6. Variation of dynamic parameters with the change in depth of placement of geocell.

Numerical Modeling

Finite difference based three dimensional package FLAC 3D was used to conduct the numerical analysis. The numerical methodology was followed in two major steps. Primarily, the subsurface profile up to a depth of 10 m was simulated using brick element. The subsoil conditions may also have significant influence on the dynamic response of any soil system (Gazetas, 1991). In addition, selection of mesh size, boundary distance, and conditions can significantly affect the accuracy of the model. Thus, the sensitivity analysis was carried out systematically to determine the optimal values of these parameters. Based on the results of sensitivity study, 12B was found an optimum boundary distance from the dynamic actuation for not affecting the dynamic response even at higher frequencies. In addition, mesh density was found to have minimum influence on the results. Hence, the numerical model having the dimensions of 15 × 15 × 10 m was developed. The coarse mesh was selected for discretizing the model. At the ground surface, the subgrade sections of 2 × 2 × 0.5 m was simulated as similar to the experimental study. Venkateswarlu et al. (2018a) reported the details of subsurface profile and their modeling parameters. The loading plate behavior was simulated using linear elastic material. Whereas, the response of subgrade soil was modeled using Mohr-Coulomb yield criteria. The displacement along the bottom plane of the model was restrained in all the three directions (i.e., U_x = U_y = U_z = 0). The vertical faces were restrained only in the horizontal direction. Therefore, the displacement was permitted in the vertical direction (i.e., U_x = U_y = 0 and U_z # 0). In addition, viscous (quiet) boundary conditions were assigned to the vertical faces to prevent wave reflections from the boundary of the model.

Figure 7A shows the FLAC3D model for unreinforced case with the boundary conditions. To simulate the geocell-reinforced section, geocell was created at the required position as shown in Figure 7B. The actual honeycomb curvature was considered while developing the geocell. The geocell and infill material were assigned with linear elastic and Mohr-Coulomb constitutive behavior, respectively to simulate the real case conditions. Geocell was modeled using the geogrid structural element. The modeling parameters used for the development of geocell reinforced bed are listed in Table 5. In the second stage, the dynamic excitation similar to experimental study was applied over the loading plate using FISH code. To monitor the vibration parameters, zonal points were selected along the longitudinal direction. The variation in dynamic force with the increase in frequency is shown in Figure 7C. The figure represents the magnitude of dynamic force acted over the loading plate at different operating frequencies. The dynamic force corresponding to the each operating frequency was applied for the duration of 10 s.

FIGURE 7

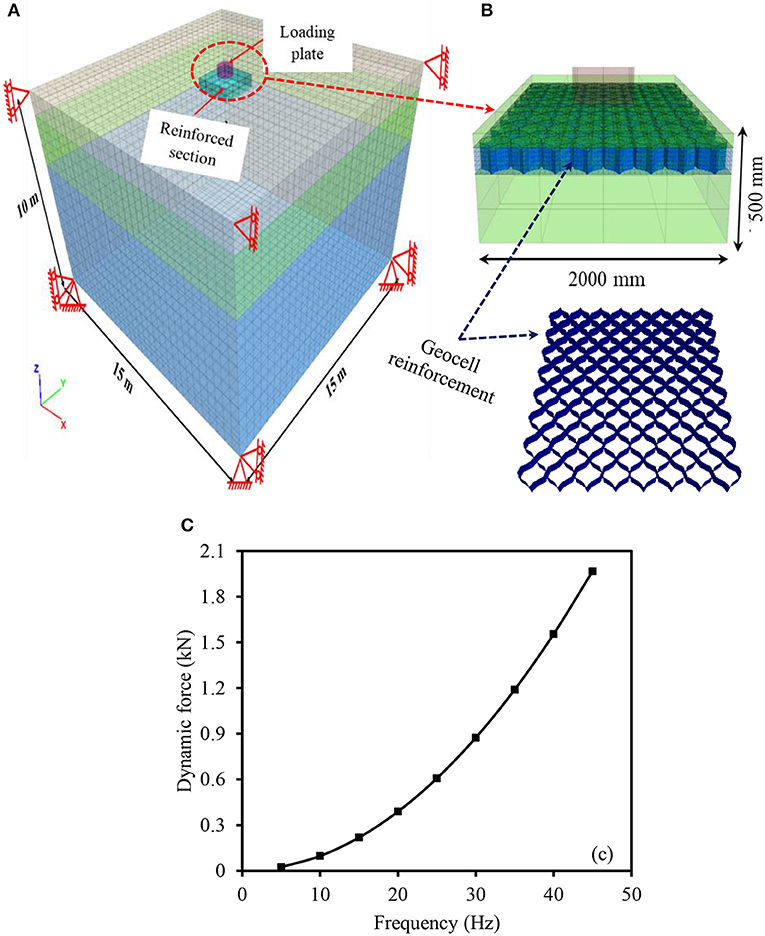
Figure 7. FLAC3D numerical model: (A) unreinforced case with boundary conditions; (B) geocell reinforced subgrade (modified after Ujjawal et al., 2019); and (C) loading variation with the frequency.

TABLE 5

Table 5. Properties of different materials used in modeling for dynamic loading condition.

Analytical Study

Various studies reported the use of mass spring dashpot (MSD) analogy for predicting the response of pavements and rail track systems. Loizos et al. (2003) carried out the dynamic analysis of pavement subgrade using MSD approach. Choudhury et al. (2008) suggested MSD system with 2-degree of freedom to predict the displacement magnitude of subgrade and ballast layers. The unique advantage of this method is that the consideration of damping and stiffness characteristics during the analysis. In this study, single degree MSD analogy was used to predict the displacement amplitude vs. frequency response of different subgrade sections. Based on MSD model, the subgrade soil was considered as an isotropic and elastic soil medium. It was characterized using linear elastic weight less spring. The dashpot system was used to replicate the damping behavior of the subgrade material. The dynamic excitation applied over the reinforced sections was considered as vertical during the analogy. The loading plate and oscillator assembly was represented with the rigid mass of M. Figure 8 shows the MSD idealization of subgrade subjected to the vertical mode dynamic excitation.

FIGURE 8

Figure 8. Analogy of a system: (a) actual reinforced subgrade section; and (b) MSD idealization.

The generalized equation of motion used to describe the system can be written as,

$\begin{array}{ll}M\ddot{Z}+C\dot{Z}+KZ=X(t)& (4)\end{array}$

where X(t) is the total vertical dynamic force, Z is the displacement amplitude, Ż and $\ddot{Z}$ are the first and second derivatives of Z over time t, C is the damping coefficient, and K is the equivalent stiffness. The variation in displacement amplitude (Z) of various sections at each frequency is determined using

$\begin{array}{ll}Z=\frac{\left(\frac{m_{e}e}{M}\right){\left(\frac{\omega }{{\omega }_n}\right)}^2}{\sqrt{{\left(1-{\left(\frac{\omega }{{\omega }_n}\right)}^2\right)}^2+{\left(2D\left(\frac{\omega }{{\omega }_n}\right)\right)}^2}}& (5)\end{array}$

where m_e is the mass of the rotating elements, ω_n is the natural frequency of the subgrade condition, ω is the operating frequency of dynamic excitation, and D is the damping ratio. The displacement amplitude becomes maximum at the resonance condition (when the ω_n matches with the ω). The peak displacement amplitude (Z_m) of the vibration at the resonance is determined by,

$\begin{array}{ll}\frac{Z_{m}M}{m_{e}e}=\frac{1}{2D\sqrt{1-D^2}}& (6)\end{array}$

Comparison of experimental results with the results of numerical and analytical studies for unreinforced section is shown in Figure 9A. The good agreement was noticed among the results of experimental, numerical and analytical studies. However, the numerical results has shown close agreement with the experimental results as compared to the analytical results. The similar observation was also noticed in the case of geocell reinforced subgrade as shown in Figure 9B. The analytical model has exhibited a slight deviation in predicting the post resonance behavior of the geocell reinforced subgrade. It might be due to the lack of consideration of parameters representing the interaction between the soil and geocell reinforcement. In addition, the subgrade is generally considered as a linear elastic weightless spring in the case of analytical study. In spite of these limitations, the analytical model has predicted the resonance response of the geocell reinforced case reasonably well. The reported amplitude vs. frequency is corresponding to the optimum (U = 0.1B) geocell reinforced case. About 7 and 12% variation in the resonant frequency was observed between the experimental and analytical studies for unreinforced and geocell reinforced sections. Whereas, the deviation between numerical and experimental resonant frequency was noticed as 3 and 2% for unreinforced and geocell reinforced subgrade cases.

FIGURE 9

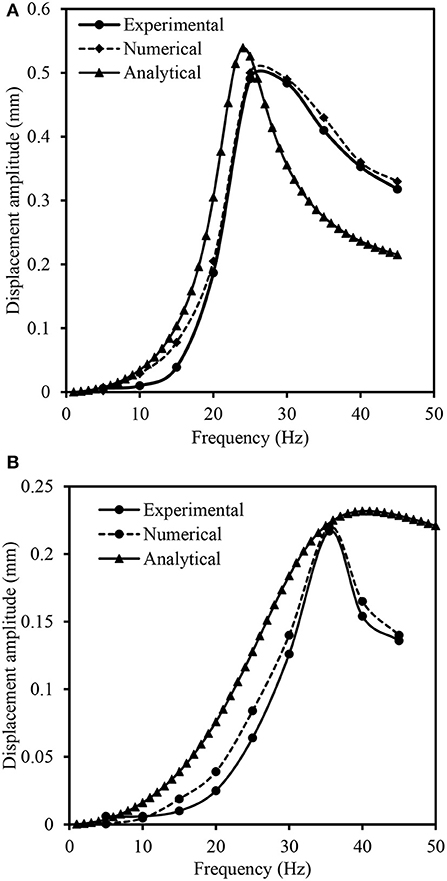
Figure 9. Comparison of the results: (A) unreinforced; and (B) geocell reinforced subgrade sections.

The influence of geocell properties, namely, elastic modulus and the width of geocell on the ARR and natural frequency (f_n) of the subgrade was numerically investigated and presented in Figures 10A,B. The geocell modulus was varied as 0.25, 0.5, 1, and 2 times Young's modulus (E) of geocell used in the present study. The E of the geocell used in the present study was 280 MPa. The width of geocell was considered as 3.3B while studying the effect of geocell modulus. From Figure 10A, the reduction in ARR and improvement in f_n was found with the increase in modulus of the geocell mattress. It was due to the increase in additional confinement offered by the geocell with the increase in its modulus. Further, to study the effect of geocell width, it was increased from 1.6B to 6.7B with an increment of 1.7B. The geocell modulus was considered as 1E while studying the effect of width of geocell mattress. The increase in geocell width resulted in the decrease in ARR and increase in f_nof the subgrade as shown in Figure 10B. The improvement in f_n was found marginal beyond the geocell width of 5B.

FIGURE 10

Figure 10. Effect of geocell properties on ARR and f_n: (A) geocell modulus; and (B) geocell width.

Conclusions

The efficacy of geocell in mitigating the traffic induced vibration was systematically studied in the present study. The vibration caused by traffic was generated over the subgrade sections with and without geocell reinforcement using the oscillator. The reduction in vibration parameters namely, displacement amplitude and peak particle velocity were measured to assess the geocell efficiency. From the experimental results, the reduction in peak particle velocity of subgrade was decreased from 48 to 34% with the change in depth of placement of geocell from 0.1B to 0.5B. Thus, 0.1B was suggested as an optimum depth for the effective mitigation of traffic vibration. At the optimum depth of placement, 1.4 times increase in natural frequency of subgrade was observed. The elasticity of the subgrade was improved by 96%. Similarly, the peak displacement amplitude of the subgrade was reduced by 57% in the presence of geocell reinforcement. The numerical and analytical methods were successfully used to predict the displacement amplitude response of the subgrade sections considered in the present study. The amplitude vs. frequency responses predicted from the analytical and numerical studies have shown good agreement with the experimental results. However, the resonant frequency predicted from the analytical study has exhibited the slightly higher deviation as compared to the numerical results. In overall, the inclusion of geocell not only mitigate the traffic induced vibration but also enriches the dynamic properties of the subgrade section.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

HV performed the studies and prepared the manuscript based on the inputs and guidance of the AH. AH and HV reviewed and accepted the final version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Alzawi, A., and El Naggar, M. H. (2011). Full scale experimental study on vibration scattering using open and in-filled (GeoFoam) wave barriers. Soil Dyn. Earthq. Eng. 31, 306–317. doi: 10.1016/j.soildyn.2010.08.010

CrossRef Full Text | Google Scholar

Amick, H., and Gendreau, M. (2000). “Construction vibrations and their impact on vibration-sensitive facilities,” in Construction Congress VI: Building Together for a Better Tomorrow in an Increasingly Complex World (Orlando, FL) 758–767. doi: 10.1061/40475(278)80

CrossRef Full Text | Google Scholar

Azzam, W. R. (2015). Utilization of the confined cell for improving the machine foundation behavior-numerical study. J. Geoeng. 10, 17–23. doi: 10.6310/jog.2015.10(1).3

CrossRef Full Text | Google Scholar

Baidya, D. K., Muralikrishna, G., and Pradhan, P. K. (2006). Investigation of foundation vibrations resting on a layered soil system. J. Geotech. Geoenviron. Eng. 132, 116–123. doi: 10.1061/(ASCE)1090-0241(2006)132:1(116)

CrossRef Full Text | Google Scholar

Baidya, D. K., and Rathi, A. (2004). Dynamic response of footings resting on a sand layer of finite thickness. J. Geotech. Geoenviron. Eng. 130, 651–655. doi: 10.1061/(ASCE)1090-0241(2004)130:6(651)

CrossRef Full Text | Google Scholar

Baker, N. H. (1982). “Planning and performing structural chemical grouting,” in ASCE Specialty Conference on Grouting in Gectechnical Engineering (New Orleans, LA), 515–539.

Google Scholar

Barneich, J. A. (1985). “Vehicle induced ground motion,” in Vibration Problems in Geotechnical Engineering (Detroit, MI: ASCE), 187–202.

Google Scholar

Biabani, M. M., and Indraratna, B. (2015). An evaluation of the interface behaviour of rail subballast stabilised with geogrids and geomembranes. Geotex. Geomembr. 43, 240–249. doi: 10.1016/j.geotexmem.2015.04.002

CrossRef Full Text | Google Scholar

Biabani, M. M., Indraratna, B., and Ngo, N. T. (2016). Modelling of geocell-reinforced subballast subjected to cyclic loading. Geotex. Geomembr. 44, 489–503. doi: 10.1016/j.geotexmem.2016.02.001

CrossRef Full Text | Google Scholar

Biswas, A., and Krishna, A. M. (2017). Geocell-reinforced foundation systems: a critical review. Int. J. Geosynth. Ground Eng. 3:17. doi: 10.1007/s40891-017-0093-7

CrossRef Full Text | Google Scholar

Boominathan, S., Senathipathi, K., and Jayaprakasam, V. (1991). Field studies on dynamic properties of reinforced earth. Soil Dyn. Earthq. Eng. 10, 402–406. doi: 10.1016/0267-7261(91)90054-4

CrossRef Full Text | Google Scholar

Çelebi, E., Firat, S., Beyhan, G., Çankaya, I., Vural, I., and Kirtel, O. (2009). Field experiments on wave propagation and vibration isolation by using wave barriers. Soil Dyn. Earthq. Eng. 29, 824–833. doi: 10.1016/j.soildyn.2008.08.007

CrossRef Full Text | Google Scholar

Choudhury, D., Bharti, R. K., Chauhan, S., and Indraratna, B. (2008). Response of multilayer foundation system beneath railway track under cyclic loading. J. Geotech. Geoenviron. Eng. 134, 1558–1563. doi: 10.1061/(ASCE)1090-0241(2008)134:10(1558)

CrossRef Full Text | Google Scholar

Coulier, P., Cuéllar, V., Degrande, G., and Lombaert, G. (2015). Experimental and numerical evaluation of the effectiveness of a stiff wave barrier in the soil. Soil Dyn. Earthq. Eng. 77, 238–253. doi: 10.1016/j.soildyn.2015.04.007

CrossRef Full Text | Google Scholar

Crispino, M., and D'apuzzo, M. (2001). Measurement and prediction of traffic-induced vibrations in a heritage building. J. Sound Vibrat. 246, 319–335. doi: 10.1006/jsvi.2001.3648

CrossRef Full Text | Google Scholar

D'Apuzzo, M. (2007). “Some remarks on the prediction of road traffic induced ground-borne vibrations,” in Proceedings of the 4th International SIIV Congress (Palermo). 1–13.

Google Scholar

DIN 4150 (1999). Erschütterungen im Bauwesen Teil 1: Vorermittlung von Schwingungsgrößen. Einwirkungen auf Menschen in Gebäuden. Einwirkungen auf bauliche, Anlagen.

Google Scholar

Ekanayake, S. D., Liyanapathirana, D. S., and Leo, C. J. (2014). Attenuation of ground vibrations using in-filled wave barriers. Soil Dyn. Earthq. Eng. 67, 290–300. doi: 10.1016/j.soildyn.2014.10.004

CrossRef Full Text | Google Scholar

Gazetas, G. (1991). Formulas and charts for impedances of surface and embedded foundations. J. Geotech, Eng. 117, 1363–1381. doi: 10.1061/(ASCE)0733-9410(1991)117:9(1363)

CrossRef Full Text | Google Scholar

Haldar, S., and Sivakumar Babu, G. L. (2009). Improvement of machine foundations using reinforcement. Proc. Instit. Civil Eng. Ground Improve. 162, 199–204. doi: 10.1680/grim.2009.162.4.199

CrossRef Full Text | Google Scholar

Hegde, A. (2017). Geocell reinforced foundation beds-past findings, present trends and future prospects: a state-of-the-art review. Construct. Build. Mater. 154, 658–674. doi: 10.1016/j.conbuildmat.2017.07.230

CrossRef Full Text | Google Scholar

Hegde, A., and Sitharam, T. G. (2016). Behaviour of geocell reinforced soft clay bed subjected to incremental cyclic loading. Geomech. Eng. 10, 405–422. doi: 10.12989/gae.2016.10.4.405

CrossRef Full Text | Google Scholar

IRC: 37 (2012). Tentative Guidelines for the Design of Flexible Pavements. New Delhi: The Indian Roads Congress.

Google Scholar

IS 2720-29 (1975). Methods of Test for Soil - Part XXIX: Determination of Dry Density of Soils in-Place. Delhi: Prabhat Offset Press, 4–8.

Google Scholar

ISO, E. 10319. (2015). Geotextiles, Wide Width Tensile Test. Brussels: Comité Européen de Normalisation.

Google Scholar

Kim, M., Lee, P., Kim, D., and Kwon, H. (2000). “Vibration isolation using flexible rubber chip barriers,” in Proceedings of the International Workshop Wave (Rotterdam), 289–298.

Google Scholar

Loizos, A., Boukovalas, G., and Karlaftis, A. (2003). Dynamic stiffness modulus for pavement subgrade evaluation. J. Transp. Eng. 129, 434–443. doi: 10.1061/(ASCE)0733-947X(2003)129:4(434)

CrossRef Full Text | Google Scholar

Mandal, A., Baidya, D. K., and Roy, D. (2012). Dynamic response of the foundations resting on a two-layered soil underlain by a rigid layer. Geotech. Geol. Eng. 30, 775–786. doi: 10.1007/s10706-012-9497-2

CrossRef Full Text | Google Scholar

Massarsch, K. R. (2005). “Vibration isolation using gas-filled cushions,” in Soil Dynamics Symposium in Honor of Professor Richard D. Woods (Austin, TX), 1–20. doi: 10.1061/40780(159)7

CrossRef Full Text | Google Scholar

Miller, G. F., and Pursey, H. (1955). On the partition of energy between elastic waves in a semi-infinite solid. Proc. R. Soc. Lond. A 233, 55–69. doi: 10.1098/rspa.1955.0245

CrossRef Full Text | Google Scholar

Mitchell, J. K. (1981). “Soil improvement state-of-theart report,” in Proceedings of the Tenth International Conference on Soil Mehanics and Foundation Engineering (Stockholm), 509–565.

Google Scholar

Murillo, C., Thorel, L., and Caicedo, B. (2009). Ground vibration isolation with geofoam barriers: centrifuge modeling. Geotex. Geomembr. 27, 423–434. doi: 10.1016/j.geotexmem.2009.03.006

CrossRef Full Text | Google Scholar

Nimbalkar, S., and Indraratna, B. (2016). Improved performance of ballasted rail track using geosynthetics and rubber shockmat. J. Geotech. Geoenviron. Eng. 142:04016031. doi: 10.1061/(ASCE)GT.1943-5606.0001491

CrossRef Full Text | Google Scholar

Paolucci, R., Maffeis, A., Scandella, L., Stupazzini, M., and Vanini, M. (2003). Numerical prediction of low-frequency ground vibrations induced by high-speed trains at Ledsgaard, Sweden. Soil Dyn. Earthq. Eng. 23, 425–433. doi: 10.1016/S0267-7261(03)00061-7

CrossRef Full Text | Google Scholar

Saride, S., and Dutta, T. T. (2016). Effect of fly-ash stabilization on stiffness modulus degradation of expansive clays. J. Mater. Civil Eng. 28:04016166. doi: 10.1061/(ASCE)MT.1943-5533.0001678

CrossRef Full Text | Google Scholar

Thompson, D. J., Jiang, J., Toward, M. G. R., Hussein, M. F. M., Dijckmans, A., Coulier, P., et al. (2015). Mitigation of railway-induced vibration by using subgrade stiffening. Soil Dyn. Earthq. Eng. 79, 89–103. doi: 10.1016/j.soildyn.2015.09.005

CrossRef Full Text | Google Scholar

Thompson, D. J., Jiang, J., Toward, M. G. R., Hussein, M. F. M., Ntotsios, E., Dijckmans, A., et al. (2016). Reducing railway-induced ground-borne vibration by using open trenches and soft-filled barriers. Soil Dyn. Earthq. Eng. 88, 45–59. doi: 10.1016/j.soildyn.2016.05.009

CrossRef Full Text | Google Scholar

Timoshenko, S. P., and Goodier, J. N. (1970). Theory of Elasticity, 3rd Edn. New York, NY: McGraw-Hill. doi: 10.1115/1.3408648

CrossRef Full Text | Google Scholar

Ujjawal, K. N., Venkateswarlu, H., and Hegde, A. (2019). Vibration isolation using 3D cellular confinement system: a numerical investigation. Soil Dyn. Earthq. Eng. 119, 220–234. doi: 10.1016/j.soildyn.2018.12.021

CrossRef Full Text | Google Scholar

Venkateswarlu, H., and Hegde, A. (2018). Numerical analysis of machine foundation resting on the geocell reinforced soil beds. Geotech. Eng. 49, 55–62.

Google Scholar

Venkateswarlu, H., Ujjawal, K. N., and Hegde, A. (2018a). Laboratory and numerical investigation of machine foundations reinforced with geogrids and geocells. Geotex. Geomembr. 46,882–896. doi: 10.1016/j.geotexmem.2018.08.006

CrossRef Full Text | Google Scholar

Venkateswarlu, H., Ujjawal, K. N., and Hegde, A. (2018b). “FLAC based 3D numerical analysis of machine foundations resting on geosynthetics reinforced soil bed,” in Proceedings of the 11th International Conference on Geosynthetics (Seoul).

Google Scholar

Watts, G. R., and Krylov, V. V. (2000). Ground-borne vibration generated by vehicles crossing road humps and speed control cushions. Appl. Acoust. 59, 221–236. doi: 10.1016/S0003-682X(99)00026-2

CrossRef Full Text | Google Scholar

Welsh, J. P. (1986). “Construction considerations for ground modification projects,” in Proc. Intl. Conf. on Deep Foundations (Beijing).

Google Scholar

Wiss, J. F. (1981). Construction vibrations: state-of-the-art. J. Geotech. Geoenviron. Eng. 107:16030.

Google Scholar

Woods, R. D. (1968). Screening of surface waves in soils. J. Soil Mech. Found. Div. 94, 951–979.

Google Scholar

Nomenclature