Robustness Evaluation of Base-Isolation Building-Connection Hybrid Controlled Building Structures Considering Uncertainties in Deep Ground

An evaluation method of robustness of base-isolation building-connection hybrid controlled building structures is developed by introducing a measure for robustness (robustness function) and considering shallow and deep ground uncertainties. The earthquake ground-motion amplitude at the earthquake bedrock is evaluated by the Boore’s stochastic method including the fault rupture and the wave propagation into the earthquake bedrock. Then, the phase angle property at the earthquake bedrock is investigated by introducing the concept of phase difference, which is defined for each earthquake type. The ground-motion amplification in the shallow and deep ground is expressed by the one-dimensional wave propagation theory. The robustness of base-isolation building-connection hybrid controlled building structures is measured by use of the robustness function due to Ben-Haim (2006) and is evaluated by taking full advantage of the updated-reference-point method. It is shown that, as the total quantity of damping coefficients of connection dampers increases, the robustness for the deformation of the base-isolation story becomes larger without the drastic reduction of the robustness for the top acceleration.

Introduction

The great Tohoku earthquake occurred on March 11, 2011 and stuck the east part of Japan. Extensive areas of Tohoku district were attacked by many terrible tsunamis. Many high-rise buildings in Tokyo were also shaken by this aggressive earthquake although Tokyo is located 200–500 km far from the fault region. More specifically, a super high-rise steel building standing at the bay area of Osaka was shaken more severely regardless of the fact that Osaka is located about 800 km far from the fault region. Takewaki et al. (2011, 2013) pointed out that the deep ground characteristic of the building actually influenced such phenomenon. This means that the deep ground characteristic and its uncertainty should be studied carefully and taken into account in the design of super tall buildings. Unfortunately, this kind of long-period, long-duration ground motions was not considered in the design of super tall buildings, which were designed around 1960–1980.

The proper treatment of uncertainties in deep grounds seems difficult due to the lack of information (epistemic uncertainty) and the intrinsic randomness (aleatory uncertainty) (Abrahamson et al., 1998, Taniguchi and Takewaki, 2015). To respond to such issue, the interval analysis was introduced as a representative of the reliable analysis methods. It appears that the research field of interval analysis was introduced by Moore in 1966 (Moore, 1966). Afterward, a pioneering work was achieved by Alefeld and Herzberger (1983). Linear interval equations, nonlinear interval equations, and interval eigenvalue analysis were investigated by introducing interval arithmetic. It is well known that the interval arithmetic is a kind of mathematical tool for the sets of intervals introduced in 1924. Subsequently, the interval arithmetic algorithm was developed. To derive the bounds of static structural response, Qiu et al. (1996) used the interval arithmetic algorithm by introducing a convergent series expansion of the uncertain structural response. Furthermore, the interval arithmetic algorithm was extended to the Neumann series expansion of the inverse stiffness matrix by Qiu and Elshakoff (1998). Then, the envelopes of the static structural response were derived by Mullen and Muhanna (1999) with the aid of the interval arithmetic. Related works have been done by many researchers on the interval analysis for the static response or eigenvalue. Moens and Hanns (2011) provided a state of the art for the interval analysis. More recently, the interval analysis using Taylor series expansion was proposed in the references (Chen et al., 2002, 2009; Chen and Wu, 2004; Fujita and Takewaki, 2011; Fujita et al., 2015; Okada et al., 2016).

In this article, a method of robustness evaluation of base-isolation building-connection hybrid controlled building structures (Murase et al., 2013, 2014; Kasagi et al., 2016; Fukumoto and Takewaki, 2017) is proposed by introducing a measure for robustness (robustness function) due to Ben-Haim (2006) and considering shallow and deep ground uncertainties. Although the base-isolation building-connection hybrid controlled building structures are known (Murase et al., 2013, 2014; Kasagi et al., 2016; Fukumoto and Takewaki, 2017) to be effective both for impulsive and long-period and long-duration earthquake ground motions, the response sensitivity of such hybrid structures to uncertainties in ground properties is not necessarily clear. Therefore, it appears useful to investigate this sensitivity in terms of robustness measures under the condition that the fault–rupture mechanism, the wave propagation property and the ground amplification property are reflected appropriately.

The earthquake ground-motion amplitude at the earthquake bedrock is evaluated by using the Boore’s stochastic method (Boore, 1983) including the fault rupture and the wave propagation into the earthquake bedrock. Then, the phase angle property at the earthquake bedrock is investigated by introducing the concept of phase difference, which is defined for each earthquake type. The ground-motion amplification in the shallow and deep ground is expressed by the one-dimensional wave propagation theory. The robustness of base-isolation building-connection hybrid controlled building structures is measured by use of the robustness function due to Ben-Haim (2006). Since Ben-Haim (2006) introduced only the concept of the robustness function, a general practical solution method, called the updated-reference-point (URP) method, is used here. It is shown that, as the total quantity of damping coefficients of connection dampers increases, the robustness for the deformation of the base-isolation story becomes larger without the drastic reduction of the robustness for the top acceleration.

Generation of Earthquake Ground Motion at Free-Ground Surface

The schematic diagram of a scenario for evaluating the response of a base-isolation building-connection hybrid controlled structure is shown in Figure 1. The earthquake ground motion at the earthquake bedrock is generated by specifying the Fourier amplitude and the phase angle. There are many researches on the generation of simulated earthquake ground motions. In particular, the stochastic method is one of the most reliable methods (see Boore, 2003). Recently, some further developments have been made (Motazedian and Atkinson, 2005; Boore, 2009; Ghofrani et al., 2013; Yenier and Atkinson, 2015). The Fourier amplitude is obtained by using the Boore’s method (Boore, 1983), including the fault rupture and the wave propagation into the earthquake bedrock, which is based on the works due to Aki (1967), Brune (1970), and Kanamori and Anderson (1975). On the other hand, the phase property at the earthquake bedrock is constructed by introducing the phase difference, which is defined for each earthquake type (for example, Thrainsson and Kiremidjian, 2002; Yamane and Nagahashi, 2008). Once the earthquake ground motion at the earthquake bedrock is generated, the free-ground surface motion is obtained by using the one-dimensional wave propagation theory for the deep and shallow ground (Schnabel et al., 1972; Kramer, 1996).

FIGURE 1

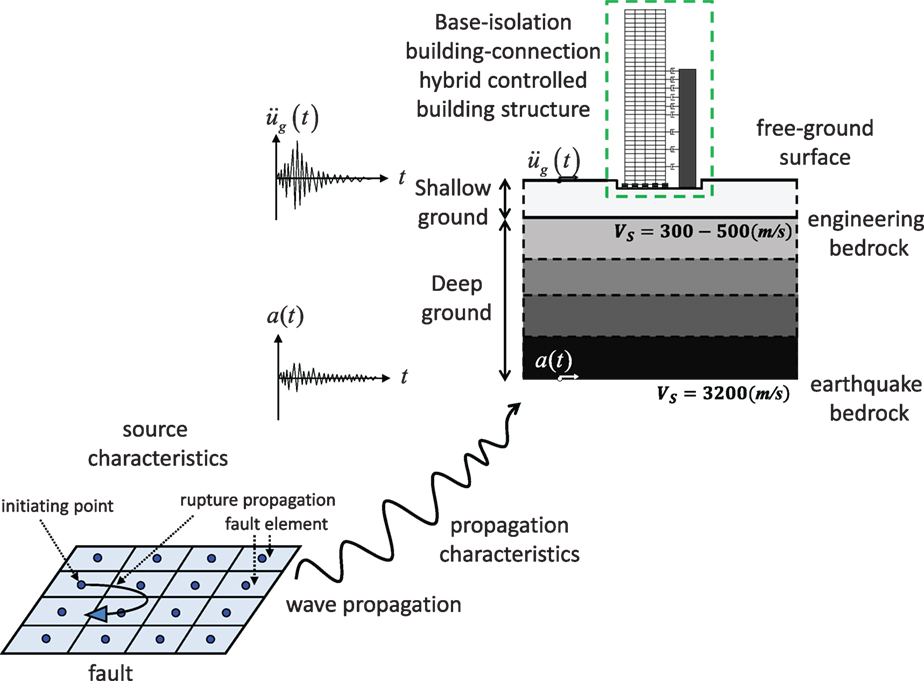
Figure 1. Schematic diagram of a scenario for evaluating the response of a base-isolation building-connection hybrid controlled structure taking into account the fault rupture, wave propagation, and ground-motion amplification in deep ground.

Generation of Earthquake Ground Motion at Earthquake Bedrock

The frequency-domain acceleration wave A(ω) at the earthquake bedrock can be expressed by the following equation:

$A\left(\mathrm{\omega }\right)=\left|A\left(\mathrm{\omega }\right)\right|e^{i\mathrm{\varphi }\left(\mathrm{\omega }\right)},$ (1)

where ϕ(ω) is the phase angle. On the other hand, the time-domain acceleration wave a(t) at the earthquake bedrock can be described by the following equation:

$a\left(t\right)={\displaystyle \sum _{k=0}^{N∕2}}{a}_k\cos \left({\mathrm{\omega }}_{k}t+{\mathrm{\varphi }}_k\right),$ (2)

where ω_k, a_k, and ϕ_k denote the kth circular frequency, the corresponding amplitude, and the corresponding phase angle.

The Fourier amplitude of the acceleration wave at the earthquake bedrock can be obtained by using the Boore’s method (Boore, 1983),

$\left|A\left(\mathrm{\omega }\right)\right|=C{M}_{0}S\left(\mathrm{\omega },{\mathrm{\omega }}_C\right)P\left(\mathrm{\omega },{\mathrm{\omega }}_m\right)\frac{e^{-\mathrm{\omega }R∕2Q{V}_s}}{R},$ (3)

where M₀, R, Q, V_s, and ω_m are the seismic moment, the fault distance, the Q-value, the shear wave velocity of the earthquake bedrock, and the cutoff circular frequency (ω_m = 2πf_m). The seismic moment M₀ is related to the moment magnitude M_w through $M_0={10}^{1.5\left(M_w+10.7\right)}$. Other parameters are given by the following equations:

$\begin{array}{l}\hfill C=\frac{R_{\mathrm{\theta }\varphi }\cdot \text{FS}\cdot \text{PRTITN}}{4\pi {\mathrm{\rho }}_E{V_s}^3},\end{array}$ (4a)

$\begin{array}{l}\hfill S\left(\mathrm{\omega },{\mathrm{\omega }}_C\right)=\frac{{\mathrm{\omega }}^2}{1+{\left(\mathrm{\omega }∕{\mathrm{\omega }}_C\right)}^2},\end{array}$ (4b)

$\begin{array}{l}\hfill {\mathrm{\omega }}_C=\frac{4.9\times 10^6}{2\pi }\times V_s{\left(\frac{\mathrm{\Delta }{\mathrm{\sigma }}_F}{M_0}\right)}^{1∕3},\end{array}$ (4c)

$\begin{array}{ll}\hfill P\left(\mathrm{\omega },{\mathrm{\omega }}_m\right)& ={\left\{1+{\left(\mathrm{\omega }∕{\mathrm{\omega }}_m\right)}^{2s}\right\}}^{-1∕2}\left(s=4\right),\end{array}$ (4d)

where R_θϕ, FS, PRTITN, ρ_E, and Δσ_F are the radiation pattern, the amplification due to the free surface (=2), the reduction factor that accounts for the partitioning of energy into two horizontal components $\left(=1∕\sqrt{2}\right)$, the mass density of the earthquake bedrock, and the stress drop.

Compared with the Fourier amplitude, the theory on the phase angle is quite limited (for example, Thrainsson and Kiremidjian, 2002; Yamane and Nagahashi, 2008). In this article, the phase difference is introduced to represent the phase angle characteristics depending on the earthquake type. This topic was introduced first by Ohsaki in 1979 (Ohsaki, 1979), and the related developments have been made. Especially, the research by Yamane and Nagahashi (2008) is used here,

${\mathrm{\varphi }}_{k+1}={\mathrm{\varphi }}_k+\mathrm{\Delta }{\mathrm{\varphi }}_k\left(k=1,2,\dots ,N∕2-1\right).$ (5)

In Eq. 5, $\mathrm{\Delta }\varphi$ denotes the phase difference and can be expressed in terms of the mean μ and the standard deviation (SD) σ,

$\mathrm{\Delta }\mathrm{\varphi }=-\left(\mathrm{\mu }+s\cdot \mathrm{\sigma }\right),$ (6)

where s is the Gaussian random number with 0 mean and unit SD. Due to the research by Yamane and Nagahashi (2008), the SD σ can be given in terms of the fault distance R for each earthquake type.

For inland earthquake,

$\mathrm{\sigma }∕\mathrm{\pi }=0.06+0.0003R.$ (7)

For plate boundary earthquake,

$\text{fault rupture direction}:\mathrm{\sigma }∕\mathrm{\pi }=0.05+0.0003R,$

$\begin{array}{l}\hfill \text{perpendicular to fault rupture}:\mathrm{\sigma }∕\mathrm{\pi }=0.08+0.0003R.\end{array}$ (8a,b)

Equation 7 indicates that the influence of directivity is small in inland earthquakes. Equations 7 and 8 were derived from the regression analysis for free-ground surface motions. Since it is known that the phase differences of the ground motions at the earthquake bedrock and the free-ground surface are similar, these relations are used also at the earthquake bedrock. Figure 2 shows some examples of the SD of phase difference given by Eqs 8a,b.

FIGURE 2

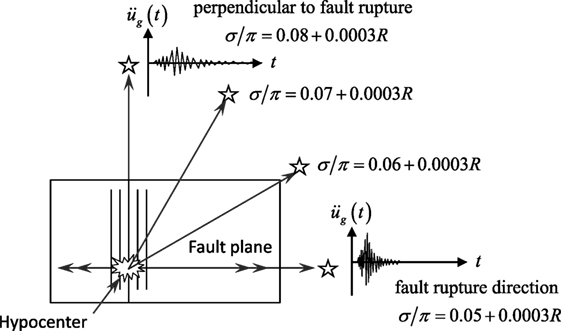
Figure 2. SD of phase difference at observation site for plate boundary earthquake [replotted based on Yamane and Nagahashi (2008)].

Figure 3 shows two examples of the relation of accelerograms with distributions of phase difference with different means of phase difference −0.5π, −1.5π for the plate boundary earthquake given by Eq. 8b. It can be observed that the mean of phase difference does not affect the maximum response of structures and influences only the location of time history (Ohsaki, 1979; Yamane and Nagahashi, 2008).

FIGURE 3

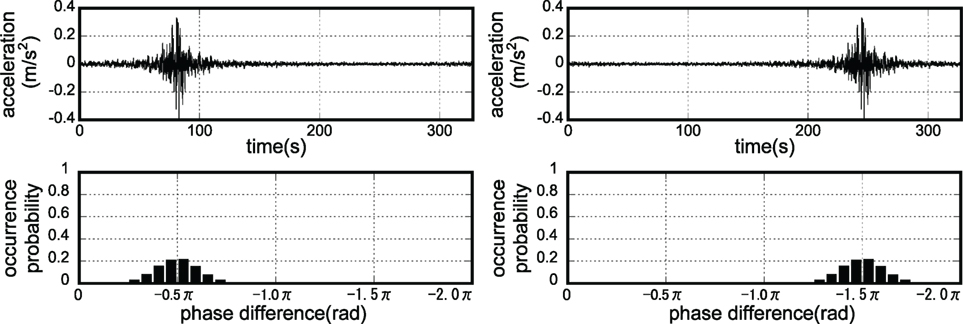
Figure 3. Accelerograms and distributions of phase difference with different means of phase difference −0.5π, −1.5π.

Amplification of Ground Motion in Deep and Shallow Ground

The free-ground surface acceleration ${Ü}_g\left(\mathrm{\omega }\right)$ in the frequency domain can be related to the frequency-domain acceleration wave A(ω) at the earthquake bedrock through

$\begin{array}{l}\hfill {Ü}_g\left(\mathrm{\omega }\right)=H_G\left(\mathrm{\omega }\right)A\left(\mathrm{\omega }\right).\end{array}$ (9)

This relation is based on the one-dimensional wave propagation theory (Schnabel et al., 1972; Kramer, 1996). Let G_i, ρ_i, V_i, and β_i denote the shear modulus, the mass density, the shear wave velocity, and the damping ratio, respectively, of the ith layer. The numbering of ground layer is made from the top (ground surface). H_G(ω) is the transfer function between the acceleration wave A(ω) at the earthquake bedrock and the free-ground surface acceleration ${Ü}_g\left(\mathrm{\omega }\right)$,

$\begin{array}{l}\hfill H_G\left(\mathrm{\omega }\right)=H_{G1}\left(\mathrm{\omega }\right)H_{G2}\left(\mathrm{\omega }\right)\cdots H_{\mathrm{GN}}\left(\mathrm{\omega }\right).\end{array}$ (10)

H_Gi(ω) in Eq. 10 can be expressed by the following equation:

$\begin{array}{l}\hfill H_{\mathrm{Gi}}\left(\mathrm{\omega }\right)=\frac{1}{\cos k_i{h}_i+i{\mathrm{\alpha }}_i\sin k_i{h}_i},\end{array}$ (11)

where k_i, ${G_i}^{\ast }$, and α_i are the complex wave number, the complex shear modulus, and the complex impedance, respectively, defined by the following equation:

$\begin{array}{lll}\hfill k_i=\mathrm{\omega }\sqrt{{\mathrm{\rho }}_i∕{G_i}^{\ast }},{G_i}^{\ast }=\left(1+2{\mathrm{\beta }}_{i}i\right)G_i,& & \hfill \\ \hfill {\mathrm{\alpha }}_i=\sqrt{{\mathrm{\rho }}_i{G_i}^{\ast }}∕\sqrt{{\mathrm{\rho }}_{i+1}{G_{i+1}}^{\ast }}.\end{array}$ (12)

Earthquake Response Considering the Fault Rupture, Wave Propagation, and Deep Ground Characteristics

The free-ground surface acceleration ${Ü}_g\left(\mathrm{\omega }\right)$ in the frequency domain obtained in the previous section is input to the base-isolation building-connection hybrid controlled building structure. The time-history response of the deformation u(t) of the base-isolation story in the hybrid model can be evaluated by using the following inverse Fourier transform:

$\begin{array}{ll}\hfill & u\left(t\right)=\frac{1}{2\pi }{\int }_{-\infty }^{\infty }U\left(\mathrm{\omega }\right)e^{i\mathrm{\omega }t}\mathrm{d}\mathrm{\omega }\\ \hfill & =\frac{1}{2\pi }{\int }_{-\infty }^{\infty }{H}_D\left(\mathrm{\omega }\right){Ü}_g\left(\mathrm{\omega }\right)e^{i\mathrm{\omega }t}\mathrm{d}\mathrm{\omega }& \hfill & \\ \hfill & (H_D\left(\mathrm{\omega }\right):\text{transfer function).}\end{array}$ (13)

The absolute acceleration at the top of the main building can also be obtained in a similar manner.

Robustness Evaluation Using Robustness Function

The robustness of the base-isolation building-connection hybrid controlled building structure is evaluated by using the robustness function introduced by Ben-Haim (2006). Although a concept for dealing with the robustness quantitatively was proposed by Ben-Haim, actual algorithms had to be developed later. Some simple examples were presented (Takewaki and Ben-Haim, 2005, 2008). However, further developments were needed for introducing general procedures. In this article, the URP method by Fujita and Takewaki (2011) is used. As the response parameters, the maximum deformation of the base-isolation story and the maximum absolute acceleration at the top of the main building are adopted.

To explain the robustness function, let us introduce the uncertain variables X(α) in terms of an uncertain parameter α,

$\begin{array}{l}\hfill X\left(\mathrm{\alpha }\right)=\left\{X_i^I\in R\left|\left[{X_i}^c-\mathrm{\alpha }\Delta X_i,{X_i}^c+\mathrm{\alpha }\Delta X_i\right],i=1,\dots ,N\right.\right\}.\end{array}$ (14)

In Eq. 14, ( )^I and [a, b] represent an interval parameter where the parameters a and b denote the lower and upper bounds of the interval parameter, respectively. Furthermore, ( )^c and Δ( ) indicate the nominal value of an interval parameter and half the varied range of the interval parameter, respectively.

Let f (X) and f_c denote the response (deformation or acceleration) of the structure with parameters X and its constrained value. The robustness function can then be defined as follows:

$\begin{array}{l}\hfill \widehat{\mathrm{\alpha }}\left(\tilde{X},f_c\right)=\max \left\{\mathrm{\alpha }\left|\max \left\{f\left(X^I\right)|X^I\in X\left(\mathrm{\alpha }\right)\right\}\right.<f_c\right\}.\end{array}$ (15)

In Eq. 15, it is necessary to specify a parameter α successively and conduct the maximization procedure for variables, which are defined by X(α). Since f (X) is not necessarily a convex function, the maximization procedure needs elaborated work. This procedure can be done by the interval analysis. In this section, the general-form interval analyses are explained which, use an approximation of first- and second-order Taylor series expansion. In the interval analysis, the uncertainty of parameters X is defined by the following equation:

$\begin{array}{l}\hfill X^I=\left[X^c-\mathrm{\Delta }X,X^c+\mathrm{\Delta }X\right].\end{array}$ (16)

When the uncertainty in M interval parameters is described by the interval vector as shown in Eq. 16, the feasible domain of interval parameters is expressed by an M-dimensional rectangle. The purpose of the robustness evaluation analysis is to find the upper and lower bounds of the objective function in this feasible domain. The general problem of interval analysis can be described as follows:

$\left.\begin{array}{cc}\hfill & \text{Find\hspace{0.17em}}\mathbf{X}\hfill \\ \hfill & \text{so as tomaximize}\left(\text{orminimize}\right)f\left(\mathit{\text{X}}\right)\hfill \\ \hfill & \text{subject\hspace{0.17em}to\hspace{0.17em}}\mathbf{X}\in {\mathit{\text{X}}}^I\hfill \\ \hfill \end{array}\right\}$ (17)

From the practical point of view, an efficient method was desired and developed, which can predict the upper and lower bounds of the objective function without huge computational load. For this purpose, the interval analysis using the approximation of Taylor series expansion has been developed so far. Among them, the URP method by Fujita and Takewaki (2011) is used in this article. The variation Δf of the objective function from the value f (X^c) at the nominal parameters X^c can be expressed by the following equation:

$\begin{array}{l}\hfill \mathrm{\Delta }f\left(d{X}_i\right)=\frac{1}{2}{f}_{,X_i{X}_i}{\left(d{X}_i+\frac{f_{,X_i}}{f_{,X_i{X}_i}}\right)}^2-\frac{f_{,{X_i}^2}}{2f_{,X_i{X}_i}},\end{array}$ (18)

where $d{X}_i=X_i-{X_i}^c$. In Eq. 18, $f_{,X_i}$ means the partial differentiation of the function f (X) with respect to X_i. Figure 4 shows the schematic algorithm of the URP method by Fujita and Takewaki (2011). More detailed explanation of the URP method can be found in Fujita and Takewaki (2011).

FIGURE 4

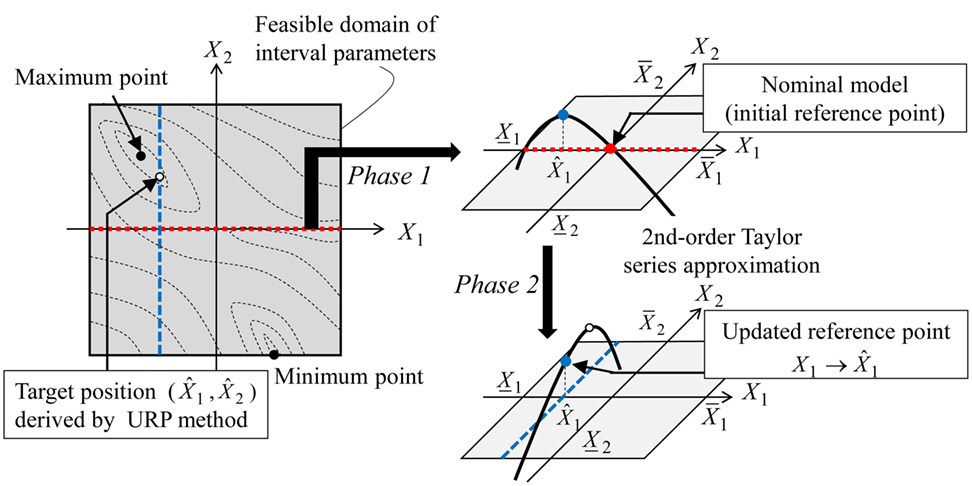
Figure 4. Schematic diagram of updated-reference-point (URP) method by Fujita and Takewaki (2011) (cited from Fujita and Takewaki, 2011).

Numerical Examples

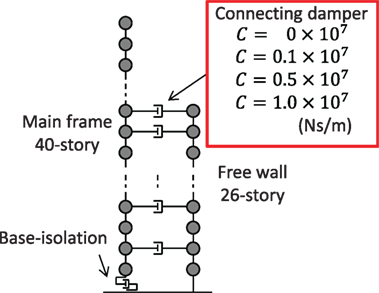
Numerical examples are presented in this section. The robustness of a base-isolation building-connection hybrid controlled building structure as shown in Figure 5 is evaluated for uncertain parameters in shallow and deep grounds.

FIGURE 5

Figure 5. Base-isolation building-connection hybrid controlled building structure.

Comparison of Simulated Ground Motions with Recorded Ground Motions

To investigate the validity of the present simulation method of ground motions, the comparison of simulated ground motions with recorded ground motions was made in the reference (Yamane and Nagahashi, 2008). The 2000 Western Tottori Prefecture earthquake (inland earthquake) and the 2003 Tokachi-oki earthquake (plate boundary earthquake) were taken as example ones. It was demonstrated that not only the overall shape of time-history response envelope and frequency content but also the response spectra exhibit good correspondence.

Examples of Robustness Evaluation

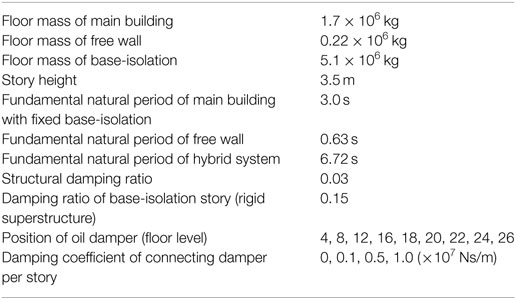
The parameters of a base-isolation building-connection hybrid controlled building structure are shown in Table 1. The number of stories of the main building is 40 and that of free wall is 26.

TABLE 1

Table 1. Structural parameters.

Case of Tokyo, Japan

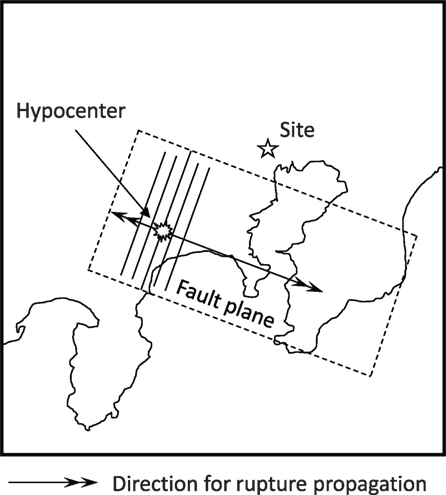
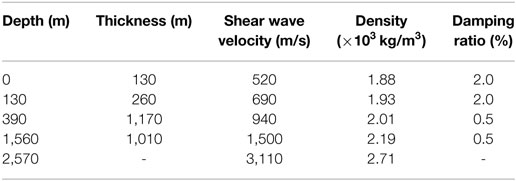
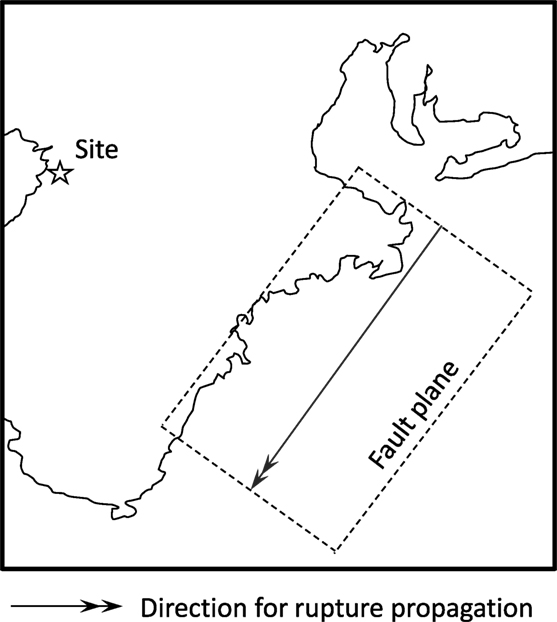
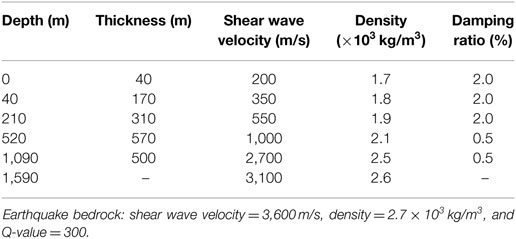
Consider a scenario of fault plane and hypocenter in Tokyo area (Great Kanto earthquake in 1923) as shown in Figure 6 (Kanamori, 1974; Wald and Somerville, 1995). Fault parameters are presented in Table 2. This earthquake is a plate boundary earthquake. The soil conditions at Chiyoda-ku, Tokyo are summarized in Table 3. The uncertain parameters are the thickness, shear wave velocity, mass density, and damping ratio of ground. Since there are four soils layers, the number of uncertain parameters is 16. The phase angle ϕ₁ for ω₁ was set to 0, and the mean of phase difference was set to μ = − π/2. Since the hypocenter-site direction is about π/3 from Figure 6, σ/π = 0.07 + 0.0003R was used.

FIGURE 6

Figure 6. Assumed fault plane and hypocenter in Tokyo area together with observed site.

TABLE 2

Table 2. Fault parameters of Great Kanto earthquake in 1923.

TABLE 3

Table 3. Soil conditions at Chiyoda-ku, Tokyo.

In the response analysis, five earthquake ground motions were generated at the earthquake bedrock, and the mean of the maximum responses was adopted as the maximum response for the evaluation of the robustness function.

Figure 7 shows a generated acceleration wave at the earthquake bedrock, a generated acceleration wave at the free-ground surface, and a generated deformation at the base-isolation story for two uncertainty levels $\widehat{\mathrm{\alpha }}=0,0.4$ of ground properties in Tokyo area. It can be found that, as the uncertainty level $\widehat{\mathrm{\alpha }}$ becomes larger, the acceleration waves at the free-ground surface and at the base-isolation story become larger, and the maximum deformation at the base-isolation story becomes larger considerably.

FIGURE 7

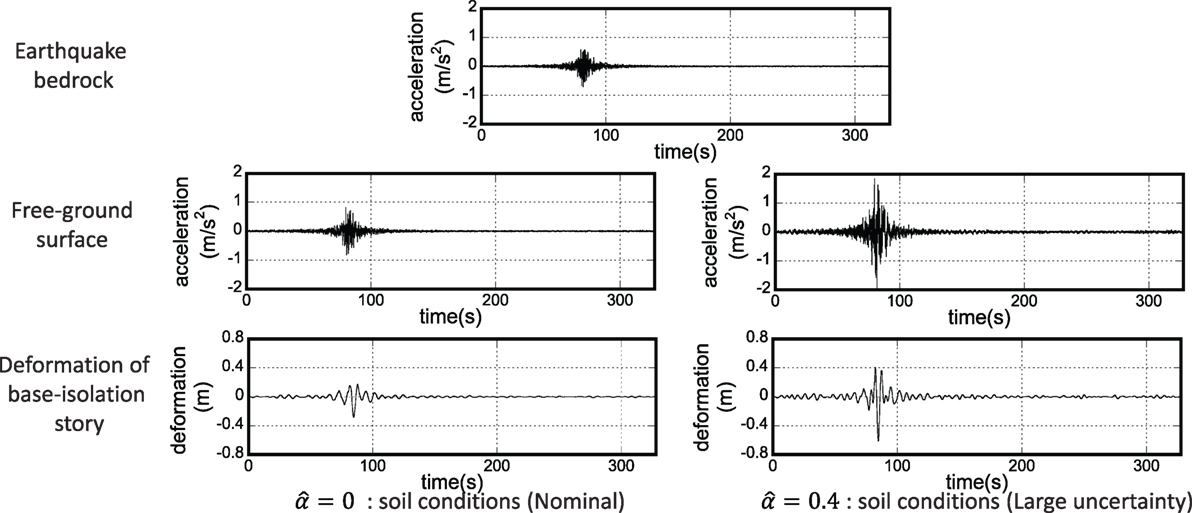
Figure 7. Generated acceleration wave at earthquake bedrock, generated acceleration wave at free-ground surface, and generated deformation at base-isolation story for two uncertainty levels $\widehat{\mathrm{\alpha }}=0,0.4$ of deep ground properties (Tokyo area).

Figure 8A shows the robustness function with respect to the deformation of the base-isolation story. It may be beneficial to note that, once the value $\widehat{\mathrm{\alpha }}$ in the vertical axis is fixed, the corresponding deformation of the base-isolation story in the horizontal axis indicates the maximum value for varied ground parameters prescribed by $\widehat{\mathrm{\alpha }}$. Especially, the deformation of the base-isolation story for $\widehat{\mathrm{\alpha }}=0$ indicates the maximum response for the nominal parameters of ground. It can be observed that, as the total quantity of the connecting dampers becomes larger, the robustness function for the deformation of the base-isolation story becomes larger. This means that the total quantity of the connecting dampers plays a key role for increasing the robustness of the base-isolation building-connection hybrid controlled building structure in terms of the deformation of the base-isolation story. The robustness function for C = 0 shows a non-monotonic curve. This may result from the local maximum in Eq. 17.

FIGURE 8

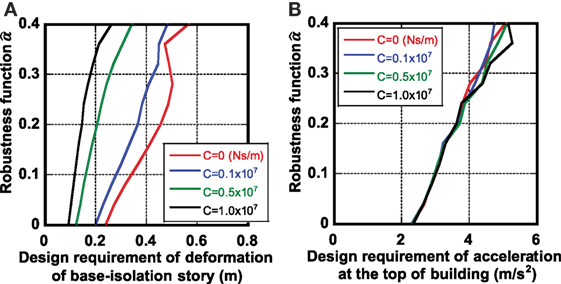
Figure 8. Robustness function with respect to design requirement, (A) deformation of the base-isolation story and (B) absolute acceleration at the top of the main structure (Tokyo area).

Figure 8B presents the robustness function with respect to the absolute acceleration at the top of the main structure. This indicates that, although the increase of the total quantity of the connecting dampers decreases the robustness for acceleration, its degree of decrease is not so large. In other words, this means that, while the increase of the total quantity of the connecting dampers is very beneficial for the increase of the robustness for the deformation of the base-isolation story, its influence on the performance degradation in the acceleration response is not large.

Case of Osaka, Japan

Consider a scenario of fault plane and hypocenter in Osaka area (Tonankai earthquake in 1944) as shown in Figure 9 (Kanamori, 1972). Fault parameters are presented in Table 4. This earthquake is also a plate boundary earthquake. The soil conditions at Kita-ku, Osaka are summarized in Table 5. As in the previous case for Tokyo area, uncertain parameters are the thickness, shear wave velocity, mass density, and damping ratio of ground. Since there are five soil layers, the number of uncertain parameters is 20. The phase angle ϕ₁ for ω₁ was set to 0, and the mean of phase difference was set to μ = − π/2 as in Tokyo area. Since the location of hypocenter was not determined, R was given approximately by 100 km, and Eq. 8B was used for σ/π.

FIGURE 9

Figure 9. Assumed fault plane and observed site in Osaka area.

TABLE 4

Table 4. Fault parameters of Tonankai earthquake in 1944.

TABLE 5

Table 5. Soil conditions at Kita-ku, Osaka.

As in the previous case for Tokyo area, five earthquake ground motions were generated at the earthquake bedrock, and the mean of the maximum responses was adopted as the maximum response for the evaluation of the robustness function.

Figure 10 shows a generated acceleration wave at the earthquake bedrock, a generated acceleration wave at the free-ground surface and a generated deformation at the base-isolation story for two uncertainty levels $\widehat{\mathrm{\alpha }}=0,0.4$ of ground properties in Osaka area. As in Tokyo area, it can be found that, as the uncertainty level $\widehat{\mathrm{\alpha }}$ becomes larger, the acceleration waves at the free-ground surface and at the base-isolation story become larger and the maximum deformation at the base-isolation story becomes larger considerably. It is interesting to note that, although the free-ground surface acceleration (about 0.8 m/s²) for $\widehat{\mathrm{\alpha }}=0.4$ in Osaka area is smaller than that (about 2 m/s²) in Tokyo area, the deformation of the base-isolation story in Osaka area is larger than that in Tokyo area. This may result from the relation between the fundamental natural period of the hybrid controlled building structure and the dominant period of the simulated ground motion at the free-ground surface.

FIGURE 10

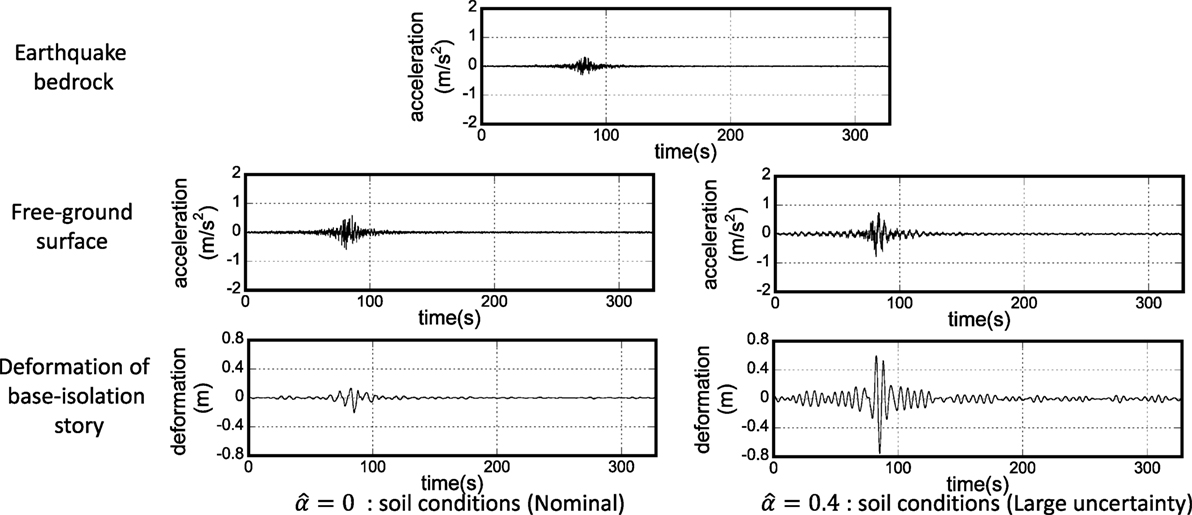
Figure 10. Generated acceleration wave at earthquake bedrock, generated acceleration wave at free-ground surface, and generated deformation at base-isolation story for two uncertainty levels $\widehat{\mathrm{\alpha }}=0,0.4$ of deep ground properties (Osaka area).

Figure 11A shows the robustness function with respect to the deformation of the base-isolation story. It can be observed that, as the total quantity of the connecting dampers becomes larger, the robustness function with respect to the deformation of the base-isolation story becomes larger as in Tokyo area. This means that the total quantity of the connecting dampers plays a key role for increasing the robustness of the base-isolation building-connection hybrid controlled building structure in terms of the deformation of the base-isolation story. It can also be found that, while the maximum deformation of the base-isolation story does not change so much in the small range of $\widehat{\mathrm{\alpha }}$, that increases drastically in the large range of $\widehat{\mathrm{\alpha }}$ (in the range of large uncertainty), especially, for smaller total quantity of the connecting dampers.

FIGURE 11

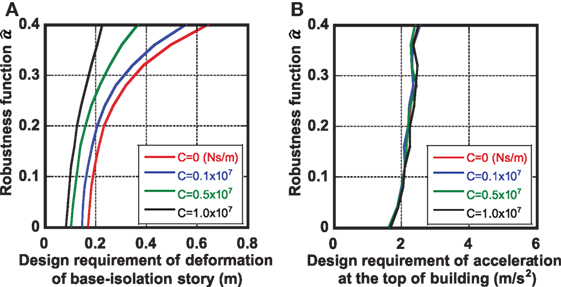
Figure 11. Robustness function with respect to design requirement, (A) deformation of the base-isolation story and (B) absolute acceleration at the top of the main structure (Osaka area).

Figure 11B presents the robustness function with respect to the absolute acceleration at the top of the main structure. This indicates that, although the increase of the total quantity of the connecting dampers decreases the robustness for acceleration, its degree of decrease is slight. In other words, this means that, while the increase of the total quantity of the connecting dampers is very beneficial for the increase of the robustness for the deformation of the base-isolation story, its influence on the performance degradation in the acceleration response is not large as in Tokyo area. Furthermore, it can also be observed that the increase of the absolute acceleration at the top of the main structure is so small for the increasing uncertainty level of ground. This phenomenon is completely different from that in Tokyo case.

It can be observed from Figures 8 and 11 that, because the fault distance in Tokyo area is smaller than that in Osaka area and the moment magnitude in Tokyo area is smaller than that in Osaka area, the deformation of the base-isolation story in Tokyo area is approximately equal to that in Osaka area. On the other hand, the acceleration at the top of the main building in Tokyo area is larger than that in Osaka area. This indicates that the robustness for the deformation of the base-isolation story and the robustness for the top-story acceleration with respect to ground uncertainties are greatly dependent on the moment magnitude and fault distance.

Conclusion

An evaluation method of robustness of base-isolation building-connection hybrid controlled building structures has been developed by introducing a measure for robustness (robustness function due to Ben-Haim, 2006) and considering shallow and deep ground uncertainties. The earthquake ground-motion amplitude at the earthquake bedrock has been evaluated by the Boore’s stochastic method including the fault rupture and the wave propagation into the earthquake bedrock. Then, the phase angle property at the earthquake bedrock has been constructed by introducing the concept of phase difference, which is defined for each earthquake type. The ground-motion amplification in the shallow and deep ground has been described by the one-dimensional wave propagation theory. The following conclusions have been drawn.

(1) An integrated evaluation method of robustness of base-isolation building-connection hybrid controlled building structures can be constructed for uncertain properties of shallow and deep grounds. The method consists of two parts, i.e., the part 1 is the generation of simulated ground motions at the earthquake bedrock, and the part 2 is the search of the worst combination of uncertain parameters. This method has been accomplished by combining the response evaluation system based on the Boore’s stochastic method for the fault rupture and the wave propagation to the earthquake bedrock and on the phase difference method with the method of robustness analysis using the robustness function.

(2) It has been shown that, as the total quantity of damping coefficients of connection dampers increases in the base-isolation building-connection hybrid controlled building structure, the robustness for the deformation of the base-isolation story becomes larger without the drastic reduction of the robustness for the top-story acceleration.

(3) The robustness for the deformation of the base-isolation story and the robustness for the top-story acceleration with respect to ground uncertainties are greatly dependent on the moment magnitude and fault distance. Earthquake structural engineers can grasp the sensitivity of deformation and acceleration response with respect to ground uncertainty level by using the proposed integrated evaluation method.

Author Contributions

KM formulated the problem, conducted the computation, and wrote the article. MM provided the parameter data and discussed the results. KK conducted the computation and discussed the results. IT supervised the research and wrote the article.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

Part of the present work is supported by the Grant-in-Aid for Scientific Research (KAKENHI) of Japan Society for the Promotion of Science (No. 15H04079, 17J00407). This support is greatly appreciated. The authors are grateful to Dr. K. Goda of University of Bristol and Dr. T. Yamane of Nikken Sekkei for their important comments on our research.

References

Abrahamson, N., Ashford, S., Elgamal, A., Kramer, S., Seible, F., and Somerville, P. (1998). Proc. of the 1st PEER Workshop on Characterization of Special Source Effects. San Diego: Pacific Earthquake Engineering Research Center, University of California, 1998.

Google Scholar

Aki, K. (1967). Scaling law of seismic spectrum. J. Geophys. Res. 72, 1217–1231. doi: 10.1029/JZ072i004p01217

CrossRef Full Text | Google Scholar

Alefeld, G., and Herzberger, J. (1983). Introduction to Interval Computations. New York: Academic Press, 1983.

Google Scholar

Ben-Haim, Y. (2006). Info-Gap Decision Theory: Decisions Under Severe Uncertainty, 2nd Edn. London: Academic Press.

Google Scholar

Boore, D. M. (1983). Stochastic simulation of high-frequency ground motions based on seismological models of the radiated spectra. Bull. Seismol. Soc. Am. 73, 1865–1894.

Google Scholar

Boore, D. M. (2003). Simulation of ground motion using the stochastic method. Pure Appl. Geophys. 160, 635–676. doi:10.1007/PL00012553

CrossRef Full Text | Google Scholar

Boore, D. M. (2009). Comparing stochastic point-source and finite-source ground-motion simulations: SMSIM and EXISIM. Bull. Seismol. Soc. Am. 99, 3202–3216. doi:10.1785/0120090056

CrossRef Full Text | Google Scholar

Brune, J. N. (1970). Tectonic stress and the spectra of seismic shear waves from earthquake. J. Geophy. Res. 75, 4997–5009. doi:10.1029/JB075i026p04997

CrossRef Full Text | Google Scholar

Chen, S. H., Lian, H., and Yang, X. (2002). Interval static displacement analysis for structures with interval parameters. Int. J. Numer. Methods Eng. 53, 393–407. doi:10.1002/nme.281

CrossRef Full Text | Google Scholar

Chen, S. H., Ma, L., Meng, G. W., and Guo, R. (2009). An efficient method for evaluating the natural frequency of structures with uncertain-but-bounded parameters. Comput. Struct. 87, 582–590. doi:10.1016/j.compstruc.2009.02.009

CrossRef Full Text | Google Scholar

Chen, S. H., and Wu, J. (2004). Interval optimization of dynamic response for structures with interval parameters. Comput. Struct. 82, 1–11. doi:10.1016/j.compstruc.2003.09.001

CrossRef Full Text | Google Scholar

Fujita, K., Kojima, K., and Takewaki, I. (2015). Prediction of worst combination of variable soil properties in seismic pile response. Soil Dyn. Earthq. Eng 77, 369–372. doi:10.1016/j.soildyn.2015.06.009

CrossRef Full Text | Google Scholar

Fujita, K., and Takewaki, I. (2011). An efficient methodology for robustness evaluation by advanced interval analysis using updated second-order Taylor series expansion. Eng. Struct. 33, 3299–3310. doi:10.1016/j.engstruct.2011.08.029

CrossRef Full Text | Google Scholar

Fukumoto, Y., and Takewaki, I. (2017). Dual control high-rise building for robuster earthquake performance. Front. Built. Environ. 3:12. doi:10.3389/fbuil.2017.00012

CrossRef Full Text | Google Scholar

Ghofrani, H., Atkinson, G. M., Goda, K., and Assatourians, K. (2013). Stochastic finite-fault simulations of the 2011 Tohoku, Japan, earthquake. Bull. Seismol. Soc. Am. 103, 1307–1320. doi:10.1785/0120120228

CrossRef Full Text | Google Scholar

Kanamori, H. (1972). Tectonic implications of the 1944 Tonankai and the 1946 Nankaido earthquakes. Phys. Earth Planet. Inter. 5, 129–139. doi:10.1016/0031-9201(72)90082-9

CrossRef Full Text | Google Scholar

Kanamori, H. (1974). Long-period ground motion in the epicentral area of major earthquakes. Tectonophysics 21, 341–356. doi:10.1016/0040-1951(74)90002-X

CrossRef Full Text | Google Scholar

Kanamori, H., and Anderson, L. (1975). Theoretical basis of some empirical relations in seismology. Bull. Seismol. Soc. Am. 65, 1073–1095.

Google Scholar

Kasagi, M., Fujita, K., Tsuji, M., and Takewaki, I. (2016). Automatic generation of smart earthquake-resistant building system: hybrid system of base-isolation and building-connection. Heliyon 2, e00069. doi:10.1016/j.heliyon.2016.e00069

PubMed Abstract | CrossRef Full Text | Google Scholar

Kramer, S. L. (1996). Geotechnical Earthquake Engineering. Upper Saddle River, NJ: Prentice Hall.

Google Scholar

Moens, D., and Hanns, M. (2011). Non-probabilistic finite element analysis for parametric uncertainty treatment in applied mechanics: recent advances. Finite Elem. Anal. Des. 47, 4–16. doi:10.1016/j.finel.2010.07.010

CrossRef Full Text | Google Scholar

Moore, R. E. (1966). Interval Analysis. Englewood Cliffs, New Jersey: Prentice-Hall, 1966.

Google Scholar

Motazedian, D., and Atkinson, G. M. (2005). Stochastic finite-fault modeling based on a dynamic corner frequency. Bull. Seismol. Soc. Am. 95, 995–1010. doi:10.1785/0120030207

CrossRef Full Text | Google Scholar

Mullen, R. L., and Muhanna, R. L. (1999). Bounds of structural response for all possible loading combinations. J. Struct. Eng. ASCE 125, 98–106. doi:10.1061/(ASCE)0733-9445(1999)125:1(98)

CrossRef Full Text | Google Scholar

Murase, M., Tsuji, M., and Takewaki, I. (2013). Smart passive control of buildings with higher redundancy and robustness using base-isolation and inter-connection. Earthq. Struct. 4, 649–670. doi:10.12989/eas.2013.4.6.649

CrossRef Full Text | Google Scholar

Murase, M., Tsuji, M., and Takewaki, I. (2014). Hybrid system of base isolation and building connection for control robust for broad type of earthquake ground motions. J. Struct. Eng. AIJ 60, 413–422.

Google Scholar

Ohsaki, Y. (1979). On the significance of phase content in earthquake ground motions. Earthq. Eng. Struct. Dyn. 7, 427–439. doi:10.1002/eqe.4290070504

CrossRef Full Text | Google Scholar

Okada, T., Fujita, K., and Takewaki, I. (2016). Robustness evaluation of seismic pile response considering uncertainty mechanism of soil properties. Innov. Infrastruct. Solut. 1:5. doi:10.1007/s41062-016-0009-8

CrossRef Full Text | Google Scholar

Qiu, Z. P., Chen, S. H., and Song, D. (1996). The displacement bound estimation for structures with an interval description of uncertain parameters. Commun. Numer. Methods Eng. 12, 1–11. doi:10.1002/(SICI)1099-0887(199601)12:1<1::AID-CNM884>3.0.CO;2-N

CrossRef Full Text | Google Scholar

Qiu, Z. P., and Elshakoff, I. (1998). Antioptimization of structures with large uncertain- but-nonrandom parameters via interval analysis. Comput. Methods Appl. Mech. Eng. 152, 361–372. doi:10.1016/S0045-7825(96)01211-X

CrossRef Full Text | Google Scholar

Schnabel, P. B., Lysmer, J., and Seed, H. B. (1972). SHAKE: A Computer Program for Earthquake Response Analysis of Horizontally Layered Sites. A computer program distributed by NISEE/Computer Applications. Berkeley: The University of California.

Google Scholar

Takewaki, I., and Ben-Haim, Y. (2005). Info-gap robust design with load and model uncertainties, special issue: uncertainty in structural dynamics. J. Sound Vib. 288, 551–570. doi:10.1016/j.jsv.2005.07.005

CrossRef Full Text | Google Scholar

Takewaki, I., and Ben-Haim, Y. (2008). “Chapter 19—Info-gap robust design of passively controlled structures with load and model uncertainties,” in Structural Design Optimization Considering Uncertainties, eds Y. Tsompanakis, N. D. Lagaros, and M. Papadrakakis (Leiden: Taylor & Francis), 531–548.

Google Scholar

Takewaki, I., Fujita, K., and Yoshitomi, S. (2013). Uncertainties in long-period ground motion and its impact on building structural design: case study of the 2011 Tohoku (Japan) earthquake. Eng. Struct. 49, 119–134. doi:10.1016/j.engstruct.2012.10.038

CrossRef Full Text | Google Scholar

Takewaki, I., Murakami, S., Fujita, K., and Tsuji, M. (2011). The 2011 off the Pacific coast of Tohoku earthquake and response of high-rise buildings under long-period ground motions. Soil Dyn. Earthq. Eng. 3, 1511–1528. doi:10.1016/j.soildyn.2011.06.001

CrossRef Full Text | Google Scholar

Taniguchi, M., and Takewaki, I. (2015). Bound of earthquake input energy to building structure considering shallow and deep ground uncertainties. Soil Dyn. Earthq. Eng 77, 267–273. doi:10.1016/j.soildyn.2015.05.011

CrossRef Full Text | Google Scholar

Thrainsson, H., and Kiremidjian, S. A. (2002). Simulation of digital earthquake accelerograms using the inverse discrete Fourier transform. Earthq. Eng. Struct. Dyn. 31, 2023–2048. doi:10.1002/eqe.198

CrossRef Full Text | Google Scholar

Wald, D. J., and Somerville, P. G. (1995). Variable-slip rupture model of the great 1923 Kanto Japan earthquake. Bull. Seismol. Soc. Am. 85, 159–177.

Google Scholar

Yamane, T., and Nagahashi, S. (2008). “A generation method of simulated earthquake groung motion considering phase difference characteristics,” in Proc. of the 14th World Conference on Earthquake Engineering (Beijing, China).

Google Scholar

Yenier, E., and Atkinson, G. M. (2015). Regionally adjustable generic ground-motion prediction equation based on equivalent point-source simulations: application to Central and Eastern North America. Bull. Seismol. Soc. Am. 105, 1989–2009. doi:10.1785/0120140332

CrossRef Full Text | Google Scholar