Tsunami-Driven Debris Motion and Loads: A Critical Review

Recent natural disasters, such as the 2004 Indian Ocean and 2011 Tohoku Tsunami, exhibited the importance of tsunami-resistant infrastructure in high-risk coastal areas. The failure of critical infrastructure in tsunami-stricken communities has led to a recent emphasis on extreme loading conditions associated with tsunami events. One of the critical loads identified by previous research was debris loads. Debris is defined as solid objects entrained within the inundating flows and can range from construction materials to shipping vessels. The emphasis of tsunami loading has led to recent progression in the understanding of debris loads and effects, particularly in evaluating the impact of a single debris piece on a structure. The following paper reviews state-of-the-art research in tsunami-driven debris motion and loads and identifies future directions of research into debris loads and effects to aid in the design of tsunami-resistant infrastructure.

Introduction

Tsunamis are among the most destructive and deadly natural disasters. Several recent events, such as the 2004 Indian Ocean Tsunami, the 2010 Chilean Tsunami, and the 2011 Tohoku Tsunami, have emphasized the importance of studying tsunami-induced loading conditions. The failure of critical infrastructure (Yeh et al., 2014) and the lack of a clear understanding of the tsunami-induced loading conditions highlighted the deficiency of current building design in tsunami-prone areas (Taubenböck et al., 2013). In the aftermath of tsunami events, reviews of current building standards have clearly shown that existing standards do not properly account for, or in some cases explicitly address, tsunami loads and effects (Palermo et al., 2009). These findings have led to an increased emphasis on the need to understand tsunami flow conditions and associated loads by researchers, engineers, and policy makers in an attempt to design tsunami-resilient infrastructure. In North America, this effort resulted in the addition of a new chapter in the upcoming ASCE Minimum Design Loads for Buildings and Other Structures (ASCE 7, 2016) for the design of structures in tsunami-prone areas of the United States: West Coast, Alaska, and Hawaii (Chock, 2016).

Tsunami engineering research has primarily focused on hydrodynamic loading, as generally field observations have identified hydrodynamic conditions as the critical load (Charvet et al., 2014). Additionally, information regarding critical flow features, such as maximum inundation and run-up, is available from post-tsunami field surveys. However, many field observations of tsunami-affected built areas have shown that debris loads and effects can play an important role in structural failure (Yeh et al., 2013). Until recently, existing guidelines have conservatively addressed debris impact recommending that all structures be designed for the impact of a single object (FEMA, 2012). Similarly, in research, the focus has been on quantifying the load of a single debris impact (Haehnel and Daly, 2004; Matsutomi, 2009; Aghl et al., 2015). Another aspect in the design of tsunami-resilient infrastructure is the identification of critical areas for debris impact. This aspect has been significantly more difficult due to the random nature of debris motion (Matsutomi, 2009) and to the wide range of variables that affect debris motion (Naito et al., 2014).

The objective of this review is to (1) evaluate the current state-of-the-art research into tsunami-driven debris motion and loads, (2) indicate areas of research needs, (3) highlight results from a collaborative research effort by the University of Ottawa, Canada, the University of Hannover, Germany, and Waseda University, Japan, to develop new experimental methods to evaluate debris motion, and, finally, (4) evaluate debris impact loads on structures. These objectives have been reached by conducting a comprehensive literature review and further drawing conclusions regarding research gaps and outlining the methodological requirements and facilities to address current and future research needs.

Literature Review

Debris Transport

The focus of post-tsunami forensic engineering surveys of affected coastal communities has primarily evaluated the hydraulic conditions of the tsunami inflow, such as inundation depth, flow velocity, and spatial inundation limits (Saatcioglu et al., 2005; Borrero et al., 2006; Fritz et al., 2006). However, information regarding debris impact cannot easily be identified from the field data, aside from the fact that debris impact may have occurred. Critical information such as the flow conditions, debris velocity, and debris orientation at the time of impact cannot be determined without a video or images of the impact (Charvet et al., 2014). Therefore, very little information regarding debris dynamics within extreme hydrodynamic flows can be derived directly from field impact sites in the aftermath of a disaster.

Debris motion has been equally challenging to evaluate in the field, as the type of debris can vary significantly and few studies have performed a comprehensive survey of debris in the aftermath of a tsunami event. Any rigid or deformable objects entrained within the inundating flow, such as construction materials, vehicles, or shipping vessels, all common to many coastal communities, can become debris (Naito et al., 2014). Additionally, multiple potential debris sources make the identification of the source of debris challenging, particularly in the post-event site surveys. The work of Naito et al. (2014) was among the first field survey to examine overall transport of the debris after the 2011 Tohoku Tsunami. Naito et al. (2014) examined the position of displaced shipping containers and vessels after the 2011 Tohoku Tsunami as they originated from a clear source (the port area) for which substantial documentation of their position before the tsunami existed. From the survey, Naito et al. (2014) were able to develop a conservative estimate of the maximum spreading angle of the shipping vessels in relation to their original location.

Based on the identified sources and subsequent field investigations, Naito et al. (2014) proposed a method to determine the maximum spreading area of the debris. Their method considered the origin of the debris as the geometric center of the debris source (black dot in Figure 1). The debris was assumed to propagate in a shore normal direction (dashed line) and conservatively estimated to propagate within a ±22.5° spreading sector in the inundation direction to the onshore extent of the tsunami inundation limit. From the point if maximum debris displacement, a similar ±22.5° spreading sector was considered as a potential motion area a result of the outgoing flow. Based on the limited observations collected from field data, the majority of debris fell well within the proposed spreading angle.

FIGURE 1

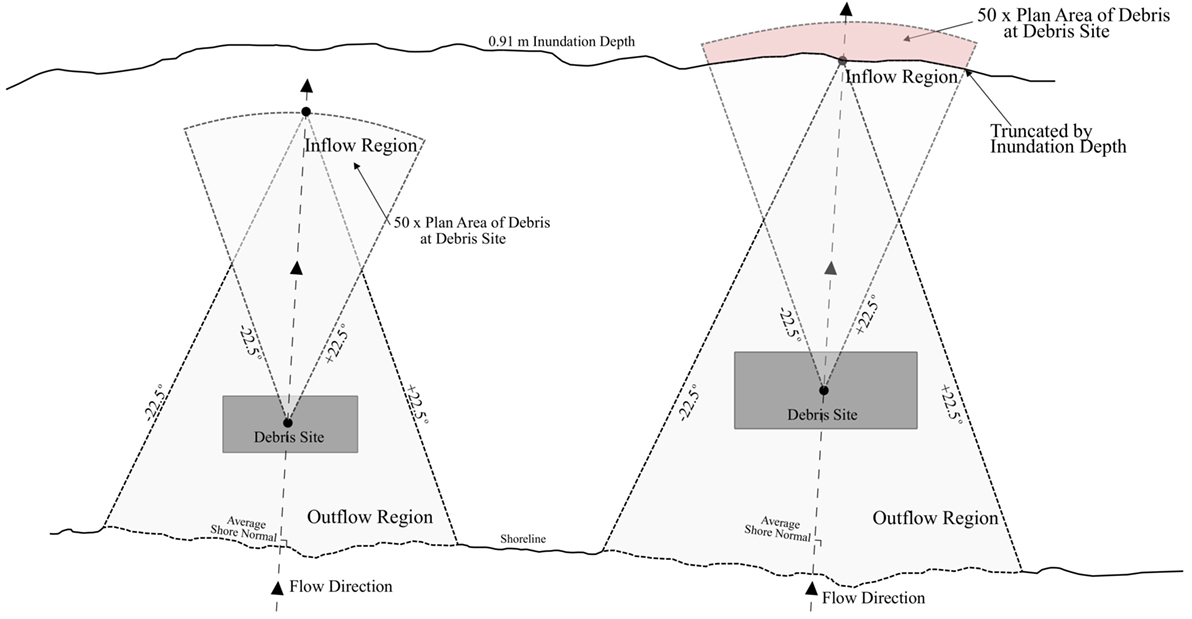
Figure 1. Identification of area for potential debris impact [adapted from Naito et al. (2014)].

The maximum displacement limit of the debris was calculated based on the debris concentration, which was defined as the plane area of the debris at the source divided by the spreading area of the debris. A conservative estimate was made to establish a debris concentration of 2% that would contain the majority of the debris. The debris limits for the inundating flow are defined by the ±22.5° sector area defining a spreading area that gave a debris concentration of 2% (50 times the plane area of the debris), termed the inflow region. However, if the spreading area encroached on an area where the inundation depth is less than 0.91 m (the “prescribed” floatation threshold for debris), this area is not considered as it was expected that debris would ground and no longer propagate forward (red area in Figure 1). As a result, the maximum inundation limit of the debris would be truncated. Additionally, from the center of the inundation limit, a return spreading area can be again determined using the ±22.5° conical area from the inundation limit toward the shoreline. The second area represents the potential spreading sector as a result of the outflow and is termed the outflow region. Based on the method outlined by Naito et al. (2014), any critical structures located within the two spreading areas (indicated by the light gray area in Figure 1) should be designed for debris impact. A detailed design example using this method can be found in Naito et al. (2016).

While the method of Naito et al. (2014) provided a conservative approach to evaluating the debris impact potential, several assumptions are associated with their proposed method. The topography of the spreading area has a substantial influence on the flow conditions and therefore the debris motion. Naito et al. (2016) indicated that, in cases with large topographical features that would divert flow, the spreading area should be shifted to account for these irregularities. Naito et al. (2014) also indicated that buildings could act as obstacles in the path of debris motion. In the case of industrial areas, large reinforced concrete buildings would act as a barrier to debris motion as long as the inundation depths were less than 0.91 m than the top of the building. However, in cases where the inundation depths’ area greater than 0.91 m above the maximum height of the building or when the surrounding buildings are likely to be destroyed by the inundating flow (wooden structures), the buildings should not be considered as obstacles to the debris. Additionally, the method only examined one type of debris whereas debris are of wide variety of sizes and properties, such as buoyancy, that would influence their propagation distance.

To provide a larger dataset examining the spreading area of debris in tsunami-like flow conditions, Nistor et al. (2016) examined the transport of multiple scaled-down shipping containers in controlled laboratory conditions, over a flat horizontal topography and with no obstacles. The study found that the spreading angle of the debris increased as the number of debris increased. This was attributed to the inter-debris collisions and flow perturbations caused by the debris within the flow. Nevertheless, the motion trajectories of all debris occurred well within the spreading angle of ±22.5° proposed by Naito et al. (2014). Nistor et al. (2016) determined that as the number of debris increased, the longitudinal displacement of the debris decreased. The latter conclusion counters the method proposed by Naito et al. (2014), which suggested that as the number of debris increased, the spreading area also increased. Additionally, Nistor et al. (2016) noted that the debris tended to propagate as an agglomeration which counters assumptions, made in the FEMA P646 (FEMA, 2012), that the likelihood of multiple debris impacts occurring is unlikely.

Goseberg et al. (2016b) built upon the study of Nistor et al. (2016) by including a scaled-down built environment, to act as obstacles to the propagating debris. Their study found that the obstacles acted as a macro-roughness feature for both the debris and inundating flow, resulting thus in significantly shorter longitudinal displacements of the debris. However, the obstacles appeared to have no influence on the spreading angle and the debris once again fell well within the ±22.5° spreading angle proposed by Naito et al. (2014). Due to scaling issues related to debris transport in a scaled experimental environment, further work is needed to properly understand the momentum transfer for debris–debris and debris–fluid interactions to possibly amend the method proposed by Naito et al. (2014).

There are still multiple challenges that must be overcome to properly model debris motion in a reduced scale experimental setting. The foremost issue is the scaling of tsunami flow conditions (Madsen et al., 2008; Rossetto et al., 2011; Goseberg et al., 2013). Related to debris transport, the motion of debris was shown to be a highly variable process (Bocchiola et al., 2006; Matsutomi, 2009). Hence, extensive information is required to obtain meaningful results. To retrieve the necessary information, tracking of the debris’ transient motion requires experimental methods that do not influence the debris motion while providing high-quality data regarding the debris’ position, orientation, acceleration, and velocity.

Braudrick and Grant (2000) examined the entrainment of individual large woody debris (LWD) in steady flow conditions. Experiments were performed to test a simple entrainment model of a single piece of LWD based on a balance of forces as depicted in Figure 2. The original model considered the LWD as a smooth cylinder lying on a smooth bed; however, the debris cross-sectional geometry may also be rectangular. The initial movement of the LWD was by sliding, though Braudrick and Grant (2000) noted that the initial movement tends to be more complex with significant pivoting involved. Figure 2 outlines the basic force balance used in the model considering a flow downstream with a channel of slope θ. The gravity force is the effective weight (W_eff = F_g − F_Buoyant) of the debris. The friction force (F_f = F_Nμ) acts in the upstream direction and is a function of the normal force (F_N) and the friction coefficient (μ) between the bed and the LWD. The drag force (F_d) is a function of the water velocity, flow depth, drag coefficient, and angle that the log is traveling in relation to the flow direction. The model performed reasonably well under experimental scrutiny though the pivoting, which was not captured by the model, was an important aspect of the LWD motion.

FIGURE 2

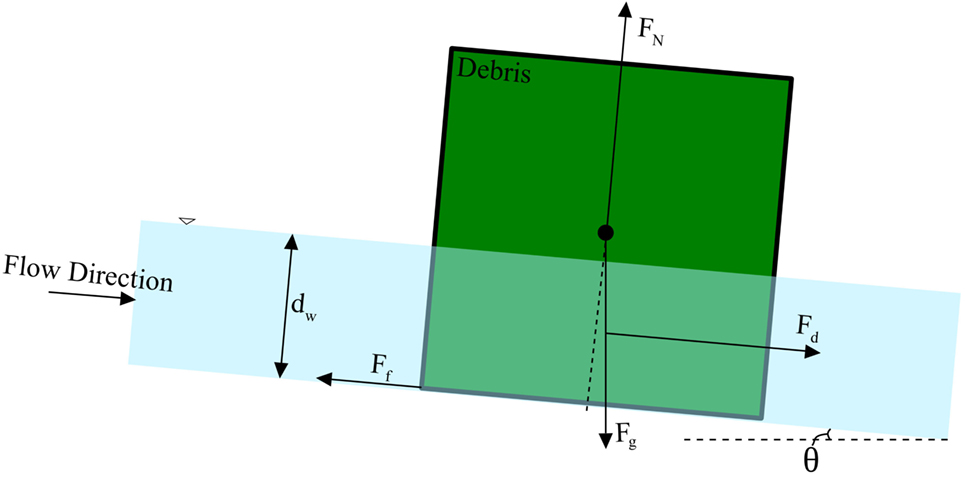
Figure 2. Debris entrainment force balance [adapted from Braudrick and Grant (2000)].

Imamura et al. (2008) experimentally evaluated the transport of boulders in a dam-break flow and developed a simple model for estimating their motion. Imamura et al. (2008) determined that the boulders tended to be transported by saltation or rolling initially (within the higher velocity flow). When flow velocity began to decrease, as the bore reached the point of maximum inundation and as the bore receded, the boulders would be transported by sliding. Their study also found that the debris orientation affected the motion of the boulder. The boulder would always pivot to have the long axis perpendicular to the flow direction, using some of the hydrodynamic energy, resulting thus in the boulder aligning with the long axis perpendicular to the flow and having thus a greater displacement under inflow conditions.

The model developed by Imamura et al. (2008) was based on a force balance of the boulder in contact with the ground. The forces to be considered for the boulder transport are the hydraulic force, the frictional force, and the component of the gravitational force on the slope. The balance of these forces resulted in:

$\begin{array}{ll}\hfill {\mathrm{\rho }}_s{k}_r{d}^{3}X″& =\frac{1}{2}{C}_D{\mathrm{\rho }}_f\left(U-v\right)\left|U-u\right|\left(k_r{d}^2\right)+C_M{\mathrm{\rho }}_{f}U\prime \left({\mathit{kd}}^3\right)-\left(C_M-1\right){\mathrm{\rho }}_{f}u\prime \left(k_r{d}^3\right)\\ & -k_r{F}_b-k_r{F}_g,\end{array}$ (1)

$\begin{array}{l}\hfill F_b=\frac{\mathrm{\mu }\left({\mathrm{\rho }}_s-{\mathrm{\rho }}_f\right)k_r{d}^{3}g\cos \mathrm{\theta }X\prime }{\left|X\prime \right|},\end{array}$ (2)

$\begin{array}{l}\hfill F_g=\left({\mathrm{\rho }}_s-{\mathrm{\rho }}_f\right)k{d}^{3}g\sin \mathrm{\theta },\end{array}$ (3)

where ρ_s is the density of the boulder, k_r is the ratio between the long axis and short axis of the boulder, d is the length of the short axis, u′ is the acceleration of the boulder, C_D is the drag coefficient, ρ_f is the density of the fluid, U is the current velocity, u is the velocity of the boulder, θ is the angle of topographic slope, μ is the coefficient of friction, and C_M is the mass coefficient. This model tends to underestimate the propagation of the boulders, likely because the friction was always considered (even when saltation or rolling occurred) and the model does not consider the initial pivoting of the boulder, influencing thus the exposed surface area of the debris.

Matsutomi et al. (2008) examined the correlation between debris concentration and debris velocity as well as the hydrodynamic conditions in a dam-break flow. Debris concentration was expressed as the void ratio (1 − plan area of debris/area of flume bed). An increase in the debris concentration resulted in increased flow resistance in the bore front. The flow resistance in turn increased bore depth as well as decreased debris velocity and bore front propagation. The debris velocity was found to be always less than or equal to the bore front velocity.

Matsutomi (2009) evaluated the motion of driftwood pieces in steady-state, high-velocity flow to determine the probability of the driftwood colliding with a structure. The probability of impact was determined based on the lateral diffusion (y-direction) of the driftwood as the driftwood propagated downstream, therefore assuming that the structure would be in the center of the flume. The Gaussian probability distribution of the driftwood location (K_y) in the x- and y-direction was expressed as:

$K_y\left(x,y\right)=\frac{1}{\sqrt{2\pi \overline{{\mathrm{\delta }}_y}}}\exp \left(-\frac{{\left(y-\overline{y}\right)}^2}{2{\overline{{\mathrm{\delta }}_y}}^2}\right),$ (4)

where $\overline{{\mathrm{\delta }}_y}$ is the variance as a function of x (flow direction), roughly expressed as:

$\frac{{\overline{{\mathrm{\delta }}_y}}^2\left(x\right)}{L_w^2}=\frac{\frac{1}{n}{\sum }_{i=1}^n\left(y-\overline{y}\right)}{L_w^2}=a{\left(\frac{x}{L_w}\right)}^b,$ (5)

where L_w is the length of the driftwood, a and b are a function of the debris’ physical properties and geometry. Extensive work is still needed in the classification of the a and b coefficients due to the variety of debris that are potentially present during a tsunami (Naito et al., 2014). The mere utilization of wooden debris with uniform draft restrains the validity of such approach in relation with different material debris.

As a preliminary investigation of debris motion in tsunami-like flow conditions, Yao et al. (2014) evaluated the motion of scaled-down coastal house models in flow conditions developed by the shoaling and subsequent breaking of a solitary wave over a sloping bed. Their study examined the maximum debris inundation compared to the limit of the maximum flow inundation. The debris initially propagated within the overflow of the bore due to high flow velocities and water depths. As the overflow approached maximum inundation, the flow velocity and depth decreased, resulting in the debris contacting the bed and slowing down, falling thus behind the advancing bore front. In the case of smaller offshore waves, the debris fell behind the bore front earlier due to an earlier contact with the bed. For the most part, the debris were unaffected by the receding flow, except when they had grounded significantly earlier and were thus much closer to the coastline. The receding wave, in this case, pulled the debris further seaward than their initial position.

Recent improvements in non-intrusive laboratory techniques for tracking debris motion have allowed for more a more detailed evaluation of the intermediate variables important for debris motion, such as changes in their orientation during displacement as well as their velocity (Goseberg et al., 2016a; Stolle et al., 2016). Rueben et al. (2014) used a novel camera-based tracking algorithm to assess the repeatability of the motion of square boxes on a sloped bed. The camera-based tracking algorithm was developed to identify a pattern of dots painted on the top of each box. The number of dots drawn on the top of each box was the identifier of each box as well as the orientation. The algorithm performed well for experiments conducted at larger scale comparing to smaller scale experiments for which the algorithm failed to identify the pattern on the top of each box.

Rueben et al. (2014) found the motion of the debris was generally 1-D and repeatable during the onshore direction phase. However, once a debris reached its maximum inundation, it would then ground and be subsequently washed seaward by the receding flow. The trajectory of the debris in the receding stage was significantly more variable, possibly due to eddies induced by the grounded debris within the returning flow.

Rueben et al. (2014) additionally examined the effect of multiple debris and fixed obstacles on debris motion. For multiple debris, the motion remained qualitatively similar to that of the single debris case. However, the presence of more debris led to the grounding point being significantly closer to the shore and the peak onshore velocity also occurred later. Alternatively, in offshore direction, peak velocities were similar to the case of single debris experiments. This is likely due to less disturbance induced in the local flow fields by debris as they had already dispersed. To examine the effect of obstacles, a fixed box was placed in front of the debris to initiate a forced rotation. The rotation of the debris resulted in a significantly more random trajectory and grounding point. The obstacle also reduced the peak onshore velocity of the debris, likely as a result of the energy lost during their rotation.

Shafiei et al. (2016) used a sensor-based tracking system, which recorded the accelerations of debris within dam-break flow conditions. The acceleration was then integrated over time to obtain debris velocity. Using a force balance and based on the assumption that debris entrainment begins after the leading edge of the bore passes the debris and that average stream-wise velocity behind the bore is constant, the following equation can be derived regarding the velocity profile (u) of the debris propagation:

$u\left(t\right)=U-{\left(\frac{C_d{\mathrm{\rho }}_f{A}_d}{2m_d}t+\frac{1}{U}\right)}^{-1}$ (6)

where U is the bore velocity, C_d is the drag coefficient, ρ_f is the density of fluid, A_d is the area of the debris projected to the incoming bore direction, m_d is the mass of the debris, and t is the debris travel time. The study showed that the debris velocity matched well to the proposed model and indicated the limit of Eq. 6 is the bore velocity.

Debris Impact

The primary approach to the modeling of debris loads has been on the impact force of a single debris on a structure (FEMA, 2012). As a result, the focus of current tsunami guidelines solely considers the impact of single debris; the likely occurrence of multiple, simultaneous debris impacts has not yet been evaluated. Nouri et al. (2010) examined the impact of a single wooden log on a structure. The debris impact resulted in an increase of the peak forces acting on the structure from 250 to 650 N. It was noted that while the debris impact load can be large, the dynamics of the impact are significantly different than those of the hydrodynamic loads, which are sustained. Nouri et al. (2010) also examined the impact duration of the debris and found that the impact duration was constant regardless of variation in log mass and velocity.

The majority of debris impact research has gone into determining maximum debris impact forces, as the maximum force will conservatively be included in the future design guidelines. The determination of the debris impact load has been based on the one-degree-of-freedom model proposed by Haehnel and Daly (2002) (Figure 3). Where the structure is considered to be rigid, the impact zone is considered to have a stiffness (k_i), the debris propagating at velocity (u_d) with a stiffness (k_d) impacts the zone causing a net displacement of x₀. Due to the relatively short duration of the impact, the damping has generally been ignored.

FIGURE 3

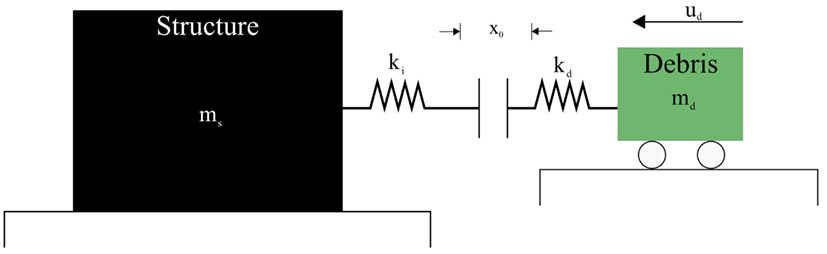
Figure 3. Schematic of the one-degree-of-freedom model proposed by Haehnel and Daly (2002).

There are several methods of solving for the maximum impact force, the most common approach being the contact-stiffness method, which is the approach used by the FEMA P646 (FEMA, 2012). The basis for this prescription is given by a debris modeled as a log impacting a rigid structure (Haehnel and Daly, 2004). Maximum impact force is thus expressed as:

$F_{i,\text{max}}=u\sqrt{k\left(m_d+C_M{m}_f\right)},$ (7)

where u is the velocity of the debris, k is the effective contact stiffness $\left(k=\frac{1}{k_i}+\frac{1}{k_d}\right)$, m_d is the mass of the debris, C_M is the added mass coefficient (dependent on debris geometry and density), and m_f is the mass of displaced fluid. In considering the maximum impact force, Matskevitch (1997), in a study of ice impacts, included a reduction in the impact force as a result of the eccentricity (e) and Haehnel and Daly (2004) considered the obliqueness (β) of the impact.

$\begin{array}{l}\hfill e=\frac{1}{\sqrt{1+\left(\frac{{\mathrm{\epsilon }}_0}{r_i}\right)\left(1+\mathrm{\mu }\left(\frac{r_0}{{\mathrm{\epsilon }}_0}\right)\right)}},\end{array}$ (8)

$\begin{array}{l}\hfill \mathrm{\beta }=\text{sin}\mathrm{\phi },\end{array}$ (9)

where ε₀ is the distance from the center of gravity of the debris to the point of impact, r_i is the radius of gyration of the debris, μ is the coefficient of friction between the debris and structure, r₀ is the radius of the log, and φ is the angle of impact relative to the log surface. Haehnel and Daly (2004) examined the effects of impact eccentricity, the distance from the impact axis to the center of gravity of the debris, and obliqueness, angle of the impact face to the structural face, on the impact force.

From the analysis of the impact force, Haehnel and Daly (2004) derived Eq. 10. The eccentricity of the debris impact results in a decrease in the impact force proportional to the distance of the impact away from the center of gravity of the debris. The obliqueness of impact generally decreased in a sine function from the 90° impact (long axis perpendicular to the structure). However, for a 0° angle of impact, the impact force was maximum. Although eccentricity resulted in a decrease in the maximum impact force, torque around the vertical axis of a structural member might be a side-product and no guidance exists at present to address such an additional load.

$F_{i,\text{max}}=e\mathrm{\beta }u\sqrt{k\left(m_D+C_D{m}_f\right)}.$ (10)

Riggs et al. (2014) evaluated the added mass coefficient by examining the impact of an aluminum box on a structure in-air and in-water. The in-water tests were performed by connecting an aluminum specimen to guidewires within a flume. The flume used a long wave generator to generate a wave that propagated the aluminum specimen along the guidewire toward the structure. The in-air tests were performed by connecting the aluminum specimen to a pendulum system that accelerated the specimen to a velocity matching the velocity in the in-water tests. The study found very little difference in the peak impact force between the in-air and in-water tests. Moreover, Riggs et al. (2014) determined that the difference in impact force between the in-air and in-water tests was unaffected by the debris impact velocity. Based on these findings, Riggs et al. (2014) did not support the use of the added mass coefficient in the evaluation of debris impact force. However, Shafiei et al. (2016) performed a similar study examining the effect of the added mass coefficient with denser debris and found the peak impact force to be up to 1.5 times greater in-water than in-air. More research is needed to determine if the added mass coefficient is necessary in the design for debris impact at full scale.

Aghl et al. (2014) expanded upon the work by Riggs et al. (2014) to develop a 1-D bar model that accurately estimated the impulse demand of a debris impact event. The model considered the structure to be rigid, therefore the impact force which was fully dependent on the properties of the debris. The impact force (F) was derived from the 1-D wave equation, assuming that the debris responds uniaxially to impact (Eq. 11). The impact force equation was very similar to that of the contact-stiffness approach (Eq. 7), without the added mass of the fluid. For the 1-D wave equation to be correctly evaluated, the stiffness of the debris must be considered as the equivalent stiffness of a 1-D bar (k_d) (Eq. 12).

$\begin{array}{l}\hfill F=u\sqrt{k_d{m}_d},\end{array}$ (11)

$\begin{array}{l}\hfill k_d=\frac{E{A}_d}{L_d},\end{array}$ (12)

where u is the impact velocity, m_d is the mass of the debris, E is the Young’s modulus, A_d is the cross-sectional area of the debris, and L_d is the length of the debris. The derived formula also resulted in a constant impact force for the duration of the elastic impact, resulting in a rectangular impact pulse with a duration of t_d.

$t_d=2\sqrt{\frac{m_d}{k_d}}.$ (13)

Aghl et al. (2014) evaluated the 1-D bar model with in-air experiments performed by accelerating debris (at full scale) to impact structures using a pendulum system. The experiments were performed with a wood pole, a steel tube, and shipping containers. The peak impact force was demonstrated to be within 5% for all the impact experiments when compared to the model equation. The impact duration was also well predicted in the cases of direct or close to direct impact of the shipping container. However, as the container impacted at the corners, the impact was not elastic, as was modeled, resulting in a significant difference between the analytical and experimental impact duration. Each debris impact force–time history had a characteristic impulse shape for the different debris types: half-sine (wood pole), rectangular (steel tube), and trapezoidal (shipping container). For all experiments, the impulse (area under the curve) for the impact model was less than the experimental results, indicating that the impact model is a conservative estimate of the impulse.

Ikeno et al. (2016) performed large-scale experiments evaluating the impact of large wood logs using a dam-break hydraulic boundary condition as well as in-air testing. The study compared the results of both test conditions to available debris impact models. The authors noted that the impact force using a hydraulic boundary condition had a significantly lower impact force than the in-air experiments as well as the impact models. As a result, they considered the potential effects of water cushioning between the wood-log and the impact surface. Additionally, Ikeno et al. (2016) considered the effect of oblique collisions using the transformation of kinetic energy to rotational energy during oblique debris impacts by defining a reduction coefficient λ:

$\mathrm{\lambda }=\frac{1+{\left(\frac{{\mathrm{\epsilon }}_0}{r}\right)}^2{\cos }^2\mathrm{\theta }}{1+{\left(\frac{{\mathrm{\epsilon }}_0}{r}\right)}^2},$ (14)

where θ is the collision angle between the debris face and the impact surface. The authors noted that the improved equation still overpredicted the experimental results, though it did not reproduce the reduction in force observed in the experimental data.

The ASCE7–Chapter 6: Tsunami Loads and Effects is the first guideline which approaches the design of coastal structures in tsunami-prone areas in mandatory language (Chock, 2016). The code uses the approach outlined by Aghl et al. (2014) for calculating the maximum impact force and duration. In the event that the structure being designed is in close proximity to debris sources with large debris, such as shipping containers and shipping vessels, the code also uses the approach proposed by Naito et al. (2014) to determine if the structure must be designed for the larger debris impact loads.

Debris Damming

Debris entrained within the flow can result in additional loads and effects on structures, particularly when the debris forms a “dam” in front of the structure or between columns, referred to as debris damming or accumulation (Robertson et al., 2007). The hydrodynamic force on a structure can be estimated by using a similar equation to the drag force (F_D) (Bremm et al., 2015):

$F_D=\frac{1}{2}{C}_D{\mathrm{\rho }}_{f}A{U}^2\text{,}$ (15)

where C_D is the drag coefficient, ρ_f is the density of the fluid, A is the cross-sectional area, and U is the flow velocity. The debris dam created by the debris will increase the cross-sectional area (A), which will in turn increase the hydrodynamic force linearly (Yeh et al., 2014). Alternatively, the properties of the dam will influence the drag coefficient as well as the surrounding hydrodynamic conditions (Parola, 2000).

While very little research has gone into debris damming in tsunami flows, research has been done within river engineering. Debris damming, in river flows, has been extensively studied due to the buildup of debris at bridge piers, depending on the shape of the structure the drag coefficient may vary as a result of the dam (Parola, 2000). The dam creates a blockage, further restring the flow path, the blockage results in a large increase in the flow depth. The debris dams also can result in increased scour as they tend to redirect the flow pattern resulting in increased scour underneath the debris dam (Pagliara and Carnacina, 2013). Due to the more diverse nature of debris in tsunami flows and due to different obstacle settings found in tsunami inundation areas, further research is expected to clarify whether river engineering findings on debris damming can be applicable to tsunami engineering.

Numerical Modeling of Debris

The numerical modeling of fluid–structure interactions (FSI) is a common topic in several fields of engineering. One of the main issues is that the numerical model needs to be able to reproduce all the physically relevant scales that affect the FSI (Canelas et al., 2015). However, the physical scales that affect the interaction are often not clear, resulting in these models requiring a high level spatial and temporal resolution. This difficulty has led to attempts to simplify the FSI by providing one-way coupling between model elements: fluid–structure or fluid–air–structure. One-way solid–fluid coupling considers the solids as massless marker particles that moved unconstrained on the water surface (Wu et al., 2014). One-way fluid–solid coupling causes the solids to move in relation to the fluid without the solids affecting the fluid. The one-way coupling methods can provide good results if the scale of the interaction between the phases is disproportionate in one direction, however, for many cases this is not the case. Two-way dynamic coupling of fluid and solid numerical solvers have become increasingly popular as computational resources are able nowadays to handle the significant computational demands of the two-way models. However, the development is still very much in its early stages.

Wu et al. (2014) used the Navier–Stokes equations coupled with the VOF free-surface tracking technique and a large eddy simulation turbulence model to calculate the flow field around the solids. Additionally, Wu et al. (2014) used partial cell treatment (PCT) to locate the faces of the solids. The basic principle of the PCT is similar to the VOF method where each cell was assigned a value between 0 and 1 indicating the phases present in the cell. When the solid phase was present within the cell, the cell is assigned a porosity that reduces the effective volume of the cell, and in the case where the cell was completely solid, the cell was removed from the Navier–Stokes equation calculations. The calculated porosity was used to adjust fluxing quantities, such as momentum and mass. The motion of the floating body was determined using the discrete element method (DEM) to calculate the translation and rotation. The translation was calculated using Newton’s equations of motion, and the rotation was calculated using Euler’s equations. The forces on the solid were calculated by integrating the fluid pressures on the surface of the solid.

The model from Wu et al. (2014) was validated using two laboratory experiments: a positively buoyant box in a tank of water (0.15 m × 0.14 m × 0.14 m) and a negatively buoyant box (0.02 m × 0.02 m × 0.02 m) in a tank of water. The boxes were released in the tank, and the motion of the box was tracked using cameras. Generally, good comparison between the numerical and experimental results was observed, with a maximum difference in displacement of 0.0044 m over a 0.06 m water column. The difference was due to the numerical simulation showing the negatively buoyant box rebounding off the bottom of the tank whereas the experimental results showed no such phenomena.

Smoothed-particle hydrodynamics (SPH) has been increasingly used in the modeling of free-surface flows (Gomez-Gesteira et al., 2012) and has been shown to be able to simultaneously deal with multiple body dynamics (Amicarelli et al., 2015). However, few current models can capably handle the transport of moving bodies in free-surface flow. Primarily, the current models have modeled the moving bodies as a rigid body of moving particle simulations (MPS) fluid particles with an imposed rigidity (Canelas et al., 2013). While the models have achieved generally good results (Manenti et al., 2008; Rogers et al., 2009), the modeling of the interactions between the body and the fluid was not based on rigid body contact laws (Canelas et al., 2013).

Canelas et al. (2013) incorporated a DEM model where the interparticle rigid body forces are taken from rigid body contact laws. The boundary particles of the rigid body are taken as fluid particle allowing the DEM model to be coupled with the SPH model. The contact force between the fluid and rigid body particles is decomposed into a repulsion force, which also takes into consideration the deformation of the particle, and a damping force, which takes in consideration for energy lost during deformation. The coupled model was validated using a dam-break experiment entraining PVC cubes. While the model and the experimental results had qualitatively similar results, the study noted that that the bottom friction was not properly modeled resulting in the motion of the debris (particularly of the bottom box) to lag behind the experimental results. Moreover, due to the high computational cost associated with the coupled model resulted in the particle resolution being too low to properly resolve the water surface and bore profile.

Amicarelli et al. (2015) modeled the moving bodies using the MPS method. However, the authors used a modified boundary condition, originally proposed by Adami et al. (2012), for a more stable pressure gradient around the moving bodies. The solid–solid interactions were also adjusted by the addition of a coefficient to the repulsive boundary conditions proposed by Monaghan (2005) to better preserve global momentum and kinetic energy through the body–body interactions. The SPH model was validated using a 2D wedge falling into a water tank. The study compared the acceleration of the experimental and numerical model with generally good accuracy. Pressure fluctuations were common throughout the experimental runs, which is a commonly noted problem with SPH models (Gomez-Gesteira et al., 2012; St-Germain et al., 2013).

The numerical model used in Amicarelli et al. (2015) was also used to qualitatively examine 3-D test cases where debris interacted with a bore front and two sets of obstacles. The bore was developed using a dam-break, and the debris was tracked using cameras. The numerical model resulted in good results when comparing both the trajectory and the orientation of the debris was also relatively well reproduced. The presence of the obstacles resulted in the formation of recirculation zones in front of the obstacles furthest downstream, and the body dynamics were maintained through this highly non-linear zone.

Canelas et al. (2015) presented the most recent version of the DualSPHysics with its many improvements on current modeling of fluid–solid interactions. The primary difference in the model presented by Canelas et al. (2015) was the addition of a δ-SPH term to the continuity equation which helps in the interface description between the solid and fluid phase. The rapid change in the density at the interface results in the pressure and density fluctuations that can be seen in many SPH fluid–solid modeling. The SPH model showed promising results when examining the rising of a submerged positively buoyant cylinder. The SPH model compared well to the analytical solution for the linear acceleration when the Reynold’s number was laminar and showed a noticeable shift in acceleration as the boundary layer transitioned to turbulent flow. The model also showed the stabilization of the density fields indicating that the δ-SPH term helping handle that particular common problem.

While the work by Canelas et al. (2015) and Amicarelli et al. (2015) showed a lot of promise in the SPH fluid–solid modeling, there are still many issues that have yet to be thoroughly evaluated. Amicarelli et al. (2015) presented a method of handling solid–solid interactions, yet, the contact mechanics were not fully evaluated. Canelas et al. (2013) coupled the SPH model with a DEM; however, the large computational cost associated with the coupling makes the use of the coupled model unfeasible for many studies. The addition of solid deformation and inelastic collisions would also greatly improve the applicability of the model throughout coastal and hydraulic engineering.

Critical Review and Future Research Directions

The above presented literature review outlines the state-of-the-art knowledge on debris-induced loading and associated effects in the context of extreme hydrodynamic flows as arising from natural disasters, such as storm surges, tsunami, and flash floods. The current body of literature covers fundamental processes of impacts on vertical structures, either derived from experimental or analytical strategies. To date, this knowledge has started to improve guidelines and standards written in mandatory language, yet many aspects of the problem of debris exerting forces on or interacting with the build environment remain unclear.

The study of debris within the context of tsunami engineering has been difficult due to the random nature of debris transport (Matsutomi, 2009). Determining aspects of debris dynamics from post-event engineering survey has been challenging due to a lack of documentation regarding potential debris sources (Naito et al., 2014). Moreover, determining impact forces without the flow conditions at the time of impact makes drawing conclusions from impact sites equally challenging. Due to these challenges, along with the relative rare occurrence of tsunami events, available field data to be compared to experimental and numerical modeling results are limited to few post-tsunami forensic engineering surveys. Therefore, the determination of debris dynamics and impact loads has primarily been performed in an experimental setting.

The study of tsunami flows and their interaction with coastal infrastructure in a laboratory setting has fundamental scaling issues related to the period of a tsunami wave. Historically, the study of tsunami loads was performed using a broken solitary wave as the hydrodynamic boundary condition (Arnason et al., 2009). However, Madsen et al. (2008) showed that the spatial and temporal duration of a solitary wave was not on the same order of magnitude of observed tsunamis. Despite these observations, broken solitary waves have still be used to examine the near-shore impact of tsunami waves as well as incipient debris transport (Arnason et al., 2009; Chinnarasri et al., 2013; Yao et al., 2014; Nistor et al., 2016). Chanson (2006) indicated that the dam-break solution was a good representation of tsunami surge profile over a coastal plain. The application of the dam-break in an experimental setting has shown better results representing the period of a tsunami wave (Imamura et al., 2008; Al-Faesly et al., 2012; Shafiei et al., 2016), though large experimental facilities are needed to achieve these flow durations at an appropriate scale. Other techniques, such as the use of N-waves (Tadepalli and Synolakis, 1994), cnoidal waves (Synolakis et al., 1988), and pump-driven long wave generation (Goseberg et al., 2013), have been shown to better represent tsunami inundation temporal features in a variety of cases. However, these experiments were performed at small scales. In determining maximum debris loads, the hydrodynamic boundary conditions must be carefully considered within the experimental procedure; it is generally recommended to aim at scales as large as possible to accurately model debris impact processes (Chock, 2016).

The problem of experimental scales extends to debris dynamics and impact loads, where little research has been done to determine minimum scales at which experiments can be performed. Studies of debris transport have mentioned the effects of turbulent eddies on debris transport (Rueben et al., 2014; Yao et al., 2014). However, as with most coastal physical models, studies are often scaled using the Froude number. The scaling of a model using the Froude number often does not adequately scale turbulent length scales (She and Leveque, 1994), resulting in an unproportioned effect of turbulence on the debris transport. Another scaling concern for debris transport is the effect of viscosity on the transport of debris at small scales. Similar to the modeling of dam-breaks (Lauber and Hager, 1998), there is likely a scale at which the viscosity of the fluid will have a significant effect on debris transport, and hence, the scaling of physical properties using Froude would no longer be adequate. A determination of the minimum scales required would help evaluate the applicability of studies to debris transport problems.

Additionally, the scaling of the debris for impact loads must also be taken into consideration. Studies of impact loads have often focused on scaling the physical properties of the debris, such as length, width, height, and mass; however, little research has been performed in examining the scaling of mechanical properties, such as stiffness and elasticity, which is critical in determining maximum impact loads. The minimum scales at which these experiments can be performed would be dependent on the material as the study must consider the loads at which the debris maintains elastic properties. A determination of the minimum scales would help identify experimental facilities capable of modeling debris impact loads. Moreover, the scaling of the plastic region of impact needs to consider the effect of debris deformation on maximum impact forces, building upon the studies by Aghl et al. (2015). Other physical properties, such as the draft of the debris, also need to be considered, as was shown in Shafiei et al. (2016) where the draft of the debris had a significant effect on the added mass coefficient.

In overcoming scaling issues related to debris dynamics, the physical modeling of debris is essential to provide benchmarking data for the numerical models, particularly due to the lack of available field or prototype data. Numerical modeling has made recent strides in the development of two-way coupled fluid–solid interactions. The availability of high temporal and spatial resolution of the various drivers of debris transport and impact would allow for numerical models to be accurately validated and calibrated. In particular, the momentum transfer between the fluid and free-floating solids needs to be thoroughly evaluated to be applied to numerical models. The momentum transfer between the fluid and the solid objects, as well as the reciprocal effects, is critical in resolving the entrainment and transport of debris within extreme hydrodynamic events.

In the determination of debris impact loads and effects, the primary objective is to apply the findings of the research to propose accurate methods of determining design loads on structures in extreme hydrodynamic events. One of the difficult aspects in designing for extreme hydrodynamic events, like tsunamis, is determining the design conditions and maximum loads associated with such rare events. Commonly, the design conditions for tsunamis are taken from historical maximum tsunamis (Okada et al., 2005). However, as observed during the 2011 Tohoku Tsunami, historical maximums may not always provide a measure of maximum conditions (Esteban et al., 2015). As a result, recent efforts have been made to implement probabilistic tsunami hazard analysis and tsunami-resistant design (Chock, 2015).

Assessing debris impact is currently considered as a deterministic design condition (Chock, 2016), despite the motion of debris being a random process (Matsutomi, 2009). The FEMA P-55 and FEMA P-646 (2012) guidelines maintain a conservative approach where debris impact should always be considered. The upcoming ASCE7 Chapter 6 also maintains a conservative approach when referring to debris ubiquitous to coastal areas, such as hydro poles and concrete debris (Chock, 2016). However, for larger debris, the ASCE7 uses the empirical approach proposed by Naito et al. (2014), based on a limited data set. The limited data set was due to difficulties in assessing debris sources in the aftermath of the 2011 Tohoku Tsunami, limiting the data set to debris with clearly defined debris sources, such as shipping vessels and shipping containers.

To better design structures for debris impact within the probabilistic assessment of tsunami hazard and account for the random nature of debris motion, the probabilistic assessment of debris motion would improve the quantification of debris loads. Considering the effect of the proximity of the debris site, the debris’ physical properties, local topography, surround obstructions, and potential flow conditions on debris dynamics and entrainment would also help assess the likelihood of debris impact, as well as identify the type of debris impacting a structure.

Additional consideration is needed to quantity of debris entrained within the flow. Currently, design guidelines only consider the possibility of single debris impacts. However, in a study of the transport of shipping containers in extreme hydrodynamic events, Nistor et al. (2016) determined that the debris often tended to propagate as an agglomeration. Based on this finding, an assessment of multiple debris impact needs to be studied to determine if building standards need to consider multiple debris impacts as the critical load. Additionally, the agglomeration of debris would also increase the risk of debris accumulating at the upstream face of structures, therefore increasing the risk of debris damming.

Conclusions

Several post-tsunami forensic field surveys over the past decade have led to increased awareness about loads associated with tsunami-induced coastal inundation. One of the loads identified from these field surveys is debris loads, where objects entrained within the flow can impact and accumulate onto structures, causing supplementary loads in addition to the previously considered hydraulic ones. Due to the random nature of debris motion and the relative rarity of tsunami events, the assessment of debris motion loads in the field has been limited. However, recent advancements in the determination of debris dynamics using an experimental setting have allowed for improvements in the methods available for the assessment of mechanisms of debris load as well as of the potential maximum impact loads. Based on an extensive literature review of debris dynamics in extreme hydrodynamic conditions, the following conclusions can be drawn:

1. An assessment of the lower bounds for experimental scales and conditions is needed to determine the type of experimental facilities necessary to accurately assess debris loading conditions. Consideration is needed in scaling of the debris mechanical properties, such as their stiffness and/or elasticity. This is particularly necessary when assessing their plastic deformation, as these properties vary widely and would have to be accounted for in scaled models.

2. As there are several means of reproducing hydrodynamic boundary conditions used in tsunami engineering, the hydrodynamic forcing factor in an experimental setting needs to consider what the critical condition is when assessing debris loads.

3. Rigorous, high-resolution studies are needed to provide detailed, tailored benchmark data sets to aid in the calibration and validation of numerical models developed for debris impact.

4. Fundamental research is needed on the various factors governing the actual debris entrainment and the solid–solid/solid–fluid momentum transfer which are critical for validating numerical models.

5. Due to the random nature of debris motion and recent consideration to probabilistic tsunami hazards design, a probabilistic design approach is needed to assess the likelihood of debris loads occurring, which would be a function of the proximity of debris sources, debris properties, and surrounding environment.

6. It is important to evaluate of multiple impact events, as well as the increased likelihood of debris damming as they propagate as an agglomeration.

Author Contributions

IN–lead author, leader of the research project, and wrote the critical discussion. NG–author, part of collaboration, and helped in the writing of both the review and critical discussion. JS–author, graduate student working on debris project, and helped in writing of the review and critical discussion.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Funding

The authors acknowledge the financial support by the Strategic Research Foundation Grant-aided Project for Private Universities (No. S1311028) from Japanese Ministry of Education and by Waseda University, of the NSERC Discovery Grant (Canada) and of the Kajima Foundation (Japan). NG acknowledges that this research was supported by a Marie Curie International Outgoing Fellowship within the 7th European Community Framework Programme (No. 622214).

References

Adami, S., Hu, X., and Adams, N. (2012). A generalized wall boundary condition for smoothed particle hydrodynamics. J. Comput. Phys. 231, 7057–7075. doi: 10.1016/j.jcp.2012.05.005

CrossRef Full Text | Google Scholar

Aghl, P., Naito, C., and Riggs, H. (2014). Full-scale experimental study of impact demands resulting from high mass, low velocity debris. J. Struct. Eng. 140, 04014006. doi:10.1061/(ASCE)ST.1943-541X.0000948

CrossRef Full Text | Google Scholar

Aghl, P. P., Naito, C., and Riggs, H. (2015). Estimation of demands resulting from inelastic axial impact of steel debris. Eng. Struct. 82, 11–21. doi:10.1016/j.engstruct.2014.10.021

CrossRef Full Text | Google Scholar

Al-Faesly, T., Palermo, D., Nistor, I., and Cornett, A. (2012). Experimental modeling of extreme hydrodynamic forces on structural models. Int. J. Protect. Struct. 3, 477–506. doi:10.1260/2041-4196.3.4.477

CrossRef Full Text | Google Scholar

Amicarelli, A., Albano, R., Mirauda, D., Agate, G., Sole, A., and Guandalini, R. (2015). A smoothed particle hydrodynamics model for 3D solid body transport in free surface flows. Comput. Fluids 116, 205–228. doi:10.1016/j.compfluid.2015.04.018

CrossRef Full Text | Google Scholar

Arnason, H., Petroff, C., and Yeh, H. (2009). Tsunami bore impingement onto a vertical column. J. Disaster Res. 4, 391–403. doi:10.20965/jdr.2009.p0391

CrossRef Full Text | Google Scholar

Bocchiola, D., Rulli, M., and Rosso, R. (2006). Transport of large woody debris in the presence of obstacles. Geomorphology 76, 166–178. doi:10.1016/j.geomorph.2005.08.016

CrossRef Full Text | Google Scholar

Borrero, J. C., Sieh, K., Chlieh, M., and Synolakis, C. E. (2006). Tsunami inundation modeling for western Sumatra. Proc. Natl. Acad. Sci. U.S.A. 103, 19673–19677. doi:10.1073/pnas.0604069103

PubMed Abstract | CrossRef Full Text | Google Scholar

Braudrick, C. A., and Grant, G. E. (2000). When do logs move in rivers? Water Resour. Res. 36, 571–583. doi:10.1029/1999WR900290

CrossRef Full Text | Google Scholar

Bremm, G. C., Goseberg, N., Schlurmann, T., and Nistor, I. (2015). Long wave flow interaction with a single square structure on a sloping beach. J. Mar. Sci. Eng. 3, 821. doi:10.3390/jmse3030821

CrossRef Full Text | Google Scholar

Canelas, R. B., Dominguez, J. M., Crespo, A. J., ómez-Gesteira, M. G., and Ferreira, R. M. (2015). A smooth particle hydrodynamics discretization for the modelling of free surface flows and rigid body dynamics. Int. J. Numer. Methods Fluids 78, 581–593. doi:10.1002/fld.4031

CrossRef Full Text | Google Scholar

Canelas, R. B., Ferreira, R. M., Crespo, A., and Domínguez, J. M. (2013). “A generalized SPH-DEM discretization for the modelling of complex multiphasic free surface flows,” in Proceedings of the 8th International SPHERIC Workshop, Trondheim.

Google Scholar

Chanson, H. (2006). Tsunami surges on dry coastal plains: application of dam break wave equations. Coast. Eng. J. 48, 355–370. doi:10.1142/S0578563406001477

CrossRef Full Text | Google Scholar

Charvet, I., Suppasri, A., and Imamura, F. (2014). Empirical fragility analysis of building damage caused by the 2011 Great East Japan tsunami in Ishinomaki city using ordinal regression, and influence of key geographical features. Stoch. Environ. Res. Risk Assess. 28, 1853–1867. doi:10.1007/s00477-014-0850-2

CrossRef Full Text | Google Scholar

Chinnarasri, C., Thanasisathit, N., Ruangrassamee, A., Weesakul, S., and Lukkunaprasit, P. (2013). The impact of tsunami-induced bores on buildings. P I Civil Eng-Mar. En. 166, 14–24.

Google Scholar

Chock, G. Y. (2015). “The ASCE 7 tsunami loads and effects design standard,” in Structures Congress 2015 (Portland, OR: ASCE), 1446–1456.

Google Scholar

Chock, G. Y. (2016). Design for tsunami loads and effects in the ASCE 7-16 standard. J. Struct. Eng. 142, 04016093. doi:10.1061/(ASCE)ST.1943-541X.0001565

CrossRef Full Text | Google Scholar

Esteban, M., Takagi, H., and Shibayama, T. (2015). Handbook of Coastal Disaster Mitigation for Engineers and Planners, Waltham, MA: Butterworth Heinemann, Elsevier.

Google Scholar

FEMA. (2012). P646 Guidelines for Design of Structure for Vertical Evacuation from Tsunamis. Redwood City, CA: Federal Emergency Management Agency.

Google Scholar

Fritz, H. M., Borrero, J. C., Synolakis, C. E., and Yoo, J. (2006). 2004 Indian Ocean tsunami flow velocity measurements from survivor videos. Geophys. Res. Lett. 33, L24605. doi:10.1029/2006GL026784

CrossRef Full Text | Google Scholar

Gomez-Gesteira, M., Rogers, B. D., Crespo, A. J., Dalrymple, R., Narayanaswamy, M., and Dominguez, J. M. (2012). SPHysics – development of a free-surface fluid solver – part 1: theory and formulations. Comput. Geosci. 48, 289–299. doi:10.1016/j.cageo.2012.02.029

CrossRef Full Text | Google Scholar

Goseberg, N., Nistor, I., Mikami, T., Shibayama, T., and Stolle, J. (2016a). Nonintrusive spatiotemporal smart debris tracking in turbulent flows with application to debris-laden tsunami inundation. J. Hydraul. Eng. 142, 04016058. doi:10.1061/(ASCE)HY.1943-7900.0001199

CrossRef Full Text | Google Scholar

Goseberg, N., Stolle, J., Nistor, I., and Shibayama, T. (2016b). Experimental analysis of debris motion due the obstruction from fixed obstacles in tsunami-like flow conditions. Coast. Eng. 118, 35–49. doi:10.1016/j.coastaleng.2016.08.012

CrossRef Full Text | Google Scholar

Goseberg, N., Wurpts, A., and Schlurmann, T. (2013). Laboratory-scale generation of tsunami and long waves. Coast. Eng. 79, 57–74. doi:10.1016/j.coastaleng.2013.04.006

CrossRef Full Text | Google Scholar

Haehnel, R. B., and Daly, S. F. (2002). Maximum Impact Force of Woody Debris on Floodplain Structures. Hanover: USACE.

Google Scholar

Haehnel, R. B., and Daly, S. F. (2004). Maximum impact force of woody debris on floodplain structures. J. Hydraul. Eng. 130, 112–120. doi:10.1061/(ASCE)0733-9429(2004)130:2(112)

CrossRef Full Text | Google Scholar

Ikeno, M., Takabatake, D., Kihara, N., Kaida, H., Miyagawa, Y., and Shibayama, A. (2016). Improvement of collision force formula for woody debris by airborne and hydraulic experiments. Coast. Eng. J. 58, 1640022. doi:10.1142/S0578563416400222

CrossRef Full Text | Google Scholar

Imamura, F., Goto, K., and Ohkubo, S. (2008). A numerical model for the transport of a boulder by tsunami. J. Geophys. Res. Oceans 197, 113. doi:10.1029/2007JC004170

CrossRef Full Text | Google Scholar

Lauber, G., and Hager, W. H. (1998). Experiments to dambreak wave: horizontal channel. J. Hydraul. Eng. 36, 291–307. doi:10.1080/00221689809498601

CrossRef Full Text | Google Scholar

Madsen, P. A., Fuhrman, D. R., and Schäffer, H. A. (2008). On the solitary wave paradigm for tsunamis. J. Geophys. Res. Oceans 113, 1–22. doi:10.1029/2008JC004932

CrossRef Full Text | Google Scholar

Manenti, S., Panizzo, A., Ruol, P., and Martinelli, L. (2008). “SPH simulation of a floating body forced by regular waves,” in Proceedings of 3rd SPHERIC Workshop (Lausanne: Swiss Federal Institute of Technology), 38–41.

Google Scholar

Matskevitch, D. (1997). Eccentric impact of an ice feature: linearized model. Cold Reg. Sci. Technol. 25, 159–171. doi:10.1016/S0165-232X(96)00009-2

CrossRef Full Text | Google Scholar

Matsutomi, H. (2009). Method for estimating collision force of driftwood accompanying tsunami inundation flow. J. Disaster Res. 4, 435–440. doi:10.20965/jdr.2009.p0435

CrossRef Full Text | Google Scholar

Matsutomi, H., Fujii, M., and Yamaguchi, T. (2008). “Experiments and development of a model on the inundated flow with floating bodies,” in Proceedings of the 31st International Conference on Coastal Engineering (Hamburg: ASCE), 1458–1470.

Google Scholar

Monaghan, J. J. (2005). Smoothed particle hydrodynamics. Rep. Progr. Phys. 68, 1703. doi:10.1088/0034-4885/68/8/R01

CrossRef Full Text | Google Scholar

Naito, C., Cercone, C., Riggs, H. R., and Cox, D. (2014). Procedure for site assessment of the potential for tsunami debris impact. J. Waterw. Port Coast. Ocean Eng. 140, 223–232. doi:10.1061/(ASCE)WW.1943-5460.0000222

CrossRef Full Text | Google Scholar

Naito, C., Riggs, H., Wei, Y., and Cercone, C. (2016). Shipping-container impact assessment for tsunamis. J. Waterw. Port Coast. Ocean Eng. 142, 05016003. doi:10.1061/(ASCE)WW.1943-5460.0000348

CrossRef Full Text | Google Scholar

Nistor, I., Goseberg, N., Mikami, T., Shibayama, T., Stolle, J., Nakamura, R., et al. (2016). Hydraulic experiments on debris dynamics over a horizontal plane. J. Waterw. Port Coast. Ocean Eng. 04016022. doi:10.1061/(ASCE)WW.1943-5460.0000371

CrossRef Full Text | Google Scholar

Nouri, Y., Nistor, I., Palermo, D., and Cornett, A. (2010). Experimental investigation of tsunami impact on free standing structures. Coast. Eng. J. 52, 43–70. doi:10.1142/S0578563410002117

CrossRef Full Text | Google Scholar

Okada, T., Sugano, T., Ishikawa, T., Ohgi, T., Takai, S., and Hamabe, C. (2005). Structural Design Method of Buildings for Tsunami Resistance (Proposed). Tokyo: Building Technology Research Institute, Building Centre for Japan, 15.

Google Scholar

Pagliara, S., and Carnacina, I. (2013). Bridge pier flow field in the presence of debris accumulation. P I Civil Eng-Water Manag. 187–198.

Google Scholar

Palermo, D., Nistor, I., Nouri, Y., and Cornett, A. (2009). Tsunami loading of near-shoreline structures: a primer. Can. J. Civ. Eng. 36, 1804–1815. doi:10.1139/L09-104

CrossRef Full Text | Google Scholar

Parola, A. C. (2000). Debris Forces on Highway Bridges. Washington, DC: Transportation Research Board.

Google Scholar

Riggs, H., Cox, D., Naito, C., Kobayashi, M., Aghl, P. P., Ko, H.-S., et al. (2014). Experimental and analytical study of water-driven debris impact forces on structures. J. Offshore Mech. Arctic Eng. 136, 041603. doi:10.1115/1.4028338

CrossRef Full Text | Google Scholar

Robertson, I., Riggs, H. R., Yim, S. C., and Young, Y. L. (2007). Lessons from Hurricane Katrina storm surge on bridges and buildings. J. Waterw. Port Coast. Ocean Eng. 133, 463–483. doi:10.1061/(ASCE)0733-950X(2007)133:6(463)

CrossRef Full Text | Google Scholar

Rogers, B. D., Dalrymple, R. A., and Stansby, P. K. (2009). “SPH modeling of floating bodies in the surf zone,” in Proc. 31st Int. Conf. Coastal Eng. 2008. 204–215.

Google Scholar

Rossetto, T., Allsop, W., Charvet, I., and Robinson, D. I. (2011). Physical modelling of tsunami using a new pneumatic wave generator. Coast. Eng. 58, 517–527. doi:10.1016/j.coastaleng.2011.01.012

CrossRef Full Text | Google Scholar

Rueben, M., Cox, D., Holman, R., Shin, S., and Stanley, J. (2014). Optical measurements of tsunami inundation and debris movement in a large-scale wave basin. J. Waterw. Port Coast. Ocean Eng. 141, 04014029. doi:10.1061/(ASCE)WW.1943-5460.0000267

CrossRef Full Text | Google Scholar

Saatcioglu, M., Ghobarah, A., and Nistor, I. (2005). Effects of the December 26, 2004 Sumatra earthquake and tsunami on physical infrastructure. ISET J. Earthq. Technol. 42, 79–94.

Google Scholar

Shafiei, S., Melville, B. W., Shamseldin, A. Y., Beskhyroun, S., and Adams, K. N. (2016). Measurements of tsunami-borne debris impact on structures using an embedded accelerometer. J. Hydraul. Res. 54, 435–449. doi:10.1080/00221686.2016.1170071

CrossRef Full Text | Google Scholar

She, Z.-S., and Leveque, E. (1994). Universal scaling laws in fully developed turbulence. Phys. Rev. Lett. 72, 336. doi:10.1103/PhysRevLett.72.336

CrossRef Full Text | Google Scholar

St-Germain, P., Nistor, I., Townsend, R., and Shibayama, T. (2013). Smoothed-particle hydrodynamics numerical modeling of structures impacted by tsunami bores. J. Waterw. Port Coast. Ocean Eng. 140, 66–81. doi:10.1061/(ASCE)WW.1943-5460.0000225

CrossRef Full Text | Google Scholar

Stolle, J., Nistor, I., and Goseberg, N. (2016). Optical tracking of floating shipping containers in a high-velocity flow. Coast. Eng. J. 58, 1650005. doi:10.1142/S0578563416500054

CrossRef Full Text | Google Scholar

Synolakis, C. E., Deb, M. K., and Skjelbreia, J. E. (1988). The anomalous behavior of the runup of cnoidal waves. Phys. Fluids 31, 3–5. doi:10.1063/1.866575

CrossRef Full Text | Google Scholar

Tadepalli, S., and Synolakis, C. E. (1994). The run-up of N-waves on sloping beaches. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 445, 99–112. doi:10.1098/rspa.1994.0050

CrossRef Full Text | Google Scholar

Taubenböck, H., Goseberg, N., Lämmel, G., Setiadi, N., Schlurmann, T., Nagel, K., et al. (2013). Risk reduction at the “last-mile”: an attempt to turn science into action by the example of Padang, Indonesia. Nat. Hazards 65, 915–945. doi:10.1007/s11069-012-0377-0

CrossRef Full Text | Google Scholar

Wu, T.-R., Chu, C.-R., Huang, C.-J., Wang, C.-Y., Chien, S.-Y., and Chen, M.-Z. (2014). A two-way coupled simulation of moving solids in free-surface flows. Comput. Fluids 100, 347–355. doi:10.1016/j.compfluid.2014.05.010

CrossRef Full Text | Google Scholar

Yao, Y., Huang, Z., Lo, E. Y. M., and Shen, H.-T. (2014). A preliminary laboratory study of motion of floating debris generated by solitary waves running up a beach. J. Earthq. Tsunami 8, 1440006. doi:10.1142/S1793431114400065

CrossRef Full Text | Google Scholar

Yeh, H., Barbosa, A. R., Ko, H., and Cawley, J. G. (2014). Tsunami loadings on structures: review and analysis. Coast. Eng. Proc. 34, 1–13. doi:10.9753/icce.v34.currents.4

CrossRef Full Text | Google Scholar

Yeh, H., Sato, S., and Tajima, Y. (2013). The 11 March 2011 East Japan earthquake and tsunami: tsunami effects on coastal infrastructure and buildings. Pure Appl. Geophys. 170, 1019–1031. doi:10.1007/s00024-012-0489-1

CrossRef Full Text | Google Scholar