Improved blockchain-based ECDSA batch verification scheme

Introduction: Blockchain technology has attracted much attention due to its decentralization, transparency and security. Initially applied in the financial field, it has now expanded to various fields such as Internet of Things (IoT), electronic cash and healthcare. However, the open nature of blockchain has raised potential security concerns about sensitive transaction data, and the increasing number of transactions requires low-latency solutions. Most blockchain applications still rely on the lightweight Elliptic Curve Digital Signature Algorithm (ECDSA). Due to complex operations such as vectorized multiplication and modular inversion, this may introduce significant additional overhead.

Methods: To address these issues, a new scheme named KTP-ECDSA is proposed. This scheme is based on the improved two-parameter Elliptic Curve Digital Signature Algorithm (TP-ECDSA) and the KGLP algorithm. In both the signing and verification processes, this scheme eliminates modular inverse operations and reduces scalar multiplications during the verification stage by using batch verification.

Result: The experimental results show that, compared with the traditional ECDSA, KTP-ECDSA has achieved a speed increase of over 50% in both independent verification and batch verification, significantly improving the efficiency of signature verification.

Discussion: By adopting the KTP-ECDSA algorithm and using the digital signature batch verification method, multiple signatures can be verified simultaneously, thus reducing the computational burden of the traditional single-verification method. This greatly increases the overall transaction throughput and improves resource utilization efficiency.

1 Introduction

Blockchain is essentially a new type of distributed database that integrates a series of emerging information technologies (Lin, 2023), including consensus mechanisms, encryption algorithms, network communication, and smart contracts. These technologies also contribute to the decentralization, transparency, traceability, and immutability of blockchain, which plays a significant role in finance (Puthiyidam et al., 2023; Wang et al., 2020), electronic cash (Jiarui et al., 2023), and the Internet of Things (IoT) (Mahajan and Junnarkar, 2023). In particular, the development of blockchain in cryptocurrency has made it a modern network technology (Zhang et al., 2022). As Blockchain 1.0, Bitcoin has received widespread attention for its successful deployment and application of ECDSA. ECDSA is gradually becoming the default signature mechanism for the current mainstream blockchain platforms and projects. The efficient development of any network technology must consider its cybersecurity factors (Khizar et al., 2022; Marcos et al., 2023), and digital signature technology in cryptography can effectively solve some security problems in blockchain.

The digital signature algorithm (DSA) uses asymmetric encryption technology to achieve information identity authentication, data integrity verification, and tamper resistance (Fang et al., 2020). In blockchain, each transaction needs to be verified by a digital signature before being added to the block. However, blockchain faces the challenge of large-scale data transactions in electronic cash applications. With the rapid development of the electronic cash market, the number of transactions and the scale of transaction data are increasing. In order to obtain real-time results, it is important to verify multiple signatures at any given point in time, and the signature verification of large-scale transaction tasks can cause cumbersome overhead to nodes (Rahman Taleb and Vergnaud, 2021). Therefore, finding a way to improve the efficiency and security of ECDSA signature verification has become a key issue. Currently, ECDSA remains one of the mainstream algorithms in the blockchain field (Yehuda, , 2021). Nevertheless, the implementation of this algorithm presents two significant mathematical challenges. The first is modular inversion, which is 10 times slower than multiplication (Kittur et al., 2017). The second is ECC scalar multiplication (Binbin et al., 2024), which is performed in both the signature and verification stages, making it a crucial factor influencing the efficiency of ECDSA.

In response to the above two problems, various schemes have been proposed to improve the ECDSA modular inversion and scalar multiplication operations. Zhang et al. (2008) proposed a fast verification ECDSA scheme that only performs scalar multiplication and modular multiplication operations to increase the operation speed. The limitations to the above scheme are that although the computational efficiency is improved, simply increasing the efficiency of signatures by reducing the number of inverse operations can lead to security issues with forged signatures, and forward security cannot be guaranteed. Therefore, Xiao et al. (2020) proposed an ECDSA scheme without modular inversion, which introduces two random parameters to improve efficiency while effectively ensuring the security of the scheme. Cao and Wei (2018) proposed an improved ECDSA protocol that effectively avoids modular inversion operations by using the SHA-256 algorithm to improve efficiency.

However, the above solutions are all based on independent verification methods. In the face of the signature verification task of large-scale transactions, using independent verification schemes is not sufficient to meet strict low-latency requirements (Liu et al., 2021). In 1994, Fiat (1997) introduced the concept of batch verification, a method that verifies multiple signatures simultaneously, reduces repetitive computation operations, and greatly saves the verifier’s computational resources and verification latency. In signature schemes such as DSA and RSA, batch verification has been widely applied (Lim and Lee, 1994; Bao et al., 2006). For ECDSA, researchers have proposed various batch verification schemes (Karati et al., 2014). Although there are technologies for batch verification of multiple ECDSA signatures, many of them have a major drawback that they are not efficient for larger batch verification. Therefore, in real-time scenarios, where a large number of signatures need to be verified at once, it is important to have a performance solution that can perform well, regardless of the signature size without compromising security. Kittur and Pais (2017) introduced a batch verification scheme for multiple ECDSA signatures. This scheme introduces batch verification technology, which combines multiple signature verification steps into one step, thereby reducing the computational and communication overhead and improving the efficiency of signature verification while ensuring security. Xiong et al. introduced an ECDSA signature scheme based on blockchain with fault-tolerant batch verification. Using batch verification technology, the verification of multiple signatures is combined into a set operation, thereby improving the efficiency of verification.

Although existing technologies attempt to reduce the overhead of verification time, for large-scale signature verification, the verification efficiency of most batch verification schemes is not high (Yu et al., 2023). To improve the efficiency of large-scale verification tasks, this paper proposes a blockchain-based dual-parameter ECDSA batch verification scheme based on the improvement of ECDSA. The scheme can verify multiple signatures at once based on the modulo inversion algorithm, and it introduces the KGLP algorithm to accelerate the scalar multiplication operation, thus greatly reducing the verification time and significantly improving the efficiency of the scheme. It can also prevent digital signature forgery attacks.

The rest of this paper is organized as follows: Section 2 introduces the basics of ECDSA and cryptography in blockchain. Section 3 proposes a signature algorithm based on two-parameter ECDSA using the KGLP algorithm and batch verification technique. Section 4 analyzes the scheme in terms of security. Section 5 analyzes the performance of the scheme. Finally, Section 6 summarizes the paper.

2 Preliminaries

2.1 Scheme parameters and interpretation instructions

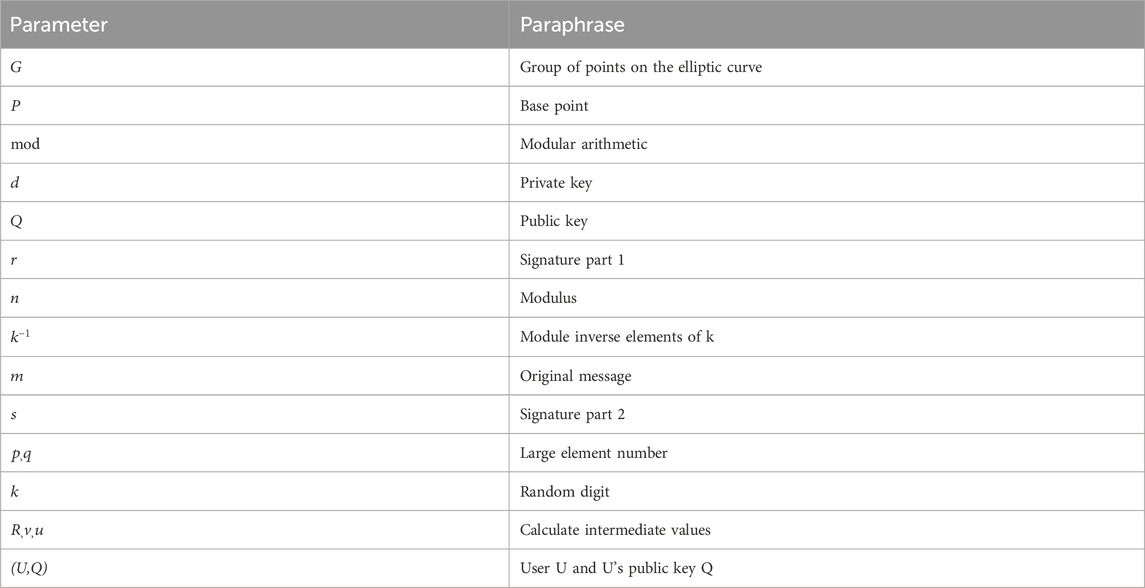
The symbols and definitions of the parameters involved in this scheme description are shown in Table 1.

Table 1

Table 1. Parameter symbols and definitions.

2.2 Elliptic curve

Elliptic curve cryptography (ECC) is an algebraic structure defined over a finite field, which is commonly used in cryptography such as encryption and digital signatures. With it set as an elliptic curve, $F_p$ representing a prime field ($p$ large prime number), and the elliptic curve satisfies the following Equation 1:

$E\left(F_p\right):y^2=x^3+ax+b,(1)$

where $a,b\in F_p$ and are constants for any $a,b\in F_p$.

2.3 Elliptic curve digital signature algorithm

ECDSA is a digital signature algorithm based on elliptic curves, which can be used to verify the integrity and non-repudiation of messages. The key pair of ECDSA $a,b\in F_p$ consists of a public key $Q$ and a private key $d$ that satisfy $Q=\mathit{dP}$, where $P$ is a base point of order $q$ on $E\left(F_p\right)$. If the order of $E\left(F_p\right)$ is $N$, then $h=N/q$ is called the cofactor.

2.3.1 Key generation stage

Given the main parameters $T=\left(p,a,b,P,q,h\right)$, to generate the signer’s key pair $\left(d,Q\right)$, the main steps are as follows:

Step 1: select a base point $P\in E\left(F_p\right)$ with order $q$ from elliptic curve $E\left(F_p\right)$;

Step 2: select a random integer $d\in \left[1,q-1\right]$;

Step 3: calculate $Q=\mathit{dP}$ and generate a key pair $\left(d,Q\right)$.

2.3.2 Signature stage

The signer generates an ECDSA signature $\left(m,r,s\right)$ for the message $m$ with the following main steps:

Step 1: the signer randomly selects a temporary secret value $k\in \left[1,q-1\right]$ and calculates $R=\mathit{kP}$;

Step 2: calculate $r=x\left(R\right)\left(\mathit{mod}q\right)$, where $x\left(R\right)$ is the x-coordinate of $R$. If $r=0$, go back to step 1;

Step 3: calculate $s=k^{-1}\left(H\left(m\right)+dr\right)\left(\mathit{mod}q\right)$, where $H\left(m\right)$ is a hash function. If $s=0$, go back to step 1;

Step 4: the signer generates the signature $\left(m,r,s\right)$ of the message $m$ and sends it to the verifier.

2.3.3 Verification stage

After receiving the signature $\left(m,r,s\right)$ from the signer, the verifier performs the following verification steps:

Step 1: the verifier first checks whether $r,s\in \left[1,q-1\right]$ holds, and if it does not, the verification fails;

Step 2: calculate $e=H\left(m\right)$, followed by $v=e{s}^{-1}\left(\mathit{mod}q\right)$ and $u=r{s}^{-1}\left(\mathit{mod}q\right)$;

Step 3: compute $R=\mathit{vP}+\mathit{uQ}$ and $r^{\prime }=x\left(R\right)\left(\mathit{mod}q\right)$;

Step 4: the verifier verifies whether $r^{\prime }=r$ is valid or not. If it is valid, then the signature is accepted; otherwise, it is rejected.

In ECDSA, one modulo-inverse operation is required for each of the signature and verification phases. If the data size is $N$, the complexity of one modulo operation is $O\left(N^2\ln N\right)$, while the complexity of modulo inverse operation is $O\left(N^3\right)$, which is one order of magnitude higher than the modulo operation. Therefore, the mode inverse operation should be avoided as much as possible in this algorithm to improve the efficiency (Na et al., 2022) of signature verification.

2.4 Elliptic curve discrete logarithm problem

The elliptic curve discrete logarithmic problem (ECDLP) is recognized as a difficult mathematical problem, and its intractability is based on the inability of the current computational power of computers to solve large-scale elliptic curve discrete logarithmic problems in a reasonable amount of time. The ECDLP takes the specific form of solving an elliptic curve $E\left(F_p\right)$, given a point $Q$ and a base point $P$, where $d$ satisfies equation $Q=\mathit{dP}$.

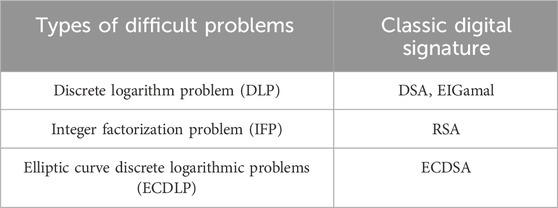
Three common types of difficult problems in current public key cryptosystem-based digital signatures are given in Table 2, among which, ECDLP is the most difficult to solve (Abdelkrim et al., 2022).

Table 2

Table 2. Signatures for different difficult problems.

2.5 Batch validation for ECDSA

Batch verification is a technology that can verify multiple signatures at the same time, which is applicable to ECDSA. In the large-scale transaction of blockchain systems, there are many message signatures to be verified, and a lot of time and computational resources will be consumed if they are verified one by one. Batch verification technology can verify multiple message signatures at the same time, which can effectively improve the verification efficiency of signatures and also reduce the computational cost of verification. The standard methods for batch verification of ECDSA signatures generated by multiple or single signers are shown in Equations 2, 3.

The standard ECDSA signature verification equation is R = uP + vQ. When verifying the ECDSA signature $\left(m_1,r_1,s_1\right),\left(m_2,r_2,s_2\right),\cdots ,\left(m_t,r_t,s_t\right)$ of t signers, in order to improve the efficiency of ECDSA signature verification and save computational resources, these signatures can be aggregated as follows:

${\displaystyle \sum _{i=1}^t}{R}_i=\left({\displaystyle \sum _{i=1}^t}{v}_i\right)P+{\displaystyle \sum _{i=1}^t}{u}_i{Q}_i.(2)$

In the event that all signatures originate from a single signer, the public key utilized in the verification process is identical, $Q_1=Q_2=\cdots =Q_t=Q$, and the equation for bulk verification can be simplified as follows:

${\displaystyle \sum _{i=1}^t}{R}_i=\left({\displaystyle \sum _{i=1}^t}{v}_i\right)P+\left({\displaystyle \sum _{i=1}^t}{u}_i\right)Q.(3)$

The ECDSA batch verification scheme can reduce the scalar multiplication operation in the verification phase from 2t to [2, t+1], which greatly reduces the time overhead of signature verification. To detect the equivalence of Equations 2, 3, Karati et al. proposed the plain batch verification algorithm and the symbolic batch verification algorithm.

2.6 Blockchain cryptography

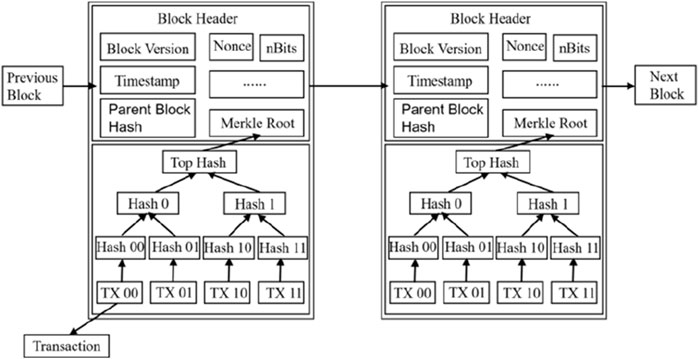
Blockchain is a distributed ledger technology that originated with the digital cryptocurrency Bitcoin. In a blockchain, each block consists of two main parts, the block header and the block body, where the block header contains a unique hash value as the block address. By recording the hash value of the previous block, the blockchain links each block into a chain structure, the specific structure of which is shown in Figure 1. Each transaction consists of a list of “inputs” and “outputs,” and the “inputs” of a transaction contain digitally signed data, ensuring that the transaction data cannot be tampered with or forged.

Figure 1

Figure 1. Blockchain data structure.

In the Bitcoin trading system, ECDSA is used to verify the identity of the account holder and prevent misuse of the account. To ensure the validity of transactions, each transaction must be verified with a digital signature. When a node receives a transaction, it first verifies the correctness of the digital signature to ensure that the transaction was initiated by the account holder. Only after verifying the digital signature will the node broadcast the transaction to other nodes and join the blockchain. Therefore, ECDSA is an important guarantee for the security of Bitcoin transactions, making transactions safe and efficient in a decentralized blockchain system. However, with the increasing volume of transactions, the verification efficiency of ECDSA has gradually become a challenge. To address this challenge, several optimization measures can be taken to reduce the latency of transaction broadcasting and verification while ensuring the security and reliability of transactions.

3 Proposed scheme

3.1 The KTP-ECDSA digital signature algorithm

The traditional ECDSA scheme has time-consuming mode reversal operations in both the signature phase and the verification phase, and its computation time overhead is 10 times that of the dot product operation. In order to improve the efficiency of the ECDSA scheme, an improved elliptic curve digital signature algorithm (KTP-ECDSA) is proposed, which introduces the KGLP algorithm under the premise of the TP-ECDSA (Guang-fu et al., 2024) scheme and uses Hamming weights instead of message hash to avoid the mode reversal operation. The KTP-ECDSA algorithm is mainly divided into key generation, signature, and verification stages, and the specific process is as follows.

3.1.1 Key generation stage

Given the main parameters $T=\left(p,a,b,P,q,h\right)$, to generate the signer’s key pair $\left(d,Q\right)$, the main steps are as follows:

Step 1: select a base point $P\in E\left(F_p\right)$ with order $q$ from the elliptic curve $E\left(F_p\right)$;

Step 2: select a random integer $d\in \left[1,q-1\right]$;

Step 3: calculate $Q=\mathit{dP}$ and generate the key pair $\left(d,Q\right)$.

3.1.2 Signature stage

The signer generates an ECDSA signature $\left(m,r,s,\beta \right)$ for the message $m$ with the following main steps:

Step 1: the signer randomly selects a temporary secret value $k\in \left[1,q-1\right]$ and calculates $\mathrm{R}=\text{kP}$;

Step 2: calculate $r=x\left(R\right)\left(\mathit{mod}q\right)$, where $x\left(R\right)$ is the x-coordinate of $R$. If $r=0$, go back to step 1;

Step 3: the signer uses a random number generator to generate two numbers $\alpha ,\beta \in \left[1,q-1\right]$ at random that satisfy $k=\alpha r+\beta m$;

Step 4: calculate $e=H\left(m\right)$ and its Hamming weight $w$;

Step 5: calculate $s=\alpha r+\left(w+r\right)d\left(\mathit{mod}q\right)$. If $s=0$, return to step 1;

Step 6: the signer generates the signature $\left(m,r,s,\beta \right)$ of the message $m$ and sends it to the verifier.

3.1.3 Verification stage

Any verifier can test the validity of a sign $\left(m,r,s,\beta \right)$ by following the steps below:

Step 1: the verifier first tests whether $r,s,\beta \in \left[1,q-1\right]$ holds; if otherwise, the verification fails;

Step 2: compute $e=H\left(m\right)$ and its Hamming weights $w$;

Step 3: compute $v=\left(s+\beta m\right)\left(\mathit{mod}q\right)$ and $u=\left(w+r\right)\left(\mathit{mod}q\right)$;

Step 4: calculate $R=\mathit{vP}-\mathit{uQ}$ and $r^{\prime }=x\left(R\right)\left(\mathit{mod}q\right)$;

Step 5: the verifier checks whether $r^{\prime }=r$ is valid. If so, the signature is accepted; otherwise, it is rejected.

3.2 KGLP algorithms

The KGLP algorithm is a fast scalar multiplication algorithm for elliptic curve cryptography, which is widely used in scenarios such as digital signature and public key encryption. Compared with the traditional scalar multiplication algorithm, the KGLP algorithm has higher computational efficiency and better performance. The KGLP algorithm transforms the original scalar multiplication operation into multiple sub-operations based on the addition and multiplication of elliptic curve points and improves the execution speed of the whole algorithm through parallel processing. In practice, the KGLP algorithm can significantly improve the security and efficiency of elliptic curve cryptography, especially when dealing with large data and performing high-strength encryption.

In general, the most time-consuming operations in the ECDSA batch verification scheme are scalar multiplication and the modulo inverse operation. In contrast, the TP-ECDSA scheme does not require the latter, with the former, therefore, representing the most time-consuming operation in this scheme. In order to enhance the efficiency of the TP-ECDSA batch verification scheme, we employ the KGLP algorithm to accelerate the scalar multiplication operation, thereby improving the overall verification efficiency. The KGLP algorithm can calculate scalar multiplications of multiple points at the same time, which reduces the number of doubling operations and improves the computational efficiency. For example, in batch verification of t TP-ECDSA signatures, the KGLP algorithm can calculate and sum the scalar multiplications of t points simultaneously, i.e., ${\sum }_{i=1}^t{u}_i{Q}_i$. The KGLP algorithm is shown in Algorithm 1. Assuming that $v_i$ is, at most, $l$ bits, the binary representation of all multipliers can be written as a $t\times l$ matrix. It is possible to arbitrarily combine the expected results of t scalar sums, perform scalar multiplication operations on t points, and then perform scalar addition based on the value of column i of the $t\times l$ matrix. Utilizing this algorithm in the batch validation of TP-ECDSA requires only $l$ scalar doubling and $l\cdot \left[1-{\left(1/2\right)}^t\right]$ scalar addition, whereas $t\times l$ scalar multiplication doubling and $t\times l/2+t-1$ scalar addition are required when this operation is not used.

Algorithm 1.KGLP algorithm.

Input: u_i = (u_i,l,u_i,l−1, … ,u_i,1), Q_i∈E (F_P), i∈[1,t]

Output: R = ∑u_iQ_i

1. QQ_j = j_tQ_t + j_t−1Q_t−1 + … + j₁Q₁, j=(j_t, … ,j₁)₂, j∈[0,2^t−1]; //pre-calculated results for any combination of t-point scalar summation

2. R = ∞;

3. for i = t; i ≥ 0;i--do

4.     R = 2R;

5.     for j = t; j ≥ 0; j--do

6.        bit = u_j,i ≪ j;

7.     R = R + QQ_bit;

8.     return R;

3.3 KTP-ECDSA batch verification scheme

ECDSA batch verification schemes are good at checking lots of signatures at once, but they get slower as the number of signatures in a batch gets bigger. Blockchain transactions are large, so existing schemes may not work. Our scheme is fast for all sizes of message signature verification with few modulo and scalar multiplication operations. The main time-consuming operation in the KTP-ECDSA batch verification scheme is the scalar multiplication operation. We propose a KTP-ECDSA batch verification scheme using the KGLP algorithm to reduce this operation and the time overhead of signature verification. The KTP-ECDSA batch verification scheme is given below from the perspective of the same signer and different signers.

3.3.1 KTP-ECDSA batch verification scheme for same signers

For batch verification of same signers, we can utilize the same public key and different messages and signatures. The public key of the same signer is the same; when verifying t message signatures $\left(m_i,r_i,s_i,{\beta }_i\right)\left(i=1,2,\cdots ,t\right)$, according to the verification algorithm of the TP-ECDSA scheme, 2t scalar multiplication operations are needed, while this scheme only needs two scalar multiplication operations, and the KGLP algorithm accelerates the scalar multiplication operations, which can greatly improve the efficiency of the verification of signatures. The specific process of the KTP-ECDSA batch verification scheme for the same signer is as follows:

Step 1: the verifier first tests whether $r_i,s_i,{\beta }_i\in \left[1,q-1\right]$ holds. If otherwise, the verification fails;

Step 2: compute $e_i=H\left(m_i\right)$ and its Hamming weights $w_i$;

Step 3: compute ${\sum }_{i=1}^t{v}_i={\sum }_{i=1}^t\left(s_i+{\beta }_i{m}_i\right)\left(\mathit{mod}q\right)$;

Step 4: calculate ${\sum }_{i=1}^t{u}_i={\sum }_{i=1}^t\left(w_i+r_i\right)\left(\mathit{mod}q\right)$;

Step 5: calculate $R={\sum }_{i=1}^t{r}_i$;

Step 6: based on the equations in steps 3 and 4, the KGLP algorithm is applied to perform scalar multiplication to calculate $T={\sum }_{i=1}^t{v}_{i}P-{\sum }_{i=1}^t{u}_{i}Q$;

Step 7: the verifier computes $R^{\prime }=x\left(T\right)\left(\mathit{mod}q\right)$ and verifies whether $R^{\prime }=R$ holds. If it does, then the batch of signatures is accepted; otherwise, the batch of verifications fails.

3.3.2 KTP-ECDSA batch verification scheme for different signers

For batch verification of different signers, there are varying public keys and message signatures to be verified. It is assumed that there are t signers whose key pairs are $\left(d_i,Q_i\right)\left(i=1,2,\cdots ,t\right)$ and t signatures $\left(m_i,r_i,s_i,{\beta }_i\right)\left(i=1,2,\cdots ,t\right)$ are generated for different messages $m$. The use of TP-ECDSA requires 2t scalar multiplication operations in the verification phase, while this scheme only requires t+1, and the KGLP algorithm accelerates the scalar multiplication operations, so the efficiency of signature verification is greatly improved. The specific process of KTP-ECDSA batch verification scheme for different signers is as follows:

Step 1: the verifier first tests whether $r_i,s_i,{\beta }_i\in \left[1,q-1\right]$ holds. If otherwise, the verification fails;

Step 2: tor t different signers, have ${\sum }_{i=1}^t{Q}_i={\sum }_{i=1}^t{d}_{i}P$;

Step 3: compute $e_i=H\left(m_i\right)$ and its Hamming weights $w_i$;

Step 4: compute ${\sum }_{i=1}^t{v}_i={\sum }_{i=1}^t\left(s_i+{\beta }_i{m}_i\right)\left(\mathit{mod}q\right)$;

Step 5: calculate ${\sum }_{i=1}^t{u}_i={\sum }_{i=1}^t\left(w_i+r_i\right)\left(\mathit{mod}q\right)$;

Step 6: calculate $R={\sum }_{i=1}^t{r}_i$;

Step 7: based on the above equation, the KGLP algorithm is applied to calculate the scalar multiplication operation to compute $T={\sum }_{i=1}^t{v}_{i}P-{\sum }_{i=1}^t{u}_i{Q}_i$;

Step 8: the verifier computes $R^{\prime }=x\left(T\right)\left(\mathit{mod}q\right)$ and verifies whether $R^{\prime }=R$ holds. If it does, then the batch of signatures is accepted; otherwise, the batch of verifications fails.

Our scheme uses the TP-EDCSA implementation, which uses the KGLP algorithm to further reduce the time overhead of the scalar multiplication operation. As the number of signatures increases, the time spent verifying them decreases. The KTP-ECDSA scheme uses the KGLP algorithm to reduce the time spent on verification. It can verify large numbers of transactions in the blockchain efficiently and reduces the time spent on signature verification.

3.4 Correctness

The signature verification phase of the TP-ECDSA scheme meets the computational correctness of individual verification processes and batch verification processes, as shown in Equations 4–6.

3.4.1 Individual verification

$\begin{array}{l}Right=uP-vQ=\left(s+\beta m\right)P-\left(w+r\right)dP\\ =\left[\left(\alpha r+\left(w+r\right)d+\beta m\right)-\left(w+r\right)d\right]P\\ =\left(\alpha r+\beta m\right)P\\ =\text{kP}\\ =\mathrm{R}=\text{Left}.\end{array}(4)$

3.4.2 Batch verification

For batch verification of different signers, there are $r_i=x\left(k_{i}P\right)\left(\mathit{mod}q\right)$ and $k_i={\alpha }_i{r}_i+{\beta }_i{m}_i$ in the signing phase. So, it is only necessary to verify that Equation 5 holds.

${\displaystyle \sum _{i=1}^t}{k}_{i}P={\displaystyle \sum _{i=1}^t}{v}_{i}P-{\displaystyle \sum _{i=1}^t}{u}_i{Q}_i.(5)$

Then, the following equation holds:

$\begin{array}{l}Right={\displaystyle \sum _{i=1}^t}{v}_{i}P-{\displaystyle \sum _{i=1}^t}{u}_i{Q}_i={\displaystyle \sum _{i=1}^t}\left(s_i+{\beta }_i{m}_i\right)P-{\displaystyle \sum _{i=1}^t}\left(w_i+r_i\right)d_{i}P\\ =\left[\left({\displaystyle \sum _{i=1}^t}\left({\alpha }_i{r}_i+\left(w_i+r_i\right)d+{\beta }_i{m}_i\right)\right)-{\displaystyle \sum _{i=1}^t}\left(w_i+r_i\right)d_i\right]P\\ ={\displaystyle \sum _{i=1}^t}\left({\alpha }_i{r}_i+{\beta }_i{m}_i\right)P\\ ={\displaystyle \sum _{i=1}^t}{k}_{i}P=Left.\end{array}(6)$

4 Security analysis

4.1 Security formalism analysis

This section shows how the security model works in a game between a challenger $\mathcal{C}$ and an attacker $\mathcal{A}$. There are three types of attackers: ordinary, strong, and super. Ordinary attackers usually forge a signature with a specific public key by eavesdropping on network communications. Strong attackers forge signatures when they work with legitimate participants to obtain private keys. Super-attackers can even forge signatures using only selected public keys. They can also extract private keys from public keys and sign messages using a “black box” tool.

Attacker $\mathcal{A}$ can denote the super attacker. The challenger $\mathcal{C}$ is constructed by an algorithm with $\mathcal{A}$ as a black box and can simulate $\mathcal{A}$ to gain accesses to the prediction machine. In the next interaction game, we assume the existence of super type I and type II attackers ${\mathcal{A}}_I$ and ${\mathcal{A}}_{II}$.

4.1.1 Game

Super type I and type II attackers ${\mathcal{A}}_I$ and ${\mathcal{A}}_{II}$ and challenger $\mathcal{C}$ play an interactive game with adaptively chosen users U and messages $m$. The game is played by the attackers. During system initialization, $\mathcal{C}$ generates public parameters and releases them to the attackers. Attackers ${\mathcal{A}}_I$ and ${\mathcal{A}}_{II}$ can submit multiple queries, e.g., user-created queries, hash queries, etc., to the prediction machine under the random prediction machine model in polynomial time. After submitting all the necessary queries, if attacker ${\mathcal{A}}_I$ or ${\mathcal{A}}_{II}$ successfully outputs a legitimate forged signature, it means that ${\mathcal{A}}_I$ or ${\mathcal{A}}_{II}$ wins the game; otherwise, the forged signature fails.

Theorem 1:. Under the intractability assumption based on the elliptic curve discrete logarithmic problem, the proposed scheme suffers from unforgeability under the adaptive choice of message attack against the super type I attacker ${\mathcal{A}}_I$.

4.1.2 Proof

Under the stochastic predicate machine model, a legitimate signature can be forged assuming that in polynomial time, the attacker ${\mathcal{A}}_I$ can successfully crack the ECDLP puzzle with non-negligible probability after executing qc user-created queries, qh hash queries, qs secret-value queries, qk public-key queries, and qs signature queries. We can construct a challenger $C$ that runs ${\mathcal{A}}_I$ as a subroutine for solving difficult ECDLP problems. Given an ECDLP instance $\left(P,Q=dP\right)$, for $C$, the ultimate goal is to compute $d$. $C$ and ${\mathcal{A}}_I$ will play the following game:

4.1.3 Initialization phase

Challenger $\mathcal{C}$ runs the system initialization program, generates the public parameter $T=\left(p,a,b,P,q,h\right)$, sends the parameter to ${\mathcal{A}}_I$, and randomly selects user U as the forgery target.

4.1.4 Query phase

${\mathcal{A}}_I$ performs the following randomized predicator query.

User creation query: challenger $\mathcal{C}$ maintains the list L_c with element contents in the format of (U,Q) and an empty initial state. When $\mathcal{C}$ receives a user-created query from ${\mathcal{A}}_I$ about U, $\mathcal{C}$ searches L_c and responds directly to ${\mathcal{A}}_I$ if the corresponding tuple exists; otherwise, $\mathcal{C}$ randomly selects $d\in \left[1,q-1\right]$, computes $Q=\mathit{dP}$, and adds (U,Q) to the list L_c, and $Q$ will respond to ${\mathcal{A}}_I$.

Hash query: challenger $\mathcal{C}$ maintains list L_h, whose element contents are in the format of $\left(\mathrm{U},m,w\right)$ and whose initial state is empty. When $\mathcal{C}$ receives a $\left(m,w\right)$ query from ${\mathcal{A}}_I$ about, it searches the list L_h and responds directly to ${\mathcal{A}}_I$ if the corresponding tuple exists; otherwise, $\mathcal{C}$ chooses a random number $w\in Z^{*}$, computes the weight value $w$ of the message $m$, adds it to the list L_h, and responds to ${\mathcal{A}}_I$.

Secret value query: challenger $\mathcal{C}$ maintains the list L_s, whose element contents are in the format of $\left(\mathrm{U},k,R,r,\alpha ,\beta \right)$ and whose initial state is empty. When $\mathcal{C}$ receives a secret value query from ${\mathcal{A}}_I$ about user U, $\mathcal{C}$ searches the list L_s and responds directly to ${\mathcal{A}}_I$ if the corresponding tuple exists; otherwise, $\mathcal{C}$ randomly selects $k,\alpha ,\beta \in \left[1,q-1\right]$, computes $R=\mathit{kP}$, $r=x\left(R\right)\left(\mathit{mod}q\right)$, and then $\alpha$ and $\beta$ that satisfy the equation by $k=\alpha r+\beta m$, adds the result to the list L_s, and responds to ${\mathcal{A}}_I$.

Public key query: when $\mathcal{C}$ receives the public key query from ${\mathcal{A}}_I$ about U, it searches the list L_c and re-executes the user-created query if the tuple (U,Q) does not exist; otherwise, challenger $\mathcal{C}$ responds $Q$ to ${\mathcal{A}}_I$.

Signature query: when challenger $\mathcal{C}$ receives a signature query from ${\mathcal{A}}_I$ about message $m$, $\mathcal{C}$ searches lists L_c, L_h, and L_s for the required data and randomly selects $s\in \left[1,q-1\right]$; and if the equation $kP=\left(s+\beta m\right)P-\left(w+r\right)Q$ is valid, $\mathcal{C}$ responds to ${\mathcal{A}}_I$ with the formed signature $\sigma =\left(r,s\right)$.

4.1.5 Forging phase

${\mathcal{A}}_I$ completes all the necessary queries and finally outputs a valid message signature $\left(\mathrm{U},m,\sigma =\left(r,s\right)\right)$. According to the forking lemma, ${\mathcal{A}}_I$ chooses a different hash function answer in the same stochastic predicate machine model and obtains another message signature pair $\left(\mathrm{U},m,{\sigma }^{\prime }=\left(r,s^{\prime }\right)\right)$ with the same r-value by replaying the above process. Thus, Equations 7, 8 can be obtained as follows:

$kP=\left(s^{\prime }+\beta m\right)P-\left(w^{\prime }+r\right)Q,(7)$

$kP=\left(s^{\prime }+\beta m\right)P-\left(w^{\prime }+r\right)Q.(8)$

Based on the above two equations, $\left(s-s^{\prime }\right)=\left(w-w^{\prime }\right)d$ can be obtained, and then, $d=\left(s-s^{\prime }\right){\left(w-w^{\prime }\right)}^{-1}$ can be calculated.

Challenger $\mathcal{C}$ eventually computes $d$ as a solution to ECDLP instance $\left(P,Q=dP\right)$ with non-negligible probability. However, this contradicts the hardness of the ECDLP hard problem assumed in the previous section. Therefore, the scheme in this paper is secure under the stochastic predicate machine model with the existence of unforgeability of the adaptive message selection attack by the super type I attacker ${\mathcal{A}}_I$.

Theorem 2:. Under the intractability assumption based on the elliptic curve discrete logarithmic problem, the proposed scheme suffers from unforgeability under the adaptive choice of message attack against the super type II attacker ${\mathcal{A}}_{II}$.

The proof of Theorem 2 has the same idea and method as Theorem 1, so the proof process will not be repeated in this paper.

4.2 Security analysis

1) Message integrity: Message integrity is achieved through hash functions and Hamming weights. A hash function is a function that maps the data on arbitrary length to a fixed length hash value, which is unique and irreversible. Any minor changes to the message will result in a completely different hash digest. Hamming weights can further verify the integrity of the message. When the data are tampered with, the Hamming weight gives different results. Therefore, the scheme in this paper has message integrity and can effectively prevent data tampering. In the event that a signature is identified as being fraudulent as a result of the injection of a fictitious signature, the verification process will be unsuccessful.

2) Non-repudiation: in the scheme of this paper, the sender of the message signs the message using its own private key. Since the private key is owned only by the sender, no one else can forge the sender’s signature. Therefore, once the signature of a message has been verified, it can be determined that the message was indeed sent by the sender, and the sender cannot deny that it sent the message.

3) Forward security: assume that an illegal user can get the public key of U. Due to $Q_U=d_{U}P$, even if the attacker knows $Q_U$ and $P$, by the elliptic curve discrete logarithm problem (ECDLP), it is difficult for the attacker to compute $d_U$, i.e., he cannot get the private key of user U. Therefore, the scheme is forward secure.

4) Resistant weak randomness: after taking the first random number $k$, the scheme in this paper, since $k$ is randomly selected in the range of $\left[1,q-1\right]$. With $r$ and $m$ known, there must exist an integer $\beta \in \left[1,q-1\right]$ that satisfies the equation $k=\alpha r+\beta m$ when $\alpha$ is randomly selected from the interval $\left[1,q-1\right]$. The structure of the TP-ECDSA scheme in this paper is reasonable and randomized, and it has the ability to resist weak randomness.

5) Anti man-in-the-middle attack: if the two communicating parties do not know each other’s identity, the establishment of a critical session is vulnerable to man-in-the-middle attack. This solution realizes two-way authentication through digital signature technology so that illegal users cannot impersonate either party and can effectively prevent man-in-the-middle attacks.

5 Efficiency analysis

We compare ECDSA with KTP-ECDSA for verification to check how well they work. The computer-based experimental runtime environment is Windows 11, 64-bit CPU. Intel Core i5 CPU @ 1.60 GHz; 8 GB RAM.

We use C to implement the schemes in this paper, calling the parameters of the security curve in the OpenSSL source code (OpenSSL is an open-source cryptographic library that provides a large number of cryptographic algorithms and key protocols) and programmed in Visual Studio 2021. The OpenSSL Development Kit program is used to verify ECDSA and KTP-ECDSA for large prime number domains.

The current mainstream batch algorithms include Schnorr and SM2. However, Schnorr has not been widely adopted by all mainstream blockchains, and the international adoption rate of SM2 is lower than that of ECDSA and Schnorr. Consequently, in the experimental efficiency analysis, we primarily compared with the ECDSA algorithm.

The ECDSA is employed in conjunction with KTP-ECDSA, as detailed in this paper, to facilitate the individual and batch verification of a single signatory and multiple signatories. Each scheme is executed 100 times, and the resulting data are averaged. The time required for the key generation phase differs between the same-signer and different-signer signature verification schemes. This is due to the fact that the same-signer scheme necessitates the generation of a single set of key pairs but the different-signer scheme requires the generation of multiple sets of key pairs. Furthermore, the time required for each stage of the signature verification process is almost identical. Table 3 presents the runtime overhead of independent and bulk verification by the same signers for varying message signature sizes. Table 4 presents the runtime overhead of independent and bulk verification by different signers. The use of a hyphen in tables III and IV indicates the absence of pertinent data. As can be seen from table III, when verifying 16 message signatures, ECDSA consumes 4,737 ms for individual verification and 431 ms for batch verification, while KTP-EDCSA consumes 58 ms for individual verification and only 4.8 ms for batch verification. It is evident from tables III and IV that the batch verification can markedly reduce the time overhead of verification in comparison to individual verification. In particular, the KTP-ECDSA batch verification scheme proposed in this paper requires even less time for the verification of signatures.

Table 3

Table 3. Time overhead for identical signers with independent and batch verification (ms).

Table 4

Table 4. Time overhead for different signers with independent and batch verification (ms).

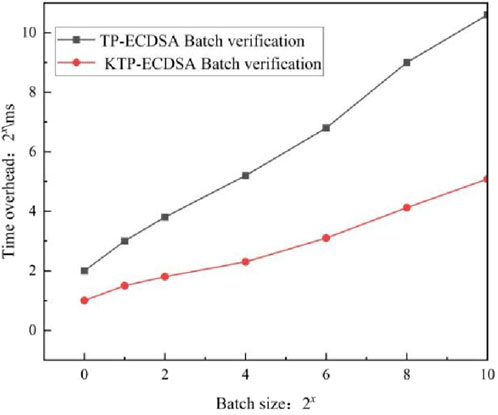
In Figure 2, we show whether the TP-ECDSA batch verification scheme uses the KGLP algorithm to accelerate the time overhead of the verification algorithm, i.e., comparing the time overhead of TP-ECDSA and KTP-ECDSA batch verification, which can be shorter and more efficient in the latter. The horizontal coordinate $2^x\left(x=0,2,\cdots ,10\right)$ in Figure 2 indicates the number of signatures, and the vertical coordinate $2^x\left(x=0,2,\cdots ,10\right)$ indicates the time overhead of verification. As demonstrated in Figure 2, TP-ECDSA batch verification’s time overhead grows rapidly as the size of the number of signatures grows exponentially, whereas KTP-ECDSA batch verification’s time overhead grows more gradually. When the number of signatures is 1,024, TP-ECDSA batch verification takes approximately 1,540 ms, and TP-ECDSA batch verification takes only 32.9 m, which optimizes the operation speed by approximately 97.8%. Therefore, for simultaneous verification of large-scale message signatures, KTP-ECDSA batch verification with the introduction of the KGLP algorithm can greatly reduce the verification time and significantly improve the efficiency.

Figure 2

Figure 2. Time overhead of Tp-ECDSA and KTP-ECDSA batch verifications.

6 Conclusion

The present study proposes a batch verification scheme with the objective of enhancing the efficiency of large-scale message signature verification in blockchain. The proposed scheme builds upon the TP-ECDSA scheme with a modeless inverse operation, employing the KGLP algorithm in a dual-parameter elliptic curve digital signature for batch verification. In comparison to independent verification, the TP-ECDSA batch verification scheme reduces the number of scalar multiplications and utilizes the KGLP algorithm to accelerate the time-consuming scalar multiplication operation, thereby significantly improving the verification speed. A security analysis indicates that the proposed scheme ensures data security, possesses non-forgeability, and can resist weak randomness attacks on ECDSA. Experimental analysis demonstrates that in comparison to existing schemes, the proposed scheme has a significant advantage in terms of verification time costs and can achieve the final verification result with fewer computational operations. It is our belief that this scheme will prove to be a valuable addition to blockchain systems in the future.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

GW: writing–original draft. JZ: writing–review and editing. XF: writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdelkrim, I., Ahmed, E., and Fouzia, O. (2022). ECDSA-based certificateless conditional privacy-preserving authentication scheme in Vehicular ad hoc Network. Veh. Commun. 37, 100504. doi:10.1016/j.vehcom.2022.100504

CrossRef Full Text | Google Scholar

Bao, F., Lee, C. C., and Hwang, M. S. (2006). Cryptanalysis and improvement on batch verifying multiple RSA digital signatures. Appl. Math. Comput. 172 (2), 1195–1200. doi:10.1016/j.amc.2005.03.016

CrossRef Full Text | Google Scholar

Binbin, T., Chen, Y., Cui, H., and Wang, X. (2024). Fast two-party signature for upgrading ECDSA to two-party scenario easily. Theor. Comput. Sci. 986, 114325. doi:10.1016/j.tcs.2023.114325

CrossRef Full Text | Google Scholar

Cao, X., and Wei, S. M. (2018). Improved elliptic curve digital signature algorithm. J. Huaibei Normal Univ. Nat. Sci. Ed. 34 (2), 1–3.

Google Scholar

Fang, W., Chen, W., Zhang, W., Pei, J., Gao, W., Wang, G., et al. (2020). Digital signature scheme for information non-repudiation in blockchain: a state of the art review. EURASIP J. Wirel. Commun. Netw. 10, 1366–1385. doi:10.1186/s13638-020-01665-w

CrossRef Full Text | Google Scholar

Fiat, A. (1997). Batch RSA. J. Cryptol. 10 (2), 75–88. doi:10.1007/s001459900021

CrossRef Full Text | Google Scholar

Guang-fu, W., Xiao-yan, F., and Jian-dong, Z. (2024). An efficient and lightweight two-parameter ECDSA batch verification scheme. J. Jiamusi Univ. Nat. Sci. Ed. 42 (01), 1–5.

Google Scholar

Jiarui, Y., Cui, J., Tu, H., Yu, C., and Zhou, M. (2023). A SM2 based efficient and lightweight batch verification approach for IC cards. J. Inf. Secur. Appl. 73, 103409. doi:10.1016/j.jisa.2022.103409

CrossRef Full Text | Google Scholar

Karati, S., Das, A., Roychowdhury, D., Bellur, B., Bhattacharya, D., and Iyer, A. (2014). New algorithms for batch verification of standard ECDSA signatures. J. Cryptogr. Eng. 4 (4), 237–258. doi:10.1007/s13389-014-0082-x

CrossRef Full Text | Google Scholar

Khizar, H., Garg, S., Amin, M. B., Kang, B., and Khan, A. (2022). A context-aware information-based clone node attack detection scheme in Internet of Things. J. Netw. Comput. Appl. 197, 103271. doi:10.1016/j.jnca.2021.103271

CrossRef Full Text | Google Scholar

Kittur, A. S., and Roshan Pais, A. (2017). Batch verification of digital signatures: approaches and challenges. J. Inf. Secur. Appl. 37, 15–27. doi:10.1016/j.jisa.2017.09.005

CrossRef Full Text | Google Scholar

Kittur, A. S., and Pais, A. R. (2017). Batch verification of digital signatures: approaches and challenges. J. Inf. Secur. Appl. 37, 15–27. doi:10.1016/j.jisa.2017.09.005

CrossRef Full Text | Google Scholar

Lim, C. H., and Lee, P. J. (1994). Security of interactive DSA batch verification. Electron. Lett. 30 (19), 1592–1593. doi:10.1049/el:19941112

CrossRef Full Text | Google Scholar

Lin, H.Yi (2023). Secure data transfer based on a multi-level blockchain for Internet of vehicles. Sensors 23 (5), 2664. doi:10.3390/s23052664

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, S. G., Chen, W. Q., and Liu, J. L. (2021). An efficient double parameter elliptic curve digital signature algorithm for blockchain. IEEE Access 9, 77058–77066. doi:10.1109/access.2021.3082704

CrossRef Full Text | Google Scholar

Mahajan, H. B., and Junnarkar, A. A. (2023). Smart healthcare system using integrated and lightweight ECC with private blockchain for multimedia medical data processing. Multimedia tools Appl. 82 (28), 44335–44358. doi:10.1007/s11042-023-15204-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Marcos, A., León, D. L., Cerón, S., Pareja, A., Pacheco, E., Leal, A., et al. (2023). Quantum-resistance in blockchain networks. Sci. Rep. 13 (1), 5664. doi:10.1038/s41598-023-32701-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Na, J., Kim, Y. H., Park, N., and Seo, B. (2022). Comparative analysis of Schnorr digital signature and ECDSA for efficiency using private ethereum network. IEIE Trans. Smart Process. and Comput. 11 (3), 231–239. doi:10.5573/ieiespc.2022.11.3.231

CrossRef Full Text | Google Scholar

Puthiyidam, J. J., Shelbi, J., and Bharat, B. (2023). Enhanced authentication security for IoT client nodes through T-ECDSA integrated into MQTT broker. J. Supercomput. 80 (7), 8898–8932. doi:10.1007/s11227-023-05789-w

CrossRef Full Text | Google Scholar

Rahman Taleb, A., and Vergnaud, D. (2021). Speeding-up verification of digital signatures. J. Comput. Syst. Sci. 116, 22–39. doi:10.1016/j.jcss.2020.08.005

CrossRef Full Text | Google Scholar

Wang, Z., Yu, H., Zhang, Z., Piao, J., and Liu, J. (2020). ECDSA weak randomness in Bitcoin. Future Gener. Comput. Syst. 102, 507–513. doi:10.1016/j.future.2019.08.034

CrossRef Full Text | Google Scholar

Xiao, S., Wang, X. A., and Pan, F. (2020). Elliptic curve digital signature algorithm for modeless inverse operations. Comput. Eng. Appl. 56 (11), 118–123.

Google Scholar

Yehuda, L. (2021). Fast secure two-party ECDSA signing. J. Cryptol. 34 (4), 44. doi:10.1007/s00145-021-09409-9

CrossRef Full Text | Google Scholar

Yu, J., Cui, J., Tu, H., Yu, C., and Zhou, M. (2023). A SM2 based efficient and lightweight batch verification approach for IC cards. J. Inf. Secur. Appl. 73 (C), 103409. doi:10.1016/j.jisa.2022.103409

CrossRef Full Text | Google Scholar

Zhang, P., Li, Y., Liu, M., Shang, Y., and Fu, Z. (2022). An ECC-based digital signature scheme for privacy protection in wireless communication network. Wirel. Commun. Mob. Comput. 2022, 1–9. doi:10.1155/2022/1977798

CrossRef Full Text | Google Scholar

Zhang, Q. S., Guo, B. A., and Cheng, D. F. (2008). Fast elliptic curve verification algorithm. Comput. Eng. Des. 29 (17), 4425–4427.

Google Scholar