Enhanced scalability and privacy for blockchain data using Merklized transactions

Blockchain technology has evolved beyond the use case of electronic cash and is increasingly used to secure, store, and distribute data for many applications. Distributed ledgers such as Bitcoin have the ability to record data of any kind alongside the transfer of monetary value. This property can be used to provide a source of immutable, tamper-evident data for a wide variety applications spanning from the supply chain to distributed social media. However, this paradigm also presents new challenges regarding the scalability of data storage protocols, such that the data can be efficiently accessed by a large number of users, in addition to maintaining privacy for data stored on the blockchain. Here, we present a new mechanism for constructing blockchain transactions using Merkle trees comprised of transaction fields. Our construction allows for transaction data to be verified field-wise using Merkle proofs. We show how the technique can be implemented either at the system level or as a second layer protocol that does not require changes to the underlying blockchain. This technique allows users to efficiently verify blockchain data by separately checking targeted individual data items stored in transactions. Furthermore, we outline how our protocol can afford users improved privacy in a blockchain context by enabling network-wide data redaction. This feature of our design can be used by blockchain nodes to facilitate easier compliance with regulations such as GDPR and the right to be forgotten.

1 Introduction

The use of the blockchain as a data source for various applications has significantly increased in recent years Ali et al. (2017); Sgantzos and Grigg (2019), Liang et al. (2020). Blockchains such as Bitcoin and its derivatives utilise a scripting language to lock and spend the native blockchain token. These scripts generally contain opcodes that operate on small items of data, such as public keys and digital signatures, for the purpose of transferring funds and verifying transactions. However, it is also possible to use these scripts to embed any kind of data on the blockchain. This data is sometimes called ‘arbitrary’ data because it does not relate to the conditions used to transfer the funds themselves Matzutt et al. (2018). There are several ways in which data can be embedded on Bitcoin-like chains using the scripting language, and the use of these methods has grown substantially over time Bartoletti and Pompianu (2017). One of the primary motivations for including such data on the blockchain is that it creates an immutable record for the data, which can improve transparency for a wide range of applications by enabling reliable proofs of data integrity Bartoletti and Pompianu (2017); Sgantzos and Grigg (2019); Aitsam and Chantaraskul (2020).

Despite the compelling use case for embedding arbitrary, non-payment data on the blockchain, the ability to do so has given rise to new problems and challenges. Most notably the inclusion of illicit data on the blockchain Zhang et al. (2021); Aitsam and Chantaraskul (2020); Deuber et al. (2019). These are cases where illegal or inappropriate data has been added to the ledger either for directly nefarious purposes or to undermine the credibility of the blockchain itself. In addition, issues have been raised regarding the “right to be forgotten” Ateniese et al. (2017) and the need for compliance with legal requirements around data processing, such as the General Data Protection Regulation (GDPR) Shah et al. (2019). The existence of these concerns when embedding data on the blockchain has brought with it calls for blockchain implementations and designs to build in mitigations for these issues, such as the ability for illegal data to be redacted from the blockchain Matzutt et al. (2018).

A range of previous efforts have been made to address these problems by introducing data redaction capabilities to blockchain designs Zhang et al. (2021). Early proposals Rajasekhar et al. (2018); Ateniese et al. (2017) that sought to enable redaction for blockchain data relied upon Chameleon hashes. While tackling the issue directly, these solutions also introduce the problems of needing central coordination and allowing mutability of block data, undermining the desired immutability property in general. The use of voting or consensus-based mechanisms to remove data from the blockchain at the system level have also been proposed Deuber et al. (2019); Zhang et al. (2021). Such techniques require a high level of network-wide coordination and do not allow individual nodes to unilaterally remove data locally, whilst also requiring changes at the blockchain protocol level.

As identified in Zhang et al. (2021), other mechanisms include the creation of “meta-transactions” or by pruning data directly from the blockchain. The creation of such meta-transactions leads to general transaction mutability and in some cases allows for the removal of full transaction history from the blockchain. The pruning-based mechanisms introduce the concept of block expiry for older data, which may force users to spend transactions within a given time period to avoid their loss in the system. However, these mechanisms benefit from their efficiency as they do not rely on heavy cryptographic primitives and are lightweight in nature. More recently, ring signatures have been suggested as a method to improve the scalability and privacy of blockchain redaction techniques Huang et al. (2021), but this also mandates changes to the underlying blockchain protocol and can sacrifice immutability as a system-wide property.

In related problem spaces, Liang et al. (2020) addresses the challenge of resilience to data loss within a network, while Yang et al. (2018) outlines a method to provide secure proof of deletion using the blockchain. These mechanisms utilise the blockchain to improve concerns around the use of data, but they do not directly address the issue of ensuring blockchain data can be handled efficiently and privately in compliance with GDPR and other laws.

This paper presents a novel approach to the redaction and management of sensitive blockchain data. The proposed mechanism builds on concepts from the meta-transaction and pruning frameworks Zhang et al. (2021) to solve the problem using Merklized transactions. The solution has the following properties:

• enables transaction redaction without introducing mutability to the underyling blockchain

• does not require a central authority to coordinate data redaction

• allows any blockchain node to unilaterally redact transaction data from their copy of the blockchain

• is scalable and allows lightweight proof-of-existence verification for blockchain data

We also build on the core solution to outline how blockchain regulatory protocols can be implemented to enable nodes to more easily comply with GDPR and other legislation.

2 Background

In the following we describe the necessary background to build up our proposed blockchain redaction mechanism. In general the mechanism we outline in this paper is blockchain-agnostic, and can therefore be applied to any blockchain that uses a typical transaction-based ledger. The protocol outlined in this paper can be applied to any such blockchain by choosing appropriate fields of the transaction as the leaves of each transaction Merkle tree, as explained in Section 3. The proposed design does not depend on the consensus algorithm (e.g., Proof-of-Work, Proof-of-Stake) of the underlying blockchain, and can be applied whether the blockchain uses a UTXO-based transaction structure like Bitcoin or an account-based structure like Ethereum. For the purposes of this paper, we use Bitcoin as an illustrative example to show directly how the solution applies to Bitcoin-like chains, such as Bitcoin Core (BTC), Bitcoin Cash (BCH), or Bitcoin Satoshi’s Vision (BSV).

2.1 Bitcoin

Bitcoin is a peer-to-peer electronic cash system that enables multiple parties to transact directly with one another, without needing to rely on trusted third party as a mediator. The system maintains a distributed ledger, formed of blocks of many transactions, and utilises a Proof-of-Work (PoW) consensus algorithm to append new blocks to the chain. The native token of the blockchain, denominated in Satoshis, can be transferred between users through new transactions whereby digital signatures allow the movement of funds to be validated.

The blockchain ledger is maintained by a network of nodes. Each node is responsible for aggregating and ordering users’ transactions into blocks and attempting to find a PoW solution for their block by expending computational power. The nodes are incentivised to do this through a block reward, which itself contains a block subsidy and transaction fees. The block subsidy halves approximately every 4 years, meaning that over time the incentive to create blocks is increasingly made up of the fees paid in each transaction.

Once a transaction has been included in the blockchain, or has reached a certain depth due to subsequent blocks built on top, it becomes computationally infeasible to alter the its data or claim an alternative record existed in its place. This is a statement of the immutability property of Bitcoin-like chains. This property should be distinguished from indelibility, or the property that data can be removed from the blockchain. Bitcoin-like chains are immutable due to the PoW process, but they are not indelible since data can be pruned from the blockchain. The data that can typically be pruned from the blockchain is anything that cannot be used in a future spending transaction, such as in transactions whose outputs have already been spent. The data stored using the most common embedding methods Bartoletti and Pompianu (2017) can also be pruned in this way.

2.2 Blocks

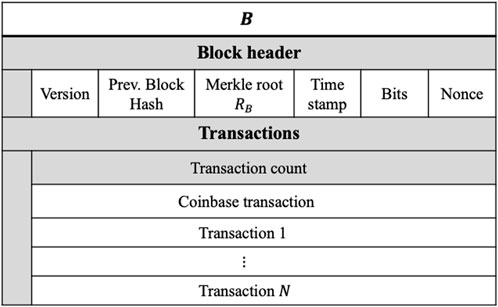
A Bitcoin block (B) is used to collect and order a batch of transactions. These blocks are produced by Bitcoin nodes in regular time intervals of approximately 10 min and comprise three core components as shown in Figure 1.

FIGURE 1

FIGURE 1. The data structure of a Bitcoin block.

2.2.1 Block header

The block header contains the metadata of a block including the protocol version number, timestamp, previous block hash and two PoW parameters (bits and nonce). The header also contains a Merkle root, which uniquely summarises the ordered set of transactions contained in the block using a Merkle tree Merkle (1980).

2.2.2 Transaction list

The second component is the full list of transactions included in the block. Each transaction is itself a separate data structure containing additional fields, and the first transaction in the block is called the coinbase transaction. The transaction count is simply a variable field which encodes the total number of transactions included within the block.

The block header has multiple important functions. First, it creates a one-way link to the previous block header, which gives rise to the chain of blocks that constitute the overall blockchain data structure. The block header also encodes the PoW expended to create the block that can be easily verified by other nodes and entities using only the chain of successive block headers. Finally, the block header contains the Merkle root as a cryptographic commitment to the set of transactions in the block, which we exploit in our protocol to achieve blockchain data redaction.

2.3 Transactions

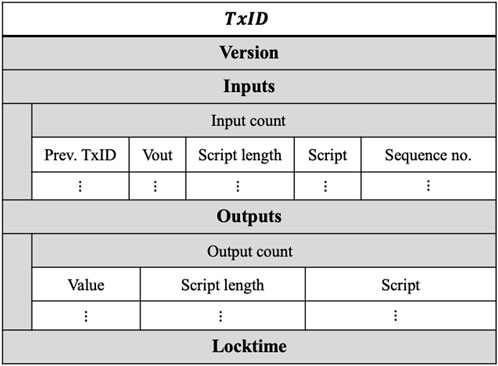
A Bitcoin transaction (Tx) is used to convey a transfer or value between users or to record data on the blockchain. Each transaction has a unique identifier defined as the double SHA-256 hash of the transaction contents TxID≔H(Tx).

2.3.1 Transaction structure

The contents of each transaction must conform to a common structure as outlined in Figure 2. Each transaction contains a version number and a locktime, in addition to a list of inputs and a list of outputs. The inputs are defined by a separate data structure containing a previous transaction identifier (TxID_Prev), a previous output index (vout), an unlocking script and its length, as well as a sequence number. Similarly, the outputs are defined by a separate structure, containing a Satoshi-denominated output value, a locking script and the length of the locking script.

FIGURE 2

FIGURE 2. The data structure of a Bitcoin transaction.

2.3.2 Coinbase transactions

The first transaction in each block is a special case, the coinbase transaction. These transactions are used to distribute new tokens to the node that created the block, and as such these transactions are subject to different transaction validation rules. Specifically, coinbase transactions do not spend a previous transaction output, meaning the input script of a coinbase transaction can contain any arbitrary data as the script will not be validated by the blockchain protocol. We call these “coinbase scripts”, and we utilise them in our solution to enable redaction as a second-layer protocol that can be implemented voluntarily by any node.

2.4 Merkle proofs

In Bitcoin, the use of a Merkle tree to encode the set of transactions in a block allows for efficient lightweight verification that a given transaction is part of a block. The mechanism used to perform such a check, given a candidate transaction Tx_i, located at index i in a block B, and the Merkle root R_B of the block, is known as a Merkle proof (π) Merkle (1980). This proof comprises a set of hash values used to recover a candidate Merkle root R′. If R′ = R_B then the proof is valid and Tx_i is contained in B. Note that the entire data of Tx_i is required to verify such a proof.

3 Merklized transactions

The goal of the following is to define a framework for managing blockchain data that has two properties. First, it should allow for the efficient verification of any item of data on the blockchain without the need for the full transaction data. Second, the scheme should enable data to be easily redacted from the chain at the discretion of a given node to increase the levels of privacy available to blockchain data.

An additional design principle of the proposed mechanism is that it may be implemented without change to the underlying consensus protocol of a given blockchain. While the design outlined in this section may be implemented more simply at the base layer (“layer 1”) for a chosen blockchain, it has been designed in such a way that it can also be deployed as a “layer 2” solution on top of most blockchain networks. This choice is to ensure that the proposed mechanism can be used to enable transaction data redaction regardless of whether the protocol is adopted uniformly by the nodes of a blockchain network. In what follows, we focus on the design details for the layer 2 approach, which allows any individual node to facilitate data redaction unilaterally. This can help any node meet the regulatory and legal obligations of the jurisdiction in which it operates without requiring that other nodes on the network also use this protocol.

The core of the proposed mechanism is to use a Merkle tree to represent the contents of each transaction stored on the blockchain. This allows for smaller subsets of the transaction data to be verified as included on the blockchain, after the transaction has been mined, without requiring the whole transaction data for the post hoc verification. In any given implementation of this mechanism, transactions may be split into different fields to form the Merkle tree to allow different subsets of information to be verified after the transaction is mined. The protocol may also be adapted to each underlying blockchain protocol by choosing different fields or subsets of transaction data to be used as leaves of the transaction Merkle tree, as appropriate.

3.1 Transaction identifiers

As described previously, every Bitcoin transaction Tx has a unique identifier TxID associated with it. Because this identifier is derived from the double-hash of the transaction, this means that the entire transaction must be possessed in order to verify whether any subset of the transaction content exists on the blockchain.

The first aspect of the proposed solution is that a secondary identifier can be generated for each transaction. In general this can be thought of as a “meta” transaction identifier, and we can use the notation MTxID to refer to it. We propose that such a secondary transaction identifier must be some function F of the full transaction data, such that MTxID≔F(Tx). This ensures that all of the data within Tx can be identified by MTxID. However, to fulfil our stated goals, we must also ensure that only a subset of the contents of Tx are required to verify that something is contained within Tx. Furthermore, we must ensure that MTxID is unique to Tx.

3.2 Merkle-based transaction identifiers

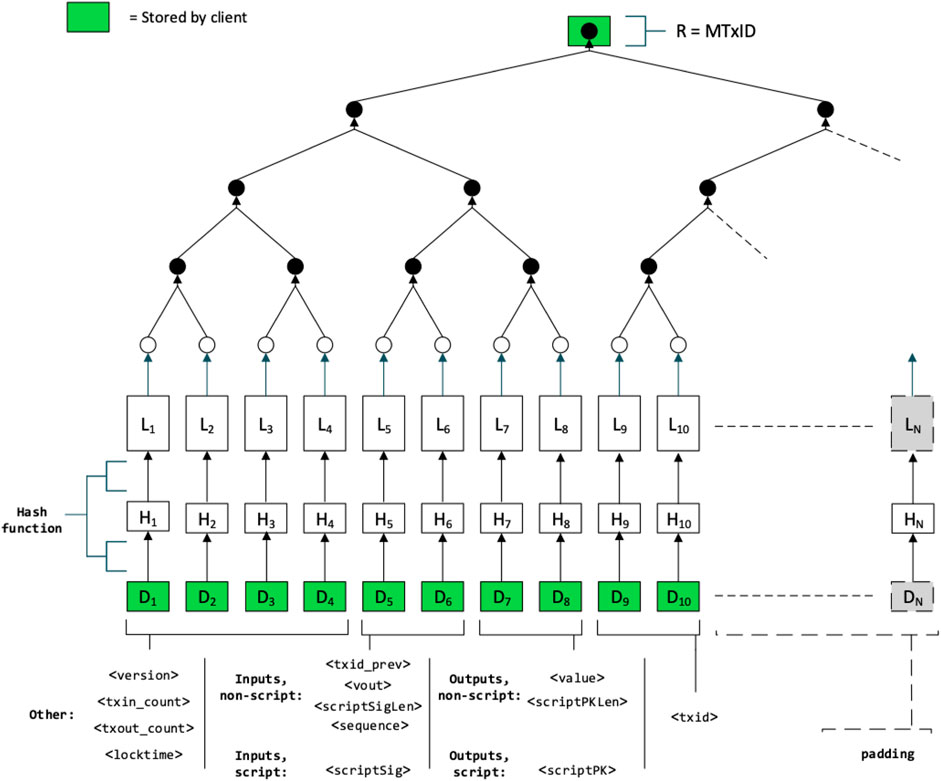
The proposed mechanism to generate a secondary transaction identifier that is unique and only requires a subset of Tx to verify is to use a Merkle tree. In this approach, we define the secondary identifier as MTxID = R, where R is the root of a Merkle tree T. In our construction, the leaves of T are comprised of the contents of Tx split into discrete segments, such that the entirety of Tx is collectively contained within the set of leaves of T.

This approach ensures the uniqueness of MTxID because the root is derived from successively hashing the leaves of the Merkle tree using a one-way cryptographic hash function (e.g., SHA-256). Changing any of the data within the leaves, or the order of the leaves of T, will necessarily alter the resulting MTxID identifier. An example structure of such a transaction-based Merkle tree T is shown in Figure 3.

FIGURE 3

FIGURE 3. A schematic outline of Merkle-based transaction identifier generation.

3.3 Transaction splitting

As outlined in other Merkle-based protocols for blockchain data applications such as Bruschi et al. (2021), the use of a Merkle tree inherently allows for compact and efficient proofs of existence. The proposed system extends this property to individual fields of blockchain transactions, such that any item of data within any blockchain transaction can be independently verified in isolation. This presents a signficant efficiency gain when compared with existing blockchain Merkle proofs where the entire transaction is required.

In our scheme, a transaction Tx is segmented into a set of M data packets D₁, …D_M. There are many possible ways the transaction data can be split and we here outline a few options as examples.

3.3.1 Field-wise splitting

The transaction can be split simply into its component fields, whereby each field will correspond to a single leaf of the transaction Merkle tree T used to generate MTxID. For improved efficiency, some fields may be grouped together by concatenation. An example would be to group the “non-script” fields together and leave each script to a separate leaf of the tree, since data redaction will most likely occur for script fields.

3.3.2 Field-wise granular splitting

A variant of field-wise splitting would be to further split each script field into multiple data leaves, such that individual elements of a single script can later be redacted without removing the entire script.

3.3.3 Fixed number of packets

Each transaction may alternatively be split into a fixed number of packets, meaning packet size will be constant for a given transaction and determined by its size. Different transactions will have different sizes and therefore have different packet sizes in this scenario.

3.3.4 Fixed packet size

A similar strategy would be to fix the packet size for the Merkle tree and allow its number of leaves to increase depending on the size of the transaction.

Our scheme is agnostic to the choice of splitting methodology and can be implemented in any of these ways, depending on the use requirements of nodes or the particular use case.

3.4 Binding to original transaction identifier

The proposed mechanism can be implemented as a layer 1 protocol simply be replacing the TxIDs with MTxIDs within the base consensus algorithm of the blockchain used. However, in a layer 2 setting where we do not modify the underlying consensus protocol, we require an alternative way to bind the secondary transaction identifier MTxID to the original identifier TxID. This can be achieved either by including TxID as an additional leaf in the transaction Merkle tree or by prepending the TxID to each leaf in the transaction Merkle tree. Both options ensure that the entire transaction Tx must be processed when MTxID is first generated and that each other leaf is inextricably linked to the full original transaction data.

3.5 Identifier generation

The steps to generate an MTxID for a given transaction Tx are outlined in the Algorithm 1. In this algorithm the function Merklize() generates a typical binary Merkle tree from a set of leaf data items, whose Merkle root is labelled R.

Algorithm 1.Transaction Identifier Generation.

Input: Transaction Tx

Output: Transaction Identifier MTxID

  1: Generate TxID ← H²(Tx)

  2: Split Tx into M packets D₁, …, D_M

  3: Generate T ← Merklize(D₁, …, D_M, TxID)

  4: Set MTxID ← R

  5: return MTxID

The generation algorithm is intended to be used by a node when it first receives a new transaction in the blockchain network. In the layer 1 setting, this algorithm would be used to directly generate MTxID as the canonical transaction identifier for a given transaction Tx used for the consensus algorithm and block generation process.

When used at layer 2, this generation algorithm can be used by any node voluntarily using our proposed mechanism to prepare transactions for potential data redaction at a future time. If the node wishes to include a transaction in its own block, it should construct the block according to a modified block generation process (see Algorithm 3) that incorporates the above algorithm to ensure that the MTxID is bound to the canonical TxID for this transaction, such that the node can later redact data contained in Tx without sacrificing the ability to prove the existence of the non-redacted content of Tx, as required. If the node does not wish to include Tx in its own block, it may still store the corresponding MTxID locally for similar purposes.

3.6 Identifier verification

The corresponding protocol for verifying a secondary transaction identifier, given MTxID and Tx, is detailed in Algorithm 2. The root of the generated tree T′ is labelled R′.

Algorithm 2.Transaction Identifier Verification.

Input: Transaction Identifier MTxID, Transaction Tx  

Output: True/False

  1: Generate TxID ← H2(Tx)

  2: Split Tx into M packets D1, …, DM

  3: Generate T′ ← Merklize(D1, …, DM, TxID)

  4: Set MTxID′ ← R′

  5: if MTxID = MTxID′ then

  6: Result ← True

  7: else

  8: Result ← False

  9: end if

  10: return Result

This algorithm is used to verify that a given MTxID has been correctly generated for a given Tx, and therefore requires the full data of the transaction. For this reason, Algorithm 2 is only directly relevant to blockchain nodes in a layer 1 implementation of the mechanism and during the consensus process, while a new transaction is propagating through the network for inclusion on the blockchain and when verifying a new block that contains the transaction. Algorithm 2 may nonetheless be used at any time in a layer 2 setting by a node or a third party external to the blockchain network in possession of the full transaction data Tx to verify it has been correctly associated with an MTxID by nodes voluntarily using our proposed mechanism as a layer 2 protocol.

The transaction identifier verification process should not be conflated with the process of verifying, in the absence of the full transaction data Tx, whether an individual data portion D_i of the transaction has been included on the blockchain. This process is instead referred to as a lightweight proof of existence verification and is outlined in Section 4.4.

4 Data redaction

The previous section outlined a process for generating secondary transaction identifiers for blockchain transactions. These identifiers are Merkle-based to allow the granular verification of data fields. The verification of an individual field using an MTxID is more efficient that using the traditional TxID because it does not require the verifier to obtain the full transaction data Tx. We now use this technique as a building block to enable data redaction for Bitcoin-like ledgers.

4.1 Trusting transaction identifiers

Previously, deleting any part of a transaction would compromise the ability of a blockchain node to prove the existence of data contained within the rest of the transaction. The introduction of MTxIDs now enables data to be redacted from the blockchain by allowing nodes to simply delete particular leaves from a transaction Merkle tree T. Deleting these leaves does not prohibit the node from providing compact proofs of existence for the remainder of the transaction, or even verifying future spending relationships with the transaction in question. However, the addition of an MTxID for each transaction is only part of the solution. Specifically, we need a mechanism to establish trust that a given MTxID has been generated correctly for the corresponding transaction. Without having a publicly known and reliable attestation of the MTxIDs for each transaction, we cannot use them to prove with confidence that a particular data item actually exists on the blockchain.

To prove that a data element D_i is included in a transaction on the blockchain, we must prove both of the following:

• there must be a valid proof π_M connecting D_i to a secondary identifier MTxID; and

• there must be a valid proof π_B that MTxID corresponds to a valid transaction Tx on the blockchain that can also be identified by TxID

If both conditions are met, we can be convinced that D_i exists at the claimed location on the blockchain.

The first condition is met simply by obtaining π_M, which is the set of hashes corresponding to a standard Merkle proof Merkle (1980) that proves the leaf data D_i is a member of the set of leaves of the Merkle tree corresponding the Merkle root R = MTxID for the transaction in question.

The second condition is easily met in a layer 1 setting, where MTxID is simply the canonical transaction identifier for the transaction, assuming that the consensus algorithm has been modified appropriately to ensure this. In this case, the proof π_B is simply the standard Merkle proof that connects MTxID to the Merkle root R_B of a valid block B in the blockchain, in the same way that there exists a Merkle proof in the Bitcoin consensus algorithm that currently connects each transaction identifier TxID to a root R_B.

In a layer 2 setting however, a participating node must perform additional steps during the block generation process to ensure that a valid π_B will exist for a given MTxID. In the following subsections, we outline how a node may generate a secondary block Merkle tree, in addition to the standard Merkle tree of a Bitcoin block, and include the root R_M of this secondary tree in a coinbase transaction during block generation. By including both R_B and this additional root R_M when generating a block, the participating node establishes the required information for a valid proof π_B in the layer 2 setting. The use of π_B to verify the existence of a transaction data portion on the blockchain is then outlined in Section 4.4.

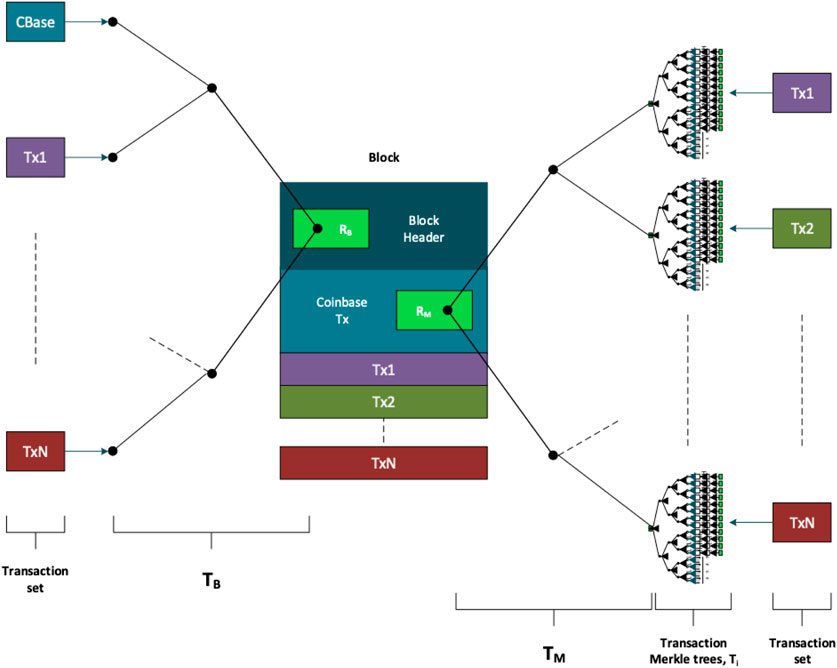
4.2 Secondary block Merkle tree

To achieve such a proof, we introduce a secondary block Merkle tree denoted by T_M and whose root is R_M. For a block B containing N transactions, the leaves of T_M correspond to the set of secondary transaction identifiers MTxID₁, …, MTxID_N for the transactions Tx₁, …, Tx_N contained with the block. In other words, T_M is effectively a tree of Merkle trees. The proposed redaction mechanism relies on a node including the root R_M in the coinbase transaction of blocks they successfully generate.

The structure of a secondary block Merkle tree is outlined in Figure 4. As shown, the order of the transactions used to derive T_M must be the same as the order of the transactions as they appear in block B and its original block Merkle tree T_B. The exception is the coinbase transaction, which does not appear in the secondary tree. The coinbase transaction is necessarily excluded from T_M because our redaction protocol requires R_M to be stored in the coinbase transaction itself.

FIGURE 4

FIGURE 4. A schematic outline of the block generation protocol for Merklized transactions.

4.3 Block generation protocol

To facilitate the redaction of data after it has been included on the blockchain in a block B, we require only that the node responsible for generating B also includes the root R_M in the coinbase transaction. This represents a minor modification of the standard process of generating Bitcoin blocks that a node participating in this redaction scheme. The details of the updated block-generation protocol is shown in Algorithm 3. The modified process requires that the node generates the secondary Merkle tree T_M and includes its root R_M in the coinbase transaction. A suitable option is to include the root in the coinbase script. The node can then generate the standard block Merkle tree T_B and generate the final block B by finding a valid proof of work solution. Crucially, the proposed solution operates at a layer above the base blockchain protocol and does not require any change to the underlying rule set used to maintain and validate the blockchain.

Algorithm 3.Block Generation for Redactable Data.

Input: Transaction set $\mathbb{T}≔\{T{x}_1,\dots T{x}_N\}$

Output: Block B

  1: for Tx_i in Tx₁, …Tx_N do

  2: Split Tx_i into M packets D₁, …, D_M

  3: Generate R_i ← Merklize(D₁, …, D_M, TxID_i)

  4: Set MTxID_i ← R_i

  5: end for

  6: Generate T_M ← Merklize(MTxID₁, …, MTxID_N)

  7: Add R_M to coinbase transaction Tx_C

  8: Generate T_B ← Merklize(Tx_C, Tx₁, …, Tx_N)

  9: Generate block B including R_B

  10: return B

4.4 Lightweight proof of existence

The core goal of the mechanism outlined in Section 3 is to prepare a transaction Tx, when it is added to the blockchain, such that a subset of its data can be verified as included on the blockchain at a later time in the absence of the full original transaction data. In other words, to allow for the verification that a data portion D_i ∈ D₁, …, D_M has been included in the blockchain without access to one or more of the remaining data portions D_j≠i of the original Tx. As outlined previously, we require two proofs π_M and π_B to satisfy our conditions that prove the data portion exists on the blockchain in the absence of the full transaction data.

The first proof π_M is the Merkle proof connecting the data portion D_i to the secondary identifier MTxID and can be checked simply using a standard Merkle proof verification. This check is performed by verifying the Merkle proof π_M for the leaf D_i against the Merkle root MTxID, which we denote by C₁ ← MerkleVerify(D_i, MTxID, π_M), setting C₁ to True if the check is successful and False otherwise.

In the layer 2 context we are considering, the second proof π_B = (π_MTxID, π_TxID) in fact comprises two further Merkle proofs π_MTxID and π_TxID, which connect MTxID to the secondary root R_M and TxID to the standard root R_B respectively. In order to verify the second condition using π_B, we must perform a total of three checks C₂, C₃, C₄. Checks C₂, C₃ are simply Merkle proof verifications similar to C₁ and using the same notation. The final check C₄ is to confirm that both R_M and R_B have been included in the same block header H_B by a participating node. In combination, checks C₂ to C₄ prove that MTxID corresponds to the same transaction as TxID included in the block B.

The full lightweight proof of existence process is outlined in Algorithm 4. This mechanism allows anybody to verify that a data portion D_i has been included on the blockchain as part of Tx without requiring the other data portions D_j≠i comprising the original transaction.

Algorithm 4.Layer 2 Lightweight Proof of Existence.

Input: D_i, MTxID, TxID, R_M, R_B, block header H_B, proof π_M, proofs π_B = (π_MTxID, π_TxID)

Output: Result

  1: C₁ ← MerkleVerify(D_i, MTxID, π_M)

  2: C₂ ← MerkleVerify(MTxID, R_M, π_MTxID)

  3: C₃ ← MerkleVerify(TxID, R_B, π_TxID)

  4: C₄ ← Check(R_M, R_B ∈ H_B)

  5: if C₁ and C₂ and C₃ and C₄ then

  6: Result ← True

  7: else

  8: Result ← False

  9: end if

  10: return Result

This proof of existence protocol is lightweight because it only requires the portion of the transaction D_i that is to be verified. For instance, if a large transaction 100 Megabytes in size has been split into 1 Kilobyte portions the verifier only needs to retrieve 0.001% of the transaction data. This represents a significant storage and bandwidth saving for any application that needs to verify small items of data stored within large transactions. The flexibility and granularity of data portions D_i that can be verified in this manner is constrained by the choice of how the transaction Tx was originally split into packets in Algorithm 3 by the participating blockchain node.

It is anticipated that the lightweight proof of existence verification process may be performed by any blockchain node or third party that needs to verify the existence of a portion of data on the blockchain. An example application using this feature would be a video streaming service to allow users to check the metadata of a video file stored on the blockchain without needing to download the entire media file itself.

In both layer 1 and layer 2 implementations of the Merklized transaction protocol, it should be noted that lightweight verifications are expected to be performed at a later time after the transaction has been initially added to the blockchain. This means that transactions are still expected to be processed in the usual manner at the time they are added to the blockchain. However, by implementing the transaction Merklization process during block generation, whether at layer 1 or 2, individual fields can be later verified by any party in a lightweight manner.

4.5 Data redaction

A key benefit of the proposed transaction Merklization protocol is that individual data elements within transactions can be verified as existing on the blockchain without possessing the full transaction data. This feature is crucial to allow nodes to selectively delete some portions of transaction data without sacrificing the ability to verify others.

This is particularly advantageous in the event that a node is compelled by law to delete or redact some data from its local copy of the blockchain database. Typically, if a node is required to delete or redact a portion of transaction data it must delete the full transaction, making it impossible to preserve other parts of the transaction not subject to the redaction. This can render nodes unable to prove legally-compliant data exists on the blockchain in the case that it is stored in the same transaction as data which must be redacted.

Conversely, our mechanism allows nodes to redact only the portions of data to which legal deletion or regulations such as GDPR apply. The use of Merklized transactions, and the extensions outlined for support as a layer 2 protocol, ensure that the remaining portions of the transaction data can still be proven as part of the blockchain database even after the node has removed other components as required.

In this regime, the redaction of a data portion from a transaction simply involves a node deleting the specific leaves from a transaction Merkle tree T that correspond to the data that must be redacted. The deletion of a subset of leaves from a given transaction by one node does not preclude other nodes from storing and serving the remaining leaves from the same tree. This is because the Merkle tree structures used allow any node to prove the existence of any of the remaining leaves without needing to hold or access the deleted leaves. In practice, this may be done in response to a request for deletion to comply with the right to be forgotten or GDPR laws Ateniese et al. (2017); Shah et al. (2019). Each such request may only apply to different nodes on a jurisdictional or regional basis. Crucially, when implemented as a layer 2 protocol this allows individual nodes to act unilaterally in redacting data as required by the legal jurisdiction in which they operate, without affecting the operations of other nodes in the network. This therefore allows each node to comply with local rules and regulations regarding data protection and privacy without impinging on other nodes which may not be subject to the same legilsation across the world.

5 Discussion

We have defined a framework enabling data to be redacted from Bitcoin-like blockchains without sacrificing the integrity and utility of storing the remaining data on the blockchain. Finally we consider the properties, advantages, and limitations of the solution.

5.1 Properties

The proposed protocol introduced redactability for blockchain data that can be implemented on top of the base Bitcoin protocol. This means that there is no requirement to modify the underlying blockchain infrastructure to facilitate better GDPR compliance for nodes. Moreover, the mechanism can be implemented independently by any individual node, whether in their own interest or as a public service to the network. This also presents a significant privacy benefit for the end users of blockchain networks who can now demand that their data is removed from public blockchain ledgers.

Our solution is also efficient because it does not rely on any heavy cryptographic primitives and is based primarily on Merkle trees which are a scalable data structure allowing compact proofs of existence. The efficiency of this method allows partial transaction verification that can allow a user to check individual aspects of a transaction, such as the transaction value or the number of outputs, without downloading the entire transaction using Merkle proofs. This presents a new way for blockchain analytics to be conducted using lower bandwidths suitable for Internet of Things devices or low-powered user hardware.

5.2 Complexity

As discussed, the key efficiency benefit afforded by the proposed protocol is during the lightweight verification processes, where only a minimal portion of the transaction data is required to verify its existence. In extreme cases, this may represent a significant saving in terms of storage and bandwidth required to obtain the data necessary for verification.

When assessing the overall scalability of the solution as compared with current blockchain protocols, we must consider the complexity of the process used to generate an MTxID and to generate the corresponding secondary root R_M used to encode these identifiers in a block by participating nodes.

The time complexity of computing a standard transaction identifier TxID is determined by the time complexity of the hash function used to generate the identifier. In the case of Bitcoin, the SHA-256 hash function is used, whose complexity scales as $\mathcal{O}(n)$, where n is the number of 512-bit message blocks contained in the full data of Tx Rachmawati et al. (2018). The complexity associated with generating the MTxID for a given transaction will therefore depend on the size of the data packets D_i into which the transaction is split. If it is split into packets of approximately 512-bits, the process of generating a MTxID will scale as $\mathcal{O}(n+log(n))$, where the additional log(n) arises due to the definition of MTxID as a Merkle tree requiring additional hashes to be computed upon the leaf hash values. This shows the additional time complexity required to compute MTxID is small compared to the existing complexity for generating a TxID, and therefore does not significantly impact the performance of nodes when processing transactions.

The generation of the additional root R_M to be included in the coinbase transaction has the same complexity as generating the standard root R_B, which scales as $\mathcal{O}(N)$ where N is the total number of transactions contained in the block. However, this should not increase the time taken to generate a block significantly as both roots can be generated in parallel and either computation represents a small fraction of the total verification process for transactions which is generally dominated by the verification of elliptic curve digital signatures.

5.3 Protocol extensions

The protocol in its current form is limited because only the transactions in blocks mined by participating miners are eligible for redaction. In addition, the protocol still requires a level of trust in the nodes themselves to faithfully create the correct secondary tree T_M for each of their blocks. Here we propose potential extensions to improve these aspects.

5.3.1 Accounting for interim periods

We do not anticipate that all nodes will simultaneously implement the redaction protocol since it is not a protocol-level requirement. However, the nodes that do choose to provide the redaction service can also account for the interim periods between their blocks by creating secondary trees for the interim blocks and combining them into a summary root hash R_Int. This additional root can be included in a node’s blocks alongside the root R_M for the current block each time the node successfully generates a new block.

5.3.2 Trusting participating nodes

In the case where the protocol is implemented at layer 1, the underlying consensus mechanism can be updated such that the secondary identifiers MTxID are made canonical according to the protocol. This means that there is no additional trust placed on network nodes as the Merklized transaction identifier is enforced by the protocol rules directly.

However, when implemented at layer 2 volunatrily by individual nodes, there is no verification by the underlying blockchain protocol that the secondary Merkle tree T_M has been generated correctly and that the correct corresponding root R_M has been included in the coinbase transaction. For instance, it is possible that the root R_M may be malformed either due to error or malicious intent of a participating node. This creates the need for greater trust in the participating nodes when performing lightweight proofs of verification on individual portions of transaction data.

Trust in participating nodes may be improved by implementing a reputation system for nodes providing this service, where reputation can be based on the proportion of successfully-generated secondary Merkle roots. In addition, it is possible for the generation of each secondary root to be checked far in advance of a data redaction request. This means that faulty roots can be easily detected in advance and incorrect proofs of existence mitigated. Additional third parties such as regulators could perform the checking procedure to support the blockchain ecosystem and prevent fraud.

6 Conclusion

In conclusion, we have presented a novel, Merkle-based data redaction mechanism for public blockchain networks such as BTC, BCH, and BSV. Our design enables improved privacy for the users of such blockchains by enabling nodes to redact transaction data on a granular level. This allows them to provide improved compliance guarantees and additional protections for users and applications putting data on the blockchain. Moreover, the protocol can be implemented on top of any Bitcoin-like chain, without the need to modify the underlying blockchain system, by a single participating node. The mechanism we have proposed is also highly efficient and scalable through its use of Merkle tree structures. This has the added advantage that individual characteristics of transactions, such as size or value, can be checked without obtaining the full transaction data. The effect is that our proposal reduces the bandwidth costs required to interact with blockchain-based applications that use distributed ledgers as an underlying data source. The proposed system we have outlined overcomes limitations in existing redaction protocols by removing the requirement of a central coordinating party and by ensuring that blockchain-level mutability is not introduced by our design.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of interest

Author JD was employed by nChain.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aitsam, M., and Chantaraskul, S. (2020). Blockchain technology, technical challenges and countermeasures for illegal data insertion. Eng. J. 24, 65–72. doi:10.4186/ej.2020.24.1.65

CrossRef Full Text | Google Scholar

Ali, M., Shea, R., Nelson, J., and Freedman, M. J. (2017). Blockstack: a new decentralized internet. Whitepaper.

Google Scholar

Ateniese, G., Magri, B., Venturi, D., and Andrade, E. (2017). “Redactable blockchain–or–rewriting history in bitcoin and friends,” in 2017 IEEE European symposium on security and privacy (EuroS&P) (IEEE), Paris, April 26-28, 2017, 111.

Google Scholar

Bartoletti, M., and Pompianu, L. (2017). “An analysis of bitcoin op_return metadata,” in International Conference on Financial Cryptography and Data Security, Sliema, Malta, April 3-7, 2017, 218–230.

CrossRef Full Text | Google Scholar

Bruschi, F., Rana, V., Pagani, A., and Sciuto, D. (2021). Tunneling trust into the blockchain: a merkle based proof system for structured documents. IEEE Access 9, 103758–103771. doi:10.1109/ACCESS.2020.3028498

CrossRef Full Text | Google Scholar

Deuber, D., Magri, B., and Thyagarajan, S. A. K. (2019). “Redactable blockchain in the permissionless setting,” in 2019 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, May 19 2019 to May 23 2019, 124. doi:10.1109/SP.2019.00039

CrossRef Full Text | Google Scholar

Huang, K., Zhang, X., Mu, Y., Rezaeibagha, F., and Du, X. (2021). Scalable and redactable blockchain with update and anonymity. Inf. Sci. 546, 25–41. doi:10.1016/j.ins.2020.07.016

CrossRef Full Text | Google Scholar

Liang, W., Fan, Y., Li, K.-C., Zhang, D., and Gaudiot, J.-L. (2020). Secure data storage and recovery in industrial blockchain network environments. IEEE Trans. Industrial Inf. 16, 6543–6552. doi:10.1109/TII.2020.2966069

CrossRef Full Text | Google Scholar

Matzutt, R., Hiller, J., Henze, M., Ziegeldorf, J. H., Müllmann, D., Hohlfeld, O., et al. (2018). “A quantitative analysis of the impact of arbitrary blockchain content on bitcoin,” in Financial cryptography and data security. Editors S. Meiklejohn, and K. Sako (Berlin, Heidelberg: Springer Berlin Heidelberg), 420–438.

CrossRef Full Text | Google Scholar

Merkle, R. C. (1980). “Protocols for public key cryptosystems,” in 1980 IEEE Symposium on Security and Privacy, Oakland, California, USA, April 14-16, 1980, 122. doi:10.1109/SP.1980.10006

CrossRef Full Text | Google Scholar

Rachmawati, D., Tarigan, J., and Ginting, A. (2018). A comparative study of message digest 5 (md5) and sha256 algorithm. J. Phys. Conf. Ser. 978, 012116. doi:10.1088/1742-6596/978/1/012116

CrossRef Full Text | Google Scholar

Rajasekhar, K., Yalavarthy, S. H., Mullapudi, S., and Gowtham, M. (2018). Redactable blockchain and it’s implementation in bitcoin. Int. J. Eng. Technol. 7, 401–405. doi:10.14419/ijet.v7i1.1.9861

CrossRef Full Text | Google Scholar

Sgantzos, K., and Grigg, I. (2019). Artificial intelligence implementations on the blockchain. use cases and future applications. Future Internet 11, 170. doi:10.3390/fi11080170

CrossRef Full Text | Google Scholar

Shah, P., Forester, D., Berberich, M., Raspé, C., and Mueller, H. (2019). Blockchain technology: data privacy issues and potential mitigation strategies. Pract. Law. Available at: https://www.davispolk.com/sites/default/files/blockchain_technology_data_privacy_issues_and_potential_mitigation_strategies_w-021-8235.pdf.

Google Scholar

Yang, C., Chen, X., and Xiang, Y. (2018). Blockchain-based publicly verifiable data deletion scheme for cloud storage. J. Netw. Comput. Appl. 103, 185–193. doi:10.1016/j.jnca.2017.11.011

CrossRef Full Text | Google Scholar

Zhang, D., Le, J., Lei, X., Xiang, T., and Liao, X. (2021). Exploring the redaction mechanisms of mutable blockchains: a comprehensive survey. Int. J. Intelligent Syst. 36, 5051–5084. doi:10.1002/int.22502

CrossRef Full Text | Google Scholar