A review of model evaluation metrics for machine learning in genetics and genomics

Miller, Catriona; Portlock, Theo; Nyaga, Denis; O'Sullivan, Justin M.

doi:10.3389/fbinf.2024.1457619

REVIEW article

Front. Bioinform., 10 September 2024

Sec. Genomic Analysis

Volume 4 - 2024 | https://doi.org/10.3389/fbinf.2024.1457619

A review of model evaluation metrics for machine learning in genetics and genomics

Catriona Miller¹*

Theo Portlock¹

Denis M. Nyaga¹

Justin M. O’Sullivan^1,2,3,4*

¹The Liggins Institute, The University of Auckland, Auckland, New Zealand
²The Maurice Wilkins Centre, The University of Auckland, Auckland, New Zealand
³MRC Lifecourse Epidemiology Unit, University of Southampton, Southampton, United Kingdom
⁴Singapore Institute for Clinical Sciences, Agency for Science Technology and Research, Singapore, Singapore

Machine learning (ML) has shown great promise in genetics and genomics where large and complex datasets have the potential to provide insight into many aspects of disease risk, pathogenesis of genetic disorders, and prediction of health and wellbeing. However, with this possibility there is a responsibility to exercise caution against biases and inflation of results that can have harmful unintended impacts. Therefore, researchers must understand the metrics used to evaluate ML models which can influence the critical interpretation of results. In this review we provide an overview of ML metrics for clustering, classification, and regression and highlight the advantages and disadvantages of each. We also detail common pitfalls that occur during model evaluation. Finally, we provide examples of how researchers can assess and utilise the results of ML models, specifically from a genomics perspective.

1 Introduction

The general hype around the generative artificial intelligence (AI) era has increased the popularity of machine learning (ML) for a range of applications. Alongside this, the advent of “plug and play” style ML tools, such as PyCaret, has dramatically increased the accessibility of ML to scientists and researchers without a traditional computational background (Ali, 2020; Manduchi et al., 2022; Whig et al., 2023). In genomics, ML is becoming increasingly used to analyse large and complex datasets, including sequencing data (Caudai et al., 2021; Chafai et al., 2024). Therefore, it is increasingly important that “all” researchers understand what happens after an ML model has been deployed. This is particularly true for the choice of performance metrics and how to interpret the validity of the results. As such, without understanding the common metrics used in ML, together with an awareness of the inherent strengths and weaknesses of such metrics, there is a possible risk of result inflation (Kapoor and Narayanan, 2023). Therefore, understanding the potential biases within the input data is essential to successfully interpret the results (Vokinger et al., 2021).

Existing reviews of ML applications to genetic and genomic datasets either focus on earlier stages of the ML pipeline (e.g., feature selection, method selection), or give an overview of the whole process (Libbrecht and Noble, 2015; Ho et al., 2019; Musolf et al., 2022; Pudjihartono et al., 2022). This review addresses an important gap in the literature by focusing on the final section of the ML pipeline – model evaluation. Specifically, we cover the most common use cases of ML in genomics before an in-depth analysis of the metrics used to evaluate each subtype, including the advantages and disadvantages of each. We finalise by cautioning researchers and scientists of the common pitfalls that can bias model performance and inflate the metrics reported.

1.1 Types of ML typically used in genomics

Supervised learning, unsupervised learning, semi-supervised learning, and reinforcement learning are the four main types of ML algorithms used within genetic and genomic datasets (Figure 1) (Libbrecht and Noble, 2015; Ho et al., 2019; Koumakis, 2020; Bracher-Smith et al., 2021). Here we focus on unsupervised and supervised learning and their subcategories: clustering (unsupervised learning), classification and regression (supervised learning).

Figure 1

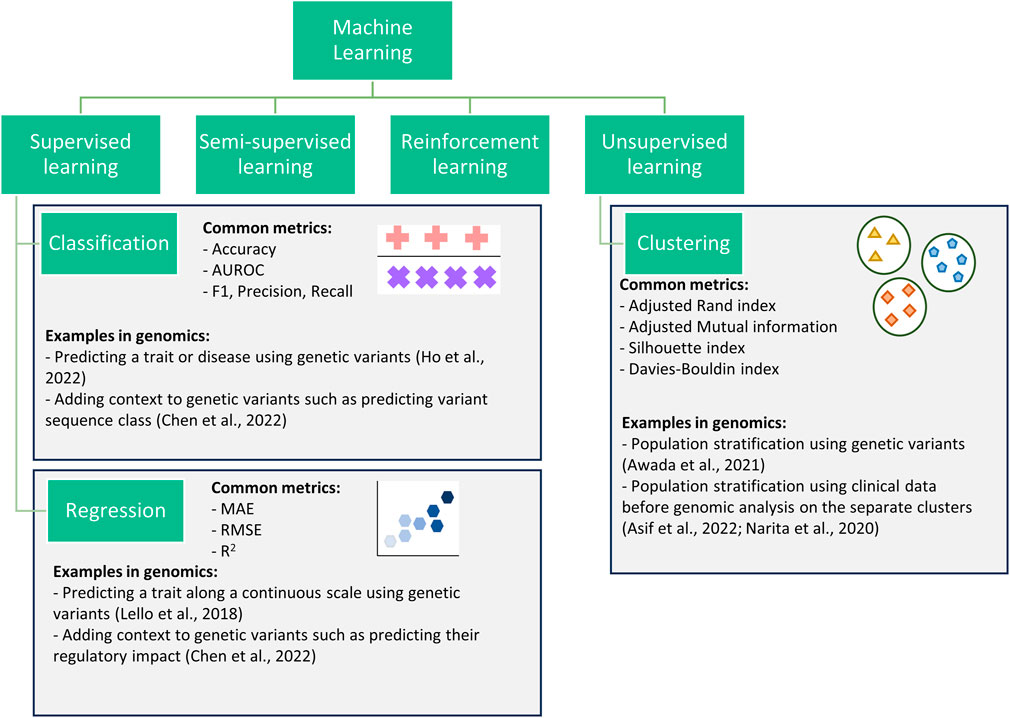
Figure 1. Flowchart showing four categories of machine learning. This review focuses on three subcategories (classification, regression, and clustering) within the supervised and unsupervised categories.

Clustering algorithms are processes for the identification of subgroups within a population. Clustering can be performed when data is prelabelled (e.g., known disease subtypes) or with no a priori information. Clustering has been successfully used to improve prediction (Alyousef et al., 2018), to identify disease-related gene clusters (Di Giovanni et al., 2023), or to better define complex traits/diseases (Lottaz et al., 2007; Lopez et al., 2018; Yin et al., 2018; Awada et al., 2021).

Classification algorithms encompass all machine learning methods where pre-labelled data is used to train an algorithm to predict the correct class, where class refers to all data points with a given label (e.g., control class or a specific disease class). These are commonly used within genomics to predict a trait/disease (i.e., diagnostics) (Trakadis et al., 2019; Lee and Lee, 2020; Ho et al., 2022), or to identify potential biomarkers (Al-Tashi et al., 2023). However, they can struggle with imbalanced datasets, where one class is significantly more prevalent than the other, leading to biased predictions (Ramyachitra and Manikandan, 2014).

Regression algorithms, like classification algorithms, predict a target variable for each datapoint or individual; however, they are applied in applications involving continuous variables. For example, regression algorithms are commonly used for the prediction of highly heterogeneous traits with known scales such as height, systolic blood pressure, and waist-hip ratio (Bellot et al., 2018; Lello et al., 2018). While regression algorithms can capture complex relationships between variables, they are sensitive to outliers which can impact the reliability of predictions (Wang, 2021). This review only covers regression for continuous variables. Other methods, such as negative binomial and Poisson used in mutation burden analysis and differential gene expression analysis (Sun et al., 2017; Li et al., 2019; Zhang et al., 2020), are outside of the scope.

Classification and regression algorithms have also been applied to add context to genomic data such as predicting the regulatory impacts of single nucleotide polymorphisms (SNPs). For example, the interpretable deep learning sequence model Sei predicts sequence regulatory activity based on chromatin profiles (Chen et al., 2022). Such a framework can be considered both classification and regression as it predicts a variant’s sequence class (classification) and provides a regulatory impact score (regression). In this case, classification provides users with a more understandable output (e.g., promoter) but loses some of the information, whereas the regression score captures more information but is less interpretable. Therefore, by providing both a classification and regression output, users can decide between increased interpretability and information.

Clustering, classification, and regression algorithms all have multiple metrics for evaluating their performance and this review focuses on the most commonly used ones in genomics (Figure 1). This review focuses on their applicability for evaluating models in the fields of genetics and genomics. However, the majority of the metrics detailed are also used for hyperparameter tuning during cross-validation. The choice of the metric for tuning can greatly impact the model produced, often resulting in a model that scores highly for the provided metric at the expense of the other metrics. Therefore, the advantages and disadvantages (both general and genomic specific) discussed for each metric in this review are still largely relevant when choosing a metric for hyperparameter tuning. Yang and Shami (2020) provides a review of hyperparameter optimisation.

2 ML metrics for clustering

The choice of metric for evaluating clustering algorithms largely depends on whether there is access to a “ground truth” (Box 1). If there are known categories to compare the clusters to, extrinsic measures can be used such as the Adjusted Rand Index (Hubert and Arabie, 1985) or Mutual Information (Vinh et al., 2010) (Figure 2). Without a ground truth, intrinsic measures must be used (e.g., the Sillhouette index or Davies Bouldin index). Intrinsic metrics measure the similarities between points within the same cluster compared to the similarity between clusters (Figure 2). They score highly if the intra-cluster similarity is greater than the inter-cluster similarity. Extrinsic metrics score highly if the clusters are similar to the known ground truth clusters (Figure 2).

Box 1 | Glossary
Class – a group of samples or individuals with the same target variable. For example, a control and asthmatic would be two classes in a classification analysis.

Clustering ground truth – a known set of clusters for a given dataset.

Decision boundary – a score threshold used in classification algorithms to assign individuals to classes.

Euclidean distance – the length of the line segment that would connect two points.

Imbalanced dataset – a dataset where one class(es) appears at a much higher rate than the other class(es).

Intra-cluster similarity – similarity between datapoints assigned to the same cluster.

Inter-cluster similarity – similarity between datapoints assigned to different clusters.

True positive rate (TPR) – also known as recall. The percentage of “positive” samples that have been correctly labelled as “positive”.

False positive rate (FPR) – the percentage of ‘negative’ samples that are incorrectly classified as “positive”.

Figure 2

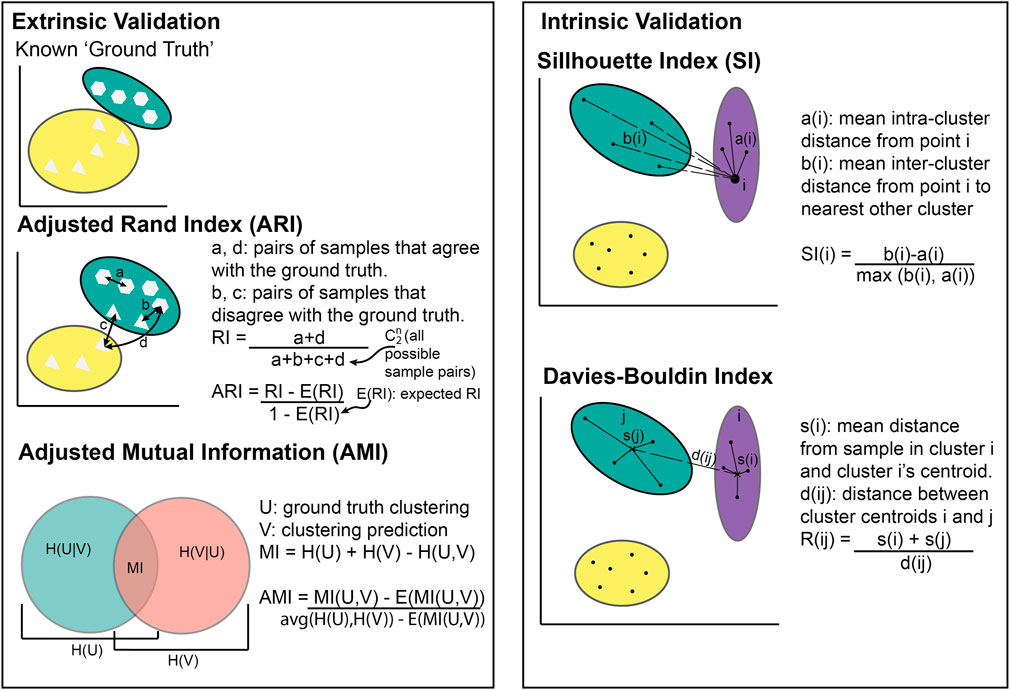
Figure 2. Illustration of cluster metric calculations. Extrinsic validation methods require known clusters to compare against whilst intrinsic validation does not.

2.1 Adjusted Rand Index

The Adjusted Rand Index (ARI) is a measure of similarity between two clusterings of the same dataset, while accounting for similarities that occur by chance (Hubert and Arabie, 1985). For example, the ARI can be used to compare the similarity between calculated clusters within a disease group and known clusters based on disease subtypes.

A R I = \frac{R I - E}{1 - E} w h e r e R I = \frac{a + d}{C_{2}^{n}} a n d E = \frac{\sum (C_{2}^{n_{i}}) \times \sum (C_{2}^{n_{j}})}{C_{2}^{n}}

Given:

- n = number of samples in the dataset

- a and d = number of pairs of samples in the same and different clusters between the two clusterings respectively

- n_i and n_j = number of samples in clusters i and j respectively

If ARI = −1, it indicates complete disagreement (i.e., no individuals are in the same cluster as the known ground truth), while ARI = 0 indicates an agreement equivalent to that from random chance, and ARI = 1 indicates perfect agreement (i.e., all individuals are in the same cluster as the known ground truth). Figure 2 shows most individuals placed in the same cluster as the known ground truth, meaning the ARI would be between 0 and 1.

ARI is a common metric choice for validating the performance of a clustering technique within biology (Shi et al., 2022; Zhen et al., 2022). However, ARI is based on the assumption that the known clusters are correct for the use case. For example, if the aim of clustering is to identify novel groups within a population (diseased or otherwise) or to identify similarities between genetic variants, comparing against known clusters would be detrimental to the problem (Awada et al., 2021). Another limitation is ARI’s bias to cluster size. If a clustering contains a mixture of large and small sized clusters, ARI will be predominantly influenced by the large clusters (Warrens and van der Hoef, 2022).

2.2 Adjusted Mutual Information

Adjusted Mutual Information (AMI) is a clustering metric that comes from information theory (Vinh et al., 2010). It calculates how much information is shared between two clusterings (i.e., known clusters and calculated clusters).

A M I (U, V) = \frac{M I (U, V) - E (M I (U, V))}{a v g (H (U), H (V)) - E (M I (U, V))}

- U and V = two clusterings (e.g., calculated clusters and known clusters)

- H = individual entropy – a measure of expected uncertainty

- MI = mutual information algorithm described by Vinh et al. (2010).

- E = the expected value based on chance.

Both AMI and ARI adjust for chance and can be used to calculate an algorithm’s performance when a “ground truth” is known. Therefore, deciding when it is appropriate to prioritize one metric over the other can be difficult. The key differentiating factor derives from the fact that ARI scores solutions with similar sized clusters higher. By contrast, AMI is biased towards “pure” clusters, consisting of only one class type and are often imbalanced (Romano et al., 2016). For example, if some disease subtypes are rarer than others resulting in imbalanced cluster sizes, AMI is likely to be a more accurate metric than ARI. Variations of AMI measures have been used in biology, including to create gene regulatory networks (Shachaf et al., 2023), identify SNP interactions (Cao et al., 2018), and to analyse similarities between biomarkers (Keup et al., 2021).

2.3 Silhouette index

The Silhouette Index (SI) is a common metric that is typically used when there are no labels for the data being clustered. It compares the similarity within a cluster to the similarity between clusters (Rousseeuw, 1987).

S I = \frac{1}{N} \sum s (i) w h e r e s (i) = \frac{b (i) - a (i)}{\max \{a (i), b (i)\}}

Given:

- N = number of samples in the dataset

- a(i) = mean within cluster distance for sample i

- b(i) = mean distance between sample i and samples within the nearest cluster

SI values range from −1 to 1 with negative values indicating that the average sample has been assigned to “the wrong cluster.” Higher scores (approaching 1) indicate robust clustering and the presence of dense, well-separated clusters. In biological use cases, stratifying individuals can be nuanced meaning clusters could be weaker. As such, there is no guideline for an SI value that acts as a cut-off for “good” clustering for biological data. Rather, the SI threshold varies between use cases (Pagnuco et al., 2017; Zhao et al., 2018).

The SI metric does not rely on labels or measure prediction validity. Therefore, the SI metric is helpful for evaluating the comparative performances of different clustering methods. However, the SI metric cannot detect if the clustering is due to a bias in the data that is unrelated to the trait (Chhabra et al., 2021). For example, when clustering whole genome sequencing data, the clusters may be related to ancestry, sex, or other traits distributed across the population and not the actual trait being studied. Another disadvantage is the key assumption that clusters are Gaussian, meaning that any SI values for data that does not follow a spherical shape will be misleading (Thrun, 2018). For example, if a disease has a limited number of genes associated with it, the genes would not cover enough dimensions to be spherical and satisfy this assumption. Sparsity can also result in irregular shapes. Therefore, the SI metric would not be suitable in some cases, such as rare disease clustering, and should always be used with caution. Nonetheless, it is a useful method in genetics and genomics where clusters are often unknown so there are no labels to compare against (Lopez et al., 2018; Yin et al., 2018).

2.4 Davies-Bouldin Index

A less common intrinsic method for evaluating clustering performance is the Davies-Bouldin Index (DBI). This metric compares the similarity between each cluster and the cluster most similar to it (Davies and Bouldin, 1979).

D B I = \frac{1}{N} \sum_{i = 1}^{N} \max (R_{i j}) w h e r e R_{i j} = \frac{s_{i} + s_{j}}{d_{i j}} a n d i \neq j

Given:

- N = number of clusters

- s_i = the mean distance between each sample in cluster i and cluster i’s centroid

- d_ij = the distance between cluster centroids i and j

DBI is an intrinsic method and shares many advantages and disadvantages with the SI. However, unlike the SI, the lower the DBI, the better the samples are clustered with zero being the minimum score. The computation of the DBI is simpler and more efficient than for the SI (Petrovi’c, 2006). This is a particularly valid consideration for the analysis of large genomics datasets, particularly if the data being clustered is whole-genome sequencing data. A limitation of DBI is that the clustering algorithm for its generation requires the Euclidean distance between cluster centroids (Davies and Bouldin, 1979). This is typically not a problem for genomics as Euclidean distance is a common choice in bioinformatic analyses. However, different distance matrices can provide different, even conflicting results and there are times when another distance measure may be more suitable for the research question (Jaskowiak et al., 2014). For example, genomics datasets such as whole genome sequencing data often suffer from sparsity meaning that most of the data is zeroes (Yazdani et al., 2015). In these cases, DBI would not be suitable.

2.5 Other clustering metrics

While these four clustering metrics cover the majority of use cases within genomics, there are other metrics that have their advantages. These include internal metrics such as the Calinski-Harabasz index (variance ratio criterion) (Caliñski and Harabasz, 1974; Babichev et al., 2017; Huang et al., 2021) as well as external metrics such as the Fowlkes-Mallows index (Fowlkes and Mallows, 1983; Ryšavý and Železný, 2017; Lee et al., 2023). Methods such as gap statistics are predominantly used for selecting the number of clusters, however, can be used as a metric (Tibshirani et al., 2001; Lugner et al., 2021). Advantages and disadvantages as well as previous uses of these are included in Table 1.

Table 1

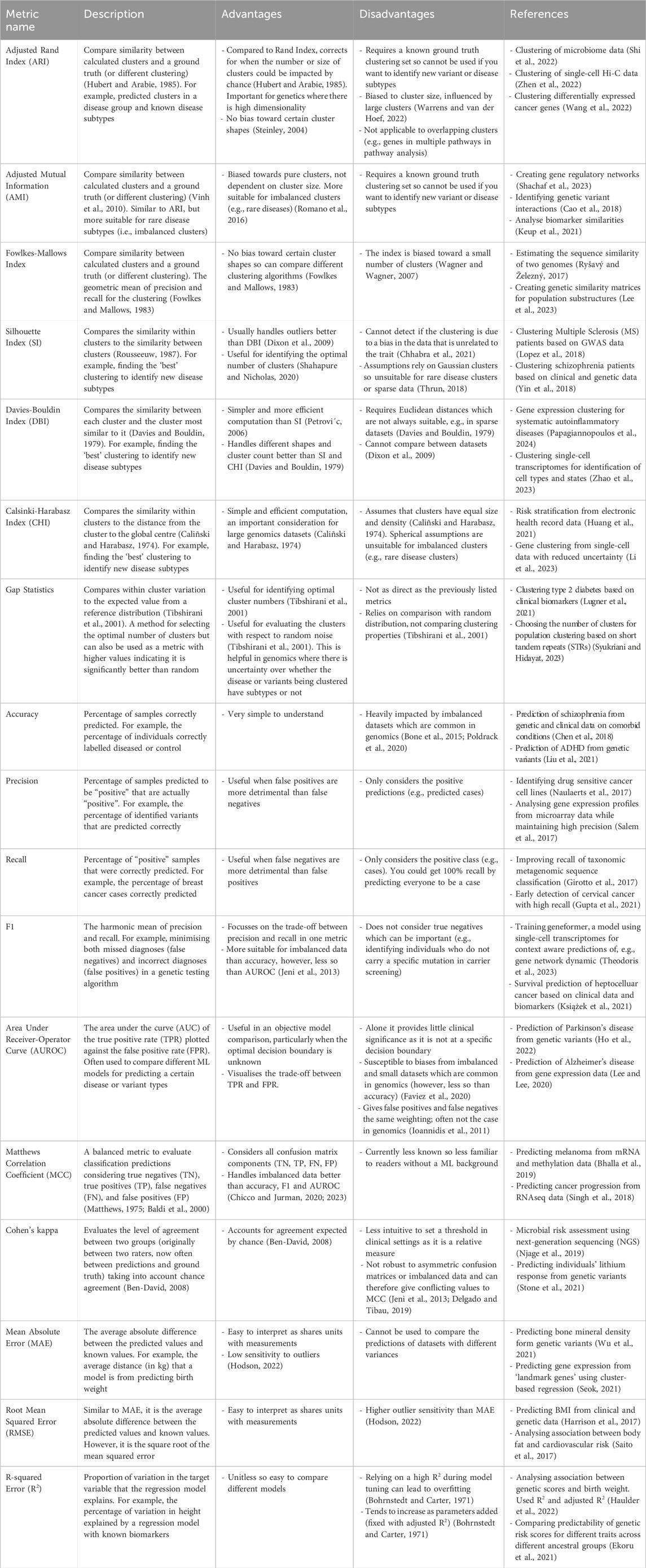
Table 1. Overview of the common clustering, classification, and regression metrics including their advantages, disadvantages, and example uses in genetics and genomics.

3 ML metrics for classification

Classification is the machine learning category most frequently used in genetics and genomics (Al-Tashi et al., 2023; Ho et al., 2022; Lee and Lee, 2020; Trakadis et al., 2019). Whilst the classification method complexity can range from simple logistic regression to complicated deep learning algorithms, the metrics remain predominantly the same. For parametric classifiers, the choice of metric largely depends on (1) the distribution of the data and (2) an understanding of the aim of the study. Nonparametric decision boundaries do not make assumptions about the data’s distribution (e.g., DD-classifier (Li et al., 2012)), however, these are not covered in this paper. Common metrics include: accuracy, area under the receiver-operator curve (AUROC), precision, recall, and F1.

3.1 Accuracy

Accuracy is the simplest classification metric to understand and is often reported in genomics papers (Chen et al., 2018; Trakadis et al., 2019; Liu et al., 2021). Accuracy provides a measure of the percentage of individuals who are correctly classified.

A c c u r a c y = \frac{n o . o f c o r r e c t c l a s s i f i c a t i o n s}{t o t a l n o . o f c l a s s i f i c a t i o n s} \times 100

The accuracy metric is used to evaluate how well an algorithm assigns individuals to the correct category (e.g., predicting whether someone has a particular trait or not). However, accuracy is heavily impacted by imbalanced datasets (Bone et al., 2015; Poldrack et al., 2020). For example, if a dataset of 100 individuals contains 10 diseased individuals and 90 healthy, an algorithm could get an accuracy of 90% by predicting everyone to be healthy. This is a real issue for genomic analyses, as they are often imbalanced due to the ease of obtaining data from control in comparison to the affected individuals, especially when dealing with rare traits/diseases (Devarriya et al., 2020; Faviez et al., 2020; Dai et al., 2021). Therefore, it is important to understand the dataset structure to enable an objective assessment of the accuracy measure.

3.2 Precision, recall, and F1

Confusion matrices (Figure 3A) are a simple way to display predictions for a population by separating them into those that were correctly predicted to be controls (true negatives; TN), correctly predicted to be cases (true positives; TP), incorrectly predicted to be controls (false negatives; FN), and incorrectly predicted to be cases (false positives; FP) (Figures 3A, B). The precision, recall, and F1 classification scores can be calculated from these four groups.

P r e c i s i o n = \frac{T P}{T P + F P} R e c a l l = \frac{T P}{T P + F N} F 1 = \frac{2 \times P \times R}{P + R}

Given:

- TP: number of true positives

- FP: number of false positives

- FN: number of false negatives

- P: precision

- R: recall

Figure 3

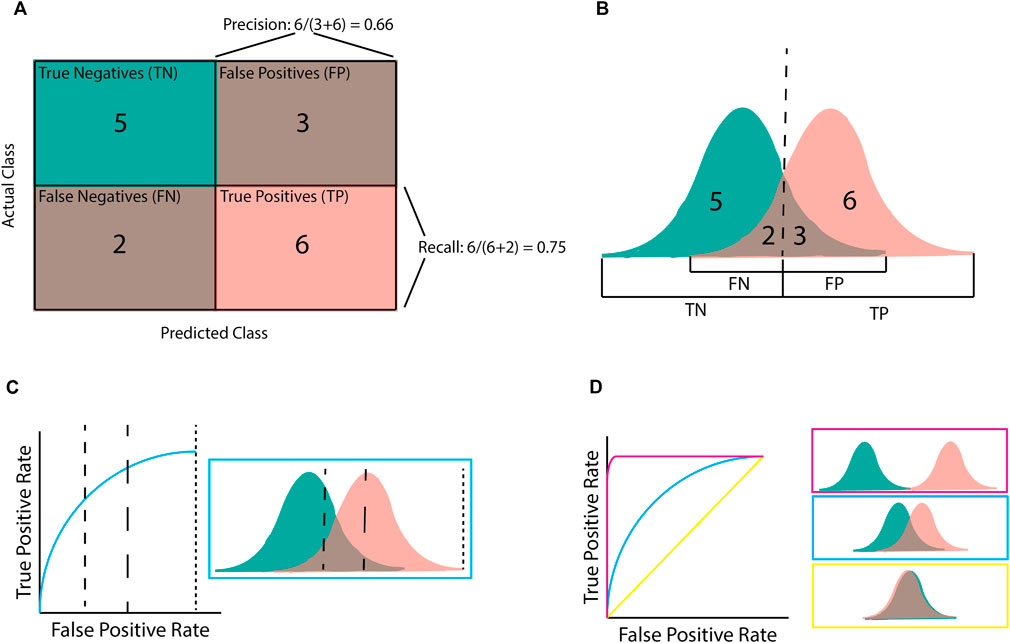
Figure 3. Illustration of classification metrics. (A) Confusion matrix used to calculate precision and recall. (B) the score distribution and threshold that gives the confusion matrix in (A). Every score below the dashed line is assigned to the negative class whilst scores after the dashed line are assigned to the positive class. (C) An Area Under the Receiver-Operator Curve (AUROC) graph for the given score distribution. Different chosen thresholds (dashed lines) give different ratios of FPR to TPR. (D) AUROC graphs for the three distribution patterns. Pink shows complete separation, blue is partial separation, and yellow is complete crossover.

Precision (or positive predictive value [PPV]) refers to the percentage of samples predicted to be “positive” that are actually “positive”; that is, a 100% precision means that there were no samples incorrectly labelled as “positive”. However, precision does not consider positive samples that were incorrectly labelled “negative”. By contrast, recall (or sensitivity) refers to the percentage of “positive” samples that were correctly labelled as positive; that is, a 100% recall score means that no positive samples were incorrectly labelled as negative. The F1 score is the harmonic mean of these precision and recall metrics. Therefore, a high F1 score requires both a high precision and a high recall. The importance of the precision and recall metrics varies according to the problem. For example, if an algorithm has been designed for disease diagnosis, incorrectly labelling an individual as health would be more harmful, making recall more important than precision (Chen et al., 2017). On the contrary, if an algorithm focuses on identifying genetic variants of interest or transcriptional effects, it is more important that the majority of the identified variants are correctly predicted, even at the expense of missed variants (false negatives). In this case precision would be more important than recall (Ioannidis et al., 2011).

3.3 Area under a receiver-operator curve

Area under a Receiver-Operator Curve (AUROC) is a common metric used in genomics as it is helpful for model comparison (Lee and Lee, 2020; Gupta et al., 2022; Ho et al., 2022). AUROC is calculated by plotting the true positive rate (TPR; equivalent to recall) against the false positive rate (FPR) and finding the area underneath this curve (Figures 3C, D). AUROC quantifies how well a model distinguishes between different classes by summarising the model’s performance at all decision boundaries (Box 1) into one value. This is different from other metrics (e.g., accuracy, precision, and recall) that only consider the model at a given decision boundary. However, even though AUROC is commonly used in genomics, it is not always useful on its own as, despite being helpful for model comparison, using AUROC alone provides little measure of clinical significance. For example, AUROC does not provide insight into how well a specific model will perform upon deployment (e.g., for diagnosing a disease) as this requires a decision boundary to have been chosen and validated.

Two keys assumptions limit the use of AUROC. Firstly, AUROC assumes false positives and false negatives are equally undesirable, which is not always the case in genomic analyses where the consequences of incorrectly predicting someone has not got a particular condition (false negative) can be far greater than the consequences of incorrectly predicting that they do (false positives) (Ioannidis et al., 2011). Secondly, AUROC is susceptible to biases from imbalanced and small datasets, both of which are common in genomics, particularly within studies of rare diseases (Faviez et al., 2020). Given these limitations, many studies will report the AUROC metric alongside metrics that include accuracy, precision, and recall, which are calculated at a given decision boundary and thus provide more clinical significance (Gao et al., 2021; Liu et al., 2021).

3.4 Matthew’s correlation coefficient and Cohen’s kappa

The above metrics are a selection of those most commonly used in ML for genomics and are arguably the easiest to understand. However, like with clustering, there are many other metrics available. Two metrics that are increasing in popularity and address some of the disadvantages of the metrics listed above are Matthew’s correlation coefficient (MCC) (Singh et al., 2018; Bhalla et al., 2019; Chicco and Jurman, 2020) and Cohen’s kappa (Ben-David, 2008; Njage et al., 2019; Yu et al., 2019; Stone et al., 2021). Particularly, MCC has been suggested as a preferential metric to the more popular ones discussed in this section due to its increased reliability with imbalanced datasets (Chicco and Jurman, 2020; 2023). Advantages, disadvantages, and use cases for these are listed in Table 1.

4 ML metrics for regression

Regression is less common in genomic studies than classification. However, it is helpful in predicting highly heterogenous traits with known scales such as height, systolic blood pressure, and waist-hip ratio (Bellot et al., 2018; Lello et al., 2018). The choice of regression metric for a particular analysis is also more nuanced than in classification studies, as the advantages and disadvantages of each option are less obvious. However, regression metrics that are commonly used include mean absolute error (Shahid and Singh, 2020), root mean squared error (Shmoish et al., 2021), and R² (Harrison et al., 2017; Haulder et al., 2022).

4.1 Mean absolute error

Mean absolute error (MAE) is a common method for measuring the average difference between the predicted values and the known values.

M A E = \sum_{i = 1}^{n} \frac{|y_{i} - x_{i}|}{n}

Given:

- $x_{i}$ = predicted value i

- $y_{i}$ = true value i

- $n$ = number of data points

The units for MAE are the same as the data points, making it easier to understand. However, this means it is hard to compare different predictions if the underlying data have different units. For example, Lello et al. (2018) used machine learning to predict height, heel bone density, and educational attainment from the same dataset (UK Biobank). They chose to look at the total variance explained by the model, however, had they chosen MAE as their metric instead, they would not be able to easily compare the predictability of the three traits – due to the different units used to measure each trait.

MAE has several strengths that make it useful, in particular MAE is less sensitive to outliers as it gives equal weight to all errors (Hodson, 2022). However, giving equal weighting to all errors means MAE cannot be used to compare the predictions of datasets with different variances even when these incorporate the same measurement units (e.g., predicting two body measurements in datasets with differing variance).

To take advantage of the strengths and restrict the impact of the limitations associated with the use of MAE, many researchers choose to report MAE alongside other metrics, such as root mean squared error and R² (see below) (Shahid and Singh, 2020; Shmoish et al., 2021; Zhang et al., 2021).

4.2 Root mean squared error

Root mean squared error (RMSE) is another frequently used metric for measuring the average difference between the predicted values and actual values in regression.

R M S E = \sqrt{\frac{\sum_{i = 1}^{n} {(y_{i} - x_{i})}^{2}}{n}}

Given:

- $x_{i}$ = predicted value i

- $y_{i}$ = true value i

- $n$ = number of data points

Similar to MAE, the units for RMSE are the same as those used for the data points. However, RMSE is more sensitive to outliers than MAE. This means RMSE gives larger weightings to these errors (Hodson, 2022). As such, whether MAE or RMSE is a better error metric has been hotly debated. Willmott et al. (2009) argued that sums-of-square-based statistics such as RMSE can not be used to represent average error as they vary in response to both error variability and central location. Chai and Draxler (2014) debated this, using simulations to show that RMSE is not only not ambiguous, but is more valuable than the MAE when the expected error distribution is Gaussian. It has also been suggested that a ratio of the two metrics is a more accurate metric than either option individually (Karunasingha, 2022).

RMSE has been used in genomic studies as a metric for predicting heterogeneous traits (Harrison et al., 2017; Shmoish et al., 2021). However, like MAE, RMSE is typically reported alongside the R² error, which measures the proportion of variation explained by the model (see below) (Harrison et al., 2017; Shmoish et al., 2021).

4.3 R-squared error

The R-squared error (R²), also known as the coefficient of determination, provides a measure of the proportion of variation in the variable being predicted (target variable) that the regression model explains.

R^{2} = 1 - \frac{\sum_{i = 1}^{n} {(y_{i} - x_{i})}^{2}}{\sum_{i = 1}^{n} {(y_{i} - y_{m e a n})}^{2}}

Given:

- $x_{i}$ = predicted value i

- $y_{i}$ = true value i

- $y_{m e a n}$ = mean of true values

- $n$ = number of data points

Unlike MAE and RMSE, R² error is not measured in the same units as the data points but instead varies from 0 (model explains 0% of target variable variance) to 1 (model explains 100% of target variable variance). Because of this, R² error is easily used to compare different models. A large R² suggests that the model is a good fit for the data. On the other hand, low R² values can mean that there is a significant amount of noise compared to signal (i.e., low signal-to-noise ratio). A low R² is not always bad, however, as it may just be indicative of low effect sizes which are common in complex disease genetics (Marian, 2012). Conversely, a high R² is not always good. Relying on a high R² for model tuning can result in overfitting as it is not robust to the number of predictors (Bohrnstedt and Carter, 1971). Notably, R² tends to increase when new variables are added to the model, even if they do not cause significant improvement(s) (Bohrnstedt and Carter, 1971). This can be compensated for by using the adjusted R².

A d j u s t e d R^{2} = 1 - \frac{(1 - R^{2}) (n - 1)}{n - p - 1}

Given:

- n = number of data points

- p = number of independent variables/predictors

The adjusted R² decreases if the additional parameters do not increase the model’s predictability. Therefore, the adjusted R² is often a more suitable measure for genomic studies, where models frequently use many variables (e.g., many genes, clinical scores, sex, and anthropometric measures) to predict target variables (e.g., birthweight) (Haulder et al., 2022).

5 Common pitfalls that lead to exaggerated metrics

Regardless of the chosen metric, some common pitfalls can result in the wrong conclusions being drawn. This can be particularly problematic in genetic and genomic studies, especially if a published model is thought to be more accurate at predicting a disease than it is. However, overfitting of data is the main cause of exaggerated metrics (England and Cheng, 2019). A model is considered overfit if it predicts extremely well for the training data but is a poor predictor outside the context. The chance of overfitting is greatly reduced by splitting the data into a training and test dataset, however, if enough models are trained on the training dataset, it is possible to find one that performs well on the test dataset by chance. For example, Chekroud et al. (2024) found that a machine learning model designed to predict patient outcomes of individuals in schizophrenia drug trials had high accuracy for predictions within the trial dataset used to train the model. However, in other trials its performance was no better than chance (Chekroud et al., 2024). Therefore, when optimising a model to achieve higher scores in the chosen metrics, it is crucial to remember that the scores are only relevant for the dataset(s) that the model is trained and tested on. This relates to the concept “bias-variance tradeoff” where high bias comes from a simplified model and leads to underfitting whereas high variance comes from a complex model with low training errors, leading to overfitting (Geman et al., 1992). As mentioned in the previous section, some metrics (including R²) are more prone to overfitting, and adjustments can be made to minimise this problem (e.g., adjusted R²). Reproducibility is critical so that the pipeline can be repeated on another dataset to confirm the validity of the model’s claims (Pineau et al., 2021) and identify overfitting.

Another common cause of exaggerated metrics is if the test data does not remain unseen by the model during training. That is, the test data must be kept hidden throughout feature selection and model training. Otherwise the model may learn features from the test dataset that it would not have otherwise learnt. A common mistake is to split the data after feature selection has begun (e.g., after genes or SNPs have been selected based on a statistical test), however, doing so will lead to inflated metrics (Kapoor and Narayanan, 2023). For example, Barnett et al. (2023) found that 44% of the genomic studies they investigated had inflated metrics due to data leakage during feature selection. On average, they saw an AUROC increase of 0.18 because of this data leakage. Unlike with overfitting, all metrics are equally impacted by this bias so care must be taken both during model training and when evaluating the metric scores. Again, reproducibility is essential to confirm the validity of the model’s claims and identify any biases.

Even if an effort is made to ensure the data is not overfit to the training data and the test data remains unseen, it is important to understand the limitations of the dataset. Models created with data from a specific subpopulation may not be meaningful when applied to other populations (De Roos et al., 2009; Gurdasani et al., 2019). For example, an algorithm using SNP information within a European population to predict a disease may not be as accurate when applied to different population groups. Understanding the dataset means it is easier to check for any biases inflating the reported metrics. For a dataset of individuals with and without a particular disease, if there is information on ancestry or sex, a simple check should be performed to confirm that the model remains unbiased toward a specific group. If there is a disparity in metric scores between groups, reporting the metrics for the different groups separately brings awareness to these biases.

A checklist of standards for publishing papers on AI-based science has been created that covers eight sections, including metrics and reproducibility (Kapoor et al., 2023). Specific reproducibility standards for the life sciences have also been published (Heil et al., 2021).

6 Discussion

Machine learning is a powerful tool within genetic and genomic research and has become increasingly accessible to researchers. However, care must be taken when choosing a metric for evaluating model outputs and interpreting the results. There is no one-size-fits-all metric available. We contend that multiple suitable performance metrics should be chosen based on an understanding of the dataset and the research question. Result reproducibility is crucial for readers to trust the reported metrics, as is a discussion of potential biases within the data and model that could have impacted the metrics. After reporting on the model’s performance, biases should be considered. It is best to keep the research question and data context in mind throughout the process to ensure reliable and confident results.

Author contributions

CM: Conceptualization, Visualization, Writing–original draft, Writing–review and editing. TP: Supervision, Writing–review and editing. DN: Supervision, Writing–review and editing. JO’S: Conceptualization, Supervision, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. C Miller was funded by the University of Auckland Doctoral Scholarship. D Nyaga was funded by the Dines Family Foundation.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ali, M. (2020). PyCaret: an open source, low-code machine learning library in Python. Available at: https://www.pycaret.org.

Google Scholar

Al-Tashi, Q., Saad, M. B., Muneer, A., Qureshi, R., Mirjalili, S., Sheshadri, A., et al. (2023). Machine learning models for the identification of prognostic and predictive cancer biomarkers: a systematic review. Int. J. Mol. Sci. 2023, 7781. doi:10.3390/ijms24097781

PubMed Abstract | CrossRef Full Text | Google Scholar

Alyousef, A. A., Nihtyanova, S., Denton, C., Bosoni, P., Bellazzi, R., and Tucker, A. (2018). Nearest consensus clustering classification to identify subclasses and predict disease. J. Healthc. Inf. Res. 2, 402–422. doi:10.1007/s41666-018-0029-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Awada, H., Durmaz, A., Gurnari, C., Kishtagari, A., Meggendorfer, M., Kerr, C. M., et al. (2021). Machine learning integrates genomic signatures for subclassification beyond primary and secondary acute myeloid leukemia. Blood 138, 1885–1895. doi:10.1182/blood.2020010603

PubMed Abstract | CrossRef Full Text | Google Scholar

Babichev, S., Lytvynenko, M. A. T., and Osypenko, V. (2017). “Criterial analysis of gene expression sequences to create the objective clustering inductive technology,” in 2017 IEEE 37th international conference on electronics and nanotechnology (ELNANO) (IEEE).