A Review of Feature Selection Methods for Machine Learning-Based Disease Risk Prediction

Machine learning has shown utility in detecting patterns within large, unstructured, and complex datasets. One of the promising applications of machine learning is in precision medicine, where disease risk is predicted using patient genetic data. However, creating an accurate prediction model based on genotype data remains challenging due to the so-called “curse of dimensionality” (i.e., extensively larger number of features compared to the number of samples). Therefore, the generalizability of machine learning models benefits from feature selection, which aims to extract only the most “informative” features and remove noisy “non-informative,” irrelevant and redundant features. In this article, we provide a general overview of the different feature selection methods, their advantages, disadvantages, and use cases, focusing on the detection of relevant features (i.e., SNPs) for disease risk prediction.

1 Introduction

1.1 Precision Medicine and Complex Disease Risk Prediction

The advancement of genetic sequencing technology over the last decade has re-ignited interest in precision medicine and the goal of providing healthcare based on a patient’s individual genetic features (Spiegel and Hawkins, 2012). Prediction of complex disease risk (e.g., type 2 diabetes, obesity, cardiovascular diseases, etc…) is emerging as an early success story. Successful prediction of individual disease risk has the potential to aid in disease prevention, screening, and early treatment for high-risk individuals (Wray et al., 2007; Ashley et al., 2010; Manolio, 2013).

Genome-wide association studies (GWAS) have identified single nucleotide polymorphisms (SNPs) within the human genome that are associated with complex diseases at the population level (Altshuler et al., 2008; Donnelly, 2008; Hindorff et al., 2009). However, most of the SNPs that have been associated with phenotypes have small effect sizes (Visscher et al., 2017), and collectively they only explain a fraction of the estimated heritability for each phenotype (Makowsky et al., 2011). This is known as the missing heritability problem. One possible explanation for the missing heritability is that GWAS typically utilize univariate filter techniques (such as the χ² test) to evaluate a SNP’s association with a phenotype SNP separately (Han et al., 2012). While univariate filter techniques are popular because of their simplicity and scalability, they do not account for the complex interactions between SNPs (i.e., epistasis effects). Ignoring interactions amongst genetic features might explain a significant portion of the missing heritability of complex diseases (Maher, 2008; König et al., 2016). Furthermore, being population-based, GWAS do not provide a model for predicting individual genetic risk. Thus, translation of GWAS association to individualized risk prediction requires quantification of the predictive utility of the SNPs that are identified. Typically, genetic risk prediction models are built by: 1) Polygenic risk scoring; or 2) Machine learning (ML) (Abraham and Inouye, 2015).

1.2 Machine Learning for Individualized Complex Disease Risk Prediction

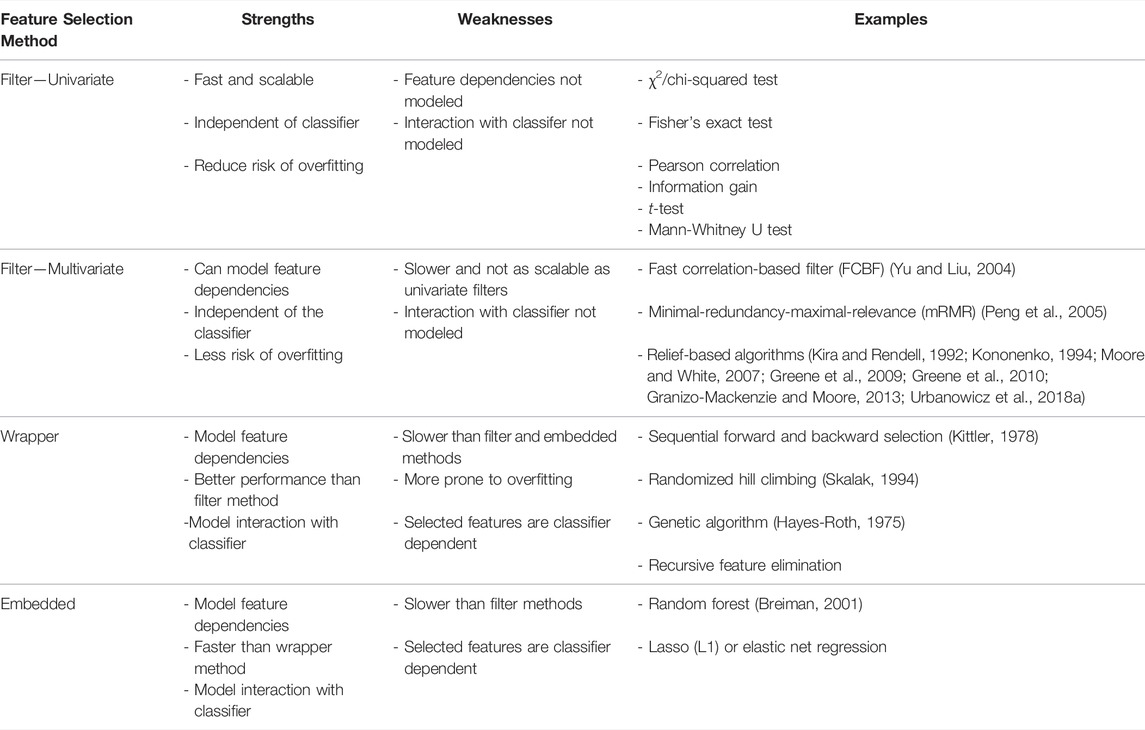
ML-based approaches are a potentially effective way of predicting individualized disease risk (Figure 1). Unlike other popular predictive models (e.g., Polygenic Risk Scores, which use a fixed additive model), ML has the potential to account for complex interactions between features (i.e. SNP-SNP interaction) (Ho et al., 2019). ML algorithms utilize a set of advanced function-approximation algorithms (e.g., support-vector machine, random forests, K-nearest neighbor, artificial neural network, etc…) to create a model that maps the association between a set of risk SNPs and a particular phenotype (Kruppa et al., 2012; Mohri et al., 2018; Uddin et al., 2019). Thus, a patient’s genotype data can be used as an input to the predictive ML algorithm to predict their risk for developing a disease (Figure 1B).

FIGURE 1

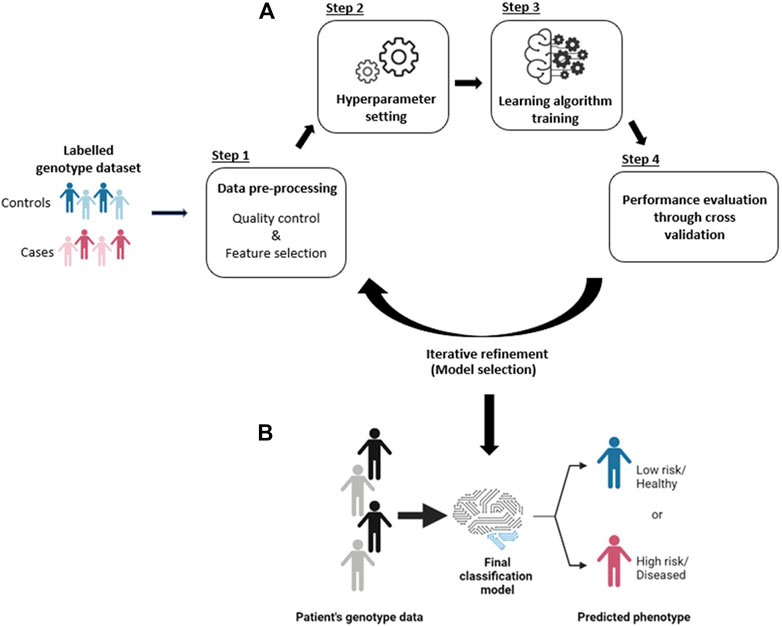
FIGURE 1. (A) Generalized workflow for creating a predictive ML model from a genotype dataset. (B) The final model can then be used for disease risk prediction.

The prediction of disease risk using SNP genotype data can be considered as a binary classification problem within supervised learning. There is a generalized workflow for creating a predictive ML model from a case-control genotype dataset (Figure 1A). The first step is data pre-processing, which includes quality control and feature selection (Figure 1A, step 1). Quality control includes, but is not limited to, removing low-quality SNPs (e.g., those with low call rates or that deviate from the Hardy-Weinberg Equilibrium), and samples (e.g. individuals with missing genotypes). SNPs with low minimum allele frequency (e.g., less than 0.01) can also be removed. Feature selection reduces the training dataset’s dimensionality by choosing only features that are relevant to the phenotype. Feature selection is crucial in order to produce a model that generalizes well to unseen cohorts (see Section 1.3). The goal of data pre-processing is to produce a high-quality dataset with which to train the prediction model.

The second step in a generalized predictive ML modelling workflow is the selection of the specific learning algorithm and setting the learning parameters (i.e. the “hyperparameters”) (Figure 1A, step 2). Hyperparameters are algorithm-specific parameters whose values are set before training. Examples include the number of trees in a random forest, the type of kernel in an SVM, or the number of hidden layers in an artificial neural network. Different learning algorithms use different hyperparameters, and their values affect the complexity and learning behaviour of the model.

Once the hyperparameters have been set, the pre-processed dataset is used to train the chosen algorithm (Figure 1A, step 3). This training step allows the algorithm to “learn” the association between the features (i.e., SNPs) and the class labels (i.e., phenotype status). Once learnt, the trained model’s predictive performance (e.g. accuracy, precision, AUC) is validated (Figure 1A, step 4). This is typically performed by K-fold cross-validation to estimate the model’s performance on unseen data. Cross-validation on unseen data ensures that the trained model does not overfit the training data. During cross-validation, the training dataset is equally split into K parts, and each part will be used as a validation/testing set. For example, in 5-fold (K = 5) cross-validation, the dataset is divided into 5 equal parts. The model is then trained on four of these parts and the performance is tested on the one remaining part. This process is repeated five times until all sections have been used as the testing set. The average performance of the model across all testing sets is then calculated.

The estimated model performance from cross-validation can be used as a guide for iterative refinement. During iterative refinement different aspects of the model building process (step 1–4) are repeated and refined. For example, different: hyperparameters (hyperparameter tuning); learning algorithms, feature selection methods, or quality control thresholds can all be tried. The combination that produces the best average performance (in cross-validation) is chosen to build the final classification model. The process of selecting the best model development pipeline is known as model selection. The final classification model can then be tested against an independent (external) dataset to confirm the model’s predictive performance, and finally be used for disease risk prediction (Figure 1B).

1.3 Feature Selection to Reduce SNP Data Dimensionality

Overcoming the curse of dimensionality is one of the biggest challenges in building an accurate predictive ML model from high dimensional data (e.g. genotype or GWAS data). For example, a typical case-control genotype dataset used in a GWAS can contain up to a million SNPs and only a few thousands of samples (Szymczak et al., 2009). Using such data directly to train the ML classification algorithms is likely to generate an overfitted model, which performs well on the training data but poorly on unseen data. Overfitting happens when the model picks up the noise and random fluctuations in the training data as a learned concept. Furthermore, the excessive number of features increases the learning and computational time significantly because the irrelevant and redundant features clutter the learning algorithm (Yu and Liu, 2004).

Feature selection is a common way to minimize the problem of excessive and irrelevant features (Figure 2). Generally, feature selection methods reduce the dimensionality of the training data by excluding SNPs that: 1) have low or negligible predictive power for the phenotype class; and 2) are redundant to each other (Okser et al., 2014). Effective feature selection can increase learning efficiency, predictive accuracy, and reduce the complexity of the learned results (Koller and Sahami, 1996; Kohavi and John, 1997; Hall, 2000). Furthermore, the SNPs that are incorporated into the predictive model (following feature selection) are typically assumed to be associated with loci that are mechanistically or functionally related to the underlying disease etiology (Pal and Foody, 2010; López et al., 2018). Therefore, extracting a subset of the most relevant features (through feature selection) could help researchers to understand the biological process(es) that underlie the disease (Cueto-López et al., 2019). In this context, feature selection can be said to be analogous to the identification of SNPs that are associated with phenotypes in GWAS.

FIGURE 2

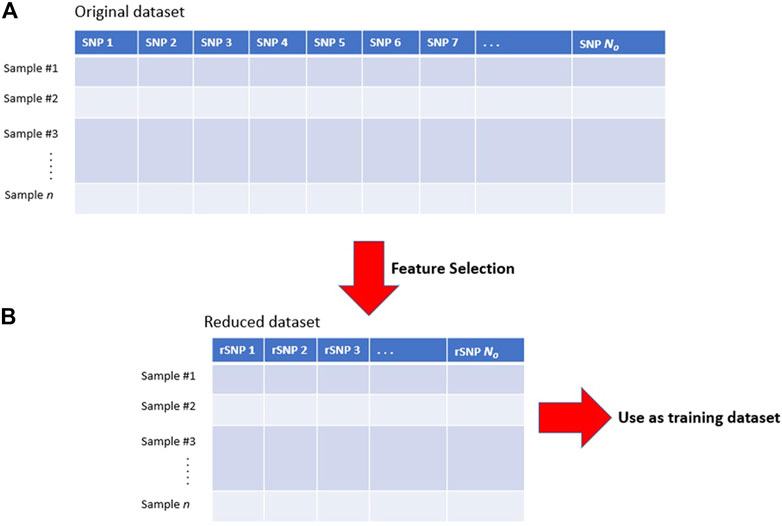
FIGURE 2. Illustration of feature selection process. (A) The original dataset may contain an excessive number of features and a lot of irrelevant SNPs. (B) Feature selection reduces the dimensionality of the dataset by excluding irrelevant features and including only those features that are relevant for prediction. The reduced dataset contains relevant SNPs (rSNPs) which can be used to train the learning algorithm. N_o: original number of features, N_r: number of remaining relevant SNPs.

1.4 The Problem of Feature Redundancy and Feature Interaction in SNP Genotype Dataset

GWAS typically identify multiple SNPs close to each other within a genetic window to be associated with a disease (Broekema et al., 2020). This occurs because of linkage disequilibrium (LD), which is the correlation between nearby variants such that they are inherited together within a population more often than by random chance (Figure 3). In ML and prediction contexts, these highly correlated SNPs can be considered redundant because they carry similar information and can substitute for each other. The inclusion of redundant features has been shown to degrade ML performance and increase computation time (Kubus, 2019; Danasingh et al., 2020). Therefore, ideally, feature selection techniques should select one SNP (e.g., the SNP with the highest association score) to represent the entire LD cluster as a feature for prediction. However, since the SNP with the highest association signal is not necessarily the causal variant of that locus (Onengut-Gumuscu et al., 2015), geneticists often link an association signal to the locus they belong to rather than the SNP itself (Brzyski et al., 2017). If a researcher aims to identify the true causal variant within an association locus then fine-mapping techniques must be employed (see (Spain and Barrett, 2015; Broekema et al., 2020))

FIGURE 3

FIGURE 3. Lead SNPs in GWAS studies need not be the causal variant due to linkage disequilibrium. Illustration of GWAS result where SNPs (circles) are colored according to linkage disequilibrium (LD) strength with the true causal variant within the locus (indicated with a black star). Due to LD, several SNPs near the true causal variant may show a statistically significant association with the phenotype. In ML, these highly correlated SNPs can be considered redundant to each other, therefore only one representative SNP for this LD cluster is required as a selected feature. In this example, the causal variant is not the variant with the strongest GWAS association signal.

Relevant features may appear irrelevant (or weakly relevant) on their own but are highly correlated to the class in the presence of other features. This situation arises because these features are only relevant to the phenotype when they interact with other features (i.e., they are epistatic). Figure 4 shows a simplified example of a feature interaction that arises because of epistasis. In this example, there is an equal number of SNP 1 = AA, Aa, or aa in cases and controls, which means that SNP 1 does not affect the distribution of the phenotype class. The same is true for SNP 2. However, the allele combinations between SNP1 and SNP2 does affect phenotype distribution. For example, there are more combinations of SNP1 = AA and SNP2 = AA in cases than controls, consistent with this allele combination conferring increased risk (Figure 4B).

FIGURE 4

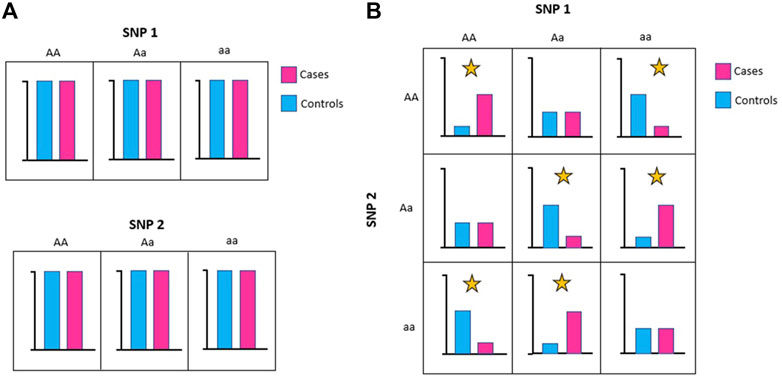
FIGURE 4. The functional impacts of SNPs can interact and may be epistatic. (A) Individually, neither SNP1 nor SNP2 affect phenotype distribution. (B) Taken together, allele combinations between SNP1 and SNP2 can affect phenotype distribution (marked with yellow star).

It is generally advisable to consider both feature redundancy and feature interaction during feature selection. This is especially true when dealing with genotype data, where linkage disequilibrium (LD) and the non-random association of alleles create redundant SNPs within loci. Moreover, complex epistatic interactions between SNPs can account for some of the missing heritability of complex diseases and should be considered when undertaking feature selection. Indeed, studies have demonstrated the benefits to predictive power of ML approaches that consider feature interactions when compared to those that only consider simple additive risk contributions (Couronné et al., 2018; Ooka et al., 2021). However, searching for relevant feature interactions undoubtedly comes with additional computational costs. As such, deciding whether different aspects of it must be done (i.e., searching for relevant interactions) is a problem-specific question that depends upon the nature of the input data and the a priori assumptions of the underlying mechanisms of the disease. For example, if the genetic data originates from whole-genome sequencing (WGS), or a genotyping array, and the target phenotype is a complex disease (i.e. best explained by non-linear interactions between loci) then using a feature selection approach that considers interactions will be beneficial. By contrast, if the input genetic data does not uniformly cover the genome (i.e., the density of the SNPs is much higher in known disease associated loci; e.g. Immunochip genotyping array) then interactions may not aid the selection as the lack of data leads to potentially important interactions with SNPs outside known disease associated loci being missed. Furthermore, not all diseases are recognized as involving complex epistatic effects. In such cases, searching for feature interactions might lead to additional computation complexity without obvious predictive benefits. For example, Romagnoni et al. (Romagnoni et al., 2019) reported that searching for possible epistatic interactions did not yield a significant increase in predictive accuracy for Crohn’s disease. Notably, the authors concluded that epistatic effects might make limited contributions to the genetic architecture of Crohn’s disease, and the use of the Immunochip genotyping array might have caused interaction effects with SNPs outside of the known autoimmune risk loci to have been missed.

The goal of feature selection is to select a minimum subset of features (which includes individually relevant and interacting features) that can be used to explain the different classes with as little information loss as possible (Yu and Liu, 2004). It is possible that there are multiple possible minimum feature subsets due to redundancies. Thus, this is “a minimum subset” and not “the minimum set.”

In the remainder of this manuscript we discuss the advantages and disadvantages of representative filter, wrapper, and embedded methods of feature selection (Section 2). We then assess expansions of these feature selection methods (e.g. hybrid, ensemble, and integrative methods; Sections 3.1–3.2) and exhaustive search methods for higher-order (≥3) SNP-SNP interaction/epistasis effects (Section 4).

2 Feature Selection Techniques

The feature selection methods that are routinely used in classification can be split into three methodological categories (Guyon et al., 2008; Bolón-Canedo et al., 2013): 1) filters; 2) wrappers; and 3) embedded methods (Table 1). These methods differ in terms of 1) the feature selection aspect being separate or integrated as a part of the learning algorithm; 2) evaluation metrics; 3) computational complexities; 4) the potential to detect redundancies and interactions between features. The particular strengths and weaknesses of each methodological category mean they are more suitable for particular use cases (Saeys et al., 2007; Okser et al., 2013; De et al., 2014; Remeseiro and Bolon-Canedo, 2019) (Table 1).

TABLE 1

TABLE 1. Strengths, weaknesses, and examples of the three main feature selection categories.

2.1 Filter Methods for Feature Selection

Filter methods use feature ranking as the evaluation metric for feature selection. Generally, features are ranked based on their scores in various statistical tests for their correlation with the class. Features that score below a certain threshold are removed, while features that score above it are selected. Once a subset of features is selected, it can then be presented as an input to the chosen classifier algorithm. Unlike the other feature selection methods (wrapper and embedded), filter methods are independent/separate from the classifier algorithm (Figure 5A). This separation means that filter methods are free from classifier’s bias which reduces overfitting. However, this independence also means that interaction with the classifier is not considered during feature selection (John et al., 1994). Thus, the selected feature set is more general and not fine-tuned to any specific classifier (Zhang et al., 2013). This lack of tuning means that filter methods tend to produce models that have reduced predictive performance compared to those produced by wrapper or embedded methods. The main advantage of filter methods over other feature selection methods is that they are generally less computationally demanding, and thus can easily be scaled to very high dimensional data (e.g. SNP genotype datasets).

FIGURE 5

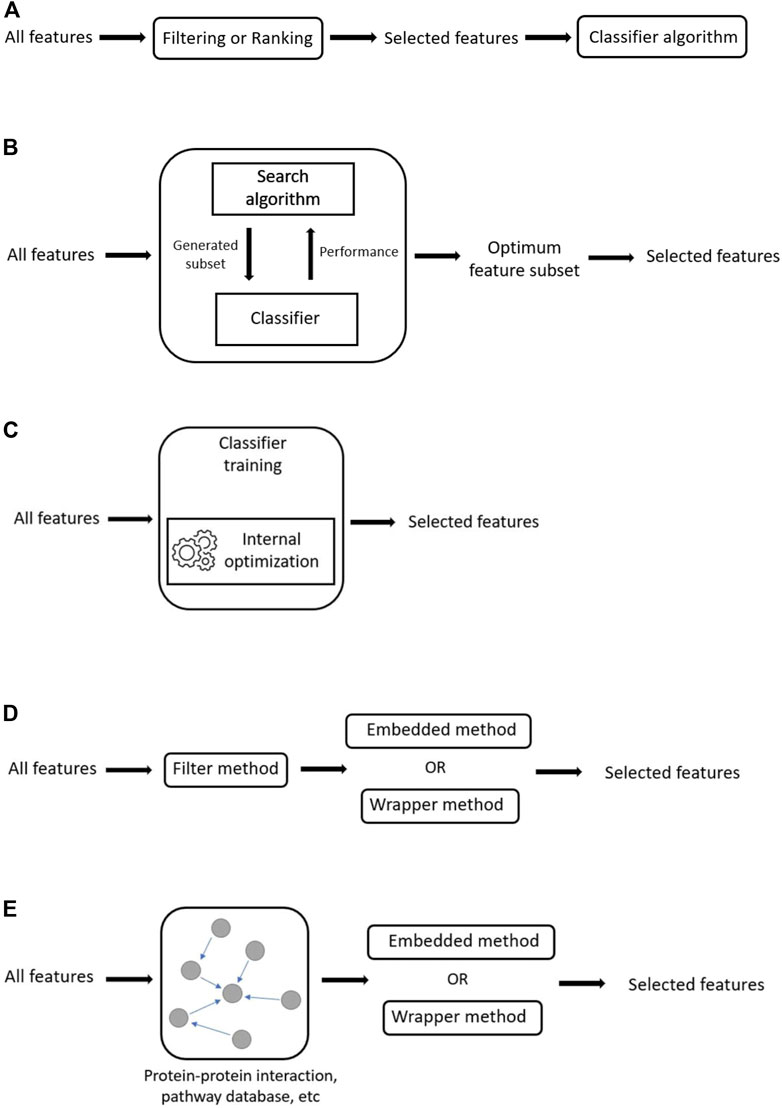
FIGURE 5. Generalized illustrations of methods. (A) Schematic of filter method, where feature selection is independent of the classifier. (B)The wrapper method. Feature selection relies on the performance of the classifier algorithm on the various generated feature subsets. (C) The embedded method. In embedded methods, feature selection is integrated as a part of the classifier algorithm. (D) Hybrid methods. In hybrid methods, features are reduced through the application of a filter method before the reduced feature set is passed through a wrapper or embedded method to obtain the final feature subset. (E) Integrative methods. In integrative methods, external information is used as a filter to reduce feature search space before the reduced feature set is passed through a wrapper or embedded method to obtain the final feature subset.

Existing filter methods can be broadly categorized as either univariate or multivariate. Univariate methods test each feature individually, while multivariate methods consider a subset of features simultaneously. Due to their speed and simplicity, univariate methods (e.g., χ2 test, Fisher’s exact test, information gain, Euclidean distance, Pearson correlation, Mann-Whitney U test, t-test, etc...) have attracted the most attention in fields that work with high dimensional datasets (Saeys et al., 2007; Bolón-Canedo et al., 2014). However, since each feature is considered separately, univariate methods only focus on feature relevance and cannot detect feature redundancy, or interactions. This decreases model predictor performance because: 1) the inclusion of redundant features makes the feature subset larger than necessary; and 2) ignoring feature interactions can lead to the loss of important information.

More advanced multivariate filter techniques, including mutual information feature selection (MIFS) (Battiti, 1994), minimal-redundancy-maximal-relevance (mRMR) (Peng et al., 2005), conditional mutual information maximization (CMIM) (Schlittgen, 2011), and fast correlation-based filter (FCBF), (Yu and Liu, 2004), have been developed to detect relevant features and eliminate redundancies between features without information loss. Other algorithms like BOOST (Wan et al., 2010), FastEpistasis (Schüpbach et al., 2010), and TEAM (Zhang et al., 2010) have been designed to exhaustively search for all possible feature interactions. However, they are restricted to two-way (pairwise) interactions and they cannot eliminate redundancy. More recent algorithms (e.g., the feature selection based on relevance, redundancy and complementarity [FS-RRC] (Li et al., 2020), Conditional Mutual Information-based Feature Selection considering Interaction [CMIFSI] (Liang et al., 2019)) have been demonstrated to be able to detect feature interactions and eliminate redundancies. However, again, they are mostly constrained to pair-wise feature interactions. Another popular family of filter algorithms is the Relief-based algorithm (RBA) family (e.g., Relief (Kira and Rendell, 1992), ReliefF (Kononenko, 1994), TURF (Moore and White, 2007), SURF (Greene et al., 2009), SURF* (Greene et al., 2010), MultiSURF (Urbanowicz et al., 2018a), MultiSURF* (Granizo-Mackenzie and Moore, 2013), etc…). Relief does not exhaustively search for feature interactions. Instead, it scores the importance of a feature according to how well the feature’s value distinguishes samples that are similar to each other (e.g., similar genotype) but belong to different classes (e.g., case and control). Notably, RBAs can detect pair-wise feature interactions, some RBAs (e.g., ReliefF, MultiSURF) can even detect higher order (>2 way) interactions (Urbanowicz et al., 2018a). However, RBAs cannot eliminate redundant features. Different RBAs have been reviewed and compared previously (Urbanowicz et al., 2018a; Urbanowicz et al., 2018b).

Despite its advantages, it should be noted that multivariate methods are more computationally heavy than univariate methods and thus cannot as effectively be scaled to very high dimensional data. Furthermore, multivariate filters still suffer from some of the same limitations as univariate filters due to their independence from the classifier algorithm (i.e., it ignores interaction with the classifier). In this context, wrapper and embedded methods represent an alternative way to perform multivariate feature selection while allowing for interactions with the classifier although again there is a computational cost (see Sections 2.2, 2.3).

2.1.1 The Multiple Comparison Correction Problem and Choosing the Appropriate Filter Threshold

Filter methods often return a ranked list of features rather than an explicit best subset of features (as occurs in wrapper methods). For example, univariate statistical approaches like χ2 test and fisher exact test rank features based on p value. Due to the large number of hypothesis tests made, relying on the usual statistical significance threshold of p < 0.05 will result in a preponderance of type 1 errors (false positive). As an illustration, if we perform hypothesis tests on 1 million SNPs at a p value threshold <0.05, we can expect around 50,000 false positives, which is a considerable number. Therefore, choosing an appropriate threshold for relevant features adds a layer of complexity to predictive modelling when using feature selection methods that return ranked feature lists.

For methods that return a p value, the p value threshold is commonly adjusted by controlling for FWER (family-wise error rate) or FDR (false discovery rate). FWER is the probability of making at least one type 1 error across all tests performed (i.e., 5% FWER means there is 5% chance of making at least one type 1 error across all hypothesis tests). FWER can be controlled below a certain threshold (most commonly <5%) by applying a Bonferroni correction (Dunn, 1961). The Bonferroni correction works by dividing the desired probability of type 1 error p (e.g., p < 0.05) by the total number of independent hypotheses tested. This is a relatively conservative test that assumes that all the hypotheses being tested are independent of each other. However, this assumption is likely to be violated in genetic analyses where SNPs that are close to each other in the linear DNA sequence tend to be highly correlated due to LD (Figure 3). Thus, the effective number of independent hypothesis tests is likely to be smaller than the number of SNPs examined. Not taking LD into account will lead to overcorrection for the number of tests performed. For example, the most commonly accepted p value threshold used in GWAS (p < 5 × 10⁻⁸) is based on a Bonferroni correction on all independent common SNPs after taking account of the LD structure of the genome (Dudbridge and Gusnanto, 2008; Xu et al., 2014). Despite its widespread use in GWAS, this threshold has been criticized for being too conservative, leading to excessive false negatives (Panagiotou and Ioannidis, 2012). Panagiotou et al. (Panagiotou and Ioannidis, 2012) noted that a considerable number of legitimate and replicable associations can have p values just above this threshold; therefore, a possible relaxation of this commonly accepted threshold has been suggested.

Alternatively, one can apply p value adjustment to control for FDR instead of FWER. Controlling for FDR is a less stringent metric than controlling for FWER because it is the allowed proportion of false positives among all positive findings (i.e., 5% FDR means that approximately 5% of all positive findings are false). Despite potentially including more false positives in the selected features, FDR has been shown to be more attractive if prediction (rather than inference) is the end goal (Abramovich et al., 2006).

FDR can be controlled by applying the Benjamini-Hochberg (B-H) procedure (Benjamini and Hochberg, 1995). However, like the Bonferroni correction, the B-H procedure assumes independent hypothesis tests. To satisfy this assumption, for example, Brzyski et al. (2017) proposed a strategy that clusters tested SNPs based on LD before applying B–H. Alternatively, there also exist procedures that control FDR without making any assumptions such as the Benjamini-Yekutieli (B-Y) procedure (Benjamini and Yekutieli, 2001). However, the B-Y procedure is more stringent, leading to less power compared to procedures that assume independence like B-H (Farcomeni, 2008).

The question remains, when applying a Bonferroni, B-H or B-Y correction, which FWER/FDR threshold is optimum (e.g., 5, 7, or 10%)? In a ML context, this threshold can be viewed as a hyperparameter. Thus, the optimum threshold that produces the best performance can be approximated by cross-validation as a part of the model selection process (Figure 1A, step 5). The threshold for feature selection methods that do not directly produce a p value (e.g., multivariate algorithms like mRMR (Peng et al., 2005)) can also be chosen using cross validation (e.g. by taking the top n SNPs as the selected features).

2.2 Wrapper Methods for Feature Selection

In contrast to filter methods, wrapper methods use the performance of the chosen classifier algorithm as a metric to aid the selection of the best feature subset (Figure 5B). Thus, wrapper methods identify the best-performing set of features for the chosen classifier algorithm (Guyon and Elisseeff, 2003; Remeseiro and Bolon-Canedo, 2019). This is the main advantage of wrapper methods, and has been shown to result in higher predictive performance than can be obtained with filter methods (Inza et al., 2004; Wah et al., 2018; Ghosh et al., 2020). However, exhaustive searches of the total possible feature combination space are computationally infeasible (Bins and Draper, 2001). Therefore, heuristic search strategies across the space of possible feature subsets must be defined (e.g., randomized (Mao and Yang, 2019), sequential search (Xiong et al., 2001), genetic algorithm (Yang and Honavar, 1998; Li et al., 2004), ant colony optimization (Forsati et al., 2014), etc…) to generate a subset of features. A specific classification algorithm is then trained and evaluated using the generated feature subsets. The classification performances of the generated subsets are compared, and the subset that results in the best performance [typically estimated using AUC (area under the receiver operating characteristic curve)] is chosen as the optimum subset. Practically, any search strategy and classifier algorithm can be combined to produce a wrapper method.

Wrapper methods implicitly take into consideration feature dependencies, including interactions and redundancies, during the selection of the best subset. However, due to the high number of computations required to generate the feature subsets and evaluate them, wrapper methods are computationally heavy (relative to filter and embedded methods) (Chandrashekar and Sahin, 2014). As such, applying wrapper methods to SNP genotype data is usually not favored, due to the very high dimensionality of SNP data sets (Kotzyba - Hibert et al., 1995; Bolón-Canedo et al., 2014).

Wrapper methods are dependent on the classifier used. Therefore, there is no guarantee that the selected features will remain optimum if another classifier is used. In some cases, using classifier performance as a guide for feature selection might produce a feature subset with good accuracy within the training dataset, but poor generalizability to external datasets) (i.e., more prone to overfitting) (Kohavi and John, 1997).

Unlike filter methods which produce a ranked list of features, wrapper methods produce a “best” feature subset as the output. This has both advantages and disadvantages. One advantage of this is that the user does not need to determine the most optimum threshold or number of features selected (because the output is already a feature subset). The disadvantage is that it is not immediately obvious which features are relatively more important within the set. Overall, this means that although wrapper methods can produce better classification performance, they are less useful in exposing the relationship between the features and the class.

2.3 Embedded Methods for Feature Selection

In an embedded method, feature selection is integrated or built into the classifier algorithm. During the training step, the classifier adjusts its internal parameters and determines the appropriate weights/importance given for each feature to produce the best classification accuracy. Therefore, the search for the optimum feature subset and model construction in an embedded method is combined in a single step (Guyon and Elisseeff, 2003) (Figure 5C). Some examples of embedded methods include decision tree-based algorithms (e.g., decision tree, random forest, gradient boosting), and feature selection using regularization models (e.g., LASSO or elastic net). Regularization methods usually work with linear classifiers (e.g., SVM, logistic regression) by penalizing/shrinking the coefficient of features that do not contribute to the model in a meaningful way (Okser et al., 2013). It should be noted that like many filter methods, decision tree-based and regularization methods mentioned above also return a ranked list of features. Decision tree-based algorithms rank feature importance based on metrics like the Mean Decrease Impurity (MDI) (Louppe et al., 2013). For regularization methods, the ranking of features is provided by the magnitude of the feature coefficients.

Embedded methods are an intermediate solution between filter and wrapper methods in the sense that the embedded methods combine the qualities of both methods (Guo et al., 2019). Specifically, like filter methods, embedded methods are computationally lighter than wrapper methods (albeit still more demanding than filter methods). This reduced computational load occurs even though the embedded method allows for interactions with the classifier (i.e., it incorporates classifier’s bias into feature selection, which tends to produce better classifier performance) as is done for wrapper methods.

Some embedded methods (i.e…, random forest and other decision tree-based algorithms) do allow for feature interactions. Notably, unlike most multivariate filters, tree-based approaches can consider higher-order interactions (i.e., more than two). Historically, random forest is rarely applied directly to whole-genome datasets due to computational and memory constraints (Szymczak et al., 2009; Schwarz et al., 2010). For example, it has been shown that the original Random Forest algorithm (developed by Breiman and Cutler, 2004) can be applied to analyze no more than 10,000 SNPs (Schwarz et al., 2010). Indeed, many applications of random forest have been focused on low-dimensional dataset. For example, Bureau et al. (Bureau et al., 2005), identified relevant SNPs from a dataset of just 42 SNPs. Lopez et al. (López et al., 2018) implemented a random forest algorithm to identify relevant SNPs from a dataset that contains a total of 101 SNPs that have been previously associated with type 2 diabetes.

Nevertheless, recent advances in computational power, together with optimizations and modifications of the random forest algorithm (e.g., the Random Jungle (Schwarz et al., 2010)) have resulted in efficiency gains that enable it to be applied to whole-genome datasets. However, studies have indicated that the effectiveness of random forest to detect feature interactions declines as the number of features increases, thus limiting the useful application of random forest approaches to highly dimensional datasets (Lunetta et al., 2004; Winham et al., 2012). Furthermore, the ability of standard random forest to detect feature interactions is somewhat dependent on strong individual effects, potentially losing epistatic SNPs with a weak individual effect. Several modified random forest algorithms have been developed to better account for epistatic interactions between SNPs with weak individual effect (e.g., T-tree (Botta et al., 2014), GWGGI (Wei and Lu, 2014)). These modified algorithms are still less sensitive than exhaustive search methods (Section 4).

Unlike some multivariate filters (Section 2.1), random forest does not automatically eliminate redundant features. Indeed, Mariusz Kubus (Kubus, 2019) showed that the presence of redundant features decreases the performance of the random forest algorithm. A potential solution to this problem includes filtering out the redundant features before applying random forest [see hybrid method (Section 3.1)]. Another possible solution might be aggregating the information carried by these redundant features (e.g., using haplotypes instead of SNPs to build the model). Some software packages like T-tree (Botta et al., 2014) have a built-in capability to account for redundancy by transforming the input SNPs into groups of SNPs in high-LD with each other.

In contrast to decision tree-based algorithms, penalized methods (e.g., LASSO) can discard redundant features, but it have no built-in ability to detect feature interactions (Barrera-Gómez et al., 2017). Instead, interaction terms must be explicitly included in the analysis (Signorino and Kirchner, 2018). This is commonly achieved by exhaustively including all (usually pairwise) interaction terms for the features. While this approach can be effective for data with low dimensionality, it can be inaccurate and computationally prohibitive in highly dimensional data settings. Two-stage or hybrid strategies that result in reduced search spaces are potential solutions to this problem (Section 3.1).

2.4 Which Feature Selection Method Is Optimal?

The “no free lunch” theorem states that in searching for a solution, no single algorithm can be specialized to be optimal for all problem settings (Wolpert and Macready, 1997). This is true for feature selection methods, each of which has its own strengths and weaknesses (Table 1), relying on different metrics and underlying assumptions. Several studies have compared the predictive performance of the different feature selection methods (Forman, 2003; Bolón-Canedo et al., 2013; Aphinyanaphongs et al., 2014; Wah et al., 2018; Bommert et al., 2020). These comparative studies have resulted in the widely held opinion that there is no such thing as the “best method” that is fit for all problem settings.

Which feature selection method is best is a problem-specific question that depends on the dataset being analyzed and the specific goals that the researcher aims to accomplish. For example, suppose the aim is to identify which features are relatively the most important (which can be useful to help uncover the biological mechanism behind the disease). In that case, filter methods are better because they produce a ranked list of features and are the most computationally efficient. If the dataset contains a relatively low number of features (e.g., tens to hundreds), applying wrapper methods likely results in the best predictive performance. Indeed, in this case, model selection algorithms can be applied to identify which wrapper algorithm is the best. By contrast, for the typical SNP genotype dataset with up to a million features, computational limitations mean that directly applying wrapper or embedded methods might not be computationally practical even though they model feature dependencies and tend to produce better classifier accuracy than filter methods.

New feature selection strategies are emerging that either: 1), use a two-step strategy with a combination of different feature selection methods (hybrid methods); or 2), combine the output of multiple feature selection methods (ensemble methods). These strategies take advantage of the strengths of the different feature selection methods that they include.

3 Hybrid Methods—Combining Different Feature Selection Approaches

Hybrid methods combine different feature selection methods in a multi-step process to take advantage of the strengths of the component methods (Figure 5D). For example, univariate filter-wrapper hybrid methods incorporate a univariate filter method as the first step to reduce the initial feature set size, thus limiting the search space and computational load for the subsequent wrapper step. In this instance, the filter method is used because of its simplicity and speed. By contrast, the wrapper method is used because it can model feature dependencies and allow interactions with the classifier, thus producing better performance. Typically, a relaxed scoring threshold is used for the filtering step because the main goal is to prioritize a subset of SNPs for further selection by the wrapper method. For example, when using the univariate χ2 test in the initial feature selection step, instead of the genome-wide significance threshold commonly used in GWAS (p > 5 × 10^–8), one might choose a less stringent threshold (e.g., p > 5 × 10^–4), or adjust by FDR instead. While this might result in more false positives, these can be further eliminated and SNPs with weak individual effects, but strong interacting effects will be able to survive the filtering step and thus can be detected by the wrapper method in the subsequent step. Practically, any filter, wrapper, or embedded method can be combined to create a hybrid method.

In a hybrid method, implementing the filter step reduces the feature search space thus allowing for the subsequent use of computationally expensive wrapper or embedded methods for high-dimensional datasets (which might otherwise be computationally unfeasible). For example, Yoshida and Koike (Yoshida and Koike, 2011) presented a novel embedded method to detect interacting SNPs associated with rheumatoid arthritis called SNPInterForest (a modification of random forest algorithm). To accommodate the computational load of the proposed algorithm, the authors first narrowed the feature size from 500,000 SNPs to 10,000 SNPs using a univariate filter before further selection using SNPInterForest.

Wei et al. (2013) built a Crohn’s disease prediction model that employed a single SNP association test (a univariate filter method), followed by logistic regression with L1 (LASSO) regularization (an embedded method). The first filtering step reduced the original feature size from 178,822 SNPs to 10,000 SNPs for further selection with LASSO. The final predictive model achieved a respectable AUC of 0.86 in the testing set.

There is always a trade-off between computational complexity and performance in feature selection. In this context, hybrid methods can be considered a “middle ground” solution between the simple filter method and the more computationally complex but performant wrapper and embedded methods. Indeed, many examples in the literature have shown that a hybrid method tends to produce better performance than a simple filter while also being less computationally expensive than a purely wrapper method. For example, Alzubi et al. (2017) proposed a feature selection strategy using a hybrid of the CMIM filter and RFE-SVM wrapper method to classify healthy and diseased patients. They used SNP datasets for five conditions (thyroid cancer, autism, colorectal cancer, intellectual disability, and breast cancer). The authors showed that generally, the SNPs selected by the hybrid CMIM + RFE-SVM produce better classification performance than using any single filter method like mRMR (Peng et al., 2005), CMIM (Schlittgen, 2011), FCBF (Yu and Liu, 2004), and ReliefF (Urbanowicz et al., 2018b), thus showing the superiority of the hybrid method.

Ghosh et al. (2020) demonstrated that a hybrid filter-wrapper feature selection technique, based on ant colony optimization, performs better than those based solely on filter techniques. The proposed hybrid method was less computationally complex than those based on the wrapper technique while preserving its relatively higher accuracy than the filter technique. Similarly, Butler-Yeoman et al. (2015) proposed a novel filter-wrapper hybrid feature selection algorithm that was based on particle swarm optimisation (FastPSO and RapidPSO). The authors further showed that the proposed hybrid method performs better than a pure filter algorithm (FilterPSO), while being less computationally complex than a pure wrapper algorithm (WrapperPSO).

Hybrid methods still have limitations despite their advantages when compared to purely filter, embedded, and wrapper methods. For example, relevant interacting SNPs with no significant individual effects (i.e., exclusively epistatic) can potentially be lost during the filtering step. This is because most filter methods cannot model feature-feature interactions. This can be mitigated by using filter algorithms that can model feature interactions (Section 2.1).

3.1 Integrative Method—Incorporating External Knowledge to Limit Feature Search Space

Integrative methods incorporate biological knowledge as an a priori filter for SNP pre-selection (Figure 5E). This enables the researcher to narrow the search space to “interesting” SNPs that are recognized as being relevant to the phenotype of interest. Limiting the search space means limiting the computational complexity for downstream analysis.

To integrate external knowledge, one can obtain information from public protein-protein interaction databases (e.g., IntAct, ChEMBLOR, BioGRID) or pathway databases (KEGG, Reactome). Software (e.g., INTERSNP (Herold et al., 2009)) has also been developed to help select a combination of “interesting” SNPs based on a priori knowledge (e.g., genomic location, pathway information, and statistical evidence). This information enables a reduction in the search space to only those SNPs that are mapped to genes that researchers contend are involved in relevant protein interactions or pathways of interest. For example, Ma et al. (2015) successfully identified SNP-SNP interactions that are associated with high-density lipoprotein cholesterol (HDL-C) levels. The search space was reduced by limiting the search to SNPs that have previously been associated with lipid levels, SNPs mapped to genes in known lipid-related pathways and those that are involved in relevant protein-protein interactions. In other examples, the SNP search space has been limited to SNPs that are located within known risk loci. For example, D’angelo et al. (D’Angelo et al., 2009) identified significant gene-gene interactions that are associated with rheumatoid arthritis (RA) by restricting their search to chromosome 6 (a known as risk locus for RA (Newton et al., 2004)) and using a combined LASSO-PCA approach.

An obvious limitation with these types of integrative approaches is the fact that online databases and our current biological knowledge are incomplete. Therefore, relying on external a priori knowledge will hinder the identification of novel variants outside our current biological understanding.

3.2 Ensemble Method—Combining the Output of Different Feature Selections

Ensemble feature selection methods are based on the assumption that combining the output of multiple algorithms is better than using the output of a single algorithm (Figure 6) (Bolón-Canedo et al., 2014). In theory, an ensemble of multiple feature selection methods allows the user to combine the strengths of the different methods while overcoming their weaknesses (Pes, 2020). This is possible because different feature selection algorithms can retain complementary but different information. Several studies have shown that ensemble feature selection methods tend to produce better classification accuracy than is achieved using single feature selection methods (Seijo-Pardo et al., 2015; Hoque et al., 2017; Wang et al., 2019; Tsai and Sung, 2020). Furthermore, ensemble feature selection can improve the stability of the selected feature set (i.e., it is more robust to small changes in the input data) (Yang and Mao, 2011). Stability and reproducibility of results is important because it increase the confidence of users when inferring knowledge from the selected features (Saeys et al., 2008).

FIGURE 6

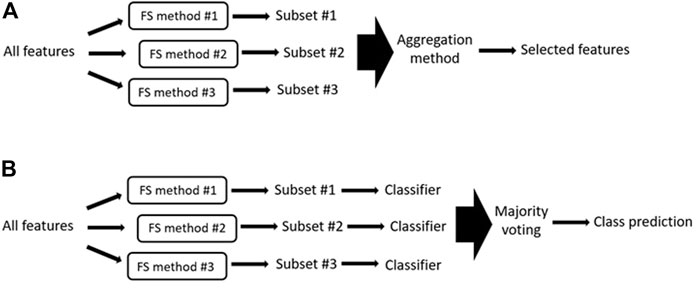
FIGURE 6. (A) Generalized illustration of ensemble methods. In ensemble methods, the outputs of several feature selection methods are aggregated to obtain the final selected features. FS = feature selection. (B) Generalized illustration of majority voting system where the different generated feature subsets are used to train and test a specific classifier. The final output is the class predicted by the majority of the classifiers.

When designing an ensemble approach, the first thing to consider is the choice of individual feature selection algorithms to be included. Using more than one feature selection method will increase the computation time, therefore filter and (to a lesser extent) embedded methods are usually preferred. By contrast, wrappers are generally avoided. Researchers must also make sure that the included algorithms will output diverse feature sets because there is no point in building an ensemble of algorithms that all produce the same results. Several metrics can be used to measure diversity (e.g. pair-wise Q statistics (Kuncheva et al., 2002)).

It is also important to consider how to combine the partial outputs generated by each algorithm into one final output; this is known as the aggregation method. Several aggregation methods have been proposed, the simplest works by taking the union or intersection of the top-ranked outputs of the different algorithms. While taking the intersection seems logical (i.e., if all algorithms select a feature, it might be highly relevant), this approach results in a restrictive set of features and tends to produce worse results than selecting the union (Álvarez-Estévez et al., 2011). To overcome this, other popular aggregation methods assign each feature the mean or median position it has achieved among the outputs of all algorithms and use these positions to produce a final ranked feature subset. The final fusion rank of each feature can also be calculated as a weighted sum of the ranks assigned by the individual algorithms, where the weight of each algorithm is determined based on metrics such as the classification performance of the algorithm (Long et al., 2001). Alternatively, majority voting systems (Bolón-Canedo et al., 2012) (Figure 6B) can be used to determine the final class prediction. In majority voting systems, the different feature subsets generated by each algorithm are used to train and test a specific classifier. The final predicted output is the class that is predicted by the majority of the classifiers (see (Guan et al., 2014; Bolón-Canedo and Alonso-Betanzos, 2019) for reviews about ensemble methods).

Verma et al. (2018) proposed the use of a collective feature selection approach that combined the union of the top-ranked outputs of several feature selection methods (MDR, random forest, MultiSURFNTuRF). They applied this approach to identify SNPs associated with body mass index (BMI) and showed that the ensemble approach could detect epistatic effects that were otherwise missed using any single individual feature selection method.

Bolón-Canedo et al. (2012) applied an ensemble of five filter methods (CFS, Consistency-based, INTERACT, Information Gain and ReliefF) to ten high dimensional microarray datasets. The authors demonstrated that the ensemble of five filter methods achieved the lowest average error for every classifier tested (C4.5, IB1, and naïve Bayes) across all datasets, confirming the advantage of using the ensemble method over individual filters.

4 Exhaustive Searches for Higher-Order SNP-SNP Interactions

There are instances where scientists are mainly interested in inference, not prediction (e.g., the research interest lies in interpreting the biology of the selected SNPs). Recently, researchers within the GWAS field have recognized the importance of identifying significant SNP-SNP interactions, especially for complex diseases. The wrapper and embedded methods (e.g., decision tree-based algorithms) that can detect feature interactions (see Section 2.2–2.3) have some limitations: 1). Despite modifications that enable epistasis detection (Section 2.3), random forest-based algorithms are not exhaustive and are still prone to miss epistatic SNPs with low individual effects; 2) wrapper methods return a subset of features but do not identify which are relatively more important than others.

In theory, the most reliable (albeit naïve) way to detect relevant SNP-SNP interactions is by exhaustively testing each possible SNP combination and how it might relate to the phenotype class. Indeed, several exhaustive filter methods have been proposed (see (Cordell, 2009; Niel et al., 2015)). Some examples include, BOolean Operation-based Screening and Testing” (BOOST), FastEpistasis (Schüpbach et al., 2010), and Tree-based Epistasis Association Mapping (TEAM) (Zhang et al., 2010). However, these methods are restricted to testing and identifying pair-wise SNP interactions. Therefore, any epistatic effects of ≥3 orders will be missed. This contrasts with random forest (and many of its modifications), which despite its lower sensitivity (compared to exhaustive filters), can identify higher order interactions.

For higher-order interactions, exhaustive filter methods have been developed (e.g., Multifactor Dimensionality Reduction (MDR) (Ritchie et al., 2001) or the Combinatorial Partitioning Method (CPM) (Nelson et al., 2001)) and shown to be able to detect SNP-SNP interactions across ≥3 orders. However, due to the computational complexity of these analyses, these methods are effectively constrained to a maximum of several hundred features and they cannot be applied to genome-wide datasets (Lou et al., 2007). Goudey et al. (Goudey et al., 2015) estimated that evaluating all three-way interactions in a GWAS dataset of 1.1 Million SNPs could take up to 5 years even on a parallelized computing server with approximately 262,000 cores.

The application of exhaustive methods to genome-wide data can be achieved using an extended hybrid approach (i.e., applying a filter method as a first step, followed by an exhaustive search), or an integrative approach (incorporating external knowledge) that reduces the search space for the exhaustive methods (Pattin and Moore, 2008). For example, Greene et al. (Greene et al., 2009) recommended the use of SURF (a Relief-based filter algorithm) as a filter before using MDR to exhaustively search for relevant SNP interactions. Collins et al. (2013) used MDR to identify significant three-way SNP interactions that are associated with tuberculosis from a dataset of 19 SNPs mapped to candidate tuberculosis genes. Similarly, algorithms that incorporate two-stage strategies to detect high-order interactions have been developed (e.g., dynamic clustering for high-order genome-wide epistatic interactions detecting (DCHE) (Guo et al., 2014) and the epistasis detector based on the clustering of relatively frequent items (EDCF) (Xie et al., 2012)). DCHE and EDCF work by first identifying significant pair-wise interactions and using them as candidates to search for high-order interactions. More recently, swarm intelligence search algorithms have been proposed as an alternative way to look for candidate higher-order feature interactions, prior to application of an exhaustive search strategy. For example, Tuo et al. (2020) proposed the use of multipopulation harmony search algorithm to identify candidate k-order SNP interactions to reduce computation load before applying MDR to verify the interactions. Notably, the multi-stage algorithm (MP-HS-DHSI) that Tuo et al. developed is scalable to high-dimensional datasets (>100,000 SNPs), much less computationally demanding than purely exhaustive searches, and is sensitive enough to detect interactions where the individual SNPs have no individual effects (Tuo et al., 2020).

Despite being time demanding, the exhaustive search for pair-wise SNP interaction is possible (Marchini et al., 2005). However, exhaustive searches for higher-order interactions are not yet available. Researchers must resort to hybrid, integrative, or two-stage approaches to reduce the feature space prior to exhaustive search (Table 2). Several (non-exhaustive) embedded methods (e.g., approaches based on decision tree algorithms) have been proposed as viable options to identify SNP interactions and increase the best predictive power of the resulting information. However, the need for an efficient and scalable algorithm to detect SNP-SNP interactions remains, especially for higher-order interactions.

TABLE 2

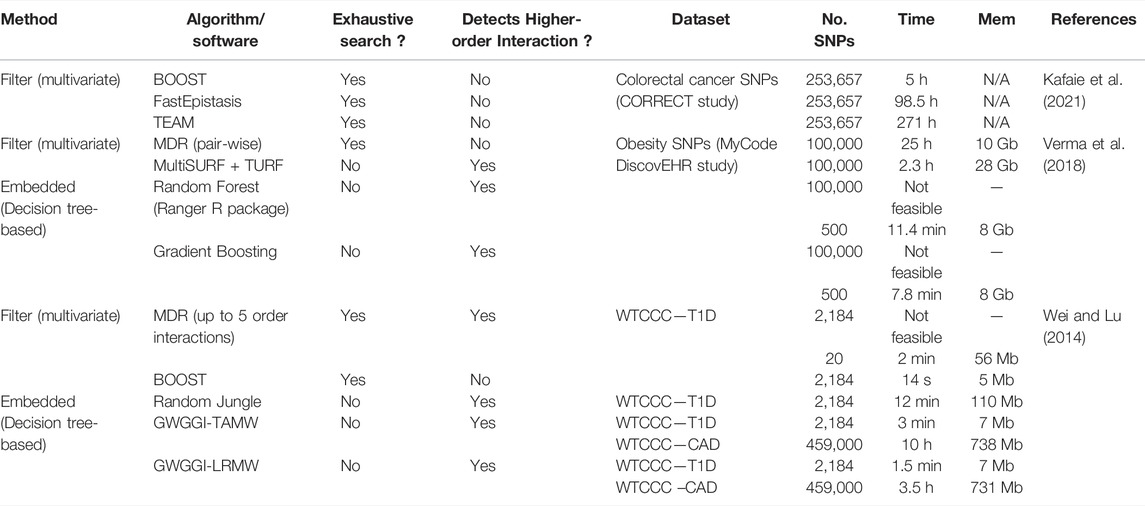
TABLE 2. Summary of algorithms reviewed to detect epistasis along with datasets applications, computational time, and memory requirements. Data are taken from three comparative studies, each of which are colour coded differently. N/A, not available.

5 Conclusion

Supervised ML algorithms can be applied to genome-wide SNP datasets. However, this is often not ideal because the curse of dimensionality leads to long training times and production of an overfitted predictive model. Therefore, the reduction of the total feature numbers to a more manageable level by selection of the most informative SNPs is essential before training the model.

Currently, no single feature selection method stands above the rest. Each method has its strengths and weaknesses (Table 1, Table 3, discussed in Section 2.4). Indeed, it is becoming rarer for researchers to depend on just a single feature selection method. Therefore, we contend that the use of a two-stage approach or hybrid approach should be considered “best practice.” In a typical hybrid approach, a filter method is used in the first stage to reduce the number of candidate SNPs to a more manageable level, so that more complex and computationally heavy wrapper, embedded, or exhaustive search methods can be applied. Depending on the available resources, the filter used should be multivariate and able to detect feature interactions. Alternatively, biological knowledge can be used as an a priori filter for SNP pre-selection. Multiple feature selection methods can also be combined in a parallel scheme (ensemble method). By exploiting strengths of the different methods, ensemble methods allow better accuracy and stability than relying on any single feature selection method.

TABLE 3

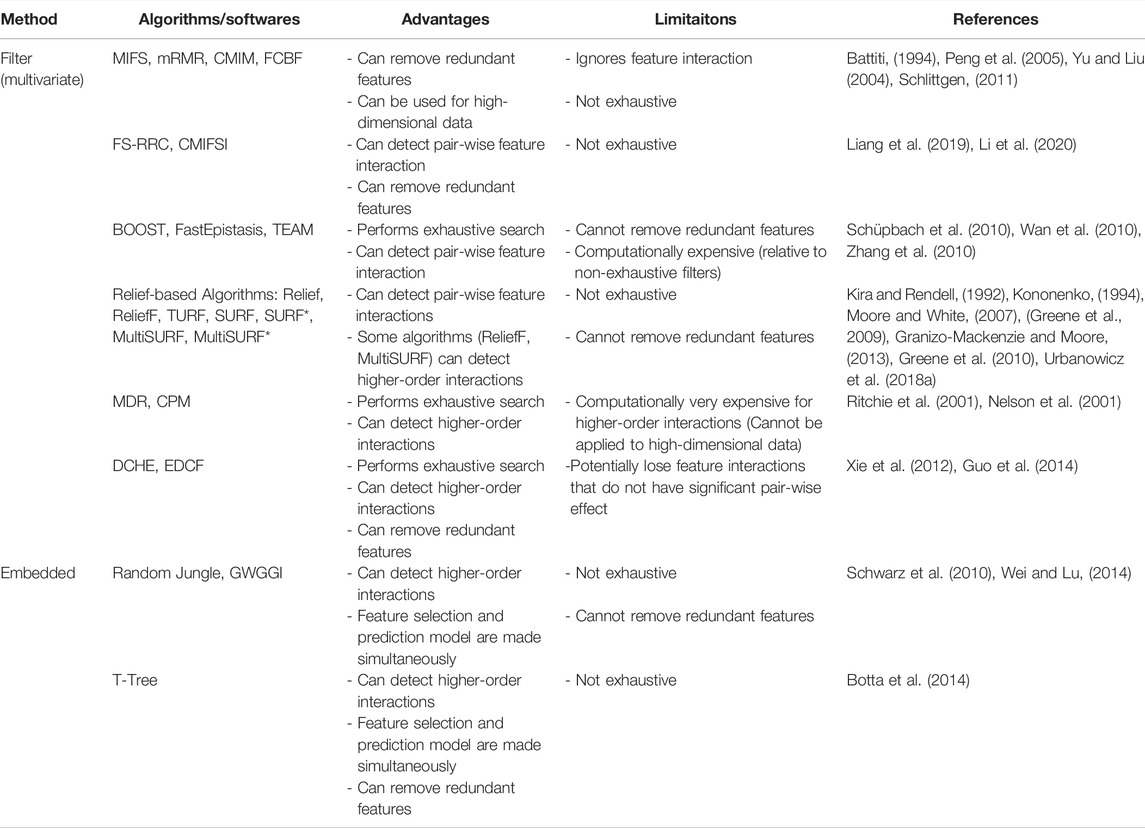
TABLE 3. Advantages, limitations, and references for the feature selection algorithms reviewed in this paper.

Author Contributions

NP conceived and wrote the review. TF, AK, and JOS conceived and commented on the review.

Funding

NP received a University of Auckland PhD Scholarship. TF and JOS were funded by a grant from the Dines Family Foundation.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abraham, G., and Inouye, M. (2015). Genomic Risk Prediction of Complex Human Disease and its Clinical Application. Curr. Opin. Genet. Dev. 33, 10–16. doi:10.1016/j.gde.2015.06.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Abramovich, F., Benjamini, Y., Donoho, D. L., and Johnstone, I. M. (2006). Adapting to Unknown Sparsity by Controlling the False Discovery Rate. Ann. Stat. 34, 584–653. doi:10.1214/009053606000000074

CrossRef Full Text | Google Scholar

Altshuler, D., Daly, M. J., and Lander, E. S. (2008). Genetic Mapping in Human Disease. Science 322, 881–888. doi:10.1126/science.1156409

PubMed Abstract | CrossRef Full Text | Google Scholar

Álvarez-Estévez, D., Sánchez-Maroño, N., Alonso-Betanzos, A., and Moret-Bonillo, V. (2011). Reducing Dimensionality in a Database of Sleep EEG Arousals. Expert Syst. Appl. 38, 7746–7754.

Google Scholar

Alzubi, R., Ramzan, N., Alzoubi, H., and Amira, A. (2017). A Hybrid Feature Selection Method for Complex Diseases SNPs. IEEE Access 6, 1292–1301. doi:10.1109/ACCESS.2017.2778268

CrossRef Full Text | Google Scholar

Aphinyanaphongs, Y., Fu, L. D., Li, Z., Peskin, E. R., Efstathiadis, E., Aliferis, C. F., et al. (2014). A Comprehensive Empirical Comparison of Modern Supervised Classification and Feature Selection Methods for Text Categorization. J. Assn Inf. Sci. Tec. 65, 1964–1987. doi:10.1002/asi.23110

CrossRef Full Text | Google Scholar

Ashley, E. A., Butte, A. J., Wheeler, M. T., Chen, R., Klein, T. E., Dewey, F. E., et al. (2010). Clinical Assessment Incorporating a Personal Genome. Lancet 375, 1525–1535. doi:10.1016/S0140-6736(10)60452-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Barrera-Gómez, J., Agier, L., Portengen, L., Chadeau-Hyam, M., Giorgis-Allemand, L., Siroux, V., et al. (2017). A Systematic Comparison of Statistical Methods to Detect Interactions in Exposome-Health Associations. Environ. Heal. A Glob. Access Sci. Source 16, 74. doi:10.1186/s12940-017-0277-6

CrossRef Full Text | Google Scholar

Battiti, R. (1994). Using Mutual Information for Selecting Features in Supervised Neural Net Learning. IEEE Trans. Neural Netw. 5, 537–550. doi:10.1109/72.298224

PubMed Abstract | CrossRef Full Text | Google Scholar

Benjamini, Y., and Hochberg, Y. (1995). Controlling the False Discovery Rate: A Practical and Powerful Approach to Multiple Testing. J. R. Stat. Soc. Ser. B Methodol. 57, 289–300. doi:10.1111/j.2517-6161.1995.tb02031.x

CrossRef Full Text | Google Scholar

Benjamini, Y., and Yekutieli, D. (2001). The Control of the False Discovery Rate in Multiple Testing under Dependency. Ann. Stat. 29, 1165–1188. doi:10.1214/aos/1013699998

CrossRef Full Text | Google Scholar

Bins, J., and Draper, B. A. (2001). Feature Selection from Huge Feature Sets. Proc. IEEE Int. Conf. Comput. Vis. 2, 159–165. doi:10.1109/ICCV.2001.937619

CrossRef Full Text | Google Scholar

Bolón-Canedo, V., and Alonso-Betanzos, A. (2019). Ensembles for Feature Selection: A Review and Future Trends. Inf. Fusion 52, 1–12. doi:10.1016/j.inffus.2018.11.008

CrossRef Full Text | Google Scholar

Bolón-Canedo, V., Sánchez-Maroño, N., and Alonso-Betanzos, A. (2013). A Review of Feature Selection Methods on Synthetic Data. Knowl. Inf. Syst. 34, 483–519.

Google Scholar

Bolón-Canedo, V., Sánchez-Maroño, N., and Alonso-Betanzos, A. (2012). An Ensemble of Filters and Classifiers for Microarray Data Classification. Pattern Recognit. 45, 531–539.

Google Scholar

Bolón-Canedo, V., Sánchez-Maroño, N., Alonso-Betanzos, A., Benítez, J. M., and Herrera, F. (2014). A Review of Microarray Datasets and Applied Feature Selection Methods. Inf. Sci. (Ny) 282, 111–135.

Google Scholar

Bommert, A., Sun, X., Bischl, B., Rahnenführer, J., and Lang, M. (2020). Benchmark for Filter Methods for Feature Selection in High-Dimensional Classification Data. Comput. Statistics Data Analysis 143, 106839. doi:10.1016/j.csda.2019.106839

CrossRef Full Text | Google Scholar

Botta, V., Louppe, G., Geurts, P., and Wehenkel, L. (2014). Exploiting SNP Correlations within Random Forest for Genome-wide Association Studies. PLoS One 9, e93379. doi:10.1371/journal.pone.0093379

PubMed Abstract | CrossRef Full Text | Google Scholar

Breiman, L. (2001). Random Forests. Mach. Learn. 45, 5–32. doi:10.1023/a:1010933404324

CrossRef Full Text | Google Scholar

Broekema, R. V., Bakker, O. B., and Jonkers, I. H. (2020). A Practical View of Fine-Mapping and Gene Prioritization in the Post-genome-wide Association Era. Open Biol. 10, 190221. doi:10.1098/rsob.190221

PubMed Abstract | CrossRef Full Text | Google Scholar

Brzyski, D., Peterson, C. B., Sobczyk, P., Candès, E. J., Bogdan, M., and Sabatti, C. (2017). Controlling the Rate of GWAS False Discoveries. Genetics 205, 61–75. doi:10.1534/genetics.116.193987

PubMed Abstract | CrossRef Full Text | Google Scholar

Bureau, A., Dupuis, J., Falls, K., Lunetta, K. L., Hayward, B., Keith, T. P., et al. (2005). Identifying SNPs Predictive of Phenotype Using Random Forests. Genet. Epidemiol. 28, 171–182. doi:10.1002/gepi.20041

PubMed Abstract | CrossRef Full Text | Google Scholar

Butler-Yeoman, T., Xue, B., and Zhang, M. (2015). “Particle Swarm Optimisation for Feature Selection: A Hybrid Filter-Wrapper Approach,” in 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25-28 May 2015, 2428–2435. doi:10.1109/CEC.2015.7257186

CrossRef Full Text | Google Scholar

Chandrashekar, G., and Sahin, F. (2014). A Survey on Feature Selection Methods. Comput. Electr. Eng. 40, 16–28. doi:10.1016/j.compeleceng.2013.11.024

CrossRef Full Text | Google Scholar

Collins, R. L., Hu, T., Wejse, C., Sirugo, G., Williams, S. M., and Moore, J. H. (2013). Multifactor Dimensionality Reduction Reveals a Three-Locus Epistatic Interaction Associated with Susceptibility to Pulmonary Tuberculosis. BioData Min. 6, 4–5. doi:10.1186/1756-0381-6-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Cordell, H. J. (2009). Detecting Gene-Gene Interactions that Underlie Human Diseases. Nat. Rev. Genet. 10, 392–404. doi:10.1038/nrg2579

PubMed Abstract | CrossRef Full Text | Google Scholar

Couronné, R., Probst, P., and Boulesteix, A.-L. (2018). Random Forest versus Logistic Regression: a Large-Scale Benchmark Experiment. BMC Bioinforma. 19, 270. doi:10.1186/s12859-018-2264-5

CrossRef Full Text | Google Scholar

Cueto-López, N., García-Ordás, M. T., Dávila-Batista, V., Moreno, V., Aragonés, N., and Alaiz-Rodríguez, R. (2019). A Comparative Study on Feature Selection for a Risk Prediction Model for Colorectal Cancer. Comput. Methods Programs Biomed. 177, 219–229. doi:10.1016/j.cmpb.2019.06.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Danasingh, A. A. G. S., Subramanian, A. a. B., and Epiphany, J. L. (2020). Identifying Redundant Features Using Unsupervised Learning for High-Dimensional Data. SN Appl. Sci. 2, 1367. doi:10.1007/s42452-020-3157-6

CrossRef Full Text | Google Scholar

D’Angelo, G. M., Rao, D., and Gu, C. C. (2009). Combining Least Absolute Shrinkage and Selection Operator (LASSO) and Principal-Components Analysis for Detection of Gene-Gene Interactions in Genome-wide Association Studies. BMC Proc. 3, S62. doi:10.1186/1753-6561-3-S7-S62

PubMed Abstract | CrossRef Full Text | Google Scholar

De, R., Bush, W. S., and Moore, J. H. (2014). Bioinformatics Challenges in Genome-wide Association Studies (Gwas). Methods Mol. Biol. 1168, 63–81. doi:10.1007/978-1-4939-0847-9_5

PubMed Abstract | CrossRef Full Text | Google Scholar

Donnelly, P. (2008). Progress and Challenges in Genome-wide Association Studies in Humans. Nature 456, 728–731. doi:10.1038/nature07631

PubMed Abstract | CrossRef Full Text | Google Scholar

Dudbridge, F., and Gusnanto, A. (2008). Estimation of Significance Thresholds for Genomewide Association Scans. Genet. Epidemiol. 32, 227–234. doi:10.1002/gepi.20297

PubMed Abstract | CrossRef Full Text | Google Scholar

Dunn, O. J. (1961). Multiple Comparisons Among Means. J. Am. Stat. Assoc. 56, 52–64. doi:10.1080/01621459.1961.10482090

CrossRef Full Text | Google Scholar

Farcomeni, A. (2008). A Review of Modern Multiple Hypothesis Testing, with Particular Attention to the False Discovery Proportion. Stat. Methods Med. Res. 17, 347–388. doi:10.1177/0962280206079046

PubMed Abstract | CrossRef Full Text | Google Scholar

Forman, G. (2003). An Extensive Empirical Study of Feature Selection Metrics for Text Classification. J. Mach. Learn. Res. 3, 1289–1305. doi:10.5555/944919.944974

CrossRef Full Text | Google Scholar

Forsati, R., Moayedikia, A., Jensen, R., Shamsfard, M., and Meybodi, M. R. (2014). Enriched Ant Colony Optimization and its Application in Feature Selection. Neurocomputing 142, 354–371. doi:10.1016/j.neucom.2014.03.053

CrossRef Full Text | Google Scholar

Ghosh, M., Guha, R., Sarkar, R., and Abraham, A. (2020). A Wrapper-Filter Feature Selection Technique Based on Ant Colony Optimization. Neural Comput. Applic 32, 7839–7857. doi:10.1007/s00521-019-04171-3

CrossRef Full Text | Google Scholar

Goudey, B., Abedini, M., Hopper, J. L., Inouye, M., Makalic, E., Schmidt, D. F., et al. (2015). High Performance Computing Enabling Exhaustive Analysis of Higher Order Single Nucleotide Polymorphism Interaction in Genome Wide Association Studies. Health Inf. Sci. Syst. 3, S3. doi:10.1186/2047-2501-3-S1-S3

PubMed Abstract | CrossRef Full Text | Google Scholar

Granizo-Mackenzie, D., and Moore, J. H. (2013). “Multiple Threshold Spatially Uniform ReliefF for the Genetic Analysis of Complex Human Diseases,” in Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) (Berlin, Heidelberg: Springer), 7833, 1–10. doi:10.1007/978-3-642-37189-9_1

CrossRef Full Text | Google Scholar

Greene, C. S., Penrod, N. M., Kiralis, J., and Moore, J. H. (2009). Spatially Uniform ReliefF (SURF) for Computationally-Efficient Filtering of Gene-Gene Interactions. BioData Min. 2, 5–9. doi:10.1186/1756-0381-2-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Greene, C. S., Himmelstein, D. S., Kiralis, J., and Moore, J. H. (2010). “The Informative Extremes: Using Both Nearest and Farthest Individuals Can Improve Relief Algorithms in the Domain of Human Genetics,” in Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) (Berlin, Heidelberg: Springer), 6023, 182–193. doi:10.1007/978-3-642-12211-8_16

CrossRef Full Text | Google Scholar

Guan, D., Yuan, W., Lee, Y. K., Najeebullah, K., and Rasel, M. K. (2014). “A Review of Ensemble Learning Based Feature Selection,” in IETE Technical Review (India): Institution of Electronics and Telecommunication Engineers), 31, 190–198. doi:10.1080/02564602.2014.906859

CrossRef Full Text | Google Scholar

Guo, X., Meng, Y., Yu, N., and Pan, Y. (2014). Cloud Computing for Detecting High-Order Genome-wide Epistatic Interaction via Dynamic Clustering. BMC Bioinforma. 15, 102–116. doi:10.1186/1471-2105-15-102

PubMed Abstract | CrossRef Full Text | Google Scholar

Guo, Y., Chung, F.-L., Li, G., and Zhang, L. (2019). Multi-Label Bioinformatics Data Classification with Ensemble Embedded Feature Selection. IEEE Access 7, 103863–103875. doi:10.1109/access.2019.2931035

CrossRef Full Text | Google Scholar

Guyon, I., and Elisseeff, A. (2003). An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 3, 1157–1182. doi:10.5555/944919.944968

CrossRef Full Text | Google Scholar

Guyon, I., Gunn, S., Nikravesh, M., and Zadeh, L. (2008). Feature Extraction: Foundations and Applications, 207. Berlin: Springer.

Google Scholar

Hall, M. (2000). “Correlation-based Feature Selection of Discrete and Numeric Class Machine Learning,” in Proceedings of the Seventeenth International Conference on Machine Learning (ICML 2000), Stanford University, Stanford, CA, USA, June 29 - July 2, 2000.

Google Scholar

Han, B., Chen, X. W., Talebizadeh, Z., and Xu, H. (2012). Genetic Studies of Complex Human Diseases: Characterizing SNP-Disease Associations Using Bayesian Networks. BMC Syst. Biol. 6 Suppl 3, S14. doi:10.1186/1752-0509-6-S3-S14

PubMed Abstract | CrossRef Full Text | Google Scholar

Hayes-Roth, F. (1975). Review of "Adaptation in Natural and Artificial Systems by John H. Holland", the U. Of Michigan Press, 1975. SIGART Bull. 53, 15. doi:10.1145/1216504.1216510

CrossRef Full Text | Google Scholar

Herold, C., Steffens, M., Brockschmidt, F. F., Baur, M. P., and Becker, T. (2009). INTERSNP: Genome-wide Interaction Analysis Guided by A Priori Information. Bioinformatics 25, 3275–3281. doi:10.1093/bioinformatics/btp596

PubMed Abstract | CrossRef Full Text | Google Scholar

Hindorff, L. A., Sethupathy, P., Junkins, H. A., Ramos, E. M., Mehta, J. P., Collins, F. S., et al. (2009). Potential Etiologic and Functional Implications of Genome-wide Association Loci for Human Diseases and Traits. Proc. Natl. Acad. Sci. U. S. A. 106, 9362–9367. doi:10.1073/pnas.0903103106

PubMed Abstract | CrossRef Full Text | Google Scholar

Ho, D. S. W., Schierding, W., Wake, M., Saffery, R., and O'Sullivan, J. (2019). Machine Learning SNP Based Prediction for Precision Medicine. Front. Genet. 10, 267. doi:10.3389/fgene.2019.00267

PubMed Abstract | CrossRef Full Text | Google Scholar

Hoque, N., Singh, M., and Bhattacharyya, D. K. (2017). EFS-MI: an Ensemble Feature Selection Method for Classification. Complex Intell. Syst. 4, 105–118. doi:10.1007/s40747-017-0060-x

CrossRef Full Text | Google Scholar

Inza, I., Larrañaga, P., Blanco, R., and Cerrolaza, A. J. (2004). Filter versus Wrapper Gene Selection Approaches in DNA Microarray Domains. Artif. Intell. Med. 31, 91–103. doi:10.1016/j.artmed.2004.01.007

PubMed Abstract | CrossRef Full Text | Google Scholar

John, G. H., Kohavi, R., and Pfleger, K. (1994). “Irrelevant Features and the Subset Selection Problem,” in Machine Learning Proceedings 1994 (Burlington, MA: Morgan Kaufmann Publishers), 121–129, 121–129. doi:10.1016/b978-1-55860-335-6.50023-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Kafaie, S., Xu, L., and Hu, T. (2021). Statistical Methods with Exhaustive Search in the Identification of Gene-Gene Interactions for Colorectal Cancer. Genet. Epidemiol. 45, 222–234. doi:10.1002/gepi.22372

PubMed Abstract | CrossRef Full Text | Google Scholar

Kira, K., and Rendell, L. A. (1992). “Feature Selection Problem: Traditional Methods and a New Algorithm,” in Proceedings Tenth National Conference on Artificial Intelligence 2, 129–134.

Google Scholar

Kittler, J. (1978). “Feature Set Search Alborithms,” in Pattern Recognition and Signal Processing. Dordrecht, Netherlands: Springer Dordrecht, 41–60. doi:10.1007/978-94-009-9941-1_3

CrossRef Full Text | Google Scholar

Kohavi, R., and John, G. H. (1997). Wrappers for Feature Subset Selection. Artif. Intell. 97, 273–324. doi:10.1016/s0004-3702(97)00043-x

CrossRef Full Text | Google Scholar

Koller, D., and Sahami, M. (1996). “Toward Optimal Feature Selection,” in International Conference on Machine Learning. Stanford, CA: Stanford InfoLab, 284–292.

Google Scholar

König, I. R., Auerbach, J., Gola, D., Held, E., Holzinger, E. R., Legault, M. A., et al. (2016). Machine Learning and Data Mining in Complex Genomic Data-Aa Review on the Lessons Learned in Genetic Analysis Workshop 19. BMC Genet. 17, 1. BioMed Central. doi:10.1186/s12863-015-0315-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Kononenko, I. (1994). “Estimating Attributes: Analysis and Extensions of RELIEF,” in Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) (Berlin, Heidelberg: Springer), 784, 171–182. doi:10.1007/3-540-57868-4_5710.1007/3-540-57868-4_57

CrossRef Full Text | Google Scholar

Kotzyba‐Hibert, F., Kapfer, I., and Goeldner, M. (1995). Recent Trends in Photoaffinity Labeling. Angewandte Chemie Int. Ed. Engl. 34, 1296–1312.

Google Scholar

Kruppa, J., Ziegler, A., and König, I. R. (2012). Risk Estimation and Risk Prediction Using Machine-Learning Methods. Hum. Genet. 131, 1639–1654. doi:10.1007/s00439-012-1194-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Kubus, M. (2019). The Problem of Redundant Variables in Random Forests. Folia Oeconomica 6, 7–16. doi:10.18778/0208-6018.339.01

CrossRef Full Text | Google Scholar

Kuncheva, L. I., Skurichina, M., and Duin, R. P. W. (2002). An Experimental Study on Diversity for Bagging and Boosting with Linear Classifiers. Inf. Fusion 3, 245–258. doi:10.1016/s1566-2535(02)00093-3

CrossRef Full Text | Google Scholar

Li, C., Luo, X., Qi, Y., Gao, Z., and Lin, X. (2020). A New Feature Selection Algorithm Based on Relevance, Redundancy and Complementarity. Comput. Biol. Med. 119, 103667. Elsevier. doi:10.1016/j.compbiomed.2020.103667

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, L., Umbach, D. M., Terry, P., and Taylor, J. A. (2004). Application of the GA/KNN Method to SELDI Proteomics Data. Bioinformatics 20, 1638–1640. doi:10.1093/bioinformatics/bth098

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, J., Hou, L., Luan, Z., and Huang, W. (2019). Feature Selection with Conditional Mutual Information Considering Feature Interaction. Symmetry 11, 858. doi:10.3390/sym11070858

CrossRef Full Text | Google Scholar

Long, A. D., Mangalam, H. J., Chan, B. Y., Tolleri, L., Hatfield, G. W., and Baldi, P. (2001). Improved Statistical Inference from DNA Microarray Data Using Analysis of Variance and A Bayesian Statistical Framework. Analysis of Global Gene Expression in Escherichia coli K12. J. Biol. Chem. 276, 19937–19944. doi:10.1074/jbc.M010192200

PubMed Abstract | CrossRef Full Text | Google Scholar

López, B., Torrent-Fontbona, F., Viñas, R., and Fernández-Real, J. M. (2018). Single Nucleotide Polymorphism Relevance Learning with Random Forests for Type 2 Diabetes Risk Prediction. Artif. Intell. Med. 85, 43–49. doi:10.1016/j.artmed.2017.09.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Lou, X. Y., Chen, G. B., Yan, L., Ma, J. Z., Zhu, J., Elston, R. C., et al. (2007). A Generalized Combinatorial Approach for Detecting Gene-By-Gene and Gene-By-Environment Interactions with Application to Nicotine Dependence. Am. J. Hum. Genet. 80 (6), 1125–1137. Elsevier. doi:10.1086/518312

PubMed Abstract | CrossRef Full Text | Google Scholar

Louppe, G., Wehenkel, L., Sutera, A., and Geurts, P. (2013). “Understanding Variable Importances in Forests of Randomized Trees,” in Advances in Neural Information Processing Systems 26.

Google Scholar

Lunetta, K. L., Hayward, L. B., Segal, J., and van Eerdewegh, P. (2004). Screening Large-Scale Association Study Data: Exploiting Interactions Using Random Forests. BMC Genet. 5, 32. doi:10.1186/1471-2156-5-32

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, L., Keinan, A., and Clark, A. G. (2015). Biological Knowledge-Driven Analysis of Epistasis in Human GWAS with Application to Lipid Traits. Methods Mol. Biol. 1253, 35–45. doi:10.1007/978-1-4939-2155-3_3

PubMed Abstract | CrossRef Full Text | Google Scholar

Maher, B. (2008). Personal Genomes: The Case of the Missing Heritability. Nature 456, 18–21. doi:10.1038/456018a

PubMed Abstract | CrossRef Full Text | Google Scholar

Makowsky, R., Pajewski, N. M., Klimentidis, Y. C., Vazquez, A. I., Duarte, C. W., Allison, D. B., et al. (2011). Beyond Missing Heritability: Prediction of Complex Traits. PLoS Genet. 7, e1002051. doi:10.1371/journal.pgen.1002051

PubMed Abstract | CrossRef Full Text | Google Scholar

Manolio, T. A. (2013). Bringing Genome-wide Association Findings into Clinical Use. Nat. Rev. Genet. 14, 549–558. doi:10.1038/nrg3523

PubMed Abstract | CrossRef Full Text | Google Scholar

Mao, Y., and Yang, Y. (2019). A Wrapper Feature Subset Selection Method Based on Randomized Search and Multilayer Structure. Biomed. Res. Int. 2019, 9864213. doi:10.1155/2019/9864213

PubMed Abstract | CrossRef Full Text | Google Scholar

Marchini, J., Donnelly, P., and Cardon, L. R. (2005). Genome-wide Strategies for Detecting Multiple Loci that Influence Complex Diseases. Nat. Genet. 37, 413–417. doi:10.1038/ng1537

PubMed Abstract | CrossRef Full Text | Google Scholar

Mohri, M., Rostamizadeh, A., and Talwalkar, A. (2018). Foundations of Machine Learning. Cambridge, MA: MIT Press.

Google Scholar

Moore, J. H., and White, B. C. (2007). “Tuning ReliefF for Genome-wide Genetic Analysis,” in Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) (Berlin, Heidelberg: Springer), 4447, 166–175.

Google Scholar

Nelson, M. R., Kardia, S. L., Ferrell, R. E., and Sing, C. F. (2001). A Combinatorial Partitioning Method to Identify Multilocus Genotypic Partitions that Predict Quantitative Trait Variation. Genome Res. 11, 458–470. doi:10.1101/gr.172901

PubMed Abstract | CrossRef Full Text | Google Scholar

Newton, J. L., Harney, S. M., Wordsworth, B. P., and Brown, M. A. (2004). A Review of the MHC Genetics of Rheumatoid Arthritis. Genes. Immun. 5, 151–157. doi:10.1038/sj.gene.6364045

PubMed Abstract | CrossRef Full Text | Google Scholar

Niel, C., Sinoquet, C., Dina, C., and Rocheleau, G. (2015). A Survey about Methods Dedicated to Epistasis Detection. Front. Genet. 6, 285. doi:10.3389/fgene.2015.00285

PubMed Abstract | CrossRef Full Text | Google Scholar

Okser, S., Pahikkala, T., Airola, A., Salakoski, T., Ripatti, S., and Aittokallio, T. (2014). Regularized Machine Learning in the Genetic Prediction of Complex Traits. PLoS Genet. 10, e1004754. doi:10.1371/journal.pgen.1004754

PubMed Abstract | CrossRef Full Text | Google Scholar

Okser, S., Pahikkala, T., and Aittokallio, T. (2013). Genetic Variants and Their Interactions in Disease Risk Prediction - Machine Learning and Network Perspectives. BioData Min. 6, 5. doi:10.1186/1756-0381-6-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Onengut-Gumuscu, S., Chen, W. M., Burren, O., Cooper, N. J., Quinlan, A. R., Mychaleckyj, J. C., et al. (2015). Fine Mapping of Type 1 Diabetes Susceptibility Loci and Evidence for Colocalization of Causal Variants with Lymphoid Gene Enhancers. Nat. Genet. 47, 381–386. doi:10.1038/ng.3245

PubMed Abstract | CrossRef Full Text | Google Scholar

Ooka, T., Johno, H., Nakamoto, K., Yoda, Y., Yokomichi, H., and Yamagata, Z. (2021). Random Forest Approach for Determining Risk Prediction and Predictive Factors of Type 2 Diabetes: Large-Scale Health Check-Up Data in Japan. Bmjnph 4, 140–148. doi:10.1136/bmjnph-2020-000200

CrossRef Full Text | Google Scholar

Pal, M., and Foody, G. M. (2010). Feature Selection for Classification of Hyperspectral Data by SVM. IEEE Trans. Geosci. Remote Sens. 48, 2297–2307. doi:10.1109/tgrs.2009.2039484

CrossRef Full Text | Google Scholar

Panagiotou, O. A., and Ioannidis, J. P. (2012). What Should the Genome-wide Significance Threshold Be? Empirical Replication of Borderline Genetic Associations. Int. J. Epidemiol. 41, 273–286. doi:10.1093/ije/dyr178

PubMed Abstract | CrossRef Full Text | Google Scholar

Pattin, K. A., and Moore, J. H. (2008). Exploiting the Proteome to Improve the Genome-wide Genetic Analysis of Epistasis in Common Human Diseases. Hum. Genet. 124, 19–29. doi:10.1007/s00439-008-0522-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Peng, H., Long, F., and Ding, C. (2005). Feature Selection Based on Mutual Information: Criteria of Max-Dependency, Max-Relevance, and Min-Redundancy. IEEE Trans. Pattern Anal. Mach. Intell. 27, 1226–1238. doi:10.1109/TPAMI.2005.159

PubMed Abstract | CrossRef Full Text | Google Scholar

Pes, B. (2020). Ensemble Feature Selection for High-Dimensional Data: a Stability Analysis across Multiple Domains. Neural Comput. Applic 32, 5951–5973. doi:10.1007/s00521-019-04082-3

CrossRef Full Text | Google Scholar

Remeseiro, B., and Bolon-Canedo, V. (2019). A Review of Feature Selection Methods in Medical Applications. Comput. Biol. Med. 112, 103375. doi:10.1016/j.compbiomed.2019.103375

PubMed Abstract | CrossRef Full Text | Google Scholar

Ritchie, M. D., Hahn, L. W., Roodi, N., Bailey, L. R., Dupont, W. D., Parl, F. F., et al. (2001). Multifactor-dimensionality Reduction Reveals High-Order Interactions Among Estrogen-Metabolism Genes in Sporadic Breast Cancer. Am. J. Hum. Genet. 69, 138–147. doi:10.1086/321276

PubMed Abstract | CrossRef Full Text | Google Scholar

Romagnoni, A., Jégou, S., Van Steen, K., Wainrib, G., and Hugot, J. P. (2019). Comparative Performances of Machine Learning Methods for Classifying Crohn Disease Patients Using Genome-wide Genotyping Data. Sci. Rep. 9, 10351. doi:10.1038/s41598-019-46649-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Saeys, Y., Inza, I., and Larrañaga, P. (2007). A Review of Feature Selection Techniques in Bioinformatics. Bioinformatics 23, 2507–2517. doi:10.1093/bioinformatics/btm344

PubMed Abstract | CrossRef Full Text | Google Scholar

Saeys, Y., Abeel, T., and Van De Peer, Y. (2008). “Robust Feature Selection Using Ensemble Feature Selection Techniques,” in Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) (Berlin, Heidelberg: Springer), 5212, 313–325. doi:10.1007/978-3-540-87481-2_21

CrossRef Full Text | Google Scholar

Schlittgen, R. (2011). A Weighted Least-Squares Approach to Clusterwise Regression. AStA Adv. Stat. Anal. 95, 205–217. doi:10.1007/s10182-011-0155-4

CrossRef Full Text | Google Scholar

Schüpbach, T., Xenarios, I., Bergmann, S., and Kapur, K. (2010). FastEpistasis: a High Performance Computing Solution for Quantitative Trait Epistasis. Bioinformatics 26, 1468–1469. doi:10.1093/bioinformatics/btq147

PubMed Abstract | CrossRef Full Text | Google Scholar

Schwarz, D. F., König, I. R., and Ziegler, A. (2010). On Safari to Random Jungle: a Fast Implementation of Random Forests for High-Dimensional Data. Bioinformatics 26, 1752–1758. doi:10.1093/bioinformatics/btq257

PubMed Abstract | CrossRef Full Text | Google Scholar

Seijo-Pardo, B., Bolón-Canedo, V., Porto-Díaz, I., and Alonso-Betanzos, A. (2015). “Ensemble Feature Selection for Rankings of Features,” in Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) (Cham: Springer-Verlag), 9095, 29–42. doi:10.1007/978-3-319-19222-2_3

CrossRef Full Text | Google Scholar

Signorino, C. S., and Kirchner, A. (2018). Using LASSO to Model Interactions and Nonlinearities in Survey Data. Surv. Pract. 11, 1–10. doi:10.29115/sp-2018-0005

CrossRef Full Text | Google Scholar

Skalak, D. B. (1994). “Prototype and Feature Selection by Sampling and Random Mutation Hill Climbing Algorithms,” in Machine Learning Proceedings 1994. Burlington, MA: Morgan Kauffmann, 293–301. doi:10.1016/b978-1-55860-335-6.50043-x

CrossRef Full Text | Google Scholar

Spain, S. L., and Barrett, J. C. (2015). Strategies for Fine-Mapping Complex Traits. Hum. Mol. Genet. 24, R111–R119. doi:10.1093/hmg/ddv260

PubMed Abstract | CrossRef Full Text | Google Scholar

Spiegel, A. M., and Hawkins, M. (2012). 'Personalized Medicine' to Identify Genetic Risks for Type 2 Diabetes and Focus Prevention: Can it Fulfill its Promise? Health Aff. (Millwood) 31, 43–49. doi:10.1377/hlthaff.2011.1054

PubMed Abstract | CrossRef Full Text | Google Scholar

Szymczak, S., Biernacka, J. M., Cordell, H. J., González-Recio, O., König, I. R., Zhang, H., et al. (2009). Machine Learning in Genome-wide Association Studies. Genet. Epidemiol. 33 Suppl 1, S51–S57. doi:10.1002/gepi.20473

PubMed Abstract | CrossRef Full Text | Google Scholar

Tsai, C.-F., and Sung, Y.-T. (2020). Ensemble Feature Selection in High Dimension, Low Sample Size Datasets: Parallel and Serial Combination Approaches. Knowledge-Based Syst. 203, 106097. doi:10.1016/j.knosys.2020.106097

CrossRef Full Text | Google Scholar

Tuo, S., Liu, H., and Chen, H. (2020). Multipopulation Harmony Search Algorithm for the Detection of High-Order SNP Interactions. Bioinformatics 36, 4389–4398. doi:10.1093/bioinformatics/btaa215

PubMed Abstract | CrossRef Full Text | Google Scholar

Uddin, S., Khan, A., Hossain, M. E., and Moni, M. A. (2019). Comparing Different Supervised Machine Learning Algorithms for Disease Prediction. BMC Med. Inf. Decis. Mak. 19, 281. doi:10.1186/s12911-019-1004-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Urbanowicz, R. J., Meeker, M., La Cava, W., Olson, R. S., and Moore, J. H. (2018b). Relief-based Feature Selection: Introduction and Review. J. Biomed. Inf. 85, 189–203. doi:10.1016/j.jbi.2018.07.014

PubMed Abstract | CrossRef Full Text | Google Scholar

Urbanowicz, R. J., Olson, R. S., Schmitt, P., Meeker, M., and Moore, J. H. (2018a). Benchmarking Relief-Based Feature Selection Methods for Bioinformatics Data Mining. J. Biomed. Inf. 85, 168–188. doi:10.1016/j.jbi.2018.07.015

CrossRef Full Text | Google Scholar

Verma, S. S., Lucas, A., Zhang, X., Veturi, Y., Dudek, S., Li, B., et al. (2018). Collective Feature Selection to Identify Crucial Epistatic Variants. BioData Min. 11, 5. doi:10.1186/s13040-018-0168-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Visscher, P. M., Wray, N. R., Zhang, Q., Sklar, P., McCarthy, M. I., Brown, M. A., et al. (2017). 10 Years of GWAS Discovery: Biology, Function, and Translation. Am. J. Hum. Genet. 101, 5–22. doi:10.1016/j.ajhg.2017.06.005

PubMed Abstract | CrossRef Full Text | Google Scholar

Wah, Y. B., Ibrahim, N., Hamid, H. A., Abdul-Rahman, S., and Fong, S. (2018). Feature Selection Methods: Case of Filter and Wrapper Approaches for Maximising Classification Accuracy. Pertanika J. Sci. Technol. 26, 329–340.

Google Scholar

Wan, X., Yang, C., Yang, Q., Xue, H., Fan, X., Tang, N. L. S., et al. (2010). BOOST: A Fast Approach to Detecting Gene-Gene Interactions in Genome-wide Case-Control Studies. Am. J. Hum. Genet. 87 (3), 325–340. Elsevier. doi:10.1016/j.ajhg.2010.07.021

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Xu, J., Zhao, C., Peng, Y., and Wang, H. (2019). An Ensemble Feature Selection Method for High-Dimensional Data Based on Sort Aggregation. Syst. Sci. Control Eng. 7, 32–39. doi:10.1080/21642583.2019.1620658

CrossRef Full Text | Google Scholar

Wei, C., and Lu, Q. (2014). GWGGI: Software for Genome-wide Gene-Gene Interaction Analysis. BMC Genet. 15, 101. doi:10.1186/s12863-014-0101-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Wei, Z., Wang, W., Bradfield, J., Li, J., Cardinale, C., Frackelton, E., et al. (2013). Large Sample Size, Wide Variant Spectrum, and Advanced Machine-Learning Technique Boost Risk Prediction for Inflammatory Bowel Disease. Am. J. Hum. Genet. 92, 1008–1012. doi:10.1016/j.ajhg.2013.05.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Winham, S. J., Colby, C. L., Freimuth, R. R., Wang, X., de Andrade, M., Huebner, M., et al. (2012). SNP Interaction Detection with Random Forests in High-Dimensional Genetic Data. BMC Bioinforma. 13, 164. doi:10.1186/1471-2105-13-164

PubMed Abstract | CrossRef Full Text | Google Scholar

Wolpert, D. H., and Macready, W. G. (1997). No Free Lunch Theorems for Optimization. IEEE Trans. Evol. Comput. 1, 67–82. doi:10.1109/4235.585893

CrossRef Full Text | Google Scholar

Wray, N. R., Goddard, M. E., and Visscher, P. M. (2007). Prediction of Individual Genetic Risk to Disease from Genome-wide Association Studies. Genome Res. 17, 1520–1528. doi:10.1101/gr.6665407

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, M., Li, J., and Jiang, T. (2012). Detecting Genome-wide Epistases Based on the Clustering of Relatively Frequent Items. Bioinformatics 28, 5–12. doi:10.1093/bioinformatics/btr603

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiong, M., Fang, X., and Zhao, J. (2001). Biomarker Identification by Feature Wrappers. Genome Res. 11, 1878–1887. doi:10.1101/gr.190001

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, C., Tachmazidou, I., Walter, K., Ciampi, A., Zeggini, E., and Greenwood, C. M. T. (2014). Estimating Genome‐Wide Significance for Whole‐Genome Sequencing Studies. Genet. Epidemiol. 38, 281–290. Wiley Online Libr. doi:10.1002/gepi.21797

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, F., and Mao, K. Z. (2011). Robust Feature Selection for Microarray Data Based on Multicriterion Fusion. IEEE/ACM Trans. Comput. Biol. Bioinform 8, 1080–1092. doi:10.1109/TCBB.2010.103

PubMed Abstract | CrossRef Full Text | Google Scholar

Yang, J., and Honavar, V. (1998). Feature Subset Selection Using a Genetic Algorithm. IEEE Intell. Syst. 13, 44–49. doi:10.1109/5254.671091

CrossRef Full Text | Google Scholar

Yoshida, M., and Koike, A. (2011). SNPInterForest: a New Method for Detecting Epistatic Interactions. BMC Bioinforma. 12, 469. doi:10.1186/1471-2105-12-469

PubMed Abstract | CrossRef Full Text | Google Scholar

Yu, L., and Liu, H. (2004). Efficient Feature Selection via Analysis of Relevance and Redundancy. J. Mach. Learn. Res. 5, 1205–1224. doi:10.5555/1005332.1044700

CrossRef Full Text | Google Scholar

Zhang, X., Huang, S., Zou, F., and Wang, W. (2010). TEAM: Efficient Two-Locus Epistasis Tests in Human Genome-wide Association Study. Bioinformatics 26, i217–27. doi:10.1093/bioinformatics/btq186

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, Y., Li, S., Wang, T., and Zhang, Z. (2013). Divergence-based Feature Selection for Separate Classes. Neurocomputing 101, 32–42. doi:10.1016/j.neucom.2012.06.036

CrossRef Full Text | Google Scholar