- Department of Computer Science, Universidad Rey Juan Carlos, Madrid, Spain
This work describes a computational methodology for the design of braces for adolescent idiopathic scoliosis. The proposed methodology relies on a personalized simulation model of the patient’s trunk, and automatically searches for the brace geometry that optimizes the trade-off between clinical improvement and patient comfort. To do this, we introduce a formulation of differentiable biomechanics of the patient’s trunk, the brace, and their interaction. We design a simulation model that is differentiable with respect to both the deformation state and the brace design parameters, and we show how this differentiable model is used for the efficient update of brace design parameters within a numerical optimization algorithm. To evaluate the proposed methodology, we have obtained trunk models with personalized geometry for five patients of adolescent idiopathic scoliosis, and we have designed Boston-type braces. In a simulation setting, the designed braces improve clinical metrics by 45% on average, under acceptable comfort conditions. In the future, the methodology can be extended beyond synthetic validation, and tested with physical braces on the actual patients.
1 Introduction
Scoliosis is a clinical condition marked mostly by a lateral curvature of the spine. Moderate cases of adolescent idiopathic scoliosis (AIS) are typically treated through conservative methods (Karimi and Rabczuk, 2018), which try to naturally correct scoliosis during the growth of the patients. A common conservative treatment is to use orthotic brace structures (Negrini et al., 2022) that transmit forces to the spine and try to correct the existing deformities (Kuroki, 2018; Kaelin, 2020). Such scoliosis braces are designed in a variety of shapes and procedures, but most design methods rely to date on physical experimentation and prototyping. Even though computational strategies have been studied to some extent (Cobetto et al., 2016; Vergari et al., 2016), they are typically limited to evaluating design iterations. The design decisions on the braces are not made by intelligent computer programs; they are instead made by clinical experts, using information from simulation models.
In our work, we try to answer if brace design can be further automated, devising an intelligent computer program that can automatically explore the design space of a brace, and select optimal design parameters. The development of such a brace design solution faces two important research challenges. First, it requires a personalized biomechanical model of brace-trunk interaction. Using this biomechanical model, it is possible to predict trunk deformations as a function of changes to the brace design. This simulation is key for computer evaluation of design metrics, such as a clinical objective and a comfort objective. Second, the biomechanical model must be embedded within a numerical optimization solver, which will automatically search for brace design parameters. State-of-the-art optimization methods use gradients to efficiently and robustly search for optimal parameters; therefore, the biomechanics formulation must allow for the computation of gradients with respect to design parameters.
In this work, we propose a differentiable biomechanics model for the optimization of scoliosis brace designs. By formulating biomechanics simulation as a differentiable function, we can embed the simulation model within advanced optimization procedures, and automatically achieve effective brace designs, with flexible definition of design goal metrics.
The first major component of our approach, presented in Section 3, is a predictive model of the passive biomechanics of the trunk. We put the focus on modeling biomechanics elements that affect the deformation of the thoracolumbar spine under forces produced by a scoliosis brace. To this end, we largely rely on previous work for the development of the trunk model (Koutras et al., 2021) and personalization of its geometry (Koutras et al., 2022) (mechanical personalization is left as future work).
The second major component of our approach, presented in Section 4, is an optimization algorithm that relies on differentiable biomechanics. We show that differentiable biomechanics can be efficiently formulated by implicitly linearizing the equilibrium constraints of a biomechanics simulation engine, and we provide insight into the design of all elements of the biomechanics model to ensure efficient and robust differentiation.
We have tested our personalized brace design approach on a cohort of 5 (potential) patients of AIS. For each patient, we personalize the trunk model, initialize a Boston brace design (Périé et al., 2003), and then optimize this design using the differentiable biomechanics formulation. The results of our experiments show that a fully automated algorithm manages to reduce Cobb angle by an average of 7.8°, while keeping brace forces within a comfortable range of 220 N. To date, we have limited our experiments to a synthetic study, considering only simulated brace-trunk interactions. Our work demonstrates the feasibility of the approach, but real-world application requires further iterating other aspects of the brace design, as well as validating the clinical and comfort objectives before letting actual patients wear the resulting braces.
2 Related work
2.1 Trunk modeling and parameter estimation
Designing a personalized biomechanical model entails two tasks: fitting the morphology and connections of anatomical elements to those of the patient, and parameterizing the mechanical models to match the response of the patient’s body. Biomechanical modeling of the spine has received a lot of attention, with popular approaches largely divided into two categories. One category follows the Finite Element Method (FEM, please see (Wang et al., 2014) for a survey of methods); the other category uses a simpler but more efficient solution based on multi-body models.
In terms of FEM models, many approaches have been developed for the lumbar (Xu et al., 2017; Finley et al., 2018; Dong et al., 2020), thoracic (Aroeira et al., 2017; Aroeira et al., 2018) or the cervical spine (Lasswell et al., 2017). Furthermore, Dicko et al., (2015) developed a hybrid lumbar spine model containing rigid bodies, FEM and contact mechanics, while Clin et al., (2011) developed a novel method to include gravitational forces in an FE model. While these methods are potentially accurate, they require careful estimation of model parameters for personalized design applications.
FE models of the trunk have been coupled to brace models and patient geometry for personalized brace design in the context of AIS (Gignac et al., 2000; Liao et al., 2007; Nie et al., 2009). Some studies include the evaluation of the effectiveness of these techniques on large cohorts of patients (Cobetto et al., 2017; Vergari et al., 2020; Guy et al., 2021).
In terms of multi-body models, de Zee et al., (2007) made a generic detailed rigid-body model of the lumbar spine. Bayoglu et al., (2019) developed a multi-body muscoloskeletal model of the human spine in order to study the spinal loads. Raabe and Chaudhari, (2016) investigated the jogging biomechanics using a full-body spine model developed in OpenSim, an open-source musculoskeletal simulation software. Le Navéaux et al., (2016) developed biomechanical models based on multi-body dynamics to analyze the effects of implant density and distribution on curve correction and the resulting forces on the vertebrae. Ignasiak et al., 2016 predicted the dynamic spinal loading using a multi-body thoracolumbar spine model with articulated rib cage.
In the category of multi-body models, a strong effort has been devoted to finding accurate simplifications of the models and designing parameter estimation techniques. In our design and parameterization of a spine-and-trunk model, we borrow insight and design choices from this collection of work.
Panjabi et al., (1994) studied the mechanical behavior of the human lumbar and lumbosacral spine as shown by three dimensional load-displacement curves. Panjabi et al., (1976) estimated the rotational stiffness coefficients of the thoracic spine from experiments. Bisschop et al., (2012) and Panjabi et al., (1976) found the translational stiffness coefficients of the thoracic spine through experimental studies. Moroney et al., (1988) estimated the load displacement properties of the cervical spine from experiments. Andriacchi et al., (1974) estimated the stiffness coefficients of the elastic properties of the rib cage through simulations. Wilke et al., (2017) examined the flexibility of every thoracic spinal segment in an in vitro experiment. Liebsch et al., (2017); Liebsch et al., (2019) investigated the kinematic and stiffness properties of the thoracic spine and the rib cage through experimental studies.
Moreover, many studies tried to estimate the mechanical parameters of the soft tissue in the human’s body. Choi and Zheng, (2005) estimated Young’s modulus and Poisson’s ratio of soft tissue from indentation using two different-sized indentors in a finite element analysis. Song et al., (2006) studied the elasticity of the living abdominal wall in laparoscopic surgery. Hostettler et al., (2010) measured the Bulk modulus and volume variation of the liver and the kidneys in vivo. McKee et al., (2011) compared the reported values of Young’s modulus obtained from indentation and tensile deformations of soft biological tissues.
2.2 Optimization-based shape design
As mentioned earlier, some works have considered computational optimization of scoliosis braces leveraging simulation models of brace-trunk interaction (Gignac et al., 2000; Liao et al., 2007; Nie et al., 2009). These works suffer strong limitations though. On one hand, the biomechanics models they use are limited, e.g., some limit brace interaction to point forces applied on the skin surface (Gignac et al., 2000). On the other hand, the optimization solvers require complex simulation of trunk biomechanics for every small optimization step, which turns into large inefficiencies.
The computational approach explored in this work considers tight connection between the optimization formulation and the biomechanics engine, to design efficient search methods. This approach is popular in the fields of parameter estimation and computational fabrication, and it relies on implicit differentiation of the biomechanics model. For instance, the work of Miguel et al., (2012) used implicit differentiation of a cloth model to execute efficient parameter estimation of cloth simulation models, and the works of Pérez et al., (2015); Pérez et al., (2017) used implicit differentiation of rod meshes to explore shape designs later produced through 3D printing. Recently, differentiable simulation methodologies have also seen success in robotics. The applications include the optimization of control policies (Du et al., 2021; Murthy et al., 2021), or even the design of sensor networks (Tapia et al., 2020).
It is important to note that computational optimization methods have been explored for various objects, very different from braces, but the methodologies could be applicable. Montes et al., (2020) recently developed a design method for tight clothing that considers design and comfort metrics, and accounts for simulation models of both clothing and the body. Zhao et al., (2021) recently developed a similar method to design supporting surfaces for the human body, accounting for metrics that optimize ergonomics.
3 Trunk and brace simulation model
In this section, we describe the biomechanical model of the torso, the model and parameterization of the brace, and the interaction between both. We put all these elements together in a biomechanics simulation engine that, given a brace geometry as input, outputs the deformation of the trunk and the forces between trunk and brace. We borrow the biomechanical model of the trunk from the work of Koutras et al., (2021), and we refer to their publication for details.
In the definition of the biomechanical model of the trunk and brace, we seek a formulation that can be differentiated, to be efficiently embedded within a design optimization approach. To this end, we model all biomechanical components using smooth energy potentials.
3.1 Biomechanical model of the trunk
The purpose of the trunk simulation model is to predict the deformation of the spine under the action of a scoliosis brace. To this end, we characterize the trunk as a multi-body system, consisting of articulated rigid bodies to model the skeleton, and surrounding soft tissue to model the skin, muscles and organs. In particular, and following the rationale of (Koutras et al., 2021), we consider the trunk model passive, without muscle activation. While the exact instantaneous trunk deformation depends on the instantaneous muscle activity, we consider a passive trunk model as an approximate average of muscle activity conditions.
We group all degrees of freedom (DoFs) of the trunk in a large vector xtrunk. This vector includes: 1) translation and rotation of all bones in the trunk skeleton (the rotation is parameterized using incremental axis angle (Taylor and Kriegman, 1994)); and 2) nodes of a tetrahedral mesh of the soft tissue. The trunk skeleton includes the bones relevant for predicting the deformation of the lumbar and thoracic spine, which are: all lumbar and thoracic vertebrae, the sternum, the rib cage, and the pelvis. The soft-tissue mesh is constructed from the surface of the trunk between neck and waist, and clipped at the shoulders. We provide as input this surface as a triangle mesh, together with sample points on the surfaces of the bones, and we produce a conformal tetrahedral mesh (Si, 2015). Introducing mesh nodes on the surfaces of bones facilitates the coupling between skeleton and soft tissue. We rigidly couple these nodes to the bones, and we remove them from the DoF vector xtrunk.
The mechanics of the trunk are modeled as a sum of energy terms parameterized by the DoFs xtrunk. The energy terms include compliant joint models between skeletal bones Wjoints (xtrunk), and the soft-tissue internal energy Wtissue (xtrunk). We describe the joint energies Wjoints as 6-DoF joints between pairs of bones, acting on both their translation and rotation. By tuning the stiffness of each constraint axis, we effectively model different types of joints and their anisotropy. We describe the soft-tissue energy Wtrunk using a Neo-Hookean strain energy density model, integrated on the volume of the tetrahedral mesh using a finite-element formulation. As mentioned above, we refer to (Koutras et al., 2021) for details on the biomechanical model of the trunk, such as the definition of the energy terms.
In our study, we use the trunk model to simulate the biomechanical response of different subjects suffering from AIS. To adapt the model to each subject, we start from a template geometry corresponding to a healthy (non-scoliotic) adolescent female, and then we apply the morphing method in (Koutras et al., 2022), using as input low-dose radiographs of the subjects. Full personalization would also require estimating subject-specific mechanical parameters, but in this synthetic study we limit ourselves to the default mechanical parameters listed in (Koutras et al., 2021).
3.2 Model and parameterization of the brace
There are many different types of scoliosis braces. Designing a computational solution that explores the different brace types is a complex task, as the design space is not continuous. Therefore, for our solution we focus on one particular type of brace, specifically the classic Boston brace (Périé et al., 2003), which concentrates brace-trunk forces on three locations. One of these locations corresponds to the location of peak curvature in the spine, and the other two locations are above and below, to produce counteracting forces and a net torque that rotates the spine in a corrective direction. Note that more modern variants of the Boston brace consider also other design principles, but we leave such extensions for future work.
We describe the geometry of the Boston brace as a parametric surface
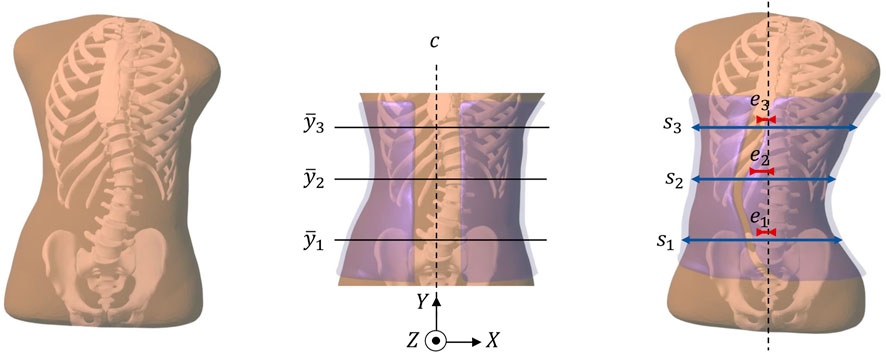
FIGURE 1. This figure summarizes the pipeline of our computational brace design methodology. From left to right: (i) Starting from radiographs of a patient, we obtain a personalized simulation model of the trunk (including the spine, the rib cage, and the surrounding soft tissue). (ii) We initialize a brace geometry (in semi-transparent purple) by trimming and slightly offsetting the patient´s skin. In this initial brace geometry, we identify the frontal center line c, and three heights
In addition to the design transformation, the initial shape of the brace is transformed to provide pressure on the trunk, and thus forces on the spine that produce an incremental correction. This produces the actual brace surface
3.3 Contact and regularization
To model the interaction between the brace and the trunk, we use a potential-based contact model. An alternative would be to solve contact with hard constraints, but the differentiation of hard constraints is considerably more expensive (Liang et al., 2019). Among potential-based contact models, some recent methods propose highly nonlinear potentials to strongly enforce non-penetration (Li et al., 2020). However, we opt for a quadratic potential to improve the convergence of the design optimization solver.
Given a deformation of the trunk defined by its DoFs xtrunk, we define a distance field of its surface, ϕtrunk (x, xtrunk), x ∈ R3. The distance is positive outside the trunk and negative inside. Based on this distance field, we define a potential energy that penalizes interpenetration between the brace surface
We approximate the integral through finite-element integration on the triangular surface elements of the brace surface
In our contact model, we do not account for friction between the brace and the trunk. Friction indeed exists in the real world when the trunk moves, but it is always possible to adjust the brace and let skin relax to remove such friction. Therefore, we are interested in modeling frictionless interaction.
This said, friction plays another important role in simulation, as it ensures that the trunk cannot slip through the brace. We replace this effect with a small regularization term that tries to maintain the brace in place, by penalizing the norm of the brace DoFs.
3.4 Simulation engine
Based on the various energy terms defined in the previous sections, the total energy of the trunk-brace system can be computed as:
Given a set of brace design parameters p, we wish to predict the deformation of the trunk produced by the brace. We do this by solving a static equilibrium problem. For convenience, we concatenate all DoFs in one large vector
At the configuration of minimum energy, the biomechanics satisfy static equilibrium, i.e., zero net energy gradient or zero net force everywhere in the brace-trunk system:
Note that the forces on the DoFs, f, are simply the (negative) gradient of the energy. Static equilibrium is a direct consequence of the optimality conditions of the optimization. We can also regard these optimality conditions as biomechanics constraints.
To solve the optimization (Eq. 5), we use Newton’s method with line search (Nocedal and Wright, 2006). On every Newton iteration, we compute the Jacobian of the forces, i.e., the (negative) energy Hessian,
4 Brace optimization
In this section, we describe the formulation of an optimization problem for brace design. We start with the formulation of a design objective function, and we continue with efficient computation of the objective gradient using our differentiable biomechanics formulation.
4.1 Design optimization problem
To guide the change of the brace shape, we need a merit function that quantifies the impact on the spine from a clinical standpoint. In our approach, we use the Cobb angle (Safari et al., 2019) to characterize the severity of scoliosis. More complex, multi-objective merit functions are left for future work, but are briefly discussed in Section 6. The Cobb angle measures the largest angle between the superior end plate of a vertebra and the inferior end plate of some other vertebra, thus characterizing the maximum bending of the spine. The Cobb angle Ψ(xtrunk) can be computed from the DoFs of the vertebrae embedded in xtrunk. Then, our clinical merit function is:
Note that the metric is normalized by the initial Cobb angle
However, optimizing the Cobb angle might produce braces that are uncomfortable or even impossible to wear. Therefore, we also add the total force applied by the brace on the trunk as a comfort function, penalizing designs that would be too uncomfortable. We obtain per-point forces by differentiating the penalty potential in (Eq. 2), we compute its squared norm, and we integrate the result over the surface of the brace:
Adding the clinical metric (Eq. 7) and the comfort metric (Eq. 8), we obtain the full objective function of the brace design problem:
where λ is the relative weight of the two components of the objective function. A proper weight adjustment λ of the clinical and comfort metrics produces designs that are both effective and comfortable to wear. We consider a Cobb angle of 75% as a sufficient objective, and a force of 250 N as a reasonable contact force. Then, a value of λ = 9e−6 assigns equal weight to both the clinical and comfort metrics.
4.2 Optimization algorithm
Given the brace design objective
We rely on numerical optimization methods to automatically search for brace geometries that produce optimal designs. In our implementation, we choose the bounded L-BFGS optimization algorithm (Nocedal and Wright, 2006), as it offers a good balance between speed and convergence. L-BFGS requires the evaluation of the gradient of the objective function with respect to the design parameters, i.e.,
The challenge in the evaluation of this gradient is that a change of design parameters p affects the DoFs x in a complex way, through the equilibrium condition (Eq. 6). Due to this complexity, a common approach to evaluate
where ei is a unit vector in the direction of the ith parameter, and ɛ is a small value. For small parameter sets, finite-differences may be computationally effective, but their cost grows linearly with the number of design parameters, and they soon become the bottleneck of the optimization.
4.3 Differentiable biomechanics
Instead of using finite differences, we leverage our differentiable biomechanics formulation to compute the gradient of DoFs with respect to design parameters,
With the definition of the objective function (Eq. 9), we note that the clinical metric
Thanks to the implicit function theorem (IFT), the biomechanics equilibrum constraints (Eq. 6) must be satisfied for small changes to the DoFs and the design parameters. Then, we can differentiate those constraints to obtain:
IFT provides an implicit definition of the Jacobian of the DoFs with respect to design parameters, such that the equilibrium constraints remain satisfied.
We leverage this Jacobian to differentiate the objective (Eq. 9) analytically, and substitute it in (Eq. 12) to obtain:
The evaluation of the gradient (Eq. 14) requires substituting the implicit derivative (Eq. 13). In practice, however, this is done using the adjoint method:
On each step of L-BFGS, given a new tentative set of brace parameters p, we solve the static equilibrium (Eq. 5) to obtain the trunk and brace DoFs. Then, we solve for the adjoint u in (Eq. 15), and we evaluate the full objective gradient.
4.4 Implementation details
Our optimization is built in Python, using the L-BFGS solver in scipy. As mentioned in Section 3.4, we use SOFA for the biomechanics, and then we build the full gradient in Python and we feed it to the L-BFGS solver. By defining smooth biomechanics functions with respect to both DoFs x and design parameters p, we can efficiently evaluate the objective gradient
The Jacobian of forces
The gradient of the comfort metric with respect to the DoFs can be obtained trivially from the contact forces. From (Eq. 8), we derive that
The gradient of the comfort metric with respect to the brace parameters does not differ much from the contact forces. It can be computed as
The most complex term is probably the Jacobian of forces with respect to brace parameters,
The last necessary term is the gradient of the clinical metric with respect to the DoFs,
The IFT applied in (Eq. 13) to implicitly define the derivative of DoFs with respect to design parameters is only valid when the biomechanics constraints (Eq. 6) are satisfied. For this reason, the static equilibrium is solved on each L-BFGS iteration. We have experimented with the accuracy required by the static equilibrium solve, which in turn affects the accuracy of
5 Experiments
This section describes the cases that were evaluated in our study. We start with a description of the patient data, and then we provide an analysis of performance of the brace design methodology. As discussed in the introduction, to date we have limited our experiments to a synthetic study, and we evaluate the performance of brace designs only on simulation models of the patients.
5.1 Test cohort
The proposed computational brace design method was applied to a cohort of five female potential AIS patients, ranging from 10 to 13 years old, with an average height of 163.6 cm (±11 cm). The subjects were selected because they had to be screened for scoliosis based on previous diagnosis or examination, but subject #2 was not considered an AIS patient after all, and subject #3 would not require brace treatment in clinical practice. As discussed in the definition of the clinical metric in Section 4.1, in our study we use the Cobb angle metric (Safari et al., 2019) to characterize the severity of scoliosis, as it is the standard clinical metric for this purpose. The average Cobb angle measured on the subjects was 17.4° (±8.9°).
In order to proceed with the study, all patients provided oral and written consent according to national Danish guidelines and the Helsinki Declaration, and with approval of the local ethics committee at University Hospital of Hvidovre (No H-17034237). For each subject, we captured biplanar radiographs of the trunk, as they are readily available as part of the regular check-up of scoliotic patients, using a DelftDI D2RS system with fluoroscopic exposure (Wong et al., 2021). Then, we followed the procedure in (Koutras et al., 2022) to morph a template trunk geometry and obtain personalized trunk biomechanical models. Table 1 provides the individual patient data, as well as the complexity of the simulation models, characterized by the number of triangles of the surface mesh (which dominates the cost of contact computations) and the number of tetrahedra of the soft-tissue mesh (which dominates the cost of deformation computations).
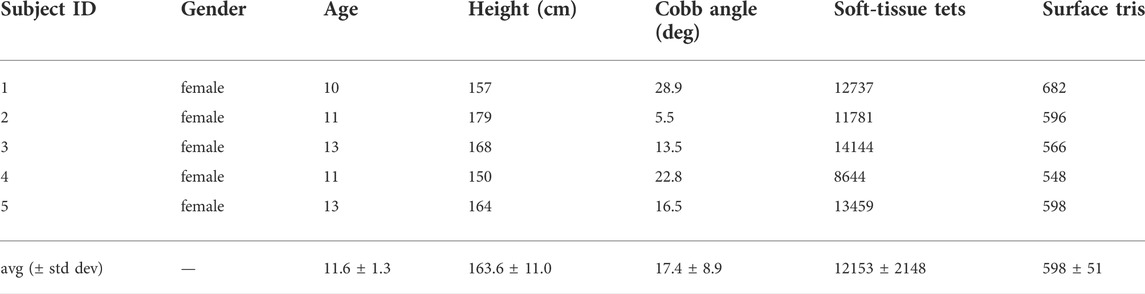
TABLE 1. Features of the subjects evaluated in our study. The table indicates the severity of the main spine curve (i.e., the Cobb angle) of each subject, as well as the size of the simulation meshes used in our optimization algorithm.
5.2 Brace optimization results
Figure 2 illustrates the result of brace optimization for each subject evaluated in the study. The figure shows the trunk geometry and the brace geometry before and after the computational optimization. As evidenced in the images, the optimization algorithm automatically finds brace designs that push on the rib cage at the appropriate location to induce a correction of the spine curvature.
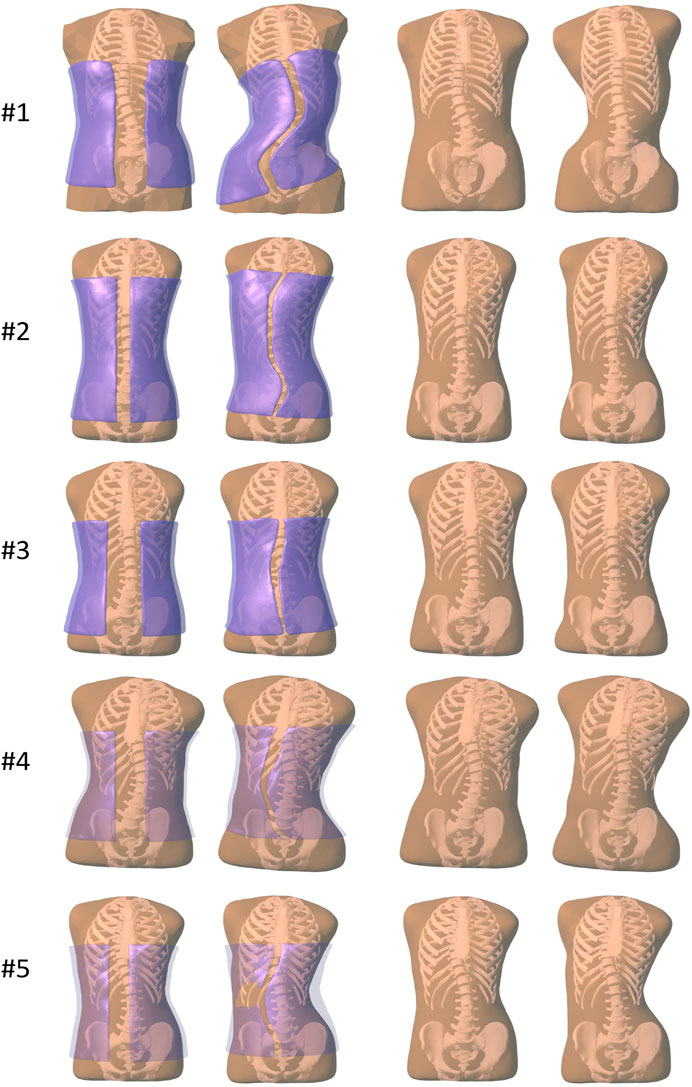
FIGURE 2. Images of all the subjects evaluated in our study. From left to right, (i) before brace optimization, with the initial brace geometry shown semi-transparent purple, (ii) after brace optimization, with the final brace geometry shown semi-transparent purple, (iii) before brace optimization, just the initial trunk geometry, (iv) after brace optimization, showing the deformed trunk geometry.
Table 2 compares the Cobb angle before and after applying the scoliosis brace to each of the subjects. Note that we refer to the in-brace correction of Cobb angle; our work has no way of predicting the correction of Cobb angle after brace removal, as this temporal process is not handled by our simulation model. On average, the Cobb angle was reduced by 7.8° (±4.9°), which amounts to a reduction of 45.4% ± 18.9%. Moreover, thanks to the comfort metric described in Section 4.1, this reduction in Cobb angle was achieved under average contact forces of 185.8 N (±29.8 N). None of the subjects reached the limit of 250 N in contact force, indicating a good balance of the clinical and comfort metrics in (Eq. 9). An average reduction of 7.8° in Cobb angle may be considered low with respect to the reduction achieved by real-world braces (in particular in the case of subject #3), and we consider two reasons behind this limitation: 1) The degrees of freedom of our computational braces are currently far fewer than those of real braces; 2) The comfort metric may be too conservative. Both limitations are avenues for further improvement, but they do not challenge the overall methodology.

TABLE 2. Quantitative results achieved by optimization-based brace design on each of the test subjects. The table lists the reduction in Cobb angle (in degrees and in percentage of the initial angle), as well as the total force on the subject’s trunk as a measure of comfort.
Finally, Table 3 summarizes the computational performance of our proposed optimization algorithm. Thanks to differentiable biomechanics and the efficient computation of gradients, the optimizations take 16.4 min on average (±7.3 min). This is in contrast to the average of 94.1 min required by state-of-the-art optimization using finite-difference gradients. The average speed-up across subjects is of 9.2×. This number is particularly affected by the performance of subject #4, for whom the finite-difference version suffered considerably worse convergence. Even removing this outlier case, the average speed-up across subjects is of 4.5×. In our current parameterization of the brace, described in Section 3.2, we use just 6 parameters. With a larger number of parameters, the speed-up of our differentiable biomechanics formulation would be even higher, as the computation of gradients is insensitive to the number of parameters.
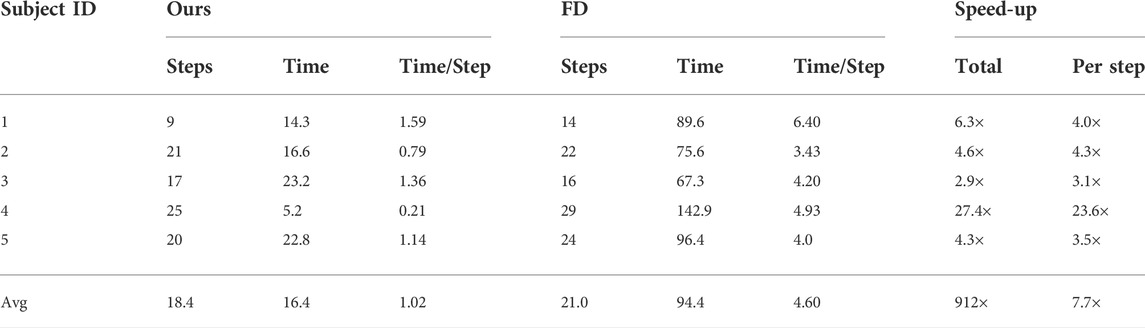
TABLE 3. Performance of our method, using differentiable biomechanics, compared with state-of-the-art optimization using finite differences (FD) for the computation of gradients. All timings are measured in minutes. We report the number of steps of each optimization, the total time, the time per step, the total speed-up, and the speed-up per step.
6 Discussion
In this paper, we have presented a computational method to design personalized scoliosis Boston braces. The main novelty of the proposed method is to leverage differentiable biomechanics to enable efficient use of numerical optimization methods. Differentiable biomechanics formulates static equilibrium equations as constraints, and evaluates the relationship between deformation state and design variables through implicit differentiation. This relationship is then used within the numerical optimization algorithm to quickly advance toward optimal brace design parameters. We have shown that the differentiable biomechanics formulation provides a large speed-up over state-of-the-art numerical optimization approaches. And this already large speed-up can even increase as the versatility of brace designs grows with more complex parameterizations.
We have demonstrated the use of differentiable biomechanics to design personalized scoliosis braces for five different potential AIS patients. The overall methodology combines personalized trunk simulation models with the differentiable-biomechanics technical contribution. Altogether, we demonstrate that it is possible to design scoliosis braces following a fully computational methodology. The braces balance a clinical metric and a comfort metric, ensuring that they are both effective and practical.
Our study and evaluation are to date limited to synthetic experiments. While the input data belong to real (potential) AIS patients, we have not fabricated and physically tested the brace designs. The contribution of our work is to demonstrate that a computational design methodology is feasible and efficient, but further work is necessary before actual braces are physically tested on real patients. One of the elements that requires further study is the design of the comfort metric. Our current metric considers the total force on the body surface, but this metric is not proven to be suitable or sufficient. Therefore, our work should be complemented with a specific analysis on comfort metrics for scoliosis braces. Another element that requires further study is the accuracy of the overall computational approach, as well as the sensitivity of its various elements. The different computational elements (i.e., the model geometry, the mechanical model, the model parameters, or the weight of the clinical vs comfort metrics) introduce error in the estimated Cobb angle and contact forces. It is necessary to understand the degree of possible error, and thus design a tolerance on the contact forces computed in the simulation. Once the computational model is fully validated, it will be necessary to execute a clinical study concentrated on patient-reported outcome measures, including treatment acceptance and compliance.
In addition to the work necessary for bringing the method to practice, our methodology could also see some improvements on the technical choices. Some of the possible extensions include a richer parameterization of the brace geometry (e.g., using spline surfaces with control points), or personalization of the mechanical parameters of the trunk model. Regarding this last extension, using personalized vs default parameters poses a trade-off between complexity and accuracy. While designing a personalized model would indeed increase accuracy, it is interesting to understand the error produced in practice by a default model.
To conclude, our work has been applied so far only to one type of scoliosis brace, the Boston-type brace, and considering only Cobb angle as clinical metric. It would be interesting to address other types of braces, which would require a different geometric design and a different parameterization. For practical cases, the optimization methodology may even search among different brace types, and find the one that is most convenient for each patient. However, the challenge is two-fold. First, more complex braces require more modeling effort; but this can always be approached by progressively including brace elements of higher impact. Second, some of the design parameters define a continuous parametric space, which can be explored by our current numerical optimization method, but others may define discontinuous or discrete spaces, which require different optimization methods. For instance, optimizing the expansion chambers of Chêneau braces might require topology optimization methods. It would also be interesting to address richer clinical metrics, which are accounted for in the design of braces in practice. One example is the addition of a sagittal-plane metric on top of our current frontal-plane-only metric (e.g., sagittal-plane isostatic balance as a function of lumbopelvic incidence). Our overall approach can be extended to include more advanced multi-objective clinical metrics. For such extension to be possible without critical changes to the overall methodology, the new metrics must be computed from the geometry available in the trunk model, and they must be (locally) continuous and differentiable.
Data availability statement
The data analyzed in this study is subject to the following licenses/restrictions: The dataset was obtained in the context of the MSCA Rainbow project, and use is limited to research within that project. Requests to access these datasets should be directed to miguel.otaduy@urjc.es.
Ethics statement
The studies involving human participants were reviewed and approved by University Hospital of Hvidovre. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
Author contributions
KK led the development of the models, implementation of the methods, and testing and evaluation of results. CK contributed to the development of the model and the obtention of the input data. MO contributed to the design of the methodology, evaluation of results and writing of the paper. All authors reviewed and agreed to the final manuscript.
Funding
This project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No. 764644, Rainbow.
Acknowledgments
The authors would like to thank the reviewers for their help in improving the paper, Christian Wong for his help in the obtention of the patient data, Jesús Pérez for many insightful discussions, and Maxime Tournier, Matthieu Nesme and Francois Faure for their help with the simulation software.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Author disclaimer
This paper only contains the author’s views and the Research Executive Agency and the Commission are not responsible for any use that may be made of the information it contains.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbioe.2022.1014365/full#supplementary-material
References
Andriacchi, T., Schultz, A., Belytschko, T., Galante, J., and Galante, J. (1974). A model for studies of mechanical interactions between the human spine and rib cage. J. Biomechanics 7, 497–507. doi:10.1016/0021-9290(74)90084-0
Aroeira, R. M. C., Pertence, A. E. d. M., Kemmoku, D. T., and Greco, M. (2017). Three-dimensional geometric model of the middle segment of the thoracic spine based on graphical images for finite element analysis. Res. Biomed. Eng. 33, 97–104. doi:10.1590/2446-4740.08916
Aroeira, R. M. C., Pertence, A. E. M., Kemmoku, D. T., and Greco, M. (2018). The effect of hypokyphosis on the biomechanical behavior of the adolescent thoracic spine. J. Braz. Soc. Mech. Sci. Eng. 40, 128. doi:10.1007/s40430-018-1061-4
Bayoglu, R., Galibarov, P. E., Verdonschot, N., Koopman, B., and Homminga, J. (2019). Twente spine model: A thorough investigation of the spinal loads in a complete and coherent musculoskeletal model of the human spine. Med. Eng. Phys. 68, 35–45. doi:10.1016/j.medengphy.2019.03.015
Bisschop, A., Mullender, M. G., Kingma, I., Jiya, T. U., van der Veen, A. J., Roos, J. C., et al. (2012). The impact of bone mineral density and disc degeneration on shear strength and stiffness of the lumbar spine following laminectomy. Eur. Spine J. 21, 530–536. doi:10.1007/s00586-011-1968-2
Choi, A., and Zheng, Y. (2005). Estimation of young’s modulus and Poisson’s ratio of soft tissue from indentation using two different-sized indentors: Finite element analysis of the finite deformation effect. Med. Biol. Eng. Comput. 43, 258–264. doi:10.1007/bf02345964
Clin, J., Aubin, C.-É., Lalonde, N., Parent, S., and Labelle, H. (2011). A new method to include the gravitational forces in a finite element model of the scoliotic spine. Med. Biol. Eng. Comput. 49, 967–977. doi:10.1007/s11517-011-0793-4
Cobetto, N., Aubin, C.-É., Parent, S., Barchi, S., Turgeon, I., and Labelle, H. (2017). 3d correction of ais in braces designed using cad/cam and fem: A randomized controlled trial. Scoliosis Spinal Disord. 12, 24–28. doi:10.1186/s13013-017-0128-9
Cobetto, N., Aubin, C. E., Parent, S., Clin, J., Barchi, S., Turgeon, I., et al. (2016). Effectiveness of braces designed using computer-aided design and manufacturing (CAD/CAM) and finite element simulation compared to CAD/CAM only for the conservative treatment of adolescent idiopathic scoliosis: A prospective randomized controlled trial. Eur. Spine J. 25, 3056–3064. doi:10.1007/s00586-016-4434-3
de Zee, M., Hansen, L., Wong, C., Rasmussen, J., and Simonsen, E. B. (2007). A generic detailed rigid-body lumbar spine model. J. Biomechanics 40, 1219–1227. doi:10.1016/j.jbiomech.2006.05.030
Dicko, A. H., Tong-Yette, N., Gilles, B., Faure, F., and Palombi, O. (2015). Construction and validation of a hybrid lumbar spine model for the fast evaluation of intradiscal pressure and mobility. Int. J. Med. Health Sci. 9 (2). 139–150.
Dong, E., Shi, L., Kang, J., Li, D., Liu, B., Guo, Z., et al. (2020). Biomechanical characterization of vertebral body replacement in situ: Effects of different fixation strategies. Comput. Methods Programs Biomed. 197, 105741. doi:10.1016/j.cmpb.2020.105741
Du, T., Wu, K., Ma, P., Wah, S., Spielberg, A., Rus, D., et al. (2021). Diffpd: Differentiable projective dynamics. ACM Trans. Graph. 41, 1–21. doi:10.1145/3490168
Faure, F., Duriez, C., Delingette, H., Allard, J., Gilles, B., Marchesseau, S., et al. (2012). “Sofa: A multi-model framework for interactive physical simulation,” in Soft tissue biomechanical modeling for computer assisted surgery. Editor Y. Payan (Springer), 11, 283–321. of Studies in Mechanobiology, Tissue Engineering and Biomaterials. doi:10.1007/8415_2012_125
Finley, S. M., Brodke, D. S., Spina, N. T., DeDen, C. A., and Ellis, B. J. (2018). Febio finite element models of the human lumbar spine. Comput. methods biomechanics Biomed. Eng. 21, 444–452. doi:10.1080/10255842.2018.1478967
Gignac, D., Aubin, C.-É., Dansereau, J., and Labelle, H. (2000). Optimization method for 3d bracing correction of scoliosis using a finite element model. Eur. spine J. 9, 185–190. doi:10.1007/s005860000135
Guy, A., Labelle, H., Barchi, S., Audet-Duchesne, E., Cobetto, N., Parent, S., et al. (2021). Braces designed using cad/cam combined or not with finite element modeling lead to effective treatment and quality of life after 2 years: A randomized controlled trial. Spine 46, 9–16. doi:10.1097/brs.0000000000003705
Hostettler, A., George, D., Rémond, Y., Nicolau, S. A., Soler, L., and Marescaux, J. (2010). Bulk modulus and volume variation measurement of the liver and the kidneys in vivo using abdominal kinetics during free breathing. Comput. methods programs Biomed. 100, 149–157. doi:10.1016/j.cmpb.2010.03.003
Ignasiak, D., Dendorfer, S., and Ferguson, S. J. (2016). Thoracolumbar spine model with articulated rib cage for the prediction of dynamic spinal loading. J. Biomechanics 49, 959–966. doi:10.1016/j.jbiomech.2015.10.010
Kaelin, A. J. (2020). Adolescent idiopathic scoliosis: Indications for bracing and conservative treatments. Ann. Transl. Med. 8, 28. doi:10.21037/atm.2019.09.69
Karimi, M., and Rabczuk, T. (2018). Scoliosis conservative treatment: A review of literature. J. Craniovertebr. Junction Spine 9, 3–8. doi:10.4103/jcvjs.JCVJS_39_17
Koutras, C., Pérez, J., Kardash, K., and Otaduy, M. A. (2021). A study of the sensitivity of biomechanical models of the spine for scoliosis brace design. Comput. Methods Programs Biomed. 207, 106125. doi:10.1016/j.cmpb.2021.106125
Koutras, C., Shayestehpour, H., Pérez, J., Wong, C., Rasmussen, J., Tournier, M., et al. (2022). Biomechanical morphing for personalized fitting of scoliotic torso skeleton models. Front. Bioeng. Biotechnol. 10, 945461. doi:10.3389/fbioe.2022.945461
Kuroki, H. (2018). Brace treatment for adolescent idiopathic scoliosis. J. Clin. Med. 7, 136. doi:10.3390/jcm7060136
Lasswell, T. L., Cronin, D. S., Medley, J. B., and Rasoulinejad, P. (2017). Incorporating ligament laxity in a finite element model for the upper cervical spine. Spine J. 17, 1755–1764. doi:10.1016/j.spinee.2017.06.040
Le Navéaux, F., Larson, A. N., Labelle, H., Wang, X., and Aubin, C.-É. (2016). How does implant distribution affect 3d correction and bone-screw forces in thoracic adolescent idiopathic scoliosis spinal instrumentation? Clin. Biomech. 39, 25–31. doi:10.1016/j.clinbiomech.2016.09.002
Li, M., Ferguson, Z., Schneider, T., Langlois, T., Zorin, D., Panozzo, D., et al. (2020). Incremental potential contact: Intersection-and inversion-free, large-deformation dynamics. ACM Trans. Graph. 39. doi:10.1145/3386569.3392425
Liang, J., Lin, M., and Koltun, V. (2019). “Differentiable cloth simulation for inverse problems,” in Advances in neural information processing systems. Editors H. Wallach, H. Larochelle, A. Beygelzimer, F. d’ Alché-Buc, E. Fox, and R. Garnett (Vancouver: Curran Associates, Inc.), 32.
Liao, Y.-C., Feng, C.-K., Tsai, M.-W., Chen, C.-S., Cheng, C.-K., and Ou, Y.-C. (2007). Shape modification of the boston brace using a finite-element method with topology optimization. Spine 32, 3014–3019. doi:10.1097/brs.0b013e31815cda9c
Liebsch, C., Graf, N., Appelt, K., and Wilke, H.-J. (2017). The rib cage stabilizes the human thoracic spine: An in vitro study using stepwise reduction of rib cage structures. PLoS One 12, e0178733. doi:10.1371/journal.pone.0178733
Liebsch, C., Graf, N., and Wilke, H.-J. (2019). In vitro analysis of kinematics and elastostatics of the human rib cage during thoracic spinal movement for the validation of numerical models. J. biomechanics 94, 147–157. doi:10.1016/j.jbiomech.2019.07.041
McKee, C. T., Last, J. A., Russell, P., and Murphy, C. J. (2011). Indentation versus tensile measurements of young’s modulus for soft biological tissues. Tissue Eng. Part B Rev. 17, 155–164. doi:10.1089/ten.teb.2010.0520
Miguel, E., Bradley, D., Thomaszewski, B., Bickel, B., Matusik, W., Otaduy, M. A., et al. (2012). Data-driven estimation of cloth simulation models. Comput. Graph. Forum 31, 519–528. doi:10.1111/j.1467-8659.2012.03031.x
Montes, J., Thomaszewski, B., Mudur, S., and Popa, T. (2020). Computational design of skintight clothing. ACM Trans. Graph. 39. doi:10.1145/3386569.3392477
Moroney, S. P., Schultz, A. B., Miller, J. A., and Andersson, G. B. (1988). Load-displacement properties of lower cervical spine motion segments. J. biomechanics 21, 769–779. doi:10.1016/0021-9290(88)90285-0
Murthy, J. K., Macklin, M., Golemo, F., Voleti, V., Petrini, L., Weiss, M., et al. (2021). “gradsim: Differentiable simulation for system identification and visuomotor control,” in International conference on learning representations.
Negrini, S., Aulisa, A., Cerny, P., de Mauroy, J., McAviney, J., Mills, A., et al. (2022). The classification of scoliosis braces developed by sosort with srs, ispo, and posna and approved by esprm. Eur. Spine J. 31, 980–989. Publisher Copyright: ⓒ 2022, The Author(s). doi:10.1007/s00586-022-07131-z
Nie, W.-Z., Ye, M., Liu, Z.-D., and Wang, C.-T. (2009). The patient-specific brace design and biomechanical analysis of adolescent idiopathic scoliosis. J. Biomech. Eng. 131, 041007. doi:10.1115/1.3049843
Panjabi, M. M., Brand, R. A., and White, A. A. (1976). Three-dimensional flexibility and stiffness properties of the human thoracic spine. J. biomechanics 9, 185–192. doi:10.1016/0021-9290(76)90003-8
Panjabi, M. M., Oxland, T., Yamamoto, I., and Crisco, J. J. (1994). Mechanical behavior of the human lumbar and lumbosacral spine as shown by three-dimensional load-displacement curves. J. Bone Jt. Surg. 76, 413–424. doi:10.2106/00004623-199403000-00012
Pérez, J., Otaduy, M. A., and Thomaszewski, B. (2017). Computational design and automated fabrication of Kirchhoff-plateau surfaces. ACM Trans. Graph. 36, 1–12. doi:10.1145/3072959.3073695
Pérez, J., Thomaszewski, B., Coros, S., Bickel, B., Canabal, J. A., Sumner, R., et al. (2015). Design and fabrication of flexible rod meshes. ACM Trans. Graph. 34, 1–12. doi:10.1145/2766998
Périé, D., Aubin, C., Petit, Y., Beauséjour, M., Dansereau, J., and Labelle, H. (2003). Boston brace correction in idiopathic scoliosis: A biomechanical study. Spine 28, 1672–1677. doi:10.1097/01.brs.0000083165.93936.6d
Raabe, M. E., and Chaudhari, A. M. (2016). An investigation of jogging biomechanics using the full-body lumbar spine model: Model development and validation. J. biomechanics 49, 1238–1243. doi:10.1016/j.jbiomech.2016.02.046
Safari, A., Parsaei, H., Zamani, A., and Pourabbas, B. (2019). A semi-automatic algorithm for estimating cobb angle. J. Biomed. Phys. Eng. 9, 317–326. doi:10.31661/jbpe.v9i3jun.730
Si, H. (2015). Tetgen, a delaunay-based quality tetrahedral mesh generator. ACM Trans. Math. Softw. 41, 1–36. doi:10.1145/2629697
Song, C., Alijani, A., Frank, T., Hanna, G., and Cuschieri, A. (2006). Elasticity of the living abdominal wall in laparoscopic surgery. J. biomechanics 39, 587–591. doi:10.1016/j.jbiomech.2004.12.019
Tapia, J., Knoop, E., Mutný, M., Otaduy, M. A., and Bächer, M. (2020). Makesense: Automated sensor design for proprioceptive soft robots. Soft Robot. 7, 332–345. doi:10.1089/soro.2018.0162
Taylor, C. J., and Kriegman, D. J. (1994). Minimization on the lie group SO(3) and related manifolds. Tech. Rep.. Yale University.
Vergari, C., Chen, Z., Robichon, L., Courtois, I., Ebermeyer, E., Vialle, R., et al. (2020). Towards a predictive simulation of brace action in adolescent idiopathic scoliosis. Comput. Methods Biomechanics Biomed. Eng. 24, 874–882. 1–8. doi:10.1080/10255842.2020.1856373
Vergari, C., Courtois, I., Ebermeyer, E., Bouloussa, H., Vialle, R., and Skalli, W. (2016). Experimental validation of a patient-specific model of orthotic action in adolescent idiopathic scoliosis. Eur. Spine J. 25, 3049–3055. doi:10.1007/s00586-016-4511-7
Wang, W., Baran, G. R., Betz, R. R., Samdani, A. F., Pahys, J. M., and Cahill, P. J. (2014). The use of finite element models to assist understanding and treatment for scoliosis: A review paper. Spine Deform. 2, 10–27. doi:10.1016/j.jspd.2013.09.007
Wilke, H.-J., Herkommer, A., Werner, K., and Liebsch, C. (2017). In vitro analysis of the segmental flexibility of the thoracic spine. PLoS One 12, e0177823. doi:10.1371/journal.pone.0177823
Wong, C., Adriansen, J., Jeppsen, J., and Balslev-Clausen, A. (2021). Intervariability in radiographic parameters and general evaluation of a low-dose fluoroscopic technique in patients with idiopathic scoliosis. Acta Radiol. Open 10, 205846012110432. doi:10.1177/20584601211043258
Xu, M., Yang, J., Lieberman, I. H., and Haddas, R. (2017). Lumbar spine finite element model for healthy subjects: Development and validation. Comput. methods biomechanics Biomed. Eng. 20, 1–15. doi:10.1080/10255842.2016.1193596
Keywords: computational design, biomechanical models, differentiable simulation, scoliosis, computational modeling, spine, scoliosis braces
Citation: Kardash K, Koutras C and Otaduy MA (2022) Design of personalized scoliosis braces based on differentiable biomechanics—Synthetic study. Front. Bioeng. Biotechnol. 10:1014365. doi: 10.3389/fbioe.2022.1014365
Received: 08 August 2022; Accepted: 24 October 2022;
Published: 10 November 2022.
Edited by:
Stephen Ferguson, ETH Zürich, SwitzerlandReviewed by:
Maciej Płaszewski, Józef Piłsudski University of Physical Education in Warsaw, PolandJean Claude De Mauroy, Independent Researcher, Switzerland
Vigilio Fontanari, University of Trento, Italy
Copyright © 2022 Kardash, Koutras and Otaduy. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Miguel A. Otaduy, bWlndWVsLm90YWR1eUB1cmpjLmVz
 Kateryna Kardash
Kateryna Kardash Christos Koutras
Christos Koutras Miguel A. Otaduy
Miguel A. Otaduy