
94% of researchers rate our articles as excellent or good
Learn more about the work of our research integrity team to safeguard the quality of each article we publish.
Find out more
ORIGINAL RESEARCH article
Front. Bioeng. Biotechnol. , 04 November 2021
Sec. Biomechanics
Volume 9 - 2021 | https://doi.org/10.3389/fbioe.2021.687951
Effective contact (
Ground contact
Different techniques to identify gait events are available and depend on the placement of the IMU on the human body (Moe-Nilssen, 1998; Lee et al., 2010; Flaction et al., 2013; Giandolini et al., 2014; Norris et al., 2014; Giandolini et al., 2016; Gindre et al., 2016; Falbriard et al., 2018; Falbriard et al., 2020). Among them, when the IMU is positioned near the sacrum, that is, close to the center of mass, the vertical acceleration signal can be used to determine effective contact
Using effective timings or
Nonetheless, the vertical ground reaction force can be approximated using a sine wave as
which could not be solved analytically for
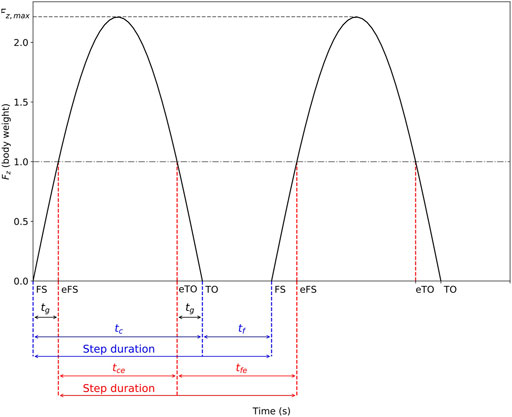
FIGURE 1. Vertical ground reaction force
Hence, the purpose of this study was to obtain a mathematical modeling of
Brent’s method (also known as van Wijngaarden Dekker Brent method) (Brent, 1973; Press et al., 1992) was used to find the zeros of Eq. 1 for any pair of
The numerical analysis showed that a linear boundary relationship is present between
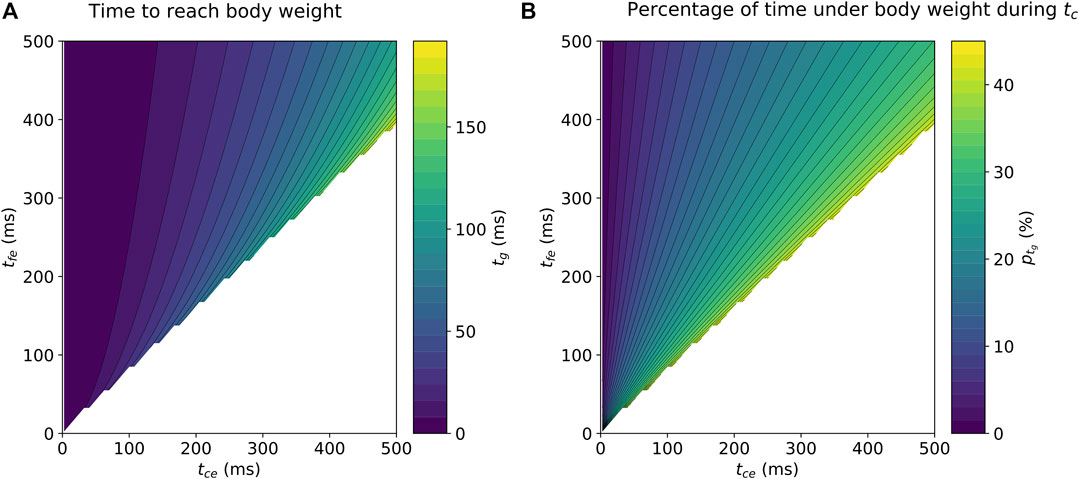
FIGURE 2. Contour plots depicting a) the numerically calculated time
The numerical analysis showed that
One hundred recreational runners (Honert et al., 2020), 75 males (age: 31 ± 8 years, height: 180 ± 6 cm, body mass: 70 ± 7 kg, and weekly running distance: 37 ± 24 km) and 25 females (age: 30 ± 7 years, height: 169 ± 5 cm, body mass: 61 ± 6 kg, and weekly running distance: 20 ± 14 km), voluntarily participated in the present study. For study inclusion, participants were required to be in good self-reported general health with no current or recent lower extremity injury (≤1 month), to run at least once a week, and to have an estimated maximal aerobic speed ≥14 km/h. The study protocol was approved by the Ethics Committee (CER-VD 2020–00334) and adhered to the latest Declaration of Helsinki of the World Medical Association.
After providing written informed consent, each participant performed a 7-min warm-up run on an instrumented treadmill (Arsalis T150—FMT-MED, Louvain-la-Neuve, Belgium). Speed was set to 9 km/h for the first 3 min and was then increased by 0.5 km/h every 30 s. This was followed, after a short break (<5 min), by three 1-min runs (9, 11, and 13 km/h) performed in a randomized order (1-min recovery between each run). 3D kinetic data were collected during the first 10 strides following the 30-s mark of running trials. All participants were familiar with running on a treadmill as part of their usual training program and wore their habitual running shoes.
3D kinetic data (1,000 Hz) were collected using the force plate embedded into the treadmill and using Vicon Nexus software v2.9.3 (Vicon, Oxford, UK). The laboratory coordinate system was oriented such that x-, y-, and z-axes denoted mediallateral (pointing toward the right side of the body), posterioranterior, and inferiorsuperior axis, respectively. Ground reaction force (analog signal) was exported in .c3d format and processed in Visual3D Professional software v6.01.12 (C-Motion Inc, Germantown, MD, United States). 3D ground reaction force signal was low-pass–filtered at 20 Hz using a fourth-order Butterworth filter and down-sampled to 200 Hz to represent a sampling frequency corresponding to typical measurements recorded using a central inertial unit.
For each running trial, eFS and eTO events were identified within Visual3D by applying a body weight threshold to the z-component of the ground reaction force (Cavagna et al., 1988). More explicitly, eFS was detected at the first data point greater or equal to mg within a running step, while eTO was detected at the last data point greater or equal to mg within the same running step.
In addition, FS and TO events were also identified within Visual3D. These events were detected by applying a 20 N threshold to the z-component of the ground reaction force (Smith et al., 2015). More explicitly, FS was detected at the first data point greater or equal to 20 N within a running step, while TO was detected at the last data point greater or equal to 20 N within the same running step.
The recorded vertical ground reaction force permitted to precisely measure
All data are presented as mean ± standard deviation. The reconstructed
Systematic bias, lower and upper limit of agreements, and 95% confidence intervals (CI) were computed as well as RMSE. The difference between reconstructed and ground truth
The numerically calculated
The linear regression gave the model (Eq. 2):
Applying this model to the testing set led to an
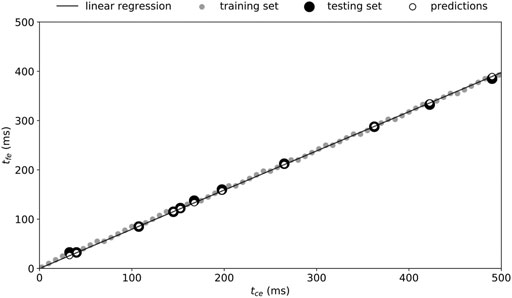
FIGURE 3. Boundary relationship between
The grid points which did not satisfy the previously obtained boundary relationship (Eq. 2) were discarded (1814 discarded points). RMSE computed for each multivariate polynomial regression (order 1–15) is depicted in Figure 4. The polynomial which provided an RMSE smaller than 0.5 ms was kept as the final model of choice (RMSE = 0.43 ms;
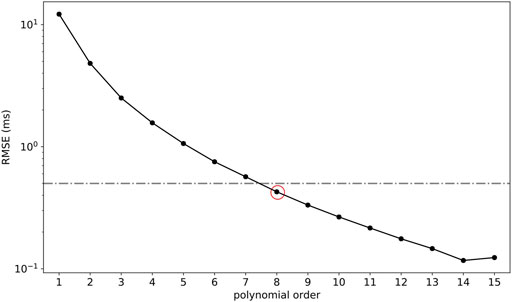
FIGURE 4. Root-mean-square error (RMSE) computed on the testing set (15% points) for polynomial fits of order 1 to 15 performed on the training set (85% points). The red circle denotes the final model of choice, an eighth-order polynomial model (RMSE = 0.43 ms;
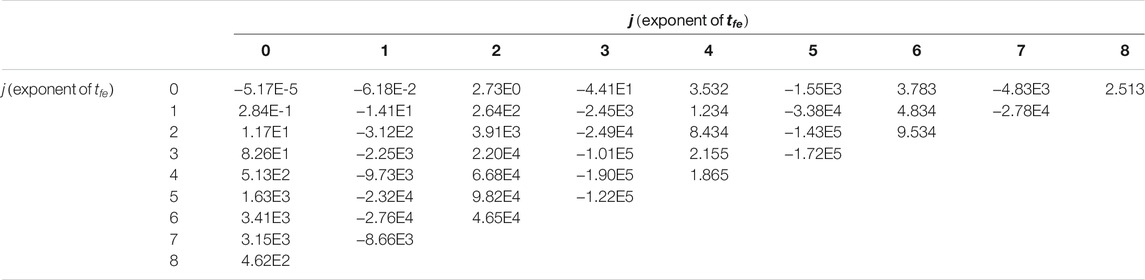
TABLE 1. Coefficients (
Noteworthy, the threshold on RMSE ensured an error smaller than 1 ms on the reconstructed
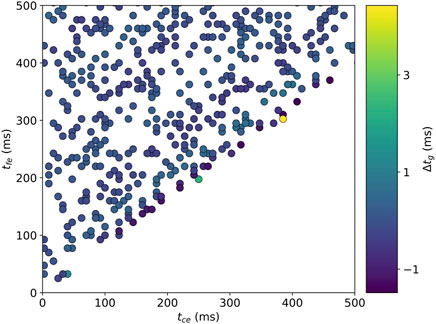
FIGURE 5. Differences between
Reconstructed
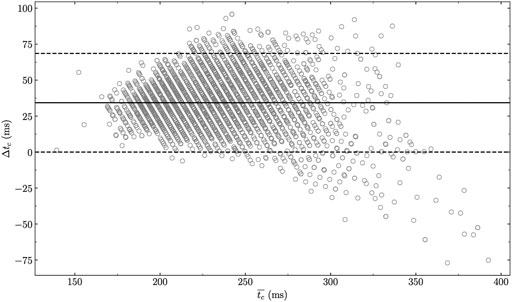
FIGURE 6. BlandAltman plot comparing experimentally measured and reconstructed
The proposed eighth-order multivariate polynomial model (Eq. 3) could be used to obtain
In the case where an algorithm based on effective timings is running on the fly to provide live feedbacks, such as in sports watches, one could simply add the proposed model in the end of the algorithm chain, right before computing the biomechanical outcomes. However, many operations should be performed in a very small amount of time, where the number of operations is directly related to the order of the polynomial. Indeed, knowing that the number of terms in an
The multivariate polynomial model (Eq. 3) was applied to experimentally measured
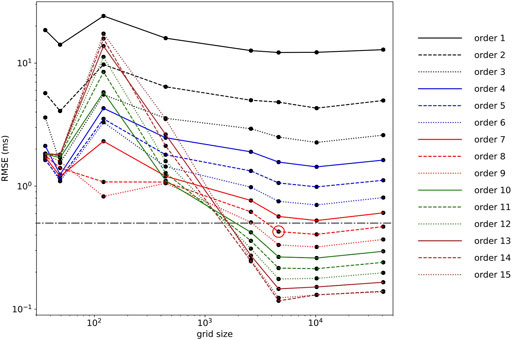
FIGURE 7. Root-mean-square error as a function of grid size ranging from 36 to 40,804 total points and for each polynomial regression (1st to 15th order). The red circle denotes RMSE corresponding to a polynomial (eighth order) chosen in Section 3.2 (0.43 ms), and the gray line depicts an RMSE threshold of 0.5 ms.
To conclude, in the present study, an eighth-order multivariate polynomial model was constructed based on the numerical solution of the transcendental equation given by Eq. 1. The proposed model permitted to compute
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
The studies involving human participants were reviewed and approved by the Ethics Committee (CER-VD 2020–00334). The patients/participants provided their written informed consent to participate in this study.
Conceptualization, AP, TL, CG, and DM; methodology: AP, TL, CG, and DM; investigation: AP, TL, and BB; formal analysis: AP and BB; writing—original draft preparation: AP; writing—review and editing: AP, TL, BB, CG, and DM; supervision: AP, TL, CG, and DM
This study was supported by Innosuisse (grant no. 35793.1 IP-LS).
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
The authors warmly thank the participants for their time and cooperation.
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbioe.2021.687951/full#supplementary-material
Abendroth-Smith, J. (1996). Stride Adjustments during a Running Approach toward a Force Plate. Res. Q. Exerc. Sport 67, 97–101. doi:10.1080/02701367.1996.10607930
Alcantara, R. S., Day, E. M., Hahn, M. E., and Grabowski, A. M. (2021). Sacral Acceleration Can Predict Whole-Body Kinetics and Stride Kinematics across Running Speeds. PeerJ 9, e11199. doi:10.7717/peerj.11199
Alexander, R. M. (1989). On the Synchronization of Breathing with Running in Wallabies (Macropusspp.) and Horses (Equus caballus). J. Zoolog. 218, 69–85. doi:10.1111/j.1469-7998.1989.tb02526.x
Ammann, R., Taube, W., and Wyss, T. (2016). Accuracy of PARTwear Inertial Sensor and Optojump Optical Measurement System for Measuring Ground Contact Time during Running. J. Strength Conditioning Res. 30, 2057–2063. doi:10.1519/jsc.0000000000001299
Atkinson, G., and Nevill, A. M. (1998). Statistical Methods for Assessing Measurement Error (Reliability) in Variables Relevant to Sports Medicine. Sports Med. 26, 217–238. doi:10.2165/00007256-199826040-00002
Backes, A., Skejø, S. D., Gette, P., Nielsen, R. Ø., Sørensen, H., Morio, C., et al. (2020). Predicting Cumulative Load during Running Using Field‐based Measures. Scand. J. Med. Sci. Sports 30, 2399–2407. doi:10.1111/sms.13796
Bland, J. M., and Altman, D. G. (1995). Comparing Methods of Measurement: Why Plotting Difference against Standard Method Is Misleading. The Lancet 346, 1085–1087. doi:10.1016/s0140-6736(95)91748-9
Brent, R. P. (1973). Algorithms for Minimization without Derivatives. Englewood Cliffs, NJ: Prentice-Hall.
Broyden, C. G. (1970). The Convergence of a Class of Double-Rank Minimization Algorithms 1. General Considerations. IMA J. Appl. Math. 6, 76–90. doi:10.1093/imamat/6.1.76
Camomilla, V., Bergamini, E., Fantozzi, S., and Vannozzi, G. (2018). Trends Supporting the In-Field Use of Wearable Inertial Sensors for Sport Performance Evaluation: A Systematic Review. Sensors 18, 873. doi:10.3390/s18030873
Cavagna, G. A., Franzetti, P., Heglund, N. C., and Willems, P. (1988). The Determinants of the Step Frequency in Running, Trotting and Hopping in Man and Other Vertebrates. J. Physiol. 399, 81–92. doi:10.1113/jphysiol.1988.sp017069
Cavagna, G. A., Legramandi, M. A., and Peyré-Tartaruga, L. A. (2008). Old Men Running: Mechanical Work and Elastic Bounce. Proc. R. Soc. B. 275, 411–418. doi:10.1098/rspb.2007.1288
Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences. Oxfordshire, England, UK: Routledge.
Da Rosa, R. G., Oliveira, H. B., Gomeñuka, N. A., Masiero, M. P. B., Da Silva, E. S., Zanardi, A. P. J., et al. (2019). Landing-takeoff Asymmetries Applied to Running Mechanics: A New Perspective for Performance. Front. Physiol. 10, 415. doi:10.3389/fphys.2019.00415
Dalleau, G., Belli, A., Viale, F., Lacour, J. R., and Bourdin, M. (2004). A Simple Method for Field Measurements of Leg Stiffness in Hopping. Int. J. Sports Med. 25, 170–176. doi:10.1055/s-2003-45252
Debaere, S., Jonkers, I., and Delecluse, C. (2013). The Contribution of Step Characteristics to Sprint Running Performance in High-Level Male and Female Athletes. J. Strength Conditioning Res. 27, 116–124. doi:10.1519/jsc.0b013e31825183ef
Falbriard, M., Meyer, F., Mariani, B., Millet, G. P., and Aminian, K. (2018). Accurate Estimation of Running Temporal Parameters Using Foot-Worn Inertial Sensors. Front. Physiol. 9, 610. doi:10.3389/fphys.2018.00610
Falbriard, M., Meyer, F., Mariani, B., Millet, G. P., and Aminian, K. (2020). Drift-Free Foot Orientation Estimation in Running Using Wearable IMU. Front. Bioeng. Biotechnol. 8, 65. doi:10.3389/fbioe.2020.00065
Flaction, P., Quievre, J., and Morin, J. B. (2013). An Athletic Performance Monitoring Device. Washington, DC: U.S. Patent and Tradematk Office patent application.
Fletcher, R. (1970). A New Approach to Variable Metric Algorithms. Comp. J. 13, 317–322. doi:10.1093/comjnl/13.3.317
Folland, J. P., Allen, S. J., Black, M. I., Handsaker, J. C., and Forrester, S. E. (2017). Running Technique Is an Important Component of Running Economy and Performance. Med. Sci. Sports Exerc. 49, 1412–1423. doi:10.1249/mss.0000000000001245
Giandolini, M., Horvais, N., Rossi, J., Millet, G. Y., Samozino, P., and Morin, J.-B. (2016). Foot Strike Pattern Differently Affects the Axial and Transverse Components of Shock Acceleration and Attenuation in Downhill Trail Running. J. Biomech. 49, 1765–1771. doi:10.1016/j.jbiomech.2016.04.001
Giandolini, M., Poupard, T., Gimenez, P., Horvais, N., Millet, G. Y., Morin, J.-B., et al. (2014). A Simple Field Method to Identify Foot Strike Pattern during Running. J. Biomech. 47, 1588–1593. doi:10.1016/j.jbiomech.2014.03.002
Gindre, C., Lussiana, T., Hebert-Losier, K., and Morin, J.-B. (2016). Reliability and Validity of the Myotest for Measuring Running Stride Kinematics. J. Sports Sci. 34, 664–670. doi:10.1080/02640414.2015.1068436
Goldfarb, D. (1970). A Family of Variable-Metric Methods Derived by Variational Means. Math. Comp. 24, 23. doi:10.1090/s0025-5718-1970-0258249-6
Halilaj, E., Rajagopal, A., Fiterau, M., Hicks, J. L., Hastie, T. J., and Delp, S. L. (2018). Machine Learning in Human Movement Biomechanics: Best Practices, Common Pitfalls, and New Opportunities. J. Biomech. 81, 1–11. doi:10.1016/j.jbiomech.2018.09.009
Hébert-losier, K., Mourot, L., and Holmberg, H.-C. (2015). Elite and Amateur Orienteers' Running Biomechanics on Three Surfaces at Three Speeds. Med. Sci. Sports Exerc. 47, 381–389. doi:10.1249/mss.0000000000000413
Honert, E. C., Mohr, M., Lam, W.-K., and Nigg, S. (2020). Shoe Feature Recommendations for Different Running Levels: A Delphi Study. PLOS ONE 15, e0236047. doi:10.1371/journal.pone.0236047
Kram, R., and Dawson, T. J. (1998). Energetics and Biomechanics of Locomotion by Red Kangaroos (Macropus rufus). Comp. Biochem. Physiol. B: Biochem. Mol. Biol. 120, 41–49. doi:10.1016/s0305-0491(98)00022-4
Lee, J. B., Mellifont, R. B., and Burkett, B. J. (2010). The Use of a Single Inertial Sensor to Identify Stride, Step, and Stance Durations of Running Gait. J. Sci. Med. Sport 13, 270–273. doi:10.1016/j.jsams.2009.01.005
Lussiana, T., Patoz, A., Gindre, C., Mourot, L., and Hébert-Losier, K. (2019). The Implications of Time on the Ground on Running Economy: Less Is Not Always Better. J. Exp. Biol. 222, jeb192047. doi:10.1242/jeb.192047
Lussiana, T., and Gindre, C. (2016). Feel Your Stride and Find Your Preferred Running Speed. Biol. Open 5, 45–48. doi:10.1242/bio.014886
Maiwald, C., Sterzing, T., Mayer, T. A., and Milani, T. L. (2009). Detecting Foot-To-Ground Contact from Kinematic Data in Running. Footwear Sci. 1, 111–118. doi:10.1080/19424280903133938
Minetti, A. E. (1998). A Model Equation for the Prediction of Mechanical Internal Work of Terrestrial Locomotion. J. Biomech. 31, 463–468. doi:10.1016/s0021-9290(98)00038-4
Moe-Nilssen, R. (1998). A New Method for Evaluating Motor Control in Gait under Real-Life Environmental Conditions. Part 1: The Instrument. Clin. Biomech. 13, 320–327. doi:10.1016/s0268-0033(98)00089-8
Moore, I. S., Ashford, K. J., Cross, C., Hope, J., Jones, H. S. R., and Mccarthy-Ryan, M. (2019). Humans Optimize Ground Contact Time and Leg Stiffness to Minimize the Metabolic Cost of Running. Front. Sports Act Living 1, 53. doi:10.3389/fspor.2019.00053
Morin, J.-B., Dalleau, G., Kyröläinen, H., Jeannin, T., and Belli, A. (2005). A Simple Method for Measuring Stiffness during Running. J. Appl. Biomech. 21, 167–180. doi:10.1123/jab.21.2.167
Norris, M., Anderson, R., and Kenny, I. C. (2014). Method Analysis of Accelerometers and Gyroscopes in Running Gait: A Systematic Review. Proc. Inst. Mech. Eng. P: J. Sports Eng. Tech. 228, 3–15. doi:10.1177/1754337113502472
Novacheck, T. F. (1998). The Biomechanics of Running. Gait & Posture 7, 77–95. doi:10.1016/s0966-6362(97)00038-6
Patoz, A., Lussiana, T., Thouvenot, A., Mourot, L., and Gindre, C. (2020). Duty Factor Reflects Lower Limb Kinematics of Running. Appl. Sci. 10, 8818. doi:10.3390/app10248818
Press, W. H., Teukolsky, S. A., and Vetterling, W. T. (1992). Numerical Recipes in FORTRAN: The Art of Scientific Computing. Cambridge, England: Cambridge University Press.
Purcell, B., Channells, J., James, D., and Barrett, R. (2006). Use of Accelerometers for Detecting Foot-Ground Contact Time during Running. Proc. SPIE - Int. Soc. Opt. Eng. 6036, 292–299. doi:10.1117/12.638389
Shanno, D. F. (1970). Conditioning of Quasi-Newton Methods for Function Minimization. Math. Comp. 24, 647. doi:10.1090/s0025-5718-1970-0274029-x
Smith, L., Preece, S., Mason, D., and Bramah, C. (2015). A Comparison of Kinematic Algorithms to Estimate Gait Events during Overground Running. Gait & Posture 41, 39–43. doi:10.1016/j.gaitpost.2014.08.009
To justify the grid choice, a similar numerical analysis was carried out but using different grid spacings (2.5, 5, 7.5, 10, 25, 50, 75, and 100 ms).
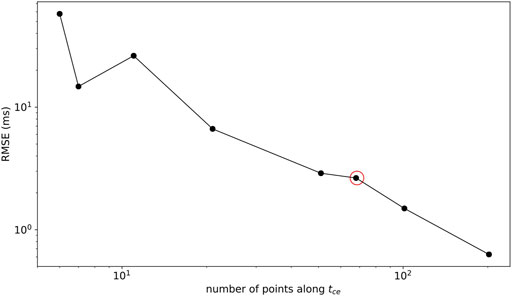
FIGURE A1. Root-mean-square error (RMSE) as a function of the number of points along tce and ranging from 6 to 202. The red circle denotes RMSE corresponding to the boundary relationship computed in Section 3.1 (3.2 ms).
For this reason, a multivariate polynomial regression (polynomial order from 1 to 15) was performed on 85% of the points composing these different grids, after having discarded the points which were not within the corresponding boundary relationship. RMSE on the testing set (15% points) as a function of grid size is depicted for each polynomial order in Figure A1. It can be noticed that the eighth-order polynomial is the lowest order polynomial, leading to an RMSE smaller than 0.5 ms on the testing set. In addition, the smallest grid to obtain such an RMSE threshold is given by a grid using a spacing of 7.5 ms, that is, 4,624 grid points. As for the grid spacing of 10 ms, it requires a polynomial of order 10 to achieve the requested RMSE threshold, which is less convenient as it requires 21 extra coefficients than the eighth-order polynomial. Therefore, these previous statements justify the grid choice used to construct the multivariate polynomial model (Eq. 3).
Keywords: running, biomechanics, sensors, inertial measurement unit, machine learning
Citation: Patoz A, Lussiana T, Breine B, Gindre C and Malatesta D (2021) A Multivariate Polynomial Regression to Reconstruct Ground Contact and Flight Times Based on a Sine Wave Model for Vertical Ground Reaction Force and Measured Effective Timings. Front. Bioeng. Biotechnol. 9:687951. doi: 10.3389/fbioe.2021.687951
Received: 30 March 2021; Accepted: 29 September 2021;
Published: 04 November 2021.
Edited by:
Yang Liu, Hong Kong Polytechnic University, Hong Kong, SAR ChinaCopyright © 2021 Patoz, Lussiana, Breine, Gindre and Malatesta. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Aurélien Patoz, YXVyZWxpZW4ucGF0b3pAdW5pbC5jaA==
Disclaimer: All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.
Research integrity at Frontiers

Learn more about the work of our research integrity team to safeguard the quality of each article we publish.