Synthetic biology outside the cell: linking computational tools to cell-free systems

As mathematical models become more commonly integrated into the study of biology, a common language for describing biological processes is manifesting. Many tools have emerged for the simulation of in vivo synthetic biological systems, with only a few examples of prominent work done on predicting the dynamics of cell-free synthetic systems. At the same time, experimental biologists have begun to study dynamics of in vitro systems encapsulated by amphiphilic molecules, opening the door for the development of a new generation of biomimetic systems. In this review, we explore both in vivo and in vitro models of biochemical networks with a special focus on tools that could be applied to the construction of cell-free expression systems. We believe that quantitative studies of complex cellular mechanisms and pathways in synthetic systems can yield important insights into what makes cells different from conventional chemical systems.

Introduction

Synthetic biologists seek to simplify the understanding of biological systems by constructing biochemical pathways and building computational models to simulate the behavior of those pathways (De Jong, 2002; Andrianantoandro et al., 2006). This shift toward an engineering model of experimentation has revealed intriguing details about the architecture of biological networks (Milo et al., 2002), but has largely neglected to integrate older methods of biological inquiry, especially in vitro biology.

In vitro synthetic biology is an emerging area that focuses on complex biosynthesis, directed evolution, and reconstitution of biological functions (Forster and Church, 2007; Hodgman and Jewett, 2012; Swartz, 2012; Guterl and Sieber, 2013). In vitro reactions, also termed cell-free systems in this review, are defined as a collection of biochemical components used to quantify properties of biological systems and/or produce biological products, such as nucleic acids, polypeptides, or metabolites. Conventional in vitro systems are routinely used in biochemistry to measure binding affinity (Shutt and Cox, 1972; Poland et al., 1976; Strauch, 1995), assess reactivity (Waugh, 1954; Bekhor et al., 1969; Assmann and Brewer, 1974; Mari, 2002), and determine molecular structure (Solomon and Varshavsky, 1985; Weeks, 2010) of cellular components. Reconstituted in vitro systems are used to demonstrate the molecular basis of transcription and translation in vivo (Hoagland et al., 1958; Nathans et al., 1962). In vitro systems are also used in high-throughput screening of proteins (Hanes and Pluckthun, 1997; Zhu et al., 2001; Goshima et al., 2008), RNA (Koizumi et al., 1999; Robertson and Ellington, 1999; Goler et al., 2014), and DNA (Higuchi et al., 1988). High-throughput screening of RNA compounds is often used in directed evolution experiments to develop riboswitches and other auto-catalytic RNA structures that have utility in biosynthetic applications (Koizumi et al., 1999; Robertson and Ellington, 1999; Goler et al., 2014). In these examples, in vitro systems are applied as minimal and biomimetic model systems to study single cellular components in isolation (Zubay, 1973). These properties of in vitro systems resonate with the bottom-up approaches of synthetic biology and have indeed been exploited to create complex circuitry in cell-free systems (Kim et al., 2006; Kim and Winfree, 2011; Padirac et al., 2012). For example, an in vitro oscillator was developed by using cellular machinery to transcribe a pair of nicked-promoter constructs (Kim and Winfree, 2011). The first construct produces a transcript that inhibits the second construct by strand displacement, while the second construct produces an RNA oligo that activates the first construct (Kim and Winfree, 2011). As a result, the system forms a negative feedback loop that produces oscillation in the activities of the promoters (Kim and Winfree, 2011).

In vitro systems can be integrated with other materials to create hybrid constructs (Holtz and Asher, 1997; Murakami and Maeda, 2005; He et al., 2012; Langecker et al., 2012; Singh et al., 2013; Munkhjargal et al., 2014). A recent work develops freeze-dried in vitro reactions stored on paper disks (Pardee et al., 2014). These in vitro systems are easily stored and can be activated with water, greatly increasing the portability and flexibility of cell-free systems for applications in mobile diagnostic systems. Another intriguing class of hybrid constructs is the encapsulated cell-free system, which can also be referred to as artificial cells. These artificial cells were originally created to study the origin of cellular life, but have recently been used as biomimetic systems to address other biological questions. Pioneer work on these systems include the synthesis of poly-A RNA in self-reproducing vesicles (Walde et al., 1994), the replication of an RNA template in liposomes (Oberholzer et al., 1995b), and the compartmentalization of PCR (Oberholzer et al., 1995a). These work demonstrated that enzymatic activity could occur inside a liposome and direct the de novo synthesis and replication of nucleic acids. Further efforts in the field yielded enzymatic synthesis of membrane lipids inside liposomes to increase compartment size (Wick and Luisi, 1996), evidence of base pair recognition between components of a phosphatidyl nucleoside membrane (Berti et al., 1998), and poly(Phe) production inside liposomes loaded with ribosomal components (Oberholzer et al., 1999). With the advent of encapsulated protein synthesis, there was a focused attempt to reproduce key features of cellular systems using artificial cells, including the production of functional proteins (Yu et al., 2001), implementation of a transcriptional cascade (Ishikawa et al., 2004), and the membrane targeting of a translated protein (Noireaux et al., 2005).

In addition, artificial cells can perform fundamental functions associated with natural cells, such as formation of membrane pores via alpha hemolysin expression (Chalmeau et al., 2011), execution of genetic programs like a positive feedback loop (Kobori et al., 2013), and other processes associated with sensing and responding to the environment (Martini and Mansy, 2011; Lentini et al., 2014). While artificial cells cannot currently undergo self-reproduction (Noireaux et al., 2011), they have been used to gain insight into features of natural cells, including molecular crowding (Sokolova et al., 2013; Tan et al., 2013), compartmentalization (Matsuura et al., 2012), and RNA-facilitated encapsulation (Black et al., 2013). Furthermore, artificial cells have potential applications in drug delivery (Safra et al., 2000; Kaneda et al., 2009), biosensors (Martini and Mansy, 2011; Hamada et al., 2014; Lentini et al., 2014), biosynthesis (Kuruma et al., 2009; Moritani et al., 2010; Maeda et al., 2012), and bioenergy. Due to the tractability and bio-compatibility of artificial cells, they represent a potentially safer strategy when compared to natural cells for targeted therapeutic treatment.

Perhaps, the most intriguing ramification of developing in vitro synthetic biology will come from the establishment of new algorithms to simulate the behavior of these systems. Computational models of artificial cells could unite chemical and biological theory, combining the defined and predictable nature of in vitro reactions with the robust and sensitive qualities of natural cells. To date, however, computational tools for modeling artificial cell systems have not been established.

The computational toolbox for cell-free synthetic biology could be developed using two sources of models. On the one hand, physical models of single cellular components can be created from first principles, which lead to conventional focus on tools to predict structure and dynamics of single components (Bradley et al., 2005; Park et al., 2006; Tang et al., 2006; Zanghellini et al., 2006; Shaw et al., 2010; Lindorff-Larsen et al., 2011; Wijma and Janssen, 2013). For example, the enzyme glycoxylase II was re-designed to lose its original catalytic action and instead carry a functional beta-lactamase domain, which conferred antibiotic resistance to bacteria that carried the modified protein (Park et al., 2006). On the other hand, the advent of systems biology creates a wide-range of mathematical models for predicting system dynamics of natural cells (Klumpp et al., 2009; Jamshidi and Palsson, 2010; Park et al., 2010; Scott et al., 2010). Computational tools have been used to describe diverse biological functions, including somitogenesis, T-cell antigen discrimination, and heterogeneous vesicle formation (Lewis, 2003; Altan-Bonnet and Germain, 2005; Heinrich and Rapoport, 2005; Gunawardena, 2014). These tools describe interactions between many biological components and emergent dynamics due to the complex relationships between them. Can these tools be integrated into the modeling of complex cell-free systems?

In this review, we present computational tools created for both in vivo and in vitro systems that are validated experimentally. In accordance with synthetic biologists’ goal of composing biological components into rational arrangements, we seek to bridge the gap between our understanding of complex biological networks and fundamental biochemical processes by comparing modeling algorithms for both systems (Figure 1). We will also examine some of the challenges that researchers face when engineering artificial cells. We intend to propose a framework for synthetic biologists to build novel artificial cellular systems and to identify underserved research areas for computational model development.

FIGURE 1

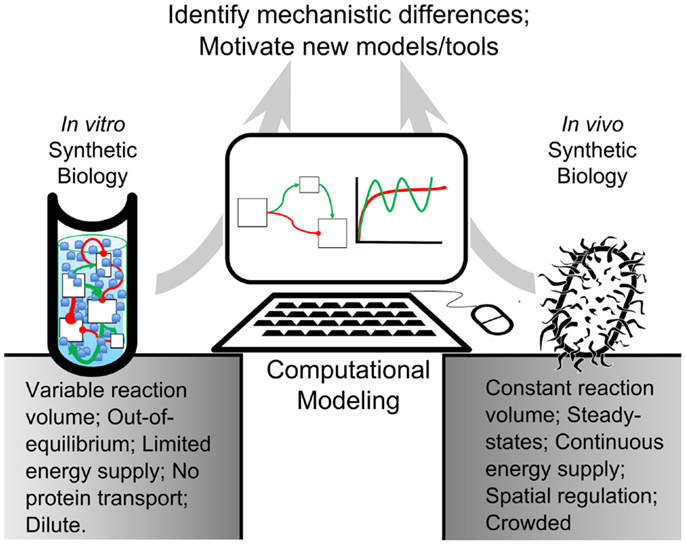
Figure 1. Modeling-based inquiry of cell-free and in vivo synthetic systems. An abstracted synthetic pathway (boxes and arrows) is modeled on a computer. The simulated expression dynamics are compared to biological and cell-free iterations of the process of interest. By using computational models to establish quantitative differences between in vitro reactions and in vivo systems, we could identify mechanisms in living organisms that contribute to desirable network behavior. These mechanisms could be added to in vitro reactions, bestowing useful properties on their processes. This way, computational modeling would bridge the gap between in vitro and in vivo reactions.

Modeling Algorithms

Deterministic Modeling

Deterministic models typically consist of differential equations that predict the kinetics of a biological network based on past dynamics of the system and its initial conditions (Di Ventura et al., 2006). Deterministic models have been used to simulate synthetic gene networks, including inverters (Yokobayashi et al., 2002; Karig and Weiss, 2005), switches (Michalowski et al., 2004; Collins et al., 2006; Ham et al., 2008), band-pass filters (Basu et al., 2004; Sohka et al., 2009), multi-cellular networks (You et al., 2004; Basu et al., 2005; Tabor et al., 2009; Danino et al., 2010), and oscillators (Elowitz and Leibler, 2000; Stricker et al., 2008). Deterministic models have also been applied to simulate the behavior of tumor-invading bacteria (Danino et al., 2012), prokaryotic circuits capable of producing artificial analog computation (Daniel et al., 2013), and a transcriptional oscillator that retains its period across a range of temperatures (Hussain et al., 2014). These models utilize Michaelis–Menten equations to describe each chemical reaction.

For the modeling of in vivo systems, a baseline level of expression is typically included to model leaky activity of promoters. The leaky expression is attributed to the relationship between transcription factor binding strength and the corresponding RNA polymerase-promoter affinity. The typical model also assumes that all parameters are constant, which may not be true in vivo due to fluctuating states of intracellular environments.

In contrast to in vivo systems, cell-free systems could offer greater predictability by having well-defined parameters, easily controlled inputs, and fewer unknown interactions. Therefore, cell-free systems may be more accurately simulated than in vivo reactions using deterministic models. These cell-free systems can perform many of the same functions of natural organisms with circuits including oscillators (Kim and Winfree, 2011; Montagne et al., 2011; Weitz et al., 2014), switches (Kim et al., 2006; Padirac et al., 2012), and logic elements (Takinoue et al., 2008). A recent work modeled in vitro expression by accounting for the rate of green fluorescent proteins (GFP) maturation, which is often ignored for in vivo models (Stogbauer et al., 2012). Constructing computational models of in vitro systems can also provide insights into the effects of network architecture on the dynamic behavior of genetic circuits. Previous work has shown that biological pathways can achieve oscillatory behavior via bi-stable, hysteretic loops, and demonstrated in vitro that these mechanisms could be used in living systems to control the transition to the mitotic phase in Xenopus embryogenesis (Hasty et al., 2001; Pomerening et al., 2003). Subsequent research into the modeling of synthetic in vitro transcriptional oscillators was used to determine the optimum system parameters required for sustained circuit behavior and to identify the network’s period and amplitude limitations (Kim and Winfree, 2011). Recently, this same model was applied to simulate the behavior of an in vitro oscillator after compartmentalization in emulsion droplets and was found to accurately represent the trend observed in individual encapsulated circuits (Weitz et al., 2014).

Models of in vitro systems are also used to explore the impact of biological phenomena that are missing in reconstituted systems. Molecular crowding represents such a phenomenon and has been incorporated into models of gene expression to explain some of the desirable properties of biological systems. Recent work demonstrated that molecular crowding, either induced by crowding agents such as dextran or coacervation of encapsulated circuits can greatly increase the expression rate and total protein production of in vitro systems (Sokolova et al., 2013; Tan et al., 2013). One of these works investigates the mechanisms of enhanced transcriptional output induced by coacervation of encapsulated cell lysate (Sokolova et al., 2013). Coacervation was induced by treating encapsulated cell lysate with a concentrated salt solution, drawing water out from the droplets by osmotic pressure (Sokolova et al., 2013). Protein synthesis was dramatically increased within coacervated systems (Sokolova et al., 2013). A computational model of transcription–translation reactions revealed that the rise in mRNA output could not be explained simply by the increase in density of transcription machinery induced by coacervation (Figure 2) (Sokolova et al., 2013). The model instead suggested that the increase in gene expression was due to an elevated kinetic transcription constant in coacervated compartments, and a rise in the T7 polymerase association constant caused by increased molecular crowding (Sokolova et al., 2013).

FIGURE 2

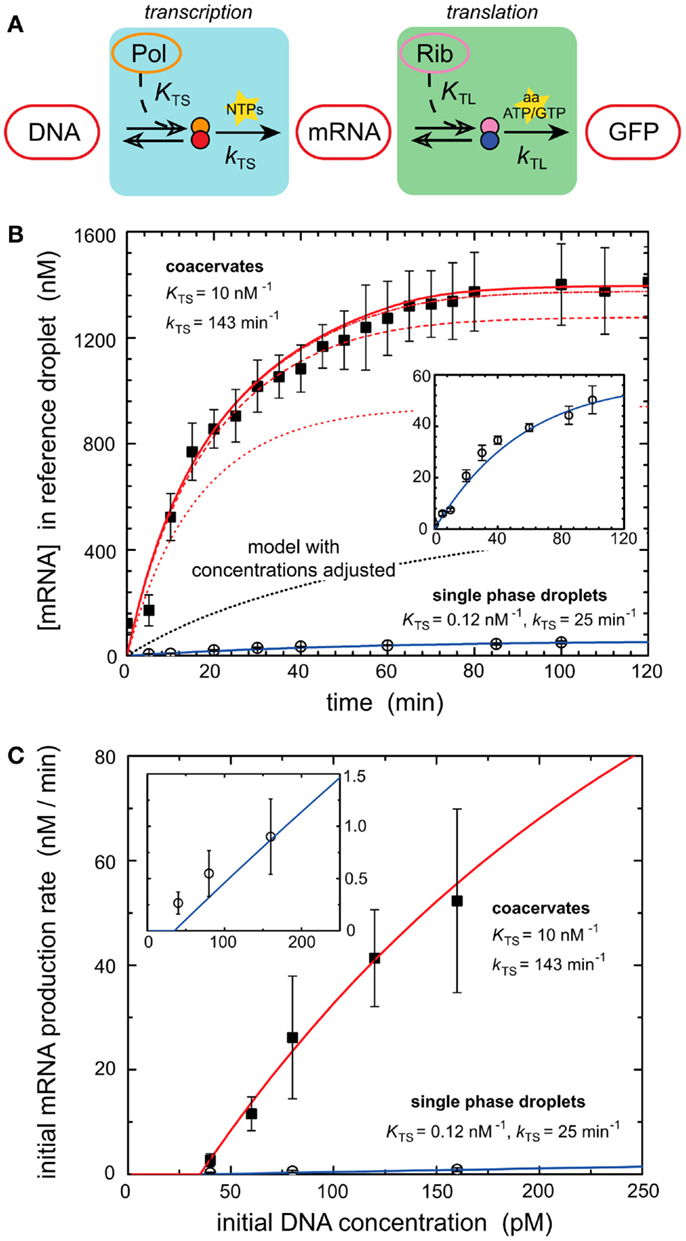
Figure 2. Enhancement of transcription by coacervation. (A) A schematic of biochemical processes that produce GFP from a DNA template via transcription and translation. Key reactants such as NTPs, amino acids, ATP, and GTP are depicted at their active steps. (B) Graph of mRNA production (nanomoles) over time from a genetic module encapsulated in coacervates and droplets. Dark squares represent experimental results for coacervate reactions. Open circles represent experimental results for droplet reactions. Lines represent deterministic simulations of the genetic module. Solid blue line corresponds to simulation of droplet reaction. Inset is a re-scaled view of the same experimental and simulated results of droplet reaction. The dotted black line represents a deterministic model of GFP production in coacervates with adjusted concentrations of transcription machinery. Red lines represent simulation results using altered T7 RNA polymerase binding constant K_TS and transcription rate constant k_TS. The series of red lines represents simulation results for a constant k_TS of 143 min⁻¹ and different values of K_TS, 0.12 nM⁻¹ (dotted), 1.0 nM⁻¹ (dashed), 10 nM⁻¹ (dash-dot), and 100 nM⁻¹ (solid). Predicted values of K_TS and k_TS are listed for both coacervates and single phase droplets. (C) Initial rates of mRNA production as dictated by the initial concentrations of DNA (picomoles), which contain the genetic module. Dark squares represent experimental results for coacervate reactions. Open circles represent experimental results for droplet reactions. The red line represents simulation of coacervate with altered K_TS and k_TS parameters established in (B). The solid blue line represents simulation of droplet reaction. Inset is a re-scaled view of the same experimental and simulated results of droplet reaction. Figure modified with permission from Sokolova et al. (2013).

Stochastic Modeling

To investigate the impact of random fluctuations, stochastic models of cellular processes can be formulated following the master equations. For in vivo systems, noise arises due to intrinsic and extrinsic factors (Elowitz et al., 2002). Extrinsic noise is variation caused by incomplete distribution of reactants within a system, whereas intrinsic noise is variation caused by the discrete nature of small-scale chemical reactions (Elowitz et al., 2002). Both kinds of noise can have a profound impact on biological systems, including partitioning noise observed during replication (Huh and Paulsson, 2011a), variance observed at small reaction volumes within a cell (Karig et al., 2013), and bursts of translation caused by limited transcriptional activity (Pedraza and Paulsson, 2008). Stochastic models have been applied to understand sporulation dynamics of Bacillus subtilis (Chastanet et al., 2010), robustness of a genetic circuit in response to varying environmental conditions (Toni and Tidor, 2013), exoprotease levels in bacterial populations (Davidson et al., 2012), and control of a bacterial population composition with a gene circuit (Sekine et al., 2011; Ishimatsu et al., 2013).

In vitro systems are minimal, which should intuitively simplify the development of computational models based on our experience in cell biology. However, due to this minimality, in vitro systems do not inherently contain mechanisms of natural cells that facilitate robust behavior. These missing mechanisms could increase sensitivity of in vitro systems to non-genetic factors, such as partial degradation products (Kim and Winfree, 2011), stochastic variation at femtoliter volumes (Karig et al., 2013), and molecular crowding (Tan et al., 2013). These factors, while commonly being neglected in models of natural cells, could reduce predictive power of models for cell-free systems. In addition, in vitro systems lack cellular infrastructure, including sub-cellular compartments, transport proteins, and a replication cycle. These missing cellular features could complicate the direct application of computational tools created for natural cells to in vitro systems, necessitating the development of stochastic models to predict and control noise in cell-free systems.

One notable cause of stochastic variation in cell-free expression is the process of encapsulation, which could be simulated using stochastic models. For instance, during the compartmentalization of the PURE system in small liposomes (580 nm > diameter > 35 nm), the distribution of reactants between compartments was shown to follow power law statistics instead of a Poisson distribution as previously assumed (Lazzerini-Ospri et al., 2012). A subsequent study of in vitro systems encapsulated in larger liposomes (575 nm and 2.67 μm, respectively) predicted resulting reactant concentrations via a stochastic model following the Gillespie algorithm (Calviello et al., 2013). Another example of stochastic variation in an encapsulated in vitro system comes from a recent work detailing the behavior of a compartmentalized transcriptional oscillator (Weitz et al., 2014). The performance of the circuit within an emulsion was highly variable and was originally assumed to be the result of intrinsic noise of the system acting stochastically at small volumes (Weitz et al., 2014). However, the model of the reaction demonstrated that intrinsic noise was insufficient to describe the variability exhibited by the system; instead, the dominant cause of the deviation from the deterministic model was more likely to be extrinsic noise caused by heterogeneous distribution of reactants within the emulsion (Figure 3) (Weitz et al., 2014). This kind of discrepancy from the deterministic model is also observed during replication when cytoplasmic components are unequally distributed between daughter cells (Huh and Paulsson, 2011a,b; Weitz et al., 2014). The significant impact of extrinsic noise on this minimal system suggests that reactant distribution is an important factor in encapsulated in vitro reactions, which could be overlooked when considering the source of stochastic variation within in vivo systems (Huh and Paulsson, 2011a,b; Weitz et al., 2014).

FIGURE 3

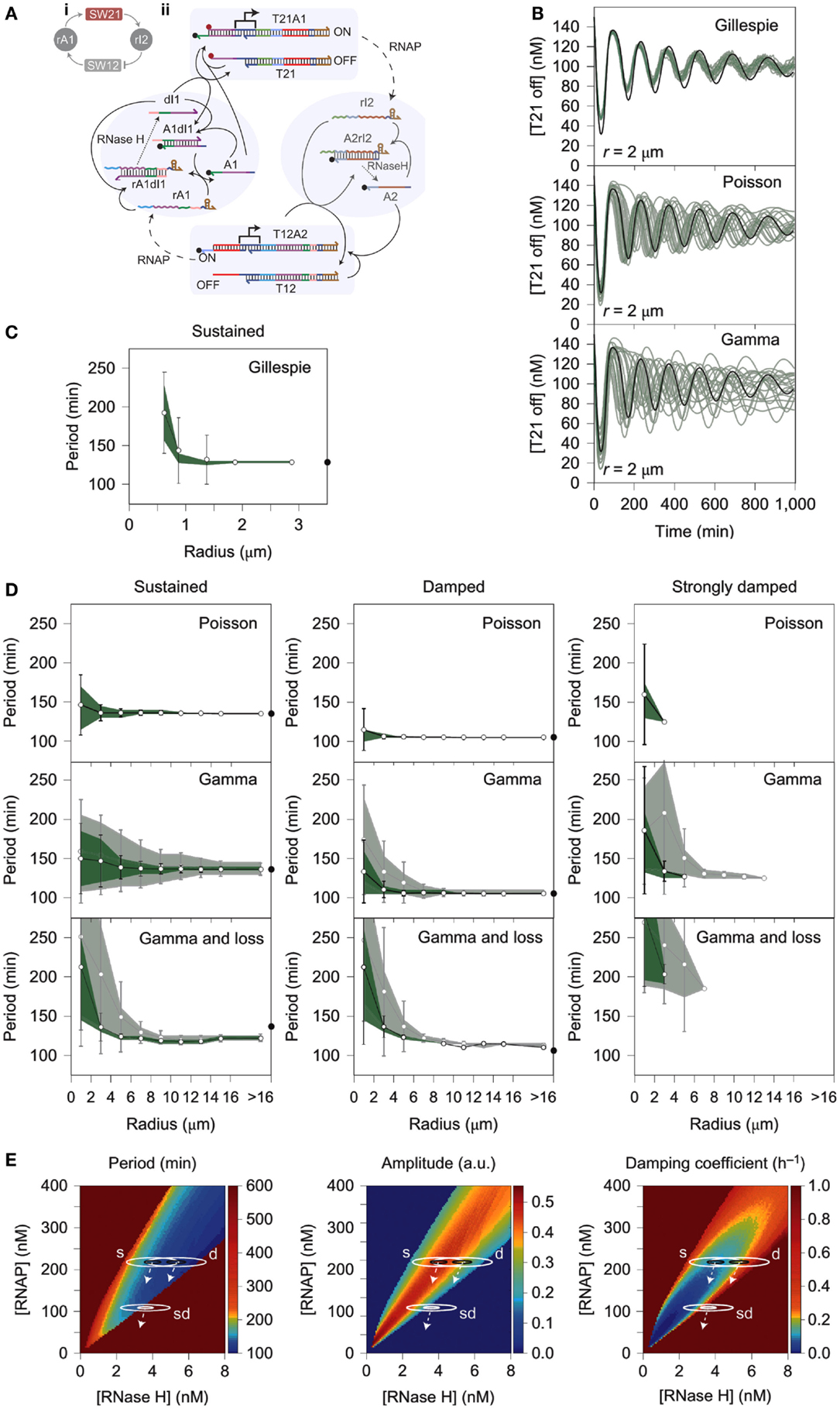
Figure 3. Stochastic simulation of a compartmentalized oscillator. (A) A linear construct (T21A1) transcribes a short RNA oligo (rI2) that base-pairs with a nicked region of another linear DNA promoter (T12A2). Base pairing of rI2 with the nicked DNA region A2 deactivates T12A2 because T7 promoter region of the switch becomes single stranded, referred to as T12. Deactivation of the T12 construct reduces transcription of RNA oligo rA1, which base pairs with nicked DNA region A1 of the T21A1 construct. Base pairing of rA1 with dl1 causes A1, a quencher labeled-strand of DNA, to separate from T21. T21 also has a fluorescent labeled strand of DNA. This reaction activates the fluorescent signal, but deactivates transcription of RNAP because the T7 promoter of T21 becomes single stranded. Essentially, the oscillator is formed by the T21A1 module (SW21) that inhibits the T12A2 module (SW12), which in turn activates SW21. The delayed negative feedback loop causes a temporal delay between ON and OFF cycles of T21A1. (B) The panels show concentrations of T21 in the OFF position (low fluorescence, high transcriptional activity) over time according to the Gillespie algorithm, Poisson Distribution, and Gamma Distribution, respectively. Droplet radius is always 2 μm. (C) The oscillator period is plotted against the radius of the compartment housing the in vitro circuit. The results suggest that only a small percentage of the variability experienced by the system can be attributed to the intrinsic noise of biochemical reactions. (D) Fluctuations of the oscillator period with increasing radius of the compartment. Panels show partitioning variance (error caused by incomplete distribution of reactants) of period following a Poisson distribution, Gamma distribution, or a Gamma distribution that accounts for loss of enzyme activity. Dark green shading corresponds to a scale factor β = 10, and light green shading corresponds to β = 100. (E) Phase diagrams that indicate period, amplitude, and dampening coefficient as a function of RNAP and RNase H concentrations. Solution space that achieves sustained oscillations, dampened oscillations, and severely dampened oscillations are referred to in the diagram as s, d, and sd, respectively. The white arrows represent behavioral trends experienced by the circuit when it loses RNAP and/or RNAse H. Figure modified with permission from Weitz et al. (2014).

The study of molecular crowding revealed how molecular distribution can impact stochastic variation in vitro. Molecular crowding has long been recognized as an important phenomenon for accurately reconstituting the function of biological systems, and recent research efforts have demonstrated that molecular crowding increases expression levels in vitro (Minton and Wilf, 1981; Morelli et al., 2011; Sokolova et al., 2013; Tan et al., 2013). Stochastic models of in vitro systems have also revealed decreased variation of gene expression rates in the presence of molecular crowding conditions, along with increased robustness to environmental perturbations of molecules known to affect the binding affinity of transcription–translation machinery (Tan et al., 2013).

Exploratory Models

Exploratory modeling is used to guide the design of biological circuits. To emulate labor-saving strategies from the engineering disciplines, there has been a push for automated biological design, combining known modules into more complicated architecture (Cheng and Lu, 2012). An automated design algorithm first registers a library of biochemical parts with defined kinetic parameters and interactions described in terms of ordinary differential equations (Marchisio and Stelling, 2008). Next, the algorithm selects certain parts and arranges them into motifs that satisfy a user’s query (Marchisio and Stelling, 2011; Beal et al., 2012; Huynh et al., 2012; Yaman et al., 2012; Huynh et al., 2013). Exploratory models can also be used to analyze the impact of intrinsic noise, extrinsic noise, and variation of kinetic parameters on synthetic genetic machinery (Chiang and Hwang, 2013; Toni and Tidor, 2013). These exploratory models have been used to design in vivo pathways, such as a Boolean network of transcriptional switches implemented in yeast (Marchisio, 2014), a multiplexor circuit in E. coli (Huynh et al., 2013), and an inducible bi-stable system of fluorescent reporters in mammalian cells (Beal et al., 2012).

In theory, these automated genetic design programs could be applied in the development of in vitro expression systems. On the one hand, transcriptional networks in vivo and in vitro have the same circuit architecture and basic components. Furthermore, the parameters used by these automatic genetic design programs are actually determined in vitro, which would make the assembly of in vitro circuits more accurate than in vivo circuits. On the other hand, genetic design programs optimized for in vivo conditions may not account for the chemical conditions experienced by in vitro expression systems. For instance, cell-free expression systems have limited substrates, contain molecular components with different reaction efficiencies than their in vivo counterparts, and do not inherently contain complex mechanisms (such as metabolic feedback loops, assisted protein folding, and protein trafficking) that maintain robustness of cellular functions.

Parameter Definition

While there are a wide variety of equations that describe the behavior of synthetic biological systems, parameters of these equations are mostly unknown. There are several established databases for obtaining enzymatic reaction constants such as KEGG (Kanehisa and Goto, 2000; Kanehisa et al., 2014), BRENDA (Schomburg et al., 2013), SABIO-RK (Wittig et al., 2012), and ExPASy (Artimo et al., 2012). BioNumbers has also collected measurements of biological systems (Milo et al., 2010) and has been used in the modeling of a yeast–bacteria ecosystem (Biliouris et al., 2012), a predictor of anti-microbial protein efficacy (Melo et al., 2011), and a computational representation of distributive metabolic networks (De la Fuente et al., 2013). The difficulty of modeling in vivo systems stems from the context-dependency of reaction parameters. The kinetic constants of biological molecules used in modeling in vivo systems are often measured in vitro, where conditions may not reflect the pH or molecular crowding conditions experienced by those molecules in natural cells. In contrast, these kinetic constants that are quantified in vitro could be directly applied to cell-free reactions, thus creating models with high accuracy and predictive power. We compare kinetic constants determined for the two dominant in vitro expression platforms: whole cell extracts and the PURE system (Table 1). The table contrasts the transcription rate constant, translation rate constant, and mRNA degradation rate. The transcription rate is slightly higher in the PURE system, but the whole cell extract has a significantly higher translation rate and mRNA degradation rate. These results suggest the presence of critical factors in whole cell extracts that have not been fully reconstituted in the PURE system. We note that the two studies used different genes, suggesting potential follow-up work to systematically compare and model different in vitro systems.

TABLE 1

Table 1. Expression constants for in vitro systems.

Now that we have outlined the broad classes of models available for synthetic biologists and identified some areas of potential growth for researchers interested in developing tools for cell-free systems, we will discuss the specific applications of computational tools to the design of an in vitro gene expression platform known as the artificial cell.

The Components of Artificial Cells

To layout the vision toward a comprehensive model of artificial cells, we have classified the system into the Input, Processor, Output, and Shell (Figure 4). Here, we define the Input as the starting concentrations of enzymes, metabolites, and inducers that are present in a system. The Processor is defined as the cellular circuit that dictates genetic composition and functional relationship between genes. The Output is described as the concentration of the final product(s) of a system. The Shell refers to the liposome barrier that controls interaction between artificial cells and the environment. We discuss mathematical design and optimization of each component and assemble a suite of computational tools that could be applied for predictive modeling of artificial cells.

FIGURE 4

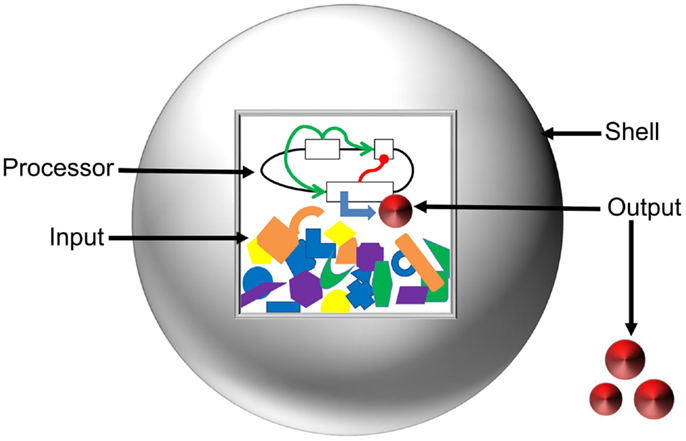
Figure 4. Anatomy of artificial cells. Input and Processor are contained inside the liposome Shell (gray sphere). The Inputs, represented by orange, blue, purple, yellow, and green shapes, are the energy supply, enzymatic co-factors, and substrates necessary for gene expression. The Processor is the cellular circuit (represented by black lines and white boxes) that controls protein production. The Processor determines the network architecture of cellular components (functional relationships represented by green and red lines) and the machinery required to interpret the information. The action of the Processor on the Input produces the Output (red disks) in the form of either a metabolite or a protein. The Shell serves to modulate diffusion of signals from the environment, maintain chemical conditions favorable for gene expression, and allow for export of the Output.

Input

The Input is defined as the co-factors, substrates, and chemical energy used in the execution of in vitro reactions. Although these factors are known to significantly alter gene expression, concentrations of these molecules are difficult to be perturbed in vivo, making their effects on gene expression elusive (Jewett et al., 2008, 2009). Mathematical modeling offers a unique solution to this problem by providing a formalized framework to evaluate the accuracy of a predicted Input concentration. A few publications have sought to quantify the impact of the Input on gene expression in cell-free systems. However, given the intricate complexity required to produce proteins in vitro, there is still substantial room for innovation. One computational model was created to determine the epistatic interactions between 69 elements of an in vitro transcription–translation system (Matsuura et al., 2009). Another model utilized a machine learning algorithm to stochastically vary different components of the Input (Caschera et al., 2011). Reaction systems with the highest expression levels were found to have two primary expression patterns: one with a rapid rise of protein production and the other with an initial decrease in protein level before a rapid rise (Caschera et al., 2011). A stochastic model of an in vitro transcription–translation system was used to vary reaction components such as potassium, magnesium, and spermidine to investigate the impact of environmental perturbations on gene expression (Tan et al., 2013). To aid the development of subsequent models that describe the effects of the Input on gene expression in vitro, a recent work has compared physiological and supplemented concentrations of intracellular components within cell-free systems (Jewett et al., 2008).

Processor/Output

The Processor is defined as the DNA sequence that dictates genetic composition and functional relationship between genes, together with the machinery required to interpret it [RNA polymerases (RNAPs), transcription factors (TFs), translation machinery]. The Output is defined as the final product of a system. In the context of this review, we define Output as the product of the activity of the Processor (mRNA for transcription systems, protein for coupled transcription–translation systems, and metabolites for enzymatic reactions). We will review Processor and Output together because they are required for the integral understanding of gene expression. These modules are critical to connect input signals to functions of synthetic biological systems. In the following sections, we will review some of the strategies developed to predict activities of Processor modules and to control the expression of genes. Many of these approaches have been validated primarily in natural cells, but could be adapted for cell-free systems.

Sequence-Based Control of Promoter Transcriptional Activity

Cells have evolved mechanisms to regulate both transcription and translation rates to adjust the expression levels of target proteins (Figure 5). The promoter region allows the binding of RNAPs to DNA to initiate the synthesis of mRNA. Prokaryotic RNAPs typically bind promoters through the specific recognition of their σ-subunits to conserved sequences at the −10 and −35 promoter positions (transcription starts at position + 1), while RNAP α-subunits interact with elements located upstream of the −35 site. Furthermore, the activity of RNAP is modulated by activators and repressors. Following RNAP–DNA interactions, mRNA is synthesized until the RNAP reaches a terminator.

FIGURE 5

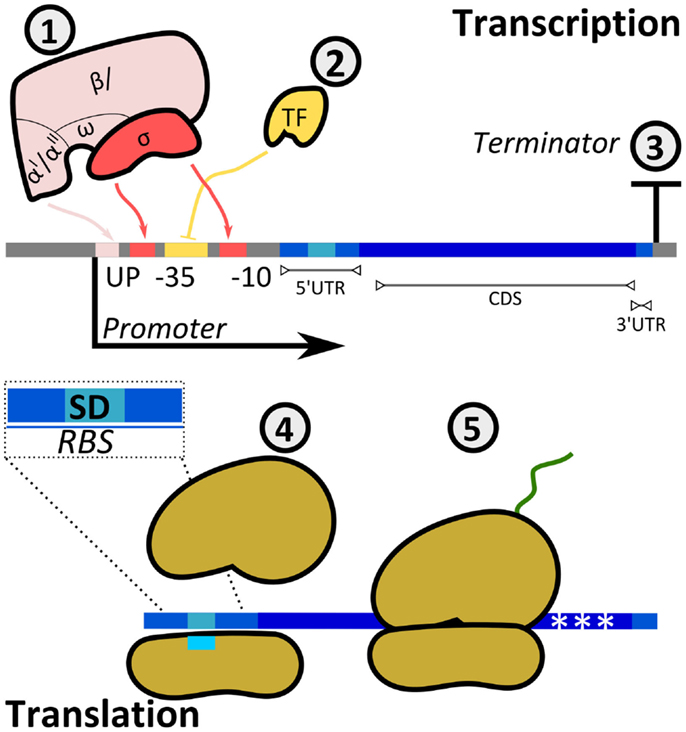
Figure 5. Regulatory mechanisms of protein production rates. The synthesis rate of a protein can be controlled at either transcriptional (1, 2, 3) or translational (4, 5) levels. (1) The multi-subunit bacterial RNAP interacts with the promoter at boxes −35 and −10 (σ-factor) and at the UP element (α-subunits). The sequence of the promoter defines the specificity and affinity of the binding. (2) Transcription factors (TFs) either enhance or inhibit the binding of RNAP to the promoter (in the example, TF is a repressor inhibiting RNAP–DNA interactions). TF–RNAP–DNA interactions determine the initiation of transcription. The synthesized mRNA contains a 5′-untranslated region (UTR), a coding sequence (CDS), and a 3′-UTR. (3) The terminator sequence determines RNAP release from DNA. (4) Translation initiation is the rate limiting step for translation. It is determined by interactions between the ribosomal binding site and the small ribosomal subunit, with specific heteroduplex mRNA:rRNA formation between the Shine–Dalgarno (SD) sequence in the transcript and the 16S rRNA. In addition, codon usage (5) can affect the amount of translated protein.

Several studies have established libraries of artificial promoters with different sequences, which are compared by measuring the accumulation of reporter proteins (Hammer et al., 2006; De Mey et al., 2007; Ellis et al., 2009; Rhodius and Mutalik, 2010; Lu et al., 2012; Rhodius et al., 2012; Temme et al., 2012; Iyer et al., 2013; Shis and Bennett, 2013). In some of these studies, the experimental data collected have been used to build inference models (Gunawardena, 2014), in order to establish causal relationships between promoter sequence and its strength. Next, we will describe approaches used to predict promoter strengths, which we define as the association rate constants of RNAP–promoter complex. Therefore, if the binding affinity of RNAP to a promoter is high, the promoter is “strong,” which increases Output accumulation. Conversely, a promoter is “weak” if the affinity between RNAP and promoter is low, resulting in a reduced transcription rate.

Promoter Strength Can be Predicted Based on RNAP and Transcription Factors Binding Dynamics

Cellular biochemical functions, including gene transcription, have been grouped into defined subsets according to their approximated fitting to differential equations in the form of Hill functions. This approach is useful for predicting the activity of a promoter, which depends on the binding affinity of RNAP and regulatory TFs to DNA, the position of the promoter, and the position of other regulatory sequences in the promoter (Ang et al., 2013). For example, the transcription of a gene controlled by a promoter with binding sites for an RNAP and a TF can be expressed as Eq. 1 for an activator and Eq. 2 for a repressor.

$\frac{\mathit{dy}}{\mathit{dt}}=k^{\prime }+k\left(\frac{x^n}{K^n+x^n}\right)-k_{d}y$ (1)

$\frac{\mathit{dy}}{\mathit{dt}}=k^{\prime }+k\left(\frac{K^n}{K^n+x^n}\right)-k_{d}y$ (2)

For both Eqs (1) and (2), y is the Output (mRNA), k_d represents the degradation rate constant. For Eq. 1, k′ is the basal rate of Output production associated to RNAP affinity for the promoter and k is the maximum production rate (measured by the energy binding of activator TF to RNAP). The bracketed term corresponds to a Hill function, where x is the concentration of the TF and K is the Hill’s constant corresponding to the binding affinity of TF to DNA. Finally, n is the Hill coefficient that indicates TF cooperative effect. For Eq. 2, k′ + k accounts for the expression rate in un-repressed conditions and corresponds to the binding affinity of RNAP to the promoter. In this case, the Hill function has a decreasing sigmoidal shape. In the absence of TFs (either activators or repressors), as for the case of constitutive promoters, the Output production will depend exclusively on the binding affinity of RNAP to DNA.

A recent work described a novel method based on the Hill functions to characterize regulatory elements in cell-free systems (Chappell et al., 2013). In this study, the relative activities of σ⁷⁰-promoters were demonstrated to correlate well between cell-free systems and bacterial systems (Figure 6A). Furthermore, they tested the activity of a promoter in the presence of an activator transcription factor, LasR (Figure 6B). After the addition of acylhomoserine lactone (AHL), LasR affinity for the promoter increases, allowing recruitment of RNAP and subsequent gene transcription. Output levels (GFP) of different LasR-regulated promoters were found to correlate well between in vivo and in vitro systems (Figure 6B). However, the authors observed that estimated RNAP binding efficiency did not correlate well between in vivo and in vitro systems. Several factors could account for the observed differences: (1) concentrations of macromolecules (i.e., proteins, DNA, and ribosomes), (2) ratios between proteins and other co-factors (proteins or enzymes), (3) structure and supercoiling of DNA, (4) molecular crowding (confinement vs. non-confined environment), (5) composition of energy and/or redox power regeneration systems. Due to these differences, it remains unclear when it is appropriate to extrapolate kinetic information between in vitro and in vivo systems. To this end, mathematical modeling could help to identify and potentially resolve the differences.

FIGURE 6

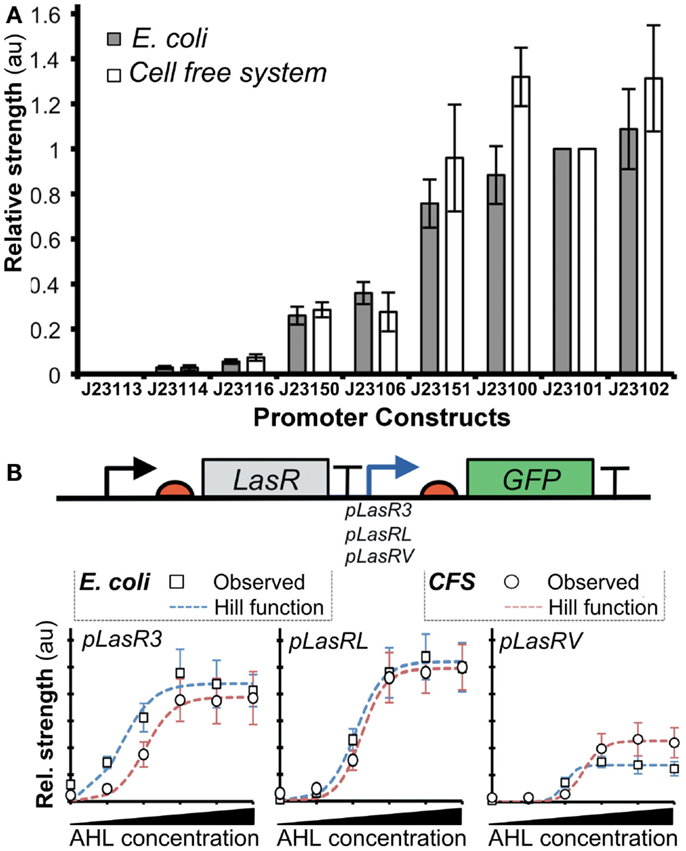
Figure 6. Comparison of promoter strengths in vivo and in vitro. (A) Several promoters controlling expression of GFP showed comparable activities when assayed in cell-free systems and E. coli. The x-axis shows different promoter-GFP constructs. The y-axis shows relative promoter strengths measured by GFP intensities (au). (B) GFP expression is regulated by pLas promoters that are bound by an activator LasR with different affinities. Fluorescence intensities were determined for the constructs both in vitro (open circles) and in vivo (gray squares). A model of gene expression was built using the Hill function (red dashed lines represent cell-free systems; blue dashed lines represent E. coli). The result shows that Hill functions can be used for quantifying gene expression in cell-free systems. Figures modified with permission from Chappell et al. (2013).

Prediction of Promoter Strengths Based on Its Nucleotide Sequence

In order to predict the strength of a given promoter sequence, extensive effort has been made to build models that describe the causal relationships between promoter sequences and their affinity to RNAP. In general, the binding energy of RNAPs to DNA has been considered to be a linear addition of the individual energy barriers of each base in the promoter sequence (thermodynamic-based models; Figure 7A) (Mulligan et al., 1984; von Hippel and Berg, 1986; Berg, 1988; Takeda et al., 1989; Stormo, 2000; Benos et al., 2002; Segal et al., 2008; Rhodius and Mutalik, 2010). However, inconsistencies have been observed between models and experimental observations. For example, several promoters were predicted to exhibit strong transcription rates, but were either weak or inactive in vivo (false positives) (Stormo, 2000; Man and Stormo, 2001; Rhodius and Mutalik, 2010). A fraction of strong promoters were also not identified by the models (false negatives) (Maerkl and Quake, 2007).

FIGURE 7

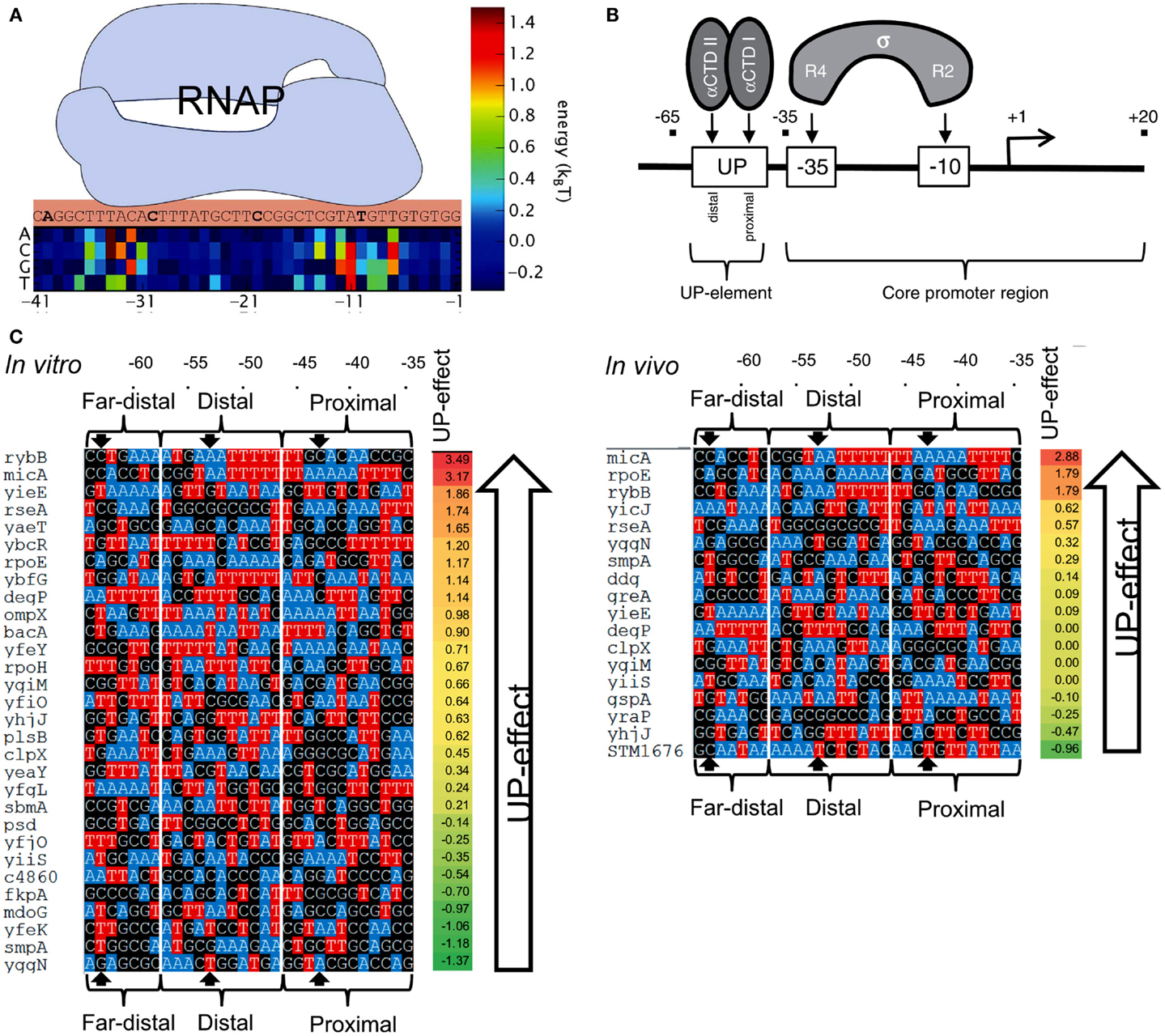
Figure 7. Prediction of promoter strengths based on DNA sequences. (A) The binding energy of RNAP (light blue shape) to a promoter can be estimated based on its DNA sequence. A position matrix defines the contribution of each base to the total binding energy. Bases at sites −10 and −35 are major contributors to the overall binding energy. At some positions, the occurrence of certain bases decreases RNAP binding energy. (B) The approach is used to determine the effect of UP elements on gene transcription. UP elements are recognized by the α-subunit of RNAP and located upstream of the −35/−10 sites (core). (C) The activities of several E. coli promoters containing an UP element (with three distinguished substrings, termed proximal, distal, and far-distal) were determined both in vitro (left) and in vivo (right), and compared to the activity of the core promoter (promoter lacking the UP element). The impact of UP elements on gene transcription was calculated by the ratio between the activity of a complete promoter (a core promoter plus an UP element) and the activity of the corresponding core promoter. The bases A and T are colored to indicate the AT tracts in the promoters. AT tracts are known to increase the influence of UP elements on gene transcription. Figures modified with permission from Brewster et al. (2012) and Rhodius et al. (2012).

Despite these drawbacks revealed by genome scale studies of promoter activity, additional models have been developed and used to predict bacterial RNAP-promoter activity in vivo based on their sequences. For example, a set of promoters with variable RNAP-σ⁷⁰ binding sites were tested for their strengths, in terms of both transcriptional activity and activity of the encoded gene (β-galactosidase) (Brewster et al., 2012). The sequences of the promoters were chosen based on a predictive model, built with sequence-based position weight matrices and binding energies. The model predictions correlated strongly with observed promoter strengths in vivo. The model was also applied to promoters that were regulated by a repressive transcription factor, confirming that the model can be used for prediction of promoter strengths. In another study, a library of Escherichia coli lac promoters was generated (Kinney et al., 2010). The promoters contained mutations in binding sites of both RNAP-σ⁷⁰ and CRP, as well as an activator TF. Promoters with both or either binding sites were assembled and their strengths were measured according to reporter GFP fluorescence intensity. RNAP–DNA, CRP–DNA, and RNAP–CRP interaction strengths determine the overall promoter strengths. The promoter strengths were estimated using a model based on position matrices for each binding site, which assigned a quantitative value to the influence of each position along the promoter on its activity. Through this strategy, the authors were able to model RNAP– and CRP–DNA binding strengths, and also RNAP–CRP interaction energy, to establish relationships between promoter sequences and transcription rates.

Predictive models of promoter strengths in vitro are less well established when compared to in vivo models. Rhodius et al. (2012) assessed strengths of promoters with mutations in −35/−10 sequences and the upstream UP elements (Figure 7B). Using a library of core promoters (containing regions −35/+20) and their corresponding full-length versions (core promoter plus UP element, −65/+20), the authors determined the activity of the promoters both in vivo (Output: GFP) and in vitro (Output: mRNA). They built a model to estimate the effects of the UP elements on promoter strengths. The authors built position weight matrices (PWMs) for each motif in the promoters (Stormo, 1990; Rhodius and Mutalik, 2010). The relative binding affinity of σ^E to a DNA sequence was estimated by adding the individual weights of each nucleotide in the motif. The scores of core promoters, UP elements, and full-length promoters were used to calculate the overall promoter strengths (Figure 7C). Based on the approach, the predicted and observed promoter strengths showed strong correlation between in vivo and in vitro systems.

Theoretic Basis for Modeling T7 Promoter Activity for Cell-Free Circuits

In cell-free systems and artificial cells, the use of bacterial RNAPs has been challenging due to their multimeric composition and low transcription efficiency. Instead, the use of monomeric, phage-derived RNAPs, such as T7-RNAP and SP6 RNAP, can simplify the design and application of in vitro genetic circuits. In addition, T7-RNAP is a highly processive polymerase, is not regulated by TFs, and binds to specific T7 promoters (Bintu et al., 2005). To date, no sequence-based and predictive models of T7 promoter strength have been published. To this end, predictive thermodynamic models for T7 promoter strengths could be developed following existing models for bacterial RNAPs.

Tremendous biophysical information is available for T7 RNAP and its associated T7 promoters. A collection of T7 promoters with different DNA sequence was tested in vivo (Imburgio et al., 2000) by quantifying mRNA as Output signals. In another study, T7 promoters with mutations in −11 to −8 bases were assayed using a split T7 RNAP, where C-terminal and N-terminal fragments were individually expressed (Shis and Bennett, 2013). When both fragments are expressed, T7 RNAP becomes functional (Output: GFP). Mutations were also introduced in the C-terminal fragment’s specificity loop of T7 RNAP, which gave rise to combination of promoters and T7-RNAP variants with a broad range of transcriptional activity. Recently, a library of 21 T7 promoters was characterized in cell-free platforms using an in vitro transcription–translation system (Chizzolini et al., 2013). In addition, detailed kinetic data of T7-RNAP–promoter interactions are available (Bandwar et al., 2002), as well as protein:DNA structural data (Cheetham and Steitz, 2000). Taken together, these data suggest that a sequence-based predictive model of T7 promoter strength could be developed and subsequently validated for in vitro control of gene expression levels.

Control of Translation Initiation Rate by Modification of Ribosomal Binding Sequence

Translation initiation rates can be controlled to modulate Output accumulation in vitro (corresponding to protein accumulation). The translation process involves three main steps, including initiation, elongation, and termination (Simonetti et al., 2009). In bacteria, the 16S rRNA (from the small ribosomal subunit 30S) interacts with the Shine–Dalgarno (SD) sequence present in the 5′-untranslated region (UTR) of mRNAs (Kozak, 1999) (Figure 5). The initiation complex is completed with the binding of initiation factors and the large ribosomal subunit 50S. Additional sequences upstream and downstream the SD sequence determine the initial translation rate (Espah Borujeni et al., 2014). These sequences together with the SD sequence are termed ribosomal binding site (RBS).

Ribosomal binding site strengths can be predicted using multiple tools, including RBS calculator (Salis, 2011) (Figure 8A), UTR Designer (Seo et al., 2013), and RBSDesigner (Bujara et al., 2010). These tools compute differences of free energy between the folded secondary structures of a RBS (representing the state when mRNA is not bound to ribosomes) and its unfolded state (bound to the ribosome). The relative functionality and limitations of these RBS models were recently reviewed elsewhere (Reeve et al., 2014).

FIGURE 8

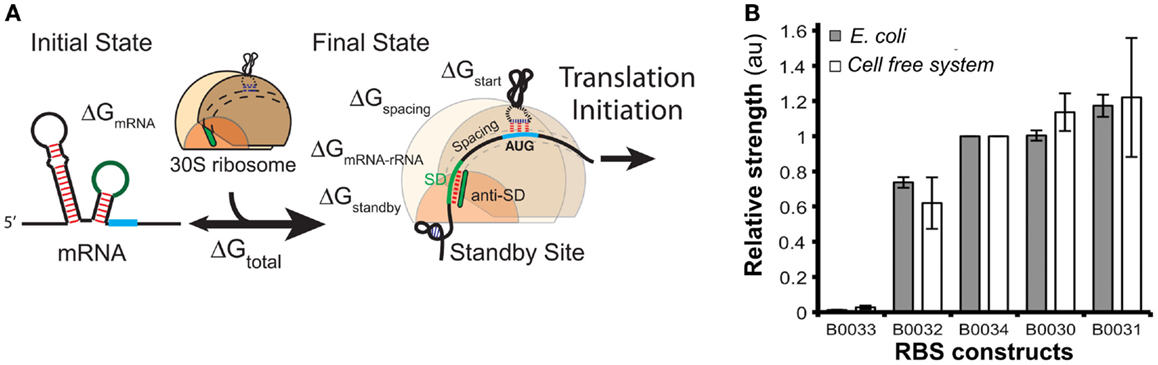
Figure 8. Models of ribosome binding sites (RBS) and their potential applications for in vitro systems. (A) A thermodynamic model for the calculation of RBS strength based on its sequence. The RBS calculator (Salis, 2011) is based on the calculation of the mRNA–ribosome binding energy (ΔG_total). The sequence upstream of the Shine–Dalgarno (SD) site determines a penalty score ΔG_standby that is due to the work required to unfold secondary structures in this region. (B) The strengths of several RBS (controlling translation of GFP) were comparable when assayed both in vivo and in vitro [different RBS-GFP constructs in the x-axis, relative fluorescence (au) in the y-axis]. Figures modified with permission from Espah Borujeni et al. (2014) and Chappell et al. (2013).

These tools have been successfully applied to fine-tune protein translation in natural cells. For example, RBS calculator was used to adjust translation rates of genes in the nif operon, which was responsible for nitrogen fixation in Klebsiella oxytoca (Temme et al., 2012). RBS calculator was also used to demonstrate that modification of RBS sequence altered protein levels, but not mRNA accumulation (Pothoulakis et al., 2013). UTR designer (Lim et al., 2013; Seo et al., 2014) and RBSDesigner (Lee et al., 2013) were used in vivo to adjust translation rates of genes in metabolic operons, build a predictive library of RBS strengths, and fine-tune accumulation of reporter genes in a light-inducible expression system. These results suggest that RBS-based models can be used to predict the accumulation of target proteins in vivo.

In contrast, there are few publications that evaluate RBS strengths in cell-free systems. A recent report (Chappell et al., 2013) showed that relative strengths of RBS are similar for in vitro and in vivo systems (Figure 8B). The authors measured GFP translation both in whole cells and in cell-free systems using several RBS sequences with different predicted strengths. Despite the differences in the in vivo and in vitro biochemical environments, the accumulation of Output (GFP) was comparable for each tested RBS. These results suggest that RBS strengths in vitro could be estimated using existing tools developed for in vivo systems likely because RBS models rely solely on RBS sequence and secondary structures, as well as interactions between RBS and ribosomes.

Other Factors Influencing Gene Output Accumulation

The control of transcription and translation initiation accounts for most of the common strategies used to control accumulation of target proteins. However, other factors could be considered to improve target accumulation at desired levels. Terminators are necessary to promote detachment of RNAP from DNA and release of the synthesized RNA (Figure 5). In the absence of efficient terminators, the RNAP will continue transcribing throughout the DNA, reducing the pool of RNAP available to initiate productive transcription rounds. Intrinsic terminators are recognized by RNAP without requirement of additional factors. Several biophysical models have been developed to estimate strengths of intrinsic terminators using solely their DNA sequence (Carafa et al., 1990; von Hippel and Yager, 1991; Cambray et al., 2013). Recently, a library of more than 500 terminators was characterized in E. coli, and the strengths of the terminators agreed with predicted strengths based on a simple thermodynamic model (Chen et al., 2013). Similar to bacterial RNAP, T7 RNAP recognizes a specific terminator sequence, which functions at low termination efficiency of 50–70% (MacDonald et al., 1993). Recently, T7-RNAP terminators with efficiencies of up to 99% have been developed (Mairhofer et al., 2014). Although these models were tested in vivo, the fact that intrinsic terminators do not require additional factors suggests that they could potentially be applied to cell-free systems.

Two other factors can also control Output accumulation. First, translation efficiency can be affected by the target gene sequence (Figure 5), affecting the concentrations of synthesized proteins. For example, codon usage can be specifically designed and optimized for a particular host or in vitro system (Chung and Lee, 2012), maximizing protein production. Second, the activity of a promoter and RBS depends on upstream and downstream sequences (Kammerer et al., 1986; Leirmo and Gourse, 1991; Salis et al., 2009; Espah Borujeni et al., 2014). Therefore, the implementation of insulator sequences that “buffer” the effects of surrounding sequences over the regulatory sequences (Davis et al., 2011; Mutalik et al., 2013) should be considered when designing cell-free systems.

Metabolites as Output: Prediction and Control of Metabolic Pathways

Biocommodities are metabolites that have high economic values, including antibiotics, chiral compounds, and proteins (Zhang, 2010). Typically, biocommodities are produced using microorganisms with engineered metabolic pathways. However, the complexity of the biosynthetic pathway of interest can be reduced by isolating it from cellular metabolic network and engineered specifically to produce the desired target at determined rates. The decrease in the complexity of the cell-free isolated metabolic pathway could potentially lead to improved control over the system behavior and simplified purification of the target metabolite. In vitro production of metabolites could also avoid potential toxicity associated with synthesizing a biocommodity in vivo. Furthermore, theoretical calculations of product-to-biocatalyst weight ratios (total turnover number, TTN_W) show that in vitro systems achieve TTN_W at several orders of magnitude higher than microbial-based production (Zhang, 2010), likely due to the removal of non-essential metabolic pathways. Indeed, theoretical calculations suggest that in vitro systems could be important tools for the production of biocommodities such as ethanol and butanol (Welch and Scopes, 1985; Zhang et al., 2010). Cell-free systems have been shown to efficiently produce metabolites (Bujara et al., 2010) and proteins (Calhoun and Swartz, 2005). For example, the granulocyte macrophage colony-stimulating factor, a multi-sulfide bonds protein, was produced at scales ranging from 250 μL to 100 L using synthetic expression systems (Zawada et al., 2011). In this context, the development of models that accurately predict productivity of in vitro systems could improve synthesis of biocommodities.

Several tools are available for the design of cell-free metabolic pathways. Public access databases such as KEGG (Kanehisa et al., 2014), MetaCyc (Caspi et al., 2014), ChEBI (de Matos et al., 2010), and RHEA (Alcantara et al., 2012), are useful for the design of metabolic pathways using parts from different organisms. BRENDA (Schomburg et al., 2013), a database containing molecular and biochemical data of enzymes, can be useful to select the core pathway that will produce the metabolite of interest. Web servers, such as From-Metabolite-To-Metabolite (FMM) (Chou et al., 2009) and Metabolic Route Search and Design (MRSD) (Xia et al., 2011), can also be used for designing synthetic and unique metabolic pathways in cell-free systems. Metabolic Tinker (McClymont and Soyer, 2013) can be used to identify and rank thermodynamically favorable pathways between two compounds, which may include novel, non-natural pathways. The XTMS platform (Carbonell et al., 2014) can help to rank pathways based on enzymatic efficiency and maximum pathway yields.

Together with the definition of metabolic pathways, it is important to establish the relative contribution of each enzyme to the accumulation of the target metabolite. Flux balance analysis (FBA) is commonly used to calculate the relative contribution of each enzymatic step in the pathway when optimization of particular objective function is required (Orth et al., 2010). FBA is based on the stoichiometry of the metabolic pathway and requires the selection of constraints to limit the solution space (Gianchandani et al., 2010). The system has to be solved for the maximization (or minimization) of an objective function, including metabolic fluxes, metabolite production, and biomass production. Several computational tools are available to solve FBA (and its variants, see Gianchandani et al., 2010), such as COBRA toolbox for MATLAB (Schellenberger et al., 2011) and the open-source version COBRApy (Ebrahim et al., 2013). Therefore, FBA can be useful for determining enzymatic steps and the required concentrations of the enzymes in the pathway. Thus, the combination of these tools will be valuable for designing cell-free systems as biocommodity production factories.

Shell

The Shell is defined as the barrier that isolates the Input and the Processor from the environment. The diameter of the Shell can influence the degree of molecular crowding and reaction rates of the Processor. Furthermore, the Shell controls the import of signals from the environment and export of Output compounds from intracellular space of artificial cells.

The advent of synthetic biology brings forth the desire to harness functioning principles of natural membranes for the control of the Shell of artificial cells. Natural membranes use many strategies, such as membrane proteins and lipid rafts to achieve information exchange with the environment (Klingenberg, 1981; Simons and Ikonen, 1997; Korade and Kenworthy, 2008). Currently, it is difficult to engineer artificial membranes to achieve the same complexity of natural membranes due to limited knowledge about the dynamics of lipid bilayers. To this end, computational tools have been implemented to close the gap between natural and artificial membranes by simulating dynamics of lipid bilayers and their interactions with the environment (Sum et al., 2003; Rog et al., 2007; Risselada and Marrink, 2008; Thakkar and Ayappa, 2010; Stepniewski et al., 2011). Here, we will discuss two types of molecular dynamic models, all-atom (AA) and coarse-grained (CG) models, which are categorized by the level of detail (Figure 9A). The degree of detail addressed by each algorithm is determined by force fields that make up these models. A force field consists of a set of mathematical functions and parameters that describe interactions between molecules. Development of various force fields is outside the scope of this review. Detailed reviews (Xiang and Anderson, 2006; Marrink et al., 2009) or comparisons (Baron et al., 2006; Siu et al., 2008; Perlmutter et al., 2011) of different force fields, such as CHARMM, GROMOS, AMBER, and MARTINI can be found elsewhere. This section of the review presents some examples on how computational modeling can boost our understanding of membrane behavior and dynamics, which could provide important insights into efficacious design of the Shell.

FIGURE 9

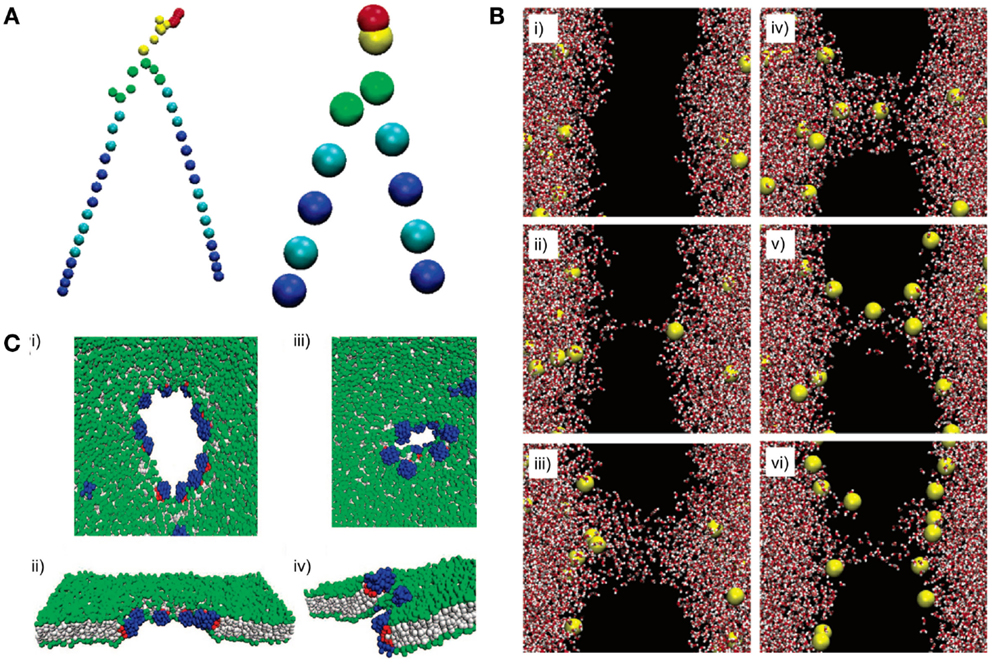
Figure 9. All-atom (AA) and coarse-grained (CG) models can reveal lipid dynamics at different length and time scales. (A) A DPPC lipid is represented with an AA model (left) and a CG model (right). All atoms are explicitly simulated in the AA model. In contrast, atoms are simplified into “beads” in the CG model. (B) A pore formation and closure event induced by ionic charge imbalance is simulated using an AA model. The dynamic is illustrated at different time points from (i) to (vi). Time points: (i) 20 ps, (ii) 450 ps, (iii) 1000 ps, (iv) 1070 ps, (v) 9180 ps, and (vi) 60 ns. The lipid bilayer is not shown (black space). Red and white shapes represent water molecules. Yellow shapes represent sodium ions. (C) Pore formation on a lipid membrane by nanoparticles is simulated using a CG model. (i–ii) The pore is formed and opened by applying an external stress. (iii–iv) Closure of the pore after the stress is removed. Gray shapes represent lipid tails. Green shapes represent lipid headgroups. Blue and red shapes represent hydrophilic and hydrophobic portions of the nanoparticle, respectively. Figures modified with permission from Gurtovenko and Vattulainen (2005), Baron et al. (2006), and Alexeev et al. (2008).

All-Atom Models

All-atom models are useful tools in lipid membrane simulation. In AA models, every atom of the solute and solvent in the system is explicitly simulated. Thus, when applied to the simulation of lipid bilayers, AA models can provide fine details at the molecular level. Due to the computational cost, AA models are often limited to small-scale simulations (Xiang and Anderson, 2006; Marrink et al., 2009; Perlmutter et al., 2011).

All-atom models have been applied to simulate membrane defection by an electrical field (Tieleman, 2004; Bockmann et al., 2008) and pore-forming agents (Jean-Francois et al., 2008). For instance, Bennett et al. demonstrated spontaneous pore formation by restraining a single phosphate group at the center of the lipid bilayers. The simulated results agreed with previous computational (Tieleman, 2004; Bockmann et al., 2008) and experimental work (Paula et al., 1996). With tremendous detail at the atomic level, the simulation was able to reveal thermodynamics of transient pore formation and closure, which illustrated membrane defects from a novel perspective (Bennett et al., 2014). Similarly, Gurtovenko et al. used an AA model and illustrated that pore formation and closure could be induced by ionic charge imbalance (Figure 9B) (Gurtovenko and Vattulainen, 2005). Permeation of water or small solutes across lipid bilayers may be attributed to transient membrane defects (Deamer and Bramhall, 1986). The understanding of the dynamics of pore formation could be exploited to modulate the rates of molecular diffusion across membranes of artificial cells. This understanding could enhance our control of the activation of Processor by environmental signals and the rates of Output release from artificial cells.

Coarse-Grained Models

In contrast to AA models, CG models are simpler and contain fewer details. Instead of explicitly describing every atom in the system, CG models consist of “beads,” which represent groups of atoms, potentially reducing the resolution of the simulation and decreasing computer resources required to simulate AA models (Baron et al., 2006; Marrink et al., 2007; Marrink et al., 2009). As a result, CG models are preferable when simulating large scale dynamics where atomic details may not be critical. For example, CG models have been used to simulate lipid phase behaviors, such as phase separation and phase transition (Risselada and Marrink, 2008; Prates Ramalho et al., 2011). Lipid bilayers have several phases that are generally characterized by relative mobility of lipid molecules. Phase changes can alter mechanical properties of membranes, such as fluidity and rigidity. Indeed, a simulation study using a mesoscopic model suggests that phase separation could impact liposome fusion dynamics (Smith et al., 2007). Thus, phase behaviors may need to be considered when designing the Shell to achieve certain mechanical properties. In one study, Risselada et al. used MARTINI force field to simulate lipid phase behaviors in a ternary lipid system. The simulation demonstrated that a mixture of saturated, unsaturated lipids, and cholesterol could spontaneously segregate into different domains. The liquid-ordered (L_o) domains consisted mostly of saturated lipid and cholesterol, whereas the liquid disordered (L_d) domains consisted mostly of unsaturated lipid (Risselada and Marrink, 2008). This simulation had been validated by experiments (Veatch et al., 2004). In addition, the simulation suggested that cholesterol was the key driving force for the phase separation.

Coarse-grained models have also been used to study interactions between lipid bilayers and other molecules. Ramalho et al. investigated the effect of nanoparticles on fluid-gel transformation of lipid bilayers. Nanoparticles were shown to induce local disorder of a lipid bilayer and delay the transformation of the lipid bilayer from fluid to gel states (Prates Ramalho et al., 2011). Other computational studies have shown that amphiphilic nanoparticles (Alexeev et al., 2008) (Figure 9C) and nanotubes (Dutt et al., 2011) interact with lipid membranes to form controllable pores and channels. These simulations could be used in conjunction with AA models of pore formation to provide guidelines when designing a permeable Shell.

Model Tradeoffs and Prospect

The choice of AA or CG model depends on the context of scientific questions. When detailed atom–atom interactions are not a concern, CG models are suitable to compromise the computational cost. However, as computational hardware and software continue to improve, it is possible to use AA models to describe dynamics over a longer time scale (Sodt et al., 2014). Some studies have also combined AA and CG models to achieve long, yet fine time-scale simulation (Thogersen et al., 2008; Perlmutter et al., 2011). Briefly, CG models are first used to perform large time-scale simulation and then switched to AA models by mapping “beads” to single atoms.

Most simulation tools are focused on dynamics of the lipid membrane itself. To date, models integrating the Shell and the Processor/Output modules have not been established. The main hurdle for the integration lies in the difficulty of linking physical concepts used in membrane modeling and chemical dynamics utilized in transcription–translation modeling. Recent studies have shown that liposomes can affect gene expression (Bui et al., 2008; Umakoshi et al., 2009). The models discussed in this section only consider microscopic (atomistic) scale of membrane dynamics, but integrated simulation may be necessary for predicting dynamics of artificial cells. Beyond the atomistic scale, mesoscopic (about 0.1–10 μm) models where individual molecules are CG to single fluid volume are potential options for simulation of lipid bilayers (Ayton and Voth, 2002; Goujon et al., 2008). Other options are hybrid models where atomistic scale information is obtained and then “transformed” to lower resolution representations to achieve simulations at larger time- and/or length-scales (Ayton and Voth, 2002, 2009). This transformation can be challenging due to the lack of direct links between micro- and macro-scale dynamics. A recent work has developed a framework and attempted to incorporate physical (spatial location and diffusion) and chemical (biochemical reactions) methods to simulate cellular functions (Loew and Schaff, 2001). To this end, we envision that computational modeling of interactions between lipid membranes and transcription–translation machinery will provide unique insights into robustness of gene expression and enhance our capacity to control artificial cells.

Conclusion

In this review, we have outlined differences between in vitro and in vivo synthetic biological systems. Current cell-free expression systems lack the spatial arrangement, protein transport, and folding, as well as various non-DNA binding factors that modulate gene expression in living organisms. These qualitative differences between in vivo and in vitro reactions could produce quantifiable differences in dynamical behavior between the two systems, which would require different modeling approaches. Molecular crowding, encapsulation, and reaction volumes all profoundly affect stochastic variation of gene expression, which in turn impacts the choice between mass-action and ordinary differential equations for prediction of protein synthesis. In addition, cell-free systems lack a continuous supply of substrates, supplementary TFs, and chaperones, which could dramatically alter the rates of peptide and/or metabolite production in vivo. These factors could change kinetic parameters that in vitro systems operate within. There are other cellular processes, such as self-repair (Witkin, 1976; Demple and Halbrook, 1983; Demple and Harrison, 1994; Aas et al., 2003) and proofreading (Brutlag and Kornberg, 1972; Cline et al., 1996) that have not been considered when constructing cell-free synthetic systems.

While these missing features of in vitro systems could make it non-trivial to adapt existing computational tools for the design of cell-free systems, the minimality of cell-free systems provides a unique research opportunity to understand functioning of cells from a bottom-up perspective. We have detailed several projects that quantify the effects of molecular phenomena such as encapsulation, molecular crowding, and reaction volumes on the performance of in vitro transcription and translation. These projects could provide insights into key molecular phenomena that impact gene expression in vivo. Models that detail the impact of energy supply and molecular building blocks on protein synthesis in cell-free systems could similarly demonstrate how molecular transporters and secondary metabolic reactions modulate homeostasis of natural cells. Exploratory models for in vitro pathways could considerably speed the assembly of cell-free circuits, and provide excellent platforms for testing hypotheses of how complex processes, such as self-repair and proofreading, influence dynamical behavior of synthetic circuits. These automatic in vitro network assemblers could also form the fundamental tools for creating an integrated model of artificial cells.

Artificial cells represent unique in vitro platforms for studying fundamental principles of biochemical pathways. Indeed, they have been used to measure differences in the expression and stochastic variation of gene circuits caused by encapsulation. To create predictive models of artificial cells, existing design tools of gene circuits could be integrated with models of liposomes. Such whole-artificial-cell models could be used to predict the response of artificial cells to osmotic pressure and to understand plausible co-regulation of system dynamics by membranes and gene circuits.

The computational tools consolidated in this review establish a foundation for mathematical comparison between in vivo and in vitro biological phenomena. Computer simulation allows researchers to accelerate the pace of scientific inquiry and build a common framework for designing biological networks. In vitro reactions remain a powerful tool for experimental biologists, and as the field of biology becomes increasingly quantitative, it is important to take advantage of the flexibility of cell-free systems to test model predictions under simplified and minimal conditions. We envision that studies of cell-free and in vivo synthetic systems will reveal cryptic non-genetic factors, network structures, and spatial organization of cellular components that may modulate robustness of synthetic biological systems.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Dr. Yunfeng Ding for providing important bibliographic sources on artificial cells. This work is supported by Society-in-Science: Branco-Weiss Fellowship.

References

Aas, P. A., Otterlei, M., Falnes, P. O., Vagbo, C. B., Skorpen, F., Akbari, M., et al. (2003). Human and bacterial oxidative demethylases repair alkylation damage in both RNA and DNA. Nature 421, 859–863. doi: 10.1038/nature01363

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Alcantara, R., Axelsen, K. B., Morgat, A., Belda, E., Coudert, E., Bridge, A., et al. (2012). Rhea – a manually curated resource of biochemical reactions. Nucleic Acids Res. 40, D754–D760. doi:10.1093/nar/gkr1126

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Alexeev, A., Uspal, W. E., and Balazs, A. C. (2008). Harnessing janus nanoparticles to create controllable pores in membranes. ACS Nano 2, 1117–1122. doi:10.1021/nn8000998

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Altan-Bonnet, G., and Germain, R. N. (2005). Modeling T cell antigen discrimination based on feedback control of digital ERK responses. PLoS Biol. 3:e356. doi:10.1371/journal.pbio.0030356

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Andrianantoandro, E., Basu, S., Karig, D. K., and Weiss, R. (2006). Synthetic biology: new engineering rules for an emerging discipline. Mol. Syst. Biol. 2, 0028. doi:10.1038/msb4100073

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Ang, J., Harris, E., Hussey, B. J., Kil, R., and McMillen, D. R. (2013). Tuning response curves for synthetic biology. ACS Synth. Biol. 2, 547–567. doi:10.1021/sb4000564

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Artimo, P., Jonnalagedda, M., Arnold, K., Baratin, D., Csardi, G., De Castro, E., et al. (2012). ExPASy: SIB bioinformatics resource portal. Nucleic Acids Res. 40, W597–W603. doi:10.1093/nar/gks400

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Assmann, G., and Brewer, H. B. Jr. (1974). Lipid-protein interactions in high density lipoproteins. Proc. Natl. Acad. Sci. U.S.A. 71, 989–993. doi:10.1073/pnas.71.3.989

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Ayton, G., and Voth, G. A. (2002). Bridging microscopic and mesoscopic simulations of lipid bilayers. Biophys. J. 83, 3357–3370. doi:10.1016/S0006-3495(02)75336-8

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Ayton, G. S., and Voth, G. A. (2009). Systematic multiscale simulation of membrane protein systems. Curr. Opin. Struct. Biol. 19, 138–144. doi:10.1016/j.sbi.2009.03.001

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Bandwar, R. P., Jia, Y., Stano, N. M., and Patel, S. S. (2002). Kinetic and thermodynamic basis of promoter strength: multiple steps of transcription initiation by T7 RNA polymerase are modulated by the promoter sequence†. Biochemistry 41, 3586–3595. doi:10.1021/bi0158472

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Baron, R., De Vries, A. H., Hunenberger, P. H., and Van Gunsteren, W. F. (2006). Configurational entropies of lipids in pure and mixed bilayers from atomic-level and coarse-grained molecular dynamics simulations. J. Phys. Chem. B 110, 15602–15614. doi:10.1021/jp061627s

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Basu, S., Gerchman, Y., Collins, C. H., Arnold, F. H., and Weiss, R. (2005). A synthetic multicellular system for programmed pattern formation. Nature 434, 1130–1134. doi:10.1038/nature03461

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Basu, S., Mehreja, R., Thiberge, S., Chen, M. T., and Weiss, R. (2004). Spatiotemporal control of gene expression with pulse-generating networks. Proc. Natl. Acad. Sci. U.S.A. 101, 6355–6360. doi:10.1073/pnas.0307571101

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Beal, J., Weiss, R., Densmore, D., Adler, A., Appleton, E., Babb, J., et al. (2012). An end-to-end workflow for engineering of biological networks from high-level specifications. ACS Synth. Biol. 1, 317–331. doi:10.1021/sb300030d

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Bekhor, I., Kung, G. M., and Bonner, J. (1969). Sequence-specific interaction of DNA and chromosomal protein. J. Mol. Biol. 39, 351–364. doi:10.1016/0022-2836(69)90322-2

CrossRef Full Text | Google Scholar

Bennett, W. F., Sapay, N., and Tieleman, D. P. (2014). Atomistic simulations of pore formation and closure in lipid bilayers. Biophys. J. 106, 210–219. doi:10.1016/j.bpj.2013.11.4486

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Benos, P. V., Bulyk, M. L., and Stormo, G. D. (2002). Additivity in protein-DNA interactions: how good an approximation is it? Nucleic Acids Res. 30, 4442–4451. doi:10.1093/nar/gkf578

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Berg, O. G. (1988). Selection of DNA binding sites by regulatory proteins: the LexA protein and the arginine repressor use different strategies for functional specificity. Nucleic Acids Res. 16, 5089–5105. doi:10.1093/nar/16.11.5089

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Berti, D., Baglioni, P., Bonaccio, S., Barsacchi-Bo, G., and Luisi, P. L. (1998). Base complementarity and nucleoside recognition in phosphatidylnucleoside vesicles. J. Phys. Chem. B 102, 303–308. doi:10.1021/jp972954q

CrossRef Full Text | Google Scholar

Biliouris, K., Babson, D., Schmidt-Dannert, C., and Kaznessis, Y. N. (2012). Stochastic simulations of a synthetic bacteria-yeast ecosystem. BMC Syst. Biol. 6:58. doi:10.1186/1752-0509-6-58

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Bintu, L., Buchler, N. E., Garcia, H. G., Gerland, U., Hwa, T., Kondev, J., et al. (2005). Transcriptional regulation by the numbers: models. Curr. Opin. Genet. Dev. 15, 116–124. doi:10.1016/j.gde.2005.02.007

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Black, R. A., Blosser, M. C., Stottrup, B. L., Tavakley, R., Deamer, D. W., and Keller, S. L. (2013). Nucleobases bind to and stabilize aggregates of a prebiotic amphiphile, providing a viable mechanism for the emergence of protocells. Proc. Natl. Acad. Sci. U.S.A. 110, 13272–13276. doi:10.1073/pnas.1300963110

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Bockmann, R. A., De Groot, B. L., Kakorin, S., Neumann, E., and Grubmuller, H. (2008). Kinetics, statistics, and energetics of lipid membrane electroporation studied by molecular dynamics simulations. Biophys. J. 95, 1837–1850. doi:10.1529/biophysj.108.129437

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Bradley, P., Misura, K. M., and Baker, D. (2005). Toward high-resolution de novo structure prediction for small proteins. Science 309, 1868–1871. doi:10.1126/science.1113801

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Brewster, R. C., Jones, D. L., and Phillips, R. (2012). Tuning promoter strength through RNA polymerase binding site design in Escherichia coli. PLoS Comput. Biol. 8:e1002811. doi:10.1371/journal.pcbi.1002811

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Brutlag, D., and Kornberg, A. (1972). Enzymatic synthesis of deoxyribonucleic acid. 36. A proofreading function for the 3′ leads to 5′ exonuclease activity in deoxyribonucleic acid polymerases. J. Biol. Chem. 247, 241–248.

Google Scholar

Bui, H. T., Umakoshi, H., Ngo, K. X., Nishida, M., Shimanouchi, T., and Kuboi, R. (2008). Liposome membrane itself can affect gene expression in the Escherichia coli cell-free translation system. Langmuir 24, 10537–10542. doi:10.1021/la801962j

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Bujara, M., Schumperli, M., Billerbeck, S., Heinemann, M., and Panke, S. (2010). Exploiting cell-free systems: implementation and debugging of a system of biotransformations. Biotechnol. Bioeng. 106, 376–389. doi:10.1002/bit.22666

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Calhoun, K. A., and Swartz, J. R. (2005). Energizing cell-free protein synthesis with glucose metabolism. Biotechnol. Bioeng. 90, 606–613. doi:10.1002/bit.20449

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Calviello, L., Stano, P., Mavelli, F., Luisi, P. L., and Marangoni, R. (2013). Quasi-cellular systems: stochastic simulation analysis at nanoscale range. BMC Bioinformatics 14:S7. doi:10.1186/1471-2105-14-S7-S7

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Cambray, G., Guimaraes, J. C., Mutalik, V. K., Lam, C., Mai, Q.-A., Thimmaiah, T., et al. (2013). Measurement and modeling of intrinsic transcription terminators. Nucleic Acids Res. 41, 5139–5148. doi:10.1093/nar/gkt163

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Carafa, Y. D. A., Brody, E., and Thermes, C. (1990). Prediction of rho-independent Escherichia coli transcription terminators: a statistical analysis of their RNA stem-loop structures. J. Mol. Biol. 216, 835–858. doi:10.1016/S0022-2836(99)80005-9

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Carbonell, P., Parutto, P., Herisson, J., Pandit, S. B., and Faulon, J.-L. (2014). XTMS: pathway design in an extended metabolic space. Nucleic Acids Res. 42, W389–W394. doi:10.1093/nar/gku362

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Caschera, F., Bedau, M. A., Buchanan, A., Cawse, J., De Lucrezia, D., Gazzola, G., et al. (2011). Coping with complexity: machine learning optimization of cell-free protein synthesis. Biotechnol. Bioeng. 108, 2218–2228. doi:10.1002/bit.23178

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Caspi, R., Altman, T., Billington, R., Dreher, K., Foerster, H., Fulcher, C. A., et al. (2014). The MetaCyc database of metabolic pathways and enzymes and the BioCyc collection of pathway/genome databases. Nucleic Acids Res. 42, D459–D471. doi:10.1093/nar/gkt1103

CrossRef Full Text | Google Scholar

Chalmeau, J., Monina, N., Shin, J., Vieu, C., and Noireaux, V. (2011). α-Hemolysin pore formation into a supported phospholipid bilayer using cell-free expression. Biochim. Biophys. Acta 1808, 271–278. doi:10.1016/j.bbamem.2010.07.027

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Chappell, J., Jensen, K., and Freemont, P. S. (2013). Validation of an entirely in vitro approach for rapid prototyping of DNA regulatory elements for synthetic biology. Nucleic Acids Res. 41, 3471–3481. doi:10.1093/nar/gkt052

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Chastanet, A., Vitkup, D., Yuan, G. C., Norman, T. M., Liu, J. S., and Losick, R. M. (2010). Broadly heterogeneous activation of the master regulator for sporulation in Bacillus subtilis. Proc. Natl. Acad. Sci. U.S.A. 107, 8486–8491. doi:10.1073/pnas.1002499107

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Cheetham, G. M., and Steitz, T. A. (2000). Insights into transcription: structure and function of single-subunit DNA-dependent RNA polymerases. Curr. Opin. Struct. Biol. 10, 117–123. doi:10.1016/S0959-440X(99)00058-5

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Chen, Y.-J., Liu, P., Nielsen, A. A. K., Brophy, J. A. N., Clancy, K., Peterson, T., et al. (2013). Characterization of 582 natural and synthetic terminators and quantification of their design constraints. Nat. Methods 10, 659–664. doi:10.1038/nmeth.2515

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Cheng, A. A., and Lu, T. K. (2012). Synthetic biology: an emerging engineering discipline. Annu. Rev. Biomed. Eng. 14, 155–178. doi:10.1146/annurev-bioeng-071811-150118

CrossRef Full Text | Google Scholar

Chiang, A. W., and Hwang, M. J. (2013). A computational pipeline for identifying kinetic motifs to aid in the design and improvement of synthetic gene circuits. BMC Bioinformatics 14(Suppl. 16):S5. doi:10.1186/1471-2105-14-S16-S5

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Chizzolini, F., Forlin, M., Cecchi, D., and Mansy, S. S. (2013). Gene position more strongly influences cell-free protein expression from operons than T7 transcriptional promoter strength. ACS Synth. Biol. 3, 363–371. doi:10.1021/sb4000977

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Chou, C. H., Chang, W. C., Chiu, C. M., Huang, C. C., and Huang, H. D. (2009). FMM: a web server for metabolic pathway reconstruction and comparative analysis. Nucleic Acids Res. 37, W129–W134. doi:10.1093/nar/gkp264

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Chung, B., and Lee, D.-Y. (2012). Computational codon optimization of synthetic gene for protein expression. BMC Syst. Biol. 6:134. doi:10.1186/1752-0509-6-134

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Cline, J., Braman, J. C., and Hogrefe, H. H. (1996). PCR fidelity of pfu DNA polymerase and other thermostable DNA polymerases. Nucleic Acids Res. 24, 3546–3551. doi:10.1093/nar/24.18.3546

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Collins, C. H., Leadbetter, J. R., and Arnold, F. H. (2006). Dual selection enhances the signaling specificity of a variant of the quorum-sensing transcriptional activator LuxR. Nat. Biotechnol. 24, 708–712. doi:10.1038/nbt0806-1033c

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Daniel, R., Rubens, J. R., Sarpeshkar, R., and Lu, T. K. (2013). Synthetic analog computation in living cells. Nature 497, 619–623. doi:10.1038/nature12148

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Danino, T., Lo, J., Prindle, A., Hasty, J., and Bhatia, S. N. (2012). In vivo gene expression dynamics of tumor-targeted bacteria. ACS Synth. Biol. 1, 465–470. doi:10.1021/sb3000639

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Danino, T., Mondragon-Palomino, O., Tsimring, L., and Hasty, J. (2010). A synchronized quorum of genetic clocks. Nature 463, 326–330. doi:10.1038/nature08753

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Davidson, F. A., Seon-Yi, C., and Stanley-Wall, N. R. (2012). Selective heterogeneity in exoprotease production by Bacillus subtilis. PLoS ONE 7:e38574. doi:10.1371/journal.pone.0038574

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Davis, J. H., Rubin, A. J., and Sauer, R. T. (2011). Design, construction and characterization of a set of insulated bacterial promoters. Nucleic Acids Res. 39, 1131–1141. doi:10.1093/nar/gkq810

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

De Jong, H. (2002). Modeling and simulation of genetic regulatory systems: a literature review. J. Comput. Biol. 9, 67–103. doi:10.1089/10665270252833208

CrossRef Full Text | Google Scholar

De la Fuente, I. M., Cortes, J. M., Pelta, D. A., and Veguillas, J. (2013). Attractor metabolic networks. PLoS ONE 8:e58284. doi:10.1371/journal.pone.0058284

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

de Matos, P., Alcantara, R., Dekker, A., Ennis, M., Hastings, J., Haug, K., et al. (2010). Chemical entities of biological interest: an update. Nucleic Acids Res. 38, D249–D254. doi:10.1093/nar/gkp886

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

De Mey, M., Maertens, J., Lequeux, G. J., Soetaert, W. K., and Vandamme, E. J. (2007). Construction and model-based analysis of a promoter library for E. coli: an indispensable tool for metabolic engineering. BMC Biotechnol. 7:34. doi:10.1186/1472-6750-7-34

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Deamer, D. W., and Bramhall, J. (1986). Permeability of lipid bilayers to water and ionic solutes. Chem. Phys. Lipids 40, 167–188. doi:10.1016/0009-3084(86)90069-1

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Demple, B., and Halbrook, J. (1983). Inducible repair of oxidative DNA damage in Escherichia-Coli. Nature 304, 466–468. doi:10.1038/304466a0

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Demple, B., and Harrison, L. (1994). Repair of oxidative damage to DNA: enzymology and biology. Annu. Rev. Biochem. 63, 915–948. doi:10.1146/annurev.bi.63.070194.004411

CrossRef Full Text | Google Scholar

Di Ventura, B., Lemerle, C., Michalodimitrakis, K., and Serrano, L. (2006). From in vivo to in silico biology and back. Nature 443, 527–533. doi:10.1038/nature05127

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Dutt, M., Kuksenok, O., Nayhouse, M. J., Little, S. R., and Balazs, A. C. (2011). Modeling the self-assembly of lipids and nanotubes in solution: forming vesicles and bicelles with transmembrane nanotube channels. ACS Nano 5, 4769–4782. doi:10.1021/nn201260r

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Ebrahim, A., Lerman, J., Palsson, B., and Hyduke, D. (2013). COBRApy: constraints-based reconstruction and analysis for python. BMC Syst. Biol. 7:74. doi:10.1186/1752-0509-7-74

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Ellis, T., Wang, X., and Collins, J. J. (2009). Diversity-based, model-guided construction of synthetic gene networks with predicted functions. Nat. Biotech. 27, 465–471. doi:10.1038/nbt.1536

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Elowitz, M. B., and Leibler, S. (2000). A synthetic oscillatory network of transcriptional regulators. Nature 403, 335–338. doi:10.1038/35002125

CrossRef Full Text | Google Scholar

Elowitz, M. B., Levine, A. J., Siggia, E. D., and Swain, P. S. (2002). Stochastic gene expression in a single cell. Science 297, 1183–1186. doi:10.1126/science.1070919

CrossRef Full Text | Google Scholar

Espah Borujeni, A., Channarasappa, A. S., and Salis, H. M. (2014). Translation rate is controlled by coupled trade-offs between site accessibility, selective RNA unfolding and sliding at upstream standby sites. Nucleic Acids Res. 42, 2646–2659. doi:10.1093/nar/gkt1139

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Forster, A. C., and Church, G. M. (2007). Synthetic biology projects in vitro. Genome Res. 17, 1–6. doi:10.1101/gr.5776007

CrossRef Full Text | Google Scholar

Gianchandani, E. P., Chavali, A. K., and Papin, J. A. (2010). The application of flux balance analysis in systems biology. Wiley Interdiscip. Rev. Syst. Biol. Med. 2, 372–382. doi:10.1002/wsbm.60

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Goler, J. A., Carothers, J. M., and Keasling, J. D. (2014). Dual-selection for evolution of in vivo functional aptazymes as riboswitch parts. Methods Mol. Biol. 1111, 221–235. doi:10.1007/978-1-62703-755-6_16

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Goshima, N., Kawamura, Y., Fukumoto, A., Miura, A., Honma, R., Satoh, R., et al. (2008). Human protein factory for converting the transcriptome into an in vitro-expressed proteome. Nat. Methods 5, 1011–1017. doi:10.1038/nmeth.1273

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Goujon, F., Malfreyt, P., and Tildesley, D. J. (2008). Mesoscopic simulation of entanglements using dissipative particle dynamics: application to polymer brushes. J. Chem. Phys. 129, 034902. doi:10.1063/1.2954022

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Gunawardena, J. (2014). Models in biology: ‘accurate descriptions of our pathetic thinking’. BMC Biol. 12:29. doi:10.1186/1741-7007-12-29

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Gurtovenko, A. A., and Vattulainen, I. (2005). Pore formation coupled to ion transport through lipid membranes as induced by transmembrane ionic charge imbalance: atomistic molecular dynamics study. J. Am. Chem. Soc. 127, 17570–17571. doi:10.1021/ja053129n

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Guterl, J. K., and Sieber, V. (2013). Biosynthesis “debugged”: novel bioproduction strategies. Eng. Life Sci. 13, 4–18. doi:10.1002/elsc.201100231

CrossRef Full Text | Google Scholar

Ham, T. S., Lee, S. K., Keasling, J. D., and Arkin, A. P. (2008). Design and construction of a double inversion recombination switch for heritable sequential genetic memory. PLoS ONE 3:e2815. doi:10.1371/journal.pone.0002815

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Hamada, S., Tabuchi, M., Toyota, T., Sakurai, T., Hosoi, T., Nomoto, T., et al. (2014). Giant vesicles functionally expressing membrane receptors for an insect pheromone. Chem. Commun. 50, 2958–2961. doi:10.1039/c3cc48216b

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Hammer, K., Mijakovic, I., and Jensen, P. R. (2006). Synthetic promoter libraries – tuning of gene expression. Trends Biotechnol. 24, 53–55. doi:10.1016/j.tibtech.2005.12.003

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Hanes, J., and Pluckthun, A. (1997). In vitro selection and evolution of functional proteins by using ribosome display. Proc. Natl. Acad. Sci. U.S.A 94, 4937–4942. doi:10.1073/pnas.94.10.4937

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Hasty, J., Isaacs, F., Dolnik, M., McMillen, D., and Collins, J. J. (2001). Designer gene networks: towards fundamental cellular control. Chaos 11, 207–220. doi:10.1063/1.1345702

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

He, X., Aizenberg, M., Kuksenok, O., Zarzar, L. D., Shastri, A., Balazs, A. C., et al. (2012). Synthetic homeostatic materials with chemo-mechano-chemical self-regulation. Nature 487, 214–218. doi:10.1038/nature11223

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Heinrich, R., and Rapoport, T. A. (2005). Generation of nonidentical compartments in vesicular transport systems. J. Cell Biol. 168, 271–280. doi:10.1083/jcb.200409087

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Higuchi, R., Krummel, B., and Saiki, R. K. (1988). A general method of in vitro preparation and specific mutagenesis of DNA fragments: study of protein and DNA interactions. Nucleic Acids Res. 16, 7351–7367. doi:10.1093/nar/16.15.7351

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Hoagland, M. B., Stephenson, M. L., Scott, J. F., Hecht, L. I., and Zamecnik, P. C. (1958). A soluble ribonucleic acid intermediate in protein synthesis. J. Biol. Chem. 231, 241–257.

Google Scholar

Hodgman, C. E., and Jewett, M. C. (2012). Cell-free synthetic biology: thinking outside the cell. Metab. Eng. 14, 261–269. doi:10.1016/j.ymben.2011.09.002

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Holtz, J. H., and Asher, S. A. (1997). Polymerized colloidal crystal hydrogel films as intelligent chemical sensing materials. Nature 389, 829–832. doi:10.1038/39834

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Huh, D., and Paulsson, J. (2011a). Non-genetic heterogeneity from stochastic partitioning at cell division. Nat. Genet. 43, 95–U32. doi:10.1038/ng.729

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Huh, D., and Paulsson, J. (2011b). Random partitioning of molecules at cell division. Proc. Natl. Acad. Sci. U.S.A. 108, 15004–15009. doi:10.1073/pnas.1013171108

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Hussain, F., Gupta, C., Hirning, A. J., Ott, W., Matthews, K. S., Josic, K., et al. (2014). Engineered temperature compensation in a synthetic genetic clock. Proc. Natl. Acad. Sci. U.S.A 111, 972–977. doi:10.1073/pnas.1316298111

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Huynh, L., Kececioglu, J., Koppe, M., and Tagkopoulos, I. (2012). Automatic design of synthetic gene circuits through mixed integer non-linear programming. PLoS ONE 7:e35529. doi:10.1371/journal.pone.0035529

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Huynh, L., Tsoukalas, A., Koppe, M., and Tagkopoulos, I. (2013). SBROME: a scalable optimization and module matching framework for automated biosystems design. ACS Synth. Biol. 2, 263–273. doi:10.1021/sb300095m

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Imburgio, D., Rong, M., Ma, K., and McAllister, W. T. (2000). Studies of promoter recognition and start site selection by T7 RNA polymerase using a comprehensive collection of promoter variants. Biochemistry 39, 10419–10430. doi:10.1021/bi000365w

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Ishikawa, K., Sato, K., Shima, Y., Urabe, I., and Yomo, T. (2004). Expression of a cascading genetic network within liposomes. FEBS Lett. 576, 387–390. doi:10.1016/j.febslet.2004.09.046

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Ishimatsu, K., Hata, T., Mochizuki, A., Sekine, R., Yamamura, M., and Kiga, D. (2013). General applicability of synthetic gene-overexpression for cell-type ratio control via reprogramming. ACS Synth. Biol. 3, 638–644. doi:10.1021/sb400102w

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Iyer, S., Karig, D. K., Norred, S. E., Simpson, M. L., and Doktycz, M. J. (2013). Multi-input regulation and logic with T7 promoters in cells and cell-free systems. PLoS ONE 8:e78442. doi:10.1371/journal.pone.0078442

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Jamshidi, N., and Palsson, B. O. (2010). Mass action stoichiometric simulation models: incorporating kinetics and regulation into stoichiometric models. Biophys. J. 98, 175–185. doi:10.1016/j.bpj.2009.09.064

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Jean-Francois, F., Elezgaray, J., Berson, P., Vacher, P., and Dufourc, E. J. (2008). Pore formation induced by an antimicrobial peptide: electrostatic effects. Biophys. J. 95, 5748–5756. doi:10.1529/biophysj.108.136655

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Jewett, M. C., Calhoun, K. A., Voloshin, A., Wuu, J. J., and Swartz, J. R. (2008). An integrated cell-free metabolic platform for protein production and synthetic biology. Mol. Syst. Biol. 4, 220. doi:10.1038/msb.2008.57

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Jewett, M. C., Miller, M. L., Chen, Y., and Swartz, J. R. (2009). Continued protein synthesis at low [ATP] and [GTP] enables cell adaptation during energy limitation. J. Bacteriol. 191, 1083–1091. doi:10.1128/JB.00852-08

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Kammerer, W., Deuschle, U., Gentz, R., and Bujard, H. (1986). Functional dissection of Escherichia coli promoters: information in the transcribed region is involved in late steps of the overall process. EMBO J. 5, 2995–3000.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Kaneda, M., Nomura, S. M., Ichinose, S., Kondo, S., Nakahama, K., Akiyoshi, K., et al. (2009). Direct formation of proteo-liposomes by in vitro synthesis and cellular cytosolic delivery with connexin-expressing liposomes. Biomaterials 30, 3971–3977. doi:10.1016/j.biomaterials.2009.04.006

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Kanehisa, M., and Goto, S. (2000). KEGG: Kyoto encyclopedia of genes and genomes. Nucleic Acids Res. 28, 27–30. doi:10.1093/nar/28.1.27

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Kanehisa, M., Goto, S., Sato, Y., Kawashima, M., Furumichi, M., and Tanabe, M. (2014). Data, information, knowledge and principle: back to metabolism in KEGG. Nucleic Acids Res. 42, D199–D205. doi:10.1093/nar/gkt1076

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Karig, D., and Weiss, R. (2005). Signal-amplifying genetic circuit enables in vivo observation of weak promoter activation in the Rhl quorum sensing system. Biotechnol. Bioeng. 89, 709–718. doi:10.1002/bit.20371

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Karig, D. K., Jung, S. Y., Srijanto, B., Collier, C. P., and Simpson, M. L. (2013). Probing cell-free gene expression noise in femtoliter volumes. ACS Synth. Biol. 2, 497–505. doi:10.1021/sb400028c

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Karzbrun, E., Shin, J., Bar-Ziv, R. H., and Noireaux, V. (2011). Coarse-grained dynamics of protein synthesis in a cell-free system. Phys. Rev. Lett. 106, 048104.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Kim, J., White, K. S., and Winfree, E. (2006). Construction of an in vitro bistable circuit from synthetic transcriptional switches. Mol. Syst. Biol. 2, 68. doi:10.1038/msb4100099

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Kim, J., and Winfree, E. (2011). Synthetic in vitro transcriptional oscillators. Mol. Syst. Biol. 7, 465. doi:10.1038/msb.2010.119

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Kinney, J. B., Murugan, A., Callan, C. G., and Cox, E. C. (2010). Using deep sequencing to characterize the biophysical mechanism of a transcriptional regulatory sequence. Proc. Natl. Acad. Sci. U.S.A. 107, 9158–9163. doi:10.1073/pnas.1004290107

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Klingenberg, M. (1981). Membrane protein oligomeric structure and transport function. Nature 290, 449–454. doi:10.1038/290449a0

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Klumpp, S., Zhang, Z., and Hwa, T. (2009). Growth rate-dependent global effects on gene expression in bacteria. Cell 139, 1366–1375. doi:10.1016/j.cell.2009.12.001

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Kobori, S., Ichihashi, N., Kazuta, Y., and Yomo, T. (2013). A controllable gene expression system in liposomes that includes a positive feedback loop. Mol. Biosyst. 9, 1282–1285. doi:10.1039/c3mb70032a

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Koizumi, M., Soukup, G. A., Kerr, J. N. Q., and Breaker, R. R. (1999). Allosteric selection of ribozymes that respond to the second messengers cGMP and cAMP. Nat. Struct. Biol. 6, 1062–1071. doi:10.1038/14947

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Korade, Z., and Kenworthy, A. K. (2008). Lipid rafts, cholesterol, and the brain. Neuropharmacology 55, 1265–1273. doi:10.1016/j.neuropharm.2008.02.019

CrossRef Full Text | Google Scholar

Kozak, M. (1999). Initiation of translation in prokaryotes and eukaryotes. Gene 234, 187–208. doi:10.1016/S0378-1119(99)00210-3

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Kuruma, Y., Stano, P., Ueda, T., and Luisi, P. L. (2009). A synthetic biology approach to the construction of membrane proteins in semi-synthetic minimal cells. Biochim. Biophys. Acta 1788, 567–574. doi:10.1016/j.bbamem.2008.10.017

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Langecker, M., Arnaut, V., Martin, T. G., List, J., Renner, S., Mayer, M., et al. (2012). Synthetic lipid membrane channels formed by designed DNA nanostructures. Science 338, 932–936. doi:10.1126/science.1225624

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Lazzerini-Ospri, L., Stano, P., Luisi, P., and Marangoni, R. (2012). Characterization of the emergent properties of a synthetic quasi-cellular system. BMC Bioinformatics 13(Suppl. 4):S9. doi:10.1186/1471-2105-13-S4-S9

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Lee, J. M., Lee, J., Kim, T., and Lee, S. K. (2013). Switchable gene expression in Escherichia coli using a miniaturized photobioreactor. PLoS ONE 8:e52382. doi:10.1371/journal.pone.0052382

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Leirmo, S., and Gourse, R. L. (1991). Factor-independent activation of Escherichia coli rRNA transcription. I. Kinetic analysis of the roles of the upstream activator region and supercoiling on transcription of the rrnB P1 promoter in vitro. J. Mol. Biol. 220, 555–568. doi:10.1016/0022-2836(91)90100-K

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Lentini, R., Santero, S. P., Chizzolini, F., Cecchi, D., Fontana, J., Marchioretto, M., et al. (2014). Integrating artificial with natural cells to translate chemical messages that direct E. coli behaviour. Nat. Commun. 5, 4012. doi:10.1038/ncomms5012

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Lewis, J. (2003). Autoinhibition with transcriptional delay: a simple mechanism for the zebrafish somitogenesis oscillator. Curr. Biol. 13, 1398–1408. doi:10.1016/S0960-9822(03)00534-7

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Lim, H. G., Seo, S. W., and Jung, G. Y. (2013). Engineered Escherichia coli for simultaneous utilization of galactose and glucose. Bioresour. Technol. 135, 564–567. doi:10.1016/j.biortech.2012.10.124

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Lindorff-Larsen, K., Piana, S., Dror, R. O., and Shaw, D. E. (2011). How fast-folding proteins fold. Science 334, 517–520. doi:10.1126/science.1208351

CrossRef Full Text | Google Scholar

Loew, L. M., and Schaff, J. C. (2001). The virtual cell: a software environment for computational cell biology. Trends Biotechnol. 19, 401–406. doi:10.1016/S0167-7799(01)01740-1

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Lu, J., Tang, J., Liu, Y., Zhu, X., Zhang, T., and Zhang, X. (2012). Combinatorial modulation of galP and glk gene expression for improved alternative glucose utilization. Appl. Microbiol. Biotechnol. 93, 2455–2462. doi:10.1007/s00253-011-3752-y

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

MacDonald, L. E., Zhou, Y., and McAllister, W. T. (1993). Termination and slippage by bacteriophage T7 RNA polymerase. J. Mol. Biol. 232, 1030–1047. doi:10.1006/jmbi.1993.1458

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Maeda, Y. T., Nakadai, T., Shin, J., Uryu, K., Noireaux, V., and Libchaber, A. (2012). Assembly of MreB filaments on liposome membranes: a synthetic biology approach. ACS Synth. Biol. 1, 53–59. doi:10.1021/sb200003v

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Maerkl, S. J., and Quake, S. R. (2007). A systems approach to measuring the binding energy landscapes of transcription factors. Science 315, 233–237. doi:10.1126/science.1131007

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Mairhofer, J., Wittwer, A., Cserjan-Puschmann, M., and Striedner, G. (2014). Preventing T7 RNA polymerase read-through transcription – a synthetic termination signal capable of improving bioprocess stability. ACS Synth. Biol. doi:10.1021/sb5000115

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Man, T. K., and Stormo, G. D. (2001). Non-independence of Mnt repressor-operator interaction determined by a new quantitative multiple fluorescence relative affinity (QuMFRA) assay. Nucleic Acids Res. 29, 2471–2478. doi:10.1093/nar/29.12.2471

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Marchisio, M. A. (2014). In silico design and in vivo implementation of yeast gene Boolean gates. J. Biol. Eng. 8, 6. doi:10.1186/1754-1611-8-6

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Marchisio, M. A., and Stelling, J. (2008). Computational design of synthetic gene circuits with composable parts. Bioinformatics 24, 1903–1910. doi:10.1093/bioinformatics/btn330

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Marchisio, M. A., and Stelling, J. (2011). Automatic design of digital synthetic gene circuits. PLoS Comput. Biol. 7:e1001083. doi:10.1371/journal.pcbi.1001083

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Mari, A. (2002). IgE to cross-reactive carbohydrate determinants: analysis of the distribution and appraisal of the in vivo and in vitro reactivity. Int. Arch. Allergy Immunol. 129, 286–295. doi:10.1159/000067591

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Marrink, S. J., De Vries, A. H., and Tieleman, D. P. (2009). Lipids on the move: simulations of membrane pores, domains, stalks and curves. Biochim. Biophys. Acta 1788, 149–168. doi:10.1016/j.bbamem.2008.10.006

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Marrink, S. J., Risselada, H. J., Yefimov, S., Tieleman, D. P., and De Vries, A. H. (2007). The MARTINI force field: coarse grained model for biomolecular simulations. J. Phys. Chem. B 111, 7812–7824. doi:10.1021/jp071097f

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Martini, L., and Mansy, S. S. (2011). Cell-like systems with riboswitch controlled gene expression. Chem. Commun. (Camb) 47, 10734–10736. doi:10.1039/c1cc13930d

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Matsuura, T., Hosoda, K., Kazuta, Y., Ichihashi, N., Suzuki, H., and Yomo, T. (2012). Effects of compartment size on the kinetics of intracompartmental multimeric protein synthesis. ACS Synth. Biol. 1, 431–437. doi:10.1021/sb300041z

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Matsuura, T., Kazuta, Y., Aita, T., Adachi, J., and Yomo, T. (2009). Quantifying epistatic interactions among the components constituting the protein translation system. Mol. Syst. Biol. 5, doi:10.1038/msb.2009.50

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

McClymont, K., and Soyer, O. S. (2013). Metabolic tinker: an online tool for guiding the design of synthetic metabolic pathways. Nucleic Acids Res. 41, e113. doi:10.1093/nar/gkt234

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Melo, M. N., Ferre, R., Feliu, L., Bardaji, E., Planas, M., and Castanho, M. A. (2011). Prediction of antibacterial activity from physicochemical properties of antimicrobial peptides. PLoS ONE 6:e28549. doi:10.1371/journal.pone.0028549

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Michalowski, C. B., Short, M. D., and Little, J. W. (2004). Sequence tolerance of the phage lambda PRM promoter: implications for evolution of gene regulatory circuitry. J. Bacteriol. 186, 7988–7999. doi:10.1128/JB.186.23.7988-7999.2004

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Milo, R., Jorgensen, P., Moran, U., Weber, G., and Springer, M. (2010). BioNumbers – the database of key numbers in molecular and cell biology. Nucleic Acids Res. 38, D750–D753. doi:10.1093/nar/gkp889

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Milo, R., Shen-Orr, S., Itzkovitz, S., Kashtan, N., Chklovskii, D., and Alon, U. (2002). Network motifs: simple building blocks of complex networks. Science 298, 824–827. doi:10.1126/science.298.5594.824

CrossRef Full Text | Google Scholar

Minton, A. P., and Wilf, J. (1981). Effect of macromolecular crowding upon the structure and function of an enzyme: glyceraldehyde-3-phosphate dehydrogenase. Biochemistry 20, 4821–4826. doi:10.1021/bi00520a003

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Montagne, K., Plasson, R., Sakai, Y., Fujii, T., and Rondelez, Y. (2011). Programming an in vitro DNA oscillator using a molecular networking strategy. Mol. Syst. Biol. 7, 466. doi:10.1038/msb.2010.120

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Morelli, M. J., Allen, R. J., and Wolde, P. R. (2011). Effects of macromolecular crowding on genetic networks. Biophys. J. 101, 2882–2891. doi:10.1016/j.bpj.2011.10.053

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Moritani, Y., Nomura, S. M., Morita, I., and Akiyoshi, K. (2010). Direct integration of cell-free-synthesized connexin-43 into liposomes and hemichannel formation. FEBS J. 277, 3343–3352. doi:10.1111/j.1742-4658.2010.07736.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Mulligan, M. E., Hawley, D. K., Entriken, R., and McClure, W. R. (1984). Escherichia coli promoter sequences predict in vitro RNA polymerase selectivity. Nucleic Acids Res. 12, 789–800. doi:10.1093/nar/12.1Part2.789

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Munkhjargal, M., Hatayama, K., Matsuura, Y., Toma, K., Arakawa, T., and Mitsubayashi, K. (2014). Glucose-driven chemo-mechanical autonomous drug-release system with multi-enzymatic amplification toward feedback control of blood glucose in diabetes. Biosens. Bioelectron. doi:10.1016/j.bios.2014.08.044

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Murakami, Y., and Maeda, M. (2005). DNA-responsive hydrogels that can shrink or swell. Biomacromolecules 6, 2927–2929. doi:10.1021/bm0504330

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Mutalik, V. K., Guimaraes, J. C., Cambray, G., Lam, C., Christoffersen, M. J., Mai, Q. A., et al. (2013). Precise and reliable gene expression via standard transcription and translation initiation elements. Nat. Methods 10, 354–360. doi:10.1038/nmeth.2404

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Nathans, D., Notani, G., Schwartz, J. H., and Zinder, N. D. (1962). Biosynthesis of the coat protein of coliphage f2 by E. coli extracts. Proc. Natl. Acad. Sci. U.S.A. 48, 1424–1431. doi:10.1073/pnas.48.8.1424

CrossRef Full Text | Google Scholar

Noireaux, V., Bar-Ziv, R., Godefroy, J., Salman, H., and Libchaber, A. (2005). Toward an artificial cell based on gene expression in vesicles. Phys. Biol. 2, 1–8. doi:10.1088/1478-3975/2/3/P01

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Noireaux, V., Maeda, Y. T., and Libchaber, A. (2011). Development of an artificial cell, from self-organization to computation and self-reproduction. Proc. Natl. Acad. Sci. U.S.A. 108, 3473–3480. doi:10.1073/pnas.1017075108

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Oberholzer, T., Albrizio, M., and Luisi, P. L. (1995a). Polymerase chain reaction in liposomes. Chem. Biol. 2, 677–682. doi:10.1016/1074-5521(95)90031-4

CrossRef Full Text | Google Scholar

Oberholzer, T., Wick, R., Luisi, P. L., and Biebricher, C. K. (1995b). Enzymatic RNA replication in self-reproducing vesicles: an approach to a minimal cell. Biochem. Biophys. Res. Commun. 207, 250–257. doi:10.1006/bbrc.1995.1180

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Oberholzer, T., Nierhaus, K. H., and Luisi, P. L. (1999). Protein expression in liposomes. Biochem. Biophys. Res. Commun. 261, 238–241. doi:10.1006/bbrc.1999.0404

CrossRef Full Text | Google Scholar

Orth, J. D., Thiele, I., and Palsson, B. O. (2010). What is flux balance analysis? Nat. Biotechnol. 28, 245–248. doi:10.1038/nbt.1614

CrossRef Full Text | Google Scholar

Padirac, A., Fujii, T., and Rondelez, Y. (2012). Bottom-up construction of in vitro switchable memories. Proc. Natl. Acad. Sci. U.S.A. 109, E3212–E3220. doi:10.1073/pnas.1212069109

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Pardee, K., Green, A. A., Ferrante, T., Cameron, D. E., Daleykeyser, A., Yin, P., et al. (2014). Paper-based synthetic gene networks. Cell 159, 940–954. doi:10.1016/j.cell.2014.10.004

CrossRef Full Text | Google Scholar

Park, H. S., Nam, S. H., Lee, J. K., Yoon, C. N., Mannervik, B., Benkovic, S. J., et al. (2006). Design and evolution of new catalytic activity with an existing protein scaffold. Science 311, 535–538. doi:10.1126/science.1118953

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Park, J. M., Kim, T. Y., and Lee, S. Y. (2010). Prediction of metabolic fluxes by incorporating genomic context and flux-converging pattern analyses. Proc. Natl. Acad. Sci. U.S.A. 107, 14931–14936. doi:10.1073/pnas.1003740107

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Paula, S., Volkov, A. G., Van Hoek, A. N., Haines, T. H., and Deamer, D. W. (1996). Permeation of protons, potassium ions, and small polar molecules through phospholipid bilayers as a function of membrane thickness. Biophys. J. 70, 339–348. doi:10.1016/S0006-3495(96)79575-9

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Pedraza, J. M., and Paulsson, J. (2008). Effects of molecular memory and bursting on fluctuations in gene expression. Science 319, 339–343. doi:10.1126/science.1144331

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Perlmutter, J. D., Drasler, W. J. II, Xie, W., Gao, J., Popot, J. L., and Sachs, J. N. (2011). All-atom and coarse-grained molecular dynamics simulations of a membrane protein stabilizing polymer. Langmuir 27, 10523–10537. doi:10.1021/la202103v

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Poland, A., Glover, E., and Kende, A. S. (1976). Stereospecific, high affinity binding of 2,3,7,8-tetrachlorodibenzo-p-dioxin by hepatic cytosol. Evidence that the binding species is receptor for induction of aryl hydrocarbon hydroxylase. J. Biol. Chem. 251, 4936–4946.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Pomerening, J. R., Sontag, E. D., and Ferrell, J. E. Jr. (2003). Building a cell cycle oscillator: hysteresis and bistability in the activation of Cdc2. Nat. Cell Biol. 5, 346–351. doi:10.1038/ncb954

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Pothoulakis, G., Ceroni, F., Reeve, B., and Ellis, T. (2013). The spinach RNA Aptamer as a characterization tool for synthetic biology. ACS Synth. Biol. 3, 182–187. doi:10.1021/sb400089c

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Prates Ramalho, J. P., Gkeka, P., and Sarkisov, L. (2011). Structure and phase transformations of DPPC lipid bilayers in the presence of nanoparticles: insights from coarse-grained molecular dynamics simulations. Langmuir 27, 3723–3730. doi:10.1021/la200236d

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Reeve, B., Hargest, T., Gilbert, C., and Ellis, T. (2014). Predicting translation initiation rates for designing synthetic biology. Front. Bioeng. Biotechnol. 2:1. doi:10.3389/fbioe.2014.00001

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Rhodius, V. A., and Mutalik, V. K. (2010). Predicting strength and function for promoters of the Escherichia coli alternative sigma factor, σ^E. Proc. Natl. Acad. Sci. U.S.A. 107, 2854–2859. doi:10.1073/pnas.0915066107

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Rhodius, V. A., Mutalik, V. K., and Gross, C. A. (2012). Predicting the strength of UP-elements and full-length E. coli σ^E promoters. Nucleic Acids Res. 40, 2907–2924. doi:10.1093/nar/gkr1190

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Risselada, H. J., and Marrink, S. J. (2008). The molecular face of lipid rafts in model membranes. Proc. Natl. Acad. Sci. U.S.A. 105, 17367–17372. doi:10.1073/pnas.0807527105

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Robertson, M. P., and Ellington, A. D. (1999). In vitro selection of an allosteric ribozyme that transduces analytes to amplicons. Nat. Biotechnol. 17, 62–66. doi:10.1038/5236

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Rog, T., Vattulainen, I., Bunker, A., and Karttunen, M. (2007). Glycolipid membranes through atomistic simulations: effect of glucose and galactose head groups on lipid bilayer properties. J. Phys. Chem. B 111, 10146–10154. doi:10.1021/jp0730895

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Safra, T., Muggia, F., Jeffers, S., Tsao-Wei, D. D., Groshen, S., Lyass, O., et al. (2000). Pegylated liposomal doxorubicin (doxil): reduced clinical cardiotoxicity in patients reaching or exceeding cumulative doses of 500 mg/m2. Ann. Oncol. 11, 1029–1033. doi:10.1023/A:1008365716693

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Salis, H. M. (2011). “Chapter two – the ribosome binding site calculator,” in Methods in Enzymology, ed. V. Christopher (New York: Academic Press), 19–42.

Google Scholar

Salis, H. M., Mirsky, E. A., and Voigt, C. A. (2009). Automated design of synthetic ribosome binding sites to control protein expression. Nat. Biotech. 27, 946–950. doi:10.1038/nbt.1568

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Schellenberger, J., Que, R., Fleming, R. M., Thiele, I., Orth, J. D., Feist, A. M., et al. (2011). Quantitative prediction of cellular metabolism with constraint-based models: the COBRA Toolbox v2.0. Nat. Protoc. 6, 1290–1307. doi:10.1038/nprot.2011.308

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Schomburg, I., Chang, A., Placzek, S., Sohngen, C., Rother, M., Lang, M., et al. (2013). BRENDA in 2013: integrated reactions, kinetic data, enzyme function data, improved disease classification: new options and contents in BRENDA. Nucleic Acids Res. 41, D764–D772. doi:10.1093/nar/gks1049

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Scott, M., Gunderson, C. W., Mateescu, E. M., Zhang, Z., and Hwa, T. (2010). Interdependence of cell growth and gene expression: origins and consequences. Science 330, 1099–1102. doi:10.1126/science.1192588

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Segal, E., Raveh-Sadka, T., Schroeder, M., Unnerstall, U., and Gaul, U. (2008). Predicting expression patterns from regulatory sequence in Drosophila segmentation. Nature 451, 535–540. doi:10.1038/nature06496

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Sekine, R., Yamamura, M., Ayukawa, S., Ishimatsu, K., Akama, S., Takinoue, M., et al. (2011). Tunable synthetic phenotypic diversification on Waddington’s landscape through autonomous signaling. Proc. Natl. Acad. Sci. U.S.A. 108, 17969–17973. doi:10.1073/pnas.1105901108

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Seo, S. W., Yang, J.-S., Cho, H.-S., Yang, J., Kim, S. C., Park, J. M., et al. (2014). Predictive combinatorial design of mRNA translation initiation regions for systematic optimization of gene expression levels. Sci. Rep. 4. doi:10.1038/srep04515

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Seo, S. W., Yang, J. S., Kim, I., Yang, J., Min, B. E., Kim, S., et al. (2013). Predictive design of mRNA translation initiation region to control prokaryotic translation efficiency. Metab. Eng. 15, 67–74. doi:10.1016/j.ymben.2012.10.006

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Shaw, D. E., Maragakis, P., Lindorff-Larsen, K., Piana, S., Dror, R. O., Eastwood, M. P., et al. (2010). Atomic-level characterization of the structural dynamics of proteins. Science 330, 341–346. doi:10.1126/science.1187409

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Shis, D. L., and Bennett, M. R. (2013). Library of synthetic transcriptional AND gates built with split T7 RNA polymerase mutants. Proc. Natl. Acad. Sci. U.S.A. 110, 5028–5033. doi:10.1073/pnas.1220157110

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Shutt, D. A., and Cox, R. I. (1972). Steroid and phyto-oestrogen binding to sheep uterine receptors in vitro. J. Endocrinol. 52, 299–310. doi:10.1677/joe.0.0520299

CrossRef Full Text | Google Scholar

Simonetti, A., Marzi, S., Jenner, L., Myasnikov, A., Romby, P., Yusupova, G., et al. (2009). A structural view of translation initiation in bacteria. Cell. Mol. Life Sci. 66, 423–436. doi:10.1007/s00018-008-8416-4

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Simons, K., and Ikonen, E. (1997). Functional rafts in cell membranes. Nature 387, 569–572. doi:10.1038/42408

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Singh, A., Deans, T. L., and Elisseeff, J. H. (2013). Photomodulation of cellular gene expression in hydrogels. Acs Macro Lett. 2, 269–272. doi:10.1021/mz300591m

CrossRef Full Text | Google Scholar

Siu, S. W., Vacha, R., Jungwirth, P., and Bockmann, R. A. (2008). Biomolecular simulations of membranes: physical properties from different force fields. J. Chem. Phys. 128, 125103. doi:10.1063/1.2897760

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Smith, K. A., Jasnow, D., and Balazs, A. C. (2007). Designing synthetic vesicles that engulf nanoscopic particles. J. Chem. Phys. 127, 084703. doi:10.1063/1.2766953

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Sodt, A. J., Sandar, M. L., Gawrisch, K., Pastor, R. W., and Lyman, E. (2014). The molecular structure of the liquid-ordered phase of lipid bilayers. J. Am. Chem. Soc. 136, 725–732. doi:10.1021/ja4105667

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Sohka, T., Heins, R. A., Phelan, R. M., Greisler, J. M., Townsend, C. A., and Ostermeier, M. (2009). An externally tunable bacterial band-pass filter. Proc. Natl. Acad. Sci. U.S.A. 106, 10135–10140. doi:10.1073/pnas.0901246106

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Sokolova, E., Spruijt, E., Hansen, M. M., Dubuc, E., Groen, J., Chokkalingam, V., et al. (2013). Enhanced transcription rates in membrane-free protocells formed by coacervation of cell lysate. Proc. Natl. Acad. Sci. U.S.A. 110, 11692–11697. doi:10.1073/pnas.1222321110

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Solomon, M. J., and Varshavsky, A. (1985). Formaldehyde-mediated DNA-protein crosslinking: a probe for in vivo chromatin structures. Proc. Natl. Acad. Sci. U.S.A. 82, 6470–6474. doi:10.1073/pnas.82.19.6470

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Stepniewski, M., Pasenkiewicz-Gierula, M., Rog, T., Danne, R., Orlowski, A., Karttunen, M., et al. (2011). Study of PEGylated lipid layers as a model for PEGylated liposome surfaces: molecular dynamics simulation and Langmuir monolayer studies. Langmuir 27, 7788–7798. doi:10.1021/la200003n

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Stogbauer, T., Windhager, L., Zimmer, R., and Radler, J. O. (2012). Experiment and mathematical modeling of gene expression dynamics in a cell-free system. Integr. Biol. (Camb) 4, 494–501. doi:10.1039/c2ib00102k

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Stormo, G. D. (1990). Consensus patterns in DNA. Meth. Enzymol. 183, 211–221. doi:10.1016/0076-6879(90)83015-2

CrossRef Full Text | Google Scholar

Stormo, G. D. (2000). DNA binding sites: representation and discovery. Bioinformatics 16, 16–23. doi:10.1093/bioinformatics/16.1.16

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Strauch, M. A. (1995). In vitro binding affinity of the Bacillus subtilis AbrB protein to six different DNA target regions. J. Bacteriol. 177, 4532–4536.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Stricker, J., Cookson, S., Bennett, M. R., Mather, W. H., Tsimring, L. S., and Hasty, J. (2008). A fast, robust and tunable synthetic gene oscillator. Nature 456, 516–519. doi:10.1038/nature07389

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Sum, A. K., Faller, R., and De Pablo, J. J. (2003). Molecular simulation study of phospholipid bilayers and insights of the interactions with disaccharides. Biophys. J. 85, 2830–2844. doi:10.1016/S0006-3495(03)74706-7

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Swartz, J. R. (2012). Transforming biochemical engineering with cell-free biology. AIChE J. 58, 5–13. doi:10.1002/aic.13701

CrossRef Full Text | Google Scholar

Tabor, J. J., Salis, H. M., Simpson, Z. B., Chevalier, A. A., Levskaya, A., Marcotte, E. M., et al. (2009). A synthetic genetic edge detection program. Cell 137, 1272–1281. doi:10.1016/j.cell.2009.04.048

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Takeda, Y., Sarai, A., and Rivera, V. M. (1989). Analysis of the sequence-specific interactions between Cro repressor and operator DNA by systematic base substitution experiments. Proc. Natl. Acad. Sci. U.S.A. 86, 439–443. doi:10.1073/pnas.86.2.439

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Takinoue, M., Kiga, D., Shohda, K.-I., and Suyama, A. (2008). Experiments and simulation models of a basic computation element of an autonomous molecular computing system. Phys. Rev. E 78, 041921.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Tan, C., Saurabh, S., Bruchez, M. P., Schwartz, R., and Leduc, P. (2013). Molecular crowding shapes gene expression in synthetic cellular nanosystems. Nat. Nanotechnol. 8, 602–608. doi:10.1038/nnano.2013.132

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Tang, Y. C., Chang, H. C., Roeben, A., Wischnewski, D., Wischnewski, N., Kerner, M. J., et al. (2006). Structural features of the GroEL-GroES nano-cage required for rapid folding of encapsulated protein. Cell 125, 903–914. doi:10.1016/j.cell.2006.04.027

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Temme, K., Zhao, D., and Voigt, C. A. (2012). Refactoring the nitrogen fixation gene cluster from Klebsiella oxytoca. Proc. Natl. Acad. Sci. U.S.A. 109, 7085–7090. doi:10.1073/pnas.1120788109

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Thakkar, F. M., and Ayappa, K. G. (2010). Effect of polymer grafting on the bilayer gel to liquid-crystalline transition. J. Phys. Chem. B 114, 2738–2748. doi:10.1021/jp9100762

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Thogersen, L., Schiott, B., Vosegaard, T., Nielsen, N. C., and Tajkhorshid, E. (2008). Peptide aggregation and pore formation in a lipid bilayer: a combined coarse-grained and all atom molecular dynamics study. Biophys. J. 95, 4337–4347. doi:10.1529/biophysj.108.133330

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Tieleman, D. P. (2004). The molecular basis of electroporation. BMC Biochem. 5:10. doi:10.1186/1471-2091-5-10

CrossRef Full Text | Google Scholar

Toni, T., and Tidor, B. (2013). Combined model of intrinsic and extrinsic variability for computational network design with application to synthetic biology. PLoS Comput. Biol. 9:e1002960. doi:10.1371/journal.pcbi.1002960

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Umakoshi, H., Suga, K., Bui, H. T., Nishida, M., Shimanouchi, T., and Kuboi, R. (2009). Charged liposome affects the translation and folding steps of in vitro expression of green fluorescent protein. J. Biosci. Bioeng. 108, 450–454. doi:10.1016/j.jbiosc.2009.05.012

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Veatch, S. L., Polozov, I. V., Gawrisch, K., and Keller, S. L. (2004). Liquid domains in vesicles investigated by NMR and fluorescence microscopy. Biophys. J. 86, 2910–2922. doi:10.1016/S0006-3495(04)74342-8

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

von Hippel, P. H., and Berg, O. G. (1986). On the specificity of DNA-protein interactions. Proc. Natl. Acad. Sci. U.S.A. 83, 1608–1612. doi:10.1073/pnas.83.6.1608

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

von Hippel, P. H., and Yager, T. D. (1991). Transcript elongation and termination are competitive kinetic processes. Proc. Natl. Acad. Sci. U.S.A. 88, 2307–2311. doi:10.1073/pnas.88.6.2307

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Walde, P., Goto, A., Monnard, P.-A., Wessicken, M., and Luisi, P. L. (1994). Oparin’s reactions revisited: enzymic synthesis of poly(adenylic acid) in micelles and self-reproducing vesicles. J. Am. Chem. Soc. 116, 7541–7547. doi:10.1021/ja00096a010

CrossRef Full Text | Google Scholar

Waugh, D. F. (1954). Protein-protein interactions. Adv. Protein Chem. 9, 325–437. doi:10.1016/S0065-3233(08)60210-7

CrossRef Full Text | Google Scholar

Weeks, K. M. (2010). Advances in RNA structure analysis by chemical probing. Curr. Opin. Struct. Biol. 20, 295–304. doi:10.1016/j.sbi.2010.04.001

CrossRef Full Text | Google Scholar

Weitz, M., Kim, J., Kapsner, K., Winfree, E., Franco, E., and Simmel, F. C. (2014). Diversity in the dynamical behaviour of a compartmentalized programmable biochemical oscillator. Nat. Chem. 6, 295–302. doi:10.1038/nchem.1869

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Welch, P., and Scopes, R. K. (1985). Studies on cell-free metabolism: ethanol production by a yeast glycolytic system reconstituted from purified enzymes. J. Biotechnol. 2, 257–273. doi:10.1016/0168-1656(85)90029-X

CrossRef Full Text | Google Scholar

Wick, R., and Luisi, P. L. (1996). Enzyme-containing liposomes can endogenously produce membrane-constituting lipids. Chem. Biol. 3, 277–285. doi:10.1016/S1074-5521(96)90107-6

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Wijma, H. J., and Janssen, D. B. (2013). Computational design gains momentum in enzyme catalysis engineering. FEBS J. 280, 2948–2960. doi:10.1111/febs.12324

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Witkin, E. M. (1976). Ultraviolet mutagenesis and inducible DNA repair in Escherichia coli. Bacteriol. Rev. 40, 869–907.

Google Scholar

Wittig, U., Kania, R., Golebiewski, M., Rey, M., Shi, L., Jong, L., et al. (2012). SABIO-RK – database for biochemical reaction kinetics. Nucleic Acids Res. 40, D790–D796. doi:10.1093/nar/gkr1046

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Xia, D., Zheng, H., Liu, Z., Li, G., Li, J., Hong, J., et al. (2011). MRSD: a web server for metabolic route search and design. Bioinformatics 27, 1581–1582. doi:10.1093/bioinformatics/btr160

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Xiang, T. X., and Anderson, B. D. (2006). Liposomal drug transport: a molecular perspective from molecular dynamics simulations in lipid bilayers. Adv. Drug Deliv. Rev. 58, 1357–1378. doi:10.1016/j.addr.2006.09.002

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Yaman, F., Bhatia, S., Adler, A., Densmore, D., and Beal, J. (2012). Automated selection of synthetic biology parts for genetic regulatory networks. Acs Synth. Biol. 1, 332–344. doi:10.1021/sb300032y

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Yokobayashi, Y., Weiss, R., and Arnold, F. H. (2002). Directed evolution of a genetic circuit. Proc. Natl. Acad. Sci. U.S.A. 99, 16587–16591. doi:10.1073/pnas.252535999

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

You, L., Cox, R. S. III, Weiss, R., and Arnold, F. H. (2004). Programmed population control by cell-cell communication and regulated killing. Nature 428, 868–871. doi:10.1038/nature02491

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Yu, W., Sato, K., Wakabayashi, M., Nakaishi, T., Ko-Mitamura, E. P., Shima, Y., et al. (2001). Synthesis of functional protein in liposome. J. Biosci. Bioeng. 92, 590–593. doi:10.1016/S1389-1723(01)80322-4

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Zanghellini, A., Jiang, L., Wollacott, A. M., Cheng, G., Meiler, J., Althoff, E. A., et al. (2006). New algorithms and an in silico benchmark for computational enzyme design. Protein Sci. 15, 2785–2794. doi:10.1110/ps.062353106

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Zawada, J. F., Yin, G., Steiner, A. R., Yang, J., Naresh, A., Roy, S. M., et al. (2011). Microscale to manufacturing scale-up of cell-free cytokine production – a new approach for shortening protein production development timelines. Biotechnol. Bioeng. 108, 1570–1578. doi:10.1002/bit.23103

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Zhang, Y., Sun, J., and Zhong, J.-J. (2010). Biofuel production by in vitro synthetic enzymatic pathway biotransformation. Curr. Opin. Biotechnol. 21, 663–669. doi:10.1016/j.copbio.2010.05.005

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Zhang, Y. H. P. (2010). Production of biocommodities and bioelectricity by cell-free synthetic enzymatic pathway biotransformations: challenges and opportunities. Biotechnol. Bioeng. 105, 663–677. doi:10.1002/bit.22630

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Zhu, H., Bilgin, M., Bangham, R., Hall, D., Casamayor, A., Bertone, P., et al. (2001). Global analysis of protein activities using proteome chips. Science 293, 2101–2105. doi:10.1126/science.1062191

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Zubay, G. (1973). In vitro synthesis of protein in microbial systems. Annu. Rev. Genet. 7, 267–287. doi:10.1146/annurev.ge.07.120173.001411

CrossRef Full Text | Google Scholar