- Department of Computer Science, University of Illinois Chicago, Chicago, IL, United States
Current approaches to A/B testing in networks focus on limiting interference, the concern that treatment effects can “spill over” from treatment nodes to control nodes and lead to biased causal effect estimation. In the presence of interference, two main types of causal effects are direct treatment effects and total treatment effects. In this paper, we propose two network experiment designs that increase the accuracy of direct and total effect estimations in network experiments through minimizing interference between treatment and control units. For direct treatment effect estimation, we present a framework that takes advantage of independent sets and assigns treatment and control only to a set of non-adjacent nodes in a graph, in order to disentangle peer effects from direct treatment effect estimation. For total treatment effect estimation, our framework combines weighted graph clustering and cluster matching approaches to jointly minimize interference and selection bias. Through a series of simulated experiments on synthetic and real-world network datasets, we show that our designs significantly increase the accuracy of direct and total treatment effect estimation in network experiments.
1. Introduction
Causal inference plays a central role in many disciplines, from economics (Varian, 2016; Holtz et al., 2020) to health sciences (Antman et al., 1992; Loucks and Thuma, 2003) and social sciences (Sobel, 2000; Gangl, 2010). The goal of causal inference is to estimate the effect of an intervention on individuals' outcomes. The gold standard for inferring causality is the use of controlled experiments, also known as A/B tests and Randomized Controlled Trials (RCTs), in which experimenters can assign treatment (e.g. a news feed ranking algorithm) to a random subset of a population and compare their outcomes with the outcomes of a control group, randomly selected from the same population (e.g., a group of users who used the old news feed ranking algorithm). Through randomization, the experimenter can control for confounding variables that can impact the treatment and outcome assignment but are not present in the data and assess whether the treatment can cause the target variable to change.
While it is straightforward to randomly assign treatment and control to units that are i.i.d., it is much harder to do that for units that interact with each other. The goal of designing network experiments is to ensure reliable causal effect estimation in controlled experiments for potentially interacting units. One of the challenges in network experiment design is dealing with interference (or spillover), the problem of treatment “spilling over” from a treated node to a control node. The presence of interference breaks the Stable Unit Treatment Value Assumption (SUTVA), the assumption that one unit's outcome is unaffected by another unit's treatment assignment, and challenges the validity of causal inference (Imbens and Rubin, 2015). Different types of causal estimands are possible in the presence of interference: 1) the difference between the average outcomes of treated and untreated individuals due to the treatment alone (Direct Treatment Effects), 2) the influence of peers' behavior on the unit's response to the treatment (Peer Effects), and 3) the combination of direct treatment effects and peer effects (Total Treatment Effects). Different estimands lead to different inference procedures—both from a design and an analysis point of view. As a motivating example, consider the problem of quantifying the effect of changing the news feed ranking algorithm of an online social network website on the time that users spend interacting with the site. Direct treatment effects capture the effect of changing the news feed ranking algorithm on the time that a user spends on the website, regardless of the behavior of other users in the study. Peer effects quantify the effect of friends time spent on the website on the time that a user spends on the website. Total treatment effects show the total effect of changing the news feed ranking algorithm on the time all users spend on the website which is equal to the sum of peer effects and direct treatment effects.
The focus of this paper is measuring direct and total treatment effects in network data. The total treatment effect of applying a treatment to all units compared with applying a different (control) treatment to all units is a common causal estimand in network experiments. Prominent methods for total treatment effect estimation rely on two-stage or cluster-based randomization, in which clusters are identified using graph clustering and cluster randomization dictates the node assignment to treatment and control (Ugander et al., 2013; Eckles et al., 2016; Saveski et al., 2017; Pouget-Abadie et al., 2018; Fatemi and Zheleva, 2020). Graph clustering aims to find densely connected clusters of nodes, such that few edges exist across clusters (Schaeffer, 2007). The basic idea of applying it to causal inference is that little interference can occur between nodes in different clusters.
Clustering a connected graph component is guaranteed to leave edges between clusters, therefore removing interference completely is impossible. At the same time, some node pairs are more likely to interact than others, and assigning such pairs to different treatment groups is more likely to lead to undesired spillover (and biased causal effect estimation) than separating pairs with a low probability of interaction. We make the key observation that there is an inherent tradeoff between interference and selection bias in cluster-based randomization based on the chosen number of clusters (as demonstrated in Figure 1). Due to the heterogeneity of real-world graphs, discovered clusters can be very different from each other, and the nodes in these clusters may not represent the same underlying population (Fatemi and Zheleva, 2020). Therefore, cluster randomization can lead to selection bias in the data with causal effects that are confounded by the difference in node features of each cluster.
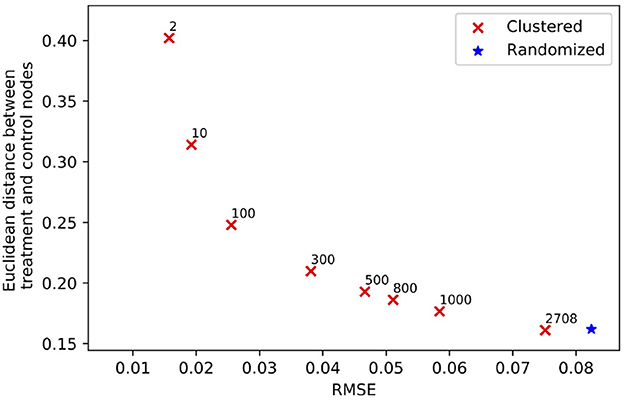
Figure 1. The tradeoff between selection bias (distance) and undesired spillover (RMSE) in cluster-based randomization; each data point is annotated with the number of clusters.
Here, we propose two methods for network experiment design in the presence of interference. First, we focus on quantifying direct treatment effects by designing a network experiment that disentangles peer effects from direct treatment effects and provides an unbiased estimation of direct treatment effects. We develop CauseIS, a framework that leverages independent algorithms on network nodes to divide nodes into two sets: 1) independent set nodes, and 2) graph nodes that are not in the independent set referred to as bystander nodes. By assigning the independent set nodes to treatment and control groups, we ensure that there are no peer effects between nodes participating in the experiment, regardless of whether they are in different treatment groups or the same treatment group. Key to the proposed experiment design is the idea that in expectation, the peer effects of bystander nodes on the treatment group are the same as the peer effect of bystander nodes on the control group, thus canceling each other in the total treatment effect estimation.
The second method focuses on total treatment effect estimation. We develop CMatch, a framework for network experiment design that minimizes both interference and selection bias through a novel objective function for matching clusters and combining node matching with weighted graph clustering to provide a more accurate estimation of total treatment effects (Fatemi and Zheleva, 2020). We introduce the concept of “edge spillover probability” as the probability of interaction between entities and account for it in the design. In this work, incorporating node matching and edge spillover probabilities into graph clustering is novel.
2. Related works
By attracting attention toward network experiments, dependent on the assumptions made in the study different causal estimands for direct, peer, and total treatment effects have been proposed (Halloran and Struchiner, 1995; Hudgens and Halloran, 2008; Green et al., 2016; Taylor and Eckles, 2018; Pouget-Abadie et al., 2019; Ugander and Yin, 2020; Aronow et al., 2021; Sävje et al., 2021). In this section, we give an overview of relevant works to quantify direct and total treatment effects in RCTs.
2.1. Direct treatment effect estimation
Estimating the effect of treatment alone has been studied in the context of network experiment design. Jagadeesan et al. (2020) propose an approach to reduce the bias of the Neymanian estimator of direct treatment effect estimation under interference and homophily. In this approach, treatment assignment is considered as a quasi-coloring on a graph and every treated node is tried to be matched with a control node with an identical number of treated and control neighbors to create a balanced interference in network experiments. In networks where perfect quasi-coloring is not possible, nodes are ordered by degree and then nodes with a similar degree are paired and assigned to treatment or control. The accuracy of causal effect estimation in this method depends on the network structure, degree distribution of the nodes, and approaching perfect quasi-coloring to perfect quasi-coloring. Recently, Li and Wager (2022) explore the problem of direct treatment effect estimation under random graph asymptotics where an interference graph is a random draw from an (unknown) graphon. Sussman and Airoldi (2017) propose an approach to estimate direct treatment effects considering a fixed design for potential outcomes. Similar to these approaches, we focus on estimating direct treatment effects in the presence of peer effects, but our approach can be applied in networks with different structural properties.
2.2. Total treatment effect estimation
Recent work that addresses interference in graphs relies on separating data samples through graph clustering (Backstrom and Kleinberg, 2011; Ugander et al., 2013; Gui et al., 2015; Eckles et al., 2016; Saveski et al., 2017; Pouget-Abadie et al., 2018), relational d-separation (Maier et al., 2010, 2013; Rattigan et al., 2011; Marazopoulou et al., 2015; Lee and Honavar, 2016), or sequential randomization design (Toulis and Kao, 2013). Among these approaches, cluster-based randomization methods attract significant attention recently. Graph clustering aims to find subgraph clusters with high intra-cluster and low inter-cluster edge density (Zhou et al., 2009; Yang and Leskovec, 2015). A number of algorithms exist for weighted graph clustering (Schaeffer, 2007). Node representation learning approaches range from graph motifs (Milo et al., 2002) to embedding representations (Hamilton et al., 2017) and statistical relational learning (SRL) (Rossi et al., 2012). Eckles et al. (2016) evaluate different methods for designing and analyzing randomized experiments and find substantial bias reduction in cluster-based randomization approaches, especially in networks with more clusters and stronger peer effects. Saveski et al. propose a procedure to detect interference bias in network experiments and propose a cluster-based randomization approach to mitigate interference bias in such studies. By comparing completely randomized and Cluster-based randomized experiments (Saveski et al., 2017) on LinkedIn's experimental platform, they indicate the presence of network effects and bias in standard RCTs in a real-world setting. However, cluster-based randomized approaches have high variance, making them more difficult to accurately estimate the treatment effect. Ugander et al. (2013) define a restricted-growth condition on the growth rate of node's connections and show that the variance of estimators is bounded by the linear function of the degrees.
In controlled experiments, the treatment assignment is randomized by the experimenter, whereas in estimating causal effects from observational data, the process by which the treatment is assigned is not decided by the experimenter and is often unknown. Matching is a prominent method for mimicking randomization in observational data by pairing treated units with similar untreated units. Then, the causal effect of interest is estimated based on the matched pairs, rather than the full set of units present in the data, thus reducing the selection bias in observational data (Stuart, 2010). There are two main approaches to matching, fully blocked and propensity score matching (PSM) (Stuart, 2010). Fully blocked matching selects pairs of units whose distance in covariate space is under a pre-determined distance threshold. PSM models the treatment variable based on the observed covariates and matches units that have the same likelihood of treatment. The few research articles that look at the problem of matching for relational domains (Oktay et al., 2010; Arbour et al., 2014) consider SRL data representations. None of them consider cluster matching for a two-stage design which is one of our contributions.
3. Preliminaries
In this section, we formally define the data model, the potential outcomes frameworks, and different types of causal estimands.
3.1. Data model
A graph G = (V, E) consists of a set of n nodes V and a set of edges E = {eij} where eij denotes that there is an edge between node vi ∈ V and node vj ∈ V. Let Ni denote the set of neighbors for node vi, i.e. set of nodes that share an edge with vi. Let vi.X denote the pre-treatment node feature variables (e.g., Twitter user features) for unit vi. Let vi.Y denote the outcome variable of interest for each node vi (e.g., voting), and vi.T ∈ {0, 1} denote whether node vi (e.g., social media user) has been treated (e.g., shown a post about the benefits of voting), vi.T = 1, or not, vi.T = 0. Let Z ∈ {0, 1}N be the treatment assignment vector of all nodes. V1 and V0 indicate the sets of units in treatment and control groups, respectively. For simplicity, we assume that both vi.T and vi.Y are binary variables. The edge spillover probability eij.p refers to the probability of interference occurring between two nodes.
3.2. Potential outcomes framework
The fundamental problem of causal inference is that we can observe the outcome of a target variable for an individual vi in either the treatment or control group but not in both. Let vi.y(1) and vi.y(0) denote the potential outcomes of vi.y if unit vi were assigned to the treatment or control group, respectively. The treatment effect (or causal effect) is the difference g(i) = vi.y(1) − vi.y(0). Since we can never observe the outcome of a unit under both treatment and control simultaneously, the effect of a treatment on an outcome is typically calculated through averaging outcomes over treatment and control groups via difference-in-means: (Stuart, 2010). For the treatment effect to be estimable, the following identifiability assumptions have to hold:
• Stable unit treatment value assumption (SUTVA) refers to the assumption that the outcomes vi.y(1) and vi.y(0) are independent of the treatment assignment of other units: {vi.y(1), vi.y(0)}⊥vj.T, ∀vj ≠ vi ∈ V.
• Ignorability (Imbens and Rubin, 2015)—also known as conditional independence (Pearl, 2009) and absence of unmeasured confoundness—is the assumption that all variables vi.X that can influence both the treatment and outcome vi.Y are observed in the data and there are no unmeasured confounding variables that can cause changes in both the treatment and the outcome: {vi.y(1), vi.y(0)}⊥vi.T∣vi.X.
• Overlap is the assumption that each unit assigned to the treatment or control group could have been assigned to the other group. This is also known as positivity assumption: P(vi.T|vi.X) > 0 for all units and all possible T and X.
3.3. Types of causal effects in networks
We follow Hudgens and Halloran (2008) to define causal estimands for different types of effects possible in the presence of interference. However, our setting is different in a way that all nodes in the same group receive a similar treatment.
Total Treatment Effects (TTE) is defined as the outcome difference between two alternative universes, one in which all nodes are assigned to treatment () and one in which all nodes are assigned to control () (Ugander et al., 2013; Saveski et al., 2017):
TTE is estimated as averages over the treatment and control group, and it accounts for two types of effects, Direct Treatment Effects (DTE) and Peer Effects (PE):
Direct Treatment effects (DTE) reflects the difference between the outcomes of treated and untreated subjects which can be attributed to the treatment alone. They are estimated as:
Peer effects (PE), known also as indirect effects in the prior studies (Halloran and Struchiner, 1995; Hudgens and Halloran, 2008; Jagadeesan et al., 2020), reflect the difference in outcomes that can be attributed to the influence of other subjects in the experiment. Let Ni.π denote the vector of treatment assignments to node vi's neighbors Ni. Average PE is estimated as having neighbors with a treatment vector:
Here, we distinguish between two types of peer effects, allowable peer effects (APE) and unallowable peer effects (UPE). Allowable peer effects are peer effects that occur within the same treatment group, and they are a natural consequence of network interactions. For example, if a social media company wants to introduce a new feature (e.g., nudging users to vote), it would introduce that feature to all users and the total effect of the feature would include both individual and peer effects. Unallowable peer effects are peer effects that occur across treatment groups and contribute to undesired spillover and incorrect causal effect estimation.
For each node vi in treatment group t, we have two types of neighbors: 1) neighbors in the same treatment class as node vi with treatment assignment set ; 2) set of neighbors in a different treatment class () with treatment assignment denoted by . The APE is defined as:
and the UPE is defined as:
4. Problem statement
The goal of designing network experiments is to ensure reliable causal effect estimation in controlled experiments by minimizing both unallowable peer effects in node assignment to treatment and control. In this work, we are interested to design two network experiments for quantifying direct and total treatment effects.
4.1. Direct treatment effect estimation
The question we are interested to answer is: What is the causal effect of the treatment alone? This question has many practical applications for estimating the effectiveness of different policy interventions. Some examples include: What is the individual protection from a disease due to vaccination alone (and not herd immunity)? What is the effect of advertisements on motivating a person to buy a new phone? In network experiments, it is challenging to disentangle DTE from PE and this is one of the main goals of this paper. More formally:
Problem 1 (Network experiment design for direct treatment effect). estimation. Given an undirected graph G = (V, E), and a set of attributes V.X associated with each node. Find a treatment assignment vector Z of a population with three different subsets of nodes, the treatment nodes V1 ∈ V, the control nodes V0 ∈ V, and nodes excluded from the experiment V2 ∈ V, such that:
a. V0 ∩ V1 ∩ V2 = ∅.
b. |V0| + |V1| is maximized.
c. PE(V1) − PE(V0) ≈ 0.
The first component aims to choose treatment, control, and bystander nodes excluded from the experiments that do not overlap. The second component ensures to choose of as many nodes as possible from V to be assigned to treatment and control groups. The third component removes peer effects from causal effect estimation.
4.2. Total treatment effect estimation
TTE is one of the most popular causal estimands in network experiments, especially in cluster-based randomization approaches (Eckles et al., 2016; Pouget-Abadie et al., 2018). There are two main challenges with causal effect estimation in graphs.
4.2.1. Challenge no. 1: it is hard to separate a graph into treatment and control nodes without leaving edges across
The presence of interference breaks the SUTVA assumption and leads to biased causal effect estimation in relational data. The two-stage experimental design addresses this problem by finding groups of units that are unlikely to interact with each other (stage 1) and then randomly assigning each group to treatment and control (stage 2). Clustering has been proposed as a way to discover such groups that are strongly connected within but loosely connected across, thus finding treatment and control subgraphs that have a low probability of spillover from one to the other. However, due to the density of real-world graphs, graph clustering techniques can leave as many as 65% to 79% of edges as inter-cluster edges (Table 2 in Saveski et al., 2017). Leaving these edges across treatment and control nodes would lead to a large amount of spillover. Incorporating information about the edge probability of spillover into the clustering helps alleviate this problem and is one of the main contributions of our work.
4.2.2. Challenge no. 2: there is a tradeoff between interference and selection bias in cluster-based network experiments
While randomization of i.i.d. units in controlled experiments can guarantee ignorability and overlap, the two-stage design does not. One of the key observations in our work is that dependent on the number of clusters, there is a tradeoff between interference and selection bias in terms of the treatment and control group not representing the same underlying distribution. Figure 1 illustrates this tradeoff for Cora, one of the datasets in our experiments, using reLDG as the clustering method. When a network is separated into very few clusters, the Euclidean distance between nodes in treatment and control clusters is larger than the Euclidean distance when a lot of clusters are produced over the same network (e.g., 0.4 vs. 0.18 for 2 and 1, 000 clusters). This is intuitive because as the clusters get smaller and smaller, their randomization gets closer to mimicking full node randomization (shown as a star). At the same time, a larger number of clusters translates to a higher likelihood of edges between treatment and control nodes, which leads to higher undesired spillover and causal effect estimation error (e.g., 0.015 vs. 0.059 for 2 and 1000 clusters).
Ideally, we would like to measure TTE = DTE(V) + APE(V1) − APE(V0). Due to undesired spillover in a controlled experiment, what we are able to measure instead is the overall effect that comprises both allowable and unallowable peer effects TTE = DTE(V) + APE(V1) − APE(V0) + UPE(V1) − UPE(V0). Therefore, when we design an experiment for minimum interference, we are interested in setting it up in a way that makes UPE(V1) = 0 and UPE(V0) = 0. More formally:
Problem 2 (Network experiment design for total treatment effect estimation). Given a graph G = (V, E), a set of attributes V.X associated with each node and a set of spillover probabilities E.P associated with the graph edges, we want to construct two sets of nodes, the control nodes V0 ∈ V and the treatment nodes V1 ∈ V such that:
a. V0 ∩ V1 = ∅.
b. |V0| + |V1| is maximized.
c. θ = UPE(V1) − UPE(V0) is minimized.
d. V0.X and V1.X are identically distributed.
This problem definition describes the desired qualities of the experiment design at a high level. The first component ensures that the treatment and control nodes do not overlap. The second component aims to keep as many nodes as possible from V in the final design. The third component minimizes unallowable spillover. The fourth component requires that there is no selection bias between the treatment and control groups. The second and third components are at odds with one another and require a tradeoff because the lower θ, the lower the number of selected nodes for the experiment |V0| + |V1|. As we showed in Figure 1, there is also a tradeoff between the third and fourth components.
5. CauseIS: a network experiment design framework for direct treatment effect estimation
In this section, we define an objective function corresponding to the problem of this paper and describe our proposed framework which we refer to as CauseIS for estimating direct treatment effects in network experiments.
Typically, total treatment effect estimation includes both APE and UPE. In a randomized approach, TTE is estimated as:
In this work, we propose an approach that makes APE(V1)=0 and APE(V0)=0 and in expectation makes UPE(V1)-UPE(V0)=0, thus making the estimated TTE correspond to DTE. We first define an objective function that addresses the goals specified in Problem 1.
5.1. Objective function
The goal of the objective function is to find a subset of V with maximum cardinality (Problem 1.b) such that by randomizing treatment assignment over the selected subset, the allowable peer effects from the experiment are removed (Problem 1.c). We define s ∈ {0, 1} such that si = 1 if node vi is in the set of selected nodes, else si = 0.
The two constraints together guarantee that adjacent nodes are not included in our network experiment design. This optimization can be solved by reducing our problem to the maximum independent set problem in graph theory (Eisenbrand et al., 2003) such that nodes in the independent set correspond to the nodes selected for the network experiment.
Given a graph G = (V, E), IS ⊆ V is a subset of nodes such that for each pair of nodes vi ∈ IS and vj ∈ IS there is no shared edge between them (ei,j ∉ E). A maximal independent set is an independent set that is not a subset of any other independent sets of the graph. Using a greedy sequential approach, a maximal independent set of a graph can be found in O(|E|) (Blelloch et al., 2012) but there are parallel algorithms that can solve this problem much faster in O(log(N)) (Luby, 1985; Yves et al., 2009). A maximal independent set with the largest possible size for a given graph is known as a maximum independent set. Finding maximum independent sets in graphs is known to be NP-hard. There are exact algorithms that can find maximum independent sets in O(1.1996nnO(1)) (Xiao and Nagamochi, 2017) and also approximation algorithms that can find it in O(n/(logn)2) (Boppana and Halldórsson, 1990).
5.2. CauseIS Framework
We propose CauseIS, a network experiment design for robust estimation of Direct Treatment Effects by disentangling peer effects from DTE. CauseIS has two main steps:
1. Finding a maximum independent set of the graph (Independent set graph in Figure 2).
2. Assigning nodes of the maximum independent set to treatment and control in a randomized fashion (CauseIS output graph in Figure 2).
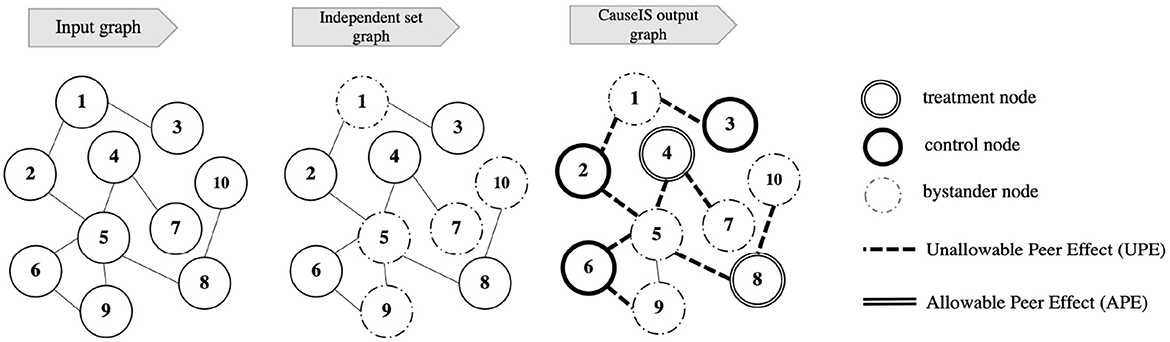
Figure 2. Illustration of CauseIS frameworks in network experiments. Input graph: a graph of nodes and the connection between them. Independent set graph: a graph of bystander and independent set nodes selected by the independent set algorithm. CauseIS output graph: the output graph that represents randomized treatment assignment of independent set nodes and peer effects that exists in the experiment.
In this framework, we find the treatment assignment vector Z of nodes by dividing the population into treatment, control, and bystander nodes. Considering the proposed objective function, we first use an algorithm to find the maximum independent set of the given graph which partitions the graph into two sets of nodes: 1) nodes in the maximum independent set denoted by MIS (MIS ⊆ V) where by randomizing treatment assignment over these nodes, we achieve treatment (V1) and control (V0) groups, and 2) bystander nodes (V2) that are not in MIS where V2 ⊆ V, V2 ∩ MIS = ∅, and V2 ∪ MIS = V. The main idea is to assign nodes of MIS to treatment and control at random and ensure that there is no peer effect across treatment and control nodes.
Figure 2 represents the pipeline of the CauseIS framework. Input graph shows the graph of the network that the network experiment is conducted on. After using an independent set algorithm on the Input graph, independent set and bystander nodes are selected from the graph that is shown in Independent set graph. Finally, by randomizing treatment assignment over independent set nodes, treatment, and control nodes are selected. CauseIS output graph shows the assignment of Input graph nodes to three treatment groups where APE is removed from the experiment.
We remove bystander nodes from the randomized treatment assignment because of the interaction within these nodes which leads to APE in treatment effect estimation. However, it is still possible that information flows from peers in V2 to V0 and V1, leading to undesired peer effects (nodes 1, 5, 7, 9, 10 in Figure 2). In the running example, an infected person in V2 may infect his peers in V0 and V1.
By removing APE from Equation (6), we have . By randomizing the treatment assignment over MIS nodes, we aim to provide a chance for treatment and control nodes to have the same number of peers in bystander nodes V2. Let α1 be the set of bystander nodes that are activated neighbors of treatment nodes, and α2 be the set of bystander nodes that are activated neighbors of control nodes at time t-1. Let V1,α and V0,α represent the set of treatment and control nodes activated by α1 and α0 at time t, and let V1,−α and V0,−α denote the set of treatment and control nodes not activated by bystander nodes, respectively. Through randomization over set MIS, we obtain |α1| ≈ |α0|. In this setup, TTE can be estimated as:
If the probability of activating a treatment and a control node by a bystander node is equal, then, in expectation, an equal number of nodes in treatment and control nodes would get activated by bystander nodes (|V1,α| ≈ |V0,α|) and UPE(V1) is equal to UPE(V0), i.e., . As a result, we have:
Since by design there are no peer effects between the treatment and control groups, Equation (8) estimates the DTE (TTE ≈ DTE).
6. CMatch: a network experiment design framework for total treatment effect estimation
In this section, we describe our proposed CMatch framework that increases the accuracy of TTE by combining clustering and matching techniques.
6.1. CMatch framework
Our network experiment design framework CMatch, illustrated in Figure 3, has two main goals: 1) spillover minimization which it achieves through weighted graph clustering, and 2) selection bias minimization which it achieves through cluster matching. Clusters in each matched pair are assigned to different treatments, thus achieving covariate balance between treatment and control (Fatemi and Zheleva, 2020). The first goal addresses part c of Problem 1 and the second goal addresses part d. While the first goal can be achieved with existing graph mining algorithms, solving for the second one requires developing novel approaches. To achieve the second goal, we propose an objective function, which can be solved with maximum weighted matching, and present the nuances of operationalizing each step.
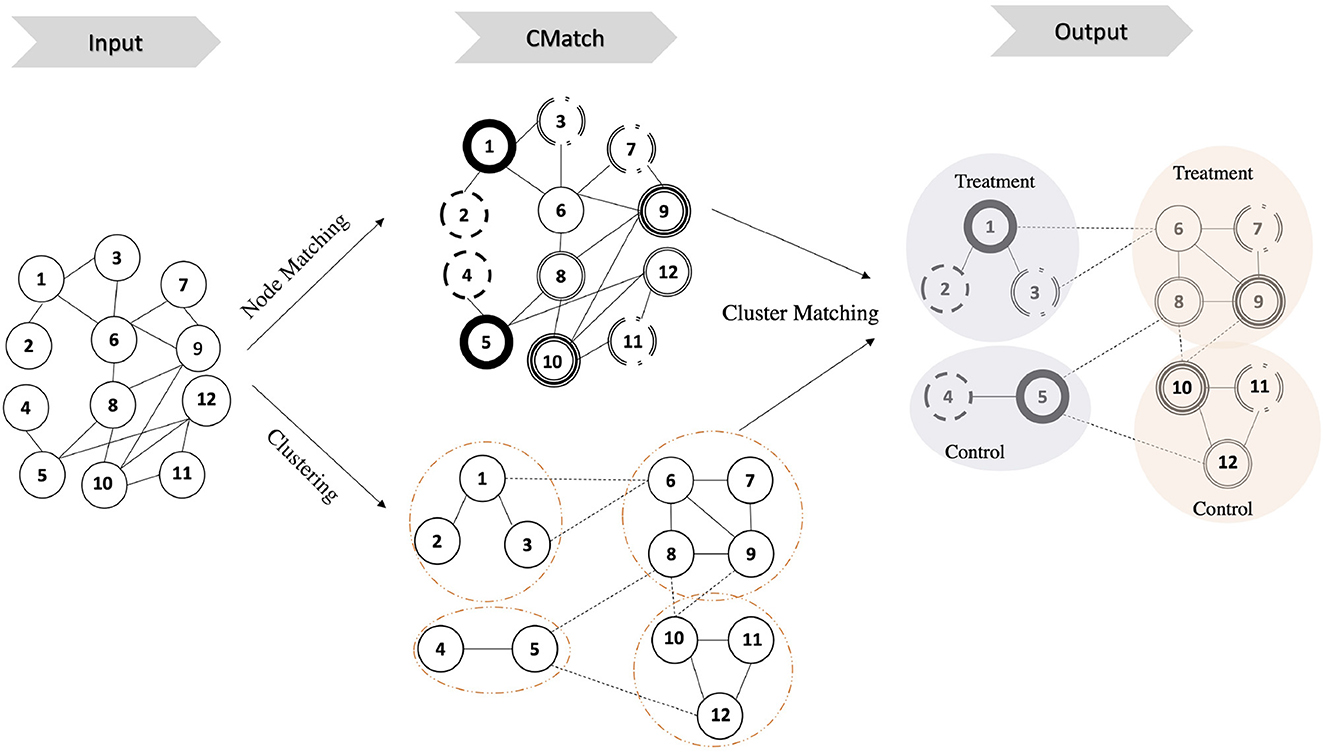
Figure 3. Illustration of CMatch framework for minimizing interference and selection bias in controlled experiments. Input: a graph of nodes and the connection between them. CMatch: node and cluster matching; the dashed circles indicates the clusters. Matched nodes are represented with a similar circle border. Output: assigning the matched cluster pairs to treatment and control randomly; circles with the same color represent matched clusters.
6.1.1. Step 1: interference minimization through weighted graph clustering
Existing cluster-based techniques for network experiment design assume unweighted graphs (Backstrom and Kleinberg, 2011; Ugander et al., 2013; Gui et al., 2015; Eckles et al., 2016; Saveski et al., 2017) and do not consider that different edges can have different likelihood of spillover. Incorporating information about the edge probability of spillover into the clustering helps alleviate this problem and is one of the main contributions of our work. In order to minimize undesired spillover, we operationalize minimizing θ as minimizing the edges, and more specifically the edge spillover probabilities, between treatment and control nodes: . To achieve this, CMatch creates graph clusters for two-stage design by employing two functions, edge spillover probability estimation and weighted graph clustering.
6.1.1.1. Edge spillover probability estimation
We consider edge strength, how strong the relationship between two nodes is, as a proxy for edge spillover probability. This reflects the notion that the probability of a person influencing a close friend to do something is higher than the probability of influencing an acquaintance. We can use common graph mining techniques to calculate edge strength, including ones based on topological proximity (Liben-Nowell and Kleinberg, 2007), supervised classification (Gilbert and Karahalios, 2009), or latent variable models (Li et al., 2010).
6.1.1.2. Weighted graph clustering
In order to incorporate edge strength into clustering, we can use any existing weighted graph clustering algorithm (Enright et al., 2002; Schaeffer, 2007; Yang and Leskovec, 2015). In our experiments, we use a prominent non-parametric algorithm, the Markov Clustering Algorithm (MCL) (Enright et al., 2002) which applies the idea of random walk for clustering graphs and produces non-overlapping clusters. We also compare this algorithm with reLDG which was the basis of previous work (Saveski et al., 2017). One of the advantages of MCL is that it automatically finds the optimal number of clusters, rather than requiring it as input. The main idea behind MCL is that nodes in the same cluster are connected with higher-weighted shortest paths than nodes in different clusters.
6.1.2. Step 2: selection bias minimization through cluster matching
Randomizing treatment assignment over clusters in a two-stage design does not guarantee that nodes within those clusters would represent random samples of the population. We propose to address this selection bias problem by cluster matching and balancing covariates across treatment and control clusters. While methods for matching nodes exist (Oktay et al., 2010; Stuart, 2010; Arbour et al., 2014), this work is the first to propose methods for matching clusters.
6.1.2.1. Objective function
The goal of cluster matching is to find pairs of clusters with similar node covariate distributions and assign them to different treatment groups. We propose to capture this through a maximum weighted matching objective over a cluster graph in which each discovered cluster from step 1 is a node and edges between clusters represent their similarity. Suppose that graph G is partitioned into C = {c1, c2, ..., cg} clusters. We define A ∈ {0, 1}, such that aij = 1 if two clusters ci and cj are matched, else aij = 0. wi, j ∈ ℝ represents the similarity between two clusters ci and cj. Then the objective function of CMatch is as follows:
This objective function maps to a maximum weighted matching problem for which there is a linear-time approximation algorithm (Duan and Pettie, 2014) and a polynomial-time exact algorithm with O(N2.376) (Mucha and Sankowski, 2004; Harvey, 2009).
6.1.2.2. Solution
In order to operationalize the solution to this objective, the main question that needs to be addressed is: what does it mean for two clusters to be similar? We propose to capture this cluster similarity through matched nodes. The more nodes can be matched based on their covariates across two clusters, the more similar the two clusters are. Thus, the operationalization comes down to the following three questions which we address next:
1. What constitutes a node match?
2. How are node matches taken into consideration in computing the pairwise cluster weights (cluster similarity)?
3. Given a cluster weight, what constitutes a potential cluster match, and thus an edge in the cluster graph?
Once these three questions are addressed, the cluster graph can be built and an existing maximum weighted matching algorithm can be applied to it to find the final cluster matches.
6.1.2.2.1. Node Matching
The goal of node matching is to reduce the imbalance between treatment and control groups due to their different feature distributions. Given a node representation, fully blocked matching would look for the most similar nodes based on that representation (Stuart, 2010). It is important to note that propensity score matching does not apply here because it models the probability of treatment in observational data and treatment is unknown at the time of designing a controlled experiment. In its simplest form, a node can be represented as a vector of attributes, including node-specific attributes, such as demographic characteristics, and structural attributes, such as node degree. For any two nodes, it is possible to apply an appropriate similarity measure sim(vi, vj), in order to match two nodes, including cosine similarity, Jaccard similarity, or Euclidean distance.
We consider two different options to match a pair of nodes in different clusters (and ignore matches within the same cluster):
• Threshold-based node matching (TNM): Node vk in cluster ci is matched with node vl from a different cluster cj if the pairwise similarity of nodes sim(vk, vl) > α. The threshold α can vary from 0, which liberally matches all pairs of nodes, to the maximum possible similarity which matches nodes only if they are exactly the same. In our experiments, we set α based on the covariate distribution of each dataset and consider different quartiles of pairwise similarity as thresholds. This allows for each node to have multiple possible matches across clusters.
• Best node matching (BNM): Node vk in cluster ci is matched with only one node vl which is most similar to vk in the whole graph; vl should be in a different cluster. This is a very conservative matching approach in which each node is uniquely matched but allows the matching to be asymmetric.
6.1.2.2.2. Cluster Weights
After the selection of a node matching mechanism, we are ready to define the pairwise similarity of clusters which is the basis of cluster matching. We consider three simple approaches and three more expensive approaches which require maximum weighted matching between nodes:
• Euclidean distance (E): This approach is the simplest of all because it does not consider node matches and it simply calculates the Euclidean distance between the node attribute vector means of two clusters.
• Matched node count (C): The first approach counts the number of matched nodes in each pair of clusters ci and cj and considers the count as the clusters' pairwise similarity: . A node in cluster ci can have multiple matched nodes in cj.
• Matched node average similarity (S): Instead of the count, this approach considers the average similarity between matched nodes across two clusters ci and cj:
.
These first two approaches allow a single node to be matched with multiple nodes in another cluster and each of those matches counts toward the cluster pair weight. In order to distinguish this from a more desirable case in which multiple nodes in one cluster are matched to multiple nodes in another cluster, we propose approaches that allow each node to be considered only once in the matches that count toward the weight. For each pair of clusters, we build a node graph in which an edge is formed between nodes vi and vj in the two clusters and the weight of this edge is sim(vi, vj). Maximum weighted matching will find the best possible node matches in the two clusters. We consider three different variants for calculating the cluster pair weight based on the maximum weighted matching of nodes:
• Maximum matched node count (MC): This method calculates the cluster weight the same way as C except that the matches (whether is 0 or 1) are based on the maximum weighted matching result.
• Maximum matched node average similarity (MS): This method calculates the cluster weight the same way as S except that the node matches are based on the maximum weighted matching result.
• Maximum matched node similarity sum (MSS): This method calculates the cluster weight similarly to MS except that it does not average the node similarity: .
6.1.2.2.3. Cluster graph
Once the cluster similarities have been determined, we need to decide what similarity constitutes a potential cluster match. Such potential matches are added as edges in the cluster graph which is considered for maximum weighted matching. We consider three different options:
• Threshold-based cluster matching (TCM): Cluster ci is considered as a potential match of cluster cj if their weight wi, j > β. The threshold β can vary from 0, which allows all pairs of clusters to be potential matches, to the maximum possible similarity which allows matching between clusters only if they are exactly the same. In our experiments, we set β based on the distribution of pairwise similarities and their quartiles as thresholds.
• Greedy cluster matching (GCM): For each cluster ci, a sorted list of the similarities between ci and all other clusters is defined. Cluster ci is considered a potential match only to the cluster with the highest similarity value in the list.
The last step in CMatch runs maximum weighted matching on the cluster graph. For every matched cluster pair, it assigns one cluster to treatment and the other one to control at random. This completes the network experiment design.
6.1.3. Analysis of the estimation bias
We follow Eckles et al. (2016) to analyze the estimation bias of the proposed cluster-based approach. One of the common approaches to measuring the causal effect μ of a treatment on an outcome is averaging outcomes over treatment and control groups via difference-in-means: where and are the mean outcomes of treatment and control nodes under experiment design d, respectively. In the presence of interference, μd does not yield the true total treatment effects (μd − μ ≠ 0). The impact of each node on the estimation bias is equal to the difference between the expected outcome of a node due to the treatment alone and the observed outcome under global treatment assignment where all nodes in the network have a treatment assignment. The experimental design can control the size of this bias by controlling the global treatment assignment. Eckles et al. prove that this bias in the cluster-based randomization approach is less than or equal to the absolute bias under randomized assignment. Following this study, if we assume that we have a linear outcome model for each node vi ∈ V as Eckles et al. (2016):
Where B is the coefficient matrix, then true TTE μ is calculated as Eckles et al. (2016):
Under cluster-based randomization assignment, we have Eckles et al. (2016):
Where C(vi) denotes the cluster assignment of vi. Under randomized assignment, we have Eckles et al. (2016):
Equations (11)–(13) imply that μ − μcbr ≤ μ − μrand. The effectiveness of cluster-based randomization in reducing bias depends on the strength of interactions within clusters. The ability of the clustering algorithm to capture the coefficient matrix B in a consistent manner also affects the degree of bias reduction. By incorporating the strength of connections between units into the clustering process, the method can better capture the structure of dependence between units, resulting in a smaller bias (μ − μcbr). Considering Equations (11)–(12), the relative bias is measured as Eckles et al. (2016):
If the clustering fails to capture the structural dependencies, the numerator in Equation (14) will be much smaller than the denominator. As a result, the method will underestimate the true total treatment effects.
7. Experiments
In this section, we evaluate the performance of CauseIS and CMatch in treatment effect estimation compared to the baselines. We first describe datasets used in our experiments and then discuss the experimental setup and results.
7.1. Data generation
Since existing network datasets do not have ground truth for treatment and its causal effect on the outcome, we use synthetic and real-world data structures and simulate the outcome and causal effect in the experiments.
7.1.1. Synthetic data
For generating synthetic networks, we use two network generation models:
• Barabási-Albert (BA) model: This model generates random scale-free networks using the preferential attachment model. In the beginning, the network is constructed from m0 connected nodes. Then, new nodes are connected to m existing nodes with a probability that is proportional to the number of edges that the existing nodes already have (Albert and Barabási, 2002). We set m = 3 in all experiments.
• Forest Fire (FF) model: In this model, a new node vi attaches to an existing node vj and then links to nodes connected to vj with forward and backward burning probabilities denoted by pf and pb, respectively. Leskovec et al. (2007) show that the synthetic network generated by this model can mimic most real-world structure characteristics. In the experiments, we generate all the graphs with forward burning probability pf = 0.3 and backward burning probability pb = 0.3.
After generating the network structure, we generate 10 attributes for each node with a uniform distribution where the values vary in [ − 1, 1].
7.1.2. Real-world data
We use five real-world datasets in our experiments. The 50 Women dataset (Michell and Amos, 1997) includes sport, smoking, drug, and alcohol habits of 50 students with 74 friendship connections. Cora and Citeseer datasets (Sen et al., 2008) incorporate the citation networks of 2, 708 and 3, 312 article with binary bag-of-words attributes for each article and 4, 675 and 5278 edges, respectively. Hamsterster dataset (Zheleva et al., 2008) includes the online friendship network of 2, 059 hamsters with 10, 943 edges. Hateful users dataset (Ribeiro et al., 2018) is a sample of Twitter's retweet graph containing 100, 386 users with 1, 024 attributes and more than two millions retweet edges. In hateful users dataset, we remove singletons and nodes with degree 1 from the graph.
7.1.3. Synthetic causal effect
We assume that the underlying probability of activating a node (changing the outcome) due to treatment and allowable peer effects in the treatment group is 0.4 and the underlying probability of activating a control node due to treatment and allowable peer effects is 0.2 which makes the true causal effect TTE = 0.2. Based on these probabilities, we randomly assign each node as activated or not. For each inactivated node, we simulate two types of interference considering both fixed values (0.1 and 0.5) and values based on the edge weights for e.p:
1. Direct interference: each treated neighbor of a control node activates the node with an unallowable spillover probability of e.p.
2. Contagion: inactive treated and untreated nodes get activated with the unallowable spillover probability of e.p if they are connected to at least one activated node in a different treatment class.
7.2. Main algorithms and baselines
Our baselines differ corresponding to the causal effect of interest. In the following, we describe the main baselines for direct and total treatment effect estimation.
7.2.1. Baselines for Direct Treatment Effect Estimation
We compare the performance of four different approaches in our experiments.
• Randomized: This algorithm assigns nodes to treatment and control randomly, ignoring the network.
• Match: This algorithm matches nodes using the maximum weighted matching algorithm and then randomly assigns nodes in each matched pair to treatment and control at random without considering clustering.
• CauseIS: In our proposed framework, we use an algorithm to find the maximum independent set MIS and then assign nodes of the set to treatment or control at random.
• CauseIS_match: This method uses the CauseIS framework, but it matches nodes of MIS and then assigns nodes of matched pairs to treatment or control at random.
The goal of comparing our method with Match and CauseIS_Match is to show whether our method has selection bias. Using matching for RCT is unusual, but in small datasets altering the randomization process by posing structural constraints on the graph may lead to worse randomization and matching can mitigate this problem.
7.2.2. Baselines for total treatment effect estimation
For TTE, all our baseline and main algorithm variants take an attributed graph as an input and produce a set of clusters, each assigned to treatment, control, or none. For graph clustering, we considered two main algorithms, Restreaming Linear Deterministic Greedy (reLDG) (Nishimura and Ugander, 2013) and Markov Clustering Algorithm (MCL) (Enright et al., 2002). reLDG takes as input an unweighted graph and desired the number of clusters and produces a graph clustering. reLDG was reported to perform very well in state-of-the-art methods for network experiment design (Saveski et al., 2017). MCL is a non-parametric algorithm that takes as input a weighted graph and produces a graph clustering. The edge weights which correspond to the probabilities of spillover are estimated based on node pair similarity using one minus the normalized L2 norm: 1 − L2(vi.x, vj.x).
The main algorithms and baselines are:
• CR (Saveski et al., 2017): The Completely Randomized (CR) algorithm was used as a baseline in Saveski et al. (2017). The algorithm clusters the unweighted graph using reLDG algorithm, assigns similar clusters to the same strata, and assigns nodes in strata to treatment and control in a randomized fashion.
• CBRreLDG (Saveski et al., 2017): Cluster-based Randomized assignment (CBR) is the main algorithm proposed by Saveski et al. (2017). The algorithm clusters the unweighted graph using reLDG, assigns similar clusters to the same strata, and randomly picks clusters within the same strata as treatment or control.
• CBRMCL: A variant of CBR that we introduce for the sake of fairness which uses MCL for weighted-graph clustering.
• CMatchreLDG: This method uses our CMatch framework but works on an unweighted graph. It uses reLDG for graph clustering.
• CMatchMCL: This is our proposed technique which uses MCL for weighted graph clustering.
We consider Randomized and Match techniques described in Section 7.2.1 as two more baselines for total treatment effect estimation. CMatch uses the maximum_weight_matching function from the NetworkX Python library.
7.3. Experimental setup
We run a number of experiments varying the underlying spillover assumptions, clustering algorithms, number of clusters, and node matching algorithms. Our experimental setup measures the desired properties for network experiment design, as described in Problem 2 and follows the experimental setups in existing work (Stuart, 2010; Maier et al., 2013; Arbour et al., 2014; Eckles et al., 2016; Saveski et al., 2017).
To measure the strength of interference bias in different estimators, we report on two metrics:
1. Root Mean Squared Error (RMSE) of the treatment effect calculated as:
where S is the number of runs and τs and are the true and estimated causal effect in run s, respectively. We set S = 10 in all experiments. The error can be attributed to undesired spillover only.
2. The number of edges and the sum of edge weights between treatment and control nodes are assigned by each algorithm.
To show the selection bias, we want to assess how different treatment vs. control nodes are. We compute the Euclidean distance between the attribute vector mean of treated and untreated nodes. We show the average and standard deviation over 10 runs.
To show the strength of UPE imposed by bystander nodes in the CauseIS framework, we calculate the difference between the percentage of edges from bystander nodes to treatment and control nodes as:
Where di,j = 1 if there is an edge between node vi and vj. T and C show the vector of treatment and control nodes.
in our experiments, we use the maximal_independent_set function from the NetworkX Python library to find a maximal independent set of each graph which implements the approach by Blelloch et al. (2012).
We run all 115 possible combinations of CMatch options for node matching, cluster weights, and cluster graphs for each dataset. We consider four different values for the threshold α in TNM: 0 (TNM0), first (TNM1), second (TNM2) and third (TNM3) quantile of pairwise nodes' similarity distribution where sim(vi, vj)= (1- the normalized L2 norm). For TCM, we consider four different β values: 0 (TCM0), first (TCM1), second (TCM2) and third (TCM3) quantile of the pairwise clusters' similarity distribution for each dataset. We use TNM2 + C + TCM2 in all the experiments of CMatchreLDG.
Unless otherwise specified, the number of clusters is the same for all CBR and CMatch versions based on the optimal determination by MCL as optimal for each respective dataset. The number of clusters determined by MCL is 2, 497 for Citeseer, 1, 885 for Cora, 1, 056 for Hamsterster and 20 in 50 Women dataset.
7.4. Results
Here, we present the experimental results for the proposed framework. We first describe the performance of the CauseIS approach in estimating direct treatment effects. Then, we show the effectiveness of the CMatch framework in mitigating interference and selection bias.
7.4.1. Performance of CauseIS framework
7.4.1.1. Evaluation of direct treatment effect estimation
To assess the accuracy of CauseIS in estimating DTE compared to the baselines, we measure causal effect estimation error for different unallowable peer effect probabilities. Figure 4 shows the RMSE of DTE in real-world data sets. In all five datasets, CauseIS and CauseIS_Match get lower estimation error, compared to Randomized and Match, especially in Hamsterster with 72.1% and 76.6% estimated error reduction for e.p = edge_weight and e.p = 0.5 and Hateful Users with 69.4% estimated error reduction for e.p = 0.1. By increasing the spillover probability from 0.1 to 0.5, we get higher estimation errors because the probability of changing treatment and control outcomes through peer effects increases.
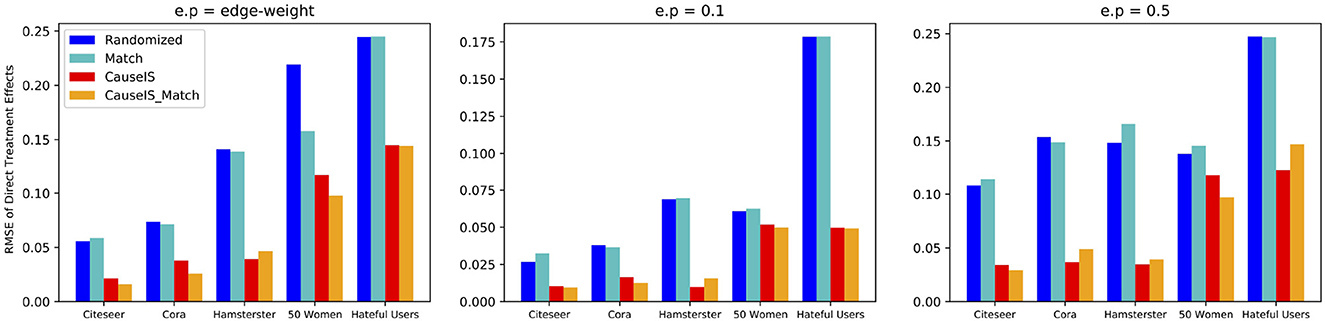
Figure 4. RMSE of direct treatment effects in real-world datasets considering different unallowable peer effect probabilities.
Synthetic data experiments depict a similar picture. Figure 5 shows the stronger performance of CauseIS and CauseIS_Match over Randomized and Match methods in reducing causal effect estimation error. For example, CauseIS's error is more than half of the error of Randomized approach (0.04 vs. 0.12 for graphs with 10, 000 nodes, 0.13 vs. 0.035 for graphs with 20, 000 nodes in Forest Fire model). In graphs with 50, 000 nodes, CauseIS obtains 63.4% and 69.9% estimation error reduction in Forest Fire and Barabási-Albert models respectively, compared to other graphs.
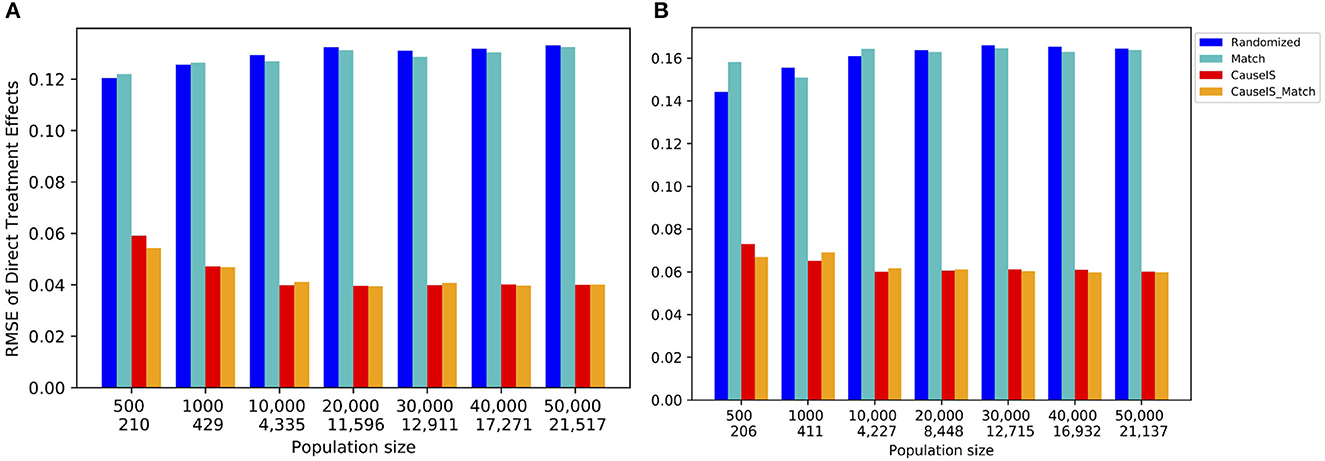
Figure 5. RMSE of direct treatment effect in synthetic data with a different number of nodes and edges. Numbers in the first row of the x-axis show the number of nodes in graphs, and the second row represents the size of MIS. (A) Forest Fire model. (B) Barab'asi-Albert model.
In both synthetic and real-world datasets, Randomized and Match on one hand and CauseIS and CauseIS_Match on the other hand show similar performances. This is intuitive because they use similar randomization techniques. While MIS size is approximately half of the population size in all datasets, by increasing the size of MIS the estimation error of CauseIS is still significantly lower than Randomized methods with smaller population size.
7.4.1.2. Sensitivity to the density of networks
To assess the impact of network density on the estimation error of various models, we computed the average estimation error across 10 randomly generated graphs containing 10,000 nodes for each density value. We adjusted the density of graphs in the Barabási-Albert model by altering the value of m within the range of 1–9, while for the Forest Fire model, we set pf = pb and varied pf between 0.01 and 0.35. Figure 6 illustrates that as the density of the graphs increases, the estimation error for all methods also increases. This observation is expected since an increase in the number of edges between treatment and control raises the possibility of unallowable peer effects in the experiment. However, the CauseIS and CauseIS_Match methods consistently outperform the other two baseline methods in all graphs. Moreover, an increase in the density of the graph leads to a decrease in the size of the MIS. A higher MIS rate (meaning fewer bystander nodes) implies fewer spillover effects from bystander nodes to treatment and control, resulting in smaller estimation errors.
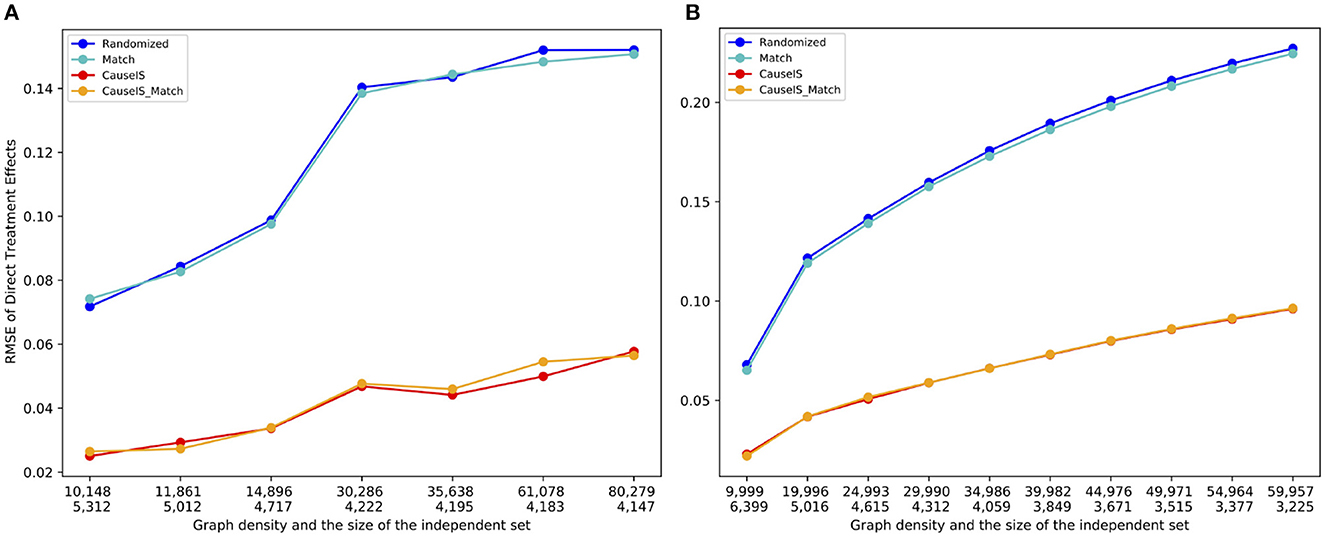
Figure 6. RMSE of direct treatment effects in synthetic data with 10, 000 nodes and different densities. Numbers in the first row of the x-axis show the number of edges in graphs, and the second row represents the size of MIS. (A) Forest Fire model. (B) Barab'asi-Albert model.
7.4.1.3. Selection bias evaluation
In this experiment, we evaluate the selection bias of different methods by comparing the Euclidean distance between treatment and control nodes' attributes in real-world and synthetic datasets with different population sizes. Figure 7 shows this comparison of real-world and synthetic data. It is not surprising that the Match method gets the lowest selection bias in all datasets because it matches most similar treatment and control nodes based on the similarity of attributes. CauseIS_Match has a higher selection bias than Match because the number of nodes matched in this approach is less than the Match method. Although CauseIS has a high selection bias, CauseIS_Match reduces selection bias to some extent.
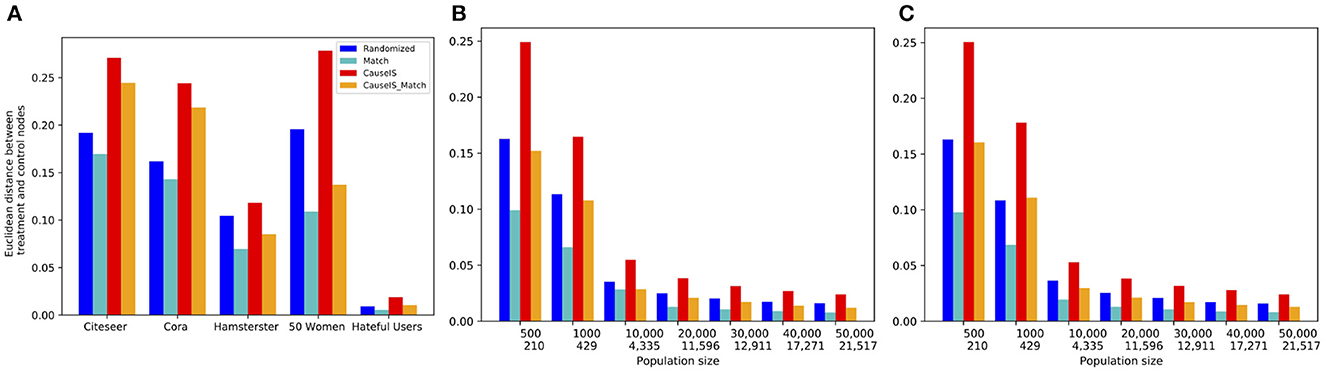
Figure 7. Euclidean distance between the attribute vector means of treatment and control nodes in real-world and synthetic datasets. In synthetic dataset plots, numbers in the first row of the x-axis show the number of nodes in graphs, and in the second row show the size of MIS. (A) Real-world data, (B) Forest Fire model, and (C) Barab'asi-Albert model.
Next, we look at how sample size impacts selection bias. We expect that asymptotically, there would be no selection bias with randomization for any design. Figure 7 shows that independent from the network generating model, by increasing the population size the similarity between treatment and control nodes' attributes reduces, and the value of matching decreases and disappears. For example, in graphs with 500 nodes generated by the Forest Fire model, the difference between Euclidean distance of treatment and control nodes in CauseIS is 0.24, while in graphs with 50, 000 nodes, this difference decreases to 0.024. These results confirm the advantage of the matching technique in small datasets.
7.4.1.4. Peer effect evaluation
To measure the extent to which UPE(V0) and UPE(V1) can cancel each other out, we consider the percentage of edges from bystander nodes to treatment and control nodes. Figure 8 shows this quantity in real-world and synthetic datasets using CauseIS and CauseIS_Match methods. As expected, results show that for graphs with fewer number of nodes, the difference between the number of edges to treatment and control nodes is higher compared to larger graphs, 2.5 vs. 0.04 in 50 Women vs. Hateful Users dataset. In synthetic data with higher population sizes (40, 000 and 50, 000), the difference between the percentages of edges to treatment and control is close to zero.
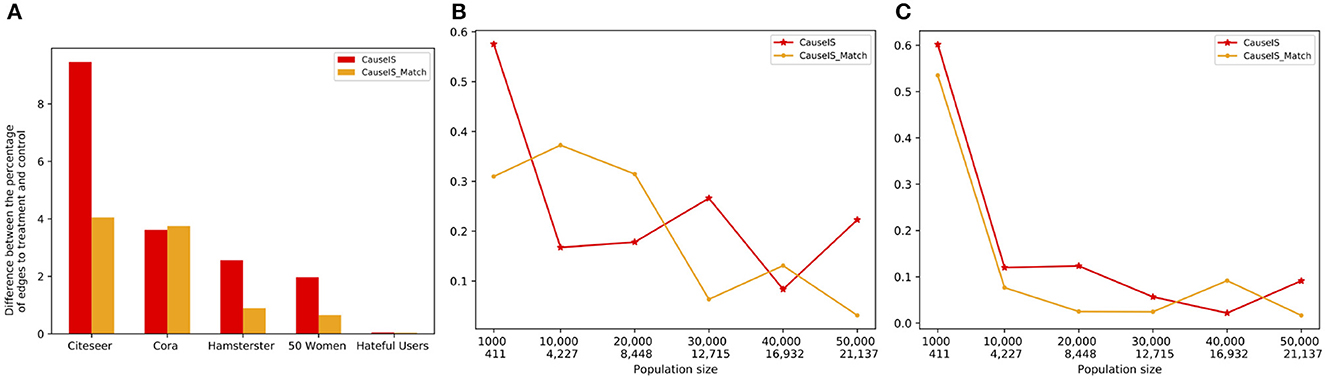
Figure 8. Difference between the percentage of edges to treatment and control nodes in real-world and synthetic datasets with a different number of nodes and edges. In synthetic dataset plots, numbers in the first row of the x-axis show the number of nodes in graphs, and in the second row show the size of MIS. (A) Real-world data, (B) Forest Fire model, and (C) Barab'asi-Albert model.
In both synthetic and real-world datasets, we observe that by increasing the sample size, the causal effect estimation error decreases because by increasing the density of the graph edges the percentage of edges from bystander nodes to treatment and control nodes becomes more similar and UPE(V1) - UPE(V0) goes to zero.
7.4.1.5. Degree distribution evaluation
To assess the extent to which the maximal independent set chosen by CauseIS biases the degree distribution of selected treatment and control nodes, we compare the degree distributions of treatment and control nodes selected by CauseIS and Randomized. Figure 9 shows that CauseIS selects treatment and control groups with roughly similar degree distribution in all datasets, except in 50 Women dataset where the assignment looks more biased, likely due to its small size. CauseIS removes high-degree nodes from the experiment which results in incorporating treatment and control groups with a more balanced degree distribution in the experiments.
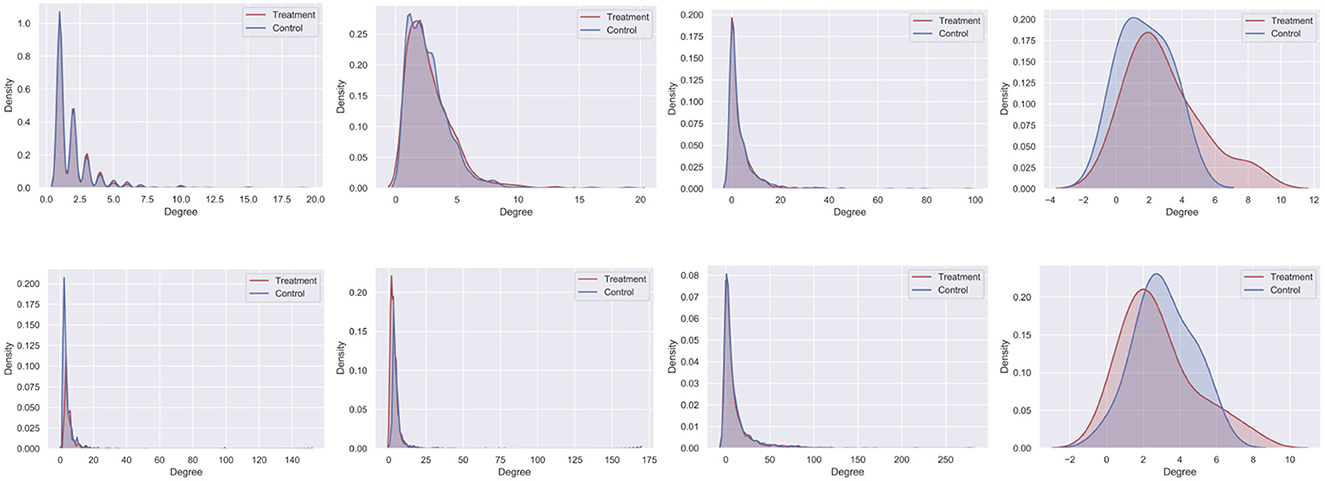
Figure 9. Degree distribution of treatment and control nodes selected by CauseIS (first row) and Randomized (second row).
7.4.2. Performance of CMatch framework
7.4.2.1. Tradeoff between interference and selection bias in CMatch variants and baselines
Given the large number of CMatch option combinations (115), we first find which ones of these combinations have a good tradeoff between RMSE and Euclidean distance (between treatment and control) with e.p = edge-weight. Depending on the node matching and cluster matching thresholds, which are specified by the user, the performance of CMatch options varies. Based on these experiments, we notice that 1) methods with stricter cluster thresholds (TCM2 and TCM3) tend to have a lower error, 2) stricter node match thresholds (TNM2 and TNM3) have lower error than others for S and MSS and 3) MS has high error across thresholds. We show the detailed results for Cora in Table 1.
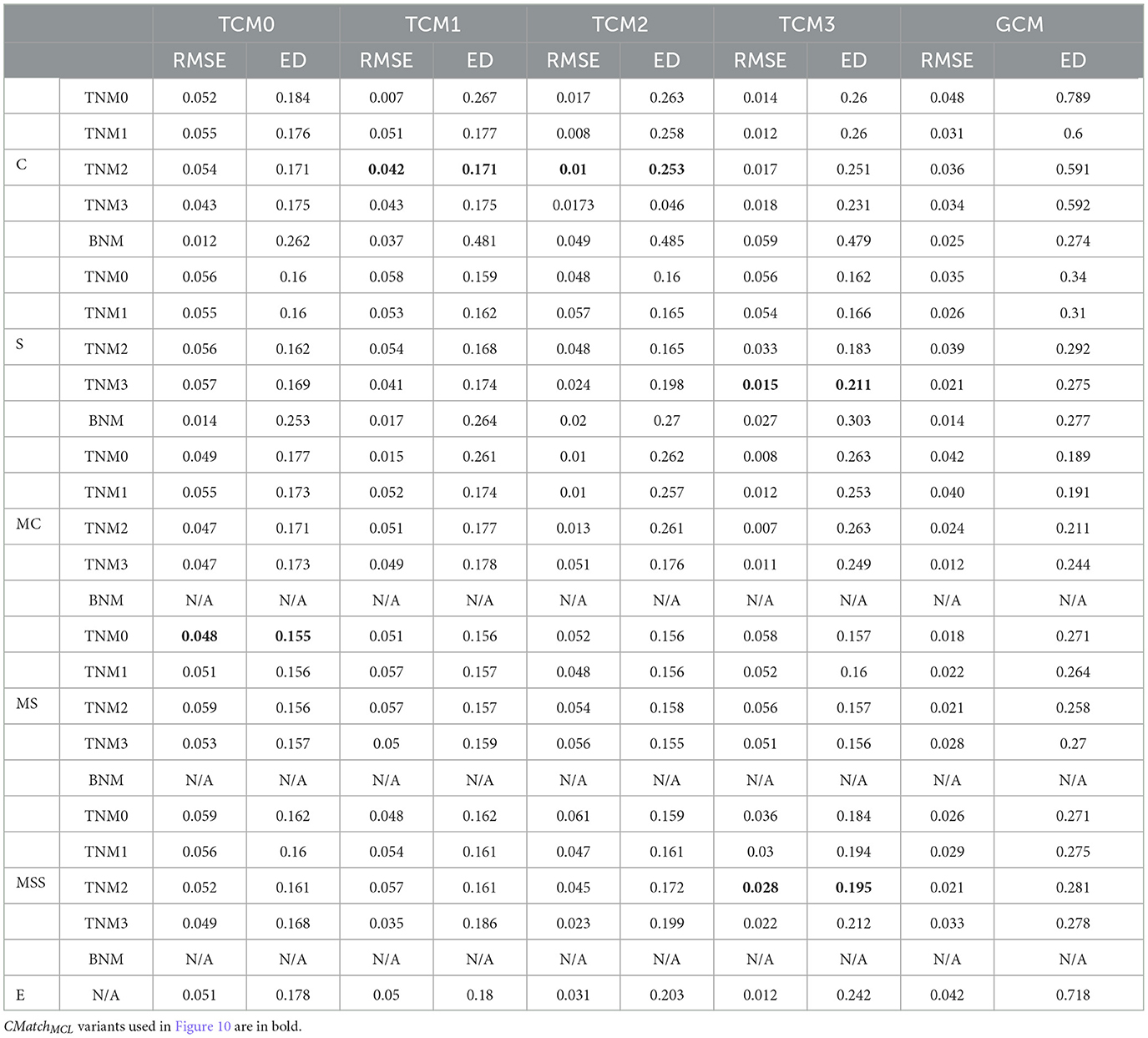
Table 1. The tradeoff between selection bias (distance) and undesirable spillover (RMSE) in CMatch variants in the Cora dataset.
Figure 10 shows the results for the CMatch variants with the best tradeoffs and their better performance when compared to the baselines for Cora. Full CMatch results can be found in Table 1. The figure clearly shows that the selection bias decreases at the expense of interference bias. For example, while the Euclidean distance for TNM0 + MS + TCM0 is low (0.155) when compared to TNM2 + C + TCM2 (0.253), its RMSE is higher, 0.048 vs. 0.01. The comparison between CBRreLDG with different possible number of clusters is consistent with the tradeoff shown in Figure 1. CBRreLDG with the highest error (annotated with 1885) and CMatchMCL have the same number of clusters. It is intuitive that the Match method has the least selection bias because all nodes have their best matches. However, similar to the Randomized method, it suffers from high interference bias (RMSE) because of the high density of edges between treatment and control nodes.
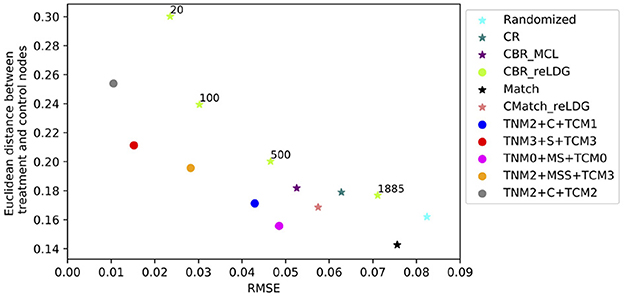
Figure 10. The tradeoff between selection bias (distance) and undesirable spillover (RMSE) in CMatchMCL variants (labeled with methods applied in) and baselines in the Cora dataset for e.p = edge-weight; CBRreLDG is annotated with the number of clusters.
7.4.2.2. Interference evaluation for contagion
We choose two CMatch variants with low estimation errors: TNM2 + MSS + TCM3 and TNM2 + C + TCM2, denoted by CMatchMCLMSS and CMatchMCLC respectively, and compare their causal effect estimation error with the baselines. The first method uses a simpler cluster weight assignment while the second one uses the expensive maximum weighted matching of nodes. Figure 11 shows that both variants of CMatchMCL get significantly lower error than other methods, especially in Citeseer and Cora with 75.5% and 81.8% estimated error reduction in comparison to CBRreLDG for e.p = edge-weight. CMatchMCLMSS has higher error than CMatchMCLC in most of the experiments which are expected as shown in Figure 10. Randomized and Match approaches have similar performance in all datasets because of their similarity in the node randomization approach. We also notice that CBRreLDG has the highest estimation error in Hamsterster data which confirms that clustering has a significant effect on the unallowable spillover. Meanwhile, CMatchreLDG outperforms other baselines in some datasets (Citeseer) but not in others (Hamsterster and 50 Women). In Citeseer, the CR method gets the largest estimation error.
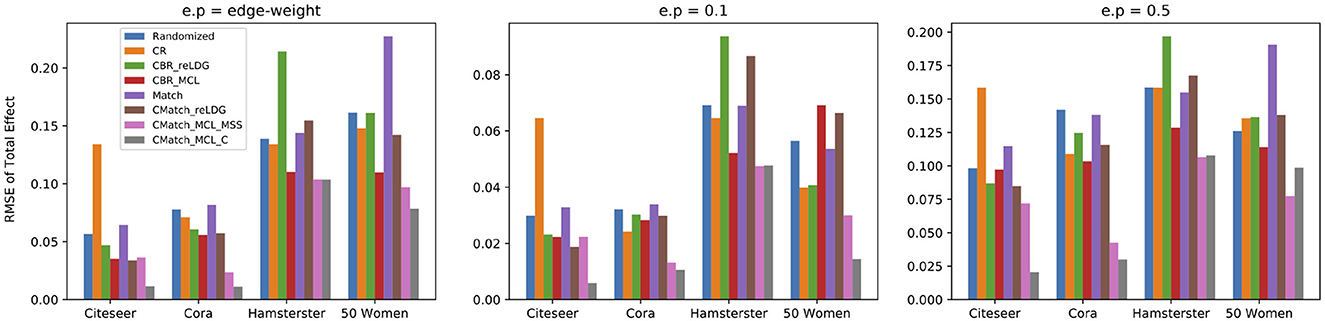
Figure 11. RMSE of total effect in the presence of contagion considering different unallowable spillover probabilities in all datasets; CMatchMCLC achieves the lowest error in all datasets.
Figure 11 also shows that the higher the unallowable spillover probability, the larger the estimation error but also the better our method becomes relative to the baselines. For example, by increasing the unallowable spillover probability from 0.1 to 0.5 in Citeseer, the estimation error increases from 0.005 to 0.02 for CMatchMCLC and from 0.023 to 0.086 for CBRreLDG.
7.4.2.3. Interference evaluation for direct interference
Figure 12 shows the difference between the RMSE of different estimators over the presence of direct interference for e.p = edge-weight. In four datasets, both variants of CMatchMCL get the lowest estimation error in comparison to baseline methods. For example, CMatchMCLC's error is approximately half of the error of CBRreLDG (0.06 vs. 0.13 for Citeseer, 0.1 vs. 0.22 for Cora, 0.31 vs. 0.54 for Hamsterster, 0.15 vs. 0.36 for 50 Women). Similar to contagion, Match, and Randomized methods have similar estimation errors.
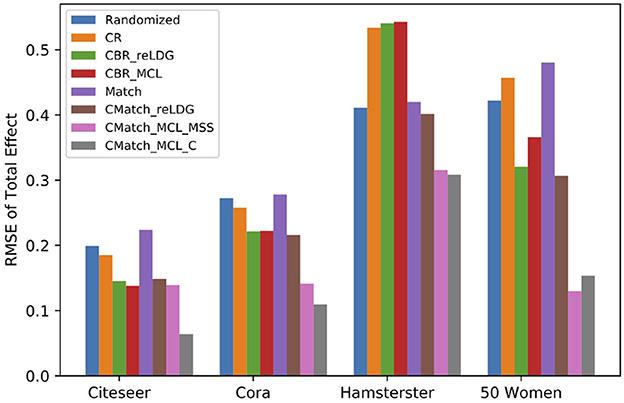
Figure 12. RMSE of total effect in the presence of direct interference (e.p = edge-weight). CMatchMCLC and CMatchMCLMSS obtain the lowest RMSE for all datasets.
7.4.2.4. Potential spillover evaluation
Table 2 shows the potential spillover between treatment and control nodes assigned by different methods. This applies to both contagion and direct interference. CMatch has the lowest sum of edges and edge weights between treatment and control nodes across all datasets. The difference between CMatchMCLC and the baselines in Cora and Citeseer is substantial: CMatchMCLC has between 13.5 and 34.8% lower number of edges between treatment and control across datasets.
7.4.2.5. Selection bias evaluation for contagion
In this experiment, we look at the relationship between the number of clusters and the difference between treatment and control nodes with and without cluster matching. Figure 13 shows the Euclidean distance between the average of treatment and control nodes' attributes in CMatchreLDG, CBRreLDG and reLDG for three different numbers of clusters and unallowable spillover probability e.p = edge-weight. Since CMatchreLDG optimizes for selection bias directly, it is not surprising that it results in treatment and control nodes that have more similar feature distributions than the other two methods. In Citeseer the differences are more subtle than in the other datasets. Error bars show the variance of averages over 10 runs which confirm the low variance of estimations in all datasets except in 50 Women, which is a small dataset.
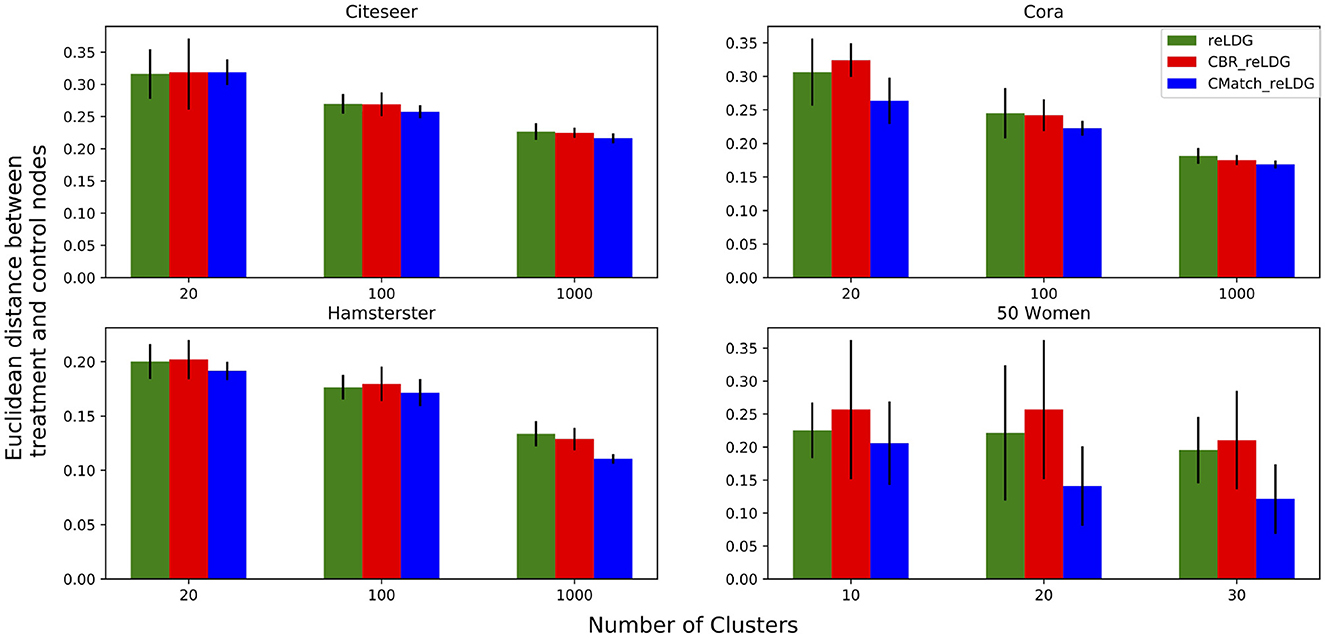
Figure 13. Euclidean distance between the attribute vector means of treatment and control nodes for a different number of clusters. The higher the number of clusters, the lower the selection bias.
7.4.2.6. Sensitivity to spillover probability metrics
Our last experiment compares metrics for calculating the spillover probability, Cosine similarity, Jaccard similarity, and the L2-based similarity used in all other experiments. We report on RMSE of total effect using CMatchMCLC and CMatchMCLMSS methods under contagion. Figure 14 shows that CMatchMCLC with L2-based similarity obtains the least error in all datasets except for Citeseer where Cosine similarity has a slightly lower error. For CMatchMCLMSS, Cosine similarity has the lowest RMSE in Citeseer and 50 Women dataset, while Euclidean similarity has the lowest error in the other datasets. Jaccard similarity has the highest estimation error in all almost all cases.
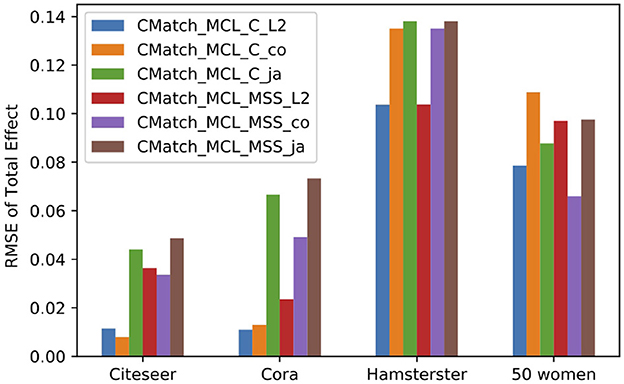
Figure 14. RMSE of total effect in the presence of contagion using three different similarity methods to calculate spillover probability: Cosine (co), Jaccard (ja) and L2 similarity.
8. Conclusion
In this paper, we proposed two different frameworks for network experiment designs that provide a more accurate estimation of two common causal estimands under interference: direct treatment effects and total treatment effects. For direct treatment effect estimation, we presented CauseIS, a framework that uses an independent set explicitly to disentangle peer effects from direct treatment effect estimation and increase the accuracy of direct treatment effect estimation. For total treatment effect estimation, we introduced CMatch, the first optimization framework that minimizes both interference and selection bias in cluster-based network experiment design. Our experiments on synthetic and real-world datasets confirm that this approach decreases direct and total treatment effect estimation error significantly. Some possible extensions of our frameworks include understanding the impact of network structural properties on estimation, jointly optimizing for interference and selection bias, and developing frameworks that are able to mitigate multiple-hop diffusions.
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Ethics statement
Ethical approval was not required for the study involving human data in accordance with the local legislation and institutional requirements. Written informed consent from the participants or their legal guardian/next of kin was not required in accordance with the national legislation and the institutional requirements.
Author contributions
ZF and EZ contributed to the brainstorming, conception, and design of the study. ZF implemented the ideas and performed the statistical analysis under EZ's supervision. ZF wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.
Funding
This research was funded in part by NSF under grant no. 2047899 and DARPA under contract number HR001121C0168.
Acknowledgments
Some of the material included in the submission originally appeared at ICWSM 2020 (Fatemi and Zheleva, 2020). We obtained permission to publish the material from AAAI. Some of the material was presented at MLG workshop 2020 which does not have an archival paper associated with it.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher's note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Albert, R., and Barabási, A.-L. (2002). Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97. doi: 10.1103/RevModPhys.74.47
Antman, E. M., Lau, J., Kupelnick, B., Mosteller, F., and Chalmers, T. C. (1992). A comparison of results of meta-analyses of randomized control trials and recommendations of clinical experts: treatments for myocardial infarction. JAMA 268, 240–248. doi: 10.1001/jama.1992.03490020088036
Arbour, D. T., Marazopoulou, K., Garant, D., and Jensen, D. D. (2014). “Propensity score matching for causal inference with relational data,” in Proceedings of the UAI 2014 Conference on Causal Inference: Learning and Prediction - Volume 1274 (Quebec City, QC), 25–34. doi: 10.5555/3020325.3020329
Aronow, P. M., Eckles, D., Samii, C., and Zonszein, S. (2021). Spillover effects in experimental data. Adv. Exp. Polit. Sci. 289, 319. doi: 10.1017/9781108777919.021
Backstrom, L., and Kleinberg, J. (2011). “Network bucket testing,” in Proceedings of the 20th International Conference on World Wide Web (New York, NY: Association for Computing Machinery), 615–624. doi: 10.1145/1963405.1963492
Blelloch, G. E., Fineman, J. T., and Shun, J. (2012). “Greedy sequential maximal independent set and matching are parallel on average,” in Proceedings of the Twenty-Fourth Annual ACM Symposium on Parallelism in Algorithms and Architectures, SPAA'12 (New York, NY: Association for Computing Machinery), 308–317.
Boppana, R., and Halldórsson, M. M. (1990). “Approximating maximum independent sets by excluding subgraphs,” in Proceedings of the Second Scandinavian Workshop on Algorithm Theory, SWAT 90 (Berlin; Heidelberg: Springer-Verlag), 13–25.
Duan, R., and Pettie, S. (2014). Linear-time approximation for maximum weight matching. J. ACM. 61, 23. doi: 10.1145/2529989
Eckles, D., Karrer, B., and Ugander, J. (2016). Design and analysis of experiments in networks: reducing bias from interference. J. Causal Inference 5, 20150021. doi: 10.1515/jci-2015-0021
Eisenbrand, F., Funke, S., Garg, N., and Könemann, J. (2003). “A combinatorial algorithm for computing a maximum independent set in a t-perfect graph,” in ACM-SIAM Symposium on Discrete Algorithms (Baltimore, MD: Society for Industrial and Applied Mathematics), 517–522. doi: 10.5555/644108.644194
Enright, A. J., van Dongen, S., and Ouzounis, C. A. (2002). An efficient algorithm for large-scale detection of protein families. Nucleic Acids Res. 30, 1575–1584. doi: 10.1093/nar/30.7.1575
Fatemi, Z., and Zheleva, E. (2020). Minimizing interference and selection bias in network experiment design. Proc. Int. AAAI Conf. Web Soc. Media 14, 176–186. doi: 10.1609/icwsm.v14i1.7289
Gangl, M. (2010). Causal inference in sociological research. Annu. Rev. Sociol. 36, 21–47. doi: 10.1146/annurev.soc.012809.102702
Gilbert, E., and Karahalios, K. (2009). “Predicting tie strength with social media,” in CHI (Association for Computing Machinery: Boston, MA: ACM), 211–220. doi: 10.1145/1518701.1518736
Green, D. P., Krasno, J. S., Coppock, A., Farrer, B. D., Lenoir, B., and Zingher, J. N. (2016). The effects of lawn signs on vote outcomes: results from four randomized field experiments. Elect. Stud. 41, 143–150. doi: 10.1016/j.electstud.2015.12.002
Gui, H., Xu, Y., Bhasin, A., and Han, J. (2015). “Network a/b testing: from sampling to estimation,” in Proceedings of the 24th International Conference on World Wide Web (Republic and Canton of Geneva: International World Wide Web Conferences Steering Committee), 399–409. doi: 10.1145/2736277.2741081
Halloran, M. E., and Struchiner, C. J. (1995). Causal inference in infectious diseases. Epidemiology 6, 142–151. doi: 10.1097/00001648-199503000-00010
Hamilton, W. L., Ying, R., and Leskovec, J. (2017). Representation learning on graphs: Methods and applications. IEEE Data Eng. Bull. 40, 52–74. Available online at: http://sites.computer.org/debull/A17sept/p52.pdf
Harvey, N. J. A. (2009). Algebraic algorithms for matching and matroid problems. SIAM J. Comput. 39, 679–702. doi: 10.1137/070684008
Holtz, D., Lobel, R., Liskovich, I., and Aral, S. (2020). Reducing interference bias in online marketplace pricing experiments. Available at SSRN 3583836. doi: 10.2139/ssrn.3583836
Hudgens, M. G., and Halloran, M. E. (2008). Toward causal inference with interference. J. Am. Stat. Assoc. 103, 832–842. doi: 10.1198/016214508000000292
Imbens, G., and Rubin, D. (2015). Causal Inference in Statistics, Social and Biomedical Sciences: An Introduction. Cambridge: Cambridge University Press.
Jagadeesan, R., Pillai, N. S., and Volfovsky, A. (2020). Designs for estimating the treatment effect in networks with interference. Ann. Stat. 48, 679–712. doi: 10.1214/18-AOS1807
Lee, S., and Honavar, V. (2016). “On learning causal models from relational data,” in Proceedings of the Thirtieth AAAI Conference on Artificial Intelligence (Phoenix. AZ: AAAI Press), 3263–3270. doi: 10.5555/3016100.3016360
Leskovec, J., Kleinberg, J., and Faloutsos, C. (2007). Graph evolution: densification and shrinking diameters. ACM Trans. Knowl. Discov. Data 1, 1217301. doi: 10.1145/1217299.1217301
Li, L., Chu, W., Langford, J., and Schapire, R. E. (2010). “A contextual-bandit approach to personalized news article recommendation,” in Proceedings of the 19th International Conference on World Wide Web (Raleigh, NC: Association for Computing Machinery), 661–670. doi: 10.1145/1772690.1772758
Li, S., and Wager, S. (2022). Random graph asymptotics for treatment effect estimation under network interference. Ann. Stat. 50, 2334–2358. doi: 10.1214/22-AOS2191
Liben-Nowell, D., and Kleinberg, J. (2007). The link-prediction problem for social networks. JASIST 58, 1019–1031. doi: 10.1002/asi.20591
Loucks, A. B., and Thuma, J. R. (2003). Luteinizing hormone pulsatility is disrupted at a threshold of energy availability in regularly menstruating women. J. Clin. Endocrinol. Metabol. 88, 297–311. doi: 10.1210/jc.2002-020369
Luby, M. (1985). “A simple parallel algorithm for the maximal independent set problem,” in Proceedings of the Seventeenth Annual ACM Symposium on Theory of Computing, STOC 85 (New York, NY: Association for Computing Machinery), 1–10.
Maier, M., Marazopoulou, K., Arbour, D., and Jensen, D. (2013). “A sound and complete algorithm for learning causal models from relational data,” in Proceedings of the Twenty-Ninth Conference on Uncertainty in Artificial Intelligence (Arlington, VA: AUAI Press), 371–380. doi: 10.5555/3023638.3023676
Maier, M., Taylor, B., Oktay, H., and Jensen, D. (2010). “Learning causal models of relational domains,” in Proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence (Atlanta, GA: AAAI Press), 531–538. doi: 10.5555/2898607.2898693
Marazopoulou, K., Maier, M., and Jensen, D. (2015). “Learning the structure of causal models with rel. and temporal dependence,” in Proceedings of the UAI 2015 Conference on Advances in Causal Inference - Volume 1504 (Amsterdam: CEUR-WS.org), 66–75. doi: 10.5555/3020267.3020274
Michell, L., and Amos, A. (1997). Girls, pecking order and smoking. Soc. Sci. Med. 44, 1861–1869. doi: 10.1016/S0277-9536(96)00295-X
Milo, R., Shen-Orr, S., Itzkovitz, S., Kashtan, N., Chklovskii, D., and Alon, U. (2002). Network motifs: simple building blocks of complex networks. Science 298, 824–827. doi: 10.1126/science.298.5594.824
Mucha, M., and Sankowski, P. (2004). “Maximum matchings via gaussian elimination,” in Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science (New York, NY: IEEE Computer Society), 248–255. doi: 10.1109/FOCS.2004.40
Nishimura, J., and Ugander, J. (2013). “Restreaming graph partitioning: simple versatile algorithms for advanced balancing,” in Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (Chicago, IL: Association for Computing Machinery), 1106–1114. doi: 10.1145/2487575.2487696
Oktay, H., Taylor, B., and Jensen, D. (2010). “Causal discovery in social media using quasi-experimental designs,” in Proceedings of the First Workshop on Social Media Analytics (Washington, DC: Association for Computing Machinery), 1–9. doi: 10.1145/1964858.1964859
Pouget-Abadie, J., Mirrokni, V., Parkes, D. C., and Airoldi, E. M. (2018). “Optimizing cluster-based randomized experiments under monotonicity,” in Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD 18 (New York, NY: Association for Computing Machinery), 2090–2099.
Pouget-Abadie, J., Saint-Jacques, G., Saveski, M., Duan, W., Ghosh, S., Xu, Y., et al. (2019). Testing for arbitrary interference on experimentation platforms. Biometrika 106, 929–940. doi: 10.1093/biomet/asz047
Rattigan, M. J., Maier, M. E., and Jensen, D. D. (2011). “Relational blocking for causal discovery,” in Proceedings of the Twenty-Fifth AAAI Conference on Artificial Intelligence (San Francisco, CA: AAAI Press) 145–151. doi: 10.5555/2900423.2900446
Ribeiro, M. H., Calais, P. H., Santos, Y. A., Almeida, V. A., and Meira Jr, W. (2018). “ Characterizing and detecting hateful users on twitter,” in ICWSM (Stanford, CA). doi: 10.1609/icwsm.v12i1.15057
Rossi, R., McDowell, L., Aha, D., and Neville, J. (2012). Transforming graph data for statistical relational learning. JAIR 45, 363–441. doi: 10.1613/jair.3659
Saveski, M., Pouget-Abadie, J., Saint-Jacques, G., Duan, W., Ghosh, S., Xu, Y., et al. (2017). “Detecting network effects: Randomizing over randomized experiments,” in KDD (Halifax, NS: Association for Computing Machinery), 1027–1035. doi: 10.1145/3097983.3098192
Sävje, F., Aronow, P., and Hudgens, M. (2021). Average treatment effects in the presence of unknown interference. Ann. Stat. 49, 673. doi: 10.1214/20-AOS1973
Schaeffer, S. E. (2007). Graph clustering. Comput. Sci. Rev. 1, 27–64. doi: 10.1016/j.cosrev.2007.05.001
Sen, P., Namata, G. M., Bilgic, M., Getoor, L., Gallagher, B., and Eliassi-Rad, T. (2008). Collective classification in network data. AI Mag. 29, 93–106. doi: 10.1609/aimag.v29i3.2157
Sobel, M. E. (2000). Causal inference in the social sciences. J. Am. Stat. Assoc. 95, 647–651. doi: 10.1080/01621459.2000.10474243
Stuart, E. A. (2010). Matching methods for causal inference: A review and a look forward. Stat. Sci. 25, 1. doi: 10.1214/09-STS313
Sussman, D. L., and Airoldi, E. M. (2017). Elements of Estimation Theory for Causal Effects in the Presence of Network Interference.
Taylor, S. J., and Eckles, D. (2018). “Randomized experiments to detect and estimate social influence in networks,” in Complex Spreading Phenomena in Social Systems, 289–322. doi: 10.1007/978-3-319-77332-2_16
Toulis, P., and Kao, E. (2013). “Estimation of causal peer influence effects,” in Proceedings of the 30th International Conference on International Conference on Machine Learning - Volume 28 (Atlanta, GA: JMLR.org), 1487–1497. doi: 10.5555/3042817.3043103
Ugander, J., Karrer, B., Backstrom, L., and Kleinberg, J. (2013). “Graph cluster randomization: network exposure to multiple universes,” in Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (Chicago, IL: Association for Computing Machinery), 329–337. doi: 10.1145/2487575.2487695
Ugander, J., and Yin, H. (2020). Randomized graph cluster randomization. arXiv preprint. arXiv, 2009.02297. doi: 10.48550/arXiv.2009.02297
Varian, H. R. (2016). Causal inference in economics and marketing. Proc. Natl. Acad. Sci. U.S.A. 113, 7310–7315. doi: 10.1073/pnas.1510479113
Xiao, M., and Nagamochi, H. (2017). Exact algorithms for maximum independent set. Inf. Comput. 255, 126–146. doi: 10.1016/j.ic.2017.06.001
Yang, J., and Leskovec, J. (2015). Defining and evaluating network communities based on ground-truth. KAIS 42, 181–213. doi: 10.1007/s10115-013-0693-z
Yves, M., Robson, J. M., Nasser, S.-D., and Zemmari, A. (2009). “An optimal bit complexity randomized distributed mis algorithm (extended abstract),” in Proceedings of the 16th International Conference on Structural Information and Communication Complexity, SIROCCO 09 (Berlin; Heidelberg: Springer-Verlag), 323–337.
Zheleva, E. J., Kuter, U., and Getoor, L. (2008). “Using friendship ties and family circles for link prediction,” in Proceedings of the Second International Conference on Advances in Social Network Mining and Analysis (Las Vegas, NV: Springer Verlag), 97–113. doi: 10.5555/1883692.1883698
Keywords: causal inference, direct treatment effects, total treatment effects, interference, spillover, selection bias
Citation: Fatemi Z and Zheleva E (2023) Network experiment designs for inferring causal effects under interference. Front. Big Data 6:1128649. doi: 10.3389/fdata.2023.1128649
Received: 21 December 2022; Accepted: 23 March 2023;
Published: 17 April 2023.
Edited by:
Xintao Wu, University of Arkansas, United StatesCopyright © 2023 Fatemi and Zheleva. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zahra Fatemi, emZhdGVtMkB1aWMuZWR1
 Zahra Fatemi
Zahra Fatemi Elena Zheleva
Elena Zheleva