- Gupta College of Business, University of Dallas, Irving, TX, United States
This paper studies contractual graphs, where the formation of edges between nodes result in dyadic exchanges. Each dyadic exchange is analyzed as a contractual agreement that is implemented upon fulfilment of underlying conditions. As these dyadic exchanges proliferate, the resulting population of these exchanges creates a contractual graph. A contractual framework for graphs is especially useful in applications where AI-enabled software is employed to create or automate smart contracts between nodes. While some smart contracts may be easily created and executed, others may contain a higher level of ambiguity which may prevent their efficient implementation. Ambiguity in contractual elements is especially difficult to implement, since nodes have to efficiently sense the ambiguity and allocate appropriate amounts of computational resources to the ambiguous contractual task. This paper develops a two-node contractual model of graphs, with varying levels of ambiguity in the contracts and examines its consequences for a market where tasks of differing ambiguity are available to be completed by nodes. The central theme of this paper is that as ambiguity increases, it is difficult for nodes to efficiently commit to the contract since there is an uncertainty in the amount of resources that they have to allocate for completion of the tasks specified in the contract. Thus, while linguistic ambiguity or situational ambiguity might not be cognitively burdensome for humans, it might become expensive for nodes involved in the smart contract. The paper also shows that timing matters—the order in which nodes enter the contract is important as they proceed to sense the ambiguity in a task and then allocate appropriate resources. We propose a game-theoretic formulation to scrutinize how nodes that move first to complete a task are differently impacted than those that move second. We discuss the applications of such a contractual framework for graphs and obtain conditions under which two-node contracts can achieve a successful coalition.
Introduction
Connections between entities are conveniently represented using graphs. The building blocks of graphs—nodes and edges—have long been used to represent various kinds of networks. The nodes represent entities involved in a transaction, and the edge represents the transaction itself. The interaction between nodes, as denoted by edges, thus represent dyadic exchanges between the nodes. As these dyadic exchanges between nodes in the network increase, it creates a population of these exchanges resulting in a graph. However, any given transaction denoted by a dyadic exchange may not occur until underlying conditions for the implementation of that transaction have been satisfied. In this context, the transaction (represented by a dyadic exchange or an edge in a graph) is not definitive, but is rather an outcome of a set of processes that have to be completed a priori. This paper studies such graphs of such contractual dyadic exchanges and their applications, where the edges between nodes are created only upon fulfilment of underlying clauses. We call such graphs as contractual graphs, since the formation of an edge is similar to the execution of a contract upon fulfilment of underlying conditions.
Contractual graphs are best exemplified by the application of smart contracts, where AI-enabled nodes are tasked with the creation or execution of contracts (Chatterjee et al., 2019). For example, upon transfer of funds from one account to another, the sale of an item is executed or a document is released. In this case, the nodes have to verify if the accounts have sufficient funds, if the transfer has taken place and if the entity has actual control over the item to be sold or the document to be released. Once these have been verified and the operations have taken place, the transaction is completed and can be represented as an edge in the contractual graph (Bartoletti and Pompianu, 2017). For example, the work in (Bigi et al., 2015) describes smart contracts for use in applications such as barter, insurance, escrow, derivatives and general business contracts.
However, not all contracts can be clearly automated. For example, if the contract is executed only upon satisfactory completion of a project, the contract will have to clearly define the threshold for “satisfactory” performance (Schneider, 2019). Any deviation from predetermined values for a task that varies in complexity will require a new smart contract to be created. Examples such as these abound in various domains, where the fuzziness of the contractual language can be parsed by humans, but poses tremendous difficulties while being converted into software. For the aforementioned example of what constitutes satisfactory performance, AI-enabled software could help by parsing through large datasets of similar projects that have been labeled as “satisfactory,” “good” or “excellent” and assign the appropriate label. Still, the ambiguity cannot always be resolved using code. Ambiguity, while helping humans achieve leeway in contractual relations, is not a welcome condition in software (Giancaspro, 2017; Clack, 2018). Ordinary qualifiers such as “few,” “some,” or “smart” cannot be programmed effectively without assigning values to these qualifiers. As AI increasingly makes its way into various facets of our lives, it is important to understand that ambiguity in the code can lead to life-altering consequences. For example, when facial recognition software identifies an individual with some probability, the inherent ambiguity in the goal of the task can create adverse outcomes with far-reaching impact (Lohr, 2018). While humans can navigate ambiguity based on situational cues (Eichberger et al., 2009), it is difficult to do so in software (Zou and Zou, 2017). Contractual relationships effected by AI, therefore, have to be cognizant of ambiguity as a key element of the human-machine and machine-machine relationships and a driver of resulting outcomes (Al-Najjar and Weinstein, 2009).
In this paper, we study how ambiguity impacts contractual graphs that are represented by dyadic exchanges. Specifically, we use a game-theoretic approach to study how tasks of varying ambiguity are perceived and completed by nodes. To do this, we assume a marketplace with ambiguous tasks (Figure 1). We model the contractual graph as a two-player game, where edges are formed only when two nodes cooperate to complete a task. We show that timing matters, i.e., there are specific advantages to the first mover and the second mover in cooperating to complete the task. Here, two contracts are formed:
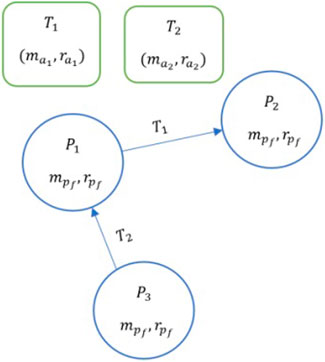
FIGURE 1. A marketplace with two ambiguous tasks
Next, using the Shapley value, we quantify the value that the first mover and the second mover bring to a coalition. These results are then used to create contractual graphs, whose edges reflect the outcomes of ambiguity and timing in task execution. Further, we provide a representation of such contractual graphs that can be used in learning important information about the community of nodes and the nature of the contracts that are formed in the marketplace.
The rest of this paper is organized as follows. Section Related Work in Contract Theory and Coalition Value presents an overview of related work in contract theory and the application of the Shapley value in diverse settings. Section Model for Contractual Graphs presents our model for contractual graphs, and Section Derivation of the Shapley Value for 2-Player Contracts derives the Shapley value for 2-player coalitions in contractual graphs. Section Results presents our findings of simulations. A kernel representation of contractual graphs is presented in Section Kernel Representation for Contractual Graphs. Finally, Sections Future Work and Conclusion present directions for future work and conclude the paper, respectively.
Related Work in Contract Theory and Coalition Value
The use of game theory to study the mechanism of contract formation has been studied in (Katz, 1990). Here, the author explored contract formation by addressing two questions. First, what are the actions or intentions that are required for a contractual obligation? Second, how do these actions or intentions affect the content of the contract itself? At the heart of this analysis, lies the issue of ambiguity in determining the set of actions or intentions that signal the formation and content of a contract. While legal rules provide a robust framework for determining the outcomes of contracts, the author emphasized the role of social norms and ethical precepts in the outcomes. To this end, the author identified different types of costs involved in contract formation and contract execution and proposes a game-theoretic economic analysis of the steps involved in contract offer, acceptance and rejection.
Another case for the incompleteness of contracts from an economics viewpoint has been made in (Tirole, 1999). Here, the author explains that most contracts are in fact, incomplete. Citing an example of mission and vision statements at higher levels of administration in various domains, the author explains how vague statements such as “increase security” or “provide robust frameworks” are often used to issue directives. The vagueness is inevitable especially since the costs of specifying every contingency and breach can be prohibitively expensive, even if such specifications can be explicitly specified. Such incomplete contract models are characterized by three types of costs: unforeseen contingencies, costs of writing contracts and costs of enforcing contracts. This theme has been continued in (Sklaroff, 2017), where the specific case of inflexibility in smart contracts was studied. The author presented the three features of smart contracts—automation, decentralization and anonymity—that require the formation of fully specified terms for entities to verify the terms of the contract without ambiguity. The author argued that contractual language offers two important attributes—linguistic ambiguity and enforcement discretion that provide powerful efficiencies in the contracting process. This is because smart contracts create transaction costs that are often inflexible. Smart contracts require future stages and terms to be clearly defined beforehand, which is difficult in volatile or unknown environments. Further, generic smart contracts lead to unpredictable and expensive litigation, and create challenging outcomes in cases of breach. Further work in the challenges of smart contracts and the law has been studied in (Verstraete, 2018) where the author presents challenges concerning enforcement and governance in smart contracts, which explicitly eschew central entities in transactions and their outcomes. Another example of developing contracts with predetermined outcomes is in (Asgaonkar and Krishnamachari, 2019) where the authors describe double-sided payment functions in smart contracts to ensure trustworthy transactions.
The aspect of cognitive burden has been addressed in (Tirole, 2015) where the author studies scenarios where having additional information is costly and therefore, players choose scenarios with less information. The paper describes such scenarios as cognitive traps, where the additional cognitive burden imposed by choosing options with higher information is the less desirable option for players. Thus, a player is hurt by choosing the cognitively burdensome option that requires the player to process larger amount of information. The paper further considers cognition-intensive contracting, where the parties to a contract attempt to understand the likely implications of the contract.
The value that players bring to a coalition can be measured in several ways, one of which is the Shapley value. In (Chalkiadakis et al., 2012), the authors present an overview of the applications of the Shapley value in cooperative game theory for AI and computer science. The Shapley value has been used extensively in feature selection in machine learning. Originally derived as a game-theoretic mechanism to characterize the value of each player in a coalition, the derivation of the Shapley value is contingent upon the fulfilment of the following conditions: symmetry (a player’s contribution and not the label assigned to the player is the factor that determines the player’s Shapley value), linearity (utility functions are linear), and carrier (dummy players are assigned a value of zero, and similarly players who make a contribution receive a value that divides the worth of the coalition among players.
The versatility of the Shapley value to diverse applications has led to development in multiple interpretations of the Shapley value. In Sundararajan and Najmi (2019), the authors study several Shapley values for application to a dataset with ten features, and show that the Shapley value with Conditional Expectations was the most sensitive for their application. In Cohen et al., (2005), the authors propose a Contribution-Selection Algorithm (CSA) that ranks each feature according to its contribution value. This algorithm is able to iteratively select
While the Shapley value offers a mechanism for determining the value of every player to a coalition, egalitarianism still remains another solution for determining the value of a player. In egalitarian solutions, the worth of each player is determined by equal division. This has led to research that combines the equal division of egalitarian solution vs. the marginalism offered by Shapley value solutions. Work in van den Brink et al., (2013) offers such a concept in the form of egalitarian Shapley values in both cooperative and non-cooperative scenarios.
Coordination games, which refer to the game-theoretic construct of rewarding players when they agree on a common strategy has been extensively studied. A thorough review of the first-mover position in marketing literature is in Kerin et al., (1992). In this paper, the authors described four categories of factors (economic, preemption, technological and behavioral) that contribute to the cost and differentiation advantages of the first-mover position. Examples include partnerships, alliance, or choice of a product. In Jackson and Watts (2002), the authors studied a coordination game in a social network where individuals periodically have the opportunity to add or sever a link.
Literature on coordination in games is extensive (Weidenholzer, 2010), and follows two broad categories. Tacit coordination, in which players communicate only by playing the game, differs from explicit coordination, in which players can send signals that are not directly related to the game (and which may not be costly). The role of communication in facilitation coordination has been studied in Ellingsen and Östling (2010), where the authors showed that communication has the potential to both hamper or hinder coordination efforts.
Work in Apt et al., (2017) studies the specific case of coordination games on finite undirected graphs, which is formulated as a problem where a player has to pick a color from a set of colors. The payoff of the player is the number of other players who pick the same color. Coordination games, here, thus refer to the scenario where it is beneficial for players to align their choices with others in the graph. Another study of a coordination game on a graph is in Rahn and Schäfer (2015), where the authors study the problem of a player having individual preference and may benefit in varying degrees by cooperating with neighbors. Efficient equilibria conditions for extreme cases are considered which allow for deviations, where on the one hand, all players choose the same strategy and on the other hand, each player chooses a unique strategy.
Another study that investigates a population of agents that can dynamically form and sever links according to varying payoffs is in Tomassini and Pestelacci (2010). The resulting co-evolution of strategies results in the formation of connected components in the network. An example of a coordination problem is the Stag Hunt problem, where a hunter must choose to hunt a stag with a group or hunt rabbits by himself (Bryant, 1994). A pure coordination game is described in Van Huyck et al., (1990), where the authors consider a tacit coordination game where strategic uncertainty contributed to inefficient outcomes. A different type of coordination game has been studied in Cason et al., (2012), where group of players are competing against each other. The effectiveness of a group is only as good as that of its weakest player. Thus, this work studies if communication within a group can help or hinder efficiency. Further investigation of strategic uncertainty is in Crawford (1995), in which players repeatedly play coordination games resulting in payoffs that depended on the player’s choices and the summative choices of the other players. A specific group of coordination games is the anti-coordination game (Bramoullé et al., 2004), in which players choose a strategy which is unlike those of her partner. They showed that as the cost of link formation increases, the equilibrium network becomes sparse.
Model for Contractual Graphs
We now introduce the model to study how ambiguity affects contract modeling by nodes/players in a marketplace. Assume two players
Figure 2 shows the steps in the process leading to a contract in a marketplace with one ambiguous task
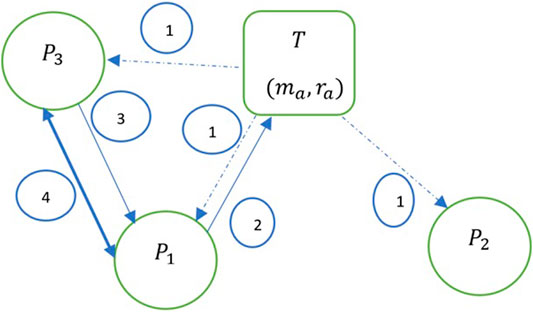
FIGURE 2. Steps leading to a contract. Assume that a task
Step 1: Players
Step 2:
Step 3: The remaining players in the marketplace
Step 4: The contract is finalized with
We assume that players are rational, intelligent and have common knowledge. A player assesses a task’s ambiguity and determines its payoff as the difference between its perception of the work it might be required to do for the task and the actual work that is required for the task. Thus, the initial payoff awareness
We define the amount of work to be performed as a product of the ambiguity and the resource commitment. Let the perceived ambiguity for the first mover node be
Similarly, let the perceived ambiguity for the second mover node be
We are interested in the difference between the perception of ambiguity and the actual ambiguity. We denote the difference in the perception and actual ambiguity for the first mover as
We now develop a matrix for the initial payoff awareness for the first mover (Table 1) and second mover (Table 2) based on the difference in ambiguity and resource consumption perception and reality. The table contains four options corresponding to the possible difference in perceptions of ambiguity (high/low), the actual levels of ambiguity (high/low), and the difference in perceptions and actual values of resource commitment (high/low).

TABLE 1. Specific conditions enumerating constraints on the initial payoff awareness (IPA) matrix for first mover.

TABLE 2. Specific conditions enumerating constraints on the initial payoff awareness (IPA) matrix for second mover.
In Tables 1, 2, we assume that each of the four cases are equally probable. This assumption can be revised to dynamically reveal different market conditions, where certain scenarios could be more probable than others. However, for simplicity, this model uses the equiprobable condition for each of these scenarios. Thus, the initial payoff awareness calculations can be obtained from Eqs. 1, 2 and Tables 1, 2 as follows. For the first mover,
Since we assume that a node allocates resources in accordance with the ambiguity, it accordingly allocates higher resources for the task. Similarly, if the node senses lower ambiguity, it allocates fewer resources for the task. This correspondence between the perception of ambiguity and the related resource allocation by a node is shown in Tables 1, 2. For both the first mover and the second mover, if the node senses a high ambiguity, it assigns more resources to the task. For example, in Table 1 for the first mover, the first row denotes that the node senses a high ambiguity, resulting in high difference between the perceived and actual ambiguity denoted by
The first term in the equation below corresponds to the first row for the first mover in Tables 1, 2, where
Similarly,
Next, we assume that nodes are motivated by reputation, which in turn is a proportional to the number of tasks completed. Reputational incentives or motivations have been extensively studied in game-theoretic modeling for applications such as cooperation in wireless networks (Jaramillo and Srikant, 2010) and human computation systems (Ghosh, 2013). Assume that reputation is function of work
Assume
We now have the framework to obtain the collective payoff from a coalition. The collective payoff function
Here,
We are implicitly assuming that total work
For best response, we set
We get
Since work
Without loss of generality, we assume constants
For simplicity, the constants
Substituting in Eq. 11, we get an equation for the relationship between the payoff factors at best response and obtain the ambiguity ratio (AR) of the first and second movers,
Thus,
Substituting this value of
Derivation of the Shapley Value for 2-Player Contracts
In this section, we analyze the two-player coalition to examine the contribution of each player to the coalition. To do this, we use the results from Eqs. 4, 5 from the above section. These results show the work of the first mover
The Shapley value offers a way to quantify the contribution of each player to the coalition. In machine-learning applications, the Shapley value has been widely used to determine the value of a particular set of features to the overall representation of the dataset. For example, in seeking to determine a predictor for longevity, which feature contributes most to longevity from a pool of features including education, genetics, diet, and others. The seminal paper by Shapley (Shapley, 1953) describes how to determine the value of the expected marginal contribution of a coalition by considering all possible orders in which coalitions can be formed between players and assigning each player her marginal contribution.
Applying this technique to the two-player coalition, we get the marginal contribution matrix (Table 4). Specifically, the Shapley value emphasizes the role of timing. If the coalition is formed with
Averaging the columns, we get P1’s contribution to the coalition as shown in Table 4.
P1’s contribution to the coalition:
Similarly, from Table 4, we get P2’s contribution to the coalition as
Dividing Eq. 18 by Eq. 19, we obtain the marginal contribution ratio (MCR) of players
Results
Figure 3 shows the relationship between the ambiguity ratio (AR) and the difference in perceived and actual ambiguity levels for the second mover
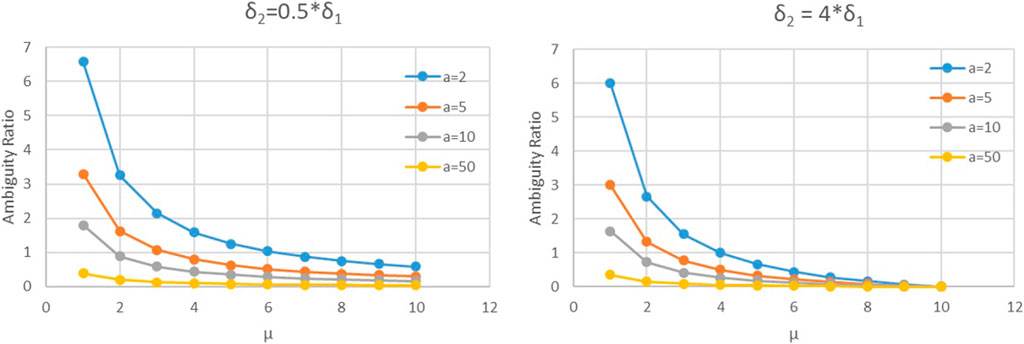
FIGURE 3. Relationship between the ambiguity ratio (AR) as a function of
The findings in Figure 3 follow from Eq. 16, which show AR and the variable costs
Next, we present the findings of the Shapley values of players involved in the coalition in terms of the marginal contribution ratio (MCR). The MCR findings depicted in Figure 4 are derived from Eq. 20. From Figure 4, we see that as
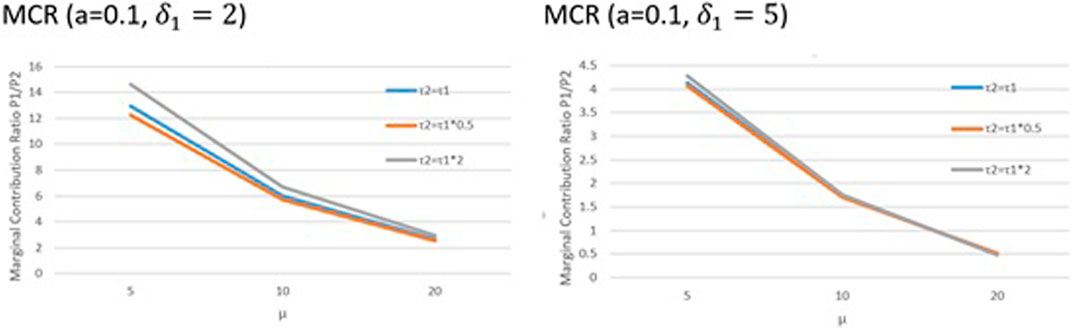
FIGURE 4. Shapley value findings. The variation of the marginal contribution ratio of the two players is explored as a function of the difference in perceived and actual ambiguity levels for the second mover
Kernel Representation for Contractual Graphs
In this section, we propose a simple kernel for contractual graphs that depict marketplaces of two-player coalitions formed to complete ambiguous tasks. Specifically, we address the question of how we can determine if two marketplaces of ambiguous tasks are similar. The implications of this question are several that range from evaluating marketplaces with similar resources, players and tasks. Several metrics can be used to study the effectiveness of a marketplace, such as number of coalitions, average size of coalitions and average task completion rate. An analysis of kernels of successful marketplaces can yield insights about the factors that significantly impact the efficiency of a marketplace of ambiguous tasks.
Since our model assumes two-player coalitions, we use the Shapley value of a two-player coalition developed in the previous section to build the kernel. Assume there are
Consider two contractual graphs in Figure 5. The Shapley value of each coalition is marked on the edge. Two graphs are considered similar if the sums of Shapley values of coalitions are equal.
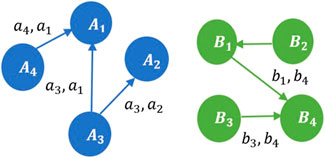
FIGURE 5. Contractual graphs
We now present the conditions under which two contractual graphs are considered similar. Let graph
Two graphs
1. Edge cardinality equivalence: The number of edges in graph
2. First mover equivalence: The sum of the Shapley values of the first movers in graph
where,
3. Second mover equivalence: The sum of the Shapley values of the second movers in graph
where,
These properties can be generalized to
Generalized Expression for Similarity of Contractual Graphs
The upper bound of the sum of the Shapley values of the coalitions in
The upper bound in Eq. 23 states that for a given contractual graph, the sum of the Shapley values of the first-movers and the second movers for all coalitions in that graph represents the term
Future Work
This paper presented an introduction to the theory of contractual graphs, by modeling contracts are commitments between two players to complete an ambiguous task. The theory of contractual graphs can be extended in several ways, some of which are summarized below.
Role of Incentives
While ambiguity of tasks can represent hurdles in task completion, incentives might be able to alleviate some of the costs involved in accepting tasks with high ambiguity. Additionally, incentives might be able to nudge the formation of coalitions thereby encouraging second movers to collaborate frequently with first movers on task completion. The role of incentives in economic literature has been widely studied (Bénabou and Tirole, 2006; DeMarzo and Saninkov, 2016). In (Bénabou and Tirole, 2006), where the authors explore the basis of incentives in psychology. Specifically, the role of incentives in intrinsic, extrinsic and reputational motivations have been considered in the development of game-theoretic models to gain insights into individual contributions and interactions. Graph theoretic representation learning can be enriched with the incorporation of additional sociological constructs such as identity (Akerlof and Kranton, 2000) to explain outcomes of interactions between nodes.
Negotiations Over Time
Our model for studying the performance of two-player coalitions in solving ambiguous tasks uses a single-stage contract. That is, the first mover assesses the ambiguity and creates a contract that the second mover accepts. In practice, however, contract formation goes through multiple stages of bargaining and negotiations over the terms of the contract. Additionally, problems related to imperfect information such as moral hazards and adverse selection can significantly impact the outcome of the contract formation, interpretation and execution.
Spectrum of Perceived Ambiguity
In our model, we chose a binary system for modeling ambiguity (high/low). While easier to model binary choices, in practice, ambiguity lies along a spectrum. Understanding the impact of ambiguity for a range of values between 0 and 1 can help further illustrate its impact on the formation of a contract.
Backing off From Contracts with Penalties/Prorated Benefits
While our model assumes that players commit to the contract and stay committed until task completion, it would be worth investigating how players would behave if they had the option to exit the contract. Similar to real-world situations where premature contract termination results in penalties or prorated rewards, modeling a marketplace of ambiguous tasks with players who have the option of exiting the contract would provide insights into real-world situations. Examples of such situations include students who sign up for classes and withdraw, renters who terminate the lease before its due date and employees who leave prior to the end of their probationary period. In all of these cases, embedded penalties/prorated rewards exist in the contractual terms and it would be worth investigating those through the lens of ambiguity. The players who have exited the contract are now freelancers of some sort, and how they impact the dynamics of the marketplace would be an interesting direction for future research.
Coalitions of Multiple Players
While our model chose two-player coalitions as dyadic exchanges, extending this model to
Conclusion
Contractual graphs arise in multiple situations. The agents involved in contractual graphs form connections among themselves upon the fulfilment of underlying conditions. For example, sending a packet from one node to another only when the packet is received with minimal distortion can be viewed as contract between two nodes only to transmit high-fidelity data. Another example of a contractual graph could be the formation of a connection in a social network, where two individuals form a “friend” connection only if they are separated by
Our findings showed how the perception of ambiguity in the contract impacts the resources allocated by a player to the task, thus displaying ambiguity aversion. Nodes model the contract by observing the parameters of the contract and allocating resources for completing the tasks specified in the contract. Using a game-theoretic formulation, we developed a model that assigns payoffs to players for the tasks completed. We distinguished between how the order in which players proceed to enter the two-player coalition affects the value that each player brings to the coalition. This metric was quantified using the Shapley value, that showed how the ambiguity of the task, costs of performing the task and resource allocation all played a part in determining the performance of the coalition. The Shapley value of a two-player coalition was then used to assign a tuple of edge weights. The set of all edge weights then formed a graph kernel for the contractual graph. We derived the conditions under which two contractual graphs are similar using edge cardinality, first-mover and second-mover equivalence. Finally, we proposed an upper limit on the sum of Shapley values of coalitions in
Contractual graphs offer several avenues for exploration due to their importance to network science. For example, we have assumed two-player coalitions where players complete the task, once they enter into the contract. In practice, however, coalition sizes may vary and players may have the option to leave the coalition even after they have entered into a contract. Similarly, new players may join the coalition even after the task has begun execution. Contractual graphs can be studied broadly, as well as in several niche environments. A better understanding of the behavior of contractual graphs can lead to the development of effective representative kernels, which in turn would facilitate learning about graphs.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the author, without undue reservation.
Author Contributions
RM designed the study, conducted the experiments and wrote the article.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Agaltsov, A. D., Molchanov, E. G., and Shananin, A. A. (2018). Inverse problems in models of resource distribution. J. Geom Anal. 28 (1), 726–765. doi:10.1007/s12220-017-9840-1
Akerlof, G. A., and Kranton, R. E. (2000). Economics and identity. Q. J. Econ. 115 (3), 715–753. doi:10.1162/003355300554881
Al-Najjar, N. I., and Weinstein, J. (2009). The ambiguity aversion literature: a critical assessment. Econ. Philos. 25 (3), 249. doi:10.1017/s026626710999023x
Apt, K. R., de Keijzer, B., Rahn, M., Schäfer, G., and Simon, S. (2017). Coordination games on graphs. Int. J. Game Theor. 46 (3), 851–877. doi:10.1007/s00182-016-0560-8
Asgaonkar, A., and Krishnamachari, B. (2019). “Solving the buyer and seller’s dilemma: a dual-deposit escrow smart contract for provably cheat-proof delivery and payment for a digital good without a trusted mediator,” in IEEE international conference on blockchain and cryptocurrency (ICBC), Seoul, South Korea, May 14–17, 2019, 262–267.
Bartoletti, M., and Pompianu, L. (2017). “An empirical analysis of smart contracts: platforms, applications, and design patterns,” in International conference on financial cryptography and data security, Sliema, Malta, April 7, 2017 (Cham: Springer), 494–509. doi:10.1007/978-3-319-70278-0_31
Bénabou, R., and Tirole, J. (2006). Incentives and prosocial behavior. Am. Econ. Rev. 96 (5), 1652–1678. doi:10.1257/aer.96.5.1652
Bigi, G., Bracciali, A., Meacci, G., and Tuosto, E. (2015). “Validation of decentralised smart contracts through game theory and formal methods,” in Programming languages with applications to biology and security, Pisa, Italy, June 2015 (Cham: Springer), 142–161. doi:10.1007/978-3-319-25527-9_11
Bilbao, J. M., Fernández, J. R., Jiménez, N., and López, J. J. (2008). The Shapley value for bicooperative games. Ann. Oper. Res. 158 (1), 99–115. doi:10.1007/s10479-007-0243-8
Bramoullé, Y., López-Pintado, D., Goyal, S., and Vega-Redondo, F. (2004). Network formation and anti-coordination games. Int. J. Game Theor. 33 (1), 1–19. doi:10.1007/s001820400178
Bryant, J. (1994). “Coordination theory, the stag hunt and macroeconomics,” in Problems of coordination in economic activity, Netherlands, January, 1994 (Dordrecht: Springer), 207–225. doi:10.1007/978-94-011-1398-4_10
Cason, T. N., Sheremeta, R. M., and Zhang, J. (2012). Communication and efficiency in competitive coordination games. Games Econ. Behav. 76 (1), 26–43. doi:10.1016/j.geb.2012.05.001
Chalkiadakis, G., Elkind, E., and Wooldridge, M. (2012). Cooperative game theory: basic concepts and computational challenges. IEEE Intell. Syst. 27 (3), 86–90. doi:10.1109/mis.2012.47
Chatterjee, K., Goharshady, A. K., and Goharshady, E. K. (2019). “The treewidth of smart contracts,” in Proceedings of the 34th ACM/SIGAPP symposium on applied computing, Limassol, Cyprus, April 8–12, 2019, 400–408.
Clack, C. D. (2018). Smart contract templates: legal semantics and code validation. J. Digital Banking 2 (4), 338–352.
Cohen, S. B., Ruppin, E., and Dror, G. (2005). “Feature selection based on the Shapley value,” in Proceedings of the IJCAI, Scotland, United Kingdom, July 30–August 5, 2005, Vol. 5, 665–670.
Crawford, V. P. (1995). Adaptive dynamics in coordination games. Econometrica 63, 103–143. doi:10.2307/2951699
DeMarzo, P. M., and Sannikov, Y. (2016). Learning, termination, and payout policy in dynamic incentive contracts. Rev. Econ. Stud. 84 (1), 182–236. doi:10.1093/restud/rdw029
Eichberger, J., Kelsey, D., and Schipper, B. C. (2009). Ambiguity and social interaction. Oxford Econ. Pap. 61 (2), 355–379. doi:10.1093/oep/gpn030
Ellingsen, T., and Östling, R. (2010). When does communication improve coordination? Am. Econ. Rev. 100 (4), 1695–1724. doi:10.1257/aer.100.4.1695
Ghosh, A. (2013). “Game theory and incentives in human computation systems,” in Handbook of human computation, New York, NY, November 2013 (New York, NY: Springer), 725–742. doi:10.1007/978-1-4614-8806-4_58
Giancaspro, M. (2017). Is a ‘smart contract’really a smart idea? Insights from a legal perspective. Comp. L. Security Rev. 33 (6), 825–835. doi:10.1016/j.clsr.2017.05.007
Jackson, M. O., and Watts, A. (2002). On the formation of interaction networks in social coordination games. Games Econ. Behav. 41 (2), 265–291. doi:10.1016/s0899-8256(02)00504-3
Jaramillo, J. J., and Srikant, R. (2010). A game theory based reputation mechanism to incentivize cooperation in wireless ad hoc networks. Ad Hoc Networks 8 (4), 416–429. doi:10.1016/j.adhoc.2009.10.002
Katz, A. (1990). The strategic structure of offer and acceptance: game theory and the law of contract formation. Mich. L. Rev. 89 (2), 215–295. doi:10.2307/1289373
Kerin, R. A., Varadarajan, P. R., and Peterson, R. A. (1992). First-mover advantage: a synthesis, conceptual framework, and research propositions. J. marketing 56 (4), 33–52. doi:10.1177/002224299205600404
Lohr, S. (2018). Facial recognition is accurate, if you’re a white guy. New York Times, February 9, 2018, 8.
Michalak, T. P., Aadithya, K. V., Szczepanski, P. L., Ravindran, B., and Jennings, N. R. (2013). Efficient computation of the Shapley value for game-theoretic network centrality. JAIR 46, 607–650. doi:10.1613/jair.3806
Narayanam, R., Skibski, O., Lamba, H., and Michalak, T. (2014). “A Shapley value-based approach to determine gatekeepers in social networks with applications,” in Proceedings of the twenty-first european conference on artificial intelligence, Prague, August 18–22, 2014, 651–656.
Rahn, M., and Schäfer, G. (2015). “Efficient equilibria in polymatrix coordination games,” in International symposium on mathematical foundations of computer science, Milan, Italy, 24–28 August, 2015 (Berlin, Heidelberg: Springer), 529–541. doi:10.1007/978-3-662-48054-0_44
Rajan, U., Seru, A., and Vig, V. (2010). Statistical default models and incentives. Am. Econ. Rev. 100 (2), 506–510. doi:10.1257/aer.100.2.506
Schneider, N. (2019). Decentralization: an incomplete ambition. J. Cult. Economy 12 (4), 265–285. doi:10.1080/17530350.2019.1589553
Sundararajan, M., and Najmi, A. (2019). The many shapley values for model explanation. arXiv preprint arXiv:1908.08474.
Tirole, J. (2015). Cognitive games and cognitive traps. Mimeo: Toulouse School of Economics Mimeo, 1.
Tirole, J. (1999). Incomplete contracts: where do we stand? Econometrica 67 (4), 741–781. doi:10.1111/1468-0262.00052
Tomassini, M., and Pestelacci, E. (2010). Coordination games on dynamical networks. Games 1 (3), 242–261. doi:10.3390/g1030242
van den Brink, R., Funaki, Y., and Ju, Y. (2013). Reconciling marginalism with egalitarianism: consistency, monotonicity, and implementation of egalitarian Shapley values. Soc. Choice Welf 40 (3), 693–714. doi:10.1007/s00355-011-0634-2
Van Huyck, J. B., Battalio, R. C., and Beil, R. O. (1990). Tacit coordination games, strategic uncertainty, and coordination failure. Am. Econ. Rev. 80 (1), 234–248.
Weidenholzer, S. (2010). Coordination games and local interactions: a survey of the game theoretic literature. Games 1 (4), 551–585. doi:10.3390/g1040551
Keywords: contractual graphs, Shapley value, kernel, game-theory, smart contracts
Citation: Murimi RM (2021) A Framework for Contractual Graphs. Front. Big Data 4:603282. doi: 10.3389/fdata.2021.603282
Received: 06 September 2020; Accepted: 27 January 2021;
Published: 04 March 2021.
Edited by:
Jiliang Tang, Michigan State University, United StatesCopyright © 2021 Murimi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Renita M. Murimi, cm11cmltaUB1ZGFsbGFzLmVkdQ==
 Renita M. Murimi
Renita M. Murimi
