Pacemaker neuron and network oscillations depend on a neuromodulator-regulated linear current

Linear leak currents have been implicated in the regulation of neuronal excitability, generation of neuronal and network oscillations, and network state transitions. Yet, few studies have directly tested the dependence of network oscillations on leak currents or explored the role of leak currents on network activity. In the oscillatory pyloric network of decapod crustaceans neuromodulatory inputs are necessary for pacemaker activity. A large subset of neuromodulators is known to activate a single voltage-gated inward current I_MI, which has been shown to regulate the rhythmic activity of the network and its pacemaker neurons. Using the dynamic clamp technique, we show that the crucial component of I_MI for the generation of oscillatory activity is only a close-to-linear portion of the current-voltage relationship. The nature of this conductance is such that the presence or the absence of neuromodulators effectively regulates the amount of leak current and the input resistance in the pacemaker neurons. When deprived of neuromodulatory inputs, pyloric oscillations are disrupted; yet, a linear reduction of the total conductance in a single neuron within the pacemaker group recovers not only the pacemaker activity in that neuron, but also leads to a recovery of oscillations in the entire pyloric network. The recovered activity produces proper frequency and phasing that is similar to that induced by neuromodulators. These results show that the passive properties of pacemaker neurons can significantly affect their capacity to generate and regulate the oscillatory activity of an entire network, and that this feature is exploited by neuromodulatory inputs.

Introduction

Recent studies have shown that linear leak currents play an important role in the generation of network oscillations (Cymbalyuk et al., 2002 ; Blethyn et al., 2006 ; Koizumi and Smith, 2008 ; Pang et al., 2009 ) and regulating excitability (Rekling et al., 2000 ; Brickley et al., 2007 ). Neuromodulatory substances are known to modify neuronal excitability by activating metabotropic receptors that can regulate ionic currents and pumps (Bayliss et al., 1992 ; Cantrell and Catterall, 2001 ; LeBeau et al., 2005 ; Tobin and Calabrese, 2005 ). In particular, the negative regulation of leak currents by several neurotransmitters has been proposed to play an important role in the regulation of neuronal excitability (Bayliss et al., 1992 ; Lee and Boden, 1997 ; Aller et al., 2005 ; Kim, 2005 ; Pratt and Aizenman, 2007 ; Weber et al., 2008 ), oscillations (Xu et al., 2007 ) and sleep-wake transitions (Goldstein et al., 2001 ). Nevertheless, few studies have directly tested the dependence of pacemaker and network oscillatory activity on leak currents and the role of neuromodulators in this process.

In this study we examine the role of linear conductances on the generation of oscillations by the pyloric network of the crab Cancer borealis. The pyloric network, located in the stomatogastric ganglion (STG), generates a rhythmic pattern of bursting activity driven by a pacemaker group of one anterior burster (AB) and two pyloric dilator (PD) neurons. The pyloric oscillations are dependent on and regulated by a variety of neuromodulators that are released hormonally or by descending projection neurons (Nusbaum and Beenhakker, 2002 ). When neuromodulators are removed, e.g., by decentralization, the bursting oscillations are usually disrupted and the pyloric neurons either spike tonically or become quiescent (Marder and Bucher, 2006 ). Using the dynamic clamp technique, we show that in a decentralized preparation, a reduction in the level of linear (leak) conductance in a single pyloric pacemaker neuron recovers oscillatory activity in that neuron, and interestingly, brings back the entire network oscillation.

Many of peptidergic and other modulators converge to unmask a voltage-dependent inward current (I_MI) characterized by an inverted bell-shaped current-voltage relationship (Golowasch and Marder, 1992b ; Swensen and Marder, 2000 ). An inverted bell-shaped I–V curve has traditionally been thought to confer a region of negative-slope conductance to the overall I–V curve of a neuron, enhancing their excitability and their tendency to produce regenerative membrane potential changes, including slow oscillations. It could be argued that an inverted bell-shaped I–V curve could be approximated by two linear segments, one with negative and one with positive slope. The positive-conductance component can depolarize the cell but reduces excitability whereas the negative-conductance component both increases excitability and reduces the stability of the membrane potential near the resting potential. Our dynamic clamp results indicate that regulation of a linear conductance with a reversal potential near the pacemaker neuron’s resting potential, controls the ability of the pyloric pacemaker neuron to generate oscillations. Furthermore, we show that the only essential element of the non-linear I_MI that contributes to the enhancement of membrane excitability and promoting membrane potential oscillations is the negative-conductance region spanning a voltage range that is aligned with the resting potential of the pacemaker neuron.

Materials and Methods

Experiments were carried on adult male crabs (Cancer borealis) purchased from local distributors (Newark, NJ, USA). The animals were maintained in artificial seawater tanks at 12–15°C until they were used, when they were first anesthetized by cooling on ice for 15–30 min prior to each dissection. The stomatogastric nervous system (including the stomatogastric ganglion, STG, the esophageal ganglion, OG, and the commissural ganglia, CoGs, Figure 1 A) was removed using standard methods (Selverston et al., 1976 ; Harris-Warrick et al., 1992 ) and each preparation was pinned down in a Sylgard-coated Petri dish. The STG was desheathed to expose the cell bodies for microelectrode impalement, and to allow effective superfusion. Preparations were superfused using normal saline containing (in mM): 11 KCl, 440 NaCl, 13 CaCl₂, 26 MgCl₂, 11.2 Trizma base, 5.1 Maleic acid, pH 7.4–7.5, and kept at ∼12°C.

FIGURE 1

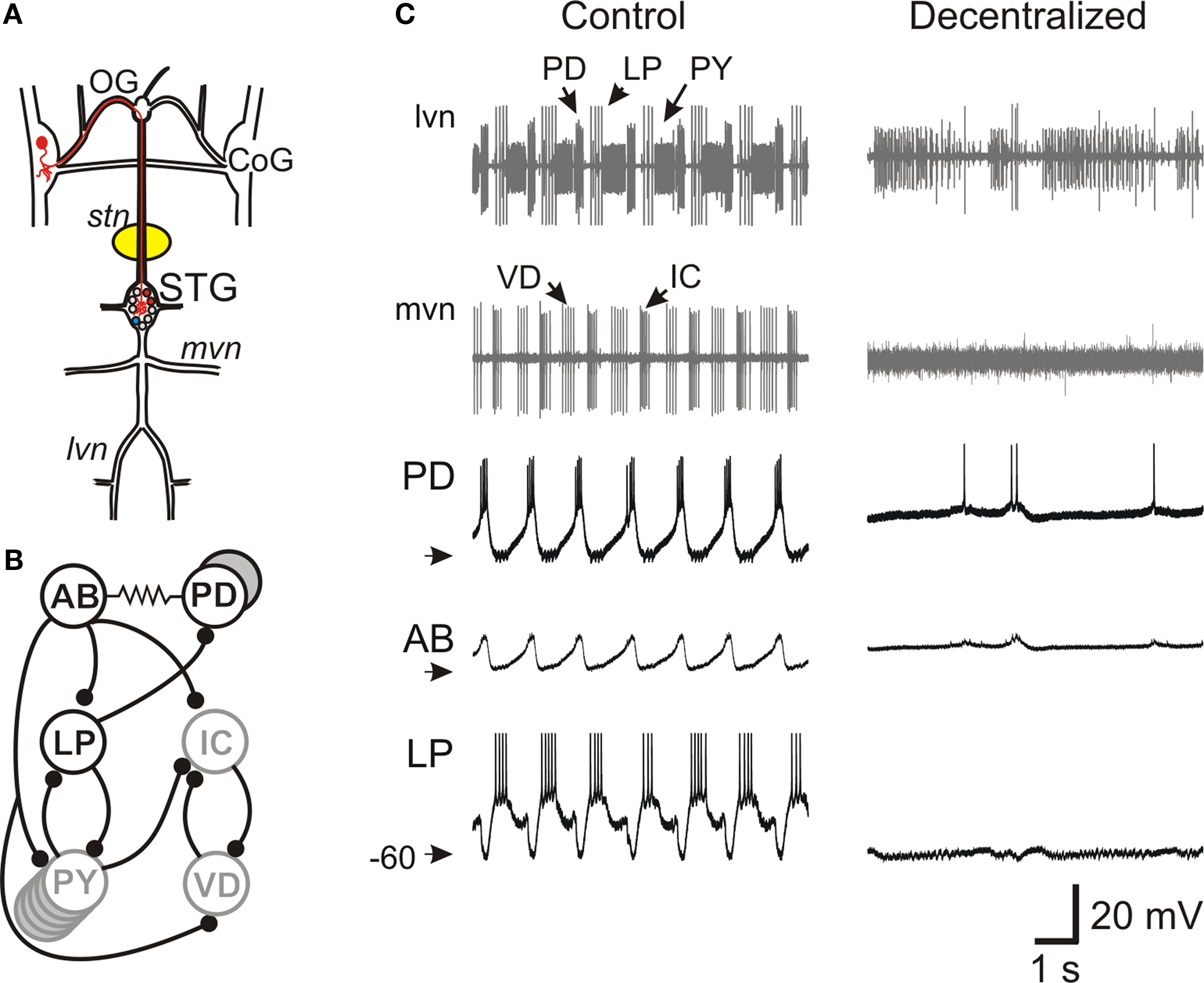
Figure 1. Effect of decentralization on the pyloric network oscillations. (A) Schematic diagram of the stomatogastric nervous system. The medial and lateral ventral motor nerves (mvn, lvn) contain axons from motor neurons located in the stomatogastric ganglion (STG). The STG receives descending projections from neurons with somata located in the oesophageal ganglion (OG) and the paired commissural ganglion (CoG, one such projection neuron is labeled in red). A petroleum jelly well (yellow) around the desheathed stomatogastric nerve (stn) is filled with 0.75-M sucrose plus 1-μM TTX to block action potential transmission of descending projections to the STG (decentralization). (B) Schematic diagram of main synaptic connections among pyloric network neurons. All chemical synapses (black circles) are inhibitory. The pacemaker neuron AB is strongly electrically coupled to the two PD neurons and, together, they make a synchronously bursting pacemaker group. (C) Extracellular recordings from lvn and mvn under Control (left) and Decentralized (right) conditions, demonstrating that removal of input from descending projections results in the cessation of pyloric oscillations. Neurons PD, LP and PY are labeled on the lvn recording and neurons IC and VD are labeled on the mvn recording. The axon of the pacemaker AB neuron runs along stn (recording not shown). Intracellular recordings of PD, AB and LP neurons are shown in the bottom three traces. AB action potentials are extremely small when recorded from the soma. Arrowheads point to −60 mV.

Microelectrodes were pulled using a Flaming-Brown micropipette puller (P97, Sutter Instruments) and filled with 0.6 M K₂SO₄ + 0.02 M KCl (resistance of 15–25 MΩ). Extracellular recordings were made with two stainless steel pins, one placed in the bath and the other within a petroleum jelly well built around the nerve of interest. Neuronal identification was accomplished by matching the intracellular action potential recordings to their corresponding extracellular nerve recordings (Selverston et al., 1976 ; Harris-Warrick et al., 1992 ). Intracellular recordings were made from the soma of the neurons using Axoclamp 2B amplifiers (Molecular Devices) and extracellular recordings were amplified using a differential AC amplifier model 1700 (A–M Systems).

We used the dynamic clamp technique (Sharp et al., 1992 ) to introduce ionic conductances into, or subtract them from, the biological neurons. A NI PCI-6070-E board (National Instruments, Austin, TX, USA) was used for current injection in dynamic clamp experiments. Data acquisition was performed using the Digidata 1332A data acquisition board and pClamp 9.2 software (Molecular Devices). The dynamic clamp software was developed in our laboratories (available for download at http://stg.rutgers.edu/software ) in the LabWindows/CVI software environment (National Instruments) on a Windows platform. In dynamic clamp, ionic currents are calculated using Hodgkin-Huxley-type equations as described below and continuously updated by recording the membrane potential (V) of the neurons in real time. I_MI was described by:

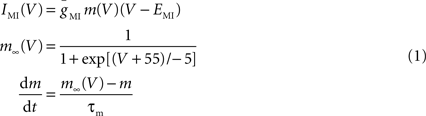
where E_MI = −10 mV and τ_m = 4 ms. The values for 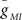varied depending on the experiment as described in the Results. The standard leak current is described by 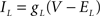where E_L = −68 mV is the leak current reversal potential and g_L is the leak conductance. When the value of leak conductance was set to be negative in the dynamic clamp software it resulted in a reduction of the total neuronal conductance. We describe this current as

The voltage-dependent current I_MI was divided into regions approximating a linear I–V curve with positive linear conductance (MI–PL) or negative linear conductance (MI–NL). The linear conductance regions were restricted in their voltage range so that they represented the negative and positive-conductance regions of I_MI:

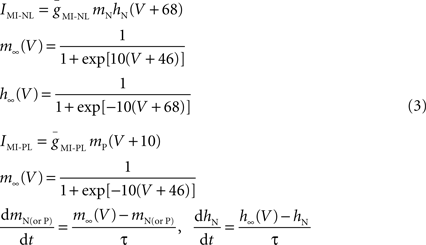
where τ = 4 ms. Although I_MI is non-inactivating, to build I_MI–NL, an inactivation variable h_N with very fast kinetics is used in dynamic clamp as a method of restricting the voltage range of activation below the upper limit of −46 mV (see Figure 6 A, red trace). A similar use of the activation variable m_P was made to produce I_MI–PL (Figure 6 A, gray trace).

It should be noted that dynamic clamp conductance manipulations introduce artificial ionic currents into the point of penetration, in this case the soma. The ionic currents in biological neurons are distributed over the entire structure of the cell and it is possible therefore that the size of the currents injected by dynamic clamp does not properly represent the equivalent biological ionic current. In particular, the currents injected in our dynamic clamp experiments may be much larger than what is actually needed for the pacemaker neurons to produce oscillations.

We measured neuronal input conductance before and after injecting negative conductances with dynamic clamp to avoid reducing the total conductance of the neuron to less than zero. When simultaneous dynamic clamp current and constant current injections were required, a Brownlee Precision Amplifier (Brownlee Precision) was used to add the currents before input to the Axoclamp amplifier. The acquired data were saved as binary files and were analyzed with the software Readscope (http://stg.rutgers.edu/software ) and Clampfit 9.2 (Molecular Devices).

For experiments performed to compare the effect of neuromodulatory input, the STG was isolated from anterior neuromodulatory inputs (i.e. decentralized) by replacing the saline solution within a petroleum jelly well built around the single stomatogastric nerve (stn, Figure 1 A) with 0.75-M sucrose and 1-μM TTX (Biotium) to block action potential transmission. In experiments to measure the input resistance of neurons 1-μM TTX was used to superfuse the ganglion.

SAS (SAS Institute), SigmaStat 2.3 (Systat Software) and Origin 7 (OriginLab) software packages were used for statistical and graphical analysis and all final figures were made in CorelDraw 12 (Corel Corp.). Reported statistical significance indicated a significance level p ≤ 0.05. In all statistical tests the data have been checked for normality by the SAS software package. All error bars shown and error values reported are standard deviations of the mean (SD).

Results

The pyloric network is a central pattern generator located in the stomatogastric ganglion, one of the four ganglia in the stomatogastric nervous system, an extension of the crab CNS (Figure 1 A). The pyloric network is an extremely well-studied network and consists, primarily, of six types of neurons that are connected with inhibitory synapses as well as gap junctions (Figure 1 B) (Nusbaum and Beenhakker, 2002 ; Marder and Bucher, 2006 ). Oscillations in the pyloric network are relatively stereotypical and consist of three phases with a cycle frequency of ∼1 Hz (Figure 1 C). All pyloric neurons take part in the network oscillation by producing bursts of action potentials on top of slow wave oscillations of their membrane potential. These oscillations are generated by a pacemaker group consisting of the AB and two PD neurons which are strongly coupled through gap junctions and produce synchronous bursting activity.

Pyloric oscillations are conditional upon the presence of neuromodulators that are released hormonally and in paracrine fashion from descending neurons that project to the STG via the stomatogastric nerve (stn; Figure 1 A). Blocking action potential conduction in the stn (decentralization) in vitro results in the disruption of the pyloric oscillations (Figure 1 C). Neuromodulatory inputs have been shown to target ionic currents in all pyloric neurons and modify the strengths of chemical synapses and gap junctions in the network (Johnson et al., 1994 ; Dickinson, 2006 ; Marder and Bucher, 2006 ). Although distinct modulators diverge in their target neurons, many modulators of the pyloric network, particularly neuropeptides and muscarinic agonists, have been shown to converge to activate a single voltage-gated inward current (I_MI) (Golowasch and Marder, 1992b ; Swensen and Marder, 2000 ). It should be noted that not all modulatory actions converge on this current and a variety of other ionic currents are also regulated by neuromodulators, particularly neuroamines (Harris-Warrick et al., 1995 ; Johnson et al., 2003 ).

The intact pyloric network is presumed to be subject to modulation by a variety of substances, each targeting a subset of neurons and synapses, the combined actions of which result in the observed triphasic pyloric oscillations. Here we examine the hypothesis that the primary action of neuromodulators that results in the triphasic pyloric oscillation is a simple modification of the leakiness of the pacemaker neurons.

During pyloric oscillations the pacemaker neurons AB and PD produce synchronous oscillations and follower neurons such as the LP neuron burst out of phase with the pacemakers (Figures 1 C and 2 A). When the preparation was decentralized, bursting oscillations in all the neurons ceased and the slow wave oscillation of their membrane potentials were suppressed and replaced with a almost completely quiescent membrane potential of −60 to −50 mV (Figure 2 B). Using the dynamic clamp technique, we reduced the magnitude of the leak current (i.e. increased the input resistance R_IN) in individual pyloric neurons in a way that the resting potential was not significantly changed. This was done by adding a negative linear conductance (Eq. 2) with a reversal potential near the resting potential of the neuron. A small value of g_NL in any of the neurons did not affect the output of a decentralized preparation. When a sufficiently large g_NL value was added to the AB neuron (N = 3), bursting activity in the AB neuron resumed and other pyloric neurons also resumed their oscillations with a triphasic pyloric activity pattern (Figure 2 C). All oscillatory activity ceased immediately as soon as the dynamic clamp current was removed (not shown). Similarly, if a sufficiently large g_NL was added to either one of the two PD neurons, it resulted in the recovery of the triphasic pyloric activity (Figure 2 D; N = 8). In contrast, addition of an I_NL to the LP neuron never resulted in the recovery of oscillations in either the LP neuron or the network no matter what conductance value g_NL was used (Figure 2 E; N = 3).

FIGURE 2

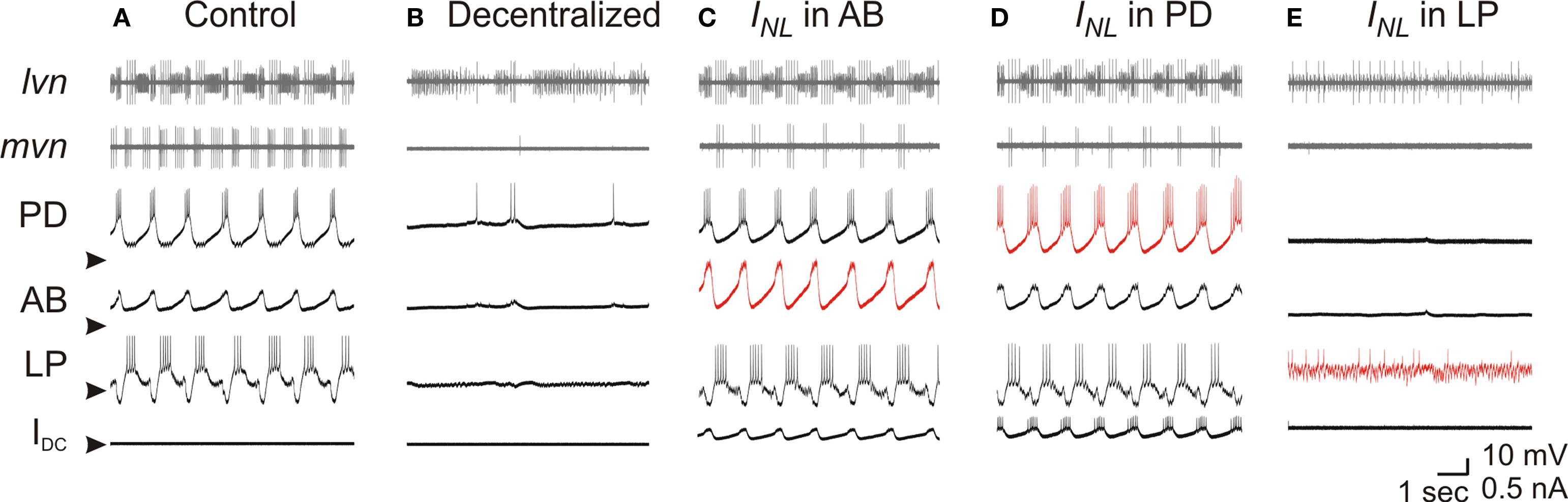
Figure 2. Effect of negative leak conductance on pyloric network activity. Simultaneous recordings of lvn and mvn (extracellular), and of PD, AB and LP neurons (intracellular) are shown in all panels. Bottom traces show the current injected with dynamic clamp (I_DC) in the respective neuron. (A) Control pyloric activity before decentralization. (B) Lack of rhythmic activity after decentralization. (C,D) Rhythmic activity that strongly resembles the control pyloric activity is observed when negative leak current I_NL (g_NL = −80 nS) is injected into the AB neuron (C) as well as into one of the two PD neurons (D). (E) No rhythmic activity can be induced when negative leak current I_NL (g_NL = −80 nS) is injected into the follower LP neuron. Arrowheads point to −60 mV and 0 nA.

These results indicated that reducing the amount of leak current in a single pacemaker neuron, but not a follower neuron, was sufficient to recover the oscillations of the entire pyloric network. There appeared to be no difference in the ability to recover the oscillations by the dynamic clamp application of I_NL in either the AB or PD neurons. Thus, from this point on we focused our experiments on the PD neurons because the single small AB neuron is often difficult to find and harder to record from than the PD neurons. Henceforth any reference to I_NL is in the PD neuron unless otherwise specified.

We examined the effect of the conductance of the I_NL on the recovered pyloric oscillation. Although in different preparations different amounts of g_NL led to the recovery of pyloric oscillations, increasingly negative g_NL in a recovered rhythm always led to a faster oscillation frequency (Figure 3 A). On average, a g_NL value of −70 to −80 nS was required to bring back the oscillation frequency to the average control value observed before decentralization (horizontal line). We also examined the effect of I_NL on the phase of activity of the individual pyloric neurons. The phase of individual neurons in the pyloric oscillation is defined as the fraction of each cycle duration (T) during which that neuron is active (Figure 3 B). As seen in Figure 3 C, the I_NL not only recovered network oscillations but produced activity phases (open boxes) that were statistically similar to those in the control pyloric oscillation recorded before decentralization (filled boxes; two-way RM ANOVA; All pair-wise p values > 0.1; N = 6). This was observed in all preparation in which I_NL led to a recovery of rhythmic pyloric activity.

FIGURE 3

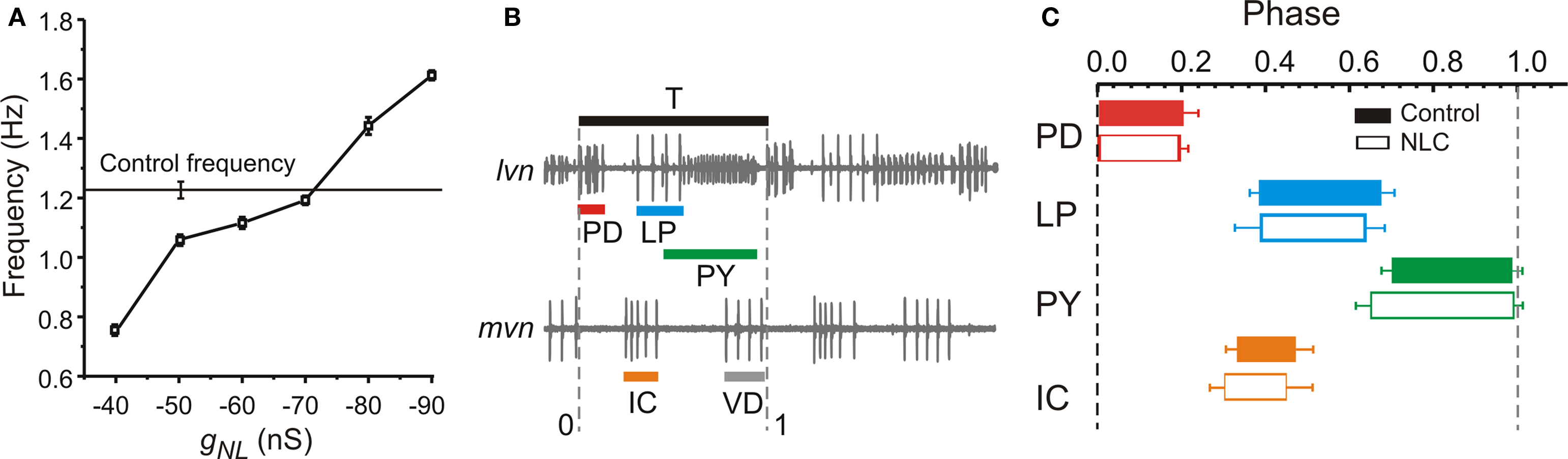
Figure 3. Effect of negative leak conductance on network frequency and phase relationships. (A) Negative leak conductance was injected into one PD neuron and the effect on rhythm frequency is plotted against the maximal conductance g_NL. Control frequency before decentralization is indicated by the horizontal line (±SD). (B) Sample extracellular recordings of lvn and mvn used to determine the phase diagram shown in (C). Black bar shows one period (T). Colored bars show duration of each neuron’s firing phase. Vertical dashed lines indicate mark the beginning and end of the cycle divided by T. (C) Phase diagram of pyloric activity. Each neuron’s spiking time is represented as a fraction of T (±SD). PD neuron firing is used as reference and thus begins at phase = 0. Filled bars are control conditions; open bars are in response to negative leak current injected with dynamic clamp (g_NL = −80 nS). (N = 6; N = 2 for the IC neuron which is not active in all preparations).

The fact that pyloric oscillations can be recovered in a decentralized preparation by reducing the leak conductance in the pacemaker neurons, leads to the hypothesis that modulatory inputs result in a conductance decrease in these neurons. We examined this hypothesis by measuring the leak conductance in the PD neurons in control and in a decentralized preparation in which action potential transmission along the stn was blocked with only 0.75-M sucrose to allow reversal of the block. These experiments were done in two-electrode voltage clamp in which the PD membrane potential was ramped from a holding value of −60 mV to a final value of −80 mV in 500 ms and the resulting I–V curve was fit with a linear function to measure the slope (Figure 4 A). The current that is blocked by decentralization can then be measured as a difference current (Figure 4 B). The average reversal potential for the difference current was −63.6 ± 9.5 mV.

FIGURE 4

Figure 4. Effect of decentralization on input conductance. (A) Current vs. voltage relationship (I–V) of a PD neuron obtained by ramping the voltage in two-electrode voltage clamp between −60 and −80 mV in 500 ms. The STG was decentralized reversibly with a solution of 0.75-M sucrose. Recovery indicates reversal of decentralization after several washes with normal saline of the sucrose well around the stn. Dashed blue lines indicate linear fits (I = aV + b; Control: a = 0.071, b = 3.67; Decentralized: a = 0.149, b = 8.14; Recovery: a = 0.127, b = 7.16). (B) Difference currents calculated from panel (A). (C) Conductance was measured as the slope of the best linear fit to the I–V curves in (A) (a values of the fits multiplied by 1000). The input conductance of the decentralized PD neurons was significantly higher than either the control or the recovered cells (One-way ANOVA, N = 6, p = 0.04).

To prevent any possible contamination of the leak conductance measurement by activation of voltage-gated currents the neuron was kept in two-electrode voltage clamp while the preparation was decentralized (see Materials and Methods) and while it recovered from decentralization after sucrose was washed from around the stn. These experiments showed that the leak conductance in the PD neuron was significantly increased when the preparation was decentralized, compared to control and recovery (Figure 4 C; N = 6; p = 0.04), supporting the hypothesis that the conductance in the decentralized system is reduced when neuromodulators are restored.

As mentioned above, several neuromodulators of the pyloric network are known to activate a single voltage-gated inward current I_MI in pyloric neurons (Swensen and Marder, 2000 ). I_MI was first characterized through actions of proctolin (Golowasch and Marder, 1992b ), an endogenously released neuromodulator that is known to activate the pyloric oscillations in a decentralized preparation (Nusbaum and Marder, 1989 ). If neuromodulators could affect the rhythm by affecting the pacemaker’s leak current or by targeting I_MI it is important to know if these effects are similar or related. We therefore compared the effect of I_NL with adding a dynamic clamp version of I_MI in the PD neuron and with bath application of 10⁻⁶ M proctolin in decentralized preparations. We found that the dynamic clamp injections of I_NL or I_MI and bath application of proctolin all had very similar effects in recovering the pyloric oscillation. A comparison of these effects on the PD neuron is shown in Figure 5 .

FIGURE 5

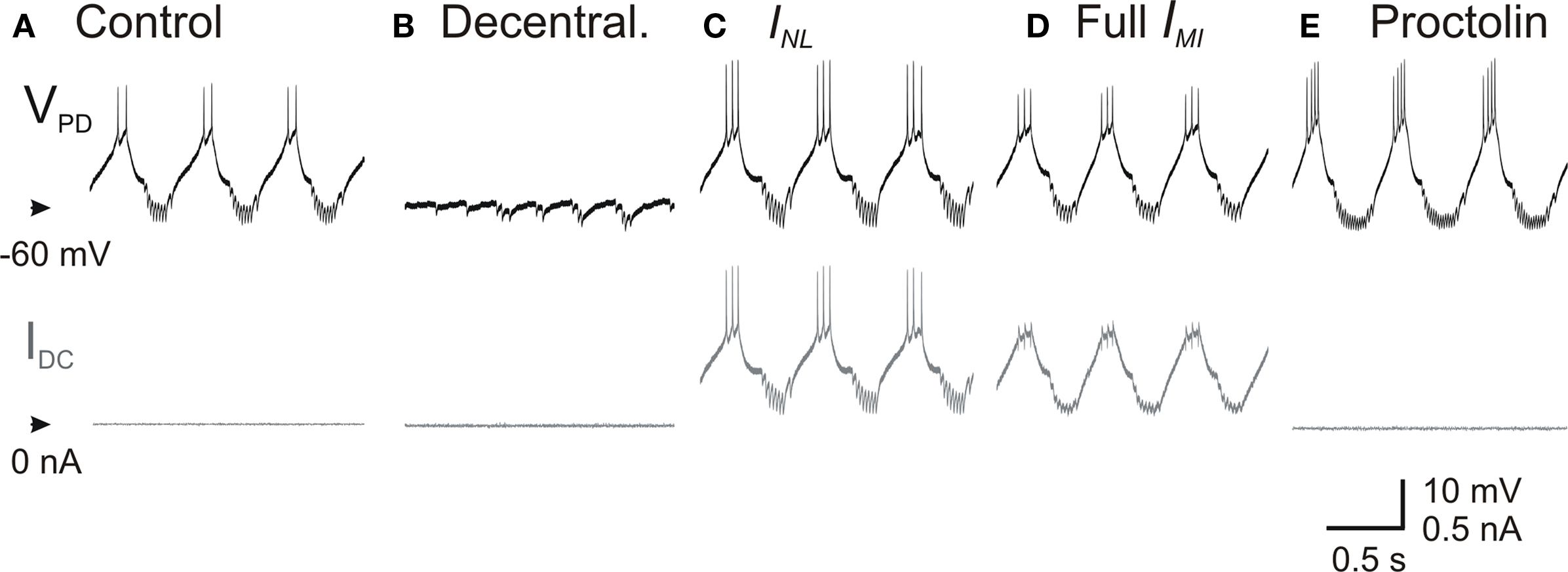
Figure 5. Effect of proctolin on the activity of PD neurons. Top traces correspond to the membrane potential of a PD neuron and the bottom traces to the injected dynamic clamp current in (A) control, (B) after decentralization, (C) during injection of I_NL (Eq. 2) with g_NL = −80 nS, (D) during injection of I_MI (Eq. 1) with g_MI = −80 nS, and (E) during bath application of 1-μM proctolin.

This result led us to the idea that I_NL and I_MI act on the PD neuron through similar mechanisms. How could the actions of a non-linear inward current and a linear current with negative conductance be similar? We explored this question by examining the I–V curve of I_MI. As shown in Figure 6 A, this typical inverted bell-shaped I–V curve (black trace) can be divided into two regions, one with negative-slope conductance (red trace) and the other with positive slope conductance (gray trace). The section of the I–V curve with negative-slope conductance can be argued to be well approximated with I_NL (dashed blue curve in Figure 6 A). We denoted the negative (positive) slope conductance section of I_MI as I_MI–NL (I_MI–PL) and compared the effect of dynamic clamp injection of I_NL, I_MI, I_MI–NL and I_MI–PL. These currents were modeled in dynamic clamp with the appropriate parameters so that I_MI was well approximated by I_MI–NL + I_MI–PL (Eq. 3) and I_NL matched the negative slope of I_MI–NL in the appropriate voltage range as shown in Figure 6 A (see Materials and Methods). When I_MI–NL, I_NL or I_MI were added to the PD neuron using dynamic clamp the result was always the recovery of oscillatory activity (Figures 6 D,F,G). In contrast, adding I_MI–PL had little effect on the PD neuron and never resulted in oscillatory activity (Figure 6 E). These results indicated that the actions of I_MI on the PD neuron were mainly through the limited region of negative-slope conductance which effectively resulted in a reduction of the leak current in the PD neuron.

FIGURE 6

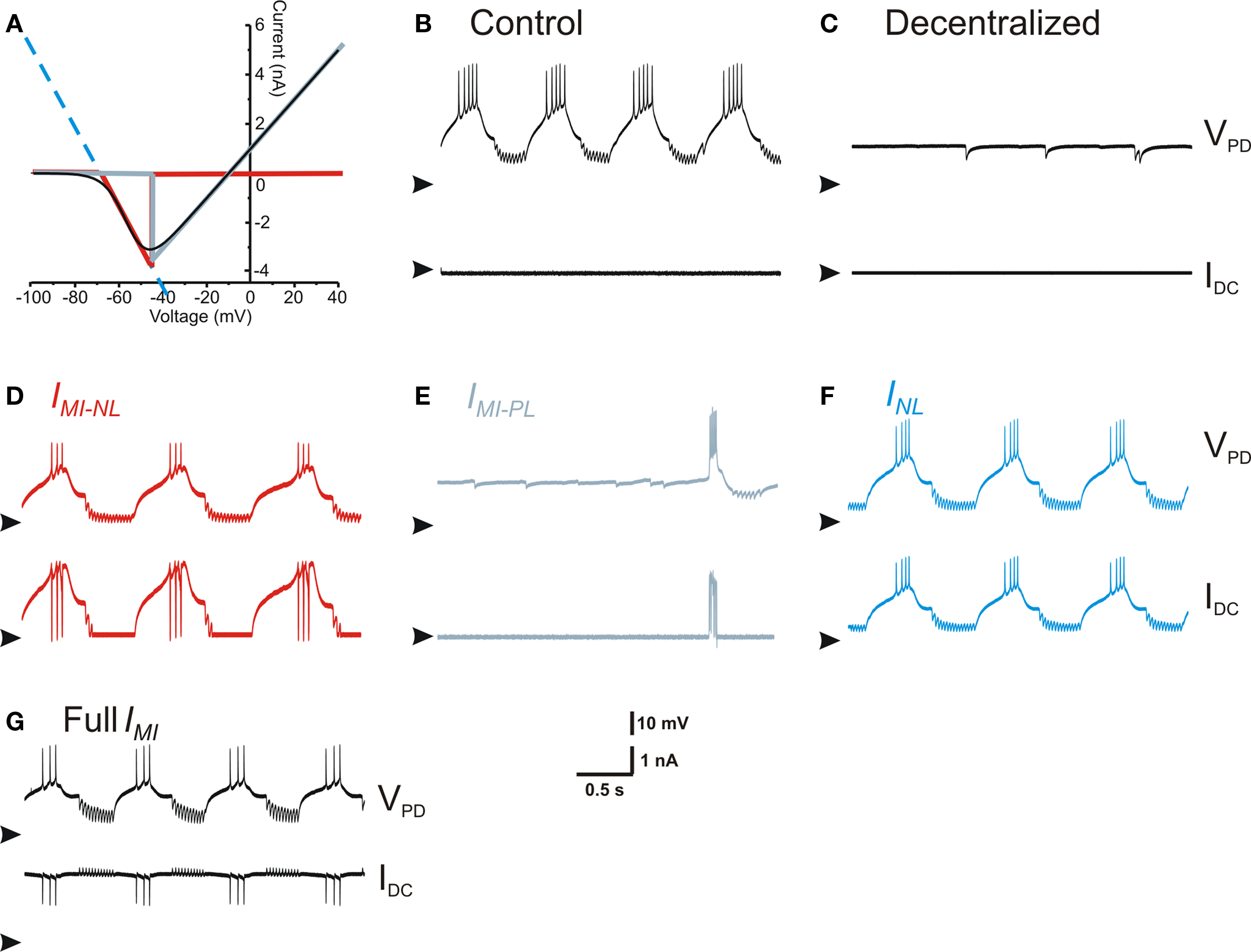
Figure 6. Effect of negative leak conductance and modulatory-activated inward current linear components. (A) I–V curve of I_MI and its linear approximations. Full I_MI is the black trace, I_NL is the dashed blue line that extends across the entire voltage range, I_MI–NL is the red trace, and I_MI–PL is the gray trace. (B) Control conditions. (C) Activity after decentralization. (D) Activity with I_MI–NL injected (red trace in (A), g_NL = −80 nS). (E) Activity with I_MI-PL injected (gray trace in (A), g_PL = 80 nS). (F) Activity with I_NL injected (dashed blue trace in (A), g_NL = −80 nS). (G) Activity with the full I_MI injected (black trace in (A), g_MI = 80 nS). All panels in (B–G) show the membrane potential of the same PD neuron (top, arrowheads point to −70 mV) and the dynamic clamp-injected current (bottom, arrowheads point to 0 nA).

Discussion

Regulation of leak currents has been proposed to play an important role in the control of neuronal excitability, oscillatory activity and sleep-wake transitions (Bayliss et al., 1992 ; Lee and Boden, 1997 ; Goldstein et al., 2001 ; Aller et al., 2005 ; Kim, 2005 ; Pratt and Aizenman, 2007 ; Xu et al., 2007 ; Weber et al., 2008 ). A number of neuromodulators acting on metabotropic receptors have been shown to negatively regulate leak currents by decreasing their conductance; these include glutamate (Blethyn et al., 2006 ; Brickley et al., 2007 ), thyrotropin-releasing hormone (TRH) (Bayliss et al., 1992 ) and serotonin (Weber et al., 2008 ). We show that the action of the neuromodulatory inputs in producing pyloric oscillations can be mimicked by a simple reduction in the leak current of the pyloric pacemaker neurons. When a leak current with negative conductance is injected, using the dynamic clamp technique, in any one of the neurons that comprise the pyloric pacemaker group, the rhythmic pattern of the entire network is recovered. This recovered rhythm is essentially identical to the ongoing pyloric rhythm prior to decentralization and to the rhythm produced by bath application of a modulatory neuropeptide in a decentralized preparation. In contrast, injecting the negative-conductance leak current into non-pacemaker neurons in the pyloric network fails to activate the pyloric rhythm or any rhythmic activity in that neuron.

How does the recovery of the pyloric rhythm by reducing the leak conductance in the pacemaker neurons relate to the known effects of neuromodulators in this network? Much of the neuromodulatory actions on individual pyloric neurons converge, through unknown second messenger mechanisms, to activate a voltage-gated inward current I_MI (Swensen and Marder, 2000 ). We show that the I–V curve of this non-linear inward current can basically be decomposed into two linear components, one with positive-conductance I_MI–PL and one with negative conductance I_MI–NL. When we introduced one or the other of these two components into the PD neuron using dynamic clamp, we found that I_MI–NL led to the recovery of oscillations whereas I_MI–PL did not. The recovered oscillation was identical to oscillations produced with the full I–V range of I_MI or that produced by bath application of the neuropeptide proctolin.

Is the linear decomposition of a continuously voltage-dependent current valid? The red and gray traces shown in Figure 6 suggest that the sum of these two linear components, restricted in their voltage range, very closely match the total current I_MI over the full voltage range. However, we observed that the linear negative-conductance component (I_MI–NL or I_NL) effectively activates the pyloric rhythm only when its reversal potential was negative relative to the membrane potentials trajectory of the pacemaker neurons’ slow wave. Reversal potential values more positive than that led to currents that were outward for most of this trajectory and thus did not enhance their excitability (not shown). Conversely, with its positive reversal potential, the positive-conductance linear component (I_MI–PL) only led to a slight depolarization of the baseline voltage but decreased the input resistance of the cells and did not enhance their excitability.

Electrical loading of a neuron can affect its membrane potential amplitude changes and temporal properties such as spiking and bursting activity. Such electrical loading can occur via two mechanisms: electrical coupling to other cells or changes in the passive membrane conductance. In the pyloric network, electrical coupling of the intrinsically oscillatory AB neuron to non-oscillatory neurons, such as the PD neuron, affects the oscillatory activity of the whole ensemble (Hooper and Marder, 1987 ; Kepler et al., 1990 ; Soto-Trevino et al., 2005 ). If the load produced by the non-oscillatory neurons is large, it would kill the oscillations. A negative conductance in any of the coupled neurons effectively reduces the electric load on the oscillatory cell, leading to an enhanced excitability. Any reduction in leak current has this effect as long as the membrane potential of the cell is more positive than the current’s reversal potential (e.g. Sirois et al., 2002 ; Blethyn et al., 2006 ; Koizumi and Smith, 2008 ). Thus, the reduction of the leak current in the PD neuron may lead to the recovery of oscillatory activity because of the strong electrical coupling of the PD neurons to the AB neuron. However, our experiments do not exclude the possibility that the PD neuron itself becomes an intrinsic oscillator under these conditions.

Previous studies of the pyloric network have shown that blocking outward currents can result in a recovery of oscillations in the AB and PD neurons, although a recovery of the full network activity was not reported (Harris-Warrick and Johnson, 1987 ). Additionally, modulatory actions by dopamine, that do not target I_MI, have also been reported to result in a significant increase of the input resistance in the AB neuron and a simultaneous decrease in the PD neuron (Johnson et al., 1993 ) and dopamine has been shown to induce oscillatory activity in the isolated AB neuron in lobsters (Johnson et al., 1992 ). It is therefore possible that recovery of oscillations may occur through mechanisms that include, among other effects, a decrease in leak conductance, but that are independent of I_MI.

Changes in leak conductance have been shown to be the likely mechanism underlying the excitatory action of several substances acting on metabotropic receptors (Bayliss et al., 1992 ; Sirois et al., 2002 ; Blethyn et al., 2006 ; Brickley et al., 2007 ; Koizumi and Smith, 2008 ; Weber et al., 2008 ). In many if not all these cases, it appears that the consequence of a reduced leak current is to move the voltage of the cell to the activation range of voltage-dependent pacemaker currents. Of course, excitability cannot result from a simple reduction in the endogenous leak current; it is necessary to produce a negative-slope conductance in the I–V curve that creates a regenerative mechanism for membrane depolarization. In the case of the pacemaker pyloric network neurons, we suggest that the negative-conductance component of I_MI is itself the pacemaker current since no other current has been reported to be active in the voltage range of this conductance component (Graubard and Hartline, 1991 ; Golowasch and Marder, 1992a ; Soto-Trevino et al., 2005 ). Although this hypothesis needs to be tested experimentally, it effectively implies that the fundamental pacemaker properties in this network result from the actions of a linear portion of a non-linear current that is activated by neuromodulatory inputs. In other words, it appears that pacemaker activity in this network depends on a linear current, whose essential properties are implemented by the modulator-activated inward current I_MI.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Dr. Vahid Tohidi for his initial experiments on this work which were published in abstract form. This research was supported by NIH grants MH64711 (Jorge Golowasch) and MH60605 (Farzan Nadim).

References

Aller, M. I., Veale, E. L., Linden, A. M., Sandu, C., Schwaninger, M., Evans, L. J., Korpi, E. R., Mathie, A., Wisden, W., and Brickley, S. G. (2005). Modifying the subunit composition of TASK channels alters the modulation of a leak conductance in cerebellar granule neurons. J. Neurosci. 25, 11455–11467.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Bayliss, D. A., Viana, F., and Berger, A. J. (1992). Mechanisms underlying excitatory effects of thyrotropin-releasing hormone on rat hypoglossal motoneurons in vitro. J. Neurophysiol. 68, 1733–1745.

Pubmed Abstract | Pubmed Full Text

Blethyn, K. L., Hughes, S. W., Toth, T. I., Cope, D. W., and Crunelli, V. (2006). Neuronal basis of the slow (<1 Hz) oscillation in neurons of the nucleus reticularis thalami in vitro. J. Neurosci. 26, 2474–2486.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Brickley, S. G., Aller, M. I., Sandu, C., Veale, E. L., Alder, F. G., Sambi, H., Mathie, A., and Wisden, W. (2007). TASK-3 two-pore domain potassium channels enable sustained high-frequency firing in cerebellar granule neurons. J. Neurosci. 27, 9329–9340.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cantrell, A. R., and Catterall, W. A. (2001). Neuromodulation of Na+ channels: an unexpected form of cellular plasticity. Nat. Rev. Neurosci. 2, 397–407.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Cymbalyuk, G. S., Gaudry, Q., Masino, M. A., and Calabrese, R. L. (2002). Bursting in leech heart interneurons: cell-autonomous and network-based mechanisms. J. Neurosci. 22, 10580–10592.

Pubmed Abstract | Pubmed Full Text

Dickinson, P. S. (2006). Neuromodulation of central pattern generators in invertebrates and vertebrates. Curr. Opin. Neurobiol. 16, 604–614.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Goldstein, S. A., Bockenhauer, D., O’Kelly, I., and Zilberberg, N. (2001). Potassium leak channels and the KCNK family of two-P-domain subunits. Nat. Rev. Neurosci. 2, 175–184.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Golowasch, J., and Marder, E. (1992a). Ionic currents of the lateral pyloric neuron of the stomatogastric ganglion of the crab. J. Neurophysiol. 67, 318–331.

Golowasch, J., and Marder, E. (1992b). Proctolin activates an inward current whose voltage dependence is modified by extracellular Ca2+. J. Neurosci. 12, 810–817.

Graubard, K., and Hartline, D. K. (1991). Voltage clamp analysis of intact stomatogastric neurons. Brain Res. 557, 241–254.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Harris-Warrick, R. M., Coniglio, L. M., Barazangi, N., Guckenheimer, J., and Gueron, S. (1995). Dopamine modulation of transient potassium current evokes phase shifts in a central pattern generator network. J. Neurosci. 15, 342–358.

Pubmed Abstract | Pubmed Full Text

Harris-Warrick, R. M., and Johnson, B. R. (1987). Potassium channel blockade induces rhythmic activity in a conditional burster neuron. Brain Res. 416, 381–386.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Harris-Warrick, R. M., Marder, E., Selverston, A. I., and Moulins, M. (1992). Dynamic Biological Networks: The Stomatogastric Nervous System. Cambridge, MA: MIT Press.

Hooper, S. L., and Marder, E. (1987). Modulation of the lobster pyloric rhythm by the peptide proctolin. J. Neurosci. 7, 2097–2112.

Pubmed Abstract | Pubmed Full Text

Johnson, B. R., Kloppenburg, P., and Harris-Warrick, R. M. (2003). Dopamine modulation of calcium currents in pyloric neurons of the lobster stomatogastric ganglion. J. Neurophysiol. 90, 631–643.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Johnson, B. R., Peck, J. H., and Harris-Warrick, R. M. (1992). Elevated temperature alters the ionic dependence of amine-induced pacemaker activity in a conditional burster neuron. J. Comp. Physiol. A 170, 201–209.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Johnson, B. R., Peck, J. H., and Harris-Warrick, R. M. (1993). Amine modulation of electrical coupling in the pyloric network of the lobster stomatogastric ganglion. J. Comp. Physiol. A 172, 715–732.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Johnson, B. R., Peck, J. H., and Harris-Warrick, R. M. (1994). Differential modulation of chemical and electrical components of mixed synapses in the lobster stomatogastric ganglion. J. Comp. Physiol. A 175, 233–249.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kepler, T. B., Marder, E., and Abbott, L. F. (1990). The effect of electrical coupling on the frequency of model neuronal oscillators. Science 248, 83–85.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Kim, D. (2005). Physiology and pharmacology of two-pore domain potassium channels. Curr. Pharm. Des. 11, 2717–2736.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Koizumi, H., and Smith, J. C. (2008). Persistent Na+ and K+-dominated leak currents contribute to respiratory rhythm generation in the pre-Botzinger complex in vitro. J. Neurosci. 28, 1773–1785.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

LeBeau, F. E., El Manira, A., and Griller, S. (2005). Tuning the network: modulation of neuronal microcircuits in the spinal cord and hippocampus. Trends Neurosci. 28, 552–561.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Lee, K., and Boden, P. R. (1997). Characterization of the inward current induced by metabotropic glutamate receptor stimulation in rat ventromedial hypothalamic neurones. J. Physiol. (Lond.) 504(Pt 3), 649–663.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Marder, E., and Bucher, D. (2006). Understanding circuit dynamics using the stomatogastric nervous system of lobsters and crabs. Annu. Rev. Physiol. 69, 291–316.

CrossRef Full Text

Nusbaum, M. P., and Beenhakker, M. P. (2002). A small-systems approach to motor pattern generation. Nature 417, 343–350.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Nusbaum, M. P., and Marder, E. (1989). A modulatory proctolin-containing neuron (MPN). II. State-dependent modulation of rhythmic motor activity. J. Neurosci. 9, 1600–1607.

Pubmed Abstract | Pubmed Full Text

Pang, D. S., Robledo, C. J., Carr, D. R., Gent, T. C., Vyssotski, A. L., Caley, A., Zecharia, A. Y., Wisden, W., Brickley, S. G., and Franks, N. P. (2009). An unexpected role for TASK-3 potassium channels in network oscillations with implications for sleep mechanisms and anesthetic action. Proc. Natl. Acad. Sci. U.S.A. 106, 17546–17551.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Pratt, K. G., and Aizenman, C. D. (2007). Homeostatic regulation of intrinsic excitability and synaptic transmission in a developing visual circuit. J. Neurosci. 27, 8268–8277.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Rekling, J. C., Funk, G. D., Bayliss, D. A., Dong, X. W., and Feldman, J. L. (2000). Synaptic control of motoneuronal excitability. Physiol. Rev. 80, 767–852.

Pubmed Abstract | Pubmed Full Text

Selverston, A. I., Russell, D. F., and Miller, J. P. (1976). The stomatogastric nervous system: structure and function of a small neural network. Prog. Neurobiol. 7, 215–290.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Sharp, A., Abbott, L. F., and Marder, E. (1992). Artificial electrical synapses in oscillatory networks. J. Neurophysiol. 67, 1691–1694.

Pubmed Abstract | Pubmed Full Text

Sirois, J. E., Lynch, C. III, and Bayliss, D. A. (2002). Convergent and reciprocal modulation of a leak K+ current and I(h) by an inhalational anesthetic and neurotransmitters in rat brainstem motoneurones. J. Physiol. (Lond.) 541, 717–729.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Soto-Trevino, C., Rabbah, P., Marder, E., and Nadim, F. (2005). Computational model of electrically coupled, intrinsically distinct pacemaker neurons. J. Neurophysiol. 94, 590–604.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Swensen, A. M., and Marder, E. (2000). Multiple peptides converge to activate the same voltage-dependent current in a central pattern-generating circuit. J. Neurosci. 20, 6752–6759.

Pubmed Abstract | Pubmed Full Text

Tobin, A. E., and Calabrese, R. L. (2005). Myomodulin increases Ih and inhibits the NA/K pump to modulate bursting in leech heart interneurons. J. Neurophysiol. 94, 3938–3950.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Weber, M., Schmitt, A., Wischmeyer, E., and Doring, F. (2008). Excitability of pontine startle processing neurones is regulated by the two-pore-domain K+ channel TASK-3 coupled to 5-HT2C receptors. Eur. J. Neurosci. 28, 931–940.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Xu, F., Tse, F. W., and Tse, A. (2007). Pituitary adenylate cyclase-activating polypeptide (PACAP) stimulates the oxygen sensing type I (glomus) cells of rat carotid bodies via reduction of a background TASK-like K+ current. J. Neurochem. 101, 1284–1293.

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text