The effect of the initial distribution of labor-related property rights on the allocative efficiency of labor markets

Introduction: The Coase Theorem posits that frictionless markets efficiently allocate scarce resources as long as property rights are fully specified. Our empirical study investigates how the initial allocation of labor-related property rights influences the allocative efficiency in labor markets for skilled workers within a highly competitive environment—professional basketball. Specifically, we compare two regimes: one where employers can trade workers to other employers without the worker's consent, and another where workers are free agents, able to negotiate and move freely without their employer's consent.

Methods: We utilize the NBA as a “laboratory” to conduct our analysis, constructing a unique panel dataset that includes 3,132 player-season observations spanning 17 regular seasons from 2003/04 to 2019/20. To address our research question, we employ linear panel regression models to analyze the data.

Results and discussion: The findings reveal a decline in productivity among workers who transition to new employers as free agents, a phenomenon not observed among non-free agents. This observation suggests that allocative efficiency might be higher when workers are traded without their consent compared to when they exercise their autonomy as free agents. These findings highlight the significant impact that the initial distribution of labor-related property rights has on labor market efficiency, potentially challenging the assumptions of the Coase Theorem. However, the lack of a statistically significant difference in productivity changes between free agents and non-free agents moving to new employers prevents us from definitively rejecting the predictions of the Coase Theorem.

1 Introduction

In his seminal paper, Coase (1960) claims that frictionless markets efficiently allocate scarce resources as long as property rights are fully specified. He specifically argues that the initial allocation of these property rights is irrelevant. The famous “Coase Theorem” (CT) has a less renowned predecessor—Rottenberg's (1956) “Invariance Principle” (IP)—that specifically addresses this point. Rottenberg argues that workers (i.e., professional baseball players) will always be efficiently allocated regardless of whether the workers' freedom to choose their employer (team) is restricted (e.g., by a reserve clause) or not (i.e., free agency).¹ In both cases, workers will end up with the employer for which they are most productive. The logic behind the IP is straightforward: Without restrictions (free agency), the employer for which a worker is most productive can offer the highest salary, and the worker will end up signing a contract with this employer. If the employer can veto a transfer (i.e., the reserve clause), the employer must be induced to let the worker transfer. Since the employer for which the worker is most productive can always make an offer that exceeds the profits the current employer can realize by keeping the worker, under the reserve clause regime, workers will also transfer to where they are most productive.

While theoretically plausible, the empirical question of whether the CT in general and the IP in particular hold in the real world is still under scrutiny. Extensive literature exists that seeks to test the predictions of CT either experimentally or empirically (Zerbe and Medema, 2000; Medema, 2020). The experimental tests of the CT offer the possibility of imitating the conditions of complete property rights and zero (or low) transaction costs. Under such perfect “frictionless” conditions, the experiments provide significant support for the predictions of the CT (Hoffman and Spitzer, 1982, 1986). However, in more complex environments with non-negligible transaction costs and information asymmetries that resemble many real-world settings, the results from experiments are mixed (Harrison et al., 1987; Shogren, 1992; Croson and Johnston, 2000; Cherry et al., 2005).

While most CT tests have been conducted with a particular focus on the theorem's efficiency proposition, some case studies and econometric analyses have tested allocative outcomes under alternative legal regimes. For example, a stream of literature tested the farmer-rancher parable of Coase in the real world and found empirical support for the theorem's predictions that agents seem to cooperate to find efficient solutions (Ellickson, 1986; Vogel, 1987; Fischel, 1995; Hanley and Summer, 1995). Another popular approach to empirically test the theorem is to turn to the dynamics of divorce (Peters, 1986; Zelder, 1993; Wolfers, 2006; Chiappori et al., 2015), where scholars find admittedly weaker support for the CT.

Understandably, professional team sports provide a fertile testing ground for the IP (Fort et al., 2016). Specifically, sports economics scholars have empirically tested whether the IP holds by examining the impact of player ownership on player mobility (Krautmann and Oppenheimer, 1994; Hylan et al., 1996; Surdam, 2006; Lin and Chang, 2011), competitive balance (Szymanski, 2007), distribution of talent (Crooker et al., 2019), winning probabilities (Surdam, 2006), and player salaries (Sanderson and Siegfried, 1997). Despite the vast array of studies, no consensus has arisen on whether the IP holds. Specifically, no study examines the influence of initial property rights allocations on player productivity.

Whether frictionless markets efficiently allocate scarce resources is thus still an open question. To answer it, one needs to be able to measure allocative efficiency, which in turn requires comparing the productivity of resources in alternative settings. This comparison is a demanding task. In most industries, it is practically impossible to isolate and objectively compare the productivity of single resources like surgeons, lawyers, or sales agents across alternative uses under ceteris paribus conditions because one cannot control for all external factors that determine the final output.

To overcome the obstacles of measuring the influence of the initial distribution of labor-related property rights on allocative efficiency, we focus on an industry where workers' productivity is highly measurable and production occurs in a laboratory-like environment. Specifically, we compare the productivity of professional basketball players in the National Basketball Association (NBA) under two different property rights regimes. In the first regime, the employer has the right to send the worker to another employer (i.e., trade the player) without the worker's consent. In the second regime, the worker can freely negotiate with other employers and move to another employer (via free agency) without the consent of the original employer.

The NBA provides an ideal “laboratory” for measuring and comparing labor productivity (Arcidiacono et al., 2017).² Compared to surgeons, lawyers, or sales agents, professional basketball players usually “work” under standardized “laboratory” conditions. The size of the court, the height of the rim, the playing time, the weight and the diameter of the ball, etc., do not change from game to game. Moreover, the standardized rules enforced by the NBA for all games ensure that labor productivity can be objectively compared. Major “external” factors that might distort productivity are held constant and/or can be observed.³

In addition, several characteristics of the NBA limit the extent to which players behave opportunistically and strategically, e.g., by shirking (Berri and Krautmann, 2006). Various relevant stakeholders, such as team managers, owners, and fans, constantly observe and measure players' productivity. At the same time, the NBA is the top basketball league in the world from both a sporting and financial point of view. For example, player salaries are among the highest in all professional team sports (Statista, 2022), translating into intense competition between and even within teams. Whether a player receives a contract strongly depends on his productivity and effort. Therefore, we argue that the “basketball laboratory” setting allows us to define comprehensive and largely objective labor productivity measures.

We empirically test the IP and, by extension, the CT by comparing the productivity of workers (players) before and after moving to a new employer (team) under two different initial distributions of property rights. If the CT holds, we should not observe significant differences in labor productivity between labor-related property rights regimes. If the CT does not hold, we should observe labor productivity differences for workers who can freely negotiate with other employers and move to another employer without the consent of the original employer compared to those workers who are bound to their original employer.

Drawing on 3,132 player-season observations from the NBA, our analysis reveals a decline in players' productivity when transitioning to new teams as free agents, a trend not observed among non-free agents. This observation suggests that the allocation of players may be more efficient when they are traded without their consent rather than when players exercise their autonomy as free agents to negotiate and move to new teams. Such findings hint at a considerable influence of the initial distribution of labor-related property rights on the allocative efficiency of labor markets, posing a potential challenge to the CT and IP. Nevertheless, the lack of a statistically significant difference in productivity changes between free agents and non-free agents moving to new teams does not allow for a definitive rejection of the CT's and IP's predictions.

The remainder of the paper is structured as follows: Section 2 describes the data and the empirical model. Section 3 presents the results of the empirical investigation, and Section 4 concludes the paper.

2 Data and empirical model

2.1 Data and sample

To test whether the initial distribution of labor-related property rights influences the allocative efficiency of labor markets, we build a unique panel dataset consisting of 8,078 player-season observations from the NBA, spanning 17 regular seasons from 2003/04 to 2019/20 and containing a total of 1,766 players and 33 teams. We use data from several publicly accessible data sources: Rod Fort's Sports Business pages for the player and team productivity measures; ESPN and the official NBA website for player and team characteristics; and Spotrac, which is based on official NBA data sources, for information on players' contract situations.⁴

We undertake several data adjustments to isolate the impact of different property rights regimes on player productivity by excluding groups of observations for various factors. There is substantial overlap among these excluded observations when considering these four reasons.

First, even though most contractual changes happen in the offseason, they can also appear during the regular season. Since we only have productivity data for one player-team combination per season, we exclude 1,791 observations where a player's contractual situation changed within a given season. Similarly, we exclude 1,571 player-season observations when a player experienced a contractual change (within and between seasons) other than moving to a new team without the consent of the existing team (free agent) or being traded to a new team without his explicit consent (non-free agent). Examples include layoffs, sending players to minor leagues, and unique contractual settings (e.g., for young players). These observations represent unique contexts that are not covered in our research question.

Second, to ensure an accurate comparison, we excluded 1,442 observations of players who played <21 games (out of 82) in a given season and had an average court time of <3.3 min (out of 48) per game. These observations represented the lowest 5% of the sample in terms of games played and average minutes played per game. This exclusion allows us to focus on members of each team with an ample amount of productivity data.⁵

Third, we exclude 1,679 observations of players with <4 years of experience in the NBA during the observation period. Again, the reason is that we want to focus on established players with sufficient skills whose employment prospects in the league are favorable.

Fourth, since we compare the productivity of a given player between seasons, we exclude 2,171 observations for players who are in their first season and players who missed entire seasons (e.g., due to injury). Our final sample consists of 3,132 unique observations, corresponding to 686 different players. Our results are robust against variations in the mentioned exclusions (see Section 3.4).

2.2 Variables and measures

This paper focuses on the impact of different property rights regimes (free agent vs. non-free agent) on player productivity. We identify this impact using dummy variables for players who become free agents, players who move to a new team as free and non-free agents, players who stay with their current team after becoming free agents, and players who remain with their current team under an ongoing contract (reference group).⁶ Table 1 gives a brief overview of the variables used in our models.

Table 1

Table 1. Variable overview.

The primary dependent variable is player productivity. To measure a player's productivity, we follow Berri (1999), Berri and Schmidt (2010), Price et al. (2010), and Berri et al. (2011), who employ Wins Produced (WP) as the productivity measure. WP connects a player's productivity to team outcome and is regarded as the best objective measure of a player's productivity in a given season (Berri and Bradbury, 2010). It is based on observable and measurable statistics of a player, his team, and the opposing teams. WP explains over 90% of the variation in team wins and is relatively stable from season to season (Berri and Schmidt, 2010).⁷

Independent variables for each player include their contractual status (free agent vs. non-free agent), minutes played in the previous season as a proxy for general (or average) productivity,⁸ experience in the NBA, tenure with their team (or in case of moving to a new team with the last team), teammates' productivity, team turnover, and fixed effects for teams and seasons.

2.3 Empirical model

To empirically examine our research question, we estimate linear panel regression models with WP as the dependent variable. We estimate the effect of a contractual change on productivity using the following specifications: First, we investigate the impact of becoming a free agent (Equation 1). Second, we distinguish between free agents and non-free agents who move to a new team (Equation 2). Third, we consider two groups of free agents: those who move to a new team and those who stay with their previous team (Equation 3). To take advantage of the panel structure of our data, we use a fixed effects linear panel regression model (FE), as shown in Equations (1, 2).⁹ One significant advantage of this model is that it allows us to capture unobserved time-invariant individual-specific effects, thereby attenuating a potential omitted variable bias (Cameron and Trivedi, 2005).¹⁰

$\begin{array}{llll}W{P}_{it}& =& X_{i,t}^{{}^{\prime }}\theta +\beta F{A}_{i,t}+{\alpha }_i+T_t+{\epsilon }_{i,t}& (1)\end{array}$

$\begin{array}{llll}W{P}_{it}& =& X_{i,t}^{{}^{\prime }}\theta +{\beta }_{1}F{A}_{i,t}+{\beta }_{2}NONF{A}_{i,t}+{\alpha }_i+T_t+{\epsilon }_{i,t}& (2)\end{array}$

$\begin{array}{l}W{P}_{it}={X^{\prime }}_{i,t}\theta +{\beta }_{1}MOVEF{A}_{i,t}+{\beta }_{2}STAYF{A}_{i,t}\\ +{\beta }_{3}NONF{A}_{i,t}+{\alpha }_i+T_t+{\epsilon }_{i,t}& (3)\end{array}$

$X_{i,t}^{{}^{\prime }}$ is a vector of the control variables described in Table 1 including team fixed effects. α_i are player-specific intercepts (player fixed effects) that capture unobserved time-invariant player characteristics. T_i are time fixed effects. θ, β, β₁, β₂, and β₃ are the coefficients (vectors) to be estimated, while our main interest is on β, β₁, β₂, and β₃. ε_{i, t} is the usual independently and identically distributed (iid) error component. We use robust standard errors to deal with heteroscedasticity and potentially clustered standard errors.¹¹

3 Results

This section presents our results and is structured as follows: First, we summarize and provide information about our sample data. Second, we report the main results of our empirical investigation. Third, we offer supplementary analyses to better understand the underlying mechanisms that drive our results. Finally, we report several robustness analyses.

3.1 Summary statistics

Table 2 presents the descriptive statistics for all main variables included in the analysis.

Table 2

Table 2. Summary statistics (n = 3,132).

The table shows that around 20% of all player-season observations consist of free agents (FA), whereas 13% are moving free agents (MOVE FA) and 7% are free agents who stayed with their previous team (STAY FA). On the other hand, 8% move as non-free agents (NON FA). In total, 21% of player-season observations moved to a new team. Therefore, 72% of season-player observations stay with their current team under an ongoing contract. The average WP is 4.24. Players in the sample averaged 1,757 min on the court in the previous season (L_MINUTES) and have 5.8 years of experience in the NBA (EXP). They stay 2.6 seasons with a given team (TENURE). The average WP of all other players on a given player's team (AV TEAM WP) amounts to 2.6, which is substantially smaller than the average of the dependent variable. This difference is because the team average considers all players, while in our model, we only focus on those players who participate in more than a quarter of the team's games and a minimum number of minutes per game. Finally, on average, 4.9 new players join a team at the beginning of each season (TURNOVER).¹²

3.2 Main estimates

In this subsection, we report our main estimates in Table 3. We proceed in three steps: First, we examine how player productivity (WP) changes for free agents compared to all non-free agents (Model 1). Second, we compare two groups of contractual changes: all free agents and non-free agents being allocated to new teams (Model 2). Third, we rerun the regression but control for three contractual statuses of players: free agents moving to a new team; free agents staying with their given team; and non-free agents being allocated to a new team (Model 3).

Table 3

Table 3. Results of fixed effects panel regression models.

In the first specification, we observe a significant decline in player productivity for free agents (FA). Specifically, the variable FA is highly significant with a coefficient of −0.37, which means that becoming a free agent corresponds to a decrease in WP of 0.37 when compared to the reference group of non-free agents. This change signifies a 9% reduction in productivity relative to the sample's average WP of 4.24.

In the second specification, we differentiate between free agents and non-free agents reallocated to new teams to assess the effect of the initial property rights distribution on allocative efficiency in terms of productivity. At first glance, contrary to the predictions of the CT, our findings suggest differences in player productivity across property rights regimes following team changes. Specifically, for free agents, productivity shows a significant decrease of 0.403, translating to a nearly 10% reduction from the sample's mean WP. In contrast, the change in productivity for non-free agents moving to new teams is not statistically significant. Yet, a direct comparison of the coefficients for free agents (FA) and non-free agents (NON FA) reveals no statistical disparity, indicating only marginal evidence, if any, for challenging the CT's predictions.

In the third specification, we additionally divide free agents in those who move to a new team (MOVE FA) and those who stay with their given team under a new contract (STAY FA). We find that the negative effect on WP for free agents according to the second specification, is driven by free agents who choose a new team. Compared to the mean of WP in our sample, free agent productivity declines by 13% after they move to a new team. In contrast, we find no statistically significant effect for free agents who stay with their current team. Again, however, the coefficients of free agents who move to a new team (MOVE FA) and players who get traded to a new team (NON FA) do not statistically differ from one another.

Our findings can be summarized as follows: Becoming a free agent typically correlates with a decrease in player productivity, but this decline is observed explicitly in free agents who choose to join a new team. Conversely, free agents who renew contracts with their existing teams and non-free agents who are transferred to new teams do not experience a drop in productivity. This pattern initially suggests that players might be allocated more efficiently under scenarios where they are traded without their consent, compared to situations where they have the autonomy to negotiate and transition freely to new teams. Such outcomes imply a significant impact of the initial distribution of labor-related property rights on the allocative efficiency of labor markets, potentially challenging the CT and IP. However, the absence of a statistically significant difference in productivity changes between (moving) free agents and (moving) non-free agents prevents us from conclusively refuting the predictions of the CT and IP. Supplementary analyses further reinforce these observations, suggesting nuanced dynamics at play in the allocative efficiency of labor markets within the context examined.

3.3 Supplemental analyses

In this subsection, we report additional results in three ways: First, we analyze a different dependent variable (minutes played) to shed light on potential mechanisms behind our main results. Second, we distinguish subsamples regarding players' current average career productivity as a proxy for skill level. Third, we analyze the persistence of the effects beyond one season.

3.3.1 Additional productivity-related measure

We consider an additional productivity-related measure to better understand the impact of a contractual change on player productivity. We use minutes played in a given season as a dependent variable (MINUTES). This variable reflects how intensively coaches deploy their players. We assume that coaches deploy players primarily based on their overall productivity (WP) to maximize team wins throughout the season. In other words, players with a high WP will play more minutes than players with a low WP. Inefficient allocation of playing time to players results in a competitive disadvantage against other teams, which is associated with negative sporting performance and, subsequently, has negative financial consequences. We therefore hypothesize that if a player experiences a drop in productivity (e.g., after moving to a new team), he will get less playing time.

The empirical model we estimate to test this hypothesis is very similar to the previous models for WP. Table 4 displays the results.

Table 4

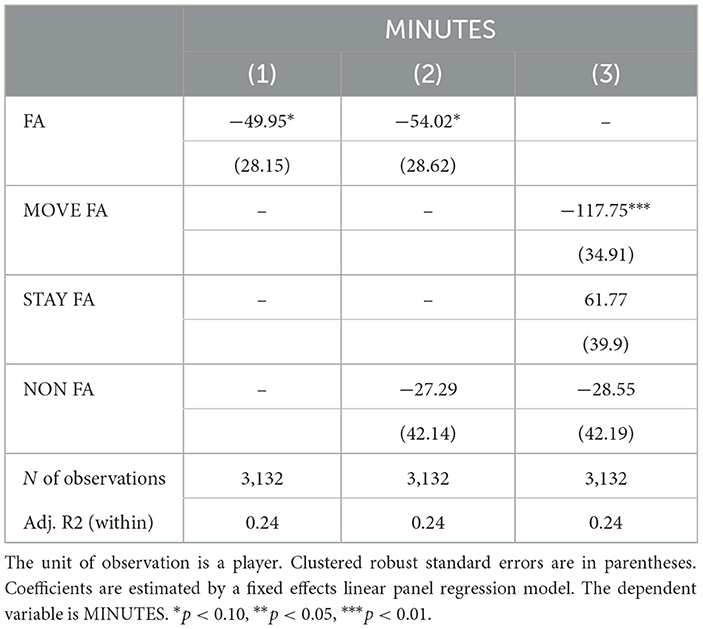
Table 4. Extract of results of fixed effects panel regression models with MINUTES as the dependent variable.

The result resembles those for WP. Specifically, we find that free agents are used for significantly fewer minutes. Free agents who move to a new team, whose minutes on the court drop by around 120 min per season, drive this result. Considering the sample average minutes per game of ~25, this decline in playtime corresponds to the equivalent of four to five games. We do not observe such a drop in productivity for non-free agents and free agents who resign from their given team. This finding is in line with our main results. To efficiently allocate court time among players, coaches reduce the court time of players who experience a drop in productivity after moving to a new team. In addition, however, the coefficients of players who become free agents (FA) and players who get traded to a new team (NON FA) do not significantly differ in model 2. We therefore come to a similar conclusion regarding the predictions of the CT and the IP as in our main results.

3.3.2 Subsample analysis

We now examine whether our results depend on a player's skill level and, thus, his productivity. More skilled and productive players may have different motives and opportunities for moving to a new team. A player's skill level may also determine how fast he can adjust to playing with new teammates. In Table 5, we estimate our models separately for the upper and lower half of the distribution of players' current average career WP (until t-1).¹³ Again, we examine how player productivity WP changes after becoming a free agent (Model 1), for free agents and non-free agents who are allocated to new teams (Model 2), and when additionally dividing free agents into those who move to a new team and those who do not (Model 3).

Table 5

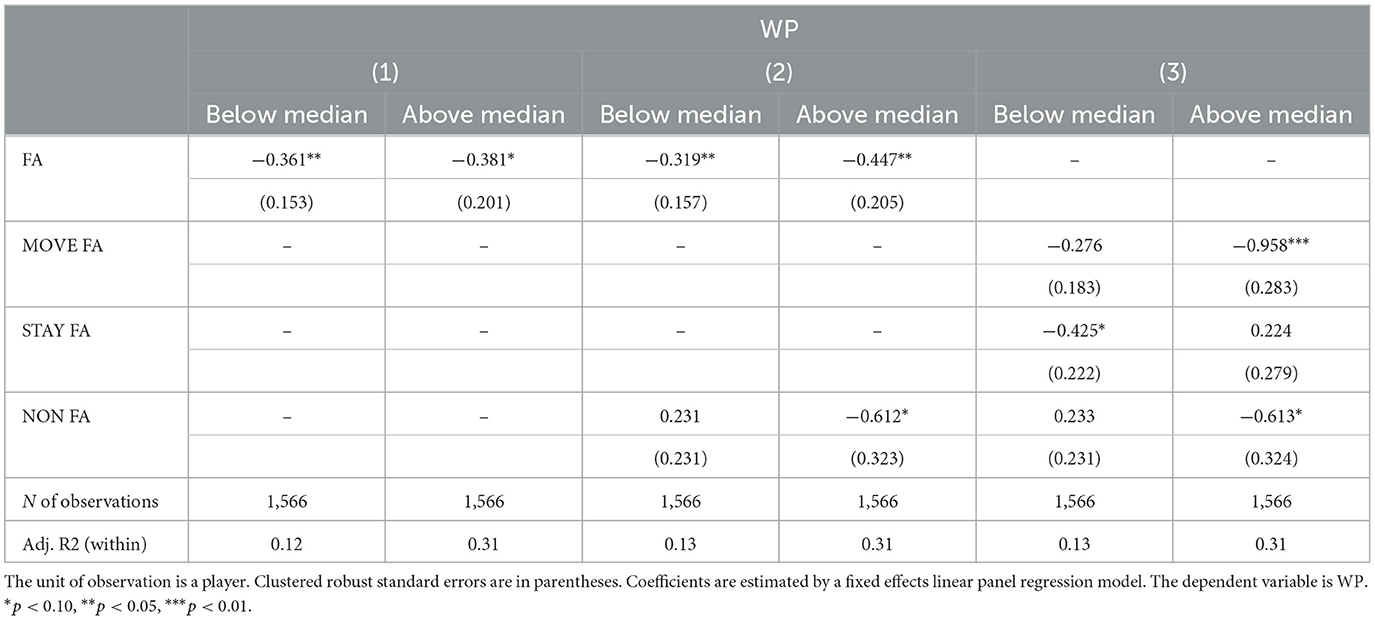
Table 5. Extract of results of fixed effects panel regression models for subsamples regarding players' current average career productivity.

When only considering free agents, we observe that the players' productivity declines almost identically for below- and above-median players. The productivity of below-median players is not affected by moving to a new team. Distinguishing between free and non-free agents allocated to a new team reveals that, in deviation from the main results, the productivity of above-median non-free agents decreases after a trade. When we separately consider free agents who move to a new team and free agents who stay with their given team, we find that productivity decreases for above-median moving free agents only, while for staying free agents, a productivity drop can only be observed for below-median players.

In sum, the skill distribution as proxied by current average career productivity does not lead to different conclusions. For the upper half of the skill distribution, when comparing free agents to non-free agents allocated to a new team, it becomes evident that the CT and IP predictions hold. For below-median players, however, we find some evidence that the change in performance differs between free agents and non-free agents allocated to new teams.¹⁴

3.3.3 Persistence

The observed decline in productivity after free agents moving to a new team could, for example, result from short-term difficulties that players experience when adjusting to a new team and environment. In this case, we would expect the adverse effects on productivity to diminish over time, which would support the predictions of the CT and the IP.

In Table 6, we examine the potential persistence of the productivity drop by re-estimating our WP model in season t+1, i.e., in the second season after the possible move to a new team, and in season t+2, i.e., the third season after becoming a free agent and/or the possible move to a new team.¹⁵

Table 6

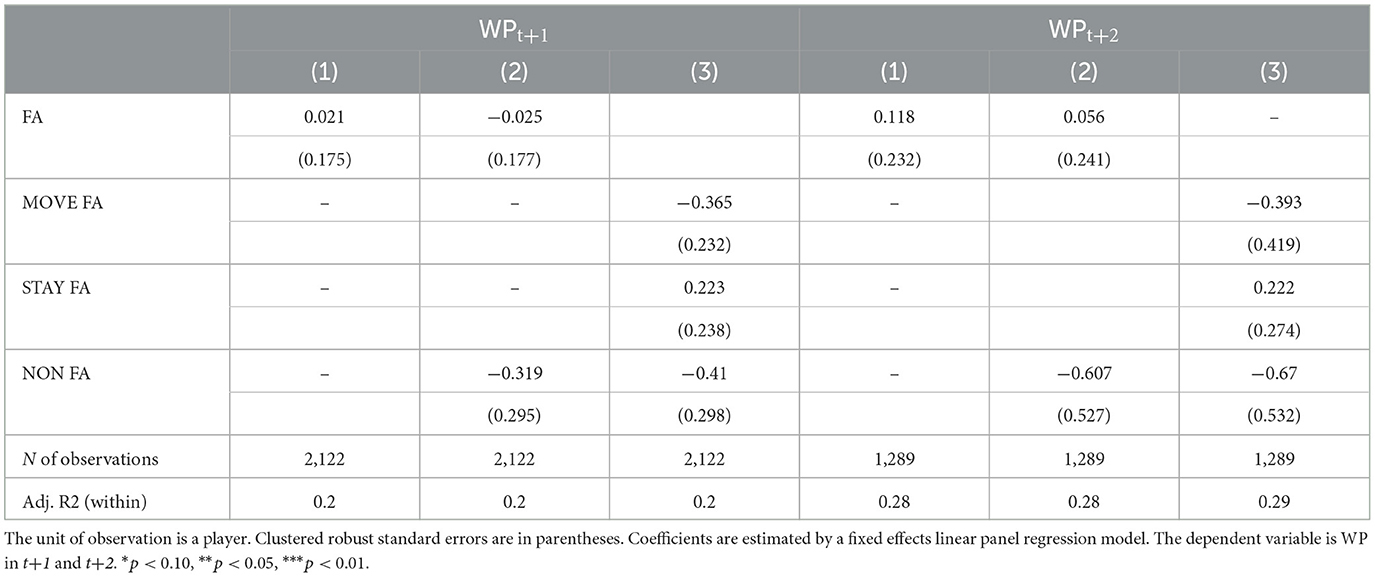
Table 6. Extract of results of fixed effects panel regression models for WP two and three seasons after players became free agents and/or moved to a new team as free and non-free agents.

Results in Table 6 indicate that none of the effects found in our main models seem to persist over time. Although the coefficient estimates are of similar magnitude, they are not statistically significant. This result underpins the above findings and additionally supports consistency with the CT and IP predictions. In other words, we find no evidence that the adverse short-term productivity effects of free agents will prevail over time. We conclude that a longer-term perspective further supports our finding and that the short term indeed could result from difficulties in adjusting for players who move to a new team.

3.4 Robustness analysis

3.4.1 Potential biases

Several endogeneity issues regarding the move to a new team could bias our results. First, teams usually trade players when they underperform. If the player improves after the trade, there is no way to tell whether the improvement results from the trade or a so-called regression to the mean (Nevill et al., 2004). Second, the prospect of free agency might affect productivity. Toward the end of their contract, players are incentivized to increase their efforts to strengthen their negotiation position for a new contract. Consequently, an adverse effect of moving to a new team on productivity could result from reduced effort (i.e., “shirking”) after a new contract has been signed (Berri and Krautmann, 2006). In the following, we try different approaches to attenuate the potential biases.

First, using simple paired samples t-tests, we compare players' WP in the last season before moving to a new team (t-1) with their WP in the previous season (t-2). For non-free agents, we find no effect. Free agents have a slightly higher performance in their season before they become free agents. This effect, while significant on the 10%-level only, would support our findings in favor of the CT and the IP.

Second, we estimate our models (including dummy variables) for the season before a player becomes a free agent or gets traded. As Table A1 shows, there is a significant change in WP for players before they become free agents, but not for non-free agents. We therefore have evidence that an upcoming change in the contractual status is related to the superior productivity of free agents. However, we do not find inferior productivity for non-free agents before a trade.

Third, we adopt a simplified version of a method developed by Freyaldenhoven et al. (2019) to correct pre-trends in panel event-study designs. In the first step, we regress WP on the player and team-season fixed effects.¹⁶ We use the fitted values ${\widehat{WP}}_t$ of this regression to calculate the change of WP against the predicted values of the previous season, $\Delta WP=W{P}_t-{\widehat{WP}}_{t-1}$. In the second step, we apply our models with ΔWP as the dependent variable and a slightly adjusted set of control variables.¹⁷ The idea behind this approach is to use some average value for each player as a basis for the potential productivity change after moving to a new team. Thereby, temporary effects that lead to under- or overperformance are (at least partially) attenuated.¹⁸ Results are shown in Table A2. The coefficients of the variables of interest are slightly smaller than in the above results, which does not lead to a different conclusion.

Finally, we test an instrumental variable (IV) approach for the variables of interest to cope with the potential endogeneity issues discussed above. The main challenge in an IV approach is to find solid and valid instruments for the potentially endogenous variables (Angrist and Pischke, 2009). We devise our own instruments since we are unaware of IV approaches in related papers. We try different specifications with different instruments that are all supposed to cause exogenous variation in the potentially endogenous variables.¹⁹ Using a standard two-stage least square approach (2SLS), we observe similar results as above.²⁰

In summary, the above robustness analyses support our main findings.

3.4.2 Additional robustness checks

We perform different additional robustness checks to validate our results. First, we further restrict the sample in the following ways: We only consider players who stay at least two seasons with their team before moving to a new team; we exclude players who play under a rookie contract, which usually lasts 2–4 years and contains specific restrictions on player movement; we do not include players in their last 2 years of their career, because there could be different incentives (“end of career effects”); and we exclude peculiar events such as a new team joining the league²¹ or the lockout season 2011/2012.²² Our results do not change qualitatively when using more restricted samples. Second, we try larger sample sizes by considering players with less court presence and fewer games played and by relaxing the restriction that players must be at least 4 years in the NBA. In other words, we consider less essential and less established players. Again, the basic pattern of results does not change qualitatively. Third, although incomplete, we have data on players who resign a contract with their given team before becoming free agents. Excluding these players from the sample does not alter our results qualitatively. Fourth, our results do not depend on how we correct standard errors. Similarly, our results are robust against excluding season and/or team fixed effects as control variables, even though each of these effects matters. Fourth, we exclude the variable L_MINUTES as a proxy for players' skills. Therefore, we aim to avoid potential bias due to lagged variables strongly correlated with the lagged dependent variable (see text footnote⁸). Estimating our models without L_MINUTES (and its square term) does not change the results qualitatively. In short, our results are robust against various sample definitions and model specifications.

4 Discussion and conclusion

This paper empirically tests the allocative efficiency of labor markets under different property rights regimes. Specifically, we compare workers' productivity before and after moving to a new employer under two different initial distributions of property rights, thereby testing the predictions of the Coase Theorem (CT) (Coase, 1960) and the Invariance Principle (IP) (Rottenberg, 1956).

While individual worker productivity is not accessible in most industries, professional sports provide a rigorous laboratory setting for measuring and comparing personal productivity data (Fonti et al., 2022). Indeed, due to the unusual granularity of sports data, many scholars use sports data to test and develop theories and explore relevant phenomena not restricted to the sports context (Bothner et al., 2007; Moliterno and Wiersema, 2007; Gould and Winter, 2009; Guryan et al., 2009; Day et al., 2012; Arcidiacono et al., 2017; Stuart and Moore, 2017). In this paper, we use the NBA as a “laboratory” for our analysis and build a unique panel dataset consisting of 3,132 player-season observations from the NBA, spanning 17 regular seasons from 2003/04 to 2019/20 and containing a total of 686 players and 33 teams.

Our findings indicate a nuanced response to different property rights regimes. Specifically, we observe a decline in productivity among workers (players) who have the initial right to negotiate freely and move to another employer (team). Intriguingly, there appears to be no such adverse effect on productivity in scenarios where employers (teams) can send their workers to another employer without the workers' consent. Moreover, we examine whether our results depend on a worker's skill level. More skilled and, therefore, more productive workers may have different motives and opportunities for moving to a new employer. Our results indicate that workers of above-median skill levels exhibit a discernible decline in productivity upon moving to a new employer as free agents. This result contrasts with free agents of below-median skill levels, whose productivity remains unaffected, suggesting that the impact of free agency on productivity is not uniform across the skill spectrum.

The overall trend of free agents showing a decrease in productivity upon joining a new team, as opposed to traded players who do not exhibit a similar decline, hints at the possibility that the initial allocation of labor-related property rights influences the allocative efficiency of labor markets, suggesting that the CT and the IP may not apply in this scenario. However, the absence of a statistically significant difference in productivity changes between free agents and non-free agents transitioning to new teams precludes a categorical dismissal of the predictions made by the CT and the IP.

Several factors can contribute to the observed phenomenon where free agents often see a dip in productivity upon moving to a new team, a trend not mirrored by traded players. At the heart of this issue is the significant role played by insider information and the strategic timing of contract renewals. Managers and scouts possess detailed knowledge of their players' skills and potential growth. Such comprehensive insights enable teams to make well-informed decisions about which players to keep and which to allow to enter free agency, often leading to a scenario where those deemed less likely to maintain or improve performance are let go. Hence, clubs tend to actively extend contracts for their key performers to secure their valuable contributions for the future. Conversely, players whose current performance might not warrant an immediate extension are more likely to end up in free agency. This inherent selection bias indicates that players transitioning to free agency might, on average, be viewed by their original clubs as having lesser prospects for future productivity.

The analysis of team decision-making closely ties into how the distribution of match surplus influences player performance. In professional sports, the concept of match surplus extends beyond simple win percentages, encompassing a broad spectrum of objectives for both clubs and individual players. For clubs, objectives may include maximizing financial returns through merchandise sales, ticket sales, and sponsorships, all of which can be significantly enhanced by the presence of high-profile players. For players, factors such as contract stability, cultural fit with the team, and quality of life in a particular city all contribute to their overall satisfaction and utility. However, our model posits that contract status does not directly affect changes in player performance, except through the choice of club.

The division of the match surplus, especially under the lens of free agency, introduces a critical layer of analysis. The prevailing hypothesis is that owners of professional sports teams exercise monopsony power whenever possible. However, according to Krautmann et al. (2009), club owners find it more challenging to extract a surplus as players' negotiating power increases. The advent of free agency bolsters a player's bargaining power, potentially leading to a more equitable distribution of the surplus in their favor, often reflected in higher salaries or more favorable contract terms. This shift provides a compelling context for investigating how variations in financial security and bargaining power affect player performance. The literature suggests that increased financial security could lead to reduced performance pressure, potentially diminishing on-court performance (“shirking”). Berri and Krautmann (2006) test this hypothesis using data from the NBA with a similar dependent variable as in the present paper. However, they find no evidence for shirking and argue that opportunistic behavior in professional basketball is prevented because team managers, owners, teammates, and fans constantly observe (and measure) players' productivity. In addition, contracts include vital incentive clauses that link compensation to individual and team productivity. In addition, a shirker might develop a bad reputation, lowering the likelihood of getting a lucrative contract in the future (and thereby losing related sources of income, such as advertising contracts), and thus, a shirking player takes a considerable risk regarding career income.

In sum, our research has explored the CT and the IP in the context of individual player productivity in professional sports, particularly through examining different property rights regimes. This approach not only broadens the existing body of literature but also applies the CT to a novel context since previous studies have primarily focused on outcomes such as the competitive balance of the league (Maxcy and Mondello, 2006; Szymanski, 2007; Lee and Fort, 2012).

Our study, while comprehensive, needs to acknowledge certain limitations in its research design. First, despite relying on WP, widely regarded as the most recognized and accepted measure of NBA player productivity (Berri, 1999; Berri and Schmidt, 2010; Price et al., 2010; Berri et al., 2011), we acknowledge that this measure is not without flaws. For example, this measure does only take on-court performance into account. Off-court performance, such as the social charisma of a player, which also highly affects a team's financial success, is not considered. A second limitation is the complexity of the contractual framework in the NBA and the lack of more detailed information on player contracts. In particular, contract duration or the number of teams interested in a free agent would have added exciting insights to our analysis. A third limitation concerns the inability to include trades and moves of players that occurred within a season. A fourth limitation arises from the challenge that a player's underperformance or overperformance could be influenced by various factors such as expectations, peer effects, coaching styles, and play styles—elements that are difficult to observe and quantify in our study.

There are several promising avenues for future research on this topic. For example, a more detailed analysis of the mechanisms driving our results could be conducted using more granular data and/or combining a quantitative analysis with a qualitative study. Examining the monetary effects (such as salaries and revenues) of moving to a new employer would also be interesting. Another possibility is to investigate whether there is a difference in performance after moving to a new team between players who received “exorbitant” contracts (relative to perceived market value) and players with “normal” contracts. Additionally, it would be valuable to determine whether the negative performance effect is also observed for free agents who move to a new team with the goal of winning the NBA championship. Many veteran NBA players reportedly prioritize winning titles over earning higher salaries.

In summary, this research contributes to our knowledge of the link between the initial distribution of labor-related property rights and the efficiency of labor markets. Although our results point to a significant influence of the initial distribution of labor-related property rights on the efficiency of labor markets we cannot refute the predictions of the CT and the IP in the context of individual productivity in a highly competitive labor market such as professional basketball. Further research is necessary to fully comprehend the mechanisms driving our findings and evaluate their potential generalizability to other settings.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material. Further inquiries can be directed to the corresponding author.

Author contributions

HD: Writing—original draft, Writing—review & editing. ML: Writing—original draft, Writing—review & editing. JO: Data curation, Writing—review & editing. PW: Data curation, Formal analysis, Software, Writing—original draft, Writing—review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. Open access funding by University of Lausanne.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^In North American professional sports, the reserve clause was part of a player contract and gave club owners an exclusive option to renew unilaterally the contracts of their players binding them to their clubs until release, retirement, or a trade. In the late 1970s, the reserve clause was replaced by free agency. A free agent is a player who is not under contract at any specific team and thus is eligible to sign with other employers.

2. ^Several other scholars have used sports as a laboratory in labor economics (Bollinger and Hotchkiss, 2003; Hendricks et al., 2003; Gould and Winter, 2009; Guryan et al., 2009; Peeters et al., 2022).

3. ^Although sports offer a relatively controlled setting for evaluating the theoretical predictions of our model, it is important to note the complexities involved. The potential impacts of team dynamics, coaching strategies, and peer interactions on player productivity are aspects that pose significant challenges in terms of quantification and accurate modeling.

4. ^Rod Fort's Sports Business page: https://sites.google.com/site/rodswebpages/codes (accessed May 26, 2021); ESPN: http://insider.espn.com/nba:hollinger/statistics (accessed October 10, 2021); Official NBA website: http://stats.nba.com/stats (accessed February 3, 2022); Spotrac: https://www.spotrac.com/nba/free-agents/ufa/ (accessed May 26, 2021).

5. ^In our robustness checks, we expanded the sample size by including players with less court time and fewer games played, but our results remained consistent.

6. ^In addition, we can identify players who forego free agency by extending their contracts early. Since we only have incomplete data on such players, we do not consider them as an own category. If we treat them as a separate group, however, we do not find any effect on WP.

7. ^We prefer WP to a more standardized measure, such as Wins Produced per 48 minutes—WP48 (Berri and Schmidt, 2010). The latter reflects a minute-based version of WP. A high WP48, however, does not necessarily translate into a high WP. The reason is that we assume WP48 to be decreasing in playing time beyond a certain player-specific threshold because basketball is a highly exhausting activity. For example, players with relatively low WP may only be given a few minutes on the court by their coaches and thus still could exhibit a high WP48. In other words, a coach presumably is much more interested in a player's WP than in his WP48. Therefore, we argue that WP is the appropriate and relevant measure for player productivity in the present context.

8. ^We cannot use lagged or aggregated values of the dependent variable as measure for players' general (or average) productivity, since in linear panel models this potentially leads to endogeneity issues (Cameron and Trivedi, 2005).

9. ^We use Stata's xtreg package to estimate our models (StataCorp, 2017).

10. ^We test the FE specification against a pooled OLS panel regression (POLS) and against a random effects specification (RE). We reject POLS using a standard F-Test for joint irrelevance of player fixed effects. Likewise, we reject the RE specification using a Hausman test. Therefore, if the model is correctly specified, coefficient estimation using a FE specification will be consistent (Cameron and Trivedi, 2005).

11. ^Formal tests of heteroskedasticity reject the null hypothesis of homoskedasticity in the error terms. We therefore use robust standard errors and cluster them at the player level. However, results are robust against different ways of correcting standard errors (see Section 3.4).

12. ^Descriptive statistics show some variation across different categories. For instance, free agents and players who move to new teams as non-free agents are generally comparable in performance, whereas players under ongoing contracts typically have higher WP and log more minutes on the court. Detailed results can be provided upon request. Importantly, our use of a panel design with player fixed effects ensures that these group differences do not confound the results, as we are comparing players' WP across two seasons.

13. ^The average values of the upper and lower half of the distribution of the current average career WP are 1.26 (below median) and 6.83 (above median). The effects remain similar if we use different variables to measure players past or general productivity.

14. ^In addition to the panel regressions, we ran quantile regressions with different fixed effects specification. Due to the limited interpretability of conditional quantile regressions (see e.g., Angrist and Pischke, 2009) we also estimated unconditional quantile regression models (see e.g., Firpo et al., 2009). Both approaches lead to results that do not contradict our findings. Results are available upon request.

15. ^A word of caution: Focusing on seasons t+1 and t+2 leads to a substantial drop in the sample size since we then must focus on players who remain with their (new) team for two and three seasons. Therefore, we see that the coefficients in Table 6 are estimated less precisely than in our main models.

16. ^We try different specifications. All of them lead to similar results.

17. ^The variables AV TEAM WP and VAR TEAM WP (see Table 1) have been adjusted to reflect changes between two seasons. Results, however, are robust against alternative definitions of controls.

18. ^The Pearson correlation coefficient between WP and $\widehat{WP}$ amounts to 0.8 in our sample.

19. ^For MOVE FA and STAY FA, we use eligibility as FA, i.e., the end of an ongoing contract, as the main instrument, an approach used by Abadie (2003) for the participation of workers in 401(k) savings plans. We instrument NON FA with variables indicating how many additional players a team traded in a given season, a player's “movement history” (previous trades and previous moves in general), and whether a player is in his last contract year or not. Some of these variables are used by Cymrot and Dunlevy (1987) to model the decision of baseball players to move to a new team.

20. ^A word of caution: Even if standard post-IV tests (e.g., F-Test of the first stage, tests for under-identification, over-identification, and weak instruments) do not indicate apparent problems, the potential lack of convincing instruments could bias results. We, therefore, consider the IV results merely as complementary evidence. Results are available upon request.

21. ^If a new team joins the NBA, it can pick players from existing teams under some conditions (the so-called expansion draft). Since these players cannot choose whether they want to join the new team or not, we treat these observations as non-free agents.

22. ^In this season, only 80% of games were played because club owners and the players labor union (National Basketball Players Association NBPA) could not agree upon a new deal about, e.g., revenue sharing between owners and players. During the negotiations that lasted until December 2011, no sign-ups of new players nor trades were allowed.

References

Abadie, A. (2003). Semiparametric instrumental variable estimation of treatment response models. J. Econom. 113, 231–263. doi: 10.1016/S0304-4076(02)00201-4

PubMed Abstract | Crossref Full Text | Google Scholar

Angrist, J. D., and Pischke, J.-S. (2009). Mostly Harmless Econometrics: An Empiricist's Companion. Princeton, NJ: Princeton University Press.

Google Scholar

Arcidiacono, P., Kinsler, J., and Price, J. (2017). Productivity spillovers in team production: evidence from professional basketball. J. Labor Econ. 35, 191–225. doi: 10.1086/687529

Crossref Full Text | Google Scholar

Berri, D. J. (1999). Who is ‘most valuable'? Measuring the player's production of wins in the National Basketball Association. Manag. Decis. Econ. 20, 411–427. doi: 10.1002/1099-1468(199912)20:8<411::AID-MDE957>3.0.CO;2-G

Crossref Full Text | Google Scholar

Berri, D. J., and Bradbury, J. C. (2010). Working in the land of the metricians. J. Sports Econ. 11, 29–47. doi: 10.1177/1527002509354891

Crossref Full Text | Google Scholar

Berri, D. J., Brook, S. L., and Fenn, A. J. (2011). From college to the pros: predicting the NBA amateur player draft. J. Prod. Analy. 35, 25–35. doi: 10.1007/s11123-010-0187-x

Crossref Full Text | Google Scholar

Berri, D. J., and Krautmann, A. C. (2006). Shirking on the court: testing for the incentive effects of guaranteed pay. Econ. Inq. 44, 536–546. doi: 10.1093/ei/cbj033

Crossref Full Text | Google Scholar

Berri, D. J., and Schmidt, M. (2010). Stumbling on Wins: Two Economists Explore the Pitfalls on the Road to Victory in Professional Sports. Edinburgh: Financial Times Press.

Google Scholar

Bollinger, C. R., and Hotchkiss, J. L. (2003). The upside potential of hiring risky workers: evidence from the baseball industry. J. Labor Econ. 21, 923–944. doi: 10.1086/377027

Crossref Full Text | Google Scholar

Bothner, M. S., Kang, J., and Stuart, T. E. (2007). Competitive crowding and risk taking in a tournament: evidence from NASCAR racing. Adm. Sci. Q. 52, 208–247. doi: 10.2189/asqu.52.2.208

PubMed Abstract | Crossref Full Text | Google Scholar

Cameron, A. C., and Trivedi, P. K. (2005). Microeconometrics: Methods and Applications. Cambridge: Cambridge University Press.

Google Scholar

Cherry, T. L., Kroll, S., and Shogren, J. F. (2005). The impact of endowment heterogeneity and origin on public good contributions: evidence from the lab. J. Econ. Behav. Org. 57, 357–365. doi: 10.1016/j.jebo.2003.11.010

Crossref Full Text | Google Scholar

Chiappori, P.-A., Iyigun, M., and Weiss, Y. (2015). The Becker–Coase theorem reconsidered. J. Demogr. Econ. 81, 157–177. doi: 10.1017/dem.2015.3

Crossref Full Text | Google Scholar

Coase, R. (1960). The problem of social cost. J. Law Econ. 3, 1–44. doi: 10.1086/466560

Crossref Full Text | Google Scholar

Crooker, J. R., Azevedo, C. D., and Fenn, A. J. (2019). Empirical shifts in Major League Baseball roster management: effects of the 1976 labor agreement. J. Econ. Insight 45, 57–83. Available online at: https://journalofeconomicinsight.com/index.php/joei/article/view/1165

Google Scholar

Croson, R., and Johnston, J. S. (2000). Experimental results on bargaining under alternatives property rights regimes. J, Law Econ. Org. 16, 50–73. doi: 10.1093/jleo/16.1.50

Crossref Full Text | Google Scholar

Cymrot, D. J., and Dunlevy, J. A. (1987). Are free agents perspicacious peregrinators? Rev. Econ. Stat. 69, 50–58. doi: 10.2307/1937900

Crossref Full Text | Google Scholar

Day, D. V., Gordon, S., and Fink, C. (2012). The sporting life: exploring organizations through the lens of sport. Acad. Manag. Ann. 6, 397–433. doi: 10.5465/19416520.2012.678697

Crossref Full Text | Google Scholar

Ellickson, R. C. (1986). Of Coase and cattle: dispute resolution among neighbors in Shasta County. Stanford Law Rev. 38, 623–687. doi: 10.2307/1228561

Crossref Full Text | Google Scholar

Firpo, S., Fortin, N. M., and Lemieux, T. (2009). Unconditional quantile regressions. Econometrica 77, 953–973. doi: 10.3982/ECTA6822

Crossref Full Text | Google Scholar

Fischel, W. A. (1995). Regulatory Takings: Law, Economics, and Politics. Cambridge, MA: Harvard University Press.

Google Scholar

Fonti, F., Ross, J.-M., and Aversa, P. (2022). Using sports data to advance management research: a review and a guide for future studies. J. Manage. 49, 325–362. doi: 10.1177/01492063221117525

Crossref Full Text | Google Scholar

Fort, R., Maxcy, J., and Diehl, M. (2016). Uncertainty by regulation: Rottenberg's invariance principle. Res. Econ. 70, 454–467. doi: 10.1016/j.rie.2016.06.004

Crossref Full Text | Google Scholar

Freyaldenhoven, S., Hansen, C., and Shapiro, J. M. (2019). Pre-event trends in the panel event-study design. Am. Econ. Rev. 109, 3307–3338. doi: 10.1257/aer.20180609

Crossref Full Text | Google Scholar

Gould, E. D., and Winter, E. (2009). Interactions between workers and the technology of production: evidence from professional baseball. Rev. Econ. Stat. 91, 188–200. doi: 10.1162/rest.91.1.188

Crossref Full Text | Google Scholar

Guryan, J., Kroft, K., and Notowidigdo, M. J. (2009). Peer effects in the workplace: evidence from random groupings in professional golf tournaments. Am. Econ. J. 1, 34–68. doi: 10.1257/app.1.4.34

PubMed Abstract | Crossref Full Text | Google Scholar

Hanley, N., and Summer, C. (1995). Bargaining over common property resources: applying the Coase theorem to Red Deer in the Scottish Highlands. J. Environ. Manage. 43, 87–95. doi: 10.1016/S0301-4797(95)90337-2

Crossref Full Text | Google Scholar

Harrison, G. W., Hoffman, E., Rutstrom, E., and Spitzer, M. L. (1987). Coasian solutions to the externality problem in experimental markets. Econ. J. 97, 388–402. doi: 10.2307/2232885

Crossref Full Text | Google Scholar

Hendricks, W., DeBrock, L., and Koenker, R. (2003). Uncertainty, hiring, and subsequent performance: the NFL draft. J. Labor Econ. 21, 857–886. doi: 10.1086/377025

Crossref Full Text | Google Scholar

Hoffman, E., and Spitzer, M. L. (1982). The Coase theorem: some experimental tests. J. Law Econ. 25, 73–98. doi: 10.1086/467008

Crossref Full Text | Google Scholar

Hoffman, E., and Spitzer, M. L. (1986). Experimental tests of the Coase theorem with large bargaining groups. J. Legal Stud. 15, 149–171. doi: 10.1086/467807

Crossref Full Text | Google Scholar

Hylan, T., Lage, M., and Treglia, M. (1996). The Coase theorem, free agency, and major league baseball: a panel study of pitcher mobility from 1961 to 1992. South. Econ. J. 62, 1029–1042. doi: 10.2307/1060946

Crossref Full Text | Google Scholar

Krautmann, A. C., and Oppenheimer, M. (1994). Free agency and the allocation of labor in Major League Baseball. Manag. Decis. Econ. 15, 459–469. doi: 10.1002/mde.4090150508

Crossref Full Text | Google Scholar

Krautmann, A. C., Von Allmen, P., and Berri, D. (2009). The underpayment of restricted players in North American sports leagues. Int. J. Sport Finan. 4:161.

Google Scholar

Lee, Y. H., and Fort, R. (2012). Competitive balance: time series lessons from the English premier league. Scott. J. Polit. Econ. 59, 266–282. doi: 10.1111/j.1467-9485.2012.00580.x

Crossref Full Text | Google Scholar

Lin, M. J., and Chang, C. C. (2011). Testing Coase theorem: the case of free agency in NBA. Appl. Econ. 43, 2545–2558. doi: 10.1080/00036840903299722

Crossref Full Text | Google Scholar

Maxcy, J., and Mondello, M. (2006). The impact of free agency on competitive balance in North American professional team sports leagues. J. Sport. Manage. 20, 345–365. doi: 10.1123/jsm.20.3.345

Crossref Full Text | Google Scholar

Medema, S. G. (2020). The Coase theorem at sixty. J. Econ. Lit. 58, 1045–1128. doi: 10.1257/jel.20191060

Crossref Full Text | Google Scholar

Moliterno, T. P., and Wiersema, M. F. (2007). Firm performance, rent appropriation, and the strategic resource divestment capability. Strat. Manag. J. 28, 1065–1087. doi: 10.1002/smj.630

Crossref Full Text | Google Scholar

Nevill, A., Holder, R., Atkinson, G., and Copas, J. (2004). The dangers of reporting spurious regression to the mean. J. Sports Sci. 22, 800–802. doi: 10.1080/02640410410001675487

PubMed Abstract | Crossref Full Text | Google Scholar

Peeters, T., Szymanski, S., and Terviö, M. (2022). The survival of mediocre superstars in the labor market. J. Law Econ. Org. 38, 840–888. doi: 10.1093/jleo/ewab035

Crossref Full Text | Google Scholar

Peters, H. E. (1986). Marriage and divorce: Informational constraints and private contracting. Am. Econ. Rev. 76, 437–454.

Google Scholar

Price, J., Soebbing, B. P., Berri, D. J., and Humphreys, B. R. (2010). Tournament incentives, league policy, and NBA team performance revisited. J. Sports Econ. 11, 117–135. doi: 10.1177/1527002510363103

Crossref Full Text | Google Scholar

Rottenberg, S. (1956). The baseball players' labor market. J. Polit. Econ. 64, 242–258. doi: 10.1086/257790

Crossref Full Text | Google Scholar

Sanderson, A. R., and Siegfried, J. J. (1997). The implications of athlete freedom to contract: Lessons from North America. Econ. Aff. 17, 7–12. doi: 10.1111/1468-0270.00035

Crossref Full Text | Google Scholar

Shogren, J. F. (1992). An experiment on Coasian bargaining over ex ante lotteries and ex post rewards. J. Econ. Behav. Org. 17, 153–169. doi: 10.1016/0167-2681(92)90084-O

Crossref Full Text | Google Scholar

StataCorp (2017). Stata 15 Base Reference Manual. College Station, TX: Stata Press.

Google Scholar

Statista (2022). Average Sports Salaries by League 2019/20. Available online at: https://www.statista.com/statistics/675120/average-sports-salaries-by-league/ (accessed April 5, 2024).

Google Scholar

Stuart, H. C., and Moore, C. (2017). Shady characters: the implications of illicit organizational roles for resilient team performance. Acad. Manag. J. 60, 1963–1985. doi: 10.5465/amj.2014.0512

Crossref Full Text | Google Scholar

Surdam, D. G. (2006). The Coase theorem and player movement in Major League Baseball. J. Sports Econ. 7, 201–221. doi: 10.1177/1527002504266227

Crossref Full Text | Google Scholar

Szymanski, S. (2007). The champions league and the Coase theorem. Scott. J. Polit. Econ. 41, 355–373. doi: 10.1111/j.1467-9485.2007.00419.x

Crossref Full Text | Google Scholar

Vogel, K. R. (1987). The Coase theorem and California animal trespass law. J. Legal Stud. 16, 149–187. doi: 10.1086/467827

Crossref Full Text | Google Scholar

Wolfers, J. (2006). Did unilateral divorce laws raise divorce rates? A reconciliation and new results. Am. Econ. Rev. 96, 1802–1820. doi: 10.1257/aer.96.5.1802

Crossref Full Text | Google Scholar

Zelder, M. (1993). Inefficient dissolutions as a consequence of public goods: the case of no-fault divorce. J. Legal Stud. 22, 503–520. doi: 10.1086/468174

Crossref Full Text | Google Scholar

Zerbe, R., and Medema, S. (2000). “The Coase theorem,” in The Encyclopedia of Law and Economics, eds. B. Bouckaert, and G. De Geest (Northampton, MA: Edward Elgar Publishing), 836–892.

Google Scholar

Appendix

Table A1

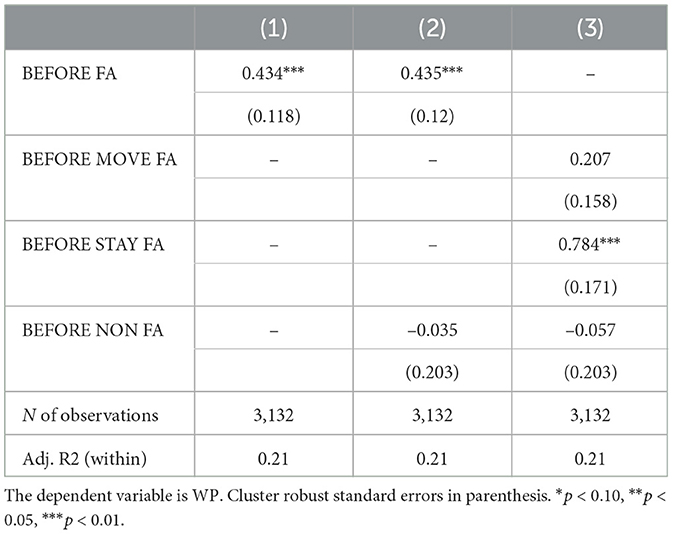
Table A1. Extract of results of fixed effects panel regression models capturing the potential change in productivity before players become free agents and/or move to a new team as free and non–free agents.

Table A2

Table A2. Extract of results of fixed effects panel regression models with ΔWP against the predicted lagged value of WP ($\widehat{WP}$) as dependent variable.