Norm focusing and losses—Evidence of ultimatum game experiments

Introduction: Human decision-making pertaining to gains compared to those pertaining losses is shown to be quite different. However, mixed evidence is provided regarding the effect on the decision-makers' prosocial behaviors; that is, losses are shown to either increase or decrease prosocial behaviors. In this context, the effect of social norms on observed behavior can play a crucial role.

Methods: To examine this aspect in more detail, we conducted incentivized ultimatum game experiments and analyzed data from three treatments, the control treatments (without specific norm focus), and two different norm-focus treatments (“average behavior” treatment and “self-interested behavior” treatment). In total, 550 participants took part in our experiment. Basically, we found no significant difference between the division of gains and losses in the “control” and “self-interested behavior” treatments.

Results and discussion: However, we found such a difference in the “average behavior” treatment. In addition, we found that inducing a norm focus leads to less variance in proposers' behavior and a greater concentration of their demands around the induced norm in the “average behavior” treatment. In contrast, we found a higher variance in proposers' behavior in the “self-interested behavior” treatment. In terms of responders' behaviors, we observed a tendency toward a higher frequency of responders' rejections in the loss domain compared to the gains domain.

1 Introduction

The energy crisis faced by Germany and other European countries in 2022 is a prominent example, among many others, of a situation in which scarce resources must be distributed. Based on this specific scenario, a number of further distribution issues that public institutions must tackle can be derived: (1) The gas resource itself must be allocated; specifically, it is necessary to plan and prioritize how to change the distribution if there is insufficient gas to meet the demand; and (2) the increased costs for acquiring the gas must also be distributed. In this context, a debate has arisen among the interest groups on how the increased costs should be distributed fairly among the various actors. This example illustrates that, in reality, both gains and losses need to be divided. It also demonstrates that several influential factors are affecting the solution to such an allocation problem.

Of course, this problem is by no means new to sociology. It rather starts from the individuals' fundamental problem of social order as it has been stated first by Hobbes (1996[1651]), and has been at the core of sociology in textbooks (e.g., Abels, 2019), handbooks (e.g., Furedi, 2013) as much as in corresponding contemporary research (e.g., Etzrodt, 2020). Yet, though there are myriads of texts and studies on the topic in sociology and beyond, hardly any of them deals with the situation Hobbes mentions—a war of all against all—where only losses (of bodily integrity or even life) are at stake. This holds especially when it comes to the analysis of social interaction (as Hobbes did it). An early exception to this is Raub and Snijders (1997). They use a Prisoner's Dilemma as the interaction model. We make one step back and use the more simple ultimatum game as an interaction model. Furthermore, we explore the normative and moral solution, respectively for the Hobbes problem (cf. e.g., Etzrodt, 2020). Against this backdrop, our study contributes to the exploration of whether people distribute gains and losses differently, as well as which (different) impacts social norms might have in the context of allocating gains or losses. We analyze these aspects using incentivized laboratory experiments.

Since Kahneman and Tversky published their Prospect Theory in 1979, loss aversion has become a prominent research topic in different contexts (e.g., Kahneman and Tversky, 1979; Tversky and Kahneman, 1992; Yechiam and Hochman, 2013a; Gächter et al., 2022). Furthermore, loss aversion has been studied in the context of the distribution of losses through ultimatum game experiments (Buchan et al., 2005; Lusk and Hudson, 2010; Neumann et al., 2018a,b). However, the literature studying ultimatum game experiments in the loss domain is sparse.

In this regard, we contribute to two streams of a lately growing literature: (1) (experimental) studies investigating behavioral differences when people must divide gains compared to situations in which they must divide losses (e.g., Buchan et al., 2005; Lusk and Hudson, 2010; Zhou and Wu, 2011; Baquero et al., 2013; Neumann et al., 2017; Thunström, 2019); and (2) studies that apply and adapt norm theory to such allocation decisions (e.g., Bicchieri, 2006, 2017; Neumann et al., 2017). In this study, we integrate both aspects to assess the influence of norm focusing on the distribution of losses and compare the observed results with those derived in a corresponding gains setting.

In a previous study (Windrich et al., 2022), we allowed participants to play dictator games in the gains and in the loss domain with norm focusing, and we examined (1) the difference in sharing losses compared to sharing gains and (2) the focus on the game-theoretic solution and the focus on prior behavior. We found a significant difference in sharing losses compared to sharing gains in this manner, in that subjects were more self-interested when sharing losses. Only by focusing on the previous average behavior treatment did the norm focusing treatment lead to a significant effect, whereas no effect was found for the self-interested focusing. With the current study, we transferred the research questions into the context of ultimatum games. Compared to the dictator game, the ultimatum game has two-sided bargaining power that encompasses asymmetry. Consequently, with the dictator game experiments, we analyzed dictators' decisions on how to distribute losses and gains.

In this study, we let participants play an ultimatum game in the gains and loss domains with and without norm focus. The ultimatum game in the loss domain corresponds to the ultimatum game over gains, whereby instead of a gain, the proposer must decide on the sharing of a loss between themselves and a responder. The responder can then accept or reject the offer. In the case of rejection, both the proposer and the responder receive a loss of −10 EUR. In the case of acceptance, both the proposer and the responder receive the proposed division of the amount that was realized. According to our dictator game study (Windrich et al., 2022), we implemented the ultimatum games over gains as well as the game over losses in three different treatments, with each treatment played in both the gains and the loss domain. In the (1) “Control treatment”, we analyzed the behavior without an additional norm focus. However, in the (2) “Average behavior” treatment, we extended the ultimatum game instruction by showing the previous average behavior to the participants. In the (3) “Self-interested” treatment, we extended the instructions by showing the participants an equilibrium solution (i.e., the self-interested solution in which the proposer proposes the smallest possible amount and the receiver accepts it because they receive more than they would if they would reject it). In this regard, we are interested in (1) the potential differences between ultimatum bargaining behavior in the gains and loss domains and (2) the robustness of the egalitarian norm.

Previous literature has shown that in the gains domain, an equal split is a well-established norm (Güth and Kocher, 2014). Based on this, we tested whether focusing on the average behavior from previous ultimatum game experiments leads to different behavior in the gains and loss domains. Compared to the results from the dictator game experiments of Windrich et al. (2022), the rejection option makes the norm of equal sharing stable in the loss domain as well. In this regard, we investigated the robustness of usual behavior against a norm that is applied. Because the ultimatum game has two-sided bargaining power, we investigated if the equal split is more robust against norm inducing. We also contributed to answering the following questions: Does a norm over preceding behavior influence behavior in the ultimatum game? Also, does a difference in proposer behavior emerge between gains and losses when a norm is induced?

Basically, we found no significant difference between the division of gains and losses in either the reference experiments or the “Self-interested behavior” treatment; only in the “Average behavior” treatment did we find a difference in the division of losses compared to the division of gains. We did not find significant differences between the distribution of gains and losses in the “Control” treatment. However, the behavior differs in the treatment in which participants receive information (i.e., a norm focus) regarding the average behavior in previous ultimatum game experiments. Although there is no significant difference between the proposers' average demands for the various norm foci, there is a significant difference in standard deviations between the different norm foci treatments. The proposers' demands are centered around the induced previous proposers' demands in the “Average behavior” treatment. Therefore, the standard deviation is significantly smaller compared to the “Control” treatment. In contrast, for the “Self-interested behavior” treatment, the standard deviation is significantly larger than the standard deviation of the “Control” treatment. The results hold for both the gains and loss domains. Our analysis shows that the receiver behavior of rejection in the ultimatum game shows no significant difference between the norm foci, although it mainly appears in the loss domain with a small frequency.

2 Theoretical background and related literature

2.1 Ultimatum games in the gains and loss domains

Güth et al. first published the ultimatum game in 1982. In this game, the proposer can split a certain amount between themselves and a responder. After the responder receives the information about the payoffs that the proposer and responder will receive, they decide to reject or accept the proposal (Güth et al., 1982; Güth and Kocher, 2014). If the responder accepts the proposer's offer, both the proposer and the responder receive the amount proposed by the proposer. If the responder rejects the offer, both the proposer and responder receive nothing. The proposer's offer can be a decision influenced by fairness or by fear of an unfair offer being rejected; the proposers' average offer is between 40 and 50% (Güth and Kocher, 2014).

Many researchers have studied ultimatum game experiments in the gains domain. For example, time pressure (Sutter et al., 2003), gender differences (García-Gallego et al., 2012), and stake size effects (Andersen et al., 2011) have been subject to prior research in ultimatum game experiments (Güth and Kocher, 2014).

Previous research on the distribution of losses in the loss domain is scarce. For example, Buchan et al. (2005) showed that proposers' offers and responders' demands in ultimatum games are higher over losses than over gains. Further investigating those questions in three different countries (the United States, China, and Japan), they found consistent results. Meanwhile, Lusk and Hudson (2010) showed that proposers demand more for themselves and therefore make more aggressive offers when bargaining over losses than over gains. Baquero et al. (2013) found a significant generosity effect for bargaining in the loss domain compared to the gains domain. In a recent study, Neumann et al. (2017) found that proposers make higher offers in the loss domain than in the gains domain. However, one finding that comes to light when studying the literature is that the previous research is inconclusive, whereby various approaches in the experimental design have been implemented. For example, Neumann et al. (2017) used the strategic vector method (Rauhut and Winter, 2010). Furthermore, recent research has shown that the question of how to distribute losses compared to gains can also be investigated with various experimental games, such as the trust game with negative endowments (Füllbrunn and Vyrastekova, 2023). In Füllbrunn and Vyrastekova (2023), one main finding was that trust is higher in the loss context than in the gains context in the way that the loss context leads to an incentive toward trust. The results underline the difference between sharing losses and sharing gains. Nontheless, this research focuses on different aspects.

From the previous literature, we derive the first hypothesis as follows:

(H1) In ultimatum games over gains and losses, the demands in the loss domain differ from the demands in the gains domain.

2.2 Norm theory in the context of the ultimatum game

Norm following is not a new concept, neither generally to describe human behavior in decision-making situations, nor especially in sociology. To structure the concept of norm following, Bicchieri (2006, 2017) defined social norms in her norm theory as the preference to follow and expect that others will also follow.

The literature distinguishes between descriptive and injunctive norms (Cialdini et al., 1991). Descriptive norms involve the perception of what a common pattern of behavior is in a given situation (Cialdini et al., 1991), whereas injunctive norms involve behavior that is normatively expected by others (Cialdini et al., 1991).

In ultimatum games, according to Güth and Kocher (2014), “proposers are either aware of the responder's willingness to reject unfair offers or guided by own fairness concerns when offering sizable or even fair shares for Y” (p. 398). The structure of the game induces the proposer's expectation that the responder demands a fair split. The proposer has either internalized a norm of fair giving (intrinsic fairness based on morality) or gives a fair split in fear of punishment by the responder (strategic fairness).

Empirical findings from ultimatum game experiments have shown that the equal split is a common behavioral type in these experiments (Güth and Kocher, 2014). The rejection rate increases when the proposers' offer is below 20% (Güth and Kocher, 2014).

The standard game theoretical prediction for the ultimatum game is the subgame perfect equilibrium (Selten, 1965, 1975), where the proposer offers the minimum possible amount and the responder accepts it. However, as Binmore (2010) argued, there is a continuum of Nash equilibria for the ultimatum game, and there is no reasonable argument that only the subgame perfect equilibrium can be used to empirically predict how subjects will play. Binmore (2010) further stated that subjects face an equilibrium selection problem regarding which of the many Nash equilibria they should coordinate. Social norms (e.g., dividing fairly) serve as one attempt to reach a solution. Often, empirically, it can be seen that subjects behave according to the egalitarian norm so that the equal split is chosen (Güth and Kocher, 2014).

According to Chen et al. (2017) and Windrich et al. (2022), we intervened in this equilibrium selection problem by focusing participants on other possible solutions. This means that we asked subjects (i.e., proposers) to freely indicate their offer. However, in our first treatment, we focused the subjects on the average offer of other proposers (in prior experiments) by telling them what the average offer was. This focus should coordinate players on the Nash equilibrium nearest to the focal point of the average offer. In addition, this focus on the average offer induces a descriptive norm of what is usually done in the game. We know from the experimental literature that empirical expectations of what others do are a better predictor for behavior than normative expectations of what should be done when the social norm demands an egalitarian offer (cf. Bicchieri and Xiao, 2009). Hence, we expect proposers to orientate their offers around the given focus on the average offer. Our corresponding second hypothesis reads as follows:

(H2) Focusing on “Average behavior” leads to a concentration of demands around the focal point of the previous average proposal.¹

In a second treatment, we focused proposers on the subgame perfect equilibrium of offering the smallest possible amount. We knew from the empirical literature on ultimatum games (Güth and Kocher, 2014) that this Nash equilibrium seldom holds as a good prediction for behavior. By focusing participants on it, we made it more focal for the proposer and more acceptable for the responder. Therefore, our third hypothesis reads as follows:

(H3) Focusing on “Self-interested behavior” leads to a dispersion of the standard deviation of proposers' demands and a decrease in fairness.

2.3 Responders' behavior

Part of the ultimatum game analysis is the responders' behavior toward the proposed amount. In the ultimatum game, the responder has two options, namely rejecting the offer or accepting the offer. Previous literature on the analysis of responder behavior has shown that offer acceptance decreases with increasing proposer demand under an average offer of 40–50%, with the responders' acceptance approaching zero for offers below 20% (Güth and Kocher, 2014). As described in Section 2.2., a proposer's offer is driven by their own fairness considerations or by the awareness of the responder's willingness to reject the offer. The ultimatum game over losses leads to a costly rejection for the responder and the proposer. In the ultimatum game over gains, if the responder rejects the proposer's offer, both receive nothing. However, in the ultimatum game over losses, the responder and the proposer have to pay an amount (−10 EUR) if the responder rejects the offer. Neumann et al. (2017) found that responders are more frequently willing to accept higher proposer demands in the loss domain than in the gains domain (Neumann et al., 2017). Nevertheless, the ultimatum game design differs from our design as it uses the strategy vector method (Rauhut and Winter, 2010). In an early study, Camerer et al. (1993) found that the proposers' average offer does not differ between the gains and loss domains but that rejections are more frequent in the loss domain compared to the gains domain (Camerer et al., 1993). In a more recent study, the responders' behavior was analyzed by implementing a design that asymmetrically endowed the responder in the loss domain while the proposer is in the gains domain. With the strategic vector method (Rauhut and Winter, 2010), the modified ultimatum game, particularly the responders' behavior, was analyzed (Neumann et al., 2018b). Neumann et al. (2018b) found that the responder's demand is guided strongly by their desire to break even. The previous literature has implied that responders' behavior can differ between the gains and loss domains. Nevertheless, the fact that rejection by the responder is costly has two implications. First, the rejection frequency can differ between the gains and loss domains. Second, the proposer may anticipate and realize that the rejection is costly for the responder and that this could impact their offer. We herein analyze the responders' rejection frequency and compare it, in particular, between the gains and loss domains.

3 Methods and treatments

In this paper, we analyzed the behavior observed in two versions of the ultimatum game: (1) an ultimatum game over gains and (2) an ultimatum game over losses. We implemented the games as a one-shot game without role uncertainty, meaning that half the participants played the role of the proposer in all treatments, whereas the other half played the role of the responder.² We also ensured that each participant could only take part in one treatment, meaning that we conducted our experiments with perfect stranger matching. Both games (i.e., the ultimatum game over gains and the ultimatum game over losses) used monetary incentives and, thus, were not played hypothetically.

3.1 Game description and domains

3.1.1 Ultimatum game over gains

As proposers, the players were asked to distribute a pie of size (s = 10 EUR) by choosing how much of the pie, a (in 50 cent increments), the proposer wanted to keep for themselves and, thus, how much the responders would receive, s−a. Then, the responder had to decide whether they accepted or rejected the proposer's offer. If the responder accepted the offer, the proposer received a and the responder received s−a. Otherwise, both players received nothing for the ultimatum game. In the case of rejection, both the proposer and the responder received an outcome of 0 EUR. The sessions in the gains domain were played in one part. Also, in the case of the gains domain, the participants played the ultimatum game experiment and received their payoff following the experiment.

3.1.2 Ultimatum game over losses

In the corresponding game over losses, the proposers were asked to distribute a pie of size s = −10 EUR by, again, choosing how much of the pie, −a (in −50 cent increments), the proposer was willing to bear themselves and, thus, how much the responders would have to bear s−a. If the responder accepted the offer, the suggested allocation was implemented. If, however, the responder rejected the offer, the players each incurred a loss of −10.00 EUR (see Table 1). Regardless of the decisions made in the experiment, all participants received a show-up payment of 5 EUR.

Table 1

Table 1. Payoff structure of the ultimatum game in the gains and loss domains.

3.2 Implementation of losses in the laboratory

We decided to conduct our study using incentivized rather than hypothetical experiments. Previous literature has provided various approaches to implement losses in the laboratory in this regard. According to our reference treatment—reported in Neumann et al. (2018a), we used the prepaid mechanism with real monetary payoffs to induce losses.³ As a consequence, the sessions in the loss domain were divided into two subsessions. We invited the participants in the loss treatments to the laboratory 2 weeks before playing the ultimatum game experiments (Rosenboim and Shavit, 2012). In the first part of the sessions, the participants received 15 EUR to compensate for their potential losses in the ultimatum game experiments. In the second part, the participants played the ultimatum game and had to pay back their losses. The prepaid mechanism has two main advantages: (1) Due to mental accounting, participants feel that they are experiencing a real loss,⁴ and (2) this overcomes the “house-money-effect”⁵ (Thaler and Johnson, 1990) because participants feel they own the money they receive. It is important that enough time has passed between the two parts of the sessions. We kept it constant at 2 weeks in advance for all sessions, which was considered sufficient time. To our knowledge, this is the best way to implement monetary losses in the laboratory, corresponding to Rosenboim and Shavit (2012).

3.3 Treatments

We are interested in (1) the potential differences between behavior in the gains and loss domains and (2) the robustness of the egalitarian norm. Regarding (1), we implemented all treatments in both domains (i.e., gains and losses, respectively). With regard to (2), we studied the behavior in three different treatments: the control treatment, the average behavior treatment, and the self-interested behavior treatment.

3.3.1 “Control” treatment

In Neumann et al. (2018a), we published the results of an experimental comparison of behavior in a standard ultimatum game over gains with that in a corresponding ultimatum game over losses. In this study, we focused on the behavior in the games without further manipulation; that is, we did not implement explicit norm foci. The obtained results from Neumann et al. (2018a) serve as reference data and are, hereinafter, referred to as the “Control” treatment. The participants received similar instructions in all treatments. However, we operationalized the norm focus by adding sentences to the instructions of the “Control” treatment. This means that we instructed the participants in all treatments of the ultimatum game in the gains domain (i.e., the “control”, the “average behavior”, and the “self-interested behavior” treatment) using the same instructions, supplemented by sentences in case of the two latter treatments. The same was true for the loss domain. In the following, we explain this procedure in more detail.

We use the results of the “Control” treatment to perform the comparison of the behavior observed in the two different treatments, which we describe in the following.

3.3.2 “Average behavior” treatment

In the “Average behavior” treatments, the participants played the game as described above (i.e., either the ultimatum game over gains or the ultimatum game over losses, and in either the proposer's or the receiver's role). However, to implement a specific norm focus, we integrated one additional sentence into the instructions. Specifically, we informed the participants what the average offer of the proposers in previous (comparable) ultimatum games had been. More precisely, we stated the results from the “Control” treatments, reported as treatment T1 (ultimatum game over gains) and treatment T3 (ultimatum game over losses) in Neumann et al. (2018a). In the corresponding sentences, Player 1 refers to the proposer and Player 2 refers to the responder. Thus, the corresponding sentences read as follows: For the ultimatum gain over gains, “In a series of experiments that took place last year, Player 1 claimed an average share of €5.33.”⁶ For the ultimate game over losses, “In a series of experiments that took place last year, the player 1s bore on average –€4.29 of the loss.”⁷

3.3.3 “Self-interested behavior” treatment

In the “self-interested behavior” treatment, we focused the players on one of the subgame perfect Nash equilibria of the ultimatum game (Selten, 1965; Güth et al., 1982). Only one sentence was added at the end of the instruction, as follows: “A rational Player 1 who wants to maximize their payoff would, in this game, offer Player 2 the smallest possible amount greater than zero. A rational Player 2 who wants to maximize their payoff would accept any amount greater than zero.”⁸ Because we used an increment of 0.50 EUR, the subgame perfect solution of the ultimatum game experiments was to propose 0.50 EUR to the responder. This solution maximizes the payoff for Player 1, and a rational player, Player 2, accepts this offer because they receive more than the 0 EUR they would receive if they rejected the offer.

The corresponding sentence for the “Self-interested behavior” treatments in the loss domain was as follows: “A rational Player 1 who wants to maximize their payoff would, in this game, offer Player 2 the largest possible loss that is less than the full loss. A rational Player 2 who wants to maximize their payoff would accept any loss that is better than the full loss of −10 €.”⁹ This is the corresponding offer that maximizes the payoff of Player 1, and a rational player, Player 2, accepts this offer because they bear a smaller loss than the loss of 10 EUR they would have received had they rejected the offer.

3.4 Experimental procedure and sample description

We conducted our incentivized ultimatum game experiments in two laboratories: 236 participants in the Magdeburg Experimental Laboratory of Economic Research (MaXLab) and 314 participants in the Leipzig Experimental Laboratory for Social Science (LEx). Experiments were implemented using z-Tree (Fischbacher, 2007), and participants were recruited using hroot (Bock et al., 2014) from the subject pools of MaXLab and LEx. Both subject pools have similar structures in terms of subjects' characteristics. The majority of subjects in both pools were university-enrolled students from different faculties.

In total, subjects (N = 550) participated in the ultimatum game experiments, with 312 female and 238 male participants. We recruited participants who were mostly students (87%) with a predominance toward human science and social science. The age of participants varies from 18 to 82 (mean= 26.9, SD = 8.1).

Based on the payoff structure in Neumann et al. (2018a), Table 1 shows the payoffs of the ultimatum game experiments in the gains and loss domains.

In Section 4, we describe and analyze the results of our experimental investigations.

4 Results

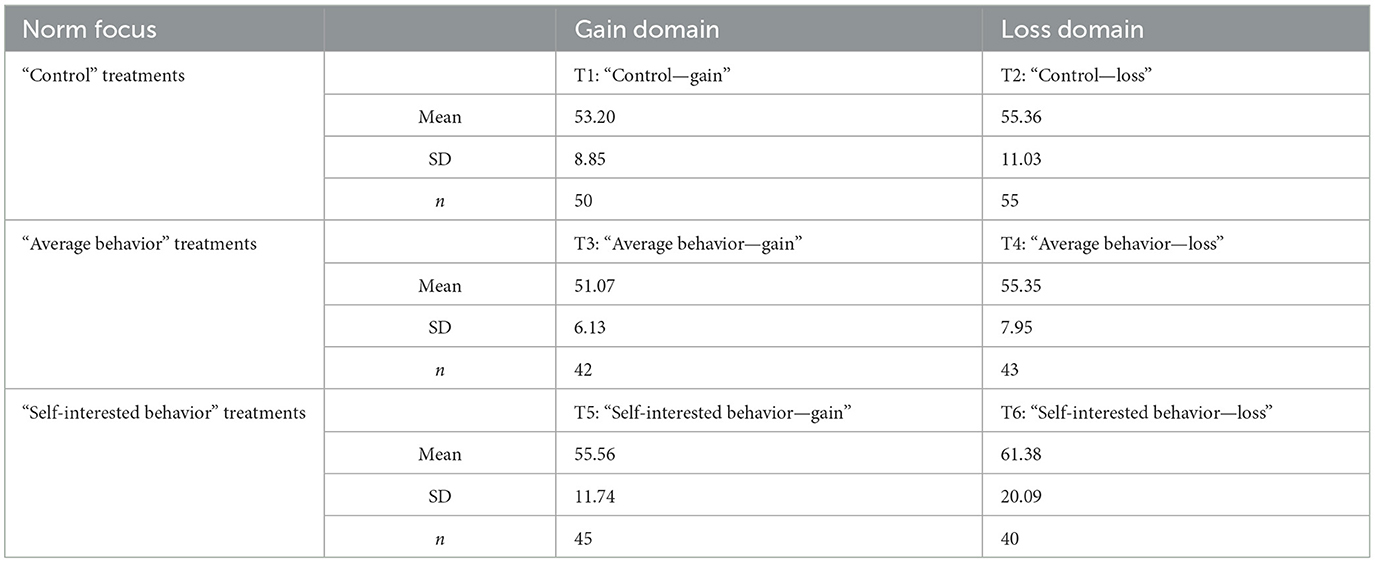
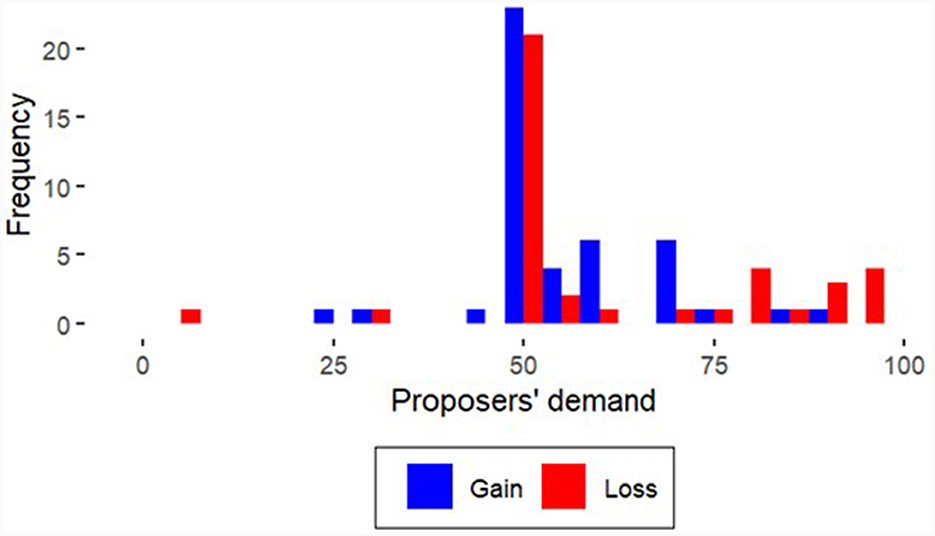
The descriptive results show that proposers have a different behavior in the loss domain compared to the gains domain. Table 2 presents the proposers' average demands and the corresponding standard deviation and provides an overview of the number of participants in the six different treatments. In all treatments, the median is 50. Figure 1 shows the proposers' demands as a percentage and the difference between gains and losses in the “Control”, “Average behavior”, and “Self-interested behavior treatments. Graphically and descriptively, we show that proposers are less generous in the loss domain than in the gains domain. To compare the offers in the gains and loss domains, the offers are presented as proposers' demands (i.e., the share that the proposers demand for themselves). In the loss domain, it is the total amount that is passed on to the responder. This transformation makes the amounts comparable, both in the analysis and graphically between gains and losses.

Table 2

Table 2. Treatment overview.

Figure 1

Figure 1. Means of proposers' demands per treatment.

Next, we analyze how the number of proposers making certain demands is distributed among three categories, namely those demanding (1) more than 50%, (2) exactly 50% (equal split), and (3) < 50%. Table 3 provides an overview of the three categories and the different distributions between the gains and loss domains. Furthermore, we analyze this separately for each norm focus treatment.

Table 3

Table 3. Overview of the distribution of proposers' demands.

Particularly in the “average behavior” treatments, we found a different distribution between the gains and loss domains. In these treatments, more proposers (n = 20) demanded more than 50% in the loss domain than in the gains domain (n = 8), while an equal split was offered more frequently by proposers in the gains domain (n = 31) than in the loss domain (n = 23). The distribution between the gains and loss domains is significantly different (X² = 9.3176, p = 0.0095). For the “Control” treatments, the distribution between the gains and loss domains is not significantly different (X² = 0.5910, p = 0.7441). The same is true for the “Self-interested behavior” treatments (X² = 0.1082, p = 0.9473).

4.1 Effect of “average behavior” treatment

In the “Average behavior” treatments, the proposers are less generous in the loss domain than in the gains domain. In T3, Average behavior—Gains, the proposers' average demand is 51.07 (SD = 6.13) and in T4, Average behavior—Loss, it is 55.35 (SD = 7.95) (see Table 2). At first glance, the difference is not surprising because, even in the “Control” treatments, proposers behave less generously in the loss domain than in the gains domain.

However, only in this norm focus treatment is the difference significant (Wilcoxon rank-sum test, z = −2.8103, p = 0.0050), which is a moderate effect with a Cohen's d = −0.59. As shown in the reference treatment in Neumann et al. (2018a), there is only a small but non-significant difference in the proposers' demand between the gains and loss domains in the “Control” treatments.

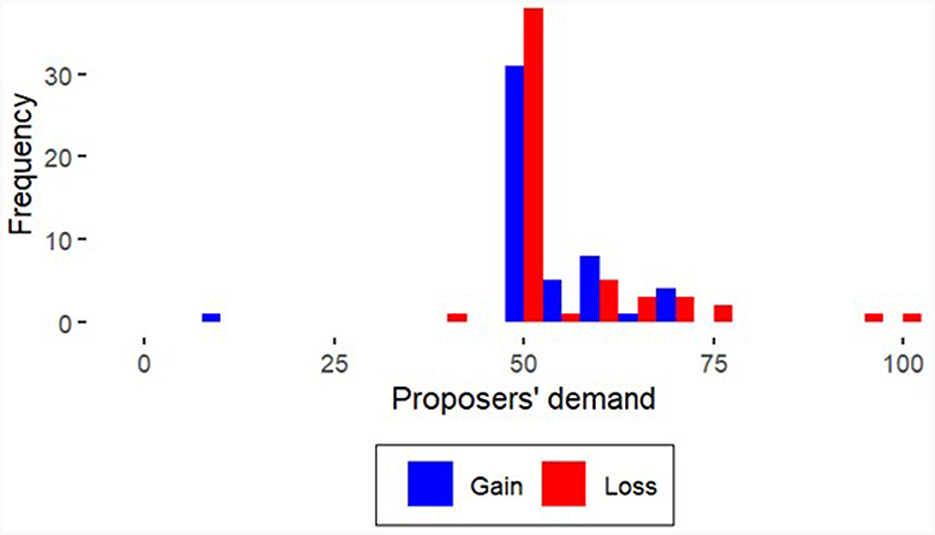
One explanation for this significant difference in the “Average behavior” treatments is the low variance, which is significantly lower according to the F-test [F_{(41, 49)} = 0.4910, p = 0.0211] in T3, “Average behavior—Gains”, compared to T1, “Control—Gains”, and according to the F-Test [F_{(42, 54)} = 0.5225, p = 0.0308] between T2,” Control—Losses”, and T4, “Average behavior—Losses”. We expected that the proposers' average demand would be centered around the previous proposers' average demand shown in the instruction, resulting in a lower variance in the “Average behavior” treatment compared to the “Control” treatment. Thus, (H2) Focusing on “Average behavior” leads to a concentration of demands around the focal point of the previous average proposal is confirmed by the significantly lower variance in both the gains and losses. The effect of norm focusing on the prior proposers' average demand has two significant effects: (1) The proposers' demand centers on the prior proposers' average demand with lower variance (2) and the difference in the proposers' demand between the gains and loss domains becomes significant, with proposers being less generous in the loss domain. The hypothesis, (H1) In ultimatum games over gains and losses, the demands in the loss domain differ from the demands in the gains domain, can also be confirmed for the “Average behavior treatments.

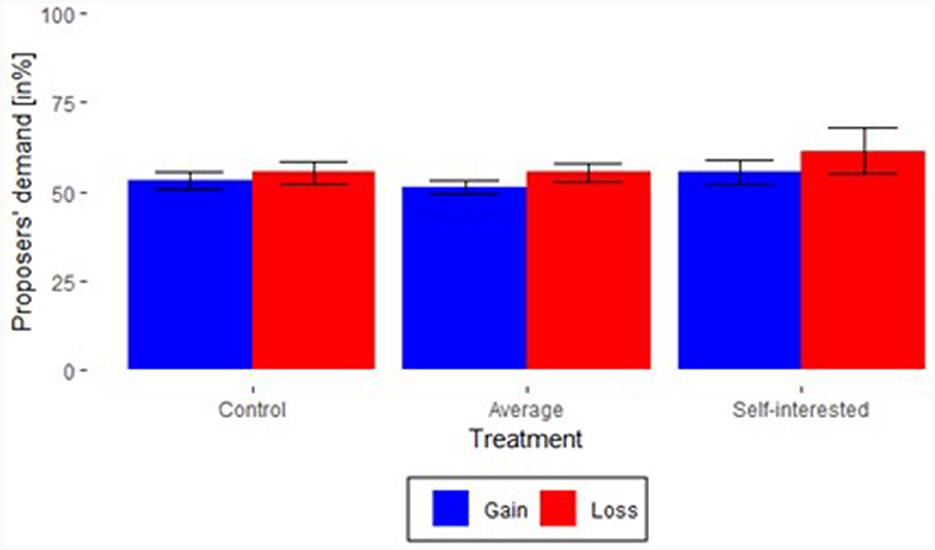
In addition, we compare the distribution of the proposers' demand in the “Control” treatments, shown in Figure 2, with the distribution of the proposers' demand in the “Average behavior” treatments, in Figure 3. In the loss domain, there is a shift from an equal split in the “Control” treatments toward the previous proposers' average demand indicated in the participant instructions. This suggests that the “Average behavior” focus appears to have a stronger influence on behavior in the loss domain than in the gains domain.

Figure 2

Figure 2. Distribution of the proposers' demands in the “control” treatments.

Figure 3

Figure 3. Distribution of the proposers' demands in the “average behavior” treatments.

4.2 Effect of “self-interested behavior” treatments

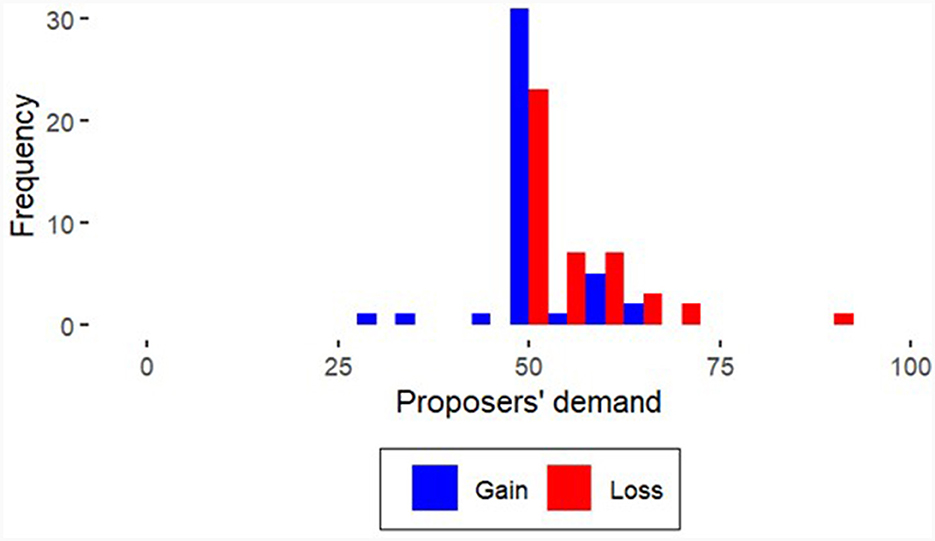
Comparing Figures 2, 4 shows a shift toward self-interested proposer demands as the proposers' average demand in the “Self-interested behavior” treatments is higher than in the “Control” treatments in both the gains and loss domains. Nevertheless, the difference within the “Self-interested” treatments between the prospers' demands in the gains and loss domains is not significant (for the gains domain: Wilcoxon rank-sum test, z = −0.6538, p = 0.5133; for the loss domain: Wilcoxon rank-sum test, z = −1.5608, p = 0.1186). Although the variance in the “Average behavior” treatments is lower than in the “Control” treatments, the variance in the “Self-interested behavior” treatments is significantly higher in the gains domain between T5 and T1, according to the F-test [F_{(49, 44)} = 0.5549, p = 0.0459], and in the loss domain between T6 and T2 [F_{(54, 39)} = 0.29931, p = 0.00005].

Figure 4

Figure 4. Distribution of the proposers' demands in the “self-interested” treatments.

Thus, we can confirm the hypothesis through the analysis of the data: (H3) Focusing on “Self-Interested behavior” leads to a dispersion of the standard deviations of proposers' demands and a decrease in fairness.

In particular, the “Self-interested behavior” treatment has a stronger effect in the loss domain than in the gains domain in terms of both the variance and the shift toward self-interested proposers' average demand. The initial situation is different; that is, in the “Control” treatments, the ultimatum game was predominantly solved by an equal split between the players, with the legitimation of the subgame perfect solution offering a large margin in which the proposer can at least somewhat adjust in the direction of selfish behavior.

4.3 Effect of loss treatment

As described above, the proposers' demands in the loss domain are higher than in the gains domain in all three treatments variants. Nevertheless, only in the “Average behavior” treatments is the difference between the proposers' demand significant with a moderate effect size due to a low variance in this treatment with norm focus. We find a difference in fairness behavior in the ultimatum games over losses in the norm focus treatment for “Average behavior”. Therefore, we can accept the following: (H1) In ultimatum games over gains and losses, the demands in the loss domain differ from the demands in the gains domain for the “Average behavior” treatments.

4.4 Responders' behavior

As shown in Table 3, selfish solutions exist, and we learned from the previous literature that selfish proposals are frequently rejected, mostly if the proposals are under 20% (Güth and Kocher, 2014). In the gains domain, we found only three responders rejecting proposer demands of 50, 60, and 70%, whereas we found 15 such rejections in the loss domain. Specifically, the responders' rejections in the loss domain are distributed as follows: 60% (4 times), 65% (1 time), 70% (2 times), 80% (1 time), 90% (3 times), 95% (3 times), and 100% (1 time) of proposers' demands. We thus observed a tendency toward a more frequent proposal rejection in the loss domain than in the gains domain. The distribution of responders' rejections between the different norm foci in the gains domain is as follows: no rejections in the “Control” treatment, two in the “Average behavior” treatment, and one in the “Self-interested behavior treatment. For the loss domain, there were four rejections in the control treatment, five in the “Average behavior” treatment, and six in the “Self-interested” treatment. Consequently, the tendency toward more frequent rejections by responders in the loss domain compared to the gains domain occurs in each norm foci treatment. In Table 4, we show the proposers' demands and responders' rejection per treatment and domain.

Table 4

Table 4. Proposers' demands and rejection per treatment and domain.

5 Discussion, limitation, and conclusion

5.1 Discussion

Social norms and losses are of great importance in distributive bargaining situations on both the individual and societal levels. The current energy crisis and shortage of gas is only one example that highlights the relevance of understanding the distribution of losses among various actors. While norm theory straightforward applies to the problem of distributing of losses in social situations, the consequential predictions had been hardly tested empirically. We tackled the research gap using ultimatum game experiments in the gains and loss domains, wherein we designed ultimatum game experiments with two different norm foci, namely (1) on the previous average behavior and (2) on the self-interested solution. We used the prepaid mechanism to implement losses in the laboratory.

In our experimental study, we found that the proposers demanded more in the loss domain than in the gains domain in both norm foci treatments. However, only in the “Average behavior” treatments was the difference in the proposers' demands significant, and it had a moderate effect. One explanation for this is the small variance created by the focus on the prior average proposer demand. In line with previous literature (e.g., Lusk and Hudson, 2010), we showed that proposers demanded more for themselves in the loss domain than in the gains domain. Our results confirm that there is a difference in the distribution of losses compared to gains (Buchan et al., 2005; Lusk and Hudson, 2010; Baquero et al., 2013; Neumann et al., 2017).

In line with norm theory (Bicchieri, 2006; Bicchieri and Xiao, 2009), we hypothesized that norm focusing leads to a different distribution of proposers' demands between the different norm foci. This was confirmed by our results from the ultimatum game experiments. We found that the standard deviation in proposers' demands in the ultimatum game experiments with the focus on “Average behavior” was smaller than in the “Control” experiments in both the gains and loss domains, as the proposers' demands concentrated around the shown average offer of the “Control” treatments. In contrast, we found significantly higher standard deviations in the norm focus treatment of “Self-interested behavior” compared to the “Control” treatments. The focus on self-interest leads to higher variance because the presented solution legitimizes a higher demand from proposers.

We found a tendency toward a higher frequency of rejections in the loss domain compared to the gains domain. This finding is in line with previous research on responders' behavior (Camerer et al., 1993). For future research, we suggest analyzing subjects' behavior in that subjects also use norm focus to determine their expectations or limits of acceptability in the loss domain compared to the gains domain. With this, the responders' behavior could be analyzed in more detail (see, e.g., Neumann et al., 2018b). The results show that behavior reacts with norm focusing and with the domain of gains and losses when making an offer in the Ultimatum Game.

5.2 Limitation

In our study, the losses occurred by chance for the participants; that is, they were caused by what may be perceived as bad luck and were not the result of their own efforts. Following Weiner's attribution theory (Weiner, 1985, 2005; Weiner et al., 2011), this may have had an influence on the subjects' behavior. The subjects could therefore have assumed that they (like the other subjects, i.e., the responders) were not responsible for the loss and therefore behaved more prosocially (cf. Fong, 2001; Weiner et al., 2011).

Besides these limitations, the ultimatum game experiments took place only in Germany, so it is a single country subject pool. Furthermore, it is predominantly a student-subject pool (Bader et al., 2021). Due to cultural differences, the proposition and the behavior of the responder can differ from country to country (Oosterbeek et al., 2004). The results of the ultimatum game are not fully transferable to countries other than Germany.

5.3 Conclusion

The different behavior in the loss domain compared to the gains domain toward more selfishness in the loss domain, due to higher proposer demands and a tendency toward a higher amount of responder rejections, can be explained by the loss aversion aspect of prospect theory (Kahneman and Tversky, 1979; Tversky and Kahneman, 1986; i.e., “losses loom larger”), which leads to higher proposer demands. Other approaches, such as the loss attention model, can be also applied as an explanation for why losses lead to a higher sensitivity compared to gains (Yechiam and Hochman, 2013a,b). This psychological model also indicates that losses are perceived differently, and in the distribution of losses, it provides an explanation for the deviating behavior seen in the comparison.

To conclude, losses change the behavior of participants in the ultimatum game as compared to gains by making the more self-oriented. In addition, it is possible to trigger the participants behavior by focusing them on a norm. Yet, the latter effect is rather weak, and it remains unsure if it would remain stable in real situations with more costly losses. These results are in accordance with Hobbes (1996[1651]) fundamental remark on the problem. Firstly, he also states that humans tend to be selfish if they interact in situation with losses. Secondly, Hobbes advises to encounter this by combining (unstable focusing on) norms with social sanctions to enforce compliance to norms.¹⁰

To take the example of the introduction out, in particular, the scarcity of the gases and thus its rising costs will lead to more self-oriented behavior in the distribution of these costs, and (focusing on) norms, probably will not overcome the problem.

In any case, we recommend further research investigating the distribution of losses, especially investigations into responder behavior to explain their perception and behavior regarding the distribution of losses.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

Ethical approval was not required for the studies involving humans because the study was conducted in accordance with ethical standards for human research and under the terms and conditions of the MaXLab and LeX, according to which additional ethical approval for this kind of experiment was not required. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.

Author contributions

BV, RB, and TN: conception and design. IW, SK, and TN: collection and analysis of data. IW, SK, TN, RB, and BV: interpretation of the data and revising the article. SK: drafting the article. RB and BV: funding acquisition. All authors contributed to the article and approved the submitted version.

Funding

This research was funded by the DFG (German Science Foundation) under grant numbers BE 2373/4-1 and VO 1677/4-1 as part of the research project The fair division of losses (project number 362787969).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

1. ^The proposer's demand is the portion that the proposer keeps for themselves; see Section 3.1.

2. ^In the dictator game, role uncertainty leads to an underestimation of selfish preferences (Iriberri and Rey-Biel, 2008).

3. ^In addition to this method, we are aware of the method of implementing losses using a waiting time (Berger et al., 2012; Kroll et al., 2014; Noussair and Stoop, 2015), which requires participants to wait a certain amount of time and/or bargain over the waiting time instead of receiving a monetary loss (Berger et al., 2012). Another approach is the cold pressor test, in which a specific duration of pain corresponds to a monetary loss (Schosser et al., 2016). However, these approaches to inducing losses in the laboratory have their drawbacks as they are difficult to compare to money.

4. ^Mental accounting means that money is broken down into categories, which can in this context be categorized into time sets (Thaler, 1999).

5. ^The house money effect describes that people tend to increase their risk-seeking if they received a gain upfront. This has also been described as “windfall gains” (Arkes et al., 1994) and the “manna economy” (Güth and Kliemt, 2003).

6. ^The instruction was written in German because all participants are German speakers. The original sentence is German and reads as follows: “In einer Experimentreihe im letzten Jahr haben die Spieler 1 im Schnitt einen Anteil von 5,33 € für sich beansprucht.”

7. ^The instruction was written in German because all participants are German speakers. The original sentence is German and reads as follows: “In einer Experimentreihe im letzten Jahr haben die Spieler 1 im Schnitt −4.29 € vom Verlust getragen.”

8. ^The instruction was written in German because all participants are German speakers. The original sentence is German and reads as follows: “Ein rationaler Spieler 1, der seine Auszahlung maximieren möchte, würde in diesem Spiel den kleinstmöglichen Betrag größer Null an Spieler 2 anbieten. Ein rationaler Spieler 2, der seine Auszahlung maximieren möchte, würde jeden Betrag größer Null annehmen.”

9. ^The instruction was written in German because all participants are German speakers. The original sentence is German and reads as follows: “Ein rationaler Spieler 1, der seine Auszahlung maximieren möchte, würde in diesem Spiel den größtmöglichen Verlust an Spieler 2 anbieten, der kleiner ist als der volle Verlust. Ein rationaler Spieler 2, der seine Auszahlung maximieren möchte, würde jeden Verlust annehmen, der besser ist als der volle Verlust von −10 €.”

10. ^In his example with definitely much harsher losses than in our experiments this sanctioning institution is the well know “Leviathan”, namely an absolute state.

References

Abels, H. (2019). “Soziale Ordnung oder: Wie ist Gesellschaft möglich?” in Einführung in die Soziologie. Studientexte zur Soziologie (Wiesbaden: Springer).

Google Scholar

Andersen, S., Erta,ç, S., Gneezy, U., Hoffman, M., and List, J. A. (2011). Stakes matter in ultimatum games. Am. Econ. Rev. 101, 3427–3439. doi: 10.1257/aer.101.7.3427

Crossref Full Text | Google Scholar

Arkes, H. R., Joyner, C. A., Pezzo, M. V., Nash, J. G., Siegel-Jacobs, K., and Stone, E. (1994). The psychology of windfall gains. Organ. Behav. Hum. Decis. Process. 59, 331–347. doi: 10.1006/obhd.1994.1063

Crossref Full Text | Google Scholar

Bader, F., Baumeister, B., Berger, R., and Keuschnigg, M. (2021). On the transportability of laboratory results. Sociol. Methods Res. 50, 1452–1481. doi: 10.1177/0049124119826151

Crossref Full Text | Google Scholar

Baquero, G., Smit, W., and Wathieu, L. (2013). The Generosity Effect: Fairness in Sharing Gains and Losses. ESMT-13-08. Berlin: ESMT European School of Management and Technology.

Google Scholar

Berger, R., Rauhut, H., Prade, S., and Helbing, D. (2012). Bargaining over waiting time in ultimatum game experiments. Soc. Sci. Res. 41, 372–379. doi: 10.1016/j.ssresearch.2011.09.009

PubMed Abstract | Crossref Full Text | Google Scholar

Bicchieri, C. (2006). The Grammar of Society: The Nature and Dynamics of Social Norms. Cambridge: Cambridge University Press.

Google Scholar

Bicchieri, C. (2017). Norms in the Wild: How to Diagnose, Measure, and Change Social Norms. Oxford; New York, NY: Oxford University Press.

Google Scholar

Bicchieri, C., and Xiao, E. (2009). Do the right thing: but only if others do so. J. Behav. Decis. Mak. 22, 191–208. doi: 10.1002/bdm.621

Crossref Full Text | Google Scholar

Binmore, K. (2010). Social norms or social preferences? Mind Soc. 9, 139–157. doi: 10.1007/s11299-010-0073-2

Crossref Full Text | Google Scholar

Bock, O., Baetge, I., and Nicklisch, A. (2014). hroot: Hamburg Registration and Organization Online Tool. Eur. Econ. Rev. 71, 117–120. doi: 10.1016/j.euroecorev.2014.07.003

Crossref Full Text | Google Scholar

Buchan, N., Croson, R., Johnson, E., and Wu, G. (2005). “Gain and loss ultimatums,” in Advances in Applied Microeconomics, Vol. 13, Experimental and Behavioral Economics, ed ed J. Morgan (Bingley: Emerald Group Pub), 1–23.

Google Scholar

Camerer, C. F., Johnson, E. J., Rymon, T., and Sen, S. (1993). “Cognition and framing in sequential bargaining for gains and losses,” in Frontiers of Game Theory, eds K. G. Binmore, A. P. Kirman, and P. Tani (Cambridge: MIT Press), 27–47.

Google Scholar

Chen, Y.-H., Chen, Y.-C., Kuo, W.-J., Kan, K., Yang, C. C., and Yen, N.-S. (2017). Strategic motives drive proposers to offer fairly in ultimatum games: an FMRI study. Sci. Rep. 7:527. doi: 10.1038/s41598-017-00608-8

PubMed Abstract | Crossref Full Text | Google Scholar

Cialdini, R. B., Kallgren, C. A., and Reno, R. R. (1991). A focus theory of normative conduct: a theoretical refinement and reevaluation of the role of norms in human behavior. Adv. Exp. Soc. Psychol. 24, 201–234. doi: 10.1016/S0065-2601(08)60330-5

Crossref Full Text | Google Scholar

Etzrodt, C. (2020). From the hobbes-parsons problem to a non-linear dimensionalist model of cultures. Sociol. Mind 10, 35–53. doi: 10.4236/sm.2020.101004

Crossref Full Text | Google Scholar

Fischbacher, U. (2007). z-Tree: Zurich toolbox for ready-made economic experiments. Exp. Econ. 10, 171–178. doi: 10.1007/s10683-006-9159-4

Crossref Full Text | Google Scholar

Fong, C. (2001). Social preferences, self-interest, and the demand for redistribution. J. Public Econ. 82, 225–246. doi: 10.1016/S0047-2727(00)00141-9

Crossref Full Text | Google Scholar

Füllbrunn, S., and Vyrastekova, J. (2023). Does trust break even? A trust-game experiment with negative endowments. J. Behav. Exp. Econ. 103:101982. doi: 10.1016/j.socec.2023.101982

Crossref Full Text | Google Scholar

Furedi, F. (2013). Authority: a Sociological History. Cambridge: Cambridge University Press.

Google Scholar

Gächter, S., Johnson, E. J., and Herrmann, A. (2022). Individual-level loss aversion in riskless and risky choices. Theor. Decis. 92, 599–624. doi: 10.1007/s11238-021-09839-8

Crossref Full Text | Google Scholar

García-Gallego, A., Georgantzís, N., and Jaramillo-Gutiérrez, A. (2012). Gender differences in ultimatum games: despite rather than due to risk attitudes. J. Econ. Behav. Organ. 83, 42–49. doi: 10.1016/j.jebo.2011.06.012

Crossref Full Text | Google Scholar

Güth, W., and Kliemt, H. (2003). “Experimentelle Ökonomik: Modell-Platonismus in neuem Gewande?” in Jahrbuch normative und institutionelle Grundfragen der Ökonomik, Bd. 2, Experimente in der Ökonomik, eds M. Held, G. Kubon-Gilke, and R. Sturn (Marburg: Metropolis-Verlag), 315–43.

Google Scholar

Güth, W., and Kocher, M. G. (2014). More than thirty years of ultimatum bargaining experiments: motives, variations, and a survey of the recent literature. J. Econ. Behav. Organ. 108, 396–409. doi: 10.1016/j.jebo.2014.06.006

Crossref Full Text | Google Scholar

Güth, W., Schmittberger, R., and Schwarze, B. (1982). An experimental analysis of ultimatum bargaining. J. Econ. Behav. Organ. 3, 367–388. doi: 10.1016/0167-2681(82)90011-7

Crossref Full Text | Google Scholar

Hobbes, T. (1996[1651]). Leviathan. Cambridge: Cambridge University Press.

Google Scholar

Iriberri, N., and Rey-Biel, P. (2008). The role of role uncertainty in modified dictator games. Exp. Econ. 14, 160–180. doi: 10.1007/s10683-010-9261-5

Crossref Full Text | Google Scholar

Kahneman, D., and Tversky, A. (1979). Prospect theory: an analysis of decision under risk. Econometrica 47, 263–292. doi: 10.2307/1914185

Crossref Full Text | Google Scholar

Kroll, E. B., Morgenstern, E., Neumann, T., Schosser, S., and Vogt, B. (2014). Bargaining power does not matter when sharing losses – Experimental evidence of equal split in the Nash bargaining game. J. Econ. Behav. Organ. 108, 261–272. doi: 10.1016/j.jebo.2014.10.009

Crossref Full Text | Google Scholar

Lusk, J. L., and Hudson, M. D. (2010). Bargaining over losses. Int. Game Theory Rev. 12, 83–91. doi: 10.1142/S0219198910002532

Crossref Full Text | Google Scholar

Neumann, T., Kierspel, S., Windrich, I., Berger, R., and Vogt, B. (2018a). How to split gains and losses? Experimental evidence of dictator and ultimatum games. Games 9:78. doi: 10.3390/g9040078

Crossref Full Text | Google Scholar

Neumann, T., Schosser, S., and Vogt, B. (2017). Ultimatum bargaining over losses and gains - An experimental comparison. Soc. Sci. Res. 67, 49–58. doi: 10.1016/j.ssresearch.2017.08.009

PubMed Abstract | Crossref Full Text | Google Scholar

Neumann, T., Schosser, S., and Vogt, B. (2018b). “Non-acceptance of losses—an experimental study on the importance of the sign of final outcomes in ultimatum bargaining,” in Operations Research Proceedings, Operations research proceedings 2017: Selected Papers of the Annual International Conference of the German Operations Research Society (GOR), Freie Universität Berlin, Germany, September 6-8, 2017, eds N. Kliewer, J. F. Ehmke, and R. Borndörfer (Cham: Springer), 287–292.

Google Scholar

Noussair, C. N., and Stoop, S. (2015). Time as a medium of reward in three social preference experiments. Exp. Econ. 18, 442–456. doi: 10.1007/s10683-014-9415-y

Crossref Full Text | Google Scholar

Oosterbeek, H., Sloof, R., and Kuilen, G. (2004). Cultural differences in ultimatum game experiments: evidence from a meta-analysis. Exp. Econ. 7, 171–188. doi: 10.1023/B:EXEC.0000026978.14316.74

Crossref Full Text | Google Scholar

Raub, W., and Snijders, C. (1997). Gains, losses, and cooperation in social dilemmas and collective action: the effects of risk preferences. J. Math. Sociol. 22, 263–302. doi: 10.1080/0022250X.1997.9990204

Crossref Full Text | Google Scholar

Rauhut, H., and Winter, F. (2010). A sociological perspective on measuring social norms by means of strategy method experiments. Soc. Sci. Res. 39, 1181–1194. doi: 10.1016/j.ssresearch.2010.06.009

Crossref Full Text | Google Scholar

Rosenboim, M., and Shavit, T. (2012). Whose money is it anyway? Using prepaid incentives in experimental economics to create a natural environment. Exp. Econ. 15, 145–157. doi: 10.1007/s10683-011-9294-4

Crossref Full Text | Google Scholar

Schosser, S., Trarbach, J. N., and Vogt, B. (2016). How does the perception of pain determine the selection between different treatments?: Experimental evidence for convex utility functions over pain duration and concave utility functions over pain intensity. J. Econ. Behav. Organ. 131:174–182. doi: 10.1016/j.jebo.2015.08.009

Crossref Full Text | Google Scholar

Selten, R. (1965). Spieltheoretische Behandlung eines Oligopolmodells mit Nachfrageträgheit. Zeitschrift für die gesamte Staatswissenschaft.

Google Scholar

Selten, R. (1975). Reexamination of the perfectness concept for equilibrium points in extensive games. Int. J. Game Theory 4, 25–55. doi: 10.1007/BF01766400

Crossref Full Text | Google Scholar

Sutter, M., Kocher, M., and Strauß, S. (2003). Bargaining under time pressure in an experimental ultimatum game. Econ. Lett. 81, 341–347. doi: 10.1016/S0165-1765(03)00215-5

Crossref Full Text | Google Scholar

Thaler, R. H. (1999). Mental accounting matters. J. Behav. Decis. Making 12, 183–206. doi: 10.1002/(SICI)1099-0771(199909)12:3<183::AID-BDM318>3.0.CO

Crossref Full Text | Google Scholar

Thaler, R. H., and Johnson, E. J. (1990). Gambling with the house money and trying to break even: the effects of prior outcomes on risky choice. Manage. Sci. 36, 643–660. doi: 10.1287/mnsc.36.6.643

Crossref Full Text | Google Scholar

Thunström, L. (2019). Preferences for fairness over losses. J. Behav. Exp. Econ. 83:101469. doi: 10.1016/j.socec.2019.101469

Crossref Full Text | Google Scholar

Tversky, A., and Kahneman, D. (1986). Rational choice and the framing of decisions. J. Bus. 59, 251–278. doi: 10.1086/296365

Crossref Full Text | Google Scholar

Tversky, A., and Kahneman, D. (1992). Advances in prospect theory: cumulative representation of uncertainty. J. Risk Uncertain. 5, 297–323. doi: 10.1007/BF00122574

Crossref Full Text | Google Scholar

Weiner, B. (1985). An attributional theory of achievement motivation and emotion. Psychol. Rev. 92, 548–573. doi: 10.1037/0033-295X.92.4.548

PubMed Abstract | Crossref Full Text | Google Scholar

Weiner, B. (2005). Social Motivation, Justice, and the Moral Emotions: An Attributional Approach. Mahwah: Taylor & Francis. Available online at: https://ebookcentral.proquest.com/lib/kxp/detail.action?docID=261422 (accessed October 04, 2023).

Google Scholar

Weiner, B., Osborne, D., and Rudolph, U. (2011). An attributional analysis of reactions to poverty: the political ideology of the giver and the perceived morality of the receiver. Pers. Soc. Psychol. Rev. 15, 199–213. doi: 10.1177/1088868310387615

PubMed Abstract | Crossref Full Text | Google Scholar

Windrich, I., Kierspel, S., Neumann, T., Berger, R., and Vogt, B. (2022). Experiments on norm focusing and losses in dictator games. Front. Sociol. 7:930976. doi: 10.3389/fsoc.2022.930976

PubMed Abstract | Crossref Full Text | Google Scholar

Yechiam, E., and Hochman, G. (2013a). Loss-aversion or loss-attention: the impact of losses on cognitive performance. Cogn. Psychol. 66, 212–231. doi: 10.1016/j.cogpsych.2012.12.001

PubMed Abstract | Crossref Full Text | Google Scholar

Yechiam, E., and Hochman, G. (2013b). Losses as modulators of attention: review and analysis of the unique effects of losses over gains. Psychol. Bull. 139, 497–518. doi: 10.1037/a0029383

PubMed Abstract | Crossref Full Text | Google Scholar

Zhou, X., and Wu, Y. (2011). Sharing losses and sharing gains: increased demand for fairness under adversity. J. Exp. Soc. Psychol. 47, 582–588. doi: 10.1016/j.jesp.2010.12.017

Crossref Full Text | Google Scholar