Multi-scale energy release events in the quiet Sun: a possible source for coronal heating

The coronal heating problem remains one of the most challenging questions in solar physics. The energy driving coronal heating is widely understood to be associated with convective motions below the photosphere. Recent high-resolution observations reveal that photospheric magnetic fields in the quiet Sun undergo complex and rapid evolution. These photospheric dynamics are expected to be reflected in the coronal magnetic field. Motivated by these insights, our research aims to explore the relationship between magnetic energy and coronal heating. By combining observations from Solar Orbiter and SDO with a magnetic field extrapolation technique, we estimate the magnetic free energy of multi-scale energy release events in the quiet Sun. Interestingly, our results reveal a strong correlation between the evolution of free energy and the integrated intensity of extreme ultraviolet emission at 171 Å in these events. We quantitatively assess the potential energy flux budget of these events to evaluate their contribution to coronal heating. Our study implies a link between photospheric magnetic field evolution and coronal temperature variations, paving the way for further research into similar phenomena.

1 Introduction

The coronal heating problem remains one of the most fundamental unsolved mysteries in solar physics and space physics in the 21st century (Klimchuk, 2006; Parnell and De Moortel, 2012; Priest, 2014; Klimchuk, 2015). A fundamental paradox arises from the remarkable temperature disparity between the solar corona and its underlying photosphere. Namely, the photosphere maintains a temperature of approximately 6000 K, while the outer corona reaches temperatures of 1–2 MK, separated only by a thin transition region of a few hundred kilometers (Yang et al., 2009; Priest, 2014; De Moortel and Browning, 2015). This extraordinary temperature gradient challenges fundamental physical principles. It is well established that the energy source originates from convective motions below the photosphere. Then how is the energy transferred through the cooler photosphere to the hotter corona, as the apparent upward heat flow from cooler to hotter regions seems to contradict the Second Law of Thermodynamics. The precise physical process behind this dramatic temperature increase remains elusive. The challenge extends beyond merely explaining the high temperatures. Although the corona’s low density (typically ${10}^8$-${10}^9$ ${\text{cm}}^{-3}$) results in smaller energy flux, which helps maintain its high temperature, the continuous radiative and conductive losses ($\sim$ $3\times 10$⁵ erg ${\text{cm}}^{-2}$ ${\text{s}}^{-1}$ in quiet Sun and $\sim {10}^7$ erg ${\text{cm}}^{-2}$ ${\text{s}}^{-1}$ in active regions) to the surrounding cooler atmosphere require a persistent energy supply (Withbroe and Noyes, 1977; Aschwanden, 2004; Reale, 2014). Observations from various space-based instruments show that coronal temperatures remain remarkably stable over various temporal and spatial scales (Reale, 2014; Del Zanna and Mason, 2018), indicating continuous heating is necessary to prevent the rapid cooling. Therefore, solving the coronal heating problem requires not only explaining the extremely high temperatures but also identifying the specific physical mechanisms that sustain this high-temperature state.

In simple terms, the coronal heating mechanisms are generally categorized into two main types: wave-based heating and nanoflare-driven heating. Wave-based heating, primarily through Alfv$\acute{e}$n and magnetoacoustic waves, offers an explanation for continuous heating with efficient energy transport (Ionson, 1978; Heyvaerts and Priest, 1983). However, this mechanism faces challenges including chromospheric damping, mode conversion processes, and the identification of precise dissipation mechanisms in the corona such as phase mixing and resonant absorption (Van Doorsselaere et al., 2020). The nanoflare-driven heating mechanism, proposed by Parker (1988), attributes coronal heating to magnetic braiding and subsequent reconnection events triggered by photospheric convective motions. While this model effectively explains impulsive heating and observations of high-temperature plasma (Klimchuk, 2006), questions remain regarding the frequency of nanoflares, their spatial-temporal distribution, and whether their total energy budget is sufficient for sustained coronal heating Priest et al. (2018). Contemporary theoretical frameworks suggest that these mechanisms likely coexist and interact (De Moortel and Browning, 2015), with wave-based heating potentially providing background heating while nanoflares contribute to intermittent strong heating events. Different mechanisms may dominate in different coronal regions, and their coupling effects could be crucial for maintaining the corona’s high temperature state (Klimchuk, 2015). The relative importance and interaction of these mechanisms remain active areas of research in solar physics.

It is widely accepted that the energy driving coronal or chromospheric heating associated with convective motions below the photosphere. Recent high-resolution observations reveal the quiet-Sun photosphere to be complex and rapidly evolving. Since photospheric magnetic fields extend into the solar corona, these photospheric complexity and dynamics are expected to be reflected in the coronal magnetic field. Meyer et al. (2013) investigated magnetic energy storage and dissipation in the quiet-Sun corona. They concluded that the magnetic free energy stored in the coronal field is sufficiently abundant to explain small-scale phenomena such as X-ray bright points and other impulsive events, providing crucial insights into the underlying mechanisms of solar coronal heating. In this report, we aim to study the characteristics of free energy evolution in multi-scale quiet-Sun eruptions and their relation to coronal heating, by combining extensive temporal coverage observations from the Solar Dynamics Observatory (SDO; Pesnell et al., 2012) with high spatial and temporal resolution observations from the Solar Orbiter (SolO; Müller et al., 2020). Furthermore, we quantitatively assess the potential energy flux of these eruptive events to evaluate their significance in coronal heating. In Section 2, we present the data analysis of the imaging results and magnetic field, and in Section 3, we engage in discussions.

2 Data analysis and results

For joint observations, we select the SolO observation data from 2022 March 8, when it was positioned almost midway along the Sun-Earth line ($\sim$0.49 au to the Sun). The extreme ultraviolet (EUV) High Resolution Imager (${\text{HRI}}_{\mathit{EUV}}$) of the Extreme Ultraviolet Imager (EUI; Rochus et al., 2020) on SolO provides continuous observations with a time resolution of 3 s for half an hour starting from 00:00 UT on March 8. The angular pixel size is $0^{\prime \prime }$.492, corresponding to about 175 km on the solar surface, which is about 2.5 times better than the spatial resolution of the Atmospheric Imaging Assembly (AIA; Lemen et al., 2012) on board SDO ($0^{\prime \prime }$.6/pixel, $\sim$440 km on the solar surface). The light travel time difference between the Sun and each instrument is about 250 s. We select three representative small-scale flare events (see F1, F2, and F3 of Animation 1) in the quiet Sun near the disk center. These regions exhibit obvious small-scale solar activities. Their sizes range from a few megameters to 20 Mm. Figure 1A shows an eruption of similar spatial scale to the small-scale dimming events catalogued in Table one of Wang et al. (2023) using EUI/${HRI}_{\mathit{EUV}}$ observations. Combining the animation and Figure 1B, we find that this should be a failed eruption, where the material is ejected outward and then falls back to the solar surface along the black arc shown in Figure 1A. The animation also shows that there are relatively obvious material ejections in the south of the eruption source. These phenomena suggest that: (1) the material and energy from the quiet-Sun eruptions may have difficulty propagating to higher altitudes, and (2) these small-scale eruptions may be composed of or accompanied by even smaller-scale events.

Figure 1

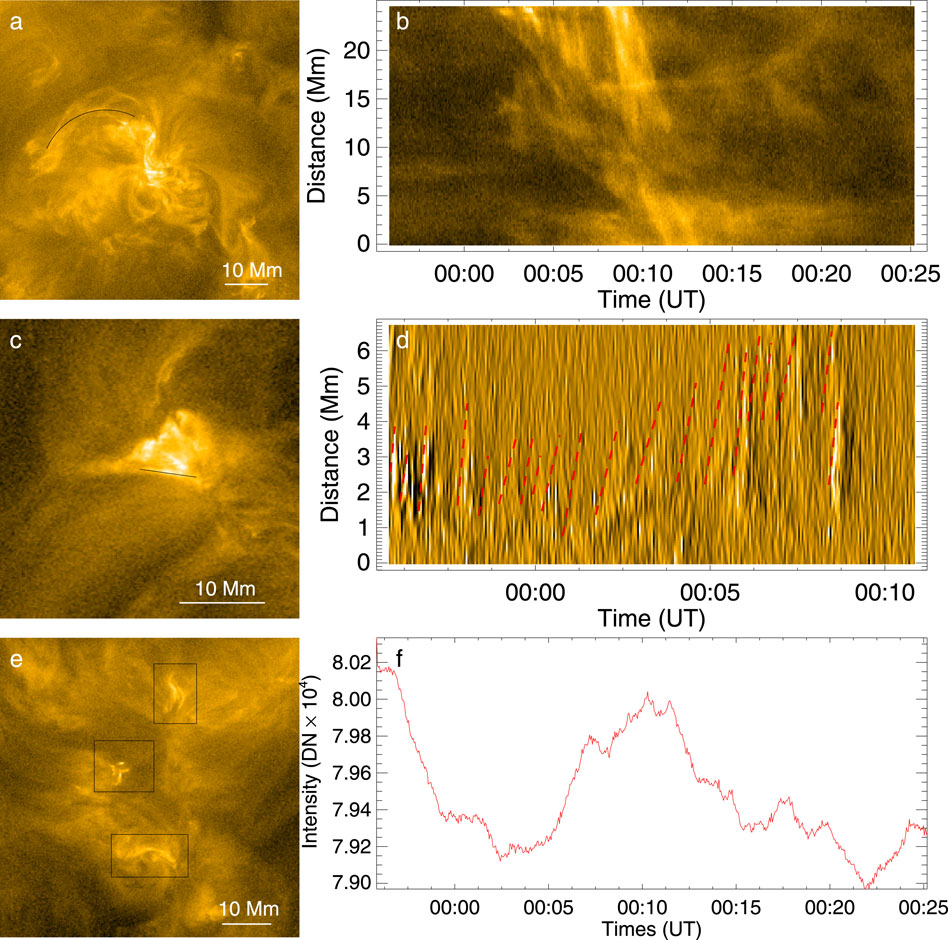
Figure 1. EUI/${HRI}_{\mathit{EUV}}$ 174 Å observations. (A) A failed small-scale filament eruption. (B) Time-distance plot along the black arc in (A) (right endpoint = 0). (C) A confined eruption with multiple EUV brightenings and mini-jets. (D) Time-distance difference plot along the black line in (C) (right endpoint = 0), with the projected speeds of small jets annotated by red dashed lines. (E) Three smaller-scale flares. (F) Light curve showing the sum of integrated intensities within the three black boxes in (E). All times are in SDO reference frame. F1, F2, and F3 in the animation align with areas shown in panels (A, C, E).

Figure 1C shows a smaller region compared to Figure 1A. F2 does not exhibit obvious filament or flare eruptions, but it does show clear EUV brightenings. Careful examination of the animation reveals jet-like structures along the black line in Figure 1C and its adjacent regions. We believe these jet-like structures are likely associated with outflows related to magnetic reconnection. Figure 1D shows that these jet-like structures have relatively high speeds, and it would have been difficult to identify them without the high temporal resolution of ${\text{HRI}}_{\mathit{EUV}}$. The average speed of 20 small jets within 15 min is 113 km ${\text{s}}^{-1}$, with a median of 106 km ${\text{s}}^{-1}$, ranging from 55 km ${\text{s}}^{-1}$ to 200 km ${\text{s}}^{-1}$, which is the typical speed range associated with small-scale jets related to reconnection events (Chitta et al., 2021; Cheng et al., 2023). Note that the measured speeds are projected in the plane of the sky. Figure 1E shows multi-scale eruptions, some of which exhibit jet-like features, while others only show EUV brightenings (see F3 of Animation 1). We aim to investigate whether these small-scale solar activities shown in Figure 1 could potentially serve as an energy source for coronal heating.

The energy driving coronal and chromospheric heating is widely understood to be associated with convective motions below the photosphere. The magnetic free energy in the quiet-Sun coronal field, influenced by photospheric magnetic field evolution, reflects energy storage and dissipation dynamics in the quiet-Sun corona. Solar flares and similar energy releases are fundamentally facilitated by magnetic reconnection, which generates observable EUV brightenings. Motivated by these insights, our research aims to quantify the relationship between temporal variations in emission intensity within eruption source regions and concurrent changes in magnetic free energy, seeking to unravel the intricate mechanisms underlying coronal heating. The AIA offers observations in six channels, with a broader temporal coverage than the ${\text{HRI}}_{\mathit{EUV}}$ data, which facilitates the study of energy evolution. We use data from 1 hour before and after the period of interest. However, the time resolution of some AIA channels is only 96 s during the period from 23:00 UT on March 7 to 02:00 UT on March 8. Therefore, to align the data across all channels, we uniformly adopte a time interval of 96 s.

Figure 2 shows the EUV image at 171 Å and photospheric magnetogram in the quiet Sun. The white boxes outline the regions selected for intensity integration and magnetic free energy. To calculate the magnetic free energy, we use a nonlinear force-free (NLFFF) magnetic field extrapolation method (Wiegelmann, 2004; Wiegelmann et al., 2012) to obtain the coronal magnetic field. The Helioseismic and Magnetic Imager (HMI; Scherrer et al., 2012; Schou et al., 2012) on board SDO does not provide the direct boundary data for NLFFF extrapolation in the quiet Sun. We adopt the “bvec2cea.pro” routine in SSW packages to convert the disambiguated full-disk vector magnetic field “hmi.B_720s” series from the native CCD coordinates to the cylindrical equal area heliographic coordinates (Hoeksema et al., 2014), which is appropriate for extrapolation. The “bvec2cea.pro” routine uses a radial-acute method (Hoeksema et al., 2014) to resolve the 180$°$ azimuthal uncertainty in the transverse field direction. This method has been demonstrated effective and reliable by previous studies (Wang et al., 2023). They successfully reconstruct the magnetic flux-rope structures in the quiet Sun, which show good agreement with observations of the filaments.

Figure 2

Figure 2. Distribution of small-scale eruptive events. Top: AIA 171 Å image showing events F1, F2, and F3 (corresponding to microflares in Figures 1A, C, E). White boxes mark the regions for intensity integration in Figure 3. Helioprojective coordinates are shown at the lower-left corner. Bottom: White boxes correspond to those in the top panel overlaid on magnetogram (Bz), which define the free energy calculation regions. Actual extrapolation boundary extends roughly twice the box size.

Figure 3 demonstrates a strong correlation between the integrated intensity in the 171 Å channel (red curve in the second row) and magnetic free energy $[\int \frac{B^2}{2{\mu }_0}dV]$ (black curve in the third row), with correlation coefficients ranging from 0.60 to approximately 0.86 across the three regions. The integrated intensity curves for all EUV channels are plotted in the first row to detect potential microflares. Similar to active region flares, we detect distinct impulsive intensity enhancements in high-temperature channels (e.g., 131 Å and 94 Å) in each region. These impulsive peaks largely coincide with the peaks in free energy, suggesting a correlation between energy release and EUV emission intensity. Among all channels, the 171 Å intensity curve shows the strongest correlation with free energy variations. Furthermore, we integrate the intensity from higher-resolution ${\text{HRI}}_{\mathit{EUV}}$ images at 174 Å and compare it with the light curve of AIA 171 Å, which displays nearly identical curve patterns (shown in Figure 1F and the dashed box in Figure 3F). This indicates that multiple small-scale eruptions, when integrated, can characterize the intensity variations across the entire region.

Figure 3

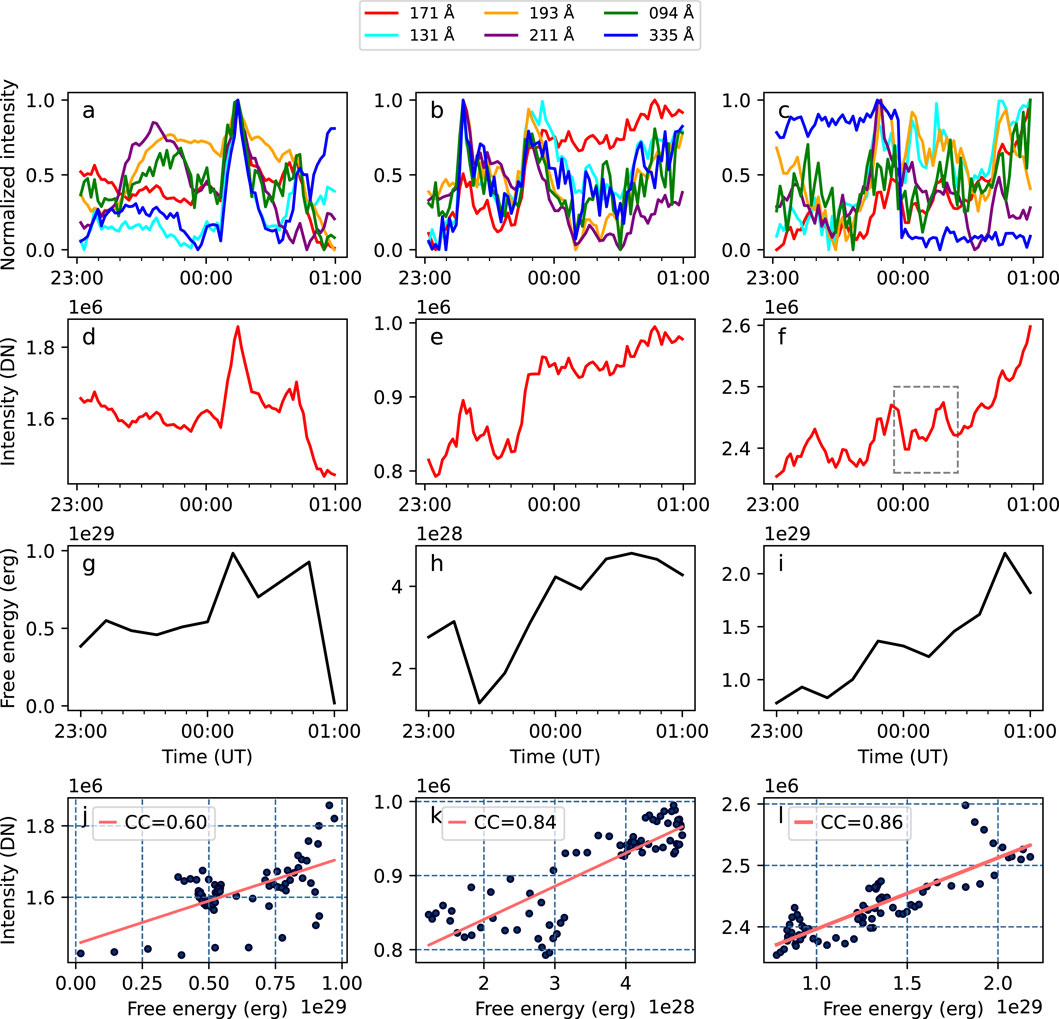
Figure 3. Time evolution of AIA EUV intensity and magnetic free energy. (A–C): Normalized intensity curves for six EUV channels. (D–F): Intensity curves at 171 Å. The dashed box in (F) marking the time period shown in Figure 1F. (G–I): Magnetic free energy evolution. (J–L) Scatter plots of the correlation coefficient between the free energy and the corresponding EUV 171 Å intensity above. The linear fit is shown by the red solid line. Columns from left to right correspond to F1, F2, and F3 shown in Figure 2.

We choose the range of EUV intensity to encompass the source region of the eruption as much as possible, such as the box corresponding to F1. In addition to capturing the sigmoid hot channel structures of the eruption core region, we also need to capture the region where the material falls along the arc trajectory as shown in Figure 1A. For the selection of the region F2, besides enclosing the wizard hat structure, we also try to avoid including another similar eruption structure in the west, so the region cannot be chosen too large. For the region F3, we choose the three neighboring eruption regions. Figure 1F reveals that the overall intensity variation is mainly determined by these three major eruptions occurring at different times. As for the calculation of the magnetic energy, we keep the calculation regions of magnetic energy and EUV intensity as consistent as possible, which encompass the main magnetic poles related to the eruptions.

In fact, the change in region size does not significantly affect the trend of magnetic field or EUV intensity changes, but only their amplitudes. Through our investigations, we find that as long as the core region of the eruption source is included, the overall trend of intensity and magnetic energy changes will not change too much, and the larger the region, the smaller the impact on the amplitude when scaling the region area, because most of the contribution comes from the intensity and magnetic energy of the core region.

Compared to the 171 Å channel, the correlation with other channels is not as strong. We attribute this primarily to the characteristic emission temperatures of different types of solar features. The 171 Å exhibits a better temperature response to the quiet corona, while the 131 Å and 94 Å are more sensitive to the flaring corona (Lemen et al., 2012). We observe that F1, a small-scale filament eruption with flaring characteristics located in a quiet region, contrasts with F2, which shows no sigificant eruption but rather a slow release of energy through tiny jets driven by reconnection. The magnetic energy of F2 may accumulate through quasi-static processes. AIA 171 Å observations are more effective in capturing such features during non-eruptive periods, whereas the 131 Å and 94 Å channels are better suited for detecting high-temperature plasma during impulsive flares. As a result, F2 shows a stronger correlation between magnetic energy and EUV intensity at 171 Å compared to the 131 Å and 94 Å channels, and this difference in correlation is more pronounced than in region F1.

3 Discussion

Our analysis reveals an interesting finding: the integrated EUV intensity shows strong correlation with magnetic free energy within the specified time intervals. The three regions exhibit eruptions of different scales. F1 corresponds to a failed small-scale filament eruption, where we believe the magnetic free energy is partially converted into thermal energy through dissipation, while a significant portion transform into kinetic energy of the upward-moving material, which eventually falls back to the solar surface due to gravitational and magnetic confining force. Figure 4 illustrates the magnetic confining force changes with height above each eruption source region, characterized by the decay index (Kliem and Török, 2006). We use PFSS model to calculate the decay index (Stansby et al., 2020). The critical heights for torus instability in all three regions exceed 150 Mm. Such heights are typically beyond the reach of small-scale filaments, which makes torus instability-driven eruptions and subsequent interplanetary mass and energy transport unlikely. In other words, even if the eruption energy is fully converted to kinetic energy, it ultimately dissipates as thermal energy within the corona.

Figure 4

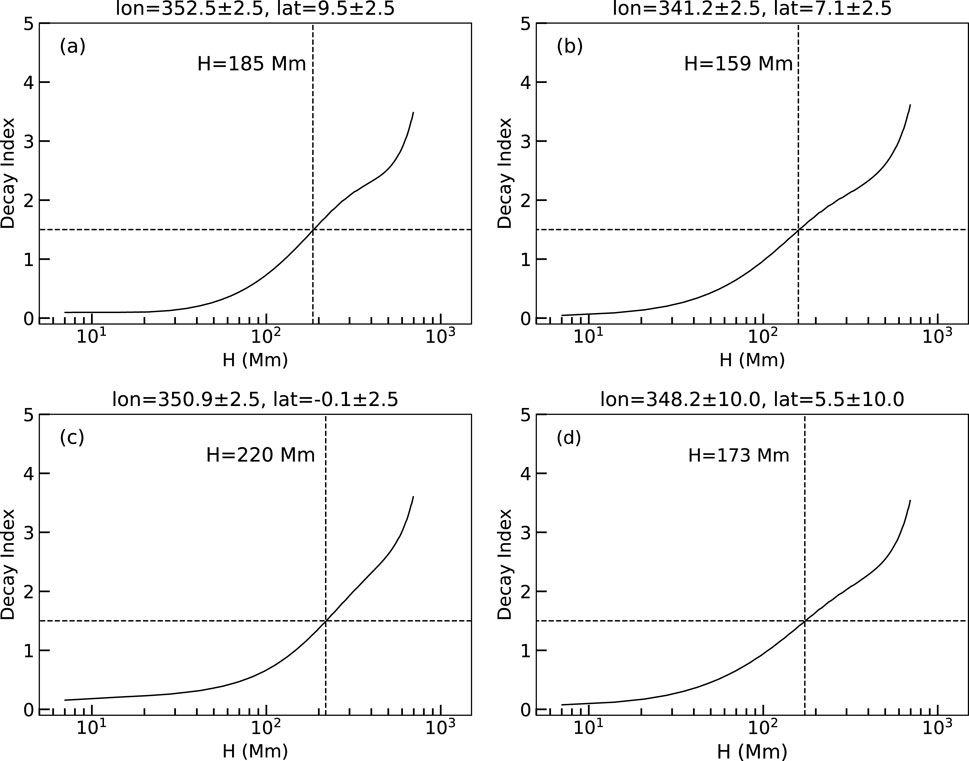
Figure 4. Decay index $n$ from PFSS model. (A–C) Decay index profiles above regions F1, F2, and F3, with calculation ranges in Carrington coordinates shown above each panel. Critical height H for torus instability onset ($n$ = 1.5) is marked. Panel (D) shows the average decay index profile over a larger region encompassing all three events.

Unlike active region flares, where EUV peaks are followed by significant energy drops, the EUV intensity here reveals an unexpected correlation with magnetic free energy. We propose this occurs because, in contrast to large-scale eruptive events, there is no significant mass or energy transfer outside the computation domain. Moreover, these small-scale eruptions may not significantly impact the photospheric magnetic field causing irreversible changes, as observed in the studies of active region eruptions (Wang et al., 1992; Hudson, 2000; Wang et al., 2014). Additionally, the NLFFF extrapolation method cannot adequately capture the nonlinear processes of magnetic reconnection, which prevents the free energy from showing a significant decrease associated with energy release. Nevertheless, we believe that using the continuous increase in free energy to represent magnetic energy deposition is reasonable. In essence, the extrapolated free energy changes primarily reflect the evolution of the photospheric magnetic field, which transfers and deposits energy into coronal magnetic fields. However, this deposited free energy is expected to be actually released through magnetic reconnection to heat the corona. In contrast, EUV integrated intensity depends on real-time emission changes, which typically intensify during flares or magnetic reconnection events through the photospheric motions. The 171 Å emission is particularly sensitive to coronal temperature changes, which corresponds to the background magnetic structure of quiet regions. All these above lead to our hypothesis, i.e., the continuous shuffling and intermixing of field footpoints in the photospheric convection causes coronal magnetic fields to wind and interweave. This process continuously leads to energy dissipation through magnetic reconnection of the braiding coronal magnetic fields, with the dissipated energy manifesting as a deposition of the free energy.

This aligns well with the nanoflare hypothesis proposed by Parker (1988). Therefore, we can expect that continuous smaller-scale magnetic reconnection events, similar in size to the observed quiet-Sun coronal brightenings, may provide a relatively stable, continuous heating source. For instance, the integrated intensity curve of F3 is the result of three smaller-scale eruptive features. The sum of their individual integrated intensity curve (Figure 1F) has almost the same shape with the integrated intensity curve obtained over the entire region (Figure 3F). The intensity curve correlates well with the changes in magnetic free energy, with a correlation coefficient of 0.86. Based on the strong correlation between the free energy and the EUV intensity, we hypothesize that most of the deposited free energy is actually released through magnetic reconnection, which enables us to estimate the energy for heating the corona within these areas by calculating ($\mathrm{\Delta }$ ${\text{E}}_{\mathit{free}}$).

Considering only the change from the minimum to the maximum free energy during a time interval, and ignoring the fluctuations within the time interval, we can roughly estimate that the three events could provide energy fluxes of $\sim$ $1.8\times 10$⁶ erg cm^-2 s^-1, $\sim$ $7\times 10$⁵ erg cm^-2 ${\text{s}}^{-1}$, and $\sim$ $1.2\times 10$⁶ erg ${\text{cm}}^{-2}$ ${\text{s}}^{-1}$, respectively. While these values are larger than the average quiet-Sun coronal energy loss rate ($\sim$ $3\times 10$⁵ erg ${\text{cm}}^{-2}$ ${\text{s}}^{-1}$; Withbroe and Noyes, 1977; Klimchuk, 2006), we have not excluded the energy from the chromosphere, the loss rate of which can be significantly higher ($\sim$ $4\times 10$⁶ erg ${\text{cm}}^{-2}$ ${\text{s}}^{-1}$). Previous similar implementations by Wiegelmann et al. (2013) and Chitta et al. (2014) suggested that the energy was too small to explain coronal heating in the quiet Sun. However, Wiegelmann et al. (2013) used a potential field extrapolation model, which did not take into account the magnetic free energy associated with field tangling and twisting. Chitta et al. (2014) only calculated the energy conducted and radiated below the base of the corona, without considering the energy released through magnetic reconnection in the corona.

On the other hand, our calculations of the energy flux are still relatively crude and could be optimized in several ways, as we do not account for the energy rises and falls within our calculation intervals, which may indicate repeated energy replenishment and release. The relatively coarse temporal resolution (12 min) of HMI vector magnetograms could impact the $\mathrm{\Delta }$ ${\text{E}}_{\mathit{free}}$ measurements. Using quiet-Sun magnetic field for extrapolation may underestimate free energy estimation. A recent study by Beck et al. (2025) revealed an intriguing finding. By comparing magnetic field measurements from HMI with higher-resolution Hinode SP data, they found that HMI magnetic field data may be significantly underestimated. Specifically, the magnetic field strength in quiet regions with B $<$ 220 G might be underestimated by a factor of 3–10. Furthermore, they suggested that the free energy derived from magnetic field extrapolations across the entire field of view, including both active and quiet regions, could be underestimated by a factor of 2. Given these findings, our estimated free energy of the magnetic field is likely to be substantially lower than the true value. However, considering computational challenges and boundary condition selection that may introduce additional uncertainties, we do not intend to perform the mentioned field correction but may explore it in future research. Nevertheless, the strong correlations between magnetic free energy and EUV 171 Å integrated intensity imply a link between photospheric magnetic evolution and coronal temperature changes. We hope to uncover deeper insights into this relationship by examining more similar events in future work.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

RW: Writing–original draft, Writing–review and editing. YJ: Writing–review and editing. XZ: Writing–review and editing. CH: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The research was supported by National Key R&D Program of China (No. 2022YFF0503800), the Strategic Priority Research Program of the Chinese Academy of Sciences (No. XDB0560000), National Natural Science Foundation of China (NSFC, Grant No. 12073032), National Key R&D Program of China (No. 2021YFA0718600), and the Specialized Research Fund for State Key Laboratories of China. XZ also acknowledges support from NSFC under grants 42204176, CH acknowledges support from the Scientific Research Foundation for the PhD (Huizhou University, 2023JB008).

Acknowledgments

We thank the anonymous reviewers for their constructive feedback, which significantly improved the quality of this manuscript. We acknowledge the use of data from Solar Orbiter and SDO. Solar Orbiter is a space mission of international collaboration between ESA and NASA, operated by ESA. The EUI instrument was built by CSL, IAS, MPS, MSSL/UCL, PMOD/WRC, ROB, LCF/IO with funding from the Belgian Federal Science Policy Office (BELSPO/PRODEX PEA 4000134088); the Centre National d’Etudes Spatiales (CNES); the UK Space Agency (UKSA); the Bundesministerium für Wirtschaft und Energie (BMWi) through the Deutsches Zentrum für Luft-und Raumfahrt (DLR); and the Swiss Space Office (SSO).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aschwanden, M. (2004). Physics of the solar corona. An introduction. Berlin: Published by Praxis Publishing Ltd.

Google Scholar

Beck, C., Prasad, A., Hu, Q., Yalim, M. S., Gosain, S., and Choudhary, D. P. (2025). Derivation and application of a scaling between hinode/sp and sdo/hmi vector magnetic fields to improve magnetic field extrapolations. Astrophysical J. 978, 150. doi:10.3847/1538-4357/ad98e6

CrossRef Full Text | Google Scholar

Cheng, X., Priest, E. R., Li, H., Chen, J., Aulanier, G., Chitta, L. P., et al. (2023). Ultra-high-resolution observations of persistent null-point reconnection in the solar corona. Nat. Commun. 14, 2107. doi:10.1038/s41467-023-37888-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Chitta, L., Kariyappa, R., Van Ballegooijen, A., DeLuca, E., and Solanki, S. (2014). Nonlinear force-free field modeling of the solar magnetic carpet and comparison with sdo/hmi and sunrise/imax observations. Astrophysical J. 793, 112. doi:10.1088/0004-637x/793/2/112

CrossRef Full Text | Google Scholar

Chitta, L., Solanki, S. K., Peter, H., Cuadrado, R. A., Teriaca, L., Schühle, U., et al. (2021). Capturing transient plasma flows and jets in the solar corona. Astronomy and Astrophysics 656, L13. doi:10.1051/0004-6361/202141683

CrossRef Full Text | Google Scholar

Del Zanna, G., and Mason, H. E. (2018). Solar uv and x-ray spectral diagnostics. Living Rev. Sol. Phys. 15 (5), 5. doi:10.1007/s41116-018-0015-3

PubMed Abstract | CrossRef Full Text | Google Scholar

De Moortel, I., and Browning, P. (2015). Recent advances in coronal heating. Philosophical Trans. R. Soc. Lond. Ser. A 373, 20140269. doi:10.1098/rsta.2014.0269

PubMed Abstract | CrossRef Full Text | Google Scholar

Heyvaerts, J., and Priest, E. R. (1983). Coronal heating by phase-mixed shear alfven waves. Astronomy Astrophysics 117 (2), 220–234.

Google Scholar

Hoeksema, J. T., Liu, Y., Hayashi, K., Sun, X., Schou, J., Couvidat, S., et al. (2014). The helioseismic and magnetic imager (HMI) vector magnetic field pipeline: overview and performance. Sol. Phys. 289, 3483–3530. doi:10.1007/s11207-014-0516-8

CrossRef Full Text | Google Scholar

Hudson, H. (2000). Implosions in coronal transients. Astrophysical J. 531, L75–L77. doi:10.1086/312516

PubMed Abstract | CrossRef Full Text | Google Scholar

Ionson, J. A. (1978). Resonant absorption of alfvénic surface waves and the heating of solar coronal loops. Astrophysical J. Part 226 (1), 650–673. doi:10.1086/156648

CrossRef Full Text | Google Scholar

Kliem, B., and Török, T. (2006). Torus instability. Phys. Rev. Lett. 96, 255002. doi:10.1103/PhysRevLett.96.255002

PubMed Abstract | CrossRef Full Text | Google Scholar

Klimchuk, J. A. (2006). On solving the coronal heating problem. Sol. Phys. 234, 41–77. doi:10.1007/s11207-006-0055-z

CrossRef Full Text | Google Scholar

Klimchuk, J. A. (2015). Key aspects of coronal heating. Philosophical Trans. R. Soc. A Math. Phys. Eng. Sci. 373, 20140256. doi:10.1098/rsta.2014.0256

PubMed Abstract | CrossRef Full Text | Google Scholar

Lemen, J. R., Title, A. M., Akin, D. J., Boerner, P. F., Chou, C., Drake, J. F., et al. (2012). The atmospheric imaging assembly (AIA) on the solar dynamics observatory (SDO). Sol. Phys. 275, 17–40. doi:10.1007/s11207-011-9776-8

CrossRef Full Text | Google Scholar

Müller, D., St. Cyr, O. C., Zouganelis, I., Gilbert, H. R., Marsden, R., Nieves-Chinchilla, T., et al. (2020). The Solar Orbiter mission. Science overview. Astron. Astrophys. 642, A1. doi:10.1051/0004-6361/202038467

CrossRef Full Text | Google Scholar

Parker, E. N. (1988). Nanoflares and the solar X-ray corona. Astrophys. J. 330, 474. doi:10.1086/166485

CrossRef Full Text | Google Scholar

Parnell, C. E., and De Moortel, I. (2012). A contemporary view of coronal heating. Philosophical Trans. R. Soc. A Math. Phys. Eng. Sci. 370, 3217–3240. doi:10.1098/rsta.2012.0113

PubMed Abstract | CrossRef Full Text | Google Scholar

Pesnell, W. D., Thompson, B. J., and Chamberlin, P. C. (2012). The solar dynamics observatory (SDO). Sol. Phys. 275, 3–15. doi:10.1007/s11207-011-9841-3

CrossRef Full Text | Google Scholar

Priest, E. (2014). Magnetohydrodynamics of the Sun. Cambridge University Press.

Google Scholar

Priest, E., Chitta, L., and Syntelis, P. (2018). A cancellation nanoflare model for solar chromospheric and coronal heating. Astrophysical J. Lett. 862, L24. doi:10.3847/2041-8213/aad4fc

CrossRef Full Text | Google Scholar

Reale, F. (2014). Coronal loops: observations and modeling of confined plasma. Living Rev. Sol. Phys. 11 (4), 4. doi:10.12942/lrsp-2014-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Rochus, P., Auchère, F., Berghmans, D., Harra, L., Schmutz, W., Schühle, U., et al. (2020). The solar orbiter EUI instrument: the extreme ultraviolet imager. Astron. Astrophys. 642, A8. doi:10.1051/0004-6361/201936663

CrossRef Full Text | Google Scholar

Scherrer, P. H., Schou, J., Bush, R. I., Kosovichev, A. G., Bogart, R. S., Hoeksema, J. T., et al. (2012). The helioseismic and magnetic imager (HMI) investigation for the solar dynamics observatory (SDO). Sol. Phys. 275, 207–227. doi:10.1007/s11207-011-9834-2

CrossRef Full Text | Google Scholar

Schou, J., Scherrer, P. H., Bush, R. I., Wachter, R., Couvidat, S., Rabello-Soares, M. C., et al. (2012). Design and ground calibration of the helioseismic and magnetic imager (HMI) instrument on the solar dynamics observatory (SDO). Sol. Phys. 275, 229–259. doi:10.1007/s11207-011-9842-2

CrossRef Full Text | Google Scholar

Stansby, D., Yeates, A., and Badman, S. (2020). pfsspy: a python package for potential field source surface modelling. J. Open Source Softw. 5, 2732. doi:10.21105/joss.02732

CrossRef Full Text | Google Scholar

Van Doorsselaere, T., Srivastava, A. K., Antolin, P., Magyar, N., Vasheghani Farahani, S., Tian, H., et al. (2020). Coronal heating by mhd waves. Space Sci. Rev. 216, 140–40. doi:10.1007/s11214-020-00770-y

CrossRef Full Text | Google Scholar

Wang, H., Varsik, J., Zirin, H., Canfield, R. C., Leka, K. D., and Wang, J. (1992). Joint vector magnetograph observations at BBSO, huairou station and mees solar observatory. Sol. Phys. 142, 11–20. doi:10.1007/BF00156630

CrossRef Full Text | Google Scholar

Wang, R., Liu, Y. D., Yang, Z., and Hu, H. (2014). Magnetic field restructuring associated with two successive solar eruptions. Astrophys. J. 791, 84. doi:10.1088/0004-637X/791/2/84

CrossRef Full Text | Google Scholar

Wang, R., Liu, Y. D., Zhao, X., and Hu, H. (2023). Observations of mini coronal dimmings caused by small-scale eruptions in the quiet sun. Astrophysical J. Lett. 952, L29. doi:10.3847/2041-8213/ace437

CrossRef Full Text | Google Scholar

Wiegelmann, T. (2004). Optimization code with weighting function for the reconstruction of coronal magnetic fields. Sol. Phys. 219, 87–108. doi:10.1023/B:SOLA.0000021799.39465.36

CrossRef Full Text | Google Scholar

Wiegelmann, T., Solanki, S., Borrero, J., Peter, H., Barthol, P., Gandorfer, A., et al. (2013). Evolution of the fine structure of magnetic fields in the quiet sun: observations from sunrise/imax and extrapolations. Sol. Phys. 283, 253–272. doi:10.1007/s11207-013-0249-0

CrossRef Full Text | Google Scholar

Wiegelmann, T., Thalmann, J. K., Inhester, B., Tadesse, T., Sun, X., and Hoeksema, J. T. (2012). How should one optimize nonlinear force-free coronal magnetic field extrapolations from SDO/HMI vector magnetograms? Sol. Phys. 281, 37–51. doi:10.1007/s11207-012-9966-z

CrossRef Full Text | Google Scholar

Withbroe, G. L., and Noyes, R. W. (1977). Mass and energy flow in the solar chromosphere and corona. In: Annu. Rev. Astron. Astrophys. 15 Palo Alto, Calif., Annual Reviews, Inc., p. 363–387. doi:10.1146/annurev.aa.15.090177.002051

CrossRef Full Text | Google Scholar

Yang, S., Zhang, J., Jin, C., Li, L., and Duan, H. (2009). Response of the solar atmosphere to magnetic field evolution in a coronal hole region. Astronomy and Astrophysics 501, 745–753. doi:10.1051/0004-6361/200810601

CrossRef Full Text | Google Scholar