Modeling the transport and anisotropy of energetic electrons in solar flares

Transport of energetic electrons in the flare loop is important to understanding nonthermal emissions in solar flares. In this work, we model the propagation of electrons by numerically solving the particle transport equation which includes the physics of magnetic mirroring and turbulent pitch-angle diffusion. We find that both the fractions of electrons trapped in the looptop and precipitating into the solar surface display a non-monotonic behavior with increasing scattering rate. In the moderate diffusion regime, the precipitation fraction is highest and we expect intense nonthermal HXR and microwave emissions at the footpoints. With no or weak pitch-angle scattering, the velocity space distribution can be highly anisotropic both in the looptop and loopleg regions. Different patterns of stripes with positive gradients in the perpendicular direction can drive the electron cyclotron maser instability with higher efficiency than the classical loss-cone distribution, facilitating the excitation of coherent solar radio bursts. Our simulation results highlight the effects of turbulent pitch-angle scattering on electron trap/precipitation and anisotropic distribution in solar flares, which may help us understand the precipitation of magnetospheric electrons accounting for the aurora as well.

1 Introduction

Solar flares are the most powerful energy-release phenomena on the Sun (e.g., Fletcher et al., 2011; Benz, 2017). A large number of charged particles are accelerated to high energies, including electrons, protons, and heavy ions, which can further excite nonthermal emissions from radio to gamma-rays via different radiation mechanisms. Although the primary acceleration mechanism remains unclear (Miller et al., 1997; Zharkova et al., 2011; Kong et al., 2019; Li et al., 2021), it is generally believed that electrons are accelerated in the coronal region above flare loops. After being injected at the top of flare loops, accelerated electrons travel to the loop footpoints and deposit energy in the high-density chromosphere, resulting in chromospheric evaporation. In some strong flares, energetic particles can deliver energy to the deeper atmosphere and have impact on the photosphere, suggested as the driver of white-light flares and sunquakes (e.g., Wu et al., 2023). Therefore, the acceleration and transport of energetic electrons plays a central role in the solar flare dynamics.

Energetic electrons are not free-streaming and subject to various effects during their transport from the looptop to the footpoints. The transport effects include magnetic mirroring due to the convergence in magnetic field, pitch-angle scattering by magnetic turbulence, energy loss and pitch-angle scattering via Coulomb collisions, return current, etc (e.g., Fletcher and Martens, 1998; Minoshima et al., 2011; Jeffrey et al., 2014; Kontar et al., 2014; Bian et al., 2017; Effenberger and Petrosian, 2018; Musset et al., 2018; Allred et al., 2020; Tang et al., 2020; Kong et al., 2022). Therefore, the pitch-angle distribution of energetic electrons is time dependent and should not be isotropic. Anisotropy in the velocity space is of critical importance to nonthermal emissions. It plays a fundamental role in plasma wave excitation in coherent emission mechanisms of solar radio bursts (Melrose, 2017). For example, electron-cyclotron maser emission requires a positive gradient of perpendicular direction, such as loss cone and horseshoe distributions (e.g., Melrose andWheatland, 2016; Zhao G. Q. et al., 2016; Ning et al., 2021a; Ning et al., 2021b; Tang et al., 2024). Anisotropic distribution can also affect the intensity, spectrum, and polarization of incoherent emissions, e.g., in microwave (e.g., Kuznetsov and Fleishman, 2021) and X-rays (e.g., Kuznetsov and Fleishman, 2021) and X-rays (e.g., Charikov et al., 2012; Melnikov et al., 2013).

Magnetic turbulence is an essential element both in particle acceleration (e.g., stochastic or shock acceleration) and transport processes in solar flares. Recent observations from nonthermal broadening of spectral lines by Hinode/EIS (e.g., Stores et al., 2021) revealed the presence of turbulence throughout the flare loop, although the strongest is at the looptop. In MHD simulations of magnetic reconnection in solar flares, the impact of reconnection outflows on the flare loop can trigger various instabilities and cause a highly turbulent plasma environment (e.g., Ruan et al., 2023; Wang et al., 2023; Ye et al., 2023). Recently, Effenberger and Petrosian (2018) studied the particle escape time for different initial pitch-angle distributions by solving the Fokker-Planck transport equation and assuming isotropic pitch-angle scattering by magnetic turbulence. Melnikov and Filatov (2020) investigated the conditions for the generation of whistler turbulence in the flare loop, which can resonate with energetic electrons and significantly affect their spectral and pitch-angle distributions (Melnikov and Filatov, 2021).

In this work, we numerically model the propagation of energetic electrons after being injected into the flare loop, and focus on the effects of magnetic mirror and turbulent scattering on the transport and anisotropic distribution of electrons. The paper is organized as follows. Section 2 describes our numerical model and Section 3 presents the simulation results. Summary and discussion are given in Section 4.

2 Numerical model

For the flare loop, we use an analytical two-dimensional magnetic field model in the $x-y$ plane (Lin et al., 1995; Minoshima et al., 2010),

$A_z\left(x,y\right)=-\frac{y+d}{x^2+{\left(y+d\right)}^2}-\frac{y}{{\left(a+d\right)}^2},$

$B_x\left(x,y\right)=\frac{\partial A_z}{\partial y}=-\left[\frac{x^2-{\left(y+d\right)}^2}{{\left\{x^2+{\left(y+d\right)}^2\right\}}^2}+\frac{1}{{\left(a+d\right)}^2}\right],$

$B_y\left(x,y\right)=-\frac{\partial A_z}{\partial x}=-\frac{2x\left(y+d\right)}{{\left\{x^2+{\left(y+d\right)}^2\right\}}^2},$

where $A_z$ is the flux function, $B_x$ and $B_y$ are two components of the magnetic field, $a$ is the height of X-type neutral line at the top of flare loops, and $d$ is the depth of the dipole below the photosphere. In Figures 1A, 2, the thin curves are contours of $A_z$ and illustrate the magnetic field lines of the flare loop model. Here we assume $a$ = 80 Mm, $d$ = 50 Mm.

Figure 1

Figure 1. Simulation results for three representative electrons. (A): electron trajectories plotted over the magnetic field lines, (B, C): temporal variations of $y$ and $\mu$. The electron without scattering is plotted in black, while the two electrons with weak scattering are plotted in red and blue. Note that in panel (A) the red and blue curves are shifted to avoid overlapping.

Figure 2

Figure 2. Spatial distributions of electrons at three different energies, 5–10 keV, 20–30 keV, $>$50 keV, in $RunA$. Panels (A–C) are at three simulation times, ${\tau }_c$ (A), 2${\tau }_c$ (B), and 3${\tau }_c$ (C), respectively. Black arrows denote streams of electrons bouncing back and forth in the right side of the loop.

Following our previous work Kong et al. (2022), we model the transport of energetic electrons in the flare loop by numerically solving the focused transport equation (Roelof, 1969; Skilling, 1971; van den Berg et al., 2020). The equation includes various transport effects, such as streaming along the magnetic field, advection with the solar wind, pitch-angle scattering, magnetic focusing/mirroring, and adiabatic cooling. Therefore, it has been widely applied to study the acceleration and transport of solar energetic particles (e.g., Qin et al., 2006; Zhang et al., 2009; Dröge et al., 2010; Zuo et al., 2011; Wang et al., 2012; Zhao L. et al., 2016; Hu et al., 2017; Zhang and Zhao, 2017; Wei et al., 2019; Wijsen et al., 2019). A similar Fokker-Planck transport equation has also been used in modeling energetic electrons in solar flares, in which the effects of magnetic mirroring, Coulomb collisions, and pitch-angle scattering are often included (e.g., Hamilton and Petrosian, 1990; Fletcher, 1995; Kontar et al., 2014; Effenberger and Petrosian, 2018; Melnikov and Filatov, 2021).

In this work, we focus on the effect of pitch-angle scattering on electron trapping/precipitation and the anisotropic distribution of energetic electrons. We neglect the advection term and the energy change due to Coulomb collisions, compression and shear in plasma flow (Kong et al., 2022). Test-particle simulations in synthetic turbulence suggested that the perpendicular diffusion coefficient is a few percent of the parallel diffusion coefficient (Giacalone and Jokipii, 1999). Cross-field diffusion may affect both the size and energy dependence of nonthermal emissions (Kontar et al., 2011), and the escape of electrons to the open field line. Here it is neglected for simplicity. The reduced particle transport equation can be written as (Roelof, 1969; Effenberger and Petrosian, 2018),

$\frac{\partial f}{\partial t}=-v\mu \widehat{\mathit{b}}\cdot \nabla f-\frac{v\left(1-{\mu }^2\right)}{2L_B}\frac{\partial f}{\partial \mu }+\frac{\partial }{\partial \mu }{D}_{\mu \mu }\frac{\partial f}{\partial \mu },$

where $f$ is the distribution function of charged particles, $v$ is the particle speed, $\mu$ is the pitch-angle cosine, and $t$ is the time. The terms on the right-hand side describe the electron streaming along the direction of magnetic field $\widehat{\mathit{b}}$, the magnetic mirroring effect with the focusing length $L_B={(\widehat{\mathit{b}}\cdot \nabla lnB)}^{-1}$, and the pitch-angle diffusion with a coefficient $D_{\mu \mu }$.

The pitch-angle diffusion coefficient $D_{\mu \mu }$ describes the resonant interaction between the particle and the turbulent magnetic field. In the quasi-linear theory, it is given by (Jokipii, 1971),

$D_{\mu \mu }=\frac{\pi }{4}{\mathrm{\Omega }}_0\left(1-{\mu }^2\right)\frac{k_{r}P\left(k_r\right)}{B_0^2},$

where ${\mathrm{\Omega }}_0=q{B}_0/m$ is the particle gyrofrequency with the mass $m$ and the charge $q$, $P(k)$ is the turbulence power spectrum, and $k_r={\mathrm{\Omega }}_0/(v|\mu |)$ is the resonant wavenumber. We assume the form of Kolmogorov turbulence spectrum with the spectral index $\mathrm{\Gamma }$ = 5/3. In the non-relativistic limit, the pitch-angle diffusion coefficient can be expressed as (Beeck and Wibberenz, 1986),

$D_{\mu \mu }=D_{\mu \mu 0}{\left(\frac{p}{p_0}\right)}^{\mathrm{\Gamma }-1}\left(1-{\mu }^2\right)\left(|\mu {|}^{\mathrm{\Gamma }-1}+h_0\right).$

$D_{\mu \mu 0}$ is a constant describing the scattering rate and depends on the level of magnetic field fluctuation. $p_0$ is the particle momentum at the energy $E_0$ = 10 keV. The parameter $h_0$ is added to describe the finite scattering through $\mu$ = 0 and here we set $h_0$ = 0.05.

Because the transport equation is essentially a Fokker-Planck equation, it can be recast into a set of stochastic differential equations (SDEs) (e.g., Zhang, 1999; Strauss and Effenberger, 2017). Here we use the following time-forward SDEs to trace the particle’s position and pitch-angle (Kong et al., 2022).

$d\mathit{X}=v\mu \widehat{\mathit{b}}dt,$

$d\mu =\left[-\frac{v\left(1-{\mu }^2\right)}{2L_B}+\frac{\partial D_{\mu \mu }}{\partial \mu }\right]dt+\sqrt{2D_{\mu \mu }}d{W}_{\mu }\left(t\right),$

where $d{W}_{\mu }$ is a Wiener process.

In the simulations, we assume that electrons have been accelerated near the top of the flare loop and only consider the transport process in the loop. Energetic electrons with a power-law energy spectrum, $f(E)\sim E^{-\delta }$, are impulsively injected in the looptop region, given by $x$ = [-2, 2] Mm and $y$ = [48, 52] Mm. Here we set the electron energy spectral index $\delta$ = 3, and the energy range is between 0.7 and 153 keV (electron velocity between 0.05 $c$ and 0.64 $c$, $c$ is the speed of light). The initial electron pitch-angle distribution is assumed to be isotropic. In each simulation, a total of 6 million pseudo-particles are injected. We note that the injection of accelerated electrons is not necessarily at the top of the loop in a realistic solar flare. For example, when the reconnection takes place between a closed loop with other loops or an open field line. This may give rise to asymmetric distribution in space and anisotropy of energetic electrons.

To study the effect of turbulent scattering on electron transport and anisotropic distribution, we conduct five simulation runs with different levels of magnetic fluctuations by changing the value of $D_{\mu \mu 0}$. We take $D_{\mu \mu 0}$ = 0 $(RunA)$, 0.0272 ${\text{s}}^{-1}$ $(RunB)$, 0.272 ${\text{s}}^{-1}$ $(RunC)$, 2.72 ${\text{s}}^{-1}$ $(RunD)$, and 27.2 ${\text{s}}^{-1}$ $(RunE)$. Then, the time scale of turbulent scattering is approximately ${\tau }_d$ = 1/$D_{\mu \mu 0}$, varying between 36.8 s and 0.0368 s from $RunB$ to $RunE$. Note that for electrons with the energy $E_0$ = 10 keV, $v_{e0}$ = 0.195 $c$ = $5.85\times 10^7$ m ${\text{s}}^{-1}$, and a loop length of $L_0$ = 100 Mm, the crossing time scale in the loop where they are injected, ${\tau }_c$ = $L_0$/$v_{e0}$ = 1.71 s.

Three regimes of turbulent pitch-angle diffusion was defined in Bespalov et al. (1987), weak $({\tau }_d>\sigma {\tau }_c)$, moderate $({\tau }_c<{\tau }_d<\sigma {\tau }_c)$, and strong $({\tau }_d<{\tau }_c)$, where $\sigma$ is the mirror ratio of the flare loop. For the field lines where electrons are injected, the magnitudes of magnetic field in the looptop and at the footpoint are 40.8 G and 241 G, respectively. Then, the mirror ratio is $\sigma =B_{FP}/B_{LT}$ = 5.9, and the critical pitch angle is ${\theta }_c$ = $arcsin\sqrt{1/\sigma }$ = 24.3$°$. Therefore, $RunB$ corresponds to the weak diffusion regime, $RunC$ in the moderate diffusion regime, and $RunD$ and $RunE$ in the strong diffusion regime. We can also calculate the particle mean free path for 10 keV electrons, ${\lambda }_{\Vert 0}=3{\kappa }_{\Vert 0}/v_{e0}$, where ${\kappa }_{\Vert 0}$ is the spatial diffusion coefficient along the direction of the magnetic field and related to the pitch-angle diffusion coefficient $D_{\mu \mu }$ (Kong et al., 2022). Then, we can get ${\lambda }_{\Vert 0}$ = 4,100 Mm in $RunB$, much larger than the loop length; ${\lambda }_{\Vert 0}$ = 410 Mm in $RunC$, comparable to the loop length; ${\lambda }_{\Vert 0}$ = 41 Mm and 4.1 Mm in $RunD$ and $RunE$, smaller than the loop length.

3 Simulation results

To test the validity of the simulation, particularly the pitch-angle scattering through $\mu$ = 0, we first examine the trajectory of a single electron. Figure 1 shows the simulation results for three representative electrons, trajectories plotted over the magnetic field lines, variations of $y$ position and $\mu$ as a function of time. The three electrons are injected in the same position at the looptop with the same energy of 10 keV and initial pitch-angle of 45$°$. For the electron without turbulent scattering (as in $RunA$), the curves are plotted in black. It is reflected at $y_R$ = 35.7 Mm, where the magnetic field strength is $B_R$ = 81.7 G. We then can get the critical pitch-angle at the reflection point is $arcsin\sqrt{B_{LT}/B_R}$ = 45$°$, consistent with the initial condition. For the two electrons with weak turbulent scattering (as in $RunB$), the curves are plotted in red and blue, respectively. Due to the pitch-angle diffusion, electrons can be scattered into the loss cone. Therefore, the two electrons can go deeper than the expected reflection position $y_R$. For the electron plotted in blue, it is not reflected while moving to the left footpoint and finally precipitates into the solar surface. As seen from the evolution of $\mu$ in panel (c), the electrons can be scattered smoothly through $\mu$ = 0.

Figure 2 displays the spatial distributions of energetic electrons at three energy ranges, 5–10 keV, 20–30 keV, and $>$50 keV, in $RunA$. The simulation times in panels (a)-(c) are ${\tau }_c$ = 1.71 s, 2${\tau }_c$ = 3.42 s, and 3${\tau }_c$ = 5.13 s, respectively. Due to the trapping effect of magnetic mirror, most electrons are concentrated around the top of the flare loop. Since the initial pitch-angle distribution of injected electrons is isotropic, electrons with larger pitch-angles take much more time as they move from the loop top to lower altitudes. Therefore, we can see multiple streams of electrons bouncing back and forth in the loop, as denoted by the black arrows (only the right side is marked). The number density of streaming electrons is smaller than that trapped at the looptop and the pattern varies with energy. As shown below, the streams of electrons are the reason for the presence of stripes in the velocity space distribution. For different simulation runs, the spatial distribution is generally similar. With increasing scattering rate, the distribution gets smoother and streaming electrons are harder to be distinguished.

We now analyze the effect of different scattering rates (as described by $D_{\mu \mu 0}$) on the trapping and precipitation of electrons in the flare loop. Figure 3 shows the fractions of electrons trapped in the looptop and precipitating to the solar surface for various energies, 5 keV, 10 keV, 50 keV, and 100 keV, respectively, at the end of the simulation (3${\tau }_c$). For each energy, the trapped fraction is defined as $F_t=N_{y>45}/N_{\mathit{inject}}$, where $N_{y>45}$ is the number of electrons that remain trapped at $y>$ 45 Mm in the simulation domain and $N_{\mathit{inject}}$ is the injected population. For the precipitating fraction, it is defined as $F_p=1-N_{\mathit{loop}}/N_{\mathit{inject}}$, where $N_{\mathit{loop}}$ is the number of electrons that remain bouncing in the loop and have not reached the bottom boundary. As noted above, for the field line where electrons are initially injected, the mirror ratio $\sigma$ = 5.9 and the critical pitch angle ${\theta }_c$ = 24.3$°$. The electrons with pitch angle smaller than ${\theta }_c$ fall into the loss cone and can escape. Therefore, it results in an expected precipitating fraction $F_{pc}$ = 27%, as denoted by the dashed line in Figure 3B. In the simulation of $RunA$ without turbulent scattering, the precipitating fractions at different energies agree well with the theoretical predication.

Figure 3

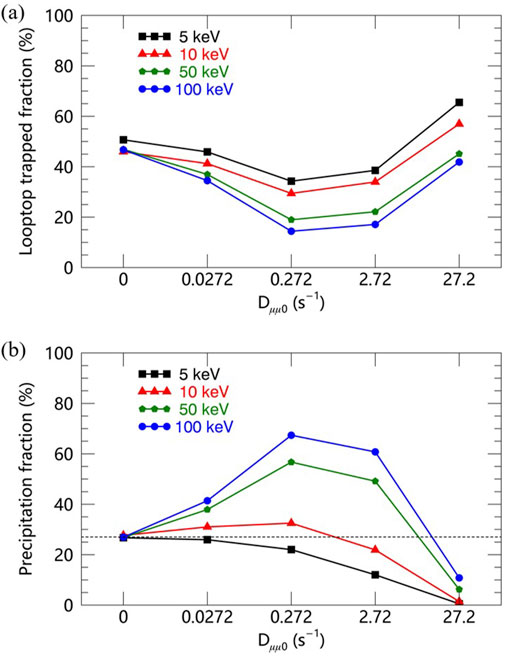
Figure 3. Fractions of electrons at various energies trapped in the looptop (A) and precipitating to the solar surface (B) at time 3${\tau }_c$ as a function of the scattering rates in the five simulation runs. The dashed line in panel (B) denotes the expected precipitating fraction $F_{pc}$ = 27% in the magnetic mirror without turbulent scattering.

As shown in Figure 3, with increasing scattering rate, the variations of both the trapped fraction $(F_t)$ and precipitation fraction $(F_p)$ display a non-monotonic pattern. From the non-scattering case in $RunA$ to the weak and intermediate scattering cases in $RunB$ and $RunC$, the trapped fraction decreases and the precipitation fraction increases. Due to pitch-angle scattering, more and more electrons with initial pitch-angle larger than the critical value ${\theta }_c$ = 24.3$°$ are scattered into the loss cone and escape. However, for the low-energy electrons of 5 keV, although the trapped fraction decreases, there is no rise in the precipitation fraction. It suggests that the electrons have not reached the solar surface while they have left the looptop, possibly due to their low speed. For the strong scattering cases in $RunD$ and $RunE$, the pitch-angle scattering is so frequent that electrons should stay at the looptop for much longer time before moving to lower altitudes. Thus, from moderate to strong scattering, the trapped fraction increases and the precipitation fraction decreases. This indicates that the precipitation fraction is highest in the moderate diffusion regime, therefore, in favor of high intensity of nonthermal HXR and microwave emissions in the footpoints. In contrast, to reproduce a bright nonthermal source in the looptop, either weak or strong scattering is required. We also find that the magnitude of variation is energy dependent. The trapped fraction decreases at higher energies, while the precipitation fraction increases with energy.

Due to the effects of magnetic mirror and turbulent scattering, the particle distribution in the velocity space varies along the flare loop and with time. Figures 4, 5 show the velocity space distribution in the looptop and loopleg regions, respectively. $v_{\Vert }$ and $v_{\perp }$ are velocity components in the parallel and perpendicular directions. Here the looptop is integrated over $x$ = [-5, 5] Mm and $y$ = [45, 55] Mm, and the loopleg on the right side is integrated over $x$ = [20, 40] Mm and $y$ = [20, 30] Mm. The simulation results in $RunA$, $RunB$, and $RunE$ are displayed in panels (a), (b), and (c), respectively. The left and right columns are at two different times, ${\tau }_c$ and 3${\tau }_c$, respectively. The dashed line in each panel illustrates the critical pitch angle ${\theta }_c$ = 24.3$°$ for the magnetic field lines where electrons are injected.

Figure 4

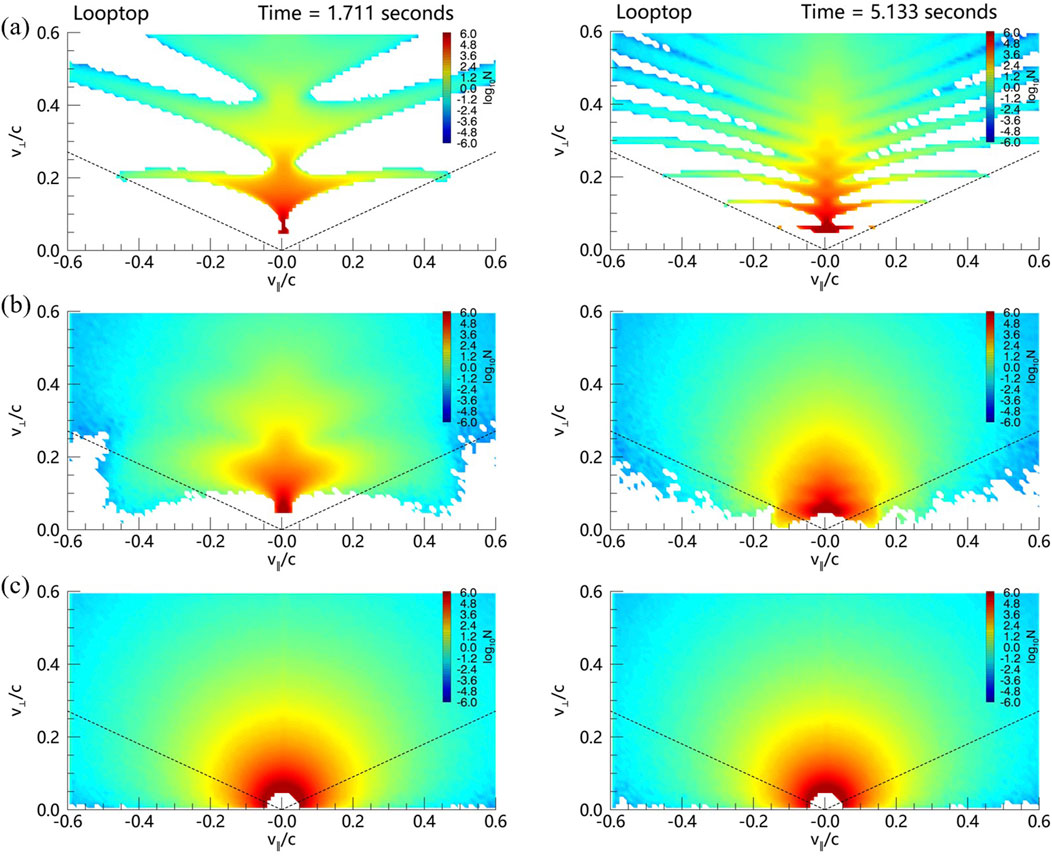
Figure 4. Velocity space distribution in the looptop region at two different times, ${\tau }_c$ (left) and 3${\tau }_c$ (right). Panels (A–C) are results in $RunA$, $RunB$, and $RunE$, respectively. The dashed line in each panel denotes the critical pitch angle ${\theta }_c$ = 24.3$°$.

Figure 5

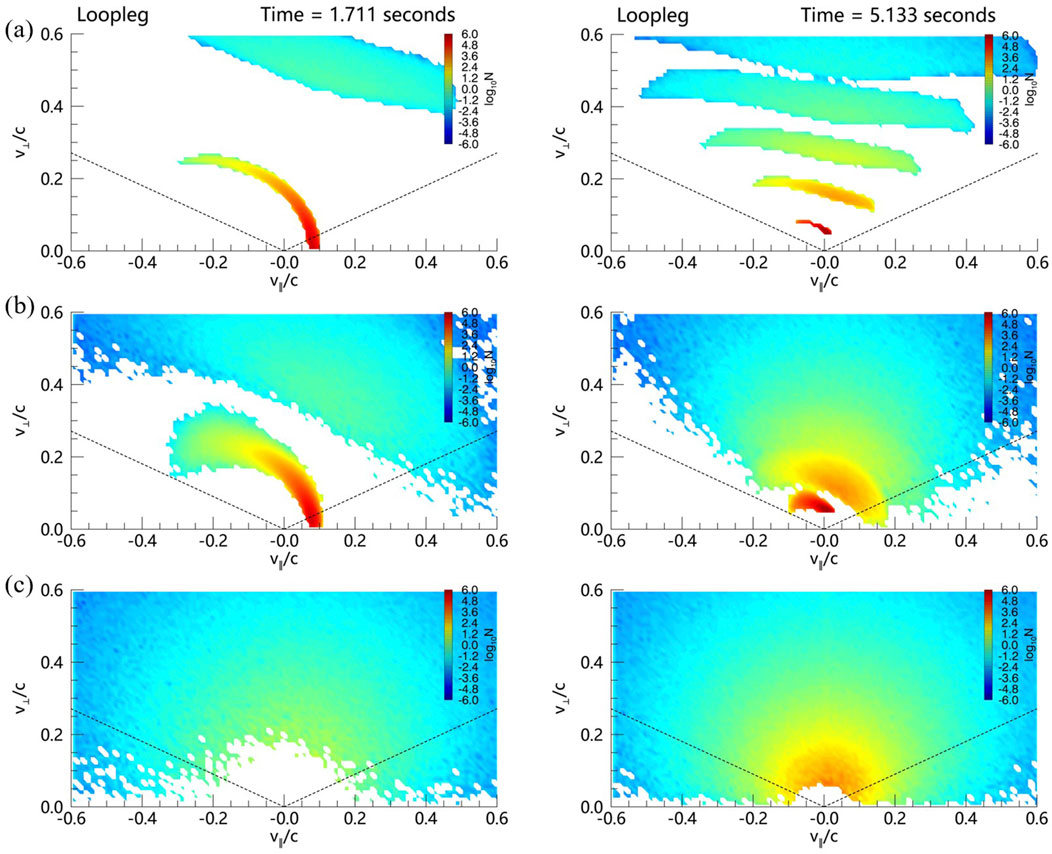
Figure 5. Same as plotted in Figure 4, but for velocity space distribution in the right loopleg region.

In the non-scattering $(RunA)$ and weak scattering $(RunB)$ runs, the velocity space distributions are obviously anisotropic, but exhibit different patterns in the looptop and loopleg regions. As shown in panel (a) in Figure 4, at the looptop, multiple narrow bands (which resemble branches or fishbone) stretch out from the vertical axis and present positive gradients in the perpendicular direction, i.e., $\partial f/\partial v_{\perp }>0$. The number of bands increases with time and they gather towards the origin of the coordinate system. If we continue to run the simulation, the gap between stripes gets smaller and the distribution will evolve into a double-sided loss cone. Those electrons at the looptop are mainly reflected and trapped electrons, therefore most electrons are distributed in the perpendicular direction. Since electrons with larger $v_{\Vert }$ can leave the looptop faster or be reflected faster, multiple streams of electrons can be observed as shown in Figure 2, leading to fishbone-like multiple bands as time goes on. As shown in panel (b) in Figure 4, with weak scattering, similar stripes can be seen at the early time, which also exhibits $\partial f/\partial v_{\perp }>0$. Due to turbulent scattering, the width of stripes increases and some electrons fill in the gaps between stripes. At later time as shown on the right, the gaps between stripes are nearly smoothed out and the distribution resemble a double-sided loss cone. As shown in panel (c), for the simulation with strong scattering $(RunE)$, the distribution has already become nearly isotropic at the early time. In addition, compared with the non-scattering case in panel (a), electrons are scattered into the loss cone (below the dashed line) at various energies as a result of pitch-angle scattering, consistent with the results as shown in Figure 3.

As shown in Figure 5, in the loopleg region, the velocity space distributions look different from that in the looptop. In panels (a) and (b), at the early time, the first stripe (close to the origin of the coordinate system) is circular-shaped and represents the contribution from the beam-like electrons before getting reflected. The distribution resembles the so-called horseshoe distribution as observed in the source of auroral kilometric radiation (AKR, see, e.g., Ergun et al., 2000; Treumann, 2006). It contains positive gradients in both parallel and perpendicular directions, i.e., $\partial f/\partial v_{\Vert }>0$ and $\partial f/\partial v_{\perp }>0$. At later time, after being reflected, $v_{\Vert }$ evolves from positive to negative values and the distribution presents mainly $\partial f/\partial v_{\perp }>0$. Similarly, the other stripes appearing later also have $\partial f/\partial v_{\perp }>0$. As in the looptop, if we continue to run the simulation, the distribution will eventually evolve into a double-sided loss cone, but it is asymmetric. For the case with strong scattering, as shown in panel (c), the distribution is nearly isotropic.

4 Summary and discussion

In this work, we numerically model the transport of energetic electrons in the flare loop after being injected around the top of the loop. We examine the effect of turbulent pitch-angle scattering on the trap/precipitation fraction and velocity space distribution by introducing different levels of scattering rates. We find that both the fractions of electrons trapped in the looptop and precipitating into the solar surface vary in a non-monotonic way with increasing scattering rate. From non-/weak to intermediate scattering, the trapped fraction decreases and the precipitation fraction increases, while from intermediate to strong scattering, the trapped fraction increases and the precipitation fraction decreases. Therefore, in the moderate diffusion regime, we expect intense nonthermal HXR and microwave emissions in the footpoints due to the highest precipitation fraction. In addition, the trap/precipitation fraction apparently shows energy dependence, which will affect the electron energy spectra both in the looptop and loopleg regions. We also find that the velocity space distribution varies both along the loop and with time. With non-/weak turbulent scattering, it presents different patterns of stripes and is highly anisotropic both in the looptop and loopleg, and gradually evolves into a double-sided loss-cone as the simulation continues. In the case of enhanced turbulent scattering, the distribution becomes nearly isotropic because a large number of electrons can be scattered into the loss-cone.

In flare regions with strong magnetic fields, the plasma frequency can be smaller compared to the electron gyro-frequency, i.e., ${\omega }_{\text{pe}}/{\mathrm{\Omega }}_{\text{ce}}<1$. Different anisotropic features in the velocity space can drive the electron cyclotron maser instability (ECMI) in different manners. In the looptop region, most electrons are distributed in the perpendicular direction, with horizontal branches stretching outward. Positive gradients along the loss-cone boundaries mainly generate fundamental X-mode emissions via ECMI, propagating along the parallel and oblique directions (see, e.g., Yoon and Ziebell, 1995; Ning et al., 2021b). According to the plasma kinetic theory, the linear growth rates of ECMI can be approximated with the integral of the velocity distribution function gradient $(\partial f/\partial v_{\perp })$ along the resonance curve in the phase space (Wu and Lee, 1979; Wu, 1985). We note that in the non-scattering case, the distribution presents branch features with sharp gradients where the resonance curve could pass through. This could drive ECMI with higher efficiency, compared to the classical loss-cone distribution. In the loopleg region, the distribution resembles the horseshoe distribution in the source of planetary AKR. Recently, the horseshoe-driven ECMI has been applied to explain the solar spikes (e.g., Melrose and Wheatland, 2016; Ning et al., 2021a). Multi-stripe distribution has been demonstrated in earlier studies (e.g., White et al., 1983). Yousefzadeh et al. (2021) carried out kinetic simulations and found that such electrons mainly generate second harmonic X-mode emissions (X2), which could solve the escaping difficulty of fundamental emission in solar corona. For the strong scattering case, the distributions in both regions are nearly isotropic, making it hard to drive the ECMI.

We used the reduced transport equation that includes magnetic mirroring and turbulent pitch-angle scattering in this study. Other effects such as Coulomb collisions and cross-filed diffusion have been neglected and will be discussed in future work. We considered different regimes of turbulent pitch-angle diffusion as defined in Bespalov et al. (1987). However, the level of magnetic turbulence in realistic flares remains unclear. Recently, some studies (Kontar et al., 2017; Stores et al., 2021) investigated the spatial and temporal distributions of turbulence in one solar flare from the observations of nonthermal broadening of spectral lines. They calculated the turbulent kinetic energy density from the nonthermal broadening velocity $(v_{\mathit{nth}})$, which approximates the energy density associated with the magnetic field fluctuations. Then, one can estimate the level of turbulent magnetic fluctuation $\delta B/B\sim v_{\mathit{nth}}/v_A$ (Kontar et al., 2017). Taking the Alfven speed $v_A\sim$2000 km ${\text{s}}^{-1}$, while $v_{\mathit{nth}}$ ranging between $\sim$10–100 km ${\text{s}}^{-1}$, we can get $\delta B/B$ is about 0.05%–5%. This indicates that the turbulence is relatively weak on average, at least for this flare event, and may provide the required condition for anisotropic distribution.

A similar electron trap and precipitation process occurs in the Earth’s magnetosphere, where the resonant interaction between energetic electrons and plasma waves such as chorus waves has been applied to explain the characteristics of aurora (e.g., Thorne et al., 2010; Zhang et al., 2022). Our simulation results may provide helpful insights to the dynamics of energetic particles in the radiation belts of magnetosphere.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

XK: Conceptualization, Investigation, Methodology, Project administration, Writing–original draft, Writing–review and editing. HN: Writing–review and editing. YC: Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. XK is supported by the National Key R&D Program of China under grant 2022YFF0503002 (2022YFF0503000), the National Natural Science Foundation of China under grants 42074203, and Yunnan Key Laboratory of Solar Physics and Space Science under grant YNSPCC202218. HN is supported by NSFC 12203031 and the China Postdoctoral Science Foundation (2022TQ0189). The work was carried out at National Supercomputer Center in Tianjin (TH-3F) and Guangzhou (TianHe-2).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Allred, J. C., Alaoui, M., Kowalski, A. F., and Kerr, G. S. (2020). Modeling the transport of nonthermal particles in flares using fokker-planck kinetic theory. Astrophys. J. 902, 16. doi:10.3847/1538-4357/abb239

CrossRef Full Text | Google Scholar

Beeck, J., and Wibberenz, G. (1986). Pitch angle distributions of solar energetic particles and the local scattering properties of the interplanetary medium. Astrophys. J. 311, 437. doi:10.1086/164784

CrossRef Full Text | Google Scholar

Benz, A. O. (2017). Flare observations. Living Rev. Sol. Phys. 14 (2B), 2. doi:10.1007/s41116-016-0004-3

CrossRef Full Text | Google Scholar

Bespalov, P. A., Zaitsev, V. V., and Stepanov, A. V. (1987). On the origin of time delays in hard X-ray and gamma-ray emission of solar flares. Sol. Phys. 114, 127–140. doi:10.1007/bf00193073

CrossRef Full Text | Google Scholar

Bian, N. H., Emslie, A. G., and Kontar, E. P. (2017). The role of diffusion in the transport of energetic electrons during solar flares. Astrophys. J. 835, 262. doi:10.3847/1538-4357/835/2/262

CrossRef Full Text | Google Scholar

Charikov, Y. E., Mel’nikov, V. F., and Kudryavtsev, I. V. (2012). Intensity and polarization of the hard X-ray radiation of solar flares at the top and footpoints of a magnetic loop. Geomagnetism Aeronomy 52, 1021–1031. doi:10.1134/S0016793212080051

CrossRef Full Text | Google Scholar

Dröge, W., Kartavykh, Y. Y., Klecker, B., and Kovaltsov, G. A. (2010). Anisotropic three-dimensional focused transport of solar energetic particles in the inner heliosphere. Astrophys. J. 709, 912–919. doi:10.1088/0004-637x/709/2/912

CrossRef Full Text | Google Scholar

Effenberger, F., and Petrosian, V. (2018). The relation between escape and scattering times of energetic particles in a turbulent magnetized plasma: application to solar flares. Appl. Sol. Flares 868, L28. doi:10.3847/2041-8213/aaedb3

CrossRef Full Text | Google Scholar

Ergun, R. E., Carlson, C. W., McFadden, J. P., Delory, G. T., Strangeway, R. J., and Pritchett, P. L. (2000). Electron-cyclotron maser driven by charged-particle acceleration from magnetic field-aligned electric fields. Astrophys. J. 538, 456–466. doi:10.1086/309094

CrossRef Full Text | Google Scholar

Fletcher, L. (1995). On the generation of loop-top impulsive hard X-ray sources. 303, L9–303L.

Google Scholar

Fletcher, L., Dennis, B. R., Hudson, H. S., Krucker, S., Phillips, K., Veronig, A., et al. (2011). An observational overview of solar flares 159, 19–106. doi:10.1007/978-1-4614-3073-5_3

PubMed Abstract | CrossRef Full Text | Google Scholar

Fletcher, L., and Martens, P. C. H. (1998). A model for hard X-ray emission from the top of flaring loops. Astrophys. J. 505, 418–431. doi:10.1086/306137

CrossRef Full Text | Google Scholar

Giacalone, J., and Jokipii, J. R. (1999). The transport of cosmic rays across a turbulent magnetic field. Astrophys. J. 520, 204–214. doi:10.1086/307452

CrossRef Full Text | Google Scholar

Hamilton, R. J., and Petrosian, V. (1990). Effects of Coulomb collisions on cyclotron maser and plasma wave growth in magnetic loops. Astrophys. J. 365, 778. doi:10.1086/169531

CrossRef Full Text | Google Scholar

Hu, J., Li, G., Ao, X., Zank, G. P., and Verkhoglyadova, O. (2017). Modeling particle acceleration and transport at a 2-D CME-driven shock. J. Geophys. Res. (Space Physics) 122, 10,938–10,963. doi:10.1002/2017JA024077

CrossRef Full Text | Google Scholar

Jeffrey, N. L. S., Kontar, E. P., Bian, N. H., and Emslie, A. G. (2014). On the variation of solar flare coronal X-ray source sizes with energy. Astrophys. J. 787, 86. doi:10.1088/0004-637x/787/1/86

CrossRef Full Text | Google Scholar

Jokipii, J. R. (1971). Propagation of cosmic rays in the solar wind. Rev. Geophys. Space Phys. 9, 27–87. doi:10.1029/rg009i001p00027

CrossRef Full Text | Google Scholar

Kong, X., Chen, B., Guo, F., Shen, C., Li, X., Ye, J., et al. (2022). Numerical modeling of energetic electron acceleration, transport, and emission in solar flares: connecting loop-top and footpoint hard X-ray sources. Astrophys. J. Lett. 941, L22. doi:10.3847/2041-8213/aca65c

CrossRef Full Text | Google Scholar

Kong, X., Guo, F., Shen, C., Chen, B., Chen, Y., Musset, S., et al. (2019). The acceleration and confinement of energetic electrons by a termination shock in a magnetic trap: an explanation for nonthermal loop-top sources during solar flares. 887, L37. doi:10.3847/2041-8213/ab5f67887L

CrossRef Full Text | Google Scholar

Kontar, E. P., Bian, N. H., Emslie, A. G., and Vilmer, N. (2014). Turbulent pitch-angle scattering and diffusive transport of hard X-ray-producing electrons in flaring coronal loops. Astrophys. J. 780, 176. doi:10.1088/0004-637x/780/2/176

CrossRef Full Text | Google Scholar

Kontar, E. P., Hannah, I. G., and Bian, N. H. (2011). Acceleration, magnetic fluctuations, and cross-field transport of energetic electrons in a solar. Flare Loop 730, L22. doi:10.1088/2041-8205/730/2/l22

CrossRef Full Text | Google Scholar

Kontar, E. P., Perez, J. E., Harra, L. K., Kuznetsov, A. A., Emslie, A. G., Jeffrey, N. L. S., et al. (2017). Turbulent kinetic energy in the energy balance of a solar flare. Phys. Rev. Lett. 118, 155101. doi:10.1103/PhysRevLett.118.155101

PubMed Abstract | CrossRef Full Text | Google Scholar

Kuznetsov, A. A., and Fleishman, G. D. (2021). Ultimate fast gyrosynchrotron codes. Astrophys. J. 922, 103. doi:10.3847/1538-4357/ac29c0

CrossRef Full Text | Google Scholar

Li, X., Guo, F., and Liu, Y.-H. (2021). The acceleration of charged particles and formation of power-law energy spectra in nonrelativistic magnetic reconnection. Phys. Plasmas 28, 052905. doi:10.1063/5.0047644

CrossRef Full Text | Google Scholar

Lin, J., Forbes, T. G., Priest, E. R., and Bungey, T. N. (1995). Models for the motions of flare loops and ribbons. Sol. Phys. 159, 275–299. doi:10.1007/BF00686534

CrossRef Full Text | Google Scholar

Melnikov, V. F., Charikov, Y. E., and Kudryavtsev, I. V. (2013). Spatial brightness distribution of hard X-Ray emission along flare loops. Geomagnetism Aeronomy 53, 863–866. doi:10.1134/S0016793213070153

CrossRef Full Text | Google Scholar

Melnikov, V. F., and Filatov, L. V. (2020). Conditions for whistler generation by nonthermal electrons in flare loops. Geomagnetism Aeronomy 60, 1126–1131. doi:10.1134/S0016793220080150

CrossRef Full Text | Google Scholar

Melnikov, V. F., and Filatov, L. V. (2021). Nonthermal electron diffusion modes in whistler turbulence in flare loops. Geomagnetism Aeronomy 61, 1189–1196. doi:10.1134/S0016793221080144

CrossRef Full Text | Google Scholar

Melrose, D. B. (2017). Coherent emission mechanisms in astrophysical plasmas. Rev. Mod. Plasma Phys. 1, 5. doi:10.1007/s41614-017-0007-0

CrossRef Full Text | Google Scholar

Melrose, D. B., and Wheatland, M. S. (2016). Is cyclotron maser emission in solar flares driven by a horseshoe distribution? Sol. Phys. 291, 3637–3658. doi:10.1007/s11207-016-1006-y

CrossRef Full Text | Google Scholar

Miller, J. A., Cargill, P. J., Emslie, A. G., Holman, G. D., Dennis, B. R., LaRosa, T. N., et al. (1997). Critical issues for understanding particle acceleration in impulsive solar flares. J. Geophys. Res. 102, 14631–14659. doi:10.1029/97ja00976

CrossRef Full Text | Google Scholar

Minoshima, T., Masuda, S., and Miyoshi, Y. (2010). Drift-kinetic modeling of particle acceleration and transport in solar flares. Astrophys. J. 714, 332–342. doi:10.1088/0004-637x/714/1/332

CrossRef Full Text | Google Scholar

Minoshima, T., Masuda, S., Miyoshi, Y., and Kusano, K. (2011). Coronal electron distribution in solar flares: drift-kinetic model. Astrophys. J. 732, 111. doi:10.1088/0004-637x/732/2/111

CrossRef Full Text | Google Scholar

Musset, S., Kontar, E. P., and Vilmer, N. (2018). Diffusive transport of energetic electrons in the solar corona: X-ray and radio diagnostics. diagnostics 610, A6. doi:10.1051/0004-6361/201731514

CrossRef Full Text | Google Scholar

Ning, H., Chen, Y., Ni, S., Li, C., Zhang, Z., Kong, X., et al. (2021a). Harmonic electron-cyclotron maser emissions driven by energetic electrons of the horseshoe distribution with application to solar radio spikes. 651, A118. doi:10.1051/0004-6361/202140427

CrossRef Full Text | Google Scholar

Ning, H., Chen, Y., Ni, S., Li, C., Zhang, Z., Kong, X., et al. (2021b). Harmonic maser emissions from electrons with loss-cone distribution in solar active regions. 920, L40. doi:10.3847/2041-8213/ac2cc6920L

CrossRef Full Text | Google Scholar

Qin, G., Zhang, M., and Dwyer, J. R. (2006). Effect of adiabatic cooling on the fitted parallel mean free path of solar energetic particles. J. Geophys. Res. (Space Physics) 111, A08101. doi:10.1029/2005JA011512

CrossRef Full Text | Google Scholar

Roelof, E. C. (1969). “Propagation of solar cosmic rays in the interplanetary magnetic field,” in Lectures in high-energy astrophysics. Editors H. Ögelman, and J. R. Wayland, 111.

Google Scholar

Ruan, W., Yan, L., and Keppens, R. (2023). Magnetohydrodynamic turbulence formation in solar flares: 3D simulation and synthetic observations. Astrophys. J. 947, 67. doi:10.3847/1538-4357/ac9b4e

CrossRef Full Text | Google Scholar

Skilling, J. (1971). Cosmic rays in the galaxy: convection or diffusion? Astrophys. J. 170, 265. doi:10.1086/151210

CrossRef Full Text | Google Scholar

Stores, M., Jeffrey, N. L. S., and Kontar, E. P. (2021). The spatial and temporal variations of turbulence in a solar flare. Astrophys. J. 923, 40. doi:10.3847/1538-4357/ac2c65

CrossRef Full Text | Google Scholar

Strauss, R. D. T., and Effenberger, F. (2017). A hitch-hiker’s guide to stochastic differential equations. Solut. Methods Energetic Part. Transp. Space Phys. Astrophysics 212, 151–192. doi:10.1007/s11214-017-0351-y

CrossRef Full Text | Google Scholar

Tang, J. F., Wu, D. J., Chen, L., Tan, C. M., and Wang, J. B. (2024). Electron cyclotron maser instability by evolving fast electron beams in the flare loops. Front. Astronomy Space Sci. 11, 1404145. doi:10.3389/fspas.2024.1404145

CrossRef Full Text | Google Scholar

Tang, J. F., Wu, D. J., Chen, L., Xu, L., and Tan, B. L. (2020). Parametric evolution of power-law energy spectra of flare accelerated electrons in the solar atmosphere. Atmosphere 904, 1. doi:10.3847/1538-4357/abc2ca

CrossRef Full Text | Google Scholar

Thorne, R. M., Ni, B., Tao, X., Horne, R. B., and Meredith, N. P. (2010). Scattering by chorus waves as the dominant cause of diffuse auroral precipitation 467, 943–946. doi:10.1038/nature09467

PubMed Abstract | CrossRef Full Text | Google Scholar

Treumann, R. A. (2006). The electron-cyclotron maser for astrophysical application. Astron. Astrophys. Rev. 13, 229–315. doi:10.1007/s00159-006-0001-y

CrossRef Full Text | Google Scholar

van den Berg, J., Strauss, D. T., and Effenberger, F. (2020). A primer on focused solar energetic particle transport. Space Sci. Rev. 216, 146. doi:10.1007/s11214-020-00771-x

CrossRef Full Text | Google Scholar

Wang, Y., Cheng, X., Ding, M., Liu, Z., Liu, J., and Zhu, X. (2023). Three-dimensional turbulent reconnection within the solar flare current sheet. Curr. Sheet 954, L36. doi:10.3847/2041-8213/acf19d

CrossRef Full Text | Google Scholar

Wang, Y., Qin, G., and Zhang, M. (2012). Effects of perpendicular diffusion on energetic particles accelerated by the interplanetary coronal mass ejection shock. Astrophys. J. 752, 37. doi:10.1088/0004-637x/752/1/37

CrossRef Full Text | Google Scholar

Wei, W., Shen, F., Yang, Z., Zhao, L., Wang, Y., Zuo, P., et al. (2019). Modeling solar energetic particle transport in 3D background solar wind: influences of the compression regions. J. Atmos. Solar-Terrestrial Phys. 182, 155–164. doi:10.1016/j.jastp.2018.11.012

CrossRef Full Text | Google Scholar

White, S. M., Melrose, D. B., and Dulk, G. A. (1983). Electron cyclotron masers during solar flares. Publ. Astron. Soc. Aust. 5, 188–191. doi:10.1017/s1323358000016829

CrossRef Full Text | Google Scholar

Wijsen, N., Aran, A., Pomoell, J., and Poedts, S. (2019). Modelling three-dimensional transport of solar energetic protons in a corotating interaction region generated with EUHFORIA 622, A28. doi:10.1051/0004-6361/201833958

CrossRef Full Text | Google Scholar

Wu, C. S. (1985). Kinetic cyclotron and synchrotron maser instabilities: radio emission processes by direct amplification of radiation. Space Sci. Rev. 41, 215–298. doi:10.1007/bf00190653

CrossRef Full Text | Google Scholar

Wu, C. S., and Lee, L. C. (1979). A theory of the terrestrial kilometric radiation. Astrophys. J. 230, 621–626. doi:10.1086/157120

CrossRef Full Text | Google Scholar

Wu, H., Dai, Y., and Ding, M. D. (2023). Highly energetic electrons accelerated in strong solar flares as a preferred driver of sunquakes. Astrophys. J. Lett. 943, L6. doi:10.3847/2041-8213/acb0d1

CrossRef Full Text | Google Scholar

Ye, J., Raymond, J. C., Mei, Z., Cai, Q., Chen, Y., Li, Y., et al. (2023). Three-dimensional simulation of thermodynamics on confined turbulence in a large-scale CME-flare current sheet. Astrophys. J. 955, 88. doi:10.3847/1538-4357/acf129

CrossRef Full Text | Google Scholar

Yoon, P. H., and Ziebell, L. F. (1995). Quasilinear evolution of cyclotron maser instability. Phys. Rev. E 51, 4908–4916. doi:10.1103/PhysRevE.51.4908

PubMed Abstract | CrossRef Full Text | Google Scholar

Yousefzadeh, M., Ning, H., and Chen, Y. (2021). Harmonic electron cyclotron maser emission excited by energetic electrons traveling inside a coronal loop. Astrophys. J. 909, 3. doi:10.3847/1538-4357/abd8d5

CrossRef Full Text | Google Scholar

Zhang, M. (1999). A markov stochastic process theory of cosmic-ray modulation. Astrophys. J. 513, 409–420. doi:10.1086/306857

CrossRef Full Text | Google Scholar

Zhang, M., Qin, G., and Rassoul, H. (2009). Propagation of solar energetic particles in three-dimensional interplanetary magnetic fields. Astrophys. J. 692, 109–132. doi:10.1088/0004-637x/692/1/109

CrossRef Full Text | Google Scholar

Zhang, M., and Zhao, L. (2017). Precipitation and release of solar energetic particles from the solar coronal magnetic field. Astrophys. J. 846, 107. doi:10.3847/1538-4357/aa86a8

CrossRef Full Text | Google Scholar

Zhang, X.-J., Artemyev, A., Angelopoulos, V., Tsai, E., Wilkins, C., Kasahara, S., et al. (2022). Superfast precipitation of energetic electrons in the radiation belts of the Earth. Nat. Commun. 13, 1611. doi:10.1038/s41467-022-29291-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhao, G. Q., Feng, H. Q., Wu, D. J., Chen, L., Tang, J. F., and Liu, Q. (2016a). Cyclotron maser emission from power-law electrons with strong pitch-angle anisotropy. Astrophys. J. 822, 58. doi:10.3847/0004-637x/822/2/58

CrossRef Full Text | Google Scholar

Zhao, L., Zhang, M., and Rassoul, H. K. (2016b). Double power laws in the event-integrated solar energetic particle spectrum. Astrophys. J. 821, 62. doi:10.3847/0004-637x/821/1/62

CrossRef Full Text | Google Scholar

Zharkova, V. V., Arzner, K., Benz, A. O., Browning, P., Dauphin, C., Emslie, A. G., et al. (2011). Recent advances in understanding particle acceleration processes in solar flares. Space Sci. Rev. 159, 357–420. doi:10.1007/s11214-011-9803-y

CrossRef Full Text | Google Scholar

Zuo, P., Zhang, M., Gamayunov, K., Rassoul, H., and Luo, X. (2011). Energy spectrum of energetic particles accelerated by shock waves: from focused transport to diffusive acceleration. Astrophys. J. 738, 168. doi:10.1088/0004-637x/738/2/168

CrossRef Full Text | Google Scholar