New insights into supradense matter from dissecting scaled stellar structure equations

The strong-field gravity in general relativity (GR) realized in neutron stars (NSs) renders the equation of state (EOS) $P(\epsilon )$ of supradense neutron star matter to be essentially nonlinear and refines the upper bound for $\varphi \equiv P/\epsilon$ to be much smaller than the special relativity (SR) requirement with linear EOSs, where $P$ and $\epsilon$ are respectively the pressure and energy density of the system considered. Specifically, a tight bound $\varphi \lesssim 0.374$ is obtained by perturbatively anatomizing the intrinsic structures of the scaled Tolman–Oppenheimer–Volkoff (TOV) equations without using any input nuclear EOS. New insights gained from this novel analysis provide EOS-model-independent constraints on the properties (e.g., density profiles of the sound speed squared $s^2=\mathrm{d}P/\mathrm{d}\epsilon$ and trace anomaly $\mathrm{\Delta }=1/3-\varphi$) of cold supradense matter in NS cores. Using the gravity-matter duality in theories describing NSs, we investigate the impact of gravity on supradense matter EOS in NSs. In particular, we show that the NS mass $M_{\text{NS}}$, radius $R$, and compactness $\xi \equiv M_{\text{NS}}/R$ scale with certain combinations of its central pressure and energy density (encapsulating its central EOS). Thus, observational data on these properties of NSs can straightforwardly constrain NS central EOSs without relying on any specific nuclear EOS model.

1 Introduction

The speed of sound squared (SSS) $s^2=\mathrm{d}P/\mathrm{d}\epsilon$ (Landau and Lifshitz, 1987) quantifies the stiffness of the equation of state (EOS) expressed in terms of the relationship $P(\epsilon )$ between the pressure $P$ and the energy density $\epsilon$ of the system considered. The principle of causality of special relativity (SR) requires the speed of sound of any signal to stay smaller than the speed of light $c\equiv 1$, that is, $s\le 1$. For a linear EOS of the form $P=w\epsilon$ with $w$ being some constant, the condition $s^2\le 1$ is globally equivalent to $\varphi =P/\epsilon \le 1$. For such EOSs, the causality condition can be equivalently written as follows:

$\text{Principle\hspace{0.17em}of\hspace{0.17em}Causality\hspace{0.17em}of\hspace{0.17em}SR\hspace{0.17em}with\hspace{0.17em}linear\hspace{0.17em}EOS\hspace{0.17em}implies\hspace{0.17em}}P\le \epsilon \leftrightarrow \varphi \equiv P/\epsilon \le 1.(1)$

The indicated equivalence between $s^2\le 1$ and $\varphi \le 1$ could be demonstrated as follows: If $P$ could be greater than $\epsilon$ somewhere, then the curve of $P(\epsilon )$ may unavoidably across the line $P=\epsilon$ from below to above, indicating the slope at the crossing point is necessarily larger than 1, as illustrated in Figure 1. In the following, we use the above causality requirement on $\varphi$ with linear EOSs as a reference in discussing properties of supradense matter in strong-field gravity.

Figure 1

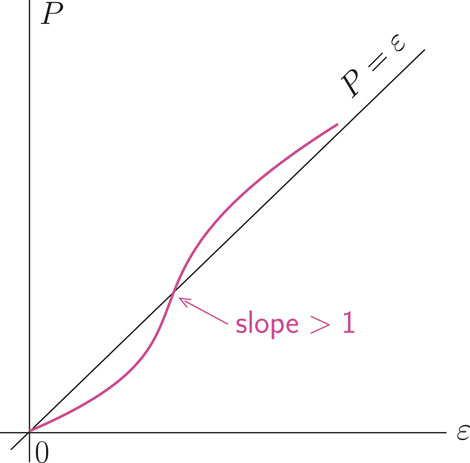
Figure 1. An illustration of the equivalence between $s^2\le 1$ with a linear EOS and $\varphi \le 1$: If $P$ could be greater than $\epsilon$ somewhere, then the curve of $P(\epsilon )$ must cross the line $P=\epsilon$ from below to above, indicating that $s^2=\mathrm{d}P/\mathrm{d}\epsilon >1$ at the crossing point.

The EOS of nuclear matter may be strongly nonlinear depending on both the internal interactions and the external environment/constraint of the system; this means that $\varphi \le 1$ is necessary but not sufficient to ensure supradense matter in all NSs always stays causal. For example, the EOS of noninteracting degenerate fermions (e.g., electrons) can be written in the polytropic form $P=K{\epsilon }^{\beta }$ (Shapiro and Teukolsky, 1983), where $\beta =5/3$ for non-relativistic and $\beta =4/3$ for extremely relativistic electrons; consequently, $\varphi \le {\beta }^{-1}<1$. Similarly, many years ago, Zel’dovich considered the EOS of an isolated ultra-dense system of baryons interacting through a vector field (Zel’dovich, 1961). In this case, $P=\epsilon \sim {\rho }^2$; here, $\rho$ is the baryon number density. Consequently, $P/\epsilon \le 1$ is obtained. The EOS of dense nuclear matter where nucleons interact through both the $\sigma$-meson and $\omega$-meson in the Walecka model (Walecka, 1974) is an example of this type. In particular, the $\omega$-field scales at asymptotically large density as $\omega \sim \rho$ while the $\sigma$-field scales $\sigma \sim {\rho }_{\text{s}}$ with the scalar density ${\rho }_{\text{s}}$ approaching some constant for $\rho \to \infty$ (Cai and Li, 2016); therefore, the vector field dominates at these densities. More generally, however, going beyond the vector field, the baryon density dependence of either $P(\rho )$ or $\epsilon (\rho )$ could be very complicated and nontrivial. The resulting EOS $P(\epsilon )$ could also be significantly nonlinear. The EOS of supradense matter under the intense gravity of NSs could be forced to be nonlinear as the equilibrium state of NSs is determined by extremizing the total action of the matter–gravity system through Hamilton’s variational principle. It is well known that the strong-field gravity in general relativity (GR) is fundamentally nonlinear; the EOS of NS matter, especially in its core, is thus also expected to be nonlinear. Therefore, the causality condition $s^2\le 1$ may be appreciably different from $\varphi \le 1$, and it may also effectively render the upper bound for $\varphi$ to be smaller than 1. Accurately determining an upper bound of $\varphi$ (equivalently a lower bound of the dimensionless trace anomaly $\mathrm{\Delta }=1/3-\varphi$) will thus help constrain properties of supradense matter in strong-field gravity.

The upper bound for $\varphi$ is a fundamental quantity essentially encapsulating the strong-field properties of gravity in GR. Its accurate determination may help improve our understanding of the nature of gravity. The latter is presently the least known among the four fundamental forces despite being the first one discovered in nature (Hoyle, 2003). An upper bound on $\varphi$ substantially different from 1 then vividly characterizes how GR affects the supradense matter existing in NSs. In some physical senses, this is similar to the effort in determining the Bertsch parameter. The latter was introduced as the ratio $E_{\text{UFG}}/E_{\text{FFG}}$ of the EOS of a unitary Fermi gas (UFG) over that of the free Fermi gas (FFG) $E_{\text{FFG}}$ (Giorgini et al., 2008); here, $E_{\text{FFG}}$ and $E_{\text{UFG}}$ are the energies per particle in the two systems considered. The EOS characterizes the strong interactions among fermions under the unitary condition. Extensive theoretical and experimental efforts have been made to constrain/fix the Bertsch parameter. Indeed, its accurate determination has already made a strong impact on understanding strongly interacting fermions (Giorgini et al., 2008; Bloch et al., 2008).

There are fundamental physics issues regarding both strong-field gravity and supradense matter EOS and their couplings. What is gravity? Is a new theory of light and matter needed to explain what happens at very high energies and temperatures? These are among the eleven greatest unanswered physics questions for this century, as identified in 2003 by the National Research Council of the U.S. National Academies (National Research Council, 2003). Compact stars provide far more extreme conditions necessary to test possible answers to these questions than terrestrial laboratories. A gravity-matter duality exists in theories describing NS properties; see, for example, Psaltis (2008) and Shao (2019) for recent reviews. Neutron stars are natural testing grounds for our knowledge of these issues. Some of their observational properties may help break the gravity-matter duality; see, for example, DeDeo and Psaltis (2003), Wen et al. (2009), Lin et al. (2014), He et al. (2015), Yang et al. (2020). Naturally, these issues are intertwined, and one may gain new insights into the EOS of supradense matter by analyzing features of strong-field gravity or vice versa. The matter-gravity duality reflects the deep connection between the microscopic physics of supradense matter and the powerful gravity effects of NSs. They both must be fully understood to unravel mysteries associated with compact objects in the Universe. In this brief review, we summarize the main physics motivation, formalism, and results of our recent efforts to gain new insights into the EOS of supradense matter in NS cores by perturbatively dissecting the intrinsic structures of the Tolman–Oppenheimer–Volkoff (TOV) equations (Tolman, 1939; Oppenheimer and Volkoff, 1939) without using any input nuclear EOS. For more details, we refer the readers to our original publications in Cai et al. (2023b), (Cai et al., 2023a), Cai and Li (2024a), and (Cai and Li, 2024b).

The rest of this article is organized as follows: First, in Section 2, we make a few remarks about some existing constraints on the EOS of supradense NS matter. Section 3 introduces the scaled TOV equations from which one can execute an effective perturbative expansion; the central SSS is obtained in Section 4. We then infer an upper bound for the ratio $\mathrm{X}\equiv {\varphi }_{\text{c}}=P_{\text{c}}/{\epsilon }_{\text{c}}$ of central pressure $P_{\mathrm{c}}$ over central energy density ${\epsilon }_{\mathrm{c}}$ for NSs at the maximum-mass configuration along the M-R curve. The generalization for the upper bound of $P/\epsilon$ is also studied in Section 4. In Section 5, we compare our prediction on the lower bound of $\mathrm{\Delta }=1/3-P/\epsilon$ with existing predictions in the literature. We summarize in Section 6 and give some perspectives for future studies. In the Appendix, we discuss an effective correction to $s_{\mathrm{c}}^2$ obtained in Section 4.

2 Remarks on some existing constraints on supradense NS matter

Understanding the EOS of supradense matter has long been an important issue in both nuclear physics and astrophysics (Walecka, 1974; Chin, 1977; Freedman and McLerran, 1977; Baluni, 1978; Wiringa et al., 1988; Akmal et al., 1998; Migdal, 1978; Morley and Kislinger, 1979; Shuryak, 1980; Bailin and Love, 1984; Lattimer and Prakash, 2001; Danielewicz et al., 2002; Steiner et al., 2005; Lattimer and Prakash, 2007; Alford et al., 2008; Li et al., 2008; Watts et al., 2016; Özel and Freire, 2016; Oertel et al., 2017; Vidaña, 2018). In fact, it has been an outstanding driver at many research facilities in both fields. For example, finding the EOS of the densest visible matter existing in our Universe is an ultimate goal of astrophysics in the era of high-precision multimessenger astronomy (Sathyaprakash et al., 2019). However, despite much effort and progress made during the last few decades using various observational data and models, especially since the discovery of GW170817 (Abbott et al., 2017a; 2018), GW190425 (Abbott et al., 2020a), GW190814 (Abbott et al., 2020b) and the recent NASA’s NICER (Neutron Star Interior Composition Explorer) mass-radius measurements for PSR J0740 + 6,620 (Fonseca et al., 2021; Riley et al., 2021; Miller et al., 2021; Salmi et al., 2022; Dittmann et al., 2024; Salmi et al., 2024), PSR J0030 + 0451 (Riley et al., 2019; Miller et al., 2019; Vinciguerra et al., 2024), and PSR J0437-4715 (Choudhury et al., 2024; Reardon et al., 2024), knowledge about the core NS EOS remains ambiguous and quite elusive (see, for example, Bose et al., 2018; De et al., 2018; Fattoyev et al., 2018; Lim and Holt, 2018; Most et al., 2018; Radice et al., 2018; Tews et al., 2018; Zhang et al., 2018; Bauswein et al., 2019; 2020; Baym et al., 2019; McLerran and Reddy, 2019; Most et al., 2019; Annala et al., 2020; 2023; Sedrakian et al., 2020; Zhao and Lattimer, 2020; Weih et al., 2020; Xie and Li, 2019; 2020; 2021; Drischler et al., 2020; 2021a; Li et al., 2020; Bombaci et al., 2021; Al-Mamun et al., 2021; Nathanail et al., 2021; Raaijmakers et al., 2021; Altiparmak et al., 2022; Breschi et al., 2022; Komoltsev and Kurkela, 2022; Perego et al., 2022; Huang et al., 2022; Tan et al., 2022a; b; Brandes et al., 2023b; a; Gorda et al., 2023; Han et al., 2023; Jiang et al., 2023; Ofengeim et al., 2023; Mroczek et al., 2023; Raithel and Most, 2023; Somasundaram et al., 2023; Zhang and Li, 2020; 2021; 2023b; a; Pang et al., 2023; Fujimoto et al., 2024; Providência et al., 2024; Rutherford et al., 2024). See recent reviews for additional discussion (for example, Baym et al., 2018; Baiotti, 2019; Li et al., 2019; Orsaria et al., 2019; Blaschke et al., 2020; Capano et al., 2020; Chatziioannou, 2020; Burgio et al., 2021; Dexheimer et al., 2021; Drischler et al., 2021b; Lattimer, 2021; Li et al., 2021; Lovato et al., 2022; Sedrakian et al., 2023; Kumar et al., 2024; Sorensen et al., 2024; Tsang et al., 2024).

Extensive theoretical investigations about the EOS of supradense NS matter have been conducted, and many interesting predictions have been made. For example, the realization of approximate conformal symmetry of quark matter at extremely high densities $\rho \gtrsim 40{\rho }_0$ with ${\rho }_0\equiv {\rho }_{\mathrm{s}\mathrm{a}\mathrm{t}}$ the nuclear saturation density implies the corresponding EOS approaches that of an ultra-relativistic Fermi gas (URFG) from below, namely (Bjorken, 1983; Kurkela et al., 2010):

$\mathrm{U}\mathrm{R}\mathrm{F}\mathrm{G}:P\lesssim \epsilon /3\leftrightarrow \varphi \lesssim 1/3,\text{\hspace{0.17em}\hspace{0.17em}at\hspace{0.17em}extremely\hspace{0.17em}high\hspace{0.17em}densities}.(2)$

For the URFG, $3P\approx \epsilon \sim {\rho }^{4/3}$. Therefore, $\varphi =P/\epsilon$ is at least upper bounded to be below 1/3 at these densities; equivalently, a lower bound on the dimensionless trace anomaly emerges:

$\mathrm{\Delta }\equiv 1/3-P/\epsilon \gtrsim 0,\text{\hspace{0.17em}\hspace{0.17em}at\hspace{0.17em}extremely\hspace{0.17em}high\hspace{0.17em}densities\hspace{0.17em}}\rho \gtrsim 40{\rho }_0.(3)$

This prompts the question of whether the bound $\varphi \le 1/3$ holds globally for dense matter or if some other bound(s) on $\varphi$ may exist. In this sense, massive NSs like PSR J1614-2230 (Demorest et al., 2010; Arzoumanian et al., 2018), PSR J0348 + 0432 (Antoniadis et al., 2013), PSR J0740 + 6,620 (Fonseca et al., 2021; Riley et al., 2021; Miller et al., 2021; Salmi et al., 2022; Dittmann et al., 2024; Salmi et al., 2024), and PSR J2215 + 5135 (Sullivan and Romani, 2024) provide an ideal testing bed for exploring such quantity. A sizable $\varphi \gtrsim \mathcal{O}(0.1)$ arises for NSs but not for ordinary stars or low-density nuclear matter (Cai and Li, 2024a). For example, considering stars such as white dwarfs (WDs), one has $P\lesssim 10^{22-23}\mathrm{d}\mathrm{y}\mathrm{n}\mathrm{e}\mathrm{s}/{\mathrm{c}\mathrm{m}}^2\approx 10^{-(11-10)}\mathrm{M}\mathrm{e}\mathrm{V}/{\mathrm{f}\mathrm{m}}^3$ and $\epsilon \lesssim 10^{8-9}\mathrm{k}\mathrm{g}/{\mathrm{m}}^3\sim 10^{-6}\mathrm{M}\mathrm{e}\mathrm{V}/{\mathrm{f}\mathrm{m}}^3$; thus, $\varphi \lesssim 10^{-(5-4)}$. The $\varphi$ could be even smaller for main-sequence stars like the Sun. Specifically, the pressure and energy density in the solar core are approximately $10^{-16}\mathrm{M}\mathrm{e}\mathrm{V}/{\mathrm{f}\mathrm{m}}^3$ and $10^{-10}\mathrm{M}\mathrm{e}\mathrm{V}/{\mathrm{f}\mathrm{m}}^3$, respectively, and therefore $\varphi \approx 10^{-6}$. These stars are Newtonian in the sense that GR effects are almost absent. Similarly, for NS matter around nuclear saturation density ${\rho }_0={\rho }_{\mathrm{s}\mathrm{a}\mathrm{t}}\approx 0.16{\mathrm{f}\mathrm{m}}^{-3}$, the pressure is estimated to be $P({\rho }_0)\approx P_0({\rho }_0)+P_{\mathrm{s}\mathrm{y}\mathrm{m}}({\rho }_0){\delta }^2\approx 3^{-1}L{\rho }_0{\delta }^2\lesssim 3\mathrm{M}\mathrm{e}\mathrm{V}/{\mathrm{f}\mathrm{m}}^3$. Its isospin-dependent part is $P_{\mathrm{s}\mathrm{y}\mathrm{m}}({\rho }_0)=3^{-1}L{\rho }_0$with $L\approx 60\mathrm{M}\mathrm{e}\mathrm{V}$ (Li et al., 2018; 2021) being the slope parameter of nuclear symmetry energy $E_{\mathrm{s}\mathrm{y}\mathrm{m}}(\rho )$at ${\rho }_0$, $\delta$is the isospin asymmetry of the system (${\delta }^2\lesssim 1$), and $P_0({\rho }_0)=0$is the pressure of symmetric nuclear matter (SNM) at ${\rho }_0$. The energy density at ${\rho }_0$is similarly estimated as $\epsilon ({\rho }_0)\approx [E_0({\rho }_0)+E_{\mathrm{s}\mathrm{y}\mathrm{m}}({\rho }_0){\delta }^2+M_{\mathrm{N}}]{\rho }_0\approx 150\mathrm{M}\mathrm{e}\mathrm{V}/{\mathrm{f}\mathrm{m}}^3$with $M_{\mathrm{N}}\approx 939\mathrm{M}\mathrm{e}\mathrm{V}$the nucleon static mass, $E_0({\rho }_0)\approx -16\mathrm{M}\mathrm{e}\mathrm{V}$the binding energy at ${\rho }_0$for SNM, and $E_{\mathrm{s}\mathrm{y}\mathrm{m}}({\rho }_0)\approx 32\mathrm{M}\mathrm{e}\mathrm{V}$ (Li, 2017), leading to $\varphi \lesssim 0.02$.

Based on the dimensional analysis and the definition of sound speed, we may write out the SSS generally as (we use the units in which $c=1$)

$s^2=\varphi f\left(\varphi \right),\varphi =P/\epsilon ,(4)$

where $f(\varphi )$ is dimensionless. For low-density matter, such as matter in ordinary stars and WDs or the nuclear matter around saturation density ${\rho }_0$, the ratio $\varphi$ is also small (as estimated in the last paragraph), indicating that $f(\varphi )$ could be expanded around $\varphi =0$ as $f(\varphi )\approx f_0+f_1\varphi +f_2{\varphi }^2+\cdots$, where $f_0>0$ (to guarantee the stability condition $s^2\ge 0$). Keeping the first leading-order term $f_0$ enables us to obtain $s^2\approx f_0\varphi$, so $s^2$ has a similar value of $\varphi$ if $f_0\sim \mathcal{O}(1)$, and the EOS does not take a linear form (except for $f_0=1$). Moreover, the causality principle requires $\varphi \lesssim f_0^{-1}$. The $s^2\approx 0.03\sim \varphi \lesssim 0.02$ at ${\rho }_0$ from chiral effective field calculations (Essick et al., 2021) confirms our order-of-magnitude estimate on $s^2$. If the next-leading-order term $f_1$ is small and positive, then the upper bound for $\varphi$ becomes $\varphi \lesssim f_0^{-1}(1-f_1/f_0^2)$, which is even reduced compared with $f_0^{-1}$. The exact form of $f(\varphi )$ should be worked out/analyzed by the general-relativistic structure equations for NSs (Tolman, 1939; Oppenheimer and Volkoff, 1939). By doing that, we demonstrated earlier that $\varphi$ is upper bounded as $\varphi \lesssim 0.374$ near the centers of stable NSs (Cai et al., 2023b; Cai et al., 2023a; Cai and Li, 2024a; Cai and Li, 2024b). The corresponding trace anomaly $\mathrm{\Delta }$ in NS cores is thus bounded to be above $-$0.04. In the next sections, we first show the main steps leading to these conclusions and then discuss their ramifications compared with existing predictions on $\mathrm{\Delta }$ in the literature.

3 Analyzing scaled TOV equations, mass/radius scalings, and central SSS

The TOV equations describe the radial evolution of pressure $P(r)$ and mass $M(r)$ of an NS under static hydrodynamic equilibrium conditions (Tolman, 1939; Oppenheimer and Volkoff, 1939). In particular, we have (adopting $c=1$)

$\frac{\mathrm{d}P}{\mathrm{d}r}=-\frac{GM\epsilon }{r^2}\left(1+\frac{P}{\epsilon }\right)\left(1+\frac{4\pi r^{3}P}{M}\right){\left(1-\frac{2GM}{r}\right)}^{-1},\frac{\mathrm{d}M}{\mathrm{d}r}=4\pi r^2\epsilon ,(5)$

Here, the mass $M=M(r)$, pressure $P=P(r)$, and energy density $\epsilon =\epsilon (r)$ are functions of the distance $r$ from NS center. The central energy density ${\epsilon }_{\text{c}}$ is a specific and important quantity, which straightforwardly connects the central pressure $P_{\text{c}}$ via the EOS $P_{\text{c}}=P({\epsilon }_{\text{c}})$. Using ${\epsilon }_{\text{c}}$, we can construct a mass scale $W$ and a length scale $Q$:

$W=\frac{1}{G}\frac{1}{\sqrt{4\pi G{\epsilon }_{\mathrm{c}}}}=\frac{1}{\sqrt{4\pi {\epsilon }_{\mathrm{c}}}},Q=\frac{1}{\sqrt{4\pi G{\epsilon }_{\text{c}}}}=\frac{1}{\sqrt{4\pi {\epsilon }_{\mathrm{c}}}},(6)$

respectively. Here, the second relations follow with $G=1$. Using $W$ and $Q$, we can rewrite the TOV equations in the following dimensionless form (Cai et al., 2023b; Cai et al., 2023a; Cai and Li, 2024a; Cai and Li, 2024b),

$\frac{\mathrm{d}\widehat{P}}{\mathrm{d}\widehat{r}}=-\frac{\widehat{\epsilon }\widehat{M}}{{\widehat{r}}^2}\frac{\left(1+\widehat{P}/\widehat{\epsilon }\right)\left(1+{\widehat{r}}^3\widehat{P}/\widehat{M}\right)}{1-2\widehat{M}/\widehat{r}},\frac{\mathrm{d}\widehat{M}}{\mathrm{d}\widehat{r}}={\widehat{r}}^2\widehat{\epsilon },(7)$

where $\widehat{P}=P/{\epsilon }_{\text{c}}$, $\widehat{\epsilon }=\epsilon /{\epsilon }_{\mathrm{c}}$, $\widehat{r}=r/Q$ and $\widehat{M}=M/W$. The general smallness of

$\mathrm{X}\equiv {\varphi }_{\mathrm{c}}\equiv {\widehat{P}}_{\mathrm{c}}\equiv P_{\mathrm{c}}/{\epsilon }_{\mathrm{c}},(8)$

together with the smallness of

$\mu \equiv \widehat{\epsilon }-{\widehat{\epsilon }}_{\mathrm{c}}=\widehat{\epsilon }-1,(9)$

near NS centers enable us to develop effective/controllable expansion of a relevant quantity $\mathcal{U}$ over $\mathrm{X}$ and $\mu$ as Cai et al. (2023b), (Cai et al., 2023a), Cai and Li (2024a), (Cai and Li, 2024b):

$\mathcal{U}/{\mathcal{U}}_{\mathrm{c}}\approx 1+{\displaystyle \sum _{i+j\ge 1}}{u}_{ij}{\mathrm{X}}^i{\mu }^j,(10)$

Here, ${\mathcal{U}}_{\mathrm{c}}$ is the quantity $\mathcal{U}$ at the center. Because both GR and its Newtonian counterpart with small $\varphi$ and $\mathrm{X}$ are nonlinear, the TOV equations are also nonlinear. One often solves the more involved nonlinear TOV equations by adopting numerical algorithms via a selected ${\epsilon }_{\text{c}}$ and an input-dense matter EOS (Cai and Li, 2016; Li et al., 2022) as well as the termination condition:

$P\left(R\right)=0\leftrightarrow \widehat{P}\left(\widehat{R}\right)=0,(11)$

which defines the NS radius $R$. The NS mass is given as

$M_{\mathrm{N}\mathrm{S}}={\widehat{M}}_{\mathrm{N}\mathrm{S}}W,\text{\hspace{0.17em}\hspace{0.17em}with\hspace{0.17em}\hspace{0.17em}}{\widehat{M}}_{\mathrm{N}\mathrm{S}}\equiv \widehat{M}\left(\widehat{R}\right)={\int }_0^{\widehat{R}}\mathrm{d}\widehat{r}{\widehat{r}}^2\widehat{\epsilon }\left(\widehat{r}\right).(12)$

Starting from the scaled TOV Equation 7, we can show that both $\widehat{P}$ and $\widehat{\epsilon }$ are even under the transformation $\widehat{r}\leftrightarrow -\widehat{r}$, while $\widehat{M}$ is odd (Cai and Li, 2024a). Therefore, we can write the general expansions for $\widehat{\epsilon }$, $\widehat{P}$ and $\widehat{M}$ near $\widehat{r}=0$:

$\widehat{\epsilon }(\widehat{r})\approx 1+a_2{\widehat{r}}^2+a_4{\widehat{r}}^4+a_6{\widehat{r}}^6+\cdots ,(13)$

$\widehat{P}(\widehat{r})\approx \mathrm{X}+b_2{\widehat{r}}^2+b_4{\widehat{r}}^4+b_6{\widehat{r}}^6+\cdots ,(14)$

$\widehat{M}(\widehat{r})\approx \frac{1}{3}{\widehat{r}}^3+\frac{1}{5}{a}_2{\widehat{r}}^5+\frac{1}{7}{a}_4{\widehat{r}}^7+\frac{1}{9}{a}_6{\widehat{r}}^9+\cdots ,(15)$

the expansion for $\widehat{M}$ follows directly from that for $\widehat{\epsilon }$. As a direct consequence, we find that $s^2(\widehat{r})=s^2(-\widehat{r})$; that is, there would be no odd terms in $\widehat{r}$ in the expansion of $s^2$ over $\widehat{r}$. The relationships between $\{a_j\}$ and $\{b_j\}$ are determined by the scaled TOV Equation 7; and the results are (Cai et al., 2023b)

$b_2=-\frac{1}{6}\left(1+3{\widehat{P}}_{\mathrm{c}}^2+4{\widehat{P}}_{\mathrm{c}}\right),(16)$

$b_4=\frac{{\widehat{P}}_{\mathrm{c}}}{12}\left(1+3{\widehat{P}}_{\mathrm{c}}^2+4{\widehat{P}}_{\mathrm{c}}\right)-\frac{a_2}{30}\left(4+9{\widehat{P}}_{\mathrm{c}}\right),(17)$

$\begin{array}{ll}\hfill b_6& =-\frac{1}{216}\left(1+9{\widehat{P}}_{\mathrm{c}}^2\right)\left(1+3{\widehat{P}}_{\mathrm{c}}^2+4{\widehat{P}}_{\mathrm{c}}\right)-\frac{a_2^2}{30}\hfill \\ \hfill & +\left(\frac{2}{15}{\widehat{P}}_{\mathrm{c}}^2+\frac{1}{45}{\widehat{P}}_{\mathrm{c}}-\frac{1}{54}\right)a_2-\frac{5+12{\widehat{P}}_{\mathrm{c}}}{63}{a}_4,\hfill \end{array}(18)$

etc., and all the odd terms of $\{b_j\}$ and $\{a_j\}$ are 0. The coefficient $a_2$ can be expressed in terms of $b_2$ via the SSS because

$s^2=\frac{\mathrm{d}\widehat{P}}{\mathrm{d}\widehat{\epsilon }}=\frac{\mathrm{d}\widehat{P}}{\mathrm{d}\widehat{r}}\cdot \frac{\mathrm{d}\widehat{r}}{\mathrm{d}\widehat{\epsilon }}=\frac{b_2+2b_4{\widehat{r}}^2+\cdots }{a_2+2a_4{\widehat{r}}^2+\cdots }.(19)$

Evaluating it at $\widehat{r}=0$ gives $s_{\mathrm{c}}^2=b_2/a_2$, or inversely, $a_2=b_2/s_{\mathrm{c}}^2$. Because $s_{\mathrm{c}}^2>0$ and $b_2<0$, we find $a_2<0$; that is, the energy density is a monotonically decreasing function of $\widehat{r}$ near $\widehat{r}\approx 0$.

According to the definition of NS radius given in Equation 11, we obtain from the truncated equation $\mathrm{X}+b_2{\widehat{R}}^2\approx 0$ that $\widehat{R}\approx {(-\mathrm{X}/b_2)}^{1/2}={[6\mathrm{X}/(1+3{\mathrm{X}}^2+4\mathrm{X})]}^{1/2}$, and therefore, the radius $R$ (Cai et al., 2023b):

$R=\widehat{R}Q\approx {\left(\frac{3}{2\pi G}\right)}^{1/2}{\nu }_{\mathrm{c}},\text{\hspace{0.17em}\hspace{0.17em}with\hspace{0.17em}\hspace{0.17em}}{\nu }_{\mathrm{c}}\equiv \frac{1}{\sqrt{{\epsilon }_{\mathrm{c}}}}{\left(\frac{\mathrm{X}}{1+3{\mathrm{X}}^2+4\mathrm{X}}\right)}^{1/2}.(20)$

Similarly, the NS mass scales as Cai et al. (2023b).

$M_{\mathrm{N}\mathrm{S}}\approx \frac{1}{3}{\widehat{R}}^3{\widehat{\epsilon }}_{\mathrm{c}}W=\frac{1}{3}{\widehat{R}}^{3}W\approx {\left(\frac{6}{\pi G^3}\right)}^{1/2}{\mathrm{\Gamma }}_{\mathrm{c}},\text{\hspace{0.17em}\hspace{0.17em}with\hspace{0.17em}\hspace{0.17em}}{\mathrm{\Gamma }}_{\mathrm{c}}\equiv \frac{1}{\sqrt{{\epsilon }_{\mathrm{c}}}}{\left(\frac{\mathrm{X}}{1+3{\mathrm{X}}^2+4\mathrm{X}}\right)}^{3/2}.(21)$

Consequently, the NS compactness $\xi$ scales as Cai and Li (2024b).

$\xi \equiv \frac{M_{\mathrm{N}\mathrm{S}}}{R}\approx \frac{2}{G}\frac{\mathrm{X}}{1+3{\mathrm{X}}^2+4\mathrm{X}}=\frac{2{\mathrm{\Pi }}_{\mathrm{c}}}{G},\text{\hspace{0.17em}\hspace{0.17em}with\hspace{0.17em}\hspace{0.17em}}{\mathrm{\Pi }}_{\mathrm{c}}\equiv \frac{\mathrm{X}}{1+3{\mathrm{X}}^2+4\mathrm{X}}.(22)$

For small $\mathrm{X}$ (Newtonian limit), $\xi \approx 2\mathrm{X}$. Relation (22) implies that $\mathrm{X}$ is the source and also a measure of NS compactness (Cai and Li, 2024b). The correlation between $\mathrm{X}$ and $\xi$ is studied and fitted numerically in the form of $\ln \mathrm{X}\approx {\sum }_i{z}_i{\xi }^i$using various EOS models (Saes and Mendes, 2022). Such fitting schemes eventually become effective as enough parameters, $z_i$, are used. However, the real correlation between $\mathrm{X}$ and $\xi$ is somehow lost. In particular, our correlation tells that $\xi \sim {\tau }_0+{\tau }_1\mathrm{X}+{\tau }_2{\mathrm{X}}^2+\cdots$with ${\tau }_0\approx 0$and ${\tau }_1\approx 2$.

The maximum-mass configuration (or the TOV configuration) along the NS M-R curve is a special point. Consider a typical NS M-R curve near the TOV configuration from right to left, the radius $R$ (mass $M_{\mathrm{N}\mathrm{S}}$) eventually decreases (increases), the compactness $\xi =M_{\mathrm{N}\mathrm{S}}/R$ correspondingly increases and reaches its maximum value at the TOV configuration. When going to the left along the M-R curve even further, the stars become unstable and may collapse into black holes (BHs). The NS at the TOV configuration is denser than its surroundings, and the cores of such NSs contain the densest stable visible matter in the Universe. The TOV configuration is indicated on a typical M-R sequence in Figure 2. Mathematically, the TOV configuration is described as

${\left.\frac{\mathrm{d}{M}_{\mathrm{N}\mathrm{S}}}{\mathrm{d}{\epsilon }_{\mathrm{c}}}\right|}_{M_{\mathrm{N}\mathrm{S}}=M_{\mathrm{N}\mathrm{S}}^{\max }=M_{\mathrm{T}\mathrm{O}\mathrm{V}}}=0.(23)$

Figure 2

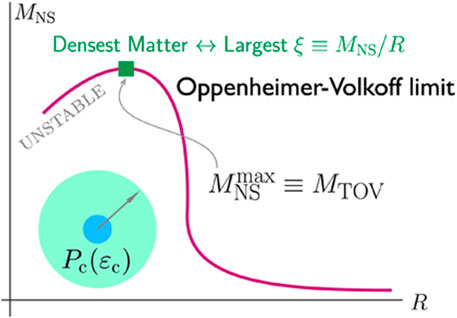
Figure 2. An illustration of the TOV configuration on a typical mass-radius sequence. The cores of NSs at the TOV configuration contain the densest visible matter in our Universe; the compactness $\xi$ for such NSs is the largest among all stable NSs.

Using the NS mass scaling of Equation 21, we obtain

$\frac{\mathrm{d}{M}_{\mathrm{N}\mathrm{S}}}{\mathrm{d}{\epsilon }_{\mathrm{c}}}=\frac{1}{2}\frac{M_{\mathrm{N}\mathrm{S}}}{{\epsilon }_{\mathrm{c}}}\left[3\left(\frac{s_{\mathrm{c}}^2}{\mathrm{X}}-1\right)\frac{1-3{\mathrm{X}}^2}{1+3{\mathrm{X}}^2+4\mathrm{X}}-1\right],\text{\hspace{0.17em}\hspace{0.17em}where\hspace{0.17em}\hspace{0.17em}}{s}_{\mathrm{c}}^2\equiv \frac{\mathrm{d}{P}_{\mathrm{c}}}{\mathrm{d}{\epsilon }_{\mathrm{c}}}.(24)$

Inversely, we obtain the expression for the central SSS (Cai et al., 2023a; Cai and Li, 2024a),

$\text{for\hspace{0.17em}stable\hspace{0.17em}NSs\hspace{0.17em}along\hspace{0.17em}M}-\text{R\hspace{0.17em}curve:\hspace{0.17em}\hspace{0.17em}}{s}_{\mathrm{c}}^2=\mathrm{X}\left(1+\frac{1+\mathrm{\Psi }}{3}\frac{1+3{\mathrm{X}}^2+4\mathrm{X}}{1-3{\mathrm{X}}^2}\right),(25)$

where

$\mathrm{\Psi }=2\frac{\mathrm{d}\ln M_{\mathrm{N}\mathrm{S}}}{\mathrm{d}\ln {\epsilon }_{\mathrm{c}}}\ge 0.(26)$

We see that the SSS is in the form of Equation 4. For NSs at the TOV configuration, we have

$\text{for\hspace{0.17em}NSs\hspace{0.17em}at\hspace{0.17em}the\hspace{0.17em}TOV\hspace{0.17em}configuration:\hspace{0.17em}\hspace{0.17em}}{s}_{\mathrm{c}}^2=\mathrm{X}\left(1+\frac{1}{3}\frac{1+3{\mathrm{X}}^2+4\mathrm{X}}{1-3{\mathrm{X}}^2}\right).(27)$

because now, $\mathrm{\Psi }=0$. Using the $s_{\mathrm{c}}^2$ of Equation 27 for NSs at the TOV configuration, we can calculate the derivative of NS radius $R$ with respect to ${\epsilon }_{\mathrm{c}}$ around the TOV point, that is, Cai et al. (2023b).

$\frac{\mathrm{d}R}{\mathrm{d}{\epsilon }_{\mathrm{c}}}\sim \frac{\mathrm{d}}{\mathrm{d}{\epsilon }_{\mathrm{c}}}{\left(\frac{\widehat{R}}{\sqrt{{\epsilon }_{\mathrm{c}}}}\right)}_{R_{\max }\leftrightarrow M_{\mathrm{N}\mathrm{S}}^{\max }}=\left(\frac{s_{\mathrm{c}}^2}{\mathrm{X}}-1\right)\frac{1-3{\mathrm{X}}^2}{1+3{\mathrm{X}}^2+4\mathrm{X}}-1=-\frac{2}{3},(28)$

That is, as ${\epsilon }_{\mathrm{c}}$ increases, the radius $R$ decreases (self-gravitating property), as expected. On the other hand, for stable NSs along the M-R curve with a nonzero $\mathrm{\Psi }$, we have $\mathrm{d}R/\mathrm{d}{\epsilon }_{\mathrm{c}}\sim (\mathrm{\Psi }-2)/3$; this means if $\mathrm{\Psi }$ is approximately 2, the dependence of the radius on ${\epsilon }_{\mathrm{c}}$ would be weak.

For verification, the scaling $R_{\max }$-${\nu }_{\mathrm{c}}$ (panel (a)) of Equation 20 and the scaling $M_{\mathrm{N}\mathrm{S}}^{\max }$-${\mathrm{\Gamma }}_{\mathrm{c}}$ (panel (b)) of Equation 21 are shown in Figure 3 by using 87 phenomenological and 17 extra microscopic NS EOSs with and/or without considering hadron-quark phase transitions and hyperons by solving the original TOV equations numerically. See Cai et al. (2023b) for more details on these EOS samples. The observed strong linear correlations demonstrate vividly that the $R_{\max }$-${\nu }_{\mathrm{c}}$ and $M_{\mathrm{N}\mathrm{S}}^{\max }$-${\mathrm{\Gamma }}_{\mathrm{c}}$ scalings are nearly universal. While it is presently unclear where the mass threshold for massive NSs to collapse into BHs is located, the TOV configuration is the closest to it theoretically. It is also well known that certain properties of BHs are universal and only depend on quantities like mass, charge, and angular momentum. One thus expects the NS mass and radius scalings near the TOV configuration to be more EOS-independent than those for light NSs. It is also interesting to notice that EOSs allowing phase transitions and/or hyperon formations consistently predict the same scalings.

Figure 3

Figure 3. Panel (A): the $R_{\max }$-${\nu }_{\mathrm{c}}$ correlation using 104 EOS samples (colored symbols); see Cai et al. (2023b) for more detailed descriptions on these EOSs. The constraints on the mass (Fonseca et al., 2021) and radius (Riley et al., 2021) of PSR J0740 + 6,620 are shown by the pink hatched bands. Panel (B): similar to the left panel but for $M_{\mathrm{N}\mathrm{S}}^{\max }$-${\mathrm{\Gamma }}_{\mathrm{c}}$. The orange arrows and captions nearby in each panel indicate the ${\nu }_{\mathrm{c}}$ and ${\mathrm{\Gamma }}_{\mathrm{c}}$ defined in Equation 20 and Equation 21, respectively. Figures taken from Cai et al. (2023b).

By performing linear fits of the results obtained from the EOS samples, the quantitative scaling relations are (Cai et al., 2023b; Cai et al., 2023a; Cai and Li, 2024a)

$R_{\mathrm{m}\mathrm{a}\mathrm{x}}/\mathrm{k}\mathrm{m}\approx 1050_{-30}^{+30}\times \left(\frac{{\nu }_{\mathrm{c}}}{{\mathrm{f}\mathrm{m}}^{3/2}/{\mathrm{M}\mathrm{e}\mathrm{V}}^{1/2}}\right)+0.64_{-0.25}^{+0.25},(29)$

$M_{\mathrm{N}\mathrm{S}}^{\mathrm{m}\mathrm{a}\mathrm{x}}/M_{\odot }\approx 1730_{-30}^{+30}\times \left(\frac{{\mathrm{\Gamma }}_{\mathrm{c}}}{{\mathrm{f}\mathrm{m}}^{3/2}/{\text{MeV}}^{1/2}}\right)-0.106_{-0.035}^{+0.035},(30)$

with their Pearson’s coefficients approximately 0.958 and 0.986, respectively. Here, ${\nu }_{\mathrm{c}}$ and ${\mathrm{\Gamma }}_{\mathrm{c}}$ are measured in ${\mathrm{f}\mathrm{m}}^{3/2}/{\mathrm{M}\mathrm{e}\mathrm{V}}^{1/2}$. In addition, the standard errors for the radius and mass fittings are approximately 0.031 and 0.003 for these EOS samples. In Figure 3, the condition $M_{\mathrm{N}\mathrm{S}}^{\max }\gtrsim 1.2M_{\odot }$ used is necessary to mitigate influences of uncertainties in modeling the crust EOS (Baym et al., 1971; Iida and Sato, 1997; Xu et al., 2009) for low-mass NSs. For the heavier NSs studied here, it is reassuring to see that although the above 104 EOSs predicted quite different crust properties, they all fall closely around the same scaling lines consistently, especially for the $M_{\mathrm{N}\mathrm{S}}^{\max }$-${\mathrm{\Gamma }}_{\mathrm{c}}$ relation.

4 Gravitational upper bound on $\mathrm{X}\equiv {\varphi }_{\mathrm{c}}=P_{\mathrm{c}}/{\epsilon }_{\mathrm{c}}$, its generalizations, and the impact on supradense NS matter EOS

Based on Equation 27 and the principle of causality of SR, we obtain immediately (Cai et al., 2023b)

$s_{\mathrm{c}}^2\le 1\leftrightarrow \mathrm{X}={\widehat{P}}_{\mathrm{c}}\lesssim 0.374\equiv {\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}.(31)$

Although the causality condition requires apparently ${\widehat{P}}_{\mathrm{c}}\le 1$, the supradense nature of core NS matter indicated by the nonlinear dependence of $s_{\mathrm{c}}^2$ on ${\widehat{P}}_{\mathrm{c}}$ essentially renders it to be much smaller.

A small $\mathrm{X}<1$ was, in fact, indicated earlier in the literature (Koranda et al., 1997; Saes and Mendes, 2022). For example, in Koranda et al. (1997), the minimum-period EOS of the form $P(\epsilon )=0$ for $\epsilon <{\epsilon }_{\mathrm{f}}$ and $P(\epsilon )=\epsilon -{\epsilon }_{\mathrm{f}}$ for $\epsilon \ge {\epsilon }_{\mathrm{f}}$ was adopted; here, ${\epsilon }_{\mathrm{f}}$ is a free parameter of the model. Such an EOS is simplified and unrealistic in the following senses: (1) both the parameter ${\epsilon }_{\mathrm{f}}\approx 2.156\times 10^{15}\mathrm{g}/{\mathrm{c}\mathrm{m}}^3\approx 8.1{\epsilon }_0$ and the central energy density ${\epsilon }_{\mathrm{c}}\approx 4.778\times 10^{15}\mathrm{g}/{\mathrm{c}\mathrm{m}}^3\approx 17.9{\epsilon }_0$ are unrealistically large for a 1.442$M_{\odot }$ NS (Koranda et al., 1997); the consequent ratio $\mathrm{X}$ in this model is $\mathrm{X}=1-{\epsilon }_{\mathrm{f}}/{\epsilon }_{\mathrm{c}}\approx 0.55$; (2) the central SSS of 1 of such model is inconsistent with Equation 27. Actually, only with $\mathrm{X}=1-{\epsilon }_{\mathrm{f}}/{\epsilon }_{\mathrm{c}}\approx 0.374$ or ${\epsilon }_{\mathrm{f}}/{\epsilon }_{\mathrm{c}}\approx 0.626$ can one make this EOS model consistent with Equation 27. That is, the parameter space for ${\epsilon }_{\mathrm{f}}$ is limited; however, a vanishing pressure up to ${\epsilon }_{\mathrm{f}}/{\epsilon }_{\mathrm{c}}\approx 0.626$ is fundamentally unsatisfactory. Therefore, $\mathrm{X}\approx 0.55$ is only qualitatively meaningful.

The bound (31) is obtained under the specific condition that it gives the upper limit for $\varphi =P/\epsilon$ at the center of NSs at TOV configurations. In order to bound a general $\varphi =P/\epsilon =\widehat{P}/\widehat{\epsilon }$, we need to take three generalizations of $\mathrm{X}\lesssim 0.374$ obtained from Equation 31 by asking (Cai et al., 2023a).

(a) How does $\varphi =\widehat{P}/\widehat{\epsilon }$ behave at a finite $\widehat{r}$ for the maximum-mass configuration $M_{\mathrm{N}\mathrm{S}}^{\max }$?

(b) How does the limit $\mathrm{X}\lesssim 0.374$ modify when considering stable NSs on the M-R curve away from the TOV configuration?

(c) By combining (a) and (b), how does $\varphi$ behave for stable NSs at finite distances $\widehat{r}$ away from their centers?

For the first question, because the pressure $\widehat{P}$ and $\widehat{\epsilon }$ are both decreasing functions of $\widehat{r}$, that is, $\widehat{P}\approx {\widehat{P}}_{\mathrm{c}}+b_2{\widehat{r}}^2<{\widehat{P}}_{\mathrm{c}}$ and $\widehat{\epsilon }\approx 1+s_{\mathrm{c}}^{-2}{b}_2{\widehat{r}}^2<1$ (notice ${\widehat{\epsilon }}_{\mathrm{c}}=1$ and $a_2=b_2/s_{\mathrm{c}}^2$), we obtain by taking their ratio:

$\begin{array}{ll}\hfill \varphi =P/\epsilon & =\widehat{P}/\widehat{\epsilon }\approx {\widehat{P}}_{\mathrm{c}}/{\widehat{\epsilon }}_{\mathrm{c}}+\left(1-\frac{{\widehat{P}}_{\mathrm{c}}}{s_{\mathrm{c}}^2}\right)b_2{\widehat{r}}^2={\widehat{P}}_{\mathrm{c}}+\left(1-\frac{{\widehat{P}}_{\mathrm{c}}}{s_{\mathrm{c}}^2}\right)b_2{\widehat{r}}^2\hfill \\ \hfill & \approx {\widehat{P}}_{\mathrm{c}}-\left(\frac{1+7{\widehat{P}}_{\mathrm{c}}}{24}\right){\widehat{r}}^2<{\widehat{P}}_{\mathrm{c}}.\hfill \end{array}(32)$

Generally, $1-{\widehat{P}}_{\mathrm{c}}/s_{\mathrm{c}}^2>0$, the small-${\widehat{P}}_{\mathrm{c}}$ expansions of $s_{\mathrm{c}}^2$ of Equation 27 and $b_2$ of Equation 16 are used in the last step. This means that not only $\widehat{P}$ and $\widehat{\epsilon }$ decrease for finite $\widehat{r}$ but also does their ratio $\widehat{P}/\widehat{\epsilon }$. Therefore, for NSs at the TOV configuration of the M-R curves, we have $\varphi =\widehat{P}/\widehat{\epsilon }\le {\widehat{P}}_{\mathrm{c}}\lesssim 0.374$. Considering the second question and for stable NSs on the M-R curve, one has $\mathrm{\Psi }>0$ (of Equation 26), and Equation 25 induces an even smaller upper bound for $\mathrm{X}$ than 0.374. Furthermore, for the last question (c), the inequality (32) still holds and is slightly modified for small ${\widehat{P}}_{\mathrm{c}}$ as

$\varphi =\widehat{P}/\widehat{\epsilon }\approx {\widehat{P}}_{\mathrm{c}}-\frac{1}{24}\frac{1+\mathrm{\Psi }}{{\left(1+\mathrm{\Psi }/4\right)}^2}\left[1+7{\widehat{P}}_{\mathrm{c}}+\mathrm{\Psi }\left({\widehat{P}}_{\mathrm{c}}+\frac{1}{4}\right)\right]{\widehat{r}}^2<{\widehat{P}}_{\mathrm{c}},(33)$

which implies that $\varphi =\widehat{P}/\widehat{\epsilon }$ for $\mathrm{\Psi }\ne 0$ also decreases with $\widehat{r}$.

Combining the above three aspects, we find

$\text{for\hspace{0.17em}stable\hspace{0.17em}NSs\hspace{0.17em}along\hspace{0.17em}M}-\text{R\hspace{0.17em}curve\hspace{0.17em}near/at\hspace{0.17em}the\hspace{0.17em}centers:\hspace{0.17em}\hspace{0.17em}}\varphi =P/\epsilon =\widehat{P}/\widehat{\epsilon }\le \mathrm{X}\lesssim 0.374.(34)$

Nevertheless, the validity of this conclusion is limited to small $\widehat{r}$ due to the perturbative nature of the expansions of $\widehat{P}(\widehat{r})$ and $\widehat{\epsilon }(\widehat{r})$. Whether $\varphi =P/\epsilon$ could exceed such upper limit at even larger distances away from the centers depends on the joint analysis of $s^2$ and $P/\epsilon$, for example, by including more higher-order contributions of the expansions (Cai et al., 2023a). The upper bound $P/\epsilon \lesssim 0.374$ (at least near the NS centers) is an intrinsic property of the TOV equations, which embody the strong-field aspects of gravity in GR, especially the strong self-gravitating nature. In this sense, there is no guarantee a priori that this bound is consistent with all microscopic nuclear EOSs (either relativistic or non-relativistic). This is mainly because the latter were conventionally constructed without considering the strong-field ingredients of gravity. The robustness of such an upper bound for $\varphi =P/\epsilon$ can be checked only by observable astrophysical quantities/processes involving strong-field aspects of gravity such as NS M-R data, NS-NS mergers, and/or NS-BH mergers (Baumgarte and Shapiro, 2010; Shibata, 2015; Baiotti and Rezzolla, 2017; Kyutoku et al., 2021). As mentioned earlier, in the NS matter-gravity inseparable system, the total action determines the matter state and the NS structure. Thus, to our best knowledge, there is no physics requirement that the EOS of supradense matter created in vacuum from high-energy heavy-ion collisions or other laboratory experiments where effects of gravity can be neglected must be the same as EOSs in NSs, as the nuclear matter in the two situations is in very different environments. Nevertheless, the ramifications of the above findings and logical arguments should be further investigated.

Next, we consider the Newtonian limit where $\varphi$ and $\mathrm{X}$ are small. We can neglect $3{\mathrm{X}}^2+4\mathrm{X}$ in the coefficient $b_2$; consequently, $b_2=-1/6$ is obtained (Chandrasekhar, 2010). In such case, we shall obtain from Equation 27:

$\text{Newtonian\hspace{0.17em}limit:\hspace{0.17em}\hspace{0.17em}}{s}_{\mathrm{c}}^2\approx 4\mathrm{X}/3,(35)$

and the principle of causality requires $\mathrm{X}\le 3/4=0.75\equiv {\mathrm{X}}_{+}^{\mathrm{N}}$. The latter can be applied to nuclear matter created in laboratory experiments where the effects of gravity can be neglected. Turning on gravity in NSs, we see that the nonlinearity of Newtonian gravity has already reduced the upper bound for $\varphi$ from 1 obtained by requiring $s^2\le 1$ in SR via a linear EOS of the form $P=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.\times \epsilon$ to 3/4; the even stronger nonlinearity of the gravity in GR reduces it further. These effects of gravity on $\varphi$ are illustrated in Figure 4. It is seen that the strong-field gravity in GR brings a relative reduction on the upper bound for $\varphi$ by approximately 100%. Though the $\varphi$ or $\mathrm{X}$ in Newtonian gravity is generally smaller, the upper bound for $\varphi$ or $\mathrm{X}$ is, however, larger than its GR counterpart. The index $s_{\mathrm{c}}^2/\mathrm{X}$, being greater than 1 in both Newtonian gravity and in GR, implies that the central EOS in NSs once considering the gravity effect could not be linear or conformal.

Figure 4

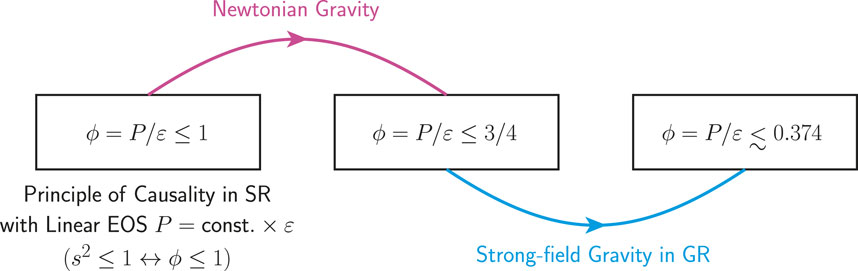
Figure 4. An illustration of the gravitational effects on supradense matter EOS in NSs: The nonlinearity of Newtonian gravity reduces the upper bound for $\varphi$ from 1 (obtained by requiring $s^2\le 1$ in SR via a linear EOS of the form $P=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}.\times \epsilon$ for supradense matter in vacuum) to 3/4 = 0.75, and the even stronger nonlinearity of the gravity in GR further refines it to be approximately 0.374.

We emphasize that all of the analyses above based on SR and GR are general from analyzing perturbatively analytical solutions of the scaled TOV equations without using any specific nuclear EOS. Because the TOV equations are the results of a hydrodynamical equilibrium of NS matter in the environment of a strong-field gravity from extremizing the total action of the matter-gravity system, features revealed above from SR and GR inherent in the TOV equations must be matched by the nuclear EOS. This requirement can then put strong constraints on the latter. In particular, the upper bound for $\varphi$ as $\varphi \lesssim {\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}\approx 0.374$ of Equation 31 enables us to limit the density dependence of nuclear EOS relevant for NS modeling.

In the following, we provide an example illustrating how the strong-field gravity can restrict the behavior of superdense matter in NSs. For simplicity, we assume that the energy per baryon takes the following form:

$E\left(\rho \right)=B_{\mathrm{F}\mathrm{F}\mathrm{G}}{\left(\frac{\rho }{{\rho }_0}\right)}^{2/3}+B{\left(\frac{\rho }{{\rho }_0}\right)}^{\sigma },(36)$

where the first term is the kinetic energy of an FFG of neutrons in NSs with $B_{\mathrm{F}\mathrm{F}\mathrm{G}}\approx 35$ MeV being its known value at ${\rho }_0$, and the second term is the contribution from interactions described with the parameters $B$ and $\sigma$. The pressure and the energy density are obtained from $P(\rho )={\rho }^2\mathrm{d}E/\mathrm{d}\rho$ and $\epsilon (\rho )=[E(\rho )+M_{\mathrm{N}}]\rho$, respectively. The ratio $\varphi =P/\epsilon$ and the SSS $s^2=\mathrm{d}P/\mathrm{d}\epsilon$ could be obtained correspondingly. After denoting the reduced density $\rho /{\rho }_0$, where $s^2\to 1$ and $\varphi \to \mathrm{X}\to {\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}$, as $\ell$ (e.g., $\ell \lesssim 8$ for realistic NSs), the following constraining equation for $\sigma$ is obtained:

$\sigma \left({\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}\sigma -1\right)+\frac{{\ell }^{2/3}}{3}\left(\frac{B_{\mathrm{F}\mathrm{F}\mathrm{G}}}{M_{\mathrm{N}}}\right)\left(\sigma -\frac{2}{3}\right)\left[\left(3\sigma +2\right){\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}-2\sigma -3\right]=0.(37)$

Thus, ${\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}$ effectively restricts the index $\sigma$ characterizing the stiffness of nuclear EOS. There are two solutions of Equation 37, with one being greater than 1 (denoted as ${\sigma }_{\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}}$) and the other smaller than 1 (denoted as ${\sigma }_{\mathrm{s}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{l}}$). They can be explicitly written as

$\begin{array}{ll}\hfill \sigma & =\frac{1}{2}{\left({\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}+\mathrm{\Lambda }\left({\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}-\frac{2}{3}\right)\right)}^{-1}\hfill \\ \hfill & \left\{1+\frac{5}{9}\mathrm{\Lambda }\pm \sqrt{1+\frac{16\mathrm{\Lambda }}{9}\left[\left({\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R},2}-\frac{3{\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}}{2}+\frac{5}{8}\right)+\mathrm{\Lambda }{\left({\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}-\frac{13}{12}\right)}^2\right]}\right\},\hfill \end{array}(38)$

where

$\mathrm{\Lambda }\equiv {\ell }^{2/3}\left(\frac{B_{\mathrm{F}\mathrm{F}\mathrm{G}}}{M_{\mathrm{N}}}\right)\ll 1.(39)$

The expression for the coefficient $B$ is

$B=\left(\frac{1+5\mathrm{\Lambda }/9}{{\sigma }^2-1}\frac{1}{{\ell }^{\sigma }}\right)M_{\mathrm{N}},(40)$

which depends on ${\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}$ through $\sigma$. As a numerical example, using $M_{\mathrm{N}}\approx 939\mathrm{M}\mathrm{e}\mathrm{V}$, $B_{\mathrm{F}\mathrm{F}\mathrm{G}}\approx 35\mathrm{M}\mathrm{e}\mathrm{V}$, and $\ell \approx 6$ leads to ${\sigma }_{\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}}\approx 3.1$ and $B_{\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}}\approx 0.45\mathrm{M}\mathrm{e}\mathrm{V}$ or ${\sigma }_{\mathrm{s}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{l}}\approx 0.06$ and $B_{\mathrm{s}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{l}}\approx -906\mathrm{M}\mathrm{e}\mathrm{V}$ (this second solution is unphysical because $B>0$ is necessarily required to make $E(\rho )>0$ at NS densities). If one artificially takes ${\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}=1$, then the two solutions (38) approach

${\sigma }_{\mathrm{s}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{l}}\to \frac{2}{3}\frac{1}{1+3/\mathrm{\Lambda }}=\frac{2}{3}{\left(1+\frac{3}{{\ell }^{2/3}}\left(\frac{M_{\mathrm{N}}}{B_{\text{FFG}}}\right)\right)}^{-1}\ll 1,\text{\hspace{0.17em}\hspace{0.17em}and\hspace{0.17em}\hspace{0.17em}}{\sigma }_{\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}}\to 1\text{\hspace{0.17em}\hspace{0.17em}from\hspace{0.17em}above}.(41)$

Now, neither solution is physical because $B_{\mathrm{s}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{l}}<0$ for ${\sigma }_{\mathrm{s}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{l}}$, while $B_{\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}}\to +\infty$ for ${\sigma }_{\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}}\to 1$ from above, according to Equation 40. The general ${\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}$-dependence of ${\sigma }_{\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}}$ and ${\sigma }_{\mathrm{s}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{l}}$ of Equation 38 is shown in Figure 5. It is seen that only as ${\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}\to 1$ does the EOS approach a linear form $E(\rho )\approx B\rho /{\rho }_0\sim \rho$ (so $P\approx B{\rho }^2/{\rho }_0$ and $\epsilon \approx B{\rho }^2/{\rho }_0+M_{\mathrm{N}}\rho$) at large densities (magenta line), which is consistent with our general analyses and expectation.

Figure 5

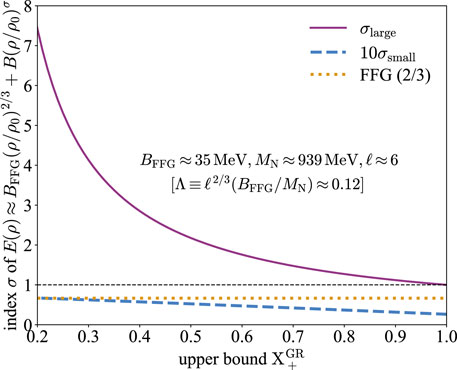
Figure 5. Gravitational impact on the EOS of supradense matter and the underlying strong interaction in NSs: the general ${\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}$-dependence of ${\sigma }_{\mathrm{l}\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{e}}$ and ${\sigma }_{\mathrm{s}\mathrm{m}\mathrm{a}\mathrm{l}\mathrm{l}}$ of Equation 38, based on the nuclear EOS model of Equation 36; here $B_{\mathrm{F}\mathrm{F}\mathrm{G}}\approx 35\mathrm{M}\mathrm{e}\mathrm{V}$, $M_{\mathrm{N}}\approx 939\mathrm{M}\mathrm{e}\mathrm{V}$, and $\ell =\rho /{\rho }_0\approx 6$.

Because the parameterization (36) is over-simplified, more density-dependent terms should be included for general cases; that is, $B{(\rho /{\rho }_0)}^{\sigma }\to {\sum }_{j=1}^J{B}_j{(\rho /{\rho }_0)}^{{\sigma }_j}$. We may then obtain two related equations from $\varphi \to \mathrm{X}\to {\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}$ and $s^2\to 1$ as (for either ${\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}=1$ or ${\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}\ne 1$):

$\begin{array}{l}\hfill {\displaystyle \sum _{j=1}^J}\left(\frac{B_j}{M_{\mathrm{N}}}\right)\left({\sigma }_j-{\mathrm{X}+}^{\mathrm{G}\mathrm{R}}\right){\ell }^{{\sigma }_j}+{\ell }^{2/3}\left(\frac{B_{\mathrm{F}\mathrm{F}\mathrm{G}}}{M_{\mathrm{N}}}\right)\left(\frac{2}{3}-{\mathrm{X}+}^{\mathrm{G}\mathrm{R}}\right)-\mathrm{X}{+}^{\mathrm{G}\mathrm{R}}=0,\\ \hfill {\displaystyle \sum _{j=1}^J}\left(\frac{B_j}{M_{\mathrm{N}}}\right)\left(1-\sigma j^2\right){\ell }^{1/3+{\sigma }_j}-{\ell }^{1/3}\left(1+\frac{5}{9}{\ell }^{2/3}\left(\frac{B\mathrm{F}\mathrm{F}\mathrm{G}}{M\mathrm{N}}\right)\right)=0.\end{array}$

These constraints for $B_j$ and ${\sigma }_j$ should be taken appropriately into account when writing an effective NS EOS based on density expansions. For example, when extending Equation 36 to be $E(\rho )=B_{\mathrm{F}\mathrm{F}\mathrm{G}}{(\rho /{\rho }_0)}^{2/3}+B_1{(\rho /{\rho }_0)}^{{\sigma }_1}+B_2{(\rho /{\rho }_0)}^{{\sigma }_2}$ under two conditions $E({\rho }_0,\delta )\approx E_0({\rho }_0)+E_{\mathrm{s}\mathrm{y}\mathrm{m}}({\rho }_0){\delta }^2\approx 15\mathrm{M}\mathrm{e}\mathrm{V}$ for pure neutron matter with $\delta =1$ and $P({\rho }_0)\approx 3\mathrm{M}\mathrm{e}\mathrm{V}/{\mathrm{f}\mathrm{m}}^3$, using $\ell \approx 6$ together with ${\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}\approx 0.374$, we may obtain ${\sigma }_1\approx 0.3$ and ${\sigma }_2\approx 3.0$ (as well as $B_1\approx -20.5\mathrm{M}\mathrm{e}\mathrm{V}$ and $B_2\approx 0.5\mathrm{M}\mathrm{e}\mathrm{V}$), respectively. This example quantitatively shows that the gravitational bound naturally leads to a constraint on the nuclear EOS and the underlying interactions in NSs.

5 Gravitational lower bound on trace anomaly $\mathrm{\Delta }$ in supradense NS matter

After the above general demonstration on the gravitational upper limit for $\varphi$ near NS centers given by (31) or (34), we equivalently obtain a lower limit on the dimensionless trace anomaly $\mathrm{\Delta }=1/3-\varphi$ as

$\mathrm{\Delta }\ge {\mathrm{\Delta }}_{\mathrm{G}\mathrm{R}}\approx -0.04.(44)$

It is very interesting to notice that such a GR bound on $\mathrm{\Delta }$ is very close to the one predicted by perturbative QCD (pQCD) at extremely high densities owning to the realization of approximate conformal symmetry of quark matter (Bjorken, 1983; Fujimoto et al., 2022), as shown in Figure 6 using certain NS modelings. A possible negative $\mathrm{\Delta }$ in NSs was first pointed out by Fujimoto et al. (2022). Since then, several studies have been made on this issue. In the following, we summarize the main findings of these studies by others and compare them with what we found above when possible.

Figure 6

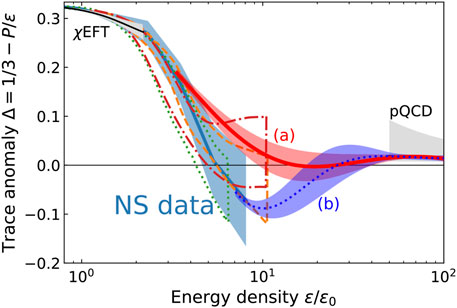
Figure 6. Trace anomaly $\mathrm{\Delta }$ as a function of energy density $\epsilon /{\epsilon }_0$. Here, the $\mathrm{\Delta }$ in NSs tends to be negative, although the pQCD prediction on it approaches zero, and ${\epsilon }_0\approx 150\mathrm{M}\mathrm{e}\mathrm{V}/{\mathrm{f}\mathrm{m}}^3$ is the energy density at nuclear saturation density. Figure taken from Fujimoto et al. (2022).

The analysis in Ecker and Rezzolla (2022) using an agnostic EOS showed that $\mathrm{\Delta }$ is very close to 0 for $M_{\mathrm{T}\mathrm{O}\mathrm{V}}\gtrsim 2.18$ $\sim 2.35M_{\odot }$ and may be slightly negative for even more massive NSs (e.g., $\mathrm{\Delta }\gtrsim -0.021_{-0.136}^{+0.039}$ for $M_{\mathrm{T}\mathrm{O}\mathrm{V}}\gtrsim 2.52M_{\odot }$); the radial dependence of $\mathrm{\Delta }$ is shown in the upper panel of Figure 7 from which one finds the $\mathrm{\Delta }$ for NS at the TOV configuration is much deeper than that in a canonical NS. Moreover, incorporating the pQCD effects $({\mathrm{\Delta }}_{\mathrm{p}\mathrm{Q}\mathrm{C}\mathrm{D}}\to 0)$ was found to effectively increase the inference on $\mathrm{\Delta }$. An updated analysis of Ecker and Rezzolla (2022) was given in Musolino et al. (2024), where $\mathrm{\Delta }\gtrsim -0.059_{-0.158}^{+0.162}$ or $\mathrm{\Delta }\gtrsim 0.019_{-0.129}^{+0.100}$ was obtained under the constraint $M_{\mathrm{T}\mathrm{O}\mathrm{V}}\gtrsim 2.35M_{\odot }$ without or with considering the pQCD effects; see the lower panel of Figure 7 for the PDFs. Similarly, if $M_{\mathrm{T}\mathrm{O}\mathrm{V}}\gtrsim 2.20M_{\odot }$ was required, these two limits become $\mathrm{\Delta }\gtrsim -0.046_{-0.166}^{+0.167}$ and $\mathrm{\Delta }\gtrsim 0.029_{-0.133}^{+0.108}$ (Musolino et al., 2024), respectively. In Takátsy et al. (2023), the central minimum value of $\mathrm{\Delta }$ is found to be about 0.04 using the NICER data together with the tidal deformability from GW170817, and a value of ${\mathrm{\Delta }}_{\min }\approx -0.04_{-0.09}^{+0.11}$ was inferred considering additionally the second component of GW190814 as an NS with mass approximately $2.59M_{\odot }$ (Abbott R. et al., 2020) using two hadronic EOS models (Takátsy et al., 2023); see the upper panel of Figure 8. By incorporating the constraints from AT2017gfo (Abbott et al., 2017b), it was found (Pang et al., 2024) that the minimum of $\mathrm{\Delta }$ is very close to 0 (approximately $-0.03$ to 0.05), as shown in the lower panel of Figure 8. Using similar low-density nuclear constraints as well as astrophysical data, including the black widow pulsar PSR J0952-0607 (Romani et al., 2022), Brandes et al. (2023a) predicted $\mathrm{\Delta }\gtrsim -0.086_{-0.07}^{+0.07}$ taken at $\epsilon \approx 1\mathrm{G}\mathrm{e}\mathrm{V}/{\mathrm{f}\mathrm{m}}^3$. Another analysis within the Bayesian framework considering the state-of-the-art theoretical calculations showed that $\mathrm{\Delta }\gtrsim -0.01$ (Annala et al., 2023) (where $M_{\mathrm{T}\mathrm{O}\mathrm{V}}\approx 2.27_{-0.11}^{+0.11}{M}_{\odot }$ is assumed). Furthermore, by considering the slope and curvature of energy per particle in NSs, Marczenko et al. (2024) showed that $\mathrm{\Delta }$ is lower bounded for $M_{\mathrm{T}\mathrm{O}\mathrm{V}}$ to be approximately $-0.02_{-0.03}^{+0.03}$. In addition, Cao and Chen (2023) found that the $\mathrm{\Delta }$ should be roughly larger than about $-0.04_{-0.09}^{+0.08}$ in self-bound quark stars while that in a normal NS is generally greater than zero.

Figure 7

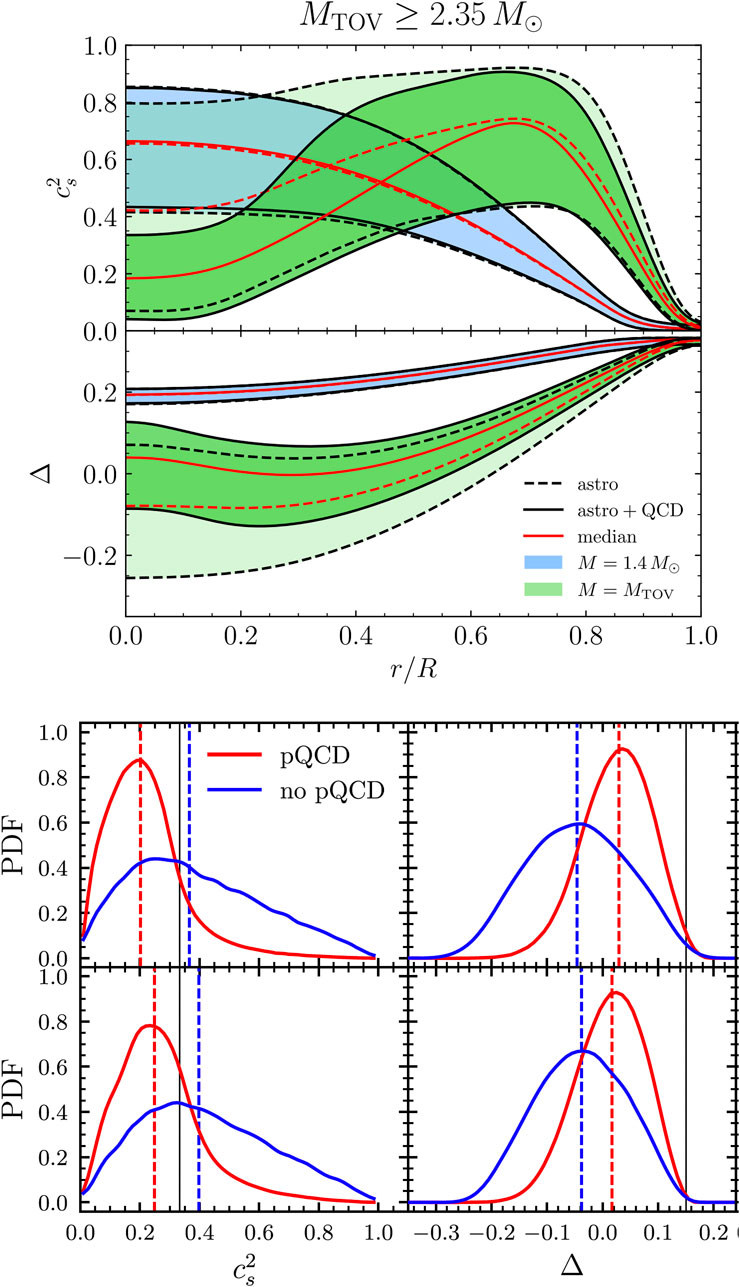
Figure 7. Upper panel: radial dependence of $\mathrm{\Delta }$ with the constraint $M_{\mathrm{T}\mathrm{O}\mathrm{V}}/M_{\odot }\gtrsim 2.35$. Figure taken from Ecker and Rezzolla (2022). Lower panel: PDF for $\mathrm{\Delta }$ with/without considering the pQCD limit at extremely high densities. The first (second) line in the lower panel is for non-rotating (Kepler rotating) NSs. Figure taken from Musolino et al. (2024).

Figure 8

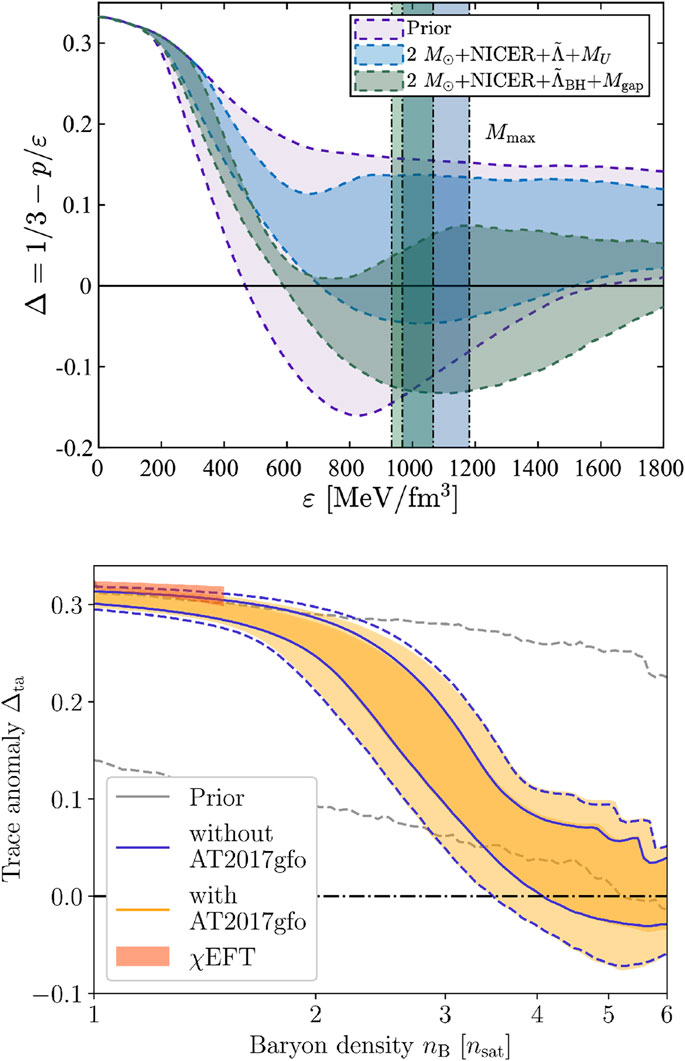
Figure 8. Two typical inferences on the energy density (or baryon density) dependence of $\mathrm{\Delta }$. Figures taken from Takátsy et al. (2023) (upper panel) and Pang et al. (2024) (lower panel).

A very recent study classified the EOSs by using the local and/or global derivative $\mathrm{d}{M}_{\mathrm{N}\mathrm{S}}/\mathrm{d}R$ of the resulting mass-radius sequences (Ferreira and Providência, 2024). Limiting the sign of $\mathrm{d}{M}_{\mathrm{N}\mathrm{S}}/\mathrm{d}R$ to positive on the M-R curve for NS masses between about $1M_{\odot }$ and $M_{\mathrm{T}\mathrm{O}\mathrm{V}}$, it was found that $\mathrm{\Delta }\gtrsim 0.008_{-0.160}^{+0.133}$ (Ferreira and Providência, 2024). On the other hand, if $\mathrm{d}{M}_{\mathrm{N}\mathrm{S}}/\mathrm{d}R<0$ is required for all NS masses, then $\mathrm{\Delta }\gtrsim -0.057_{-0.119}^{+0.119}$ is found; see the upper left panel of Figure 9. Our understanding of this behavior is as follows: A negative slope $\mathrm{d}{M}_{\mathrm{N}\mathrm{S}}/\mathrm{d}R$ along the whole M-R curve with $M_{\mathrm{N}\mathrm{S}}/M_{\odot }\gtrsim 1$ (Ferreira and Providência, 2024) implies the radius of NS at the TOV configuration is relatively smaller than the one with a positive $\mathrm{d}{M}_{\mathrm{N}\mathrm{S}}/\mathrm{d}R$ on a certain M-R segment, as indicated in the upper right panel of Figure 9. Thus, the NS compactness $\xi$ in the former case is relatively larger, which induces a larger $\mathrm{X}$ via Equation 22 and, correspondingly, a smaller $\mathrm{\Delta }$ (Cai and Li, 2024b). The smaller radius also implies that the NS is much denser, so the maximum baryon density is correspondingly larger (Ferreira and Providência, 2024). The dense matter trace anomaly in twin stars satisfying relevant static and dynamic stability conditions was recently studied (Jiménez et al., 2024). The $\mathrm{\Delta }$ was found to be deeply bounded roughly as $\mathrm{\Delta }\gtrsim -0.035$ (Jiménez et al., 2024), as shown in the bottom panel of Figure 9. A deep negative $\mathrm{\Delta }$ implies a large $\varphi$ or $\mathrm{X}$, so the compactness is correspondingly large according to Relation (22). We notice that the radii obtained in Jiménez et al. (2024) for certain NS masses (e.g., approximately $2M_{\odot }$) may be small compared with the observational data, for example, PSR J0740 + 6,620 (Riley et al., 2021).

Figure 9

Figure 9. Upper left panel: density dependence of $\mathrm{\Delta }$ inferred under the constraint $\mathrm{d}{M}_{\mathrm{N}\mathrm{S}}/\mathrm{d}R<0$ for all NS masses (blue) or $\mathrm{d}{M}_{\mathrm{N}\mathrm{S}}/\mathrm{d}R\ge 0$ for a certain mass range (red); inference in the bottom figure with astrophysical constraints. Figure taken from Ferreira and Providência (2024). Upper right panel: two types of M-R curves classified by using the derivative $\mathrm{d}{M}_{\mathrm{N}\mathrm{S}}/\mathrm{d}R$ for NS masses between about $1M_{\odot }$ and $M_{\mathrm{T}\mathrm{O}\mathrm{V}}$ to help understand the behavior of trace anomaly $\mathrm{\Delta }$s shown in the left panel. Bottom: The trace anomaly for twin stars satisfying static and dynamic stability conditions. Figure taken from Jiménez et al. (2024).

The above constraints on the lower limit of $\mathrm{\Delta }$ (realized in NSs) are summarized in the upper panel of Figure 10. Clearly, assuming all results are equally reliable within their individual errors indicated, there is a strong indication that the lower bound of $\mathrm{\Delta }$ is negative in NSs. Moreover, except for the prediction of Jiménez et al. (2024), the lower bounds of $\mathrm{\Delta }$ from various analyses are very close to the pQCD $({\mathrm{\Delta }}_{\mathrm{p}\mathrm{Q}\mathrm{C}\mathrm{D}}=0)$ or GR limit $({\mathrm{\Delta }}_{\mathrm{G}\mathrm{R}}\approx -0.04)$. It is interesting to note that the ${\mathrm{\Delta }}_{\mathrm{G}\mathrm{R}}$ and ${\mathrm{\Delta }}_{\mathrm{p}\mathrm{Q}\mathrm{C}\mathrm{D}}$ have no inner relation, to our best knowledge currently. However, we speculate that the matter-gravity duality in massive NSs mentioned earlier may be at work here. Certainly, this speculation deserves further study.

Figure 10

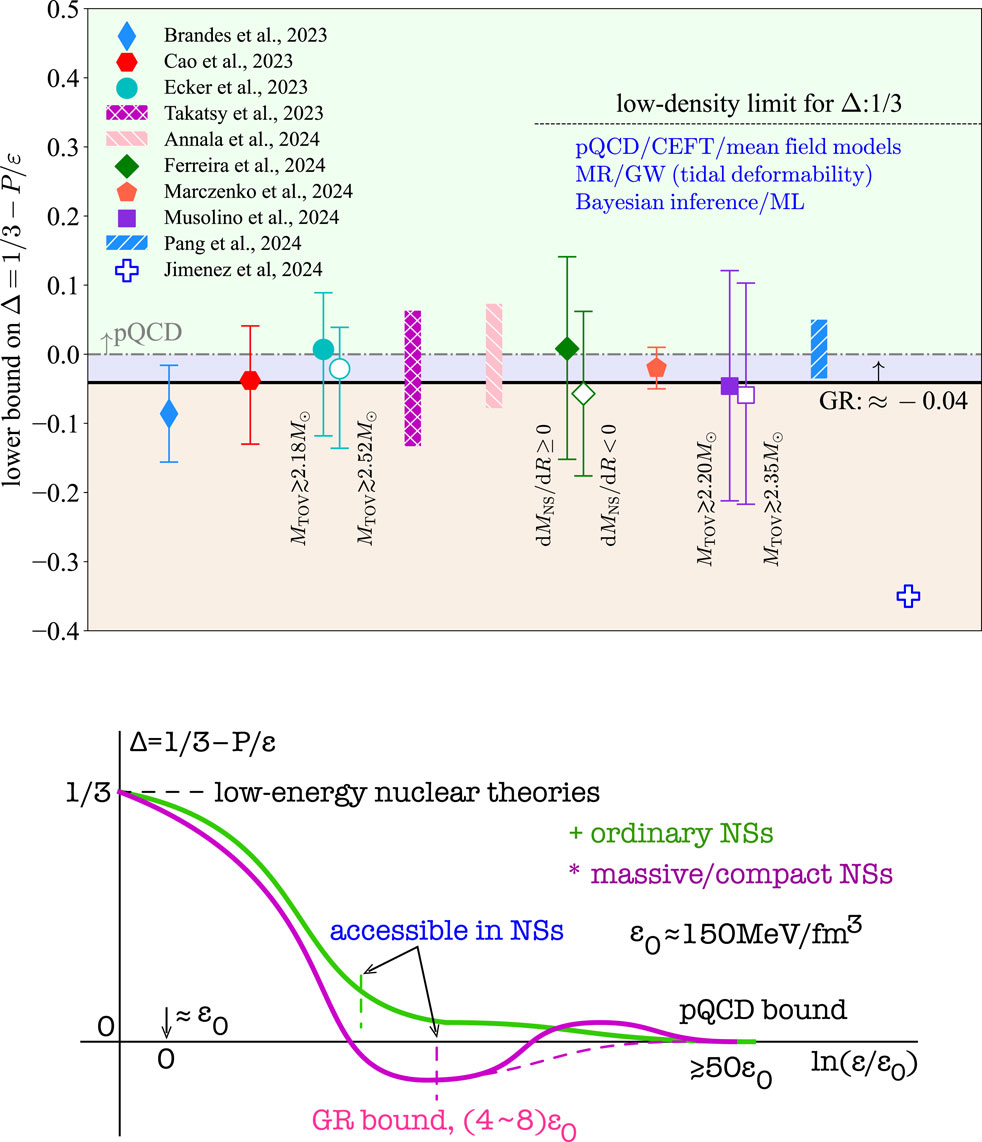
Figure 10. Upper panel: Summary of current constraints on the lower bound of trace anomaly $\mathrm{\Delta }$ in NSs from different analyses with respect to the pQCD (dot-dashed line) and GR (black solid line) predictions. See the text for details. Lower panel: Sketch of two imagined patterns for $\mathrm{\Delta }=1/3-P/\epsilon$ in NSs. The $\mathrm{\Delta }$ is well constrained around the fiducial density ${\epsilon }_0\approx 150\mathrm{M}\mathrm{e}\mathrm{V}/{\mathrm{f}\mathrm{m}}^3$ by low-energy nuclear theories and is predicted to vanish due to the approximate conformality of the matter at $\epsilon \gtrsim 50{\epsilon }_0$ (or equivalently $\rho \gtrsim 40{\rho }_0$) using pQCD theories. Figure 1 The magenta curve is based on the assumption that the causality limit is reached in the most massive NS observed, where $\epsilon /{\epsilon }_0$ being roughly around 4$\sim$8. Figure taken from Cai et al. (2023a).

How relevant are the GR or pQCD limits for understanding the trace anomaly $\mathrm{\Delta }$ in NSs? The $\mathrm{\Delta }$ and its energy density dependence are crucial for studying the $s^2$ in NSs (Fujimoto et al., 2022). For instance, one can explore whether there would be a peaked structure in the density/radius profile of $s^2$ in NSs. Sketched in the lower panel of Figure 10 (Cai et al., 2023a) are two imagined $\mathrm{\Delta }$ functions versus the reduced energy density $\epsilon /{\epsilon }_0$; here, ${\epsilon }_0\approx 150\mathrm{M}\mathrm{e}\mathrm{V}/{\mathrm{f}\mathrm{m}}^3$, around which the low-energy nuclear theories constrain the $\mathrm{\Delta }$ quite well. We notice that these two functions are educated guesses, certainly with biases. In fact, it has been pointed out that applying a particular EOS in extracting $\mathrm{\Delta }$ from observational data may influence the conclusion (Musolino et al., 2024). In the literature, there have been different imaginations/predictions/speculations on how the $\mathrm{\Delta }$ at finite energy density may vary and finally reach its pQCD limit of $\mathrm{\Delta }=0$ at very large energy densities $\epsilon \gtrsim 50{\epsilon }_0\approx 7.5\mathrm{G}\mathrm{e}\mathrm{V}/{\mathrm{f}\mathrm{m}}^3$ (Fujimoto et al., 2022; Kurkela et al., 2010) or equivalently $\rho \gtrsim 40{\rho }_0$. The latter is far larger than the energy density reachable in the most massive NSs reported so far based on our present knowledge. The pQCD limit on $\mathrm{\Delta }$ is thus possibly relevant (Zhou, 2024) but not fundamental for explaining the inferred $\varphi =P/\epsilon \gtrsim 1/3$ from NS observational data based on various microscopic and/or phenomenological models. On the other hand, we also have no confirmation in any way that the causality limit is reached in any NS. The magenta curve is based on the assumption that the causality limit under GR is reached in the most massive NSs observed so far. Based on most model calculations, in the cores of these NSs, the $\epsilon /{\epsilon }_0$ is roughly around 4$\sim$8. However, if the matter-gravity in massive NSs is indeed at work, we have no reason to expect that the GR limit is reached at an energy density lower than the one where the pQCD is applicable.

Keeping a positive attitude in our exploration of a completely uncharted area, we make a few more comments below on how the trace anomaly may reach the pQCD limit. As a negative $\mathrm{\Delta }$ is unlikely to be observed in ordinary NSs, the evolution of $\mathrm{\Delta }$ is probably more like the green curve in the lower panel of Figure 10. An (unconventional) exception may come from light but very compact NSs; for example, a $1.7M_{\odot }$ NS at the TOV configuration with radius approximately 9.3 km has its ${\mathrm{\Delta }}_{\mathrm{c}}\approx -0.02$ because ${\epsilon }_{\mathrm{c}}\approx 1.86\mathrm{G}\mathrm{e}\mathrm{V}/{\mathrm{f}\mathrm{m}}^3$ together with $P_{\mathrm{c}}\approx 654\mathrm{M}\mathrm{e}\mathrm{V}/{\mathrm{f}\mathrm{m}}^3$ should be obtained via the mass and radius scalings of (30) and (29), and so $\mathrm{X}={\widehat{P}}_{\mathrm{c}}\approx 0.351$. On the other hand, massive and compact NSs (masses $\gtrsim 2M_{\odot }$) are most relevant to observing a negative $\mathrm{\Delta }$ (as indicated by the magenta curves) and how it evolves to the pQCD bound, thus revealing more about properties of supradense matter (Cai et al., 2023a). Interestingly, both the green and magenta curves for the $\mathrm{\Delta }$ pattern are closely connected with the density dependence of the SSS using the trace anomaly decomposition of $s^2$ (Fujimoto et al., 2022) (we do not discuss these interesting topics in the current review). Unfortunately, the region with $\epsilon /{\epsilon }_0\gtrsim 8$ is largely inaccessible in NSs due to their self-gravitating nature.

6 Summary and future perspectives

In summary, perturbative analyses of the scaled TOV equations reveal interesting new insights into properties of supradense matter in NS cores without using any input nuclear EOS. In specific, the ratio $\varphi =P/\epsilon$ of pressure $P$ over energy density $\epsilon$ (the corresponding trace anomaly $\mathrm{\Delta }=1/3-\varphi$) in NS cores is bounded to be below 0.374 (above $-$0.04) by the causality condition under GR independent of the nuclear EOS. Moreover, we demonstrate that the NS mass $M_{\mathrm{N}\mathrm{S}}$, radius $R$, and compactness $\xi =M_{\mathrm{N}\mathrm{S}}/R$ strongly correlate with ${\mathrm{\Gamma }}_{\mathrm{c}}={\epsilon }_{\mathrm{c}}^{-1/2}{\mathrm{\Pi }}_{\mathrm{c}}^{3/2}$, ${\nu }_{\mathrm{c}}={\epsilon }_{\mathrm{c}}^{-1/2}{\mathrm{\Pi }}_{\mathrm{c}}^{1/2}$ and ${\mathrm{\Pi }}_{\mathrm{c}}=\mathrm{X}/(1+3{\mathrm{X}}^2+4\mathrm{X})$ with $\mathrm{X}\equiv {\varphi }_{\mathrm{c}}=P_{\mathrm{c}}/{\epsilon }_{\mathrm{c}}$, respectively; therefore observational data on $M_{\mathrm{N}\mathrm{S}}$ and $R$ as well as on $\xi$ via red-shift measurements can directly constrain the central EOS $P_{\mathrm{c}}=P_{\mathrm{c}}({\epsilon }_{\mathrm{c}})$ in a model-independent manner. In addition to the topics we have already investigated (Cai et al., 2023b; Cai et al., 2023a; Cai and Li, 2024a; Cai and Li, 2024b), there are interesting issues to be further explored in this direction. Particularly, we notice:

1. The upper limit for $\varphi =P/\epsilon$ near NS cores is obtained by truncating the perturbative expansion of $P$ and $\epsilon$ to low orders in reduced radius $\widehat{r}$. While the results are quite consistent with existing constraints from state-of-the-art simulations/inferences, refinement by including even higher-order $\widehat{r}$ terms would be important for studying the radius profile of $\varphi$ or $\mathrm{\Delta }$ in NSs. In the Appendix, we estimate such an effective correction.

2. Ironically, the upper bound $\varphi =P/\epsilon \lesssim 0.374$ from GR is very close to that $(P/\epsilon \lesssim 1/3)$ from pQCD at extremely high densities (Bjorken, 1983; Kurkela et al., 2010; Fujimoto et al., 2022). While we speculated that the well-known matter-gravity duality in massive NSs may be at work, it is currently unclear whether there is a fundamental connection between them. Efforts to understand their relationships may provide useful hints for developing a unified theory for strong-field gravity and elementary particles in supradense matter.

Author contributions

B-JC: writing–original draft and writing–review and editing. B-AL: writing–original draft and writing–review and editing.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This work was supported in part by the U.S. Department of Energy, Office of Science, under Award Number DE-SC0013702 and the CUSTIPEN (China-U.S. Theory Institute for Physics with Exotic Nuclei) under the U.S. Department of Energy Grant No. DE-SC0009971.

Acknowledgments

We would like to thank James Lattimer and Zhen Zhang for their helpful discussions.

Conflict of interest

Author B-JC was employed by Shadow Creator, Inc.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abbott, B. P., Abbott, R., Abbott, T. D., Abraham, S., Acernese, F., Ackley, K., et al. (2020a). Gw190425: observation of a compact binary coalescence with total mass 3.4 m_⊙. Astrophysical J. Lett. 892, L3. doi:10.3847/2041-8213/ab75f5

CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T. D., Acernese, F., Ackley, K., Adams, C., et al. (2017a). Gw170817: observation of gravitational waves from a binary neutron star inspiral. Phys. Rev. Lett. 119, 161101. doi:10.1103/PhysRevLett.119.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T. D., Acernese, F., Ackley, K., Adams, C., et al. (2017b). Multi-messenger observations of a binary neutron star merger. Astrophysical J. Lett. 848, L12. doi:10.3847/2041-8213/aa91c9

CrossRef Full Text | Google Scholar

Abbott, B. P., Abbott, R., Abbott, T. D., Acernese, F., Ackley, K., Adams, C., et al. (2018). Gw170817: measurements of neutron star radii and equation of state. Phys. Rev. Lett. 121, 161101. doi:10.1103/PhysRevLett.121.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

Abbott, R., Abbott, T. D., Abraham, S., Acernese, F., Ackley, K., Adams, C., et al. (2020b). Gw190814: gravitational waves from the coalescence of a 23 solar mass black hole with a 2.6 solar mass compact object. Astrophysical J. Lett. 896, L44. doi:10.3847/2041-8213/ab960f

CrossRef Full Text | Google Scholar

Akmal, A., Pandharipande, V. R., and Ravenhall, D. G. (1998). Equation of state of nucleon matter and neutron star structure. Phys. Rev. C 58, 1804–1828. doi:10.1103/PhysRevC.58.1804

CrossRef Full Text | Google Scholar

Alford, M. G., Schmitt, A., Rajagopal, K., and Schäfer, T. (2008). Color superconductivity in dense quark matter. Rev. Mod. Phys. 80, 1455–1515. doi:10.1103/RevModPhys.80.1455

CrossRef Full Text | Google Scholar

Al-Mamun, M., Steiner, A. W., Nättilä, J., Lange, J., O’Shaughnessy, R., Tews, I., et al. (2021). Combining electromagnetic and gravitational-wave constraints on neutron-star masses and radii. Phys. Rev. Lett. 126, 061101. doi:10.1103/PhysRevLett.126.061101

PubMed Abstract | CrossRef Full Text | Google Scholar

Altiparmak, S., Ecker, C., and Rezzolla, L. (2022). On the sound speed in neutron stars. Astrophysical J. Lett. 939, L34. doi:10.3847/2041-8213/ac9b2a

CrossRef Full Text | Google Scholar

Annala, E., Gorda, T., Hirvonen, J., Komoltsev, O., Kurkela, A., Nättilä, J., et al. (2023). Strongly interacting matter exhibits deconfined behavior in massive neutron stars. Nat. Commun. 14, 8451. doi:10.1038/s41467-023-44051-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Annala, E., Gorda, T., Kurkela, A., Nättilä, J., and Vuorinen, A. (2020). Evidence for quark-matter cores in massive neutron stars. Nat. Phys. 16, 907–910. doi:10.1038/s41567-020-0914-9

CrossRef Full Text | Google Scholar

Antoniadis, J., Freire, P. C. C., Wex, N., Tauris, T. M., Lynch, R. S., van Kerkwijk, M. H., et al. (2013). A massive pulsar in a compact relativistic binary. Science 340, 448, 1233232. doi:10.1126/science.1233232

PubMed Abstract | CrossRef Full Text | Google Scholar

Arzoumanian, Z., Brazier, A., Burke-Spolaor, S., Chamberlin, S., Chatterjee, S., Christy, B., et al. (2018). The nanograv 11-year data set: high-precision timing of 45 millisecond pulsars. Astrophysical J. Suppl. Ser. 235, 37. doi:10.3847/1538-4365/aab5b0

CrossRef Full Text | Google Scholar

Bailin, D., and Love, A. (1984). Superfluidity and superconductivity in relativistic fermion systems. Phys. Rep. 107, 325–385. doi:10.1016/0370-1573(84)90145-5

CrossRef Full Text | Google Scholar

Baiotti, L. (2019). Gravitational waves from neutron star mergers and their relation to the nuclear equation of state. Prog. Part. Nucl. Phys. 109, 103714. doi:10.1016/j.ppnp.2019.103714

CrossRef Full Text | Google Scholar

Baiotti, L., and Rezzolla, L. (2017). Binary neutron star mergers: a review of einstein’s richest laboratory. Rep. Prog. Phys. 80, 096901. doi:10.1088/1361-6633/aa67bb

PubMed Abstract | CrossRef Full Text | Google Scholar

Baluni, V. (1978). Non-abelian gauge theories of fermi systems: quantum-chromodynamic theory of highly condensed matter. Phys. Rev. D. 17, 2092–2121. doi:10.1103/PhysRevD.17.2092

CrossRef Full Text | Google Scholar

Baumgarte, S., and Shapiro, S. (2010). Numerical relativity: solving einstein’s equations on the computer. Cambridge: Cambridge Unversity Press.

Google Scholar

Bauswein, A., Bastian, N.-U. F., Blaschke, D. B., Chatziioannou, K., Clark, J. A., Fischer, T., et al. (2019). Identifying a first-order phase transition in neutron-star mergers through gravitational waves. Phys. Rev. Lett. 122, 061102. doi:10.1103/PhysRevLett.122.061102

PubMed Abstract | CrossRef Full Text | Google Scholar

Bauswein, A., Blacker, S., Vijayan, V., Stergioulas, N., Chatziioannou, K., Clark, J. A., et al. (2020). Equation of state constraints from the threshold binary mass for prompt collapse of neutron star mergers. Phys. Rev. Lett. 125, 141103. doi:10.1103/PhysRevLett.125.141103

PubMed Abstract | CrossRef Full Text | Google Scholar

Baym, G., Furusawa, S., Hatsuda, T., Kojo, T., and Togashi, H. (2019). New neutron star equation of state with quark–hadron crossover. Astrophysical J. 885, 42. doi:10.3847/1538-4357/ab441e

CrossRef Full Text | Google Scholar

Baym, G., Hatsuda, T., Kojo, T., Powell, P. D., Song, Y., and Takatsuka, T. (2018). From hadrons to quarks in neutron stars: a review. Rep. Prog. Phys. 81, 056902. doi:10.1088/1361-6633/aaae14

PubMed Abstract | CrossRef Full Text | Google Scholar

Baym, G., Pethick, C., and Sutherland, P. (1971). The ground state of matter at high densities: equation of state and stellar models. Astrophysical J. 170, 299. doi:10.1086/151216

CrossRef Full Text | Google Scholar

Bjorken, J. D. (1983). Highly relativistic nucleus-nucleus collisions: the central rapidity region. Phys. Rev. D. 27, 140–151. doi:10.1103/PhysRevD.27.140

CrossRef Full Text | Google Scholar

Blaschke, D., Ayriyan, A., Alvarez-Castillo, D. E., and Grigorian, H. (2020). Was GW170817 a canonical neutron star merger? Bayesian analysis with a third family of compact stars. Universe 6, 81. doi:10.3390/universe6060081

CrossRef Full Text | Google Scholar

Bloch, I., Dalibard, J., and Zwerger, W. (2008). Many-body physics with ultracold gases. Rev. Mod. Phys. 80, 885–964. doi:10.1103/RevModPhys.80.885

CrossRef Full Text | Google Scholar

Bombaci, I., Drago, A., Logoteta, D., Pagliara, G., and Vidaña, I. (2021). Was gw190814 a black hole–strange quark star system? Phys. Rev. Lett. 126, 162702. doi:10.1103/PhysRevLett.126.162702

PubMed Abstract | CrossRef Full Text | Google Scholar

Bose, S., Chakravarti, K., Rezzolla, L., Sathyaprakash, B. S., and Takami, K. (2018). Neutron-star radius from a population of binary neutron star mergers. Phys. Rev. Lett. 120, 031102. doi:10.1103/PhysRevLett.120.031102

PubMed Abstract | CrossRef Full Text | Google Scholar

Brandes, L., Weise, W., and Kaiser, N. (2023a). Evidence against a strong first-order phase transition in neutron star cores: impact of new data. Phys. Rev. D. 108, 094014. doi:10.1103/PhysRevD.108.094014

CrossRef Full Text | Google Scholar

Brandes, L., Weise, W., and Kaiser, N. (2023b). Inference of the sound speed and related properties of neutron stars. Phys. Rev. D. 107, 014011. doi:10.1103/PhysRevD.107.014011

CrossRef Full Text | Google Scholar

Breschi, M., Bernuzzi, S., Godzieba, D., Perego, A., and Radice, D. (2022). Constraints on the maximum densities of neutron stars from postmerger gravitational waves with third-generation observations. Phys. Rev. Lett. 128, 161102. doi:10.1103/PhysRevLett.128.161102

PubMed Abstract | CrossRef Full Text | Google Scholar

Burgio, G., Schulze, H.-J., Vidaña, I., and Wei, J.-B. (2021). Neutron stars and the nuclear equation of state. Prog. Part. Nucl. Phys. 120, 103879. doi:10.1016/j.ppnp.2021.103879

CrossRef Full Text | Google Scholar

Cai, B.-J., and Li, B.-A. (2016). Symmetry energy of cold nucleonic matter within a relativistic mean field model encapsulating effects of high-momentum nucleons induced by short-range correlations. Phys. Rev. C 93, 014619. doi:10.1103/PhysRevC.93.014619

CrossRef Full Text | Google Scholar

Cai, B.-J., and Li, B.-A. (2024a). Strong gravity extruding peaks in speed of sound profiles of massive neutron stars. Phys. Rev. D. 109, 083015. doi:10.1103/PhysRevD.109.083015

CrossRef Full Text | Google Scholar

Cai, B.-J., and Li, B.-A. (2024b). Unraveling trace anomaly of supradense matter via neutron star compactness scaling. arXiv:2406, 05025.

Google Scholar

Cai, B.-J., Li, B.-A., and Zhang, Z. (2023a). Central speed of sound, the trace anomaly, and observables of neutron stars from a perturbative analysis of scaled tolman-oppenheimer-volkoff equations. Phys. Rev. D. 108, 103041. doi:10.1103/PhysRevD.108.103041

CrossRef Full Text | Google Scholar

Cai, B.-J., Li, B.-A., and Zhang, Z. (2023b). Core states of neutron stars from anatomizing their scaled structure equations. Astrophysical J. 952, 147. doi:10.3847/1538-4357/acdef0

CrossRef Full Text | Google Scholar

Cao, Z., and Chen, L.-W. (2023). Neutron star vs quark star in the multimessenger era. arXiv:2308, 16783.

Google Scholar

Capano, C. D., Tews, I., Brown, S. M., Margalit, B., De, S., Kumar, S., et al. (2020). Stringent constraints on neutron-star radii from multimessenger observations and nuclear theory. Nat. Astron 4 (4), 625–632. doi:10.1038/s41550-020-1014-6

CrossRef Full Text | Google Scholar

Chandrasekhar, S. (2010). An introduction to the study of stellar structure. New York: Dover Press. Chapter 4).

Google Scholar

Chatziioannou, K. (2020). Neutron star tidal deformability and equation of state constraints. Gen. Rel. Grav. 52, 109. doi:10.1007/s10714-020-02754-3

CrossRef Full Text | Google Scholar

Chin, S. (1977). A relativistic many-body theory of high density matter. Ann. Phys. 108, 301–367. doi:10.1016/0003-4916(77)90016-1

CrossRef Full Text | Google Scholar

Choudhury, D., Salmi, T., Vinciguerra, S., Riley, T. E., Kini, Y., Watts, A. L., et al. (2024). A nicer view of the nearest and brightest millisecond pulsar: psr j0437–4715. Astrophysical J. Lett. 971, L20. doi:10.3847/2041-8213/ad5a6f

CrossRef Full Text | Google Scholar

Danielewicz, P., Lacey, R., and Lynch, W. G. (2002). Determination of the equation of state of dense matter. Science 298, 1592–1596. doi:10.1126/science.1078070

PubMed Abstract | CrossRef Full Text | Google Scholar

De, S., Finstad, D., Lattimer, J. M., Brown, D. A., Berger, E., and Biwer, C. M. (2018). Tidal deformabilities and radii of neutron stars from the observation of gw170817. Phys. Rev. Lett. 121, 091102. doi:10.1103/PhysRevLett.121.091102

PubMed Abstract | CrossRef Full Text | Google Scholar

DeDeo, S., and Psaltis, D. (2003). Towards new tests of strong-field gravity with measurements of surface atomic line redshifts from neutron stars. Phys. Rev. Lett. 90, 141101. doi:10.1103/PhysRevLett.90.141101

PubMed Abstract | CrossRef Full Text | Google Scholar

Demorest, P. B., Pennucci, T., Ransom, S. M., Roberts, M. S. E., and Hessels, J. W. T. (2010). A two-solar-mass neutron star measured using shapiro delay. Nature 467, 1081–1083. doi:10.1038/nature09466

PubMed Abstract | CrossRef Full Text | Google Scholar

Dexheimer, V., Noronha, J., Noronha-Hostler, J., Yunes, N., and Ratti, C. (2021). Future physics perspectives on the equation of state from heavy ion collisions to neutron stars. J. Phys. G Nucl. Part. Phys. 48, 073001. doi:10.1088/1361-6471/abe104

CrossRef Full Text | Google Scholar

Dittmann, A. J., Miller, M. C., Lamb, F. K., Holt, I., Chirenti, C., Wolff, M. T., et al. (2024). A more precise measurement of the radius of psr j0740+6620 using updated nicer data. Astrophysical Jouranl. doi:10.3847/1538-4357/ad5f1e

CrossRef Full Text | Google Scholar

Drischler, C., Furnstahl, R. J., Melendez, J. A., and Phillips, D. R. (2020). How well do we know the neutron-matter equation of state at the densities inside neutron stars? a bayesian approach with correlated uncertainties. Phys. Rev. Lett. 125, 202702. doi:10.1103/PhysRevLett.125.202702

PubMed Abstract | CrossRef Full Text | Google Scholar

Drischler, C., Han, S., Lattimer, J. M., Prakash, M., Reddy, S., and Zhao, T. (2021a). Limiting masses and radii of neutron stars and their implications. Phys. Rev. C 103, 045808. doi:10.1103/PhysRevC.103.045808

CrossRef Full Text | Google Scholar

Drischler, C., Holt, J., and Wellenhofer, C. (2021b). Chiral effective field theory and the high-density nuclear equation of state. Annu. Rev. Nucl. Part. Sci. 71, 403–432. doi:10.1146/annurev-nucl-102419-041903

CrossRef Full Text | Google Scholar

Ecker, C., and Rezzolla, L. (2022). Impact of large-mass constraints on the properties of neutron stars. Mon. Notices R. Astronomical Soc. 519, 2615–2622. doi:10.1093/mnras/stac3755

CrossRef Full Text | Google Scholar

Essick, R., Tews, I., Landry, P., and Schwenk, A. (2021). Astrophysical constraints on the symmetry energy and the neutron skin of ²⁰⁸Pb with minimal modeling assumptions. Phys. Rev. Lett. 127, 192701. doi:10.1103/PhysRevLett.127.192701

PubMed Abstract | CrossRef Full Text | Google Scholar

Fattoyev, F. J., Piekarewicz, J., and Horowitz, C. J. (2018). Neutron skins and neutron stars in the multimessenger era. Phys. Rev. Lett. 120, 172702. doi:10.1103/PhysRevLett.120.172702

PubMed Abstract | CrossRef Full Text | Google Scholar

Ferreira, M., and Providência, C. m. c. (2024). Constraining neutron star matter from the slope of the mass-radius curves. Phys. Rev. D. 110, 063018. doi:10.1103/PhysRevD.110.063018

CrossRef Full Text | Google Scholar

Fonseca, E., Cromartie, H. T., Pennucci, T. T., Ray, P. S., Kirichenko, A. Y., Ransom, S. M., et al. (2021). Refined mass and geometric measurements of the high-mass psr j0740+6620. Astrophysical J. Lett. 915, L12. doi:10.3847/2041-8213/ac03b8

CrossRef Full Text | Google Scholar

Freedman, B. A., and McLerran, L. D. (1977). Fermions and gauge vector mesons at finite temperature and density. iii. the ground-state energy of a relativistic quark gas. Phys. Rev. D. 16, 1169–1185. doi:10.1103/PhysRevD.16.1169

CrossRef Full Text | Google Scholar

Fujimoto, Y., Fukushima, K., Kamata, S., and Murase, K. (2024). Uncertainty quantification in the machine-learning inference from neutron star probability distribution to the equation of state. Phys. Rev. D. 110, 034035. doi:10.1103/PhysRevD.110.034035

CrossRef Full Text | Google Scholar

Fujimoto, Y., Fukushima, K., McLerran, L. D., and Praszałowicz, M. (2022). Trace anomaly as signature of conformality in neutron stars. Phys. Rev. Lett. 129, 252702. doi:10.1103/PhysRevLett.129.252702

PubMed Abstract | CrossRef Full Text | Google Scholar

Giorgini, S., Pitaevskii, L. P., and Stringari, S. (2008). Theory of ultracold atomic fermi gases. Rev. Mod. Phys. 80, 1215–1274. doi:10.1103/RevModPhys.80.1215

CrossRef Full Text | Google Scholar

Gorda, T., Komoltsev, O., and Kurkela, A. (2023). Ab-initio qcd calculations impact the inference of the neutron-star-matter equation of state. Astrophysical J. 950, 107. doi:10.3847/1538-4357/acce3a

CrossRef Full Text | Google Scholar

Han, M.-Z., Huang, Y.-J., Tang, S.-P., and Fan, Y.-Z. (2023). Plausible presence of new state in neutron stars with masses above 0.98mtov. Sci. Bull. 68, 913–919. doi:10.1016/j.scib.2023.04.007

CrossRef Full Text | Google Scholar

He, X.-T., Fattoyev, F. J., Li, B.-A., and Newton, W. G. (2015). Impact of the equation-of-state–gravity degeneracy on constraining the nuclear symmetry energy from astrophysical observables. Phys. Rev. C 91, 015810. doi:10.1103/PhysRevC.91.015810

CrossRef Full Text | Google Scholar

Hoyle, C. D. (2003). The weight of expectation. Nature 421, 899–900. doi:10.1038/421899a

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, Y.-J., Baiotti, L., Kojo, T., Takami, K., Sotani, H., Togashi, H., et al. (2022). Merger and postmerger of binary neutron stars with a quark-hadron crossover equation of state. Phys. Rev. Lett. 129, 181101. doi:10.1103/PhysRevLett.129.181101

PubMed Abstract | CrossRef Full Text | Google Scholar

Iida, K., and Sato, K. (1997). Spin down of neutron stars and compositional transitions in the cold crustal matter. Astrophysical J. 477, 294–312. doi:10.1086/303685

CrossRef Full Text | Google Scholar

Jiang, J.-L., Ecker, C., and Rezzolla, L. (2023). Bayesian analysis of neutron-star properties with parameterized equations of state: the role of the likelihood functions. Astrophysical J. 949, 11. doi:10.3847/1538-4357/acc4be

CrossRef Full Text | Google Scholar

Jiménez, J. C., Lazzari, L., and Gonçalves, V. P. (2024). How the qcd trace anomaly behaves at the core of twin stars? arXiV:2408, 11614.

Google Scholar

Komoltsev, O., and Kurkela, A. (2022). How perturbative qcd constrains the equation of state at neutron-star densities. Phys. Rev. Lett. 128, 202701. doi:10.1103/PhysRevLett.128.202701

PubMed Abstract | CrossRef Full Text | Google Scholar

Koranda, S., Stergioulas, N., and Friedman, J. L. (1997). Upper limits set by causality on the rotation and mass of uniformly rotating relativistic stars. Astrophysical J. 488, 799–806. doi:10.1086/304714

CrossRef Full Text | Google Scholar

Kumar, R., Dexheimer, V., Jahan, J., Noronha, J., Noronha-Hostler, J., Ratti, C., et al. (2024). Theoretical and experimental constraints for the equation of state of dense and hot matter. Living Rev. Relativ. 27, 3. doi:10.1007/s41114-024-00049-6

CrossRef Full Text | Google Scholar

Kurkela, A., Romatschke, P., and Vuorinen, A. (2010). Cold quark matter. Phys. Rev. D. 81, 105021. doi:10.1103/PhysRevD.81.105021

CrossRef Full Text | Google Scholar

Kyutoku, K., Shibata, M., and Taniguchi, K. (2021). Coalescence of black hole–neutron star binaries. Living Rev. Relativ. 24, 5. doi:10.1007/s41114-021-00033-4

CrossRef Full Text | Google Scholar

Landau, L., and Lifshitz, E. (1987). Fluid mechanics, 64. New York: Pergamon Press.

Google Scholar

Lattimer, J. M. (2021). Neutron stars and the nuclear matter equation of state. Ann. Rev. Nucl. Part. Sci. 71, 433–464. doi:10.1146/annurev-nucl-102419-124827

CrossRef Full Text | Google Scholar

Lattimer, J. M., and Prakash, M. (2001). Neutron star structure and the equation of state. Astrophysical J. 550, 426–442. doi:10.1086/319702

CrossRef Full Text | Google Scholar

Lattimer, J. M., and Prakash, M. (2007). Neutron star observations: prognosis for equation of state constraints. Phys. Rep. 442, 109–165. The Hans Bethe Centennial Volume 1906-2006. doi:10.1016/j.physrep.2007.02.003

CrossRef Full Text | Google Scholar

Li, A., Zhu, Z. Y., Zhou, E. P., Dong, J. M., Hu, J. N., and Xia, C. J. (2020). Neutron star equation of state: quark mean-field (QMF) modeling and applications. JHEAp 28, 19–46. doi:10.1016/j.jheap.2020.07.001

CrossRef Full Text | Google Scholar

Li, B.-A. (2017). Nuclear symmetry energy extracted from laboratory experiments. Nucl. Phys. News 27, 7–11. doi:10.1080/10619127.2017.1388681

CrossRef Full Text | Google Scholar

Li, B.-A., Cai, B.-J., Chen, L.-W., and Xu, J. (2018). Nucleon effective masses in neutron-rich matter. Prog. Part. Nucl. Phys. 99, 29–119. doi:10.1016/j.ppnp.2018.01.001

CrossRef Full Text | Google Scholar

Li, B.-A., Cai, B.-J., Xie, W.-J., and Zhang, N.-B. (2021). Progress in constraining nuclear symmetry energy using neutron star observables since gw170817. Universe 7, 182. doi:10.3390/universe7060182

CrossRef Full Text | Google Scholar

Li, B.-A., Chen, L.-W., and Ko, C. M. (2008). Recent progress and new challenges in isospin physics with heavy-ion reactions. Phys. Rep. 464, 113–281. doi:10.1016/j.physrep.2008.04.005

CrossRef Full Text | Google Scholar

Li, B.-A., Krastev, P. G., Wen, D.-H., and Zhang, N.-B. (2019). Towards understanding astrophysical effects of nuclear symmetry energy. Eur. Phys. J. A 55, 117. doi:10.1140/epja/i2019-12780-8

CrossRef Full Text | Google Scholar

Li, F., Cai, B.-J., Zhou, Y., Jiang, W.-Z., and Chen, L.-W. (2022). Effects of isoscalar- and isovector-scalar meson mixing on neutron star structure. Astrophysical J. 929, 183. doi:10.3847/1538-4357/ac5e2a

CrossRef Full Text | Google Scholar

Lim, Y., and Holt, J. W. (2018). Neutron star tidal deformabilities constrained by nuclear theory and experiment. Phys. Rev. Lett. 121, 062701. doi:10.1103/PhysRevLett.121.062701

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, W., Li, B.-A., Chen, L.-W., Wen, D.-H., and Xu, J. (2014). Breaking the EOS-gravity degeneracy with masses and pulsating frequencies of neutron stars. J. Phys. G. 41, 075203. doi:10.1088/0954-3899/41/7/075203

CrossRef Full Text | Google Scholar

Lovato, A., Dore, T., Pisarski, R. D., Schenke, B., Chatziioannou, K., Read, J. S., et al. (2022). Long range plan: dense matter theory for heavy-ion collisions and neutron stars. arXiv:2211, 02224.

Google Scholar

Marczenko, M., Redlich, K., and Sasaki, C. (2024). Curvature of the energy per particle in neutron stars. Phys. Rev. D. 109, L041302. doi:10.1103/PhysRevD.109.L041302

CrossRef Full Text | Google Scholar

McLerran, L., and Reddy, S. (2019). Quarkyonic matter and neutron stars. Phys. Rev. Lett. 122, 122701. doi:10.1103/PhysRevLett.122.122701

PubMed Abstract | CrossRef Full Text | Google Scholar

Migdal, A. B. (1978). Pion fields in nuclear matter. Rev. Mod. Phys. 50, 107–172. doi:10.1103/RevModPhys.50.107

CrossRef Full Text | Google Scholar

Miller, M. C., Lamb, F. K., Dittmann, A. J., Bogdanov, S., Arzoumanian, Z., Gendreau, K. C., et al. (2019). Psr j0030+0451 mass and radius from nicer data and implications for the properties of neutron star matter. Astrophysical J. Lett. 887, L24. doi:10.3847/2041-8213/ab50c5

CrossRef Full Text | Google Scholar

Miller, M. C., Lamb, F. K., Dittmann, A. J., Bogdanov, S., Arzoumanian, Z., Gendreau, K. C., et al. (2021). The radius of psr j0740+6620 from nicer and xmm-Newton data. Astrophysical J. Lett. 918, L28. doi:10.3847/2041-8213/ac089b

CrossRef Full Text | Google Scholar

Morley, P., and Kislinger, M. (1979). Relativistic many-body theory, quantum chromodynamics and neutron stars/supernova. Phys. Rep. 51, 63–110. doi:10.1016/0370-1573(79)90005-X

CrossRef Full Text | Google Scholar

Most, E. R., Papenfort, L. J., Dexheimer, V., Hanauske, M., Schramm, S., Stöcker, H., et al. (2019). Signatures of quark-hadron phase transitions in general-relativistic neutron-star mergers. Phys. Rev. Lett. 122, 061101. doi:10.1103/PhysRevLett.122.061101

PubMed Abstract | CrossRef Full Text | Google Scholar

Most, E. R., Weih, L. R., Rezzolla, L., and Schaffner-Bielich, J. (2018). New constraints on radii and tidal deformabilities of neutron stars from gw170817. Phys. Rev. Lett. 120, 261103. doi:10.1103/PhysRevLett.120.261103

PubMed Abstract | CrossRef Full Text | Google Scholar

Mroczek, D., Miller, M. C., Noronha-Hostler, J., and Yunes, N. (2023). Nontrivial features in the speed of sound inside neutron stars. arXiv:2309.02345

Google Scholar

Musolino, C., Ecker, C., and Rezzolla, L. (2024). On the maximum mass and oblateness of rotating neutron stars with generic equations of state. Astrophysical J. 962, 61. doi:10.3847/1538-4357/ad1758

CrossRef Full Text | Google Scholar

Nathanail, A., Most, E. R., and Rezzolla, L. (2021). Gw170817 and gw190814: tension on the maximum mass. Astrophysical J. Lett. 908, L28. doi:10.3847/2041-8213/abdfc6

CrossRef Full Text | Google Scholar

National Research Council (2003). Connecting quarks with the cosmos: eleven science questions for the new century. Washington, DC: The National academies Press.

Google Scholar

Oertel, M., Hempel, M., Klähn, T., and Typel, S. (2017). Equations of state for supernovae and compact stars. Rev. Mod. Phys. 89, 015007. doi:10.1103/RevModPhys.89.015007

CrossRef Full Text | Google Scholar

Ofengeim, D. D., Shternin, P. S., and Piran, T. (2023). Maximal mass neutron star as a key to superdense matter physics. Astron. Lett. 49, 567–574. doi:10.1134/s1063773723100055

CrossRef Full Text | Google Scholar

Oppenheimer, J. R., and Volkoff, G. M. (1939). On massive neutron cores. Phys. Rev. 55, 374–381. doi:10.1103/PhysRev.55.374

CrossRef Full Text | Google Scholar

Orsaria, M. G., Malfatti, G., Mariani, M., Ranea-Sandoval, I. F., García, F., Spinella, W. M., et al. (2019). Phase transitions in neutron stars and their links to gravitational waves. J. Phys. G Nucl. Part. Phys. 46, 073002. doi:10.1088/1361-6471/ab1d81

CrossRef Full Text | Google Scholar

Özel, F., and Freire, P. (2016). Masses, radii, and the equation of state of neutron stars. Ann. Rev. Astron. Astrophys. 54, 401–440. doi:10.1146/annurev-astro-081915-023322

CrossRef Full Text | Google Scholar

Pang, P. T. H., Dietrich, T., Coughlin, M. W., Bulla, M., Tews, I., Almualla, M., et al. (2023). An updated nuclear-physics and multi-messenger astrophysics framework for binary neutron star mergers. Nat. Commun. 14, 8352. doi:10.1038/s41467-023-43932-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Pang, P. T. H., Sivertsen, L., Somasundaram, R., Dietrich, T., Sen, S., Tews, I., et al. (2024). Probing quarkyonic matter in neutron stars with the bayesian nuclear-physics multimessenger astrophysics framework. Phys. Rev. C 109, 025807. doi:10.1103/PhysRevC.109.025807

CrossRef Full Text | Google Scholar

Perego, A., Logoteta, D., Radice, D., Bernuzzi, S., Kashyap, R., Das, A., et al. (2022). Probing the incompressibility of nuclear matter at ultrahigh density through the prompt collapse of asymmetric neutron star binaries. Phys. Rev. Lett. 129, 032701. doi:10.1103/PhysRevLett.129.032701

PubMed Abstract | CrossRef Full Text | Google Scholar

Providência, C., Malik, T., Albino, M. B., and Ferreira, M. (2024). “Relativistic description of the neutron star equation of state,”. Florida, United States: CRC Press, 111–143. chap. 5. doi:10.1201/9781003306580-5

CrossRef Full Text | Google Scholar

Psaltis, D. (2008). Probes and tests of strong-field gravity with observations in the electromagnetic spectrum. Living Rev. rel. 11, 9. doi:10.12942/lrr-2008-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Raaijmakers, G., Greif, S. K., Hebeler, K., Hinderer, T., Nissanke, S., Schwenk, A., et al. (2021). Constraints on the dense matter equation of state and neutron star properties from nicer’s mass–radius estimate of psr j0740+6620 and multimessenger observations. Astrophysical J. Lett. 918, L29. doi:10.3847/2041-8213/ac089a

CrossRef Full Text | Google Scholar

Radice, D., Perego, A., Zappa, F., and Bernuzzi, S. (2018). Gw170817: joint constraint on the neutron star equation of state from multimessenger observations. Astrophysical J. Lett. 852, L29. doi:10.3847/2041-8213/aaa402

CrossRef Full Text | Google Scholar

Raithel, C. A., and Most, E. R. (2023). Degeneracy in the inference of phase transitions in the neutron star equation of state from gravitational wave data. Phys. Rev. Lett. 130, 201403. doi:10.1103/PhysRevLett.130.201403

PubMed Abstract | CrossRef Full Text | Google Scholar

Reardon, D. J., Bailes, M., Shannon, R. M., Flynn, C., Askew, J., Bhat, N. D. R., et al. (2024). The neutron star mass, distance, and inclination from precision timing of the brilliant millisecond pulsar j0437-4715. Astrophysical J. Lett. 971, L18. doi:10.3847/2041-8213/ad614a

CrossRef Full Text | Google Scholar

Riley, T. E., Watts, A. L., Bogdanov, S., Ray, P. S., Ludlam, R. M., Guillot, S., et al. (2019). A nicer view of psr j0030+0451: millisecond pulsar parameter estimation. Astrophysical J. Lett. 887, L21. doi:10.3847/2041-8213/ab481c

CrossRef Full Text | Google Scholar

Riley, T. E., Watts, A. L., Ray, P. S., Bogdanov, S., Guillot, S., Morsink, S. M., et al. (2021). A nicer view of the massive pulsar psr j0740+6620 informed by radio timing and xmm-Newton spectroscopy. Astrophysical J. Lett. 918, L27. doi:10.3847/2041-8213/ac0a81

CrossRef Full Text | Google Scholar

Romani, R. W., Kandel, D., Filippenko, A. V., Brink, T. G., and Zheng, W. (2022). Psr j0952-0607: the fastest and heaviest known galactic neutron star. Astrophysical J. Lett. 934, L17. doi:10.3847/2041-8213/ac8007

CrossRef Full Text | Google Scholar

Rutherford, N., Mendes, M., Svensson, I., Schwenk, A., Watts, A. L., Hebeler, K., et al. (2024). Constraining the dense matter equation of state with new nicer mass–radius measurements and new chiral effective field theory inputs. Astrophysical J. Lett. 971, L19. doi:10.3847/2041-8213/ad5f02

CrossRef Full Text | Google Scholar

Saes, J. A., and Mendes, R. F. P. (2022). Equation-of-state-insensitive measure of neutron star stiffness. Phys. Rev. D. 106, 043027. doi:10.1103/PhysRevD.106.043027

CrossRef Full Text | Google Scholar

Salmi, T., Choudhury, D., Kini, Y., Riley, T. E., Vinciguerra, S., Watts, A. L., et al. (2024). The radius of the high mass pulsar psr j0740+6620 with 3.6 years of nicer data. Astrophys. J.

Google Scholar

Salmi, T., Vinciguerra, S., Choudhury, D., Riley, T. E., Watts, A. L., Remillard, R. A., et al. (2022). The radius of psr j0740+6620 from nicer with nicer background estimates. Astrophysical J. 941, 150. doi:10.3847/1538-4357/ac983d

CrossRef Full Text | Google Scholar

Sathyaprakash, B. S., Buonanno, A., Lehner, L., Broeck, C. V. D., Ajith, P., Ghosh, A., et al. (2019). Extreme gravity and fundamental physics. Astro2020 Science White Paper. arXiv:1903.09221v3. doi:10.48550/arXiv.1903.09221

CrossRef Full Text | Google Scholar

Sedrakian, A., Li, J. J., and Weber, F. (2023). Heavy baryons in compact stars. Prog. Part. Nucl. Phys. 131, 104041. doi:10.1016/j.ppnp.2023.104041

CrossRef Full Text | Google Scholar

Sedrakian, A., Weber, F., and Li, J. J. (2020). Confronting gw190814 with hyperonization in dense matter and hypernuclear compact stars. Phys. Rev. D. 102, 041301. doi:10.1103/PhysRevD.102.041301

CrossRef Full Text | Google Scholar

Shao, L. (2019). Degeneracy in studying the supranuclear equation of state and modified gravity with neutron stars. AIP Conf. Proc. 2127, 020016. doi:10.1063/1.5117806

CrossRef Full Text | Google Scholar

Shapiro, S. L., and Teukolsky, S. A. (1983). Black holes, white dwarfs, and neutron stars: the physics of compact objects. John Wiley and Sons. doi:10.1002/9783527617661

CrossRef Full Text | Google Scholar

Shibata, M. (2015). Numerical relativity. Singapore: World Scientific Press. Chapter 8 and Chapter 9).

Google Scholar

Shuryak, E. V. (1980). Quantum chromodynamics and the theory of superdense matter. Phys. Rep. 61, 71–158. doi:10.1016/0370-1573(80)90105-2

CrossRef Full Text | Google Scholar

Somasundaram, R., Tews, I., and Margueron, J. (2023). Investigating signatures of phase transitions in neutron-star cores. Phys. Rev. C 107, 025801. doi:10.1103/PhysRevC.107.025801

CrossRef Full Text | Google Scholar

Sorensen, A., Agarwal, K., Brown, K. W., Chajjȩcki, Z., Danielewicz, P., Drischler, C., et al. (2024). Dense nuclear matter equation of state from heavy-ion collisions. Prog. Part. Nucl. Phys. 134, 104080. doi:10.1016/j.ppnp.2023.104080

CrossRef Full Text | Google Scholar

Steiner, A., Prakash, M., Lattimer, J., and Ellis, P. (2005). Isospin asymmetry in nuclei and neutron stars. Phys. Rep. 411, 325–375. doi:10.1016/j.physrep.2005.02.004

CrossRef Full Text | Google Scholar

Sullivan, A. G., and Romani, R. W. (2024). The intrabinary shock and companion star of redback pulsar j2215+5135. arXiV:2405, 13889.

Google Scholar

Takátsy, J., Kovács, P., Wolf, G., and Schaffner-Bielich, J. (2023). What neutron stars tell about the hadron-quark phase transition: a bayesian study. Phys. Rev. D. 108, 043002. doi:10.1103/PhysRevD.108.043002

CrossRef Full Text | Google Scholar

Tan, H., Dexheimer, V., Noronha-Hostler, J., and Yunes, N. (2022a). Finding structure in the speed of sound of supranuclear matter from binary love relations. Phys. Rev. Lett. 128, 161101. doi:10.1103/PhysRevLett.128.161101

PubMed Abstract | CrossRef Full Text | Google Scholar

Tan, H., Dore, T., Dexheimer, V., Noronha-Hostler, J., and Yunes, N. (2022b). Extreme matter meets extreme gravity: ultraheavy neutron stars with phase transitions. Phys. Rev. D. 105, 023018. doi:10.1103/PhysRevD.105.023018

CrossRef Full Text | Google Scholar

Tews, I., Carlson, J., Gandolfi, S., and Reddy, S. (2018). Constraining the speed of sound inside neutron stars with chiral effective field theory interactions and observations. Astrophysical J. 860, 149. doi:10.3847/1538-4357/aac267

CrossRef Full Text | Google Scholar

Tolman, R. C. (1939). Static solutions of einstein’s field equations for spheres of fluid. Phys. Rev. 55, 364–373. doi:10.1103/PhysRev.55.364

CrossRef Full Text | Google Scholar

Tsang, C. Y., Tsang, M. B., Lynch, W. G., Kumar, R., and Horowitz, C. J. (2024). Determination of the equation of state from nuclear experiments and neutron star observations. Nat. Astron 8, 328–336. doi:10.1038/s41550-023-02161-z

CrossRef Full Text | Google Scholar

Vidaña, I. (2018). Hyperons: the strange ingredients of the nuclear equation of state. Proc. R. Soc. Lond. Ser. A 474, 20180145. doi:10.1098/rspa.2018.0145

CrossRef Full Text | Google Scholar

Vinciguerra, S., Salmi, T., Watts, A. L., Choudhury, D., Riley, T. E., Ray, P. S., et al. (2024). An updated mass–radius analysis of the 2017–2018 nicer data set of psr j0030+0451. Astrophysical J. 961, 62. doi:10.3847/1538-4357/acfb83

CrossRef Full Text | Google Scholar

Walecka, J. (1974). A theory of highly condensed matter. Ann. Phys. 83, 491–529. doi:10.1016/0003-4916(74)90208-5

CrossRef Full Text | Google Scholar

Watts, A. L., Andersson, N., Chakrabarty, D., Feroci, M., Hebeler, K., Israel, G., et al. (2016). Colloquium: measuring the neutron star equation of state using x-ray timing. Rev. Mod. Phys. 88, 021001. doi:10.1103/RevModPhys.88.021001

CrossRef Full Text | Google Scholar

Weih, L. R., Hanauske, M., and Rezzolla, L. (2020). Postmerger gravitational-wave signatures of phase transitions in binary mergers. Phys. Rev. Lett. 124, 171103. doi:10.1103/PhysRevLett.124.171103

PubMed Abstract | CrossRef Full Text | Google Scholar

Wen, D.-H., Li, B.-A., and Chen, L.-W. (2009). Super-soft symmetry energy encountering non-Newtonian gravity in neutron stars. Phys. Rev. Lett. 103, 211102. doi:10.1103/PhysRevLett.103.211102

PubMed Abstract | CrossRef Full Text | Google Scholar

Wiringa, R. B., Fiks, V., and Fabrocini, A. (1988). Equation of state for dense nucleon matter. Phys. Rev. C 38, 1010–1037. doi:10.1103/PhysRevC.38.1010

PubMed Abstract | CrossRef Full Text | Google Scholar

Xie, W.-J., and Li, B.-A. (2019). Bayesian inference of high-density nuclear symmetry energy from radii of canonical neutron stars. Astrophysical J. 883, 174. doi:10.3847/1538-4357/ab3f37

CrossRef Full Text | Google Scholar

Xie, W.-J., and Li, B.-A. (2020). Bayesian inference of the symmetry energy of superdense neutron-rich matter from future radius measurements of massive neutron stars. Astrophysical J. 899, 4. doi:10.3847/1538-4357/aba271

CrossRef Full Text | Google Scholar

Xie, W.-J., and Li, B.-A. (2021). Bayesian inference of the dense-matter equation of state encapsulating a first-order hadron-quark phase transition from observables of canonical neutron stars. Phys. Rev. C 103, 035802. doi:10.1103/PhysRevC.103.035802

CrossRef Full Text | Google Scholar

Xu, J., Chen, L.-W., Li, B.-A., and Ma, H.-R. (2009). Nuclear constraints on properties of neutron star crusts. Astrophysical J. 697, 1549–1568. doi:10.1088/0004-637X/697/2/1549

CrossRef Full Text | Google Scholar

Yang, S.-H., Pi, C.-M., Zheng, X.-P., and Weber, F. (2020). Non-Newtonian gravity in strange quark stars and constraints from the observations of PSR J0740+6620 and GW170817. Astrophys. J. 902, 32. doi:10.3847/1538-4357/abb365

CrossRef Full Text | Google Scholar

Zel’dovich, Y. B. (1961). The equation of state at ultrahigh densities and its relativistic limitations. Zh. Eksp. Teor. Fiz. 41, 1609–1615.

Google Scholar

Zhang, N.-B., and Li, B.-A. (2020). Gw190814’s secondary component with mass 2.50-2.67 m_⊙ as a superfast pulsar. Astrophysical J. 902, 38. doi:10.3847/1538-4357/abb470

CrossRef Full Text | Google Scholar

Zhang, N.-B., and Li, B.-A. (2021). Impact of nicer’s radius measurement of psr j0740+6620 on nuclear symmetry energy at suprasaturation densities. Astrophysical J. 921, 111. doi:10.3847/1538-4357/ac1e8c

CrossRef Full Text | Google Scholar

Zhang, N.-B., and Li, B.-A. (2023a). Impact of symmetry energy on sound speed and spinodal decomposition in dense neutron-rich matter. Eur. Phys. J. 59, 86. doi:10.1140/epja/s10050-023-01010-x

CrossRef Full Text | Google Scholar

Zhang, N.-B., and Li, B.-A. (2023b). Properties of first-order hadron-quark phase transition from inverting neutron star observables. Phys. Rev. C 108, 025803. doi:10.1103/PhysRevC.108.025803

CrossRef Full Text | Google Scholar

Zhang, N.-B., Li, B.-A., and Xu, J. (2018). Combined constraints on the equation of state of dense neutron-rich matter from terrestrial nuclear experiments and observations of neutron stars. Astrophysical J. 859, 90. doi:10.3847/1538-4357/aac027

CrossRef Full Text | Google Scholar

Zhao, T., and Lattimer, J. M. (2020). Quarkyonic matter equation of state in beta-equilibrium. Phys. Rev. D. 102, 023021. doi:10.1103/PhysRevD.102.023021

CrossRef Full Text | Google Scholar

Zhou, D. (2024). What does perturbative qcd really have to say about neutron stars. arXiv:2307.

Google Scholar

AppendixEstimate of an effective correction to $s_{\mathrm{c}}^2$

In this appendix, we estimate an effective correction to $s_{\mathrm{c}}^2$ given in Equation 27 for NSs at the TOV configuration (Cai et al., 2023a). When writing down $M_{\mathrm{N}\mathrm{S}}$ in Equation 21, we adopt $M_{\mathrm{N}\mathrm{S}}=3^{-1}{\widehat{R}}^{3}W$, which only includes the first term in the systematic expansion (Equation 14); necessarily, we may include higher-order terms from Equation 14 in $M_{\mathrm{N}\mathrm{S}}$. As an effective correction, we now include $5^{-1}{a}_2{\widehat{R}}^5$ from Equation 14 to the NS mass, which modifies Equation 21 as

$\begin{array}{ll}\hfill M_{\mathrm{N}\mathrm{S}}& \approx \left(\frac{1}{3}{\widehat{R}}^3+\frac{1}{5}{a}_2{\widehat{R}}^5\right)W=\frac{1}{3}{\widehat{R}}^{3}W\left(1+\frac{3}{5}{a}_2{\widehat{R}}^2\right)=\frac{1}{3}{\widehat{R}}^{3}W\left(1-\frac{3}{5}\frac{\mathrm{X}}{s_{\mathrm{c}}^2}\right)\hfill \\ \hfill & \sim {\mathrm{\Gamma }}_{\mathrm{c}}\left(1-\frac{3}{5}\frac{\mathrm{X}}{s_{\mathrm{c}}^2}\right),\hfill \end{array}(\mathrm{A1})$

where $\widehat{R}$ is given by Equation 20 through $\mathrm{X}+b_2{\widehat{R}}^2\approx 0$, the coefficient ${\mathrm{\Gamma }}_{\mathrm{c}}\sim {\widehat{R}}^{3}W$ is defined in Equation 21, and the general relation $a_2=b_2/s_{\mathrm{c}}^2$ is used to write $3a_2{\widehat{R}}^2/5=-3\mathrm{X}/5s_{\mathrm{c}}^2$. The factor “$1+3a_2{\widehat{R}}^2/5$” is actually the averaged reduced energy density $⟨\widehat{\epsilon }⟩$ by including the $a_2$-term in $\widehat{\epsilon }$ of Equation 13, namely, $M_{\mathrm{N}\mathrm{S}}/W\approx 3^{-1}{\widehat{R}}^3⟨\widehat{\epsilon }⟩$ with

$⟨\widehat{\epsilon }⟩={\int }_0^{\widehat{R}}\mathrm{d}\widehat{r}{\widehat{r}}^2\widehat{\epsilon }\left(\widehat{r}\right)/{\int }_0^{\widehat{R}}\mathrm{d}\widehat{r}{\widehat{r}}^2=1+\frac{3}{5}{a}_2{\widehat{R}}^2,\widehat{\epsilon }\left(\widehat{r}\right)\approx 1+a_2{\widehat{r}}^2.(\mathrm{A2})$

Moreover, the $s_{\mathrm{c}}^2$ in Equation A1 is now not given by Equation 27 but should include corrections due to including the $a_2$-term in $\widehat{\epsilon }(\widehat{r})$. Generally, we write it as:

$s_{\mathrm{c}}^2\approx \mathrm{X}\left(1+\frac{1}{3}\frac{1+3{\mathrm{X}}^2+4\mathrm{X}}{1-3{\mathrm{X}}^2}\right)\left(1+{\kappa }_1\mathrm{X}\right)\approx \frac{4}{3}\mathrm{X}+\frac{4}{3}\left(1+{\kappa }_1\right){\mathrm{X}}^2+\mathcal{O}\left({\mathrm{X}}^3\right),(\mathrm{A3})$

where ${\kappa }_1$ is a coefficient to be determined. In addition, we have $1-3\mathrm{X}/5s_{\mathrm{c}}^2\approx (11/20)[1+9(1+{\kappa }_1)\mathrm{X}/11]$ using the $s_{\mathrm{c}}^2$ of Equation A3; taking $\mathrm{d}{M}_{\mathrm{N}\mathrm{S}}/\mathrm{d}{\epsilon }_{\mathrm{c}}=0$ with $M_{\mathrm{N}\mathrm{S}}$ given by Equation A1 gives the expression for $s_{\mathrm{c}}^2$ (which is quite complicated). We then expanding the latter over $\mathrm{X}$ to order ${\mathrm{X}}^2$ to give

$s_{\mathrm{c}}^2\approx \frac{4}{3}\mathrm{X}+\frac{1}{11}\left(\frac{38}{3}-2{\kappa }_1\right){\mathrm{X}}^2+\mathcal{O}\left({\mathrm{X}}^3\right).(\mathrm{A4})$

Matching the two expressions (Equations A3, A4) at order ${\mathrm{X}}^2$ gives ${\kappa }_1=-3/25$. After that, we determine $\mathrm{X}\lesssim 0.381$ via $s_{\mathrm{c}}^2\le 1$, which is close to and consistent with 0.374 obtained in the main text; and similarly, $\mathrm{\Delta }\gtrsim -0.048$. The magnitude of the correction “$+{\kappa }_1\mathrm{X}$” in $s_{\mathrm{c}}^2$ is smaller than 5% while the corresponding correction on ${\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}$ is smaller than 2%. In addition, the NS mass now scales as

$M_{\mathrm{N}\mathrm{S}}\sim \frac{1}{\sqrt{{\epsilon }_{\mathrm{c}}}}{\left(\frac{\mathrm{X}}{1+3{\mathrm{X}}^2+4\mathrm{X}}\right)}^{3/2}\cdot \left(1+\frac{18}{25}\mathrm{X}\right).(\mathrm{A5})$

In order to obtain the corrections to $s_{\mathrm{c}}^2$ more self-consistently and improve the accuracy of ${\mathrm{X}}_{+}^{\mathrm{G}\mathrm{R}}$, one may include more terms in the expansion of $\widehat{P}$ over $\widehat{R}$ of Equation 14 (i.e., $b_2$-term, $b_4$-term and $b_6$-term, etc.), the expansion of $\widehat{M}$ over $\widehat{R}$ of Equation 15 (i.e., $a_2$-term, $a_4$-term, $a_6$-term, etc.), and in the mean while introduce corrections “$1+{\kappa }_1\mathrm{X}+{\kappa }_2{\mathrm{X}}^2+{\kappa }_3{\mathrm{X}}^3+\cdots$” in $s_{\mathrm{c}}^2$ as we did in Equation A3. Then, determine the coefficients ${\kappa }_1$, ${\kappa }_2$, and ${\kappa }_3$, etc. The procedure eventually becomes involved as more terms are included.