The first photometric investigation of two short-period Algol-type eclipsing binaries: IW UMa and V367 Gem

Introduction: The first multi-color photometric observations and low-resolution spectra of the Algol-type short-period eclipsing binary systems IWUMa and V367 Gem are presented here. The stellar atmospheric parameters of the primary stars were derived through spectral analysis. Ground-based and TESS-based light curves were analyzed.

Methods: ULySS software was employed to obtain atmospheric parameters by fitting full spectra with model spectra. Wilson–Devinney code was used to analyze the light curves.

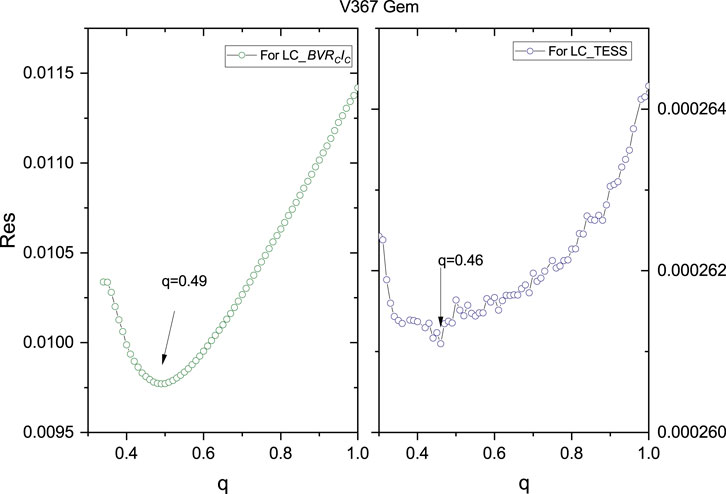
Results: The photometric solutions suggest that IW UMa and V367 Gem are both typical Algol systems in a semidetached configuration, with secondary stars filling their Roche lobes. The mass ratios of IW UMa and V367 Gem are 0.145 (3) and 0.478 (15), respectively. A third light was detected in the light curve analysis of V367 Gem with a luminosity contribution of $L_3/L_{\mathit{total}}=44.38\%$. Using O$-$C analysis, we found that the period of IW UMa is likely increasing over the long term, superposed with cyclic variation. The period of V367 Gem is decreasing at a rate of $dP/dt=-7.40(\pm 0.43)\times 10^{-8}d\cdot {yr}^{-1}$ on a long time scale.

Discussion: The period decrease of V367 Gem may be due to the mass and angular momentum loss from the system. Additionally, a probable cyclic variation has been identified for the period of V367 Gem, which may be caused by the third body.

1 Introduction

Algol-type binaries are a unique subset of semi-detached eclipsing binaries (EB systems) characterized by mass transfer between their components, which significantly influences their evolution. In these systems, the more luminous and massive component, referred to as the “primary”, is typically composed of B-, A-, or F-type stars. The less luminous and less massive “secondary” component may be an evolved giant or subgiant star. In these systems, the primary component is a main sequence star, while the secondary component fills its Roche lobe, leading to mass transfer from the secondary to the primary. These systems began as binary systems with unequal masses. The more massive component (the future secondary) evolved from the main sequence more quickly than the less massive component (the future primary). When the former primary fills its Roche lobe, a significant mass-transfer episode occurs during which a substantial amount of mass from the former primary is transferred to the less massive component, causing it to become more massive than the Roche-lobe-filling star (the former more massive component). Therefore, current Algols are systems undergoing slow mass transfer from a Roche-lobe-filling giant or subgiant low-mass star (the former massive star) to a main sequence, massive, mass-accreting component (the current primary). The mass transfer results in an increase in the orbital period. Secondary components with later spectral types are magnetically active, producing features such as spots, plages, flares, and winds (e.g., Hall, 1989). These systems lose angular momentum due to magnetic stellar winds, suggesting that mass transfer between the components should be non-conservative (e.g., Sarna et al., 1997; 1998). The observed period decrease in the orbital periods may be attributed to mass loss and transfer and angular momentum loss (AML) (Qian, 2000; 2001; Yang and Wei, 2009; Erdem et al., 2010; Soydugan et al., 2011; Ibanoǧlu et al., 2006). In addition, a magnetic braking mechanism is often referenced to explain the observed orbital shrinkage. Chen et al. (2006) suggested that, in addition to magnetic braking, a circumbinary disk may play an important role in AML from Algol-type binaries, which could explain the low-mass ratio systems undergoing rapid mass transfer.

IW UMa (ASASSN-V J064643.50 + 205322.1) is a confirmed Algol-type variable binary with a short orbital period of 0.7747182 (1) d (Kreiner, 2004). IW UMa was identified as eclipsing Am binary candidates by confirming the relationship between different spectral types, based on the low-resolution spectra of the Large Sky Area Multi$-$Object Fiber Spectroscopic Telescope (LAMOST) (Tian et al., 2023). The MK spectral type of primary component is kA5hA5mA9 (Tian et al., 2023). Borovicka and Sarounova (1996) first released the VR band light curves of IW UMa.

V367 Gem (SVS 863, ASASSN-V J092900.54 + 434402.7) is an Algol-type variable binary with a short orbital period of 0.699229 (1) d as revised by Hintz and Brown (2007). V367 Gem was also identified as eclipsing Am binary candidates with an MK spectral type of the primary component classified as kA3hA5mA7 by Tian et al. (2023). Hintz and Brown (2007) also released the light curves and found some minimal color changes with values of (B$-$V) = 0.27$\pm$0.01 and (V$-$R) = 0.18$\pm$0.01. Based on the measured colors and the shape of the light curve, V367 Gem was classified as an Algol-type system by Hintz and Brown (2007). Unfortunately, the two Algol-type eclipsing binaries have not been investigated in more detail.

In this study, we obtain the multi-color high-precision light curves and low-resolution spectra of both targets. Based on the times of the light minimum collected and calculated from the TESS database, the O$-$C diagrams with long time-spanning eclipse timings were obtained for the short-period Algol-type eclipsing binaries IW UMa and V367 Gem. We thus obtained more accurate geometric and physical parameters.

2 Observation and data reduction

2.1 Photometric observations

The new complete multi-color light curves of IW UMa in Johnson$-$Cousin $BV{R}_c{I}_c$ filters (Ažusienis and Straižys, 1969; Bessell, 1983) were observed on 30 January and 24–26 March, 2023 and on 7 February, 2024, with a PI VersArray 1300B LN CCD (size: $1340\times 1300$ pixel) photometric system attached to the 80 $cm$ telescope (Tsinghua-NAOC Telescope) at the Xinglong Station of the National Astronomical Observatories of China (NAOC). New complete Johnson$-$Cousin $BV{R}_c{I}_c$ (Ažusienis and Straižys, 1969; Bessell, 1983) multi-color light curves of V367 Gem were observed on 11–13 January, 2024. The observations were also made with the 80 $cm$ telescope (Tsinghua-NAOC Telescope) at NAOC. The PHOT package of IRAF was used to process all images. The comparison and check stars were chosen to determine the differential magnitudes. For IW UMa, the non-variable star TYC 2997-1178-1 was selected as the comparison, and TYC 2997-1377-1 and TYC 2997-1501-1 were the check stars. GSC 01342-01119 and UCAC4 555-033241 were selected as comparison stars for V367 Gem, and TYC 1342-417-1 was the check star. Table 1 shows information for the comparison and check stars and for both targets. The comparison stars have a similar brightness to the targets. The observed CCD images of both targets are shown in Figures 1 and 2; the variable star is marked “V”, the comparison star is marked “C”, and the check star is marked “Ch”. The two check stars for IW UMa are marked “Ch1” and “Ch2” in Figure 1, and the two comparison stars for V367 Gem are marked “C1” and “C2” in Figure 2. The light curves of IW UMa and V367 Gem are shown in Figures 3 and 4, respectively. The data observed on different nights are marked with different colors, and the B, V, $R_c$ and $I_c$ band data are represented by a square, circle, triangle, and inverted triangle, respectively. The magnitude difference of the comparison and check stars in all filters are shown at the bottom of the figures. In Figure 3, the mean standard deviations of the magnitude difference in each filter are approximately 0.00678 in the B band, 0.00637 in the V band, 0.00589 in the $R_c$ band, and 0.00527 in the $I_c$ band. In Figure 4, the mean standard deviations of the magnitude difference of each filter are 0.01075 in the B band, approximately 0.01175 in the V band, 0.00695 in the $R_c$ band, and 0.00818 in the $I_c$ band.

Table 1

Table 1. Information of IW UMa, V367 Gem, and the corresponding comparison and check stars.

Figure 1

Figure 1. CCD image of IW UMa in the $I_c$ band. “Variable star”, “Comparison star”, and “Check star” are marked V, C, and Ch respectively. The two check stars are marked Ch1 and Ch2.

Figure 2

Figure 2. CCD image of V367 Gem in the $I_c$ band. “Variable star”, “Comparison star”, and “Check star” are marked V, C, and Ch respectively. The two comparison stars are marked C1 and C2.

Figure 3

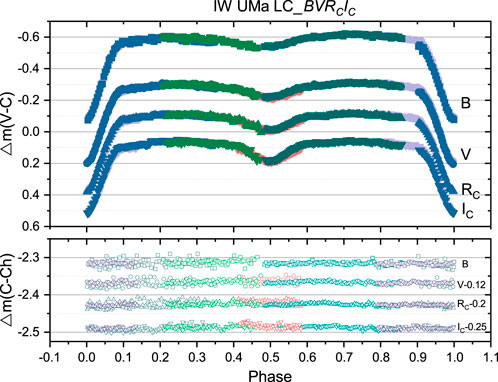
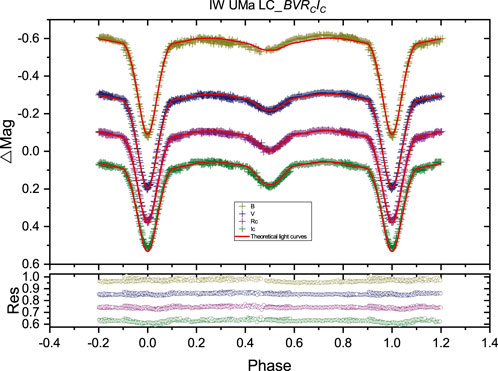
Figure 3. Light curves of IW UMa in the $BV{R}_c{I}_c$ bands (top panel). The magnitude differences of the comparison star and check star in all filters are shown at the bottom.

Figure 4

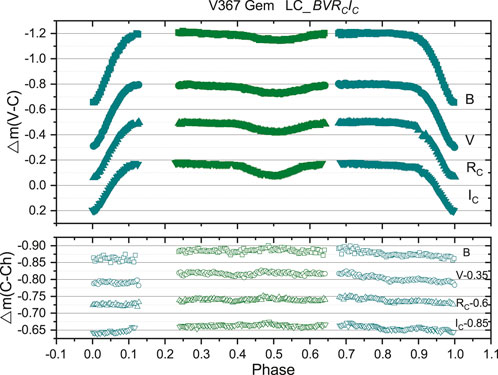
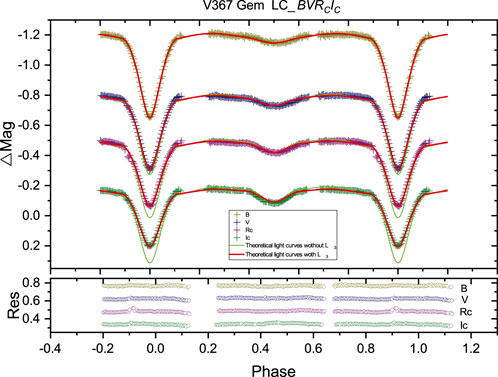
Figure 4. Light curves of V367 Gem in the $BV{R}_c{I}_c$ bands (top panel). The magnitude differences of the comparison star and check star in all filters are shown at the bottom.

2.2 TESS observations

The Transiting Exoplanet Survey Satellite (TESS) is an all-sky transit survey whose principal goal is to detect Earth-sized planets orbiting bright stars that are amenable to follow-up observations to determine planet masses and atmospheric compositions (Ricker et al., 2014). These targets are read out as postage stamps and made available to the community as target pixel files (TPFs) and corrected light curves. These files comprise several time series, including a simple aperture photometry, a corrected light curve, position vectors, and quality flags. The aperture photometry flux series is termed “SAP_FLUX”, while the flux series that has the common instrumental systematics removed using cotrending basis vectors (CBV) files is termed “PDCSAP_FLUX”. SAP_Flux was used to obtain the light curves of IW UMa and V367 Gem in this study.

IW UMa (TESS target identifier: TIC 105439439) and V367 Gem (TESS target identifier: TIC 56897408) have been observed by TESS for many days in different sectors. The data were retrieved using the Python package $lightkurve$ (Lightkurve Collaboration et al., 2018) from the MAST data archive (http://https://mast.stsci.edu/), which provides three different types of data products. Two kinds of light curves from the authors TESS-SPOC and QLP, and the other is the TESScut cutouts of the calibrated full frame images from the author TESScut. Using the TESScut tool, we downloaded $20\times 20$ pixel files centered on IW UMa and V367 Gem. Then, the Python procedure dat.to_lightcurve was used to obtain a simple aperture photometry light curve. The flux data are normalized. We thus obtained the light curves of IW UMa from sector 48 with a cadence of 600 s and that of V367 Gem from sectors 71 and 72 with a cadence of 200s. The observation time of the light curves of IW UMa from sector 48 lasted from 29 January to 11 February and from 14 to 25 February 2023. The observation time of light curves of V367 Gem from sectors 71 and 72 lasted 19–28 October, 1–10 and 15–24 November, and 28 November to 7 December 2023. The time-series light curves of each sector and phase-binned light curve of IW UMa and V367 Gem obtained from the TESS database are presented in Figures 5 and 6. The phase-binned light curves of both targets were based on the part of the data in corresponding sectors.

Figure 5

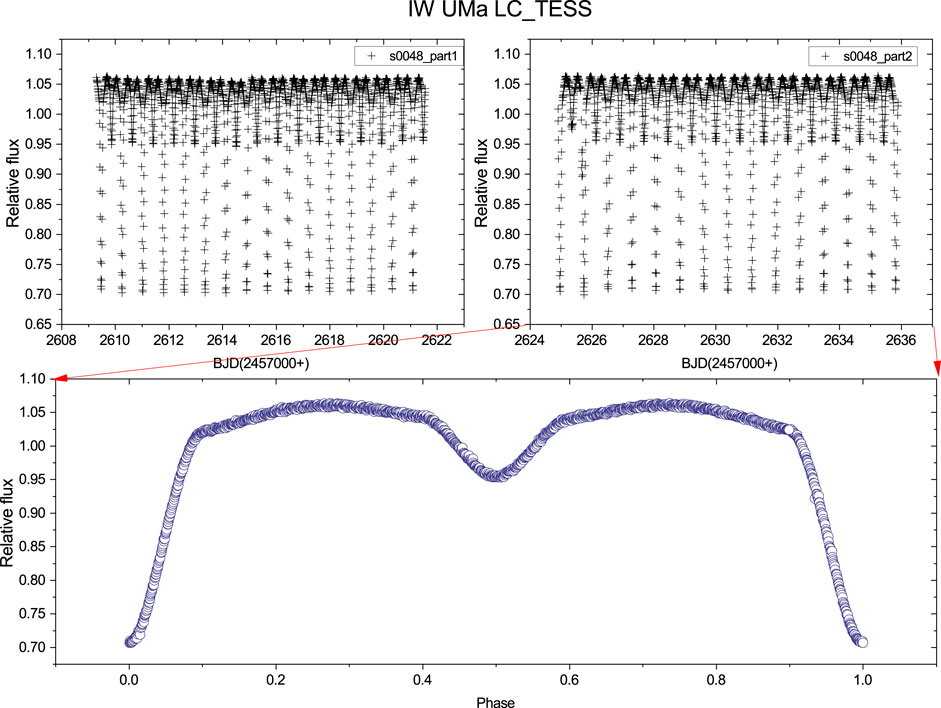
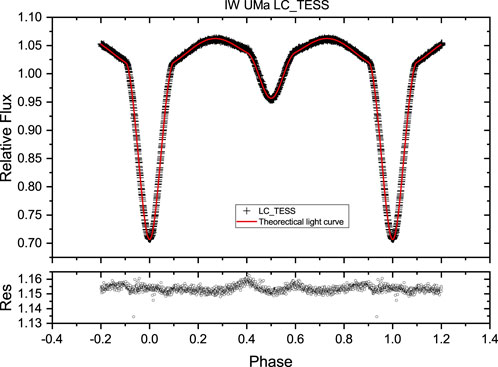
Figure 5. Continuous time-series and phase-binned light curves of IW UMa obtained from the TESS database. Top panels show the continuous time-series light curves from sector 48. The phase-binned light curve is shown in the bottom panel calculated from the light curves shown in the top-right panel.

Figure 6

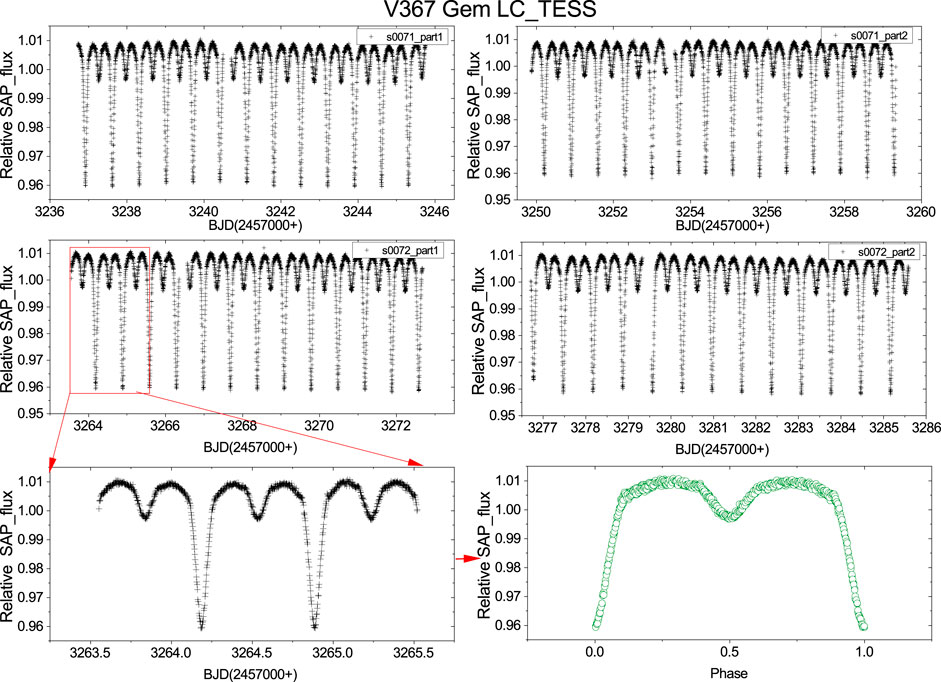
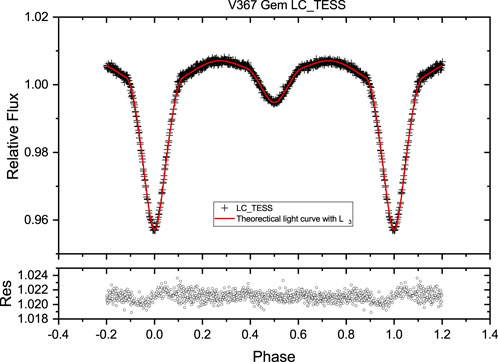
Figure 6. Continuous time-series and phase-binned light curves of V367 Gem obtained from the TESS database. The top and middle panels display the continuous time-series light curves from sector 71 and 72, respectively. The bottom-left panel presents the partial light curves highlighted in the middle-left panel. Finally, the phase-binned light curve derived from these partial light curves is illustrated in the bottom-right panel.

2.3 Spectroscopic observations

The spectra of IW UMa and V367 Gem were observed using the Beijing Faint Object Spectrograph and Camera (BFOSC), which was mounted on the 2.16 m telescope of the Xinglong station of the National Astronomical Observatories of China (NAOC), Chinese Academy of Sciences (CAS). The observations were made on 14 January 2023, using a low-dispersion spectrometer BFOSC and grism G6. The slit width and line dispersion of grism G6 are 1.8 arcsec and 88 Å ${\text{mm}}^{-1}$, respectively. The observations cover the wavelength range 330–545 nm (Fan et al., 2016). The spectra resolution per pixel is 1.98 Å. IRAF was used to process the observation images and extract the spectra. Normalized flux was obtained, and the atmospheric absorption lines were also corrected. Low-resolution spectra can only show the spectral lines of the primary star, and the lines of the secondary star may be too faint to be detected. The observed spectra of both targets are shown in Figure 7 with black lines.

Figure 7

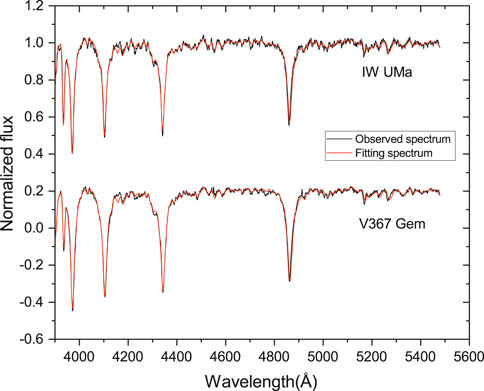
Figure 7. Spectra of IW UMa and V367 Gem observed on 14 January 2023. The black and red lines represent the observed and fitting spectrum, respectively.

University of Lyon Spectroscopic Analysis Software (ULySS) (Koleva et al., 2009) was employed to obtain atmospheric parameters by fitting full spectra with model spectra generated by an interpolator with the ELODIE library (Prugniel and Soubiran, 2001).

The red lines in Figure 8 represent the fitting spectra. The atmospheric stellar parameters were derived—for IW UMa: $T_{\mathit{eff}}$ = 7378$\pm$70 K, $\log \mathit{\text{g}}$ = 4.18$\pm$0.04 cm/s², [Fe/H] = −0.29$\pm$0.04 dex; for V367 Gem: $T_{\mathit{eff}}$ = 8290$\pm$52 K, $\log \mathit{\text{g}}$ = 4.28$\pm$0.04 cm/s², [Fe/H] = 0.04$\pm$0.05 dex. For the two targets, the spectra were analyzed as single-star spectra, ignoring the secondary (faint) component in the spectra analysis program, the spectra of the primary component, which is casually diluted by the secondary component, will mimic a low metallicity. The atmospheric parameters obtained by ULySS can be used to describe the atmospheric characteristics of the primary star.

Figure 8

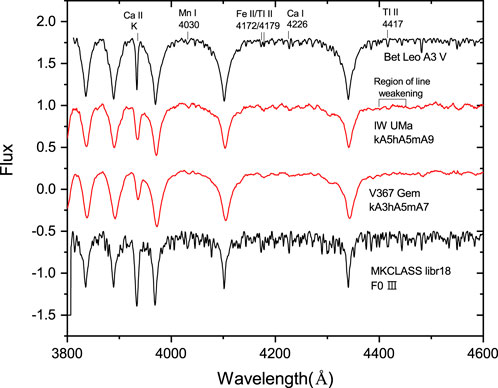
Figure 8. Comparison of the blue–violet spectrum (3800–4600 Å) of IW UMa and V367 Gem with the part of the spectrum of two MK standards.

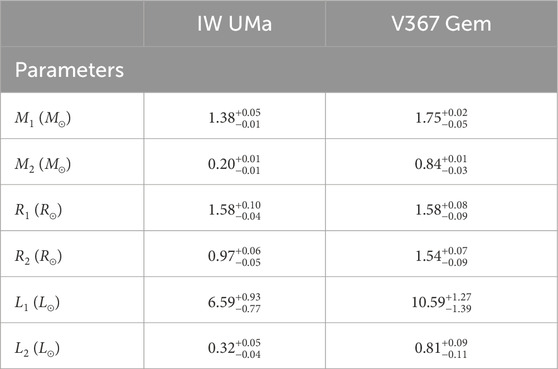
The physical properties of the primary can be estimated from the atmosphere parameters by matching with stellar isochrones for normal single stars, assuming that the mass-accreting component is in thermal equilibrium (Zhang et al., 2019), using the PARSEC (Padova and Trieste Stellar Evolution Code) isochrone database (Bressan et al., 2012; Chen et al., 2014; 2015; Tang et al., 2014) along with the lognormal form initial mass function by Chabrier (2001). The primary stars’ physical properties can then be determined, including mass and radius—for IW UMa: $M_1=1.38_{-0.01}^{+0.05}{M}_{\odot }$, $R_1=1.58_{-0.04}^{+0.10}{R}_{\odot }$, $log{L}_1=0.819_{-0.054}^{+0.057}{L}_{\odot }$; for V367 Gem: $M_1=1.75_{-0.05}^{+0.02}{M}_{\odot }$, $R_1=1.58_{-0.09}^{+0.08}{R}_{\odot }$, $log{L}_1=1.025_{-0.061}^{+0.049}{L}_{\odot }$.

The blue-violet spectrum (3800–4600 Å) of IW UMa, V367 Gem, and part of the spectrum of two MK standard spectra with a type of A3 V (Bet Leo) and F0 III are shown in Figure 8. It is clear that the Ca II K lines of IW UMa and V367 Gem are quite weaker in strength than that of the A3 and F0 MK standards, which exhibit typical characteristics similar to Am stars. The low resolution of the spectral data means that many metallic properties are not adequately captured. Indeed, the Am classification of the primary components of Algol undergoing mass accretion and experiencing high atmospheric turbulence dynamics contradicts the theories of Am star formation. The accurate determination of chemical composition should be based on multi-element chemical composition analysis conducted through high-resolution spectroscopy.

3 O$-$C diagram analyses

All available light minimum times of IW UMa and V367 Gem were collected from the literature. Meanwhile, we computed the light minima based on the TESS data for both targets in HJD time—listed in the Appendix of Supplementary Tables A1 and B1 marked “This study*” in the corresponding reference column.

3.1 IW UMa

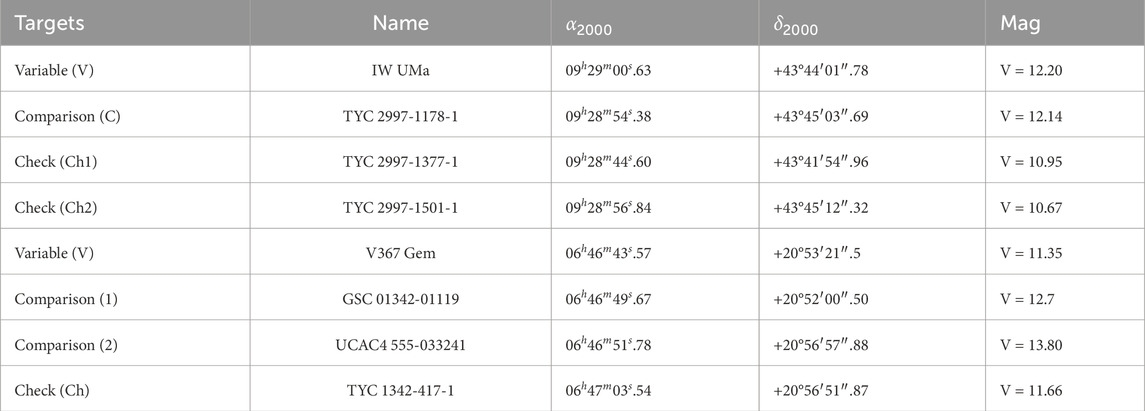
A total of 95 eclipse times of IW UMa spanning approximately 28 years were used to structure the O$-$C diagram, including two eclipse times observed by us and 62 eclipse times obtained from the TESS data. All eclipse times used for the period analysis are listed in the Supplementary Table A1 Appendix. For the reference items marked “*”, the original publications unavailable online. The corresponding O$-$C were obtained with the following ephemeris:

$\begin{array}{ccc}\hfill Min.\mathit{\text{I}}& =\hfill & HJD 2460030.1425\left(2\right)\hfill \\ \hfill & \hfill & +0.7747182{\left(1\right)}^d\times E\hfill \end{array}(1)$

In Equation 2, “Min I” are the observed primary eclipse times and 2460030.1425 (2) is the primary eclipse time of the multi-color light curves.

The O$-$C diagram of IW UMa is shown in Figure 9. In particular, the open square was used to mark the light minimum obtained from the TESS database. The same weight of 1 was taken for all CCD data, including the TESS data in the O$-$C analysis. Using the least squares method, Equation 2 can be used to describe the O$-$C diagram:

$\begin{array}{ccc}\hfill Min.\mathit{\text{I}}& =\hfill & HJD2460030.1433\left(41\right)\hfill \\ \hfill & \hfill & +0.7747187\left(1\right)\times E\hfill \\ \hfill & \hfill & +1.78\left(\pm 8.03\right)\times 10^{-11}\times E^2\hfill \end{array}(2)$

Figure 9

Figure 9. O$-$C diagram of IW UMa.

The error associated with the coefficient of the quadratic term is quite large. The black line in Figure 9 represents the fitting curve. We noticed that this parabolic fit is statistically insignificant. The fitting residuals are shown in the middle panel of Figure 9, which may indicate a cyclic variation. The final residuals are shown at the bottom of Figure 9. The period of IW UMa is likely increasing over the long term superposed with cyclic variation. Considering the large fitting error, this conclusion requires further confirmation.

3.2 V367 Gem

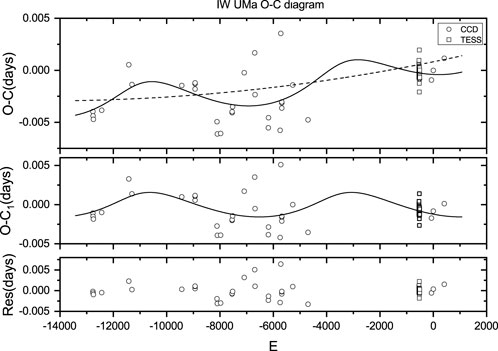
For V367 Gem, 117 eclipse times crossing approximately 25 years were used to calculate the O$-$C diagram, including two new observed and 103 eclipse timings estimated from the TESS data by this study (Supplementary Table B1 Appendix). Equation 3 is used to obtained the corresponding O$-$C and E.

$\begin{array}{ccc}\hfill Min\mathit{\text{I}}& =\hfill & HJD2460322.2221\left(3\right)\hfill \\ \hfill & \hfill & +0.699229^d\times E\hfill \end{array}(3)$

The O$-$C diagram with error bars of V367 Gem based on all the eclipsing times is shown in the top$-$left panel of Figure 10; the light minimum obtained from the TESS database is marked with green color. In the O$-$C analysis program, the same weight of 1 was adopted for all the CCD data. Using the least square method, the O$-$C of V367 Gem can be described by Equation 4.

$\begin{array}{ccc}\hfill Min\mathit{\text{I}}& =\hfill & HJD2460322.2232\left(1\right)\hfill \\ \hfill & \hfill & +0.699227234\left(78\right)\times E\hfill \\ \hfill & \hfill & -0.71\left(41\right)\times 10^{-10}\times E^2\hfill \end{array}(4)$

Figure 10

Figure 10. O$-$C diagram of V367 Gem.

The quadratic term in the above polymerization indicates that the period is undergoing a long-term decrease at a rate of $dP/dt=-7.40(\pm 0.43)\times 10^{-8}d\cdot {yr}^{-1}$. The black line in Figure 10 represents the corresponding fitting curve. The fitting residuals are shown in the left-bottom panel of Figure 10. We found that the O$-$C diagram constructed by the light eclipse timings obtained from TESS data may exhibit an incomplete cycle of a sinusoidal variation with a short period. The cyclic variation can be fitted by Equation 5:

$\begin{array}{ccc}\hfill \tau & =\hfill & A\left[\left(1-e^2\right)\frac{\sin \left(\nu +\omega \right)}{1+e\cos \left(\nu \right)}+e\sin \left(\omega \right)\right]\hfill \\ \hfill & =\hfill & A\left[\sqrt{\left(1-e^2\right)}\sin E^{*}\cos \omega +\cos E^{*}\sin \omega \right]\hfill \end{array}(5)$

in which: $A={a_{12}}^{\prime }\sin i^{\prime }/c$ $(day)$ is the projected semi-major axis and $c$ is the velocity of light; $e$, $\nu$, and $\omega$ are the eccentricity, true anomaly, and longitude of the periastron passage, respectively; $E^{*}$ is the eccentric anomaly.

The O$-$C diagram based only on the mid-times of eclipses obtained from TESS are shown in the top-right panel in Figure 10, and the residuals are shown in the right-bottom panel. The incomplete cyclic variation fits the O$-$C diagram only based on TESS data well, indicating a cyclic variation with a short period of $P_3=$0.26 (37) years and an amplitude of A$=$0.002 (24) days. The O$-$C diagram analysis demonstrates that the orbital period of V367 Gem is undergoing a continuous decrease and a probable cyclic variation simultaneously. The cyclic variation shown in the O-C of TESS mid-times requires further confirmation.

4 Light curve analyses

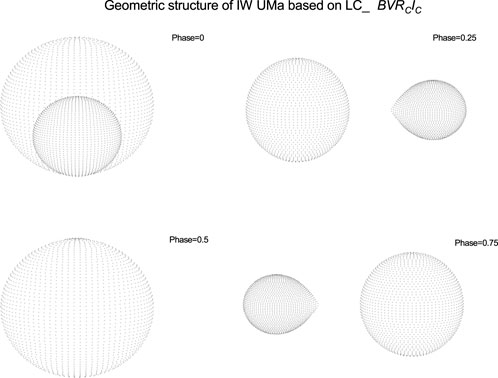
The Wilson–Devinney (WD) program (Wilson and Devinney, 1971; Wilson, 1990; 2012) was used to analyze all the light curves (including these based on the TESS data) of the two targets. The gravity-darkening coefficients and bolometric albedos were taken according to temperature (Ruciński, 1969). The bandpass limb-darkening coefficients were taken from van Hamme (1993), and the logarithmic bolometric coefficients were applied. There are various modes for different binary configurations in the WD program. We acquired the converged solutions of both targets with Mode 5 (the semidetached case with the secondary component filling the critical RL). The corresponding adjustable parameters of Mode 5 are: the monochromatic luminosity of star 1, $L_{1B}$, $L_{1V}$, $L_{1R_c}$, $L_{1I_c}$; the orbital inclination i; the mean temperature of star 2, $T_2$; the dimensionless potential of the primary star, ${\mathrm{\Omega }}_1$. We also set the third light $L_3$ as one adjustable parameter. In order to confirm a reliable mass ratio, the photometric solutions based on a group of assumed mass ratio values from 0.01 to 1 were obtained with the differential correction program. The search-step length was set to 0.01. The value of q resulted in the lowest sum of weighted squared deviations $(\sum {{(O-C)}_i}^2)$ was chosen as the initial value for q in the WD modeling. Thence, q was treated as an adjustable parameter to achieve the final converged solution.

4.1 IW UMa

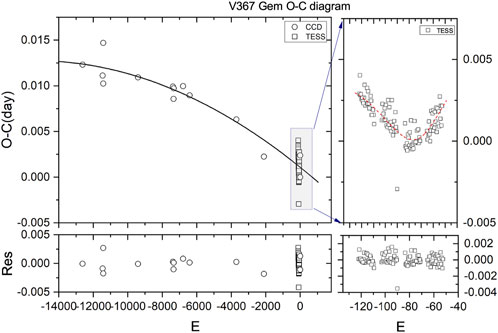
The first multi-color light curves of IW UMa were observed. The TESS observation data from sector 48 (covering HJD 2459625 to HJD 2459636) were utilized to generate the light curve for analysis. The light curves are shown at the bottom of Figure 5. In the figures below, the observed multi-color light curve is labeled “LC_$BV{R}_c{I}_c$”, while the light curve obtained from the TESS database is labeled “LC_TESS”. Different linear ephemerides were used to calculate the phased light curves. For the multi-color light curves, the ephemeris given by Equation 1 was employed. For the TESS-based light curve, the linear ephemeris Equation 6 was used:

$\begin{array}{ccc}\hfill Min\mathit{\text{I}}& =\hfill & HJD2459625.7383\left(17\right)\hfill \\ \hfill & \hfill & +0.7747182{\left(1\right)}^d\times E\hfill \end{array}(6)$

in which the epoch 2460030.14246 (12) is the new observed eclipse time and 2459625.73832 (168) is the eclipse time based on the TESS database.

The effective temperature of the primary star obtained as $T_1$ = 7378 K from our spectral analysis. The effective temperature of the primary star was fixed at 7378 K in the WD modeling. The gravity-darkening coefficients and bolometric albedos are taken as $g_1$ = 1, $g_2$ = 0.32, $A_1$ = 1, and $A_2$ = 0.5 (Ruciński, 1969). The third light $L_3$ was set as an adjustable parameter, but no converged result was obtained. The process of q search was confirmed. For all assumed values of q, the sums of weighted square deviations $(\sum {{(O-C)}_i}^2)$ based on two sets of light curves are displayed in Figure 11. The minimal values achieved at q = 0.15 and q = 0.20 were based on the observed multi-color light curves and the TESS-based light curves, respectively. Then, q was made as an adjustable parameter, and q = 0.15 and q = 0.20 were taken as the initial value in the WD modeling for the two sets of light curves, respectively. The theoretical light curves for the multi-color light curves and TESS-based light curve are shown in Figures 12, 13 in red lines, respectively. The theoretical light curves fitted the light curves very well. All converged photometric solutions are listed in Table 2. The geometric structure is shown in Figure 14.

Figure 11

Figure 11. $\sum {{(O-C)}_i}^2$-q curves of the preliminary search for the most optimal mass ratio of IW UMa.

Figure 12

Figure 12. Theoretical and observed multi-color light curves of IW UMa.

Figure 13

Figure 13. Theoretical and TESS-based light curve of IW UMa.

Table 2

Table 2. Photometric solutions of IW UMa and V367 Gem.

Figure 14

Figure 14. Geometrical structure of IW UMa.

4.2 V367 Gem

The first multi-color light curves of V367 Gem were observed. Different linear ephemeris was used to calculate the phased light curves for the observed multi-color light curves and TESS observation. For multi-color light curves, the ephemeris given by Equation 3 was used. For the TESS-based light curves, the linear ephemeris Equation 7 was used:

$\begin{array}{ccc}\hfill Min\mathit{\text{I}}& =\hfill & HJD2460264.18578\left(8\right)\hfill \\ \hfill & \hfill & +0.699229{\left(1\right)}^d\times E\hfill \end{array}(7)$

in which the epoch 2460322.22210 (25) is the new observed eclipse times and 2460264.18578 (8) is the eclipse times based on the TESS data.

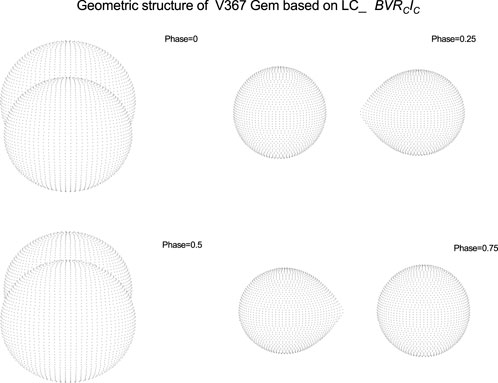
In the WD modeling, the effective temperature of the primary star was fixed at 8280 K, which was obtained from our spectral analysis. The convergent solutions were confirmed with Mode 5. The third light $L_3$ was set as an adjustable parameter, and a converged solution was obtained. The mass ratio search was also confirmed for V367 Gem based on the two sets of light curves. The sums of the weighted square deviations $(\sum {{(O-C)}_i}^2)$ for all assumed values of q are displayed in Figure 15 based on the two sets of light curves. In order to make the minimal q value more obvious, only the trend of change from q = 0.3 to q = 1 was plotted. The minimal value achieved q = 0.49 and q = 0.46 for observed multi-color light curves and TESS light curves, respectively. We thus make “q” an adjustable parameter and set q = 0.49 and q = 0.46 as the initial value in the WD modeling for the two sets of light curves, respectively. The theoretical light curves with and without a third light for multi-color light curves are shown in Figure 16 in red and green lines, respectively. The residual of the theoretical light curves with a third light is shown at the bottom of Figure 16, where the theoretical light curves with a third light fit the light curves better. For LC_TESS, the converged solution with a third light was obtained. The theoretical light curves with a third light for the TESS light curve are shown in Figure 17 in red lines. All of the converged photometric solutions with a third light are listed in Table 2. The geometric structure of V367 Gem is plotted in Figure 18.

Figure 15

Figure 15. $\sum {{(O-C)}_i}^2$-q curves of the preliminary search for the optimal mass ratio of V367 Gem.

Figure 16

Figure 16. Theoretical and observed multi-color light curves of V367 Gem.

Figure 17

Figure 17. Theoretical and TESS-based light curve of V367 Gem.

Figure 18

Figure 18. Geometrical structure of V367 Gem.

5 Discussion and conclusion

The atmospheric parameters of the primary components of the Algol-like short-period eclipsing Am binaries IW UMa and V367 Gem are obtained based on the spectra analyses: for IW UMa, $T_{\mathit{eff}}$ = 7378$\pm$70 K, $\log \mathit{\text{g}}$ = 4.18$\pm$0.04 cm/s², [Fe/H] = -0.29$\pm$0.04 dex; for V367 Gem, $T_{\mathit{eff}}$ = 8290$\pm$52 K, $\log \mathit{\text{g}}$ = 4.28$\pm$0.04 cm/s², [Fe/H] = 0.04$\pm$0.05 dex. The physical properties of the primary can be estimated from the atmospheric parameters by matching with stellar isochrones, using the PARSEC database. For IW UMa: $M_1=1.38_{-0.01}^{+0.05}{M}_{\odot }$, $R_1=1.58_{-0.04}^{+0.10}{R}_{\odot }$, $log{L}_1=0.819_{-0.054}^{+0.057}{L}_{\odot }$; for V367 Gem: $M_1=1.75_{-0.05}^{+0.02}{M}_{\odot }$, $R_1=1.58_{-0.09}^{+0.08}{R}_{\odot }$, $log{L}_1=1.025_{-0.061}^{+0.049}{L}_{\odot }$. Light curve analysis of both targets used the WD program. The light curves of both targets show Algol-like characteristics. The theoretical light curves with mode 5 fitted the light curves of both targets quite well. The fill-degree factors of the primary components of IW UMa and V367 Gem are 0.3178 (38) and 0.3426 (26) based on the multi-color light curve solutions. The mass ratio of IW UMa is estimated as 0.145 (3), which is quite low. The mass ratio of V367 Gem is 0.478 (15). We detected a third body in the light curve analysis of V367 Gem. The luminosity contribution of the third light is about $L_3/L_{\mathit{total}}=44.38\%$ based on the observed multi-color light curves. The value is higher based on the TESS light curve because of the high background light interference of TESScut files, so such a value is not informative. The orbital inclinations of two targets are $i=80.66(31)°$ for IW UMa and $i=80.45(32)°$ for V367 Gem, which means that the photometric solutions can be reliable. Based on the physical properties of the primary and photometric solutions, the absolute parameters of the two binaries are estimated and are listed in Table 3.

Table 3

Table 3. Absolute parameters of IW UMa and V367 Gem.

All available eclipse times were used to investigate the variations of the orbital period by analyzing the O$-$C diagram. We have attempted a parabolic fit superposed with a cyclic variation to describe the O$-$C diagram of IW UMa but failed to obtain reliable conclusions due to the dispersion of data. It appears that the period of IW UMa is likely increasing over the long term. The period of V367 Gem is decreasing at a rate of $dP/dt=-7.40(\pm 0.43)\times 10^{-8}d\cdot {yr}^{-1}$ on a long time scale. Additionally, the O$-$C diagram derived from the TESS data may show an incomplete cycle of a sinusoidal variation. A cyclic variation was identified with a short period of $P_3=$0.26 (37) years and an amplitude of A$=$0.002 (24) days. Long-term monitoring is essential to confirm the existence of this cyclic variation. The long-term period increase or decrease change occurs commonly in systems with semi-detached configurations.

IW UMa and V367 Gem are typical Algol systems in a semidetached phase with the secondary star filling the RL. The period increase of IW UMa may be the cause of the mass transfer from the secondary to the primary star (e.g., Qian, 2002; Tian and Zhu, 2019). The period decrease of V367 Gem may mainly be caused by the mass and angular momentum loss (AML) via an enhanced stellar wind of the more evolved secondary star (e.g., Tout and Eggleton, 1988; Liao et al., 2017; 2019). The probable cyclic variation may be caused by the magnetic activity of one or both components (Applegate, 1992) and the light travel time effect (LTTE) through the presence of a tertiary companion. In light curve analysis, the detection of a third light may indicate the existence of a distant companion, which could plausibly explain the cyclic variation observed in V367 Gem due to LTTE. The third body plays an important role in the evolution of the binaries; it will cause the cyclic variation of an orbital period and also will take away the angular momentum of the system, leading to the orbital contraction process and then promoting the evolution of contact binaries (Tokovinin et al., 2006; Qian et al., 2013a; 2014b; 2017). Both targets are in a semidetached configuration, with the secondary star filling the RL, and then will evolve into a marginal-contact phase with poor thermal contact (e.g., Liao et al., 2012; Qian et al., 2013b; 2014a; Liao and Sarotsakulchai 2019), such as GW Gem and V723 Per (Tian and Zhu, 2019).

The components in very-short-period near-contact systems are likely to be rotating synchronously. For a circular orbit, the following equation can be used to obtain the equatorial rotational velocity $v=50.6(R/R_{\odot })/(P/d)km{s}^{-1}$(Carquillat and Prieur, 2007), where $R$ is the radius of the considered component and $P$ is the orbital period. The projected rotation velocity $v\sin i$ of the components of IW UMa and V367 Gem can be estimated. For IW UMa, $v_1\sin i=102km{s}^{-1}$ and $v_2\sin i=62km{s}^{-1}$; for V367 Gem, $v_1\sin i=113km{s}^{-1}$ and $v_2\sin i=110km{s}^{-1}$.

The spectra types and temperature of primary stars in IW UMa and V367 Gem indicate that both systems are AF-type Algols, with primary components classified as A- or F- type stars. We combined our two targets with the AF-type Algols collected by Wang et al. (2022) to investigate the evolutionary stages of these systems. The distributions of a Hertzsprung–Russell (HR) diagram are illustrated in Figure 19. Different symbols are used to differentiate AF-type Algols from our target stars, while various colors indicate the primary and secondary components. The primary components of AF-type Algol systems are predominantly located near the zero-age main sequence, whereas nearly all secondary components have evolved away from the main sequence. The mass-luminosity (M-L) relation, mass-radius (M-R) relation, and mass-temperature (M-T) relation of the components are shown in Figure 20. Different symbols are used to differentiate AF-type Algols and our target stars, and various colors indicate the primary and secondary components, respectively. The blue dash lines indicate the corresponding empirical relationships of main sequence (MS) stars (Eker et al., 2018). The primary components of AF-type Algols closely follow the empirical relationships of main sequence stars. In contrast, the secondary components are brighter, larger, and a little hotter than MS stars of the same mass.

Figure 19

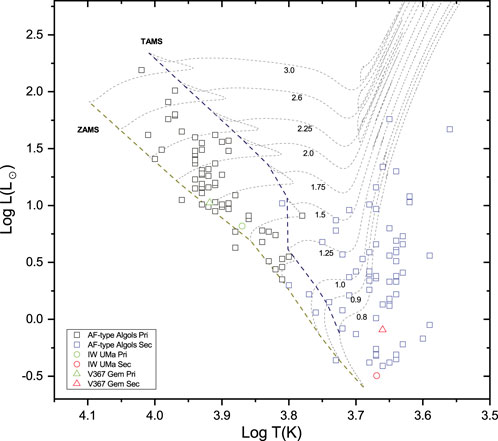
Figure 19. Hertzsprung–Russell diagram of AF-type Algols including IW UMa and V367 Gem. The evolutionary tracks (thin dash lines) for the labeled masses, as well as the zero-age main sequence (ZAMS) and the terminal-age main sequence (TAMS), were taken from Bressan et al. (2012), which were calculated for Y = 0.279, Z = 0.017.

Figure 20

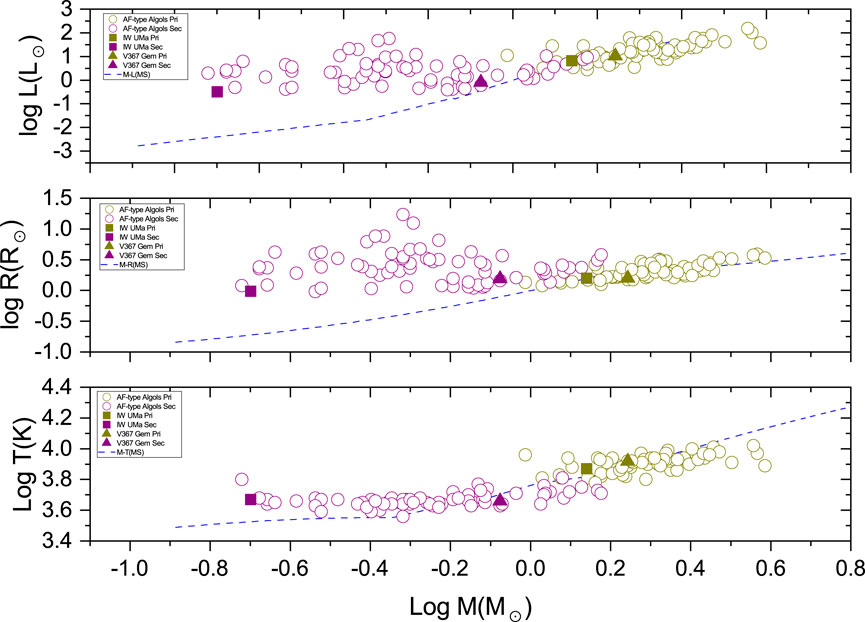
Figure 20. M-R, M-L, and M-T distributions of AF-type Algols including IW UMa and V367 Gem. The blue dash-lines represent the corresponding empirical relationships of main sequence stars (Eker et al., 2018).

We noticed that the primary components contribute about $95.35\%$ and $92.92\%$ to the luminosity of IW UMa and V367 Gem, respectively. The primary component of IW UMa is approximately 19 times brighter than the secondary, while the radius of the primary component is approximately 1.6 times as large as that of the secondary. Even the primary component of V367 Gem is 13 times brighter than the secondary with nearly the same radius. The secondary components of both targets may have evolved through the red giant phase with an expanded radius.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

X-MT: conceptualization, formal analysis, funding acquisition, investigation, methodology, software, writing–original draft, and writing–review and editing. L-QJ: data curation, methodology, resources, visualization, and writing–review and editing. Z-HW: formal analysis, funding acquisition, resources, supervision, and writing–review and editing. J-JW: funding acquisition, investigation, methodology, project administration, validation, and writing–review and editing.

Funding

The authors declare that financial support was received for the research, authorship, and/or publication of this article. This work is supported by the National Natural Science Foundation of China (Grant Nos. 12103030 and 12303038), the Natural Science of Shandong Province (Grant No. ZR2021QA082), the Natural Science Foundation of Xinjiang Uygur Autonomous Region (Grant No. 2022DO1A164), the Joint Research Found (Grant No. U1831109) in Astronomy under cooperative agreement between the National Science Foundation of China (NSFC) and Chinese Academy of Sciences (CAS), and the Young Talent Project of the Yunnan Revitalization Talent Support Program and the CAS Light of West China Program. This work is partly supported by the Research Fund of the Key Laboratory of Aircraft Environment Control and Life Support, MIIT, Nanjing University of Aeronautics and Astronautics (Grant No. KLAECLS–E–202203).

Acknowledgments

We acknowledge the support of the staff of the Xinglong 80 cm and the Xinglong 2.16 m telescopes. This research was partially supported by the Open Project Program of the Key Laboratory of Optical Astronomy, National Astronomical Observatories, Chinese Academy of Sciences. This paper has used data collected by the Transiting Exoplanet Survey Satellite (TESS) mission, for which funding is provided by the NASA Explorer Program. We would like to thank the editor and the referees for the very valuable and useful comments that helped improve this paper.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fspas.2024.1497989/full#supplementary-material

References

Applegate, J. H. (1992). A mechanism for orbital period modulation in close binaries. Astrophysical J. 385, 621. doi:10.1086/170967

CrossRef Full Text | Google Scholar

Ažusienis, A., and Straižys, V. (1969). Improved determination of the response curves and parameters of the UBV system. Summary of results. Sov. Astron. 13, 316.

Google Scholar

Bessell, M. S. (1983). VRI photometry: an addendum. Publ. Astronomical Soc. Pac. 95, 480–488. doi:10.1086/131196

CrossRef Full Text | Google Scholar

Borovicka, J., and Sarounova, L. (1996). The Period and lightcurve of NSV 4497. Inf. Bull. Var. Stars 4402, 1.

Google Scholar

Bressan, A., Marigo, P., Girardi, L., Salasnich, B., Dal Cero, C., Rubele, S., et al. (2012). PARSEC: stellar tracks and isochrones with the PAdova and TRieste Stellar Evolution Code. Mon. Notices R. Astronomical Soc. 427, 127–145. doi:10.1111/j.1365-2966.2012.21948.x

CrossRef Full Text | Google Scholar

Carquillat, J. M., and Prieur, J. L. (2007). Contribution to the search for binaries among Am stars - VIII. New spectroscopic orbits of eight systems and statistical study of a sample of 91 Am stars. Mon. Notices R. Astronomical Soc. 380, 1064–1078. doi:10.1111/j.1365-2966.2007.12143.x

CrossRef Full Text | Google Scholar

Chabrier, G. (2001). The galactic disk mass budget. I. Stellar mass function and density. Astrophysical J. 554, 1274–1281. doi:10.1086/321401

CrossRef Full Text | Google Scholar

Chen, W.-C., Li, X.-D., and Qian, S.-B. (2006). Orbital evolution of Algol binaries with a circumbinary disk. Astrophysical J. 649, 973–978. doi:10.1086/506433

CrossRef Full Text | Google Scholar

Chen, Y., Bressan, A., Girardi, L., Marigo, P., Kong, X., and Lanza, A. (2015). PARSEC evolutionary tracks of massive stars up to 350 M_⊙ at metallicities 0.0001 ≤ Z ≤ 0.04. Mon. Notices R. Astronomical Soc. 452, 1068–1080. doi:10.1093/mnras/stv1281

CrossRef Full Text | Google Scholar

Chen, Y., Girardi, L., Bressan, A., Marigo, P., Barbieri, M., and Kong, X. (2014). Improving PARSEC models for very low mass stars. Mon. Notices R. Astronomical Soc. 444, 2525–2543. doi:10.1093/mnras/stu1605

CrossRef Full Text | Google Scholar

Eker, Z., Bakış, V., Bilir, S., Soydugan, F., Steer, I., Soydugan, E., et al. (2018). Interrelated main-sequence mass-luminosity, mass-radius, and mass-effective temperature relations. Mon. Notices R. Astronomical Soc. 479, 5491–5511. doi:10.1093/mnras/sty1834

CrossRef Full Text | Google Scholar

Erdem, A., Doğru, S. S., Soydugan, F., Çiçek, C., and Demircan, O. (2010). Period studies of five neglected algol-type binaries: RW cet, BO Gem, DG lac, SW oph and WY per. New Astron. 15, 628–636. doi:10.1016/j.newast.2010.02.007

CrossRef Full Text | Google Scholar

Fan, Z., Wang, H., Jiang, X., Wu, H., Li, H., Huang, Y., et al. (2016). The Xinglong 2.16-m telescope: current instruments and scientific projects. Publ. Astronomical Soc. Pac. 128, 115005. doi:10.1088/1538-3873/128/969/115005

CrossRef Full Text | Google Scholar

Hall, D. S. (1989). The relation between RS CVn and Algol. Space Sci. Rev. 50, 219–233. doi:10.1007/BF00215932

CrossRef Full Text | Google Scholar

Hintz, E. G., and Brown, P. J. (2007). Revised periods for QS geminorum and V367 geminorum. Publ. Astronomical Soc. Pac. 119, 274–283. doi:10.1086/516602

CrossRef Full Text | Google Scholar

Ibanoǧlu, C., Soydugan, F., Soydugan, E., and Dervişoǧlu, A. (2006). Angular momentum evolution of Algol binaries. Mon. Notices R. Astronomical Soc. 373, 435–448. doi:10.1111/j.1365-2966.2006.11052.x

CrossRef Full Text | Google Scholar

Koleva, M., Prugniel, P., Bouchard, A., and Wu, Y. (2009). ULySS: a full spectrum fitting package. Astronomy Astrophysics 501, 1269–1279. doi:10.1051/0004-6361/200811467

CrossRef Full Text | Google Scholar

Kreiner, J. M. (2004). Up-to-Date linear elements of eclipsing binaries. Acta Astron. 54, 207–210.

Google Scholar

Liao, W. P., Qian, S. B., Li, L. J., Zhou, X., Zhao, E. G., and Zhang, J. (2017). DI hya: a near-contact binary with a close-in companion. Publ. Astronomical Soc. Pac. 129, 034201. doi:10.1088/1538-3873/aa5869

CrossRef Full Text | Google Scholar

Liao, W. P., Qian, S. B., and Liu, N. P. (2012). A CCD photometric study of the contact binary star GSC 03526-01995. Astronomical J. 144, 178. doi:10.1088/0004-6256/144/6/178

CrossRef Full Text | Google Scholar

Liao, W. P., Qian, S. B., and Sarotsakulchai, T. (2019). Physical properties of the close-in tertiary in the southern triple-lined system VZ lib. Astronomical J. 157, 207. doi:10.3847/1538-3881/ab17d4

CrossRef Full Text | Google Scholar

Liao, W. P., and Sarotsakulchai, T. (2019). First photometric investigations of the solar-type binary FV CVn in multiple systems. Publ. Astronomical Soc. Pac. 131, 014202. doi:10.1088/1538-3873/aaeae2

CrossRef Full Text | Google Scholar

Lightkurve Collaboration Cardoso, J. V. D. M., Hedges, C., Gully-Santiago, M., Saunders, N., Cody, A. M., et al. (2018). Lightkurve: kepler and TESS time series analysis in Python. Astrophys. Source Code Libr. Rec. ascl:1812.013.

Google Scholar

Prugniel, P., and Soubiran, C. (2001). A database of high and medium-resolution stellar spectra. Astronomy Astrophysics 369, 1048–1057. doi:10.1051/0004-6361:20010163

CrossRef Full Text | Google Scholar

Qian, S. (2000). Orbital period changes and possible mass and angular momentum loss in two Algol-type binaries: RW Coronae Borealis and TU Herculis. Astronomical J. 119, 901–905. doi:10.1086/301217

CrossRef Full Text | Google Scholar

Qian, S. (2001). Possible mass and angular momentum loss in algol-type binaries. III. TU cancri, FZ delphini, AY geminorum, VZ leonis, FH orionis, IU persei, XZ persei, and BE vulpeculae. Astronomical J. 121, 1614–1622. doi:10.1086/319404

CrossRef Full Text | Google Scholar

Qian, S. (2002). Period changes in four algol-type binaries: SX dra, AV del, CU peg and DK peg. Astrophysics Space Sci. 282, 399–409. doi:10.1023/A:1020876723842

CrossRef Full Text | Google Scholar

Qian, S.-B., He, J.-J., Zhang, J., Zhu, L.-Y., Shi, X.-D., Zhao, E.-G., et al. (2017). Physical properties and catalog of EW-type eclipsing binaries observed by LAMOST. Res. Astronomy Astrophysics 17, 087. doi:10.1088/1674-4527/17/8/87

CrossRef Full Text | Google Scholar

Qian, S. B., Liu, N. P., Li, K., He, J. J., Zhu, L. Y., Zhao, E. G., et al. (2013a). BI vulpeculae: a siamese twin with two very similar cool stars in shallow contact. Astrophysical J. Suppl. Ser. 209, 13. doi:10.1088/0067-0049/209/1/13

CrossRef Full Text | Google Scholar

Qian, S. B., Liu, N. P., Liao, W. P., He, J. J., Liu, L., Zhu, L. Y., et al. (2013b). First photometric investigation of the newly discovered W UMa-type binary star MR com. Astronomical J. 146, 38. doi:10.1088/0004-6256/146/2/38

CrossRef Full Text | Google Scholar

Qian, S. B., Wang, J. J., Zhu, L. Y., Snoonthornthum, B., Wang, L. Z., Zhao, E. G., et al. (2014a). Optical flares and a long-lived dark spot on a cool shallow contact binary. Astrophysical J. Suppl. Ser. 212, 4. doi:10.1088/0067-0049/212/1/4

CrossRef Full Text | Google Scholar

Qian, S. B., Zhou, X., Zola, S., Zhu, L. Y., Zhao, E. G., Liao, W. P., et al. (2014b). AL cassiopeiae: an F-type contact binary system with a cool stellar companion. Astronomical J. 148, 79. doi:10.1088/0004-6256/148/5/79

CrossRef Full Text | Google Scholar

Ricker, G. R., Winn, J. N., Vanderspek, R., Latham, D. W., Bakos, G. Á., Bean, J. L., et al. (2014). “Transiting Exoplanet survey satellite (TESS),” in Space telescopes and instrumentation 2014: optical, infrared, and millimeter wave. Editors J. Oschmann, M. Jacobus, M. Clampin, G. G. Fazio, and H. A. MacEwen (Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series), 9143, 914320

CrossRef Full Text | Google Scholar

Ruciński, S. M. (1969). The proximity effects in close binary systems. II. The bolometric reflection effect for stars with deep convective envelopes. Acta Astron. 19, 245.

Google Scholar

Sarna, M. J., Muslimov, A., and Yerli, S. K. (1997). Magnetic activity and evolution of Algol-type stars. Mon. Notices R. Astronomical Soc. 286, 209–214. doi:10.1093/mnras/286.1.209

CrossRef Full Text | Google Scholar

Sarna, M. J., Yerli, S. K., and Muslimov, A. G. (1998). Magnetic activity and evolution of Algol-type stars - II. Mon. Notices R. Astronomical Soc. 297, 760–768. doi:10.1046/j.1365-8711.1998.01539.x

CrossRef Full Text | Google Scholar

Soydugan, F., Erdem, A., Doğru, S. S., Aliçavuş, F., Soydugan, E., Çiçek, C., et al. (2011). Period studies of classical algol-type binaries II: UX Leo, RW Mon, EQ ori, XZ UMa and AX vul. New Astron. 16, 253–264. doi:10.1016/j.newast.2010.11.006

CrossRef Full Text | Google Scholar

Tang, J., Bressan, A., Rosenfield, P., Slemer, A., Marigo, P., Girardi, L., et al. (2014). New PARSEC evolutionary tracks of massive stars at low metallicity: testing canonical stellar evolution in nearby star-forming dwarf galaxies. Mon. Notices R. Astronomical Soc. 445, 4287–4305. doi:10.1093/mnras/stu2029

CrossRef Full Text | Google Scholar

Tian, X.-M., Wang, Z.-H., Zhu, L.-Y., and Yang, X.-L. (2023). A new catalog of Am-type chemically peculiar stars based on LAMOST. Astrophysical J. Suppl. Ser. 266, 14. doi:10.3847/1538-4365/acc4b5

CrossRef Full Text | Google Scholar

Tian, X.-M., and Zhu, L.-Y. (2019). V723 Persei: a short-period Algol-like near-contact binary. Publ. Astronomical Soc. Jpn. 71, 66. doi:10.1093/pasj/psz044

CrossRef Full Text | Google Scholar

Tokovinin, A., Thomas, S., Sterzik, M., and Udry, S. (2006). Tertiary companions to close spectroscopic binaries. Astronomy Astrophysics 450, 681–693. doi:10.1051/0004-6361:20054427

CrossRef Full Text | Google Scholar

Tout, C. A., and Eggleton, P. P. (1988). Tidal enhancement by a binary companion of stellar winds from cool giants. Mon. Notices R. Astronomical Soc. 231, 823–831. doi:10.1093/mnras/231.4.823

CrossRef Full Text | Google Scholar

van Hamme, W. (1993). New limb-darkening coefficients for modeling binary star light curves. Astronomical J. 106, 2096. doi:10.1086/116788

CrossRef Full Text | Google Scholar

Wang, Z. H., Zhu, L. Y., and Yue, Y. F. (2022). Evolutionary inference and statistical constraints on Algols including SD2-type near contact binaries. Mon. Notices R. Astronomical Soc. 511, 488–500. doi:10.1093/mnras/stac037

CrossRef Full Text | Google Scholar

Wilson, R. E. (1990). Accuracy and efficiency in the binary star reflection effect. Astrophysical J. 356, 613. doi:10.1086/168867

CrossRef Full Text | Google Scholar

Wilson, R. E. (2012). Spotted star light curves with enhanced precision. Astronomical J. 144, 73. doi:10.1088/0004-6256/144/3/73

CrossRef Full Text | Google Scholar

Wilson, R. E., and Devinney, E. J. (1971). Realization of accurate close-binary light curves: application to MR cygni. Astrophysical J. 166, 605. doi:10.1086/150986

CrossRef Full Text | Google Scholar

Yang, Y. G., and Wei, J. Y. (2009). Evolutionary status of RV trianguli and its related algol-type binaries. Astronomical J. 137, 226–235. doi:10.1088/0004-6256/137/1/226

CrossRef Full Text | Google Scholar

Zhang, J., Qian, S.-B., Wu, Y., and Zhou, X. (2019). Unbiased distribution of binary parameters from LAMOST and kepler observations. Astrophysical J. Suppl. Ser. 244, 43. doi:10.3847/1538-4365/ab442b

CrossRef Full Text | Google Scholar